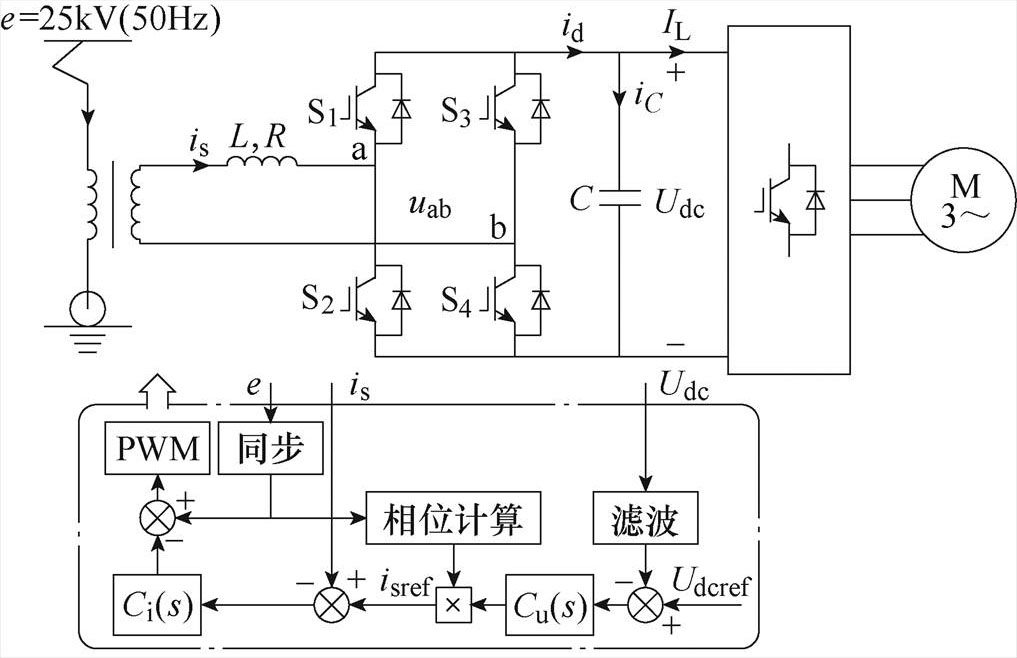
图1 机车PWM整流器及其控制
Fig.1 PWM rectifier and its control in traction systems
摘要 随着宽禁带开关器件的发展，机车中PWM整流器的开关频率逐渐提高，并网滤波器的电感和体积可随之减小，此时PWM整流器的电流控制不仅要对基波电流快速响应，也需要快速抑制直流偏置和由牵引网谐波电压造成的谐波电流。该文选用比例积分（PI）和多个矢量比例积分（VPI）控制器分别控制直流信号和基波、各次谐波交流信号。但是由于各控制器的增益相互耦合，共同影响系统的动态性能，传统增益设计方法很难应用。因此基于Nichols图提出一种增益设计方法，将增益设计转变成最小幅值裕度和相位穿越频率设计，实现增益的解耦；通过优化调整时间和超调选取最终参数，优化动态响应，并通过实验验证，使用该设计方法调优后的系统拥有良好的稳定性、动态性和鲁棒性。
关键词：电流控制 谐振控制器 PWM整流器 增益设计
随着宽禁带器件的发展，碳化硅（SiC）器件有望应用于机车牵引系统的PWM整流器中，使开关频率提高，并网滤波器的电感和体积可随之减小。但由于牵引网电压存在谐波[1]，造成的电流谐波也相应增大，增加了PWM整流器电流控制的难度。
PWM整流器的电流控制对系统的稳定、快速响应起到了至关重要的作用，选择合适的电流控制器是首先需要考虑的问题。作为单相系统，谐振控制器能够实现对特定频率信号的零稳态误差、快速瞬态响应，是非常合适的选择。对于基波和各次谐波，需要采用多个谐振控制器。其中，比例谐振（Proportional Resonant, PR）控制器是谐振控制器中最常见的实现形式[2-7]，但是PR控制器没有考虑系统被控对象的极点、计算延时和PWM延时，动态性能较差。在PR控制器基础上，加入一个能够与被控对象极点对消的零点，形成了矢量比例积分（Vector Proportional Integrator, VPI）控制器[8-10]，该控制器消除了系统极点对系统性能的影响，动态性能得到优化。如果控制频率无法远大于被控信号频率，计算延时和PWM延时的影响不能忽略，此时一般使用超前矫正比例矢量比例积分（Vector Proportional Integrator with compensation, VPIc）控制器[10-12]，进一步优化动态性能。然而VPIc控制器在s域右半平面引入了一个零点，会导致较为明显的非最小相位系统响应，加入与否需要对比实际响应，该问题是本文将要讨论的问题之一。此外，PWM整流器交流回路中可能存在直流偏置电流，原因有很多，包括不一致的开关特性[13-14]、牵引网中的2次谐波[13]、负载中的基波频率功率波动[15]等。对于实际系统，在电流控制器中加入比例积分（Proportional Integral, PI）控制器是解决直流偏置电流最简单、有效的方法[14-16]。
除了控制器的选择外，控制器增益设计对系统性能同样起到了非常关键的作用。PI控制器和各VPIc控制器都包含一个增益，且各增益之间相互耦合，目前在电流控制中涉及采用多个谐振控制器的情况时，控制器增益的选取没有完全解耦，大都需通过观察频率响应并根据经验选取，很难形成一套通用的设计方案。例如，文献[4]采用了比例加多个PR控制器，比例环节通过系统带宽确定，而各PR控制器增益选取相同数值；文献[17]采用比例加多个VPIc控制器，由于比例环节与VPIc控制器增益相互解耦，比例环节被优先提取出来通过阻尼比进行设计，再通过调整时间对单个VPIc控制器的增益进行设计，但没有涉及多个VPIc控制器增益之间的解耦；文献[14, 16]采用了PI和多个VPI控制器，其中PI控制器的增益直接给定，多个VPI控制器的增益通过观察Bode图给定。文献[5]则在保证系统稳定性的前提下直接根据Bode图给定。
为了明确各控制器增益设计的含义，本文提出了一种新的增益设计方法将各个控制器的增益进行解耦，通过Nichols图而不是Bode图进行分析，简化了分析复杂度。该方法中，PI控制器的增益被提取出来作为整体增益，给出其与最小的幅值裕度（Gain Margin, GM）的关系；随后各个VPIc控制器与PI控制器的增益比通过多个相位穿越频率wPC来进行设计，实现了与PI控制器增益的解耦；最后，通过最小化响应时间和超调来确定最优的最小幅值裕度和各个相位穿越频率。
该文首先介绍了PWM整流器电流控制，给出VPI控制器中相位补偿加入条件；然后，在Nichols图上通过幅值裕度和相位穿越频率对控制器增益解耦，通过最优化动态响应设计控制器增益，并分析了系统的鲁棒性；最后，通过实验验证了该分析方法的有效性。
机车PWM整流器及其控制如图1所示，通常使用双环控制，外环控制直流母线电压，内环控制交流电流。本文重点研究电流内环，假定同步策略工作稳定，能够给出基波电压和相位，电流环控制框图如图2所示，但牵引网谐波扰动仍然会引入电流环路中，用ed等效。
图1 机车PWM整流器及其控制
Fig.1 PWM rectifier and its control in traction systems
图2 电流环控制框图
Fig.2 Block diagram of current control loop
电流环控制中，交流侧滤波器是系统被控对象，其传递函数为
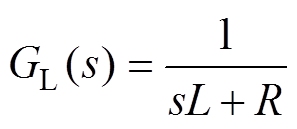（1）PWM延时等效为零阶保持器（Zero-Order Hold, ZOH），同时考虑连续域到离散域的采样，PWM延时的传递函数为
（2）
式中，T为控制周期。计算延时为一拍时延，传递函数为
（3）用Ci(s)表示控制器，那么系统开环传递函数Gol(s)为
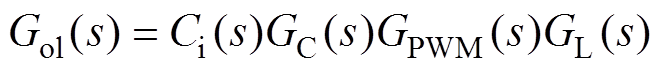（4）
从电流参考isref到电流is的传递函数为
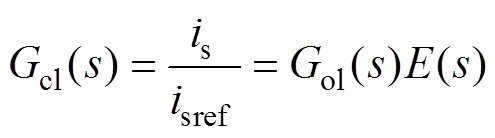（5）其中
（6）
式中，E(s)为误差传递函数。
从ed到电流is的传递函数为
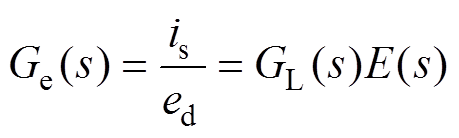（7）机车PWM整流器是单相变流器，需要使用谐振控制器控制基频交流电流；随着开关频率的提高，滤波器减小，牵引网中的谐波电压会造成较大的谐波电流，需要加入抑制谐波电流的谐波谐振控制器。此外，系统需要拥有直流调节能力以抑制因不一致的开关、牵引网中的2次谐波、基频功率波动等造成的直流偏置电流，加入PI控制器是解决该问题的简单方法。综上，系统采用PI+nVPI控制器，即
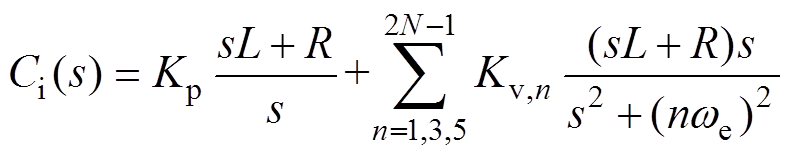（8）式中，we=2p×50rad/s；谐振控制器个数N根据实际谐波情况进行选择（本文分析中N=4）；Kp为PI控制器的增益；Kv,n为基波谐振控制器和各次谐波谐振控制器增益。为了抵消系统极点对动态性能的影响，PI控制器和谐振控制器中都包含用于补偿系统极点的零点（s=-R/L），此时谐振控制器的实现形式为VPI控制器。
如果要控制高次谐波，VPI控制器中还需要加入超前相位补偿角jn来减轻计算延时和PWM延时对动态性能的影响，形成PI+nVPIc控制器，即
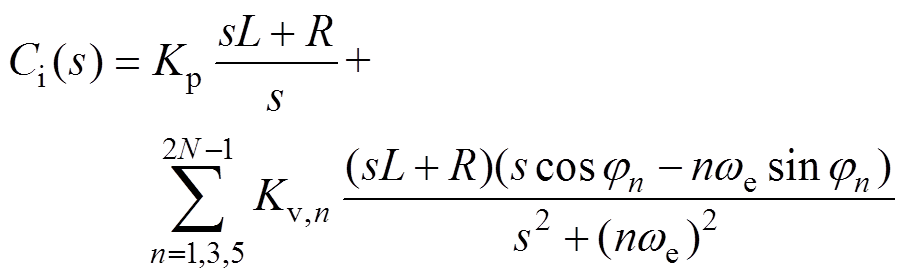（9）根据先前的研究[10, 12, 15]可知，VPIc控制器中的相位补偿角jn可表示为
（10）
但是相位补偿会引入一个在s域右平面的零点（s=nwetanjn），导致非最小相位系统响应，劣化系统动态性能，因此需要权衡相位补偿的利弊。
为了对比相位补偿对动态性能的影响，本节对比VPI控制器和VPIc控制器频率响应的敏感峰值倒数h 的大小，给出jn的加入条件。
相位延时的大小主要由控制频率f（f =1/T，本文中f =5kHz）和被控信号频率fn（fn=nwe/(2p)）的比值d（d=f/fn）决定。为了简化分析复杂度，在这里仅使用单个VPI（VPIc）控制器进行分析，系统开环频率响应为
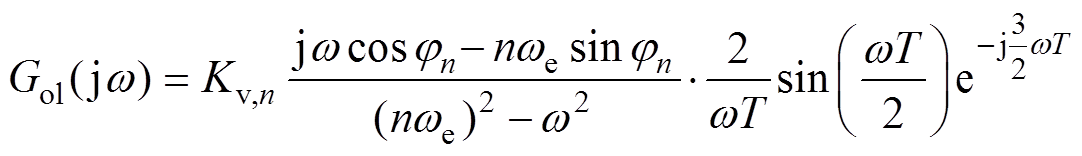（11）VPI控制器中的零点（s=-R/L）与被控对象相抵消，滤波器参数对频率响应没有影响。忽略Kv,n对jn选取的影响，使用文献[15]中的设计方法确定Kv,n，并将VPIc控制器的幅值裕度调整到6.5dB（VPI控制器使用相同大小的Kv,n进行对比）。
在Nyquist图中对比VPI控制器和VPIc控制器的敏感峰值倒数h，如图3所示（d=10，Kv,n=183.7，GMVPIc=6.5dB）。h 在图中表示开环频率响应距离(-1, j0)的最近距离。h 越大，系统稳定裕度越大。
图3 使用单VPI和单VPIc控制器敏感峰值倒数h 对比
Fig.3 Comparison of sensitivity function with VPI controller and VPIc controller
因为hVPIc位于相位穿越频率wPC处，所以
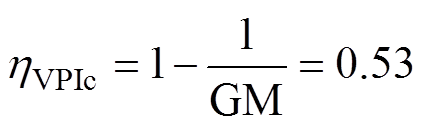（12）是恒定值。而hVPI与d相关，则
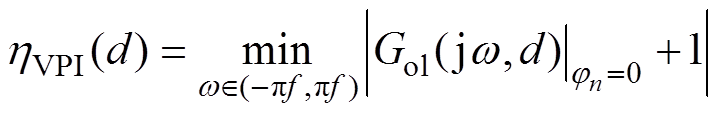（13）
敏感峰值倒数h 和调整时间随频率比变化情况如图4所示。将h 随d的变化情况绘于图4中，当d＞7.6时，hVPI与d呈正相关。系统对nwe频率信号的调整时间t2%（2%误差）也绘于图4中做对比，可以看出，hVPI＜hVPIc基本对应t2%,VPI＞t2%,VPIc，因此用h 判断是否加入jn是一种合理的方法。最终选择
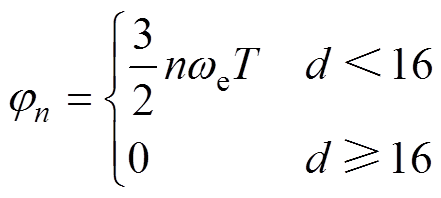（14）即当d＜16时，可以加入jn来提高系统的动态响应。
图4 敏感峰值倒数h 和调整时间随频率比变化情况
Fig.4 Sensitivity function and settling time change with different frequency ratio
在第1、2节中，选定PI+nVPI(c)控制器用于电流控制，jn由式（14）确定。但此时仍然还有Kp和Kv,n共N+1个增益需要设计。先前的文献中，增益参数大都是根据Bode图或根轨迹直接给定[4, 14, 16, 18]，没有对各个增益之间进行解耦；或者各个谐振控制器的增益都取相同数值[4, 18]，没有分别设计，无法发挥控制器的最优性能。
基于系统开环频率响应进行控制器增益设计是常用的方法。但是，使用谐振控制器后，Bode图会多次穿过0dB和(180+360k)°（kÎZ），使用不同相位补偿角开环频率响应Bode图对比如图5所示，参数如下：Kp=124，Kv,n=2Kp（n=1, 3, 5, 7），PI+ nVPI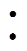
jn=0（n=1, 3, 5, 7），PI+nVPIc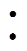jn=0（n=1, 3, 5），jn=3nweT/2（n=7）。此时图形中出现多个幅值裕度和相位裕度（Phase Margin, PM），而且PM有正有负，仅通过Bode图难以直接获知系统稳定性。本文提出使用Nichols图来进行参数设计，在Nichols图中，系统稳定性更容易观察，GM和PM更清晰，使用不同相位补偿角开环频率响应Bode图对比如图6所示（绘图参数与图5相同）。
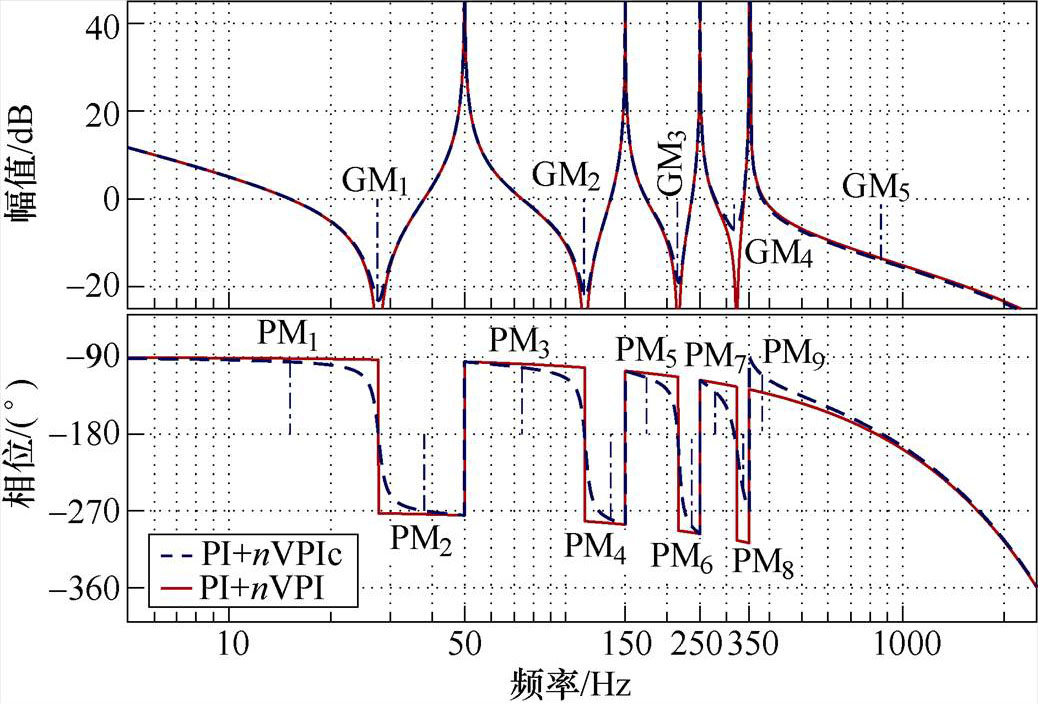
图5 使用不同相位补偿角开环频率响应Bode图对比
Fig.5 Comparison of open-loop Bode diagram with different compensating phase
3.1.1 Kp与最小幅值裕度的关系
在Nichols图上的开环频率响应曲线有一个很实用的特点：如果该开环频率响应有一个整体增益变化，频率响应曲线只会沿着幅值轴垂直向上或向下移动，接近或远离临界点((180+360k)°, 0dB)（kÎZ）（由Nyquist图中(-1, j0)点转换而来），方便确认系统稳定性。
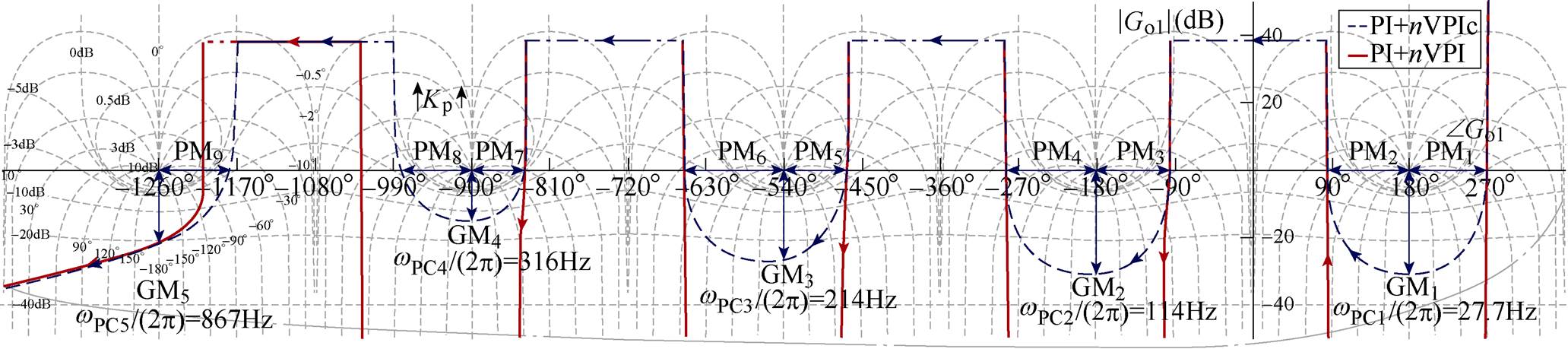
图6 使用不同相位补偿角系统开环频率响应Nichols图对比
Fig.6 Comparison of open-loop frequency response on Nichols chart with different compensating phase
将控制器中的Kp提取出来，开环频率响应为
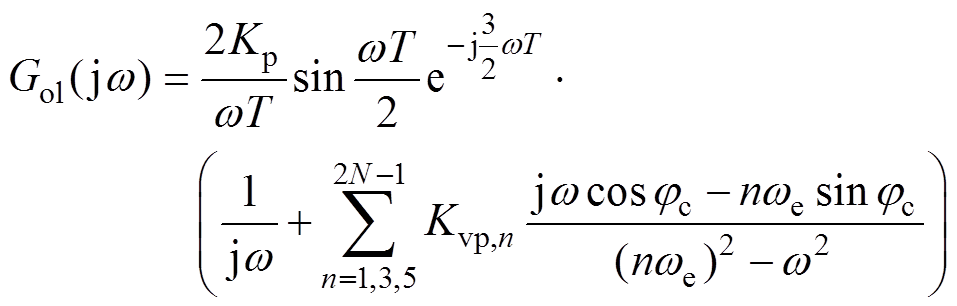（15）式中，Kvp,n=Kv,n/Kp。如果Kp增大，Gol(jw)会上移靠近临界点，所有GM都会随之减小，当曲线任意一点穿过临界点时，即任意GMm＜0dB时，系统不再稳定。GMm的定义是
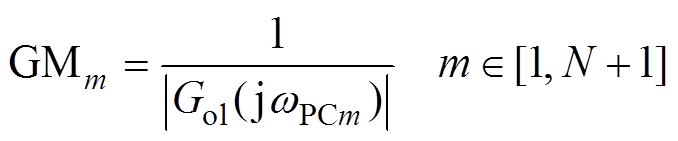（16）
根据式（16），Kp可以由GM计算得到
（17）其中
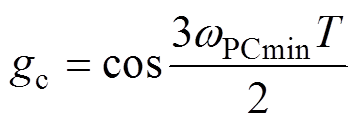
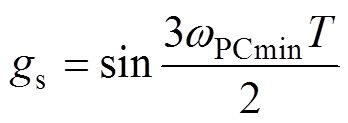
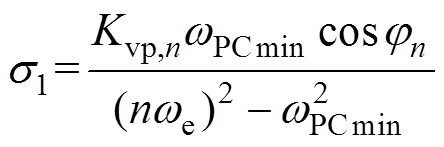
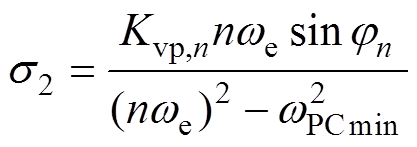
式中，wPCmin为取得最小幅值裕度GMmin时的相位穿越频率。
3.1.2 Kvp,n与相位穿越频率的关系
为了使GMmin仅与Kp相关，需要先对式（17）中的Kvp,n进行设计，并且Kvp,n必须与Kp无关，才能实现增益之间的解耦。
观察系统开环传递函数，在Gol(jw)=0时，Kp不起作用，而该等式可在相位穿越频率或幅值穿越频率处满足。因此可以通过给定相位穿越频率或幅值穿越频率来确定Kvp,n，N个增益可通过设计N个穿越频率获取。由于最大的相位、幅值穿越频率主要由系统特性决定，可设计阈值很小，不建议使用。剩余相位穿越频率wPCm相较幅值穿越频率更接近两个谐振峰之间的最小增益处，而且随着Kp增大，这些频率将会成为系统的振荡频率，因此更适合用于确定Kvp,n。
根据相位穿越频率的定义可知
（18）代入不同wPCm得到N个方程为
（19）其中
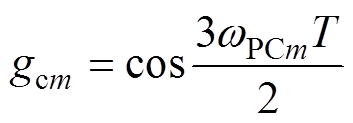
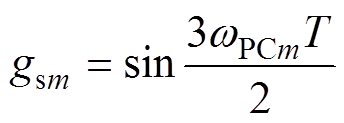
给定N个wPCm后，求解式（19）即可求得N个增益Kvp,n。
经过3.1节的解耦，增益的设计转换为相位穿越频率和系统最小幅值裕度设计，这些变量在控制系统中含义更明确。由不同Kvp,n系统开环频率响应Nichols图对比如图7所示。由图7的Nichols图（GMmin(GM4)=15dB）可以看出，只有Kvp,n变化，即相位穿越频率变化时，系统稳定性不发生变化，仅影响带宽。因此本文将通过调节系统调整时间来设计相位穿越频率。
在GMmin固定后，DwPCm=wPCm+1-wPCm (mÎ[1, N-1])与第m个谐振控制器的带宽呈正相关，将用于对比设计。系统调整时间随相位穿越频率变化情况如图8所示。为了进一步明确该数值对系统动态性能的影响，将各个DwPCm变化时调整时间对比绘于图8中（GMmin(GM4)=15dB），由于系统对直流偏置的抑制速度不是重点，本文仅对比跟踪基波指令值（见式（5））和各次谐波扰动抑制（见式（7））的调整时间。
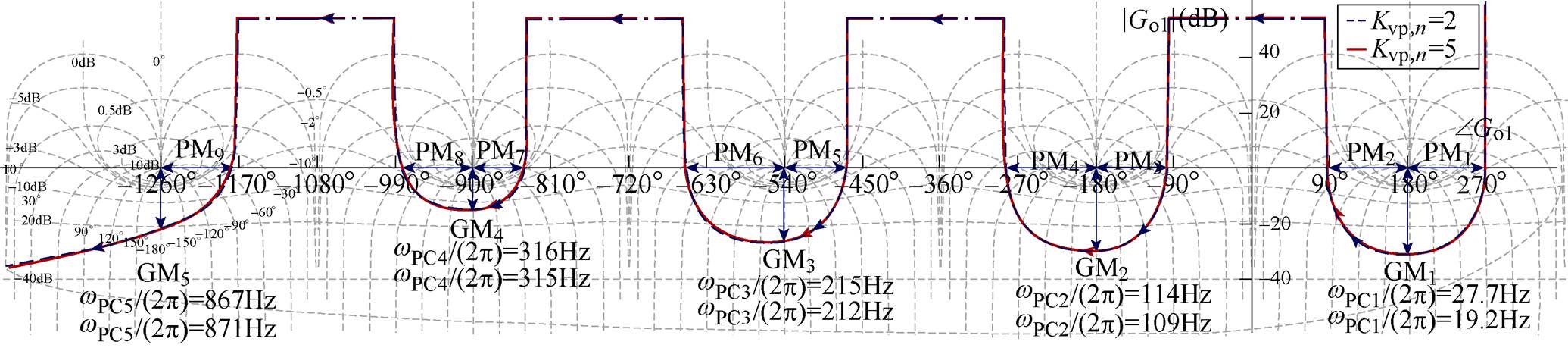
图7 使用不同Kvp,n系统开环频率响应Nichols图对比
Fig.7 Comparison of open-loop frequency response on Nichols chart with Kvp,n
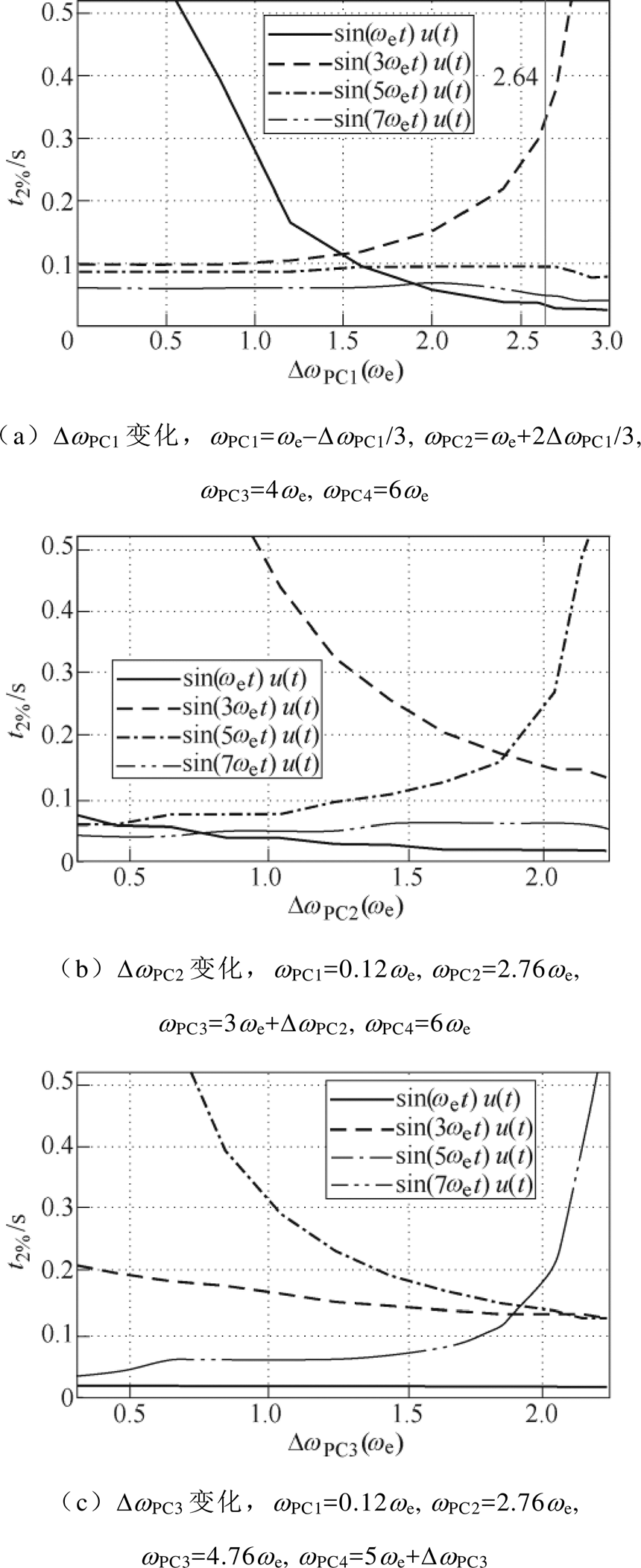
图8 系统调整时间随相位穿越频率变化情况
Fig.8 Settling times change with different phase crossover frequency
图8a对比了DwPC1变化时系统调整时间大小，可以看出，DwPC1主要影响基波和3次谐波的调整时间，而对5、7次谐波的响应影响很小。在实际控制中保证最快的基波响应速度更重要，需要较大的DwPC1，因此本文选取
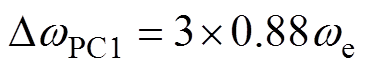（20）按照比例将wPC1和wPC2分布在we两侧，即
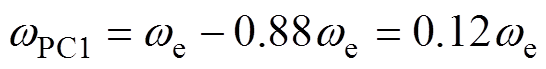（21）
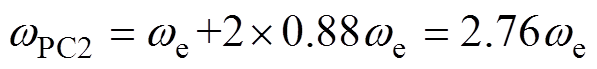（22）此时基波调整时间接近最小，而3次谐波调整时间还没有增大到不可接受的程度。剩余DwPCm则主要影响各次谐波响应速度。由图8b和图8c可以看出，二者非常相似，DwPCm越大，2m-1次谐波调整时间越小，而2m+1次谐波调整时间越大，基本不影响基波和其他次谐波响应。从平衡各次谐波响应速度的角度选择
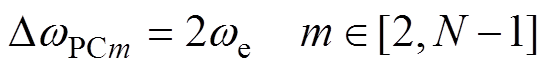（23）
由于wPC2已经确定，wPC3和wPC4可相应确定为
（24）
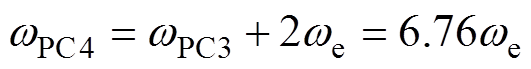（25）
确定N个wPCm后，即可由式（19）求得N个Kvp,n。
相位穿越频率设计完成后，Kvp,n全部确定。此时仅剩Kp需要设计，传统方法中的基于调整时间、超调、带宽等方法都适用。
本文通过对比基波和各次谐波调整时间t2%和基波超调Mp确定系统幅值裕度。各动态性能随GMmin的变化如图9所示。可以看出，GMmin在0～30dB之间时基波调整时间都维持较低数值，并在15～20dB之间达到最小值；基波超调随着GMmin的增大而减小；各次谐波调整时间在3～5dB之间达到最小值，然后便随着GMmin的增大而增大。折中考虑各项动态性能后，将GMmin选取为15dB。在确定GMmin后，即可由式（17）求得Kp。
图9 系统调整时间和超调随最小幅值裕度变化情况
Fig.9 Settling time and overshoot change with different minimum gain margin
一般而言，实际系统中的滤波参数与标称值存在误差，而且滤波参数的数值会随电流大小、温度等变化，被控对象的极点和增益并不准确，VPI控制器中的零点无法准确对消系统极点。实际系统开环频率响应为
（26）式中，Lr和Rr为实际滤波器参数。
对比Lr和Rr变化时系统的Nichols图，滤波器参数变化对系统开环频率响应影响如图10所示。可以看到，Lr变化时，GMmin变化很大；Lr减小，GMmin变小，当Lr=0.2L时，GMmin=1.3dB；Lr增大，GMmin变大，当Lr=5L时，GMmin=29dB。但Lr在5倍变化范围内，系统仍然稳定。Rr的变化对系统影响更小，Rr的变化对GMmin没有影响，但基波附近频率响应变化较大，动态性能会受到影响，在5倍范围内变化时系统仍然稳定。综上，本文的设计方法有较强的鲁棒性。
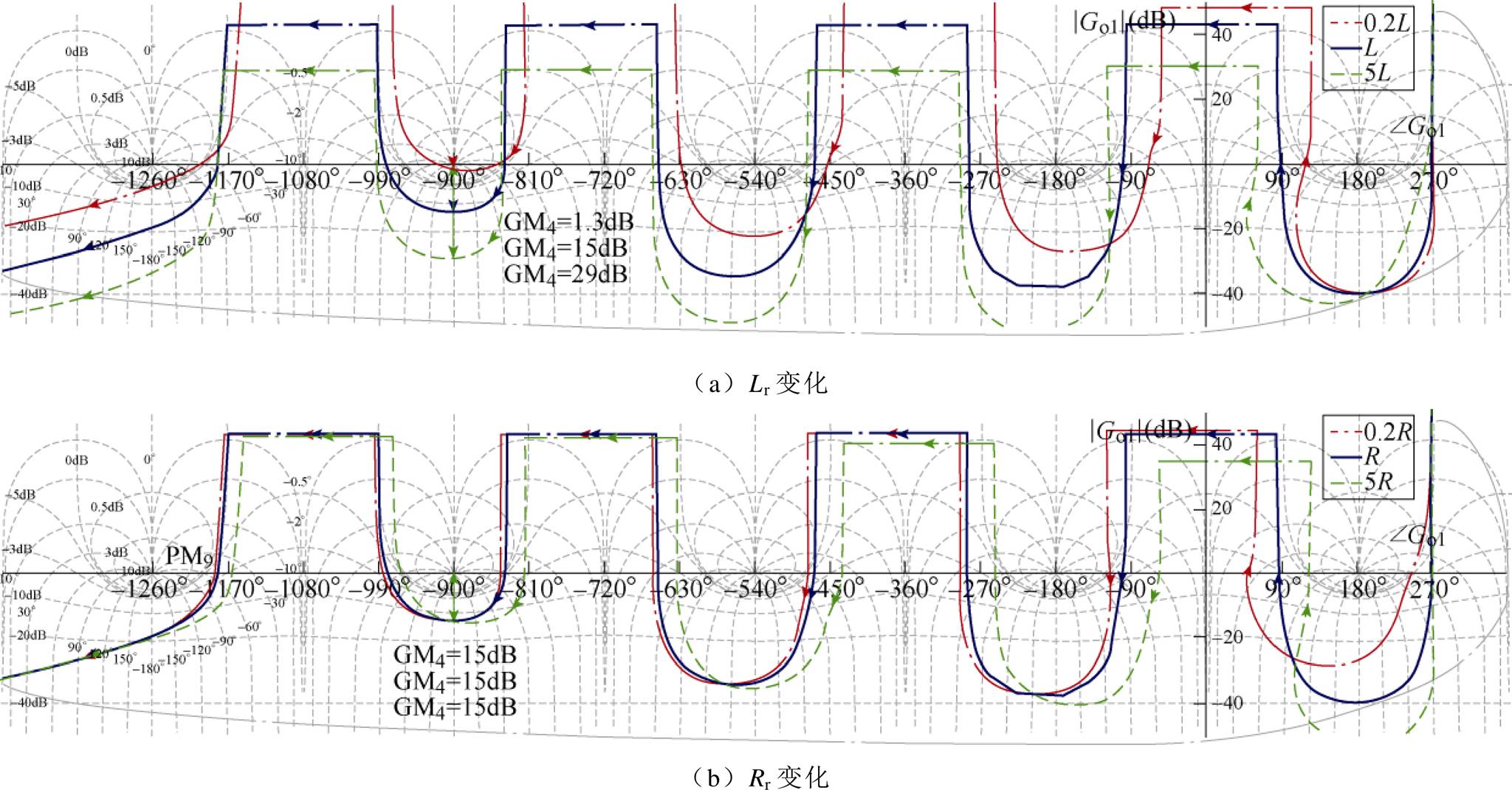
图10 滤波器参数变化对系统开环频率响应影响
Fig.10 Open-loop frequency response on Nichols chart with different filter parameters
为了验证本文电流控制器增益设计结果的实用性，对本文方法进行实验验证。由于本文重点研究电流环，需要排除电压外环的影响，因此实验将基于PWM整流器的单电流环控制，直流母线连接直流源，实验参数见表1。
验证本文设计方法的有效性。对比该方法与传统给定各个谐振控制器增益的方法的动态响应，如图11所示，控制器相位补偿角按照式（14）设计为jn=0（n=1, 3, 5），jn=3nweT/2（n=7）。增益设计方面，图11a使用本文设计方法，wPC1=0.12we，wPC2= 2.76we，wPC3=4.76we，wPC4=6.76we，GMmin(GM4)= 15dB（Kp=5.78），Kvp,1=66.5，Kvp,2=13.1，Kvp,3=8.9，Kvp,4=6.04；图11b在使用传统给定方法Kvp,n=2（n= 1, 3, 5, 7）的同时，将GMmin(GM4)也调整为15dB，Kp=49.4。整个动态过程中，电流参考值isref给定首先从0跳变为15sin(wet)，经过0.16s后在ed处注入3sin(3wet)+3sin(5wet)+3sin(7wet)的信号。
表1 实验参数
Tab.1 Parameters of experiments
参 数数 值 滤波电感L/mH1.44 滤波电阻R/W0.1 直流母线电压Udc/V100 电网电压e/V45 电网频率fe/Hz50 开关频率fsw/kHz2.5 控制频率f/kHz5 谐振控制器个数N4
图11 不同设计方法系统动态响应
Fig.11 Dynamic responses with different tuning method
可以看到，使用本文设计方法时基波跟随过程中的超调很难观察到，经过0.05s后，电流误差值ierr减小到可以忽略的大小，该数值与图9中的设计值基本相同；使用传统给定方法同样没有超调，但调整时间为0.09s，而且误差的波动明显更大。谐波抑制方面，使用本文方法的抑制速度略微慢于传统方法，但由于实际系统中谐波并不会出现很大的突变，因此本文设计方法的动态性能已经足够满足实际需求。
验证本文分析方法的准确性。对比设计方法在极限GMmin=0dB附近（GMmin=-0.5dB和GMmin= 0.5dB）的动态响应，最小幅值裕度极限取值时系统动态响应如图12所示，其中控制器相位补偿角设计和动态变化过程与图11相同；相位穿越频率设计与图11a相同。可以看到，当GMmin=-0.5dB时，系统不稳定，并逐渐发散，发散过程中的振荡频率为338Hz，与设计的最小幅值裕度GMmin(GM4)处的相位穿越频率wPC4相同。而当GMmin增大到0.5dB时，系统稳定，并逐渐收敛，但是收敛速度较慢，综上，仿真与理论分析相互匹配，验证了设计方法的准确性。同时可以看到，GMmin=0.5dB时Kp=30.7是GMmin(GM4)=15dB时Kp的5.3倍，有充足调整裕度。
图12 最小幅值裕度极限取值时系统动态响应
Fig.12 Dynamic responses with ultimate minimum gain margin
验证本文设计方法的鲁棒性，对比滤波器参数变化时系统动态响应，由于实际系统中的滤波器参数的变化不可控，因此改变控制器中的滤波器参数来模拟实际参数的变化。由于Rr变化时系统稳定裕度变化较小，在这里只对比Lr发生变化时的动态响应，滤波电感Lr变化时系统动态响应如图13所示，其中控制器所有参数设计和动态变化过程均与图11a相同。可以看到，当Lr=0.2L时，系统对基波的动态响应变慢，波动频率减小，但误差峰值减小；而当Lr=5L时，系统振荡变大，而且系统对谐波的动态响应变慢很多。两种变化下系统仍然稳定，本文设计方法有良好的鲁棒性，而且因为Lr=0.2L的动态性能要好于Lr=5L，当实际电感值不确定时，可以在控制器中取较大一些的电感值，以保证有更好的动态性能。
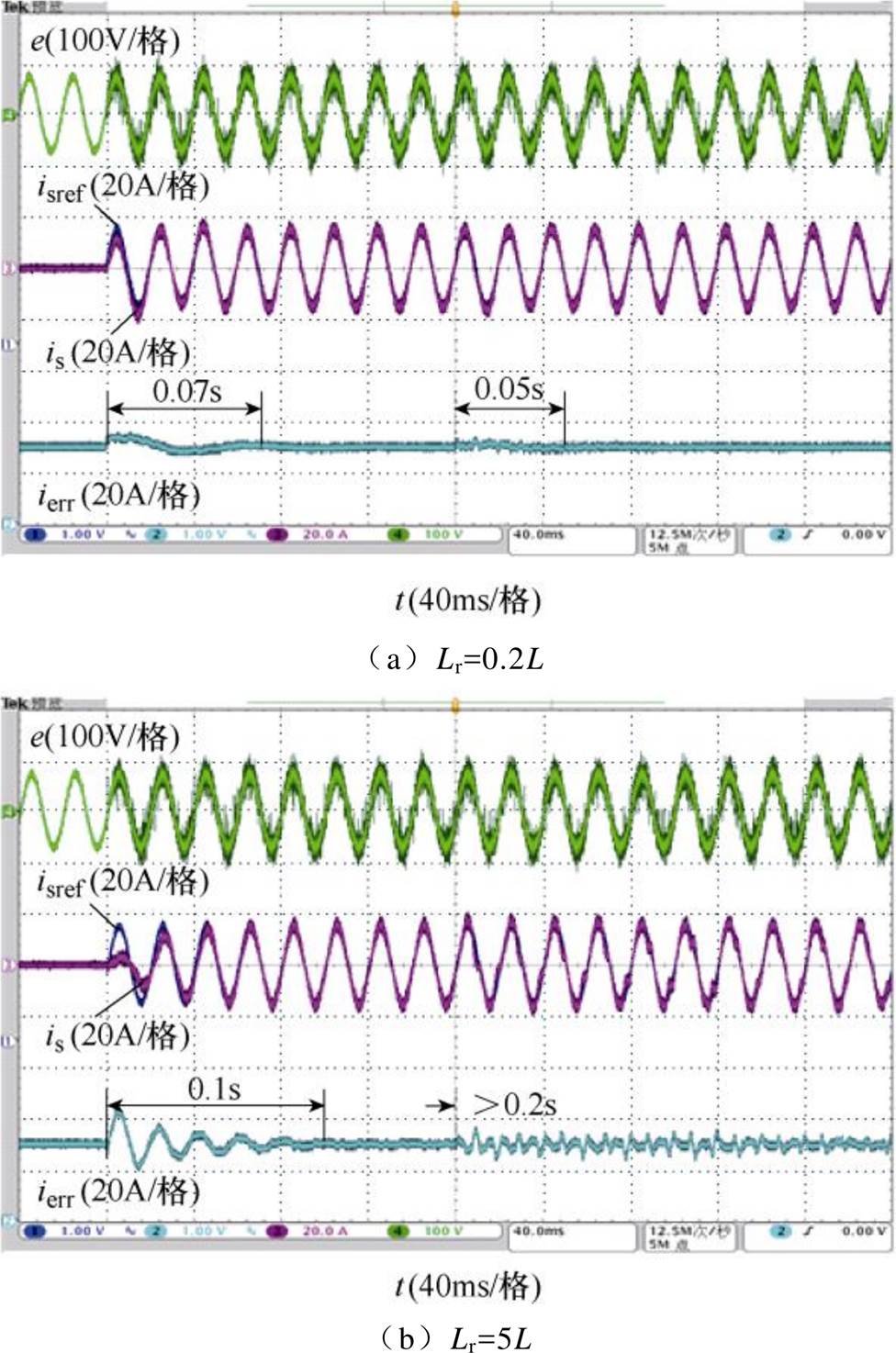
图13 滤波电感Lr变化时系统动态响应
Fig.13 Dynamic responses with different filter inductance Lr
对是否加入相位补偿角进行对比，如图14所示，其中控制器增益参数设计和动态变化过程与图11a相同。图14a对所有谐振控制器的相位都进行了补偿，但是系统对基波的调整时间没有减小，说明只有当被控信号的频率足够高的时候才应该加入相位补偿角来提高系统的动态响应。图14b则将针对7次谐波（d=14.3）的谐振控制器的相位补偿角设为0，此时系统调整时间相较图11a略微增大，说明本文给出的相位补偿角加入时刻（见式（14））的分析准确性良好，可用于实际设计中。
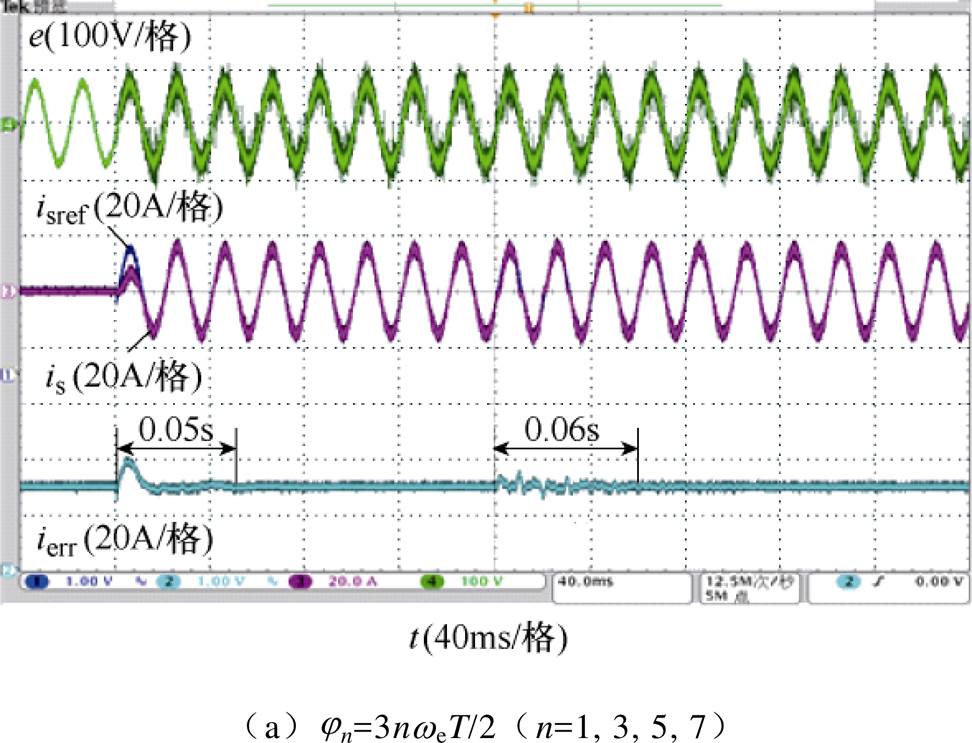
图14 相位补偿角加入与否系统动态响应
Fig.14 Dynamic responses with different compensating phase
将本文设计的电流环控制器应用在PWM整流器中，起动、加载及正常运行波形如图15所示，可以看到，系统运行稳定，低次谐波含量很少，本文设计方法有良好的实用性。
为了使开关频率提高后机车牵引系统中PWM整流器中的电流控制器能够对基波电流快速响应，快速抑制电流中的偏置和谐波，本文选用了PI+ nVPI(c)控制器，提出了该控制器的一种增益设计方法。首先，通过对比调整时间，给出VPI控制器相位补偿角的设定与控制频率和被控信号频率比值d的关系，本文推荐当d＜16时加入相位补偿；然后，通过Nichols图将控制器增益设计转换成最小幅值裕度GMmin和相位穿越频率wPCm的设计，实现了控制器增益的解耦；最后，通过系统调整时间和超调来确定最终的GMmin和wPCm，本文选取wPC1=0.12we，wPCm=2.76we+2(m-2)we（mÎ[2, N]），GMmin=15dB。实验验证了本文设计方法的有效性、准确性和鲁棒性。由于GMmin和wPCm与系统滤波器参数无关，因此本文的设计方法适用于需要多个谐振电流控制器控制的任何单相应用。
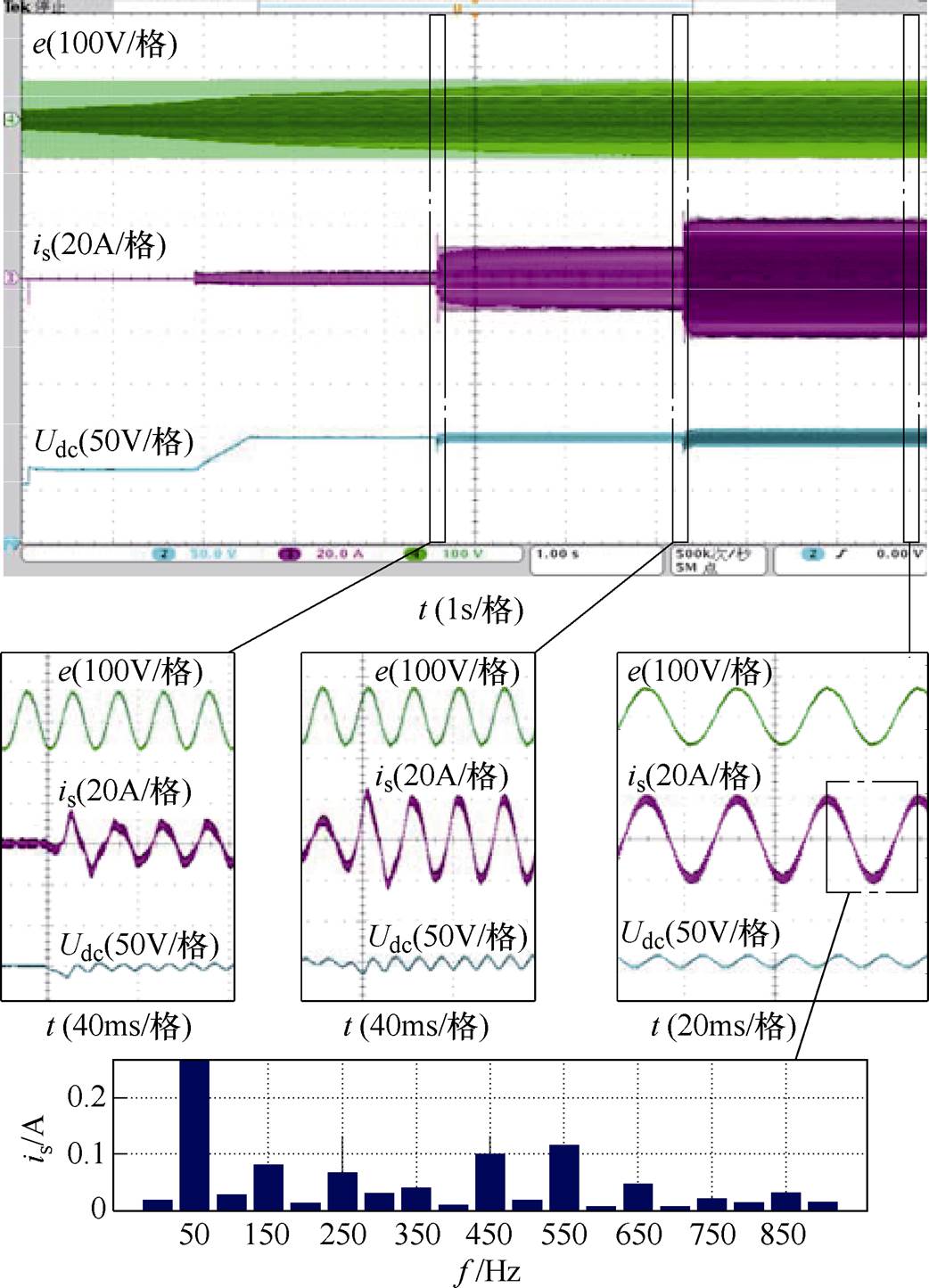
图15 PWM整流器波形
Fig.15 Waveforms of PWM rectifier
参考文献
[1] 刘秋降, 吴命利, 张俊骐, 等. 基于分层控制策略的牵引供电系统谐波阻抗测试装置[J]. 电工技术学报, 2018, 33(13): 3098-3108.
Liu Qiujiang, Wu Mingli, Zhang Junqi, et al. Harmonic impedance measuring apparatus of traction power supply system based on hierarchical control strategy[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3098-3108.
[2] Zmood N D, Holmes D G, Bode G H. Frequency- domain analysis of three-phase linear current regulators[J]. IEEE Transactions on Industry Appli- cations, 2001, 37(2): 601-610.
[3] Kuperman A. Proportional-resonant current control- lers design based on desired transient performance[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5341-5345.
[4] Vidal A, Freijedo F D, Yepes A G, et al. Assessment and optimization of the transient response of proportional-resonant current controllers for distri- buted power generation systems[J]. IEEE Transa- ctions on Industrial Electronics, 2013, 60(4): 1367- 1383.
[5] Husev O, Roncero-Clemente C, Makovenko E, et al. Optimization and implementation of the proportional- resonant controller for grid-connected inverter with significant computation delay[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1201-1211.
[6] Xie Chuan, Zhao Xin, Li Kai, et al. Phase compensated reduced order generalized integrators for grid-tied VSCs with harmonics compensation capability[J]. IEEE Transactions on Industry Appli- cations, 2018, 54(3): 2568-2578.
[7] 冯伟, 孙凯, 关雅娟, 等. 基于分层控制的微电网并网谐波电流主动抑制控制策略[J]. 电工技术学报, 2018, 33(6): 1400-1409.
Feng Wei, Sun Kai, Guan Yajuan, et al. An active harmonic grid-connecting current suppression strategy for hierarchical control based microgrid[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(6): 1400-1409.
[8] Lascu C, Asiminoaei L, Boldea I, et al. High per- formance current controller for selective harmonic compensation in active power filters[J]. IEEE Transa- ctions on Power Electronics, 2007, 22(5): 1826-1835.
[9] 易皓, 卓放, 翟灏. 基于矢量谐振调节器的有源电力滤波器网侧电流检测控制方法研究[J]. 电工技术学报, 2015, 30(7): 72-79.
Yi Hao, Zhuo Fang, Zhai Hao. Research on source current detection type APF control scheme based on vector resonant regulator[J]. Transactions of China Electrotechnical Society, 2015, 30(7): 72-79.
[10] Yepes A G, Freijedo F D, Lopez Ó, et al. Analysis and design of resonant current controllers for voltage-source converters by means of Nyquist diagrams and sensitivity function[J]. IEEE Transa- ctions on Industrial Electronics, 2011, 58(11): 5231- 5250.
[11] Yepes A G, Freijedo F D, Doval-Gandoy J, et al. Effects of discretization methods on the performance of resonant controllers[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1692-1712.
[12] Yi Hao, Zhuo Fang, Wang Feng. Analysis about overshoot peaks appearing in the current loop with resonant controller[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(1): 26-36.
[13] Gerçek C Ö, Ermis M. Elimination of coupling transformer core saturation in cascaded multilevel converter-based T-STATCOM systems[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6796-6809.
[14] Trinh Q N, Wang P, Choo F H. An improved control strategy of three-phase PWM rectifiers under input voltage distortions and DC-offset measurement errors[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 1164-1176.
[15] Yang Caiwei, Wang Jian, Wang Chenchen, et al. Tuning method of resonant current controller with DC elimination for PWM rectifiers in electric multiple units[J]. IEEE Transactions on Transportation Elec- trification, 2020, 6(2): 740-751.
[16] Trinh Q, Lee H. An advanced current control strategy for three-phase shunt active power filters[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5400-5410.
[17] Xie Chuan, Zhao Xin, Li Kai, et al. A new tuning method of multiresonant current controllers for grid-connected voltage source converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(1): 458-466.
[18] Briz F, García P, Degner M W, et al. Dynamic behavior of current controllers for selective harmonic compensation in three-phase active power filters[J]. IEEE Transactions on Industry Applications, 2013, 49(3): 1411-1420.
A Tuning Method for Proportional Integral-Resonant Current Controller in Locomotive PWM Rectifiers
Abstract With the development of wide-bandgap semiconductors, the switching frequency of locomotive or EMU PWM rectifiers is increasing, and the gird-tied filter is reduced correspondingly. Therefore, the current control in PWM rectifier must not only respond fast to the fundamental current reference, but also quickly suppress the DC bias and harmonics generated by the grid voltage. Hence, proportional integral (PI) plus multiple vector proportional integral (VPI) controllers are used in this paper to control these signals. However, because the gains of PI and multiple VPI are coupled with each other and affect the system performance together, it is difficult to use traditional gain tuning methods. Therefore, a gain tuning method based on Nichols chart is proposed to achieve the gain decoupling, and the gain design is transformed into the tuning of minimum gain margin and phase crossover frequency. The settling time and overshoot are considered for the optimal gain tuning. The experimental results show that the designed system has good stability, transient performance and robustness.
keywords：Current control, resonant controller, PWM rectifiers, gains tuning
DOI: 10.19595/j.cnki.1000-6753.tces.L90079
中图分类号：TM461
国家自然科学基金资助项目（51977006）。
收稿日期 2020-06-20
改稿日期 2020-10-21
游小杰 男，1964年生，教授，博士生导师，主要研究方向大功率电源技术、轨道交通电力牵引技术。E-mail: xjyou@bjtu.edu.cn
王 剑 男，1979年生，讲师，硕士生导师，研究方向为并网变流器的控制策略、电力机车电牵引传动系统。E-mail: jwang4@bjtu.edu.cn（通信作者）
（编辑 陈 诚）