图1 系统结构与潮流计算节点分布
Fig.1 System structure and distribution of power flow calculation nodes
摘要 针对全双向变流供电系统(双向变流装置作为唯一变流器的供电系统)中潮流计算和参数设计问题,该文建立考虑双向变流装置容量约束的系统潮流计算模型;以潮流计算算法为基础,提出一种基于改进暴力搜索算法的双向变流装置参数设计策略,该算法考虑任一牵引降压混合所(牵混所)解列的情况,以不考虑双向变流装置容量约束的仿真结果为基础,将容量、下垂率和空载电压分三层迭代以求得极限解集。对实际算例进行分析,考虑双向变流装置容量约束后牵混所整流峰值功率得到控制,相邻所可提供功率支援。提出的策略搜索次数为传统暴力搜索算法搜索次数的1.63%;算例工程中,列车为6B编组,最高速度为80km/h,采用上述策略得到解集中,双向变流装置容量下限为7MW。
关键词:双向变流装置 参数设计 改进暴力搜索 容量约束
双向变流装置可以实现能量在交直流间的双向转化,与整流机组加逆变回馈装置的方案相比,占地更小且输出可控,是智慧城轨建设的重要技术之一[1]。
双向变流装置为PWM变流器结构,文献[2]提出了双向变流装置的主电路拓扑结构和控制方法并通过实验验证。文献[3]将其应用于轻轨中并给出了并联控制策略。目前,双向变流装置容量还远小于整流机组,成为约束其大规模应用的主要原因之一,但也逐渐开始被应用于实际工程中,如宁波地铁已进行挂网实验[4-5],在回馈列车制动能量和稳定直流网压等方面有较好效果。
双向变流装置的供电系统设计理论正在起步阶段。供电系统设计的基础为系统潮流计算,文献[6]提出了含逆变回馈装置的交直流交替潮流计算算法。文献[7]中提出了含逆变回馈装置的交直流统一潮流计算算法;由于逆变回馈装置与双向变流装置拓扑结构相同,含逆变回馈装置的系统潮流计算可为含双向变流装置的系统潮流计算提供参考。文献[8-9]对逆变回馈装置下垂率进行优化。文献[10]对与整流机组并联的双向变流装置的下垂率进行优化,达到了较好的节能效果。但由于双向变流装置过载能力有限,全双向变流场景下,系统设计的重点应为双向变流装置的容量。文献[11]提出了基于双向变流装置的潮流计算算法并对双向变流装置的参数进行分析,给出了其容量参考值,但算法中并未考虑双向变流装置的容量约束,因此计算结果有一定偏差。
本文对列车模型分别以电流源和功率源模型进行建模,并建立了考虑双向变流装置容量约束外特性的模型,提出了潮流计算算法和容量选择方法,根据实际工程,对算法进行验证,并根据提出的方法对工程所需双向变流装置容量和参数进行设计。
城市轨道牵引供电系统结构主要分为集中式、分散式和混合式三种。我国普遍应用集中式结构,由城市电网外部电源接入主变电所110kV侧,主变压器二次电压等级为35kV,经中压电缆连接至各牵引降压混合所(牵混所)和降压变电所。
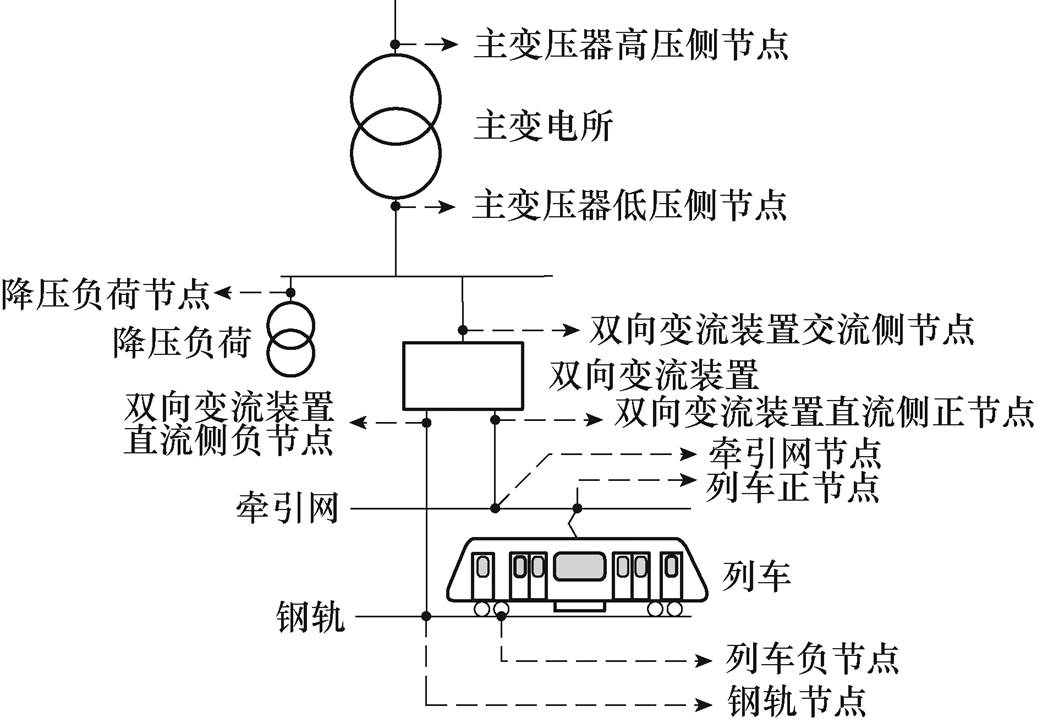
在进行城市轨道潮流计算前,需将系统等效为节点与支路。系统交流侧节点包括主变压器高压侧节点、低压侧节点、降压负荷节点和双向变流装置交流侧节点;直流侧节点包括双向变流装置正节点、负节点、牵引网节点和钢轨节点。系统结构与供电系统潮流计算节点分布如图1所示。

图1 系统结构与潮流计算节点分布
Fig.1 System structure and distribution of power flow calculation nodes
列车为移动负荷,在供电建模时可将其等效为功率源[12-13],每个扫描时刻列车功率可通过牵引计算或实地测量得到全线运行数据。列车供电计算模型如图2所示。图中,Etp为列车正节点的电压,Etn为列车负节点的电压,Pt为列车功率。
列车作为功率源时,每个列车的正节点和负节点与其他直流侧节点模型不同,因此节点类型也不
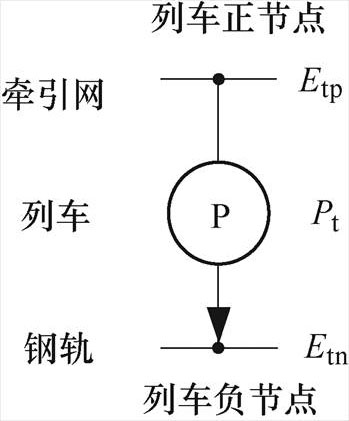
图2 列车供电计算模型
Fig.2 Power supply calculation model of trains
同,为列车正、负节点类型。同一列车的正节点、负节点i间的功率Pti均为已知量,待求变量为正、负节点的电压Etpi和Etni,根据功率平衡,列车正、负节点的偏差方程DPbpi、DPbni分别为
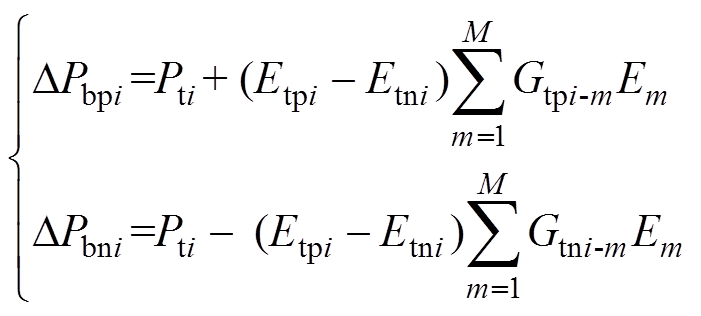 (1)
(1)式中,Gtpi-m、Gtni-m为列车正节点、负节点i与节点m间的电导。
牵混所内双向变流装置可实现牵引供电系统直流侧与交流侧电能的转换。其等效电路由等效并网阻抗、电压源型换流器等组成,如图3所示。图中,Us∠qs为双向变流装置交流侧电压;Ps和Qs为交流侧的有功功率和无功功率;Rs为等效电阻,Xs为等效电抗;Uc∠qc为电压源型换流器阀侧电压;Ud为双向变流装置直流侧电压;Ib为注入电流。
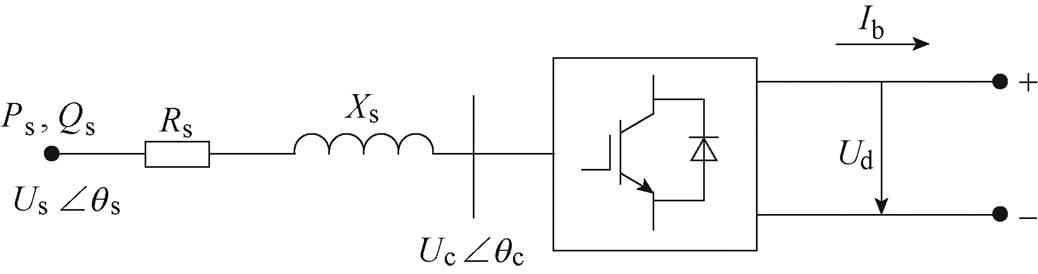
图3 双向变流装置等效电路
Fig.3 Equivalent circuit diagram of bidirectional converter device
双向变流装置交流侧节点的有功功率、无功功率偏差方程可由文献[11]推导得到。直流侧正节点、负节点i的功率偏差方程DPbpi、DPbni分别为
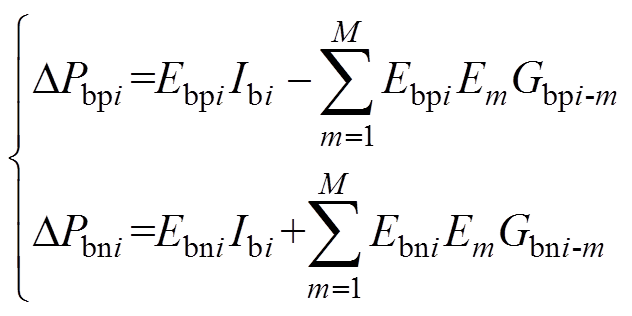 (2)
(2)式中,Ebpi、Ebni分别为双向变流装置直流侧正节点、负节点的电压;Gbpi-m、Gbni-m分别为双向变流装置直流侧正节点、负节点i与节点m间电导;Ibi为双向变流装置正负节点i的直流侧电流。
双向变流装置过载能力有限,因此进行潮流计算时需要考虑其容量约束,但传统的含双向变流装置的潮流计算模型中并未对此加以考虑[11]。
考虑双向变流装置容量约束的外特性如图4所示。图中,Id为双向变流装置直流侧的电流,其为正时为整流工况,为负时为逆变工况;U0为装置空载电压;SN为装置额定容量;Idmax为整流工况下的最大电流;Idmin为Id数值上的最小值和逆变工况下的最大电流;Udmax和Udmin为装置最高和最低电压;U1、U2为对应b、c点的电压;I1、I2为对应a、c点的电流。bc段对应双向变流装置在容量范围内的下垂外特性,a 为输出外特性的下垂率,ab段、cd段对应恒功率输出特性。
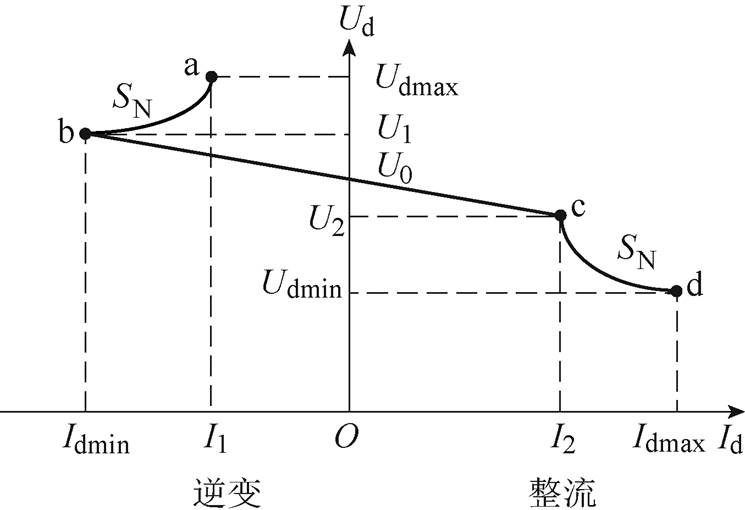
图4 双向变流装置直流侧输出外特性
Fig.4 The DC output characteristic of bidirectional converter
双向变流装置的计算模型中存在未知量,需要增加约束方程以获得潮流解。为了稳定牵引网压状态,同时兼顾补偿无功功率,可采用定Ud、定Qs控制,Qs固定值设为Qcom,考虑双向变流装置输出外特性后,双向变流装置交流侧节点i的其他修正方程为
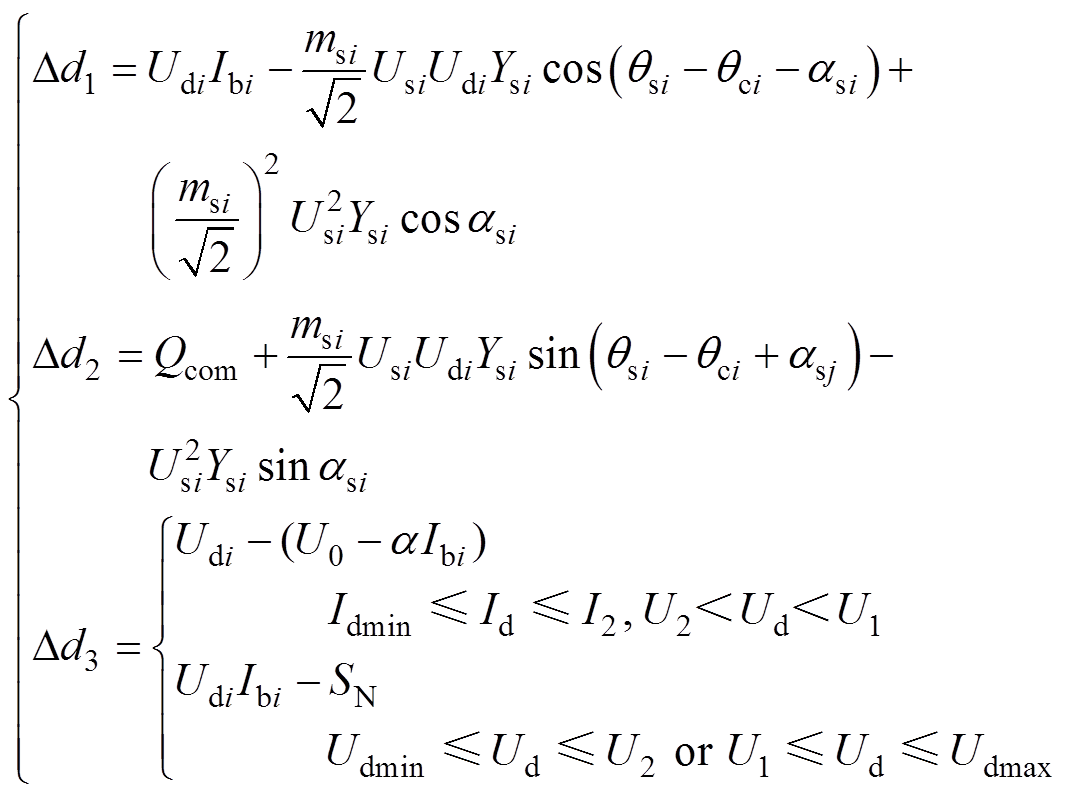 (3)
(3)式中,Udi为节点i的输出电压;Usi∠qsi为节点i输入电压;Psi和Qsi分别为节点i的有功功率和无功功率;asi=arctan(Xsi/Rsi),Rsi、Xsi分别为节点i所在双向变流装置电阻、电抗;qci为节点i阀侧电压相位;msi为调制度;Dd1~Dd3为偏差方程,Dd1对应功率平衡,Dd2对应定Qs控制,Dd3对应定Ud控制,即输出外特性。当Id在[Idmin, I2]且电压在[U2, U1]时,对应图4中bc段,当Ud在[U1, Udmax]或[Udmin, U2]时,对应图4中ab、cd段。
除双向变流装置交流侧节点外,其他交流侧节点的功率偏差方程可参考电力系统。其他直流侧节点如牵引网节点、钢轨节点i根据功率平衡,其偏差方程DPdi为
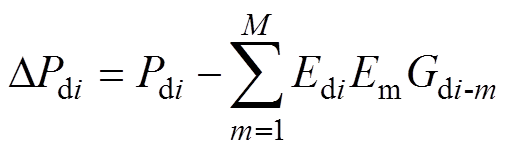 (4)
(4)式中,Pdi为直流节点i的功率;Gdi-m为i与直流侧节点m间的电导。
含双向变流装置的城市轨道供电系统交直流统一潮流算法如图5所示。
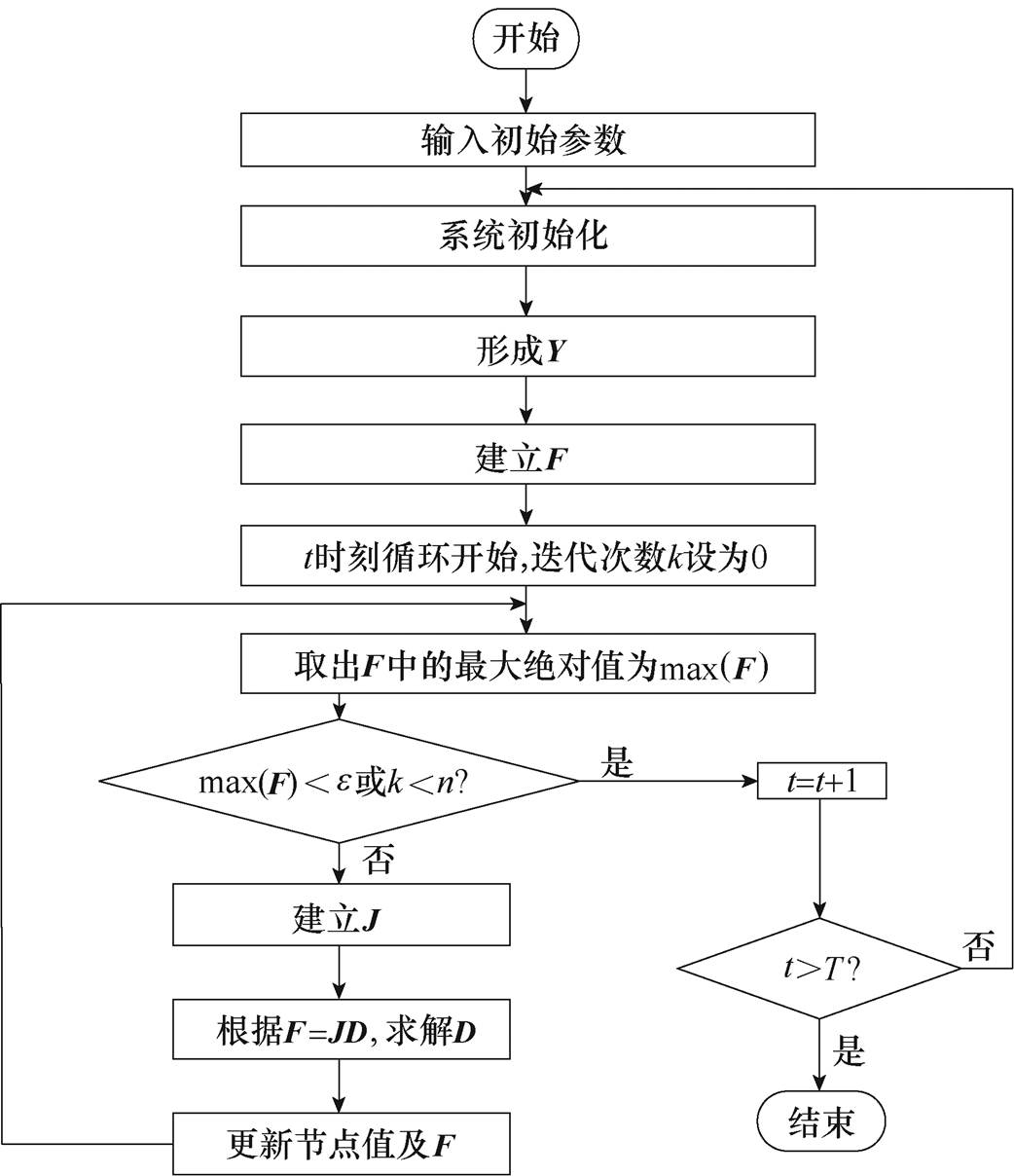
图5 含双向变流装置的城市轨道供电系统交直流统一潮流算法
Fig.5 Unified power flow algorithm for power supply system in urban rail with bidirectional converter device
图5中,输入的初始参数包括:收敛精度e、迭代次数上限n、列车全线上下行牵引计算结果、列车运行计划和城市轨道供电系统结构及相关参数等。系统初始化包括:根据列车运行计划得到行车间隔T;根据列车全线上下行牵引计算结果、列车运行计划,由运行图法得到仿真周期内列车运行图;仿真时刻t初始化。
形成系统交直流节点导纳矩阵Y的过程为:根据城市轨道供电系统结构,建立交流侧节点、支路数据并初始化交流侧各节点电压,形成交流侧节点导纳矩阵Yac;根据列车运行图确定t时刻全线列车位置、电流和功率分布,初始化直流侧各节点电压,形成直流侧节点导纳矩阵Ydc;统一Yac与Ydc,形成Y。
偏差项列矢量F根据式(1)~式(4)、节点电压、矩阵Y建立,表达式为
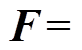
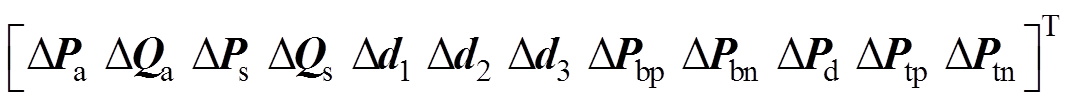 (5)
(5)式中,DPa、DQa为除双向变流装置交流节点外其他交流侧节点有功功率、无功功率偏差矢量;DPs、DQs为双向变流装置交流侧节点有功功率、无功功率偏差矢量;Dd1、Dd2、Dd3为双向变流装置交流侧补充偏差矢量;DPbp、DPbn为双向变流装置直流侧正节点、负节点功率偏差矢量;DId为直流节点电流偏差矢量;DPd为除列车节点外其他直流节点的功率偏差矢量;DPtp、DPtn为列车正节点、负节点功率偏差矢量。
J为雅克比矩阵,D为修正矢量,更新节点值即根据D求取城市轨道各交流侧、直流侧节点电压新值。
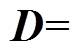
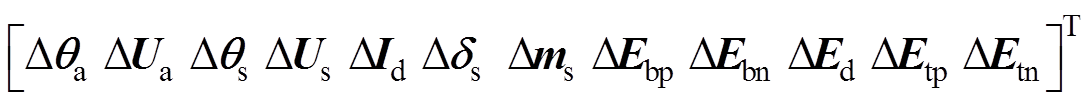 (6)
(6)式中,Dqa、DUa为除双向变流装置交流侧节点外其他交流节点的电压相为和幅值偏差矢量;Dqs、DUs为双向变流装置交流侧的电压相位、电压幅值的偏差矢量;DId为双向变流装置的偏差矢量;Dds、Dms为双向变流装置的交流侧与阀侧电压相位差、调制比的偏差矢量;DEbp、DEbn为双向变流装置正负节点的电压偏差矢量; DEbp、DEbn为列车正负节点电压的偏差矢量;DEd为除上述直流节点外其他直流节点的电压偏差矢量。
在全双向变流装置的供电系统中,设计双向变流装置容量应考虑在全线任意一所解列退出运行时,牵引供电系统仍可满足高峰时段负荷需求的情况。
根据文献[11],双向变流装置的峰值功率与S和a 均相关。双向变流装置容量实际中为一系列离散值,可根据不考虑容量约束时潮流计算,确定牵混所峰值功率最大值Smax。在考虑容量约束后,当双向变流装置容量设置过小时,全线列车负荷功率得不到满足,潮流计算结果将不收敛。因此,采用逐级递减容量约束的方式确定双向变流装置的安装容量。
根据地铁设计规范[14],牵引网网压和钢轨电位等参数需要在规定范围内。在双向变流装置容量确定后需对空载电压U0进行调整以符合牵引网网压和钢轨电位要求。
暴力搜索算法即穷举算法,是将所有可能情况一一列出求解以求取可行解的一种方法。但其搜索次数较多、占用时间长、效率较低。本文提出的改进暴力搜索算法在传统算法的基础上,设计了三层迭代算法,以S为外层迭代变量,按安装容量步长Sw递减,x为外层迭代数;a 为中层迭代变量,以0为起点,按下垂率步长aw递增。第x次外层迭代时S=Sx,第y次中层迭代时a =ax-y,即
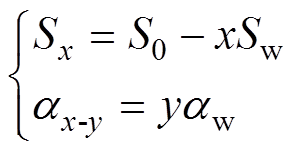 (7)
(7)式中,S0为不大于Smax的Sw的公倍数的最大值。
算法开始后,首先进行中层迭代。当容量为Sx,首次进行至结果为可行解,即仿真结果中全部时刻均收敛时,该解称为极限解。
此时进入内层迭代,Sx、ax-y不变,U0从默认值U0default开始,按U0的仿真步长U0w增大或减小,遍历所有可行域。U0default可根据运营经验确定,以减少计算次数。若存在满足牵引网网压和钢轨电位的解,则将U0最大允许值U0maxx,最小允许值U0minx记录至解集中,并跳至外层迭代;否则,继续进行中层迭代。
当在某一Sx时,所有中层迭代均无可行解,或内层迭代无满足牵引网网压和钢轨电位的解时,仿真结束。最终解集为{Sx, ax-y, U0maxx, U0minx}。
三层迭代示意图如图6所示,图中,内层迭代并未画出,极限解均为符合牵引网网压和钢轨电位的解,i、j为某一迭代次数。
基于改进暴力搜索算法的双向变流装置参数设计策略的步骤为:
(1)输入初始条件,包括列车运行计划、供电系统结构及参数,即U0default、Sw、aw、U0w。
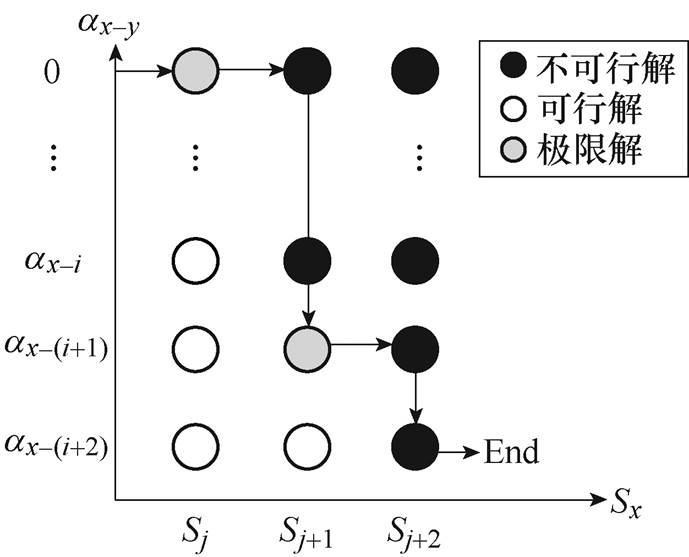
图6 三层迭代示意图
Fig.6 Triple-loop diagram
(2)依次解列每个牵混所,进行不考虑双向变流装置容量约束的城市轨道牵引供电计算,并统计计算结果,得到S0及达到最大值时解列的第n个牵混所Tn,且x=0,y=0。
(3)将全线双向变流装置S设置为Sx,a 设为ax-y,U0设为U0default,对牵混所Tn解列的情况进行考虑双向变流装置容量约束的城市轨道牵引供电计算。
(4)统计仿真结果,若所有时刻均收敛,跳至步骤(7)。
(5)y=y+1,更新ax-y。
(6)ax-y是否大于amax,amax为装置允许的最大下垂率,如果是,跳至步骤(10);否则,跳至步骤(3)。
(7)根据改进暴力搜索算法调整U0,进行全线双向变流装置容量设置为Sx,下垂率设为ax-y,牵混所Tn解列的考虑双向变流装置容量约束的城市轨道牵引供电计算,记录U0maxx、U0minx。
(8)如U0maxx、U0minx均存在,记录至解集中,跳至步骤(11)。
(9)y=y+1,更新ax-y。
(10)ax-y是否大于amax,如果是,跳至步骤(12);否则,跳至步骤(7)。
(11)x=x+1,更新Sx;跳至步骤(3)。
(12)输出仿真结果,解集为{Sx, ax-y, U0maxx, U0minx},结束。
以某地铁为算例进行研究,该线路简图如图7所示。该地铁设置主变电所2座,牵引降压混合所(简称牵混所)10座,分别为T1~T10,和降压变电所(简称降压所)10座。主变电所主变压器安装容量均为2×40MV·A,变压器联结方式为YNd11,变压器短路百分比为10.5%,短路损耗为200kW,空载损耗为50kW。牵混所内变流器均为双向变流装置。降压所负载率设为0.25。接触网电阻为0.017 3W/km,钢轨电阻为0.02W/km[12]。列车为6B型车,4动2拖编组,限速为80km/h。行车组织采用不同交路,大交路为全线运行,小交路运行区间为T3~T10区间。
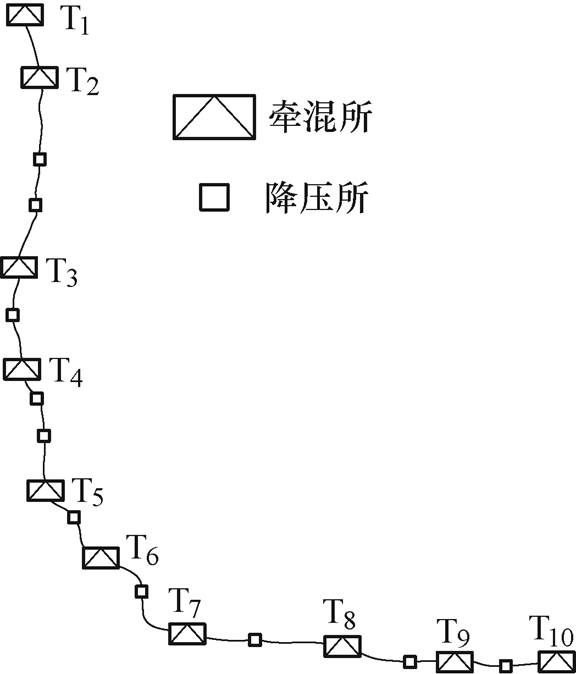
图7 某地铁线路简图
Fig.7 The sketch of the subway line
对线路的高峰时段,即发车对数为14对/小时(大交路)+7对/小时(小交路)的运行情况进行仿真。双向变流装置下垂率a 设为0。迭代收敛精度e=1×10-6,下同。设Case1为列车采用电流源模型的情况,Case2为列车采用功率源模型的情况,两者均未考虑双向变流装置容量约束。列车采用节时策略,列车力-速度曲线如图8所示。上行方向,列车牵引计算曲线如图9所示。
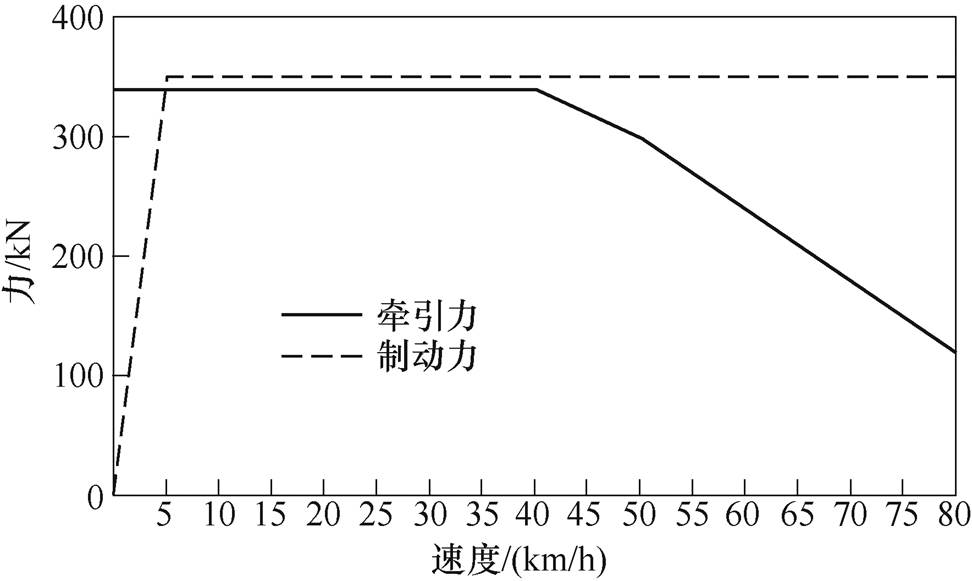
图8 列车力-速度曲线
Fig.8 The force-speed curves of trains
从图9a可以看出,由于列车采用节时策略,因此在各区间内均可达到80km/h速度左右,且均全力制动,与图9b中各区间内最大牵引电流和最大制动电流基本一致相对应。
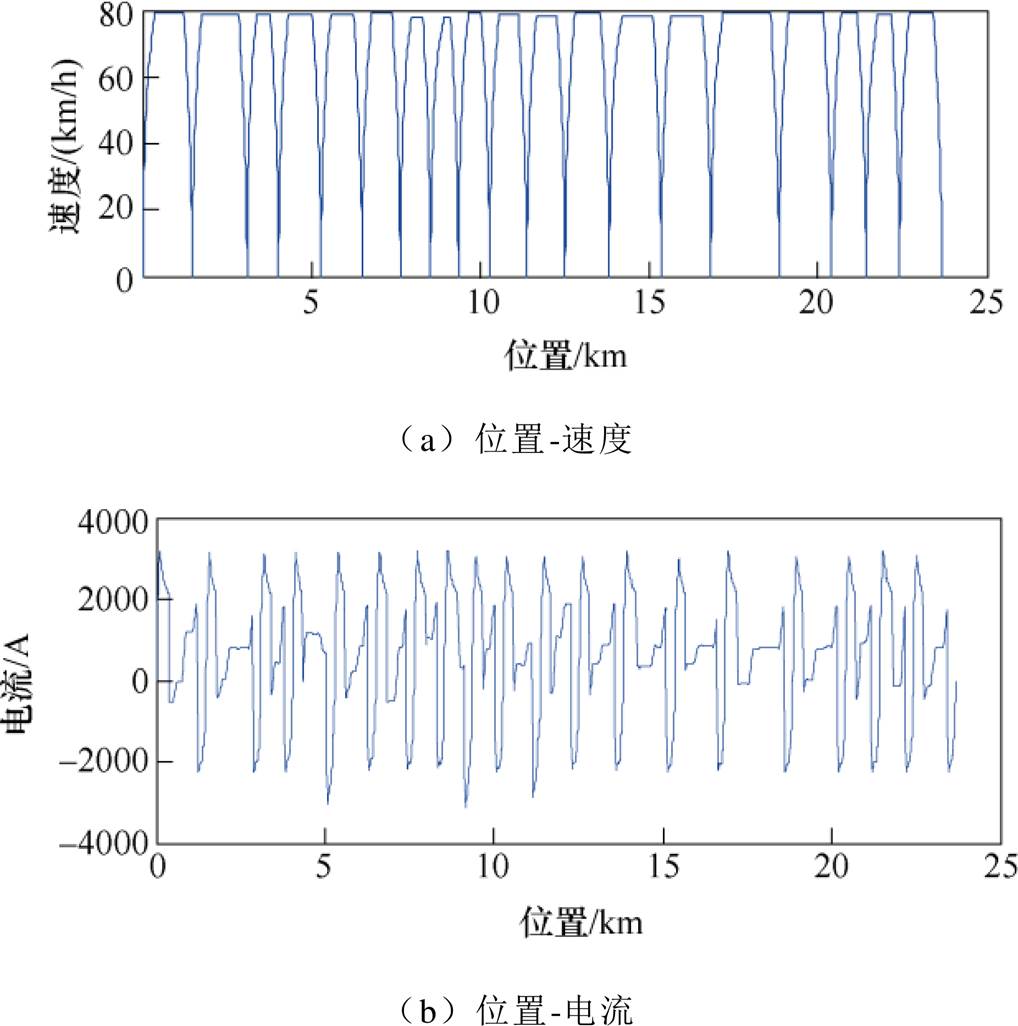
图9 列车牵引计算曲线
Fig.9 The curves of traction calculation of trains
为验证本文所提算法,选取列车在某一区间内密集启动的某一仿真时刻,如t =365s进行分析,结果如图10、图11所示。设U0=1 650V,a =0。Case1为不考虑容量约束的情况;Case2为全线双向变流装置容量为8MW的情况;Case3为全线双向变流装置容量为5MW的情况。
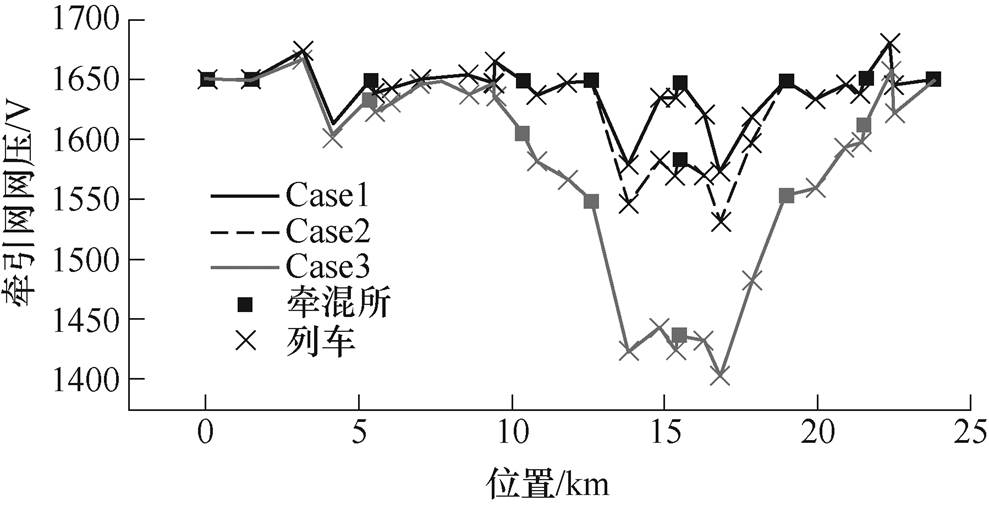
图10 t =365s时,不同情况下牵混所和列车牵引网网压
Fig.10 Network voltage of traction network and trains in different situations when t =365s
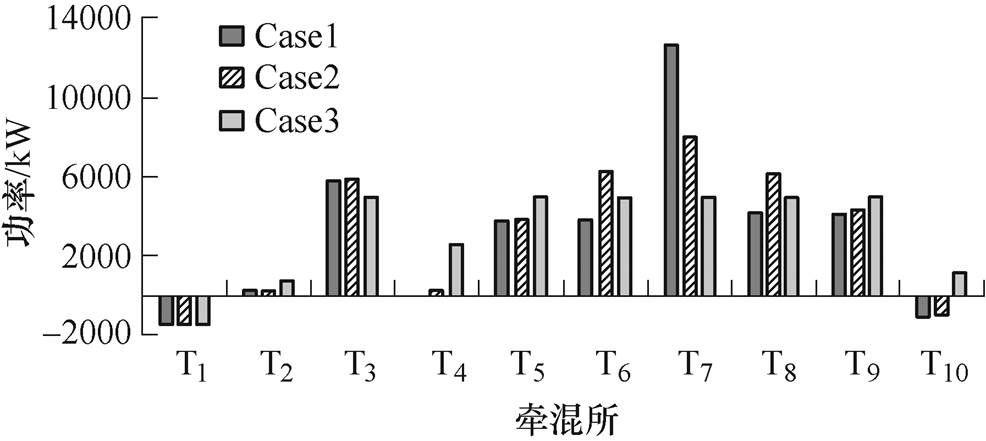
图11 t =365s时,不同情况牵混所直流侧功率
Fig.11 DC power in different situations when t =365s
从图10中可以看出,Case1中牵混所处牵引网网压均为1 650V;Case2中牵混所T7牵引网网压为1 583.7V;Case3中牵混所T7及附近多个牵混所网压低于1 650V,且附近列车网压水平也低于Case1相同位置处列车网压。由图11可知,这是由于Case2中牵混所T7的双向变流装置功率达到容量上限,为8MW,处于图4中cd阶段,且由于网压较低,相邻T6、T8对其进行功率支援。而在Case3中,T7功率被限制在5MW,牵引网网压更低,达到1 436.6V,根据牵引网网压分布,牵混所T4~T10均为其提供功率支援,T5、T6、T8、T9功率均为5MW。
不同情况下所有时刻牵混所牵引峰值功率如图12所示。
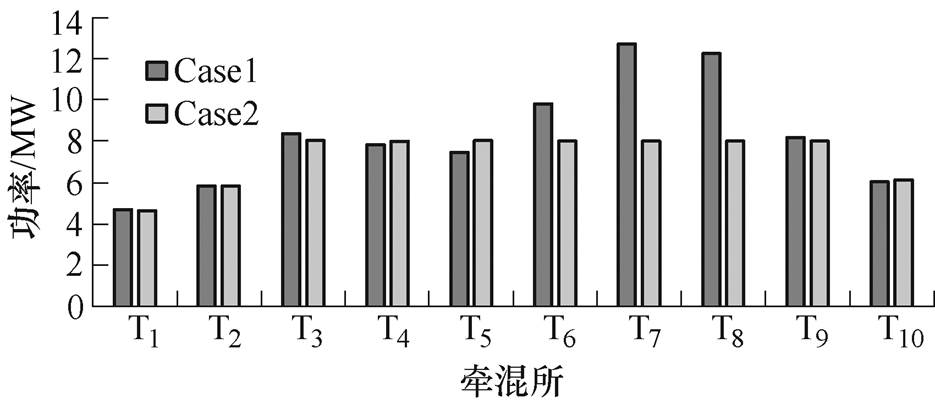
图12 不同情况下所有时刻牵混所牵引峰值功率
Fig.12 Peak power of traction substations in different situations of all seconds
T4~T9至相邻左右牵混所距离的和分别为4 954m、4 863m、5 059m、6 345m、6 082m和4 809m。可以看出,T7与T8至相邻左右牵混所距离的和均超过6km,远大于其他牵引所,这意味着在T7、T8至左右牵混所区间内列车间距较大,邻车吸收再生制动能量较少,因此Case1中T7、T8牵引功率峰值远大于其他牵混所,如图12所示。
从图12中可以看出,所有时刻仿真结果中,Case1的T7峰值功率最大为12.6MW,T3、T6、T8和T9最大牵引峰值功率均大于8MW。Case2中,T3~T9峰值功率最大值均为8MW,证明考虑容量约束算法的有效性。而由于Case3仿真结果中存在不收敛时刻,因此未统计。
根据第3节双向变流装置参数设计策略,不考虑容量约束时,a =0,所有情况下全线双向变流装置功率的最大值Smax=13.4MW,达到最大值时解列牵混所T7。Sw设为0.5MW。因此仿真起点S0= 13.0MW,a0=0.06W,aw=0.01W,U0w=10V。
采用传统暴力搜索算法,S可行域内含有26个值,a 可行域内含有7个值,U0可行域内含81个值,因此共需搜索14 742次才可得到所有可行解。采用本文提出的改进的暴力搜索算法进行求解,共搜索240次即得到所有解集,为传统算法的1.63%。所得结果中,U0、S与钢轨电位的关系如图13所示。
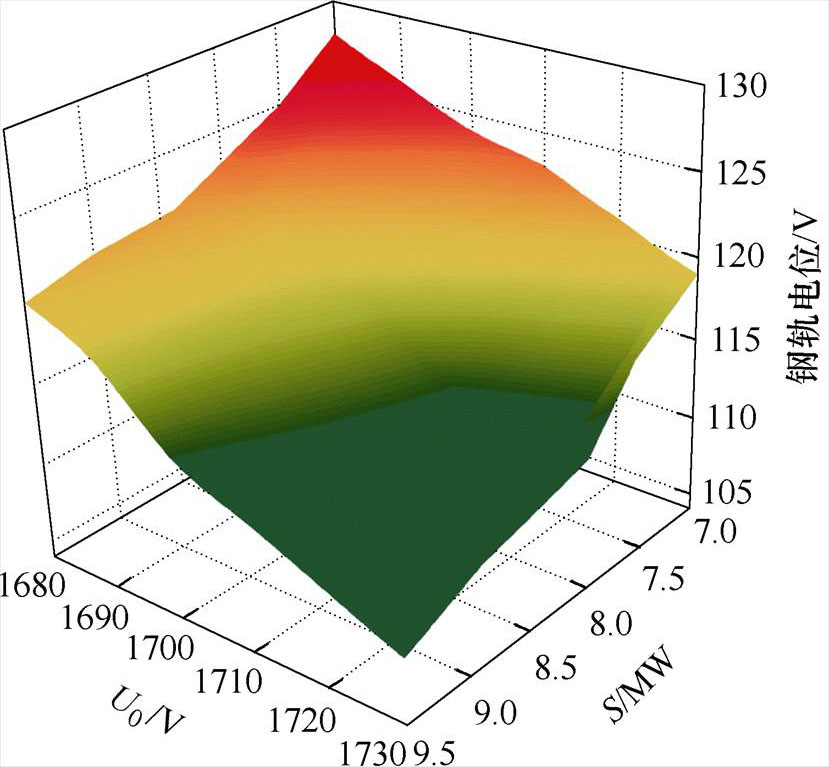
图13 不同空载电压和容量约束下最高钢轨电位
Fig.13 Maximum rail potential under different no-load voltages and capacity constraints
由图13可以看出,U0越高,轨电位越低。这是由于U0较高时,相同功率下列车所需电流越小,因此钢轨上回流电流越小,钢轨电位因而较低。容量增大时,钢轨电位有降低趋势,但容量约束为9.0MW和9.5MW时钢轨最高电位相同。由于钢轨电位最高值是牵引列车密集启动造成的,当双向变流装置容量足以提供列车牵引所需功率时,继续增加双向变流装置容量不会对系统钢轨电位最大值产生影响。
另一方面,U0越高,牵引网网压最大值越高。综合牵引网网压和钢轨电位约束,双向变流装置参数设计解集见表1。
表1 双向变流装置参数设计解集
Tab.1 The parameter sets of the bidirectional converter device
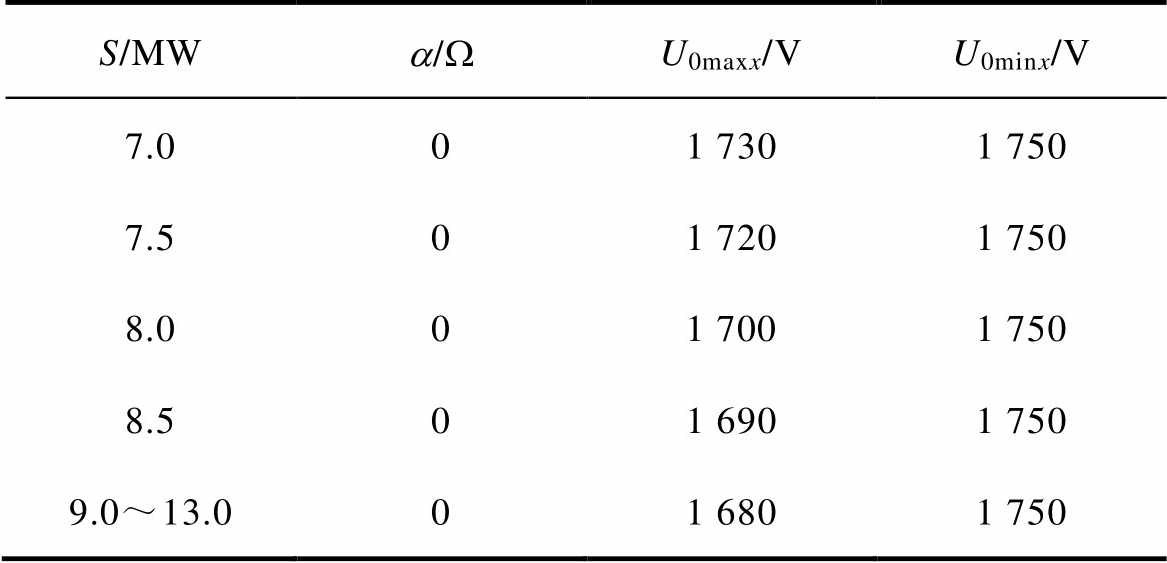
S/MWa/WU0maxx/VU0minx/V 7.001 7301 750 7.501 7201 750 8.001 7001 750 8.501 6901 750 9.0~13.001 6801 750
在改进的暴力搜索算法计算过程中,S=6.5MW,a =0,U0=1 650V为极限解,但U0遍历可行域后并无满足钢轨电位和牵引网网压的值,a 继续增大后也无解,因此解集中,容量最低为7.0MW。
本文建立了基于容量约束外特性的双向变流装置潮流计算模型,提出了含双向变流装置的城市轨道潮流计算算法,并设计了一种双向变流装置参数设计策略,对实际案例进行分析研究,得出结论如下:
1)对全线双向变流装置容量为8MW、5MW的算例与不考虑容量约束的结果进行对比分析,考虑容量约束后双向变流装置功率峰值与容量对应,且牵引网网压与实际接近,验证了算法中容量约束的有效性和合理性。
2)提出的参数设计策略考虑任一牵混所解列的情况,且含三层迭代,最终可求解得到双向变流装置容量、下垂率及空载电压3个参数。实例中,该策略搜索次数为传统暴力搜索算法的1.63%,提高了计算效率。
3)根据提出的参数设计策略(大交路),当列车为6B(小交路)编组,行车为14对/小时+7对/小时,双向变流装置最低下垂率为0,双向变流装置容量最小允许容量为7MW,空载电压最低为1 730V,最高为1 750V,此时牵引网网压和钢轨电位在国标限值内。
4)双向变流装置的容量越大,其空载电压的可选择范围越大,但同时成本越高。在进行系统设计时,应综合考虑成本及系统牵引网网压运营条件,对双向变流装置的参数进行合理选择。
目前,对双向变流装置的参数设计方法为改进暴力搜索算法,算法仍存在改进空间。后续将考虑引入人工智能算法进行参数设计以提高效率。
参考文献
[1] 中国城市轨道交通智慧城轨发展纲要[J]. 城市轨道交通, 2020(4): 8-23.
Development outline of smart urban rail in China[J]. China Metros, 2020(4): 8-23.
[2] 沈茂盛, 刘志刚, 张钢, 等. 采用三电平电压型PWM整流器的地铁牵引供电系统[J]. 电工技术学报, 2007, 22(7): 74-77.
Shen Maosheng, Liu Zhigang, Zhang Gang, et al. Traction power supply system in subway adopting three-level voltage source PWM rectifier[J]. Transa- ctions of China Electrotechnical Society, 2007, 22(7): 74-77.
[3] 卢西伟, 刘志刚, 张钢, 等. 基于电压型PWM整流器的新型轻轨牵引供电系统[J]. 电工技术学报, 2007, 22(8): 68-72.
Lu Xiwei, Liu Zhigang, Zhang Gang, et al. Research on novel light-rail traction power supply system based on voltage source PWM rectifier[J]. Transactions of China Electrotechnical Society, 2007, 22(8): 68-72.
[4] 成吉安. 城市轨道交通双向变流器牵引供电技术的应用[J]. 城市轨道交通研究, 2019, 22(12): 110-113.
Cheng Ji’an. Application of traction power supply technology with bidirectional converter for urban rail transit[J]. Urban Mass Transit, 2019, 22(12): 110- 113.
[5] 杨树松, 李辉, 朱纪法. 双向变流器应用于城市轨道交通供电系统的功能性验证[J]. 城市轨道交通研究, 2020, 23(1): 187-190.
Yang Shusong, Li Hui, Zhu Jifa. Functional veri- fication of bidirectional converter applied in urban rail transit power supply system[J]. Urban Mass Transit, 2020, 23(1): 187-190.
[6] 刘炜, 张扬鑫, 张戬, 等. 考虑牵引所多运行状态的城轨交直流供电计算[J]. 西南交通大学学报, 2020, 55(6): 1163-1170.
Liu Wei, Zhang Yangxin, Zhang Jian, et al. Calculation of urban rail AC/DC power supply with traction substation in multi-operation modes[J]. Journal of Southwest Jiaotong University, 2020, 55(6): 1163-1170.
[7] 刘炜, 娄颖, 张戬, 等. 计及城市轨道逆变回馈装置的交直流统一供电计算[J]. 电工技术学报, 2019, 34(20): 4381-4391.
Liu Wei, Lou Ying, Zhang Jian, et al. Unified AC-DC power supply calculation taking into account urban rail inverter feedback devices[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4381- 4391.
[8] Zhang Gang, Tian Zhongbei, Tricoli P, et al. Inverter operating characteristics optimization for DC traction power supply systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3400-3410.
[9] 刘志刚, 郝峰杰, 陈杰, 等. 城轨牵引供电系统车-地配合参数优化方法[J]. 北京交通大学学报, 2019, 43(1): 79-87.
Liu Zhigang, Hao Fengjie, Chen Jie, et al. Optimal method of train-ground coordination parameters for urban traction power supply system[J]. Journal of Beijing Jiaotong University, 2019, 43(1): 79-87.
[10] Hao Fengjie, Zhang Gang, Chen Jie, et al. Optimal voltage regulation and power sharing in traction power systems with reversible converters[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2726- 2735.
[11] 张戬, 刘炜, 周瑞兵, 等. 基于双向变流装置的城市轨道牵引供电系统潮流计算[J]. 中国铁道科学, 2020, 41(1): 92-98.
Zhang Jian, Liu Wei, Zhou Ruibing, et al. Power flow of traction power supply system for urban rail transit based on bidirectional converter device[J]. China Railway Science, 2020, 41(1): 92-98.
[12] 刘炜, 吴拓剑, 禹皓元, 等. 直流牵引供电系统地面储能装置建模与仿真分析[J]. 电工技术学报, 2020, 35(19): 4207-4215.
Liu Wei, Wu Tuojian, Yu Haoyuan, et al. Modeling and simulation of way-side energy storage devices in DC traction power supply system[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4207- 4215.
[13] 秦强强, 郭婷婷, 林飞, 等. 基于能量转移的城轨交通电池储能系统能量管理和容量配置优化[J]. 电工技术学报, 2019, 34(增刊1): 414-423.
Qin Qiangqiang, Guo Tingting, Lin Fei, et al. Optimal research for energy management and configuration of battery ESS in urban rail transit based on energy transfer[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 414-423.
[14] 中华人民共和国住房和城乡建设部. 地铁设计规范: GB 50157—2013[S]. 北京: 中国建筑工业出版社, 2013.
Parameter Designing in Power Supply System with Bidirectional Converter Devices as Only Converters Based on Enhanced Brute Force Algorithm
Abstract Aiming at the power flow calculation and parameter design in the power supply system (the bidirectional converter device is the only converter), this paper establishes a power flow calculation model of urban rail power supply system considering the capacity constraint of the bidirectional converter device. According to the power flow calculation algorithm, a parameter design strategy of the bidirectional converter device based on the improved brute force search algorithm is proposed, which considers the splitting of each traction substation (TS). In the iteration, to obtain the limit solution set, the capacity, droop rate and no-load voltage are divided into three layers, and the results are based on the simulation without considering the capacity constraint of the bidirectional converter device. The actual case is studied. After considering the capacity constraint of the bidirectional converter device, the peak output power of TS is controlled, and the adjacent TSs can provide power support. The search number of the proposed strategy is 1.63% of the traditional brute force algorithm. In the example case, the train is 6B marshalling with the maximum speed of 80km/h, and the minimum capacity of the bidirectional current converter in the limit solution set is 7MW.
keywords:Bidirectional converter device, parameter designing, enhanced brute force, capacity constraint
DOI: 10.19595/j.cnki.1000-6753.tces.210431
中图分类号:U231+.8
国家自然科学基金资助项目(51607148)。
收稿日期 2021-03-30
改稿日期 2021-07-12
张 戬 男,1995年生,博士研究生,研究方向为城市轨道柔性牵引供电。E-mail: zhangjian95@foxmail.com
刘 炜 男,1982年生,副教授,博士生导师,研究方向为城市轨道牵引供电与杂散电流。E-mail: liuwei_8208@swjtu.cn(通信作者)
(编辑 陈 诚)