0 引言
随着能源枯竭和环境污染问题越发严峻,目前全球海上风电开发呈现出深远海化和集群化的发展趋势[1],离海岸距离超过100km 的深远海域具有更丰富的风能资源,是未来海上风电探寻的重点方向[2]。德国等部分欧洲国家的深远海风电场已经投运[3],中国已经进行了基础前瞻性探索[4-6],其中,大规模风电跨海远距离输送是深远海域风能开发涉及的关键问题之一。
海上风电输送技术难度较大和成本较高,一般采用电缆线路。采用直流输电方式虽然可以减小损耗提升载流量,但直流电压下空间电荷积累效应给电缆绝缘带来了严峻挑战,在一定程度上限制了输送容量的提升。若采用工频交流输电,则由电容效应导致的无功电流和电磁感应引起的护套感应电流将显著影响电缆的输送容量、传输距离和经济性。而介于工频和直流之间的低频乃至分频输电方式可能在海上风电并网中得到广泛应用[7-9]。因此电缆在低频输电方式下的损耗和载流特性是深远海风电高效输送的关键因素之一。
目前,关于电缆护套感应电压、环流损耗的研究多集中于工频输电方式,采用的方法有IEC 标准法及有限元方法。文献[10]分析了多回路电力电缆不同敷设方式对环流的影响,指出了不同相序组合下的环流分布规律;文献[11]基于光电复合海缆的有限元模型,提出了光纤温度变化模型;文献[12]建立了光电复合海缆的热路模型;文献[13-15]采用有限元多物理场仿真方法,分析了不同敷设条件下海底电缆的温度和载流特性;文献[16]通过建立环形纹和螺纹护套的参数方程,提出了线芯与波纹护套的互感和等效直径方法误差的解析公式;文献[17]采用有限元法研究了护套材料磁导率、体积电阻率对护套感应电压的影响;文献[18]基于电路模型推导了双回路敷设电缆护套环流的计算方程,提出了减小护套环流的技术方案;部分学者还研究了电缆及周围媒质的温度场分布和热特性[19-21]。而关于电缆在低频输电方式下的损耗和载流特性研究较少。文献[22]基于系统技术经济性,讨论了分频输电方式下交流电缆载流量、传输极限等问题;文献[23]研究了城市电缆线路在低频输电方式下的运行特性。综上所述,关于三芯海底电缆在低频输电方式下的损耗特性,鲜有文献报道。
本文采用有限元方法,建立了三芯铠装电缆的电磁-热多物理场仿真模型,研究了其在低频运行方式下的损耗和载流特性,分析了缆芯电流在低频输电方式下的不均匀分布特性,研究了输电频率、缆芯半径等因素对护套感应电压、损耗因子及载流量的影响,并分析了IEC 标准计算误差,计算结果为提高深远海电缆线路的经济性提供了数据支撑。
1 三芯铠装电缆护套感应电压解析计算
运行过程中电缆护套损耗由护套上的感应电压和电流引起,因此在分析电缆护套损耗之前应首先明确护套感应电压的计算。相较于单芯电缆,三芯铠装电缆能大幅度节省输电走廊,提高传输容量,因此海上风电传输往往采用三芯光纤复合海底电缆,其结构示意图如图1 所示。
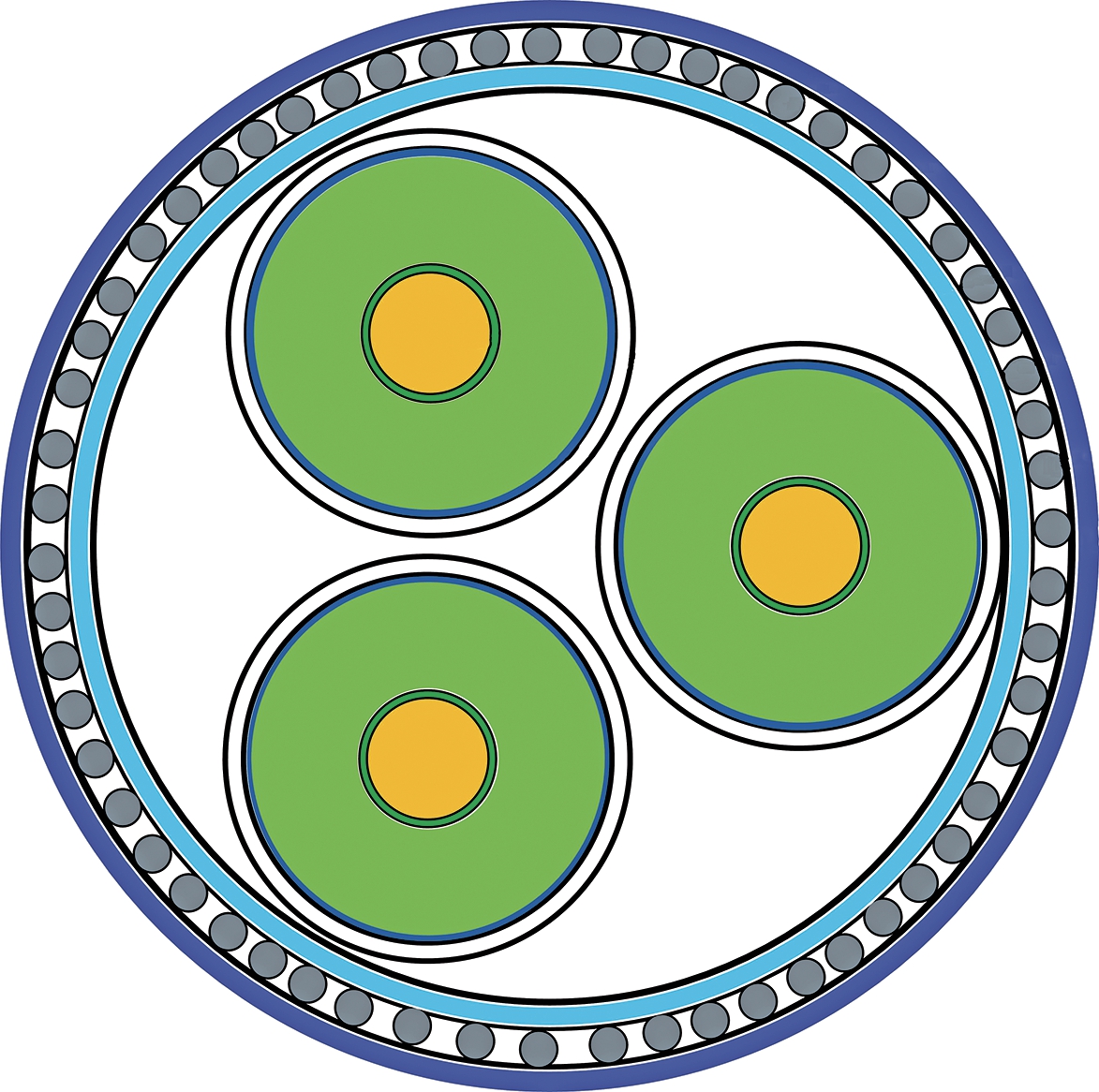
图1 三芯铠装电缆结构示意图
Fig.1 Structure of three-core armored cable
根据电磁场理论,缆芯电流激发的交变磁场将在电缆护套和铠装中产生感应电压,设三芯电缆流过三相平衡电流,其复数形式为

式中,I 为三相电流有效值。
按IEC 标准,当导体P 和A、B、C 三相缆芯平行布置时,如图2 所示,则三相电流产生的与P导体交链的磁通可表示为式中,RP 为导体P 的几何半径;S1、S2、S3 分别为三相缆芯与导体P 之间的距离。
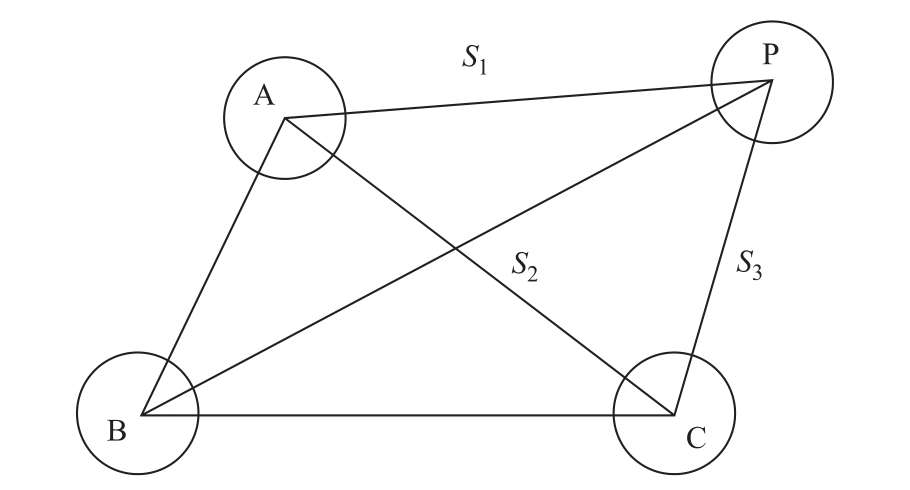
图2 电缆护套感应电压等效分析模型
Fig.2 Equivalent analysis model for induced voltage of cable sheath

对于三芯铠装海底电缆,护套可视为上述导体P 的特例,其与缆芯的间距等于护套平均半径,此时,护套感应电压计算式为
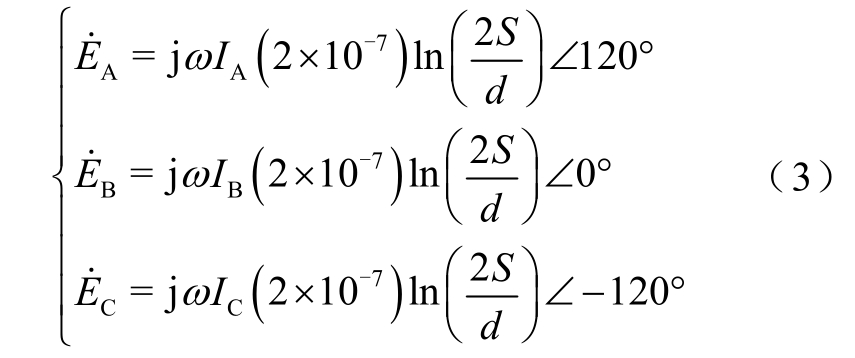
式中,d 为护套直径的几何平均值;S 为缆芯轴间距离。
上述护套感应电压计算公式是基于电缆简化模型推导得出,模型首先假设电流均匀分布,在处理某些环节时进一步假设电流集中于缆芯中央。而实际电流则由于趋肤效应和邻近效应的影响,在缆芯中并非均匀分布;且随着传输容量的上升,缆芯半径越大、结构越复杂,电流不均匀分布越明显,解析法计算就愈发困难。因此,对于三芯铠装海底电缆,采用上述解析公式进行计算,精度难以满足要求,有必要建立精确的有限元场模型进行分析。
2 三芯电缆电磁特性有限元分析
2.1 电磁-热耦合分析模型
电磁-热多物理场耦合模型以电磁场的麦克斯韦方程组和热传导的傅里叶定律为基础,电缆中电磁参数满足
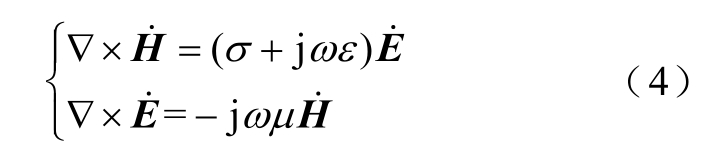
式中, ˙H 为磁场强度矢量相量(A/m); ˙E 为电场强度矢量相量(V/m);σ 为电导率(S/m);ω 为角频率(rad/s);ε 为介电常数(F/m);μ 为磁导率(H/m)。
引入相量形式的矢量磁位˙A,上述方程可以转化为频域下的二阶偏微分方程,即
由上述方程得出矢量磁位˙A 之后,可按式(6)求得磁感应强度。

式中,Φ 为与金属护套交链的磁通。
电缆实际运行过程中,缆芯和金属护套的电导率均受温度影响,其与温度的函数关系为

基于电磁场和温度场双向耦合的电缆损耗分析流程如图3 所示。
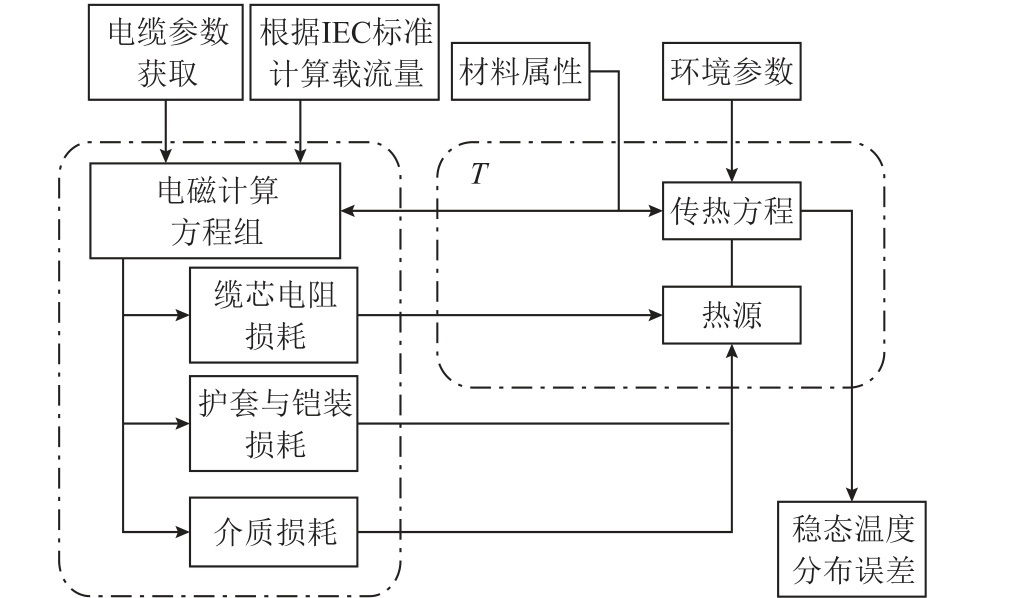
图3 电磁-热耦合分析原理
Fig.3 Principle of electromagnetic-thermal coupling analysis
2.2 缆芯电流分布及护套感应电压
三芯电缆的几何尺寸见表1,敷设条件如图4所示。通过电磁-热多物理场仿真计算,三芯铠装电缆的磁场分布如图5 所示。
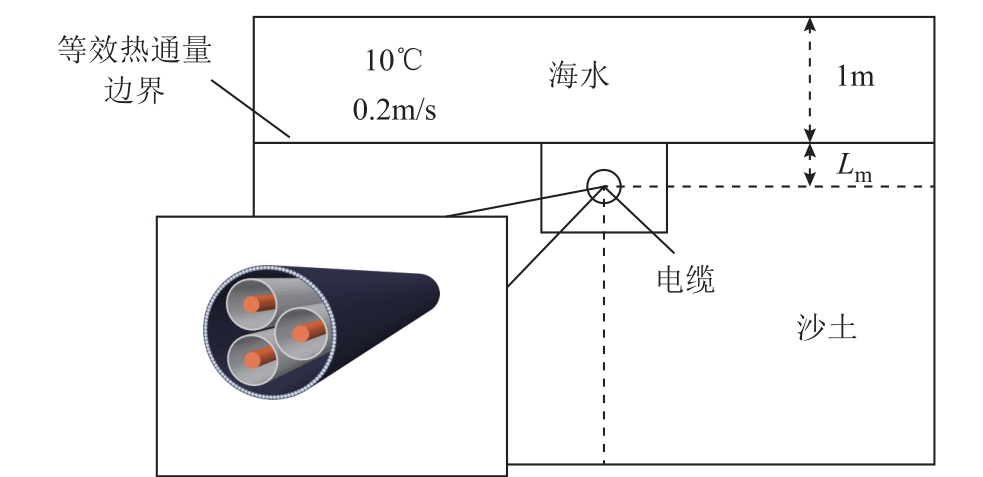
图4 电缆敷设条件
Fig.4 Cable laying conditions

图5 电缆磁场分布
Fig.5 Magnetic field distribution of cable
表1 电缆物理参数
Tab.1 Cable physical parameters
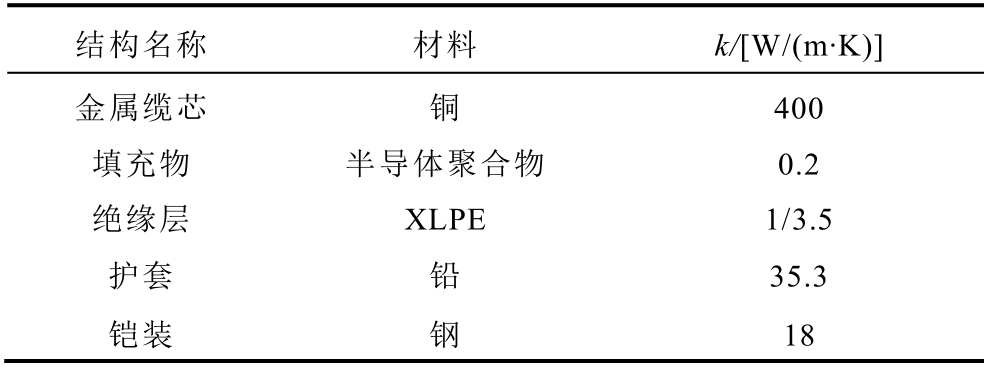
结构名称 材料 k/[W/(m·K)]金属缆芯 铜 400填充物 半导体聚合物 0.2绝缘层 XLPE 1/3.5护套 铅 35.3铠装 钢 18
当输电频率为50Hz 时,缆芯和护套中的电流分布如图6 所示。可以看出,缆芯电流明显呈不均匀分布,在三根缆芯相互靠近的一侧电流密度较大,在远离的一侧较小。缆芯电流的不均匀分布由趋肤效应和邻近效应引起。缆芯电流分布随频率的变化趋势如图7 所示。可以看出,频率越高,电流不均匀度越明显;且电流密度平均值位置和缆芯中心偏离较大,该偏离距离正是导致IEC 标准计算护套感应电压存在误差的原因之一。可以预见,电缆结构越复杂,其误差越大。
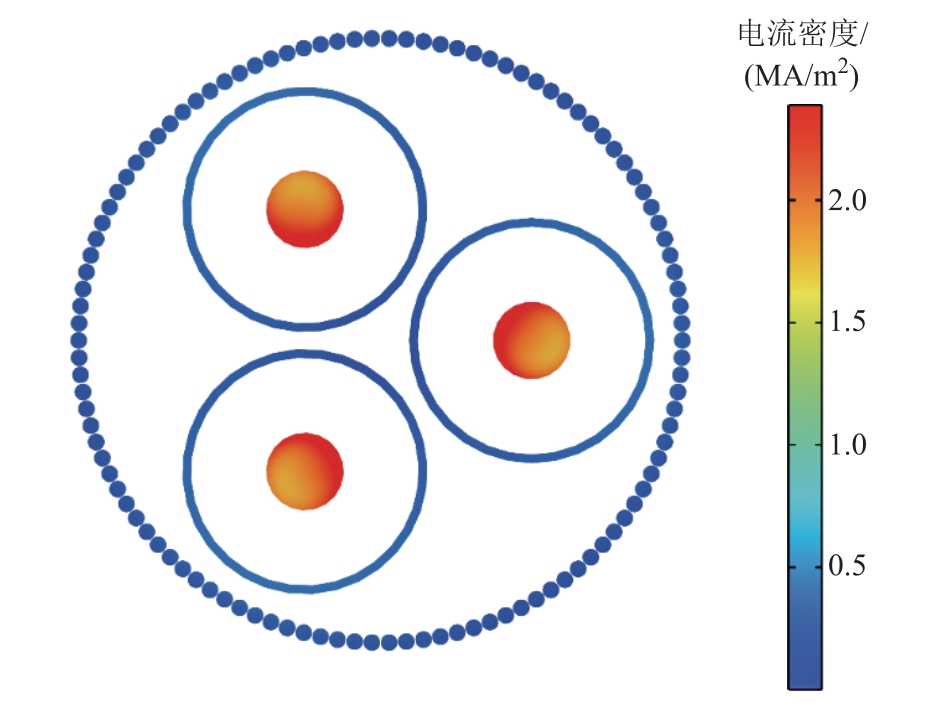
图6 缆芯与护套的电流密度
Fig.6 Current density of cable core and sheath

图7 缆芯电流径向分布
Fig.7 Radial distribution of core current
不同频率时,采用有限元法计算的护套感应电压如图8 所示,可以看出,采用电流均匀分布假设时,计算结果偏大,且随着频率增加,二者之间的偏差逐渐增大,分频时误差为8.4%,工频时的误差为13%。
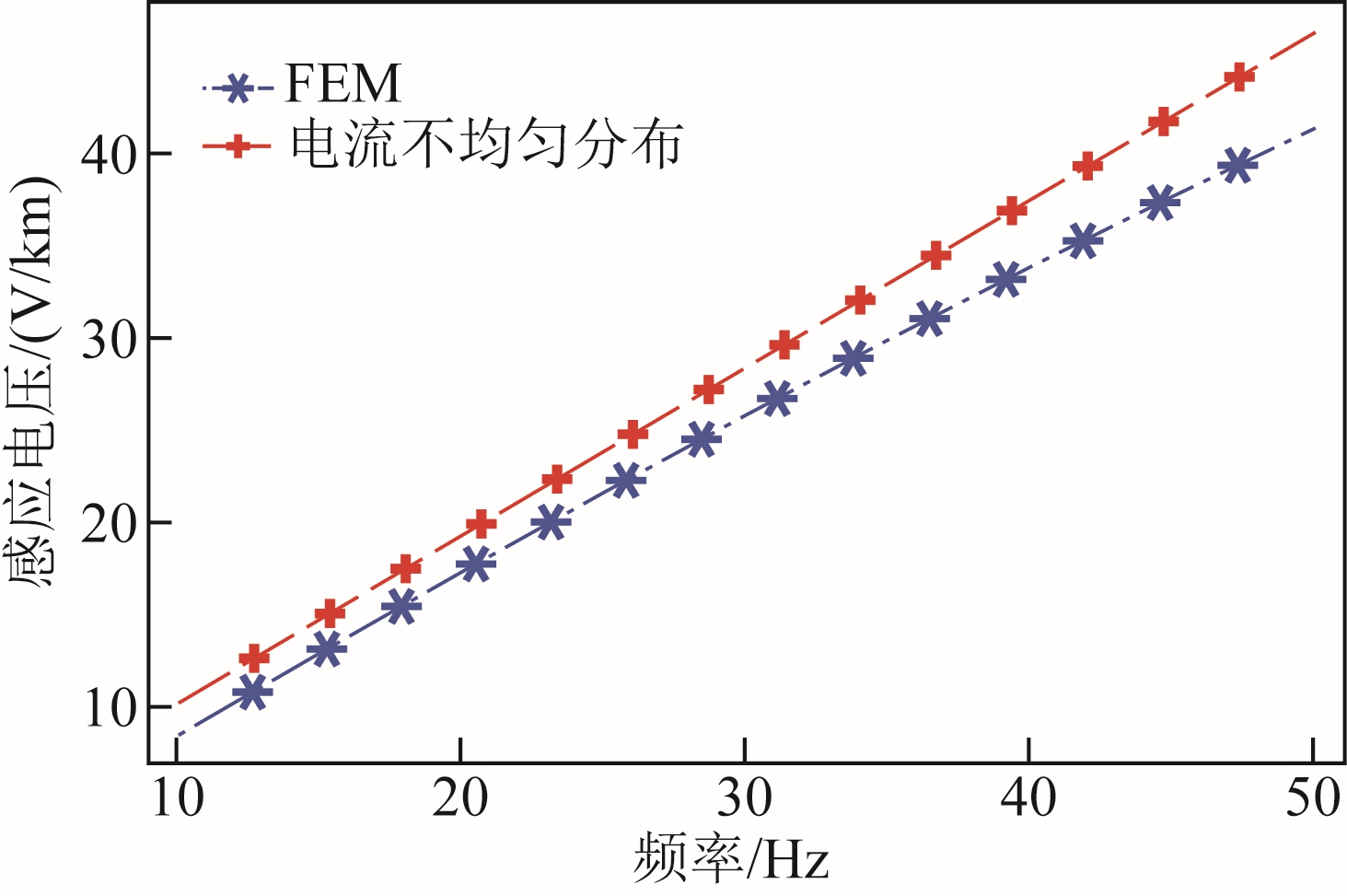
图8 电缆护套感应电压
Fig.8 Induced voltage of cable sheath
2.3 护套损耗
电缆护套中的感应电流会产生额外的损耗,从而导致电缆温度进一步上升,因此,准确计算护套损耗对于合理确定三芯海底电缆载流量,提升海上风电的经济性具有重要意义。根据IEC 标准,在不考虑铠装的情况下,护套中的总损耗由环流损耗和涡流损耗构成,损耗因子可表示为

式中,X 为电缆护套电抗(Ω/m);Rs 为护套电阻(Ω/m);R 为缆芯电阻(Ω/m);S 为三相导体间的缆芯轴间距离(m)。

式中,ts 为护套厚度(mm);Ds 为电缆护套的外径(mm);ρ0 为护套材料的电阻率(Ω·m)。
上述公式在计算λ1 时没有考虑邻近效应,这同样导致公式在计算三芯海底电缆损耗因子时精度降低。输电频率一方面影响缆芯电流分布、缆芯电阻及缆芯欧姆损耗,另一方面还影响护套感应电压及护套损耗,而IEC 标准在计算λ1 过程中做出的某些假设并未计及上述影响。此外,若考虑铠装, 1λ′可由式(14)给出,此时电缆结构更加复杂,IEC 标准的计算误差会更大。因此,需要构建有限元模型进行详细讨论。
采用有限元分析可以得出,输电频率及缆芯半径对缆芯电阻的影响如图9 所示,可以看出,由于趋肤效应和邻近效应的存在,随着频率的增加,电阻明显增加,从而将导致缆芯损耗增加。
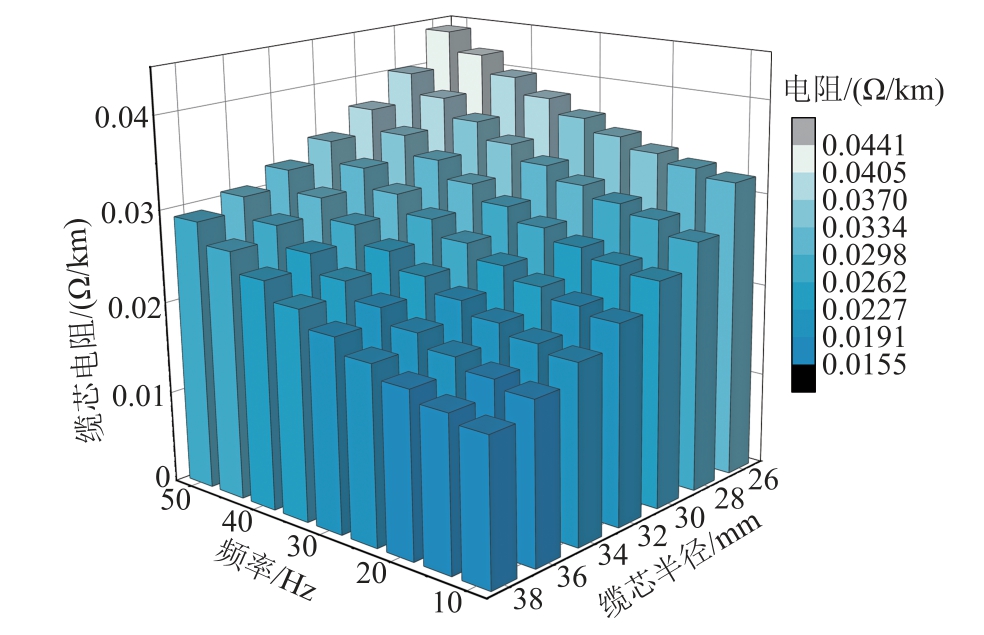
图9 输电频率及缆芯半径对电阻的影响
Fig.9 Influence of transmission frequency and core radius on resistance
输电频率对损耗因子的影响如图10 所示,可以看出,采用有限元计算时,如采用电流均匀分布模型,其计算结果和IEC 标准计算结果基本相同,且大于实际值(有限元采用电流不均匀分布模型计算结果),这一方面验证了IEC 标准的假设条件,另一方面也揭示了标准的局限性。随着频率的上升,趋肤效应和邻近效应越发明显,电流分布不均匀导致的损耗比率λ1 也明显变化,当频率由分频50/3Hz 增加到工频50Hz 时,λ1 误差由14%增加到18.4%。
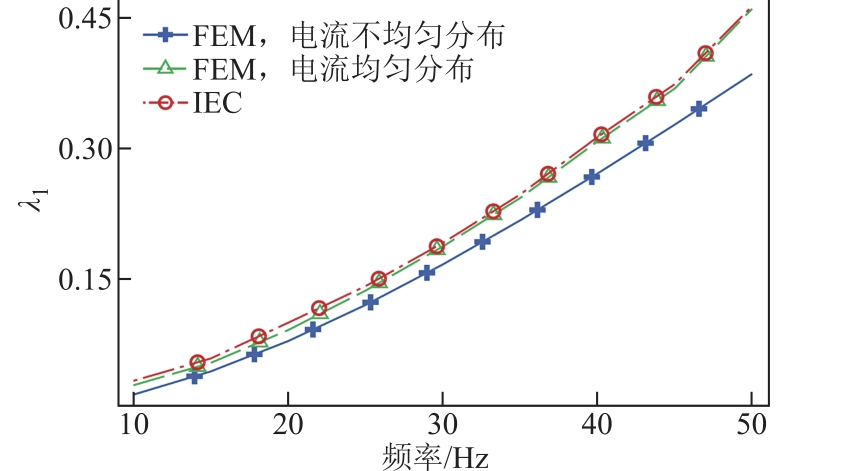
图10 频率对λ1 的影响
Fig.10 Influence of frequency on λ1
除了频率,缆芯半径同样影响损耗因子λ1,不同频率时缆芯半径对 1λ 的影响如图11 和图12 所示。在工频输电方式下,IEC 计算结果显示,λ1 随缆芯半径增加而逐渐增加,并存在饱和趋势;而有限元结果则显示,当缆芯半径小于24mm 时,λ1 随缆芯增加呈增长趋势,当缆芯半径大于24mm 时,λ1 则随缆芯增加呈现下降趋势,此时IEC 标准法误差将进一步增大,究其原因在于,缆芯半径越大,电流密度平均值位置和缆芯中心偏离越大,导致IEC 标准的电流集中分布假设和电缆实际电流分布情况相差较远,从而导致IEC 计算结果误差进一步增大。分频输电方式下,缆芯半径对λ1 的影响与工频情况下类似。总之,电流的不均匀分布对损耗有十分明显的影响,因此在计算电缆损耗时,应将电流分布情况考虑在内。
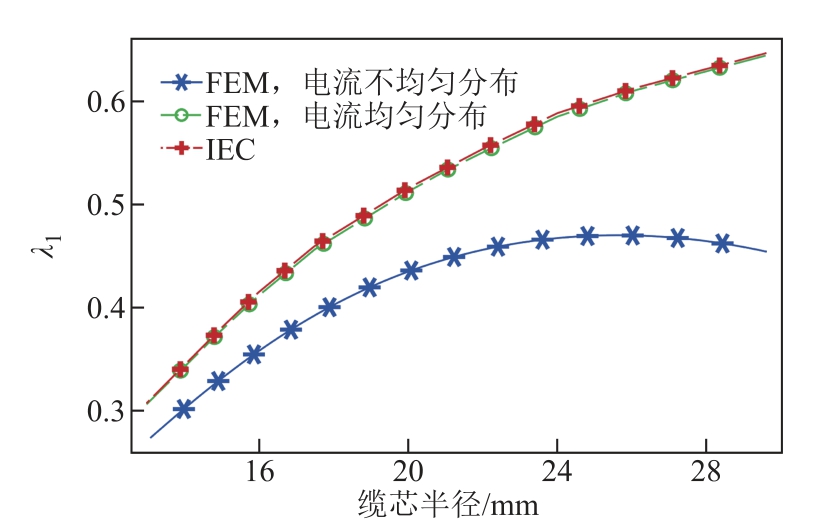
图11 50Hz 时缆芯半径对λ1 的影响
Fig.11 Influence of core radius on λ1 at 50Hz

图12 17Hz 时缆芯半径对λ1 的影响
Fig.12 Influence of core radius on λ1 at 17Hz
当同时计及护套损耗和铠装损耗时,采用有限元计算的电缆各部分损耗如图13 所示,可以看出,随着频率的上升,电缆整体电磁损耗、缆芯损耗、铠装及护套损耗均呈上升趋势。电缆总损耗比率如图14 所示。
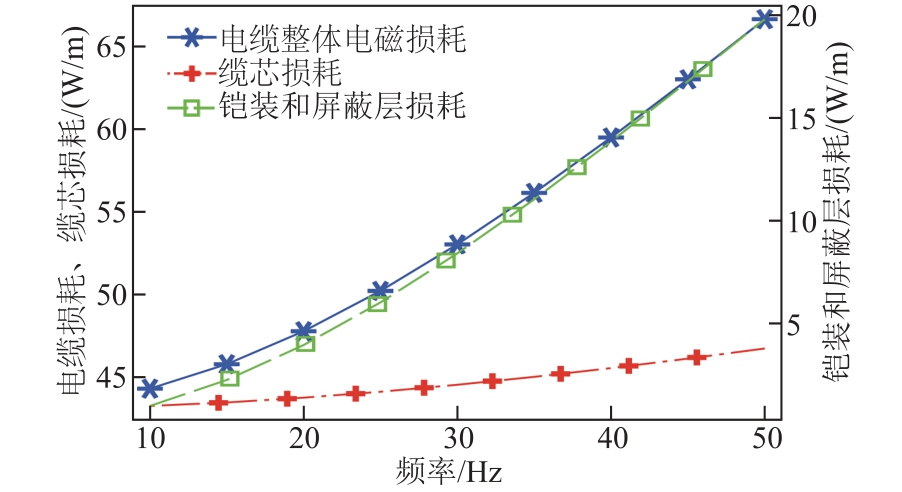
图13 电缆各部分损耗
Fig.13 Loss of each part of the cable
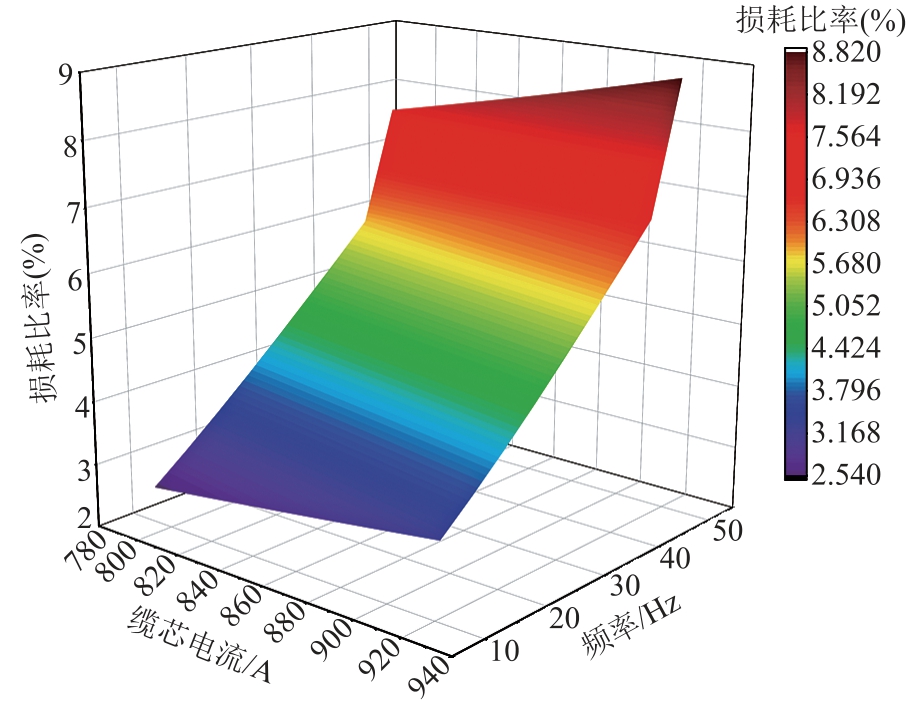
图14 电缆损耗比率
Fig.14 Cable loss ratio
2.4 载流量
基于上述分析,充分考虑缆芯电流不均匀分布,采用电磁-热耦合模型计算得到的三芯铠装海底电缆的载流量如图15 所示。

图15 电缆载流量
Fig.15 Ampacity of the cable
可以看出,相同缆芯截面积时,电缆工频载流量低于分频载流量;和有限元结果相比,IEC 计算结果偏大,随着缆芯截面积增大,IEC 计算误差有饱和趋势,工频时误差最大值约为15%,分频时误差最大值约为10%。图16 为三芯电缆满载时的温度场分布,此时缆芯温度为90℃,温度由内向外逐渐降低。
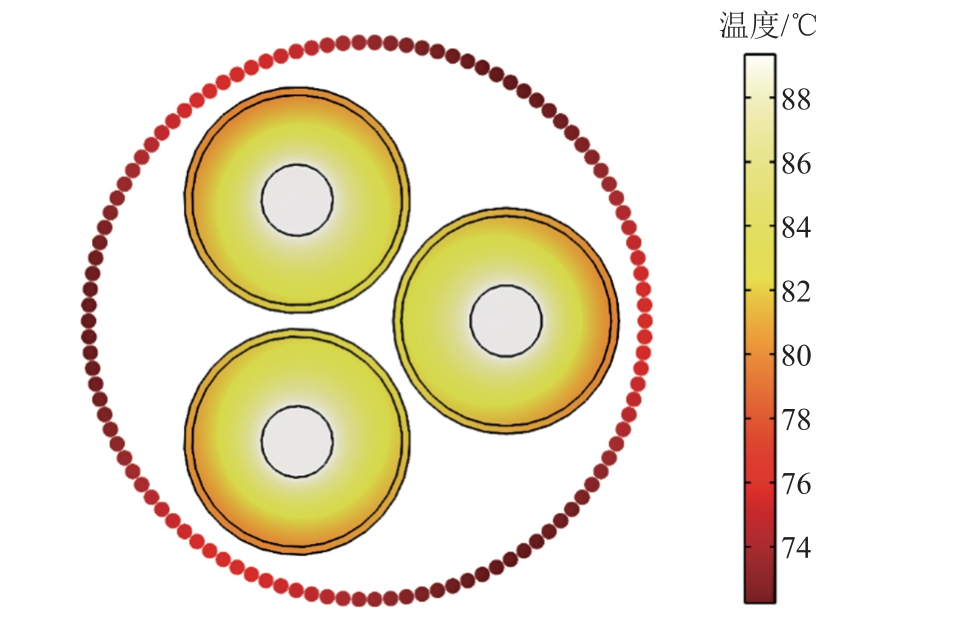
图16 电缆温度场分布
Fig.16 Distribution of cable temperature
3 结论
本文基于电磁-热耦合原理研究了三芯铠装海底电缆在低频输电方式下的损耗特性,得出如下结论:
1)缆芯电流密度平均值点偏离缆芯中心,偏离距离随输电频率的增大而增大,此偏离距离是采用IEC 标准计算感应电压、损耗因子和载流量时存在误差的重要原因之一。
2)采用IEC 标准计算的三芯铠装电缆护套损耗因子λ1 偏大,输电频率越高,缆芯半径越大,λ1误差越大,分频及工频输电时误差分别达到14%和18.4%;另外,当缆芯半径增大时,实际损耗因子λ1变化规律呈现饱和甚至减小的趋势,此时(半径为24mm)由于IEC 标准计算误差进一步增大,应慎重采用。
3)采用IEC 标准计算的电缆载流量偏小,该误差随输电频率和缆芯截面积的增加而增大,当截面积取2 000mm2 时,分频及工频下的载流量误差分别达10%和15%左右。
[1] 李响, 韩民晓. 海上风电串联多端VSC-HVDC 协调控制策略[J]. 电工技术学报, 2013, 28(5): 42-48.Li Xiang, Han Minxiao. A coordinated control strategy of series multi-terminal VSC-HVDC for offshore wind farm[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 42-48.
[2] 姜楠. 深海风力发电技术的发展现状与前景分析[J].新能源进展, 2015, 3(1): 21-24.Jiang Nan. Analysis on status and prospect of wind power generation in deep sea[J]. Advances in New and Renewable Energy, 2015, 3(1): 21-24.
[3] Wind Europe. Offshore wind in europe key trends and statistics 2017 [EB/OL]. [2018-07-18]. https://windeurope.org/wp-content/uploads/files/about-wind/statistics/WindEurope-Annual-Offshore-2017.pdf.
[4] 迟永宁, 梁伟, 张占奎, 等. 大规模海上风电输电与并网关键技术研究综述[J]. 中国电机工程学报,2016, 36(14): 3758-3771.Chi Yongning, Liang Wei, Zhang Zhankui, et al. An overview on key technologies regarding power transmission and grid integration of large scale offshore wind power[J]. Proceedings of the CSEE,2016, 36(14): 3758-3771.
[5] 杨悦, 李国庆. 基于VSC-HVDC 的海上风电小干扰稳定控制[J]. 电工技术学报, 2016, 31(13): 101-110.Yang Yue, Li Guoqing. The small signal stability control of offshore wind farm based on VSC-HVDC[J].Transactions of China Electrotechnical Society, 2016,31(13): 101-110.
[6] 王秀丽, 张小亮, 宁联辉, 等. 分频输电在海上风电并网应用中的前景和挑战[J]. 电力工程技术,2017, 36(1): 15-19.Wang Xiuli, Zhang Xiaoliang, Ning Lianhui, et al.Application prospects and challenges of fractional frequency transmission system in offshore wind power integration[J]. Electric Power Engineering Technology, 2017, 36(1): 15-19.
[7] Chen Hao, Johnson M H, Aliprantis D C. Lowfrequency AC transmission for offshore wind power[J]. IEEE Transactions on Power Delivery, 2013,28(4): 2236-2244.
[8] 王锡凡, 卫晓辉, 宁联辉, 等. 海上风电并网与输送方案比较[J]. 中国电机工程学报, 2014, 34(31):5459-5466.Wang Xifan, WEI Xiaohui, Ning Lianhui, et al.Integration techniques and transmission schemes for off-shore wind farms[J]. Proceedings of the CSEE,2014, 34(31): 5459-5466.
[9] Ruddy J, Meere R, O'louchin C, et al. Design of VSC connected low frequency AC offshore transmission with long HVAC cables[J]. IEEE Transactions on Power Delivery, 2018, 33(2): 960-970.
[10] 邹宏亮, 孙云莲, 张弛, 等. 多回路电力电缆不同敷设方式对环流的影响[J]. 高电压技术, 2016,42(8): 2426-2433.Zou Hongliang, Sun Yunlian, Zhang Chi, et al. Effects of different multi-loop laying ways on circulating current of power cable[J]. High Voltage Engineering,2016, 42(8): 2426-2433.
[11] 吕安强, 李永倩, 李静, 等. 光电复合海缆中光纤与导体温度关系的有限元分析方法[J]. 电工技术学报, 2014, 29(4): 91-96.Lü Anqiang, Li Yongqian, Li Jing, et al. Finite element analysis method for temperature relati-onship between conductor and optical fiber in optic-electric composite submarine cable[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 91-96.
[12] 王鹤, 李兴宝, 路俊海, 等. 基于叠加原理的光纤复合低压电缆热路模型建模[J]. 电工技术学报,2019, 34(7): 1381-1391.Wang He, Li Xingbao, Lu Junhai, et al. Simulation analysis of induced voltage on metal sheath of power cable based on finite element method[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1381-1391.
[13] Zhang Yiyi, Chen Xiaoming, Zhang Heng, et al.Analysis on the temperature field and the ampacity of XLPE submarine HV cable based on electro-thermalflow multiphysics coupling simulation[J]. Polymers,2020, 12(4): 952.
[14] 郝艳捧, 陈云, 阳林. 高压直流海底电缆电-热-流多物理场耦合仿真[J]. 高电压技术, 2017, 43(11):3534-3542.Hao Yanpeng, Chen Yun, Yang Lin. Coupled simulation on electro-thermal-fluid multiple physical fields of HVDC submarine cable[J]. High Voltage Engineering, 2017, 43(11): 3534-3542.
[15] 陆莹, 范明明, 刘刚, 等. 基于电磁-热-流耦合场的非开挖敷设方案的海底电缆载流量计算[J]. 广东电力, 2020, 33(5): 117-124.Lu Ying, Fan Mingming, Liu Gang, et al. Calculation of ampacity for submarine cables under trenchless laying method based on electromagnetic-thermal-flow coupled field[J]. Guangdong Electric Power, 2020,33(5): 117-124.
[16] 王航, 周文俊, 陈杰, 等. 波纹金属护套高压单芯电缆线芯护层互感的解析解[J]. 电工技术学报,2020, 35(16): 3369-3376.Wang Hang, Zhou Wenjun, Chen Jie, et al.Analytical solution of the mutual inductance of a HV single conductor cable with corrugated metallic sheath[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3369-3376.
[17] 高俊国, 于平澜, 李紫云, 等. 基于有限元法的电缆金属护套感应电压仿真分析[J]. 高电压技术,2014, 40(3): 714-720.Gao Junguo, Yu Pinglan, Li Ziyun, et al. Simulation analysis of induced voltage on metal sheath of power cable based on finite element method[J]. High Voltage Engineering, 2014, 40(3): 714-720.
[18] 刘英, 王磊, 曹晓珑. 双回路电缆护套环流计算及影响因素分析[J]. 高电压技术, 2007, 33(4): 143-146.Liu Ying, Wang Lei, Cao Xiaolong. Calculation of circulating current in sheaths of two-circuit arranged cables and analyses of influencing factors[J]. High Voltage Engineering, 2007, 33(4): 143-146.
[19] 梁永春, 李彦明, 柴进爱, 等. 地下电缆群稳态温度场和载流量计算新方法[J]. 电工技术学报, 2007,22(8): 185-190.Liang Yongchun, Li Yanming, Chai Jinai. A new method to calculate the steady-state temperature field and ampacity of underground cable system[J].Transactions of China Electrotechnical Society, 2007,22(8): 185-190.
[20] 牛海清, 郑文坚, 雷超平, 等. 基于有限元和粒子群算法的电缆周围土壤热特性参数估算方法[J].高电压技术, 2018, 44(5): 1557-1563.Niu Haiqing, Zheng Wenjian, Lei Chaoping, et al.estimation method for thermal parameters of soil around the cable based on finite element and particle swarm optimization[J]. High Voltage Engineering,2018, 44(5): 1557-1563.
[21] 曹惠玲, 王增强, 李雯靖, 等. 坐标组合法对直埋电缆与土壤界面温度场的数值计算[J]. 电工技术学报, 2003, 18(3): 59-63.Cao Huiling, Wang Zengqiang, Li Jingwen, et al.Numerical computation of temperature distribution of underground cables and soil with combina-torial coordinates[J]. Transactions of China Electrotechnical Society, 2003, 18(3): 59-63.
[22] 黄明煌, 王秀丽, 刘沈全, 等. 分频输电应用于深远海风电并网的技术经济性分析[J]. 电力系统自动化, 2019, 43(5): 167-174.Huang Minghuang, Wang Xiuli, Liu Shenquan, et al.Technical and economic analysis on fractional frequency transmission system for integration of longdistance offshore wind farm[J]. Automation of Electric Power Systems, 2019, 43(5): 167-174.
[23] Fan Huimin, Xu Yunfei, Xiao Xiangning, et al.Operation characteristics of low frequency AC cable transmission system for urban grid[C]//2016 China International Conference on Electric Distribution(CICED), Xi'an, 2016: 1-6.