U i 时，电感电流峰峰值最小，即电流应力最小。由此可见，采用该文提出的控制策略可实现双向隔离型AC-DC 变换器能量的双向流动，保证了良好的输入输出性能。通过与传统控制策略的仿真与实验对比，采用所提出控制策略的双向隔离型AC-DC 矩阵变换器在较低输出电压范围内具有更小的电感电流应力，有助于降低器件损耗，提高变换器效率，并提升系统可靠性。摘要 针对双向隔离型AC-DC 矩阵变换器，提出一种基于零矢量嵌入的分段同步控制策略。其中，前级 3-1 矩阵式变换电路采用对称双线电压调制法，以提高电压传输比；后级全桥电路采用互补控制，简单易实现；前后级电路之间分段同步，并通过在前级电路中嵌入零矢量以实现能量的双向传输。仿真和实验结果表明，网侧电流三相平衡正弦，功率因数接近于1，输出电压和电流平稳，纹波小，且电感电流峰峰值随直流侧电压增加呈先减小后增大的趋势，当nUo=U i 时，电感电流峰峰值最小，即电流应力最小。由此可见，采用该文提出的控制策略可实现双向隔离型AC-DC 变换器能量的双向流动，保证了良好的输入输出性能。通过与传统控制策略的仿真与实验对比，采用所提出控制策略的双向隔离型AC-DC 矩阵变换器在较低输出电压范围内具有更小的电感电流应力，有助于降低器件损耗，提高变换器效率，并提升系统可靠性。
随着新能源技术的发展，许多学者提出利用储能系统对可再生能源进行消纳，因此储能技术将在未来新能源发电系统中扮演重要角色。双向AC-DC变换器是连接储能单元与电网的接口，在储能系统中具有重要的作用[1-3]。近年来，双向隔离型AC-DC矩阵变换器被应用于储能系统作为接口变换器，具有能量双向传输、网侧单位功率因数、体积小、质量轻和功率密度高等优势，特别是在交流侧和直流侧之间引入高频变压器作为电气隔离，使得抗干扰能力强，升降压的范围宽。因此，获得了学术界和工业界的广泛关注[4-7]。
由于双向隔离型AC-DC 矩阵变换器拓扑结构比较复杂，前后级电路相互耦合，因而不能直接借鉴使用传统矩阵变换器的调制方法。文献[8]提出了一种针对高频链矩阵变换器的基于电压空间矢量调制和前后级移相控制的控制策略，虽然可以实现双向功率控制，但该策略导致峰值电流较大，从而降低了高频链矩阵变换器的效率。为此，本文提出了一种分段同步控制策略。其中，前级3-1 矩阵变换电路采用对称双线电压调制，后级全桥电路采用传统的互补控制，并通过在前级端口电压的脉冲信号中嵌入零矢量，以调节变换器的传输功率。为了进一步分析该控制策略的性能，对电感电流峰峰值实现了量化评估，即实现了对变换器电流应力的分析。
双向隔离型AC-DC 矩阵变换器的拓扑如图1所示，由网侧LC 滤波器、前级变换电路、高频变压器、后级变换电路和直流侧输出滤波器五个部分组成。其中，网侧LC 滤波器用于滤除高频开关动作产生的高频电流谐波，防止注入电网造成干扰；前级变换电路由3-1 矩阵电路构成，可将三相工频交流电转换为单相高频交流电，为提高变换器的功率密度，可采用12 个SiC MOSFET 以共源极连接的形式构成6 个双向开关，按照3×2 矩阵排列；高频变压器作为前级变换电路和后级变换电路之间的电气隔离环节，使变换器可以实现安全可靠的升降压变换；后级变换电路由全桥电路构成，可将单相高频交流电转换为直流电，同样由四个 SiC MOSFET 组成；直流侧滤波器可以保证直流侧电压、电流平滑稳定。
图1 双向隔离型AC-DC 矩阵变换器拓扑
Fig.1 The topology of bidirectional isolated AC-DC matrix converter
图1 所示拓扑结构可视为由3-1 AC-AC 矩阵变换器和AC-DC 变换器组合而成，无中间直流母线电容作为储能元件。因此，该变换器前后级电路之间相互耦合，无法完全独立控制，大大增加了控制难度。考虑到这一拓扑结构与双有源桥（Double Active Bridge, DAB）有相似之处，因此可以借鉴其控制思想[9-10]，建立如图2 所示双向隔离型AC-DC变换器的等效电路。其中，三相交流电压源经网侧滤波器和前级3-1 矩阵式变换电路后为高频交流电压，构成高频变压器一次电压up，可视为一个电压源；后级全桥电路、输出滤波器和直流负载，可视为单相电压源型变换器，其输入为变压器二次电压us，亦可视为一个电压源；前级串联电感及高频变压器的漏感共同等效为电感L，流过等效电感L 的电流为iL(t)。
图2 双向隔离型AC-DC 变换器等效电路
Fig.2 The equivalent circuit of the bidirectional isolated AC-DC matrix converter
根据上述等效电路可以建立两个端口电压和电感L 上的电压电流等量关系为
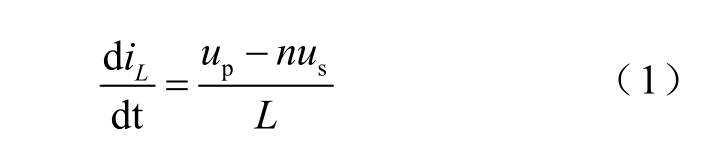
基于双向隔离型AC-DC 矩阵变换器的基本工作原理和等效电路，本文构建其控制原则如图2 所示：①前级3-1 矩阵变换电路采用双线电压调制法，以提高电压传输比，同时为了避免高频变压器出现直流饱和现象，双线电压采用正负对称的分布方式；②为配合前级电路，后级全桥电路采用分段互补控制，即按照前级的两组线电压分布情况将整个控制周期分段，在相应时段中采用互补控制；③前、后级电路之间按照输入线电压划分的时段进行分段同步控制，同时为了实现前后级之间功率的传输，在前级电路控制中嵌入零矢量以调节中间高频电感电流。
以整流模式为例，根据上述控制原则进行变换器控制得到的前后级电路电压和中间电感电流分布如图3a 所示。图中，t0 为一个控制周期的起始时刻点，一个控制周期Ts 分成最大线电压（第一占空比）作用时间d1Ts、次大线电压（第二占空比）作用时间d2Ts 和零电压作用时间d0Ts 三个部分，在两组线电压作用时段中嵌入的两段零矢量
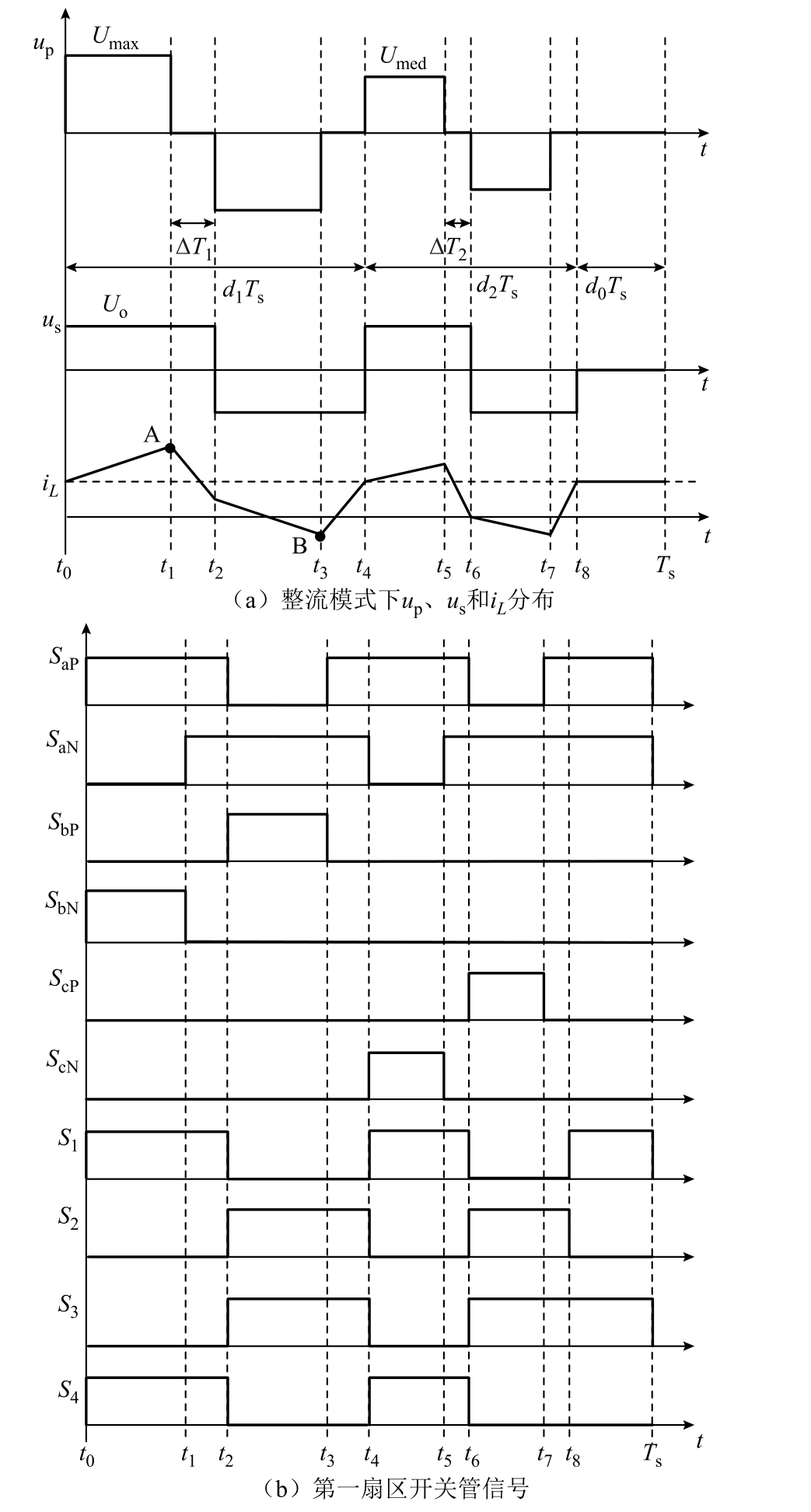
图3 整流模式下up、us、iL 的移相控制示意图和第一扇区开关管控制信号
Fig.3 up, us and iL phase-shift control in rectifier mode,control signals of the switches in sector 1
如图3a 所示，一个控制周期共分为9 段。根据式（1）所示的电压电流关系，可以推导得各段电感电流表达式为
式中，iL0 为一个控制周期起始时刻t0 时的电感电流初始值；Umax、Umed 分别为 uab、uac、ubc、uba、uca、ucb 中，极性为正，且幅值最大的和次大的输入线电压。
为保证一个控制周期内Umax、Umed 对应关系不变，将一个工频周期平均划分为12 个扇区，如图4所示。
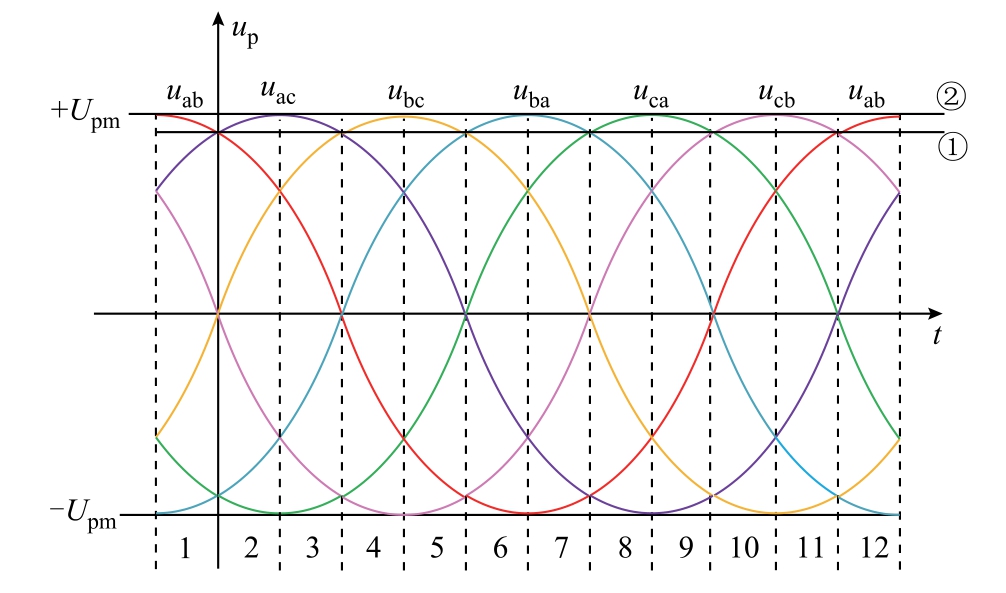
图4 前级电路输入电压扇区划分
Fig.4 Sector distribution based on input voltage of pre-stage circuit
以第一扇区为例，此时相电压ua＞uc＞ub 时，幅值最大的正极性线电压为uab，幅值次大的正极性线电压为uac，在一个控制周期Ts 内，按照本文提出的控制策略，可以得到各开关器件的控制信号如图3b 所示，其中SaP～ScN 为前级3-1 矩阵电路中6 个双向开关的控制信号，S1～S4 为后级全桥电路中4 个单向开关的控制信号。
根据当前扇区的开关状态，可以确定一个控制周期内，三相电流ia、ib、ic 的状态，如图5 所示。
图5 扇区1 时三相输入电流波形
Fig.5 Three-phase input current in sector 1
根据图5 中各相电流的方向和式（2）中每段电感电流的表达式，可得到各相电流平均值的表达式为
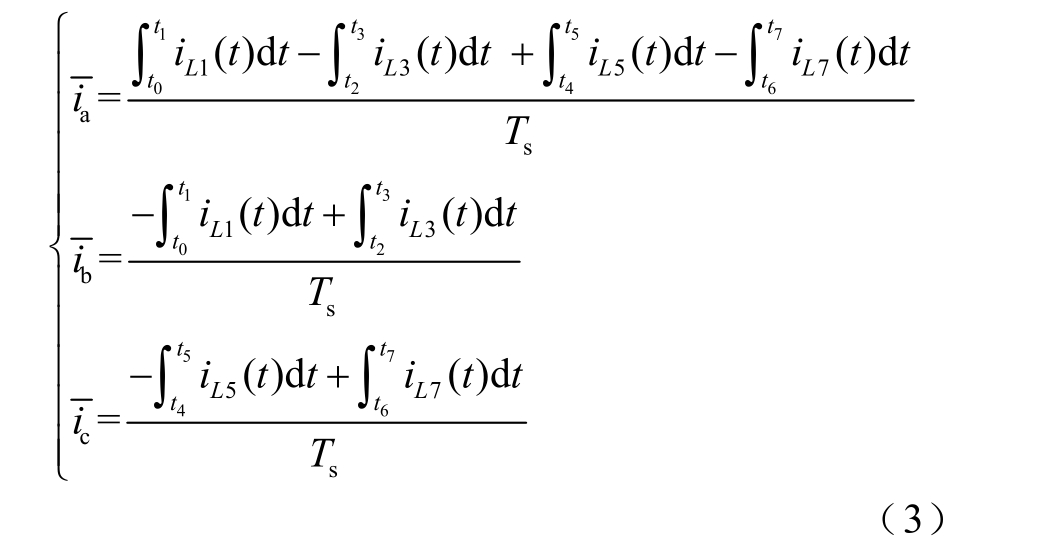
将各个物理量代入式（3）进行化简整理，得到一个控制周期Ts 内各相电流的平均值为
为保证网侧电流三相平衡正弦，网侧电流与电压相位相同，设定网侧三相电流参考值表达式为
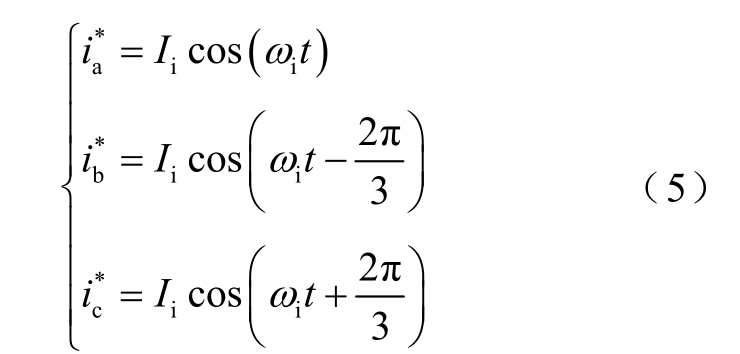
式中， Ii 为网侧三相电流幅值。
联立式（3）和式（4），可以求得第一占空比d1、第二占空比d2 和零矢量占空比d0 在第一扇区的计算公式为
同理可推导出其他11 个扇区中各占空比的表达式，整理可得到本控制策略在整流模式下第一占空比d1、第二占空比d2 和零矢量占空比d0 为
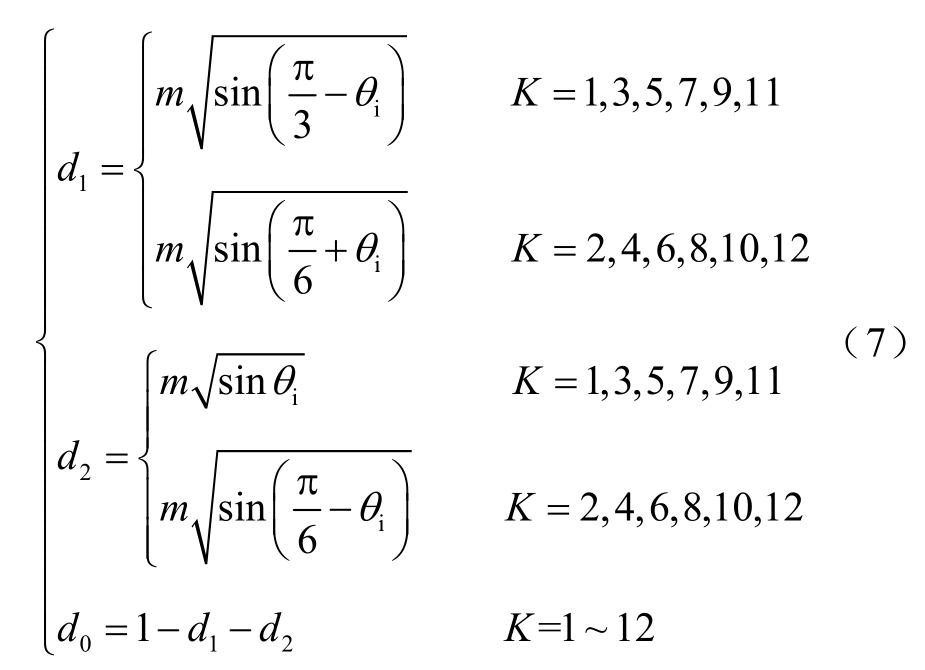
同理，建立逆变模式下的脉冲宽度调制（Pulse Width Modulation, PWM）脉冲分布如图6 所示，对其每段占空比的表达式进行理论推导，得到第一占空比d1、第二占空比d2 和零矢量占空比d0 表达式同式（7）所示。由于能量传输方向与整流模式相反，移相角φ 的取值范围为-π 2≤φ＜0 ，移相比δ 的取值范围是-1≤δ ＜0 ，其他变量的定义和取值范围与整流模式相同。
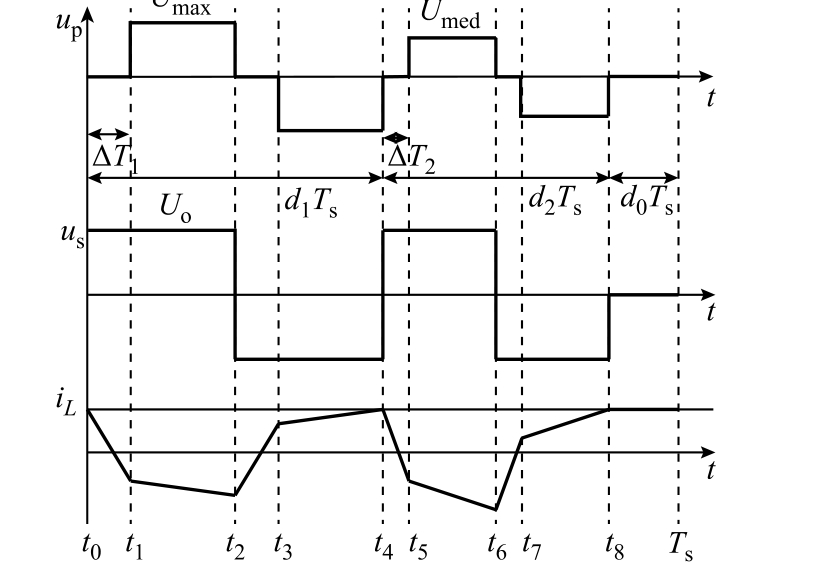
图6 逆变模式下up、us、iL 的移相控制示意图
Fig.6 up, us and iL phase-shift control in inverter mode
在保证良好输入输出性能的基础上，对所提出控制策略的性能进行了进一步评估，从而明确其优、缺点和适用范围。类比DAB 的工作特性和性能，控制策略对变换器的电流应力具有显著的作用，进而对系统的功率损耗和可靠性产生一定影响[11-15]。本文利用电感电流峰峰值对电流应力进行了量化评估，分析了在直流侧不同电压条件下，电感电流峰峰值随之发生的变化。
由于双向隔离型AC-DC 变换器可实现升、降压的变换，其直流侧电压调节范围宽，在直流侧电压Uo 递增的过程中，需对电感电流峰峰值的变化进行分情况讨论。
这里以整流模式为例，分析讨论以上三种情况时直流侧电压对电感电流峰峰值的影响。
图7 在nUo＞
Ui条件下电感电流峰峰值示意图
Fig.7 The peak to peak of inductance current under
利用Matlab/Simulink 搭建双向隔离型AC-DC矩阵变换器仿真模型，进行仿真验证，说明以上理论的正确性和有效性，系统关键参数见表1。
表1 仿真关键参数
Tab.1 The key parameters of simulation
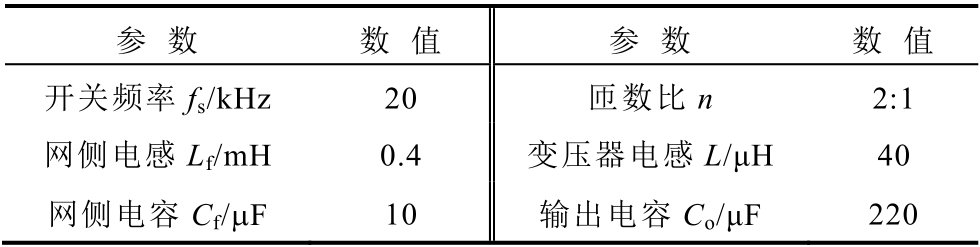
参 数 数 值 参 数 数 值开关频率fs/kHz20 匝数比n 2:1网侧电感Lf/mH0.4 变压器电感L/μH40网侧电容Cf/μF 10 输出电容Co/μF 220
仿真中交流侧相电有效值设定为80V，直流侧电压180V，控制频率为20kHz，移相比δ=0.4。仿真结果如图8 所示，在整流模式下，可以实现网侧电流与电压同相位，且网侧电流正弦度良好，总谐波畸变率（Total Harmonic Distortion, THD）为2.00%，直流侧输出电压电流波形平稳，输出电压纹波约为0.46%，即在整流模式下，实现了良好的输入输出性能，验证了所提调制策略的正确性。
图8 整流模式下的仿真结果
Fig.8 Simulation results in rectifier mode
在整流模式下，设定网侧电压幅值Ui=113V，通过只改变直流侧电压Uo，将Uo 从33.3V 一直增大到160V，进行了电感电流峰峰值的仿真计算，结果如图9 所示。
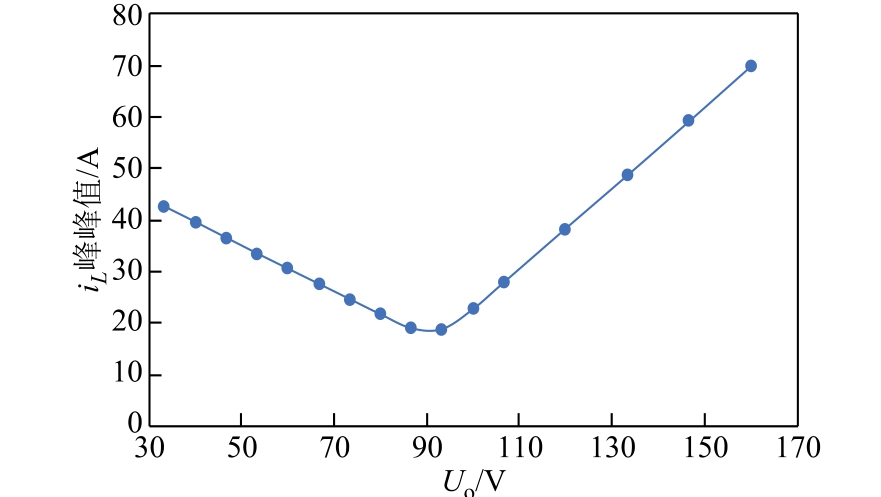
图9 整流模式下电感电流峰峰值随Uo 的变化曲线
Fig.9 The peak to peak of iL changing with Uo in rectifier mode
设定交流侧相电压有效值为80V，直流侧电压为180V，移相比δ=- 0.4。仿真结果如图10 所示，在逆变模式下，网侧电流与电压相差180°，且网侧电流THD 为1.83%，直流侧输出电压电流波形平稳，输出电压纹波约为0.58%，即在逆变模式下，同样具有良好的输入输出性能。因此，采用本文所提出控制策略可以实现功率的双向传输，且可以实现良好的电能质量及稳定的直流侧电压、电流。
图10 逆变模式下的仿真结果
Fig.10 Simulation results in inverter mode
在逆变模式下设定网侧电压幅值Ui=113V，移相比δ=- 0.4。将Uo 从33.3V 一直增大到160V，进行了电感电流峰峰值的仿真计算，仿真结果如图11 所示。
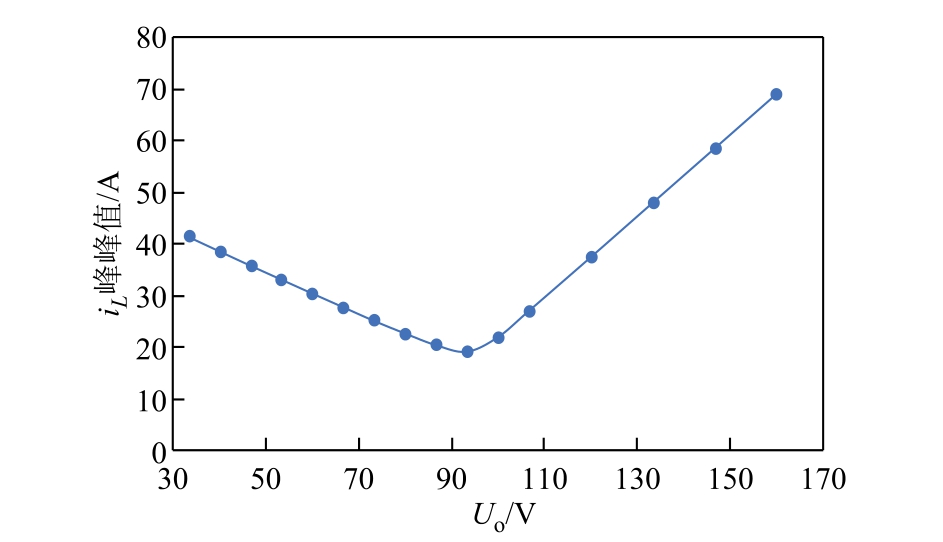
图11 逆变模式下电感电流峰峰值随Uo 的变化曲线
Fig.11 The peak to peak of iL changing with Uo in inverter mode
为了进一步验证本文所提出控制策略在减小电流应力方面的效果，将本文控制策略与文献[17]提出的“后级电路移相、前后级电路同步”控制策略进行了仿真对比分析。分别考虑整流模式和逆变模式下，电感电流峰峰值随直流侧电压变化的特性。
图12 为整流模式下两种控制策略的电感电流峰峰值随直流侧电压Uo 的变化曲线。其中，实线为本文控制策略的仿真结果，虚线为文献[17]控制策略仿真结果。由图12 可以看出，两种控制策略的电感电流峰峰值变化曲线均呈先减小后增大的趋势，但曲线斜率和对应的电感电流峰峰值略有不同。
图12 整流模式下两种控制策略对比（仿真结果）
Fig.12 Comparison of simulation results of two control strategies in rectifier mode
图13 为逆变模式下两种控制策略的电感电流峰峰值随直流侧电压Uo 的变化曲线。其中，实线为本文控制策略的仿真结果，虚线为文献[17]策略的仿真结果。可以看出，两种控制策略的电感电流峰峰值变化曲线均呈先减小后增大的趋势，但曲线斜率和对应的电感电流峰峰值略有不同。对比可得，
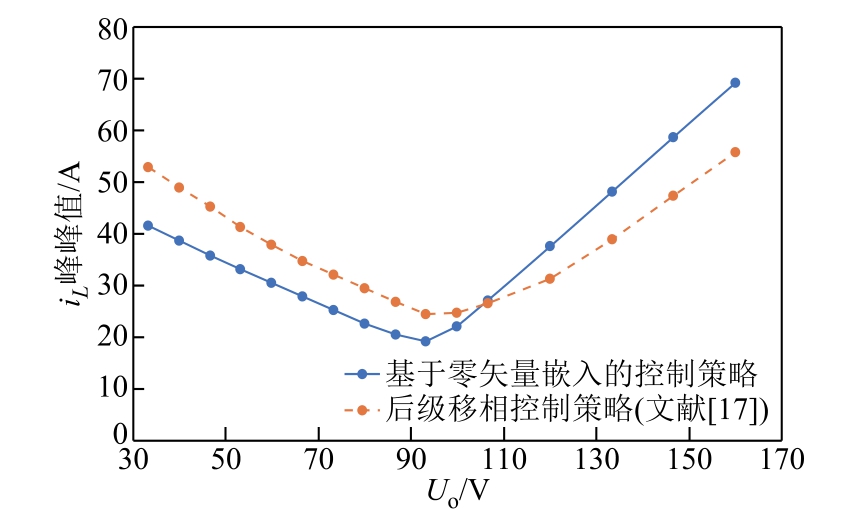
图13 逆变模式两种方法对比（仿真结果）
Fig.13 Comparison of simulation results of two control strategies in inverter mode
为验证所提出控制策略的可行性与有效性，搭建了一台2.2kW 的双向隔离型AC-DC 矩阵变换器的实验样机，如图14 所示。根据变换器的工作电压，前后级变换电路采用宽禁带器件SiC MOSFET，型号为 C3M0075120J ； 变换器控制器采用TMS320F28335PGFA 型DSP 芯片作为主控制器，进行各电压电流采集、判断扇区号、计算控制脉宽等；DSP 的输出信号送入 EPM1270T144C5N 型CPLD，进行逻辑解码和生成死区时间，实现安全换流，并根据各个故障信号进行保护逻辑处理。
图14 实验平台
Fig.14 Photo of the experimental platform
设定交流侧相电压有效值为80V，直流侧电压为180V，δ =0.4，进行实验验证。实验结果如图15所示，网侧输入电流和电压相位基本相同，测得功率因数cosφ =0.976。网侧电流三相平衡，正弦度良好，THD=2.25%，谐波含量很小。直流侧电压纹波为2.56%，对输出电压的控制性能良好。
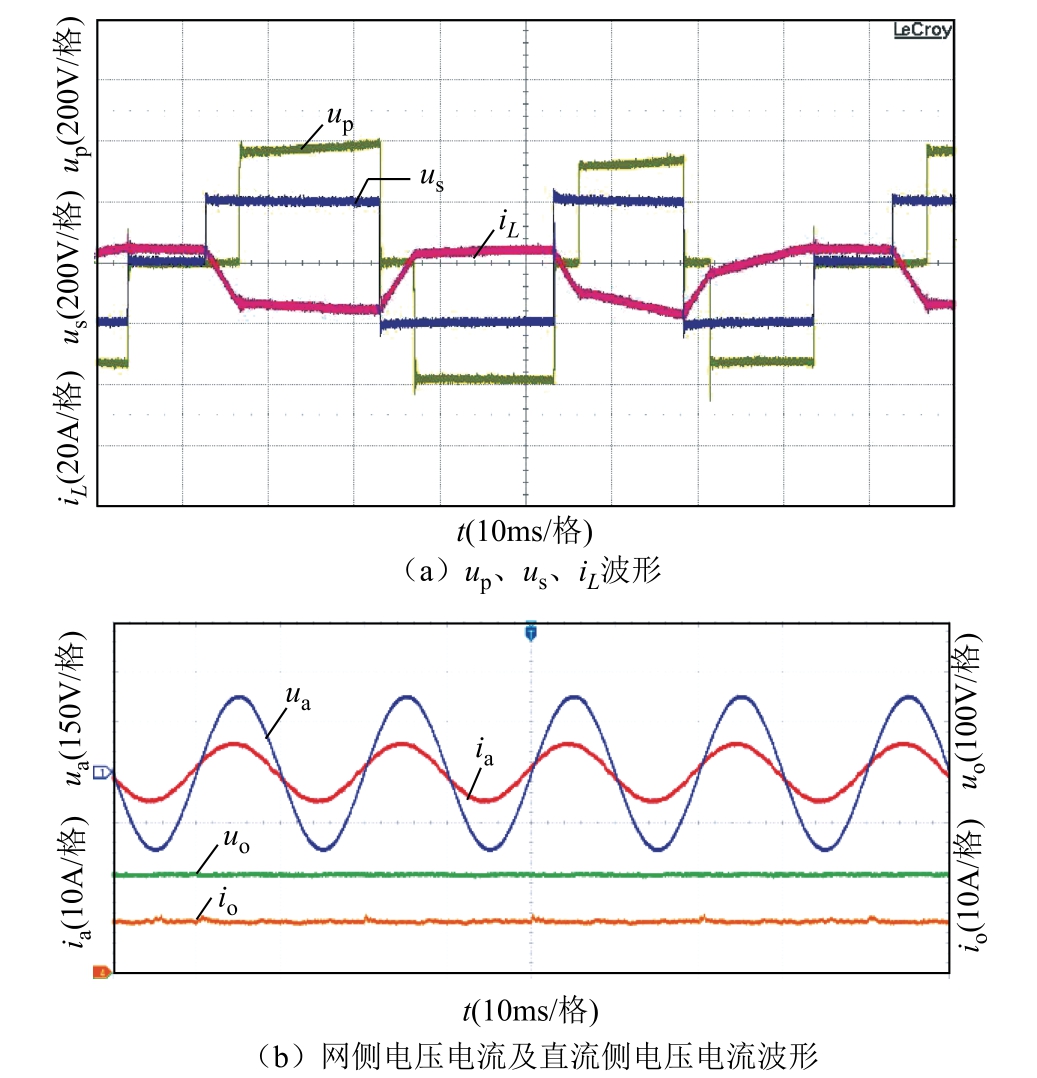
图15 整流模式下的实验结果
Fig.15 Experimental results in rectifier mode
与仿真条件相同，在整流模式下设定网侧电压幅值Ui=113V，通过只改变直流侧电压Uo，将Uo 从33.3V 一直增大到160V，测试电感电流峰峰值，实验结果如图16 所示。
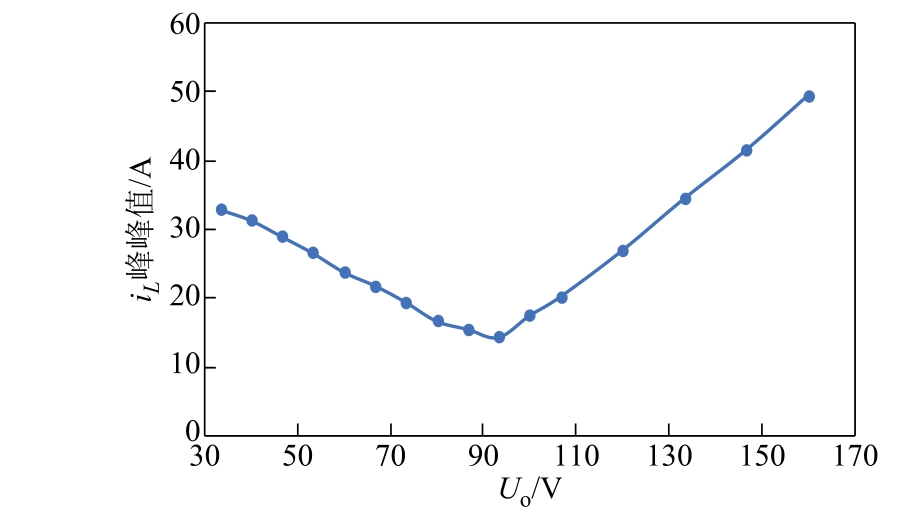
图16 整流模式下电感电流iL 峰峰值随Uo 的变化曲线
Fig.16 The peak to peak of iL changing with Uo in rectifier mode
设定交流侧相电压有效值为80V，直流侧电压为180V，δ=-0 .4，进行实验验证。实验结果如图17 所示，网侧输入电流和电压相位相反，测得功率因数cosφ=-0.976。网侧电流三相平衡，正弦度良好，THD=3.79%，谐波含量很小。直流侧电压纹波为3.45%，对输出电压的控制性能良好。
图17 逆变模式下的实验结果
Fig.17 Experimental results in inverter mode
与仿真条件相同，在逆变模式下设定网侧电压幅值Ui=113V，移相比δ =-0 .4，将Uo 从33.3V 一直增大到160V，测试电感电流峰峰值，实验结果如图18 所示。
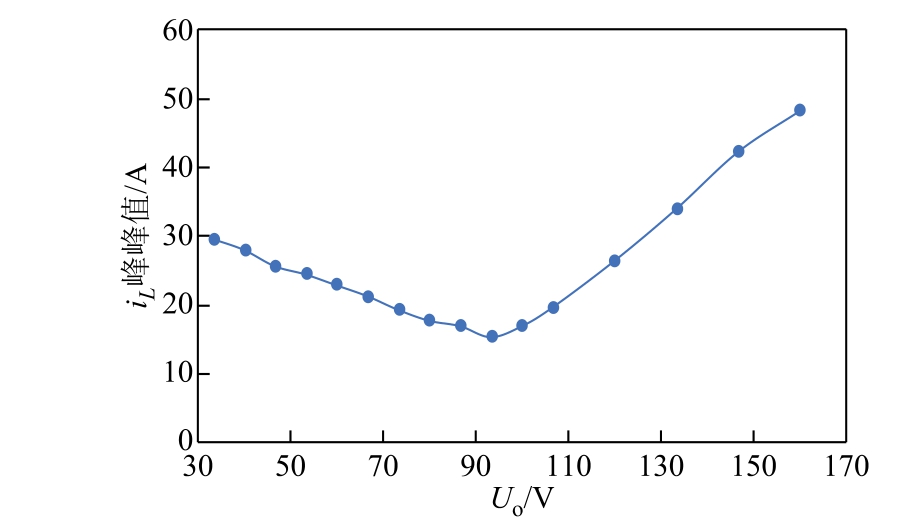
图18 逆变模式下电感电流iL 峰峰值随Uo 的变化曲线
Fig.18 The peak to peak of iL changing with Uo in inverter mode
与仿真工况相同，将本文控制策略和文献[17]控制策略在整流模式和逆变模式下，测试电感电流峰峰值随直流侧电压变化的实验结果，并进行对比分析。
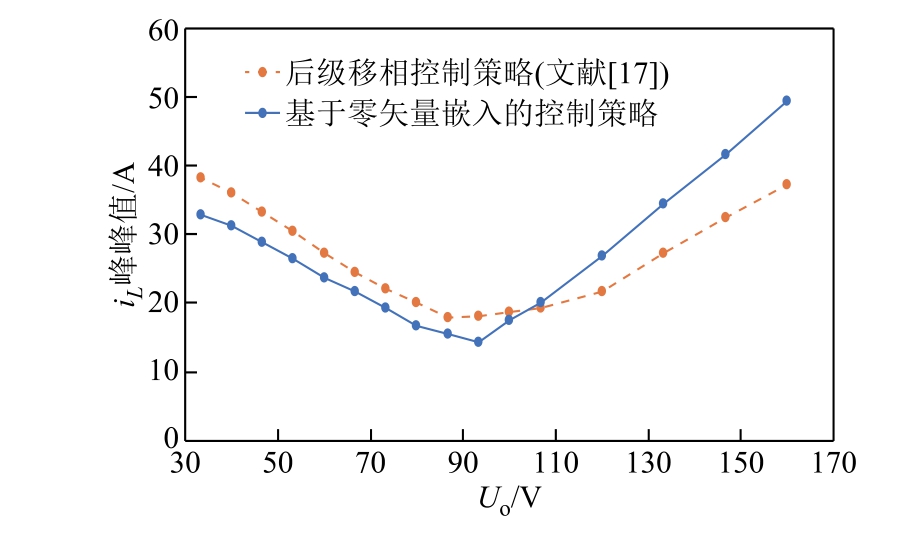
图19 整流模式两种方法对比（实验结果）
Fig.19 Comparison of experiental results of two control strategies in rectifier mode
图20 逆变模式两种方法对比（实验结果）
Fig.20 Comparison of experiental results of two control strategies in inverter mode
本文提出了一种基于零矢量嵌入的双向隔离型AC-DC 矩阵变换器分段同步控制策略。仿真和实验表明该控制策略具有如下优势：
1）网侧电流正弦度高，功率因数接近1。
2）直流侧电压、电压平滑稳定且纹波小。
综上所述，采用本文提出的控制策略可实现双向隔离型AC-DC 变换器功率的双向传输，不仅能够保证良好的输入输出性能，而且在较低输出电压范围内具有更小的电感电流应力，有助于降低器件损耗，提高变换器效率，并提升系统可靠性。
[1] 刘晓飞, 张千帆, 崔淑梅. 电动汽车 V2G 技术综述[J]. 电工技术学报, 2012, 27(2): 121-127.Liu Xiaofei, Zhang Qianfan, Cui Shumei. Review of electric vehicle V2G technology[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 121-127.
[2] Singh A K, Das P, Panda S K. Novel switching scheme for matrix based isolated three phase AC to DC conversion[C]//IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX,USA, 2015: 3324-3329.
[3] 齐磊, 杨亚永, 孙孝峰, 等. 一种电流型高增益双向DC-DC 变换器[J]. 电工技术学报, 2019, 34(18):3797-3809.Qi Lei, Yang Yayong, Sun Xiaofeng, et al. A currentfed high step-up bidirectional DC-DC converter[J].Transactions of China Electrotechnical Society, 2019,34(18): 3797-3809.
[4] 邢毅川, 牟宪民, 齐琛. 一种新的单相-三相矩阵变换器调制策略[J]. 电工技术学报, 2015, 30(8): 90-96.Xin Yichuan, Mu Xianmin, Qi Chen. A new modulation strategy for single-phase to three-phase matrix converter[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 90-96.
[5] Su Lining, Qin Xiaohui, Zhang Shang, et al. Fast frequency response of inverter-based resources and its impact on system frequency characteristics[J]. Global Energy Interconnection, 2020, 3(5): 475-485.
[6] Afsharian J, Xu Dewei, Wu Bin, et al. The optimal PWM modulation and commutation scheme for threephase isolated buck matrix type rectifier[J]. IEEE Transactions on Power Electronics, 2017, 33(1): 110-124.
[7] Fang Fanxiu, Li Yunwei. Modulation and control method for bidirectional isolated AC/DC matrix based converter in hybrid AC/DC microgrid[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE),Cincinnati, OH, USA, 2017: 37-43.
[8] Varajão D, Rui E A, Miranda L M, et al. Modulation strategy for a single-stage bidirectional and isolated AC-DC matrix converter for energy storage systems[J].IEEE Transactions on Industrial Electronics, 2017,65(4): 3458-3468.
[9] 程红, 高巧梅, 朱锦标, 等. 基于双重移相控制的双向全桥DC-DC 变换器动态建模与最小回流功率控制[J].电工技术学报, 2014, 29(3): 245-253.Cheng Hong, Gao Qiaomei, Zhu Jinbiao, et al.Dynamic modeling and minimum backflow power controlling of the bi-directional full-bridge DC-DC converters based on dual-phase-shifting control[J].Transactions of China Electrotechnical Society, 2014,29(3): 245-253.
[10] Lukas Schrittwieser, Michael Leibl, Johann W Kolar.99% efficient isolated three-phase matrix-type DAB Buck-Boost PFC rectifier[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 138-157.
[11] Matsui Yuto, Suzuki K, Takeshita T. High-frequency link AC/DC converter using matrix converter with soft-switching technique[C]//IEEE Energy Conversion Congress and Exposition, Cincinnati, OH, USA, 2017:1715-1722.
[12] 王天宇, 徐政, 姜红利, 等.电压匹配度对DAB 特性的影响及其优化控制方法[J].电气传动, 2019,49(9): 31-34.Wang Tianyu, Xu Zheng, Jiang Hongli, et al. Effects of voltage matching degree on DAB operating characteristics and its optimal control methods[J].Electric Drive, 2019, 49(9): 31-34.
[13] 张天晖. 双有源桥DC/DC 变换器多目标优化控制研究[D]. 武汉: 华中科技大学, 2019.
[14] 安峰, 杨柯欣, 王嵩, 等. 基于模型前馈的双有源全桥DC-DC 变换器电流应力优化方法[J]. 电工技术学报, 2019, 34(14): 2946-2956.An Feng, Yang Kexin, Wang Song, et al. Current stress optimized scheme with model-based feedforward for dual-active-bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2019, 34(14):2946-2956.
[15] 曾进辉, 孙志峰, 雷敏, 等. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J].电工技术学报, 2019, 34(12): 2507-2518.Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Global current stress analysis and optimal control strategy of dual-active full bridge converters based on dual phase shift control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2507-2518.
[16] Mei Yang, Liu Ziyu, Huang Weichao. A coordination control strategy for an isolated bidirectional AC/DC matrix converter[C]//2019 22nd International Conference on Electrical Machines and Systems(ICEMS), Harbin, China, 2019: 1-5.
Piecewise Synchronous Control Strategy of Bidirectional Isolated Matrix AC-DC Converter Based on Zero Vector Embedded
Abstract In this paper, a piecewise synchronous control strategy of the bidirectional isolated AC-DC matrix converter based on zero vector embedded is proposed. In this control strategy, a symmetrical double-line-voltage modulation is adopted for the front-stage three-phase to single-phase matrix converter (3-1MC), which improves the voltage transfer ratio; a complementary control is employed for the back-stage circuit full-bridge (FB) converter, which is simple and easy to implement.By embedding the zero vector into 3-1MC modulation, the 3-1MC and FB are piecewise synchronous,which enables the bidirectional power transfer. Simulation and experimental results verify that the isolated bidirectional AC-DC matrix converter features balanced sinusoidal currents at grid side,nearly unity input power factor, and stable DC output voltage/current with low ripples. The peak value of inductance current (current stress) decreases first and then increases with the increase of DC output voltage, which is at the minimum value while nUo=
U i . Hence, the bidirectional power flow and good input/output performances of the bidirectional isolated AC-DC converter can be ensured under the proposed control strategy. Compared with the traditional control strategy, the bidirectional isolated AC-DC matrix converter with the proposed control strategy has smaller inductance current stress in the lower DC voltage range, which helps to reduce device losses, enhance efficiency and improve system reliability.
梅 杨 女，1981 年生，博士，教授，研究方向为电力电子与电力传动。E-mail：meiy@ncut.edu.cn （通信作者）
许 策 男，1995 年生，硕士研究生，研究方向为力电子与电力传动。E-mail：1048085298@qq.com