0 引言
剩余电流保护装置(Residual Current Protection Device, RCD)[1]被广泛应用于末级电网,其主要作用是减小电器不正常接地及其他故障事故带来的危害,同时也作为预防生物触电的主要保护装置[2-5]。但运行结果表明,目前使用的剩余电流保护装置普遍存在误动、拒动现象。通过对剩余电流保护装置的保护特性研究发现,剩余电流保护装置检测到的剩余电流,受泄漏电流与触电电流相位差的影响,存在触电电流大于人体触电安全电流30mA 时,检测值仍小于整定值的拒动情况[6]。相关学者就此提出开发基于触电电流动作的新型剩余电流保护装置。
目前对生物触电事故的研究,主要集中于触电信号的特征识别及触电电流提取两个方面。最早李春兰等[7]提出利用神经网络模型检测触电电流,其将小波滤波后的触电信号在误差反向传播(Back Propagation, BP)神经模型下进行分离参数训练,提升了神经网络模型分离结果准确性。韩晓慧等[8-9]利用触电信号的统计特征参数,结合支持向量机提出了多种触电信号暂态特征识别及触电类型判断的检测方法。刘咏梅等[10]将标准支持向量机(Support Vector Machines, SVM)和神经网络结合,并提出触电融合判据,在较大程度上提升了单一回归预测方法的检测准确性。关海鸥等[11]利用特征频带的能量占比平均变化率,实现了触电事故的检测,同时利用小波变换结合量子神经网络算法对触电信号进行参数训练,成功实现了对触电事故类型的识别。夏兰兰等[12]利用混沌系统不同状态下的功率谱波峰数差别作为系统判据,实现了从总剩余电流中检测触电电流。关海鸥等[13]利用经验模态分解(Empirical Mode Decomposition, EMD)结合希尔伯特黄变换发现触电时刻剩余电流高频分量存在幅值突变,据此提出基于归一化预处理的生物触电时刻检测方法。李春兰等[14]提出基于局部均值分解构造虚拟通道,再结合盲源分离算法成功地从总剩余电流中分离出触电电流信号。上述针对触电特征识别和触电电流检测的研究算法复杂度高,尚无法满足触电事故对保护装置实时动作的要求,因此目前仍仅限于理论研究方面。
循环平稳理论最早由W. A. Gardner[15]提出,国内学者罗利春[16]、王洪[17]就其数学原理及物理意义做了相关研究,因其具有在展示信号傅里叶频率的同时提供一个信号广义倍频与自混频的优势,被广泛应用于通信信号的检测和调制识别[18],近年来信号一阶、二阶循环平稳特性的研究被用于机械故障特征识别[19]和医学信号的特征识别[20]。由于个体差异,不同触电个体的触电信号频谱图存在明显差异;即使同一个体在不同时间触电,其相关频谱差异仍然存在,传统频谱分析方法[21]很难提取触电时刻的特殊频率或频段来识别触电事故的发生与否。鉴于此,本文提出利用循环谱相关理论对触电信号进行循环频谱特性分析,提取生物触电特征,为研发基于触电电流动作的剩余电流保护装置提供理论依据。
1 循环谱理论
有学者将非平稳信号中按时域统计特征表现出周期特征的一类信号定义为循环平稳信号。按统计量阶数循环平稳理论又分为低阶循环平稳(一阶、二阶)和高阶循环平稳[22],循环谱相关理论是在信号的二阶统计量基础上发展起来。
1.1 循环自相关函数
设随机过程x(t)为一广义循环平稳过程,满足周期为T0,则其关于时间平均的自相关函数为

式中,n 为遍历循环周期;t 为时间参数;τ 为延时参数;*表示复共轭。对式(1)按Fourier 级数展开有

1.2 循环谱密度函数
维纳辛钦定理指出对信号的自相关函数的傅里叶变换就是信号的功率谱函数,同样对循环自相关函数进行傅里叶变换得到信号的循环功率谱密度为[23]
1.3 循环谱密度估计
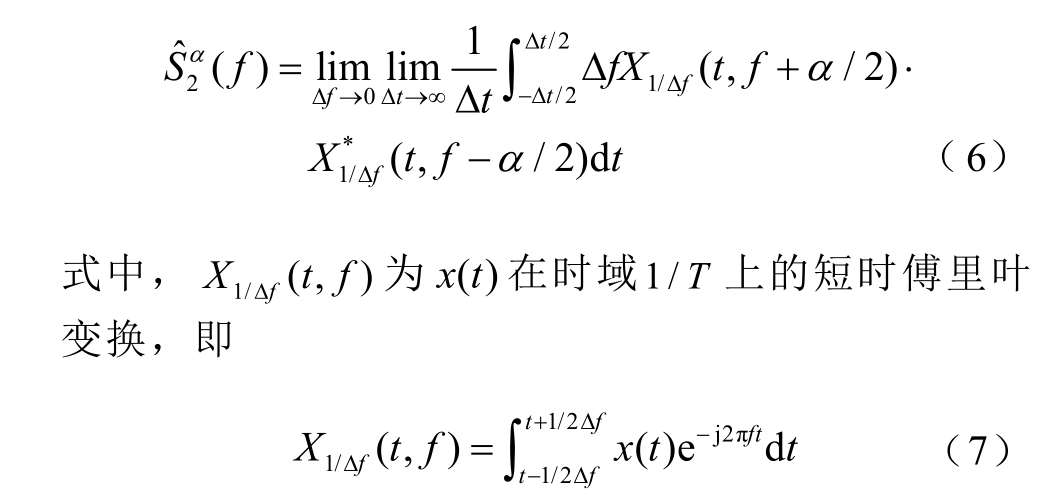
对源信号及其时延信号进行互谱分析可得信号循环谱估计式为样频率为10kHz 的故障滤波器详细记录了不同体重动物体(猪)在不同时刻触电时的触电信号。原始信号如图2 所示。

图2 原始触电信号
Fig.2 Original electric shock signal
式(6)中,积分项为信号循环周期图[24]。实际应用中对其按式(6)进行时域平滑,就是信号的时域平滑周期图循环谱密度估计式。
2 基于循环谱特征的触电时段特征提取
2.1 原始触电信号
本文所分析触电信号来源是从课题组前期所搭建生物触电物理试验平台获得[14,25],其电路原理图如图1 所示。
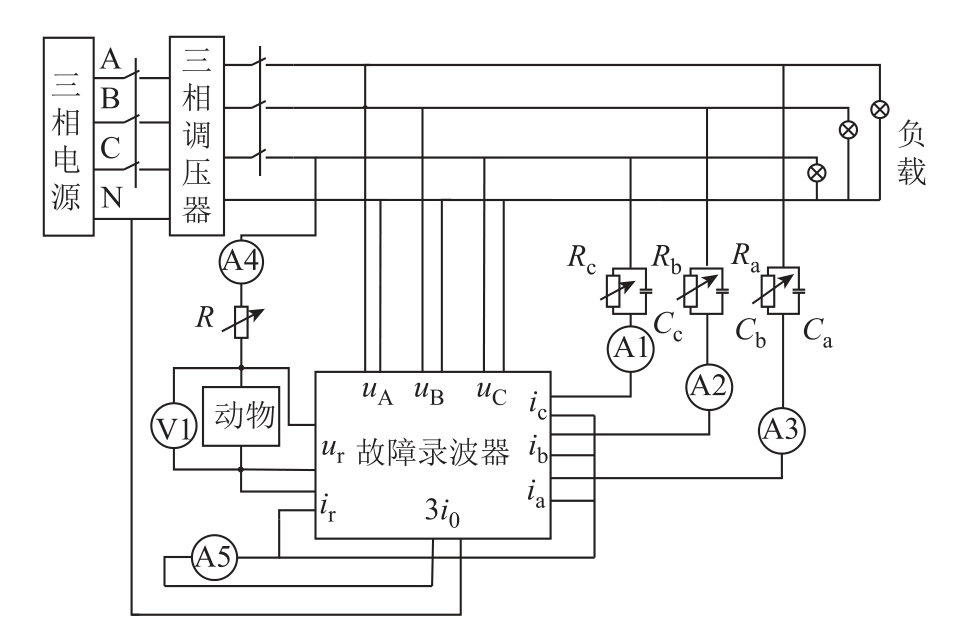
图1 生物触电实验电路原理图
Fig.1 Schematic diagram of bioelectric shock experiment circuit
图1 中分别用灯箱模拟三相负载,可变电阻、电容并联结构模拟三相对地分布阻抗。电流表A1、A2、A3 分别记录三相正常泄漏电流,A4 记录了流过动物体的触电电流,A5 记录总剩余电流,通过采
图2 为某次触电试验获得的两种电路结构下的包含触电时刻的剩余电流信号和触电电流信号,其中剩余电流为正常泄漏电流和触电电流矢量和,截取共计1 200 个采样点,触电发生在0.06s 时刻。
2.2 触电信号循环谱分析
基于循环谱相关分析法对信号采样点数及信号广义平稳特性的需求,选取剩余电流信号触电前、后各三个周期的600 个采样点,通过对比触电前、后剩余电流信号循环谱差异,实现从剩余电流中提取触电特征。
对图2 展示的触电信号进行时域平滑周期图谱相关计算,得到各信号循环频谱三维图,保留循环频谱三维图中主要线谱成分的三维图谱,如图3 所示。标注alpha/Hz 的轴代表经过时间延时和平滑处理后的信号循环频率。
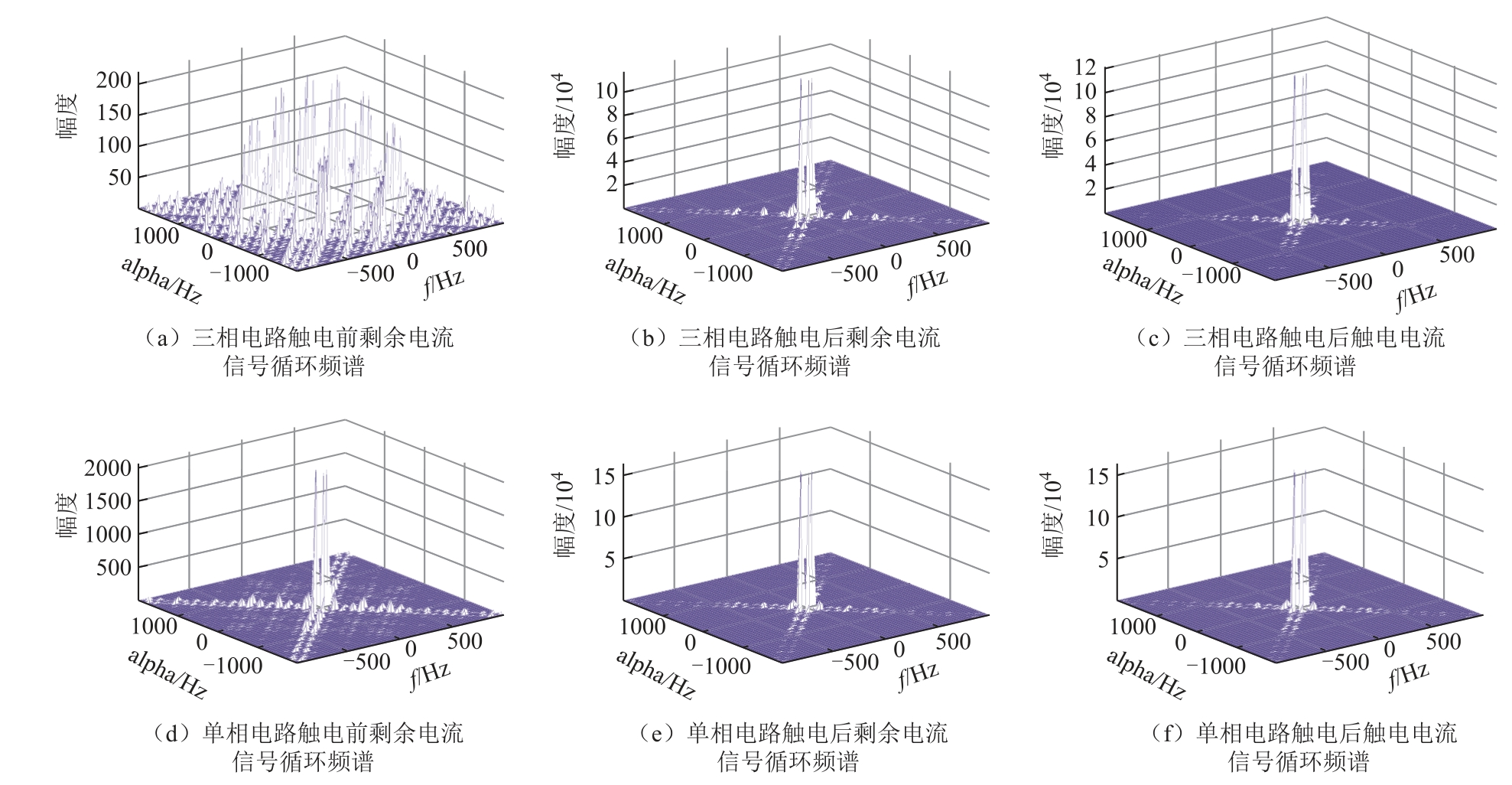
图3 触电信号循环频谱三维图
Fig.3 3D diagram of the cycle spectrum of electric shock signal
分析图3 可知:①各信号在循环三维图中均表现出线谱特征,即各信号具有二阶循环平稳特性[14]。②三相电路时,触电前正常泄漏电流的线谱分布较为密集,且各线谱幅值分布较为均匀;触电后剩余电流信号线谱表现为某一线谱含量极高,且触电后剩余电流图谱与触电电流图谱差异较小。③单相电路时,触电前剩余电流与触电后剩余电流主要线谱并无明显差异,其变化主要为高频成分对应的广义倍频与混频在频谱图中占比差异。由于触电信号中谐波成分的复杂性,对触电信号进行循环谱计算过程中涉及信号自乘,使其估计结果除信号原始成分外,同时展示了各成分与其他成分的广义倍频及混频成分,仅通过对比触电信号循环频谱三维图难以直观提取触电特征。
2.3 基于循环谱切片分析的触电特征提取
对信号的循环谱分析往往涉及切面分析,因其能较好地展示信号在各成分的细节特征。因此为进一步分析触电信号的差异寻找触电特征,对图3 的触电信号三维图进行切片分析。图4、图5 分别为单相电路和三相电路触电前、后剩余电流中频率f分别为50Hz、150Hz、250Hz、350Hz、450Hz 成分对应的alpha 切片图。
分析图4、图5 可知:①单相电路触电前、后剩余电流各频率对应的截面图中出现的线谱基本一致,各频率分量对应的循环频率截面最高线谱分别为200Hz、400Hz、400Hz、800Hz、800Hz 的循环频率;②三相电路中触电前剩余电流切片图中的线谱较触电后的含量明显复杂;③触电前三相电路各频率分量对应的循环谱切面较单相电路相比出现的线谱明显密集,触电后两种电路下的各频率分量对应的线谱基本一致,且触电后主要循环频率的幅度均明显上升;④循环频谱差异在f=150Hz 对应的切片上得到了表现,具体表现为触电后循环频率1 200Hz的线谱占比明显低于触电前。
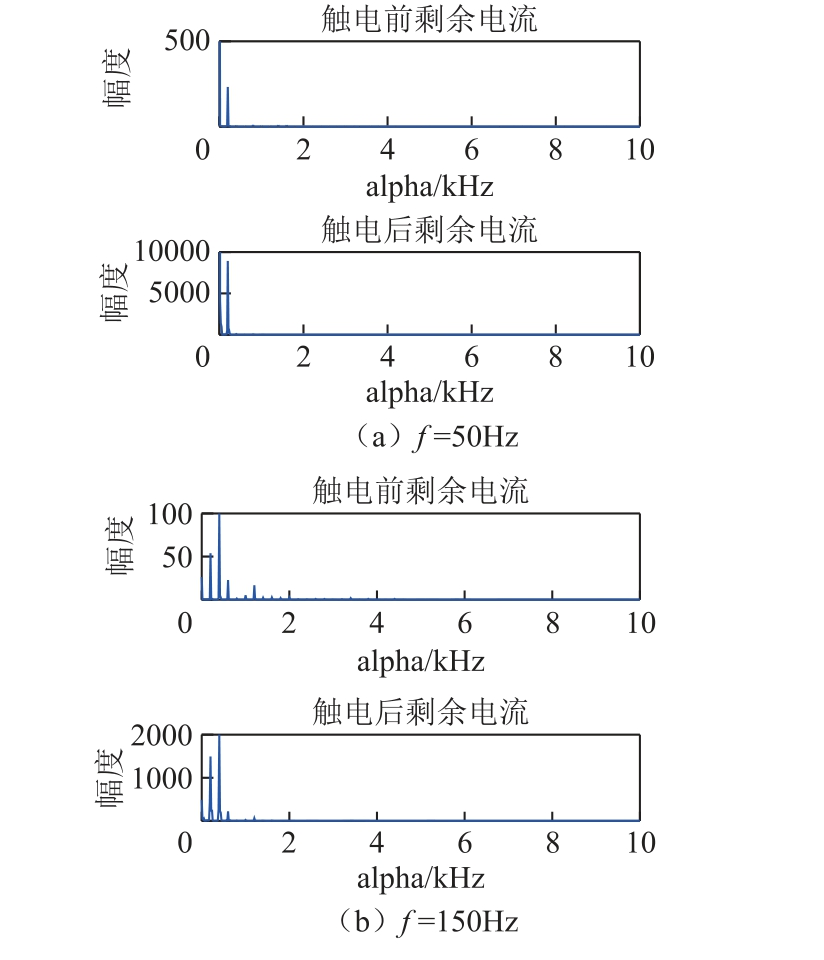
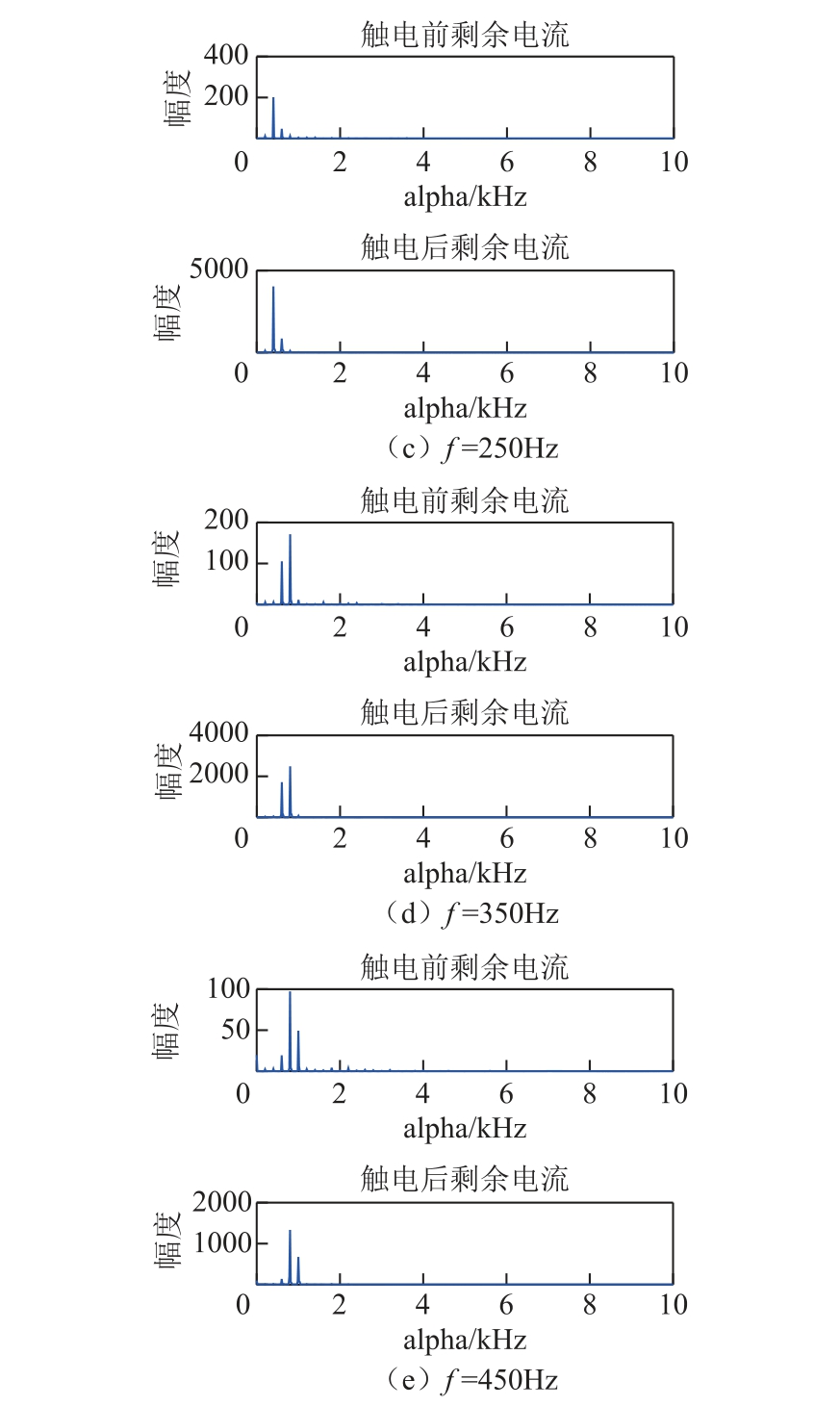
图4 单相电路时剩余电流循环谱切片图
Fig.4 Slice spectral of residual current in a single phase circuit
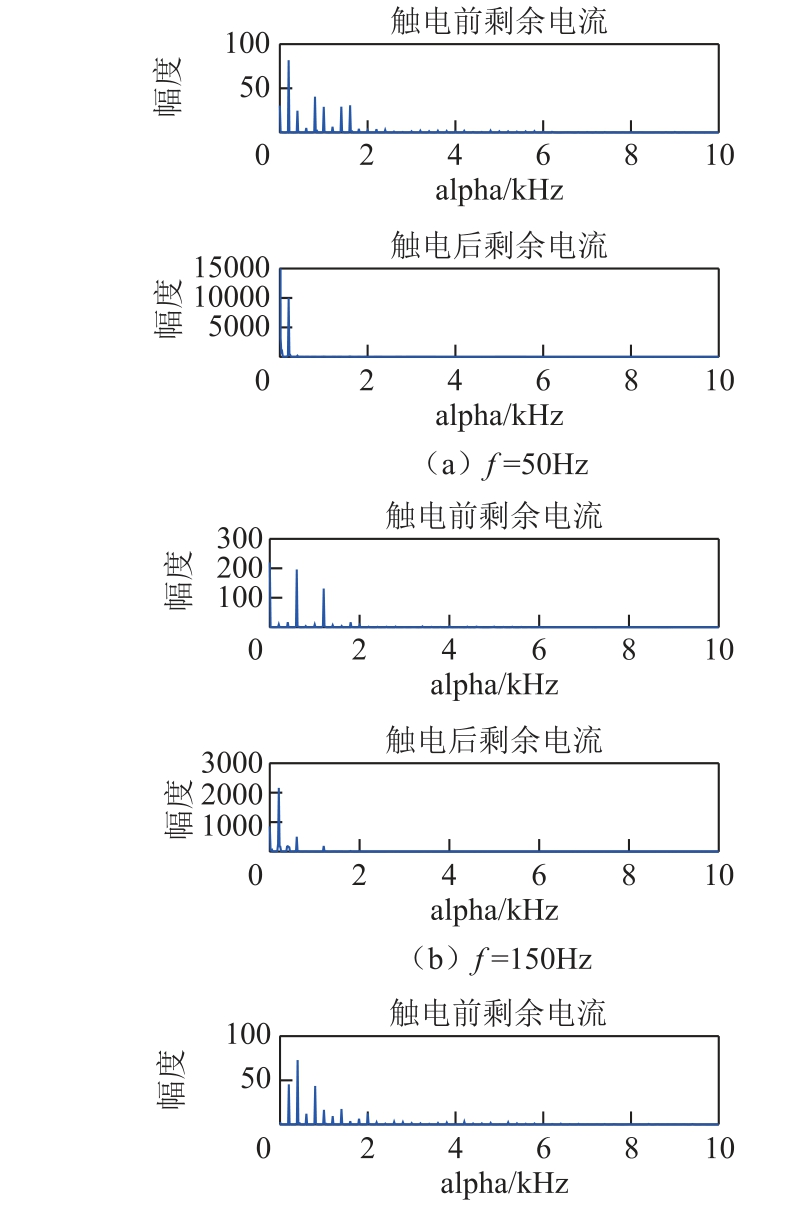
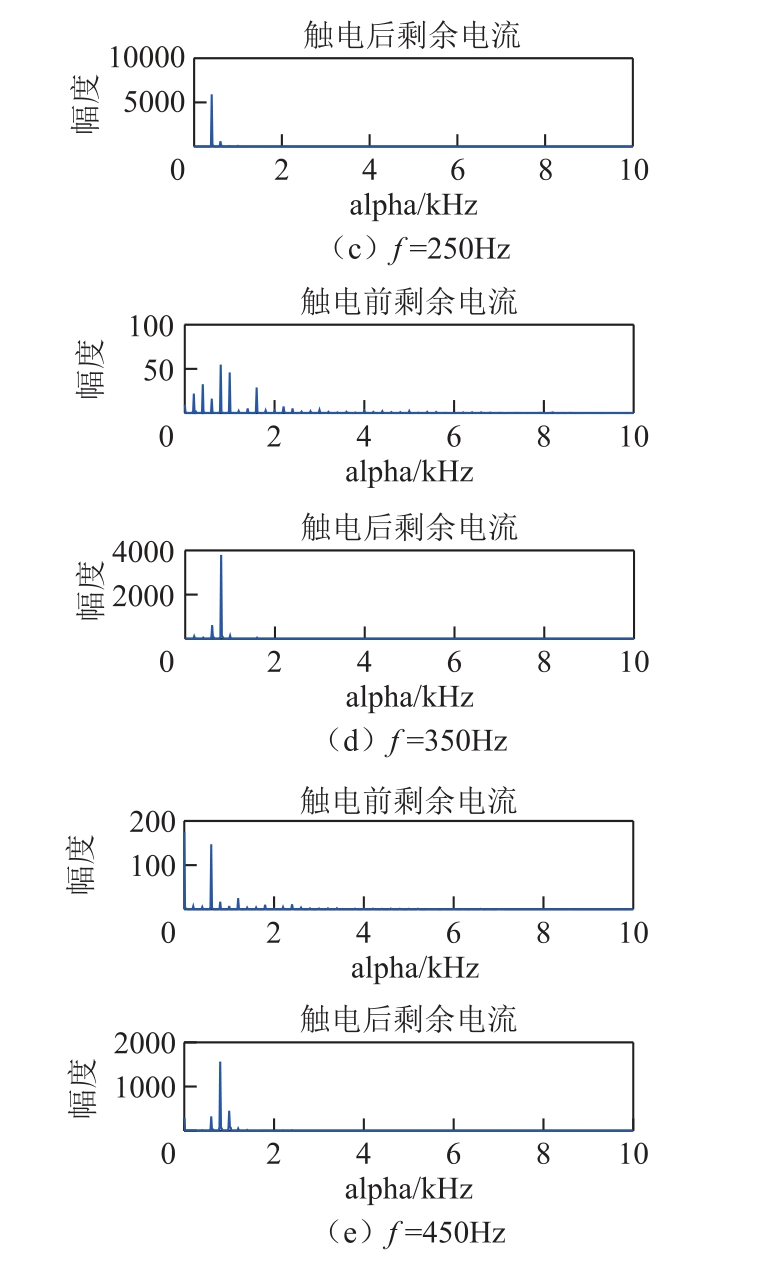
图5 三相电路时剩余电流循环谱切片图
Fig.5 Slice spectral of residual current in three-phase circuit
为研究触电前、后剩余电流在f=150Hz 下的线谱差异与触电现象的相关性,分别对课题组在三相电路和单相电路下通过触电试验获得的触电信号进行循环谱切片分析,其f=150Hz 对应的循环谱切片图如图6 所示。
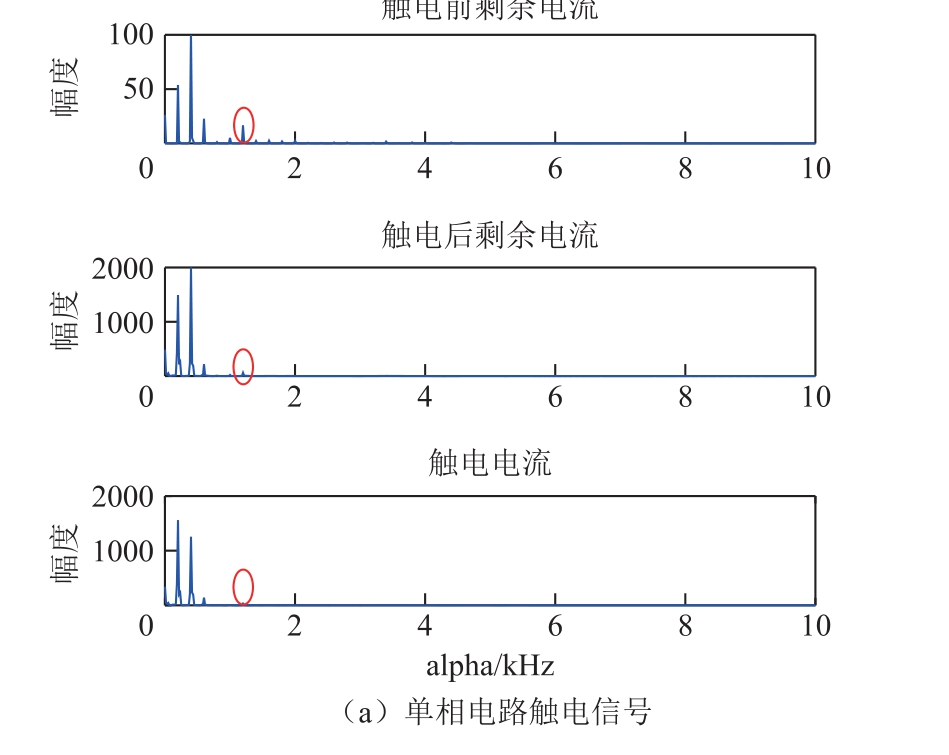
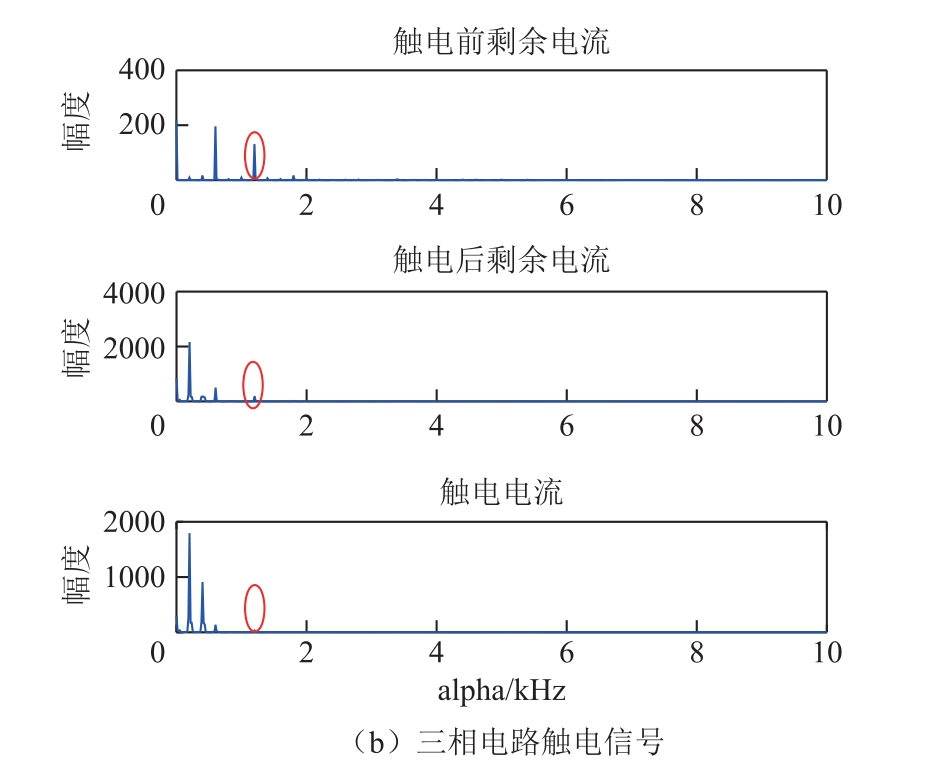
图6 触电信号特征循环谱切片图
Fig.6 Characteristic slice spectral of electric shock signal
分析图6 可知:触电电流的特征切面对应的特征循环频率(alpha=1 200Hz)线谱明显低于剩余电流触电前、后对应的循环频率的线谱,且触电后剩余电流的特征线谱比例也明显低于触电前,可考虑为触电现象造成。
为利用线谱差异描述触电现象,本文定义特征循环频率占比η 为
式中,Pα=1 200为剩余电流中150 Hz 成分对应的循环谱切面中alpha=1200Hz 线谱幅度;P 为对应切面中最高线谱幅度、次高线谱幅度、第三高线谱幅度和所有线谱幅度和之一。
考虑触电信号的随机性,单一特征难以完整描述触电现象,因此本文定义四种与特征循环频率相关的触电特征,对150 组单相电路触电试验获得的剩余电流及45 组三相电路触电试验获得的剩余电流循环谱特征计算结果见表1。
表1 触电前、后剩余电流循环谱特征
Tab.1 Before and after electric shock the cycle spectrum characteristic of residual current
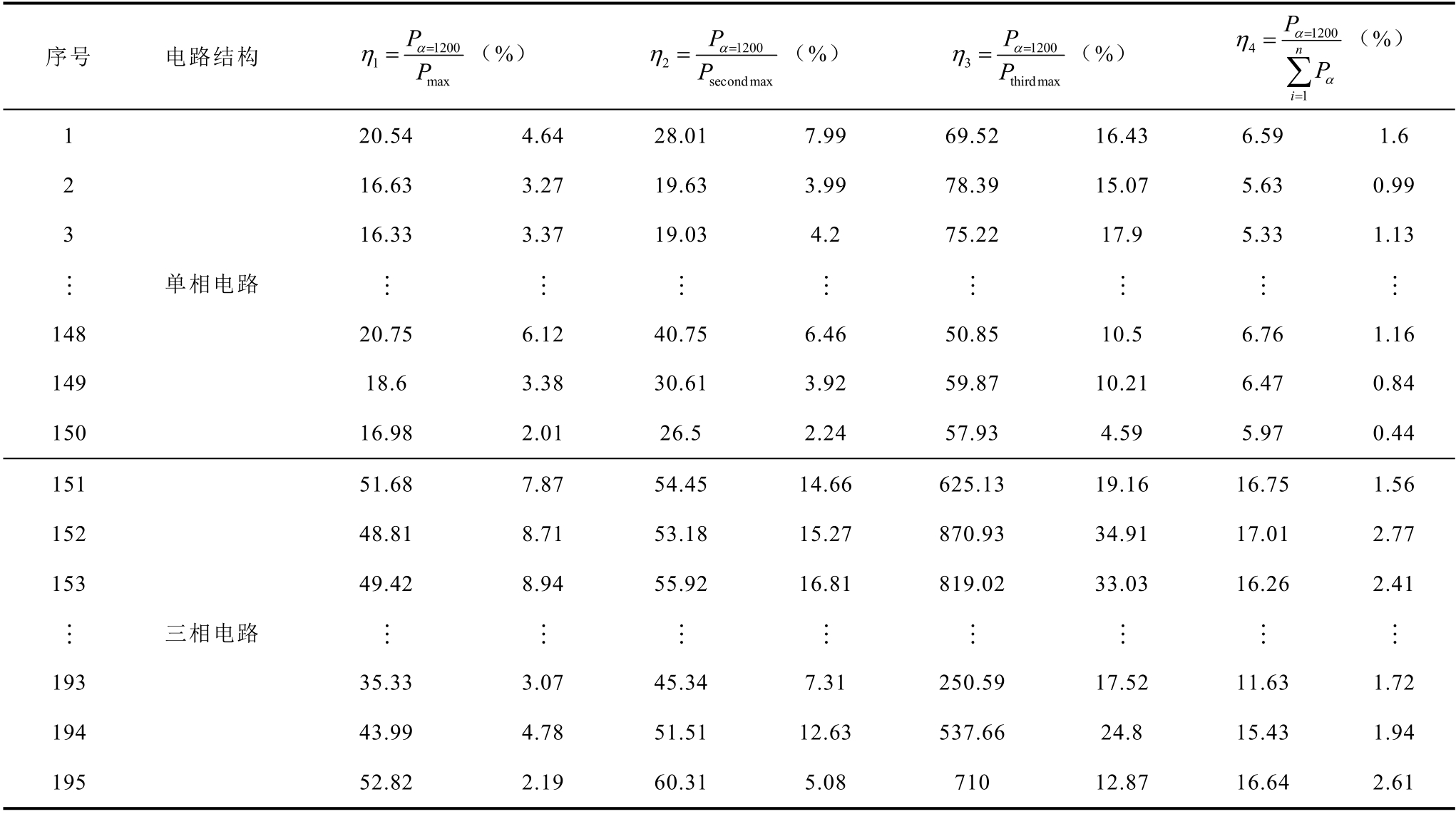
序号 电路结构P Pα η==(%)1200 1 max PP η==(%)α1200 2 secondmax PPα η==(%)1200 3 thirdmax P η=α1200 4=∑n (%)P α i=1 1 20.54 4.64 28.01 7.99 69.52 16.43 6.59 1.6 2 16.63 3.27 19.63 3.99 78.39 15.07 5.63 0.99 3 16.33 3.37 19.03 4.2 75.22 17.9 5.33 1.13⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮148 20.75 6.12 40.75 6.46 50.85 10.5 6.76 1.16 149 18.6 3.38 30.61 3.92 59.87 10.21 6.47 0.84 150 16.98 2.01 26.5 2.24 57.93 4.59 5.97 0.44 151单相电路51.68 7.87 54.45 14.66 625.13 19.16 16.75 1.56 152 48.81 8.71 53.18 15.27 870.93 34.91 17.01 2.77 153 49.42 8.94 55.92 16.81 819.02 33.03 16.26 2.41⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮193 35.33 3.07 45.34 7.31 250.59 17.52 11.63 1.72 194 43.99 4.78 51.51 12.63 537.66 24.8 15.43 1.94 195 52.82 2.19 60.31 5.08 710 12.87 16.64 2.61三相电路
表1 中,序号1~150 对应单相电路触电前、后150 组剩余电流信号相关循环谱特征计算结果,序号151~195 为三相电路触电前、后相关循环谱特征计算结果,各组循环谱特征的第一列对应触电前剩余电流循环谱特征,第二列对应触电后循环谱特征。分析表1 可知:触电后剩余电流循环谱特征与触电前相比均呈下降趋势。
2.4 多维循环谱组合特征
为提高识别准确率,减小识别误差,本文同时研究了不同维度、不同特征组合情况下的触电特征,以寻求最优触电事故判据。对提出的四种触电特征两两随机组合得到新的六组触电特征,三种触电特征随机组合条件下得到四种新的触电特征,其组合结果见表2。
表2 不同维度下的组合触电特征
Tab.2 Combined electric shock characteristics in different dimensions

特征维度 组合触电特征1 1η 、 2η 、 3η 、 4η 2 η1 2η 、 η1 3η 、 η1 4η 、 η 2 3η 、 η 2 4η 、 η 3 4η 3 1 2 3 ηη η 、 1 2 4 ηη η 、 1 3 4 ηη η 、 2 3 4 η η η ηη η η 4 1 2 3 4
3 基于K-means 聚类的触电判据提取
3.1 K-means 聚类算法
聚类分析是利用计算机进行数据处理的一类无监督学习算法[26]。其中K-means 聚类算法最早由学者MacQueen 提出[27],该算法能在给定聚类簇数下,通过随机选取K 个聚类中心样本,并通过计算簇间距离测度的平均大小确定算法的中止目标,自适应调整中心样本,被广泛应用于数理统计、聚类分析、故障识别、深度学习等领域[28-29]。算法原理如下:
对确定数据集Xk,N,其中k 表示样本属性,N 表示样本数量,随机样本与给定聚类中心样本关系由距离相似度度量,常用欧式距离度量公式为
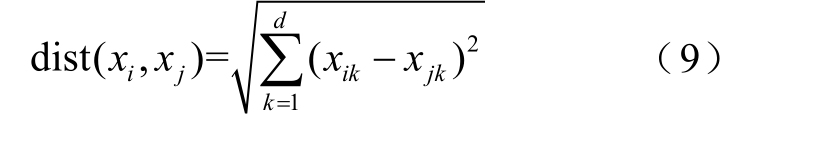
式中,i、j 为不同数据样本。欧式距离越小表示两个样本的相似度越大,差异越小,对应将随机样本与聚类中心划分为同簇。
对聚类性能的评价准则采用误差二次方和,即同一类各样本到聚类中心的距离最小。式中,p 为同类样本中的数据;mk 为该次计算的聚类中心。
其算法步骤为:
1)随机选定用于计量距离相似度的初始聚类中心,其个数由K 值决定。
2)按式(9)计算样本到聚类中心的欧式距离,并将其分配到距离最近的类。
3)按式(10)计算同类数据到聚类中心的误差二次方和。
4)聚类中心的更新,按当前输出各类样本的质心作为新的聚类中心。
5)返回步骤2)、步骤3),直到样本到所选聚类中心的评价指标最小。
6)输出所有数据所属类和聚类中心。
3.2 基于K-means 聚类的触电特征分析
为自动识别触电事故,进一步对本文所定义的触电特征进行聚类分析,提取触电识别判据,并验证其识别触电事故的有效性。按2.4 节所提议组合方法对表1 展示的两种电路结构下计算得到的触电前、后剩余电流循环谱特征进行聚类分析,结果分别如图7、图8 所示。为便于聚类分析,对一维数据进行了升维处理,其高维数据由正态分布随机产生,考虑数据大小对欧式距离测度的影响,本文在两种电路结构下的正态分布期望取值为0,标准差在单相电路时取值为0.05、三相电路时取值为0.5。

图7 单相电路时剩余电流组合循环谱特征聚类分析
Fig.7 Cluster analysis of residual current combined cyclic spectrum characteristics in single-phase circuit

图8 三相电路时剩余电流组合特征聚类分析
Fig.8 Cluster analysis of residual current combination features in three-phase circuit
图7、图8 中分别展示了两种电路结构时单一特征以及二维、三维、四维组合特征下的最佳聚类结果,其中聚类1 对应正常情况下的剩余电流特征,
聚类2 对应触电事故下的剩余电流特征,聚类中心为所提取的触电特征点,误差表示聚类结果与实际情况的差异。进一步分析可知:
1)单相电路情况下,一维特征时最佳聚类划分为特征3,其正确率为91.78%,聚类中心分别为触电前剩余电流的[58.286]和触电后剩余电流[11.753]。二维组合特征时特征2 与特征3 的组合特征为最佳聚类特征,其正确率为92.67%,聚类中心分别为触电前[20.597,57.682]和触电后[4.102,11.387]。三维组合特征时最佳组合为特征2、特征3、特征4,其聚类正确率为94.67%,聚类中心为触电前[20.597,57.682,4.773]和触电后[4.102,11.387,0.923]。四维组合特征时的识别率为94%,其聚类中心为触电前[14.378,20.597,57.862,4.773]和触电点后[3,4.102,11.387,0.921]。其中三维特征时聚类正确率最高。
2)三相电路时聚类分析的准确率并没有随组合维度的增加而增大,其中一维特征4 的聚类正确率最高达到了100%,其聚类中心为触电前剩余电流[16.136]和触电后剩余电流[2.197]。
3)各维度最优聚类结果中误差项均表现为对触电前正常剩余电流的误判。
由以上结论进一步提出触电识别方法为:单相电路时对提取的循环频谱特征2、3、4 分别计算其与触电后剩余电流聚类中心、正常剩余电流聚类中心的欧式距离,将其归属为欧式距离上较小的一类;三相电路提议循环谱特征为特征4。
3.3 改进的聚类分析
由循环谱方法提取的正常剩余电流特征在空间分布上较为离散,导致其在欧式距离上更加靠近触电后剩余电流聚类中心造成误判。为提高识别准确率,分别计算单相电路时触电前、后共计300 组剩余电流循环谱特征2、3、4 到3.2 节提取的两类聚类中心的欧式距离,计算结果如图9 所示。
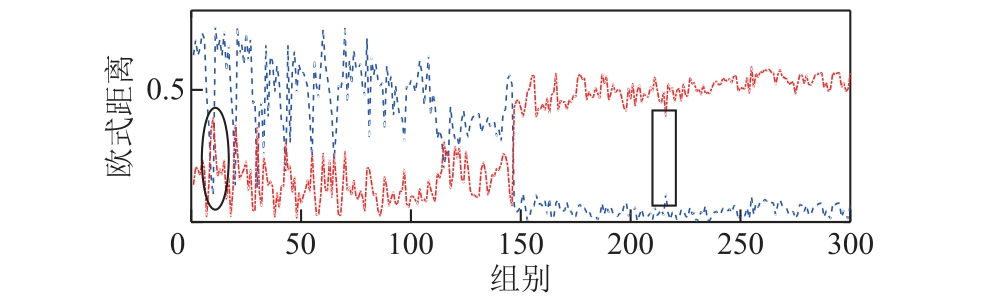
图9 单相电路时组合特征欧式距离计算结果
Fig.9 Calculation results of combined characteristic Euclidean distance for single-phase circuit
图9 中,前、后150 组分别为触电前、触电后剩余电流循环谱特征分别到正常剩余电流聚类中心、触电后剩余电流聚类中心的欧式距离。进一步分析可知,理想情况下前150 组循环谱特征到正常剩余电流聚类中心的距离应恒大于到触电后剩余电流聚类中心的距离,后150 组循环谱特征到触电后剩余电流聚类中心的距离应恒大于到正常剩余电流聚类中心的距离。但图9 中前150 组中两者存在交叉项,后150 组中两线段距离较远,使得对正常剩余电流的分类错误。因此可对循环谱特征到正常剩余电流聚类中心的欧式距离进行修正以提高分辨率。
基于以上分析,本文进一步提出基于偏置欧式距离测度的聚类划分方法。具体思路为对触电聚类中心到循环谱特征的欧式距离计算结果加上偏置项,其具体步骤为:
1)对提取的三维最佳循环谱特征进行均值聚类,获得聚类中心。
2)按式(10)计算各循环谱特征点到聚类中心的欧式距离。
3)找到第一类样本中到触电后剩余电流聚类中心的欧式距离大于到正常剩余电流聚类中心的点(对应图9 椭圆区域对应的点),并求最大差值Δ1。
4)找到第二类样本中到触电后剩余电流聚类中心和正常剩余电流聚类中心的欧式距离差值最小的点(对应图9 矩形区域对应的点),并求最小差值Δ2。
5)取偏置调整范围Δ 为:当Δ1<Δ2 时,Δ1<Δ<Δ2;当Δ1≥Δ2 时,0<Δ<Δ2。
改进后的欧式距离计算结果如图10 所示,此时前150 组中到触电特征聚类中心大于到正常泄漏特征聚类中心的点明显减少,且对触电事故的识别率仍然较好。
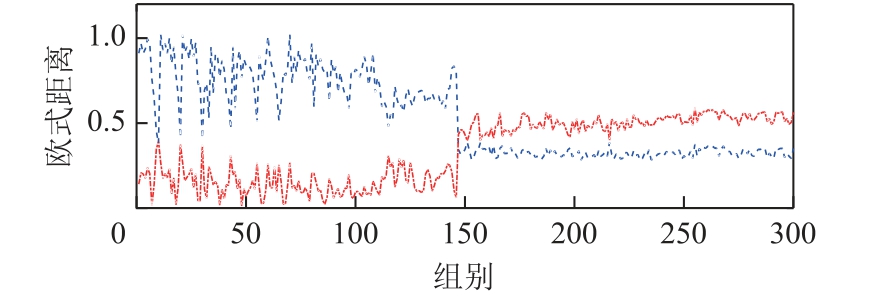
图10 改进后的欧式距离测度计算结果
Fig.10 Calculation results of Euclidean distance measure improved
本文提议的偏置Δ=0.291 9,改进后的聚类结果如图11 所示。对比图11、图7a 可知:改进后的结果误差类明显减少,且对正常情况下和触电情况下的剩余电流循环谱特征的聚类正确率达到99.33%,能更好地区分触电事故和正常泄漏的剩余电流循环谱特征。
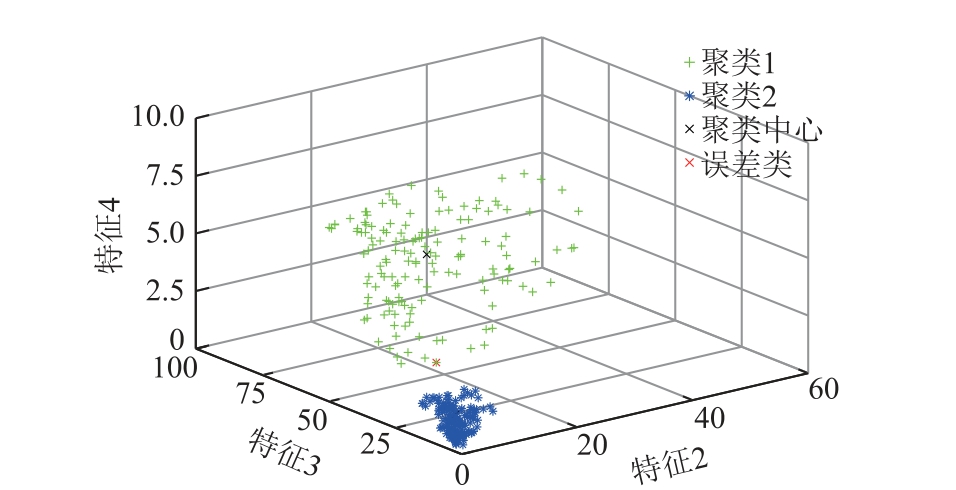
图11 改进后的聚类分析识别结果
Fig.11 Improved cluster analysis recognition results
4 结论
本文针对剩余电流保护装置因检测剩余电流受泄漏电流和触电电流相位差影响,在大负荷投入或触电事故发生时存在误动、拒动问题,利用循环谱相关理论计算触电前、后剩余电流信号的谱相关成分,并利用聚类分析提取触电判据。研究结果表明:
1)单相、三相两种电路结构下的触电前、后剩余电流信号循环频谱切片差异均表现为f=150Hz 频率对应的alpha=1 200Hz 线谱占比差异,据此提出了四种触电信号循环谱特征。
2)对单一和组合循环谱特征进行了聚类分析,其中单相电路分析结果表明特征2、3、4 三维组合特征下的聚类识别率最高为94.67%,提取的单相电路时触电后剩余电流聚类中心为[20.597,57.682,4.773],正常剩余电流聚类中心为[4.102,11.387,0.923];另三相电路时的最佳识别特征为特征4,识别率为100%,提取的三相电路时触电后剩余电流聚类中为[16.136],正常剩余电流聚类中心为[2.197]。
3)利用对欧式距离加偏置项的修正距离测度进行触电识别,其分辨率提高到了99.33%,偏置项设定阈值为0.291 9。
[1] 杜松怀, 张筱慧. 电力系统接地技术[M]. 北京: 中国电力出版社, 2011.
[2] 武一, 李奎, 王尧, 等. 磁调制式剩余电流传感器的动态励磁过程分析与仿真[J]. 电工技术学报,2014, 29(7): 244-252.Wu Yi, Li Kui, Wang Yao, et al. Analysis and simulation of dynamic process of excitation current of magnetic modulation residual current transformer[J].Transaction of China Electrotechnical Society, 2014,29(7): 244-252.
[3] 熊晓祎, 肖先勇, 左金威, 等. 触电事故特征改进近似熵检测方法[J]. 电力系统保护与控制, 2017,45(13): 27-33.Xiong Xiaoyi, Xiao Xianyong, Zuo Jinwei, et al.Electrical shock feature detection method based on improved approximate entropy[J]. Power System Protection and Control, 2017, 45(13): 27-33.
[4] 熊晓祎, 肖先勇, 赵恒. 基于自适应算法的触电事故电流检测[J]. 电力系统保护与控制, 2017, 45(4): 139-144.Xiong Xiaoyi, Xiao Xianyong, Zhao Heng. Adaptive algorithm based electrical shock current detection method[J]. Power System Protection and Control,2017, 45(4): 139-144.
[5] 李春兰, 夏兰兰, 王成斌, 等. 基于椭圆域分割的触电电流混沌检测方法研究[J]. 电力系统保护与控制, 2017, 45(15): 69-76.Li Chunlan, Xia Lanlan, Wang Chengbin, et al. Study on chaos detection method of electric shock current based on elliptic domain segmentation[J]. Power System Protection and Control, 2017, 45(15): 69-76.
[6] 李奎, 陆俭国, 武一, 等. 自适应漏电保护技术及其应用[J]. 电工技术学报, 2008, 23(10): 53-57.Li Kui, Lu Jianguo, Wu Yi, et al. Adaptive technology of leakage current operation protection and its application[J]. Transaction of China Electrotechnical Society, 2008, 23(10): 53-57
[7] 李春兰, 苏娟, 杜松怀, 等. 基于小波分析和BP 神经网络的触电信号检测模型[J]. 农业工程学报,2010, 26(增刊2): 130-134.Li Chunlan, Su Juan, Du Songhuai, et al. Detecting model of electric shock signal based on wavelet analysis and BP neural network[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(Supp: 2): 130-134.
[8] 韩晓慧, 杜松怀, 苏娟, 等. 触电信号暂态特征提取及故障类型识别方法[J]. 电网技术, 2016, 40(11):3591-3596.Han Xiaohui, De Songhuai, Su Juan, et al. Fault transient feature extraction and fault type identitfication for electrical shock signals[J]. Power System Technology, 2016, 40(11): 3591-3596.
[9] 韩晓慧, 杜松怀, 苏娟, 等. 基于参数优化的最小二乘支持向量机触电电流检测方法[J]. 农业工程学报, 2014, 30(23): 238-245.Han Xiaohui, Du Songhuai, Su Juan, et all.Determination method of electric shock current based on parameter-optimized least squares support vector machine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2014 30(23): 238-245.
[10] 刘永梅, 杜松怀, 盛万兴. 基于 SVM-神经网络融合反馈的触电电流检测方法[J]. 电网技术, 2020,44(5): 1972-1977.Liu Yongmei, Du Songhuai, Sheng Wangxin.Prediction method of electric shock current based on SVM and neural network fusion feedback[J]. Power System Technology, 2020, 44(5): 1972-1977.
[11] 关海鸥, 杜松怀, 苏娟, 等. 一种触电信号的自动快速检测模型[J]. 电网技术, 2013, 37(8): 2328-2335.Guan Haiou, Du Songhuai, Su Juan, et al. An automatic and quick detection model of electric shock signals[J]. Power System Technology, 2013, 37(8):2328-2335.
[12] 夏兰兰, 李春兰, 王成斌, 等. 基于混沌系统功率谱特征的触电信号识别研究[J]. 华北电力技术,2017(9): 1-7.Xia Lanlan, Li Chunlan, Wang Chengbin, et al. Study on detecting method of electric shock current based on chaotic system power spectrum feature[J]. North China Electric Power, 2017(9): 1-7.
[13] 关海鸥, 李伟凯, 杜松怀, 等. 基于 Hilbert-Huang变换的生物触电电流检测模型[J]. 农业工程学报,2017, 33(14): 202-209.Guan Haiou, Li Weikai, Du Songhuai, et al. Detection model of biological electric shock current based on Hilbert-Huang transform[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2017, 33(14): 202-209.
[14] 李春兰, 高阁, 张亚飞, 等. 基于局部均值分解(LMD)的单通道触电信号盲源分离算法[J]. 农业工程学报, 2019, 35(12): 200-208.Li Chunlan, Gao Ge, Zhang Yafei, et al. Single channel electric shock signals blind source separation algorithm based on local mean decomposition[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(12):200-208.
[15] Gardner W A. The spectral correlation theory of cyclosta-tionary time-series[J]. IEEE Transactions on Signal Pro-cessing, 1986, 11(7): 13-36.
[16] 罗利春. 谱相关的原理、功能与 α 截面谱表示[J].物理学报, 2002(10): 2177-2182.Luo Lichun. Spectrum correlation: principle,functionand representation in α section[J]. Acta Physica Sinica, 2002(10): 2177-2182.
[17] 王洪. 谱相关的数学关系与物理意义[J]. 电子学报,2015, 43(4): 810-815.Wang Hong. Mathematical relationships and physical functions of spectral correlation[J]. Acta Electronica Sinica, 2015, 43(4): 810-815.
[18] Swami A, Sadler B M. Hierarchical digital modulation classification using cumulants[J]. IEEE Transcation on Communication, 2000, 48(3): 416-429.
[19] 明阳, 陈进. 基于谱相关密度切片分析和 SVM 的滚动轴承故障诊断[J]. 振动与冲击, 2010, 29(1):196-199.Ming Yang, Chen Jin. Rolling element bearing fault diagnosis based on slice spectral correlation density and support vector machine[J]. Journal of Vibration and Shock, 2010, 29(1): 196-199.
[20] Gupta C N, Palaniappan R. Denoising cyclostationary framework for enhanced Electrocardiogram analysis[C]//2007 Computers in Cardiology, Durham, NC, 2007: 93-96.
[21] 刘艳丽, 郭凤仪, 王智勇, 等. 基于信息熵的串联型故障电弧频谱特征研究[J]. 电工技术学报, 2015,30(12): 488-495.Liu Yanli, Guo Fengyi, Wang Zhiyong, et al. Research on the spectral characteristics of series arc fault based on information entropy[J]. Transaction of China Electrotechnical Society, 2015, 30(12): 488-495.
[22] 柯维, 张永祥, 郭彬. 柴油机振动信号二阶循环平稳特性分析[J]. 武汉理工大学学报(交通科学与工程版), 2012, 36(2): 328-331, 336.Ke Wei, Zhang Yongxiang, Guo Bin. Second order cyclostationary analysis for diesel vibration signal[J].Journal of Wuhan University of Technology(Transportation Science & Engineering), 2012, 36(2):328-331, 336.
[23] 付海涛. 基于循环平稳的单信道时频重叠信号分析[D].成都: 电子科技大学, 2010.
[24] 郑鹏, 王泽众, 刘锋. 循环谱时域平滑循环周期图法估计性能分析[J]. 计算机与数字工程, 2011,39(11): 30-34.Zheng Peng, Wang Zezong, Liu Feng. Performance analysis for cyclic spectrum by temporally smoothed cyclic periodogram[J]. Computer & Engineering,2011, 39(11): 30-34.
[25] 叶豪, 李春兰, 高阁, 等. 基于多因素的动物触电电流特征试验与分析[J]. 江苏大学学报(自然科学),2020, 41(1): 39-45.Ye Hao, Li Chunlan, Gao Ge, et al. Experiment and analysis of animal electric shock current characteristics based on multiple factors[J]. Journal of Jiangsu University(Natural Science Edition), 2020, 41(1): 39-45.
[26] 李恩文, 王力农, 宋斌, 等. 基于混沌序列的变压器油色谱数据并行聚类分析[J]. 电工技术学报,2019, 34(24): 5104-5114.Li Enwen, Wang Linong, Song Bin, et al. Parallel clustering analysis of dissolved gas analysis data based on chaotic sequences[J]. Transaction of China Electrotechnical Society, 2019, 34(24): 5104-5114.
[27] 仇新艳, 李付亮. 基于ITD 和K 均值聚类的电能质量扰动分析与识别[J]. 电力系统及其自动化学报,2015, 27(8): 54-59.Qiu Xinyan, Li Fuliang. Analysis and identification for power quality disturbance signals based on ITD and K-mean clustering algorithm[J]. Proceedings of the CSU-EPSA, 2015, 27(8): 54-59.
[28] 严英杰, 盛戈皞, 刘亚东, 等. 基于滑动窗口和聚类算法的变压器状态异常检测[J]. 高电压技术,2016, 42(12): 4020-4025.Yan Yingjie, Sheng Gehao, Liu Yadong, et al.Anomalous state detection of power transformer based on algorithm sliding wind-ows and clustering[J]. High Voltage Engineering, 2016, 42(12): 4020-4025.
[29] 肖勇, 钱斌, 蔡梓文, 等. 电力物联网终端非法无线通信链路检测方法[J]. 电工技术学报, 2020,35(11): 2319-2327.Xiao Yong, Qian Bin, Cai Ziwen, et al. Malicious wireless communication link detection of power internet of thing devices[J]. Transaction of China Electrotechnical Society, 2020, 35(11): 2319-2327.