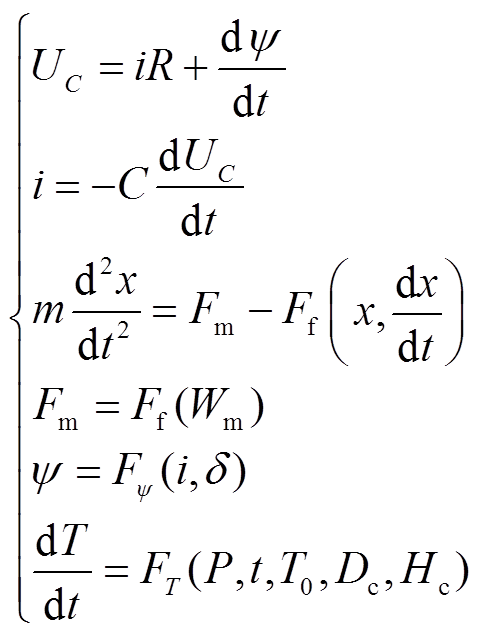（1）摘要 基于永磁操动机构的真空开关被广泛应用在电力系统中，以确保真空开关在不同环境下操动的精度和动作时间稳定，可以有效提高电力系统的稳定性。该文首先对10kV真空开关操动机构的分合闸动态特性进行分析计算，并建立仿真实验模型；利用径向基函数（RBF）神经网络与模糊PID自适应控制相结合的技术设计算法控制器，对机构的线圈电流与位移特性进行实时检测控制；通过仿真实验证明了该控制器在提高机构动作稳定性上的可行性。搭建实验测试平台，进行合闸对比实验，未加入算法控制器时，操动机构总体合闸时间在22.7～31.8ms；加入算法控制器后，合闸时间稳定在25.5～26.1ms。同时该算法控制器将机构合闸时间分散性由原来的±1.5ms降低为±0.3ms左右，不同环境温度下分散性依然可以保持在±0.3ms左右，证明加入该控制系统后，提高了动作时间的稳定性和有效性。
关键词：真空断路器 永磁操动机构 模糊径向基函数神经网络 动作稳定性
基于永磁操动机构的真空开关被广泛应用在电力系统中，提高开关动作时间的稳定性和动作特性的可控制性，对电力系统中相控开关技术的实现具有重要意义。相控开关技术可以有效地削弱电网中高压开关开合闸时产生的涌流和过电压，有效提高电力系统的稳定性[1]。永磁操动机构动作部件少，中间转换和连接机构也很少，极大地提高了动作的可控性，因此永磁操动机构为实现真空开关的智能控制提供了可靠支持[2-4]。
真空开关永磁机构动作时间的分散性是指对同一开关机构，一般采用充电电容当作控制电源，由于每次动作时，控制电压很难保证都相等，难免会有波动，必然会影响电流的大小，最终造成永磁机构分合闸的时间波动及特性曲线的变化[5-7]。控制电压的变化作为影响动作时间稳定性的关键因素之一，它的波动必然会引起动作时间的偏差，从而对整个电力系统的稳定运行产生负面影响。因此电压变化引起的时间误差是永磁操动机构亟需解决的问题之一[8]。此外，频繁地充放电及连续的动作，将导致电容的容量降低，回路中接线端子处的接触电阻也会增加，这些难以预知的变化都会引起线圈电流的变化，对开关的动作造成难以预测的影响，使开关动作分散性变大。
对于单机构而言，控制电压变化、外界温度及触头磨损等问题是无法避免的，也很难进行控制调节，因此降低机构动作时间的误差，需要考虑如何抵消这些环境因素带来的影响。目前的研究工作就是加入智能控制系统对操动机构的动作进行控制，得到不同电压环境下的动作时间，以及不同环境温度下的机构的动作特性，对比未加入智能控制系统时开关的动作特性，从而验证加入控制系统后对动作稳定性的改善效果。
本文采用模糊径向基函数（Radial Basis Function, RBF）神经网络-PID智能控制系统，保证开关操动时间的稳定性及操动过程的可控性。首先对永磁操动机构动态模型进行建模与仿真分析，建立永磁操动机构仿真模型，验证了算法控制器的可行性。在此基础上搭建了永磁操动机构动触头运动控制系统实验平台，以TMS320F28335 类型的数字信号（Digital Signal Processor, DSP）处理器为核心设计了永磁机构真空开关智能控制系统。在控制算法上选择了模糊RBF-PID控制算法，控制机构触头的行程和线圈电流。进行合闸实验并对比加入控制系统之前的合闸时间稳定性，证明模糊RBF-PID控制方案对提高真空开关动作时间稳定性的可行性及有效性。
为了完成真空开关永磁机构控制系统的设计，达到对机构的智能控制效果，需要对永磁操动机构的运动过程进行分析。
本设计主要利用电容为永磁机构的线圈供电，在此情况下对其进行动态分析，得到的微分方程组为
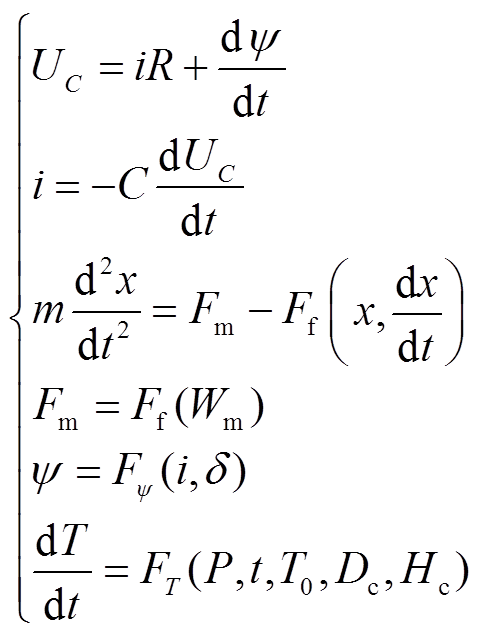（1）式中，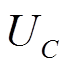
为充电电容初始电压；i为线圈中分闸或合闸电流；R为线圈的等效电阻；ψ为电磁系统的总磁链，是电流i和动铁心位移x的函数；C为充电电容容量；x为动铁心的位移；Fm为动铁心受到的电磁吸力；Ff为动铁心的运动反力；dx/dt=v为动铁心的运动速度；t为动作时间；P为永磁机构的功耗；
、
分别为线圈外径、线圈高度；m为运动部件的质量；Wm为电磁系统磁能；Fy为磁链函数；d 为磁场间隙；FT为温度变化函数；T0为环境温度。
对于永磁操动机构，无论是分闸操作还是合闸操作，动态过程都可分为两个阶段[5]。
1）第一阶段：励磁线圈电流从零逐渐增大，由于线圈电流产生的电磁力还没有足够大，动铁心还未开始运动，动铁心位移x=0，速度v=dx/dt=0，为起磁阶段（触动阶段）。
得到该阶段电容放电励磁下的动态方程为
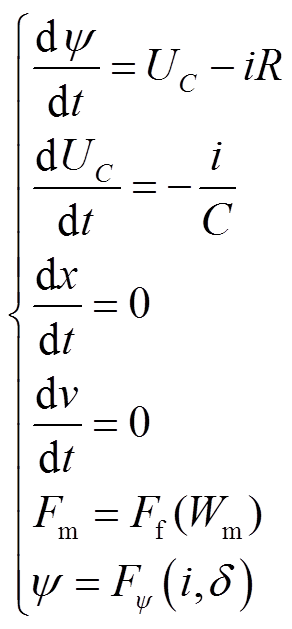（2）
2）第二个阶段：当励磁线圈的电流增大到产生的电磁力大于机构反力时，动铁心开始运动，并且一直运动到终点位置，这个过程即为第二个阶段。这个阶段的动态方程为
（3）
永磁操动机构触头在按照理想速度曲线运行时，可以获得良好的合闸特性。采用PID控制策略在非线性和可变负载的控制环境中对动触头的合闸过程进行控制。传统PID控制器的参数固定，需要工作人员反复尝试，对于复杂系统，参数调整通常很困难。模糊神经网络控制器能够根据运行条件自适应调整控制参数，以确保系统的快速跟踪和精确控制。因此本文采用模糊RBF-PID控制实现对动触头速度行程的精确控制，其控制框图如图1所示。
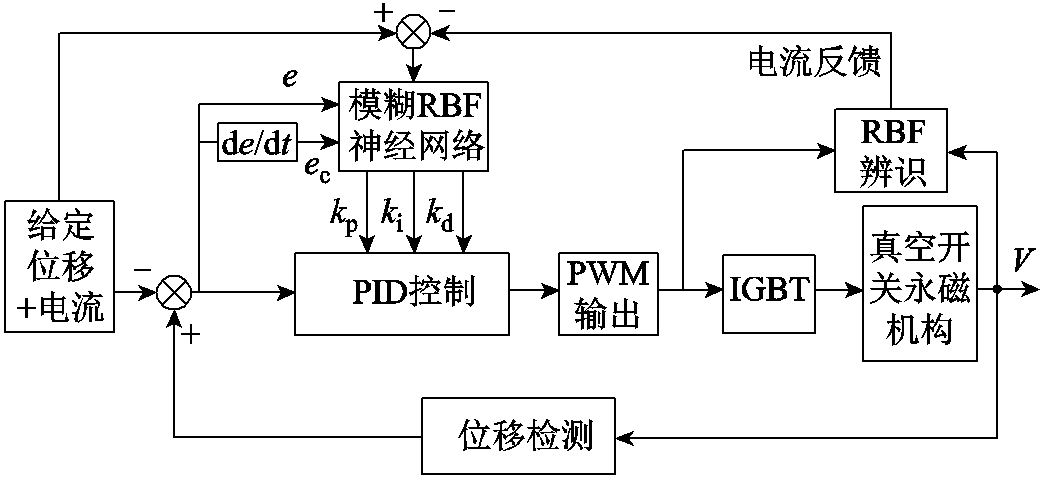
图1 永磁操动机构的模糊RBF-PID控制框图
Fig.1 Fuzzy RBF-PID control block diagram of permanent magnet operating mechanism
从模糊RBF-PID控制框图可以看出，该控制器能够实时监测机构触头的运动和线圈的电流，线圈电流的变化趋势是通过调整DSP输出的PWM的占空比来实现的。模糊RBF神经网络对触头位移和电流进行检测，并与理想的曲线进行对比，计算偏差和变化率。通过调整PID参数对PWM进行调节，进而实现对机构触头运动行程的精确控制。
本文所设计的模糊RBF神经网络是一种局部逼近网络，将神经网络的特点和模糊控制的优点结合在一起，能够体现二者的互补和相关性，可以确保系统的快速跟踪和精确控制。与目前永磁操动机构分合闸控制上使用较多的自适应控制相比，具有明显的速度优势，精确度也更高[9-12]。
综合考虑到PID和神经网络的设计需求，对算法结构的设计采用两个输入对应三个输出共四层的结构形式[13-16]，如图2所示。
图2 模糊RBF神经网络结构
Fig.2 Structure of fuzzy RBF neural network
结合本文设计与实验目的，两个输入节点分别对应采集到的位移、电流的偏差e和偏差变化率ec，三个输出节点参数被采集到DSP的算法控制器中，对输出的PWM进行相应的调节。
本文所使用的模糊RBF神经网络结构共有四层。每一层对应的作用如下所示：
（1）第一层为输入层，输入层有两个参数：①机构触头的实际采集位移y与输入理想曲线r的偏差e；②位置偏差变化率ec。节点i的个数为输入变量数量。
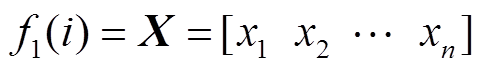（4）（2）第二层是模糊化推理层。将输入的位移偏差e和偏差变化率ec转换为模糊的矢量，通过隶属度函数计算出对应的隶属度，对输出的PWM进行预调节。定义模糊推理函数为
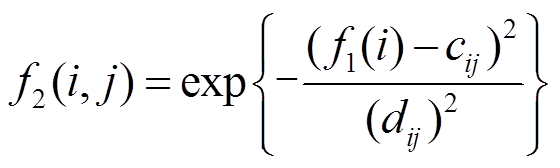（5）
（3）第三层是模糊推理层。在该层中，每个节点对应一个模糊规则，能够对节点进行模糊运算，运算乘积公式为
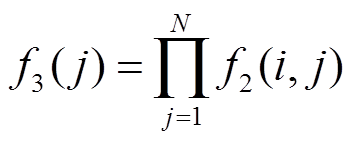（6）（4）第四层为输出层。共有三个输出节点，分别为kp、ki、kd，输出节点参数被采集到DSP的算法控制器中，根据参数的大小及上次采集到的参数变化，实现对输出PWM的最终调节。整定计算过程为
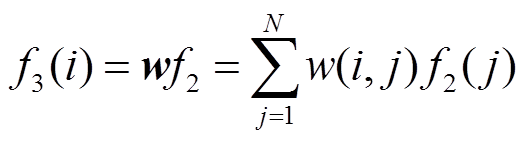（7）
式中，w为连接权矩阵；i=1,2,3；N=3。
基于2.1节中分析的模糊RBF网络的结构，输出三个节点对PID参数进行整定，定义模糊神经网络的目标函数为
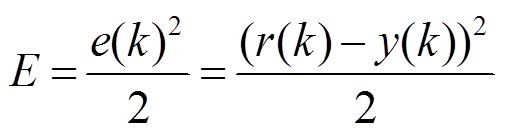（8）模糊RBF-PID控制器的输出为采用增量式的PID算法，即
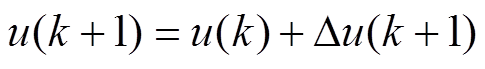（9）
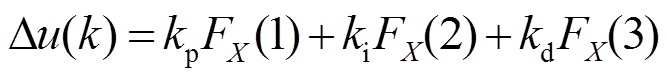（10）模糊RBF网络的理想输出为X(k)，实际输出为Y(k)，所以每次进行迭代计算，所产生的误差为X(k)-Y(k)。第k次计算中，神经网络权值的学习算法为
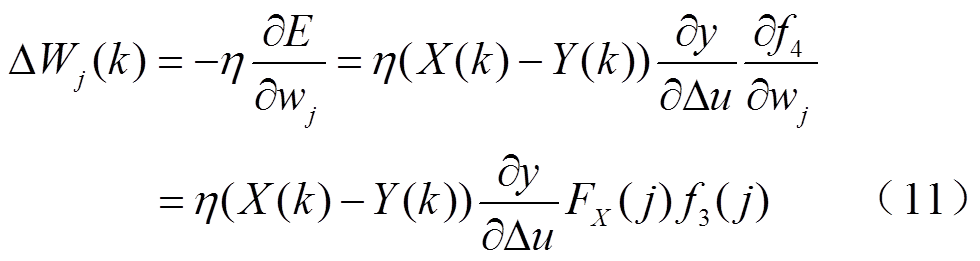
式中，
为经过算法迭代计算后得到的网络权值；wj为网络节点与上一层各节点的连接权值；h为学习率；j为模糊RBF神经网络的网络输出权值，j=1,3,…,49。
综上所述，模糊RBF-PID算法在操动机构触头控制的具体实现步骤如下：
（1）模糊RBF初始化。根据实际选定隶属度函数宽度和中心，计算权系数的初始值，选定η和量化因子α。
（2）实验开始，计算操动机构控制系统偏差，即位移、电流偏差e(k)=r(k)-y(k)和偏差变化量ec(k)=e(k)-e(k-1)。
（3）实时采集电流与位移，更新偏差与网络各层之间的输入系数、输出PID系数、根据u(k)，以及k+1时刻的实际值u(k+1)，根据u(k+1)与u(k)的偏差得出需要的参数，从而调节PWM。
（4）更新计算隶属度函数的中心Cij、基宽Bij和网络权值Wij。
（5）进行下一次迭代，令k=k+1，代入步骤2）重新进行计算，再进行循环迭代。
本文的控制系统是对真空开关永磁操动机构进行合闸操作。以电容电压为270V时的行程曲线为参考，通过合闸实验，用位移传感器检测触头的位置变化，用霍尔电流传感器采集机构合闸线圈中电流的变化，得到该电压条件下的触头运动行程曲线及合闸电流曲线，作为理想行程曲线，如图3和图4所示。
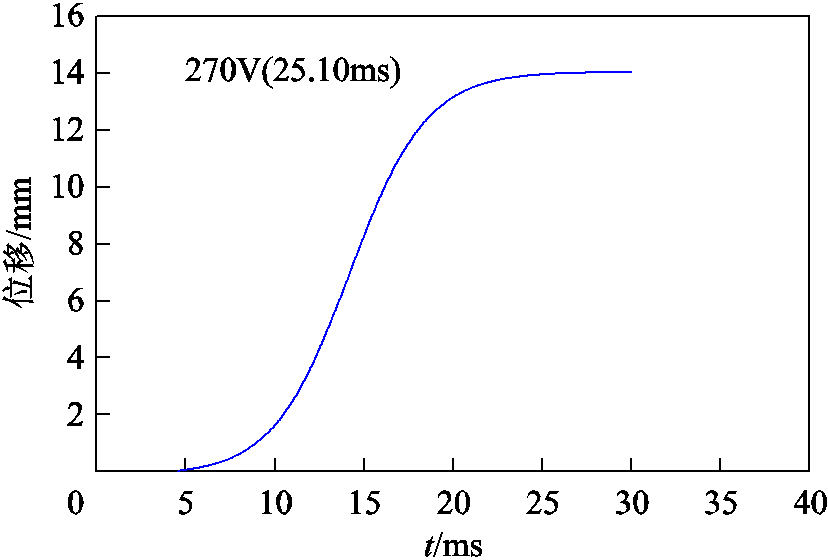
图3 给定行程曲线
Fig.3 The given stroke curve
图4 给定电流曲线
Fig.4 The given current curve
对图3中的位移变化进行计算处理，得到270V时触头合闸时的速度变化曲线，如图5所示。将该速度变化数据作为合闸理想速度对比数据。
图5 给定速度曲线
Fig.5 The given velocity curve
将电流、位移、速度三组曲线上的所有时间对应的数据存储在DSP算法控制器中，作为控制给定输入值，进行仿真和现场实验测试。
系统总体仿真时需要永磁操动机构的电磁模型，机构分合闸动态过程都需要遵循达朗贝尔运动方程。在电路上必须遵循电压平衡方程，在磁场上必须遵循麦克斯韦方程。此外根据式（1）～式（3）采用M文件S-函数编写其仿真模型。在Simulink中搭建模块，通过该模块建立的仿真模块主要是表现永磁操动系统中线圈电流与电磁斥力、机构位移三者之间的非线性关系。具体编写过程如下：
（1）初始化MdlInitializeSizes(flag=0)
定义两个连续的变量，分别是机构的输入参数x1（1）和输出变量y（2），所以NumState=2；输入的状态变量和输出的状态变量都为1。
（2）通过达朗贝尔运动方程和麦克斯韦方程，计算出状态变量Mdlderivatives(flag=1)。
（3）计算机构模块的输出子系统Mdoutput（flag=3）sys=x1(1)。
经过这三个步骤，配合整体的仿真系统，输出结果就是永磁操动机构触头的位移。完成对永磁操动机构的建模之后，在Simulink中完成对永磁操动机构模糊RBF-PID控制的系统的总体设计，如图6所示。
图6 模糊RBF神经网络PID永磁操动系统仿真
Fig.6 Simulation of fuzzy RBF neural network PID permanent magnet operating system
模糊RBF神经网络-PID控制器所用到的主要控制参数包括：kp、ki、kd和学习率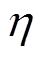
及量化因子a，其中学习速率包括PID学习率
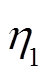和RBF神经网络学习率
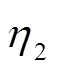[16-20]。
基于上述参数的影响，经过多次的调整验证与对比分析，在仿真过程中，将控制系统中的参数选择如下：kp=0.28、ki=0.16、kd=0.46，η1=0.8，η2=0.5，α=0.63。
由于控制电压的变化是影响机构动作时间稳定性的关键因素之一，因此在该仿真实验中，调整控制电压的变化来模拟环境的变化，分析加入算法控制器之后动作的时间稳定性情况。
由于给定的位移与电流数据是在270V测得的，为了验证系统在较大的电压波动情况下对动作时间稳定性的控制效果，选择将电压调节为290V进行对比实验。在两种情况下对电流和位移的情况进行对比分析，从而得到控制器的控制效果如图7和图8所示。
图7 仿真电流跟踪对比曲线
Fig.7 Simulation speed tracking curves
通过运行仿真，得到机构位移与线圈电流的变化数据，进行对比分析。
电流作为系统的控制变量之一，与触头的位移控制共同组成双变量的控制系统，而位移的跟踪对比结果是整个系统控制效果的直观体现，对线圈电流的调整又间接地影响位移的调节。
图8 仿真位移跟踪对比曲线
Fig.8 Simulation displacement tracking comparison curves
对仿真结果进行分析得到：在算法控制器的控制下，能够调节线圈的电流，使其按照给定的趋势进行变化。算法控制器对线圈电流和触头的位移进行双变量反馈调节，能够调整触头按照给定的位移曲线进行移动。图8所示位移曲线，290V时合闸时间是24.9ms，与给定合闸时间（270V时25.1ms）相比，时间误差为0.2ms，因此对合闸时间稳定性有一定的调节作用。
将仿真得到的290V时的触头位移变化数据进行处理，得到合闸速度变化数据，与给定速度进行对比，如图9所示。
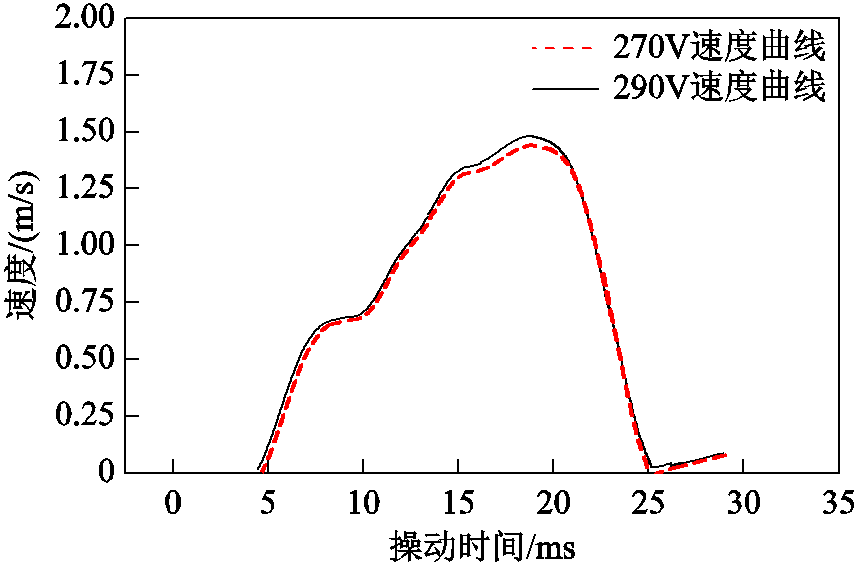
图9 仿真速度对比曲线
Fig.9 Simulation speed comparison curve
在机构合闸实验中，算法控制器对机构位移和线圈电流控制效果也体现在对触头移动速度的控制上。因此控制器控制效果的好坏，也体现在速度的跟踪上。通过对图9速度跟踪控制曲线分析得到：在合闸实验中，速度的跟踪控制存在一定的误差，在操动时间为0～15ms范围内，控制效果较好，速度跟踪误差很小，基本上能够达到实时的速度跟踪；在操动时间为15～22ms区间时，有一定的跟踪误差。但从图8可得最终的合闸时间误差为0.2ms，在允许的范围内。该模糊RBF-PID控制器方案能进行良好的速度位移跟踪控制，使断路器永磁操动机构在外界环境变化的条件下，调整机构触头的运动特性，提高合闸动作时间稳定性。
上述仿真和实验分析，证明了RBF-模糊PID控制策略能够进行速度跟踪控制，可以跟踪上目标的速度曲线变化，但在不同的电压及外部环境下，合闸时间误差的控制效果能否达到相控开关技术的要求，还需要进一步的实验验证。搭建了永磁操动机构控制回路的实验平台，电容电压的变化范围在200～300V，控制系统的整体结构框图如10所示，实验电路如图11所示。
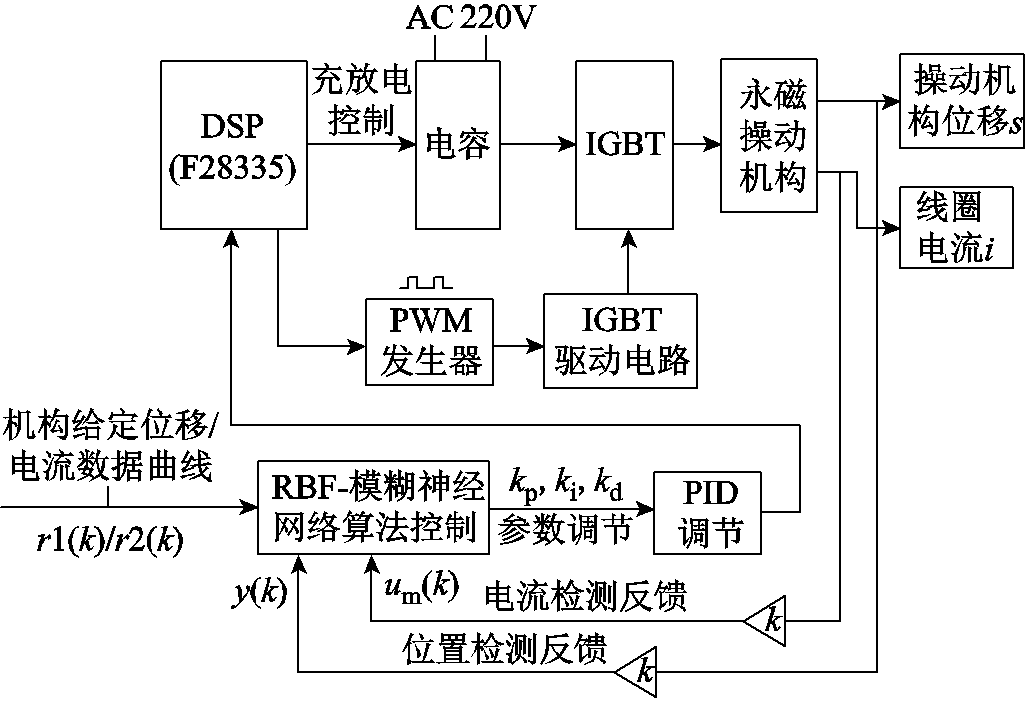
图10 现场测试系统的整体结构框图
Fig.10 Overall structural block diagram of the field test system
图11 现场测试系统整体电路图
Fig.11 Overall circuit diagram of the field test system
DSP控制回路中的检测回路包括触头位移检测回路和线圈电流检测回路，位移传感器与触头进行连接。线圈电流则通过霍尔电流传感器进行采集，传感器安装于分合闸电线上。
为验证PWM脉宽对线圈电流的调整作用，调整DSP控制系统发出不同频率的PWM，检测不同占空比的PWM对电流的控制效果。设置了PWM最高频率为100kHz，最短周期为10μs。图12为DSP发出的PWM对电流调节的结果，测试表明，驱动电路工作正常，能够对电流进行正常调节，对操动机构的运动特性进行控制以减少分合闸冲击和增加动作时间稳定性是可行的。
图12 线圈电流与PWM的相关性测试
Fig.12 Correlation test between coil current and PWM
为证明模糊RBF-PID算法控制器对机构合闸的控制效果，先进行一般的合闸测试（未加入算法控制器），测试控制电压对总体合闸时间的影响及机构的动作时间分散性。
控制电压的变化是影响机构动作时间稳定性的主要因素之一，影响较大，因此实验需要调整控制电压的变化作为外界环境的变化，分析加入算法控制器之后机构动作时间稳定性情况。
具体步骤为：以10V作为电压的调节幅度，将电容的放电电压分别控制在200V、210V、220V、
、300V进行合闸实验，采集得到机构在合闸过程中的数据，从而得到机构的总体行程趋势。
合闸时间分散性测试是在每个电压等级下进行100次实验，分别取其中的最大和最小值得出分散性。
得到在200～300V电压时测试的合闸行程总体趋势和合闸时间分散性趋势如图13和图14所示。实验结果表明：未加入算法控制器的合闸实验，合闸时间在22.7～31.8ms，合闸动作时间分散性最大为±1.5ms以上，因此不能满足选相控制的要求。
将模糊RBF-PID控制算法程序加入到DSP 控制器中，通过RBF模糊控制算法，首先进行了相应的测试和调整，设置PID参数学习率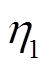
=0.75，量化因子a=0.18，RBF-模糊PID神经网络学习速率
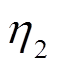=0.76。
图13 实验测试200～300V电压时合闸行程曲线
Fig.13 Experimental test of the closing stroke curve at 200～300V
图14 200～300V电压合闸时间分散性
Fig.14 Dispersion of closing time at 200～300V in experimental test
同样地，将电容的电压分别控制在200V、210V、220V、…、300V进行11组合闸实验测试，得到机构在合闸过程中的行程。另外在不同电压等级下同样进行100次合闸测试，采集得到合闸动作时间分散性数据。
在不同的电容初始电压下，进行合闸操作，分别采集线圈的电流数据，验证算法控制器对电流的跟踪反馈效果。图15为采集到的电流跟踪反馈结果图。
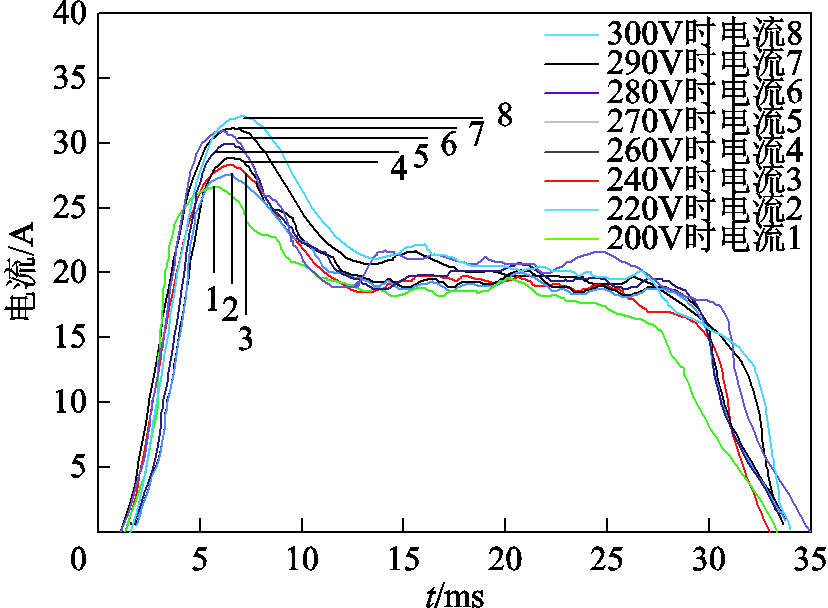
图15 实验测试200～300V电压线圈电流曲线
Fig.15 Experimental test of coil current curve at 200～300V
通过对采集结果分析可得：在算法控制器的作用下，对线圈电流进行跟踪反馈的控制，能够及时地缩小电流与给定值的误差，使电流的变化趋势与给定基本相符。
电流的跟踪反馈效果，直观地体现在机构的位移上，合闸实验同时采集不同电压条件下的位移及同一电压等级下合闸动作时间分散性数据，如图16和图17所示。
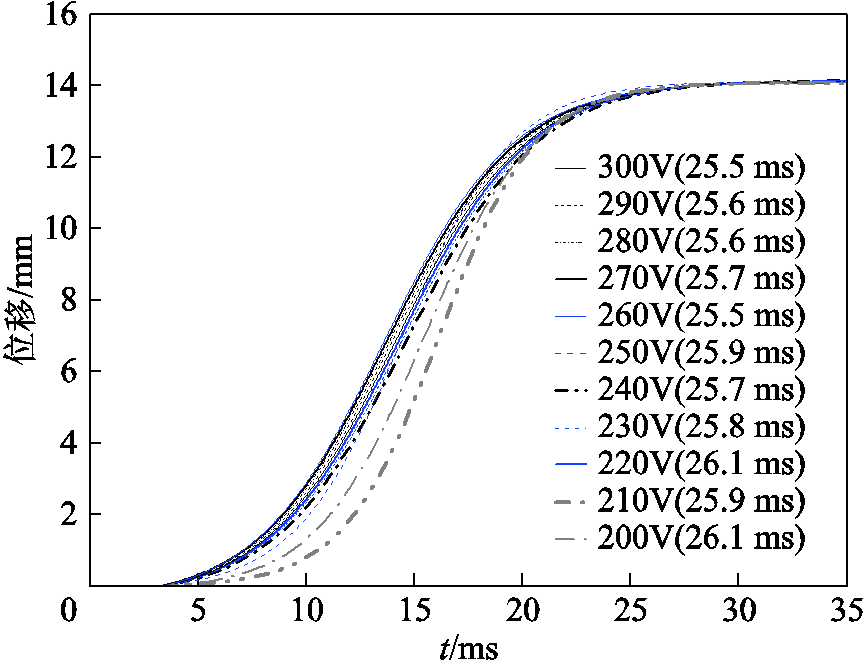
图16 实验测试200～300V电压合闸行程曲线
Fig.16 Experimental test of the closing stroke curve at 200～300V
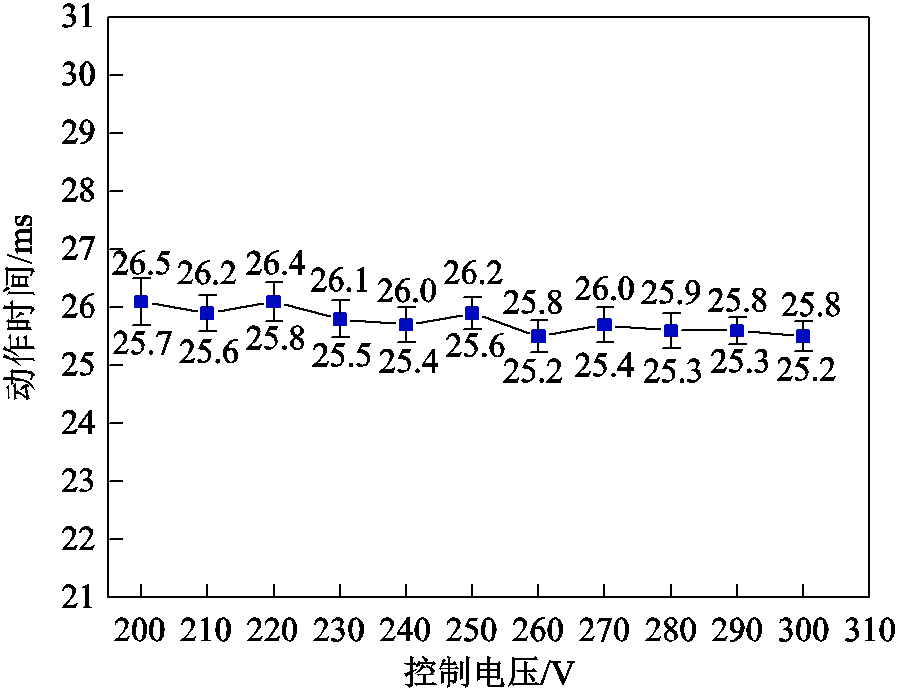
图17 实验测试200～300V合闸时间分散性
Fig.17 Overall dispersion of closing time at 200～300V in experimental test
对合闸实验及最终结果进行分析，模糊RBF-PID神经网络控制器可以将操动机构在不同外界环境下的总体合闸时间控制在25.5～26.1ms，动作时间分散性减少为±0.3ms左右，与未加入控制算法的合闸实验（分散性为±1.5ms）相比，明显提高了合闸动作时间稳定性，通过模糊RBF-PID算法控制器，对机构的位移与线圈电流进行双反馈跟踪控制，能够使操动机构触头按照给定的行程曲线运动，提高合闸动作时间稳定性，达到理想的控制效果。
控制电压的变化会造成操动机构动作时间及运动特性的变化，除此之外，环境温度的变化也会引起机构动作时间的误差，而这些环境干扰因素的存在是无法避免的，需要增加控制调节来降低影响。为证明该控制器系统可以有效降低操动机构在复杂环境下的动作时间分散性，在不同的环境温度下进行实验验证。
基于实验室的高低温环境箱进行合闸实验测试，加入算法控制器前后分别进行合闸实验，高低温环境实验箱如图18所示。低温环境模拟箱最低温度可达-40℃，高温实验箱可设置到200℃高温。在-40～60℃的环境中进行操动机构的合闸动作时间分散性实验测试，每隔10℃分别进行100次合闸测试。加入控制器前后机构动作时间分散性随温度变化曲线如图19所示。
图18 高低温环境机构合闸实验测试
Fig.18 Closing test in high and low temperature
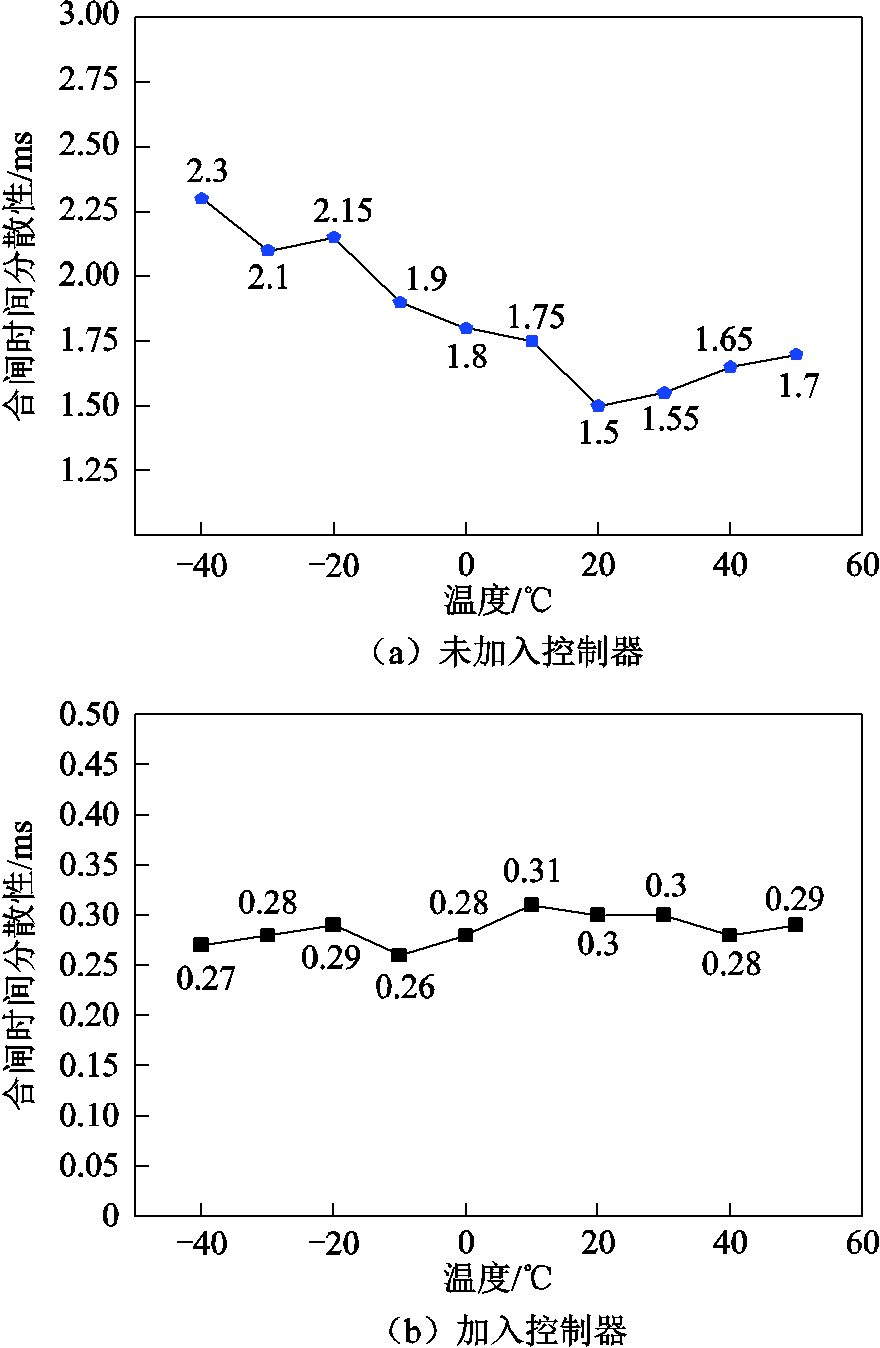
图19 动作时间误差随温度变化情况
Fig.19 Action time error changes with temperature
通过对合闸分散性实验结果进行分析可得，在复杂的环境因素影响下，加入该模糊RBF-PID控制器，可以很好地降低操动机构动作时间分散性，使得操动机构在不同的环境温度下依然能够保持动作稳定。
1）本文通过分析永磁操动机构分合闸时的受力情况，建立永磁操动机构的动态模型，提出了一种基于线圈电流补偿及位移跟踪控制的控制方案，设计了一种模糊RBF神经网络-PID控制系统，对永磁操动机构真空开关合闸进行操动控制，提高了合闸动作时间稳定性。
2）采用Matlab建立永磁操动机构控制系统的仿真模型，建立以模糊RBF-PID控制算法为核心的控制器，并进行了位移跟踪和线圈电流补偿的仿真实验。结果表明：模糊RBF-PID控制器能够对线圈电流和行程位移进行较好的跟踪控制。
3）搭建了真空开关永磁操动机构实验平台，在外界环境因素变化的情况下，进行控制效果验证。未加入算法控制器的合闸实验，总体合闸时间在22.7～31.8ms；加入算法控制器后，总体合闸时间在25.5～26.1ms，合闸动作时间分散性由原来的±1.5ms降低为±0.3ms左右。在不同的外界环境温度下，分散性依然能够保持在±0.31ms以内，验证了该控制方案的有效性。
参考文献
[1] 邓赟,武建文, 金鑫晨, 等. 基于高压断路器电机操动机构的位移分段控制策略[J]. 电工技术学报, 2018, 33(15): 3586-3595.
Deng Yun, Wu Jianwen, Jin Xinchen, et al. Displacement subsection control strategy based on motor operating mechanism of high voltage circuit breaker[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3586-3595.
[2] 程显, 葛国伟, 廖敏夫, 等. 基于真空断路器与SF6断路器串联的新型混合式高压直流断路器理论分析[J]. 电力自动化设备, 2019, 39(6): 68-74.
Cheng Xian, Ge Guowei, Liao Minfu, et al. Theoretical analysis of a new type of hybrid HVDC circuit breaker based on series connection between vacuum circuit breaker and SF6 circuit breaker[J]. Electrical Automation Equipment, 2019, 39(6): 68-74.
[3] 孙丽琼, 王振兴, 何塞楠, 等. 126kV真空断路器分离磁路式永磁操动机构[J]. 电工技术学报, 2015, 30(20): 49-56.
Sun Liqiong, Wang Zhenxing, He Sainan, et al. Separation magnetic circuit permanent magnetic actuator for 126kV vacuum circuit breaker[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 49-56
[4] 程显, 赵海洋, 葛国伟, 等. 基于螺线管和线圈盘的新型混合式斥力机构分析[J]. 电工技术学报, 2020, 35(14): 2997-3006.
Cheng Xian, Zhao Haiyang, Ge Guowei, et al. Analysis of a new hybrid repulsion mechanism based on solenoid and coil disk[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 2997-3006.
[5] 葛国伟, 廖敏夫, 黄金强, 等. 双断口真空断路器配合特性仿真与实验[J]．电工技术学报, 2016, 31(22): 57-65.
Ge Guowei, Liao Minfu, Huang Jinqiang, et al. Simulation and test of matching characteristics of double-break vacuum circuit breakers[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 57-65.
[6] 张梓莹, 梁德世, 蔡淼中, 等. 机械式高压直流真空断路器换流参数研究[J]. 电工技术学报, 2020, 35(12): 2554-2561.
Zhang Ziying, Liang Deshi, Cai miaozhong, et al. Study on commutation parameters of mechanical high voltage DC vacuum circuit breaker[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2554-2561.
[7] 孙曙光, 李勤, 杜太行, 等. 基于一维卷积神经网络的低压万能式断路器附件故障诊断[J]. 电工技术学报, 2020, 35(12): 2562-2573.
Sun Shuguang, Li Qin, Du Taihang, et al. Fault diagnosis of accessories for the low voltage conventional circuit breaker based on one-dimensional convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2562-2573.
[8] Castro-Sitiriche M J, Ofoli A R. DSP-based laboratory implementation of hybrid fuzzy-PID controller using genetic optimization for high-performance motor drives[J]. IEEE Transactions on Industry Applications, 2008, 44(6): 1977-1986
[9] Rubaai A, Castro-Sitiriche M J, Ofoli A R. DSP-based laboratory implementation of hybrid fuzzy-PID controller using genetic optimization for high-performance motor drives[J]. IEEE Transactions on Industry Applications, 2008, 44(6): 1977-1986.
[10] Akman C, Haider S, Ayarcan Y, et al. Anti-windup PID controller with integral state predictor for variable-speed motor drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1509-1516.
[11] Yubutea T, Yamada T. Neural networks controller characteristics with regard to adaptive control[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1992, 22(1): 170-177.
[12] Liu Y, Zhu Z Q, Howe D. Direct torque control of brushless DC drives with reduced torque ripple[J]. IEEE Transactions on Industry Applications, 2005, 41(2): 599-608.
[13] 刘爱民, 毕玉洁, 吴志恒, 等. 高压断路器永磁电机机构及控制系统设计[J]. 电机与控制学报, 2015, 19(1): 45-50.
Liu Aimin, Bi Yujie, Wu Zhiheng, et al. Mechanism and control system design of permanent magnet motor for high voltage circuit breaker[J]. Journal of Electrical Machinery and Control, 2015, 19(1): 45-50.
[14] 张忠蕾, 李庆民, 娄杰．电力电子控制电动机操动机构分闸运动特性的仿真分析[J]. 电网技术, 2006, 30(18): 58-63.
Zhang Zhonglei, Li Qingmin, Lou Jie. Simulation and analysis on switching-off motion characteristic of permanent magnet synchronous motor driven operating mechanism controlled by power converters for circuit breakers[J]. Power System Technology, 2006, 30(18): 58-63.
[15] 方红庆, 沈祖诒．基于改进粒子群算法的水轮发电机PID调速器参数优化[J]. 中国电机工程学报, 2005, 25(22): 120-124.
Fang Hongqing, Shen Zuyi. Parameter optimization of hydrogenerator PID governor based on improved particle swarm optimization algorithm[J]. Proceedings of the CSEE, 2005, 25(22): 120-124.
[16] 蒋宗礼．人工神经网络导论[M]．北京: 高等教育出版社, 2001．
[17] Akhyar S, Omatu S. Neuromorphic self-tuning PID controller[C]//IEEE International Conference on Neural Networks, San Francisco, California, 1993: 552-557.
[18] Orlowska-Kowalska T, Szabat K. Control of the drive system with stiff and elastic couplings using adaptive neuro-fuzzy approach[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 228-240.
[19] Liu Puyin, Li Hongxing. Efficient learning algorithms for three-layer regular feed forward fuzzy neural networks[J]. IEEE Transactions on Neural Networks, 2004, 15(3): 545-558.
[20] Maraziotis I A, Dragomir A, Bezerianos A. Gene networks reconstruction and time-series prediction from microarray data using recurrent neural fuzzy networks[J]. IET Systems Biology, 2007, 1(1): 41-50.
Permanent Magnet Mechanism Control System with High Operation Stability of Vacuum Switch
Abstract Vacuum switches based on permanent magnet actuator is widely used in power systems. To ensure the accuracy and stability of operation time of vacuum switch in different environments, the stability of power system can be effectively improved. In this paper, firstly, the dynamic characteristics of 10kV vacuum switch operating mechanism are analyzed and calculated, and the simulation test model is established. The algorithm controller is designed by combining radial basis function (RBF) neural network and fuzzy PID adaptive control technology. When the algorithm controller is not added, the overall closing time of the operating mechanism is 22.7-31.8ms, and the closing time is stable at 25.5～26.1ms after adding the algorithm controller. At the same time, the dispersion of closing time of the mechanism is reduced from ±1.5ms to ±0.3ms, and the dispersion can still be maintained at ±0.3ms under different ambient temperatures, which proves the effectiveness of the control system in improving the stability of action time.
Keywords:Vacuum switch, permanent magnet actuator, fuzzy radial basis function (RBF) neural network, action stability
DOI:10.19595/j.cnki.1000-6753.tces.201199
中图分类号：TM561
国家自然科学基金（51407163，51777025）、中国博士后科学基金（2017M622370）和河南省高校重点科研（16A470014）资助项目。
收稿日期 2020-09-12
改稿日期 2020-11-24
程 显 男，1982年生，博士，教授，博士生导师，研究方向为混合断路器和多断口真空开关等高压电器及高电压新技术。E-mail：chengxian@zzu.edu.cn
葛国伟 男，1987年生，博士，讲师，研究方向为混合断路器和多断口真空开关等高压电器及高电压新技术。E-mail：ggw@zzu.edu.cn（通信作者）
（编辑 赫蕾）