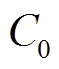 为并联电容(晶体管极间电容并入
为并联电容(晶体管极间电容并入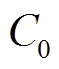 )、C1与L1构成串联谐振回路、LX为感抗所需电感、Zeq为等效阻抗(由二次侧负载RLoad归算得出)、Lr为接收线圈、Cr为补偿电容,回路中线路及寄生电阻并入Rload中,R1由线路内阻及器件寄生电阻组成。
)、C1与L1构成串联谐振回路、LX为感抗所需电感、Zeq为等效阻抗(由二次侧负载RLoad归算得出)、Lr为接收线圈、Cr为补偿电容,回路中线路及寄生电阻并入Rload中,R1由线路内阻及器件寄生电阻组成。摘要 针对基于E类逆变器的无线电能传输(WPT)系统中等效负载变化导致的硬开关问题,通过考虑源荷线圈耦合关系,分析多发射线圈等效耦合系数变化特征,得到发射端多线圈串联的线圈结构,实现了耦合系数及负载网络参数的动态调整,使等效负载在0~2Ropt(2倍理想负载)范围内均可实现软开关效果。最后通过仿真和实验验证该方法的可行性和有效性。
关键词:E类逆变器 无线电能传输 源线圈优化 软开关
随着电力能源及电子设备的发展,便携式电子设备在人类社会中的应用逐渐普及,而无线充电技术(Wireless Power Transfer,WPT)由于其便利性受到大众青睐[1-8]。2007年麻省理工学院Marin Soljacic教授成功点亮2m外的灯泡[9],无线电能传输技术再次受到学者们的广泛关注。
在磁耦合式无线电能传输系统中,为实现中近距离能量传输,需要在线圈中注入高频电流。E类逆变器因其独特的单管结构而具有高频高效的逆变特性[10-14],适用于中、近距离无线电能传输系统。然而,该拓扑易受负载变化影响[15],在无线充电应用场景中,原、副边线圈相对位置改变导致的等效负载变化易使其工作于硬开关状态,带来开关损耗增加及结温上升问题。严重情况下将造成逆变器开关管损坏,影响WPT系统的效率和可靠性。
为解决上述问题,文献[16]利用阻抗变换器消除了软开关状态下的理想负载与实际负载之间的差异。文献[17]提出了一种应用于无线充电系统的偶数路E类逆变器拓扑,通过耦合电感抑制偶数次谐波并降低逆变器的有载品质因数,增强谐振参数容差能力。文献[18]通过在晶体管两端并联饱和电抗器来解决E类逆变器的负载敏感问题,该方法需要额外引入电路元件实现宽范围软开关,增加了电路拓扑的复杂性和控制成本。文献[19]将磁化电感和漏感引入逆变器电路拓扑中,采用耦合系数统一表达的方式对逆变器参数表达式进行表达,从而实现宽范围软开关,但该方式的实现基于固定耦合系数(k=0.77),未讨论耦合系数变化下的效果。文献[20-21]采用将具有有限扼流圈的E类逆变器应用于负载范围较宽的无线充电场景,但该方式不仅会带来较大的交流电流,还会引起电磁干扰(Electromagnetic Inference, EMI)问题。
为克服E类逆变器在WPT系统中等效负载变化导致的硬开关问题,本文提出了E类逆变器宽范围软开关方法。首先,分析了逆变器负载网络中各器件参数对开关管电压波形的影响,根据E类逆变器开关电压波形,对逆变器参数及耦合系数与负载特性关系进行分析;其次,采用改进后多子线圈串联的线圈结构,提出一种线圈自互感调节的补偿方式对非理想状态下硬开关问题进行优化,实现E类逆变器宽范围软开关效果;最后,通过仿真和实验验证了所提方法的可行性和有效性。从线圈设计角度为E类逆变器实现范围软开关提供思路。
E类逆变器结构于1975年首次被Sokal提出,该电路高频、高效的特性,适用于无线电能传输系统的高频逆变环节。基于E类逆变器的WPT系统如图1所示。其中S为开关管、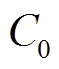 为并联电容(晶体管极间电容并入
为并联电容(晶体管极间电容并入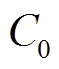 )、C1与L1构成串联谐振回路、LX为感抗所需电感、Zeq为等效阻抗(由二次侧负载RLoad归算得出)、Lr为接收线圈、Cr为补偿电容,回路中线路及寄生电阻并入Rload中,R1由线路内阻及器件寄生电阻组成。
)、C1与L1构成串联谐振回路、LX为感抗所需电感、Zeq为等效阻抗(由二次侧负载RLoad归算得出)、Lr为接收线圈、Cr为补偿电容,回路中线路及寄生电阻并入Rload中,R1由线路内阻及器件寄生电阻组成。
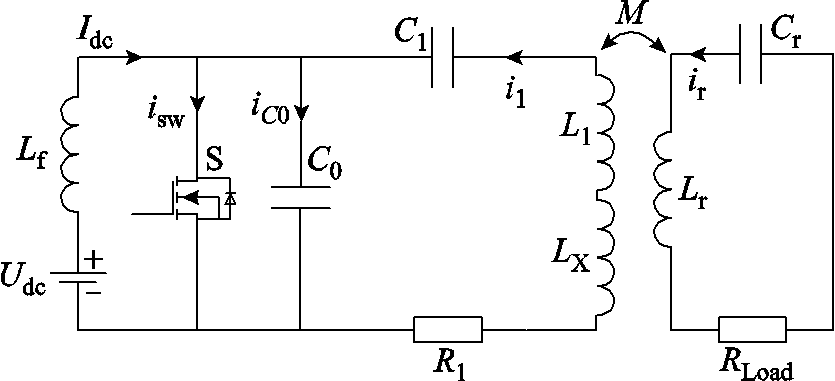
图1 基于E类逆变器的WPT系统
Fig.1 WPT system based on class E inverter
为简化逆变器工作过程分析,提出以下几点理想化假设:①开关管S的占空比D=0.5[22];②扼流圈为纯感性,电感值充分大,输入电流近似为恒定直流,无纹波;③开关管寄生电容线性,且并入并联电容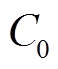 ;④开关管动作所需时间为零,且忽略导通阻抗;⑤串联谐振电路品质因数Q足够大,输出波形近似为理想正弦。
;④开关管动作所需时间为零,且忽略导通阻抗;⑤串联谐振电路品质因数Q足够大,输出波形近似为理想正弦。
E类逆变器的电压电流时间函数关系如图2所示。

图2 E类逆变器理想波形
Fig.2 Idealized waveforms of class E inverter
当开关管开通时,流过开关管S的电流为
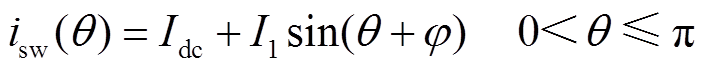 (1)
(1)式中,θ=ωt, ω=2πf,f为开关频率;Idc为输入直流电流;I1为负载回路电流峰-峰值,此时开关管两端电压恒为零(vs(θ)=0)。
开关管关断时,流过并联电容C0的电流与isw(θ)相等,即
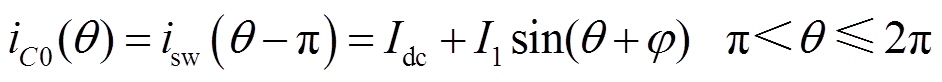 (2)
(2)此时开关管两端电压vs(θ)为关断时间内电流iC(θ)的积分
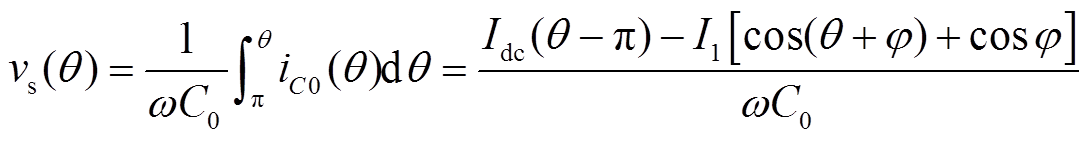 (3)
(3)
在一个周期内,开关管两端电压平均值等于输入电压。
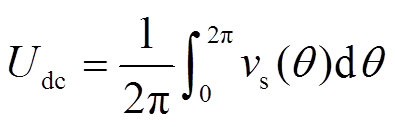 (4)
(4)首先假设开关管电压符合零电压开通(Zero Voltage Switching, ZVS)条件,可得输入输出电流关系为
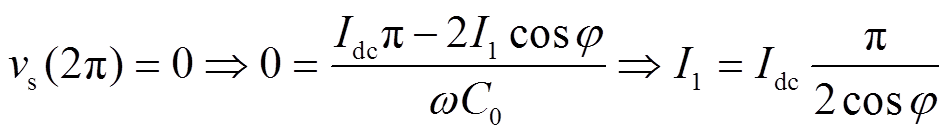 (5)
(5)
由功率守恒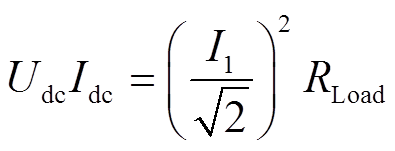 可得Idc、I1和Udc的关系
可得Idc、I1和Udc的关系
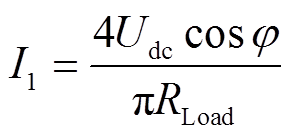 (6)
(6)
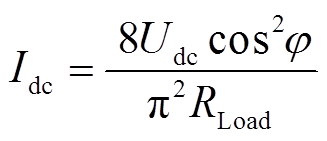 (7)
(7)若要达到理想情况,同时实现零电压开通(ZVS)及零导数开通(Zero Derivative Switching, ZDS),结合式(2)、式(6)、式(7)可得
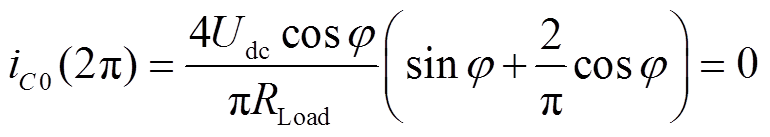 (8)
(8)
由式(8)可得同时满足ZVS和ZDS的最佳相角值φopt。
由于开关管两端电压波形非正弦波,对其进行傅里叶正交分解可得正弦部分Usin和余弦部分Ucos。由图2中可知输出电流为正弦波且负载为电阻性负载,负载网络由谐振部分和电抗LX组成,需要电抗LX对电压余弦部分进行抵消,使功率因数为1,可得RLoad、LX值为
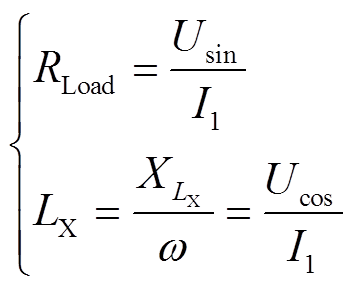 (9)
(9)至此得到理想情况下所有参数值。
结合上述分析,可得逆变器开关管电压与拓扑参数关系,如图3所示。由图3可得拓扑参数变化对vs波形影响:
(1)标称状态下,增大Req将导致vs波形波谷向上方移动,反之则向下方移动。
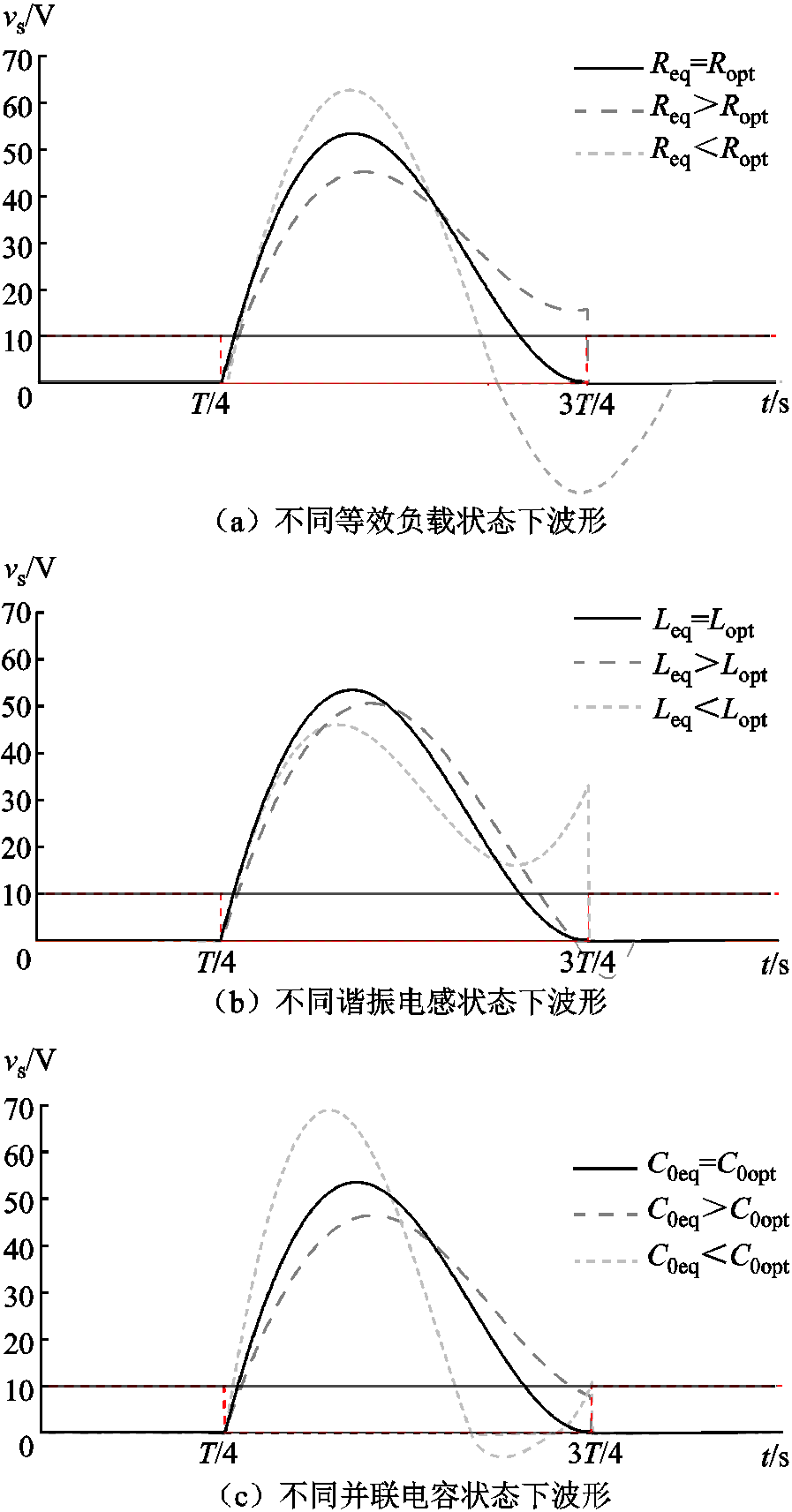
图3 不同参数变化下开关管电压波形对比
Fig.3 Voltage waveform comparison of switch under different parameter changes
(2)标称状态下,增大L1将导致vs波形波谷向右下方移动,反之则向左上方移动。
(3)标称状态下,增大C0将导致vs波形波谷向右上方移动,反之则向左下方移动。
由式(10)电容、电感的电抗公式得出,谐振电容C1参数调整后对vs波形影响与谐振电感L1基本一致。当C1增大时容抗减小,考虑串联谐振原则后,对vs波形影响等效为L1增大。
 (10)
(10)
由图3可知,可通过调节C0、L1和Req的取值,使开关管总能实现零电压开通。
二次侧负载Rload等效到一次侧后的反射阻抗为
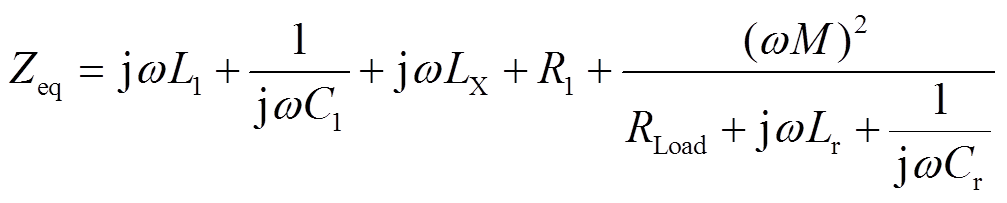 (11)
(11)通过参数的串联谐振关系化简式(11)可得
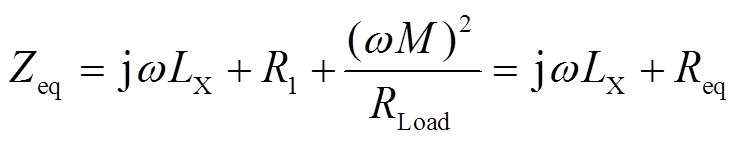 (12)
(12)
由式(12),等效负载Req直接受源荷线圈间互感M影响,为寄生电阻和二次侧反射电阻之和,可知等效负载Req与耦合系数k的二次方成正比,如图4所示。
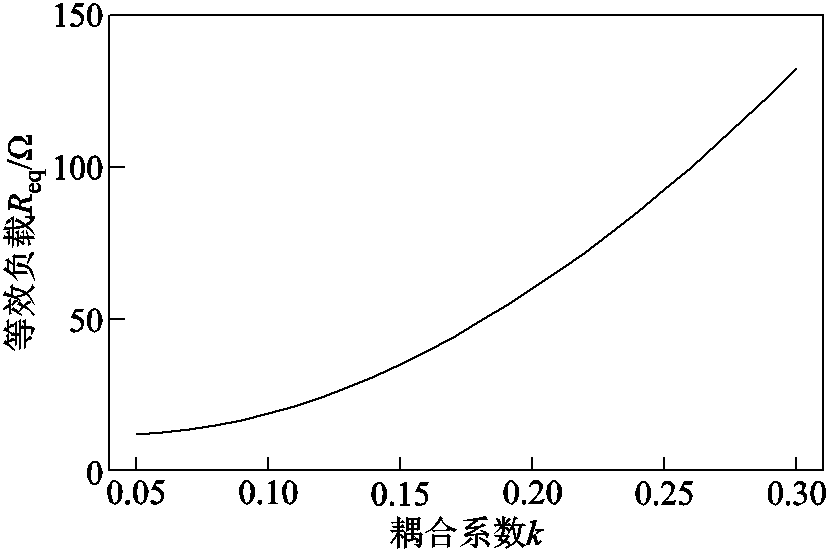
图4 等效负载与耦合系数关系
Fig.4 Relationship between equivalent load and coupling coefficient
由于负载距离越大耦合系数越小,所以当E类逆变器参数严格实现ZVS和ZDS时,负载距离的增加会减小Req,而负载距离的拉近会增大耦合系数k,进而导致Req快速增大,导通电压升高,开关管变为硬开关,极大地增加了开关损耗,开关管结温上升,影响系统稳定运行。
针对E类逆变器负载特性敏感的问题,当等效负载Req大于最佳负载Ropt时,E类逆变器处于硬开关状态,此时需对拓扑等效参数进行优化,以达到降低开通电压、减少开关损耗的目标。结合开关电压波形与拓扑参数以及耦合系数关系分析可得:
(1)在Req过大时,可以通过对C0、L1的调整,增大软开关裕度。
(2)同样,当开关管处于硬开关状态时,减小WPT系统源荷线圈间耦合系数k,可使Req减小,从而实现软开关。
考虑发射线圈为多线圈串联形式,当对各发射子线圈进行串联反接调节时,WPT系统将出现以下变化:
(1)调整线圈磁场反向,耦合系数k相应变化。
(2)由于线圈磁场方向发生变化,发射线圈自感L1的大小将随子线圈间自互感变化而改变。
为此,本文设计了一种发射端多线圈串联的线圈结构,在等效负载过大的情况下,通过在并联电容C0减小的基础上,将发射端多线圈进行串联反接调整,通过发射端线圈的自互感调节实现E类逆变器在WPT中应用的较宽范围软开关,从线圈结构角度针对网络参数和耦合系数变化提出了一种改进思路。
当两个小线圈串联时,等效电路理想化为图5所示。图5中,VIN为高频电源,VR为接收端的源荷互感电压之和,V1为发射端线圈之间互感电压之和,V2为发射端的源荷互感电压之和。
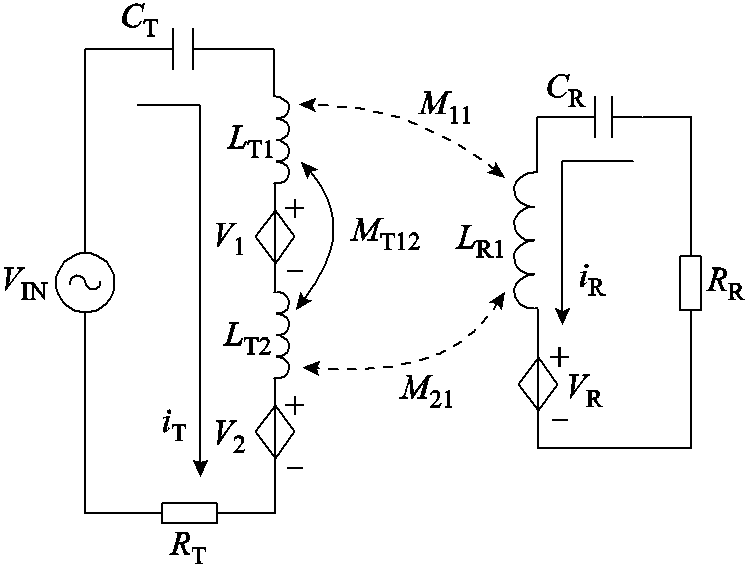
图5 发射端双线圈时源荷交叉耦合图形
Fig.5 Cross-coupling graph of source and charge for two primary coils
为简化计算,假设发射线圈等效自感LTeq与Ct完全谐振,整理后VR、V1、V2分别为
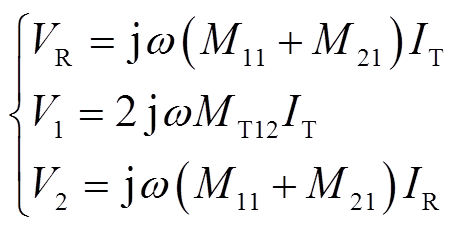 (13)
(13)式中,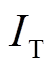 和
和 分别为发射线圈回路电流及接收线圈回路电流。
分别为发射线圈回路电流及接收线圈回路电流。
考虑串联发射线圈的耦合互感后
 (14)
(14)设
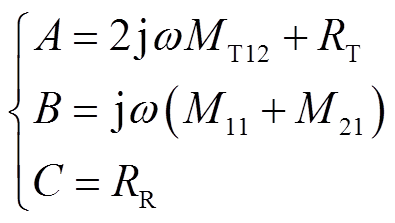 (15)
(15)
根据式(14)、式(15)化简得
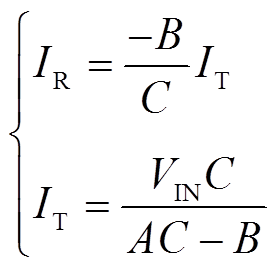 (16)
(16)
将式(15)代入式(16)并化简得
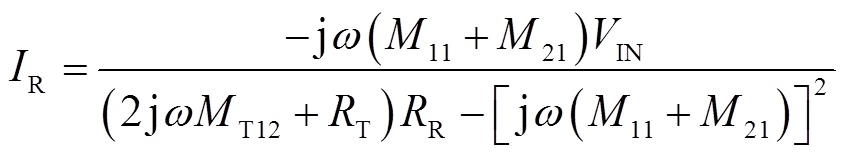 (17)
(17)根据式(17)得接收线圈回路电流关系,进一步推广到N线圈串联发射端,如图6所示。
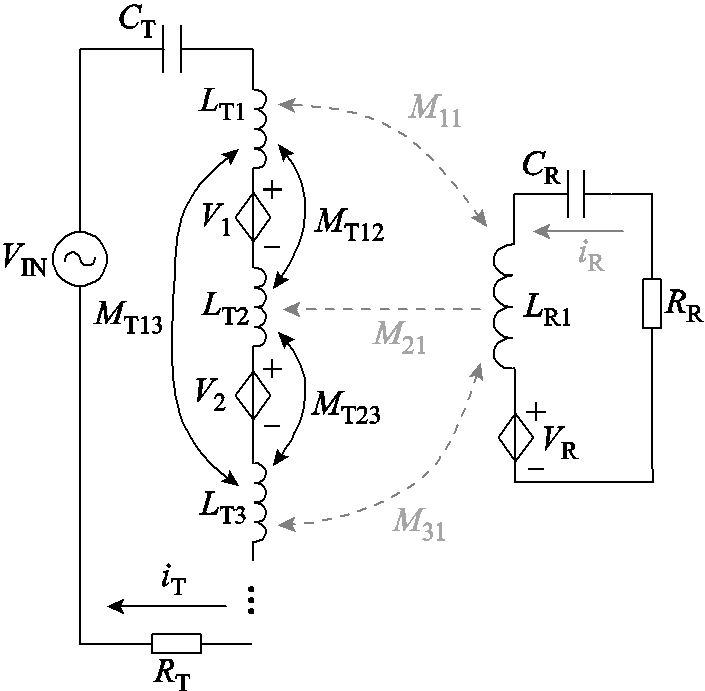
图6 发射端N/k线圈时源荷交叉耦合图形
Fig.6 Cross-coupling graph of source and charge for primary N-coils
其初始条件与双线圈时一致,化简整理后将每个发射线圈与其他发射线圈之间的互感电压向量设为Vm,即
 (18)
(18)可以得知 ,观察式(18)中互感矩阵可知,主对角线上互感值全为零,上下三角互感值对称,可进一步整理得
,观察式(18)中互感矩阵可知,主对角线上互感值全为零,上下三角互感值对称,可进一步整理得
 (19)
(19)
考虑N个串联发射线圈的线圈耦合互感后,则有
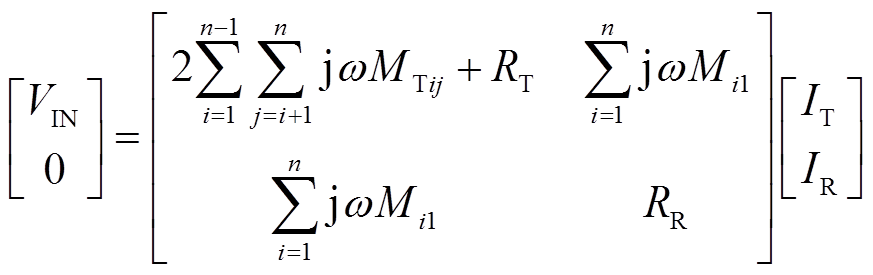 (20)
(20)根据N线圈串联发射端的互感值范围
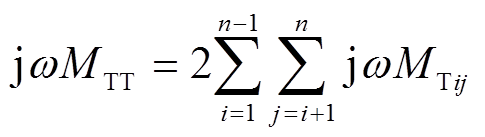 (21)
(21)
可得等效发射电感为
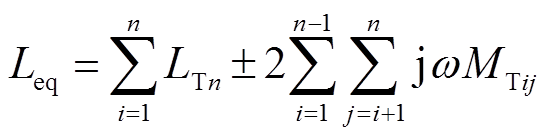 (22)
(22)根据式(21)可以得出理想状态的自互感可调范围,实际自互感调节范围受采用的线圈结构约束。
为实现自互感调节方式下的宽范围软开关效果,本文将发射线圈设计如图7所示。
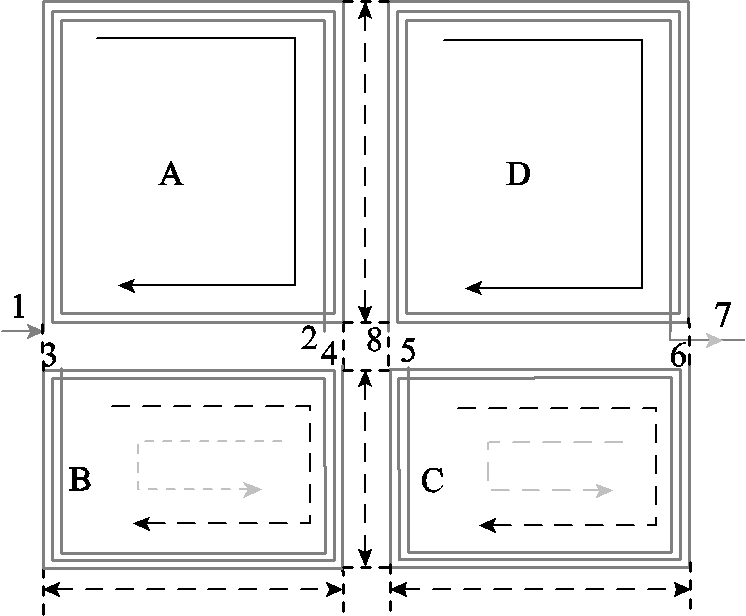
图7 多线圈串联结构
Fig.7 Multi-coils series structure
线圈采用规格为0.1´200mm2的利兹线,由外向内密绕。小线圈A、B、C、D如图7所示,其中A、D线圈参考电流方向受端口限制,均为单向流动;B、C线圈通过八个开关控制,电流参考方向均为双向;A、B、C、D线圈相邻边边长相同。在基于E类逆变器的WPT系统中,A、D线圈起到耦合机构中的主要耦合部分;B、C作为辅助线圈在系统逆变器侧起到软开关调节作用,在耦合机构侧通过耦合关系的变化接近最佳效率点。
利用该线圈结构,使谐振回路总电感由四个线圈正反串联连接组成,结合对线圈绕向以及互感变化范围分析,四个小线圈自感比值依次设为20∶2∶1∶15。该参数设计可实现宽范围软开关,且在调节过程中对耦合系数的影响较小。
开关控制框图如图8所示:通过开关S1~S8的切换实现对B、C线圈电流参考方向的控制,改变线圈磁场方向,最终实现发射线圈等效自感Lteq及互感的微调。以S1为基准,左为a通路,右为b通路。
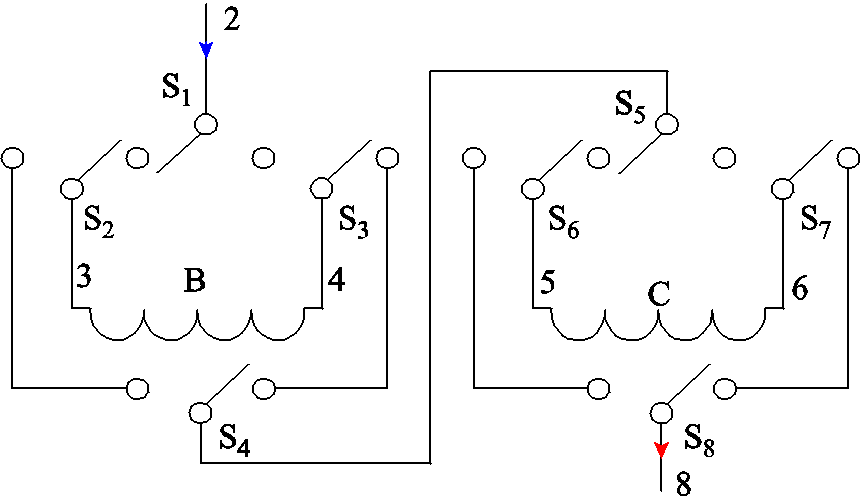
图8 自互感值切换开关组
Fig.8 Switch group for self mutual-inductance value switching
用Ansoft Maxwell软件对图7中方形线圈磁场分布进行分析,得到图9所示方形线圈磁通密度矢量图。
根据图9中磁密矢量与幅相图可知,方形线圈的磁场分布较均匀、磁感线平行于导线;四角虽然磁通密度较高但总磁通较小,因此方形线圈磁场可视为平行于导线分布。
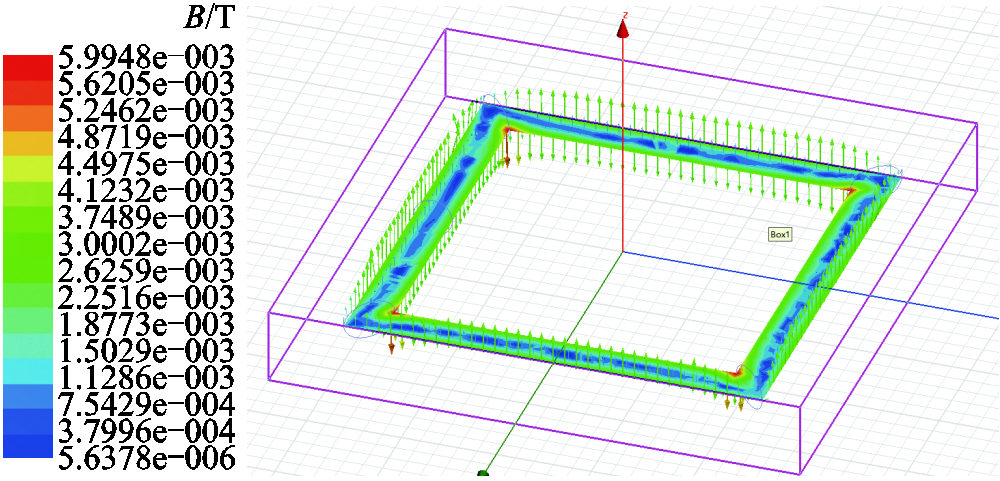
图9 方形线圈磁通密度矢量图
Fig.9 Magnetic density vector of square coil
经简化后,A、C线圈和B、D线圈的交叉互感可以忽略,对角线圈互感视为零,只需要考虑平行线圈之间的影响。
互感补偿值见表1,通过开关模态切换可以获得四种不同的互感值,选择最适合的状态进行补偿。
表1 不同开关模态下的互感补偿值
Tab.1 Mutual inductance compensation value in different switching modes

模态S1S2S3S4S5S6S7S8可调互感补偿值(ΔM) 1bbbbbbbb 2aaaaaaaa 3bbbbaaaa 4aaaabbbb
表1展示不同开关模态下的互感补偿值ΔM,a、b为开关导通通路;结合图9可知,可调互感值中MAC、MBD空间上对称,表1中未示出。
由表1及图9可知,开关1~4和开关5~8为两个开关组,每个开关组中的开关具有相同的开关状态和通路选择。这是由于开关1~4控制线圈B电流方向、开关5~8控制线圈C的电流方向。而每个线圈对应的控制开关组中的开关状态均由首个开关决定,从而降低了开关控制复杂度。
定义发射线圈间耦合系数为kt,则互感与耦合系数的关系为
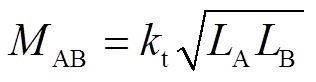 (23)
(23)线圈相对位置对称情况下,将耦合系数理想化,交叉互感的耦合系数kt视为同一值,根据式(23)可得,自互感大小仅受kt影响。
根据各线圈感值比例可得互感大小关系为
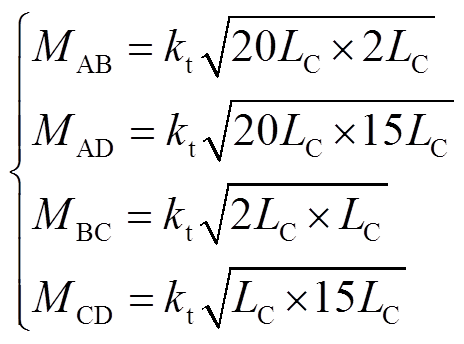 (24)
(24)归一化补偿值ΔM/LS在四个开关模态下分别为-1.522 8kt、-0.449 3kt、-0.966 2kt、-0.708 1kt,其中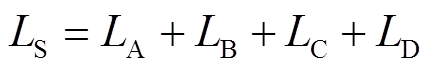 ,可以看出互感补偿值均由发射线圈间耦合系数决定。
,可以看出互感补偿值均由发射线圈间耦合系数决定。
根据图1拓扑,搭建WPT实验样机,如图10所示,实验样机具体参数见表2。

图10 实验样机
Fig.10 Experimental prototype
通过阻抗分析仪测量子线圈间互感,确定耦合系数为kt=0.062 9,C01经开关串联于C0后端,作为补偿状态投切点。通过表2参数及式(24)可得此耦合系数下四种模态的Leq,其中模态1为运行常态,其他模态为副边线圈补偿状态。
 (25)
(25)表2 实验样机主要参数取值
Tab.2 Main parameters of experimental prototype
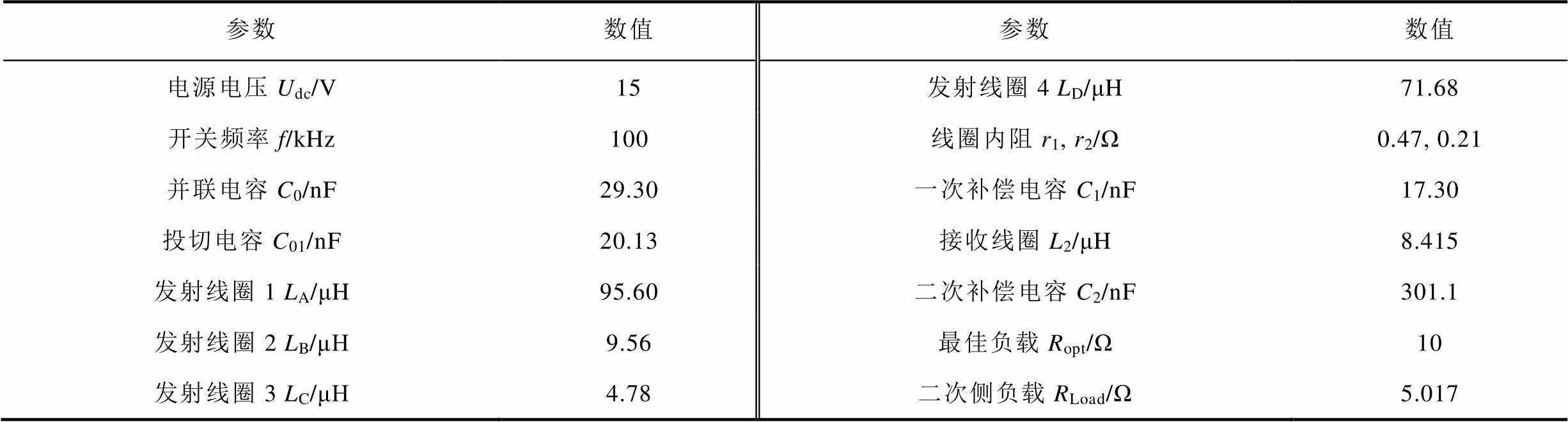
参数数值参数数值 电源电压Udc/V15发射线圈4 LD/μH71.68 开关频率f/kHz100线圈内阻r1, r2/Ω0.47, 0.21 并联电容C0/nF29.30一次补偿电容C1/nF17.30 投切电容C01/nF20.13接收线圈L2/μH8.415 发射线圈1 LA/μH95.60二次补偿电容C2/nF301.1 发射线圈2 LB/μH9.56最佳负载Ropt/Ω10 发射线圈3 LC/μH4.78二次侧负载RLoad/Ω5.017
图11a为传统E类逆变器在带不同负载时开关管电压。图中,逆变器在最佳负载Ropt时实现了ZVS与ZDS。Req≤Ropt亦可实现ZVS,但当Req>Ropt时,开关管开通电压会随Ropt的增大持续上升,严重影响软开关状态,导致开关损耗上升,故需对等效负载Req超过Ropt的情况进行补偿。图11b为改进E类逆变器在带不同负载时的开关管电压仿真结果,根据局部放大图样可知:当等效负载分别为1.5Ropt和2Ropt时,采用线圈的模态2和模态4进行补偿可获得较佳软开关效果,且所有模态均可实现1.5倍等效负载情况下的ZVS,实现了E逆变器更宽范围的软开关,降低了开关损耗。图11c为1.5倍等效负载有无补偿时实验波形对比,可知,当Req=1.5Ropt时,开关管处于硬开关状态。通过上述方法补偿后,开关管实现零电压开通,验证了上述理论分析的可行性。
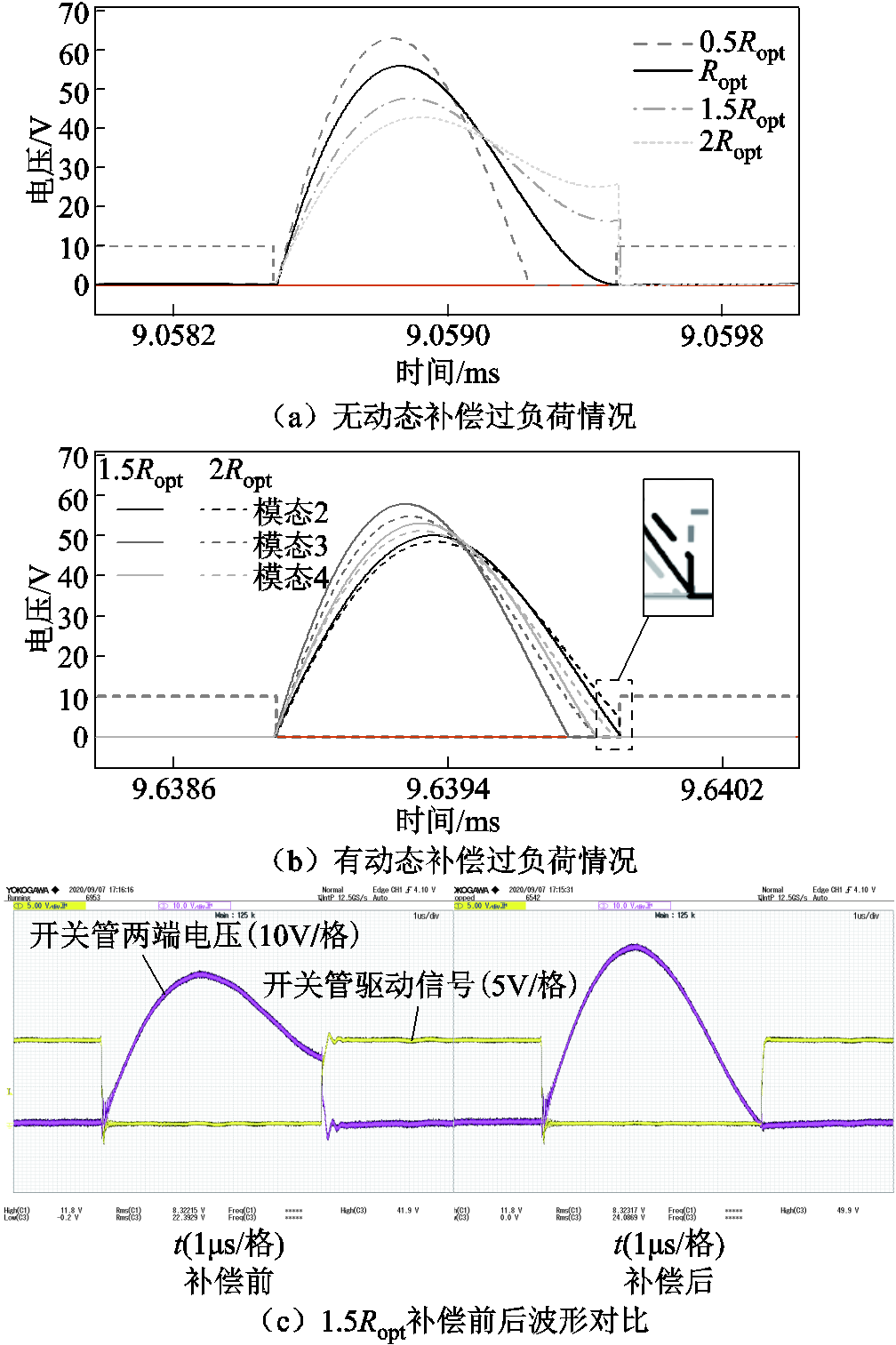
图11 自互感补偿仿真及实验验证
Fig.11 Simulation and experimental verification of self mutual-inductance compensation
图12为E类逆变器耦合系数-效率关系,由图可知,E类逆变器在Req=Ropt时存在最佳效率,随着耦合系数增大,当Req>Ropt时,逆变器效率受开通损耗影响快速下降。通过自互感补偿实现软开关后,降低开关损耗,逆变器效率得到提升,开关管发热情况被抑制。
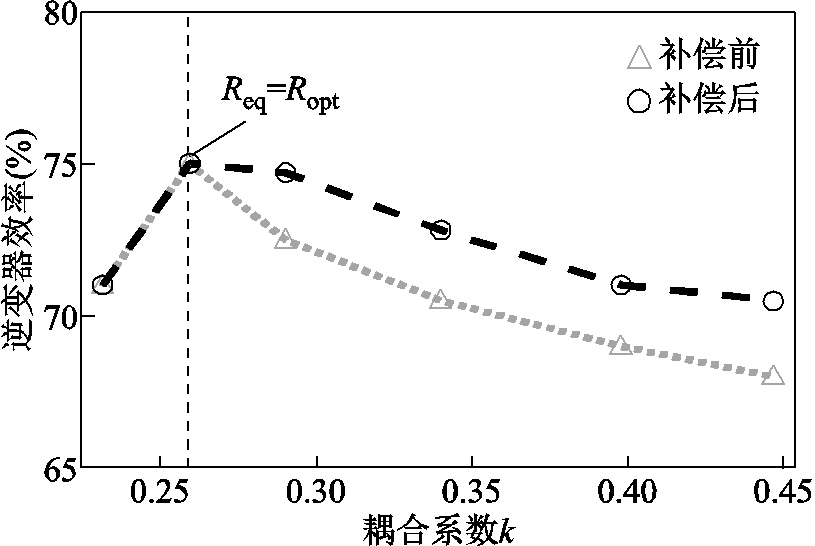
图12 E类逆变器耦合系数-效率关系
Fig.12 Inverter coupling coefficient-efficiency relationship
动态补偿前后系统效率分析如图13所示。从图13可知,在Ⅰ区中Req≤Ropt,随着距离逐渐拉近,系统效率随耦合系数增大同步提升;在Ⅱ区中Ropt<Req≤1.6Ropt,此后开关管开始呈现硬开关状态,故开始自互感补偿投切,该阶段开关损耗导致的效率下降小于耦合系数带来的效率提升,所以补偿前系统效率仍然上升;在Ⅲ区中1.6Ropt<Req≤2Ropt,此阶段中随着等效负载增大,开关管开通电压持续上升,开关损耗快速提高,且大于耦合系数带来的效率提升,导致补偿前效率开始降低;在Ⅳ区中Req>2Ropt,开关损耗持续增大,由于等效负载过大,自互感补偿无法完全实现软开关,但仍能起到大幅降低开通电压的效果,故补偿后效率开始下降,但相较无补偿状态效率仍有所提升。
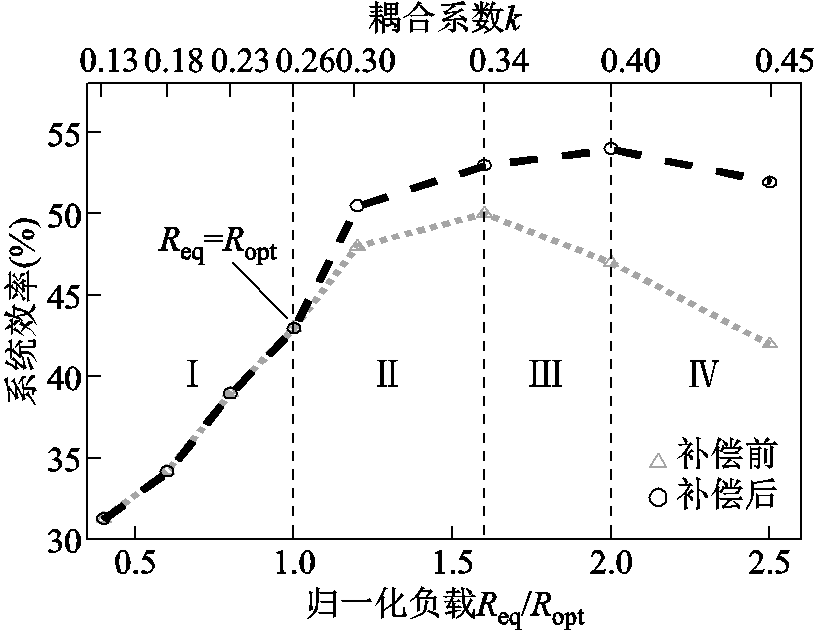
图13 动态补偿前后系统效率分析
Fig.13 System efficiency analysis before and after dynamic compensation
实验结果与理论分析一致,在本实验基础上,尤其在更高开关频率情况下,开关损耗将继续增大,此时软开关状态愈加重要,补偿效果将进一步提升;自互感补偿时,补偿值带来部分感抗,理想负载Zopt越大,则额外感抗消耗的无功功率及寄生电阻带来的有功损耗占比越小,系统效率越高。
在基于E类逆变器的无线电能传输系统中,耦合强度变化及负载特性变化将导致逆变器硬开关,降低逆变器效率。因而,改善逆变器工作状态能有效提升系统效率。
本文通过改进逆变器侧线圈结构,通过自互感调节的方式,在负载值大于最优值时,提升等效负载变化情况下的软开关裕度,实现了0~2Ropt的宽范围ZVS;通过实验对比,在两倍等效负载时系统整体效率由47%提升至54%,在其他Req>Ropt情况下系统效率也有所提升。同时,在上述情况下,该方式较好地改善了开关管硬开关导致发热问题,提升系统运行稳定性。
参考文献
[1] 黄学良, 谭林林, 陈中, 等. 无线电能传输技术研究与应用综述[J].电工技术学报, 2013, 28(10): 1-11.
Huang Xueliang, Tan Linlin, Chen Zhong, et al. Review and research progress on wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 1-11.
[2] 吴理豪, 张波. 电动汽车静态无线充电技术研究综述(上篇)[J]. 电工技术学报, 2020, 35(6): 1153-1165.
Wu Lihao, Zhang Bo. Overview of static wireless charging technology for electric vehicles: part Ⅰ[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1153-1165.
[3] 麦瑞坤, 陈阳, 张友源, 等. 基于变次级补偿参数的感应式无线充电系统研究[J]. 中国电机工程学报, 2017, 37(11): 3263-3269, 3382.
Mai Ruikun, Chen Yang, Zhang Youyuan, et al. Study on secondary compensation capacitor alteration based IPT charging system[J]. Proceedings of the CSEE, 2017, 37(11): 3263-3269, 3382.
[4] Fu Minfan, Zhang Tong, Zhu Xinen, et al. Compensation of cross coupling in multiple-receiver wireless power transfer systems[J]. IEEE Transactions on Industrial Informatics, 2016, 12(2): 474-82.
[5] 范兴明, 高琳琳, 莫小勇, 等. 无线电能传输技术的研究现状与应用综述(英文)[J]. 电工技术学报, 2019, 34(7): 1353-1380.
Fan Xingming, Gao Linlin, Mo Xiaoyong, et al. Overview of research status and application of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1353- 1380.
[6] Li Yang, Dong Weihao, Yang Qingxin, et al. An Automatic impedance matching method based on the feedforward-backpropagation neural network for a WPT system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3963-3972.
[7] 诸嘉慧, 刘之方, 高强, 等. 基于能量流理论的谐振式无线电能传输原理分析与验证[J]. 电工技术学报, 2019, 34(20): 4188-4195.
Zhu Jiahui, Liu Zhifang, Gao Qiang, et al. Analysis and verification of energy flow model of magnetic resonant coupled wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4188-4195.
[8] 苏玉刚, 谢诗云, 王智慧, 等. 基于F-F/T变结构谐振网络的恒压-恒流型电场耦合电能传输系统[J].电工技术学报, 2019, 34(6): 1127-1136.
Su Yugang, Xie Shiyun, Wang Zhihui, et al. An electric-field coupled power transfer system with constant voltage and constant current output based on F-F/T changeable resonant circuit[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1127-1136.
[9] 赵争鸣, 张艺明, 陈凯楠. 磁耦合谐振式无线电能传输技术新进展[J]. 中国电机工程学报, 2013, 33(3): 1-13, 21.
Zhao Zhengming, Zhang Yiming, Chen Kainan. New progress of magnetically-coupled resonant wireless power transfer technology[J]. Proceedings of the CSEE, 2013, 33(3): 1-13, 21.
[10] Raab F. Idealized operation of the class E tuned power amplifier[J]. IEEE Transactions on Circuits and Systems, 1977, 24(12): 725-735.
[11] Kazimierczuk M, Puczko K. Exact analysis of class E tuned power amplifier at any Q and switch duty cycle[J]. IEEE Transactions on Circuits and Systems, 1987, 34(2): 5907-5917.
[12] Oh H, Lee W, Koo H, et al. 6.78 MHz wireless power transmitter based on a reconfigurable class-E power amplifier for multiple device charging[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 5907-5917.
[13] Fu Minfan, Yin He, Liu Ming, et al. Loading and power control for a high-efficiency class E PA-driven megahertz WPT system[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 6867-6876.
[14] Liu Ming, Fu Minfan, Ma Chengbin, et al. Parameter design for a 6.78-MHz wireless power transfer system based on analytical derivation of class E current-driven rectifier[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4280-4291.
[15] 苏玉刚, 赵鱼名, 谢诗云, 等. 电场耦合无线电能传输系统负载软切换控制技术[J]. 电工技术学报, 2017, 32(18): 44-51.
Su Yugang, Zhao Yuming, Xie Shiyun, et al. Control of load soft-switched for electric-field coupled power transfer system[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 44-51.
[16] Kazimierczuk M K, Bui X T. Class E DC/DC converters with an inductive impedance inverter[J]. IEEE Transactions on Power Electronics, 1989, 4(1): 124-135.
[17] 黄晓生, 陈为, 陈庆彬. 用于WPT的双路E类逆变器功率合成拓扑及其电感耦合集成[J].中国电机工程学报, 2015, 35(21): 5577-5584.
Huang Xiaosheng, Chen Wei, Chen Qingbin. Topology of the power combination with dual class E inverters and magnetics integration of coupled inductors for WPT applications[J]. Proceedings of the CSEE, 2015, 35(21): 5577 -5584.
[18] Aldhaher S, Luk P C, Whidborne J F. Tuning class E inverters applied in inductive links using saturable reactors[J]. IEEE Transactions on Power Electronics, 2014, 29 (6): 2969-2978.
[19] Ayachit A, Corti F, Reatti A, et al. Zero-voltage switching operation of transformer class-E inverter at any coupling coefficient[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 1809-1819.
[20] Aldhaher S, Yates D C, Mitcheson P D. Load-independent class E/EF inverters and rectifiers for MHz-switching applications[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8270-8287.
[21] Roslaniec L, Jurkov A S, Bastami A A, et al. Design of single-switch inverters for variable resistance/load modulation operation[J]. IEEE Transactions on Power Electronics, 2015, 30(6): 3200-3214.
[22] Suetsugu T, Kazimierczuk M K. Design procedure of class-E amplifier for off-nominal operation at 50% duty ratio[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2006, 53(7): 1468-1476.
Research on Soft Switching Technology of Class E Inverter Based on Self Mutual-Inductance Regulation in Wireless Power Transfer
Abstract In order to solve the problem of hard switching caused by the change of equivalent load in wireless power transmission system based on class E inverter. By considering the coupling relationship between the source and load coils, and analyzing the change characteristics of the equivalent coupling coefficient of multiple transmitting coils, the coil structure of multiple coils in series at the transmitting end is obtained, and the dynamic adjustment of the coupling coefficient and load network parameters is realized. The soft switching effect can be achieved within the range of equivalent load from 0 to 2Ropt (2 times the ideal load). Finally, the feasibility and effectiveness of the method are verified by simulation and experiment.
keywords:Class E inverter, wireless power transmission system, source coil optimization, soft switch
DOI:10.19595/j.cnki.1000-6753.tces.L90292
中图分类号:TM72; TM15
国家自然科学基金资助项目(51777120)。
收稿日期 2020-07-08
改稿日期 2020-09-10
张少腾 男,1996年生,硕士研究生,研究方向无线电能传输技术。E-mail:zstsue18103133@163.com
赵晋斌 男,1972年生,教授,博士生导师,研究方向为电力电子电路、无线电能传输技术。E-mail:zhaojinbin@shiep.edu.cn(通信作者)
(编辑 郭丽军)