 (1)
(1)摘要 四管Buck-Boost变换器(FSBB)具有无源元件少、开关管电压应力低、输入输出电压同极性、控制自由度多等优势,非常适用于宽输入电压的预调节器。该文对传统三模式控制的中间模式进行优化,提出一种改进型三模式控制策略,降低了导通损耗,提升了变换器工作效率。为进一步提高功率密度、降低高频硬开关带来的开关损耗和电磁干扰,该文提出变频控制策略,能够在全电压范围内实现软开关。分析表明,改进型三模式控制可优化变频范围,与变频软开关控制具有很好的契合度。在实验室研制了一台输入80~160V,输出125V/300W的原理样机,验证了所提控制策略的正确性,并通过效率对比和损耗分析证明所提控制策略有利于FSBB实现高效率和高功率密度。
关键词:四管Buck-Boost变换器 改进型三模式控制 变频控制 软开关 电感电流
随着科技的发展和进步,许多用电场合都对电源变换器提出了更高的要求,这主要体现在高效率、高功率密度等方面[1-3]。在航天电推进单元中,电源处理单元(Power Processing Unit, PPU)阳极电源通常采用太阳能电池阵列供电,为实现最大功率跟踪,其输入电压通常会在较宽的范围内变化[4-5]。在分布式通信电源供电系统中,通常会在48V母线上并联蓄电池以保证不间断供电。由于蓄电池的充放电特性,该母线电压也会在较宽的范围内变化[6]。上述宽范围变化的输入电压给电源中的变压器优化设计带来不便,通常的应对方案是用非隔离变换器将此输入电压预调节至额定输入电压附近,再由隔离变换器将该电压变换至所需电压。这里前级预调节器的拓扑选择、特别是控制策略优化问题为提高电源的效率及功率密度提出了新的挑战。
为了在宽输入电压范围内获得高效率,文献[6-9]提出将Buck变换器和Boost变换器级联,省去中间母线电容,并采用同步整流技术,得到四管Buck- Boost(Four-Switch Buck-Boost, FSBB)变换器。FSBB不仅能够实现升降压功能,且相较于传统的非隔离型升降压变换器而言,具有无源元件数量少、开关管电压应力低、输入电压与输出电压极性相同等优点[10-11]。
针对FSBB的控制策略,文献[12-13]研究了主功率管同步开关的单模式控制策略,其控制简单、易实现,但电感电流的脉动较大,会增大功率器件的电流应力。文献[14-15]研究了两模式控制策略,当输入电压高于输出电压时,变换器工作于Buck模式,反之则工作于Boost模式。任意时刻仅有一个桥臂开关,开关损耗明显降低;此外也能有效降低电感电流有效值,从而降低导通损耗。但当输入电压接近输出电压时,变换器易在两种工作模式之间反复切换,影响系统的稳定运行。为此,文献[16]提出三模式控制策略,在两模式控制的基础上加入滞环,当输入电压位于模式分界点附近,采用Buck-Boost模式。该控制策略能够有效解决模式切换带来的问题,且能够在大部分输入电压范围内实现变换器高效率运行,但其工作于中间的Buck-Boost模式时仍然存在电感电流平均值和脉动较大的问题。
为了进一步满足高功率密度的要求,采用高频新器件并提高变换器的工作频率是必由之路。然而在传统的控制策略下,负载较重时FSBB将工作在硬开关状态,在高频工作时开关损耗明显增大,难以保证变换器的高效率[17];此外,硬开关变换器在开关管动作时产生较大的开关噪声易干扰电路的正常工作,这限制了变换器开关频率的提升[18]。而当负载较轻时,FSBB虽然能够实现软开关,但电感电流的脉动过大,导致变换器导通损耗大。
文献[19-21]针对同步整流的Boost变换器及双向DC-DC变换器,采用改变开关频率的方式使其工作在断续导通模式(Discontinuous Conduction Mode, DCM),从而在不添加辅助元件的条件下自然实现软开关,提升变换器工作效率。FSBB的控制自由度较多,包括两主功率管各自的占空比、开关频率、两主功率管开通或者关断时刻等,多个自由度为其优化控制提供了可能。可见,FSBB也可利用开关频率这一自由度来实现变换器软开关。
本文针对四管Buck-Boost的优化控制进行研究。首先,针对传统的三模式控制中间模式电感电流较大的问题,提出改进型三模式控制策略;然后,在解决模式切换问题的基础上,优化电感电流,减小导通损耗,提升变换器效率;最后,为进一步提升工作效率和功率密度,本文提出FSBB的变频控制策略,使开关管在无额外辅助元器件的条件下自然实现软开关,大幅减少开关损耗、抑制开关噪声。
图1所示为FSBB变换器的电路拓扑,其输入电压Vin与输出电压Vo的基本关系为
 (1)
(1)
式中,d1、d2分别为Buck桥臂、Boost桥臂的主功率管Q1、Q4的占空比。
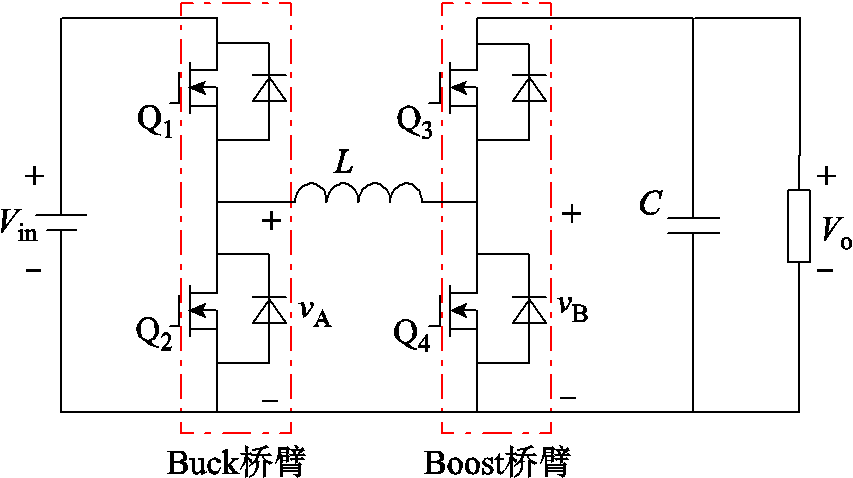
图1 四管Buck-Boost变换器的拓扑结构
Fig.1 Topology of four-switch Buck-Boost converter
由FSBB拓扑可见,电感电流在每一时刻都会流经开关管和电感本身,因此电感电流的平均值和脉动将对变换器的导通损耗产生主要影响。FSBB的传统三模式控制策略中,主要的工作模式为Buck、Boost、Buck-Boost。Buck模式下FSBB的Boost桥臂的主功率管Q4常关(d2=0),Boost模式下FSBB的Buck桥臂的主功率管Q1常开(d1=1)。传统的Buck-Boost模式下,两主开关管Q1和Q4同时开通和关断(d1=d2=d)。根据FSBB的各工作模式,对电感电流的脉动和平均值进行分析。
传统的Buck-Boost模式下,电感电流iL在Q1和Q4同时导通时上升,此时电感两端的电压为Vin,结合FSBB的输入输出关系,可知这段时间内iL上升的值即为该模式下电感电流脉动值ΔIL1,即
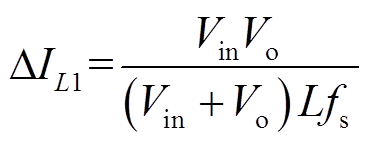 (2)
(2)当Q3导通、Q4关断时,即每个周期中(1-d2)Ts的时间内,电感向负载传递能量,此时输出电流Io与电感电流iL相等,故可得到电感电流的平均值为
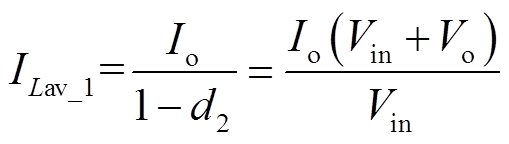 (3)
(3)
当Vin<Vo时,可以得到Boost模式下的电感电流脉动值ΔIL_Boost为
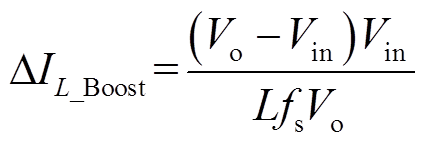 (4)
(4)在Boost模式下,在每个周期中(1-d2)Ts的时间内,电感向负载传递能量,将d1=1代入式(1),则可得Boost模式下电感电流的平均值ILav_Boost为
 (5)
(5)
当Vin >Vo时,可以得到Buck模式下电感电流脉动ΔIL_Buck为
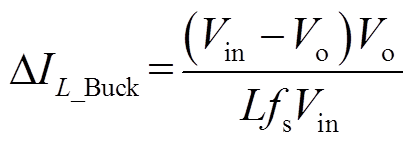 (6)
(6)在Buck模式下,由于Q3是常通(d2=0),因此FSBB电感电流平均值等于输出电流平均值,即
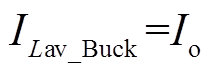 (7)
(7)
为便于分析,以输入80~160V,输出125V/300W为例,分别以传统Buck-Boost模式下输入电压为80V时的电流值为基准值,分别绘制Buck-Boost、Buck和Boost模式下电感电流的脉动值和平均值曲线如图2和图3所示。由图可见,Vin与Vo越接近,Buck-Boost模式下电感电流的脉动值越高于其他两个模式,且电感电流的平均值也较大。故在传统三模式控制下,当输入电压Vin位于[Vo-ΔV,Vo+ΔV]区间内,即工作在传统的Buck-Boost模式时,变换器的导通损耗较大。为提升变换器效率,需对传统三模式控制进行优化。
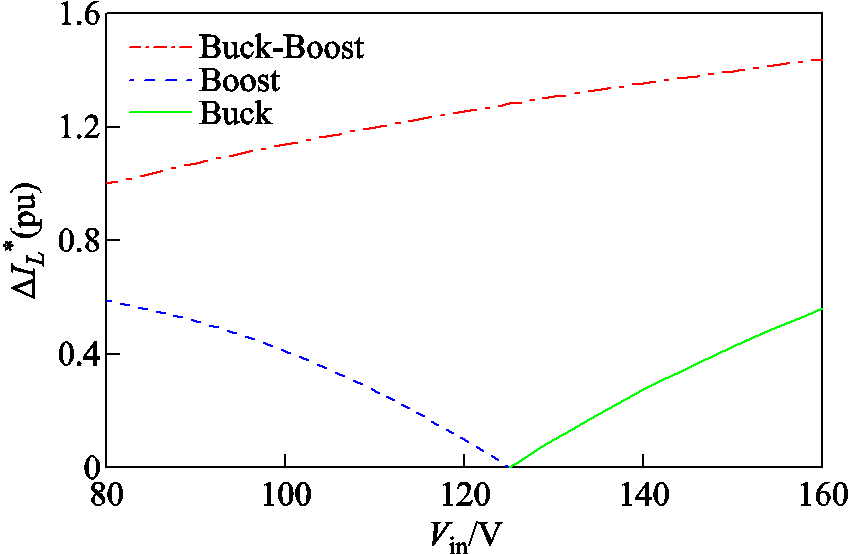
图2 各工作模式下电感电流脉动值曲线
Fig.2 Inductor current ripple curves in traditional modes
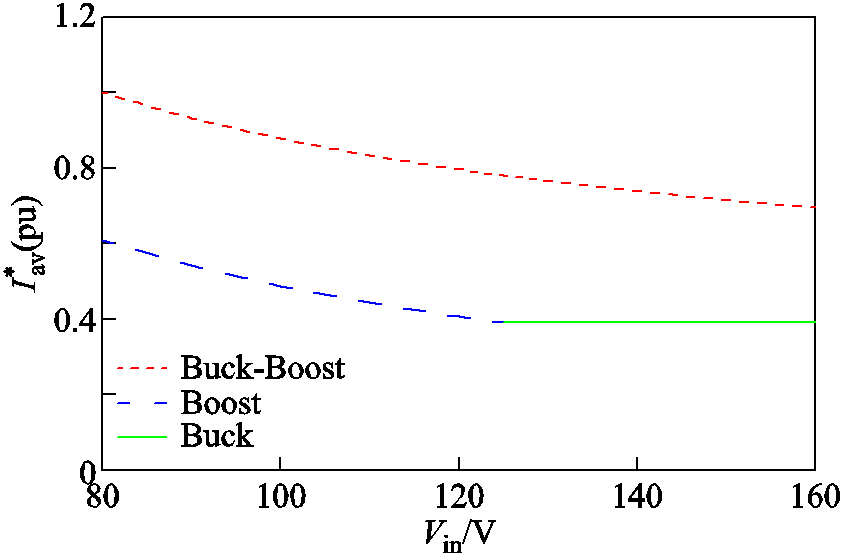
图3 各工作模式下电感电流平均值曲线
Fig.3 Inductor current average curves in traditional modes
对于FSBB的电路拓扑而言,当开关管Q1和Q3同时导通,能量由输入经电感直接传递到输出,称之为直接功率传递通路。直接功率比重越大,变换器的效率越高[13]。因此,为获得更大的直接功率比重,在FSBB工作时,希望d1尽可能大,开关管Q1导通时间长;希望d2尽可能小,开关管Q3导通时间长;并且希望Q1和Q3能够尽可能同时导通。当FSBB工作于传统的Buck-Boost模式下,d1=d2,不存在Q1和Q3同时导通的时间,即不存在直接功率传递。
为此,本文提出一种改进型三模式控制策略。用改进型Buck-Boost模式代替传统Buck-Boost模式。令Buck单元的占空比d1为小于1的固定值D,通过调节Boost单元的占空比d2进行输出电压的调节。则改进型Buck-Boost模式下,输入输出电压关系为
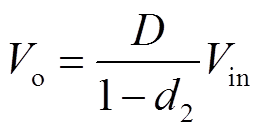 (8)
(8)
由式(8)可知,当1−d2≤D时,FSBB能实现升压功能;反之则能实现降压功能。在改进型Buck-Boost模式中,根据占空比d2与D的关系可分为如下三种情况:
1)当Vin>Vo时,d2<1-D,此时,主要电压电流波形如图4所示。其中,PWM1、PWM4分别为开关管Q1和Q4的驱动信号;vA、vB分别为Buck桥臂和Boost桥臂中点电压;iL为电感电流。在Q1和Q4同时关断期间,电感两端电压为-Vo,此时电感电流下降,电感电流的下降值等于其脉动值。因此,其脉动值可以表示为
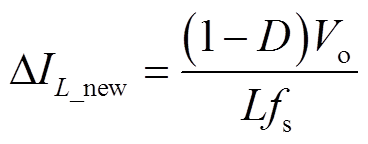 (9)
(9)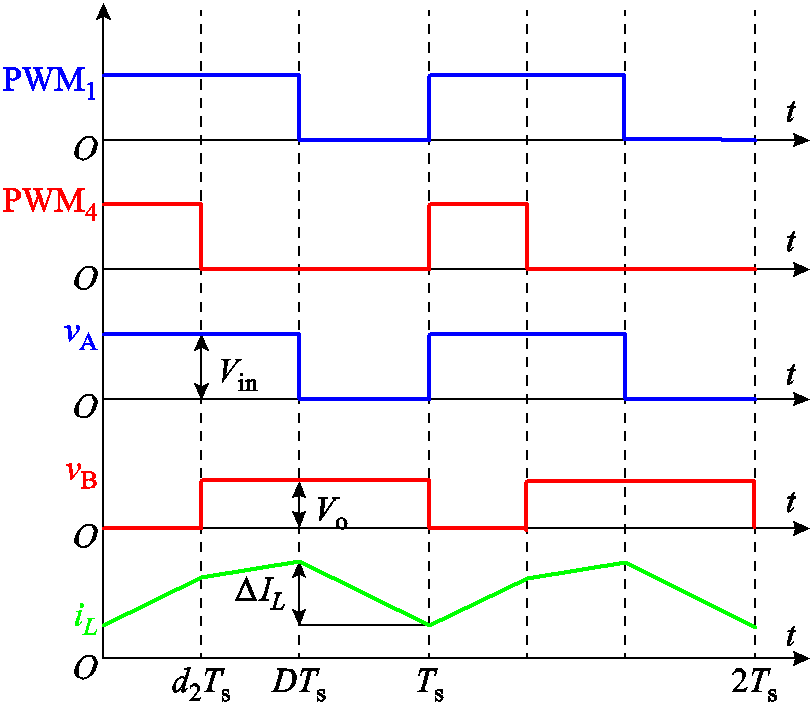
图4 d2<1-D时主要电压电流波形
Fig.4 Waveforms when d2<1-D
2)当Vin≤Vo时,则占空比d2≥1-D。其中当1-D≤d2<D时主要波形如图5所示。
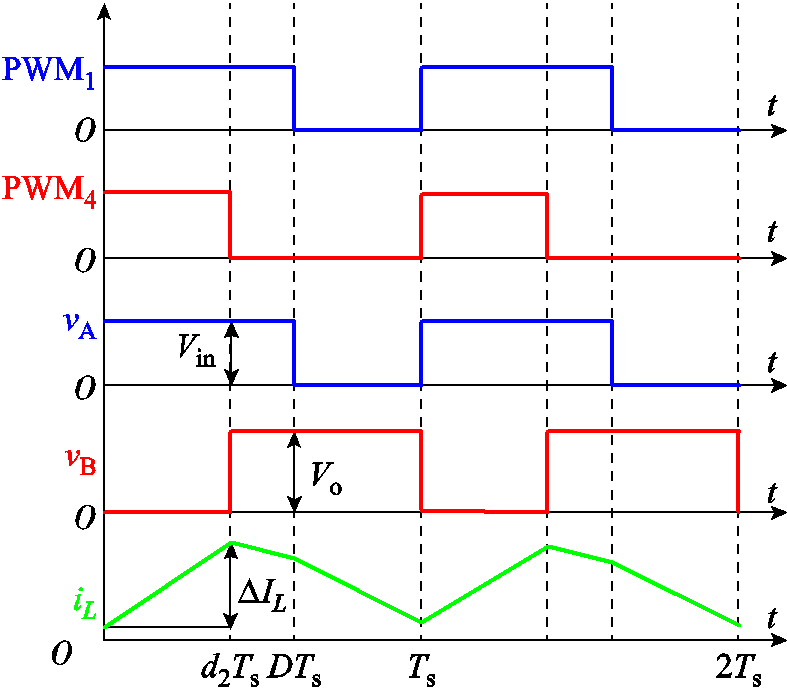
图5 1-D≤d2<D时主要电压电流波形
Fig.5 Waveforms when 1-D≤d2<D
在开关管Q1和Q4同时开通时,电感两端电压为Vin,此时电感电流上升,电感电流的上升值也即电感电流的脉动值为
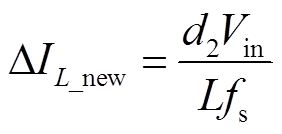 (10)
(10)
3)对于Vin≤Vo时的d2≥D情况,主要波形如图6所示。在开关管Q1开通时,电感两端电压为Vin,此时电感电流上升,其脉动值可以表示为
 (11)
(11)
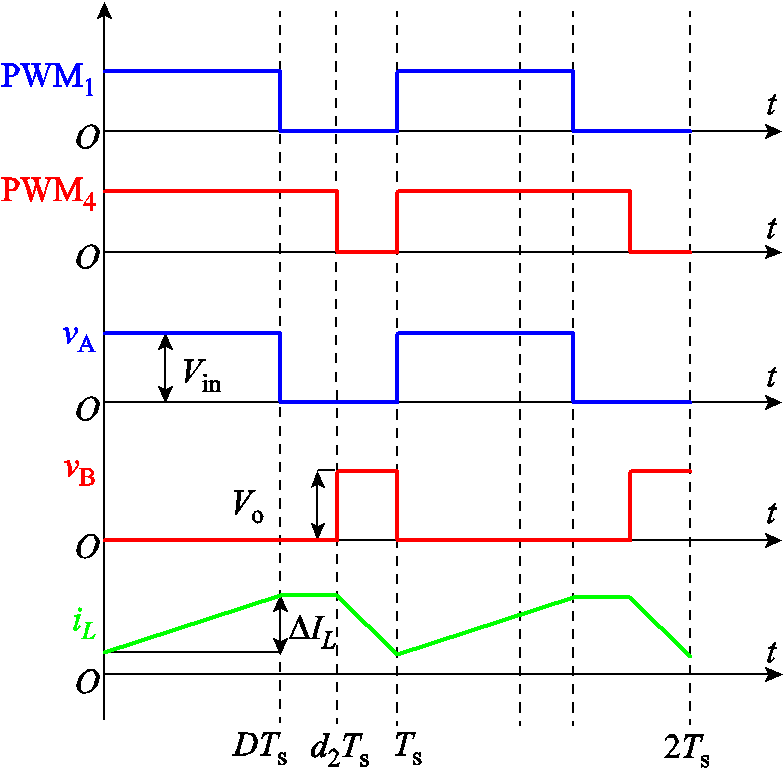
图6 d2 ≥D时主要电压电流波形
Fig.6 Waveforms when d2≥D
综合以上三种情况并结合输入输出关系,可得改进型Buck-Boost模式电感电流的脉动值为
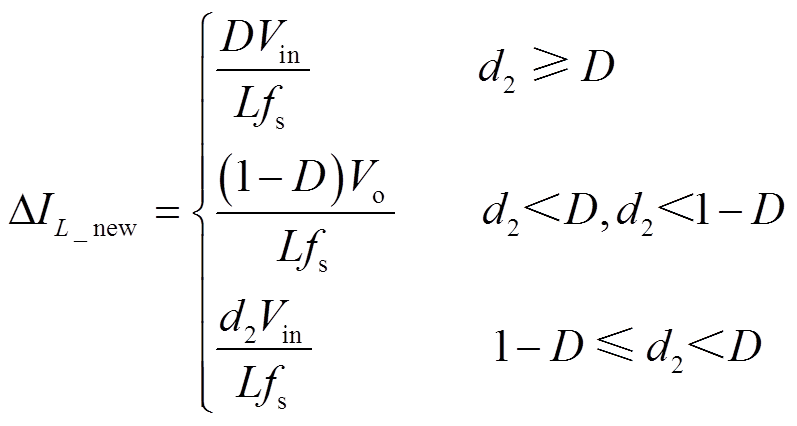 (12)
(12)在改进型Buck-Boost模式下,当Q3导通、Q4关断时,即每个周期的(1-d2)Ts期间,电感向负载传递能量。结合式(8)即可得,在上述三种情况下电感电流平均值均为
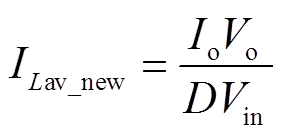 (13)
(13)
同理,以传统Buck-Boost模式下输入电压为80V时的电流值为基准值,分别绘制出全电压范围内,传统Buck-Boost模式和改进型Buck-Boost模式下电感电流的平均值和脉动值曲线如图7和图8所示。由图可见,相较于传统Buck-Boost模式,改进Buck-Boost模式下FSBB电感电流脉动值和平均值大幅降低。
在FSBB的两模式控制策略中,插入改进型Buck-Boost模式,即得到改进型三模式控制策略。改进型三模式下输入和输出电压之间的关系为
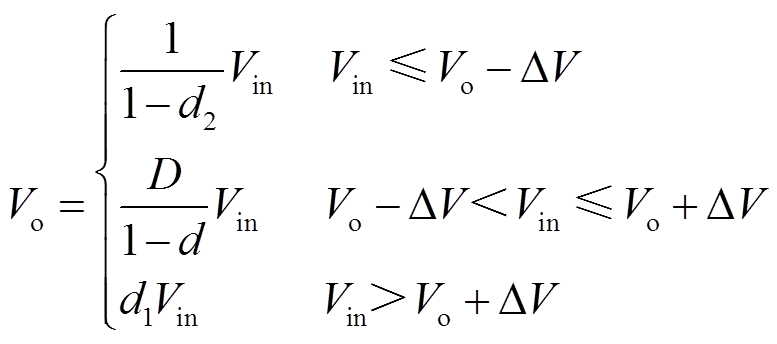 (14)
(14)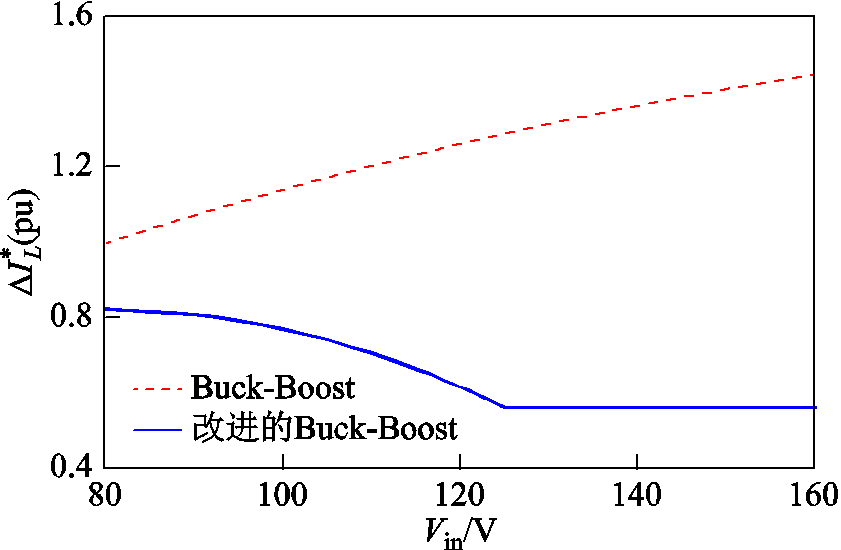
图7 电感电流脉动量标幺曲线
Fig.7 Scal-unit curves of the ripple of inductor current
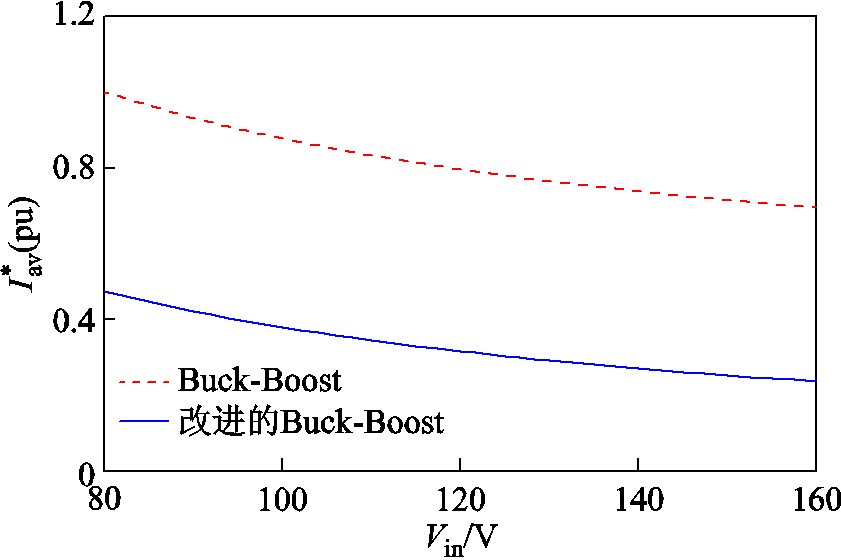
图8 电感电流标幺化均值曲线
Fig.8 Scal-unit curves of the average value of inductor current
相较于两模式控制策略,该控制方式能够解决在输入输出电压接近时,变换器在Buck模式和Boost模式下频繁切换影响系统稳定运行的问题。而相较于传统的三模式控制策略,改进型三模式控制策略能够降低中间模式下电感电流的脉动和平均值,提高升降压模式下FSBB的工作效率。
如前所述,为了进一步实现变换器的高功率密度,采用新型开关器件并提高开关频率是有效举措。然而,随着负载增加,FSBB将工作于硬开关状态,限制了开关频率及效率的提升。据此,本文提出FSBB变换器的变频软开关的控制策略。FSBB软开关工作波形如图9所示。其开关管切换的等效电路如图10所示。
假设在Vin>Vo的情况下,结合图9和图10,说明FSBB的软开关实现条件。
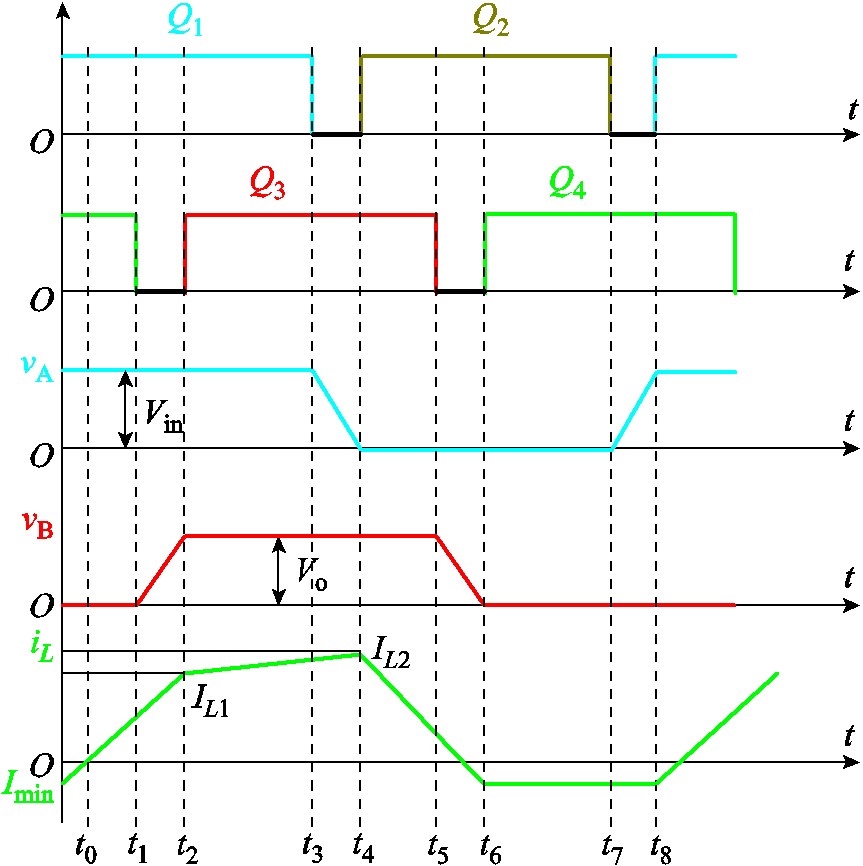
图9 FSBB软开关工作波形示意图
Fig.9 Waveforms of FSBB working in soft switching
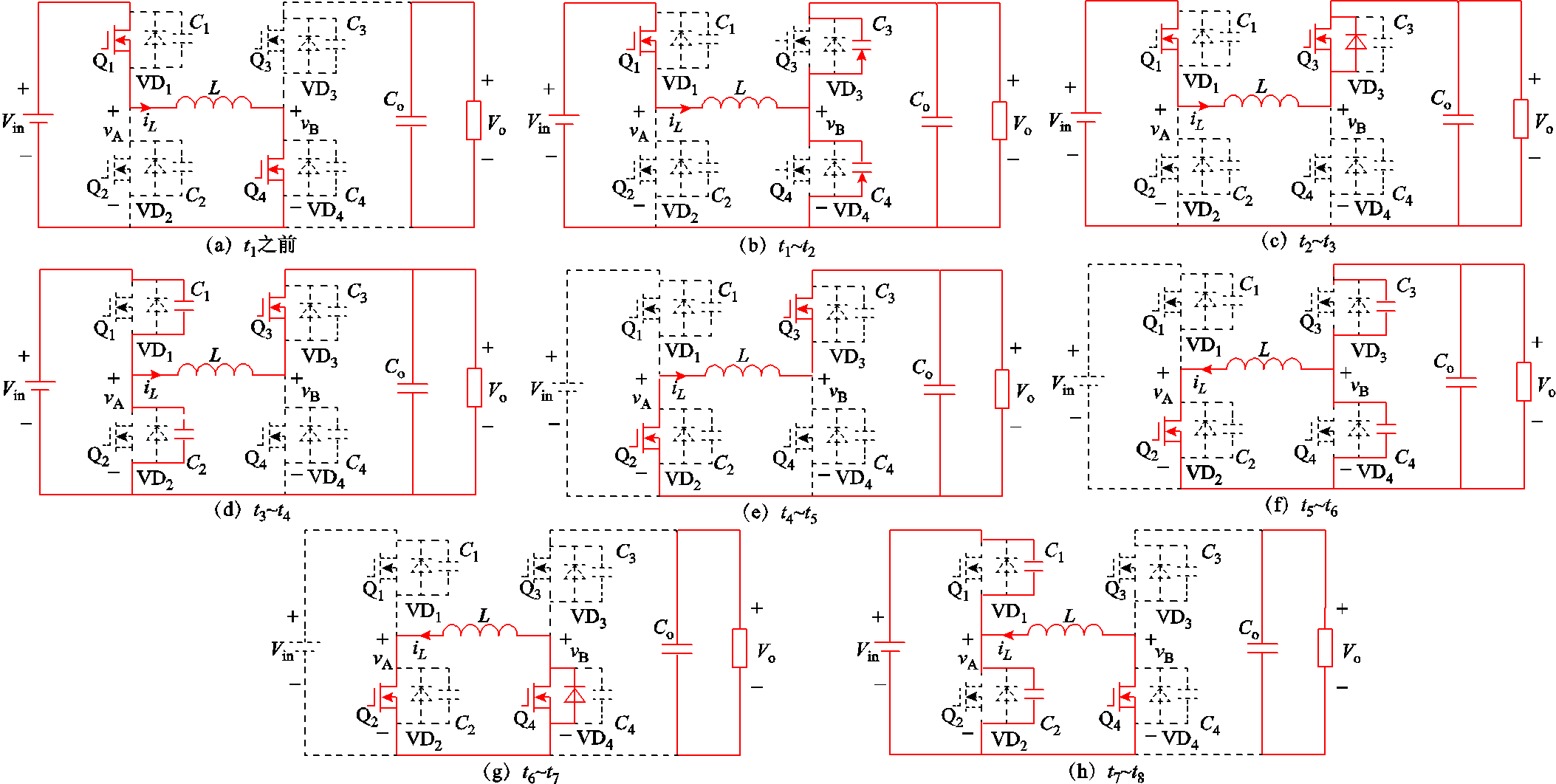
图10 开关管切换的等效电路
Fig.10 Equivalent circuits of the switching stages
开关模态0[0, t1)之前,对应图10a:开关管Q1和Q4同时开通,电感两端电压为Vin,电感电流iL线性上升。t0时刻电感电流过0,之后iL正向流动。
开关模态1 [t1, t2],对应图10b:t1时刻,开关管Q4关断,此时电感电流正向流动。在死区时间内iL对结电容C3完成放电,对结电容C4完成充电。忽略电感电流变化,以图示的电感电流值IL1作为充放电电流,那么这段时间内,C3和C4上的电压可以表示为
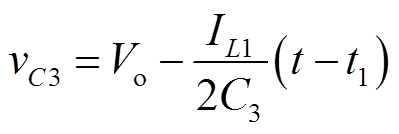 (15)
(15)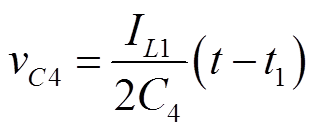 (16)
(16)
开关模态2[t2, t3],对应图10c:t2时刻之前,C3放电完全,使得体二极管VD3正向导通,将开关管Q3的漏源极电压钳位至0。t2时刻Q3的驱动导通,此时Q3为零电压开通(Zero Voltage Switching, ZVS)。然后Q1和Q3处于同时导通状态,此时两桥臂中点电压分别为Vin和Vo,电感电压为Vin-Vo,iL线性增加。
开关模态3[t3, t4],对应图10d:t3时刻,开关管Q3开通,此后iL正向流动。忽略电感电流变化,以图示的电感电流值IL2作为充放电电流,在这段时间内,C1和C2上的电压可以表示为
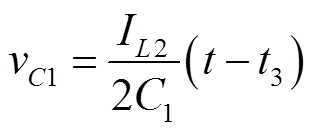 (17)
(17)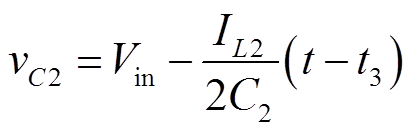 (18)
(18)
开关模态4[t4, t5],对应图10e:t4时刻C2放电完全,使得体二极管VD2正向导通,将电压钳位至0,此时Q2为零电压开通。Q2和Q3同时导通,Buck单元中点电压vA为0,Boost单元中点电压vB为Vo,电感电压为-Vo,iL线性减小。
开关模态5[t5, t6],对应图10f:t5时刻,关断开关管Q3,此时电感电流反向流动,iL完成对结电容C3充电的同时,完成对C4放电。
开关模态6[t6, t7],对应图10g:t6时刻C4放电完全,使得体二极管VD4正向导通,此时Q4零电压开通。开关管Q2和Q4同时开通时,电感经Q2、Q4形成回路,iL保持不变。
开关模态7[t7, t8],对应图10h:这段时间内,电感电流为负,iL同时向结电容C1放电,向C2充电。t8时刻,C1电压为0,C2电压为Vin。
之后FSBB进行下一个开关周期的变换。Vin≤Vo的情况与上述分析类似,这里不再赘述。
基于以上分析可见,FSBB实现软开关的条件为:在死区时间内,电感电流完成对结电容的充放电,使结电容两端电压降至零电压。
因此,在关断Q1、Q4时,希望电感电流iL正向流动,结电容完成充放电且VD2和VD3自然导通后,开通Q2和Q3,由此Q2和Q3即能实现零电压开通。在关断Q2、Q3时,希望电感电流iL反向流动,结电容完成充放电且VD1和VD4自然导通后,开通Q1和Q4,由此Q1和Q4即能实现零电压开通。因此,FSBB要实现软开关,需满足
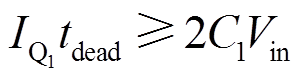 (19)
(19)
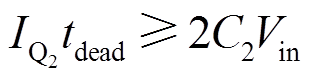 (20)
(20) 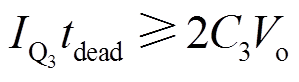 (21)
(21)
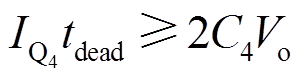 (22)
(22)
式中,tdead为死区时间;IQ1~IQ4为开关管Q1~Q4开关时刻流经开关管的电流值,此时的电流即为电感电流瞬时值iL。假设结电容C1 = C2 = C3 = C4 = Coss。由此可得电感电流绝对值IL的范围为
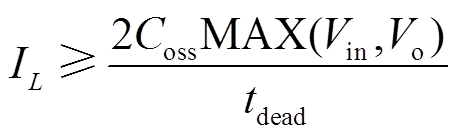 (23)
(23)式中,IL为FSBB四个开关管Q1~Q4实现ZVS所需的电感电流瞬时值的绝对值。
定频控制不同负载下电感电流波形如图11所示,开关管Q1、Q4实现软开关需要电感电流为负。但在现有控制方式下,一方面电感电流平均值IL将随着负载的增加而增大,Imin也会随之增大为正,FSBB在负载较大时将无法实现软开关;另一方面,当负载减小时,电感电流Imin1将会过小,此时Q1和Q4虽然能够实现软开关,但电感电流的脉动得不到控制,因此脉动仍然较大,导致变换器的导通损耗增加。
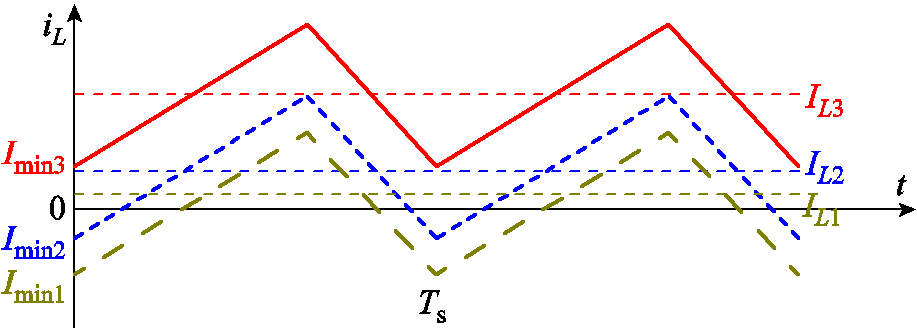
图11 定频控制不同负载下电感电流波形
Fig.11 Waveforms of inductor current for different loads under constant frequency
为保证Q1、Q4开通之前电感电流为负,本文提出一种变频控制策略。如图12所示,当负载较重时,电感电流较大,变换器开关周期Ts1较大,开关频率fs1较低;当负载减轻时,电感电流降低,变换器开关周期Ts2较小,开关频率fs2较高。通过变频控制使电感电流最小值过负且满足式(23),就能保证FSBB在实现软开关的同时减小开关损耗和导通损耗。下文将对该控制策略进行具体分析。

图12 变频控制不同负载下电感电流的波形
Fig.12 Waveforms of inductance current at different switching frequencies
图13为四管Buck-Boost变换器在Buck模式下的主要波形。
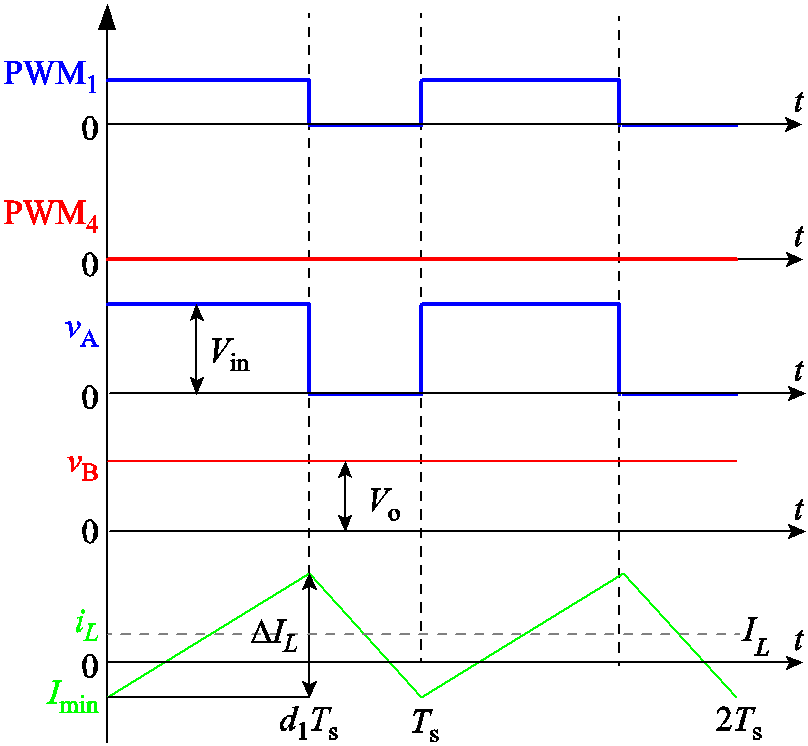
图13 Buck模式下FSBB变换器的主要波形
Fig.13 Waveforms of FSBB in Buck mode
在一个开关周期内Q1的导通时间为d1Ts,此时Q1和Q3同时导通,电感两端的电压为Vin-Vo,电感电流上升。由此可得电感电流脉动和电压的关系为
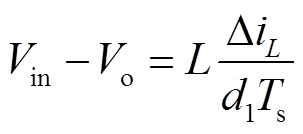 (24)
(24)经过变换,得到频率与电压、脉动值的关系式为
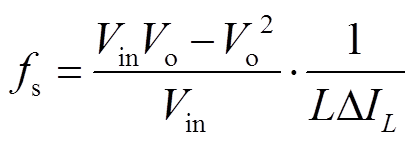 (25)
(25)
将脉动值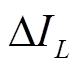 用最小电感电流值表示为
用最小电感电流值表示为
 (26)
(26)将式(26)代入式(25)得到频率的表达式为
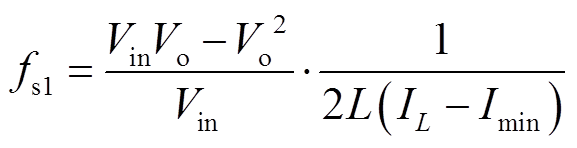 (27)
(27)
同理,根据电感电流与输入输出电压的关系,能够得到Boost模式下开关频率的表达式为
 (28)
(28)FSBB工作于改进型Buck-Boost模式时,Vin与Vo接近,此时d1与1-d2的比值接近于1。为了获得更大的直接功率传输比,希望Q1和Q3同时导通时间尽可能长,因此希望d1和1-d2都尽可能接近于1,由此容易得到d2<d1,即d1为接近于1的固定值D,且d2<D(如图4和图5所示),不会出现d2>D(如图6所示)的应用情况。由图4和图5可见,此时电感电流始终保持三段式。
为了便于分析,图14给出d2<1-D情况下FSBB能够实现ZVS的主要的波形。
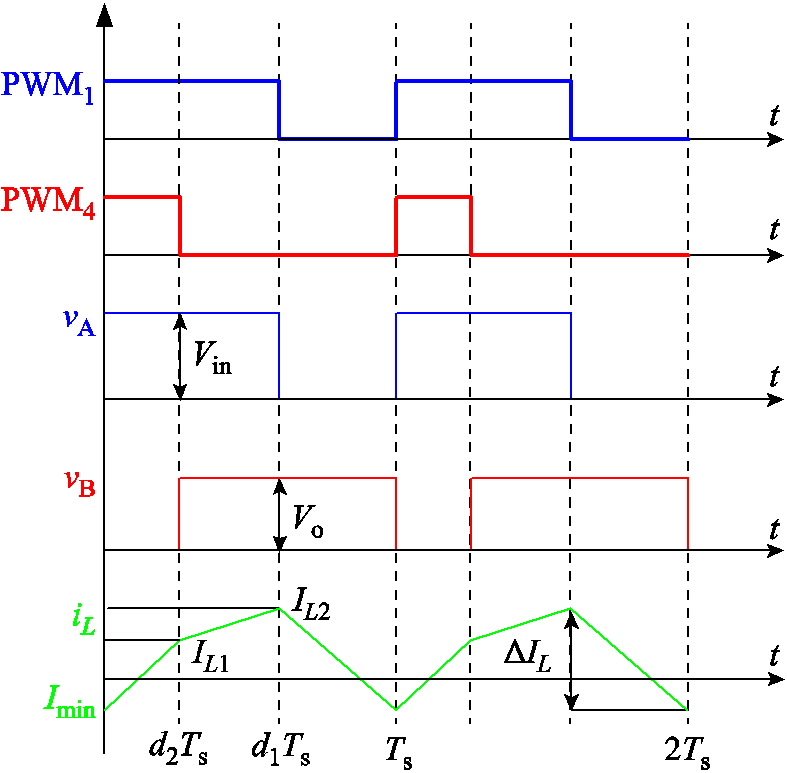
图14 d2<1-D时FSBB变换器主要电压电流波形
Fig.14 Waveforms of FSBB when d2<1-D
由图14可得,在d2Ts和(d1-d2)Ts时间段内,电感电流与输入输出电压之间的关系为
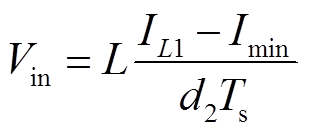 (29)
(29)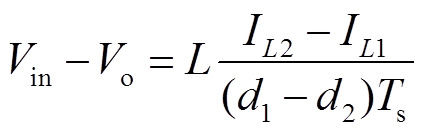 (30)
(30)
当Q3导通时输出电流与电感电流相等;当Q3关断时输出电流为0。因此输出电流的平均值Io与电感电流之间的关系为
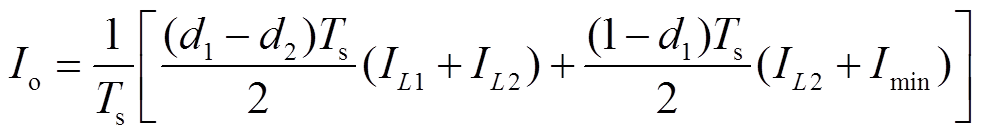 (31)
(31)结合式(29)~式(31),可得在改进型Buck-Boost模式下开关频率和电感电流最小值的关系为
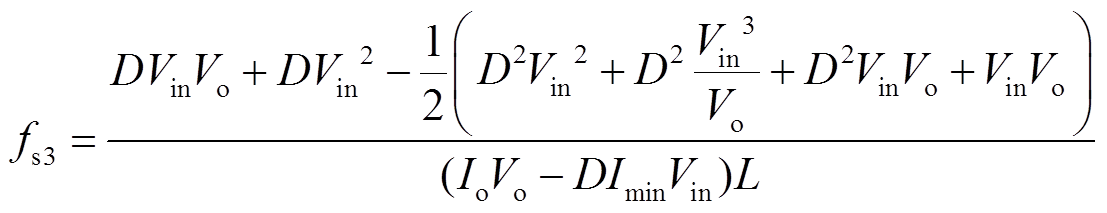 (32)
(32)
在改进型三模式控制下,可由输入输出电压关系确定FSBB的工作模式。用两主功率管的占空比控制输出电压。由式(27)、式(28)、式(32)可见,在各工作模式下均可采用开关频率这一自由度来控制电感电流的最小值Imin,使Imin为能够保证FSBB实现软开关条件下的最小电感电流。在Buck模式和Boost模式,采用该控制策略所得的脉动量ΔIL为实现软开关的最小脉动值,因此变换器的开关损耗和导通损耗均能大幅减小。另外,在优化变频范围方面,改进型三模式控制也具有显著优势。
不同的工作模式采用变频控制策略时,电感电流平均值和脉动不同,频率的变化范围差异也较大。
由图2和图3对比可见,单模式控制策略下,电感电流的平均值和脉动约为两模式控制的2倍。因此,若在此基础上采用变频方式来实现软开关,则电感电流的脉动将会进一步提升,从而进一步增大导通损耗,不利于变换器效率的提升。
两模式控制下变换器主要工作于Buck模式和Boost模式,其开关频率与电感电流的关系与式(27)、式(28)相同。
传统的三模式控制下,输入电压与输出电压接近时,FSBB工作于传统Buck-Boost模式。在Buck-Boost模式下,也可以得到电感电流最小值与开关频率之间的关系为
 (33)
(33)为保证FSBB全电压范围内均能够实现软开关,则需要在整个电压范围内选择电感电流最小值Imin最高点,设计四管Buck-Boost变换器的电感值,使得FSBB在该处的工作频率为最低频率时,Imin仍能保证实现软开关。
为优化频率变化范围,并且保证FSBB在全电压范围内实现软开关,选择输入电压Vin为110V时的频率为最低频率来设计电感。采用相同设计规则,以Vin为110V时的开关频率为基准值进行标幺化,以输入电压Vin和输出电压Po为自变量,分别绘制两模式、传统三模式和改进型三模式的频率变换范围的三维图,如图15所示。为便于理解与分析,图16亦同时给出了300W满载时,以Vin为自变量的开关频率标幺值曲线。由图15可见,以上三种控制策略下,随着负载减小,开关频率均相应提升,但频率变化趋势基本一致;而由图15及图16可见,随着输入电压的变化,以上三种控制策略仅中间模式的变频变化范围差异较大,详细分析如下:

图15 不同控制策略下fs*与Vin、Po的关系曲线
Fig.15 The relationship curve between fs* and Vin, Po under different control strategies
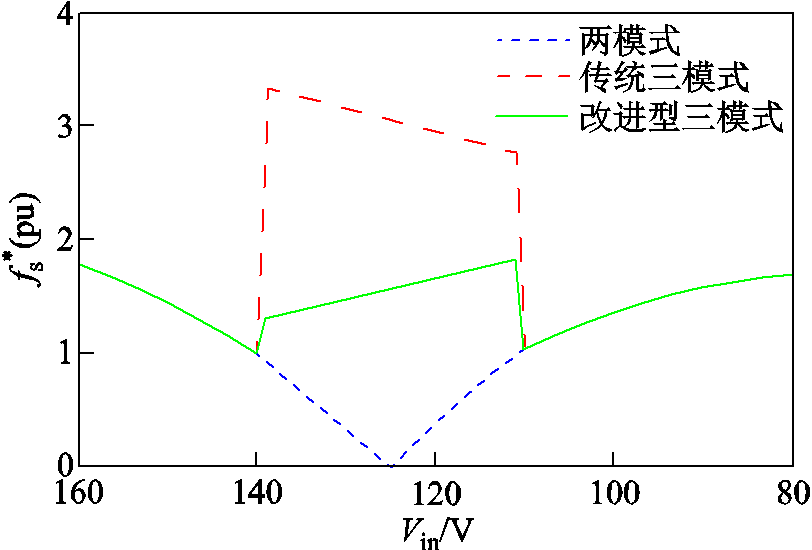
图16 不同控制策略下满载时fs*曲线
Fig.16 The curve of fs* at full load under different control strategies
(1)两模式控制下,在图15所示的电压和负载区间内,FSBB开关频率最大值为基准频率的2.17倍,最小值为0。这是因为在两模式控制下,输入电压与输出电压越接近,电感电流的脉动则越接近于0,通过改变开关频率来保证电感电流最小值过负,则必然会存在开关频率趋于零的一段工作区间。
(2)传统的三模式控制下,最低开关频率为基准频率,中间的传统Buck-Boost模式本质上是增大了电感电流的脉动,不会出现开关频率为0的工作状态。但由于此段工作区间内电感电流最小值Imin过低,因此需要更大程度提高开关频率来提升Imin,使之维持在恰好能够保证FSBB实现软开关的值附近。故其开关频率在满载时将超过3倍基准频率,而在90 W轻载时,开关频率约为基准频率的6倍。可见,该控制策略频率变化范围过大。
(3)改进型三模式控制下,FSBB在图15所示的电压和负载范围内,开关频率标幺值变化范围为1(pu)~2.17(pu)。相较于两模式控制,中间采用改进型Buck-Boost模式,在一定程度上提升了电感电流脉动,来保证开关频率不低于所设定的最低频率,解决了输入电压与输出电压接近时频率过低的问题。而相较于传统的三模式控制策略,改进型的Buck-Boost模式下电感电流的脉动大幅降低,因此电感电流最小值Imin不会远小于零,无需过高的开关频率来提升电感电流的最小值。
综上可见,两模式控制下,在Vin为125V时开关频率为0;而传统的三模式控制下,开关频率的变化范围过大,两种控制策略均不利于磁性元件设计。本文在改进型三模式的基础上采用变频控制策略来实现软开关,能够大幅缩小开关频率变化范围,更利于开关器件的选型以及变换器磁性元件的设计。同时,相较于传统三模式控制,改进型三模式能够在较低的电感电流脉动之下,解决模式切换的问题,在保证FSBB稳定工作的同时,提升变换器的工作效率和功率密度。
对于所提FSBB的改进型三模式变频软开关控制策略,本文首先通过采样输入电压Vin,并根据输入输出电压关系来确定FSBB的工作模式及占空比;然后通过采样负载电流Io,来反映电感电流值;最后根据开关频率的表达式,再结合选定最小电感电流Imin,计算出所需的开关频率,并进行调频控制。本文采用数字控制结合查表法实现前文所提控制策略,改进型三模式变频软开关控制流程如图17所示,具体步骤如下:
(1)DSP上电,初始化控制程序,执行主程序。当FSBB启动时,由于输出电压和输入电压均为0,此时DSP将输出初始工作频率和占空比。
(2)使用ePWM模块输出触发ADC采样模块,采样频率与PWM频率相同,判断输入电压、输出电压、输出电流的采样值大小。若出现过电压或过电流情况,则禁止ePWM模块输出,结束程序进程;若未出现过电压或过电流,则进入下一步。
(3)根据输入电压Vin的采样值判断其工作模式,确定FSBB的工作模式后,进入所确定工作模式的表段。
(4)根据输入电压和输出电流查二维表,确定工作频率fs、占空比d1和d2。
(5)启动ePWM模块,输出当前状态所对应的PWM信号。
(6)结合当前标志位Flag,选择触发下一周期的采样或结束程序。
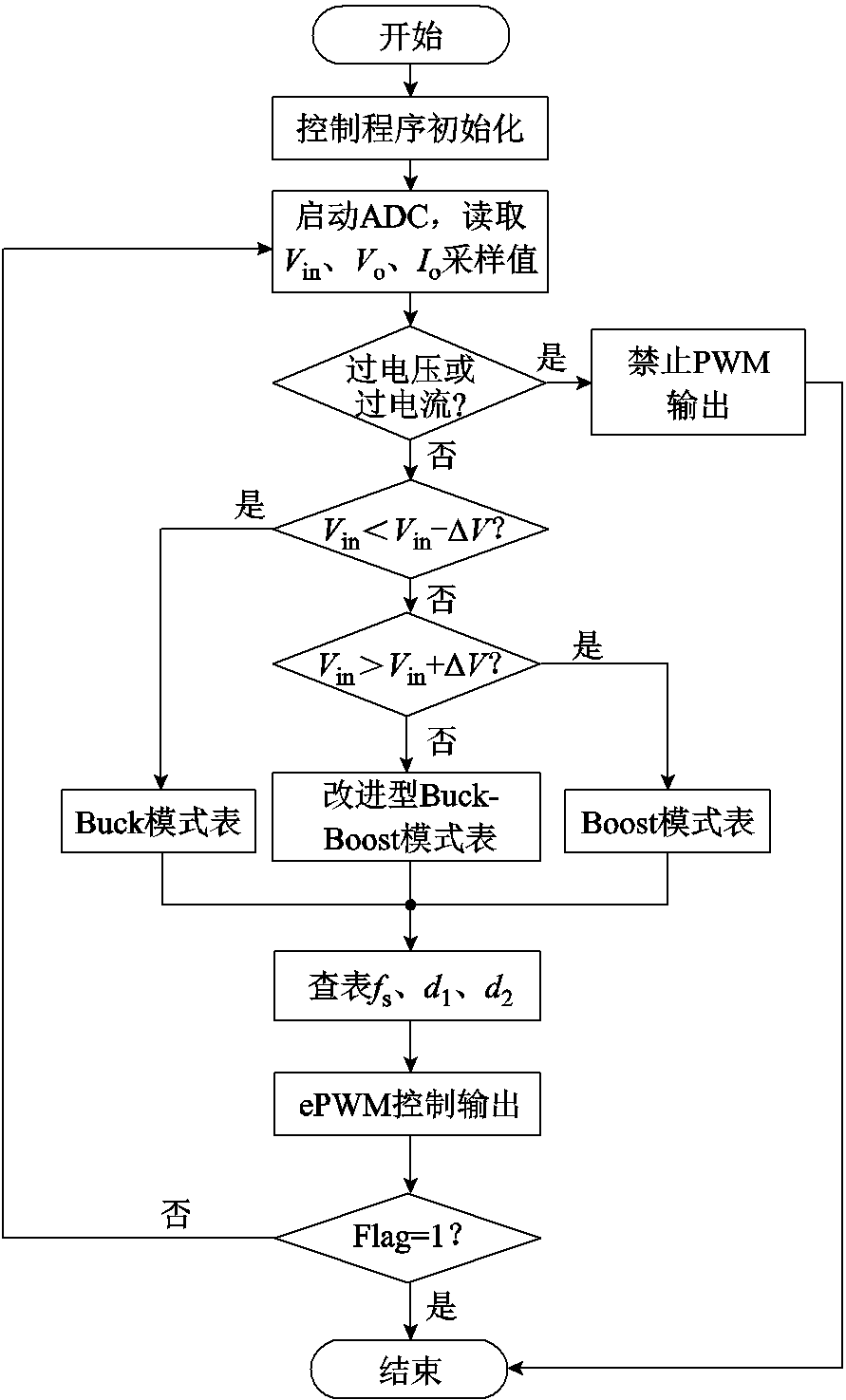
图17 改进型三模式变频软开关控制流程
Fig.17 The flow chart of the improved three-mode frequency-varying control
为验证所提改进型三模式下的变频软开关控制策略,在实验室搭建一台输入电压80~160V、输出电压125V、满载功率为300W的原理样机,并采用新型GaN器件实现高频化和高功率密度。样机主要参数见表1,原理样机图片如图18所示。
图19和图20分别给出了不同电压点,负载分别为300W和90W时的稳态实验波形。由实验波形可见,在三种模式下,电感电流的最小值基本维持在-2A,根据负载不同,开关管的开关频率能够适应负载变化,保证开关管实现零电压开通。图中,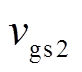 、
、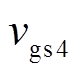 为
为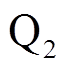 和
和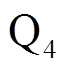 的驱动信号,
的驱动信号,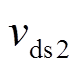 、
、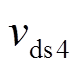 为
为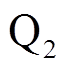 和
和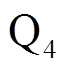 的漏源级电压。
的漏源级电压。

图18 原理样机图片
Fig.18 Photo of the prototype
表1 样机主要参数
Tab.1 The main parameters of the prototype

参数数值(型号) 开关管GS66508T 电感L/μH5.3 输出电容Co/μF25 开关频率fs/kHz0.3~650 控制芯片TMS320F28335 样机尺寸/mm3128×91×25
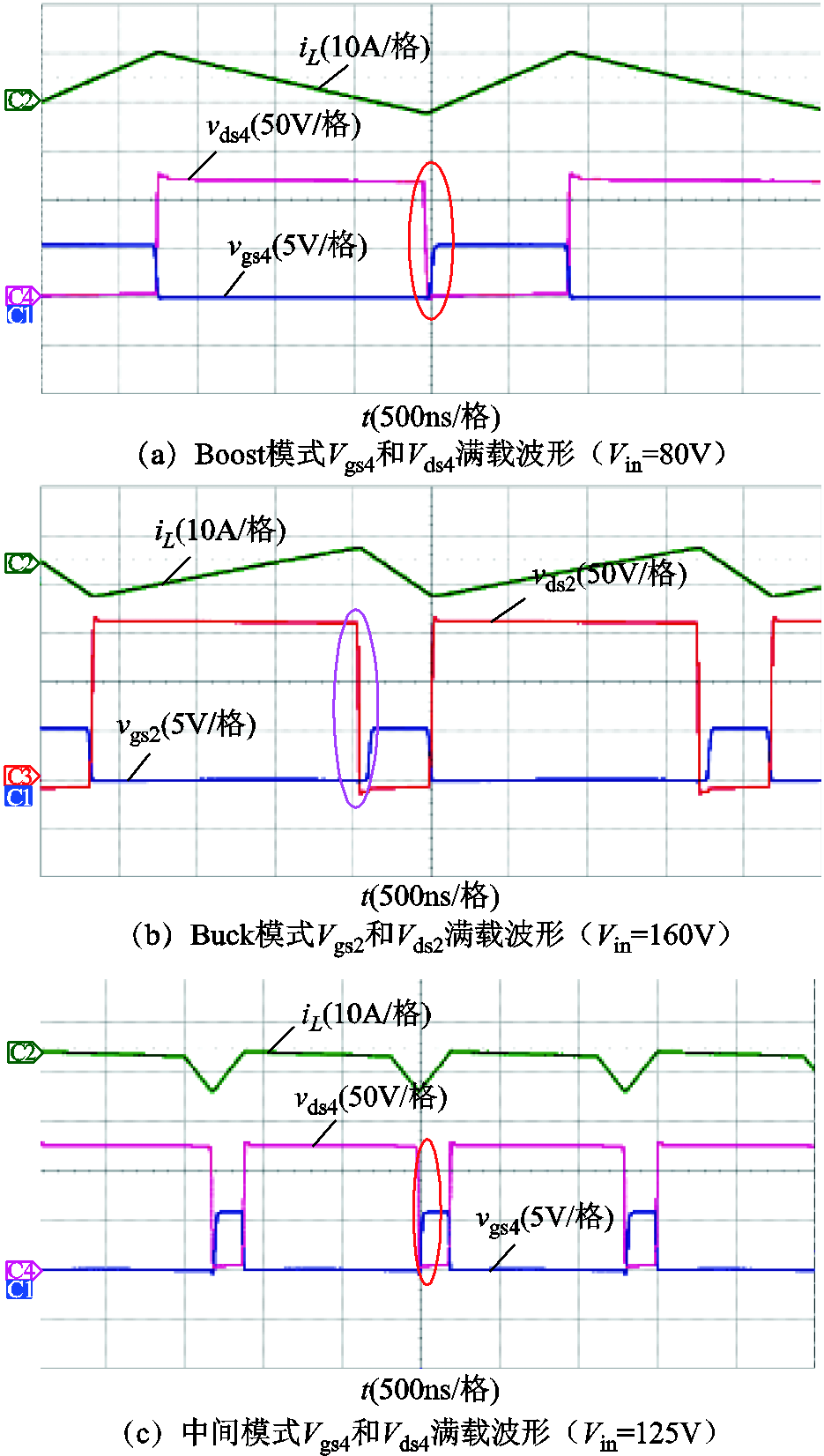
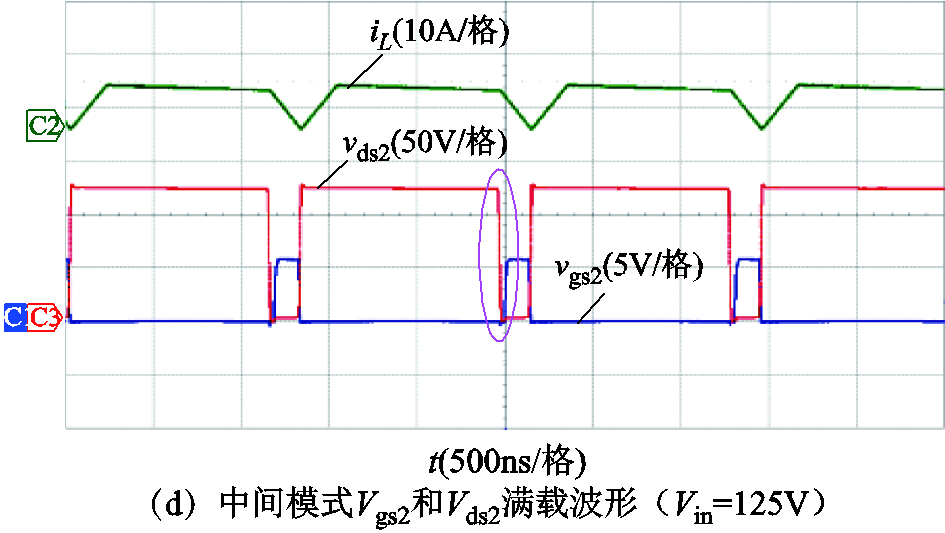
图19 不同输入电压下满载ZVS实验波形
Fig.19 Full load ZVS experimental waveforms under different input voltages

图20 不同输入电压下轻载ZVS实验波形
Fig.20 Light load ZVS experimental waveforms under different input voltages
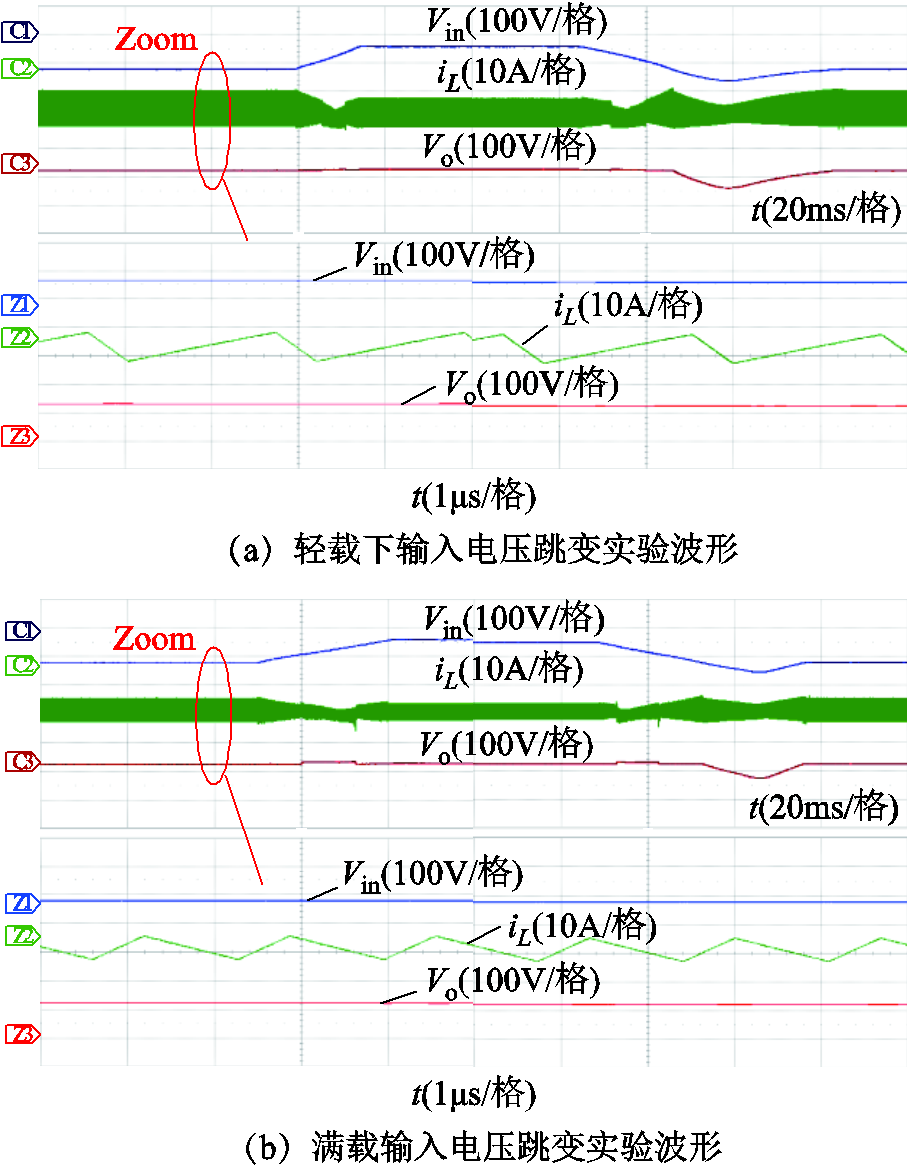
图21 不同负载下动态实验波形
Fig.21 Dynamic waveforms under different loads
由图21可见,在不同负载条件下,当输入电压Vin由80V跳变到160V,再由160V跳变到80V,输出电压和电感电流的波动很小,且均能快速恢复稳态,说明所提控制策略具有较好的动态响应能力。
图22所示为在负载300W和90W时,分别采用传统三模式控制、改进型三模式定频控制、改进型三模式变频软开关控制所测得的效率曲线。
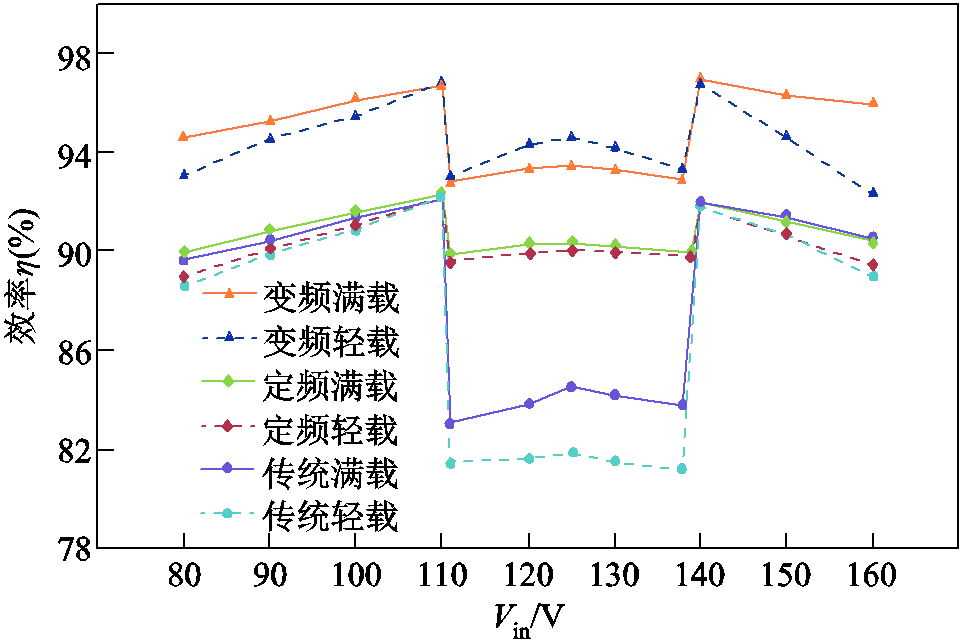
图22 效率曲线
Fig.22 Prototype efficiency curves
由于输入电压宽范围变化时FSBB工作的模式不同,因此变换器的工作效率η也会在较宽的范围内变化。以上三种控制策略下,相较于Buck模式和Boost模式而言,中间模式的电感电流脉动均有所增加,且四个开关管均进行开关动作,因此在模式分界点处存在效率突变。
传统三模式和改进型三模式定频控制下,FSBB工作于硬开关状态,开关损耗极大,因此工作效率较低;且硬开关导致器件温度升高,从而增大了晶体管的导通电阻,导通损耗也急剧上升。在输入电压Vin为139 ~ 160V范围内时,改进型三模式定频控制优化了电感电流脉动,故工作效率高于传统三模式。
当采用改进型三模式变频控制策略时,FSBB的电感电流脉动即为能够保证实现软开关条件下电感电流脉动最小,因此其导通损耗小;且由于开关管实现了零电压开通,因此其开关损耗大幅降低,变换器工作效率大幅提升。
综合以上分析结合效率曲线可见,在传统三模式控制下,FSBB整体工作效率较低,为81.1%~ 92.1%;中间模式下工作效率仅为81.1%~84.5%。在改进型三模式定频控制下,FSBB整体工作效率为88.9% ~ 92.3%;中间模式工作效率为89.6%~90.2%,改进型Buck-Boost模式对电感电流脉动的优化使得中间模式工作效率提升约6%。采用改进型三模式变频控制时,FSBB的工作效率为93%~96.9%;相较于改进型三模式定频控制,FSBB实现软开关后工作效率进一步提升了约4%。
为更直观地说明本文所提改进型三模式变频控制策略对变换器工作效率的提升,图23分别给出了FSBB在三种控制策略下满载工作时的热分布图。可见,采用传统控制策略时,由于FSBB工作于硬开关状态,且导通损耗较大,故其最高工作温度达到102.3℃;而采用改进型三模式定频控制策略时,虽然FSBB仍工作于硬开关状态,但中间模式导通损耗大幅降低,故其最高温度为82.7℃;在改进型三模式基础上采用变频控制策略,由于此时FSBB实现软开关,开通损耗和导通损耗显著降低,故其最高温度大幅下降,仅为35.7℃。


图23 FSBB满载工作热分布图
Fig.23 Heat distribution map of FSBB at full load
对于FSBB,根据改进型三模式定频控制和改进型三模式变频软开关控制下的电感电流、各工作点的开关频率、温度等参数,结合晶体管的特性,得到满载300W时FSBB的损耗分布情况,如图24所示。
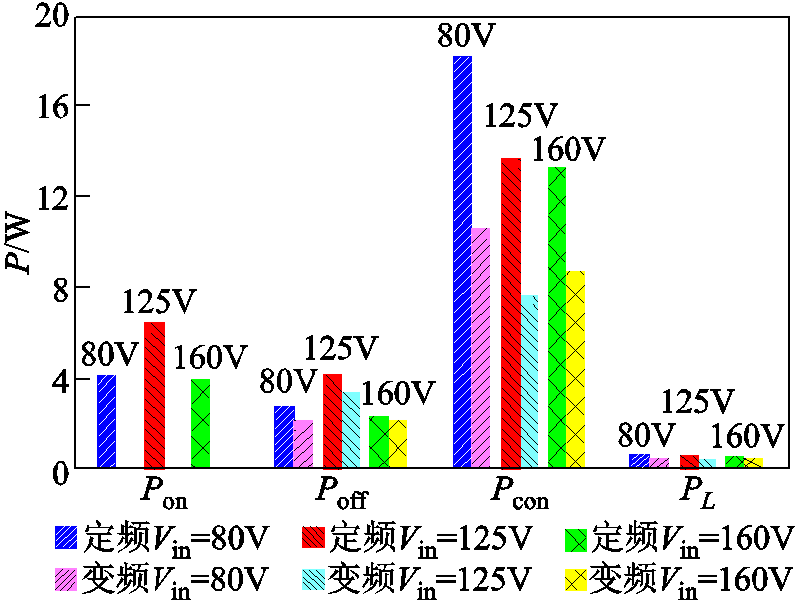
图24 FSBB满载损耗分布对比图
Fig.24 Comparison chart of loss distribution of FSBB at full load
由图24可见,采用变频软开关控制策略后,保证主功率管均能实现零电压开通,因此理论上开通损耗Pon=0。器件上的损耗通常以热的形式耗散,由于采用变频控制实现软开关,晶体管的温度大幅降低,其导通电阻Rds(on)大幅降低,因此导通损耗Pcon明显下降。在满载工作时,采用变频控制的开关频率将低于500kHz,因此关断损耗Poff也略小于定频控制状态下的值。电感上的损耗PL由磁心上的铁损和绕组上的铜损组成,在不同开关频率下电感磁心损耗密度不同,因此在满载工作时,采用变频控制策略电感上总损耗也较小。
传统的三模式控制策略下,仅中间模式与改进型三模式定频控制不同,其电感电流脉动进一步增大,因此其在Vin为125V时的损耗将进一步增大,而在Vin为80V和160V时的损耗均与定频相同,这里不再重复给出。
针对FSBB变换器,本文提出一种改进的三模式控制策略。相较于传统的三模式控制而言,在中间模式下,固定Buck单元的占空比,通过调节Boost单元占空比实现电压的升降压变换。该控制策略下,FSBB能够解决模式切换对系统稳定性的影响,并且能够减小中间模式下电感电流的平均值和脉动,降低导通损耗。
为了进一步提高效率和功率密度,本文提出一种变频软开关控制策略。选择电感电流最小值为开关管在死区时间内刚好完成结电容充放电所需的最小电感电流值。推导电感电流最小值与变换器开关频率之间的关系,通过改变开关频率,能够实现对电感电流最小值的控制,使变换器在不同负载条件下均能实现软开关。并对比了几种控制策略下开关频率的变化范围,阐明了改进型三模式下变频软开关的优越性。最后,通过实验验证、效率对比和损耗分析,证明了所提控制策略有利于FSBB提升工作效率和功率密度。
参考文献
[1] 刘俊峰, 胡仁俊, 曾君. 一种非隔离交错工作的高降压比DC-DC功率变换器[J]. 电工技术学报, 2018, 33(20): 4763-4770.
Liu Junfeng, Hu Renjun, Zeng Jun. A non-isolated interleaved step-down DC-DC converter with high ratio[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4763-4770.
[2] 张雪垠, 徐永海, 肖湘宁. 适用于中高压配电网的高功率密度谐振型级联H桥固态变压器[J]. 电工技术学报, 2018, 33(2): 310-321.
Zhang Xueyin, Xu Yonghai, Xiao Xiangning. A high power density resonance cascaded H-bridge solid-state transformer for medium and high voltage distribution network[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 310-321.
[3] 冯兴田, 邵康, 崔晓, 等. 基于多模态切换的宽电压增益LLC谐振变换器控制策略[J]. 电工技术学报, 2020, 35(20): 4350-4360.
Feng Xingtian, Shao Kang, Cui Xiao, et al. Control strategy of wide voltage gain LLC resonant converter based on multi-mode switching[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4350-4360.
[4] 康小录, 杭观荣, 朱智春. 霍尔电推进技术的发展与应用[J]. 火箭推进, 2017, 43(1): 8-17, 37.
Kang Xiaolu, Hang Guanrong, Zhu Zhicun. Developmentand application of hall electric propulsion technology[J]. Journal of Rocket Propulsion, 2017, 43(1): 8-17, 37.
[5] 王建冈, 阮新波, 陈军艳. 航空用大功率模块电源的设计及关键技术应用研究[J]. 电工技术学报, 2005, 20(12): 95-100.
Wang Jiangang, Ruan Xinbo, Chen Junyan. Develo-pment of high power aviation modular power supply and research on key application technologies[J]. Transactions of China Electrotechnical Society, 2005, 20(12): 95-100.
[6] 任小永, 唐钊, 阮新波, 等. 一种新颖的四开关Buck-Boost变换器[J]. 中国电机工程学报, 2008, 28(21): 15-19.
Ren Xiaoyong, Tang Zhao, Ruan Xinbo, et al. A novel four switch Buck-Boost converter[J]. Proceedings of the CSEE, 2008, 28(21):15-19.
[7] Cuk S M. Molding, analysis, and design of switching converters[D]. California: California Institute of Technology, 1977.
[8] Erickson R W, Maksimovic D. Fundamentals of power electronics[M]. Mew York: Kluwer Academic publishers, 2001.
[9] Chen J, Maksimovic D, Erickson R W. Buck-Boost PWM converters having two independently controlled switches[C]//2001 IEEE 32nd Annual Power Electronics Specialists Conference,Vancouver, BC, Canada, 2001: 736-741.
[10] 朱继承, 蔡丽娟. 几种新型的Buck-Boost变换器的合成[J]. 通信电源技术, 2008, 25(2): 37-40.
Zhu Jicheng, Cai Lijuan. Synthesis of several novel Buck-Boost converters[J]. Telecom Power Technology, 2008, 25(2): 37-40.
[11] 姚川, 阮新波, 王学华. 宽输入电压范围下隔离型全桥Boost变换器的高效率控制[J]. 电工技术学报, 2012, 27(2): 1-9.
Yao Chuan, Ruan Xinbo, Wang Xuehua. High efficiency control strategy for isolated full-bridge-Boost converter suitable for wide input voltage range[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 1-9.
[12] Sahu B, Rincon-Mora G A. A low voltage, dynamic, noninverting synchronous Buck-Boost converter for portable application[J]. IEEE Transactions on Power Electronics, 2004, 19(2): 443-452.
[13] Angkititrakul S, Hu H, Liang Z. Active inductor current balancing for interleaving multi-phase Buck-Boost converter[C]//2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington DC, USA, 2009: 527-532.
[14] Andersen G K, Blaabjerg F. Utilizing the free running current programed control as a power factor correction technique for the two switch Buck-Boost converter[C]//IEEE Applied Power Electronics Conference and Exposition(APEC), Anaheim, CA, USA, 2004: 1213-1219.
[15] Yao Chuan, Ruan Xinbo, Cao Weijie, et al. A two-mode control input voltage feed-forward for two-switch Buck-Boost DC-DC converter[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 2037-2048.
[16] Chen Chengwei, Chen Kunhung, Chen Yaowming. Modeling and controller design for a four-switch Buck-Boost converter in distributed maximum power point tracking PV system applications[C]//IEEE Energy Conversion Congress and Exposition(ECCE), 2012: 1663-1668.
[17] 韦莉, 刘帅, 尤伟玉, 等. 一种新型非谐振型软开关交错并联Boost电路[J]. 电工技术学报, 2017, 32(3): 172-183.
Wei Li, Liu Shuai, You Weiyu, et al. A novel interleaved Boost converter with non-resonant soft-switching[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 172-183.
[18] 陈桂鹏, 陈銮, 陶勇, 等. 基于耦合电感的零电压开关同步Buck变换器[J]. 电工技术学报, 2016, 31(1): 102-109.
Chen Guipeng, Chen Luan, Tao Yong, et al. Zero-voltage-switching synchronous Buck converter with coupled inductor[J]. Transactions of China Electrote-chnical Society, 2016, 31(1): 102-109.
[19] Rogina M R, Rodriguez A, Vazquez A, et al. Improving the efficiency of SiC-based synchronous boost converter under variable switching frequency TCM and different input/output voltage ratios[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7757-7764.
[20] Baek J B, Choi W I, Cho B H. Digital adaptive frequency modulation for bidirectional DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(11): 5167-5176.
[21] Konjedic T, Korosec L, Truntic M, et al. DCM-based zero-voltage switching control of a bidirectional DC-DC converter with variable switching frequency[J]. IEEE Transactions on Power Electronics, 2015, 31(4): 3273-3288.
An Improved Three-Mode Variable Frequency Control Strategy Based on Four-Switch Buck-Boost Converter
Abstract The four-switch Buck-Boost converter has the advantages of fewer passive components, low voltage stress of switches, the same polarity of input voltage and output voltage, and more freedom of control. And it is very suitable for pre-regulators with wide input voltage. In this paper, an improved three-mode control strategy is proposed to optimize the intermediate mode of the traditional three-mode control, which can reduce the conduction loss and improve the efficiency of FSBB. To further increase power density and reduce the switching loss and electromagnetic interference caused by high-frequency hard switching, this paper proposes a variable frequency control strategy to achieve soft switching in the full voltage range. Analysis shows that the improved three-mode control can optimize the frequency conversion range, so it has a good fit with the variable frequency soft switching control. A prototype with input 80~160V and output 125V/300W was developed in the laboratory to verify the correctness of the proposed control strategy. Through efficiency comparison and loss analysis, it is proved that the proposed control strategy is beneficial to FSBB to achieve high efficiency and high power density.
keywords:Four-switch Buck-Boost, improved three-mode control, variable frequency control, soft switching, inductive current
DOI: 10.19595/j.cnki.1000-6753.tces.201549
中图分类号:TM 46
2020年度空间电源技术国家重点实验室源创基金和南京航空航天大学研究生创新基地(实验室)开放基金(kfjj20190310)资助项目。
收稿日期 2020-11-23
改稿日期 2020-12-28
方天治 男,1977年生,博士,副教授,研究方向为串并联组合逆变器、并网逆变器、电力电子系统集成。E-mail:fangtianzhi@126.com(通信作者)
王 愿 女,1996年生,硕士研究生,研究方向为高频变换器及其软开关技术、电力电子系统集成。E-mail:yuan_wang158@126.com
(编辑 郭丽军)