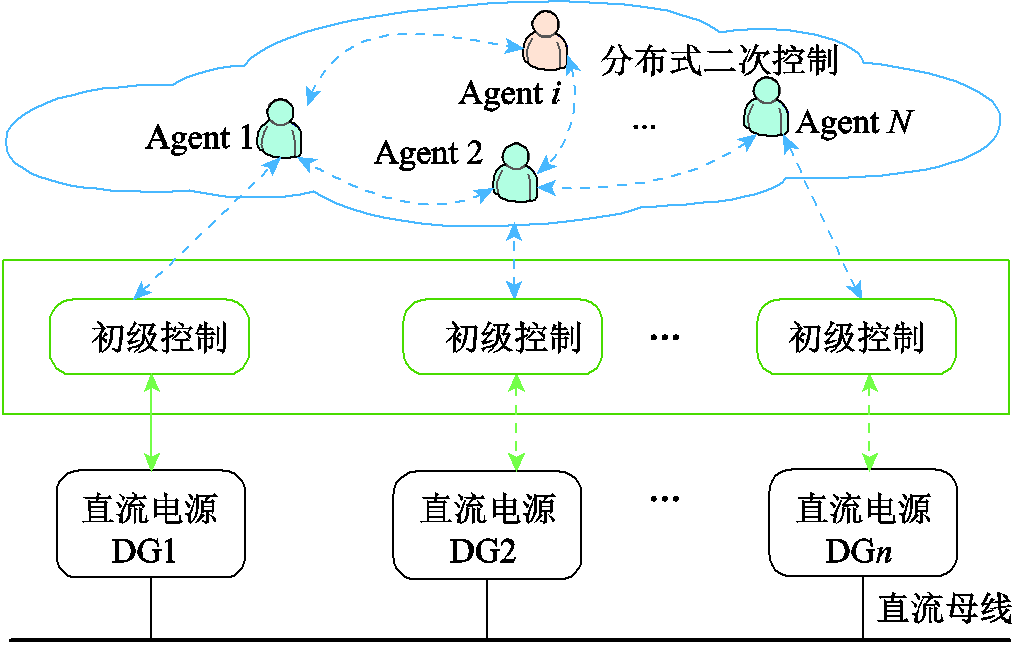
图1 直流微电网分布式分层控制结构
Fig.1 Distributed hierarchical control of a DC microgrid
摘要 基于下垂控制的直流微电网初级控制存在稳态母线电压偏差和电流难以准确分配的缺点,传统采用集中式或分布式的二次控制策略虽然可以实现直流微电网母线电压恢复和电流均分,但并没有考虑各分布式发电单元的发电成本。为提高直流微电网的稳定性和运行效率,基于分布式一致理论,设计了分布式平均母线电压恢复控制算法和分布式最优负荷分配算法,并基于上述算法设计了直流微电网新型分布式二次控制策略。该控制策略可以在二次控制层同时实现母线电压恢复和经济调度,从而提高微电网的运行效率。另外,该控制策略完全分布式实施具有更好的灵活性、鲁棒性和可扩展性。
关键词:直流微电网 分布式一致 二次控制 经济调度 电压恢复控制 多智能体
随着能源需求的增长和对环保问题的重视,可再生能源的开发利用得到越来越多的关注[1-2]。微电网技术的发展可以提高可再生能源在电网的渗透率[3-4],促进传统电网的现代化和智能化。近年来,直流型负荷(电动汽车、电子设备等)和直流分布式电源(光伏电站、储能系统等)的数量在电网中日益增加[5]。与交流微电网相比,直流微电网可以更灵活和高效地接入上述直流负荷和电源,而不需要AC-DC、DC-AC转换模块[6]。另外,直流微电网不存在交流微电网中的频率和无功调节问题。因此,直流微电网技术得到了日益广泛的研究和关注[7-8]。与传统电网类似,直流微电网通常也采用分层控制结构。
直流微电网分布式分层控制结构如图1所示,分层控制结构通常包括初级控制、二次控制和三次控制(图中未画出),并且从下层到上层时间尺度依次增加[9]。初级控制通常采用下垂控制策略,并通过控制各电源的输出电压和电流,实现负荷在各电源间的初级分配[10]。二次控制通常负责微电网系统级的稳定控制,如通过集中式或分布式的方式实现微电网母线电压的恢复控制[11-12]。三次控制通常负责管理微电网的优化运行,如经济调度[13-14]。

图1 直流微电网分布式分层控制结构
Fig.1 Distributed hierarchical control of a DC microgrid
对于直流微电网中的可控分布式电源(Distributed Generator, DG),通常采用电压-功率下垂控制策略[15-16]。下垂控制策略可以提高微电网的电压稳定性,并降低并联运行DG间的环流。然而,下垂控制是一种有差控制,存在稳态电压偏差。另外,由于受线路阻抗影响,很难实现功率的准确分配。因此,需要二次控制策略以恢复母线电压并改善功率分配。
直流微电网二次控制可以采用集中式控制策略[17]或分布式控制策略[18]。对于集中式控制策略,通常需要中央控制器处理所有相关的通信和控制任务。因此,集中式控制策略扩展性差,并容易受单点故障影响。分布式控制策略可以将复杂的计算和控制任务分解,并在各分布式控制器中并行处理。因此,分布式控制策略具有灵活性、可扩展性和不易受单点故障影响的优点。关于直流微电网分布式控制,近年来已有诸多成果[18-25]。文献[18]提出一种基于电压和斜率调整的二次控制策略以改进下垂控制型直流微电网的性能。文献[19]提出一种基于固定时间的二次控制策略以实现孤岛微电网的电压频率恢复控制。文献[20]提出一种基于分布式多智能体的微电网二次控制策略以实现微电网母线电压恢复到标称值。文献[21]设计了一种分布式控制算法以实现直流微电网中各分布式电源间的电流准确分配。文献[22]基于低速通信,设计了改进的下垂控制策略以改善直流微电网电压调节和电流分配的准确性。文献[23]提出一种直流微电网二次电压控制方法,以实现下垂控制型直流微电网母线电压的恢复。文献[24]提出一种用于直流微电网的分布式协调控制策略,以确保直流母线电压的稳定,并实现各变换器功率按用户设定值进行比例分配。文献[25]提出一种直流配电网换流站分布式有功-电压二次优化控制策略。该策略基于分布式通信实现各换流站平均功率标幺值评估与端口平均电压值评估,从而实现换流站功率按其容量成比例分配并进行电压调节。文献[26]提出一种直流微电网分布式二次控制策略以实现各电源间电流比例分配及直流母线电压恢复。然而,上述控制策略均以实现母线电压恢复或负荷的比例分配为目标,没有考虑各电源的发电成本。
针对直流微电网经济调度问题,近年来提出了一些分布式经济调度策略[27-28]。文献[27]基于有限步一致性算法设计了交直流混合微电网分布式经济调度策略。然而,该控制策略没有考虑交直流混合微电网的电压、频率二次调节。文献[28]提出一种直流微电网分布式分层控制策略:在其三次控制层,通过分布式一致算法调整下垂控制的虚拟阻抗以实现经济调度;在二次控制层,通过分布式一致算法生成下垂控制的电压补偿量以实现电压恢复。然而,三次优化调度层的时间尺度大于二次电压恢复控制层,无法在同一小时间尺度下对微电网进行控制与优化,从而无法进一步提高直流电网运行效率。此外,虚拟阻抗的大范围实时调整给系统的电压稳定控制带来挑战。
本文设计了分布式二次控制策略,以同时实现直流微电网的母线电压恢复和经济调度。本文提出的二次控制策略旨在控制直流微电网中的可控分布式电源,例如燃料电池、超级电容、微型燃气轮机、柴油发电机等。然而,直流微电网中的光伏、风力发电等新能源发电单元是不可控电源,通常运行在最大功率点跟踪模式,以按照其最大出力发电。当新能源发电及负荷波动引起系统功率不平衡时,需要调整可控电源的出力来维持系统功率平衡。虽然通过初级下垂控制可以调整可控电源的出力以维持系统功率平衡,然而,下垂控制没有考虑可控电源的发电成本,无法实现经济调度。微电网中随机性新能源发电比例高,且新能源发电量和负荷在大时间尺度下的预测误差较大。尽管,可以像传统电力系统那样,在三次控制(大时间尺度)实现微电网的经济调度,然而,大时间尺度下的预测误差会降低经济调度的性能。另外,微电网中具有大量的电力电子接口微电源,其系统惯性比传统电力系统小,需要在更小时间尺度下实现经济调度。因此,本文在二次控制层考虑了各可控电源的发电成本,通过可控电源在小时间尺度下的经济调度,降低直流微电网系统运行成本。
对于多智能体系统,通常采用图论的概念进行描述。为了将智能体之间的通信描述为图,可以用节点描述各个智能体,用边描述智能体之间的通信链路。本文用二元组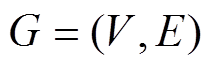 表示多智能体系统构成的图,其中
表示多智能体系统构成的图,其中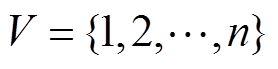 表示节点的集合,
表示节点的集合,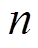 表示图中节点的个数,
表示图中节点的个数,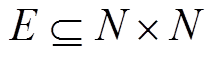 表示边的集合。第
表示边的集合。第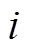 个节点的相邻节点的集合表示为
个节点的相邻节点的集合表示为 。通路表示连接一系列节点的边的序列。如果图中任意两个节点间都存在通路,则该图称为连通图。
。通路表示连接一系列节点的边的序列。如果图中任意两个节点间都存在通路,则该图称为连通图。
基于图理论,定义矩阵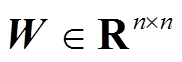 为图
为图 的拉普拉斯矩阵,其元素
的拉普拉斯矩阵,其元素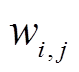 定义为[29]
定义为[29]
 (1)
(1)式中,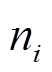 和
和 分别为智能体
分别为智能体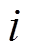 和
和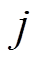 的相邻节点个数;
的相邻节点个数;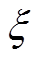 为实数,用于调整矩阵W的特征值。
为实数,用于调整矩阵W的特征值。
根据式(1)所示矩阵元素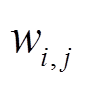 的定义,可以推出矩阵W为对称半正定矩阵。
的定义,可以推出矩阵W为对称半正定矩阵。
通常,分布式一致算法可以描述为一个线性系统,即[30-31]
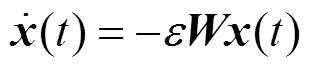 (2)
(2)式中,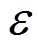 为学习因子,用于调节分布式一致算法的收敛速度;
为学习因子,用于调节分布式一致算法的收敛速度;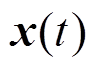 为系统状态,
为系统状态,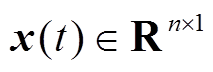 。
。
基于分布式一致理论,当系统达到一致状态,系统状态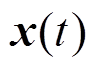 将收敛到初始状态
将收敛到初始状态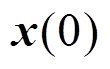 各元素的平均值。因此,分布式一致算法的收敛状态为
各元素的平均值。因此,分布式一致算法的收敛状态为
 (3)
(3)式中,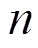 为图
为图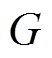 中的节点数(即系统中智能体总个数);
中的节点数(即系统中智能体总个数);
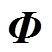 为其各元素均是1的矩阵,
为其各元素均是1的矩阵,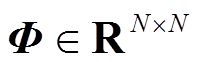 ;
;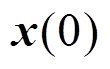 表示系统初始状态。
表示系统初始状态。
基于分布式理论,矩阵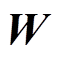 满足下面两个性质。
满足下面两个性质。
性质1:据式(1)定义的拉普拉斯矩阵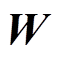 满足
满足
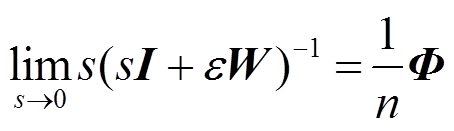 (4)
(4)证明:定义 为
为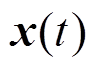 的拉氏变换,式(2)经拉氏变换后可得
的拉氏变换,式(2)经拉氏变换后可得
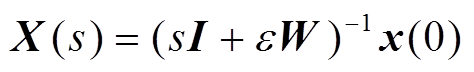 (5)
(5)
根据终值定理,式(5)可进一步转换为
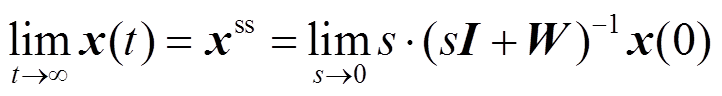 (6)
(6)根据式(3)和式(6),可以推导出
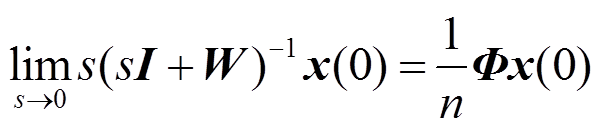 (7)
(7)
由于式(7)对于状态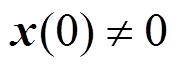 成立,因此性质1得证。
成立,因此性质1得证。
性质2:线性方程(8)的通解形式为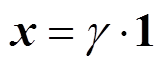 (其中
(其中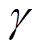 为常数),即向量
为常数),即向量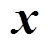 的元素具有相同的值。
的元素具有相同的值。
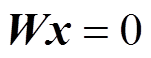 (8)
(8)
证明:由于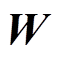 存在一个特征值0及对应的特征向量
存在一个特征值0及对应的特征向量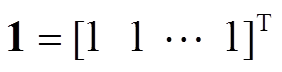 ,因此,基于线性代数理论[32],齐次方程
,因此,基于线性代数理论[32],齐次方程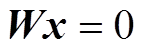 的通解为
的通解为
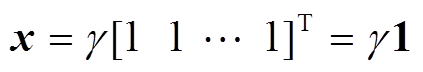 (9)
(9)因此,基于上述分析,性质2得证。
本文采用的控制结构如图1所示,包括基于下垂控制的初级控制层和基于分布式一致算法的二次控制层。本节将首先介绍本文的二次控制目标,然后设计相关分布式控制算法用于实现本文提出的二次控制目标。
在直流微电网初级控制层,通常采用下垂控制策略,以实现微电网中并联运行的可控发电源的初级负荷分配[22,33]。直流微电网的电压-功率下垂控制通常为
 (10)
(10)式中,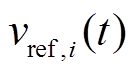 为
为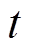 时刻第
时刻第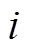 个电源的输出电压参考指令(该电源的本地电压控制器将按该指令控制其输出电压);
个电源的输出电压参考指令(该电源的本地电压控制器将按该指令控制其输出电压);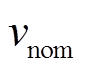 为直流母线电压的标称值;
为直流母线电压的标称值;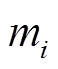 为第
为第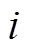 个电源的下垂系数;
个电源的下垂系数;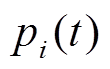 为
为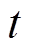 时刻第
时刻第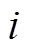 个电源的输出功率。
个电源的输出功率。
然而,上述下垂控制策略存在两个缺点:①下垂控制为有差控制,稳态时,微电网母线电压将偏离其标称值;②无法按各电源发电成本实现各电源的最优负荷分配。
为克服下垂控制上述缺点,本文提出如式(11)所示的分布式二次控制策略。
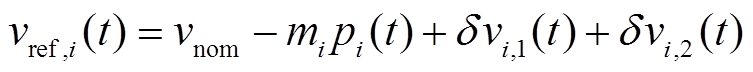 (11)
(11)式中,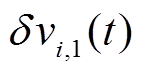 和
和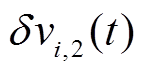 是为了克服上述下垂控制的两个缺点而提出的二次控制补偿项。
是为了克服上述下垂控制的两个缺点而提出的二次控制补偿项。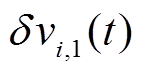 用于恢复微电网平均母线电压到标称值,
用于恢复微电网平均母线电压到标称值,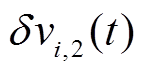 用于根据各电源发电成本实现最优负荷分配。
用于根据各电源发电成本实现最优负荷分配。
为便于后面分布式算法设计,式(11)的微分可描述为
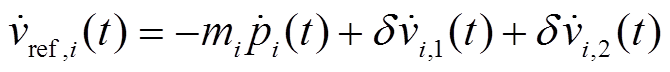 (12)
(12)式中,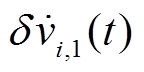 和
和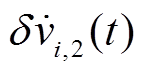 分别为补偿项
分别为补偿项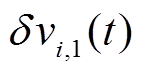 和
和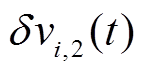 的微分形式。
的微分形式。
为了恢复微电网平均母线电压到标称值,可将式(12)中补偿项1的微分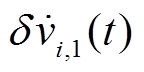 设计为
设计为
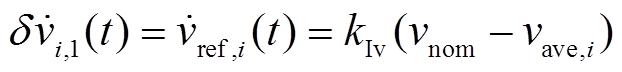 (13)
(13)式中,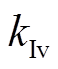 为调整算法收敛速度的积分项的系数;
为调整算法收敛速度的积分项的系数;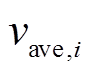 为第
为第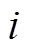 个电源对应的智能体利用后面将要介绍的分布式平均母线电压发掘算法发掘得到的微电网平均母线电压值。
个电源对应的智能体利用后面将要介绍的分布式平均母线电压发掘算法发掘得到的微电网平均母线电压值。
为了使式(13)中的微分项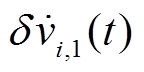 收敛到零,可采用比例积分(Proportional-Integral, PI)控制器以生成电压调整量
收敛到零,可采用比例积分(Proportional-Integral, PI)控制器以生成电压调整量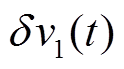 ,即
,即
 (14)
(14)式中,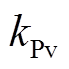 和
和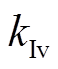 分别为PI控制器的比例项和积分项的系数。
分别为PI控制器的比例项和积分项的系数。
本文基于分布式一致算法[34],设计如下分布式平均母线电压发掘算法:
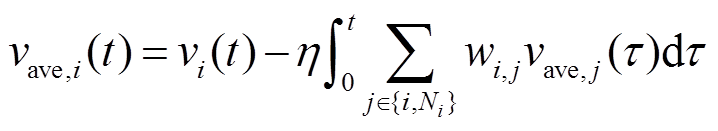 (15)
(15)式中,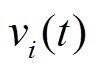 为
为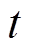 时刻第
时刻第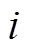 个电源所在节点的母线电压;
个电源所在节点的母线电压;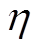 为学习率因子,用于调整分布式一致算法收敛速度,
为学习率因子,用于调整分布式一致算法收敛速度,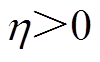 。
。
基于上述分布式平均母线电压发掘算法,各个电源只需要与其相邻智能体通信,而不需要全局信息即可实现平均母线电压的发掘。
为了证明式(15)的收敛性,定义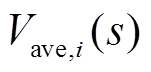 和
和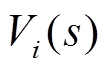 分别为
分别为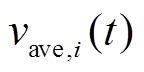 和
和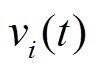 的拉氏变换。式(15)所示系统的拉氏变换可以表示为
的拉氏变换。式(15)所示系统的拉氏变换可以表示为
 (16)
(16)式中, 为复频率。
为复频率。
根据式(1)所示拉普拉斯矩阵W的定义,式(16)可以表示为
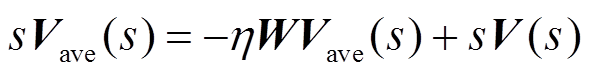 (17)
(17)其中
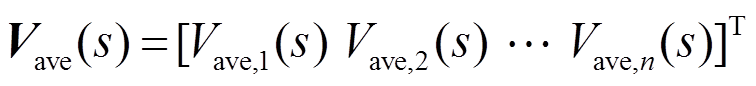

由于拉普拉斯矩阵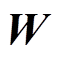 为半正定矩阵,式(17)所示系统收敛,并且式(17)所示系统可表示为
为半正定矩阵,式(17)所示系统收敛,并且式(17)所示系统可表示为
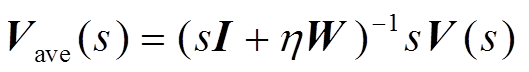 (18)
(18)
定义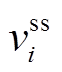 为第
为第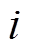 个电源所在节点的母线电压稳态值,并且定义向量
个电源所在节点的母线电压稳态值,并且定义向量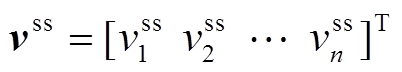 。根据拉氏变换的终值定理,可得
。根据拉氏变换的终值定理,可得
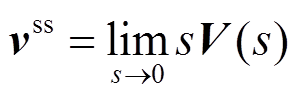 (19)
(19)
定义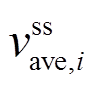 为第
为第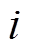 个电源发掘到的平均母线电压稳态值,且
个电源发掘到的平均母线电压稳态值,且 。对式(18)使用终值定理,并考虑式(4)和式(19)可得
。对式(18)使用终值定理,并考虑式(4)和式(19)可得
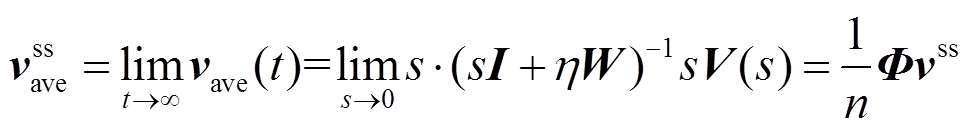 (20)
(20)由于式(4)中定义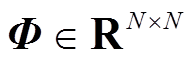 为各元素均是1的矩阵,因此,根据式(20)可得,各个电源发掘到的平均母线电压稳态值可收敛到各电源所在节点电压的平均值。
为各元素均是1的矩阵,因此,根据式(20)可得,各个电源发掘到的平均母线电压稳态值可收敛到各电源所在节点电压的平均值。
综上所述,式(15)的收敛性得证。根据式(14)和式(15)所示的分布式算法可以实现本文提出的控制目标1,即恢复微电网平均母线电压到标称值。
通常,微电网中的发电单元发电成本可以用二次函数描述[35],即
 (21)
(21)式中,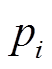 为第
为第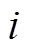 个电源的输出功率;
个电源的输出功率; 、
、 和
和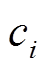 为第
为第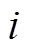 个电源的发电成本系数。
个电源的发电成本系数。
根据等耗量微增法则和分布式一致算法,分两种情况设计分布式最优负荷分配算法:①不考虑各电源容量约束;②考虑各电源容量约束的改进策略。
2.3.1 不考虑容量约束的分布式最优负荷分配算法
根据式(21)可得,各机组发电微增成本为
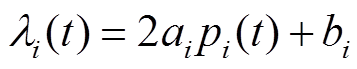 (22)
(22)式中,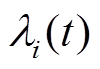 为
为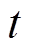 时刻机组
时刻机组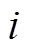 的发电微增成本。
的发电微增成本。
由式(22)可得
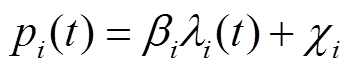 (23)
(23)式中,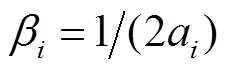 ;
;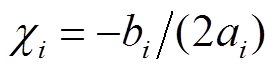 。
。
为了实现各电源间最优负荷分配,可将式(12)中补偿项2的微分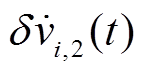 设计为
设计为
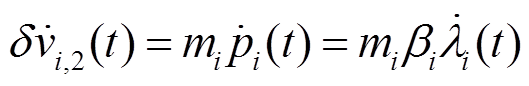 (24)
(24)根据分布式一致算法和等耗微增法则,设计等耗微增率的分布式更新规则为
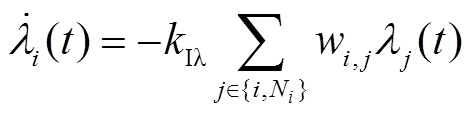 (25)
(25)
综合式(24)和式(25)设计补偿项2的分布式控制率为
 (26)
(26)式中,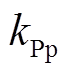 和
和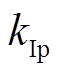 分别为调整算法收敛速度的比例项和积分项的系数。
分别为调整算法收敛速度的比例项和积分项的系数。
定义 和
和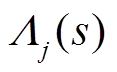 分别为
分别为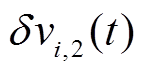 和
和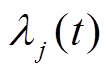 的拉氏变换。
的拉氏变换。
式(26)的拉氏变换形式可以表示为
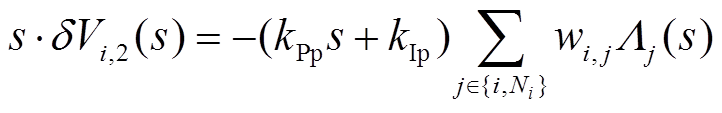 (27)
(27)定义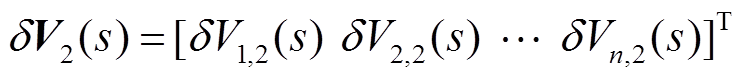 ,且
,且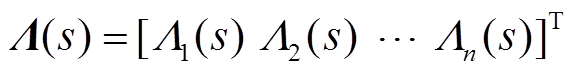 ,则式(27)可表示为
,则式(27)可表示为
 (28)
(28)
定义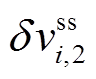 为第
为第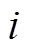 个电源控制器的电压调整量稳态值,
个电源控制器的电压调整量稳态值,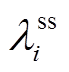 为第
为第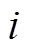 个电源发电微增成本的稳态值,并且定义向量
个电源发电微增成本的稳态值,并且定义向量 ,
,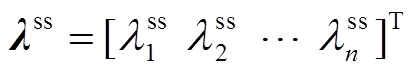 。根据拉氏变换的性质,式(28)两边同时乘以
。根据拉氏变换的性质,式(28)两边同时乘以 并应用拉氏变换的终值定理,可得
并应用拉氏变换的终值定理,可得

根据拉普拉斯矩阵W的性质2,可得各电源微增成本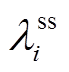 收敛到相同值。根据等耗微增法则,此条件下,各电源可实现最优负荷分配。
收敛到相同值。根据等耗微增法则,此条件下,各电源可实现最优负荷分配。
2.3.2 考虑容量约束的分布式最优负荷分配算法
由于微电网中电源的容量有限,必须设计考虑各电源容量约束的分布式最优负荷分配算法。根据等耗微增准则,在满足最优负荷分配时,各电源微增成本满足
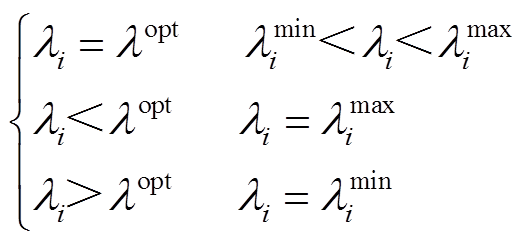 (30)
(30)式中,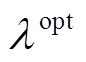 为微电网系统最优的微增成本;
为微电网系统最优的微增成本;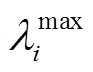 和
和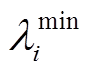 分别为第
分别为第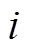 个电源的发电微增成本上、下限约束,且
个电源的发电微增成本上、下限约束,且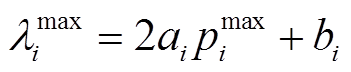 ,
, ;
;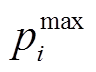 和
和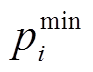 分别为第
分别为第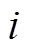 个电源的容量上、下限约束。
个电源的容量上、下限约束。
下面分三种情况考虑功率上下限约束:
(1)当电源出力满足容量约束时(即
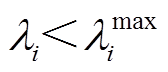 ),可以按2.3.1节设计的分布式最优功率分配算法求解。
),可以按2.3.1节设计的分布式最优功率分配算法求解。
(2)当电源出力达到上限约束时(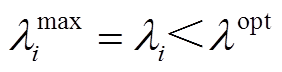 ),该电源的微增成本将低于微电网系统最优微增成本,此时,可设计该电源的虚拟微增成本
),该电源的微增成本将低于微电网系统最优微增成本,此时,可设计该电源的虚拟微增成本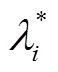 ,并令
,并令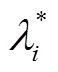 为某一相邻节点(选编号为
为某一相邻节点(选编号为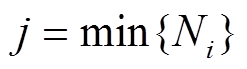 的相邻)的微增成本,并且该相邻节点应满足其容量约束,即
的相邻)的微增成本,并且该相邻节点应满足其容量约束,即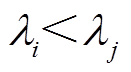 。
。
(3)当电源出力达到下限约束时( ),该电源的微增成本将大于微电网系统最优微增成本,此时,可设计该电源的虚拟微增成本
),该电源的微增成本将大于微电网系统最优微增成本,此时,可设计该电源的虚拟微增成本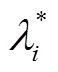 ,并令
,并令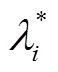 为某一相邻节点(选编号为
为某一相邻节点(选编号为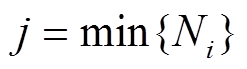 的相邻)的微增成本,并且该相邻节点应满足其容量约束,
的相邻)的微增成本,并且该相邻节点应满足其容量约束,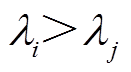 。
。
综合上面分析,定义虚拟发电微增成本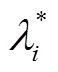 为
为
 (31)
(31)考虑电源容量约束时,式(26)所示补偿项2的分布式控制率可改进为
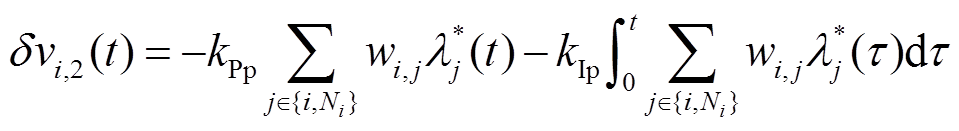 (32)
(32)
图2描述了本文所设计的分布式二次控制原理图。每个控制周期各智能体只需要与相邻智能体通信数据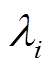 和
和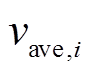 ,而不需要全局信息。因此,该算法可以完全分布式实施,并可以在各个分布式节点分配计算和通信任务。与集中式控制算法相比,该控制策略具有更好的可扩展性和灵活性。
,而不需要全局信息。因此,该算法可以完全分布式实施,并可以在各个分布式节点分配计算和通信任务。与集中式控制算法相比,该控制策略具有更好的可扩展性和灵活性。
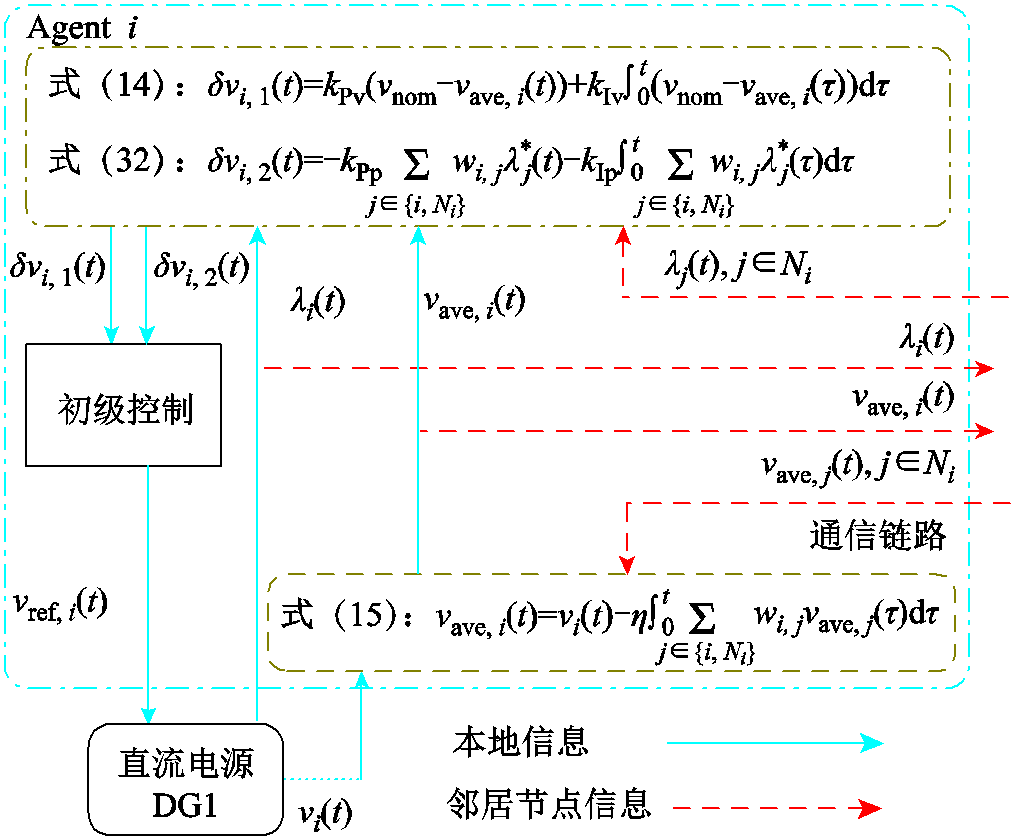
图2 分布式二次控制原理
Fig.2 Schematic diagram of the proposed distributed secondary control
为验证本文提出的分布式二次控制算法,设计如图3所示的直流微电网测试系统。系统包括五个可控分布式电源,一个不可控分布式电源(光伏发电单元),母线电压标称值为750V,传输线阻抗0.325Ω/km,传输线的长度及各节点负荷容量如图3所示。
各电源的基本参数见表1,并设定各电源启动状态下最小输出功率为其容量的5%。针对本文提出的二次控制,式(15)中的学习率因子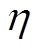 及式(14)和式(26)中的PI控制器参数可以根据PI参数整定准则[36],并考虑如下两个原则进行设计:①二次控制的响应速度应比初级控制及本地电压、电流控制环的响应速度慢;②二次控制的响应速度应比三次控制响应速度快。基于上述准则,PI控制器参数设计为
及式(14)和式(26)中的PI控制器参数可以根据PI参数整定准则[36],并考虑如下两个原则进行设计:①二次控制的响应速度应比初级控制及本地电压、电流控制环的响应速度慢;②二次控制的响应速度应比三次控制响应速度快。基于上述准则,PI控制器参数设计为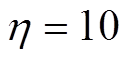 ,
,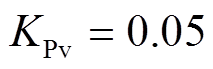 ,
,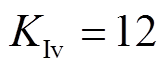 ,
,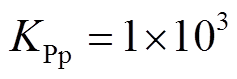 ,
, 。
。
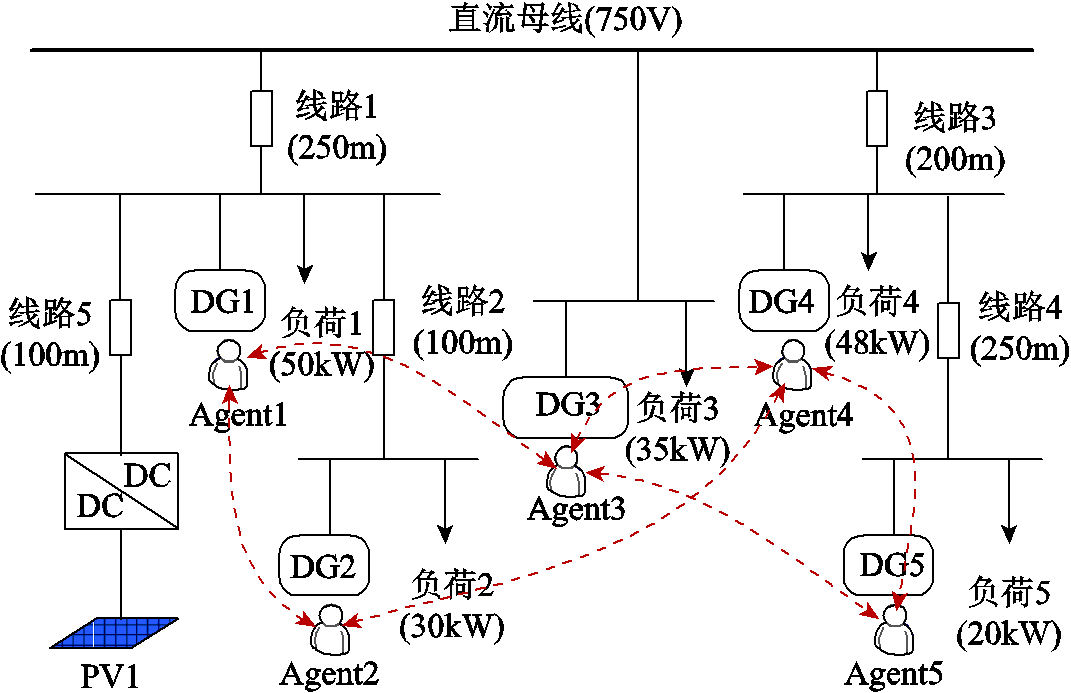
图3 直流微电网测试系统
Fig.3 DC microgrid test system
表1 各电源的基本参数
Tab.1 Parameters of the DGs
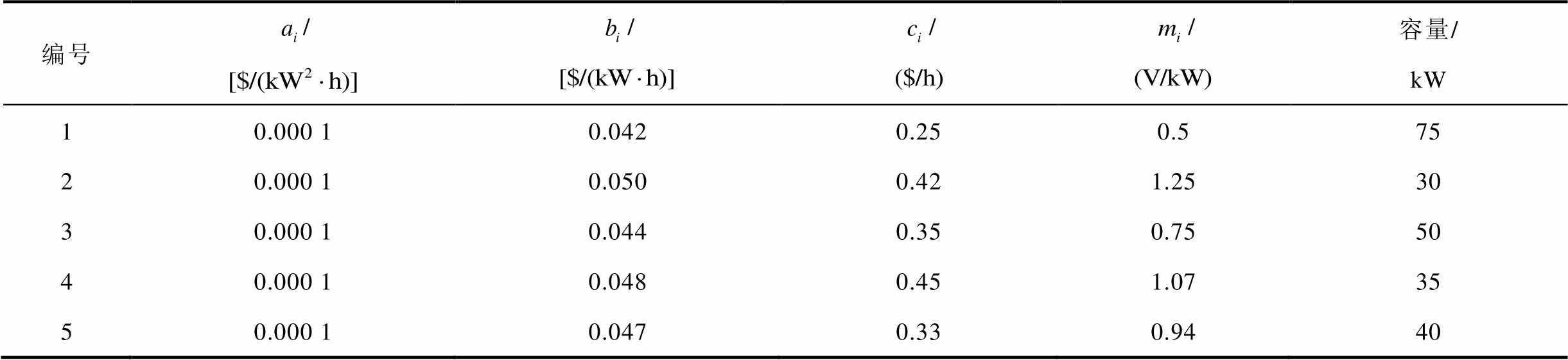
编号////容量/kW 10.000 10.0420.250.575 20.000 10.0500.421.2530 30.000 10.0440.350.7550 40.000 10.0480.451.0735 50.000 10.0470.330.9440
平均母线电压发掘算法作用前,各电源的平均母线电压发掘值初始化为该节点的电压值。在 时投入平均母线电压发掘算法,各电源发掘的平均母线电压曲线如图4所示。从图中可以看出,分布式平均母线发掘算法在1s内收敛到真实的母线电压平均值。因此,算法可以为本文提出的分布式二次控制策略实现平均母线电压恢复提供基础。
时投入平均母线电压发掘算法,各电源发掘的平均母线电压曲线如图4所示。从图中可以看出,分布式平均母线发掘算法在1s内收敛到真实的母线电压平均值。因此,算法可以为本文提出的分布式二次控制策略实现平均母线电压恢复提供基础。
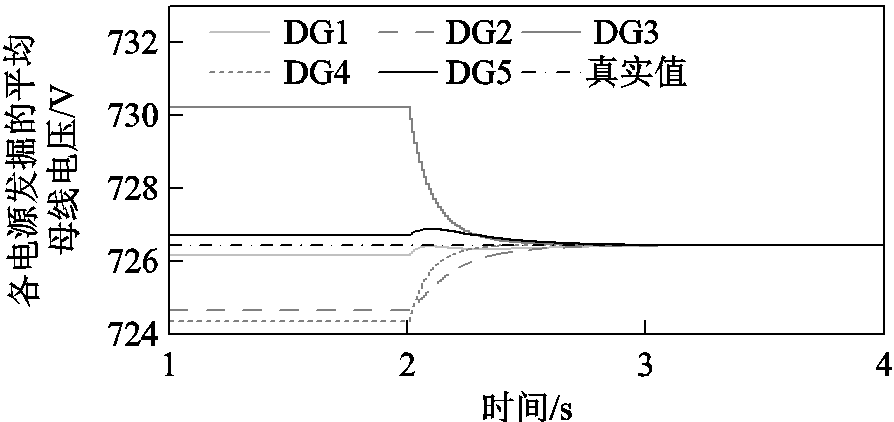
图4 分布式平均母线电压发掘算法验证
Fig.4 Performance evaluation of the proposed distributed average bus voltage discovery algorithm
本文提出的分布式二次控制算法(平均母线电压恢复控制算法和最优负荷分配算法)在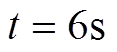 时开始实施。图5给出了分布式二次控制算法作用前后微电网的性能对比结果。
时开始实施。图5给出了分布式二次控制算法作用前后微电网的性能对比结果。
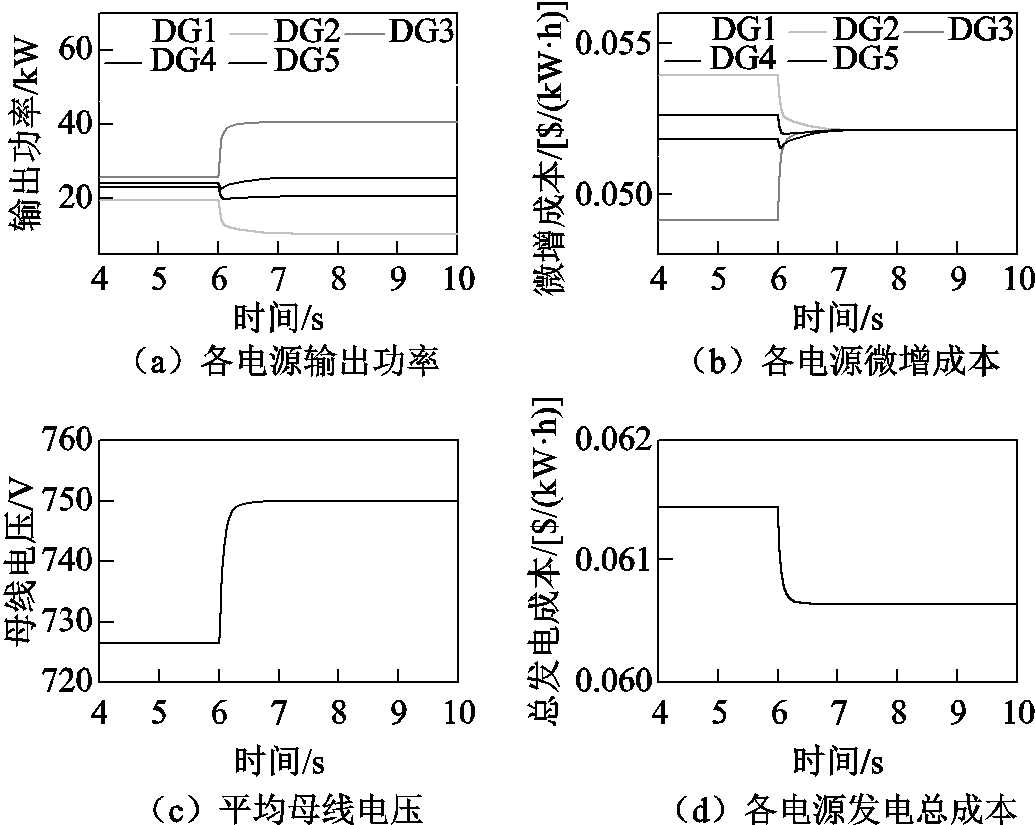
图5 分布式二次控制算法实施前后性能对比
Fig.5 Performance comparison of the DC microgrid before and after the proposed secondary control was applied
如图5a所示,算法实施后,各电源可以在1s内实现功率重新分配。根据图5b所示,实现功率分配后,各电源的微增成本可以收敛到相同值。因此,根据等耗微增原理,此时各电源发电总成本最低。如图5c所示,算法实施后,微电网平均母线电压也可以在1s内实现平均母线电压恢复到标称值。微电网中各电源的发电总成本曲线如图5d所示。算法实施后,发电总成本由0.061 5$/(kW·h)降到了0.060 6$/(kW·h)(降低了1.46%)。因此,图5验证了本文提出的分布式二次控制算法可以实现预期的两个控制目标,即实现平均母线电压恢复和实现最优负荷分配。
为验证分布式二次控制算法在负荷波动时的鲁棒性,给出五种仿真情景:①在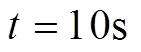 之前,负荷3未接入微电网,其余四个负荷均已接入该微电网;②在
之前,负荷3未接入微电网,其余四个负荷均已接入该微电网;②在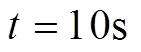 时,负荷3接入微电网;③在
时,负荷3接入微电网;③在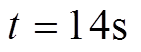 时,负荷3重新从微电网中切除;④在
时,负荷3重新从微电网中切除;④在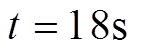 时,负荷4从微电网中切除;⑤在
时,负荷4从微电网中切除;⑤在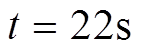 时,负荷4重新接入微电网。负荷波动时分布式二次控制算法验证如图6所示。
时,负荷4重新接入微电网。负荷波动时分布式二次控制算法验证如图6所示。
如图6a、图6b所示,在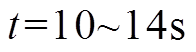 时,DG3输出功率达到了其容量上限,因此其微增成本小于最优微增成本。在
时,DG3输出功率达到了其容量上限,因此其微增成本小于最优微增成本。在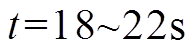 时,DG2输出功率达到了其容量下限,因此其微增成本大于最优微增成本。然而,在所有负荷波动时段,其余未达到功率容量约束的电源,其微增成本仍然可以收敛到相同值,从而实现最优负荷分配。如图6c所示,在负荷波动时,微电网的平均母线电压经过短暂的暂态过程均可以恢复到标称值。因此,图6验证了本文提出的分布式二次控制算法在负荷波动时仍然可以实现预期的两个控制目标。
时,DG2输出功率达到了其容量下限,因此其微增成本大于最优微增成本。然而,在所有负荷波动时段,其余未达到功率容量约束的电源,其微增成本仍然可以收敛到相同值,从而实现最优负荷分配。如图6c所示,在负荷波动时,微电网的平均母线电压经过短暂的暂态过程均可以恢复到标称值。因此,图6验证了本文提出的分布式二次控制算法在负荷波动时仍然可以实现预期的两个控制目标。

图6 负荷波动时分布式二次控制算法验证
Fig.6 Performance evaluation of the distributed secondary control in case of load variation
为了提高分布式二次控制算法在智能体故障情景下的鲁棒性,本文设计了如下规则:①各智能体间的通信拓扑满足“N-1”规则[37],即任一智能体故障后,其余智能体构成的图仍然是连通的(如图3所示);②各智能体周期性地向其各邻居智能体传递“心跳包”数据(包括时间戳、状态信息等),并根据式(1)更新对应的拉普拉斯矩阵元素。
基于上述策略,各智能体可以及时地识别其邻居智能体的故障并根据新的可用邻居节点信息更新拉普拉斯矩阵,从而使该控制策略能够克服系统单点故障的影响。然而,上述规则并不能处理系统面临多对相邻智能体同时故障的情景。为了进一步提高系统在多对智能体同时故障情景下的鲁棒性,可以进一步冗余设计系统通信拓扑。比如,设计通信拓扑满足“N-m”规则,即,任意m个智能体故障后,其余智能体构成的图仍然是连通的。然而,这种通信拓扑会进一步增加系统的通信成本。考虑到多对相邻智能体同时故障的概率较低,通常分布式算法的通信拓扑设计为满足“N-1”规则即可。为了进一步提高系统鲁棒性,后续将研究考虑多对相邻智能体同时故障的改进的分布式算法及通信拓扑设计规则。
为了验证分布式二次控制算法在遇到某一智能体故障时的鲁棒性,设计了如下情景:①在 时,Agent 5遇到通信故障并从通信网络中丢失,为了展示智能体故障的影响,此时引入负荷波动事件,负荷4从微电网中切除;②在
时,Agent 5遇到通信故障并从通信网络中丢失,为了展示智能体故障的影响,此时引入负荷波动事件,负荷4从微电网中切除;②在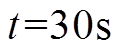 时,负荷4重新接入微电网;③在
时,负荷4重新接入微电网;③在 时,Agent 5故障恢复,并重新接入通信网络。智能体故障时分布式二次控制算法鲁棒性验证如图7所示。
时,Agent 5故障恢复,并重新接入通信网络。智能体故障时分布式二次控制算法鲁棒性验证如图7所示。
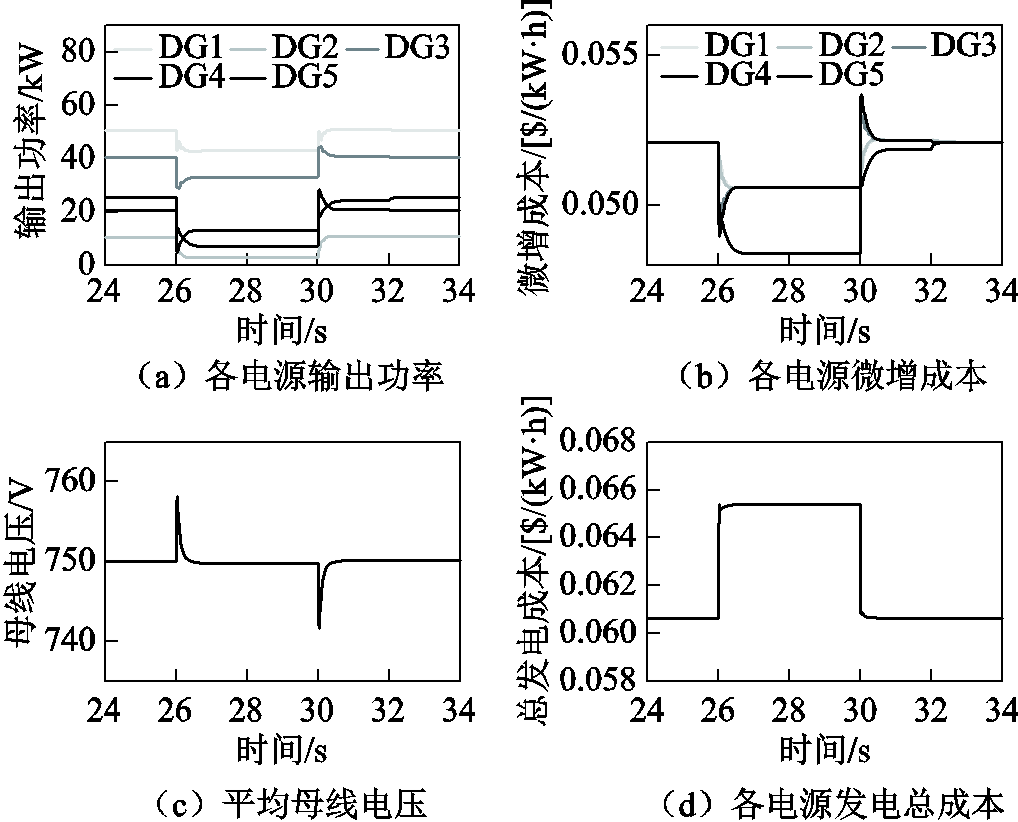
图7 智能体故障时分布式二次控制算法鲁棒性验证
Fig.7 Performance evaluation of the distributed secondary control in case of agent loss
如图7a、图7b所示,在Agent 5故障期间(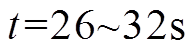 ),DG 5输出功率只能按初级下垂控制分配功率,因此,其微增成本无法收敛到其余电源的相同值。然而,对于其余正常通信的智能体,其对应的分布式电源仍然可以按最优负荷分配功率。如图7c所示,在Agent 5故障期间(
),DG 5输出功率只能按初级下垂控制分配功率,因此,其微增成本无法收敛到其余电源的相同值。然而,对于其余正常通信的智能体,其对应的分布式电源仍然可以按最优负荷分配功率。如图7c所示,在Agent 5故障期间(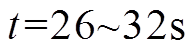 ),系统平均母线电压仍然可以恢复到标称值。因此,可以推断平均母线电压发掘算法在Agent 5故障期,仍然可以准确发掘系统平均母线电压。
),系统平均母线电压仍然可以恢复到标称值。因此,可以推断平均母线电压发掘算法在Agent 5故障期,仍然可以准确发掘系统平均母线电压。
在 后,各电源输出功率可重新调整,使各电源的发电微增成本收敛到相同值,实现最优负荷分配。因此,图7验证了本文提出的分布式二次控制算法对于智能体故障具有鲁棒性。
后,各电源输出功率可重新调整,使各电源的发电微增成本收敛到相同值,实现最优负荷分配。因此,图7验证了本文提出的分布式二次控制算法对于智能体故障具有鲁棒性。
为了验证分布式二次控制算法在分布式电源切入和切除时的鲁棒性,设计如下情景:①在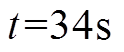 时,DG 5从电网中切除;②在
时,DG 5从电网中切除;②在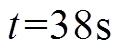 时,DG 5重新接入微电网,此时,负荷3也重新接入微电网;③在
时,DG 5重新接入微电网,此时,负荷3也重新接入微电网;③在 时,负荷3从电网中切除。电源接入切除时分布式二次控制算法鲁棒性验证如图8所示。
时,负荷3从电网中切除。电源接入切除时分布式二次控制算法鲁棒性验证如图8所示。
如图8a、图8b所示,在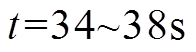 间,DG 5由于从电网中切除,其输出功率为零。然而,对于其余正常运行的分布式电源仍然可以按最优负荷分配功率。在
间,DG 5由于从电网中切除,其输出功率为零。然而,对于其余正常运行的分布式电源仍然可以按最优负荷分配功率。在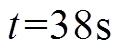 后,各电源输出功率仍然可以根据负荷波动重新调整,除DG 3达到容量上限约束外,其余各电源的发电微增成本收敛到相同值,实现最优负荷分配。因此,图8验证了本文提出的分布式二次控制算法对于电源切换具有鲁棒性。
后,各电源输出功率仍然可以根据负荷波动重新调整,除DG 3达到容量上限约束外,其余各电源的发电微增成本收敛到相同值,实现最优负荷分配。因此,图8验证了本文提出的分布式二次控制算法对于电源切换具有鲁棒性。
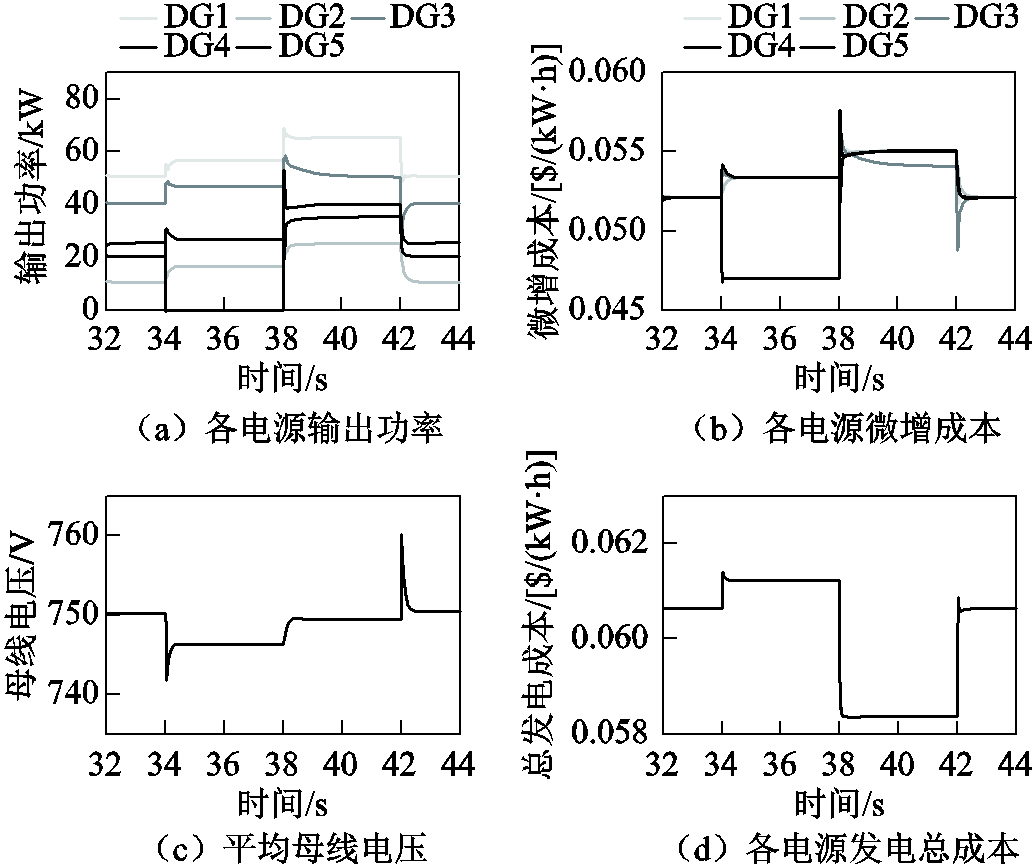
图8 电源接入切除时分布式二次控制算法鲁棒性验证
Fig.8 Performance evaluation of the distributed secondary control during the switch of DG
为验证分布式二次控制算法在不可控电源(光伏)出力波动时的鲁棒性,设计了如下情景:①在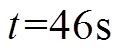 时,不可控电源投入直流微电网,且其输出功率为20kW;②在
时,不可控电源投入直流微电网,且其输出功率为20kW;②在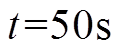 时,不可控电源输出功率从20kW降为10kW;③在
时,不可控电源输出功率从20kW降为10kW;③在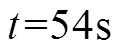 时,不可控电源输出功率从10kW升为25kW。不可控电源出力波动时分布式二次控制算法验证如图9所示。
时,不可控电源输出功率从10kW升为25kW。不可控电源出力波动时分布式二次控制算法验证如图9所示。
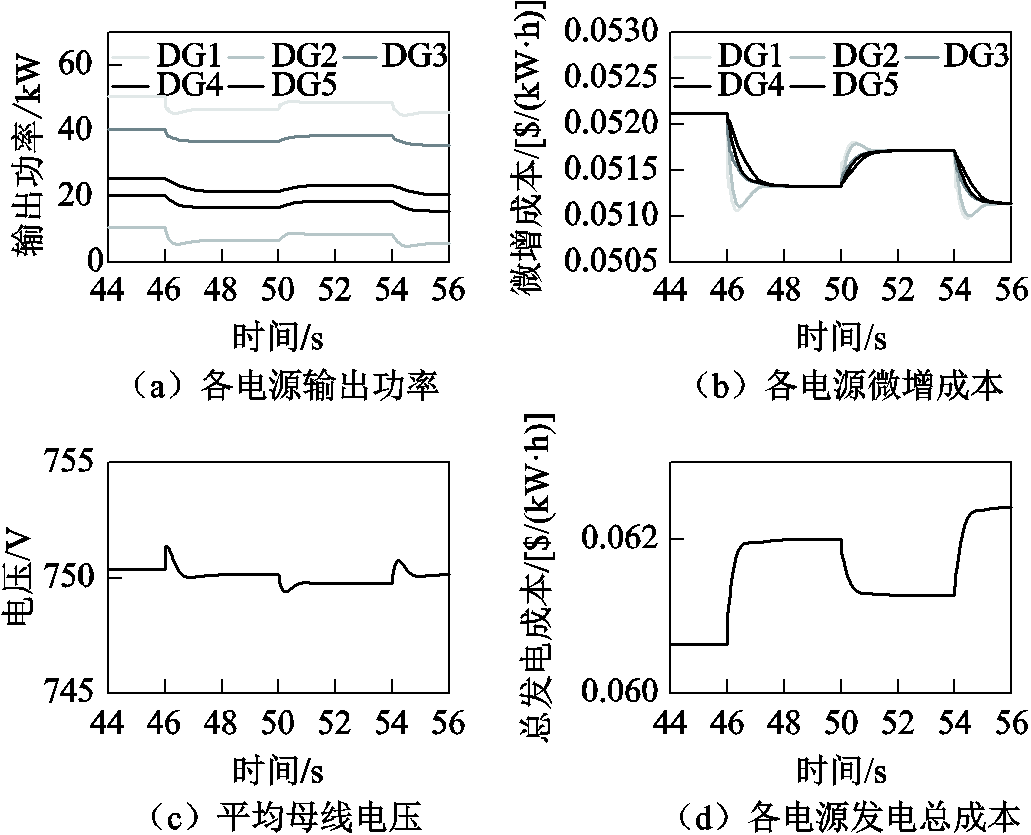
图9 不可控电源出力波动时分布式二次控制算法验证
Fig.9 Performance evaluation of the distributed secondary control in case of power fluctuation of uncontrollable power sources
如图9a、图9b所示,在不可控电源出力波动期间(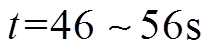 ),各可控分布式电源通过调整其输出功率可以维持系统功率平衡。此外,各可控分布式电源经过短暂的暂态过程,其微增成本仍然可以收敛到相同值,从而实现最优负荷分配。如图9c所示,在不可控电源出力波动时,微电网的平均母线电压经过短暂的暂态过程均可以恢复到标称值。因此,图9验证了本文提出的分布式二次控制算法在不可控电源出力波动时仍然可以实现预期的两个控制目标。
),各可控分布式电源通过调整其输出功率可以维持系统功率平衡。此外,各可控分布式电源经过短暂的暂态过程,其微增成本仍然可以收敛到相同值,从而实现最优负荷分配。如图9c所示,在不可控电源出力波动时,微电网的平均母线电压经过短暂的暂态过程均可以恢复到标称值。因此,图9验证了本文提出的分布式二次控制算法在不可控电源出力波动时仍然可以实现预期的两个控制目标。
本文提出了一种直流微电网分布式二次控制策略,以同时实现直流微电网平均母线电压恢复和经济调度,从而提高微电网的稳定性和运行效率。该控制策略不需要中央控制器,只需要为微电网中可控分布式电源分配一个智能体。各智能体利用本地信息并与有限的相邻智能体通信即可实现控制任务,从而提高了系统的灵活性、可扩展性以及应对单点故障的鲁棒性。仿真结果验证了本文提出的控制策略在负荷波动、智能体故障、电源切换情景下均具有良好的控制性能。
参考文献
[1] 涂春鸣, 黄红, 兰征, 等. 微电网中电力电子变压器与储能的协调控制策略[J]. 电工技术学报, 2019, 34(12): 2627-2636.
Tu Chunming, Huang Hong, Lan Zheng, et al. Coordinated control strategy of power electronic transformer and energy storage in microgrid[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2627-2636.
[2] 陈树泉, 张兆云, 李天利. 基于模糊下垂控制的直流微电网电压稳定控制研究[J]. 电气技术, 2020, 21(8): 40-45.
Chen Shuquan, Zhang Zhaoyun, Li Tianli. Research on voltage control of DC microgrid based on fuzzy droop control[J]. Electrical Engineering, 2020, 21(8): 40-45.
[3] 孟建辉, 邹培根, 王毅, 等. 基于灵活虚拟惯性控制的直流微网小信号建模及参数分析[J]. 电工技术学报, 2019, 34(12): 2615-2626.
Meng Jianhui, Zou Peigen, Wang Yi, et al. Small-signal modeling and parameter analysis of the DC microgrid based on flexible virtual inertia control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2615-2626.
[4] 李建林, 牛萌, 周喜超, 等. 能源互联网中微能源系统储能容量规划及投资效益分析[J]. 电工技术学报, 2020, 35(4): 874-884.
Li Jianlin, Niu Meng, Zhou Xichao, et al. Energy storage capacity planning and investment benefit analysis of micro-energy system in energy interconnection[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 874-884.
[5] Zhang Xing, Wang Mingda, Zhao Tao, et al. Topological comparison and analysis of medium-voltage and high-power direct-linked PV inverter[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 327-334.
[6] Cook M, Parker G, Robinett R, et al. Decentralized mode-adaptive guidance and control for DC microgrid[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 263-271.
[7] 朱珊珊, 汪飞, 郭慧, 等. 直流微电网下垂控制技术研究综述[J]. 中国电机工程学报, 2018, 38(1): 72-84.
Zhu Shanshan, Wang Fei, Guo Hui, et al. Overview of droop control in DC microgrid[J]. Proceedings of the CSEE, 2018, 38(1): 72-84.
[8] 朱晓荣, 候顺达, 李铮. 基于模型预测控制的直流微电网电压动态响应优化[J]. 电网技术, 2020, 44(6): 2187-2195.
Zhu Xiaorong, Hou Shunda, Li Zheng. Voltage dynamic response optimization of DC microgrid based on model predictive control[J]. Power System Technology, 2020, 44(6): 2187-21959.
[9] Li Zhongwen, Cheng Zhiping, Liang Jing, et al. Distributed event-triggered secondary control for economic dispatch and frequency restoration control of droop-controlled AC microgrids[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1938-1950.
[10] Messinis G, Gonzalez-Espin F, Valdivia V, et al. Application of rapid prototyping tools for a hierarchical microgrid control implementation[C]// 2014 IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems, Galway, Ireland, 2014, DOI: 10.1109/PEDG.2014. 6878688.
[11] 施永, 徐冬, 于鸿儒, 等. 基于系统辨识建模的微网二次电压频率控制器参数设计方法[J]. 电力系统自动化, 2020, 44(13): 89-97.
Shi Yong, Xu Dong, Yu Hongru, et al. Parameter design method of secondary voltage and frequency regulation controller in microgrid based on system identification modeling[J]. Automation of Electric Power Systems, 2020, 44(13): 89-97.
[12] 吴亮, 刘庆楷, 唐翀, 等. 微电网二次频率/电压控制器的反馈线性化设计及分布式实现[J]. 电力系统保护与控制, 2019, 47(14): 79-86.
Wu Liang, Liu Qingkai, Tang Chong, et al. Design of secondary frequency/voltage controller with feedback linearization and distributed implemention in microgrids[J]. Power System Protection and Control, 2019, 47(14): 79-86.
[13] Azevedo R, Cintuglu M, Ma T, et al. Multiagent-based optimal microgrid control using fully distributed diffusion strategy[J]. IEEE Transactions on Smart Grid, 2017, 8(4): 1997-2008.
[14] 周晓倩, 艾芊. 配电网与多微网联合分布式鲁棒经济调度[J]. 电力系统自动化, 2020, 44(7): 23-30.
Zhou Xiaoqian, Ai Qian. Combined distributed robust economic dispatch of distribution network and multiple microgrids[J]. Automation of Electric Power Systems, 2020, 44(7): 23-30.
[15] 施静容, 李勇, 贺悝, 等. 一种提升交直流混合微电网动态特性的综合惯量控制方法[J]. 电工技术学报, 2020, 35(2): 337-345.
Shi Jingrong, Li Yong, He Kui, et al. A comprehensive inertia control method for improving the dynamic characteristics of hybrid AC-DC microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 337-345.
[16] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC/DC distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[17] Kakigano H, Miura Y, Ise T. Distribution voltage control for DC microgrids using fuzzy control and gain-scheduling technique[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2246-2258.
[18] Wang Panbao, Lu Xiaonan, Yang Xu, et al. An improved distributed secondary control method for DC microgrids with enhanced dynamic current sharing performance[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6658-6673.
[19] 陈刚, 李志勇, 韦梦立. 孤岛微电网的分布式固定时间二次协调控制[J]. 控制与决策, 2019, 34(1): 205-212.
Chen Gang, Li Zhiyong, Wei Mengli. Distributed fixed-time secondary coordination control of islanded microgrids[J]. Control and Decision, 2019, 34(1): 205-212.
[20] 肖湘宁, 王鹏, 陈萌. 基于分布式多代理系统的孤岛微电网二次电压控制策略[J]. 电工技术学报, 2018, 33(8): 1894-1902.
Xiao Xiangning, Wang Peng, Chen Meng. Secondary voltage control in an islanded microgrid based on distributed multi-agent system[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1894-1902.
[21] Anand S, Fernandes B, Guerrero J. Distributed control to ensure proportional load sharing and improve voltage regulation in low-voltage DC microgrids[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1900-1913.
[22] Lu Xiaonan, Guerrero J, Sun K, et al. An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing accuracy[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 1800-1812.
[23] Huang P H, Liu Pochun, Xiao Weidong, et al. A novel droop-based average voltage sharing control strategy for DC microgrids[J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1096-1106.
[24] 吴济东, 汪可友, 黄鑫, 等. 孤立直流微电网多DC-DC变换器分布式协调控制策略[J]. 电力系统保护与控制, 2020, 48(11): 76-83.
Wu Jidong, Wang Keyou, Huang Xin, et al. Distributed coordinated control scheme of parallel DC-DC converters in isolated DC microgrids[J]. Power System Protection and Control, 2020, 48(11): 76-83.
[25] 周敏, 吕振宇, 王琦, 等. 直流配电网换流站分布式有功–电压二级优化控制策略[J]. 中国电机工程学报, 2020, 40(24): 8002-8011.
Zhou Min, Lü Zhenyu, Wang Qi, et al. Distributed secondary power and voltage optimal control strategy for converter station in DC distribution network[J]. Proceedings of the CSEE, 2020, 40(24): 8002-8011.
[26] Xing Lantao, Mishra Y, Guo Fanghong, et al. Distributed secondary control for current sharing and voltage restoration in DC microgrid[J]. IEEE Transactions on Smart Grid, 2020, 3(11): 2487-2497.
[27] 蒋科, 吴峰, 张新松, 等. 基于有限步一致性算法的交直流混联微电网分布式动态经济调度[J]. 南通大学学报(自然科学版), 2020, 19(1): 17-25.
Jiang Ke, Wu Feng, Zhang Xinsong, et al. Dynamic economic dispatch of AC/DC microgrid based on the finite-step consensus algorithm[J]. Journal of Nantong University (Natural Science Edition), 2020, 19(1): 17-25.
[28] Lü Zhenyu, Wu Zaijun, Dou Xiaobo, et al. Distributed economic dispatch scheme for droop-based autonomous DC microgrid[J]. Energies, 2020, 13(2): 404.
[29] Vu T, Perkins D, Diaz F, et al. Robust adaptive droop control for DC microgrids[J]. Electric Power Systems Research, 2017, 146: 95-106.
[30] Olfati-Saber R, Fax J, Murray R. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215-233.
[31] Olfati-Saber R, Murray R. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 47(9): 1520-1533.
[32] Meyer C. Matrix analysis and applied linear algebra[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2000.
[33] 米阳, 宋根新, 蔡杭谊, 等. 基于分段下垂的交直流混合微电网自主协调控制[J]. 电网技术, 2018, 42(12): 3941-3950.
Mi Yang, Song Genxin, Cai Hangyi, et al. Autonomous coordinated control of hybrid AC/DC microgrids based on segmented droop[J]. Power System Technology, 2018, 42(12): 3941-3950.
[34] Nasirian V, Davoudi A, Lewis F. Distributed adaptive droop control for DC microgrids[C]//2014 IEEE Applied Power Electronics Conference and Exposition, Fort Worth, TX, USA, 2014: 1147-1152.
[35] Hu Jian, Duan Jie, Ma Hao, et al. Distributed adaptive droop control for optimal power dispatch in DC microgrid[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 778-789.
[36] O'Dwyer A. PI and PID controller tuning rules: an overview and personal perspective[C]//2006 IET Irish Signals and Systems Conference, Dublin, Ireland, 2006: 161-166.
[37] Zhang Wei, Liu Wenxin, Zang Chuanzhi, et al. Multiagent system-based integrated solution for topology identification and state estimation[J]. IEEE Transactions on Industrial Informatics, 2017, 13(2): 714-724.
Distributed Secondary Control for Economic Dispatch and Voltage Restoration of DC Microgrid
Abstract The droop-based primary control of DC microgrid shows the drawbacks of steady-state bus voltage deviation and inaccurate current sharing. Although, the traditional centralized or distributed secondary control strategy can achieve bus voltage restoration and accurate current sharing. However, the generation cost of each DG unit is not considered in the traditional control strategy. In order to improve the stability and operation efficiency of DC microgrid, distributed average bus voltage recovery control algorithm and distributed optimal load distribution algorithm were designed based on distributed consensus theory. Based on the proposed distributed secondary control, bus voltage restoration and economic dispatch can be achieved simultaneously in the secondary control layer, thus the operational efficiency of microgrid can be improved. In addition, the proposed control strategy can be achieved in a fully distributed way, which shows the advantages of flexibility, robustness and scalability.
keywords:DC microgrid, distributed consensus, secondary control, economic dispatch, voltage restoration control, multi-agent system
DOI:10.19595/j.cnki.1000-6753.tces.201149
中图分类号:TM761
国家自然科学基金(61803343)和河南省科技厅科技攻关(202102210096, 202102210296, 212102210011)资助项目。
收稿日期 2020-09-06
改稿日期 2021-01-19
李忠文 男,1989年生,博士,副教授,硕士生导师,研究方向为微电网控制与优化、电力电子。E-mail:lzw@zzu.edu.cn
程志平 男,1974年生,副教授,硕士生导师,研究方向为新能源发电、微电网、电力电子。E-mail:zpcheng@zzu.edu.cn(通信作者)
(编辑 赫蕾)