 、
、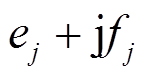 ,线路阻抗为
,线路阻抗为 ,潮流方向由i到j,交流线路模型如图1所示。
,潮流方向由i到j,交流线路模型如图1所示。摘要 弹性是衡量电网抵御扰动及故障后快速恢复能力的指标,其评估涉及对扰动的抵御、响应及恢复等多阶段过程。目前大多数研究利用仿真结果或历史数据的统计分析评估系统弹性。该文建立基于多阶段弹性力学映射的配电网模型,充分考虑系统的运行状态及物理特性,从应对扰动的抵御能力及故障后的恢复能力两个角度进行弹性的多阶段评估。对含智能软开关(SOP)的支路进行弹性力学映射,分析其在正常运行和供电恢复中的作用。通过IEEE 33节点系统与IEEE 123节点系统验证多阶段弹性力学映射评估的合理性和有效性,分析SOP对配电网弹性的影响,验证其对弹性提升的作用,比较和探讨SOP的安装位置和控制量对弹性的影响。
关键词:配电网弹性 弹性力学映射 智能软开关 等效弹性系数 供电恢复
近年来,飓风、地震、洪水等灾害事件频发,微网、新能源、电力电子器件等接入配电网,使电网运行的不确定、开放性、复杂性增加,更易受扰动的影响。电力系统关系到国家安全和国民经济命脉,在满足正常运行可靠性的同时,需要在扰动发生时最小化事件影响范围,灵活适应环境变化,快速恢复供电能力[1]。因此,建设具有弹性恢复力的电网对国家安全和国民经济的发展具有重要意义。
为了衡量严重扰动或故障下电力系统的响应和恢复能力,学术界提出了“弹性”概念[2-6]。文献[1]对不同弹性恢复力的定义进行总结归纳,提出弹性衡量电力系统对扰动的反应能力。文献[5]将电网的弹性定义为系统对扰动事件预防、抵御、快速恢复的能力,该弹性定义描述的过程与弹簧系统在外力作用下产生形变,并在外力撤销后恢复形变的过程类似。
弹性指标的计算主要分为两类。第一类依赖故障事件发生概率,将天气信息和故障率融入配电网弹性评估中。文献[7-8]在故障概率基础上构建提升系统对扰动事件故障预判能力、响应能力和恢复能力的弹性评估体系。文献[9]针对遭受台风灾害后配电网的供电能力恢复过程,提出韧性三角形评估指标。文献[10]结合覆冰荷载下线路故障率模型,构建冰雪天气下配电网弹性指标。文献[11]根据故障模型,提出防灾、减灾阶段的弹性评估指标体系。第二类根据配电网的不同运行与控制目标利用系统性能缺失量反映弹性。文献[12]用实际运行供能和期望运行供能比值量化弹性。文献[13]用满足用户需求的比例衡量系统性能。建立可以应对多种危害类型的年抗灾力指标。文献[14-16]采用简化梯形或三角形衡量系统功能损害部分。文献[17-19]选用配电网关键负荷的供电功率或供电收益衡量系统性能。
这两类弹性指标中,一类是根据故障概率等历史数据,将弹性转换成概率问题;另一类是根据仿真模拟供电恢复过程,计算从扰动到恢复过程中系统损失性能的累积量。第一种评价方法的计算基于平均值,无法描述小概率事件的影响,而且现有研究基本都针对某种特定事件,不具有普适性;第二种评估中积分法虽然涉及故障后不同阶段的全过程,但因为未考虑电网的实时变化性,性能缺失面积的计算具有理想性。
文献[3]提出弹性指标是一个多维、动态的概念,目前存在的弹性指标只能静态地量化弹性的一个或几个维度,并没有考虑多阶段系统响应及弹性的变化。根据故障发生概率,或者通过模拟仿真故障及供电恢复系统性能变化曲线得出的弹性评估指标,适用范围具有局限性,未考虑小概率-高损失事件及该场景下系统运行状态的变化性和电力系统运行的不确定性。本文根据弹性电网的特点,提出从扰动前后多阶段过程中提取能够衡量系统抵御能力和恢复能力的关键参数,以此构建配电网的弹性评估指标,将弹性指标回归系统本身。
智能软开关(Soft Open Point, SOP)是一种全控型电力电子器件,能够调节系统潮流分布[20-22]。在正常运行状态,SOP可调节两侧有功,实现负荷均衡分布[23-24]。在供电恢复过程中,通过改变换流器的控制模式,为失电区域提供电压和频率支撑,提高配电网灾后供电恢复能力[25-26]。
综上所述,本文基于文献[27]的弹性力学网络拓扑映射思路,建立电网的弹性力学映射基本模型,聚焦于配电网的弹性评估。与输电系统相比,配电网处于电网末端,与用户负荷联系密切,其应对故障扰动能力较弱[28]。微网、分布式电源、电力电子器件[5,29-30]等对于配电网弹性的影响是输电网未遇到的难题,这些都增加了配电网弹性研究的复杂性。因此合理的配电网弹性评估能有效缩小停电范围,对能源安全、经济发展、环境问题和社会稳定有重要意义[6,31-32]。本文基于潮流计算方程,建立扰动对电力系统影响机理模型,将电网映射到弹性力学模型中。在智能配电网背景下,对含SOP配电网进行弹性力学映射,建立正常运行状态和供电恢复过程中含SOP支路的等效模型,对比分析其等效弹性系数与不含SOP支路的等效弹性系数的差别。在IEEE 33节点和IEEE 123节点算例分析多阶段弹性力学映射评估的合理性和有效性。在IEEE 33节点配电网分析SOP对系统弹性的提升作用,对比不同SOP安装位置对系统弹性指标的影响,讨论SOP控制变量的变化对系统弹性的影响。
在弹性力学中,胡克定律将弹簧网络的支路弹力、支路形变和弹性系数联系起来,由文献[33]可知,在弹性力学中,胡克定律适用多自由度弹性支路。文献[27]提出功角稳定特性与弹簧所受拉力-形变的特性进行类比,通过弹性网络形变实现电网功角状态变化可视化分析。文献[34]将弹性网络的映射弹性势能作为衡量电网有功承载能力和支路负载均衡性的指标,进一步证明了电网的弹性力学网络分析的优越性。本文基于静态潮流方程,将网络支路映射成考虑受力大小和方向的两自由度弹性支路,用等效弹性系数反映整个弹性评估过程中电网应对外界扰动的反应能力。
与文献[27, 34]中定义的弹性模型相比,本文模型综合考虑有功功率和无功功率对电压和频率的影响。该模型将系统实时状态量(包括节点电压、频率、负荷功率、发电机出力等)和系统物理特性(包括拓扑结构、线路参数等)通过力学模型映射在具有物理含义的等效电网模型中。
设交流线路l两端节点为i和j,首末端电压向量为 、
、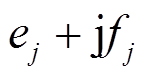 ,线路阻抗为
,线路阻抗为 ,潮流方向由i到j,交流线路模型如图1所示。
,潮流方向由i到j,交流线路模型如图1所示。
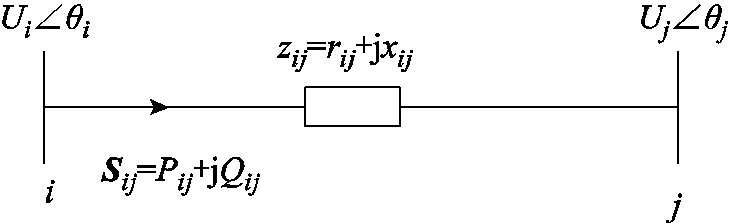
图1 交流线路模型
Fig.1 AC line model
将线路l传输功率 用直角坐标形式表示为
用直角坐标形式表示为
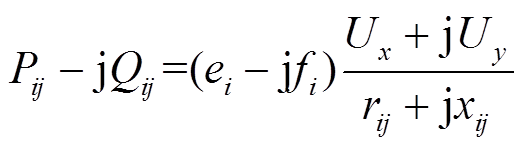 (1)
(1) (2)
(2)
式中,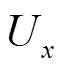 和
和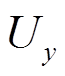 分别为电压降(
分别为电压降( )x、y方向分量,
)x、y方向分量,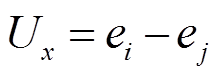 ,
,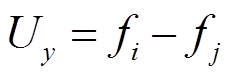 。
。
将有功功率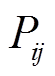 和无功功率
和无功功率 整理为由
整理为由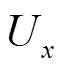 、
、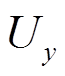 表示的形式,即
表示的形式,即
 (3)
(3)其中

两节点线路等效模型如图2所示。根据图2,可以将电气支路等效为沿电压降方向受力为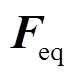 的弹簧支路[35]。
的弹簧支路[35]。
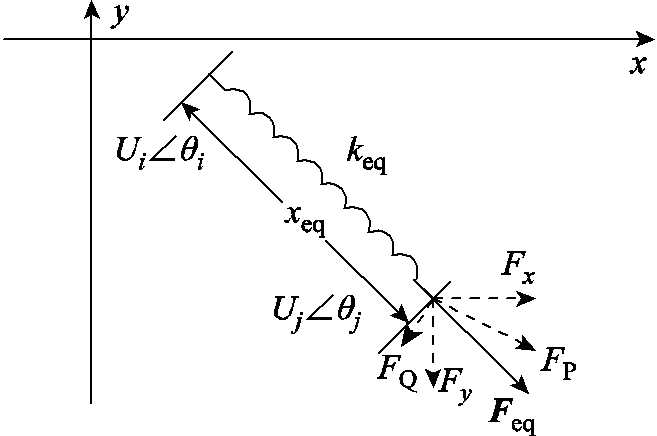
图2 两节点线路等效模型
Fig.2 Two-node line equivalent model
图2中 对应支路视在功率
对应支路视在功率 ,
,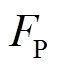 、
、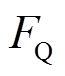 对应支路有功和无功功率
对应支路有功和无功功率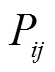 和
和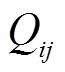 ,每一条等效弹簧支路受力方向不同,为了实现从支路到网络的拓扑映射,根据式(4)力的合成与分解计算,将其受力分解成xy方向
,每一条等效弹簧支路受力方向不同,为了实现从支路到网络的拓扑映射,根据式(4)力的合成与分解计算,将其受力分解成xy方向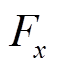 和
和 。
。
 (4)
(4)参照文献[36]的弹性力学网络模型的构建方法,将支路映射成两自由度弹簧,基本映射准则为:电气支路的电压向量对应的xy方向对应两自由度弹性支路的平面坐标系xy轴;电气支路功率的xy方向分量 、
、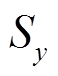 对应两自由度弹性支路的弹力
对应两自由度弹性支路的弹力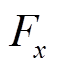 、
、 ;电压降落的xy方向分量
;电压降落的xy方向分量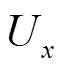 、
、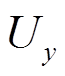 对应两自由度弹性支路的形变量
对应两自由度弹性支路的形变量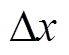 、
、 。
。
基于式(4)和映射关系可得 、
、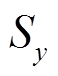 为
为
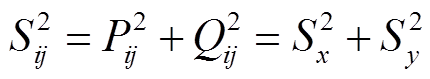 (5)
(5) (6)
(6)
类比弹性力学中等效弹性系数的定义可以得到单条支路的等效弹性系数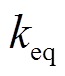 为
为
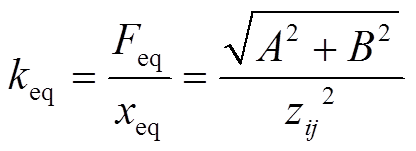 (7)
(7)在弹性力学中,弹簧受到外力后拉伸或压缩产生的弹性势能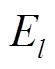 为
为
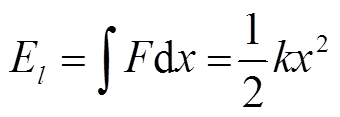 (8)
(8)
根据映射关系,支路弹性势能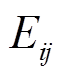 与弹簧弹性势能
与弹簧弹性势能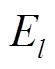 可对应定义。与暂态稳定分析中的支路势能[37]不同,本文系统是由潮流分布而具有的弹性势能,是系统本身的静态特性。
可对应定义。与暂态稳定分析中的支路势能[37]不同,本文系统是由潮流分布而具有的弹性势能,是系统本身的静态特性。
支路ij的映射弹性势能定义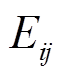 为
为
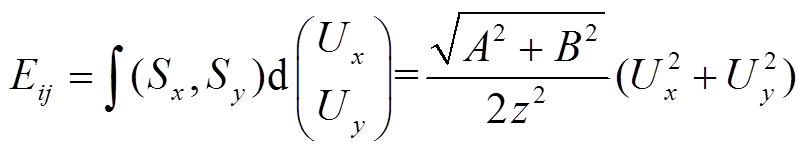 (9)
(9)由电网到弹性网络的拓扑映射以电气线路为弹簧支路,以母线节点为弹簧间的连接点,沿功率传输方向搜索而成。其中电气线路的串并联结构映射前后不变,对应到弹簧支路的串并联映射[27]。设弹性网由n条支路构成,则无论支路受力方向如何,总势能均满足线性叠加特性,电网的映射弹性势能也如此。根据广域测量系统可以得到各节点实时电压和支路阻抗等信息,得出系统弹性势能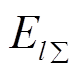 ,即
,即
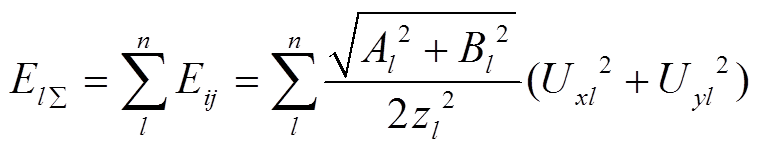 (10)
(10)
根据文献[35],在已知电网等效弹性势能和合力的情况下,根据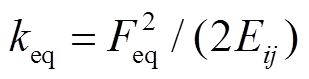 计算出的等效弹性系数
计算出的等效弹性系数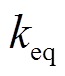 误差较小。但因为每条等效弹簧支路的受力方向不同,无法对合力进行叠加。因此将每条支路在xy方向的分力叠加,再进行合成,得到电网的等效受力。根据以下步骤计算电网的等效弹性系数:①计算总弹性势能
误差较小。但因为每条等效弹簧支路的受力方向不同,无法对合力进行叠加。因此将每条支路在xy方向的分力叠加,再进行合成,得到电网的等效受力。根据以下步骤计算电网的等效弹性系数:①计算总弹性势能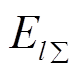 ;②计算合力
;②计算合力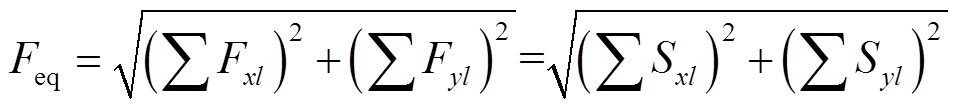 ;③构造电网等效弹性系数
;③构造电网等效弹性系数 。
。
区别于传统电网等效建模方式,通过力的合成与分解,系统的等效受力同时包含电压和频率信息,再将其映射成一条虚拟的弹性支路进行等效弹性系数的计算。该弹性力学映射模型可以形象直观地反映负荷变化对节点电压和频率的影响。
文献[5]描述了弹性电力系统应对扰动的基本过程,配电网遭受扰动事件前后的过程如图3所示。根据“弹性”的字面意义——有弹性的物体在压缩或拉伸后恢复原来形状或位置的能力[38],将弹性电力系统应对扰动的多阶段过程类比到有初始形变量的弹簧受扰动后并在外力作用下恢复全部或部分形变的过程。弹性系数可以衡量弹簧恢复形变的难易程度,借鉴其物理意义,用力学映射模型的等效弹性系数描述系统应对扰动的反应能力[39]。

图3 扰动事件发生前后弹性电网系统性能变化示意图
Fig.3 Diagram of the performance changes of the resilient power system
根据弹性电网的力学映射模型,图4模型分别对应图3的不同阶段,形变量衡量电网等效模型电压的整体水平,弹簧的受力对应负荷水平。用不同阶段的弹性系数衡量电力系统在扰动事件发生的不同阶段需要具有的应对扰动事件的能力[35]。下面对各个阶段弹性电网的特点进行详细分析,进而提出多阶段弹性评估指标。

图4 扰动事件发生前后电网力学映射模型示意图
Fig.4 Diagram of the power grid mapping mechanics model
文献[1]提出弹性电网面对扰动事件有较强的抵御能力,故障后系统有较好的恢复能力。文献[5]提出弹性电网需要满足鲁棒性、充裕性和快速性的特点。鲁棒性描述电力系统在维持自身功能时,承受外界扰动或压力的能力;充裕性描述灾难中备用设备对系统的可用性;快速性描述电力系统迅速恢复关键负荷的供电能力[6]。鲁棒性是弹性电网对抵御能力的要求,充裕性和快速性是弹性电网对恢复能力的要求。电网对扰动的抵御和恢复能力是弹性的核心特征。
图3中阶段1为遭受扰动事件前系统正常运行状态,对应为图4中阶段1弹簧系统未受外力扰动的阶段,此时的拉力为正常情况系统负荷,形变为正常的电压状态。图3中阶段2为抵御扰动事件阶段,对应为图4中阶段2弹簧系统在外力作用下产生弹性形变。因为受到等效为拉力的扰动作用,弹簧需要减少自身的负荷,以保证形变在允许范围内变化。在抵御和吸收扰动的过程中,弹性电网应具备足够的鲁棒性抵抗可能的扰动事件,在弹性评估中用系统阶段1的等效弹性系数 衡量系统的抗扰动能力。
衡量系统的抗扰动能力。
图3中阶段3为遭受扰动事件后系统的恢复准备阶段,对应为图4中阶段3弹簧系统准备接受恢复力阶段。故障期间,为维持系统稳定,切除负荷来保证其余负荷点供电,相应减少负荷拉力。图3中阶段4为扰动事件后系统快速恢复阶段,当恢复压力作用时,系统可以相应增加负荷拉力,以实现形变量(供电量)的恢复。阶段4为恢复完成阶段,对应图4中弹簧系统在外力作用下恢复全部或部分形变的过程。供电恢复阶段弹性电网需有足够的充裕性以面对变化的扰动事件场景,减少失电区域范围,即较强的恢复能力。在弹性评估中用系统阶段3的等效弹性系数 衡量系统响应和进行供电恢复的能力。
衡量系统响应和进行供电恢复的能力。
弹性电网具有两个核心特性[40-42],即应对扰动的抵抗和恢复能力,因此可以从鲁棒性和快速性两方面定义配电网的弹性指标。本文基于弹性力学映射从系统应对扰动事件的抵御能力及系统的恢复能力两个角度进行弹性评估。
定义多阶段弹性评估指标Res为
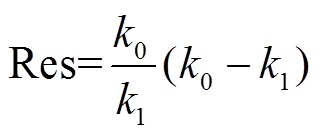 (11)
(11)弹簧的弹性系数是衡量弹簧发生形变或恢复形变的难易程度的指标,根据弹性系数可以比较不同弹簧在不同状态的弹性大小。相同受力情况下,弹性系数越大,形变量越小,即弹性越大,弹簧越“韧”;弹性系数越小,形变量越大,即越易产生形变。
基于弹性力学映射模型,在系统遭受扰动过程时,可用阶段1等效弹性系数 描述电力系统承受外界扰动的能力[6]。
描述电力系统承受外界扰动的能力[6]。 越大,对应到电力系统保持稳定和正常供电的能力越强[41],系统鲁棒性越好。在系统响应适应和快速恢复的阶段,可用阶段3的等效弹性系数
越大,对应到电力系统保持稳定和正常供电的能力越强[41],系统鲁棒性越好。在系统响应适应和快速恢复的阶段,可用阶段3的等效弹性系数 衡量系统的恢复能力。该值越小,说明系统越容易响应恢复,越容易恢复到期望的供能水平,即系统的恢复能力越强。
衡量系统的恢复能力。该值越小,说明系统越容易响应恢复,越容易恢复到期望的供能水平,即系统的恢复能力越强。
基于以上分析,建立综合考虑弹性电网的抵御能力和恢复能力要求的多阶段弹性评估指标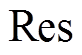 。总体来看,当系统抵御扰动能力越强,恢复能力越强时,系统的弹性指标越大。
。总体来看,当系统抵御扰动能力越强,恢复能力越强时,系统的弹性指标越大。
本文所讨论的SOP为双端背靠背电压源型换流器。正常运行时,一个换流器用于维持直流母线电压稳定,控制方式为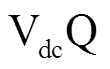 控制,另一个换流器控制SOP所传输的有功功率,控制方式为
控制,另一个换流器控制SOP所传输的有功功率,控制方式为 控制。配电网故障时,为了快速恢复失电区域供电,SOP可根据故障发生位置改变控制模式[43-46]。当图5中含SOP的支路中VSC1侧故障时,将其控制模式切换为
控制。配电网故障时,为了快速恢复失电区域供电,SOP可根据故障发生位置改变控制模式[43-46]。当图5中含SOP的支路中VSC1侧故障时,将其控制模式切换为 控制,进行负荷电压支撑,此时VSC 2侧控制模式为定直流电压
控制,进行负荷电压支撑,此时VSC 2侧控制模式为定直流电压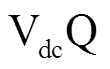 控制;VSC 2侧故障时,同理将其控制模式切换为
控制;VSC 2侧故障时,同理将其控制模式切换为 控制,此时VSC1侧为
控制,此时VSC1侧为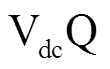 控制。
控制。

图5 含SOP的支路
Fig.5 Branch model with SOP
在弹性力学电网拓扑的映射过程中,对含SOP支路在正常运行情况和供电恢复状态进行不同的弹性力学映射,分析SOP在连接两侧交流系统时的作用。
电网的节点、支路与弹性网络模型中的节点、支路对应,每个节点的位置由节点电压的幅值和相角确定,分布于电压向量的xy坐标系中。
2.3.1 正常运行阶段
如图6在支路增加虚拟节点,以便SOP等效模型的解释。图6中未安装SOP支路的两部分分别对应为图7中弹簧 ,安装SOP支路的两部分分别对应图7中弹簧
,安装SOP支路的两部分分别对应图7中弹簧 。正常运行时SOP的VSC1侧为
。正常运行时SOP的VSC1侧为 控制,VSC2侧为
控制,VSC2侧为 控制。
控制。

图6 含虚拟节点的等效支路
Fig.6 Equivalent branch with virtual nodes
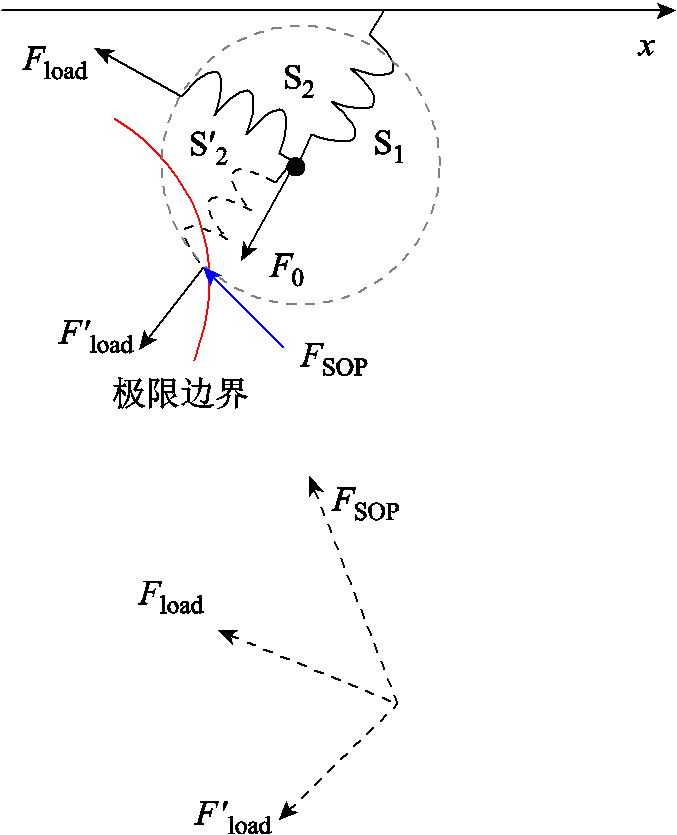
图7 含SOP的正常运行支路等效模型
Fig.7 Equivalent branch model with SOP
图7为正常运行状态含SOP支路的等效模型。 为未安装SOP时支路两端的等效受力。假设系统在安装SOP前已接近运行极限,达到电压极限映射的形变量极限边界(图中实线圆弧标注),图中弹簧
为未安装SOP时支路两端的等效受力。假设系统在安装SOP前已接近运行极限,达到电压极限映射的形变量极限边界(图中实线圆弧标注),图中弹簧 末端已处于极限边界。
末端已处于极限边界。
安装SOP的支路的等效模型中弹簧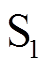 对应
对应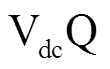 控制,可以控制其状态量保持不变,即映射位置不发生变化。而
控制,可以控制其状态量保持不变,即映射位置不发生变化。而 支路末端电压接近临界值,采用
支路末端电压接近临界值,采用 控制可改善其电压。
控制可改善其电压。 控制对应为图中力
控制对应为图中力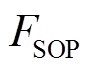 ,可在不改变支路等效受力的情况下,使弹簧支路末端远离运行的极限边界。
,可在不改变支路等效受力的情况下,使弹簧支路末端远离运行的极限边界。 为安装SOP后的
为安装SOP后的 控制侧拉力,为原拉力
控制侧拉力,为原拉力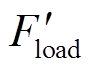 与力
与力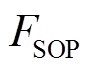 的等效合力。
的等效合力。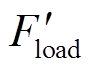 与
与 大小相等,方向不同。由图7可知,安装SOP后弹簧受合力
大小相等,方向不同。由图7可知,安装SOP后弹簧受合力 远离运行的极限边界。因为SOP相当于只改变方向的拉力,不改变力大小,所以安装SOP后支路的等效形变量减小,即等效弹性系数增加,对应为防御、抗干扰能力提升。
远离运行的极限边界。因为SOP相当于只改变方向的拉力,不改变力大小,所以安装SOP后支路的等效形变量减小,即等效弹性系数增加,对应为防御、抗干扰能力提升。
比较分析含SOP与不含SOP的单条支路的等效弹性系数,支路l的等效弹性系数计算公式为
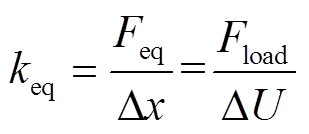 (12)
(12)根据式(12),支路是否包含SOP,会影响分母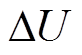 的大小。因为SOP对潮流分布的调节作用,安装SOP支路的电压水平较好,电压降差较小,即
的大小。因为SOP对潮流分布的调节作用,安装SOP支路的电压水平较好,电压降差较小,即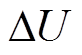 较小,对应的keq较大,即安装SOP的支路正常运行时的抵御、抗干扰能力较强。
较小,对应的keq较大,即安装SOP的支路正常运行时的抵御、抗干扰能力较强。
从弹性力学角度分析,正常运行时SOP的 控制侧等效于在原来拉力上增加力
控制侧等效于在原来拉力上增加力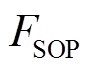 ,在不改变弹簧拉力大小的基础上改变力的方向,远离弹簧形变的极限边界。该等效与正常运行时SOP对线路有功分布的调节作用一致。力
,在不改变弹簧拉力大小的基础上改变力的方向,远离弹簧形变的极限边界。该等效与正常运行时SOP对线路有功分布的调节作用一致。力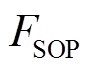 的大小和方向由控制变量P、Q决定。
的大小和方向由控制变量P、Q决定。
2.3.2 供电恢复阶段
图8在支路中增加虚拟节点,其中故障发生在VSC2侧。故障发生时,SOP切换为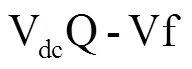 控制模式,对VSC1进行
控制模式,对VSC1进行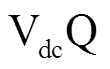 控制,对VSC2进行
控制,对VSC2进行 控制。
控制。
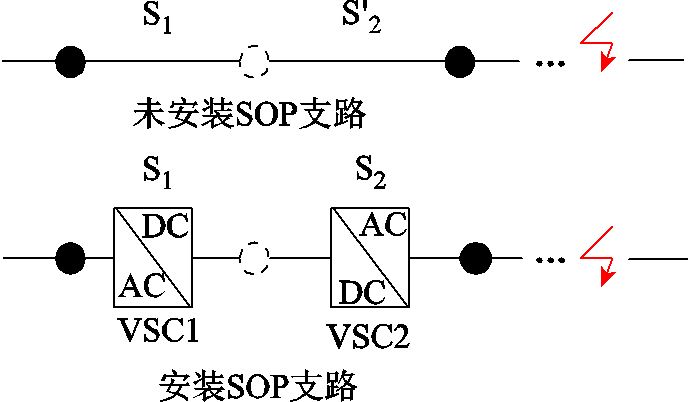
图8 含虚拟节点的等效支路
Fig.8 Equivalent branch with virtual nodes
图9为含SOP的供电恢复支路的等效模型。图9中弹簧 对应为安装SOP的支路响应、适应故障阶段。
对应为安装SOP的支路响应、适应故障阶段。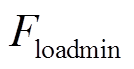 为未安装SOP时支路两端的等效受力,对应为故障后系统供电缺失状态。安装SOP支路的等效模型中弹簧
为未安装SOP时支路两端的等效受力,对应为故障后系统供电缺失状态。安装SOP支路的等效模型中弹簧 对应
对应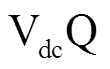 控制端支路,弹簧
控制端支路,弹簧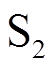 对应
对应 控制端支路。SOP迅速切换至
控制端支路。SOP迅速切换至 控制的过程对应为弹簧
控制的过程对应为弹簧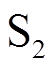 受力
受力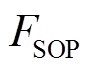 而恢复形变的过程。图中实线圆弧线为电压极限映射的形变量的边界。含SOP支路的
而恢复形变的过程。图中实线圆弧线为电压极限映射的形变量的边界。含SOP支路的 控制侧,该支路以(x0, y0)为固定端点,另一端点由(x1, y1)移动至边界(x2, y2),恢复部分负荷,受力由
控制侧,该支路以(x0, y0)为固定端点,另一端点由(x1, y1)移动至边界(x2, y2),恢复部分负荷,受力由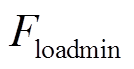 增加至
增加至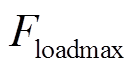 ,即SOP对失电负荷的电压支撑作用。
,即SOP对失电负荷的电压支撑作用。

图9 含SOP的供电恢复的支路等效模型
Fig.9 Equivalent branch model with SOP
支路l在供电恢复过程中接受恢复外力的等效弹性系数计算公式为
 (13)
(13)未安装SOP支路因为故障会出现大面积失电,受力迅速减少为Floadmin。SOP为故障区域提供电压支撑,实现失电区域负荷供电,受力增加为Floadmax,在恢复相同电压水平即恢复形变的过程中,对应的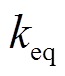 较小,即安装SOP支路的恢复能力较强。
较小,即安装SOP支路的恢复能力较强。
从弹性力学角度分析,SOP的 控制侧等效于增加力
控制侧等效于增加力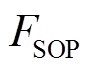 ,该动态过程可以实现形变量的恢复(对应于负荷量的恢复)。该等效与SOP通过支撑失电区域的电压和频率而快速实现重要负荷供电的作用一致。
,该动态过程可以实现形变量的恢复(对应于负荷量的恢复)。该等效与SOP通过支撑失电区域的电压和频率而快速实现重要负荷供电的作用一致。
在配电网调度[47]运行中提升电力系统弹性的措施主要为扰动前的预防措施和扰动后的恢复措施。因为扰动发生时调控中心难以取得实时详细数据并采取措施,系统需要根据自身特性和运行状态进行抵抗和防御。文献[6]提出配电网通过调整潮流分布,可以直接提升鲁棒性和提高供电恢复速度;文献[41]提出快速有效的供电恢复可以提高配电网弹性。基于以上等效模型,含SOP的配电网在正常运行状态时,功率分布均衡,防御、抗干扰能力提高。同时在供电恢复过程中因为SOP对电压的支撑作用,系统的总体失负荷量较小,更易恢复至初始运行状态,系统的恢复能力提高。综合灾前预防和灾后恢复两方面,安装SOP可以有效提高配电网弹性。
多阶段弹性评估方法的合理性分析主要针对系统抵御故障阶段和恢复响应阶段,验证阶段1的等效弹性系数 衡量系统抵御故障的能力,阶段3的等效弹性系数
衡量系统抵御故障的能力,阶段3的等效弹性系数 衡量系统响应恢复能力的合理性。该部分算例均在如图10所示的IEEE 33节点配电网进行验证分析,其中SOP安装于联络开关TS处。
衡量系统响应恢复能力的合理性。该部分算例均在如图10所示的IEEE 33节点配电网进行验证分析,其中SOP安装于联络开关TS处。

图10 IEEE 33节点算例拓扑
Fig.10 Network topology of the IEEE 33-bus system
 评估的合理性分析
评估的合理性分析在预先准备阶段,用阶段1的等效弹性系数 衡量系统抵御故障的能力,借鉴文献[48]对鲁棒性指标的计算方法,通过单次故障中系统供电性能减少的比例反映系统的抵御能力。因为系统的抵御故障能力与故障无关,由系统的负荷水平、拓扑结构等因素决定,因此要通过故障切负荷量验证系统抵御故障的能力,可以通过遍历N-1故障,得出该系统在N-1故障下的平均切负荷量,以此评价系统的抵御扰动能力。
衡量系统抵御故障的能力,借鉴文献[48]对鲁棒性指标的计算方法,通过单次故障中系统供电性能减少的比例反映系统的抵御能力。因为系统的抵御故障能力与故障无关,由系统的负荷水平、拓扑结构等因素决定,因此要通过故障切负荷量验证系统抵御故障的能力,可以通过遍历N-1故障,得出该系统在N-1故障下的平均切负荷量,以此评价系统的抵御扰动能力。
3.1.1 改变系统的负荷分布
在有功负荷和无功负荷总量不变的情况下,等功率因数随机分配每个节点的负荷,生成50个不同负荷水平的仿真场景。为了便于比较,计算每个场景负荷水平下遍历N-1故障后的平均切负荷比例和阶段1的等效弹性系数 的标幺值。
的标幺值。
根据前文分析可知,在系统遭受扰动阶段,受到故障的外力扰动时,系统的电压越不易发生变化,即扰动事件对负荷供电影响越小,阶段1的等效弹性系数 越大,系统的抵御能力越强。通过图11中不同负荷水平对应的场景可知,
越大,系统的抵御能力越强。通过图11中不同负荷水平对应的场景可知, 与N-1故障遍历平均切负荷比例的变化趋势相反,即平均切负荷量越大,系统抵御扰动故障能力越小,
与N-1故障遍历平均切负荷比例的变化趋势相反,即平均切负荷量越大,系统抵御扰动故障能力越小, 也越小。负荷分布会影响系统抵御抗干扰能力,而阶段1等效弹性系数
也越小。负荷分布会影响系统抵御抗干扰能力,而阶段1等效弹性系数 能反映遍历故障后平均切负荷比例的变化,因此用
能反映遍历故障后平均切负荷比例的变化,因此用 衡量系统抵御能力具有一定合理性。
衡量系统抵御能力具有一定合理性。
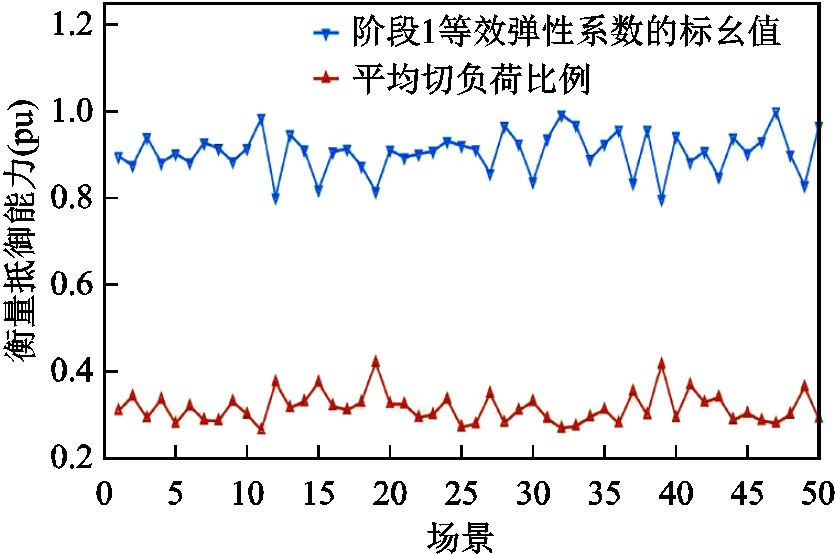
图11 衡量抵御能力指标的比较
Fig.11 Comparison between indicators for measuring resistance
3.1.2 改变系统线路参数
根据模型分析可知,线路参数也会影响系统的等效弹性系数。对IEEE 33节点标准算例的每条线路阻抗分别进行参数化,分析线路参数变化对阶段1等效弹性系数 的影响。线路参数与
的影响。线路参数与 的关系如图12所示。图12中单条线路的变化范围为[0.5,1.5],计算得到不同线路参数对应的阶段1等效弹性系数
的关系如图12所示。图12中单条线路的变化范围为[0.5,1.5],计算得到不同线路参数对应的阶段1等效弹性系数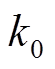 。
。
由图12可知当某条线路参数逐渐增大时,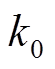 逐渐减小,但是
逐渐减小,但是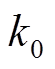 对不同线路参数变化的灵敏度不同,其中
对不同线路参数变化的灵敏度不同,其中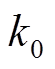 对33节点系统中的线路2-3、5-6、3-4和4-5变化的灵敏度明显大于其余线路。由系统拓扑可知,这四条线路为网络与发电机相连的主要供电支路,其参数变化对系统的抵御能力的影响较明显。与其他三条支路相比,支路5-6虽然离发电机较远,但因为线路阻抗值较大,
对33节点系统中的线路2-3、5-6、3-4和4-5变化的灵敏度明显大于其余线路。由系统拓扑可知,这四条线路为网络与发电机相连的主要供电支路,其参数变化对系统的抵御能力的影响较明显。与其他三条支路相比,支路5-6虽然离发电机较远,但因为线路阻抗值较大,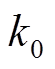 受其参数变化的影响也较大。
受其参数变化的影响也较大。

图12 线路参数与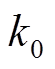 的关系
的关系
Fig.12 The relationship between line parameters and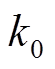
N-1潮流分析是电网安全性分析的常规方法,因此可通过故障遍历得出弹性指标下的关键线路。IEEE 33节点N-1故障场景如图13所示。对33节点系统进行N-1故障遍历,计算每条线路故障对应的系统弹性指标Res标幺值与图12中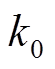 受线路参数变化影响的灵敏度进行对比分析。故障场景对应为系统故障支路号。
受线路参数变化影响的灵敏度进行对比分析。故障场景对应为系统故障支路号。
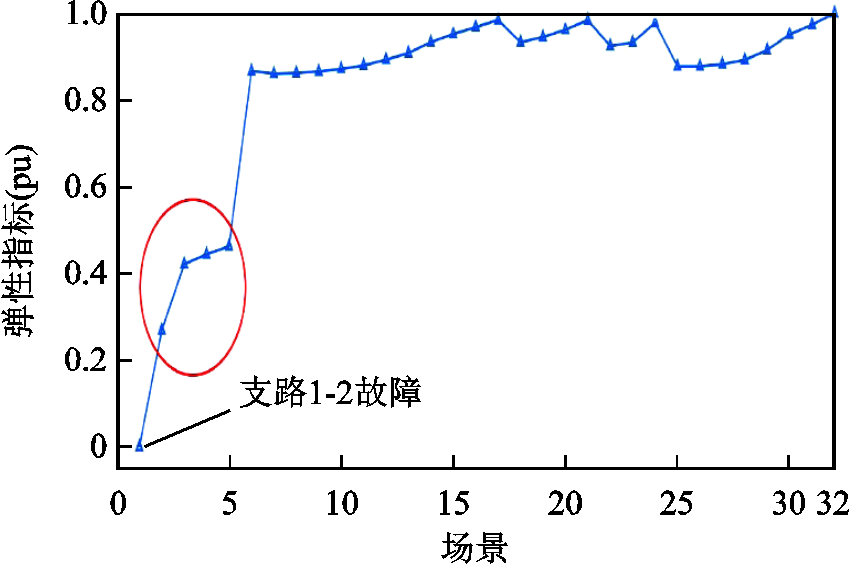
图13 IEEE 33节点N-1故障场景
Fig.13 N-1 failure scenario of IEEE 33-bus system
由图13可知,有五条支路故障时,系统弹性明显低于其他故障场景,其中与发电机相连的支路不予考虑,其余四条支路在图中已用圆圈出,分别为线路2-3、3-4、4-5和5-6。弹性指标的关键线路指该线路故障时,导致电网的弹性下降,抵御和恢复能力下降,因此这四条支路为33节点配电网的关键弹性线路。该结果与基于线路参数变化的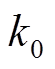 灵敏度分析得出的关键支路相一致。
灵敏度分析得出的关键支路相一致。
综合以上两部分算例,可知在系统不同负荷水平的情况下,阶段1等效弹性系数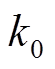 可以衡量系统对故障的抵御能力。在系统线路参数改变时,
可以衡量系统对故障的抵御能力。在系统线路参数改变时,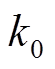 对关键线路参数变化具有较好的灵敏度。这两方面都可以反映等效弹性系数
对关键线路参数变化具有较好的灵敏度。这两方面都可以反映等效弹性系数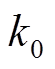 评估系统抵御能力的合理性。
评估系统抵御能力的合理性。
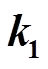 评估的合理性分析
评估的合理性分析在响应恢复阶段,阶段3等效弹性系数 衡量系统响应恢复的能力,用不同故障场景系统的恢复负荷比例来对比验证
衡量系统响应恢复的能力,用不同故障场景系统的恢复负荷比例来对比验证 的合理性。
的合理性。
在同样的负荷水平和拓扑结构的条件下,设置四种故障场景,分别计算对应的阶段1等效弹性系数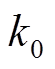 、阶段3等效弹性系数
、阶段3等效弹性系数 、弹性指标Res和相同恢复策略下的负荷恢复程度,结果见表1。为增加供电恢复效果,将系统负荷等功率因数增加至原米的1.5倍。
、弹性指标Res和相同恢复策略下的负荷恢复程度,结果见表1。为增加供电恢复效果,将系统负荷等功率因数增加至原米的1.5倍。
表1 弹性指标和恢复程度的计算结果
Tab.1 Calculation results of resilience and restoration
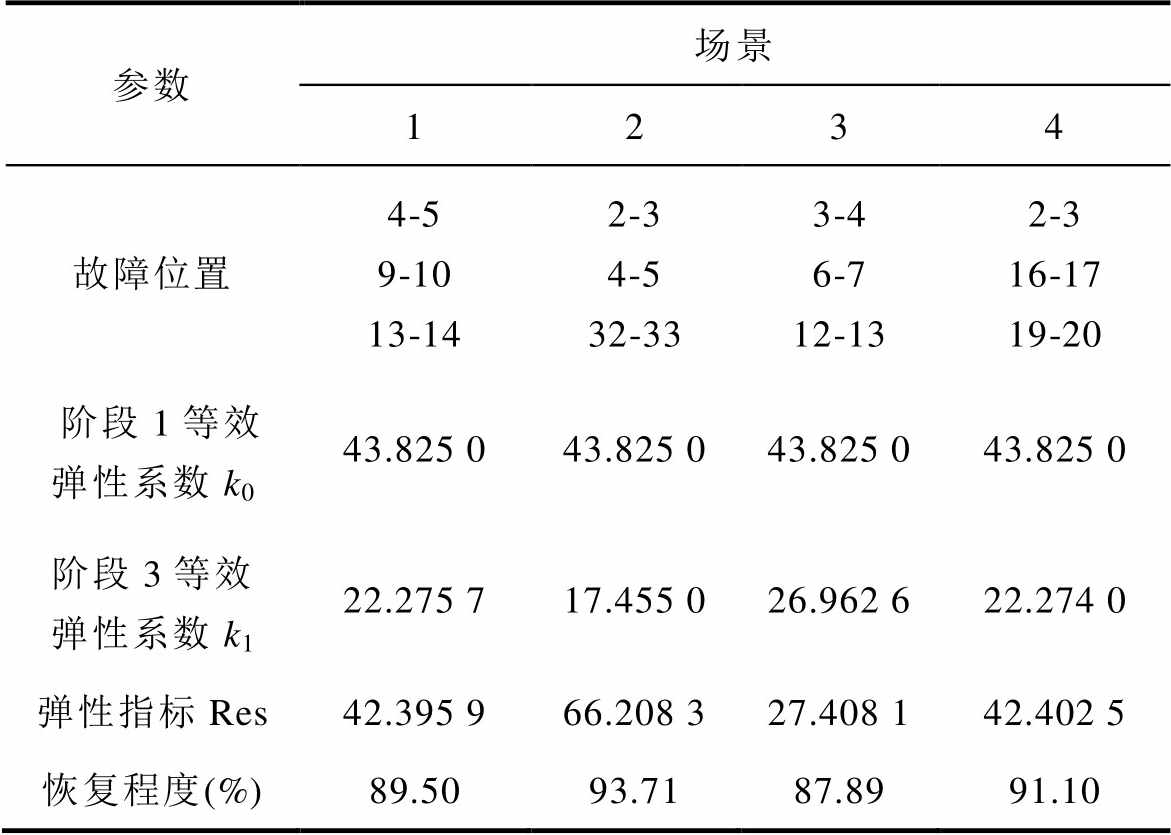
参数场景 1234 故障位置4-59-1013-142-34-532-333-46-712-132-316-1719-20 阶段1等效弹性系数k043.825 043.825 043.825 043.825 0 阶段3等效弹性系数k122.275 717.455 026.962 622.274 0 弹性指标Res42.395 966.208 327.408 142.402 5 恢复程度(%)89.5093.7187.8991.10
通过表1数据可知,不同场景下阶段1等效弹性系数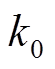 相同,因为每种场景中系统的初始状态完全相同,其应对故障的抵御能力相同。四种场景的阶段3等效弹性系数
相同,因为每种场景中系统的初始状态完全相同,其应对故障的抵御能力相同。四种场景的阶段3等效弹性系数 不同,因为断路故障发生在不同位置,对应的系统状态不同,其响应恢复的能力也不相同。根据前文
不同,因为断路故障发生在不同位置,对应的系统状态不同,其响应恢复的能力也不相同。根据前文 的类比定义,当其接受充当外力相同的恢复策略时,电压越容易变化,负荷恢复效果越好,对应的
的类比定义,当其接受充当外力相同的恢复策略时,电压越容易变化,负荷恢复效果越好,对应的 越小。因此,场景2的
越小。因此,场景2的 最小,场景3的
最小,场景3的 最大,对应可得场景2的系统恢复能力最好,场景3最差。根据表中的恢复程度,不同场景在相同的恢复策略下,场景2的恢复程度最高,场景3最低。由阶段3等效弹性系数
最大,对应可得场景2的系统恢复能力最好,场景3最差。根据表中的恢复程度,不同场景在相同的恢复策略下,场景2的恢复程度最高,场景3最低。由阶段3等效弹性系数 和恢复程度这两种指标评判系统恢复能力得出的结论相一致,因此使用阶段3等效弹性系数
和恢复程度这两种指标评判系统恢复能力得出的结论相一致,因此使用阶段3等效弹性系数 评判系统的恢复能力具有合理性。
评判系统的恢复能力具有合理性。
本文所提弹性力学映射模型是建立在潮流方程上分析扰动事件对电力系统影响的机理模型[5],不同于现有弹性研究中的概率指标。本模型可以评估某一故障场景下系统的弹性,该评估结果也可得出对系统弹性影响较大的关键支路等信息。
为验证本文所提基于弹性力学映射模型的配电网多阶段评估的合理性和有效性,将其与M. Panteli在文献[3, 17-18, 28]中所提弹性评估方法进行比较分析。该弹性评估方法采用缺电负荷量、电力不足概率、电力不足时间期望和电量不足期望值等与系统供电缺失量相关的指标来衡量弹性。
本节对如图14所示IEEE 123节点算例在同一故障情景下两种弹性评估结果进行对比分析。初始系统状态的开关13-152、18-135、54-94、115-300、60-160、97-197处于闭合状态,开关149-150、250-251、300-350、61-610、95-195、450-451处于断开状态。

图14 IEEE 123节点算例拓扑
Fig.14 Network topology of IEEE 123-node test feeder
图15对应单重故障场景,即系统中只有一条支路故障,遍历所有支路故障并进行弹性计算,故障场景即为断开支路号。图16对应多重故障场景,即系统中有两条及以上支路故障,随机生成500个故障场景并进行弹性计算,每个场景中断路支路数和支路号均为随机生成。两种弹性评价方法的单位不同,无法进行直观的对比,因此标幺化后进行比较。
图15 单重故障场景
Fig.15 Single failure scenario

图16 多重故障场景
Fig.16 Multiple failure scenarios
对比图15和图16分析可知:
(1)在单重故障场景3、7、10、115下,当系统弹性骤减时,对应的供电缺失量也大幅增加。多重故障场景的若干个系统弹性骤变的节点均对应着供电缺失量的大幅变化。从图15和图16可以看出,标幺化后的弹性指标Res和供电缺失量变化规律基本一致,即较大的供电缺失量对应着较差的弹性。
(2)图15和图16中用黑色圆圈出的较多场景,对应着的弹性指标Res变化明显,而供电缺失量基本不变。在不同的故障场景下,即使缺电负荷量相差不大,但因为不同的故障对系统的拓扑和运行状态影响不同,系统的弹性仍应表现出差异。黑色圆反映在故障对系统供电能力影响差不多时,本文的弹性指标仍能有效评估系统弹性,实现弹性的差异化量化。文献[32]提出高可靠的电力系统并不一定具有弹性,弹性指标需要同时考虑系统抵御能力和恢复能力。
(3)本文方法可以计算某一故障情景下系统弹性,区分不同故障对系统弹性的影响;M. Panteli通过概率统计模型得出的系统供电缺失量来衡量系统弹性,无法评估单一故障场景的系统弹性。
(4)缺电负荷量只能衡量系统负荷的减少量,衡量的是单方向量,且其变化范围确定,在零和负荷总量之间。而弹性是两方向量,既有提升也有下降,弹性指标应能衡量其提升和减弱作用。本文指标Res可以有效评估弹性的变化方向。
(5)根据系统在单重故障场景下的弹性计算,也可以进行基于该弹性指标的电网关键线路识别。根据图15弹性大小排序可判断出支路3、6、10是系统123节点系统的关键线路。
基于以上分析,已有的弹性评价方法和本文方法评价的结果基本一致,但本文方法适用场景更广泛且评价效果更好。
本节以图17所示的IEEE 33节点算例进行分析,算例电压等级为12.66kV,当前系统有功负荷总量为3.715MW,无功负荷总量为2.3Mvar。
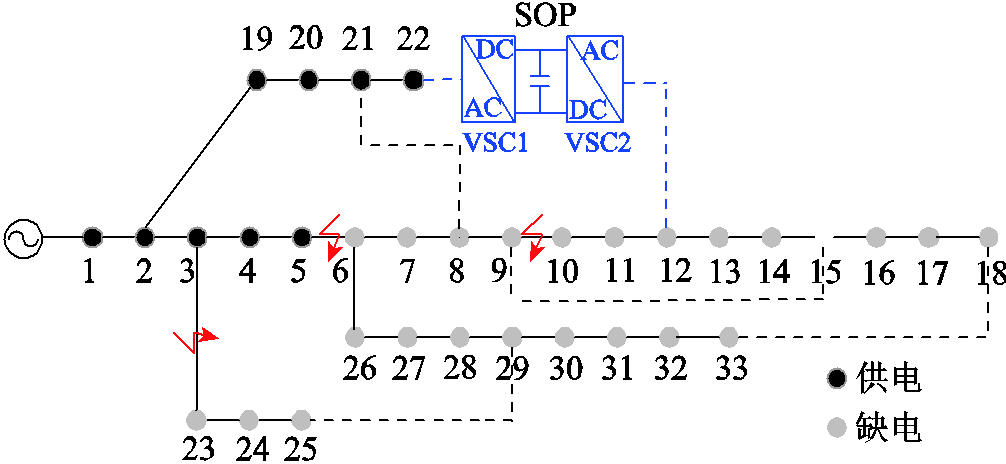
图17 IEEE 33节点多重故障情景
Fig.17 Multiple failure scenarios in IEEE 33 bus system
目前多数研究仅评估随机故障(单个故障)情形下的弹性,但实际可能为多重故障情形。本算例将基于此考虑多重故障下弹性指标的计算。借鉴文献[48]对鲁棒性指标的计算方法,根据故障造成的系统供电性能减少的比例反映系统的抵御能力,根据恢复后负荷恢复比例反映系统的恢复能力。为研究SOP对系统弹性的影响,该多阶段供电恢复在IEEE 33节点与改进的IEEE 33节点上进行测试,SOP代替22-12支路上的联络开关,对比未安装SOP与安装SOP系统的弹性指标,计算结果见表2。
表2 多重故障的计算结果
Tab.2 Calculation results of cases in multiple failure scenarios
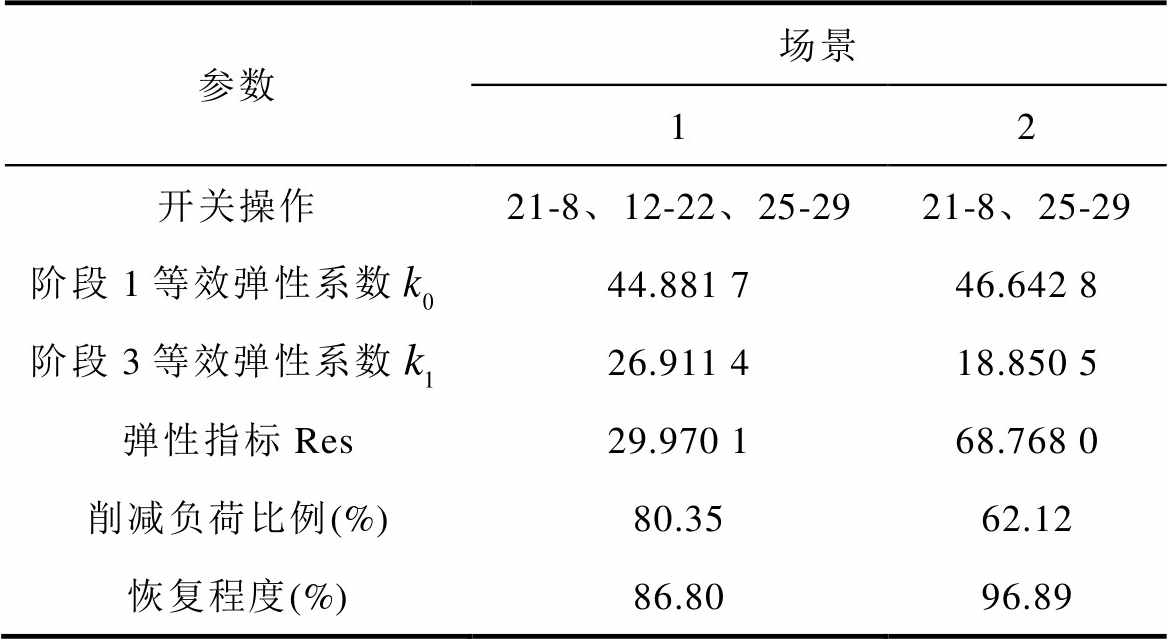
参数场景 12 开关操作21-8、12-22、25-2921-8、25-29 阶段1等效弹性系数44.881 746.642 8 阶段3等效弹性系数26.911 418.850 5 弹性指标Res29.970 168.768 0 削减负荷比例(%)80.3562.12 恢复程度(%)86.8096.89
假设支路5-6、9-10及3-23之间发生永久性故障,经故障隔离后,6-18节点与23-33节点所带负荷全部失电,设定恢复节点电压的范围为[0.95(pu), 1.05(pu)]。
根据表2的计算结果,未安装SOP的场景1的弹性低于安装SOP的场景2。场景2因故障削减负荷的比例较低,供电恢复效果较好,与较高的等效弹性系数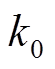 和较低的等效弹性系数
和较低的等效弹性系数 对应。
对应。
SOP在电力系统常态运行和故障恢复中的作用使系统的抵御、抗干扰能力和恢复能力得到提升,系统的整体弹性提高。两种情况的等效弹性系数和弹性指标的一致性也验证了本文所提出的多阶段弹性评估方法的合理性。
SOP的不同安装位置对系统常态运行的潮流分布及故障后的供电恢复效果有一定影响,本算例设置如图18的三种场景,SOP分别代替21-8、12-22、25-29支路的联络开关位置,通过对三种场景的系统弹性计算对比,分析不同SOP安装位置对系统弹性的影响。

图18 SOP不同安装位置
Fig.18 Different SOP installation positions
假设支路4-5之间发生了永久性故障,用SOP替代支路联络开关,计算结果见表3。
表3 SOP不同安装位置的计算结果
Tab.3 Calculation results of cases with different SOP installation positions

参数场景 345 SOP安装位置21-812-2225-29 阶段1等效弹性系数50.562 746.642 855.525 0 阶段3等效弹性系数17.428 119.327 716.129 7 弹性指标Res96.131 065.918 5135.614 6 削减负荷比例(%)30.7927.4921.12 恢复程度(%)96.7293.29100.00
根据表3的计算结果,对应SOP不同安装位置的三种场景的弹性不同,分阶段来看,其抵御能力和恢复能力也不同。SOP安装于支路25-29处的弹性最好,安装于21-8处的弹性次之。从削减负荷比例与恢复负荷比例的角度,场景5的抵御能力与恢复能力在三种场景中也是最好的。与场景4相比,场景3的抵御能力较强,其供电恢复能力较强,综合来看场景3的弹性优于场景4。
结合表2和表3的计算结果可以看出,SOP对系统弹性有一定的提升作用,SOP的不同安装位置也会影响系统弹性。对比图19的节点电压和图20的负荷分布可知,场景5的SOP安装位置处负荷量最大,电压降最大;场景4的SOP安装位置处负荷量最小,电压降最小。因为与电压降较大、负荷量较大区域相连,SOP能整体提高节点电压值,调节有功分布,同时使失电区域的电压水平波动趋于平缓[49]。通过对该算例分析可知,为了提高系统弹性,可将SOP安装在负荷量较大、压降较大的联络开关位置。
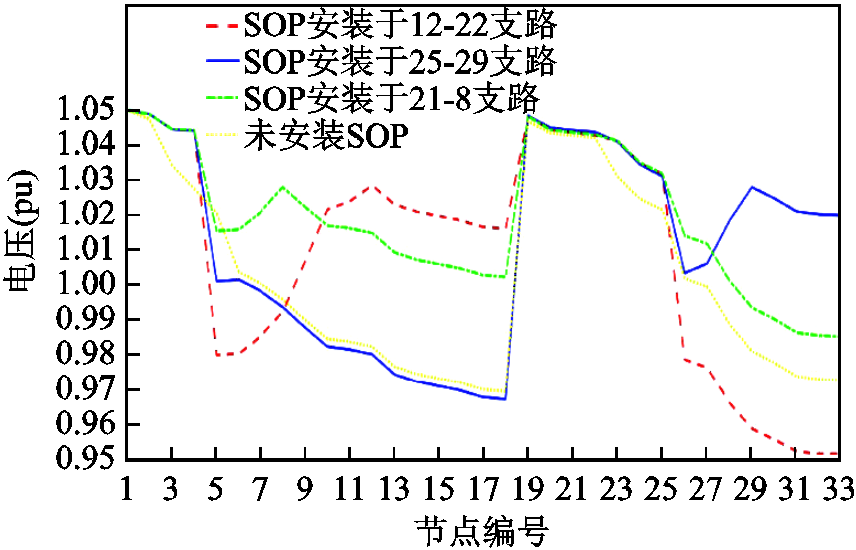
图19 不同场景节点电压
Fig.19 Node voltage for different scenarios

图20 负荷分布
Fig.20 Load distribution
基于3.2节的算例,在支路4-5发生永久性故障,SOP安装于支路25-29的场景下,分析SOP控制变量对弹性指标的影响。
当系统正常工作时,SOP两端VSC一侧控制传输的有功功率,另一侧控制直流电压,采用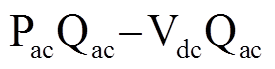 的控制模式。当SOP一侧有故障发生,则将其控制模式切换为
的控制模式。当SOP一侧有故障发生,则将其控制模式切换为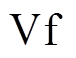 控制,保障非故障失电区域的节点电压稳定。在配电网供电恢复稳态分析中,可以将非故障侧的
控制,保障非故障失电区域的节点电压稳定。在配电网供电恢复稳态分析中,可以将非故障侧的 控制等效处理为
控制等效处理为 控制,则此时SOP的控制变量包括:非故障侧VSC输出的有功功率P和无功功率Q,故障侧VSC输出的电压U和频率f。一般将频率f设置为定值,选定控制变量U的变化范围为[0.95(pu), 1.05(pu)],通过多组实验得出不同控制变量值对应的弹性指标值,分析不同控制变量对弹性指标的影响。
控制,则此时SOP的控制变量包括:非故障侧VSC输出的有功功率P和无功功率Q,故障侧VSC输出的电压U和频率f。一般将频率f设置为定值,选定控制变量U的变化范围为[0.95(pu), 1.05(pu)],通过多组实验得出不同控制变量值对应的弹性指标值,分析不同控制变量对弹性指标的影响。
由图21a~图21c的对比可知,弹性指标Res对控制电压U的灵敏度远远大于对有功功率P和无功功率Q的灵敏度。弹性-控制电压灵敏度的最大值在8左右,而弹性-有功功率灵敏度和弹性-无功功率灵敏度均在0左右,且变化范围很小。弹性-控制电压灵敏度大于弹性-有功功率和弹性-无功功率灵敏度,即SOP的控制电压U对弹性指标Res的影响大于控制变量P和Q的影响。因为控制变量P和Q的作用主要体现在平衡系统潮流分布,电压U主要影响非故障侧失电区域的电压水平及供电恢复的速度和效果,因此可知恢复过程对系统的整体弹性影响效果更明显。为了得出Res与控制变量U之间更加准确的变化关系,由大量数据进行拟合,得出控制变量P和Q不变的情况下,Res与U之间的变化关系如图22所示。由图22可知,在控制变量U增加的过程中,弹性Res增加,当U增加至1.025(pu)时,Res达到峰值,随后U继续增加,Res开始减小。控制电压U不影响系统抵御扰动的能力,因此着重分析系统的恢复能力。负荷恢复量与控制电压的关系曲线如图23所示。由图23a可知,该场景下弹性峰值的控制电压对应着完全供电恢复的实现。由图23b可知,控制电压从0.95(pu)增加至1.025(pu), 逐渐减小,系统的恢复能力逐渐增强;控制电压从1.025(pu)增加至1.05(pu),
逐渐减小,系统的恢复能力逐渐增强;控制电压从1.025(pu)增加至1.05(pu), 逐渐增大,系统的恢复能力逐渐减弱。实现完全供电恢复后,随着控制电压的逐渐增加,虽能保证负荷恢复效果,但容易导致系统整体电压差较大,不利于其稳定运行。
逐渐增大,系统的恢复能力逐渐减弱。实现完全供电恢复后,随着控制电压的逐渐增加,虽能保证负荷恢复效果,但容易导致系统整体电压差较大,不利于其稳定运行。

图21 弹性-SOP控制变量灵敏度关系
Fig.21 The relationship between resilience index and control variables of SOP

图22 系统弹性与控制电压的关系曲线
Fig.22 The curve between resilience index and voltage of control variables

图23 负荷恢复量与控制电压的关系曲线
Fig.23 The curve between power restoration and voltage of control variable
弹性是衡量电力系统对扰动事件防御和负荷恢复能力的指标。本文将扰动前后系统变化映射到弹性力学模型,结合弹簧弹性系数的物理意义,将电力系统对扰动事件的抵御与恢复能力定量计算,构建配电网多阶段弹性评估指标。在IEEE 33节点和IEEE 123节点系统进行多阶段弹性力学映射评估的合理性和有效性分析,并分析SOP对配电网弹性的提升作用,SOP安装位置及其控制量对系统弹性的影响。本文提出的多阶段弹性力学映射为电力系统分析提供新的模型分析思路,同时含SOP的配电网弹性的合理评估对配电网运行和规划具有重要意义。
参考文献
[1] 别朝红, 林雁翎, 邱爱慈. 弹性电网及其恢复力的基本概念与研究展望[J]. 电力系统自动化, 2015, 39(22): 1-9.
Bie Zhaohong, Lin Yanling, Qiu Aici. Basic concepts and research prospects of resilient power grid and its resilience[J]. Automation of Electric Power Systems, 2015, 39(22): 1-9.
[2] Haimes Y Y. On the definition of resilient systems[J]. Risk Analysis, 2009, 29(4): 498-501.
[3] Panteli M, Mancarella P. The grid: stronger, bigger, smarter: presenting a conceptual framework of power system resilience[J]. IEEE Power & Energy Magazine, 2015, 13(3): 58-66.
[4] Francis R, Bekera B. A metric and frameworks for resilience analysis of engineered and infrastructure systems[J]. Reliability Engineering & System Safety, 2014, 121(1): 90-103.
[5] 别朝红, 林超凡, 李更丰, 等. 能源转型下弹性电力系统的发展与展望[J]. 中国电机工程学报, 2020, 40(9): 2735-2745.
Bie Zhaohong, Lin Chaofan, Li Gengfeng, et al. Development and prospect of flexible power system under energy transition[J]. Proceedings of the CSEE, 2020, 40(9): 2735-2745.
[6] 高海翔, 陈颖, 黄少伟, 等. 配电网韧性及其相关研究进展[J]. 电力系统自动化, 2015, 39(23): 1-8.
Gao Haixiang, Chen Ying, Huang Shaowei, et al. Distribution network resilience and related research progress[J]. Automation of Electric Power Systems, 2015, 39(23): 1-8.
[7] Chen Chen, Wang Jianhui, Tong Dan. Modernizing distribution system restoration to achieve grid resiliency against extreme weather events: an integrated solution[J]. Proceedings of the IEEE, 2017, 105(7): 1267-1288.
[8] Wang Yezhou, Chen Chen, Wang Jianhui, et al. Research on resilience of power systems under natural disasters—a review[J]. IEEE Transactions on Power Systems, 2016, 31(2): 1604-1613.
[9] 陈碧云, 李翠珍, 覃鸿, 等. 考虑网架重构和灾区复电过程的配电网抗台风韧性评估[J]. 电力系统自动化, 2018, 42(6): 47-52.
Chen Biyun, Li Cuizhen, Qin Hong, et al. Typhoon resilience assessment of distribution network considering grid reconfiguration and restoration process of disaster area[J]. Automation of Electric Power Systems, 2018, 42(6): 47-52.
[10] 王守相, 黄仁山, 潘志新, 等. 极端冰雪天气下配电网弹性恢复力指标的构建及评估方法[J]. 高电压技术, 2020, 46(1): 123-132.
Wang Shouxiang, Huang Renshan, Pan Zhixin, et al. Construction and evaluation method of elastic resilience index of distribution network under extreme ice and snow weather[J]. High Voltage Engineering, 2020, 46(1): 123-132.
[11] 李振坤, 王法顺, 郭维一, 等. 极端天气下智能配电网的弹性评估[J]. 电力系统自动化, 2020, 44(9): 60-71.
Li Zhenkun, Wang Fashun, Guo Weiyi, et al. Resilience assessment of smart distribution network under extreme weather[J]. Automation of Electric Power Systems, 2020, 44(9): 60-71.
[12] Henry D, Ramirez-Marquez J E. Generic metrics and quantitative approaches for system resilience as a function of time[J]. Reliability Engineering & System Safety, 2017, 99: 114-122.
[13] Ouyang Min, Dueñas-Osorio L, Xing Min. A three-stage resilience analysis framework for urban infrastructure systems[J]. Structural Safety, 2012, 36-37: 23-31.
[14] Zobel C W, Khansa L. Quantifying cyber-infrastructure resilience against multi-event attacks[J]. Decision Sciences, 2012, 43(4): 687-710.
[15] Ayyub B M. Systems resilience for multibazard environments: definition, metrics, and valuation for decision making[J]. Risk Analysis, 2014, 34(2): 340-355.
[16] Gao Haixiang, Chen Ying, Xu Yin, et al. Resilience oriented critical load restoration using microgrids in distribution systems[J]. IEEE Transactions on Smart Grid, 2016, 7(6): 2837-2848.
[17] Panteli M, Trakas D N, Mancarella P, et al. Boosting the power grid resilience to extreme weather events using defensive islanding[J]. IEEE Transactions on Smart Grid, 2017, 7(6): 2913-2922.
[18] Panteli M, Mancarella P. Influence of extreme weather and climate change on the resilience of power systems: impacts and possible mitigation strategies[J]. Electric Power Systems Research, 2015, 127(8): 259-270.
[19] 周晓敏, 葛少云, 李腾, 等. 极端天气条件下的配电网韧性分析方法及提升措施研究[J]. 中国电机工程学报, 2018, 38(2): 505-513, 681.
Zhou Xiaomin, Ge Shaoyun, Li Teng, et al. Research on analysis methods and improvement measures of distribution network resilience under extreme weather conditions[J]. Proceedings of the CSEE, 2018, 38(2): 505-513, 681.
[20] Dalhues S, Zhou Yang, Pohl O, et al. Research and practice of flexibility in distribution systems: a review[J]. CSEE Journal of Power and Energy Systems, 2019, 5(3): 285-294.
[21] 贾冠龙, 陈敏, 赵斌, 等. 柔性多状态开关在智能配电网中的应用[J]. 电工技术学报, 2019, 34(8): 1760-1768.
Jia Guanlong, Chen Min, Zhao Bin, et al. Application of flexible multi-state switch in smart distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1760-1768.
[22] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis of current research status of inverter parallel control technology in AC and DC distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[23] 孙充勃, 原凯, 李鹏, 等. 基于SOP的多电压等级混联配电网运行二阶锥规划方法[J]. 电网技术, 2019, 43(5): 1599-1605.
Sun Chongbo, Yuan Kai, Li Peng, et al. A second-order cone planning method for multi-voltage level hybrid distribution network operation based on SOP[J]. Power System Technology, 2019, 43(5): 1599-1605.
[24] 郑焕坤, 石甜静. 基于智能软开关和无功补偿装置的配电网双层优化[J]. 电力系统自动化, 2019, 43(19): 117-126.
Zheng Huankun, Shi Tianjing. Double-layer optimization of distribution network based on intelligent soft switch and reactive power compensation device[J]. Automation of Electric Power Systems, 2019, 43(19): 117-126.
[25] 彭元泉, 麦志远, 艾维, 等. 含柔性多状态开关的主动配电网有功-无功协调动态优化[J]. 电力系统自动化, 2020, 44(14): 54-64.
Peng Yuanquan, Mai Zhiyuan, Ai Wei, et al. Active power-reactive power coordination dynamic optimization of active distribution network with flexible multi-state switches[J]. Automation of Electric Power Systems, 2020, 44(14): 54-64.
[26] 祝旭焕, 童宁, 林湘宁, 等. 基于柔性多状态开关的主动配电网负荷在线紧急转供策略[J]. 电力系统自动化, 2019, 43(24): 87-101.
Zhu Xuhuan, Tong Ning, Lin Xiangning, et al. On-line emergency transfer strategy of active distribution network load based on flexible multi-state switch[J]. Automation of Electric Power Systems, 2019, 43(24): 87-101.
[27] 竺炜, 周孝信, 唐如. 电网的弹性力学网络拓扑映射[J]. 中国电机工程学报, 2011, 31(31): 109-117.
Zhu Wei, Zhou Xiaoxin, Tang Ru. Elasticity network topology mapping of power grid[J]. Proceedings of the CSEE, 2011, 31(31): 109-117.
[28] Panteli M, Mancarella P. Modeling and evaluating the resilience of critical electrical power infrastructure to extreme weather events[J]. IEEE Systems Journal, 2017, 11(3): 1733-1742.
[29] Zhang Xing, Wang Mingda, Zhao Tao, et al. Topological comparison and analysis of medium voltage and high-power direct-linked PV inverter[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 327-334.
[30] 朱永强, 刘康, 张泉, 等. 混合微电网交流侧故障传播机理及抑制方法[J]. 电机与控制学报, 2020, 24(4): 1-11.
Zhu Yongqiang, Liu Kang, Zhang Quan, et al. The AC side fault propagation mechanism and suppression method of hybrid microgrid[J]. Electric Machines and Control, 2020, 24(4): 1-11.
[31] 许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019, 34(16): 3416-3429.
Xu Yin, He Jinghan, Wang Ying, et al. Overview and prospects of distribution network failure recovery under the background of resilience[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3416-3429.
[32] Bie Zhaohong, Lin Yanling, Li Gengfeng, et al. Battling the extreme: a study on the power system resilience[J]. Proceedings of the IEEE, 2017, 105(7): 1253-1266.
[33] 徐芝纶. 弹性力学简明教程[M]. 北京: 高等教育出版社, 2013.
[34] 竺炜, 周孝信, 蒋頔, 等. 基于映射弹性势能的电网有功承载能力定量指标[J]. 中国电机工程学报, 2014, 34(13): 2088-2099.
Zhu Wei, Zhou Xiaoxin, Jiang Di, et al. Quantitative index of active power carrying capacity of power grid based on mapping elastic potential energy[J]. Proceedings of the CSEE, 2014, 34(13): 2088-2099.
[35] Qin Qing, Han Bei, Li Guojie, et al. Computation and analysis of distribution system resilience based on elastic network modeling[C]//2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, 2020: 1955-1960.
[36] 孙正龙. 弹性力学映射的电力系统能量结构及其在低频振荡分析中的应用[D]. 吉林: 东北电力大学, 2018.
[37] 蔡国伟, 穆钢, K. W. Chan, 等. 基于网络信息的暂态稳定性定量分析——支路势能法[J]. 中国电机工程学报, 2004, 24(5): 5-10.
Cai Guowei, Mu Gang, Chan K W, et al. Quantitative analysis of transient stability based on network information—branch potential energy method[J]. Proceedings of the CSEE, 2004(5): 5-10.
[38] 鞠平, 王冲, 辛焕海, 等. 电力系统的柔性、弹性与韧性研究[J]. 电力自动化设备, 2019, 39(11): 1-7.
Ju Ping, Wang Chong, Xin Huanhai, et al. Study on the flexibility, resilience and toughness of power system[J]. Electric Power Automation Equipment, 2019, 39(11): 1-7.
[39] 章雅纯, 陈树勇, 刘道伟, 等. 基于映射广义弹性系数的电网静态稳定快速评估判据[J]. 中国电机工程学报, 2015, 35(16): 4094-4101.
Zhang Yachun, Chen Shuyong, Liu Daowei, et al. Quick evaluation criterion for static stability of power grid based on mapping generalized elastic coefficient[J]. Proceedings of the CSEE, 2015, 35(16): 4094-4101.
[40] Arefifar S A, Mohamed A R I, El-Fouly T H M. Comprehensive operational planning framework for self-healing control actions in smart distribution grids[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4192-4200.
[41] Bajpai P, Chanda S , Srivastava A K . A novel metric to quantify and enable resilient distribution system using graph theory and Choquet integral[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 2918-2929.
[42] 彭寒梅, 王小豪, 魏宁, 等. 提升配电网弹性的微网差异化恢复运行方法[J]. 电网技术, 2019, 43(7): 2328-2335.
Peng Hanmei, Wang Xiaohao, Wei Ning, et al. Differential recovery method of microgrid to improve the resilience of distribution network[J]. Power System Technology, 2019, 43(7): 2328-2335.
[43] 宋毅, 孙充勃, 李鹏, 等. 基于智能软开关的有源配电网供电恢复方法[J]. 中国电机工程学报, 2018, 38(15): 4390-4398, 4639.
Song Yi, Sun Chongbo, Li Peng, et al. An active distribution network power supply restoration method based on intelligent soft switching[J]. Proceedings of the CSEE, 2018, 38(15): 4390-4398, 4639.
[44] 王成山, 孙充勃, 李鹏, 等. 基于SNOP的配电网运行优化及分析[J]. 电力系统自动化, 2015, 39(9): 82-87.
Wang Chengshan, Sun Chongbo, Li Peng, et al. Optimization and analysis of distribution network operation based on SNOP[J]. Automation of Electric Power Systems, 2015, 39(9): 82-87.
[45] 丛鹏伟, 唐巍, 娄铖伟, 等. 含高渗透率可再生能源的主动配电网两阶段柔性软开关与联络开关协调优化控制[J]. 电工技术学报, 2019, 34(6): 1263-1272.
Cong Pengwei, Tang Wei, Lou Chengwei, et al. Two-stage flexible soft open point and tie switch coordinated optimization control of active distribution network with high-permeability renewable energy[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1263-1272.
[46] 张释中, 裴玮, 杨艳红, 等. 基于柔性直流互联的多微网集成聚合运行优化及分析[J]. 电工技术学报, 2019, 34(5): 1025-1037.
Zhang Shizhong, Pei Wei, Yang Yanhong, et al. Optimization and analysis of multi-microgrid integration and aggregation operation based on flexible DC interconnection[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1025-1037.
[47] 颜宁, 潘霄, 张明理, 等. 基于多时间尺度的微电网群阶梯控制方法研究[J]. 电机与控制学报, 2019, 23(9): 26-34.
Yan Ning, Pan Xiao, Zhang Mingli, et al. Research on micro-grid group ladder control method based on multiple time scales[J]. Electric Machines and Control, 2019, 23(9): 26-34.
[48] 李雪, 孙霆锴, 侯恺, 等. 地震灾害下海岛综合能源系统韧性评估方法研究[J]. 中国电机工程学报, 2020, 40(17): 5476-5493.
Li Xue, Sun Tingkai, Hou Kai, et al. Research on the resilience assessment method of island integrated energy system under earthquake disaster[J]. Proceedings of the CSEE, 2020, 40(17): 5476-5493.
[49] 茅逸斐, 韩蓓, 李国杰, 等. 基于网络等效的配电网快速供电恢复策略并行化实现[J]. 电力系统保护与控制, 2018, 46(11): 99-108.
Mao Yifei, Han Bei, Li Guojie, et al. The parallel realization of the rapid power supply restoration strategy of distribution network based on network equivalence[J]. Power System Protection and Control, 2018, 46(11): 99-108.
Multi-Stage Elastic Mechanical Modelling and Evaluation of Distribution Networks with Soft Open Point
Abstract Resilience measures the ability of the power system to resist disturbance and quickly recover after failure. Its evaluation involves a multi-stage process of resisting, adapting, responding and recovering to disturbances. Most current researches use simulation results or statistical analysis of historical data to evaluate system resilience. This paper establishes a distribution network model based on multi-stage elastic mechanics mapping. This model fully considers the operating state and physical characteristics of the system, and conducts a multi-stage assessment of resilience from the two perspectives of resistance to disturbance and recovery after failure. It analyzes the role of soft open point (SOP) in normal operation and power supply restoration based on the elastic mechanics model. Computation and analysis conducted based on the IEEE 33-bus system and IEEE 123-node test feeder verify the rationality of the multi-stage evaluation of resilience. The influence of SOP on the resilience of the distribution network is analyzed, and the results show its effect on the improvement of resilience. The influences of different installation positions and control variables of SOP on the resilience are compared and discussed.
keywords:Resilience of power system, elastic mechanics mapping, soft open point, equivalent elastic coefficient, power restoration
DOI: 10.19595/j.cnki.1000-6753.tces.201319
中图分类号:TM744
国家重点研发计划资助项目(2016YFB0900504)。
收稿日期 2020-09-29
改稿日期 2020-12-09
秦 清 女,1998年生,硕士研究生,研究方向为配电网弹性。E-mail:qinqing@sjtu.edu.cn
韩 蓓 女,1984年生,博士,讲师,研究方向为含微网的配电网模型研究。E-mail:han_bei@sjtu.edu.cn(通信作者)
(编辑 赫蕾)