图1 交直流系统结构示意图
Fig.1 Structure of AC-DC system
摘要 针对采用牛拉（NR）法计算电力系统交直流系统潮流存在初值选取和计算量大的不足，提出一种用于交直流潮流计算的全纯嵌入方法。该方法首先依据全纯函数构造原理，通过嵌入参数，分别构建全纯交流潮流模型、直流潮流模型及换流站控制模型；然后，基于全纯函数的泰勒级数展开特性，将非线性全纯潮流方程的求解问题，转换为隐式全纯函数的显式化问题；依据同次幂系数相等原则，求取泰勒级数展开项的幂级数系数，完成全纯函数的显式化，进而对嵌入参数赋值，实现交直流潮流的快速求解；最后，通过修改的IEEE 5节点交直流系统、RTS-96交直流系统和波兰电网3012wp交直流测试系统进行分析和验证，结果表明，所提方法不依赖初值便可快速、准确地计算出交直流系统潮流，且鲁棒性强，为大规模交直流电网潮流计算提供了新思路。
关键词：交直流系统 电压源型换流器 全纯函数 潮流计算
基于电压源型换流器（Voltage Source Converter, VSC）的柔性直流输电技术具有传输容量大、可控性强等诸多优点，已成为解决用电需求增长、大规模新能源并网等问题的有效手段[1-4]。近年来，我国柔性直流输电工程数量和规模不断增加，大规模交直流混合输电已成为我国电网典型形态[5-6]。然而，大规模交直流混合输电系统拓扑结构的复杂性和直流系统控制模式的多样性，给快速、准确获取交直流电网潮流分布带来极大挑战[7-8]，研究适用于计算大规模交直流系统潮流的新方法，对交直流电网规划运行、稳定分析、可靠性评估等具有重要意义。
当前，交直流电网潮流计算方法主要分为统一求解法和交替求解法[9]：统一求解法将交流潮流方程和直流潮流方程进行联立求解[10]；交替求解法则对交流电网潮流和直流电网潮流交替求解，并利用换流站实现交直流潮流信息交互[11]。文献[10,12]将交流潮流修正方程和直流潮流修正方程进行联立，并基于牛拉（Newton Raphson, NR）法求解该修正方程，实现交直流潮流的统一求解。然而该方法在实际应用中存在以下瓶颈：①当交直流电网规模增大时，Jacobi矩阵维数剧增，修正方程求解速度降低；②换流站控制方式切换将使迭代计算次数增加。因此，统一求解法难以满足大规模交直流电网潮流计算效率的需要[11]。交替求解法可扩展性强、灵活性高，且有效降低了潮流方程的维数，在实际工程中得到了广泛应用[13-14]。文献[14-15]建立了VSC换流站的稳态潮流模型，并基于NR法分别计算交流电网潮流与直流电网潮流，实现交直流系统潮流的交替求解。然而，基于NR的交替求解法在交直流潮流信息交互的大循环和节点电压修正的小循环中均会引起节点功率变化，需修正Jacobi矩阵对应元素，并重新对Jacobi矩阵求逆，计算量较大，且节点功率变化较大时易造成Jacobi矩阵奇异[16]；其次，NR法对初值比较敏感，不合理的初值有可能导致交直流潮流计算耗时增加，甚至无法收敛[17]。
为解决NR法在潮流计算中的不足，西班牙学者A. Trias博士于2012年提出利用全纯函数嵌入法（Holomorphic Function Embedding Method, HEM）求解电力系统潮流的新思路，该方法具有良好的收敛性，且无需提供初值[18]。文献[19-20]进一步提出了PV节点的全纯潮流模型，完善了交流系统潮流计算的全纯嵌入算法。然而，现有HEM相关研究多应用于交流系统，对交直流混合系统的潮流计算鲜有研究。此外，多端互联交直流混合输电系统的潮流计算需同时考虑交流电网潮流、直流网络潮流及换流站控制方式，仅由交流全纯潮流计算方法简单地推广至直流潮流计算中，难以适用于控制方式灵活多变的多端交直流输电系统。因此，开发适用于交直流系统的全纯嵌入潮流求解算法亟待研究。
针对上述问题，本文提出了电力系统交直流潮流的全纯嵌入计算方法。首先，针对传统潮流计算中的节点功率平衡方程，通过嵌入参数构建全纯交流潮流模型和全纯直流潮流模型，同时计及换流站的控制特点，构建换流站的全纯控制模型；然后，基于全纯函数的泰勒级数展开特性，将非线性潮流方程的求解问题转换为隐式全纯函数的显式化问题；进而，依据同次幂系数相等原则，求取泰勒级数展开项的幂级数系数，以实现隐式全纯函数的显式化，并对嵌入参数赋值求取系统潮流解；最后，通过修改的IEEE 5节点交直流系统、RTS-96交直流系统和波兰电网3012wp交直流测试系统对所提方法进行分析和验证。
含VSC换流站的交直流系统结构示意图如图1所示。图1中Psp i和Qsp i分别表示第i个VSC换流站注入交流系统公共耦合点（Point of Common Coupling, PCC）的有功和无功功率，Pdc和Vdc分别表示直流节点有功功率和节点电压。
图1 交直流系统结构示意图
Fig.1 Structure of AC-DC system
图1中，交直流系统潮流模型可分为交流潮流模型、直流潮流模型和VSC换流站信息交互模型。极坐标系下交流侧潮流模型可描述为
（1）式中，Vi、Vj分别为节点i和j的电压幅值；qij为节点i与j的电压相位差；Pi与Qi分别为节点i的有功和无功注入量；Gij与Bij分别为节点i与j之间的电导与电纳；N为交流电网节点数。
直流潮流模型可表述为
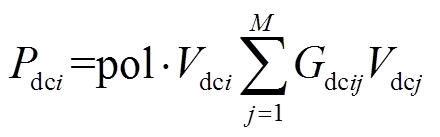（2）式中，Pdci为直流节点i的有功功率；Vdci为直流节点i的电压；Gdcij为直流节点i与直流节点j之间的电导；M为直流系统节点数；pol为直流电网输电极数。
换流站信息交互模型主要包括换流站交流侧的有功平衡方程、无功平衡方程及换流器有功功率平衡方程[9]，具体形式为
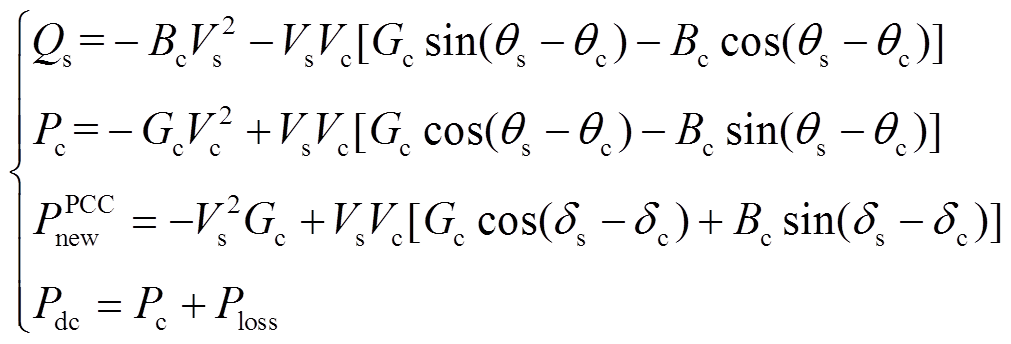（3）式中，Pc为流过换流器的有功功率；Pdc为直流侧有功功率；Ploss为换流站损耗；Qs为换流器注入PCC节点的无功功率；PPCC new为换流站注入PCC节点的更新值；Bc为换流站等效电纳；Gc为换流站等效电导；Vs为PCC节点电压幅值；Vc为换流器母线电压幅值；θs为PCC节点电压相角；θc为换流器母线电压相角。
对式（1）～式（3）所构成的交直流系统潮流方程，目前常用的求解方法是NR法。虽然NR法已在交直流系统的潮流计算中发挥出重要作用，但在实际应用时仍存在计算量较大、对初值敏感、Jacobi矩阵易奇异等不足。为此，本文提出一种基于HEM的交直流潮流全纯嵌入计算方法。
为解决传统NR法在交直流潮流计算中的不足[10-15]，本节首先基于全纯函数嵌入原理，在直角坐标系下，分别构建含全纯函数的交流潮流计算模型、直流潮流计算模型及换流站控制模型，进而实现交直流系统的全纯潮流模型构建。
2.1.1 全纯函数构造原理初始振幅系数建立
若函数z(α)定义域内每一点的邻域均无限可微，则称z(α)为全纯函数[21]，其在定义域内α0处展开的泰勒级数可表示为
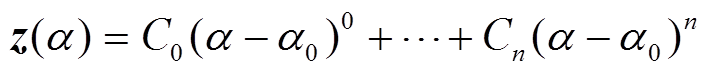（4）式中，Cn为泰勒级数展开第n项幂级数的常系数。
对非线性方程，有
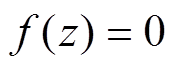（5）
若待求量z难以直接求解时，全纯函数嵌入法通过嵌入新的复变量α，构造隐式函数z(α)，并嵌入到原方程中形成含有全纯函数的方程，即
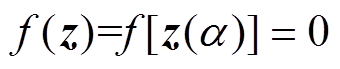（6）通过对函数z(α)进行泰勒级数展开，求解其幂级数系数Cn并代入式（4），可将该隐式函数z(α)转换为有具体表达式的显式函数，进而对变量α赋值得到z(α)的具体值，即为f(z)的解。
2.1.2 全纯函数构造条件
为保证全纯函数嵌入法的正确应用，构造全纯方程时应满足以下条件[22]：①所构造的隐式函数z(α)在定义域内连续且解析，即该函数具有全纯性；②由斯塔尔定理可知，在到达鞍节分岔点前的α路径上，f[z(α)]=0具有唯一解，不存在多个解合并的异常点，异常点仅在鞍节分岔点处存在；③当α=0时，方程f[z(0)]=0的解z[0]（即“幂级数常数项”）真实存在，且相对容易求取；④当α=1时，f[z(1)]等价于f(z)，从而保证α=1时，z(1)的值即f(z)=0的数值解。
由2.1节可知，通过对式（5）所示的非线性方程嵌入复参数构造全纯函数，可将非线性方程求解问题转换为隐式全纯函数的显式化问题，进而实现非线性方程的求解。本节将该求解思想应用于交流侧潮流求解中，分别构造如下交流系统PQ、PV及平衡节点的全纯潮流方程。
1）PQ节点全纯潮流方程。通常PQ节点注入功率已知，待求量为节点电压幅值和相角，其复数形式的节点功率平衡方程为
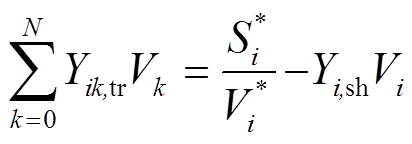（7）式中，Yik,tr为节点i与节点k之间的线路导纳；Yi,sh为节点i对地自导纳；Si为节点i注入功率；Vi为节点i电压；“*”表示共轭运算。
显然，式（7）是关于节点电压Vi的多元非线性方程，根据2.1节所述全纯函数构造原则，在原方程中嵌入复参数α（α=p+jq，其中p,q∈R），构造关于i节点电压Vi的全纯函数Vi(α)，故PQ节点全纯潮流方程为
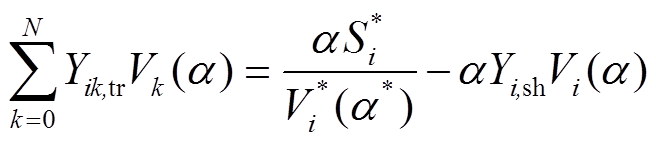（8）由全纯函数充要条件，函数V(α)满足柯西-黎曼方程，V(α)为全纯函数，且文献[18]已证明全纯潮流模型满足条件②，因此所构造PQ节点全纯潮流方程满足2.1.2小节所述构造条件①与②。
由于函数V(α)是全纯函数，将其在(0，j0)处泰数展开，并进一步化简为幂级数形式，即
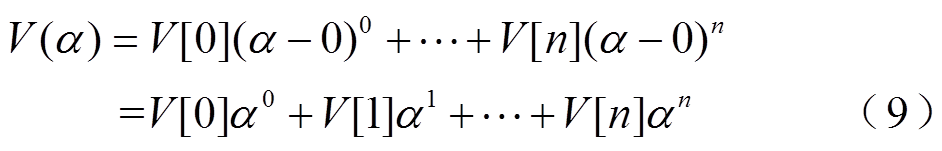
式中，V[0]、V[1]
V[n]为幂级数系数。若求取V[0]、V[1]V[n]具体数值，便可将隐式函数V(α)显式化。
又由式（8）可知，当α=0时，非线性潮流方程式（8）转换为关于Vi[0]的线性方程组，便可求取Vi[0]数值；当α=1时，式（8）与式（7）等价，故V(1)的数值即为节点电压值。因此式（8）满足2.1.2小节所述构造条件③与④。
2）PV节点全纯潮流方程。PV节点通常已知节点电压幅值和节点注入有功功率，待求量为节点电压相角和注入无功功率。同理，构造PV节点的全纯潮流方程为
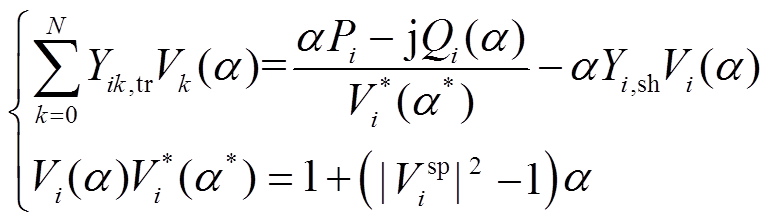（10）式中，
为节点i设定的电压幅值；
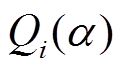为节点i注入无功功率
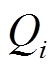的全纯函数。
3）平衡节点全纯潮流方程。平衡节点通常已知节点电压的幅值和相角，待求量为节点i注入的有功和无功功率。为便于全纯潮流模型的求解，构造平衡节点全纯潮流方程为
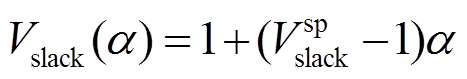（11）式中，Vsp slack为平衡节点设定的电压；V slack(α)为交流平衡节点的电压全纯函数。
不同于交流电网，直流电网的功率和电压均为实数值，但实数域包含于复数域内，故全纯嵌入法在直流电网潮流计算中依然适用。直流网络节点类型主要分为定直流功率节点和定直流电压节点，针对这两类直流网络节点类型，本节分别构造如下直流全纯潮流方程。
1）定直流功率节点全纯潮流方程。此类节点通常已知节点有功功率Pdci，待求量为节点电压Vdci。依据全纯函数的构造条件，通过嵌入实数域参数s构造节点电压Vdci的全纯函数，进而得到定直流功率节点i的全纯潮流方程为
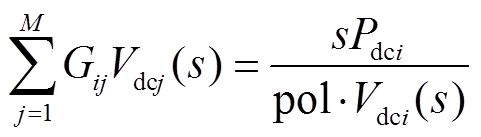（12）式中，Pdci为直流节点i的有功功率；Vdci(s)、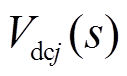
为分别直流节点i、j电压Vdci、Vdcj的全纯函数。
2）定直流电压节点全纯潮流方程。此类节点通常已知节点电压Vdci，节点有功功率Pdci待求，为便于全纯潮流模型的求解，构造该节点的全纯直流潮流方程为
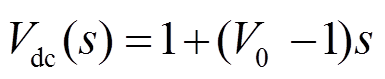（13）式中，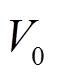
为设定的直流电压。
换流站是连接交流系统与直流网络的关键环节，在交直流系统潮流计算中，换流站潮流计算模型包括换流站等值模型、损耗模型及控制模型[23-25]。由于换流站等值模型和损耗模型的相关研究较为成熟[15]，因此，本文重点关注换流站全纯控制模型的构建，有关换流站等值模型和损耗模型可详见文献[14]。VSC换流站控制方式可分为有功类控制和无功类控制两大类，且不同控制方式间还存在转换。针对换流站的控制方式及控制方式转换特点，本节分别构建VSC换流站的有功类和无功类全纯控制模型。
2.4.1 有功类控制全纯潮流方程
有功类控制也称为直流侧控制，可直接控制直流电网的传输功率及节点电压，通常可分为定直流功率控制与定直流电压控制，其对应的全纯潮流模型构建如下：
（1）定直流功率控制全纯潮流模型。该控制方式下，VSC换流站控制量为直流侧有功功率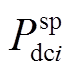
，构建定直流有功控制全纯潮流模型为
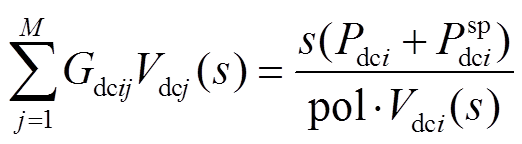（14）（2）定直流电压控制全纯潮流模型。该控制方式下，VSC换流站控制量为直流侧节点电压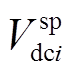
，构造的定直流电压控制全纯潮流模型为
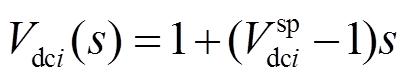（15）
2.4.2 无功类控制全纯潮流方程
无功类控制也称为交流侧控制，可间接影响交流电网传输的无功功率及电压幅值，通常分为定无功功率控制与定交流电压控制，其对应的全纯潮流模型可构建为：
（1）定无功功率控制全纯潮流模型。定无功功率控制方式下，VSC换流站注入交流侧PCC节点无功功率为定值Qsp i，构建定无功功率控制全纯潮流模型为
（16）式中，SPCC* i为交流第i个PCC节点的功率的共轭。
（2）定交流节点电压控制全纯潮流模型。定交流节点电压控制方式下，VSC换流站控制交流侧PCC节点电压幅值为定值Vsp i，构建的定交流节点电压控制全纯潮流模型为
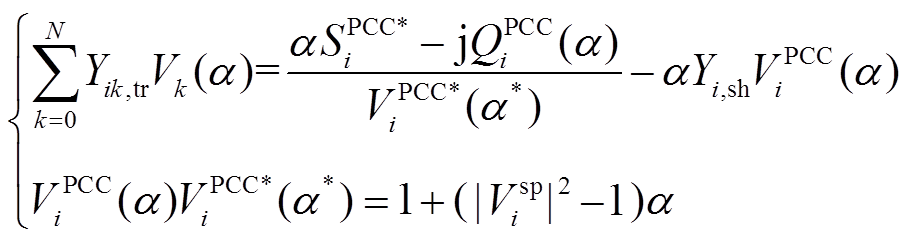（17）系统正常运行时，需根据交直流系统实际运行情况，对VSC换流站有功类和无功类控制方式进行合理的组合，常用的VSC换流站控制组合方式主要有以下四种：①直流侧定Pspdci控制，交流侧定Qsp i控制；②直流侧定Vspdci控制，交流侧定Qsp i控制；③直流侧定Pspdci控制，交流侧定Vsp i控制；④直流侧定Vspdci控制，交流侧定Vsp i控制。
2.4.3 VSC换流站控制方式转换
正常运行时，为保证换流站安全运行，换流站需适时调整其控制方式，以便换流站运行在安全区域内。图2为考虑VSC换流站电压约束和换流站传输容量约束的换流站安全运行区域。图中上、下圆弧为换流母线电压运行在上、下限时对应的无功功率边界，圆形区域为换流器传输容量约束，左侧为整流运行区域，右侧为逆变运行区域，阴影部分为VSC换流站实际运行区域。
如图2所示，若换流站无功类控制方式设置为定无功功率控制，正常运行时处于图中A点，假如交流PCC节点或与之相邻的节点负荷增加，由于无功不足将导致PCC电压幅值降低，进而导致换流母线电压低于其下限值Vc,min，如图中B点所示。此时需将定无功功率控制转变为定交流电压控制，为系统提供无功支撑能力以提高交流节点电压，系统运行点将移至图中C点，使VSC换流站电压维持在合理范围内。若换流站无功控制方式设置为定交流电压控制，正常运行时处于图2中D点。若PCC节点负荷持续大幅增加，VSC换流站注入交流系统PCC的无功功率Qs也随之增加，导致换流母线电压高于其上限值Vc,max，如图中E点所示。此时应将VSC换流站控制方式由定交流电压控制转换为定无功功率控制，无功功率设定值为换流器传输容量约束下的最大无功功率注入值，系统运行在图中F点，避免了换流器潮流越限。
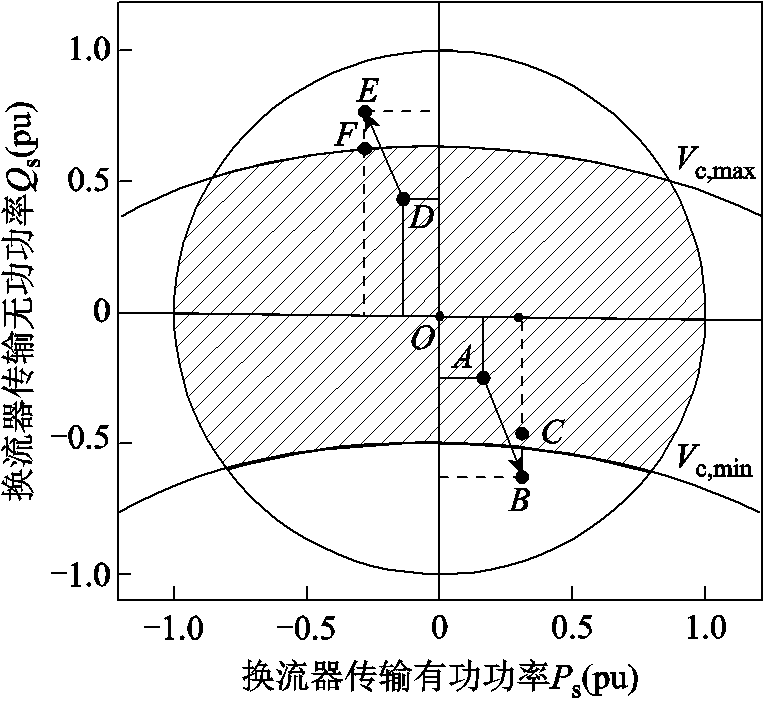
图2 电压约束和传输功率约束下换流器的运行范围
Fig.2 Operation range of converter with voltage and power constraints
针对第2节构建的交直流系统全纯潮流计算模型，本节基于交替求解算法分别对其进行求解，以实现交直流系统潮流的求解。
全纯潮流模型求解的关键是建立全纯函数幂级数系数V[n]与V[n-1]之间的递归关系，进而求取全纯函数表达式并对嵌入变量赋值，即可完成交流潮流的求解。
1）PQ节点求解
为消除式（8）中的分式，进而作如下假设
（18）将全纯函数在(0，j0)处展开为泰勒级数，并代入式（8）得
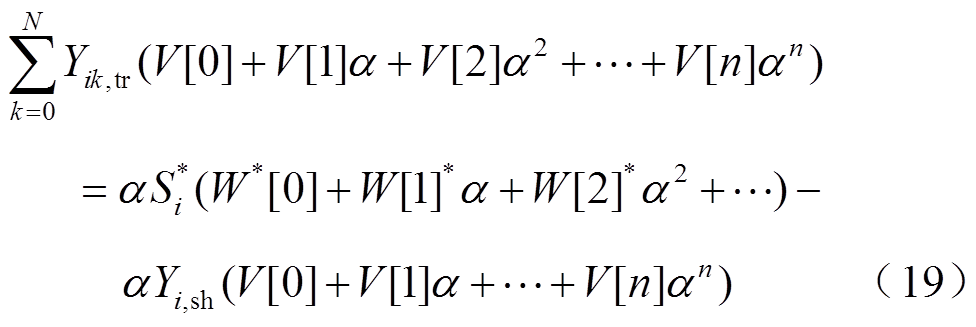
通过比较式（19）两边同次幂αn的系数（n=1,2, 3,
），得到幂级数系数递归关系为
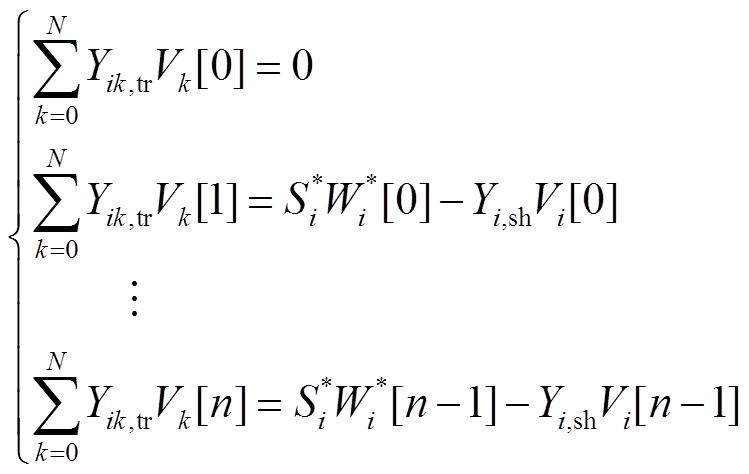（20）式中，Vk[n]为k节点电压幂级数αn的系数；n为幂级数阶次。获取递归关系式（20）后，便可利用低阶的W[n-1]和V[n-1]求取高阶的V[n]。
又因V(α)和W(α)互为倒数，故满足
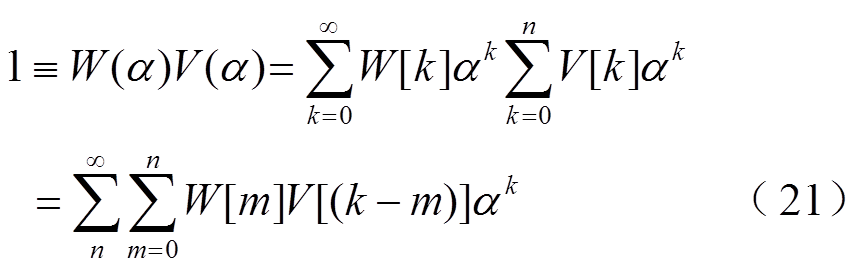
通过比较式（21）等号两边同次幂系数可得
（22）
综上所述，电压函数的幂级数系数V[n]求解过程如图3所示。
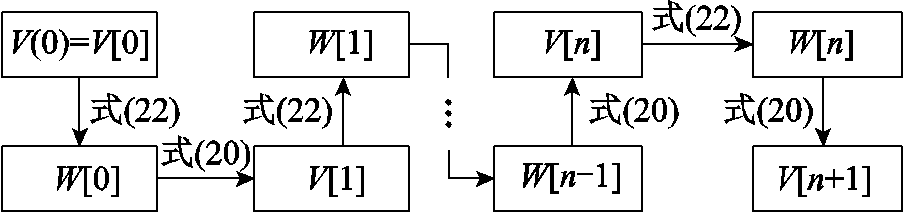
图3 幂级数系数递归求解示意图
Fig.3 Diagram of recursive solution of power series coefficients
2）PV节点求解
对PV节点，将全纯函数进行泰勒展开并代入式（10）中，对比等式两边同次αn幂级数系数，求得的幂级数系数递归式为
定义新符号Rhs_Known[n-1]为
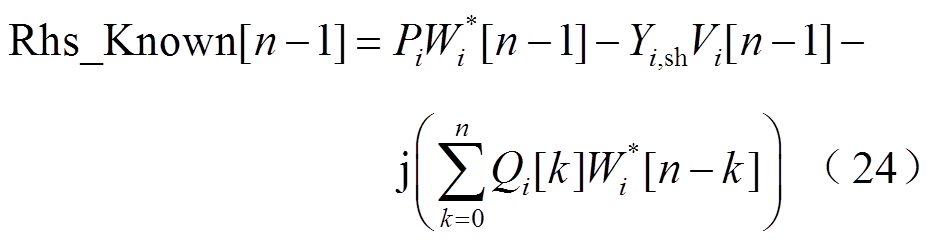
因此，式（23）可进一步表示为
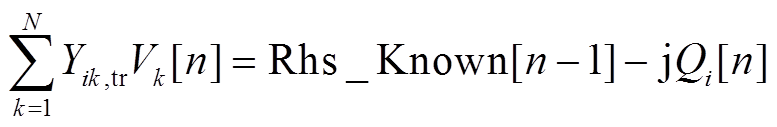（25）将式（24）中未知量Qi[n]移至等式左边，则该等式左边为第n项的系数，等式右边为第n-1项的系数，通过求解该线性方程即可求得PV节点电压幂级数αn的系数。
3）平衡节点求解
根据平衡节点全纯模型，对比式（11）等式两边同次幂系数，得递归式为
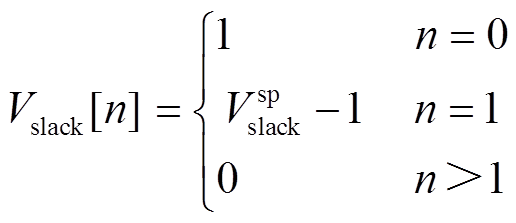（26）式中，Vslack[n]为全纯电压函幂级数αn对应系数。
综上所述，本文所提基于HEM的交流侧全纯潮流求解步骤如下：
1）根据2.1节所述全纯构造规则，对节点潮流方程嵌入变量，构造式（8）、式（10）和式（11）所示的交流全纯潮流模型。
2）将全纯函数展开为式（4）所示的泰勒级数，并代入式（8）、式（10）和式（11），依据同次幂系数相等原则，形成式（20）、式（25）和式（26）所示的系数递归式，递归求解电压幂级数系数V[0], V[1],,V[n]。
3）将求得的幂级数系数V[0],V[1],,V[n]代入式（9），获取V(α)具体表达式，实现隐式函数显式化；并令α=1，求取V(1)的值即为节点电压值。
4）利用所求得节点电压值，计算系统的最大功率不平衡量ΔPac（ΔPac=P-Re(Vac(YacVac)*)）。若ΔPac大于设定阈值，则继续计算更高阶幂级数系数；若差值小于设定阈值，结束算法，完成交流侧潮流求解。
直流全纯潮流模型求解需分别构建定直流电压节点和定直流功率节点的幂级数系数递归关系，求取电压全纯函数的表达式，直流全纯潮流求解过程如下。
1）定直流功率节点
为消除式（12）中的分式，定义电压函数Vdci(s)的倒数Wdci(s)为
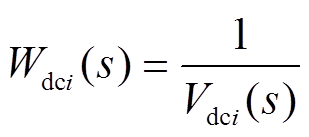（27）将函数Vdci(s)和Wdci(s)进行泰勒级数展开为
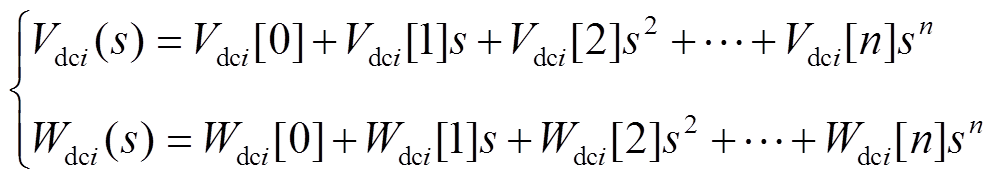（28）
式中，Vdci[n]和Wdci[n]为sn的系数；n=1,2,3,。
进而将式（28）代入式（27）得
（29）对比等式两边同次幂级数系数可得幂级数系数W和V之间递归关系为
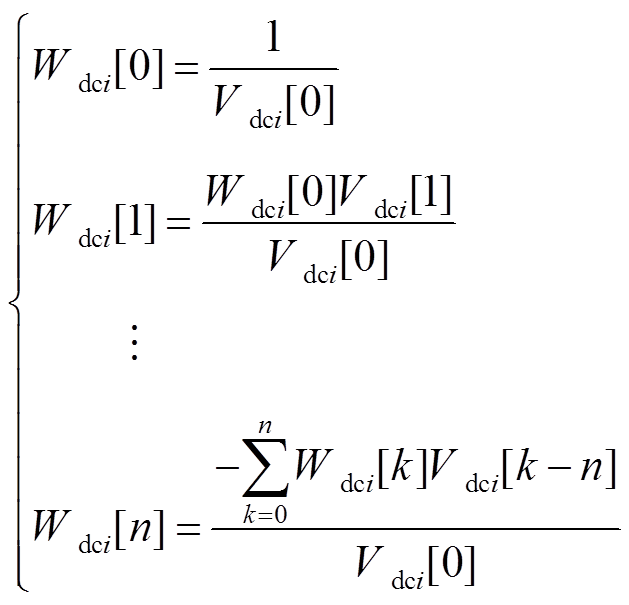（30）
将式（28）代入式（12）并进行幂级数展开为
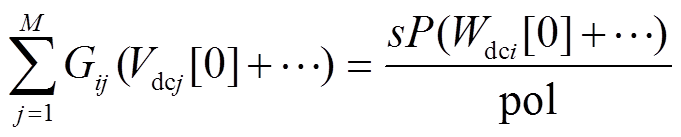（31）当s=0时，代入式（31）可得
（32）
Pi直接与嵌入变量s相乘，在s=0时，分子项全部为0，此时非线性潮流方程转换为线性方程，通过求解该线性方程组可获得幂级数常数项。
当s＞0时，比较等式（31）两边同次幂级数系数可得
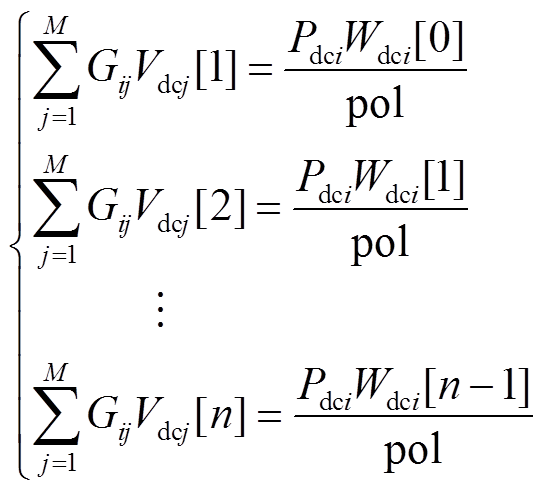（33）由式（33）得幂级数之间的递归关系式，进而可求取任意阶数的幂级数系数，实现全纯函数的显式化。
2）定直流电压节点
将定直流电压节点的Vdc(s)展开为幂级数形式代入式（13）得
（34）对比式（34）两边同次幂级数系数得定直流电压节点的幂级数系数递归关系式为
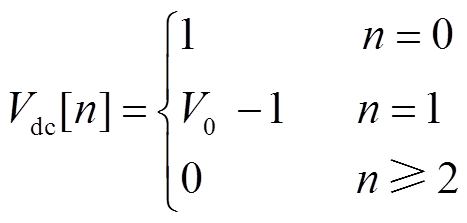（35）
3）构建求解全纯潮流模型的线性方程组
在实际潮流计算中，需基于直流电压幂级数系数的递归关系式构建线性方程组，以求解各直流节点电压的幂级数系数。此处以三节点直流网络为例，假设节点1和节点3为定直流功率节点，设定有功功率分别为Pdc1和Pdc1，节点2为定直流电压节点，构建线性方程组如式（36）所示。
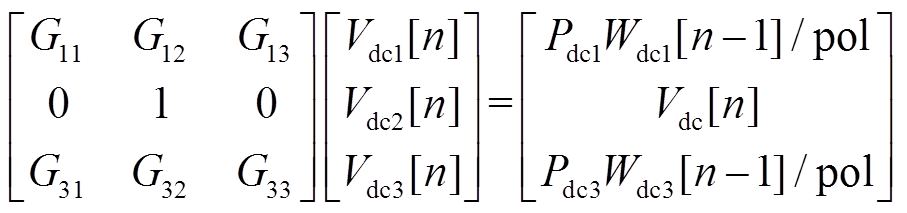（36）分析式（36）可知，该线性方程组的系数矩阵是节点导纳矩阵的一种变形，故该矩阵为常数矩阵且具有较高的稀疏度。同理可知，交流侧全纯潮流求解中，用于幂级数求解的线性方程组对应系数矩阵，也可由节点导纳矩阵变形得到，与传统NR迭代计算方法相比，潮流计算过程中仅需对该矩阵进行一次求逆运算，有效降低了低潮流计算量。
图4进一步对比了本文所提基于HEM的交直流潮流求解算法和基于NR法的交直流系统潮流求解算法的异同。显然，由图4可知，采用交替求解法求解交直流系统潮流时，本文所提求解算法与NR法在交直流潮流中交互的信息均相同，但在交流侧和直流侧潮流计算部分，两者具有显著的区别：①与NR法相比，本文所提基于HEM的交直流潮流求解算法在求解交流侧和直流侧潮流时，用于幂级数求解的线性方程组对应系数矩阵为常数阵，在整个交直流潮流交替求解过程中仅需对其进行一次求逆即可，且计算大规模交直流系统潮流时，可提前生成逆阵并存储，便于在每次递归计算中使用，大大缩短了运行时间；而NR法在整个交替求解过程中需进行频繁的Jacobi矩阵求逆运算，计算量较大。②本文所提基于HEM的交直流潮流求解算法将传统非线性代数方程的求解问题转换为隐式函数显式化的问题，无需为其提供初值便可准确计算出系统潮流解，而NR法对初值比较敏感，不合理的初值有可能导致潮流计算结果不收敛。③本文所提求解算法中，用于幂级数求解的线性方程组对应系数矩阵为常数阵，且矩阵元素仅与线路导纳有关，不会出现类似NR法在求解潮流过程中Jacobi矩阵奇异的问题，故所提算法具有较强的鲁棒性。
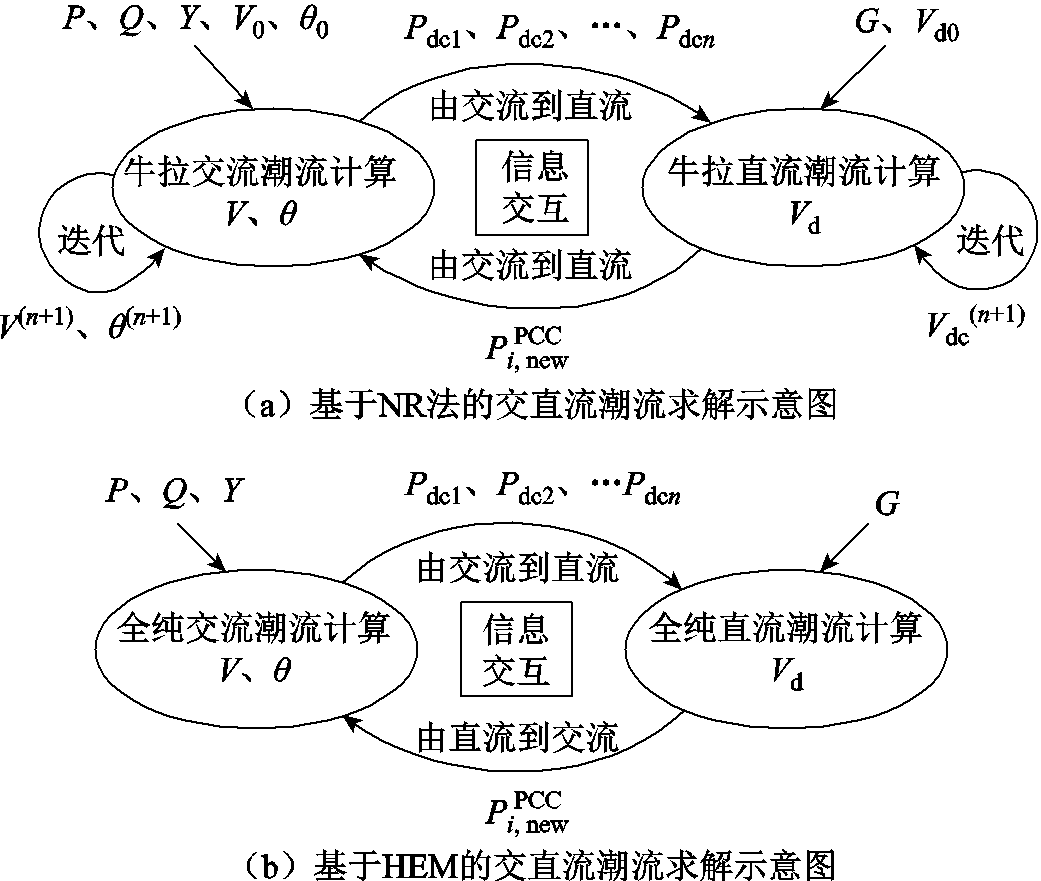
图4 交直流潮流计算方法对比
Fig.4 Comparison of AC-DC power flow calculation methods
综上所述，本文所提基于HEM的电力系统交直流潮流求解算法流程如图5所示。具体步骤如下：
1）基于HEM分别构建式（8）、式（10）和式（11）所示的交流全纯潮流模型，基于换流站控制方式，构建式（16）或式（17）PCC节点全纯潮流模型，并依据式（20）、式（25）和式（26）构建线性方程组，求取交流侧潮流分布。
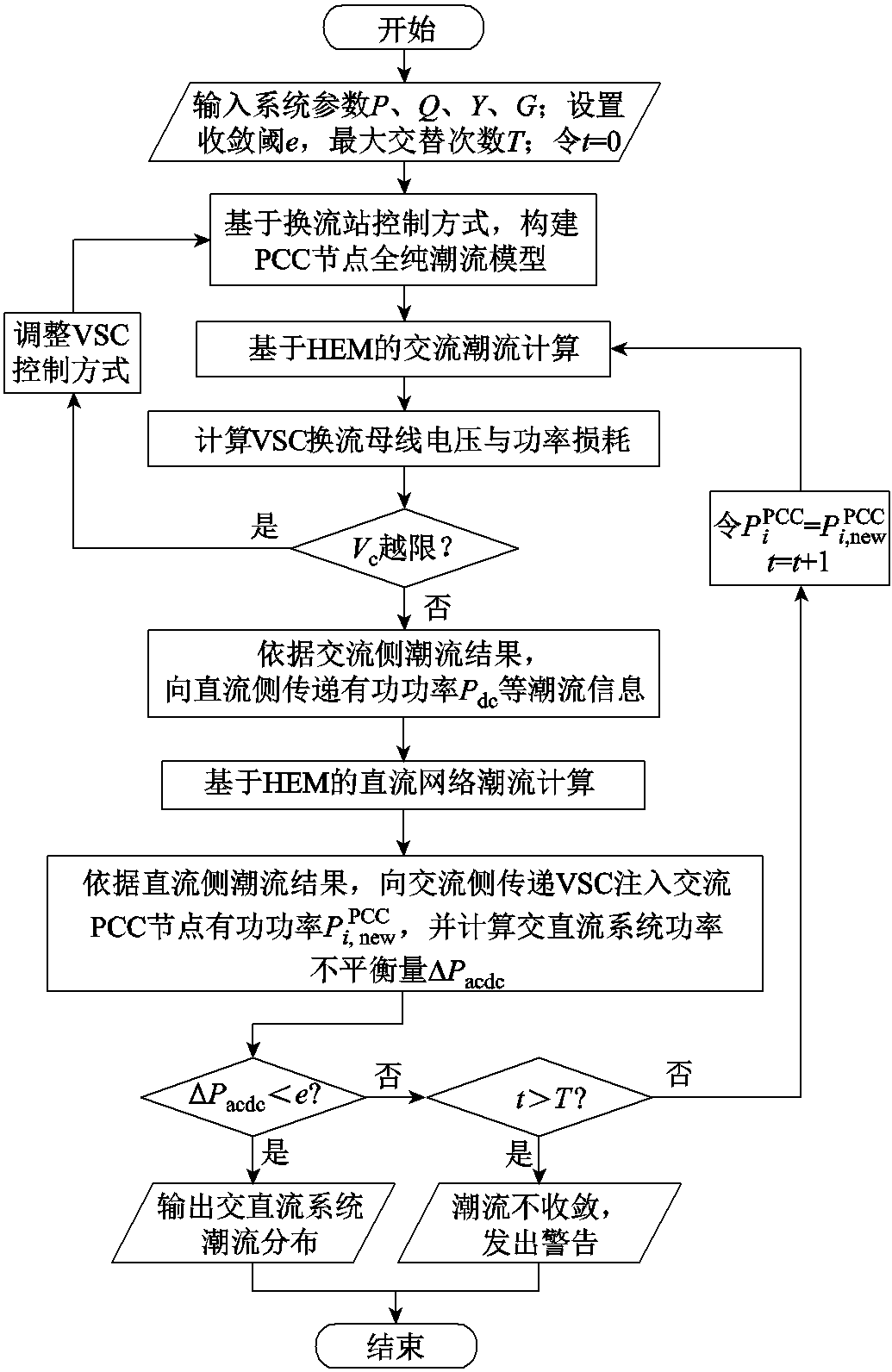
图5 电力系统交直流潮流的全纯嵌入算法流程
Fig.5 Flow chart of a holomorphic embedded method for solving power flow in hybrid AC-DC power system
2）确定交流侧潮流分布后，可将PCC节点电压VPCC i与节点功率PPCC i、QPCC i视为定值，依据图1所示换流站等效电路模型，计算换流母线电压Vc、换流站损耗Ploss等相关换流站数据，进而由式（3）求得各直流节点有功功率Pdc，将交流潮流信息传递至直流侧。
3）基于HEM构建式（12）和式（13）所示直流全纯潮流模型，并依据式（27）～式（35）进行求取直流电压函数Vdc(s)的幂级数系数递归公式，进而构建式（36）线性方程组，求取直流侧潮流分布。
4）获取直流潮流分布后，由式（3）计算“定直流电压”控制的VSC注入交流PCC节点有功功率PPCC inew，将直流潮流信息传递至交流侧；并计算交直流系统之间的功率不平衡量ΔPacdc=PPCC i-PPCC inew，若ΔP大于设定阈值e，则继续执行步骤1）；若ΔP小于设定阈值e，结束算法，输出系统潮流结果。
本节分别通过修改的IEEE 5、RTS-96和波兰电网3012wp的交直流测试系统对所提基于HEM的交直流潮流求解算法进行分析、验证，并将结果与文献[15]开发的基于NR法的交直流潮流开源计算软件MATACDC进行分析、对比，以验证所提方法的准确性、有效性和鲁棒性。
为验证所提基于HEM的交直流潮流求解算法的准确性和有效性，本文在Matlab（版本 8.3.0.532，R2014a）平台上开发了所提算法的潮流计算程序，并以修改的IEEE 5节点交直流系统为例进行分析、验证，该系统拓扑结构如图6所示。
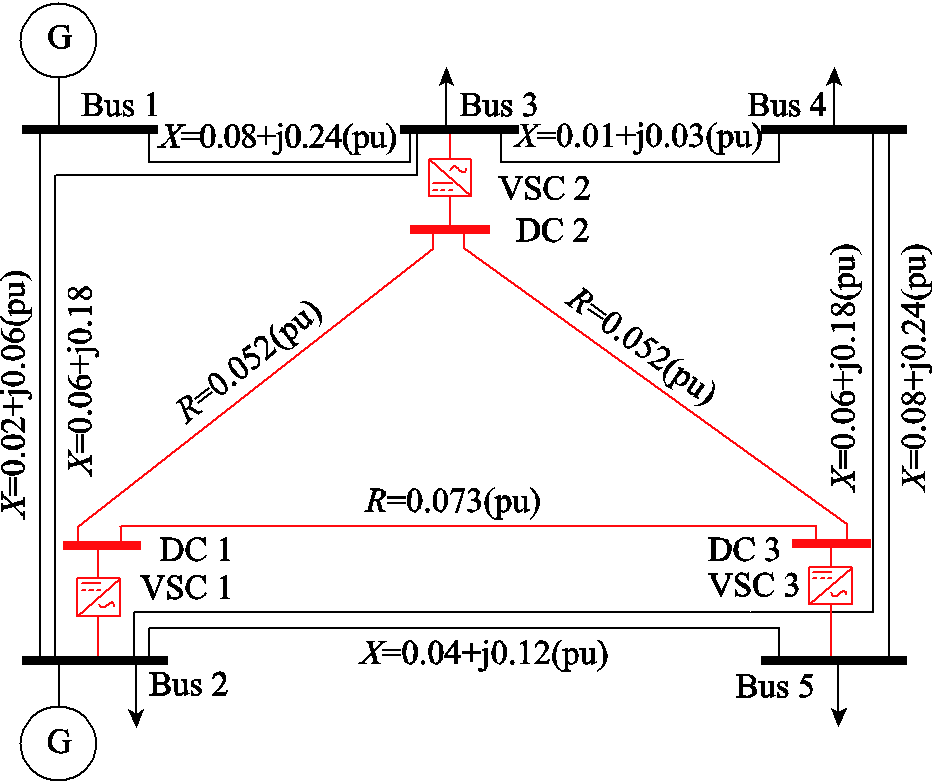
图6 修改的IEEE 5交直流测试系统
Fig.6 Modified IEEE 5 AC-DC hybrid test system
图6所示的交直流混合输电网络由5节点交流输电网络和3端直流输电网络构成，其交流和直流额定功率均为100MV·A，交流母线额定电压为345kV。图6中VSC换流站参数均相同，分别为Ztf=0.001 5+j0.112 1(pu)，Zc=0.000 1+j0.164 28(pu)，Bf=j0.088 7(pu)；直流母线额定电压为345kV；潮流收敛阈值e=10-4；换流站控制方式及参数见表1。
表1 IEEE 5节点交直流系统VSC换流站初始运行参数
Tab.1 Initial operation parameters of VSC in IEEE 5 AC-DC hybrid test system
换流站编号控制方式直流侧电压Vdc(pu)有功功率Ps/MW无功功率Qs/Mvar交流侧电压Vdc(pu) VSC1①—60.00040.000— VSC2②1.000—0.000— VSC3③—35.000—1.000
4.1.1 算法准确性验证
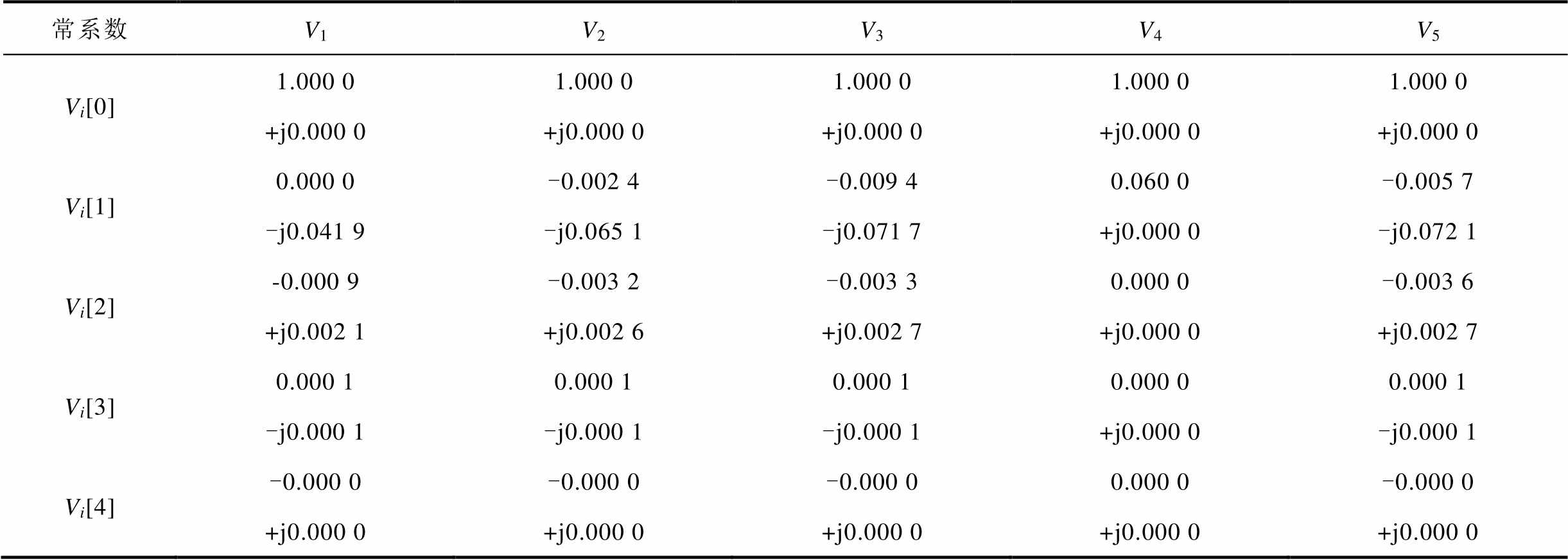
由3.4节电力系统交直流潮流的全纯嵌入算法流程图，计算交直流潮流需先进行交流侧潮流计算，求取交流电压幂级数系数见表2。
表2 IEEE 5节点交直流系统交流侧节点电压幂级数系数
Tab.2 Power series coefficients of voltage in AC side of IEEE 5 AC-DC hybrid test system
常系数V1V2V3V4V5 Vi[0]1.000 0+j0.000 01.000 0+j0.000 01.000 0+j0.000 01.000 0+j0.000 01.000 0+j0.000 0 Vi[1]0.000 0-j0.041 9-0.002 4-j0.065 1-0.009 4-j0.071 70.060 0+j0.000 0-0.005 7-j0.072 1 Vi[2]-0.000 9+j0.002 1-0.003 2+j0.002 6-0.003 3+j0.002 70.000 0+j0.000 0-0.003 6+j0.002 7 Vi[3]0.000 1-j0.000 10.000 1-j0.000 10.000 1-j0.000 10.000 0+j0.000 00.000 1-j0.000 1 Vi[4]-0.000 0+j0.000 0-0.000 0+j0.000 0-0.000 0+j0.000 00.000 0+j0.000 0-0.000 0+j0.000 0
表2中，第1行是各节点电压幂级数α0阶的系数V1[0]～V5[0]，第2行是各节点电压幂级数α1阶的系数V1[1]～V5[1]，将各节点电压函数的0阶与1阶系数代入式（9）并令α=1，求得1阶幂级数对应的交流节电压值分别为V1=1.000 0-j0.041 9(pu)、V2=0.997 6-j0.065 1(pu)、V3=0.990 6-j0.071 7(pu)、V4=1.060 0-j0.000(pu)、V5=0.994 3-j0.072 0(pu)，对应的系统最大功率不平衡量ΔPmax=0.031 1(pu)，显然不满足所设定的收敛条件，应继续计算更高阶电压幂级数系数，以提高潮流精度，图7给出了幂级数阶数与系统有功不平衡量之间关系。
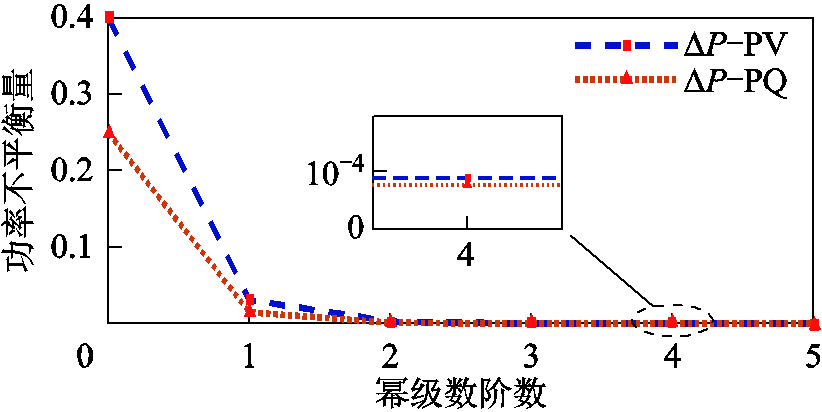
图7 幂级数阶数与功率不平衡量关系
Fig.7 Relationship between power series order and unbalance power
由图7可知，随着幂级数阶数增加，系统功率不平衡量随之减小，通过求取高阶幂级数系数可得系统高精度潮流解，本算例中仅需4阶幂级数即可满足收敛条件，完成交流侧潮流计算。
确定交流侧潮流分布后，需将交流PCC节点潮流信息传递至直流侧，此时PCC节点电压与节点功率可视为定值，依据图1所示换流站等效电路分别计算换流母线电压Vc、换流站损耗Ploss等相关换流站数据，并求取各直流节点有功功率Pdci，然后进行直流侧潮流计算，直流侧各节点电压幂级数系数见表3。
表3 IEEE 5节点交直流系统直流侧节点电压幂级数系数
Tab.3 Power series coefficients of voltage in DC side of IEEE 5 AC-DC hybrid test system
常系数Vdc1Vdc2Vdc3 Vdci[0]1.000 01.000 01.000 0 Vdci[1]0.008 0-0.000 0-0.002 2 Vdci[2]-0.000 10.000 0-0.000 1 Vdci[3]-0.000 0-0.000 0-0.000 0
表3给出了直流节点的电压幂级数s0～s3阶系数，将其代入式（20）求得各节点电压标幺值为Vdc1=1.007 9(pu)、Vdc2=1.000 0(pu)、Vdc3=0.997 7(pu)，并校验此时直流网络功率不平衡量ΔPdc，经计算直流网络功率不平衡量的最大值ΔPdc=4.518×10-5(pu)。因此，在实际计算中仅需计算出3阶幂级数即可满足收敛条件，实现直流侧潮流的准确计算。
根据直流侧潮流计算结果更新交流侧PCC节点功率，再次计算交流侧潮流，如此交替计算，直至功率不平衡量小于设定阈值，求得交直流系统潮流分布。将所得潮流计算结果与MATACDC计算结果进行对比，结果见表4和表5。
表4 IEEE 5节点交直流系统交流侧电压计算结果对比
Tab.4 Comparison of the calculated voltages in AC side of IEEE 5 AC-DC hybrid test system
交流节点电压幅值电压相角 MATACDC(pu)本文算法(pu)相对误差(%)MATACDC/(°)本文算法/(°)相对误差(%) 11.060 1.060 0.0000.000 0.000 0.000 21.000 1.000 0.000-2.383 -2.383 0.000 31.000 1.000 0.000-3.895 -3.895 0.000 40.996 0.996 0.000-4.262 -4.262 0.000 50.991 0.991 0.000-4.149 -4.149 0.000
表5 IEEE 5节点交直流系统直流侧潮流计算结果对比
Tab.5 Comparison of the calculated power flow in DC side of IEEE 5 AC-DC hybrid test system
直流节点节点电压幅值节点有功功率 MATACDC(pu)本文算法(pu)相对误差(%)MATACDC/MW本文算法/MW相对误差(%) 11.0081.0080.000-58.627-58.6270.000 21.0001.0000.00021.90121.9010.000 30.9980.9980.00036.18636.1860.000
由表4和表5可知：利用本文所提方法计算修改的IEEE 5节点交直流系统潮流结果与MATACDC的计算结果完全一致，验证了本文所提电力系统交直流潮流的全纯嵌入计算方法可实现交直流系统潮流的准确求解。
4.1.2 VSC换流站控制方式转换功能验证
为验证所提算法可实现VSC换流站控制方式转换的功能，本节对IEEE 5节点交直流系统的换流站控制方式进行切换，并将切换后的潮流计算结果与MATACDC进行对比，结果见表6。
表6 VSC换流站控制方式转换前后潮流计算误差对比
Tab.6 Comparison of calculation errors before and after VSC control mode switching
转换方式交流侧直流侧 MATACDC(pu)本文算法(pu)相对误差(%)MATACDC(pu)本文算法(pu)相对误差(%) ①→②0.9800.9800.0001.0031.0020.100 ②→③1.0001.0010.1000.9970.9970.000 ③→④0.9950.9950.0000.9980.9980.000 ①→③0.9900.9900.0001.0001.0000.000 ①→④0.9930.9940.1000.9900.9900.000 ②→④1.0601.0600.0001.0001.0000.000
由表6可知：所提方法计算的交直流节点电压幅值与MATACDC的结果一致，二者最大相对误差仅为0.1%，有效验证了所提基于HEM的交直流潮流求解算法可实现不同控制方式下交直流潮流的准确计算。
本节将所提的交直流潮流全纯嵌入计算方法应用到拓扑结构更为复杂的RTS-96多端交直流互联系统中，以验证所提方法的通用性和有效性。该多端交直流系统由三个交流系统子区域和两个直流网络构成，其系统网络结构如图8所示。
4.2.1 准确性验证
本节将所提基于HEM的交直流潮流求解算法与MATACDC所得潮流结果进行对比，按相对误差百分比降序排列，图9和图10为交流侧前10个具有最大相对误差的节点电压，表7为直流侧潮流结果对比。
由图9和图10可知：基于HEM的交直流潮流求解算法所得的交流侧节点电压幅值和相角与MATACDC的计算结果一致，满足潮流准确度要求。
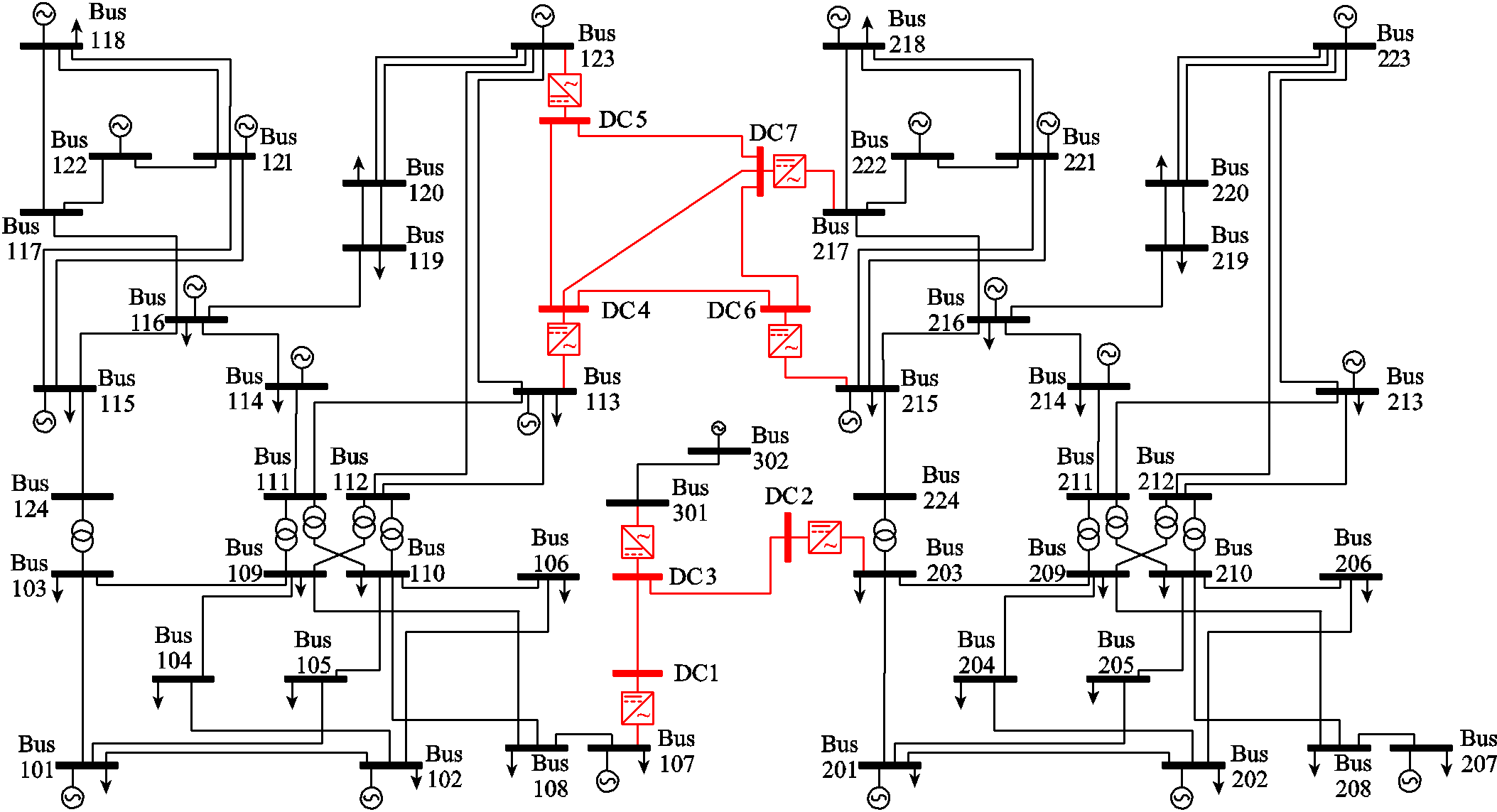
图8 RTS-96多端交直流互联系统示意图
Fig.8 RTS-96 AC-DC hybrid test system
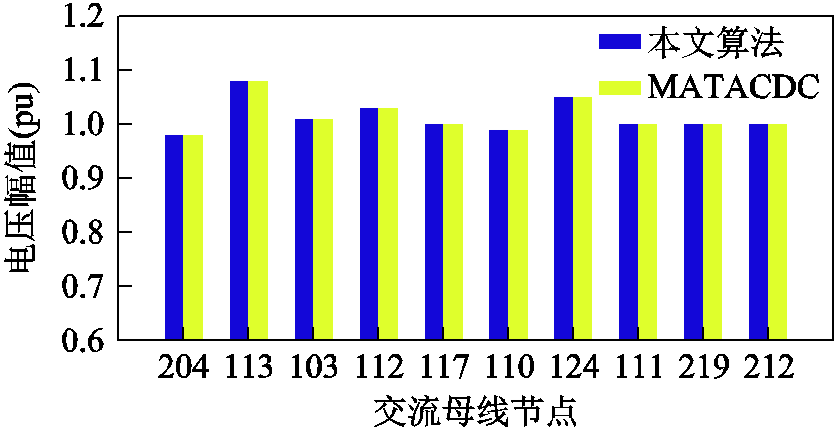
图9 RTS-96交直流系统交流侧节点电压幅值对比
Fig.9 Comparison of voltage magnitude in AC side of RTS-96 AC-DC hybrid test system
图10 RTS-96交直流系统交流侧节点电压相角对比
Fig.10 Comparison of voltage phase angle in AC side of RTS-96 AC-DC hybrid test system
由图9、图10和表7的潮流计算结果可知：采用本文所提交直流潮流求解算法得到的RTS-96系统潮流计算结果与MATACDC计算结果完全一致，由此验证了本文所提潮流求解算法同样适用于拓扑结构较复杂的多分区、多端交直流互联系统潮流计算。
表7 RTS-96交直流系统直流侧潮流计算结果对比
Tab.7 Comparison of power flow results in DC side of RTS-96 AC-DC hybrid test system
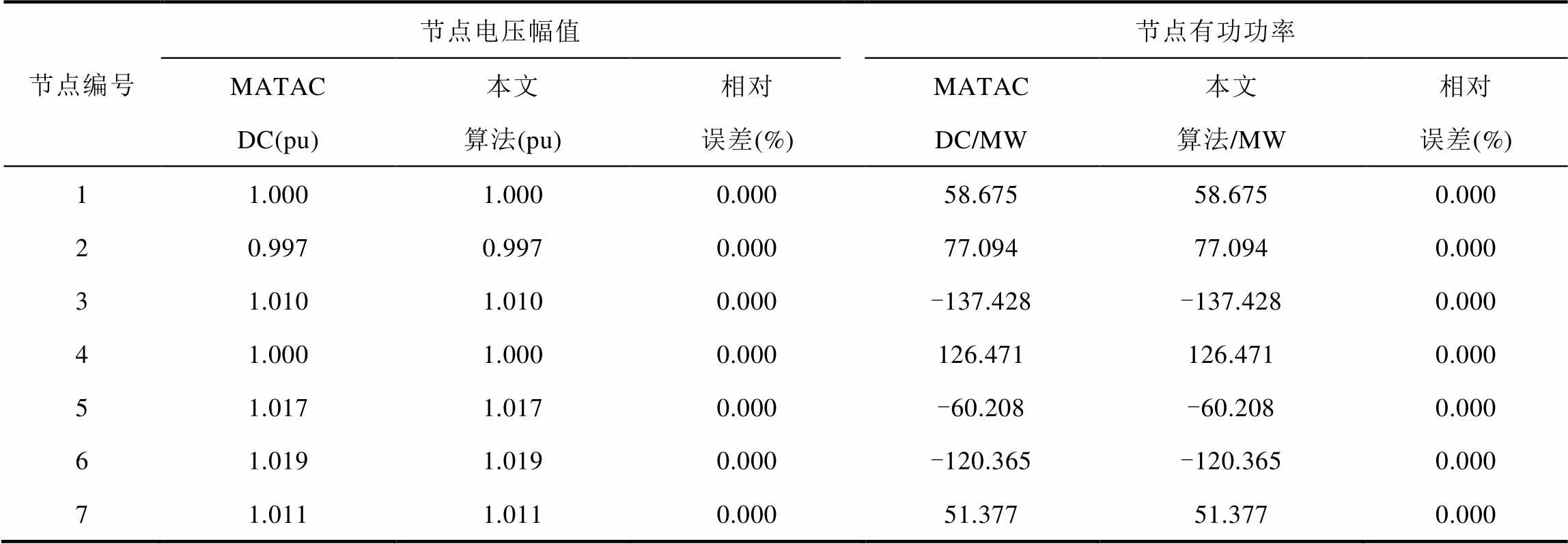
节点编号节点电压幅值节点有功功率 MATACDC(pu)本文算法(pu)相对误差(%)MATACDC/MW本文算法/MW相对误差(%) 11.0001.0000.00058.67558.6750.000 20.9970.9970.00077.09477.0940.000 31.0101.0100.000-137.428-137.4280.000 41.0001.0000.000126.471126.4710.000 51.0171.0170.000-60.208-60.2080.000 61.0191.0190.000-120.365-120.3650.000 71.0111.0110.00051.37751.3770.000
4.2.2 换流站控制策略转换
参考文献[15]，本节设置换流母线电压幅值上、下限分别为Vc,min=0.850(pu)，Vc,max=1.150(pu)。2号和7号换流器无功类控制方式均为定功率控制，若交流203和217节点无功负荷分别增大至180Mvar和230Mvar，此时该节点无功支撑能力不足，交流节点203和217的电压幅值分别为0.868(pu)和0.917(pu)，换流母线电压分别为0.742(pu)和0.823(pu)，电压越下限。将换流站控制方式由定无功功率控制改为定交流电压控制，交流电压设定值为1.000(pu)。转换前后交流系统PCC节点电压幅值如图11所示，各换流母线电压幅值如图12所示。
图11 换流站控制策略转换前后交流PCC节点电压对比
Fig.11 Comparison of voltage magnitude at PCC before and after control strategy switching
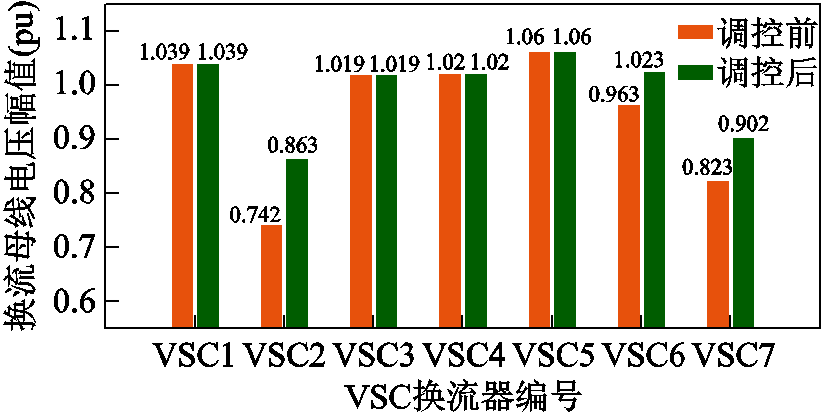
图12 换流母线电压越下限控制策略转换前后对比
Fig.12 Comparison of voltage magnitude at converter bus before and after control strategy switching with converter bus voltage violating lower limit
由图11和图12分析可知，VSC换流站交流侧控制方式由定无功功率控制转变为定交流电压控制后，VSC换流站为交流PCC提供了充足的无功功率，显著改善了交流侧节点电压。由于交流PCC节点电压的提高，换流母线电压也相应的提高，进而使得换流器在额定电压范围内安全运行。
若交流节点203和217无功负荷功率分别继续增加100Mvar和150Mvar，此时PCC节点VPCCs不变，换流站注入交流系统PCC的无功功率QPCCs持续增加，进而导致Vc越上限Vc,max。为维持换流站的稳定运行，需将交流侧控制方式由定交流电压控制转换为定无功功率控制，无功功率设定值为221Mvar和306Mvar，控制方式转换前后换流母线电压幅值如图13所示。
由图13可知，换流站控制方式由定交流电压控制转变为定无功功率控制，限制了换流站无功功率注入量，有效解决了换流母线电压越上限问题。上述结果进一步验证了所提方法可实现换流器控制策略的灵活转换。
图13 换流母线电压越上限控制策略转换前后对比
Fig.13 Comparison of voltage magnitude at converter bus before and after control strategy switching with converter bus voltage violating upper limit
4.2.3 计算效率对比
为验证所提算法的计算效率，将本文所提基于HEM的交直流潮流求解算法与MATACDC的潮流计算耗时进行对比（处理器Intel(R) Core(TM) i7-4500U CPU@1.80GHz，内存4.00GB），结果见表8。
表8 RTS-96交直流系统不同潮流算法计算耗时对比
Tab.8 Computational time comparison in RTS-96 AC-DC hybrid test system with different methods
比较内容MATACDC本文算法 交替收敛精度10-410-4 交替次数/次44 计算时间/s1.140.25
由表8中结果分析可知：当交直流交替计算收敛精度均为10-4时，本文所提基于HEM的交直流全纯潮流求解算法与MATACDC的交替计算次数均为4次，但所提算法计算耗时仅为0.25s，计算速度较MATACDC提高4.56倍。其原因为：本文所提基于HEM的交直流潮流求解算法在计算交流侧和直流侧潮流时，用于幂级数求解的线性方程组对应系数矩阵为常数阵，与传统NR法相比，交直流潮流信息交互的大循环和节点电压修正的小循环引起的节点功率变化均不会对该矩阵产生影响，所以仅需进行一次求逆运算即可满足交替计算需求，有效降低了计算负担。因此，本文所提基于HEM的交直流全纯潮流求解算法具有更高的计算效率。
进一步通过不断增加系统的负荷水平来测试所提方法的鲁棒性，不同负荷水平下两种算法的耗时对比结果见表9。
表9 不同负荷水平下两种算法的耗时对比
Tab.9 Comparisons of computational time with two algorithms under different load levels
负荷水平交替次数/次计算耗时/s MATACDC本文算法MATACDC本文算法 1.00441.140.25 1.25441.190.26 1.50551.540.45 1.75661.820.71 2.00662.100.99 2.25882.591.44 2.27不收敛8不收敛2.04
由表9可知：①在满足相同潮流收敛条件下，所提基于HEM的交直流潮流求解算法收敛用时更少，具有更高的计算效率；②当负荷增加至一定程度，系统处于重载时，易造成NR法的Jacobi矩阵奇异，导致潮流无法收敛，而所提交直流潮流求解算法不会出现类似矩阵奇异问题，故所提算法在8次交替后仍可准确计算出交直流系统的潮流解，验证了所提方法具有较强的鲁棒性。
本节进一步以图14所示波兰电网3012wp交直流测试系统为例，验证所提算法计算大规模交直流系统潮流的鲁棒性和有效性。波兰电网3012wp交直流测试系统，由原波兰电网3012wp测试系统和一个4端直流电网构成，各直流换流站接入位置如图14所示，换流站控制方式及运行参数详见表10。
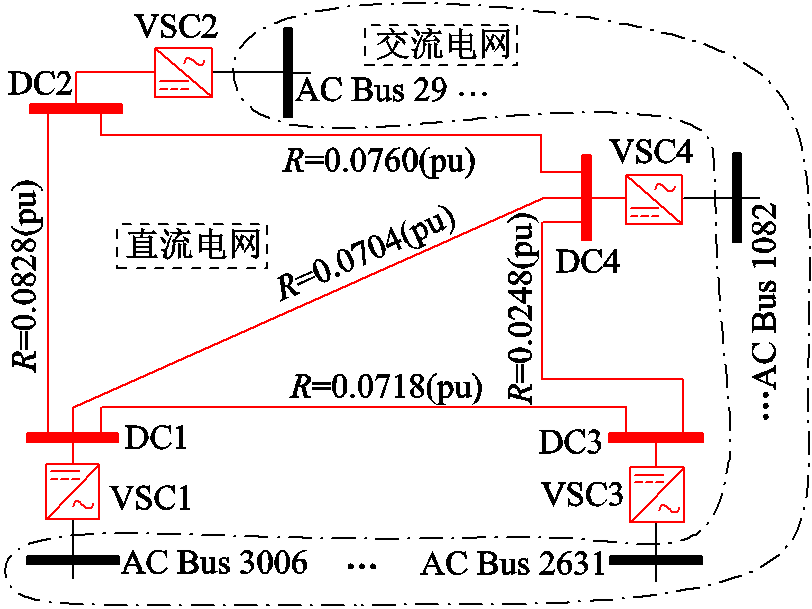
图14 波兰电网3012wp交直流测试系统示意图
Fig.14 Polish 3012wp power grid AC-DC hybrid test system
表10 VSC换流站初始运行参数
Tab.10 Initial operating parameters of VSC converter station in Polish 3012wp power grid
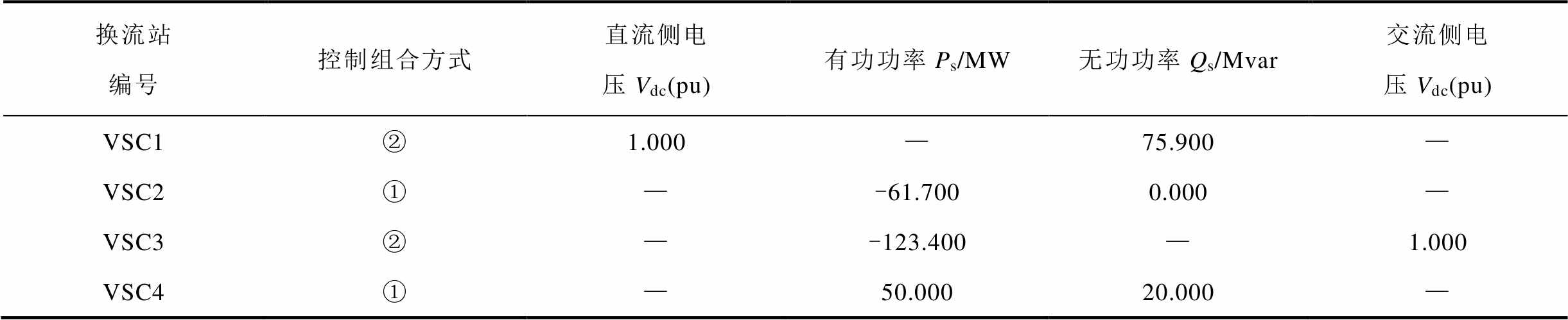
换流站编号控制组合方式直流侧电压Vdc(pu)有功功率Ps/MW无功功率Qs/Mvar交流侧电压Vdc(pu) VSC1②1.000—75.900— VSC2①—-61.7000.000— VSC3②—-123.400—1.000 VSC4①—50.00020.000—
采用本文所提基于HEM的交直流潮流求解算法对该交直流测试系统进行潮流计算，按相对误差百分比降序排列，表11给出了交流侧前10个具有最大有功计算误差的节点，直流侧各节点潮流计算结果见表12。
表11 波兰3012wp交直流系统交流侧潮流计算结果
Tab.11 Power flow results of AC side in Polish 3012wp power grid
节点编号节点电压节点有功功率/MW 电压幅值(pu)电压相角/(°)计算值设定值误差 24111.084-36.12111.75011.7501.1×10-4 391.1101.67120.09920.1001.0×10-4 30121.030-16.399589.510589.5101.0×10-4 21571.023-29.23510.95010.9509.6×10-5 27861.063-24.8533.6693.6709.2×10-5 1931.032-10.99838.18038.1808.8×10-5 17391.114-1.48713.24913.2507.9×10-5 13851.117-6.55111.44911.4507.7×10-5 5531.060-25.71812.18012.1803.0×10-5 411.0470.16860.28960.2902.1×10-5
表12 波兰3012wp交直流系统直流侧潮流计算结果
Tab.12 Power flow results of DC side in Polish 3012wp power grid
节点编号节点电压(pu)功率/MW 计算值设定值误差 11.000124.950—— 21.017-61.210-61.2106.0×10-5 31.018-121.769-121.7707.0×10-5 41.01050.88050.8801.0×10-5
由表11和表12的潮流计算结果可知：本文所提基于HEM的交直流潮流求解算法所得交直流测试系统的潮流最大功率不平衡量仅为1.1´10-4MW，验证了所提算法在计算大规模交直流系统潮流时具有较高的计算精度。
表13进一步对比了本文所提算法与MATACDC在求解该系统的计算耗时，由表中结果可知，本文所提算法仅需1.69s即可准确计算出该系统潮流，而MATACDC计算结果不收敛。
表13 波兰3012wp交直流系统潮流计算耗时对比
Tab.13 Comparison of time consumption for power flow calculation in the Polish 3012wp power grid
比较内容MATACDC本文算法 交替收敛精度10-410-4 是否收敛否是 交替次数—3 计算时间/s—1.69
上述结果表明：所提基于HEM的交直流潮流求解算法，不仅适用于较小规模交直流系统的潮流计算，对大规模交直流互联电网的潮流计算也展现出良好的计算精度、计算效率和鲁棒性。
本文提出一种基于HEM的交直流潮流计算方法，并通过修改的IEEE 5节点交直流系统、RTS-96交直流系统和波兰电网3012wp交直流测试系统进行分析、验证，结果表明：
1）所构建的全纯交流潮流模型、全纯直流潮流模型及换流站全纯控制模型合理、可行，可实现基于HEM的交直流潮流快速、准确计算。
2）所构建VSC换流站全纯控制模型，可准确、有效地计及不同控制方式间的相互转换，实现基于HEM的多种控制方式下的交直流潮流准确计算，具有较强的通用性。
3）所提基于HEM的交直流潮流计算方法不依赖初值便可快速、准确地计算出交直流系统的潮流，且相对NR法更具有较强的鲁棒性。
4）所提基于HEM的交直流潮流计算方法为交直流电网的潮流计算提供了新思路，也为电力系统运行调度和研究人员进行规划运行、稳定性分析、可靠性评估等提供了新的潮流计算工具。
需要指出的是，尽管本文所提方法可实现电力系统交直流潮流的准确计算，但现阶段VSC换流站全纯控制模型主要是主从控制模式，未对换流站下垂控制模式的全纯模型构建进行深入研究。而构建VSC换流站全纯下垂控制模型，完善基于HEM的交直流潮流求解算法中VSC换流站各项全纯控制模型，将是本文后续研究的重点。
参考文献
[1] 朱介北, 周小尧, 曾平良, 等. 英国交直流输电网规划方法及对中国电网规划的启示[J]. 全球能源互联网, 2020, 3(1): 59-69.
Zhu Jiebei, Zhou Xiaoyao, Zeng Pingliang, et al. UK AC-DC power grid planning method and its implications for China power grid planning[J]. Global Energy Internet, 2020, 3(1): 59-69.
[2] 骆悦, 姚骏, 张田, 等. 大规模风电直流外送系统单极闭锁场景下送端系统协调控制策略[J]. 电工技术学报, 2019, 34(19): 4108-4118.
Luo Yue, Yao Jun, Zhang Tian, et al. Coordinated control strategy of sending-end system in the single-pole blocking scenario of large-scale wind power DC transmission system[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4108-4118.
[3] 李岩, 滕云, 冷欧阳, 等. 含多端柔性直流互联的交直流电力系统静态安全分析[J]. 电力系统自动化, 2019, 43(10): 155-163.
Li Yan, Teng Yun, Leng Ouyang, et al. Static security analysis of AC-DC power system with multi-terminal flexible DC interconnection[J]. Automation of Electric Power Systems, 2019, 43(10): 155-163.
[4] 李国庆, 边竞, 王鹤, 等. 适用于直流电网的环流式线间直流潮流控制器[J]. 电工技术学报, 2020, 35(5): 1118-1127.
Li Guoqing, Bian Jing, Wang He, et al. Circulating line-to-line DC power flow controller for DC power grids[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1118-1127.
[5] 周晓风, 付艳, 崔晨, 等. 提高分接开关可靠性的直流输电控制策略优化[J]. 电气技术, 2020, 21(9): 54-58.
Zhou Xiaofeng, Fu Yan, Cui Chen, et al. The optimization of high voltage direct current control strategy to improve on-load tap changer reliability[J]. Electrical Engineering, 2020, 21(9): 54-58.
[6] 王浩翔, 赵冬梅, 陶然, 等. 基于分解的多目标进化算法的含MMC-HVDC交直流混合系统最优潮流研究[J]. 电工技术学报, 2020, 35(17): 3691-3702.
Wang Haoxiang, Zhao Dongmei, Tao Ran, et al. Research on optimal power flow of MMC-HVDC AC-DC hybrid system based on decomposition-based multi-objective evolutionary algorithm[J]. Transac-tions of China Electrotechnical Society, 2020, 35(17): 3691-3702.
[7] 陈厚合, 黄亚磊, 姜涛, 等. 含VSC-HVDC的交直流系统电压稳定分析与控制[J]. 电网技术, 2017, 41(8): 2429-2438.
Chen Houhe, Huang Yalei, Jiang Tao, et al. Voltage stability analysis and control of AC-DC system with VSC-HVDC[J]. Power System Technology, 2017, 41(8): 2429-2438.
[8] 杜萍静, 杨明, 曹良晶, 等. 含电压源换流器交直流系统的仿射潮流算法[J]. 电工技术学报, 2020, 35(5): 1106-1117.
Du Pingjing, Yang Ming, Cao Liangjing, et al. Affine power flow algorithm for AC-DC system with voltage source converter[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1106-1117.
[9] 郑超, 周孝信, 李若梅, 等. VSC-HVDC稳态特性与潮流算法的研究[J]. 中国电机工程学报, 2005, 25(6): 1-5.
Zheng Chao, Zhou Xiaoxin, Li Ruomei, et al. Study on VSC-HVDC steady-state characteristics and power flow algorithm[J]. Proceedings of the CSEE, 2005, 25(6): 1-5.
[10] Lei Jingting, An Ting, Du Zhengchun, et al. A general unified AC-DC power flow algorithm with MTDC[J]. IEEE Transactions on Power Systems, 2017, 32(4): 2837-2846.
[11] Beerten J, Cole S, Belmans R. Generalized steady-state VSC MTDC model for sequential AC-DC power flow algorithms[J]. IEEE Transactions on Power Systems, 2012, 27(2): 821-829.
[12] 郑超, 盛灿辉. 含VSC-HVDC的交直流混合系统潮流统一迭代求解算法[J]. 中国电力, 2007(7): 65-69.
Zheng Chao, Sheng Canhui. A uniform iterative algorithm for power flow solution of AC-DC hybrid system with VSC-HVDC[J]. China Electric Power, 2007(7): 65-69.
[13] 陈谦, 唐国庆, 王浔. 多端VSC-HVDC系统交直流潮流计算[J]. 电力自动化设备, 2005(6): 1-6.
Chen Qian, Tang Guoqing, Wang Xun. AC-DC power flow calculation for multi-terminal VSC-HVDC system[J]. Electric Power Automation Equipment, 2005(6): 1-6.
[14] Beerten J, Cole S, Belmans R. A sequential AC-DC power flow algorithm for networks containing multi-terminal VSC-HVDC systems[C]//IEEE PES General Meeting, Providence, RI, 2010: 1-7.
[15] Beerten J, Belmans R. Development of an open source power flow software for high voltage direct current grids and hybrid AC-DC systems: MATACDC[J]. IET Generation, Transmission and Distribution, 2015, 9(7): 966-974.
[16] 李雪, 刘烨, 姜涛, 等. 电力系统负荷裕度的并行计算方法研究[J]. 中国电机工程学报, 2019, 39(14): 5105-5117.
Li Xue, Liu Ye, Jiang Tao, et al. Research on the parallel calculation method of load margin in power system[J]. Proceedings of the CSEE, 209, 39(14): 5105-5117.
[17] Marcos T, Kamel S, Jurado F. Robust and efficient approach based on richardson extrapolation for solving badly-initialized/ill-conditioned power flow problems[J]. IET Generation Transmission & Distribution, 2019, 13(13): 3524-3533.
[18] Trias A. The holomorphic embedding load flow method[C]//IEEE Power and Energy Society General Meeting, San Diego, 2012: 1-8.
[19] Shruti R, Yang Feng, Daniel J, et al. The holomorphic embedding method applied to the power flow problem[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3816-3828.
[20] Muthu K, Yang Feng, Daniel T. PV bus modeling in a holomorphically embedded power-flow formulation[C]//North American Power Symposium (NAPS), Manhattan, KS, 2013: 1-6.
[21] Jonckheere EA, Ke NP. Complex-analytic theory of the μ-function*[C]//Proceedings of the 1997 American Control Conference, Albuquerque, NM, USA, 1997: 366-371.
[22] Liu Chengxi, Wang Bin, Hu Fengkai, et al. Online voltage stability assessment for load areas based on the holomorphic embedding method[J]. IEEE Transactions on Power Systems, 2018, 33(4): 3720-3734.
[23] 徐经民, 徐在德, 童超. 基于模糊下垂控制的VSC-HVDC交直流系统潮流计算方法[J]. 电力系统保护与控制, 2019, 47(20): 50-57.
Xu Jingmin, Xu Zaide, Tong Chao. VSC-HVDC AC-DC system power flow calculation method based on fuzzy droop control[J]. Power System Protection and Control, 2019, 47(20): 50-57.
[24] 陈厚合, 李国庆, 姜涛. 控制方式转换策略下的改进交直流系统潮流算法[J]. 电网技术, 2011, 35(8): 93-98.
Chen Houhe, Li Guoqing, Jiang Tao. Improved AC-DC power flow algorithm under control mode switching strategy[J]. Power System Technology, 2011, 35(8): 93-98.
[25] 刘英培, 解赛, 梁海平, 等. 计及换流站间电压误差的VSC-MTDC系统自适应下垂控制[J]. 电工技术学报, 2020, 35(15): 3270-3280.
Liu Yingpei, Xie Sai, Liang Haiping, et al. Adaptive droop control of VSC-MTDC system considering voltage error between converter stations[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3270-3280.
A Holomorphic Embedded Method for Solving Power Flow in Hybrid AC-DC Power System
Abstract In order to address the initial value selection and large calculation amount when Newton Raphson(NR) method is used to calculate AC-DC power flow, this paper proposes a holomorphic embedding method for AC-DC power flow calculation. Firstly, according to the construction principle of holomorphic function, the holomorphic AC-DC power flow model and converter station control model are constructed by embedding parameters. Then, based on the Taylor series expansion characteristics of the holomorphic function, the problem of solving nonlinear power flow equations is transformed into an explicit problem of implicit holomorphic functions. Moreover, according to the principle that the same power coefficient is equal, the power series coefficient of Taylor series expansion term is obtained, and the explicit holomorphic function is completed, and then the embedded parameters are assigned to realize the fast solution of AC-DC power flow. Finally, it is analyzed and verified through modified IEEE 5 node AC-DC system, RTS-96 AC-DC system and Polish power grid 3012wp AC-DC test system. The results show that the proposed method can quickly and accurately calculate the power flow of AC-DC power system without relying on the initial value, and has strong robustness, which provides a new idea for power flow calculation of large-scale AC-DC power grid.
Keywords：AC-DC hybrid system, voltage source converter, holomorphic function, power flow calculation
DOI:10.19595/j.cnki.1000-6753.tces.201306
中图分类号：TM744
国家自然科学基金（52077029, U2066208, 52061635103）和国家重点研发计划（2016YFB0900900）资助项目。
收稿日期 2020-09-29
改稿日期 2020-11-23
姜 涛 男，1983年生，博士，教授，博士生导师，研究方向为电力系统安全性和稳定性、可再生能源集成、综合能源系统。E-mail：t.jiang@aliyun.com
李 雪 女，1986年生，博士，副教授，硕士生导师，研究方向为电力系统安全性与稳定性、电力系统高性能计算、电力市场。E-mail：xli@neepu.edu.cn（通信作者）
（编辑 赫蕾）