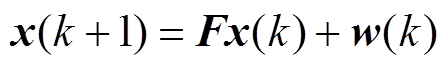 (1)
(1)摘要 传统的小波阈值去噪算法存在易丢弃真实信号、去噪效果差等缺点。该文提出了一种新的用于电能质量扰动事件的联合去噪算法。该算法首先通过强跟踪卡尔曼滤波的渐消因子大于1的次数,初步判定信号的扰动类型,然后对不同的扰动类型采取不同的去噪方法。对于仅含噪声的正弦信号和谐波信号用稀疏分解及快速傅里叶变换(FFT)做两次去噪;对暂升和暂降信号采用渐消因子准确地指示扰动起止时刻,将信号分段,并对每段信号用稀疏分解和FFT去噪;对含瞬态脉冲和暂态振荡的信号,采用不同的处理方法,首先通过稀疏分解得到稳态成分和暂态成分,对稳态成分的去噪方法与含噪声正弦信号的处理方法相同,对暂态成分的脉冲信号保留实际值,对振荡信号采用变分模态分解(VMD)去噪。大量的仿真计算表明,在不同的信噪比条件下,该文提出的算法均能够有效抑制各类扰动信号的噪声,显著提高了信噪比,且效果优于小波阈值去噪算法。
关键词:电能质量扰动 强跟踪卡尔曼滤波 稀疏分解 小波分析 去噪方法
随着国民经济的快速发展,大量电力电子设备等非线性、冲击性负荷接入电网,导致电能质量问题日益严重,有些电能质量扰动事件甚至会带来较大的经济损失。为此,部分电力用户对电能质量有着严格的标准,这对电能质量扰动事件的检测和治理提出了较高的要求。在实际情况中,电能质量信号在采集、信号处理、传输等过程中不可避免地会带来噪声[1]。因此,研究高效的电能质量信号去噪算法,对电能质量扰动信号准确分析,提出电能质量扰动事件的解决方案具有十分重要的意义。
近年来,国内外学者提出了诸多有效的信号去噪算法,包括小波分析[2]、经验模态分解(Empirical Mode Decomposition, EMD)[3]、广义S变换[4]、奇异值分解(Singular Value Decomposition, SVD)[5]和变分模态分解(Variational Mode Decomposition, VMD)[6]等算法。在以上的各类算法中,小波分析具有良好的时频分析能力,适合分析各类非平稳信号特征。其中,运用得最为广泛的方法是小波阈值去噪,以及在此基础上演变而来的各种改进的阈值算法。文献[7]提出了一种软硬混合阈值的去噪算法,对小于临界尺度层数的小波系数采用软阈值处理,对大于临界的则采用硬阈值处理,达到去噪的目的。但该方法的不足在于无法根据噪声水平自适应地确定阈值。文献[8]使用双树复小波分解信号,运用最大后验(Maximum A Posterior, MAP)估计对各层系数做噪声方差和信号方差估计,从而自适应地确定各层阈值并进行去噪,但该方法受MAP估计准确度的影响。文献[9]提出基于Bayes估计的双小波维纳滤波去噪,此方法实现小波和维纳滤波的互补,但需要采用两个小波基来构造经验维纳滤波,计算量较大。文献[10]使用平稳小波变换取得较好的效果,但其难点在于小波基函数的选取,不同的小波基对去噪效果具有较大的影响;此外,阈值函数的选取也影响到电能质量信号去噪的效果。以上的方法都难免会丢失突变时刻的信号。
除上述方法外,稀疏表示也是一种十分有效的信号分析工具。文献[11]提出了利用单位矩阵I和离散余弦变换(Discrete cosine Transform, DCT)、离散正弦变换(Discrete Sine Transform, DST)组成过完备字典[I C S], 并用于电能质量扰动的分类,但未讨论信号的去噪问题。有的学者提出单位矩阵I和单位傅里叶变换矩阵F组成过完备字典[I, F],并用于电能质量信号参数化压缩[12-13],获得了较高的压缩比,缺点在于傅里叶变换的实部和虚部数据需要占用两倍的存储空间。文献[14-15]提出哈特莱变换(Hartley Transform, HT)来替代离散傅里叶变换,并用于电能质量信号的压缩。HT的优点是相较于DCT、DST,它减少了字典长度和计算量;相较于傅里叶变换矩阵,减少了存储空间。但该文献仅仅讨论了数据压缩,未讨论电能质量信号的去噪问题。此外,针对稀疏分解计算量较大的问题,部分文献对稀疏分解的求解过程做了优化,文献[16]利用粒子群算法对过完备字典的时频原子寻优,减小了计算量,提高了收敛速度,但并未从根本上提升信号去噪的效果。另有学者对变频调速器电压暂降耐受特性进行了研究[17-18],还有学者对暂降扰动定位和电缆局部放电噪声抑制做了深入研究[19-20],但是均未讨论扰动信号去噪问题。
自卡尔曼滤波(Kalman Filter, KF)发明以来,KF在诸多领域都得到了广泛的运用。为了解决非线性系统和非线性观测条件下的参数估计等问题,许多学者在KF基础上提出了多种改进算法,如扩展卡尔曼滤波(Extended Kalman Filter, EKF)、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)[21]。为了克服状态突变情况下参数估计收敛速度慢的问题,周东华等[22]提出了强跟踪卡尔曼滤波(Strong Tracking Kalman Filter, STKF),在状态发生突变条件下有更快的收敛速度,克服了KF收敛速度慢的问题,并衍生出了强跟踪扩展卡尔曼滤波(Strong Tracking Extended Kalman Filter, STEKF)[23]、强跟踪无迹卡尔曼滤波(Strong Tracking Unscented Kalman Filter, STUKF)[24]。电能质量扰动信号去噪的关键在于准确地找到状态突变发生的时刻,而STKF的渐消因子(Fading Factor, FF)具备这样的功能。其次,EKF的计算步骤简单,计算量相对UKF较小,因此本文利用STEKF计算FF来确定突变时刻,以便对电能质量扰动信号进行处理。
此外,小波阈值去噪算法难以区分信号和噪声,在去噪过程中容易将部分信号当成噪声去除,导致去噪效果较差。为了更加有效地保留信号和抑制噪声,在现有的去噪算法的基础上,本文提出一种基于STEKF、联合字典稀疏分解、FFT和VMD的电能质量信号去噪方法。首先,通过STEKF的FF初步判定扰动信号的类型,并对信号分段,然后对分段后的各类电能质量扰动信号采取不同的去噪方法。这种算法能够根据扰动信号的特点有针对性地滤除噪声,从而提升去噪效果。仿真结果验证了算法的有效性。
对于某线性系统,其状态方程和观测方程分别为
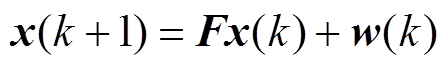 (1)
(1) (2)
(2)
式中,x(k)为系统在k时刻的状态,x(k)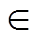 Rn;Y(k) 为系统在k时刻的观测信号,Y(k)
Rn;Y(k) 为系统在k时刻的观测信号,Y(k)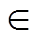 Rm;F为系统的状态转移矩阵;H为系统的观测矩阵。
Rm;F为系统的状态转移矩阵;H为系统的观测矩阵。 和
和 分别为系统的输入过程噪声和观测噪声,其均值均为零,方差矩阵分别是Q和R。
分别为系统的输入过程噪声和观测噪声,其均值均为零,方差矩阵分别是Q和R。
对于非线性系统,可以将状态方程近似线性化,即对方程中的非线性函数f(x)进行泰勒展开,保留一次项,忽略二阶及以上的展开项,得到状态转移矩阵F为
 (3)
(3)由此可得到EKF。
KF的递推公式包含下列5项公式。
状态预测为
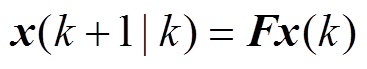 (4)
(4)状态更新为
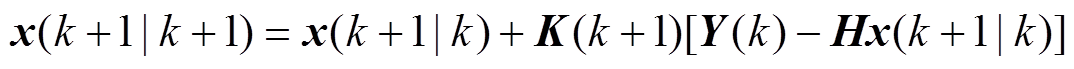 (5)
(5)
计算KF的增益为
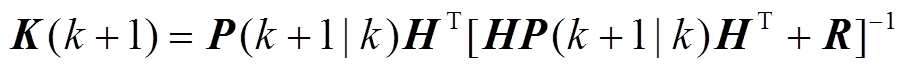 (6)
(6)其中
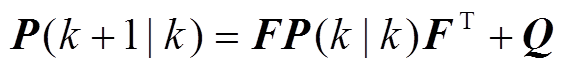 (7)
(7)
最后更新协方差为
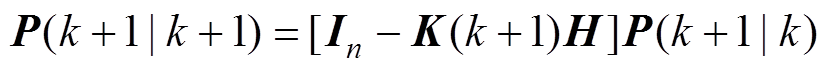 (8)
(8)式中,In为n阶单位矩阵。
STKF相对于传统的KF,不同之处在于:为了增强状态跟踪能力,在式(7)中增加了渐消因子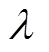 。于是式(7)变为
。于是式(7)变为
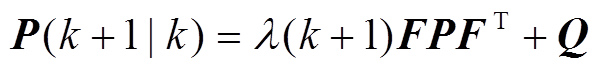 (9)
(9)式中,渐消因子的计算方法为
 (10)
(10)
式中,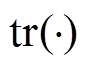 表示求矩阵的迹;
表示求矩阵的迹;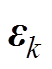 为第
为第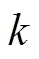 个卡尔曼滤波的计算步骤输出的残差序列;
个卡尔曼滤波的计算步骤输出的残差序列;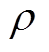 为遗忘因子,此处取0.95。
为遗忘因子,此处取0.95。
电能质量信号表示为
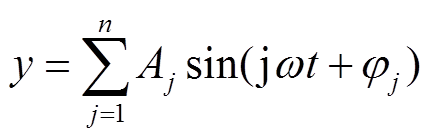 (11)
(11)式中,j为第j次谐波;Aj为第j次谐波的幅值;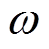 为角频率;
为角频率;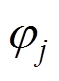 为第
为第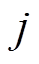 次谐波的初相位。
次谐波的初相位。
设状态空间为
 (12)
(12)故非线性状态方程中的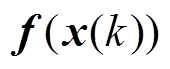 可写为
可写为
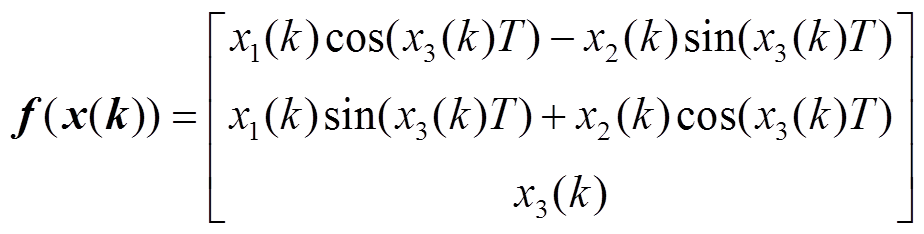 (13)
(13)
状态观测方程中的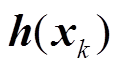 为
为
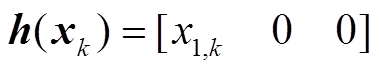 (14)
(14)在建立了非线性的状态方程和观测方程,并设置参数矩阵Q和R后,即可利用式(4)~式(10)计算STEKF,并进行参数估计,再由FF准确指示状态突变时刻,实现信号的分割,以利于对信号做分段去噪处理。
设x是一个长度为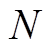 含高斯白噪声的电能质量信号。为了将信号的噪声成分从基波以及高次谐波中分离,达到去噪的目的,使用稀疏分解方法对信号进行处理。信号x可进行稀疏分解为
含高斯白噪声的电能质量信号。为了将信号的噪声成分从基波以及高次谐波中分离,达到去噪的目的,使用稀疏分解方法对信号进行处理。信号x可进行稀疏分解为
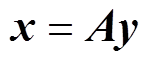 (15)
(15)
式中,A为 的联合字典矩阵,且满足M>N的条件;y为稀疏分解得到的
的联合字典矩阵,且满足M>N的条件;y为稀疏分解得到的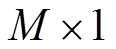 的解向量。
的解向量。
为了说明稀疏分解的优越性,本文结合图1进行说明。如图1所示,正弦信号在频域内是紧支撑的,成分单一,如图1a和图1b所示;而脉冲信号在频域内分布广泛,如图1c和图1d所示。在这样的情况下用其他方法难以将脉冲信号和正弦信号分离开来,而基于联合字典的稀疏分解可以将不同成分的信号有效分离开来。
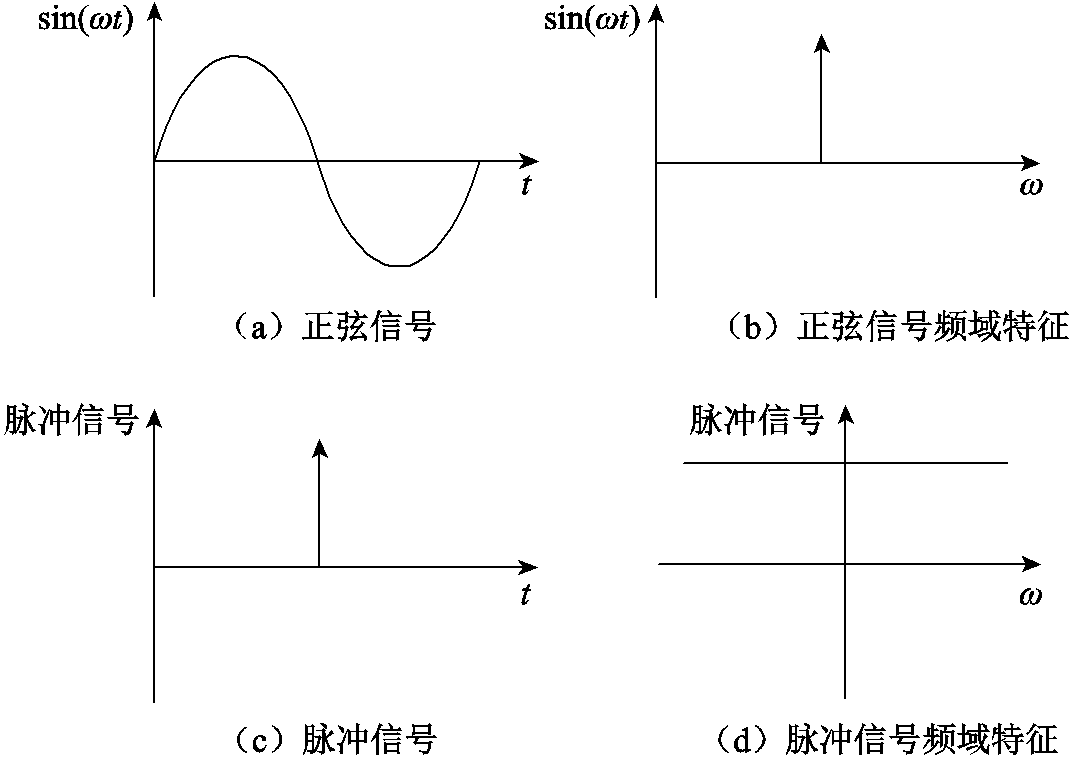
图1 电能质量扰动信号在时域和频域中的表达特征
Fig.1 Expression characteristics of power quality disturbance signal in time and frequency domain
一般用于电能质量扰动信号的稀疏分解的过完备字典有单位矩阵+离散傅里叶矩阵、单位矩阵+离散哈特来基矩阵、单位矩阵+DCT+DST矩阵等。由于DCT、DST矩阵构造简单,物理意义清晰,计算复杂度相对较小,选取单位矩阵和DCT、DST作为过完备字典。考虑到电网中3次和5次谐波占大部分,忽略7次以上谐波,所以字典中DCT、DST取到6次谐波即可。其构造方法为
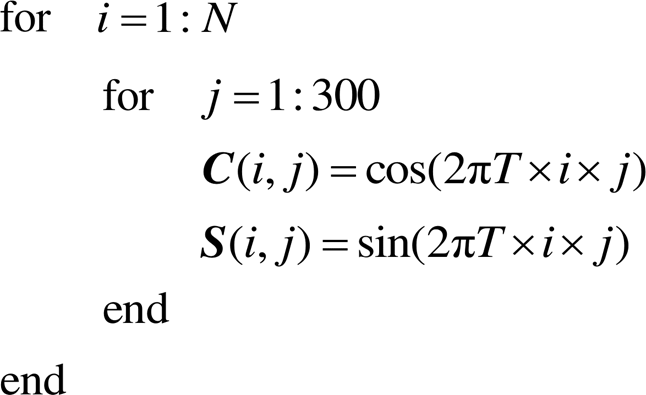
于是,过完备字典矩阵的组成为
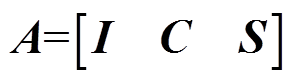 (16)
(16)
式中,C和S分别为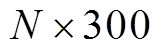 的余弦字典和正弦字典矩阵;I为N阶单位矩阵。
的余弦字典和正弦字典矩阵;I为N阶单位矩阵。
式(15)的求解是一个凸优化过程,常见的凸优化求解包括正交匹配追踪(Orthogonal Matching Pursuit, OMP)[12],以及其他改进的算法,具体步骤可参考有关文献。在凸优化计算完毕之后,计算信号的噪声和稳态成分为
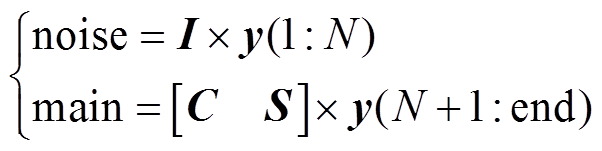 (17)
(17)式中,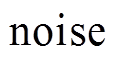 为稀疏分解得到的噪声和暂态分量;main为稀疏分解得到的稳态成分。将noise中的噪声部分抛弃(置零),对main做FFT运算,其频谱除中心频率信号的频谱外,还有少量噪声的频谱。由于稀疏分解已经分离出大部分噪声,所以少量剩余噪声频谱幅值很小。将噪声频谱的幅值置零,仅计算中心频率成分的幅值和相位,并据此重构信号,即得到二次去噪后的电能质量信号。此过程相当于先后两次去噪。
为稀疏分解得到的噪声和暂态分量;main为稀疏分解得到的稳态成分。将noise中的噪声部分抛弃(置零),对main做FFT运算,其频谱除中心频率信号的频谱外,还有少量噪声的频谱。由于稀疏分解已经分离出大部分噪声,所以少量剩余噪声频谱幅值很小。将噪声频谱的幅值置零,仅计算中心频率成分的幅值和相位,并据此重构信号,即得到二次去噪后的电能质量信号。此过程相当于先后两次去噪。
VMD算法与EMD有相似之处,但数学原理不同[25]。它将信号分解为若干个不同频率成分的本征模态函数(Intrinsic Mode Function, IMF)分量,且要求各分量的带宽之和最小,本质上它是一个在约束条件下的变分求解问题,其公式为
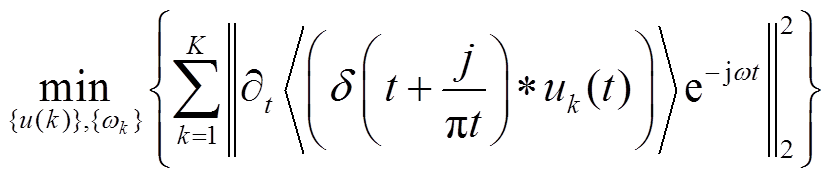 (18)
(18)且满足约束条件
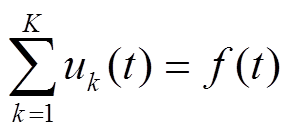 (19)
(19)
式中,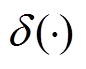 为冲击函数;
为冲击函数; 表示对t求偏导数;
表示对t求偏导数;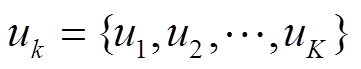 ,
,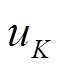 为信号
为信号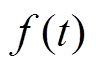 经过VMD分解后得到的K个IMF分量;
经过VMD分解后得到的K个IMF分量;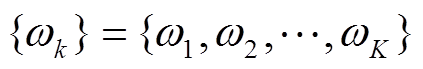 为各IMF分量
为各IMF分量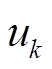 的中心频率;“*”表示求两个信号的卷积。为了求解这个问题,引入拉格朗日乘子和二次惩罚因子,于是这个变分求解问题就转换成拉格朗日函数为
的中心频率;“*”表示求两个信号的卷积。为了求解这个问题,引入拉格朗日乘子和二次惩罚因子,于是这个变分求解问题就转换成拉格朗日函数为
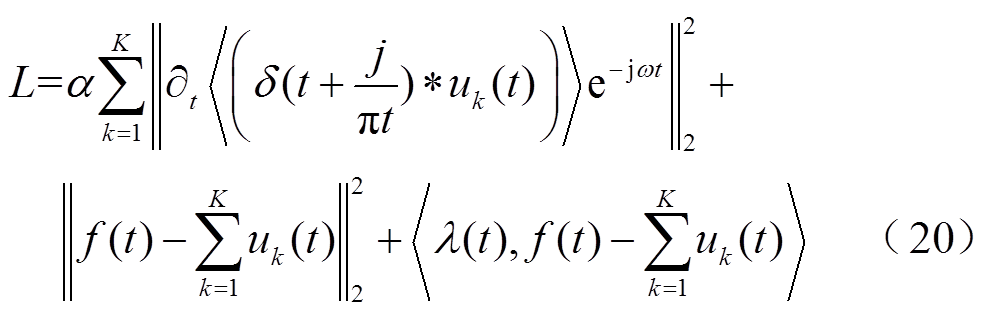
式中,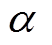 为二次项惩罚因子;
为二次项惩罚因子;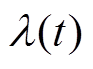 为拉格朗日惩罚因子。
为拉格朗日惩罚因子。
依据乘法算子交替法进行计算,对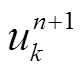 、
、 ,
,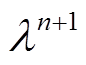 三组变量进行迭代,即可使分解后的IMF分量满足式(18)和式(19)。其具体计算步骤如下:
三组变量进行迭代,即可使分解后的IMF分量满足式(18)和式(19)。其具体计算步骤如下:
(1)对IMF分量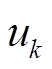 、中心频率
、中心频率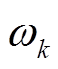 以及惩罚因子
以及惩罚因子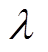 进行初始化。
进行初始化。
(2)设定分解层数K,即待分解出K个IMF分量,当k从1到K变化时,频域IMF分量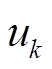 、中心频率
、中心频率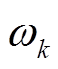 按式(21)~式(23)进行迭代。
按式(21)~式(23)进行迭代。
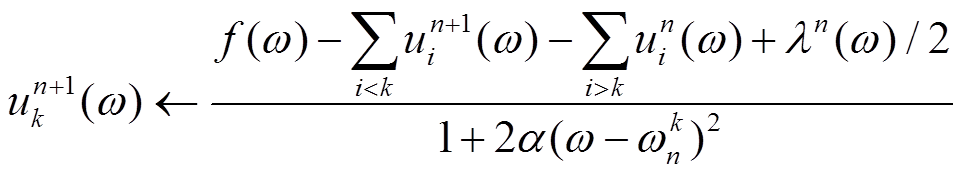 (21)
(21)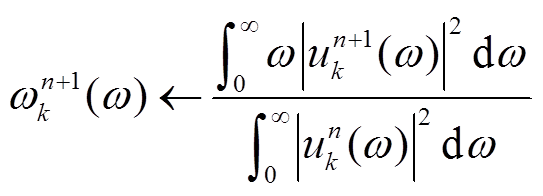 (22)
(22)
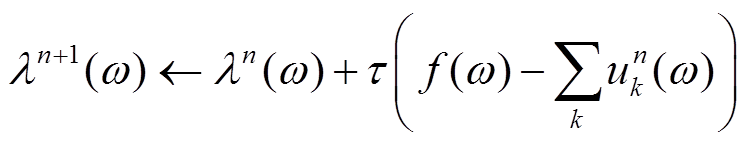 (23)
(23)
(3)判定是否达到收敛条件,此处取 =
=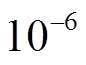 。
。
 (24)
(24)(4)在得到了频域形式的IMF分量 后,对其做傅里叶逆变换(IFFT),即得到时域形式的IMF分量
后,对其做傅里叶逆变换(IFFT),即得到时域形式的IMF分量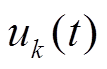 。
。
定义第k个IMF分量的平均能量 和平均周期
和平均周期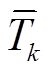 ,按式(25)和式(26)计算。
,按式(25)和式(26)计算。
 (25)
(25)
 (26)
(26)
式中,N为信号的长度;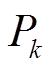 为第k个分量的极值点的个数。然后,计算乘积
为第k个分量的极值点的个数。然后,计算乘积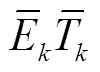 ,并将其定义为第k个IMF分量的能量周期乘积。
,并将其定义为第k个IMF分量的能量周期乘积。
文献[6]证明了对一个高斯白噪声信号做VMD分解,得到若干个IMF分量;然后对每一个IMF分量计算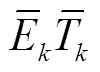 ,结果近似等于某一常数。如果对一混合高斯白噪声信号做VMD分解,计算
,结果近似等于某一常数。如果对一混合高斯白噪声信号做VMD分解,计算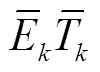 ,当第k个分量
,当第k个分量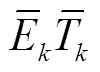 与第k+1个分量
与第k+1个分量 比值接近1,则说明第k个分量开始以后的分量均以噪声成分为主,可以去除;对剩余的前k-1个分量进行组合,即得到去噪后的信号。具体步骤如下:
比值接近1,则说明第k个分量开始以后的分量均以噪声成分为主,可以去除;对剩余的前k-1个分量进行组合,即得到去噪后的信号。具体步骤如下:
(1)对信号做K层分解并得到K个IMF分量,按中心频率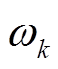 由高至低排列。
由高至低排列。
(2)逐个计算全部IMF分量的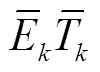 。
。
(3)计算第k个IMF分量的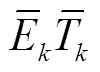 和第k+1个IMF分量的
和第k+1个IMF分量的 的比值,并判断其是否大于设定的阈值
的比值,并判断其是否大于设定的阈值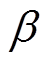 ,即
,即
 (27)
(27)
式中,取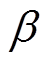 的值为1.8。若不等式成立,则把第k个分量以后的分量全部去除,剩余的分量参与重构信号。
的值为1.8。若不等式成立,则把第k个分量以后的分量全部去除,剩余的分量参与重构信号。
综上所述,本文提出一种用于电能质量扰动信号的联合去噪算法,其具体步骤可分为以下三步:
(1)利用FF的个数来判定信号的扰动类型:若有1个FF大于1,对应的信号为瞬态脉冲;若有2个FF大于1,说明信号有两次突变,对应的信号为暂升、暂降、中断;若有2个以上的FF大于1(一般多达数十个)则说明信号有暂态振荡。
(2)由单位矩阵I、DCT、DST组成的联合字典做稀疏分解,达到初步去噪的目的。把分离出来的noise置零;对main部分做FFT,舍去噪声部分对应的频谱,计算其中心频率成分的幅值和相位,并重构信号,得到先后两次去噪后的信号。
(3)对于瞬态脉冲信号,将FF大于1对应时刻的值予以保留,不做处理;对于暂态脉冲信号部分,用VMD算法做去噪处理。
为了验证本文所提出的算法的有效性,采用信噪比(Signal Noise Ratio,SNR)作为评价指标,对本文算法的去噪能力进行评估。SNR计算方法为
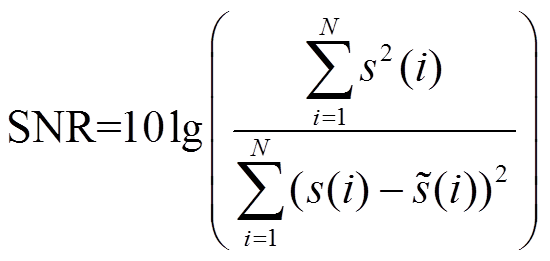 (28)
(28)式中,s(i)为不含噪声的原始信号;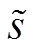 (i)为经过本文算法去噪处理后的信号。若去噪后信号的SNR越大,说明本文去噪算法越好。
(i)为经过本文算法去噪处理后的信号。若去噪后信号的SNR越大,说明本文去噪算法越好。
为了验证本文算法的有效性,利用Matlab生成各种不同的电能质量扰动信号,扰动参数采用随机生成的方法,并加入10~30dB的高斯白噪声。设置信号采样频率12.8kHz,每个周期256个采样点,然后进行去噪处理。为了消除随机误差,对每一类电能质量扰动进行20次蒙特卡罗仿真,取平均值作为去噪结果。运行环境为Matlab R2017a,操作系统win10,CPU为Intel i5-8400,主频2.8GHz,内存8GB。
一个含有高斯白噪声的电压信号可表示为
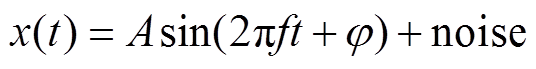 (29)
(29)式中,A为幅值,取其值为1;f为50Hz的频率; 为初相位;noise为信噪比30dB的高斯白噪声。
为初相位;noise为信噪比30dB的高斯白噪声。
首先,使用STEKF对电压信号做滤波,并计算FF,其结果如图2所示。

图2 含高斯白噪声的电压信号的渐消因子
Fig.2 Fading factor of voltage signal with white Gaussian noise
由图2可知,在全时间段内,渐消因子恒为1,说明该时间段没有发生状态突变,信号仅含有噪声;再对含噪声的电压信号应用稀疏分解去噪,分离出噪声和稳态成分,结果如图3所示。
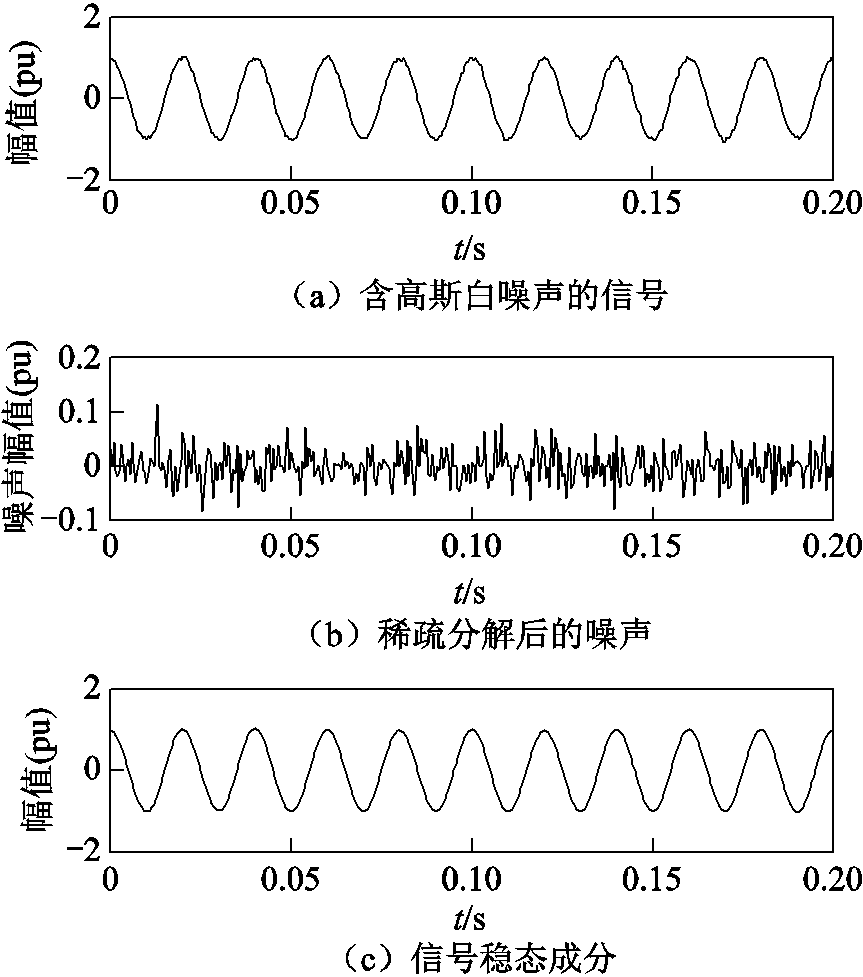
图3 电压信号的稀疏分解结果
Fig.3 Sparse decomposition results of voltage signal
由图3可知,经过稀疏分解后,图3a中的含噪声的电压被分解为噪声部分和主成分,信号中大部分噪声被分离出来,仅有少量噪声仍保留在电压波形之中。
为了进一步滤除电压波形中的噪声成分,采用FFT对信号的幅值和相位进行计算,在计算过程中噪声会被进一步滤除,从而得到信噪比更高的电压波形,如图4所示。
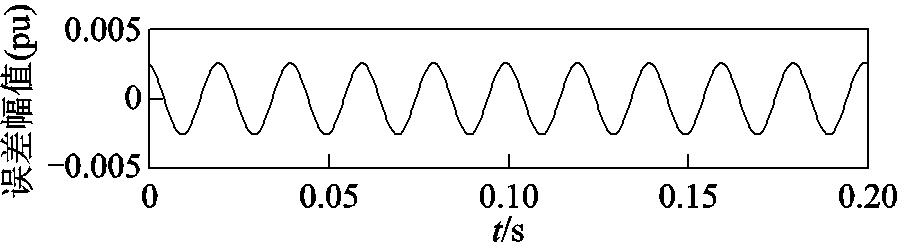
图4 去噪后的信号与原始信号的误差
Fig.4 The error between the denoised signal and the original signal
为了消除随机性,对信号做20次去噪运算,并计算每一次去噪后的SNR,其结果见表1。
表1 20次去噪后的信噪比
Tab.1 SNR after 20 times of denoising

次数信噪比/dB次数信噪比/dB 141.571147.93 241.451246.60 350.671348.36 449.951448.37 546.941551.76 650.251648.33 751.011746.13 844.031853.10 947.661943.17 1048.602045.41
取表1中20次去噪的平均值作为去噪的结果,得到平均值为47.56dB,标准差为3.24dB。由平均值可知,经过稀疏分解和FFT两次去噪后,SNR由30dB大幅度提高到47.56dB。
假设信号在某一时刻发生瞬态脉冲,含瞬态脉冲的信号表示为
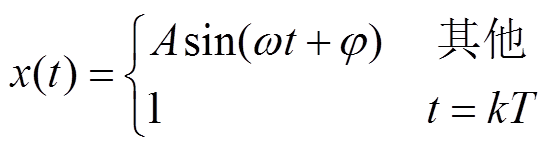 (30)
(30)式中,k为在第k个采样点处发生瞬态脉冲,此处设置为1 000;T为采样周期。
对含有瞬态脉冲的信号去噪处理方法与前面类似。但是注意到在第1 000个采样点时刻,STEKF的FF的值远大于1,说明状态在该采样点对应的时刻发生了突变,即FF准确地指示了突变发生的时刻,如图5所示。
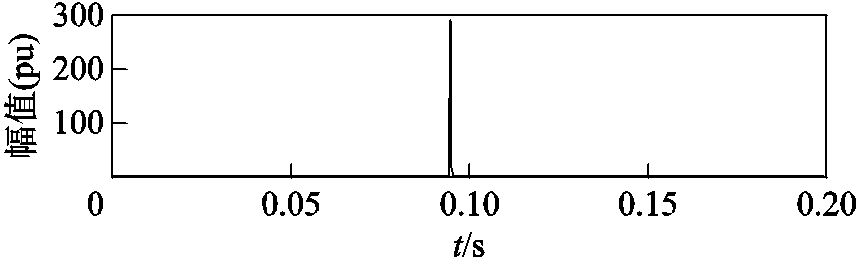
图5 含瞬态脉冲信号的渐消因子
Fig.5 Fading factor of signal with transient impulse
对含有30dB噪声的瞬态脉冲信号做稀疏分解,得到含有少部分噪声的稳态成分和含有大部分噪声的暂态成分,其结果如图6所示。
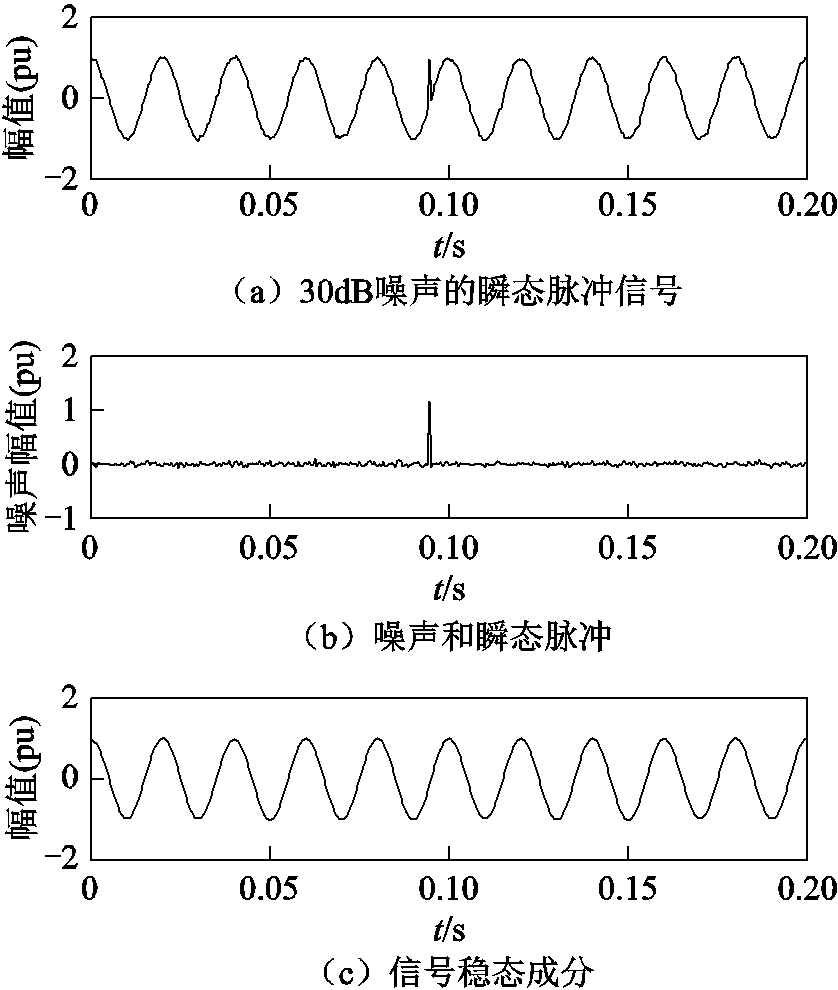
图6 瞬态脉冲信号稀疏分解结果
Fig.6 Sparse decomposition results of transient pulse signal
从图6中可以发现,经过稀疏分解以后,脉冲和噪声被分离出来。由于渐消因子准确地指示脉冲发生时刻,保留该点的信号不变,其他的部分被视为噪声去除。对含有少量噪声信号做FFT,仿照2.1节做相同处理;最后将瞬态脉冲和稳态电压波形叠加,即可得到去噪后的瞬态脉冲电压信号,如图7所示。
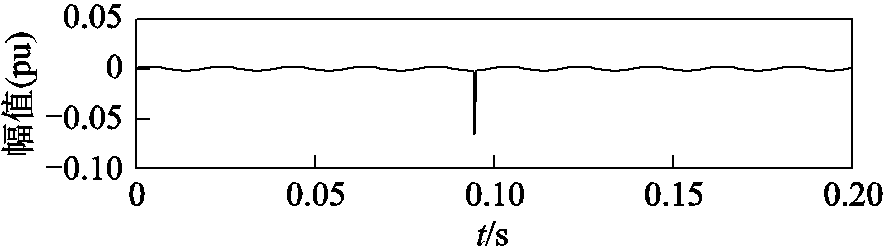
图7 去噪后的瞬态脉冲信号与原始信号的误差
Fig.7 The error between the denoised transient impulse signal and the original signal
仍然执行20次计算并取平均值,其结果为47.84dB。限于篇幅,本小节及以后若干小节的详细数据不再以列表形式给出。
考虑包含基波、3次谐波、5次谐波成分的电压信号,信号加入30dB高斯白噪声。其表达式为

本信号的处理与2.1小节的过程总体上相同。基于相同的原因,信号无突变,STEKF中的FF的值恒为1,对应的曲线与图2相同,此处不重复给出。
第二步,使用稀疏分解将噪声和基波、3次谐波、5次谐波分离开来,如图8所示。

图8 谐波信号的稀疏分解结果
Fig.8 Sparse decomposition results of harmonic signals
在分解之后将噪声置零,再使用FFT计算幅值和相位,然后据此重构信号,实现去噪。去噪后的谐波信号与原始信号的误差如图9所示。
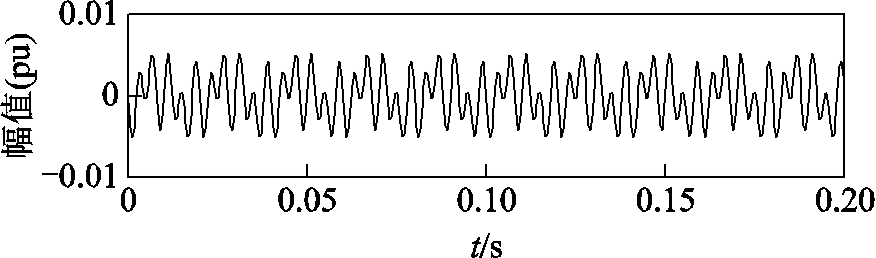
图9 去噪后的谐波信号与原始谐波信号的误差
Fig.9 The error between the denoised harmonic signal and the original harmonic signal
一个电压暂降信号的持续时间一般从一个周期到数十个周期不等。设暂降信号的起止时刻分别为0.2s和0.4s,暂降的幅度设置为0.5,其公式为
 (32)
(32)依据STEKF的原理,FF应在t=0.2s和t=0.4s处大于1,其他时刻等于1,如图10所示。

图10 暂降信号的渐消因子
Fig.10 Fading factor of sag signal
由图10可知,在0.2s和0.4s时刻FF大于1,表明暂降发生在0.2s,在0.4s电压恢复。因此,可将电压信号分为三段:初始段0~0.2s;暂降发生段0.2s~0.4s;电压恢复段0.4s~0.6s。然后分别对每一段按2.1小节的方法做去噪处理,最后再将各段信号拼接为完整的信号,即得到去噪后的信号。去噪后信号与原始信号的误差如图11所示。
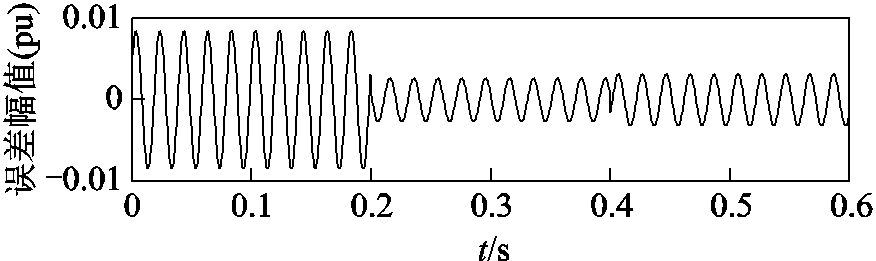
图11 去噪后的暂降信号与原始信号的误差
Fig.11 The error between the denoised sag signal and the original signal
依据本文提出的去噪算法,电压暂升信号去噪步骤和电压暂降信号去噪的步骤相同,限于篇幅,此处不再赘述。
暂态振荡信号表达式为
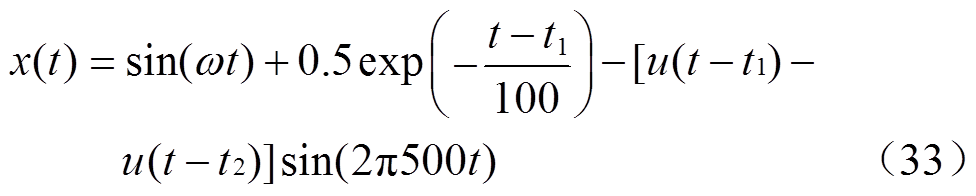
对暂态振荡信号的去噪困难之处在于振荡部分的去噪处理。本文用稀疏分解将暂态振荡和噪声一并分离出来,对稳态部分的处理与2.1节的处理方法相同;对暂态振荡的处理如下:由FF确定暂态振荡的起止时刻,对起止时刻中间的部分运用VMD去噪算法处理,其余置零。
首先,信号由STEKF处理。其中FF>1的次数会达到数十次,甚至更多,如图12所示。
由图12可知,FF>1的次数多达数十次,对应区间为第513个采样点到第1 024个采样点之间,故该段区间是暂态振荡区间。首先对该区间的振荡部分用VMD去噪,区间以外的噪声置零;最后和稳态部分组合,即实现了对信号去噪。去噪后的信号与原始信号的误差如图13所示。
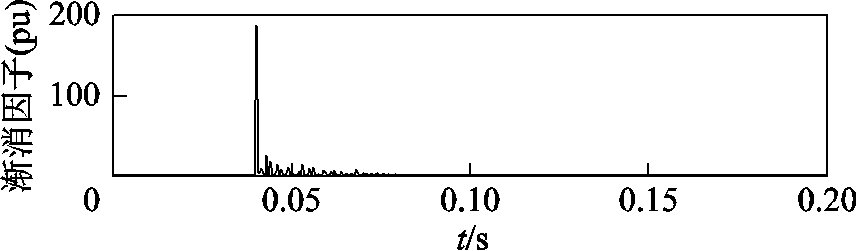
图12 暂态振荡信号的渐消因子
Fig.12 Fading factor of transient oscillation signal
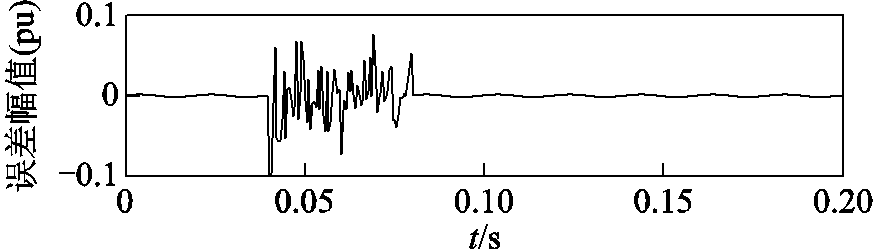
图13 去噪后的暂态振荡信号与原始信号的误差
Fig.13 The error between the denoised transient oscillation signal and the original signal
从图13可见,去噪后的信号与原始信号误差在平稳区间很小,而在振荡区间误差较大。这说明信号在振荡部分的去噪效果较差,对稳态部分的去噪效果较好。
为了验证本文算法的有效性,对2.1~2.5小节中的各类电能质量扰动信号依次添加10~30dB的高斯白噪声,并使用本文算法去噪,然后与改进小波阈值算法[26]的效果进行比较。其结果见表2。
表2 不同的去噪算法效果对比
Tab.2 Camparison of results between defferent denoising algorithms

类型信噪比/dB本文算法输出信噪比/dB改进小波阈值输出信噪比/dB 暂升1030.9824.16 1535.0928.42 2040.0333.15 2545.8435.40 3049.9139.23 暂降1027.6025.17 1532.8528.59 2037.9432.41 2542.6235.16 3047.8338.92 瞬态脉冲1025.8122.14 1530.8226.05 2037.6129.81
(续)
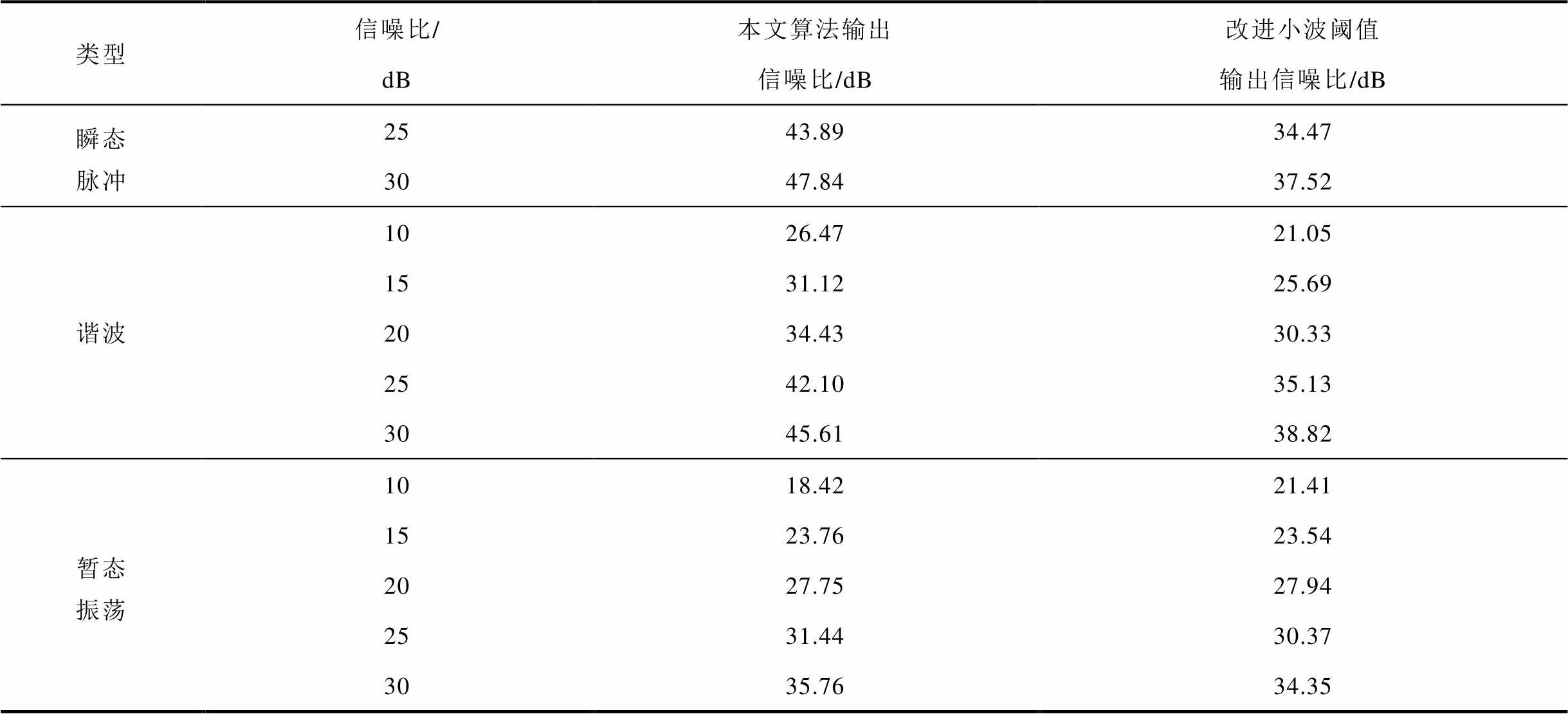
类型信噪比/dB本文算法输出信噪比/dB改进小波阈值输出信噪比/dB 瞬态脉冲2543.8934.47 3047.8437.52 谐波1026.4721.05 1531.1225.69 2034.4330.33 2542.1035.13 3045.6138.82 暂态振荡1018.4221.41 1523.7623.54 2027.7527.94 2531.4430.37 3035.7634.35
由表2可知,对于暂升、暂降、瞬态脉冲、谐波四种常见的电能质量扰动信号,本文的去噪效果优于对比算法,且改进幅度较大。以最常见的电压暂降信号为例,信噪比为30dB时,去噪后的信噪比平均值达到47.83dB。对于暂态振荡信号,当信噪比为10dB时,效果弱于改进小波阈值去噪算法;但是当信噪比为15~30dB时,与改进小波阈值效果几乎等同或优于该方法。此外,对于复合扰动本文也具有良好的效果:以暂降+谐波为例,FF仍能够精确指示暂降的起止时刻,然后用2.3节中的方法对信号分段去噪,最后将其连接成完整的信号,对于这样的复合扰动也具有良好的效果,限于篇幅此处不再赘述。综上所述,本文算法对电能质量单一扰动和复合扰动都具有良好的去噪效果,总体上是一种高效的电能质量扰动去噪方法。
本文采用基于STEKF、稀疏分解、FFT和VMD的联合去噪算法,实现了对电能质量扰动信号去噪。不同于传统的小波去噪算法,本文对不同类型的电能质量扰动信号采取了不同的去噪方法。去噪过程分为4个步骤:首先,根据FF大于1的次数判定扰动类型;然后,用稀疏分解分离稳态分量和暂态分量;之后,再用FFT对稳态分量做二次去噪;最后,对暂态分量的噪声部分置零,脉冲和暂态振荡分别采用不同的方法去噪。仿真计算结果证明,本文算法能适用于多种电能质量扰动信号,且与文献[26]中的改进小波阈值去噪算法相比,在不同的信噪比条件下,去噪效果均有了较大的提升,是一种全新且高效的去噪算法,为电能质量的准确分析和治理提供了有力支撑。
参考文献
[1] 王维博, 董蕊莹, 曾文入, 等. 基于改进阈值和阈值函数的电能质量谐波去噪方法[J]. 电工技术学报, 2019, 34(2): 409-418.
Wang Weibo, Dong Ruiying, Zeng Wenru, et al. A wavelet de-noising method for power quality based on an improved threshold and threshold function[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 409-418.
[2] Srivastava M, Anderson C L, Freed J H. A new wavelet denoising method for selecting decomposition levels and noise thresholds[J]. IEEE Access, 2016(4): 3862-3877.
[3] Shukla S, Mishra S, Singh B. Power quality event classification under noisy conditions using EMD-based de-noising techniques[J]. IEEE Transactions on Industrial Informatics, 2014, 10(2): 1044-1054.
[4] 刘宇舜, 周文俊, 李鹏飞, 等. 基于广义S变换模时频矩阵的局部放电特高频信号去噪方法[J]. 电工技术学报, 2017, 32(9): 211-220.
Liu Yushun, Zhou Wenjun, Li Pengfei, et al. Partial discharge ultrahigh frequency signal denoising method based on generalized S-transform modula time-frequency matrix[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 211-220.
[5] 胡卫红, 舒泓, 栾宇光. 基于奇异值分解的电能量信号去噪[J]. 电力系统保护与控制, 2010, 38(2): 30-33.
Hu Weihong, Shu Hong, Luan Yuguang. Power quality signals’ de-noising method based on singular value decomposition (SVD)[J]. Power System Protection and Control, 2010, 38(2): 30-33.
[6] 刘畅. 电力信号去噪与微弱信号检测的研究[D]. 武汉: 华中科技大学, 2019.
[7] 张全明, 刘会金, 兰泉妮. 基于小波混合阈值方法的电能质量信号去噪[J]. 电力自动化设备, 2008, 28(8): 28-35.
Zhang quanming, Liu Jinhui, Lan Quanni. Power quality signal denoising based on wavelet hybrid threshold method[J]. Electric Power Automation Equipment, 2008, 28(8): 28-35.
[8] 李涛, 张宇, 何怡刚. 基于MAP估计双树复小波的电能质量扰动信号去噪方法[J]. 计算技术与自动化, 2012, 31(1): 33-38.
Li Tao, Zhang Yu, He Yigang. Dual-tree disturbance signal based on MAP estimation[J]. Computing Technology and Automation, 2012, 31(1): 33-38.
[9] 张明, 李开成, 胡益胜. 基于Bayes估计的双小波维纳滤波电能质量信号去噪算法[J]. 电力系统保护与控制, 2011, 39(4): 52-57.
Zhang Ming, Li Kaicheng, Hu Yisheng. Power quality signals denoising via double-wavelet Wiener filtering based on Bayes estimation[J]. Power System Protection and Control, 2011, 39(4): 52-57.
[10] 范小龙, 谢维成, 蒋文波, 等. 一种平稳小波变换改进阈值函数的电能质量扰动信号去噪方法[J]. 电工技术学报, 2016, 31(14): 219-226.
Fan Xiaolong, Xie Weicheng, Jiang Wenbo, et al. An improved threshold function method for power quality disturbance signal de-noising based on stationary wavelet transform[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 219-226.
[11] Manikandan M S, Samantaray S R, Kwmwa I. Detection and classification of power quality disturbance using sparse signal decomposition on hybrid dictionaries[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 60(1): 27-38.
[12] 何顺帆, 李开成, 蔡得龙, 等. 电能质量扰动数据特征的最优分辨率提取[J]. 中国电机工程学报, 2018, 38(21): 6223-6232.
He Shunfan, Li Kaicheng, Cai Delong, et al. Feature extraction of power quality disturbance with optimal resolution[J]. Proceedings of the CSEE, 2018, 38(21): 6223-6232.
[13] Shunfan He, Wei Tian, Junming Zhang, et al. A high efficient approach for power disturbance waveform compression in the view of Heisenberg uncertainty[J]. IEEE Transactions on Industrial Informatics, 2019, 15(5): 2580-2591.
[14] Cai Delong, Li Kaicheng, He Shunfan, et al. On the application of joint-domain dictionary mapping for multiple power disturbance assessment[J]. Energies, 2018, 11(2): 347.
[15] 蔡得龙. 基于稀疏分解的电能质量研究[D]. 武汉: 华中科技大学, 2018.
[16] 王文飞, 周雒维, 李绍令, 等. 采用改进CPSO动态搜索时频原子的电能质量扰动信号去噪方法[J]. 电网技术, 2018, 48(12): 4129-4137.
Wang Wenfei, Zhou Luowei, Li Shaoling, et al. A time-frequency atoms dynamic search method for power quality disturbance signal de-noising based on improved chaotic particle swarm optimization[J]. Power System Technology, 2018, 48(12): 4129-4137.
[17] 陶顺, 唐松浩, 陈聪, 等. 变频调速器电压暂降耐受特性试验及量化方法研究Ⅰ:机理分析与试验方法[J]. 电工技术学报, 2019, 34(6): 1273-1281.
Tao Shun, Tang Songhao, Chen Cong, et al. Experimental research on adjustable speed drivers tolerance to voltage sags and quantitative method partⅠ: mechanism analysis and test method[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1273-1281.
[18] 唐松浩, 陶顺, 刘颖英, 等. 变频调速器电压暂降耐受特性试验及量化方法研究Ⅱ:试验及量化方法[J]. 电工技术学报, 2019, 34(10): 2207-2215.
Tang Songhao, Tao Shun, Liu Yingying, et al. Experimental research on adjustable speed drivers tolerance to voltage sags and quantitative method partⅡ: experiment and quantification method[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2207-2215.
[19] 周凯, 黄永禄, 谢敏, 等. 短时奇异值分解用于局放信号混合噪声抑制[J]. 电工技术学报, 2019, 34(11): 2435-2443.
Zhou Kai, Huang Yonglu, Xie Min, et al. Mixed noises suppression of partial discharge signal employing short-time singular value decomposition[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2435-2443.
[20] 张嫣, 林涌艺, 邵振国. 电压暂降可观约束下的定位监测点多目标优化配置[J]. 电工技术学报, 2019, 34(11): 2375-2383.
Zhang Yan, Lin Yongyi, Shao Zhenguo. Multi-objective optimal allocation of monitors for voltage sag location under observability constraint[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2375-2383.
[21] 黄小平, 王岩. 卡尔曼滤波原理及应用—MATLAB仿真[M]. 北京: 电子工业出版社, 2015.
[22] 周东华, 席裕庚, 张钟俊. 非线性系统带次优渐消因子的扩展卡尔曼滤波[J]. 控制与决策, 1990, 5(5): 1-6.
Zhou Donghua, Xi Yugeng, Zhang Zhongjun. Suboptimal fading extended Kalman filter for nonlinear systems[J]. Control and Decision, 1990, 5(5): 1-6.
[23] 陈晓静. 非平稳复合电能质量扰动检测研究[D]. 武汉: 华中科技大学, 2018.
[24] 牛胜锁, 王康乐, 梁志瑞. 基于改进强跟踪无迹卡尔曼滤波的电力系统同步相量估计方法[J]. 电网技术, 2019, 43(9): 3218-3225.
Niu Shengsuo, Wang Kangle, Liang Zhirui. Synchronous phasor estimation method for power system based on modified strong tracking unscented Kalman filter[J]. Power System Technology, 2019, 43(9): 3218-3225.
[25] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[26] 龚静. 电能质量信号去噪中小波选取特点的研究[J/OL]. 电测与仪表, 2020, https://kns.snki.net/ kcms/detail/23.1202.TH.20200728.0838.002.html.
Gong Jing. Research on the characteristics of wavelet selection in power quality signal de-noising[J/OL]. Electrical Measurement & Instrumentation, 2020, https://kns.snki.net/kcms/detail/23.1202.TH.20200728.0838.002.html
A Combined De-Noising Method for Power Quality Disturbances Events
Abstract The traditional wavelet threshold de-noising algorithm has some disadvantages, such as easy to discard the real signal and poor de-noising effect. This paper presented a new joint de-noising algorithm for power quality disturbance events. Firstly, the disturbance type of signal is preliminarily determined by the number of times that the fading factor of strong tracking Kalman filter is greater than 1, and then different de-noising methods are adopted for different disturbance types. For sinusoidal signal and harmonic signal only containing noise, sparse decomposition and fast Fourier transform (FFT) are used to de-noising twice; fading factor is used to accurately indicate the beginning and ending time of disturbance for sag and rise signal, and sparse decomposition and FFT de-noising are used for each segment of signal; different processing methods are used for signal containing transient pulse and transient oscillation. Firstly, the steady-state component and transient component are obtained by sparse decomposition. The de-noising method of steady-state component is the same as that of sinusoidal signal. The impulse signal and oscillation signal of transient component are processed by retaining the actual value and variational mode decomposition (VMD) respectively. A large number of simulation results show that under different SNR conditions, the proposed algorithm can effectively suppress the noise of various disturbance signals, significantly improve the signal-to-noise ratio, and the effect is better than the wavelet threshold de-noising algorithm.
keywords:Power quality disturbance events, strong tracking Kalman filter, sparse decomposition, wavelet analysis, de-noising method
DOI:10.19595/j.cnki.1000-6753.tces.201389
中图分类号:TM 71
国家自然科学基金资助项目(52077089)。
收稿日期 2020-10-13
改稿日期 2020-12-28
肖贤贵 男,1988年生,博士研究生,研究方向为电能质量扰动分析及信号处理、机器学习及优化方法在电能质量分析中的应用。E-mail:xiaoxiangui@hust.edu.cn
李开成 男,1962年生,教授,博士生导师,研究方向为电磁测量、电子式互感器及电能质量分析等。E-mail:likaicheng@hust.edu.cn(通信作者)
(编辑 郭丽军)