
图1 电磁超声纵波产生原理
Fig.1 Principle of electromagnetic ultrasonic longitudinal wave generation
摘要 传统电磁超声纵波换能器换能效率低,水平偏置磁场弱且无法被充分利用,导致回波信号幅值小,影响检测结果的准确性。该文应用一种新型纵波换能器,其永磁体磁极方向按照Halbach阵列排布,能够显著增强水平磁场。为提高其回波幅值,利用有限元软件进行建模,分别采用正交试验和均匀试验方法,在考虑线圈匝数的前提下,对换能器参数进行优化。仿真结果表明,降低导线间距、导线宽度和导线高度,将永磁体提离距离固定在合适范围内,均可以增强回波信号;设置合适的激励电流频率,能够使得声衰减和回波幅值处于适中水平,有利于检测。实验结果表明,优化后的换能器相较于优化前回波幅值提高了83%。
关键词:电磁超声换能器 纵波 Halbach阵列 优化设计 正交试验 均匀试验
电磁超声换能器(Electromagnetic Acoustic Transducers, EMATs)能够无接触地在金属内部激发并接收超声波,其利用通入内部线圈中的高频激励在被测试件表层趋肤深度内感生出涡流,在永磁体偏置磁场的作用下,试件表面质点受到洛仑兹力从而高频振动,继而在试件内部激发超声波。电磁超声技术在金属无损检测领域发挥了巨大作用[1-4]。与传统的压电超声检测相比,电磁超声检测无需使用耦合剂,不需要对被测试件表面进行预处理,并且可以在高温高压等恶劣工况下进行正常检测[5-9]。目前,电磁超声无损检测已经被广泛应用于金属的厚度测量、缺陷检测、塑性损伤检测等领域,逐渐成为一种国内外较为主流的无损检测手段。
尽管电磁超声检测具有诸多优点,然而相比于其他类型换能器,EMATs存在换能效率低、易受到电磁干扰等问题[10-12],其中传统电磁超声纵波换能器水平偏置磁场弱,导致换能效率极低,对测量结果造成不利影响。为此,国内外学者做了大量的研究,以提高EMATs接收信号的信噪比。Kang Lei等[13]通过三维仿真建模,使用正交试验研究了曲折线圈长度、导线宽度、提离距离等七个因素对表面波的幅值影响;江念等[14]通过对钢板实测回波进行分析,发现与换能器固有频率一致的激励频率、适中的脉冲周期数、较小的提离距离能够有效提高回波信号幅值;封礼发等[15]利用有限元软件仿真分析,研究了电流频率和线圈参数对电磁超声横波近场长度和半扩散角的影响;Sun Hongjun等[16]设计出一种新型永磁体排列结构,在不改变永磁体厚度的情况下有效增大了垂直磁通密度和回波信号峰峰值;杨理践等[17]使用电磁超声纵波对铝板厚度进行检测,研究了永磁体参数、线圈参数和电流频率对换能效率的影响;Sun Hongyu等[18-19]利用有限元仿真,运用正交试验研究了导线宽度、提离距离、激励电流幅值等七个因素对于聚焦型换能器检测效果的影响,并研究了磁铁排布列、磁铁剩磁、导线宽度等九个因素对于点聚焦型水平导波换能器检测效果的影响;Jia Xiaojun等[20]采用正交试验,分析了磁铁半径、磁铁高度、导线宽度等七个因素对点聚焦型横波换能器的信号幅值、聚焦偏移的影响;Liu Zenghua等[21]通过在永磁体下方增加磁路聚集装置,有效地减弱了磁通密度水平分量和垂直洛仑兹力,大幅削弱了A0模式波,改善了换能器的模式纯净度,提高了换能器的缺陷定位能力,并通过正交试验对换能器几何参数进行了优化。
可见,通过优化换能器的永磁体尺寸及线圈参数,能够有效提升回波幅值。然而上述优化并未考虑到线圈匝数的局限性,在永磁体可利用偏置磁场区域确定的情况下,增大导线宽度或导线间距势必会减少线圈的有效工作匝数,从而影响回波幅值。此外,正交试验优选法只适用于各参数水平较少的场合,当所要考察的水平数较多时,正交试验总试验次数过多时,宜采用均匀试验方法进行优化。
本文使用一种永磁体按照Halbach阵列排布的电磁超声纵波换能器,并对其进行优化设计。首先介绍Halbach阵列纵波换能器结构及其工作原理;然后,利用COMSOL Multiphysics有限元软件进行二维建模,分别采用正交试验和均匀试验方法,仿真中设置不同的线圈参数和匝数组合,改变永磁体提离距离,以寻求增强回波信号幅值的最佳方案,研究了不同电流频率对声衰减和一次回波幅值的影响;最后,分别使用优化前、后换能器对本文提出的优化方案进行了验证。
电磁超声换能器主要包括三部分:永磁体、线圈和被测试件。传统纵波EMATs为了得到水平磁场,通常将线圈布置于单个永磁体下方或相邻永磁体之间,然而这种排布难以产生较强的水平磁场,导致激发信号偏弱,检测准确度不高。Halbach永磁阵列能够有效地解决此类问题,其最早由美国Klaus Halbach教授提出,目前广泛应用于高速电机、高精度伺服电动机、直线电机中[22]。它是一种新型永磁体布置方式,将不同磁化方向的永磁体按照一定顺序排列,使得阵列一侧磁场显著增强而另一侧减弱,可以在不增大换能器尺寸的条件下有效增强水平磁场,相比于同尺寸传统纵波换能器,能够产生更为剧烈的纵波,接收到幅值更高的回波信号,因此拥有更高的信噪比和换能效率。Halbach阵列电磁超声换能器激发纵波原理如图1所示。

图1 电磁超声纵波产生原理
Fig.1 Principle of electromagnetic ultrasonic longitudinal wave generation
当换能器内部线圈通入激励电流J0时,感应出动态磁场强度Hd和交变磁感应强度Bd的磁场,从而在线圈附近空间激发出电场Em和感生电动势εm。根据Faraday电磁感应定律,在试件趋肤层将感应出与激励电流方向相反的涡流Je。在永磁体提供的水平偏置磁场作用下,涡流受到垂直方向的洛仑兹力,试件趋肤层质点高频振动从而激发出超声纵波并沿试件厚度方向传播。当超声波传播至接收换能器下方时,切割静磁场Bs磁力线,产生动生电动势εv。因此,换能器探头接收到的电压信号εtotal是感生电动势与动生电动势的叠加。即
 (1)
(1)
根据Faraday电磁感应定律,感生电动势εm计算式为
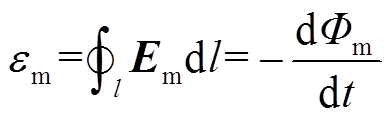 (2)
(2)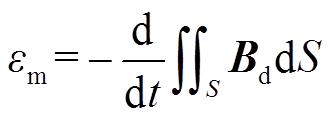 (3)
(3)
式中,Φm为感应磁通。
在检测金属材料时,磁场强度和电场强度满足
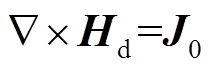 (4)
(4)
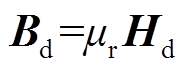 (5)
(5)
 (6)
(6)
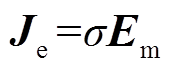 (7)
(7)
式中,μr为材料的相对磁导率;σ为材料的电导率。
考虑交变电流在被测试件趋肤深度产生交变动态场,试件表面所受洛仑兹力为
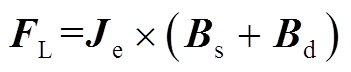 (8)
(8)铁磁性材料趋肤层质点的振动主要是由洛仑兹力FL和磁致伸缩力FMS共同作用产生,因此质点位移可以表示为
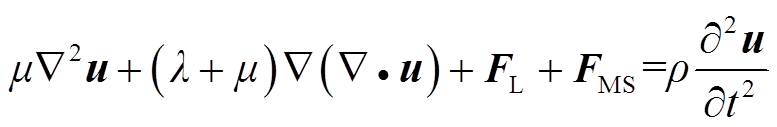 (9)
(9)
式中,ρ为材料密度;u为位移矢量;μ和λ为拉梅常数。
由于本文所检测试样为铝板,因此不存在磁致伸缩力,故FMS为0N。
利用有限元软件COMSOL Multiphysics建立Halbach阵列电磁超声纵波换能器二维模型,对其工作过程进行多物理场有限元仿真分析。
换能器采用收发一体结构布置,永磁体为方形钕铁硼磁铁,充磁方向按照Halbach阵列设计,剩余磁场强度为1.2T,矫顽力为900kA/m,尺寸为5mm×5mm。被测试件采用7075型铝合金,尺寸为40mm×5.2mm,杨氏模量为7.1×1010Pa,泊松比为0.25,电导率为3.775×107S/m,密度为2 810kg/m3。换能器线圈采用“回”形绕制,匝数为4,导线宽w为0.2mm,高度l为0.05mm,线间距d为0.2mm,永磁体底部距离待测试件上表面之间的提离距离h为0.5mm。线圈中加载峰峰值为40A、频率6MHz的激励电流。图2为Halbach阵列电磁超声换能器三维结构示意图。

图2 换能器结构示意图
Fig.2 Schematic diagram of transducer structure
由于趋肤效应的存在,铝板中的感应涡流主要存在于上表面趋肤深度层内,因此为了确保模型计算的准确性,需要对趋肤层进行网格细化,最大单元大小为0.05mm。试件域最大单元按照理论纵波波长的1/5,即0.18mm进行网格划分。空气域、线圈及永磁体区域采用自由三角形进行网格剖分。图3为细化区域局部放大图。
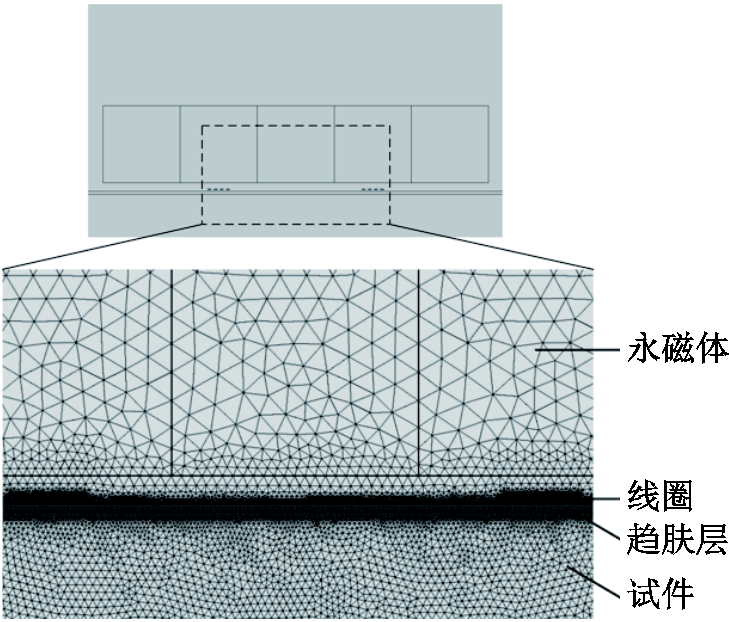
图3 模型网格细化
Fig. 3 Grid refinement of the model
图4分别为两类传统纵波换能器与Halbach阵列换能器平面磁场分布图,白色箭头表示磁场方向。可以看出,图4c中显示Halbach阵列永磁体相比于图4a、图4b两种传统永磁体排布能够显著增强水平磁场,在中间永磁体左右两侧正下方两区域磁通密度水平分量最大,垂直分量最小,为得到垂直方向的洛仑兹力以产生纵波,并且尽可能地去除横波成分,仿真中只将线圈布置于这两处,因此永磁体的有效偏置磁场区域是确定的。

图4 永磁体磁场分布
Fig.4 Magnetic field distribution of permanent magnets
设置图4a~图4c中三种纵波换能器提离距离h均为0.5mm,以左起首个永磁体边界作为x方向考察基准零点,止于最右侧永磁体边界;以试件上表面作为y方向考察基准零点,止于面下1.2mm处,考察磁通密度模水平分量在二维区域内分布情况,如图5所示。从图中可以看出,Halbach阵列型永磁体排布所产生的磁通密度模水平分量约为两种传统纵波换能器的3~4倍,而水平磁场产生垂直洛仑兹力继而激发纵波,因此Halbach阵列型换能器激发的纵波强度要大于传统纵波换能器。在x方向上,三者的水平分量最大值均位于中心左右两侧,因此仿真中将线圈布置于此处。在y方向上,随着远离试件上表面向下方延伸,可以看出水平分量总体上呈减小的趋势。
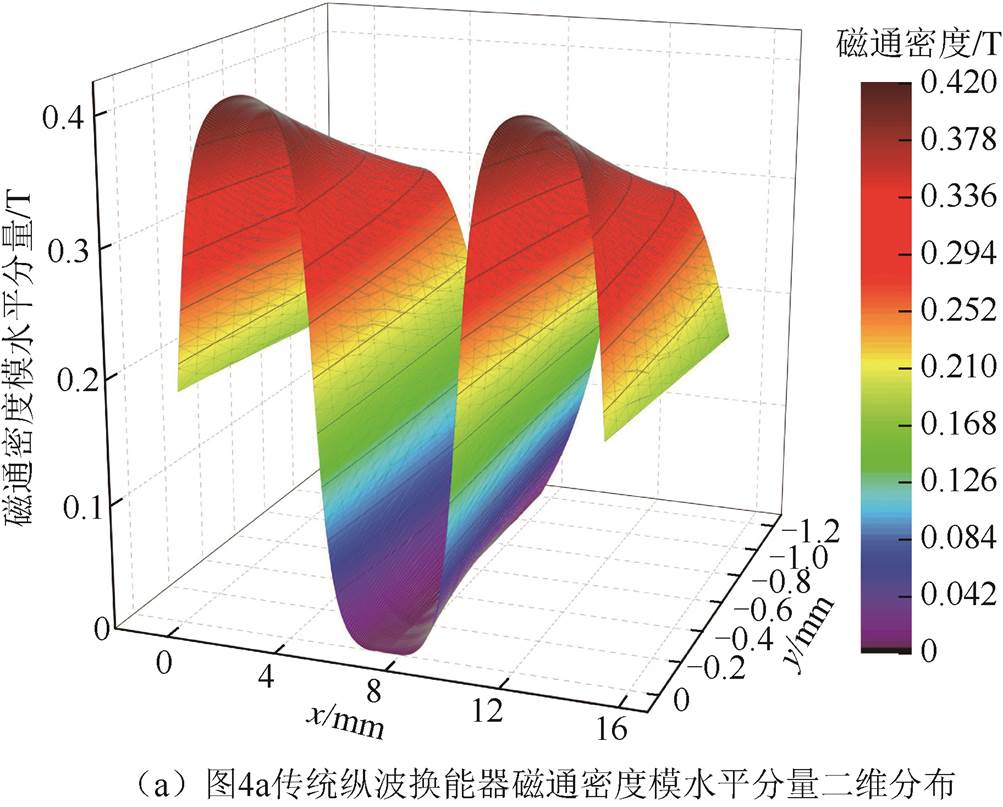
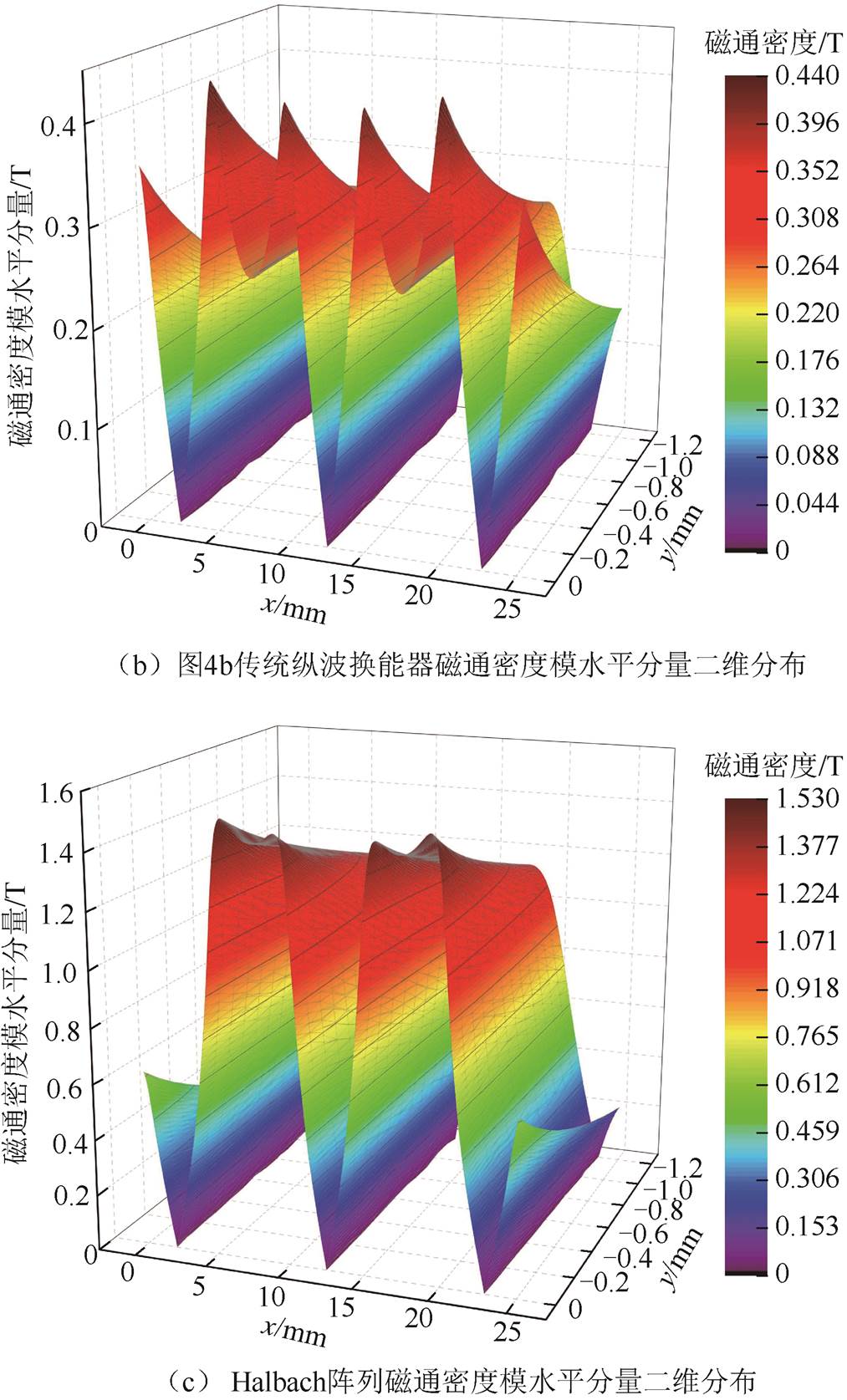
图5 磁通密度模水平分量二维分布
Fig.5 Two-dimensional distribution of the horizontal component of the magnetic flux density module
图6为超声波在铝板内部沿y负方向传播位移图。换能器激发出垂直向下的纵波和微弱的横波,均沿试件厚度方向传播。横波、纵波由于声速的差异在传播过程中逐渐分离。随着传播声程的增加,纵波的能量存在一定的衰减。当纵波触碰试件底部时将发生反射,按照原路径又传播至试件顶部,如此往复直至能量衰减耗损至零。
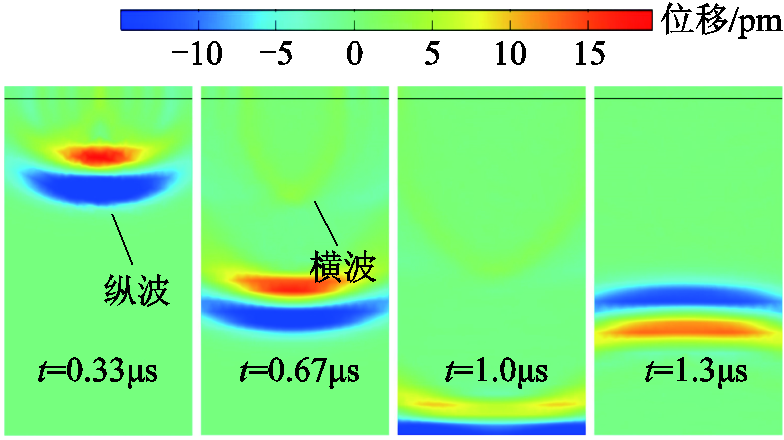
图6 不同时刻声波位移
Fig.6 Displacement of ultrasonic at different times
试件表面的涡流由换能器中线圈感应产生,线圈的几何参数势必会影响涡流的强弱和质点振动的幅度,换能器接收到的回波信号也将随着几何参数的变化发生改变,因此需要对参数进行优化以获得最佳信号。由于上述参数组合种类繁多,采用全面试验逐一进行分析工作量庞大,难以开展,因此宜采用正交试验方法。正交试验提供了一个高效且系统的方案,从全面试验中挑选出一部分具有代表性的组合进行研究,以确定各参数对结果的影响,具有“均匀分散,齐整可比”的特点,能够有效减少试验次数,从而提高优化效率[23]。
将接收到的第一次回波电压幅值作为优化对象,考察线间距、导线宽度和导线高度三个因素对其影响,不改变永磁体尺寸。图7为导线区域局部放大图。其中线间距为d,导线宽度为w,导线高度为l。仿真中永磁体底部距离被测试件上表面的提离距离h设置为0.5 mm。
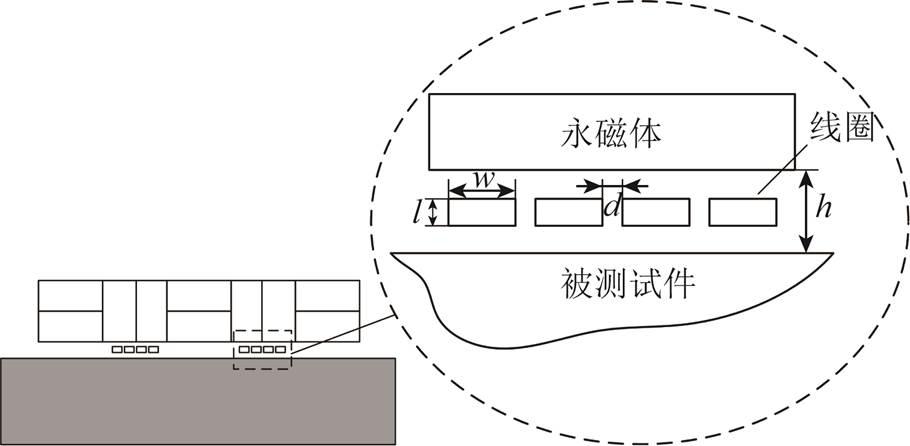
图7 线圈区域局部放大
Fig.7 Partialenlargeddetail of coil
根据EMATs线圈实际应用常用规格,确定上述三个因素的合理取值范围。当线间距和导线宽度增大时,由于永磁体有效偏置磁场区域确定,因此导线的工作匝数将减少。LA(mn)表示n因素m水平正交表,总设计试验次数为A次,且A≥m2。表1为三因素三水平的正交表L9(33)。表中Y表示第一次回波幅值;分别计算表中线间距d、导线宽度w、导线高度l在某一水平时,一次回波幅值的算数平均值ki (i表示各因素取不同值对应的序号,i = 1, 2, 3)。根据ki中最大值和最小值计算极差R,极差越大则表示该因素对一次回波幅值影响越大。正交试验结果见表2。
表1 正交试验设计方案及结果
Tab.1 Orthogonal test design scheme and results

试验序号d/mmw/mml/mm匝数Y/mV 10.20.10.02170.091 3 20.20.550.1160.043 1 30.21.00.240.015 8 40.450.10.1190.056 8 50.450.550.250.025 1 60.451.00.0230.017 1 70.70.10.270.017 8 80.70.550.0240.018 1 90.71.00.1130.013 5
表2 正交结果分析
Tab.2 The analysis of orthogonal results

dwl k1/mV0.050 10.055 30.042 2 k2/mV0.033 00.028 80.037 8 k3/mV0.016 50.015 50.019 6 R/mV0.033 60.039 80.022 6
以各因素不同取值为横坐标,以对应的ki值为纵坐标,绘制回波幅值随各因素变化趋势如图8所示。
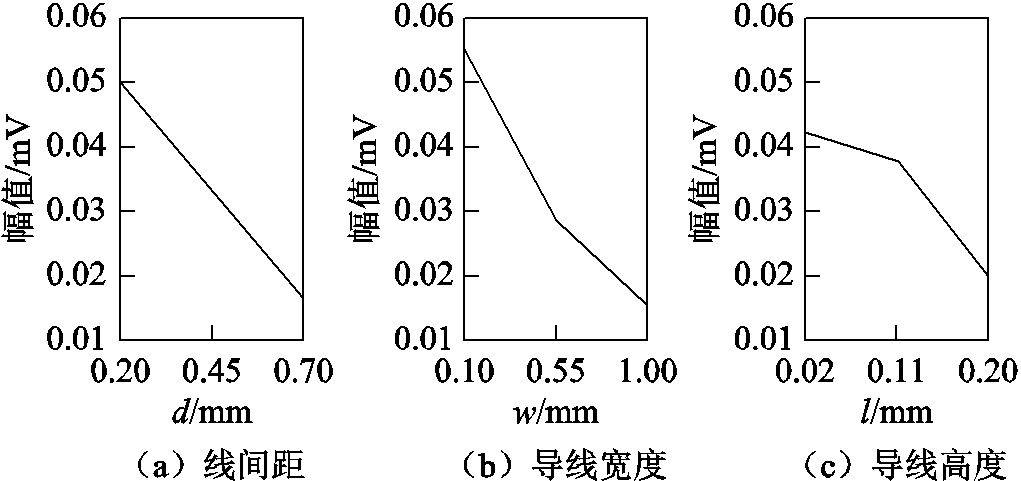
图8 各因素对回波电压幅值的影响
Fig.8 The influence of various factors on the echo voltage amplitude
从表2可以看出,对回波电压幅值影响程度从大到小依次为导线宽度w、线间距d、导线高度l。在考虑线圈匝数的条件下,三者与接收到的一次回波电压幅值均呈明显的负相关,减小线间距d、导线宽度w以及导线高度l均可以增大回波电压幅值。这是由于在仿真中通过单根导线的电流恒定,当导线宽度w、线间距d、导线高度l减小时,永磁体偏置磁场区域内导线匝数增多,使得单位截面积通过的总电流增大,试件表面感应涡流也随之提高,从而增大趋肤层质点受到的洛仑兹力,导致质点振动更加剧烈。综上分析,最优线圈参数组合为:d=0.2mm,w=0.1mm,l=0.02mm。
将使用优化组合得到的第一次回波电压,连同正交试验2(正交2)和正交试验4(正交4)的回波结果绘制于同一图中,如图9。优化参数组合得到的电压结果相比于两种未优化组合有了明显提升,正交2和正交4的归一化幅值分别为0.47和0.62,优化组合结果比优化前幅值最高的两种方案分别提升了113%和61%。
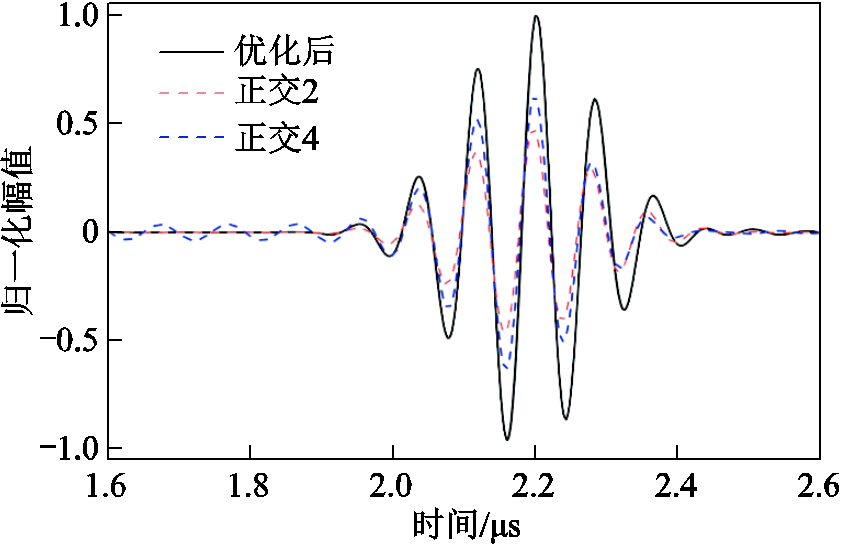
图9 优化前后回波电压幅值对比
Fig.9 Comparison of echo voltage amplitudes before and after optimization
正交试验虽然能够精简试验次数,但其只适用于各参数水平数较少的情形。在正交表LA(mn)中,水平数m增加1,则总试验次数增加2m+1次,且A≥m2,因此当线圈参数考察水平数较多时,正交总试验次数大幅增加,失去了其优势,适宜采用均匀试验来进行优化。与正交试验相比,均匀试验不需要考虑“齐整可比”,而是让各参数在试验范围内“均匀分散”[24]。UA(mn)表示n因素m水平均匀试验表,A为总试验次数,且A=m。水平数m增加1,则总试验次数A增加1次,因此均匀试验适用于参数水平数较多的情形。
均匀试验中,同样考察线间距d、导线宽度w、导线高度l三者对回波幅值的影响,且不改变永磁体尺寸。优化范围分别选为0.2mm≤d≤0.65mm, 0.1mm≤w≤1.0mm,0.02mm≤l≤0.2mm。表3为三因素十水平均匀设计表U10(103)。X1~X3分别表示线间距d、导线宽度w、导线高度l。Y表示第一次回波幅值。
对仿真结果进行多项式线性回归分析,得到回归方程
 (10)
(10)表3 均匀试验设计方案及结果
Tab.3 Uniform test design scheme and results

序号X1/mmX2/mmX3/mm匝数Y/mV 10.45(6)0.1(1)0.14(7)90.056 28 20.65(10)0.8(8)0.12(6)30.015 90 30.25(2)0.9(9)0.16(8)40.018 30 40.20(1)0.4(4)0.10(5)80.059 25 50.35(4)0.6(6)0.20(10)50.029 54 60.55(8)0.3(3)0.18(9)60.038 46 70.50(7)1.0(10)0.08(4)30.015 98 80.60(9)0.5(5)0.04(2)50.029 90 90.40(5)0.7(7)0.02(1)40.021 53 100.30(3)0.2(2)0.06(3)100.067 15
注:X(n)中( )中数字表示所取X1、X2、X3优化范围0.2mm~0.65mm、0.1mm~1.0mm、0.02mm~0.2mm内的第n个数值。
该回归方程拟合优度R2=0.917,显著性水平P=0.0012<0.05。由式(10)中各参数的回归系数,可知回波幅值Y与X1、X2、X3均成负相关。比较回归系数绝对值,各因素对回波幅值影响从大到小依次为X2>X1>X3,即w>d>l,与正交试验结论一致。为得到Y的最大值,最优的参数值为X1=0.2mm,X2=0.1mm,X3=0.02mm,与正交试验得到的最优组合结果相同。因此均匀试验在低水平数与正交试验具有同样的优化精度。
电磁超声换能器在工作时与被测试件不发生接触,永磁体和试件上表面之间的距离影响感应涡流附近的静态偏置磁场强度,因此二者之间的提离距离h将会影响回波信号。
为研究Halbach阵列纵波换能器中提离距离对接收信号的影响,仿真中依次设置h为0.5mm~ 1.5mm,步长0.1mm,分析正交试验1(正交1)、正交试验5(正交5)、正交试验9(正交9)三种方案中,不同提离距离下第一次回波电压幅值。结果如图10所示。
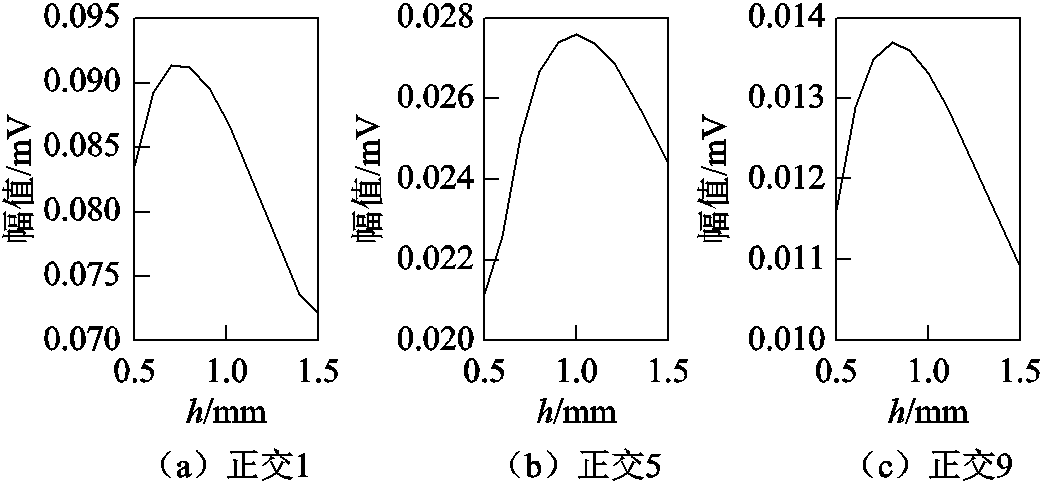
图10 提离距离对回波电压的影响
Fig.10 The effect on echo waves of lift-off distances
可以看出,与传统电磁超声换能器不同,本文所使用的Halbach阵列纵波换能器接收到的回波幅值与提离距离之间并非严格的负相关。提离距离h处于0.7mm~1.0mm之间,接收到的回波信号最强,h不在此范围时,回波信号幅值迅速衰减。造成这种差异的原因,是由于在Halbach阵列排布的永磁体中,磁通密度水平分量随着远离永磁体下表面呈现出“先增强后减弱”的趋势,因此线圈布置在合适位置上能够使换能器接收到的回波信号最强。
超声波在试件中传播时,由于存在声衰减现象,因此接收到的回波信号会随着传播声程的增大而减弱。材质的衰减系数α计算式为
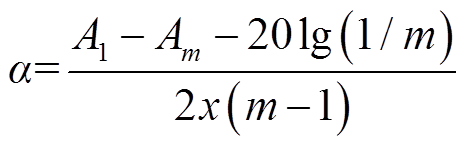 (11)
(11)式中,A1为第一次回波信号(dB);Am为第m次回波信号(dB);20lg(1/m)为修正项,是因声波的声束扩散所引起的分贝值差;x为试件厚度(mm)。本文中m设置为5,即研究第一次回波和第五次回波之间的声波衰减。
衰减系数α与激励电流频率有关。当线圈通入的电流频率较低时,声波在试件中衰减系数小,接收到的相邻回波电压幅值变化平缓,但此时幅值整体较低,导致有效回波个数较少;当电流频率较高时,虽然此时接收信号幅值较高,然而声波的衰减系数大,接收到的相邻回波电压幅值变化陡峭,因此有效回波个数同样较少。为研究激励电流频率与回波电压幅值和衰减系数二者之间的关系,并寻求回波幅值与衰减系数之间的平衡点,旨在实现回波信号在幅值大的前提下尽可能多地增加回波个数。仿真中以5.0mm厚铝板作为待测试件,设定电流频率f为1~12MHz,步长为1MHz,得到不同频率下衰减系数与第一次回波电压幅值变化趋势如图11所示。
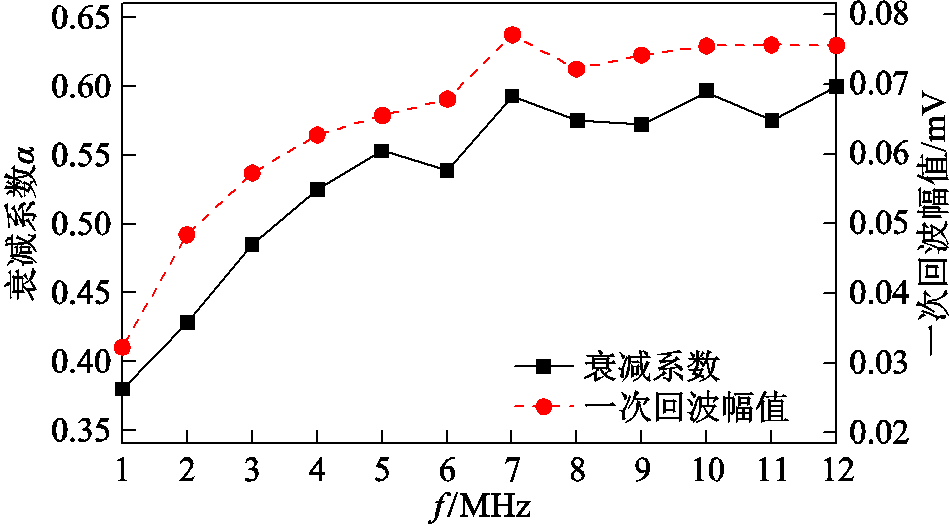
图11 衰减系数与回波电压变化趋势
Fig.11 The variation trend of attenuation coefficients and echo voltages
可以看到,衰减系数α和一次回波幅值随着激励频率增大而增大,二者的增长幅度逐渐趋于平缓。当激励频率较低时,虽然衰减系数较小,但此时的洛仑兹力不能完全激发试件趋肤层质点的振动,导致回波电压幅值太小,不便于对结果进行观测;当频率较高时,较大的衰减系数使得即便第一次回波幅值较大,后续回波幅值反而更小,线圈接收到的有效回波数减少。通过分析可知,过高和过低的激励频率都难以得到合适的回波,当激励频率为6MHz左右时,回波电压和衰减系数达到相对合适的平衡,最有利于检测。
本实验采用Ritec RAM—5000 SNAP测试系统作为实验平台,该系统能够在计算机控制下输出高频脉冲电流,激励电流经双工器、阻抗匹配器通入电磁超声换能器线圈中,涡流在垂直洛仑兹力的作用下,使得试件趋肤层质点产生高频振动,从而在试件表层激发出超声纵波。声波在试件中垂直向下传播,触及下表面后发生反射,换能器接收到电压信号,经过双工器传输至SNAP—5000系统,最后通过示波器进行回波信号的采集和观测。图12为实验系统示意图。
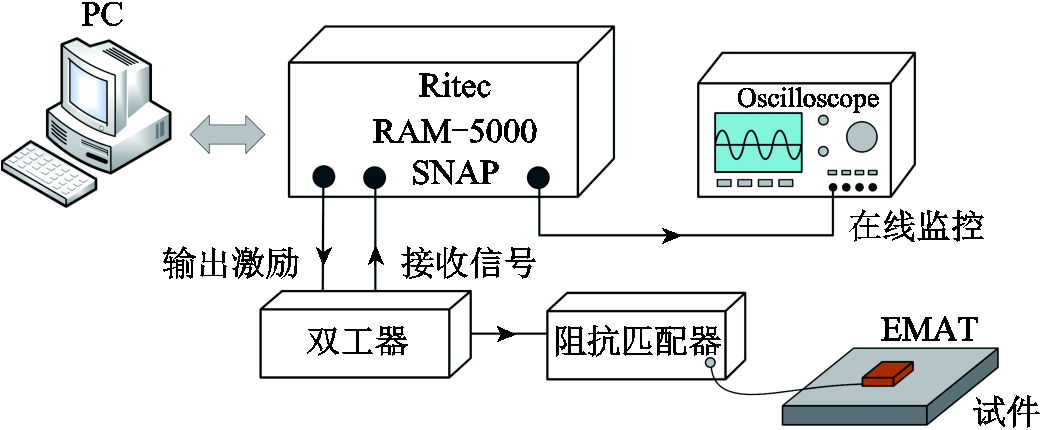
图12 实验系统示意图
Fig.12 Schematic diagram of experimental system
实验中所使用的电磁超声换能器采用25个棱长为5mm的正方体N35型钕铁硼永磁体,按照Halbach阵列进行排布。以正交试验4中各项数据作为优化前线圈参数,以正交试验和均匀试验最优组合作为优化后线圈参数进行对比试验,见表4,其余设置保持一致。对线圈按照“回”形进行绕制,并置于永磁体水平磁场最强处,以激发出纵波。Halbach换能器实物如图13所示。
考虑线圈和永磁体之间的粘合需要,以及其他材料因素的影响,实验中永磁体距离试件上表面之间的提离距离约为1 mm。
表4 优化前后线圈参数
Tab.4 The coil parameters before and after the optimization

d/mmw/mml/mm匝数 优化前0.450.10.119 优化后0.20.10.0217

图13 换能器实物图
Fig.13 Pictures of the EMAT
本实验换能器采用收发一体工作模式,利用厚度为30 mm的铝板进行测试验证。设置脉冲周期为6个,前置放大器增益70dB,激励输出电压70V,电流频率设置为6MHz。图14为分别使用优化前、后换能器得到的实测回波。

图14 换能器优化前后接收信号
Fig.14 The signals received before and after the transducer optimization
已知纵波在铝板中传播速度约为6 300m/s,根据铝板厚度计算换能器接收到相邻两次电压信号时间间隔约为9.5μs,与图14a中时差一致,证明本文所设计的Halbach阵列换能器能够成功激发出纵波。由于第一次回波信号被主脉冲所淹没,第二、三次回波信号受到主脉冲的影响并未完全稳定,故考察图中第四次回波的优化效果。由图14b得到,优化前、后换能器接收到的回波电压幅值分别为19.1mV和34.9mV,优化后幅值提高了83%,证明了优化方案的可靠性。而在仿真中,优化后的回波幅值相较于正交试验四提高了61%,二者结果出现差异。一方面是因为优化前导线高度大于优化后导线高度,在使用相同的手段将线圈与永磁体粘合在一起时,无法确保两种换能器永磁体的提离距离h保持一致,使用优化前线圈制作的换能器中永磁体的h要大于优化后的换能器,因此优化前得到的回波信号幅值要弱于理论值,故优化前后实验得到的回波信号幅值差距扩大,继而造成实验中优化后的幅值增幅大于仿真分析。另一方面,声波在试件中的衰减与激励频率、材料属性等有关,由于优化前后两次实验均保持上述参数一致,因此两种回波信号呈相同趋势的指数衰减。由于仿真和实验分别以第一次回波和第四次回波作为考察指标,当优化前后回波信号按照同样趋势呈指数衰减时,随着时间的推移,同一时刻对应的优化后、优化前幅值比值逐渐扩大,因此第四次回波中优化后幅值增幅要大于第一次回波。
本文使用一种Halbach阵列型电磁超声纵波换能器并对其进行有限元仿真分析,对线圈参数、提离距离和激励电流频率进行了优化,以增强回波信号,最后通过实验对优化方案进行了验证。结果表明:
1)Halbach阵列型永磁体排布能够显著增强水平方向磁场,增大垂直方向洛仑兹力,激发出更剧烈的纵波。
2)通过正交试验和均匀试验得到,当减小线间距、导线宽度、导线高度时,能够使得回波幅值得到提升。仿真中优化后回波幅值比优化前两种最佳方案分别提升了113%和61%,实验中优化后回波幅值比优化前提升了83%。
3)Halbach阵列纵波换能器在工作时,永磁体与被测试件上表面之间的提离距离对接收到的信号幅值影响较大,当提离距离处于0.7~1.0mm范围时,信号强度最高。
4)超声波在试件内部传播的衰减与激励电流频率有关,过高的电流频率造成较大的声波衰减,过低的电流频率产生较小的回波幅值,选取6MHz左右的激励频率可以使得回波电压幅值和有效回波数量维持在较为理想的水平,有利于进行后续检测与数据处理。
参考文献
[1] Yusa N, Song H C, Iwata D, et al. Probabilistic analysis of electromagnetic acoustic resonance signals for the detection of pipe wall thinning[J]. Nondestructive Testing and Evaluation, 2019(3): 1-16.
[2] Li Weibin, Jiang Chang, Deng Mimgxi. Thermal damage assessment of metallic plates using a nonlinear electromagnetic acoustic resonance technique[J]. NDT&E International, 2019, 108: 102172.
[3] 刘素贞, 王淑娟, 张闯, 等. 钢板电磁超声表面波的仿真分析及缺陷定量检测[J]. 电工技术学报, 2020, 35(1): 97-105.
Liu Suzhen, Wang Shujuan, Zhang Chuang, et al. Simulation analysis of electromagnetic acoustic surface wave of steel plate and quantitative defect detection[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 97-105.
[4] 张闯, 曹晓琳, 刘素贞, 等. 基于累积效应的铝材塑性损伤电磁超声非线性检测[J]. 电工技术学报, 2019, 34(19): 3961-3967.
Zhang Chuang, Cao Xiaolin, Liu Suzhen, et al. Electromagnetic ultrasonic nonlinear detection of aluminum with plastic damage based on cumulative effect[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3961-3967.
[5] Lee J K, KIM Y Y. Tuned double-coil EMATs for omnidirectional symmetric mode lamb wave generation[J]. NDT & E International, 2016, 83: 38-47.
[6] 张闯, 魏琦, 刘素贞, 等. 小尺寸试件检测用单向单模态电磁超声换能器设计[J]. 电工技术学报, 2019, 34(17): 3563-3571.
Zhang Chuang, Wei Qi, Liu Suzhen, et al. Design of unidirectional single-mode electromagnetic acoustic transducer for small size specimen detection[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3563-3571.
[7] Petcher P, Potter M, Dixon S. A new electromagnetic acoustic transducer (EMAT) design for operation on rail[J]. NDT & E International, 2014, 65(3): 1-7.
[8] Kim Y Y, Kwon Y E. Review of magnetostrictive patch transducers and applications in ultrasonic nondestructive testing of waveguides[J]. Ultrasonics, 2015, 62: 3-19.
[9] 翟国富, 梁宝, 贾文斌, 等. 横波电磁超声相控阵换能器设计[J]. 电工技术学报, 2019, 34(7): 1441-1448.
Zhai Guofu, Liang Bao, Jia Wenbin, et al. Design of the shear wave electromagnetic ultrasonic phased array transducer[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1441-1448.
[10] Pei Cuixiang, Liu Tianhao, Chen Hongen, et al. Inspection of delamination defect in first wall with a flexible EMAT-scanning system[J]. Fusion Engineering and Design, 2018, 136: 549-553.
[11] Ren Weiping, He Jianpeng, Dixon S, et al. Enhancement of EMAT’s efficiency by using silicon steel laminations back-plate[J]. Sensors and Actuators A: Physical, 2018, 274: 189-198.
[12] 蔡智超, 陈澜, 赵振勇, 等. 电磁声谐振对Q235钢压缩形变评价研究[J]. 仪器仪表学报, 2019, 40(5): 153-160.
Cai Zhichao, Chen Lan, Zhao Zhenyong, et al. Electromagnetic acoustic resonance for plastic deformation in Q235 Steel[J]. Chinese Journal of Scientific Instrument, 2019, 40(5): 153-160.
[13] Kang Lei, Dixon S, Wang Kaican, et al. Enhancement of signal amplitude of surface wave EMATs based on 3-D simulation analysis and orthogonal test method[J]. NDT&E International, 2013, 59: 11-17.
[14] 江念, 王召巴, 陈友兴, 等. 电磁超声检测钢板厚度实验的参数优化[J]. 传感技术学报, 2015, 28(4): 498-502.
Jiang Nian, Wang Zhaoba, Chen Youxing, et al.The experiment parameters of the steel-sheet thickness measurement by electromagnetic ultrasonic[J]. Chinese Journal of Sensors and Actuators, 2015, 28(4): 498-502.
[15] 阳能军, 封礼发, 唐旭明, 等. 电磁超声横波换能器中线圈的优化设计[J]. 应用声学, 2019, 38(3): 428-433.
Yang Nengjun, Feng Lifa, Tang Xuming, et al. Optimum design of coil in electromagnetic acoustic shear wave transducers[J]. Journal of Applied Acoustics, 2019, 38(3): 428-433.
[16] Sun Hongjun, Urayama R, Uchimoto T, et al. Small electromagnetic acoustic transducer with an enhanced unique magnet configuration[J]. NDT&E International, 2020, 110: 102205.
[17] 杨理践, 陈俊哲, 邢燕好. 基于电磁超声纵波的铝板厚度检测[J]. 仪表技术与传感器, 2015, 11: 67-70.
Yang Lijian, Chen Junzhe, Xing Yanhao. Thickness detection of aluminum plate based on electromagnetic ultrasonic longitudinal waves[J]. Instrument Technique and Sensor, 2015, 11: 67-70.
[18] Sun Hongyu, Huang Songling, Wang Qing, et al. Orthogonal optimal design method for point-focusing emat considering focal area dimensions[J]. Sensors and Actuators A: Physical, 2020, 312: 112109.
[19] Sun Hongyu, Wang Shen, Huang Songling, et al. Point-focusing shear-horizontal guided wave EMAT optimization method using orthogonal test theory[J]. IEEE Sensors Journal, 2020, 20(12): 6295-6304.
[20] Jia Xiaojuan, Ouyang Qi. Optimal design of point-focusing shear vertical wave electromagnetic ultrasonic transducers based on orthogonal test method[J]. IEEE Sensors Journal, 2018, 18(19): 8064-8073.
[21] Liu Zenghua, Li Aili, Zhang Yongchen, et al. Development of a directional magnetic-concentrator-type electromagnetic acoustic transducer for ultrasonic guided wave inspection[J]. Sensors and Actuators A: Physical, 2020, 303: 111859.
[22] 周赣, 黄学良, 周勤博, 等. Halbach型永磁阵列的应用综述[J]. 微特电机, 2008, 36(8): 52-55.
Zhou Gan, Huang Xueliang, Zhou Qinbo, et al. The applications of the halbach permanent magnet array: a review[J]. Small & Special Electrical Machines, 2008, 36(8): 52-55.
[23] 王淑娟, 李智超, 李鹏展, 等. 非铁磁材料表面波电磁超声换能器接收性能分析与优化设计[J]. 中国电机工程学报, 2015, 35(9): 2360-2365.
Wang Shujuan, Li Zhichao, Li Pengzhan, et al. Receiving performance analysis and optimal design of surface wave electromagnetic acoustic transducers in nonferromagnetic materials[J]. Proceedings of the CSEE, 2015, 35(9): 2360-2365.
[24] 方开泰. 均匀设计-数论方法在试验设计的应用[J]. 应用数学学报, 1980, 3(4): 363-372.
Fang Kaitai. Uniform design-application of number theory to experimental design[J]. Acta Mathematicae Applicatae Sinica, 1980, 3(4): 363-372.
Optimum Design of Electromagnetic Acoustic Longitudinal Wave Transducer Based on Halbach Array
Abstract The traditional electromagnetic acoustic longitudinal wave transducers possess low energy conversion efficiency as well as weak horizontal bias magnetic field which cannot be fully utilized, resulting in a modest echo signal and affecting the accuracy of the detection. In this paper, a new type of longitudinal wave transducer is applied, whose permanent magnet poles are arranged according to the Halbach array, which can significantly intensify the horizontal magnetic field. Aiming to improve the echo signal, the finite element software was used, and the orthogonal test and uniform test methods were operated respectively. The parameters of the transducer were optimized with considering the number of coil turns. The simulation results illustrate that reducing the spacing, width, and height of the wire can enhance the echo signal, maintaining the lift-off distance of the permanent magnet within a proper range can also be so. Make the sound attenuation and voltage amplitude at a appropriate level is conducive to detection by setting a proper excitation frequency. The experimental results demonstrate that the echo amplitude of the optimized transducer is 83 % higher than that of the previous transducer.
Keywords:Electromagnetic acoustic transducers (EMATs), longitudinal wave, Halbach array, optimum design, orthogonal test, uniform test
DOI:10.19595/j.cnki.1000-6753.tces.201541
中图分类号:TB552
国家自然科学基金青年科学基金(51807065)、江西省研究生创新专项资金(YC2020-S304)资助项目。
收稿日期 2020-11-18
改稿日期 2020-12-24
蔡智超 男,1989年生,博士,副教授,硕士生导师,研究方向为电磁无损检测技术。E-mail:zccai@foxmail.com(通信作者)
李毅博 男,1996年生,硕士研究生,研究方向为电磁无损检测技术。E-mail:liyibonix@163.com
(编辑 郭丽军)