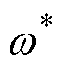 由外围自适应算法确定,决定了滤波器的中心频率,比例系数
由外围自适应算法确定,决定了滤波器的中心频率,比例系数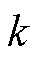 决定了滤波器的带宽,
决定了滤波器的带宽,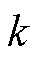 值越小,带宽越小,灵敏度越高,需要根据实际情况折中选取。
值越小,带宽越小,灵敏度越高,需要根据实际情况折中选取。摘要 基于二阶广义积分器(SOGI)的自适应滤波器(AF)在电网电量测量、电机位置、速度检测与估计等场合广泛应用。在数字化实现过程中,反馈滞后一拍的存在和所采用离散方法的不同会使系统的性能出现不同程度的退化。该文在综合考虑上述因素的前提下,用稳定性、频率偏移特性、幅值增益特性及正交特性作为衡量系统性能退化的定量指标,分别进行了理论对比分析,并给出了上述4个指标随载波比的变化规律,从而为自适应滤波器数字实现时的离散方法的选取提供理论指导依据。最后通过仿真和实验验证了理论对比分析的正确性。
关键词:自适应滤波器 二阶广义积分器 滞后一拍 频率偏移 幅值增益 正交性
基于二阶广义积分器(Second Order Generalized Integrator, SOGI)的自适应滤波器(Adaptive Filter, AF),广泛应用于电网电量测量[1-5]、电机位置、速度检测与估计[6-12]等场合。目前,使用锁频环(Frequency- Locked Loop, FLL)来实现频率自适应算法是一种较为普遍的方法[1-9, 11-12]。
在电网同步领域,基于SOGI的自适应滤波器主要用来提取电网电压中的正负序分量[1-3]。此时的信号-采样频率比较小,滞后一拍所造成的影响可以忽略不计,因此,绝大多数文献为了分析简便,通常在s域内忽略滞后一拍的影响。
在电机控制领域,基于SOGI的自适应滤波器主要用于电机位置、速度检测与估计等场合。文献[7-8]分别将基于SOGI的频率自适应滤波器应用到基于电动势的位置观测器和模糊滑模观测器来消除谐波误差。文献[9]提出一种复合SOGI-FLL用于永磁同步电机的转子位置与转速估计。文献[10]将两个SOGI的组合结构用于转子位置检测。文献[11-12]将基于SOGI的频率自适应滤波器用于异步电动机的转子磁链观测算法中。
上述文献均在s域提出新算法或新结构,然而工程实现时通常采用全数字方式来实现,即将算法从s域转换到z域,转换过程会使所研究系统产生性能的退化[13-21],特别是对于信号-采样频率比,即载波比比较大的应用场合,性能退化的影响难以忽略,因此有必要分析数字化实现对系统性能的影响。
文献[13]详细研究了SOGI的不同离散方法,提出了一种可以将SOGI应用于不同场合的通用数字结构。文献[14]讨论了谐振控制器和滤波器在定点算法实现时的一些重要问题。文献[15]针对基于双积分器的谐振控制器数字实现时的性能退化问题,对数字实现算法进行了改进。文献[16]提出了一种结构高鲁棒性的定点数字谐振控制器。文献[17]对比分析了不同离散方法对谐振控制器性能的影响,指出了离散会带来频率偏移的问题。文献[18]采用不同方法对基于SOGI的自适应滤波器进行离散化,对比分析了性能差异,由于是针对电网的应用场合,该文献只对低频50Hz进行了对比分析。
虽然上述文献详细分析了不同离散方法对数字系统性能的影响,但都未反馈滞后一拍现象,此问题是造成数字系统性能退化的主要原因[19-21],而基于SOGI的自适应滤波器为双闭环结构,因此对其进行分析时需要考虑滞后一拍的影响。
本文在考虑滞后一拍的前提下,对采用不同离散方法的数字自适应滤波器的稳定性、频率偏移特性、幅值增益及正交性等进行对比分析,并对理论对比分析结果进行仿真与实验验证。
基于SOGI的自适应滤波器s域模型如图1所示。设定频率参数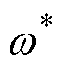 由外围自适应算法确定,决定了滤波器的中心频率,比例系数
由外围自适应算法确定,决定了滤波器的中心频率,比例系数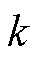 决定了滤波器的带宽,
决定了滤波器的带宽,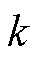 值越小,带宽越小,灵敏度越高,需要根据实际情况折中选取。
值越小,带宽越小,灵敏度越高,需要根据实际情况折中选取。

图1 自适应滤波器s域模型
Fig.1 Model of adaptive filter in s-domain
将图1的s域模型进行离散化,本文选择对各部分单独进行离散,选择的离散方法包括前向欧拉(F)、后向欧拉(B)、双线性变换法(T)、脉冲响应不变法(im)、零阶保持器法(zo)及一阶保持器法(fo)。每个积分器都可用一阶z域传递函数表示为
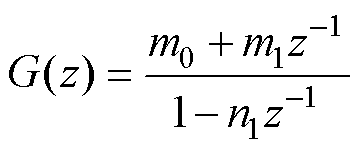 (1)
(1)式中,m0、m1、n1为系数,见表1。表中,Ts为采样周期。经分析可知,单独对积分器进行离散时,双线性变换法(T)与一阶保持器法(fo)相同,前向差分法(F)与零阶保持器法(zo)相同,后向差分法(B)与脉冲响应不变法(im)相同。
表1 离散积分器的系数
Tab.1 Coefficients of discrete-time integrators

离散方法系数 B、imTs01 F、zo0Ts1 T、foTs/2Ts/21
利用式(1)对图1所示系统进行离散化,得到数字自适应滤波器的不考虑滞后一拍的z域理想模型如图2所示。
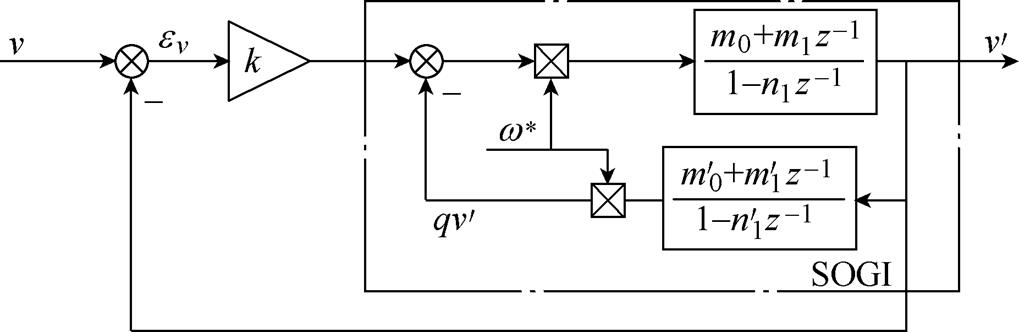
图2 自适应滤波器z域理想模型
Fig.2 The ideal model of adaptive filter in z-domain
但采用全数字方式进行物理实现时,nTs时刻的输入v(n)只能与上一时刻(n-1)Ts的反馈值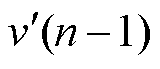 相减,得到nTs时刻的误差值
相减,得到nTs时刻的误差值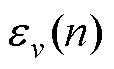 ,此误差乘以系数k后送入SOGI进行运算,在SOGI中,
,此误差乘以系数k后送入SOGI进行运算,在SOGI中,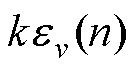 同样只能与上一时刻(n-1)Ts的反馈值
同样只能与上一时刻(n-1)Ts的反馈值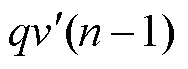 相减,然后经过一个积分器后得到nTs时刻的更新值
相减,然后经过一个积分器后得到nTs时刻的更新值 ,此值作为下一次计算的反馈值。这就造成z域实际模型如图3所示。数字系统反馈回路中存在滞后一拍,会造成数字系统的性能退化。
,此值作为下一次计算的反馈值。这就造成z域实际模型如图3所示。数字系统反馈回路中存在滞后一拍,会造成数字系统的性能退化。
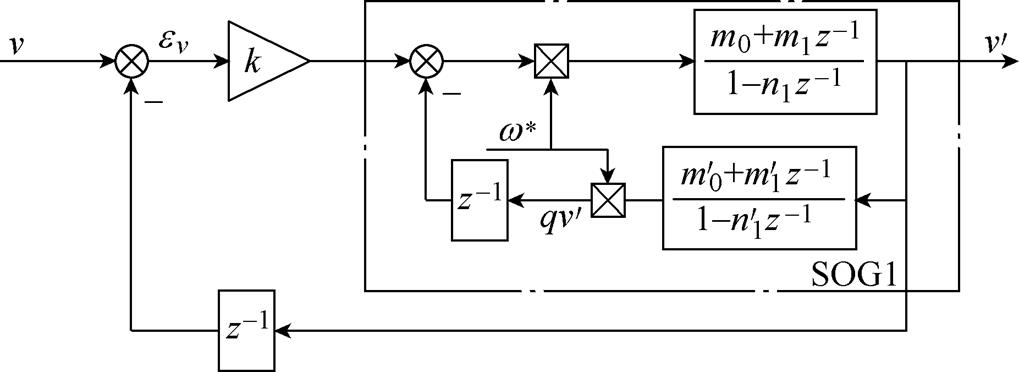
图3 自适应滤波器z域实际模型
Fig.3 The real model of adaptive filter in z-domain
图1所示理想模型的s域传递函数为
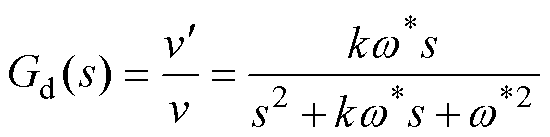 (2)
(2)式中,w*为设定频率参数。
依据稳定性判据,式(2)所示系统恒稳定。而由于滞后一拍现象的存在,系统的稳定性下降,且两个积分器的离散方法不同时,系统的稳定域各不相同。表2给出了采用不同离散方法的实际数字系统的z域传递函数以及对应的稳定域表达式。表2中,r=f */fs=Tsw*/(2p),表示系统设定信号频率f *与采样频率fs之比,即载波比。
表2中传递函数等式左边符号的下标表示两个积分器采用的离散方法。例如,T(fo)B(im)表示系统前向通路上的积分器采用双线性变换法(T)或一阶保持器法(fo)离散,反馈通路上的积分器采用后向差分法(B)或脉冲响应不变法(im)离散。本文后续内容均采用该种方式表示。
图4给出了表2中的稳定域表达式所对应的稳定区间,曲线与纵坐标所包围区域为实际数字系统稳定区域。可见,不同的离散方法对稳定域有着不同的影响。其中,采用B(im)F(zo)与F(zo)F(zo)离散的数字系统稳定域相同,B(im)T(fo)与F(zo)T(fo)相同,B(im)B(im)与F(zo)B(im)相同。结合实际情况,数字系统一般运行在载波比r<0.1的环境,k的取值范围在0~2之间,k取过大时,系统的滤波效果削弱,选频特性明显变差。从图4中可知,采用B(im)B(im)、F(zo)B(im)离散的数字系统,在0< r<0.1、0<k<2区间内恒稳定。因此,若仅从数字系统的稳定性角度考虑,B(im)B(im)、F(zo)B(im)离散结构具有优越性。当滤波器前向通道积分器采用T(fo)离散时,在稳定性约束下的载波比明显变小。而采用B(im)进行离散时,在稳定性约束下的载波比明显变大。
表2 实际数字自适应滤波器的传递函数与稳定域表达式
Tab.2 Transfer function and stability of the real digital adaptive filter

传递函数稳定域表达式
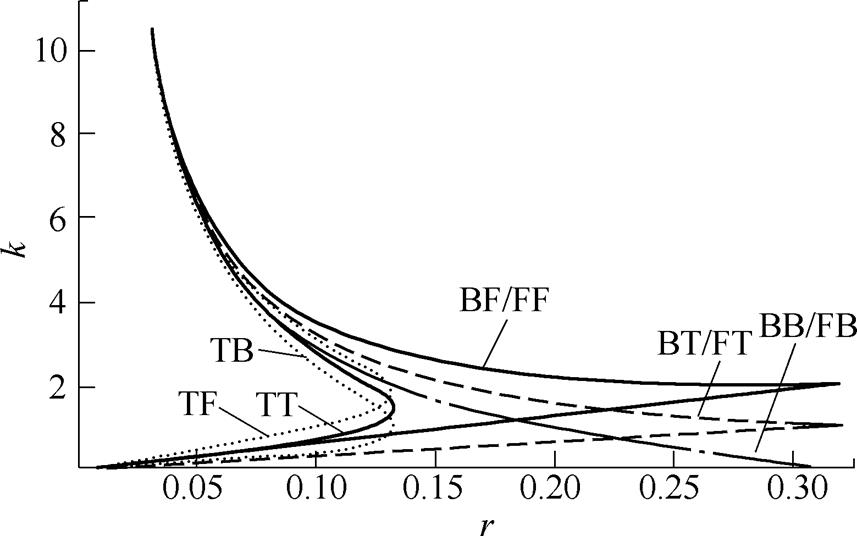
图4 自适应滤波器的稳定区间
Fig.4 Stability region of digital adaptive filter
理想自适应滤波器的选通信号频率为设定频率参数w*,但实际数字自适应滤波器的选通信号频率会相较于w*发生偏移。对系统中的积分器采用不同的离散方法时,实际数字系统的频率偏移大小不相同。现对数字系统不同离散结构下的频率偏移进行理论分析。
基于畸变预修正双线性变换的等效公式为
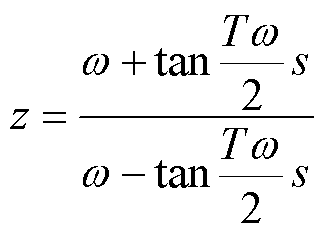 (3)
(3)将式(3)代入表2中实际数字系统的z域传递函数,可得实际数字系统的s域等效传递函数为
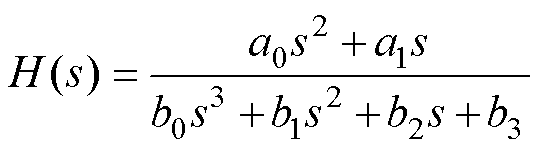 (4)
(4)
式中,a0、a1、b0~b3为系数,见表3。
知s=jw,设定存在滞后一拍的数字系统对应于w*的数字系统的实际选通信号频率为w0。当w = w0时,为H(s)相频特性曲线过0点,可得
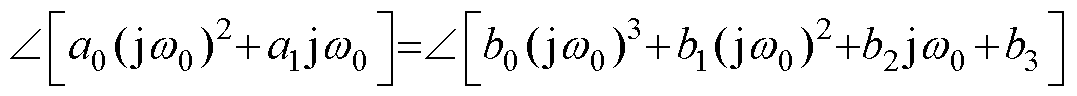 (5)
(5)整理后可得w0与w*的关系等式见表4。表中的列fq为反馈通道积分器的离散方法;表中的行qx为前向通道积分器的离散方法,为了简化表达式,定义变量a=tan(Tsw0/2)=tan(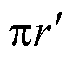 ),
),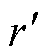 =f0/fs=Tsw0/(2p)。因此表中的关于a 与r的表达式即可表示w0与w*的关系。记数字系统的相对频率偏移量为e,则
=f0/fs=Tsw0/(2p)。因此表中的关于a 与r的表达式即可表示w0与w*的关系。记数字系统的相对频率偏移量为e,则
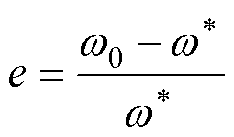 (6)
(6)
根据表4及式(6)可得图5所示的采用不同离散方法的数字系统的相对频率偏移量e与比例系数k和载波比r的关系曲线。不同离散方法的数字系统的频率偏移规律差别明显,采用F(zo)F(zo)、F(zo)B(im)、F(zo)T(fo)离散的数字系统频率偏移相同,相对偏移量e为所有离散方法中最小;B(im)B(im)离散结构频率偏移最大。因此,若仅从数字系统的选频特性考虑,采用F(zo)F(zo)、F(zo)B(im)、F(zo)T(fo)离散方法所得到的滤波器系统具有最好的选频性能。
表3 实际数字的s域等效传递函数系数
Tab.3 The coefficients of equivalent transfer function in s-domain

离散方法系 数 a0a1b0b1b2b3 T(fo)T(fo) T(fo)B(im) B(im)B(im)0 B(im)T(fo)0 F(zo)B(im)0 F(zo)T(fo)0 F(zo)F(zo)0 B(im)F(zo)0 T(fo)F(zo)
表4 数字系统不同离散结构的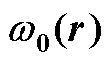 与
与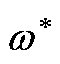 的关系等式
的关系等式
Tab.4 The relationship between w0(r) and w* in AF with different discrete methods

fqqx T(fo)B(im)F(zo) T(fo) B(im) F(zo)
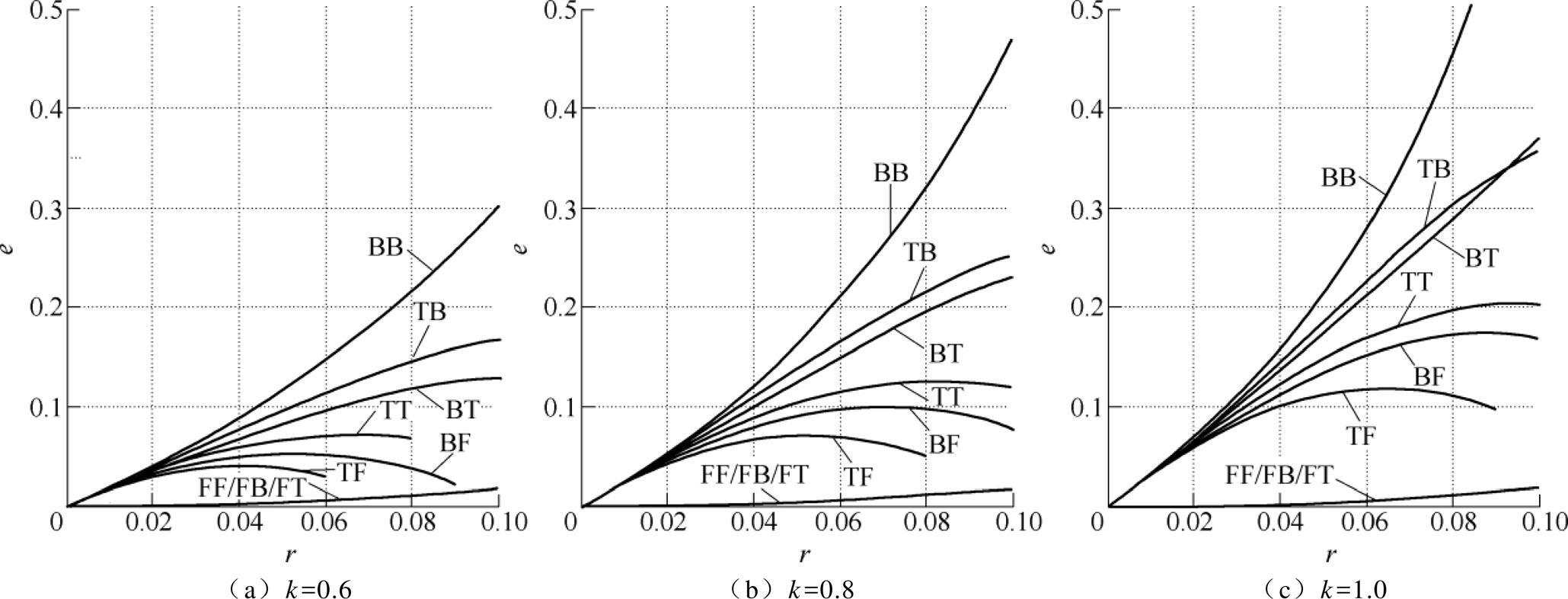
图5 相对频率偏移量e的理论数据
Fig.5 The theoretical results of relative frequency offset e
该小节在2.2节的基础上,分析数字系统不同离散结构的幅值增益现象。知s=jw,系统对应于w*的实际选通信号频率为w0。当w =w0时,为H1(s)相频特性曲线过0点,将s=jw0代入表(2)中实际数字系统的s域等效传递函数,可得通用等式为
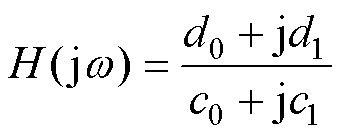 (7)
(7)式中,c0、c1、d0、d1为系数,见表5。
数字滤波器系统的幅值增益d 为
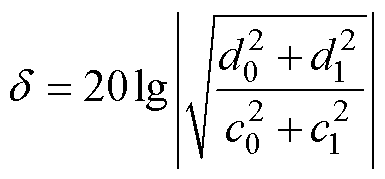 (8)
(8)由表3结合式(4)、式(7)和式(8)可得,采用不同离散方法的数字自适应滤波器的幅值增益d随着载波比r的变化曲线,如图6所示,载波比r取值范围小于0.1、k取0.6、0.8、1.0。采用不同离散方法的数字系统的幅值增益差别明显,随着载波比r的增大,B(im)B(im)、F(zo)B(im)两种离散方法的幅值增益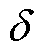 恒定为0dB,其余离散方法的幅值增益
恒定为0dB,其余离散方法的幅值增益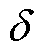 均为增大的趋势,其中,T(fo)F(zo)离散方法造成的幅值增益增加最大。因此,若仅从数字系统的幅值增益特性考虑,B(im)B(im)、F(zo)B(im)离散方法的滤波器幅值增益恒为0dB,性能最佳。
均为增大的趋势,其中,T(fo)F(zo)离散方法造成的幅值增益增加最大。因此,若仅从数字系统的幅值增益特性考虑,B(im)B(im)、F(zo)B(im)离散方法的滤波器幅值增益恒为0dB,性能最佳。
由图1可知,输出信号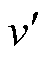 经过反馈通路的积分器后再乘以
经过反馈通路的积分器后再乘以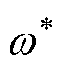 便得到输出信号
便得到输出信号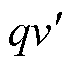 ,因此两个输出信号之间的传递函数为
,因此两个输出信号之间的传递函数为
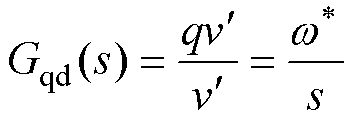 (9)
(9)s域理想情况下,当信号频率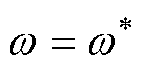 时,
时,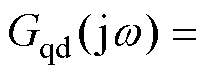
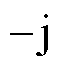 ,两个输出信号之间严格正交。
,两个输出信号之间严格正交。
实际数字系统中两输出信号之间的z域传递函数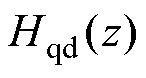 与s域等效传递函数
与s域等效传递函数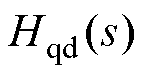 见表6。
见表6。
表5 数字AF不同离散结构的等效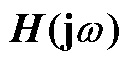 系数
系数
Tab.5 The coefficients of equivalent H(jw) of digital AF wih different discrete methods
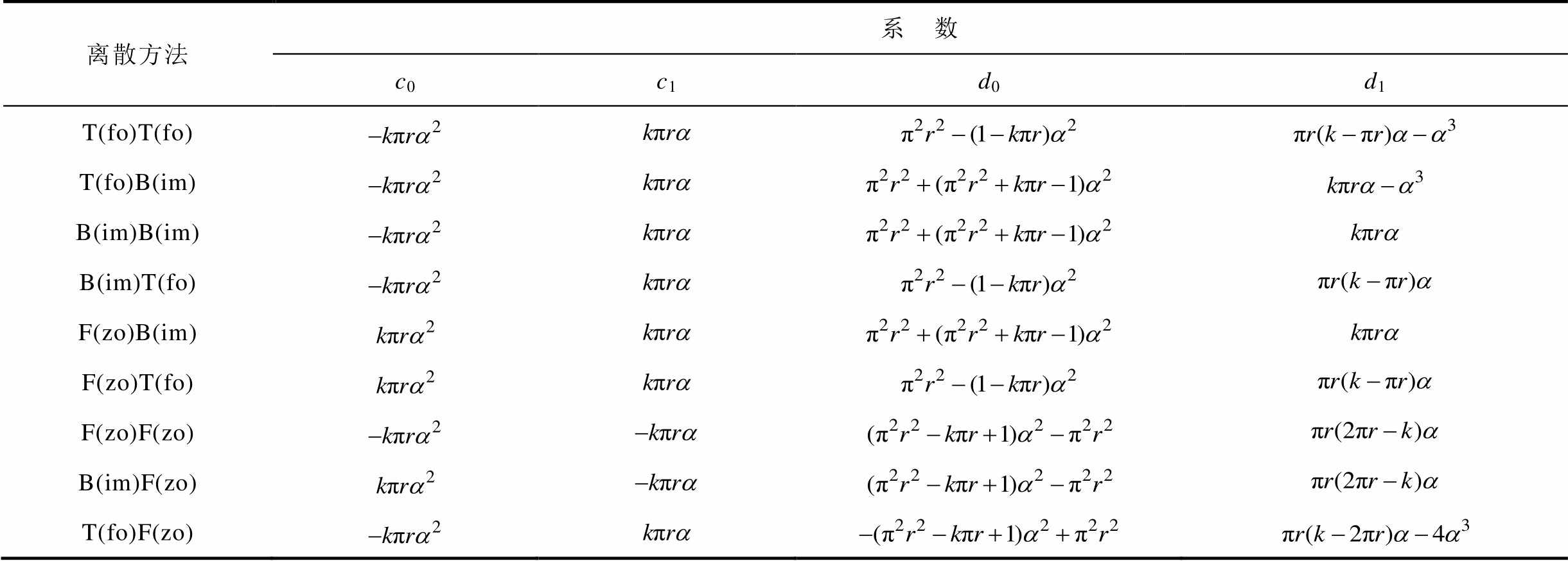
离散方法系 数 c0c1d0d1 T(fo)T(fo) T(fo)B(im) B(im)B(im) B(im)T(fo) F(zo)B(im) F(zo)T(fo) F(zo)F(zo) B(im)F(zo) T(fo)F(zo)
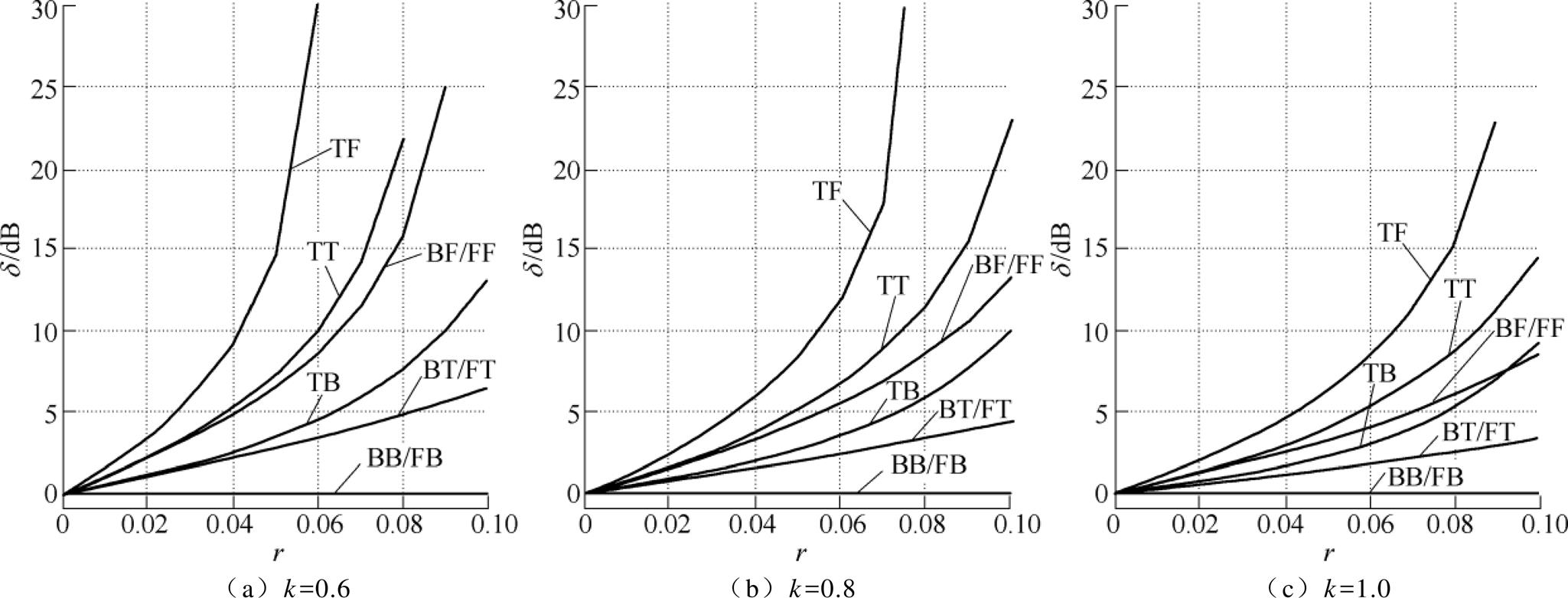
图6 幅值增益d 的理论数据
Fig.6 The theoretical results of amplitude gain d
表6 数字系统的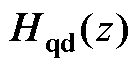 和等效
和等效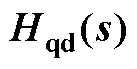
Tab.6 Hqd(z) and equivalent Hqd(s) of digital system

离散方法 B(im)T(fo)/F(zo)T(fo)/T(fo)T(fo) B(im)F(zo)/F(zo)F(zo)/T(fo)F(zo) B(im)B(im)/F(zo)B(im)/T(fo)B(im)
由2.2节分析可知,实际数字系统存在频率偏移,设定频率参数w*对应的实际选通信号频率为w0,当w=w0时,表6中的Hqd(s)可变换为
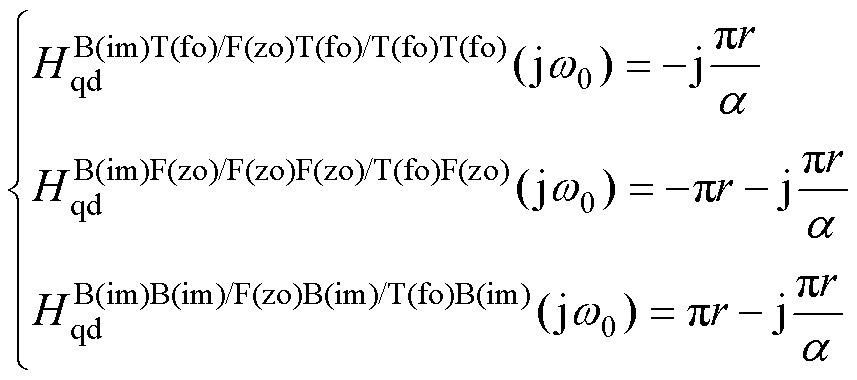 (10)
(10) 反馈通路的积分器采用不同离散方法时,可根据式(10)得到正交特性曲线,如图7所示。
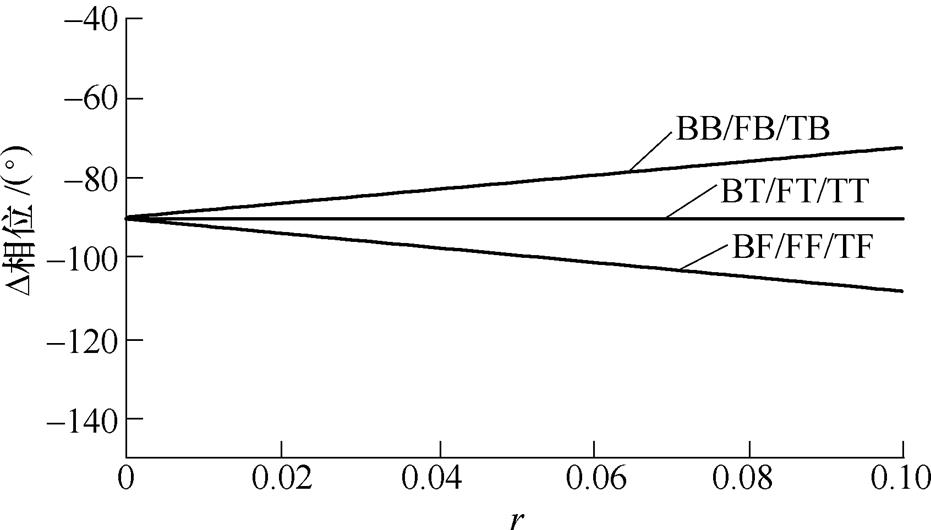
图7 AF正交特性的理论数据
Fig.7 Theoretical results of AF orthogonal characteristics
可见,前向通道积分器的离散方法并不会影响信号正交性,反馈通道积分器的离散方法影响信号的正交性,当反馈通路积分器采用T(fo)离散时,数字系统两个输出信号之间相位差恒为90°,即两者严格保持正交;当反馈通路积分器采用B(im)和F(zo)离散时,随着载波比r的增加,数字系统的正交性逐渐变差。因此,仅从数字系统的正交特性方面考虑,反馈通路积分器采用T(fo)方法离散的数字结构(B(im)T(fo)、F(zo)T(fo)、T(fo)T(fo))具有优越性。
仿真参数设定如下:采样周期Ts=10-4s;比例系数k选取为0.6、0.8、1.0;设定频率参数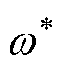 的取值范围为0~2 000prad/s,间隔200prad/s。
的取值范围为0~2 000prad/s,间隔200prad/s。
仿真过程中考虑滞后一拍,对数字自适应滤波器模型的不同离散结构进行仿真,根据数字系统的伯德图数据可以得到实际数字系统中对应着不同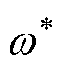 时的相对频率偏移量
时的相对频率偏移量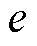 以及相频特性曲线过0点对应的幅值增益
以及相频特性曲线过0点对应的幅值增益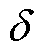 ,由于r=fs/fT=Tw*/(2p),对数据进行整理可以得到
,由于r=fs/fT=Tw*/(2p),对数据进行整理可以得到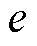 和
和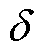 关于载波比r的变化曲线。
关于载波比r的变化曲线。
图8给出了数字系统不同离散结构的相对频率偏移量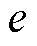 的仿真数据。由图8对比图5可知,两图一致。不同离散结构的数字系统频率偏移规律差别明显,采用F(zo)F(zo)、F(zo)B(im)、F(zo)T(fo)离散的数字系统频率偏移相同;B(im)B(im)离散结构频率偏移最大,F(zo)F(zo)、F(zo)B(im)、F(zo)T(fo)离散结构频率偏移最小。验证了数字系统频率偏移规律理论分析的正确性。
的仿真数据。由图8对比图5可知,两图一致。不同离散结构的数字系统频率偏移规律差别明显,采用F(zo)F(zo)、F(zo)B(im)、F(zo)T(fo)离散的数字系统频率偏移相同;B(im)B(im)离散结构频率偏移最大,F(zo)F(zo)、F(zo)B(im)、F(zo)T(fo)离散结构频率偏移最小。验证了数字系统频率偏移规律理论分析的正确性。
图9给出了采用不同离散方法时,系统相频特性曲线过零点处对应的幅值增益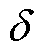 的仿真数据。可见图9与图6一致。随着载波比r的增大,除了B(im)B(im)、F(zo)B(im)两种离散结构幅值增益
的仿真数据。可见图9与图6一致。随着载波比r的增大,除了B(im)B(im)、F(zo)B(im)两种离散结构幅值增益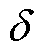 恒定为0dB,其余离散结构的幅值增益
恒定为0dB,其余离散结构的幅值增益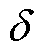 均为增大的趋势,其中,T(fo)F(zo)离散结构幅值增益随着r的增加,增大最快。验证了数字系统幅值增益规律理论分析的正确性。
均为增大的趋势,其中,T(fo)F(zo)离散结构幅值增益随着r的增加,增大最快。验证了数字系统幅值增益规律理论分析的正确性。
图10给出了不同设定参数下,Hqd(z)的相频特性仿真曲线,从图10可知,Hqd(z)的相频特性仿真曲线不受设定频率参数w*的影响,只与数字系统反馈通路积分器的离散方法有关。仿真采样周期Ts= 10-4s,频率为1 000Hz时,对应着载波比r =0.1。对比图10与图7可知,两者一致。数字系统反馈通路积分器采用T离散时,数字系统两个输出信号之间相位恒差90°,严格保持正交;数字系统反馈通路积分器采用B(im)和F(zo)离散时,随着载波比的增加,正交性逐渐变差。验证了数字滤波器两个输出信号之间正交特性理论分析的正确性。

图8 相对频率偏移量e的仿真数据
Fig.8 Simulation results of relative frequency offset e
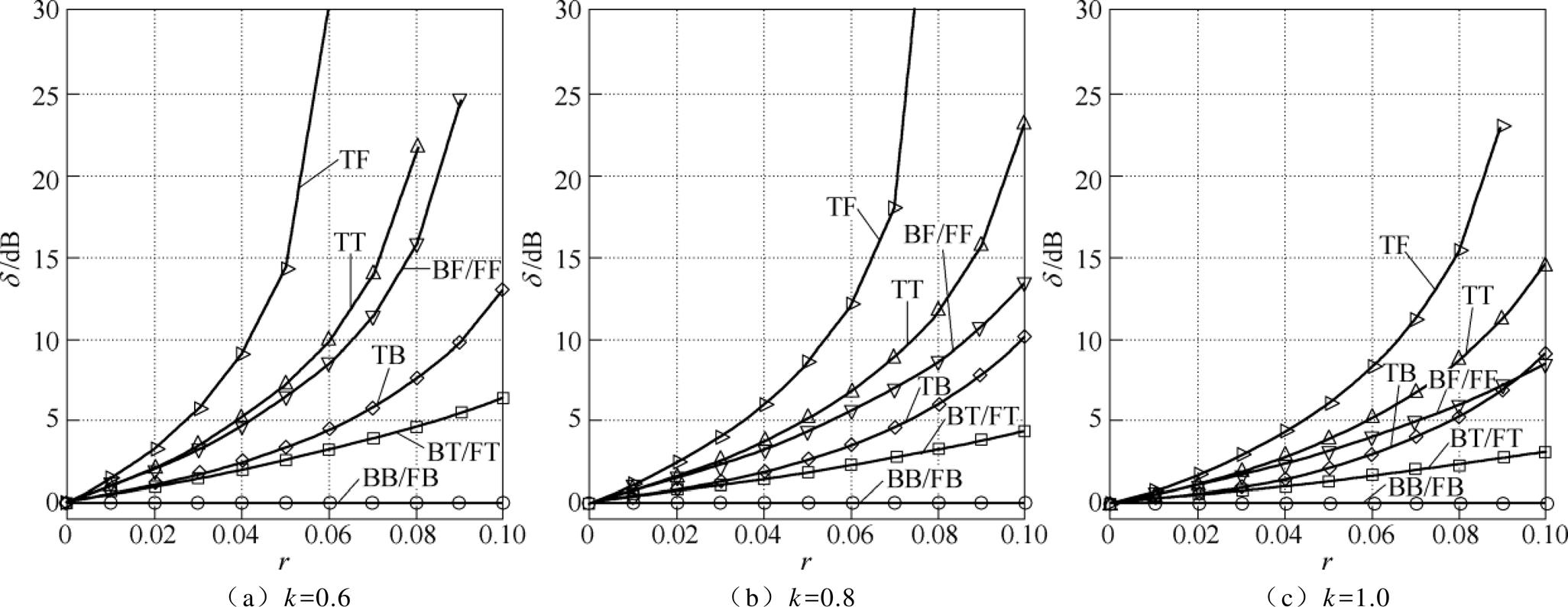
图9 幅值增益d 的仿真数据
Fig.9 Simulation results of amplitude gain d
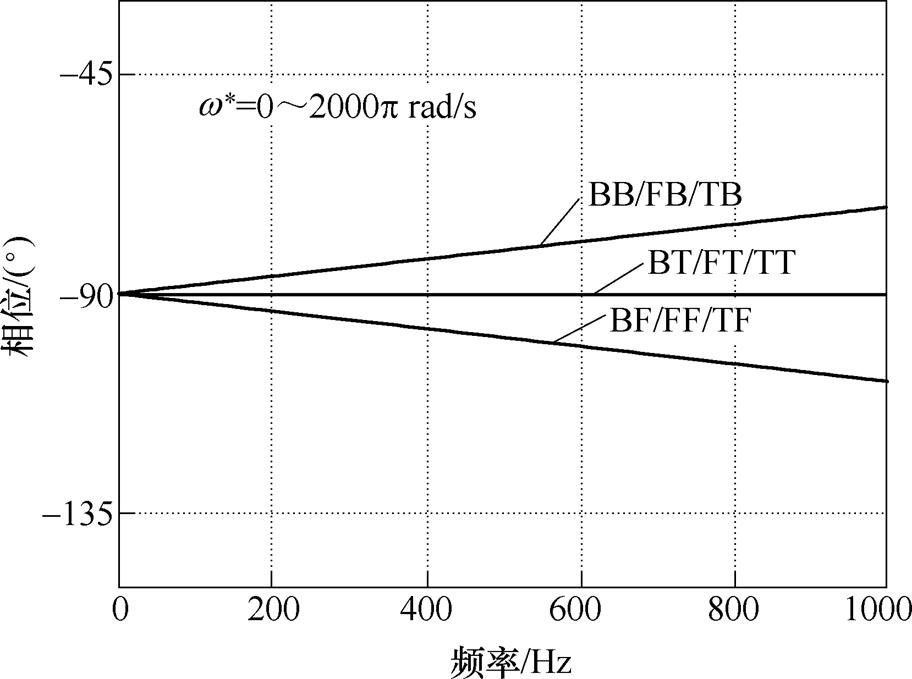
图10 AF正交特性的仿真数据
Fig.10 Simulation results of AF orthogonal characteristics
数字自适应滤波器在基于DSP28335芯片的实验平台上实现,采样周期为10-4s,自适应滤波器的参数设定与仿真一致。采用PSM1700频率响应分析仪(扫频仪)产生幅值为0.1V的等差频率正弦模拟信号,然后通过AD采样将其进行模数转换,作为数字自适应滤波器系统的输入,扫频仪对数字系统的输入、输出信号进行采样分析获得数字系统的幅相频特性曲线的数据。最后对扫频仪得到的数据进行整理分析。
图11给出了采用不同离散方法的全数字自适应滤波器的相对频率偏移量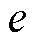 的实验数据,不同离散方法的频率偏移规律差别明显,采用F(zo)F(zo)、F(zo)B(im)、F(zo)T(fo)离散的数字系统频率偏移相同且相对偏移量e最小;B(im)B(im)离散结构频率偏移最大。对比图11与图5,两图一致。可验证数字系统频率偏移规律理论分析的正确性。
的实验数据,不同离散方法的频率偏移规律差别明显,采用F(zo)F(zo)、F(zo)B(im)、F(zo)T(fo)离散的数字系统频率偏移相同且相对偏移量e最小;B(im)B(im)离散结构频率偏移最大。对比图11与图5,两图一致。可验证数字系统频率偏移规律理论分析的正确性。
图12给出了系统的相频特性曲线过零点对应的幅值增益的实验数据,不同离散结构的数字系统幅值增益差别明显,随着载波比r的增大,除了B(im)B(im)、F(zo)B(im)两种离散结构幅值增益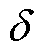 恒定为0dB,其余离散结构的幅值增益
恒定为0dB,其余离散结构的幅值增益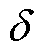 均为增大的趋势,其中,TF离散结构幅值增益随着载波比r的增加、增大最快。对比图12与图6,两图一致。可验证数字系统幅值增益规律理论分析的正确。
均为增大的趋势,其中,TF离散结构幅值增益随着载波比r的增加、增大最快。对比图12与图6,两图一致。可验证数字系统幅值增益规律理论分析的正确。
图13给出了设定参数相同时的采用不同离散方法的数字滤波器的输入/输出信号时域波形,其中,比例系数k=0.8,设定频率参数w*=1 000prad/s,已知处理器采样周期为10-4s,对应载波比r =0.05。输入正弦信号的频率为理想情况下选通信号频率,即w =1 000prad/s。从图中可知,采用不同离散方法的数字自适应滤波器的性能有着明显的差异。
为了定量分析,从而能够更加直观地进行性能对比,在上述实验条件下,得到与图13相对应的实验数据见表7,同时给出了实验数据、理论数据以及两者误差。由图13结合表7可知,采用F(zo)B(im)离散的数字系统的幅值增益实验数据为0.04dB、理论数据为-0.01dB、相差0.05dB;相位实验数据为0.07°、理论数据为0.58°、相差0.49°;输入输出正弦信号时域波形几乎重合。因此,在不考虑数字滤波器两个输出信号正交性的前提下,采用F(zo)B(im)离散的数字系统与理想系统的性能最为接近。同时验证了理论分析方法的正确性。
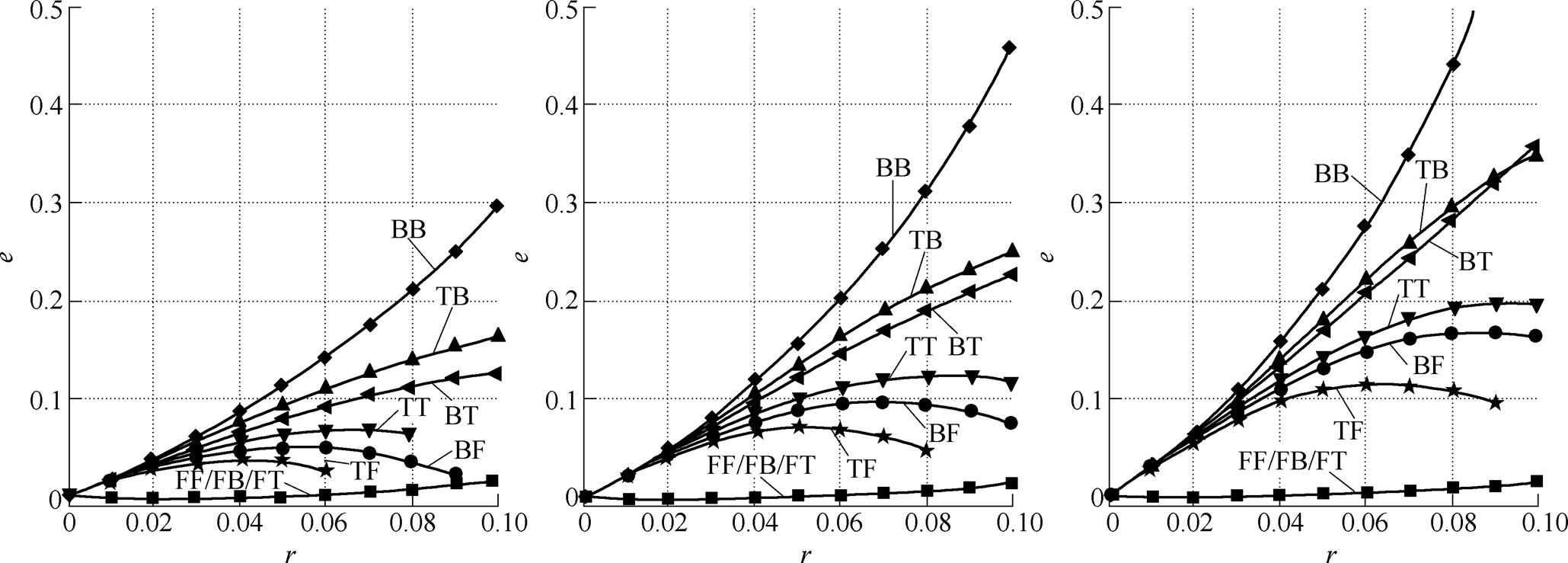
图11 相对频率偏移量e的实验数据
Fig.11 Experimental results of relative frequency offset e
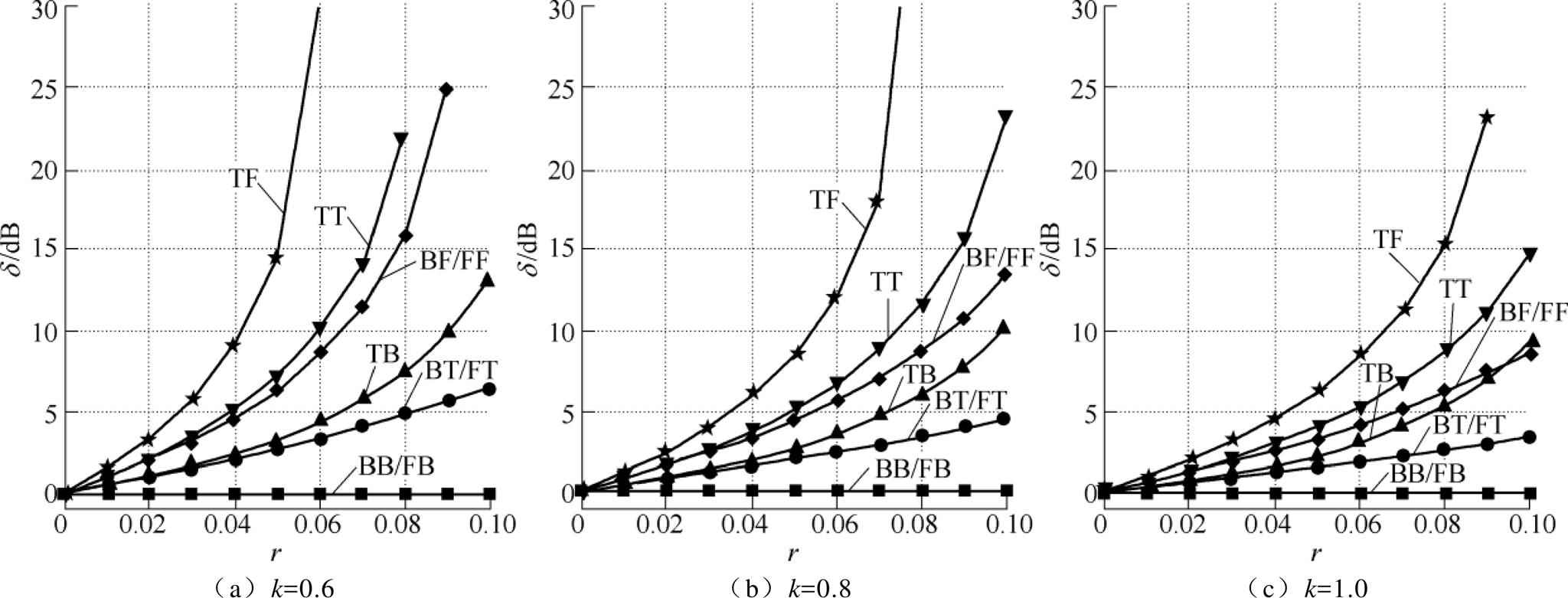
图12 幅值增益d 的实验数据
Fig.12 Experimental results of amplitude gain d

图13 自适应滤波器不同离散结构的输入、输出信号波形
Fig.13 The experimental waveforms of adaptive filter with different discrete methods
表7 与图13相对应的实验数据及相应理论数据、实验误差
Tab.7 Experimental results, theoretical results, experimental errors corresponding to Fig.13

离散方法T(fo)T(fo)T(fo)B(im)T(fo)F(zo)B(im)T(fo)B(im)B(im)B(im)F(zo)F(zo)T(fo)F(zo)B(im)F(zo)F(zo) 幅值增益实验数据/dB4.361.947.731.950.044.381.950.044.38 幅值增益理论数据/dB4.271.857.611.88-0.014.311.88-0.014.31 幅值增益实验误差/dB0.090.090.120.070.050.070.070.050.07 相位实验数据/(°)21.1520.3822.6618.1718.1318.220.110.070.17 相位理论数据/(°)21.8420.9123.6518.7218.5818.960.720.580.95 相位实验误差/(°)-0.69-0.53-0.99-0.55-0.45-0.74-0.61-0.51-0.78
本文对考虑了滞后一拍的数字自适应滤波器不同离散结构,分别从稳定性、选频特性、幅值增益特性和正交特性四个方面进行了理论对比分析,并给出了四种性能跟随载波比的变换规律,通过仿真和实验验证了变化规律的正确性。可得到如下结论:
1)从稳定性方面考虑,采用B(im)B(im)、F(zo)B(im)离散方法的数字自适应滤波器在0<r<0.1、0<k<2区间内恒稳定,稳定性能最优;从选频特性方面考虑,采用F(zo)F(zo)、F(zo)B(im)、F(zo)T(fo)离散方法的数字系统频率偏移最小,选频性能最优;从幅值增益特性方面考虑,采用B(im)B(im)、F(zo)B(im)离散方法的数字系统幅值增益恒定为0dB,具有最好的幅值跟踪效果;从正交特性方面考虑,采用B(im)T(fo)、F(zo)T(fo)、T(fo)T(fo)离散方法的数字系统两路输出信号相位恒差90°,不随载波比的增大而变化,正交性最优。
2)采用F(zo)B(im)离散的数字自适应滤波器,除正交特性以外,稳定性、选频特性和幅值增益特性在所分析的几种离散方法中均处于性能最优行列,因此,若实际应用中对正交特性要求不高,可优先选择F(zo)B(im)离散的数字自适应滤波器。若实际应用中对数字自适应滤波器的正交特性要求较高,可考虑选择F(zo)T(fo)离散的数字自适应滤波器。
参考文献
[1] Rodriguez P, Luna A, Ciobotaru M, et al. Advanced grid synchronization system for power converters under unbalanced and distorted operating con- ditions[C]//32nd Annual Conference on IEEE Indu- strial Electronics Society, Paris, France, 2006: 5173- 5178.
[2] Rodríguez P, Luna A, Candela I, et al. Grid synchronization of power converters using multiple second order generalized integrators[C]//34th Annual Conference of IEEE Industrial Electronics Society, Orlando, FL, USA, 2008: 755-760.
[3] Rodríguez P, Luna A, Muñoz-Aguilar R S, et al. A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions[J]. IEEE Transactions on Power Electronics, 2012, 27(1): 99-112.
[4] 胥芳, 王坚锋, 潘国兵, 等. LCL型有源滤波器混合状态反馈虚拟阻尼控制策略[J]. 电工技术学报, 2019, 34(23): 5014-5022.
Xu Fang, Wang Jianfeng, Pan Guobing, et al. LCL active power filter based on hybird states feedback virtual damping control strategy[J]. Transactions of China Elecrotechnical Society, 2019, 34(23): 5014- 5022.
[5] 顾长彬, 王琛琛, 王堃, 等. 单相PWM整流器虚拟矢量控制策略[J]. 电工技术学报, 2019, 34(增刊1): 202-211.
Gu Changbin, Wang Chenchen, Wang Kun, et al. Analysis on virtual vector control schemes for single-phase PWM converter based on orthogonal signals generators[J]. IEEE Transactions on Power Electronics, 2019, 34(S1): 202-211.
[6] 赵仁德, 赵斌, 徐海亮, 等. 带LC滤波器的永磁同步电机控制系统及策略研究[J]. 电工技术学报, 2019, 34(增刊1): 79-86.
Zhao Rende, Zhao Bin, Xu Hailiang, et al. Research on control method of permanent magnet synchronous motor with LC filter[J]. Transactions of China Elec- trotechnical Society, 2019, 34(S1): 79-86.
[7] Wang Gaolin, Li Ding, Li Zhuomin, et al. Enhanced position observer using second-order generalized integrator for sensorless interior permanent magnet synchronous motor drives[J]. IEEE Transactions on Energy Conversion, 2014, 29(2): 486-495.
[8] Ye Shuaichen. Fuzzy sliding mode observer with dual SOGI-FLL in sensorless control of PMSM drives[J]. ISA Transactions, 2019, 85: 161-176.
[9] 周臻, 李长磊, 王永. 基于复合二阶广义积分器的永磁同步电机转子位置与转速估计[J]. 电工技术学报, 2017, 32(7): 59-66.
Zhou Zhen, Li Changlei, Wang Yong. Position and speed estimation for a permanent magnet syn- chronous motor rotor using composite second order generalized integrator[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 59-66.
[10] 刘兵, 周波, 倪天恒, 等. 基于广义二阶积分器的表贴式永磁同步电机低速转子位置检测方法[J]. 电工技术学报, 2017, 32(23): 23-33.
Liu Bing, Zhou Bo, Ni Tianheng, et al. A novel position observer for SPMSM sensorless control based on second-order generalized integrators[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 23-33.
[11] 辛振, 赵仁德, 郭宝玲, 等. 基于广义二阶积分器- 锁频环的异步电机同步角频率估计方法[J]. 电工技术学报, 2014, 29(1): 116-122.
Xin Zhen, Zhao Rende, Guo Baoling, et al. New induction motor synchronous angular frequency estimation method based on second order generalized integrator-frequency locked loop[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 116- 122.
[12] Xin Zhen, Zhao Rende, Blaabjerg F, et al. An improved flux observer for field-oriented control of induction motors based on dual second-order gen- eralized integrator frequency-locked loop[J]. IEEE Journal of Emerging and Select Topics in Power Electronics, 2017, 5(1): 513-525.
[13] Rodriguez F J, Bueno E, Aredes M, et al. Discrete time implementation of second order generalized integrators for grid converters[C]//34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 2008: 176-181.
[14] Harnefors L. Implementation of resonant controllers and filters in fixed-point arithmetic[J]. IEEE Transa- ctions on Industrial Electronics, 2009, 56(4): 1273- 1281.
[15] Yepes A G, Freijedo F D, Lopez Ó, et al. High performance digital resonant controllers implement- ed with two integrators[J]. IEEE Transactions on Power Electronics, 2011, 26(2): 563-576.
[16] Khajehoddin S A, Karimi-Ghartemani M, Jain P K, et al. A resonant controller with high structural robu- stness for fixed-point digital implementations[J]. IEEE Transactions on Power Electronics, 2012, 27(7): 3352-3362.
[17] Alejandro G Y, Francisco D F, Jesús D G, et al. Effects of discretization methods on the perform- ance of resonant controllers[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1692-1712.
[18] 杨才伟, 王剑, 游小杰, 等. 二阶广义积分器锁频环数字实现准确性对比[J]. 电工技术学报, 2019, 34(12): 2584-2596.
Yang Caiwei, Wang Jian, You Xiaojie, et al. Accuracy comparison of digital implementation on the second-order generalized integrator frequency- locked loop[J]. Transactions of China Elecro- technical Society, 2019, 34(12): 2584-2596.
[19] 刘亚静, 范瑜. 全数字硬件化正交锁相环建模与分析[J]. 电工技术学报, 2015, 30(15): 148-155.
Liu Yajing, Fan Yu. Modeling and analysis of all-digital full-hardware quadrature phase-locked loop[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 148-155.
[20] 刘亚静, 范瑜. 全数字硬件化锁相环参数分析与设计[J]. 电工技术学报, 2015, 30(2): 172-179.
Liu Yajing, Fan Yu. Design and analysis of all-digital full-hardware phase-locked loop[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 172- 179.
[21] 孙高阳, 刘亚静, 李秉格, 等. 一种消除反馈延迟的全数字锁相环[J]. 电工技术学报, 2017, 32(20): 171-178.
Sun Gaoyang, Liu Yajing, Li Bingge, et al. An all- digital phase-locked loop with compensating feed- back unit delay[J]. Transactions of China Elecro- technical Society, 2017, 32(20): 171-178.
Performance Comparison and Analysis of All-Digital Adaptive Filter with Different Discrete Methods
Abstract The Adaptive filter (AF) based on second-order generalized integrator (SOGI) is widely applied in power grid measurement, motor position/speed detection and estimation occasions. In the process of digital realization, the existence of unit delay and different discrete methods will degrade the performance of the system. Under the premise of considering the aforementioned factors, the stability, frequency offset, amplitude gain and orthogonality were used as quantitative indicators to evaluate the performance degradation of the digital AF. And then, the performance variation with carrier ratio was given to provide the theoretical basis for digital implementation of the adaptive filter. Simulation and experimental results verified the theoretical analysis.
keywords:Adaptive filter, second-order generalized integrator, one-step-delay, frequency offset, amplitude gain, orthogonality
DOI: 10.19595/j.cnki.1000-6753.tces.200588
中图分类号:TM46
刘亚静 男,1981年生,博士,讲师,研究方向为电机数字控制系统集成化设计、伺服系统、运动控制IP核等。E-mail: lyajing@bjtu.edu.cn(通信作者)
段超 男,1994年生,硕士研究生,研究方向为伺服电机控制。E-mail: 18126083@bjtu.edu.cn
收稿日期 2020-05-23
改稿日期 2020-10-19
国家自然科学基金(51407005)、河北省重点研发计划(20351601D)和河北省高层次人才(A202003012)资助项目。
(编辑 崔文静)