 坐标轴的分量以实现对转子位置估算,动态响应速度快、简单易行,得到了较为广泛的应用。
坐标轴的分量以实现对转子位置估算,动态响应速度快、简单易行,得到了较为广泛的应用。摘要 转子位置信息的精度影响高速永磁同步电机的运行性能,在高速运行条件下,转子位置估算容易受到环路滤波器和电机参数偏差等非理想因素的影响。首先,针对转子位置估算误差,该文提出一种自适应基准锁相环,主要思想是锁相环通过误差重构,实现对基频相关误差补偿。在此基础上,以最小电流为目标自适应调节锁相环的锁相基准,实现对非基频相关误差的补偿,最终实现对位置误差的全补偿,该方法实现简单、参数依赖性低、鲁棒性强。最后,基于一台高速永磁同步电机进行仿真与实验,结果验证了所提出方法的有效性。
关键词:高速永磁同步电机 转子磁链观测器 位置估算误差 锁相环
高速永磁同步电机(High-Speed Permanent Magnet Synchronous Motor, HSPMSM)因具有体积小、质量轻和高功率密度等特点而被广泛应用于高速机床、鼓风机、压缩机以及飞轮储能等领域[1-5]。高速运行时,转子位置的精度对电机的运行性能至关重要[6]。转子位置的获取方式主要包括机械式的位置传感器和无位置传感器算法。其中,机械式的位置传感器会降低系统的可靠性,增加系统的体积与成本,因此,常采用无位置传感器算法[7]。文献[8]将无位置传感器算法分为基于电机模型的直接估算法[9-10]、基于状态观测器的闭环算法[11-13]以及信号注入法[14-15]。其中,转子磁链观测器基于电机的电压方程,直接计算出转子磁链在 坐标轴的分量以实现对转子位置估算,动态响应速度快、简单易行,得到了较为广泛的应用。
坐标轴的分量以实现对转子位置估算,动态响应速度快、简单易行,得到了较为广泛的应用。
在高速运行条件下,采用无位置传感器算法容易受到诸多非理想因素的影响,造成明显的转子位置估算误差。文献[16]为消除由于逆变器的非线性以及空间谐波所造成位置信号中存在6k次脉动,提出一种基于自适应滤波的位置估算方法。文献[17-18]通过对电机参数在线辨识,提高位置估算的准确性,但电机参数辨识模型复杂,降低了系统的实时性。文献[19]为消除信号中谐波的影响,提出一种同步频率提取滤波器,能够直接提取出信号中的基波分量。文献[20]提出一种基于误差特征量的闭环位置误差补偿方法,根据转子位置误差在直轴上的特征分量对转子位置进行闭环调节,该方法实现简单,但是对电感参数有一定的依赖。文献[21]提出一种双重锁相环,在正交锁相环的基础上,对延迟重构信号进行二次锁相以补偿位置误差。文献[22-23]通过追踪最小电流以实现对位置误差的补偿,此方法实现简单且不依赖任何参数,鲁棒性强,但是容易导引起稳态时的电流抖振,影响系统的稳定性。
本文首先对高速运行条件下环路滤波器、电感参数偏差或电压电流采样偏差等非理想因素所造成的转子位置估算误差进行分析,并归纳为基频相关和非基频两种类型。为统一补偿各类位置估测误差,本文提出一种基于自适应基准锁相环的转子位置误差全补偿方法:一方面,对误差信号进行重构,并通过锁相环(Phase-Locked Loop, PLL)得到与基频相关误差的补偿值;另一方面,锁相环基准随最小电流目标值进行自适应实时调整,从而到达对非基频相关误差的补偿。最后,本文基于一台高速永磁同步电机进行仿真与实验,验证了所提出的转子位置估算误差全补偿方法的有效性。
转子磁链在 坐标系下的数学模型为
坐标系下的数学模型为
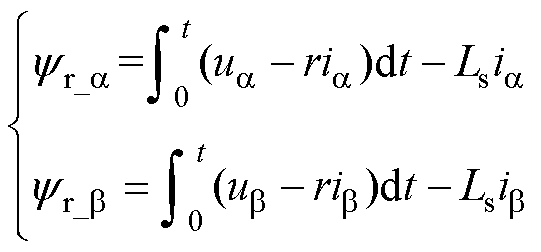 (1)
(1)式中, 、
、 为
为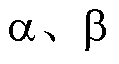 轴转子磁链分量;
轴转子磁链分量;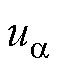 、
、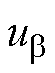 和
和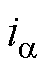 、
、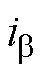 分别为
分别为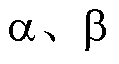 轴定子电压和定子电流分量;Ls为定子电感。根据式(1)计算得到转子磁链在
轴定子电压和定子电流分量;Ls为定子电感。根据式(1)计算得到转子磁链在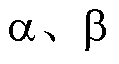 轴分量后,再通过反正切运算,即得到转子位置。
轴分量后,再通过反正切运算,即得到转子位置。
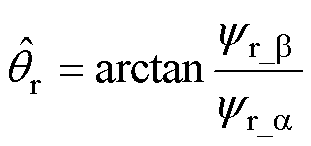 (2)
(2)
由于磁链观测器中存在纯积分环节,易受积分初值与直流分量的影响,因此,采用高通滤波器(High-Pass Filter, HPF)与纯积分环节串联。为消除高频谐波与干扰信号,还需在观测器的输入串联低通滤波器(Low-Pass Filter, LPF)。经上述改进后,转子磁链观测器的结构框图如图1所示。
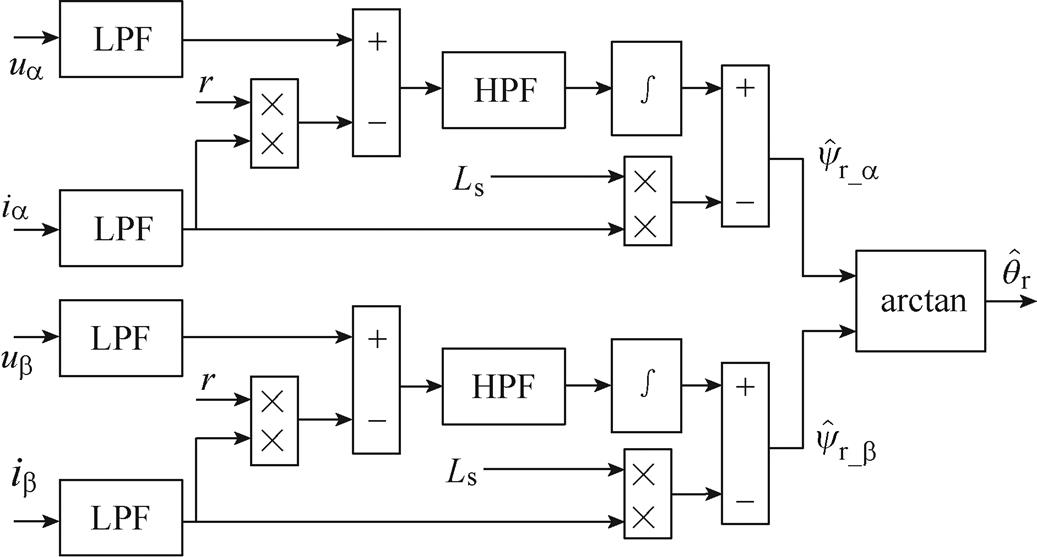
图1 转子磁链观测器结构框图
Fig.1 Structure of rotor flux observer
在高速电机驱动系统中,根据转子位置误差与基频的相关性定义为基频相关误差和非基频相关误差,下面对这两类误差进行具体分析。
1.2.1 基频相关误差
基频相关误差主要来源于环路滤波器,由1.1节分析可知,为抑制积分初值、直流分量、高频谐波以及干扰信号对位置估算的影响,加入HPF和LPF,所造成的位置估算误差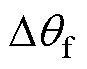 可表示为
可表示为
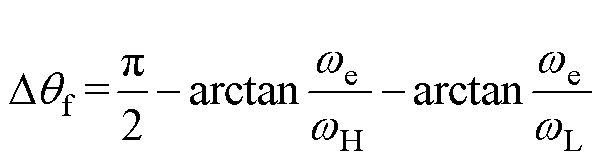 (3)
(3)式中,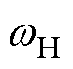 为HPF的截止频率;
为HPF的截止频率;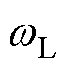 为LPF的截止频率;
为LPF的截止频率;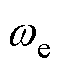 为电机角速度。由式(3)可知,环路滤波器所造成的位置误差可定量,且随基频的升高而增大。
为电机角速度。由式(3)可知,环路滤波器所造成的位置误差可定量,且随基频的升高而增大。
1.2.2 非基频相关误差
非基频误差主要包括电机参数偏差以及电压电流采样偏差等所造成的位置误差,该类误差难以准确定量,难以补偿。本文以电感参数偏差为例,定义电感偏差为 ,
,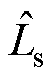 为估测电感值,
为估测电感值,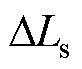 所引起的位置估算误差如图2所示,在“id=0”控制模式下,定子电流超前转子磁链p/2电角度,
所引起的位置估算误差如图2所示,在“id=0”控制模式下,定子电流超前转子磁链p/2电角度,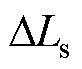 所引起的位置误差
所引起的位置误差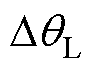 为
为
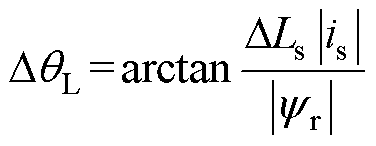 (4)
(4)
图2 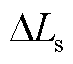 所引起的位置估算误差
所引起的位置估算误差
Fig.2 Position estimation error caused by 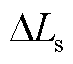
在实际运行中,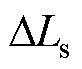 难以获取,因此,所造成的位置估算误差难以补偿。
难以获取,因此,所造成的位置估算误差难以补偿。
综上所述,采用转子磁链观测器估算转子位置时,环路滤波器和电感参数偏差均会造成一定的位置误差,其中,电感参数偏差等其他非理想因素所造成的位置误差无法准确定量,难以补偿。因此,探究有效的位置误差全补偿策略,是提升电机运行性能的关键所在。
本文所提出的转子位置估算误差全补偿方法主要包括锁相环和锁相基准自适应调整两部分,下面分别对这两部进行分析。
锁相环位置补偿原理如图3所示。在高速永磁同步电机驱动系统中,实际转子位置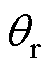 与转子磁链
与转子磁链 保持固定相位关系。磁场定向控制通过反馈的转子位置控制电流is的相位。隐极式永磁同步电机工作在最大转矩电流比状态,通常采用“id=0”控制。在“id=0”控制模式下,且无位置误差时,电流积分
保持固定相位关系。磁场定向控制通过反馈的转子位置控制电流is的相位。隐极式永磁同步电机工作在最大转矩电流比状态,通常采用“id=0”控制。在“id=0”控制模式下,且无位置误差时,电流积分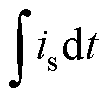 与
与 保持同相位。如图3a所示,仅考虑环路滤波器的影响,不妨假设估算的转子磁链
保持同相位。如图3a所示,仅考虑环路滤波器的影响,不妨假设估算的转子磁链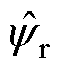 滞后于实际转子磁链
滞后于实际转子磁链 相位
相位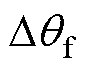 ,估算的转子位置
,估算的转子位置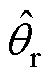 滞后于实际转子位置
滞后于实际转子位置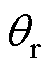 相位
相位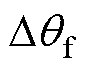 ,
,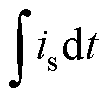 滞后于
滞后于 相位
相位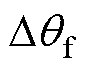 。利用电流积分环节和环路滤波器对电流信号重构得到
。利用电流积分环节和环路滤波器对电流信号重构得到 ,该信号与
,该信号与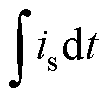 之间的相位差即为
之间的相位差即为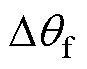 。如图3b所示,将
。如图3b所示,将 与
与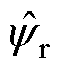 锁相(锁相基准
锁相(锁相基准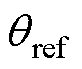 =0),当
=0),当 与
与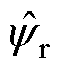 同相位时,
同相位时,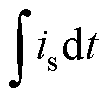 与
与 保持同相位,此时锁相环输出的补偿角度即为
保持同相位,此时锁相环输出的补偿角度即为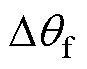 ,实现了对滤波器引起的位置估算误差的补偿。图4所示为锁相环位置误差补偿原理框图。
,实现了对滤波器引起的位置估算误差的补偿。图4所示为锁相环位置误差补偿原理框图。
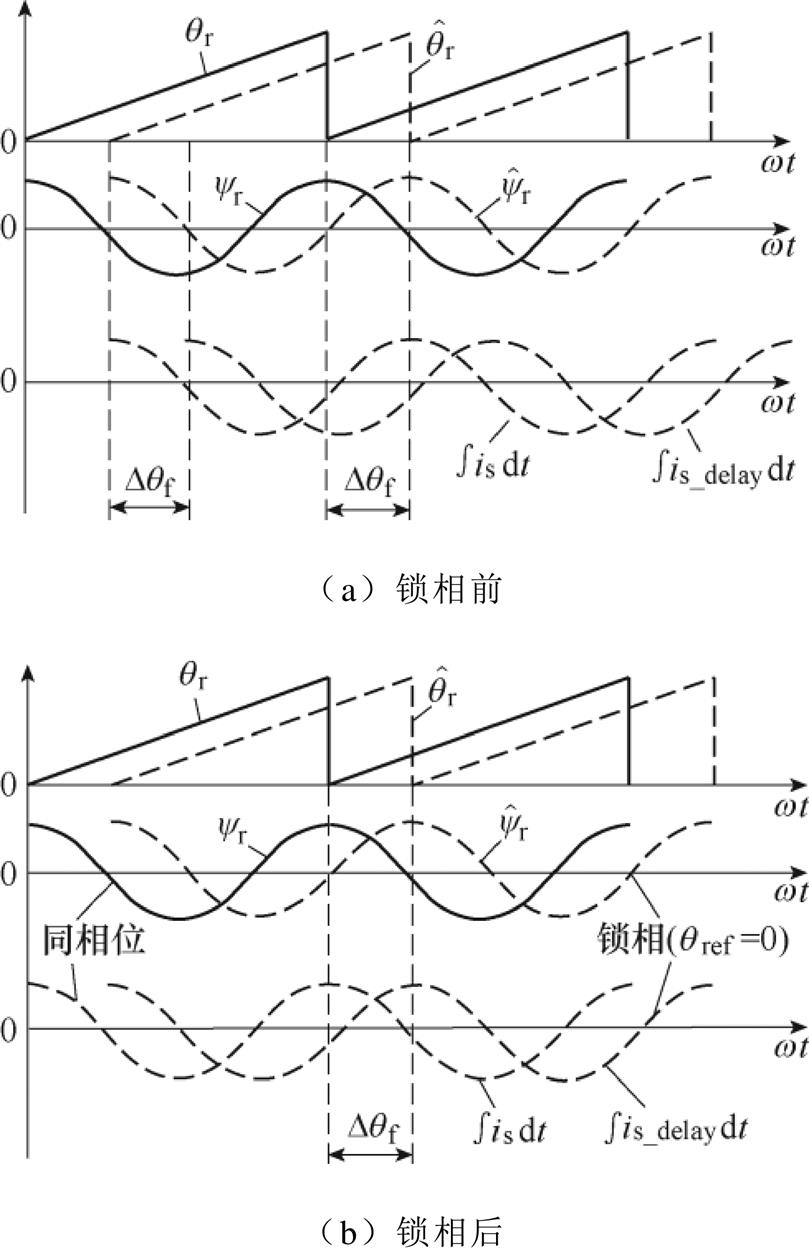
图3 锁相环位置补偿原理
Fig.3 Principle of position error compensation based on PLL
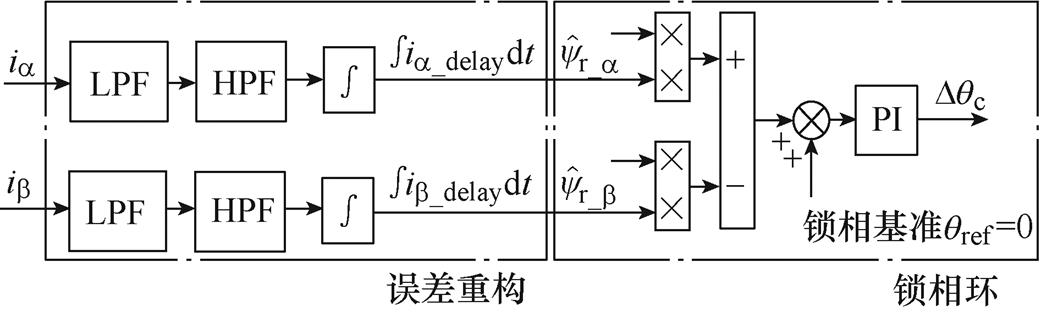
图4 锁相环位置误差补偿框图
Fig.4 Structure diagram of position error compensation based on PLL
锁相基准调整如图5所示。由2.1节分析可知,锁相环位置误差补偿的前提是对误差的精确重构。由于电感参数偏差等其他非理想因素所造成的误差无法重构,锁相环无法对其进行补偿。以电感参数偏差为例进行分析,如图5a所示,当 与
与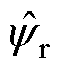 同相位时,由于电感参数偏差的影响,
同相位时,由于电感参数偏差的影响,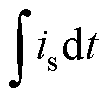 与
与 之间依然存在相位差
之间依然存在相位差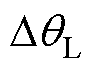 。本文所提出的自适应基准锁相环,如图5b所示,对锁相基准
。本文所提出的自适应基准锁相环,如图5b所示,对锁相基准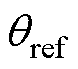 进行调整,当
进行调整,当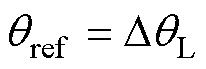 时,
时,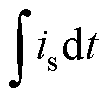 与
与 保持同相位,补偿了电感参数偏差所引起的位置估算误差。
保持同相位,补偿了电感参数偏差所引起的位置估算误差。
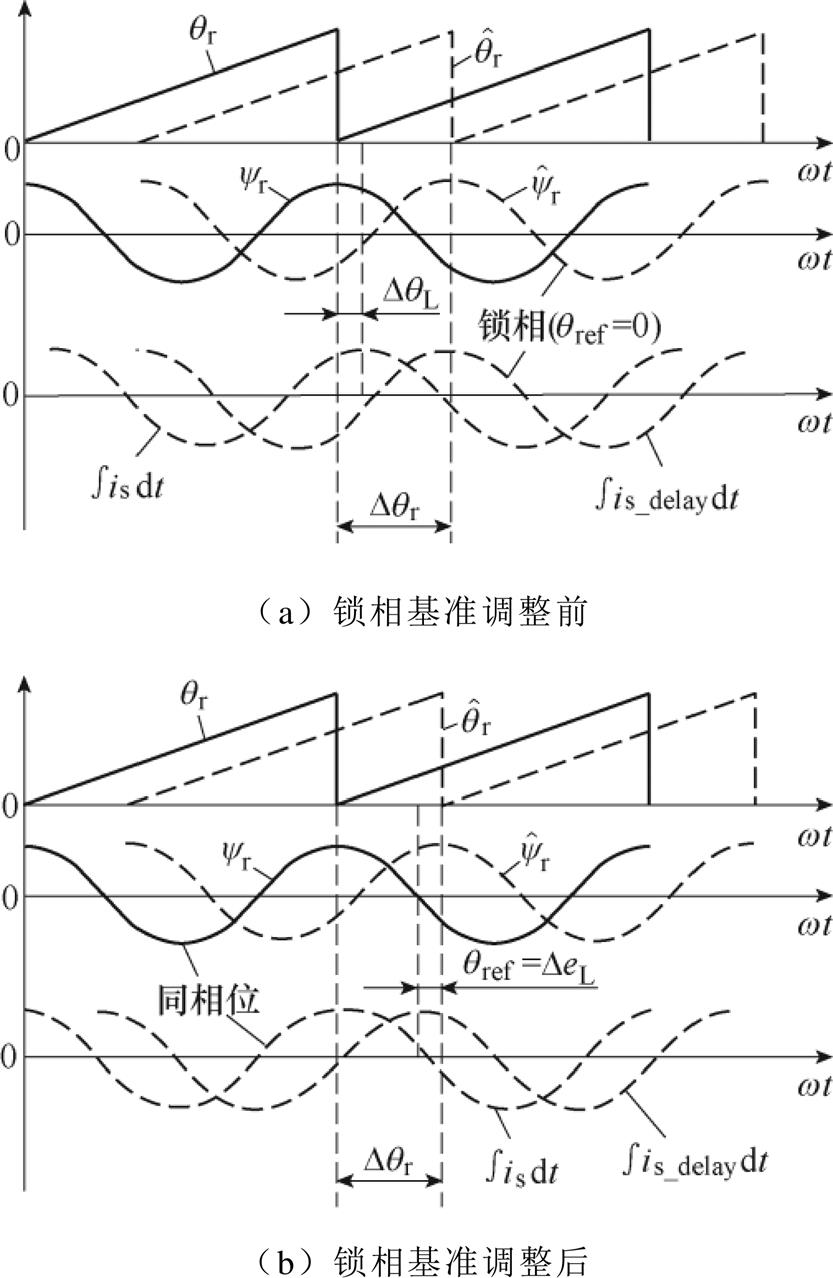
图5 锁相基准调整
Fig.5 Adjustment of the phase-locked reference
图6所示为输出电流is与位置误差的关系,在“id=0”控制模式下且负载一定时,当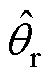 无偏差时,电机工作在最大转矩电流比状态,此时的电流全部用来产生转矩,输出电流幅值|is|为最小值。当
无偏差时,电机工作在最大转矩电流比状态,此时的电流全部用来产生转矩,输出电流幅值|is|为最小值。当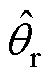 存在偏差时,只有部分电流用于产生转矩,电机偏离最大转矩电流比状态,|is|将变大。
存在偏差时,只有部分电流用于产生转矩,电机偏离最大转矩电流比状态,|is|将变大。
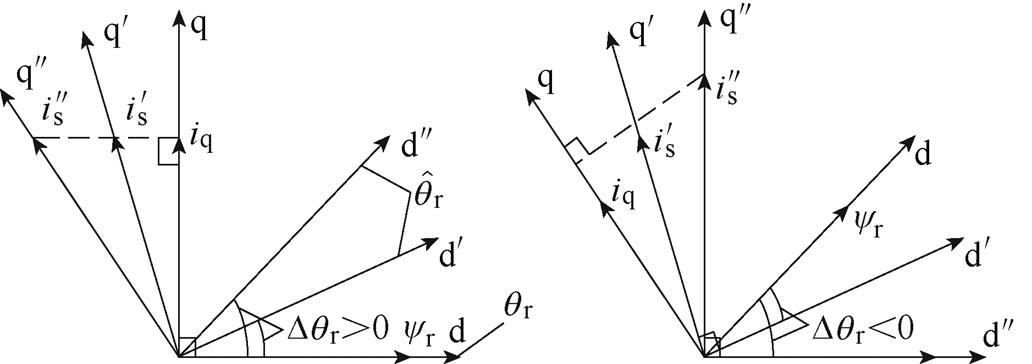
图6 电流与位置误差的关系
Fig.6 The relation between current and position error
当锁相环将 与
与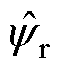 锁相(锁相基准为0)以补偿环路滤波器所造成的位置估算误差,在此基础上,以最小|is|为目标,进一步调整锁相环的锁相基准,从而调节锁相环输出的补偿角度,当|is|调节至最小值时,补偿了电感参数偏差等其他非理想因素所引起的位置估算误差,即实现转子位置估算误差的全补偿。图7所示为锁相基准自适应调整的流程,其中,
锁相(锁相基准为0)以补偿环路滤波器所造成的位置估算误差,在此基础上,以最小|is|为目标,进一步调整锁相环的锁相基准,从而调节锁相环输出的补偿角度,当|is|调节至最小值时,补偿了电感参数偏差等其他非理想因素所引起的位置估算误差,即实现转子位置估算误差的全补偿。图7所示为锁相基准自适应调整的流程,其中,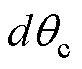 为算法的调节步长,k为算法的执行周期。根据前后周期|is|的变化来调整下一周期的步长的方向,从而动态调整锁相基准,|is|最终收敛至最小值,即实现了位置估算误差全补偿。锁相环的锁相基准可表示为
为算法的调节步长,k为算法的执行周期。根据前后周期|is|的变化来调整下一周期的步长的方向,从而动态调整锁相基准,|is|最终收敛至最小值,即实现了位置估算误差全补偿。锁相环的锁相基准可表示为
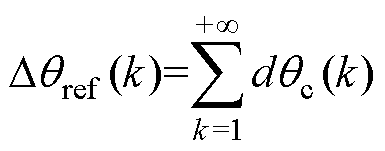 (5)
(5)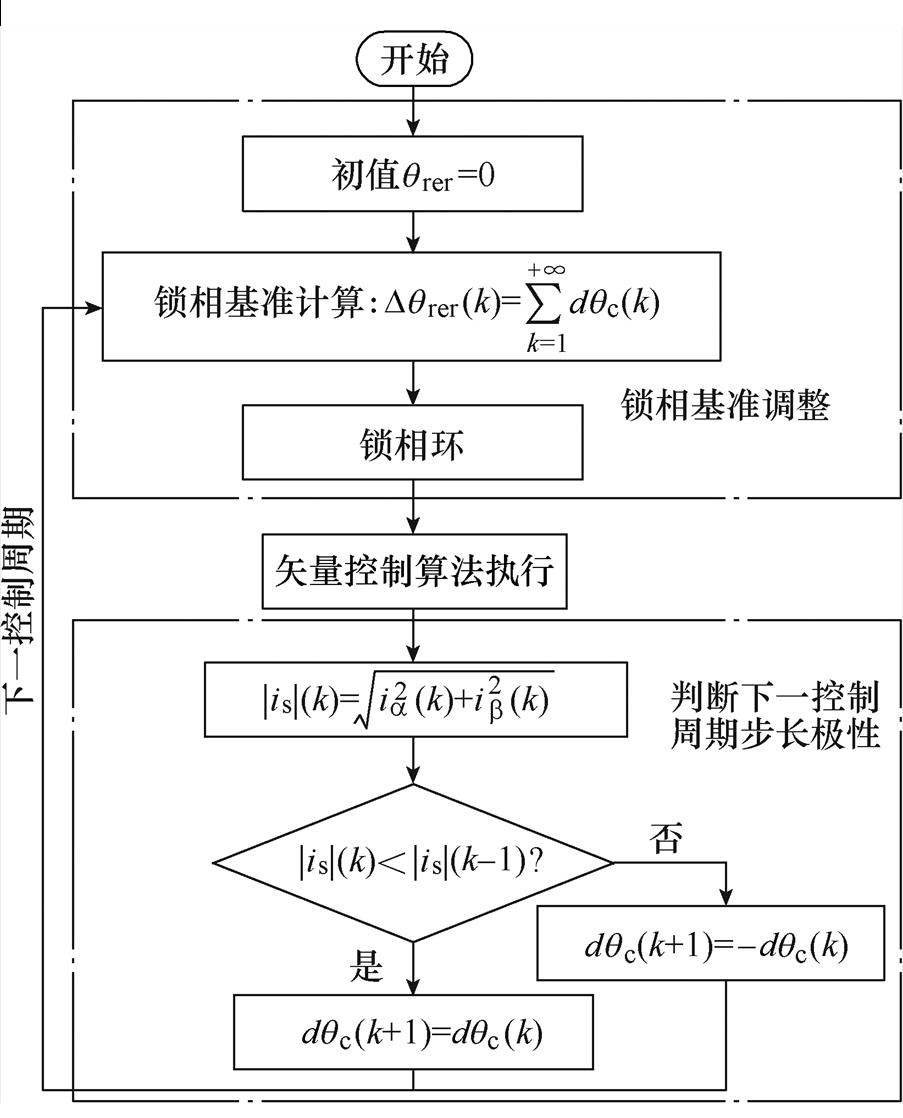
图7 锁相基准自适应调整
Fig.7 Phase-locked reference adaptive adjustment
由式(5)可知,锁相基准自适应调整算法的响应速度取决于算法的执行周期fad和调节步长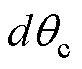 。
。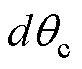 越大,补偿速度越快,
越大,补偿速度越快,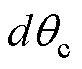 引起位置补偿角的抖振越大;
引起位置补偿角的抖振越大;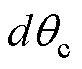 越小,抖振越小,补偿速度较慢。由香农采样定律可知,若锁相基准调整算法执行频率fad过高,算法执行周期短于电流响应时间,则前后周期采样的电流不能够反映
越小,抖振越小,补偿速度较慢。由香农采样定律可知,若锁相基准调整算法执行频率fad过高,算法执行周期短于电流响应时间,则前后周期采样的电流不能够反映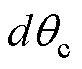 所造成电流的变化,会导致步长极性的错误判断;fad过低,则会降低误差补偿速度。fad和
所造成电流的变化,会导致步长极性的错误判断;fad过低,则会降低误差补偿速度。fad和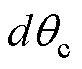 具体数值通常可通过仿真和实验测试得到,本文通过仿真和实验测试,将fad设置为40Hz,
具体数值通常可通过仿真和实验测试得到,本文通过仿真和实验测试,将fad设置为40Hz,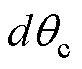 设置为0.03。
设置为0.03。
根据本节分析可设计出基于自适应基准锁相环的无位置传感器驱动系统结构如图8所示。锁相环通过误差重构以补偿环路滤波器所造成的位置估算误差,在此基础上,通过追踪最小电流自适应调整锁相环的基准,以补偿电感参数偏差等其他非理想因素所引起的位置估算误差,最终锁相环输出补偿角度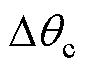 ,
,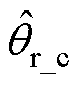 为补偿后的转子位置。经过上述流程,即可实现位置估算误差的全补偿。
为补偿后的转子位置。经过上述流程,即可实现位置估算误差的全补偿。
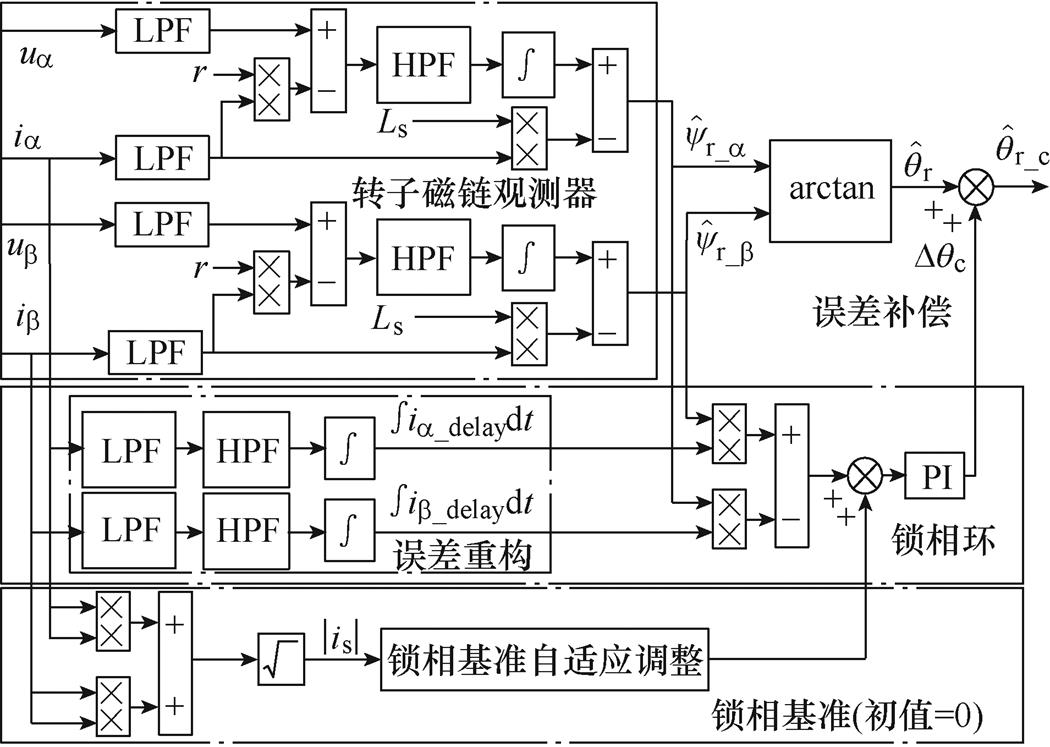
图8 基于自适应基准锁相环转子位置估计器结构
Fig.8 Structure diagram of rotor position estimator based on adaptive reference PLL
为充分验证本文所提出的转子位置估算误差全补偿方法的有效性,本文基于一台高速永磁同步电机进行仿真和实验验证,样机主要参数见表1。
表1 样机主要参数
Tab.1 The main parameters of the motor
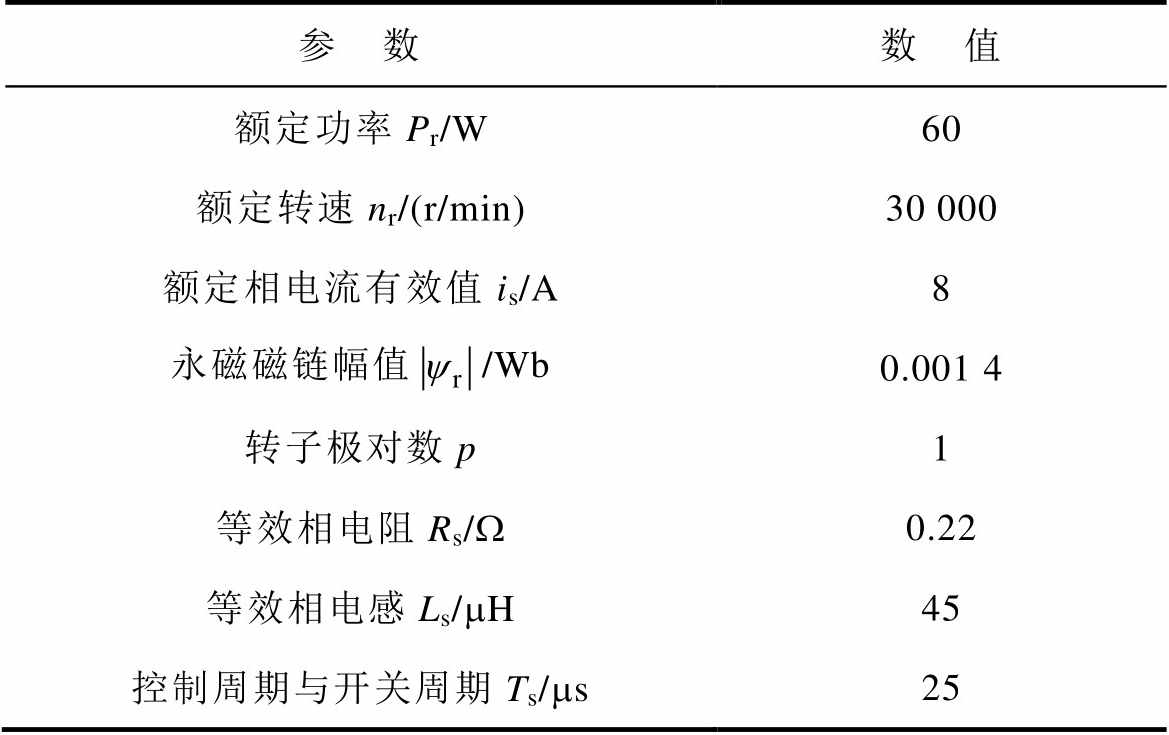
参 数数 值 额定功率Pr/W60 额定转速nr/(r/min)30 000 额定相电流有效值is/A8 永磁磁链幅值/Wb0.001 4 转子极对数p1 等效相电阻Rs/W0.22 等效相电感Ls/mH45 控制周期与开关周期Ts/ms25
本文在Matlab/Simulink环境下,搭建仿真模型,进行仿真分析。基于锁相环仿真结果(锁相基准为0)如图9所示。图9a所示为环路滤波器对转子位置估算的影响,在转速30 000r/min下,估算转子位置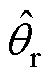 滞后于实际转子位置
滞后于实际转子位置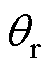 相位1.1rad,有必要对其进行补偿。重构信号
相位1.1rad,有必要对其进行补偿。重构信号 同样滞后于估算的转子磁链
同样滞后于估算的转子磁链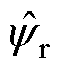 相位1.1rad,实现了对环路滤波器所造成的位置误差的精确重构。图9b所示为采用锁相环补偿位置误差,锁相环将
相位1.1rad,实现了对环路滤波器所造成的位置误差的精确重构。图9b所示为采用锁相环补偿位置误差,锁相环将 与
与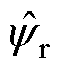 锁相后(锁相基准为0),当两者相位相同时,输出的补偿角度
锁相后(锁相基准为0),当两者相位相同时,输出的补偿角度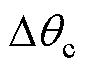 即为1.1rad,
即为1.1rad,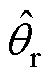 与
与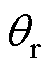 吻合,输出电流is减小。图10为锁相环切入瞬间的动态响应仿真结果,在锁相环切入后的300ms时间内,实现对环路滤波器造成的位置估算误差的补偿。
吻合,输出电流is减小。图10为锁相环切入瞬间的动态响应仿真结果,在锁相环切入后的300ms时间内,实现对环路滤波器造成的位置估算误差的补偿。
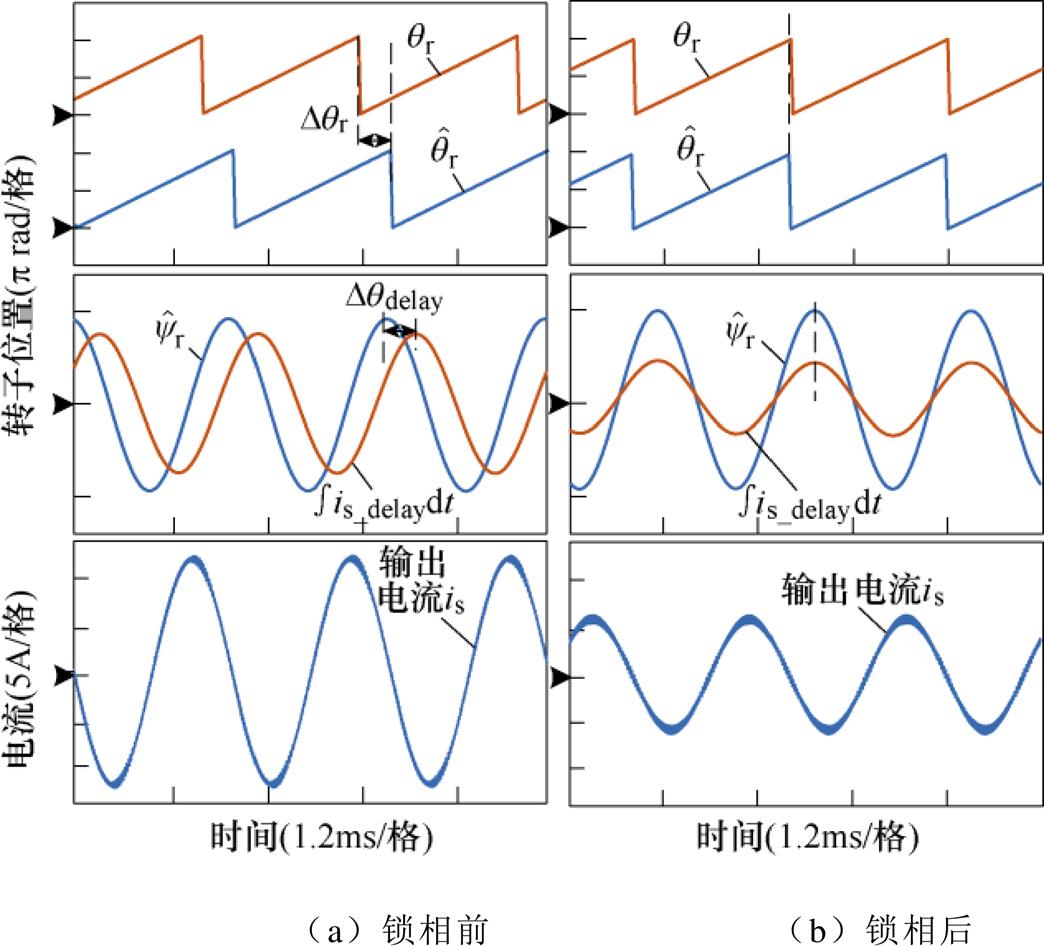
图9 基于锁相环仿真结果(锁相基准为0)
Fig.9 The simulation results based on the PLL (the phase-locked reference is 0)
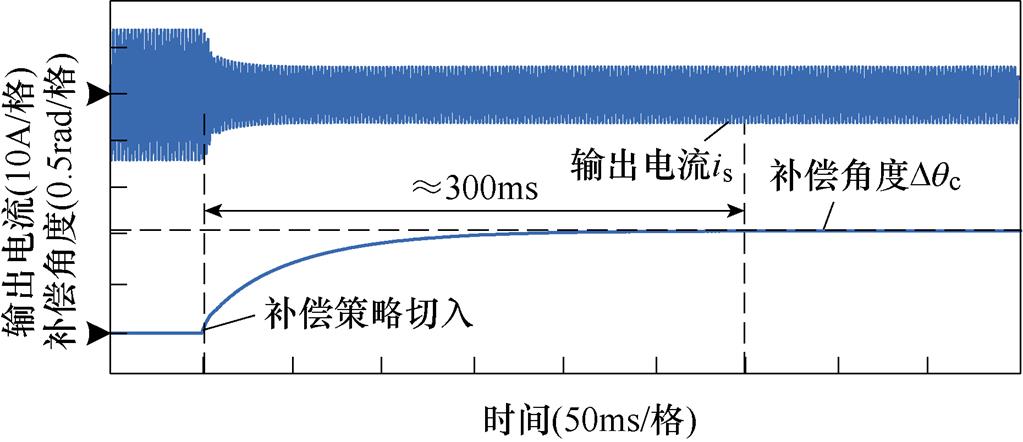
图10 锁相环的动态响应性能
Fig.10 The dynamic response performanceof PLL
为验证锁相环单独作用时无法对电感参数偏差其他非理想因素所引起的误差进行补偿,仿真中设定Ls=0mH。考虑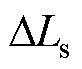 时锁相环仿真结果(锁相基准为0)如图11所示。如图11a所示,
时锁相环仿真结果(锁相基准为0)如图11所示。如图11a所示, 与
与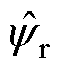 之间的相位差
之间的相位差 ,明显大于
,明显大于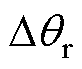 ,误差重构不准确。锁相环将
,误差重构不准确。锁相环将 与
与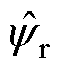 锁相后,如图11b所示,
锁相后,如图11b所示,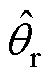 超前于
超前于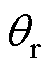 相位0.43rad,造成“过补偿”。图12所示为不同程度的
相位0.43rad,造成“过补偿”。图12所示为不同程度的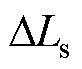 所造成的位置误差,有必要对其进行补偿。
所造成的位置误差,有必要对其进行补偿。
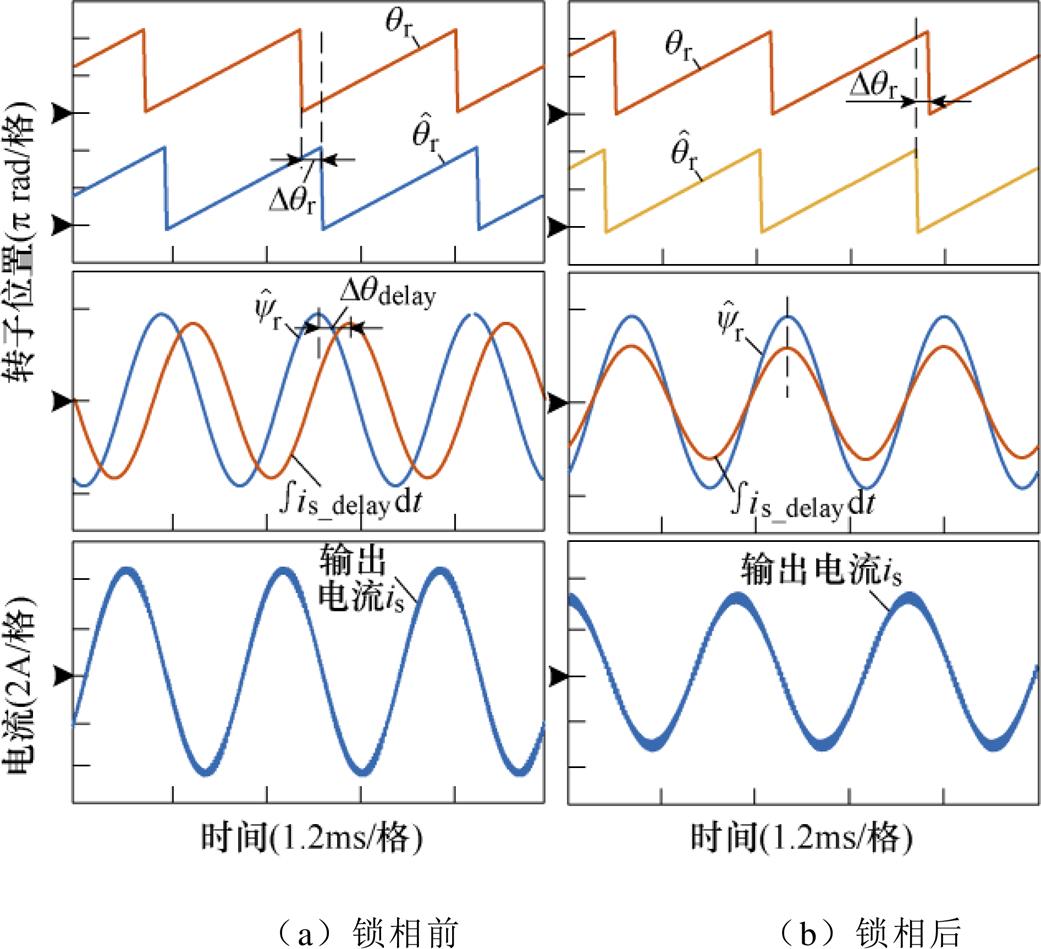
图11 考虑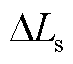 时锁相环仿真结果(锁相基准为0)
时锁相环仿真结果(锁相基准为0)
Fig.11 The simulation results based on PLL when considering 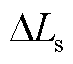 (the phase-locked reference is 0)
(the phase-locked reference is 0)
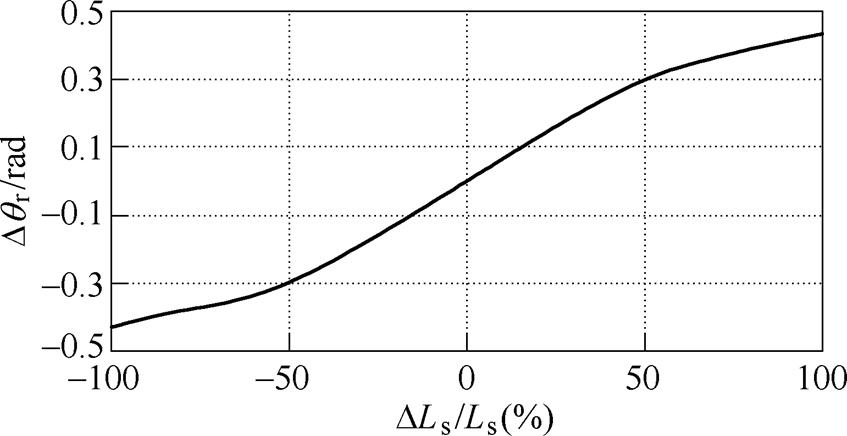
图12 不同程度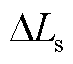 所造成的位置误差
所造成的位置误差
Fig.12 Position error caused by different 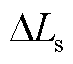
在同样的条件下,对本文所提出的锁相基准自适应调整锁相环进行仿真分析,仿真结果如图13所示。补偿后,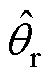 与
与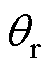 吻合,与此同时,
吻合,与此同时, 滞后于
滞后于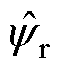 相位0.42rad,该相位即为锁相基准自适应调整的结果,相比较于锁相环单独作用时,补偿角度减小了0.42rad。图14为算法切入瞬间的动态响应仿真结果,可以看出,在前260ms时间内,锁相环通过锁相,补偿角度达到最大值以补偿环路滤波器所造成的误差,后540ms内,通过自适应调整锁相基准,使得补偿的角度逐渐减少,以补偿
相位0.42rad,该相位即为锁相基准自适应调整的结果,相比较于锁相环单独作用时,补偿角度减小了0.42rad。图14为算法切入瞬间的动态响应仿真结果,可以看出,在前260ms时间内,锁相环通过锁相,补偿角度达到最大值以补偿环路滤波器所造成的误差,后540ms内,通过自适应调整锁相基准,使得补偿的角度逐渐减少,以补偿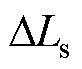 等非理想因素所造成的误差,最终,输出补偿角度
等非理想因素所造成的误差,最终,输出补偿角度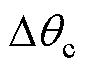 =0.68rad。通过上述两个过程,实现对位置估算误差的全补偿。
=0.68rad。通过上述两个过程,实现对位置估算误差的全补偿。

图13 基于自适应锁相基准锁相环仿真结果
Fig.13 The simulation results based on the PLL with adaptive phase-locked reference
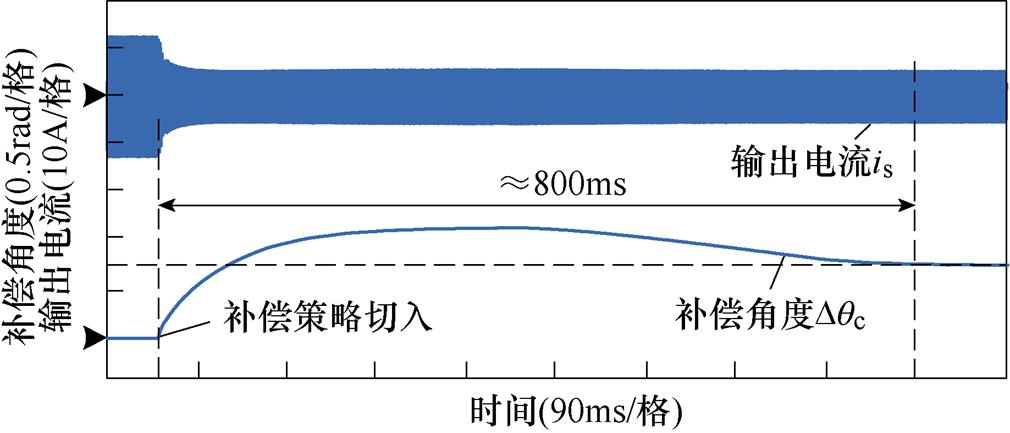
图14 自适应基准锁相环动态响应性能
Fig.14 The dynamic response performanceof PLL with adaptive phase-locked reference
锁相基准自适应调整算法根据前后周期|is|的变化来调整下一周期的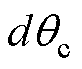 的方向。当负载突变时,电流突变,可能会导致突变后的第一个周期
的方向。当负载突变时,电流突变,可能会导致突变后的第一个周期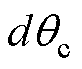 极性的错误判断,由于
极性的错误判断,由于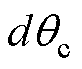 很小,对位置补偿角造成的影响很小。图15所示为负载突变时自适应基准锁相环位置估算误差补偿效果,可以看出,负载突变期间,
很小,对位置补偿角造成的影响很小。图15所示为负载突变时自适应基准锁相环位置估算误差补偿效果,可以看出,负载突变期间,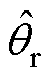 与
与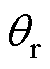 依然保持较好的吻合。
依然保持较好的吻合。
为验证自适应基准锁相环的有效性,本文搭建基于TMS320F28377D和GaNFET功率器件的高速驱动平台,相应电机与驱动平台如图16所示,该电机带叶轮负载。
采用电流-频率比控制的起动方式,当转速达到5 000r/min时,切换到转子磁链观测器,转速逐渐上升到30 000r/min,实际转子位置通过线性霍尔传感器获取。基于锁相环的实验结果(锁相基准为0)如图17所示。为验证所提出方法的有效性,在实验中设定Ls=0mH。如图17a所示,在30 000r/min下,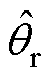 滞后于
滞后于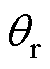 相位0.6rad。锁相环重构的误差
相位0.6rad。锁相环重构的误差 约为1.18rad,可见重构误差大于实际误差,因此,如图17b所示,锁相环将
约为1.18rad,可见重构误差大于实际误差,因此,如图17b所示,锁相环将 与
与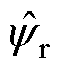 锁相后,
锁相后,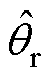 超前于
超前于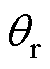 ,造成“过补偿”。由此可见,锁相环单独作用时,无法实现对转子位置估算误差的全补偿。
,造成“过补偿”。由此可见,锁相环单独作用时,无法实现对转子位置估算误差的全补偿。
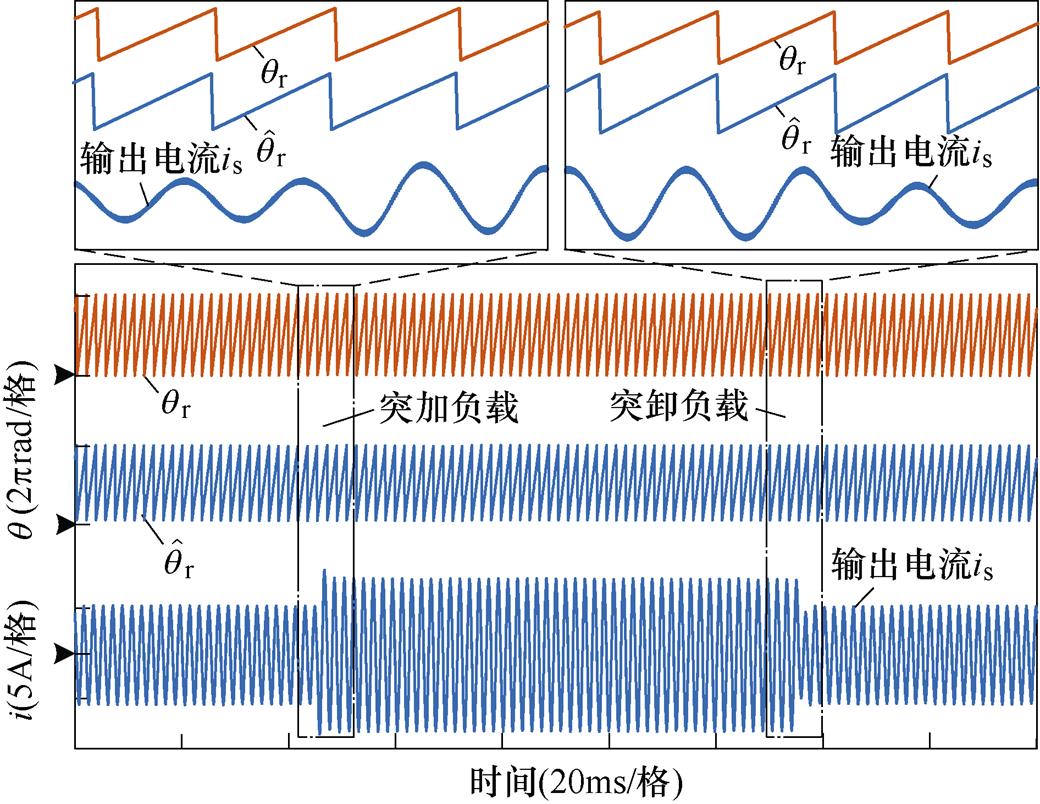
图15 负载突变时自适应锁相基准锁相环仿真结果
Fig.15 The simulation results based on the PLL with adaptive phase-locked reference under load variation

图16 高速永磁同步电机与驱动平台
Fig.16 HSPMSM and high-speed drive platform
图18所示为锁相环补偿算法切入瞬间的动态响应实验结果,可以看出,电流减小到最小值后,又稍微增大,体现出单独采用锁相环补偿位置误差时,会造成“过补偿”。
图19所示为采用自适应基准锁相环补偿位置误差,可以看出,以最小电流为目标对锁相基准进行自适应调整后,输出电流进一步减小,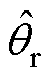 与
与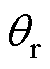 完全吻合,实现了误差的全补偿。此外,
完全吻合,实现了误差的全补偿。此外,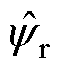 超前于
超前于 相位0.62rad,相较于锁相环单独作用时,输出的补偿角度减小了0.62rad。图20为算法切入瞬间的动态响应实验结果,在补偿算法切入后的1.2s,补偿角度达到最大值1.2rad,实现对环路滤波器造成的补偿,在随后的2.6s内自适应调整锁相基准,补偿角度减小,最终输出的补偿角度
相位0.62rad,相较于锁相环单独作用时,输出的补偿角度减小了0.62rad。图20为算法切入瞬间的动态响应实验结果,在补偿算法切入后的1.2s,补偿角度达到最大值1.2rad,实现对环路滤波器造成的补偿,在随后的2.6s内自适应调整锁相基准,补偿角度减小,最终输出的补偿角度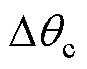 约为0.58rad,补偿
约为0.58rad,补偿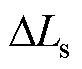 等其他非理想因素所成的误差,即实现转子位置估算误差的全补偿。
等其他非理想因素所成的误差,即实现转子位置估算误差的全补偿。
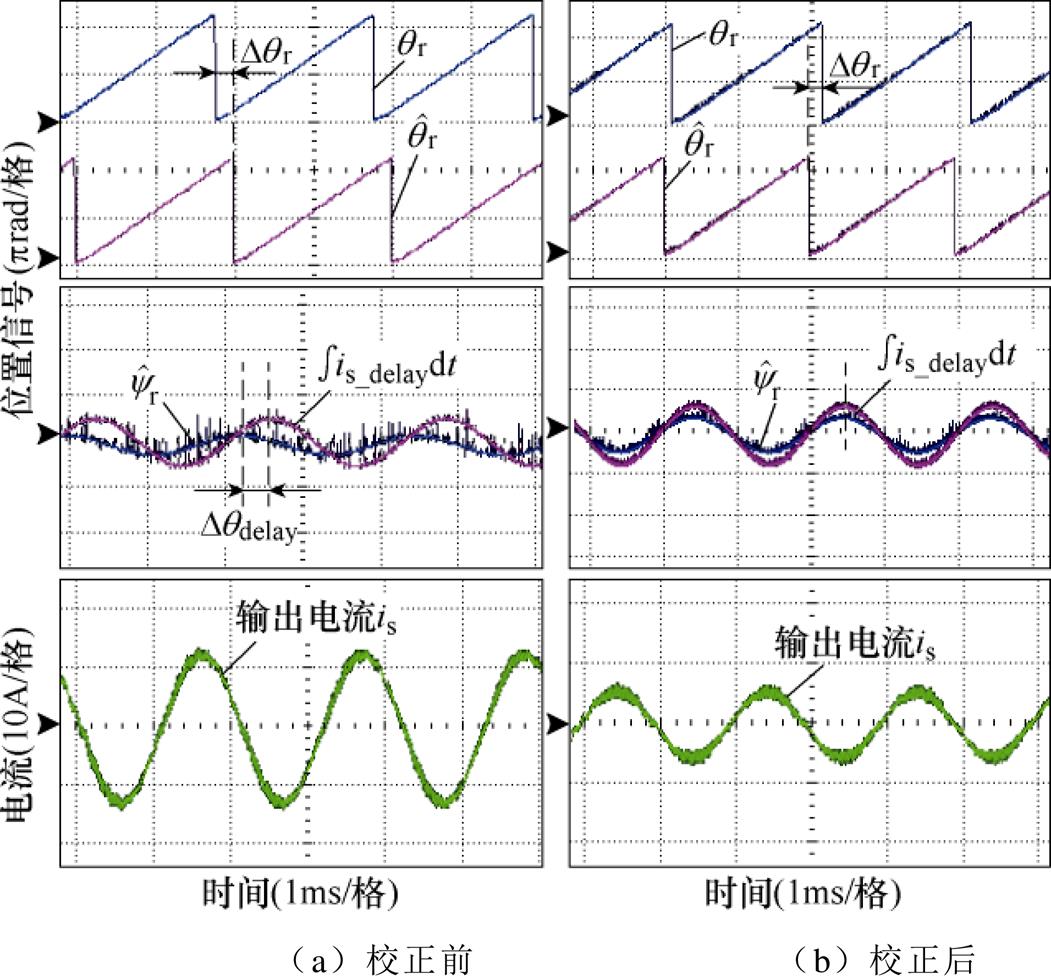
图17 基于锁相环的实验结果(锁相基准为0)
Fig.17 The experimental results based on the PLL (the phase-locked reference is 0)
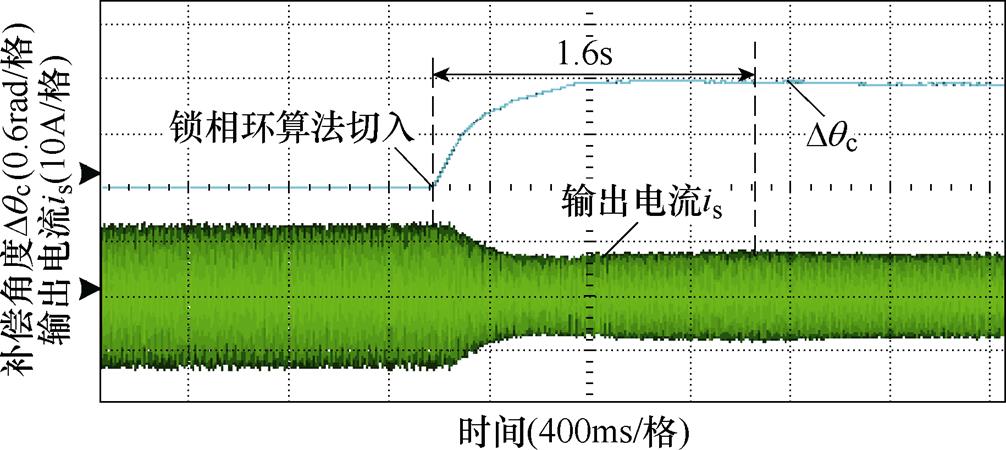
图18 锁相环动态响应性能
Fig.18 The dynamic response performanceof the PLL
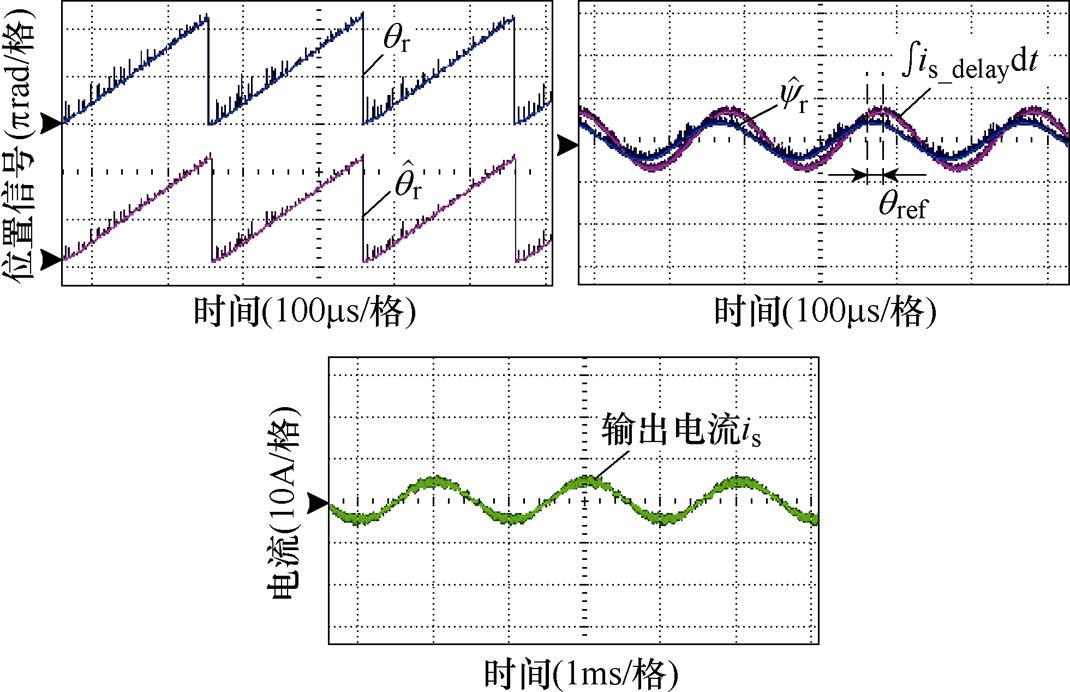
图19 基于自适应基准锁相环的补偿效果
Fig.19 The error compensation effect based on the PLL with adaptive phase-locked reference
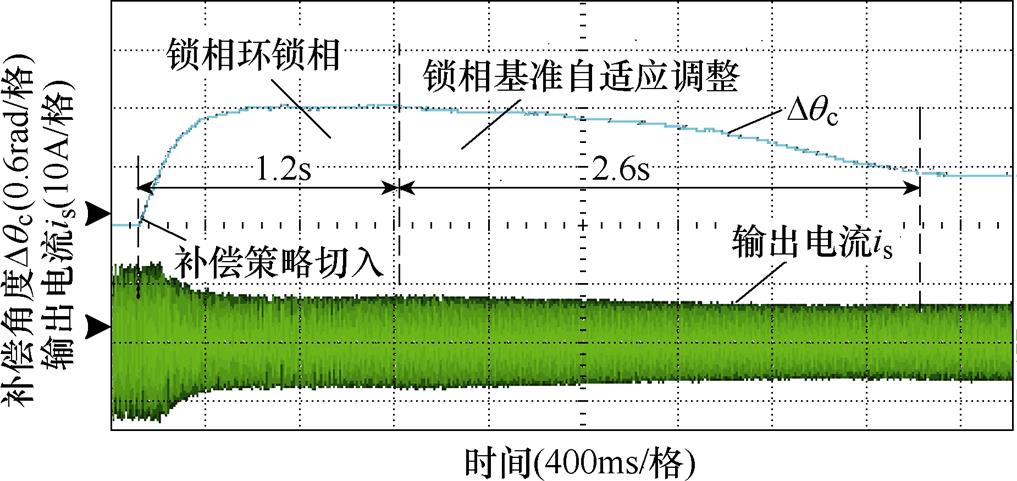
图20 自适应基准PLL动态响应性能
Fig.20 The dynamic response performanceof the PLL with adaptive phase-locked reference
图21所示为变转速时自适应基准锁相环位置估算补偿效果,实验样机带叶轮负载,转速变化,负载变化。可以看出,在变转速期间,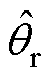 与
与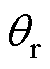 保持较好吻合。
保持较好吻合。
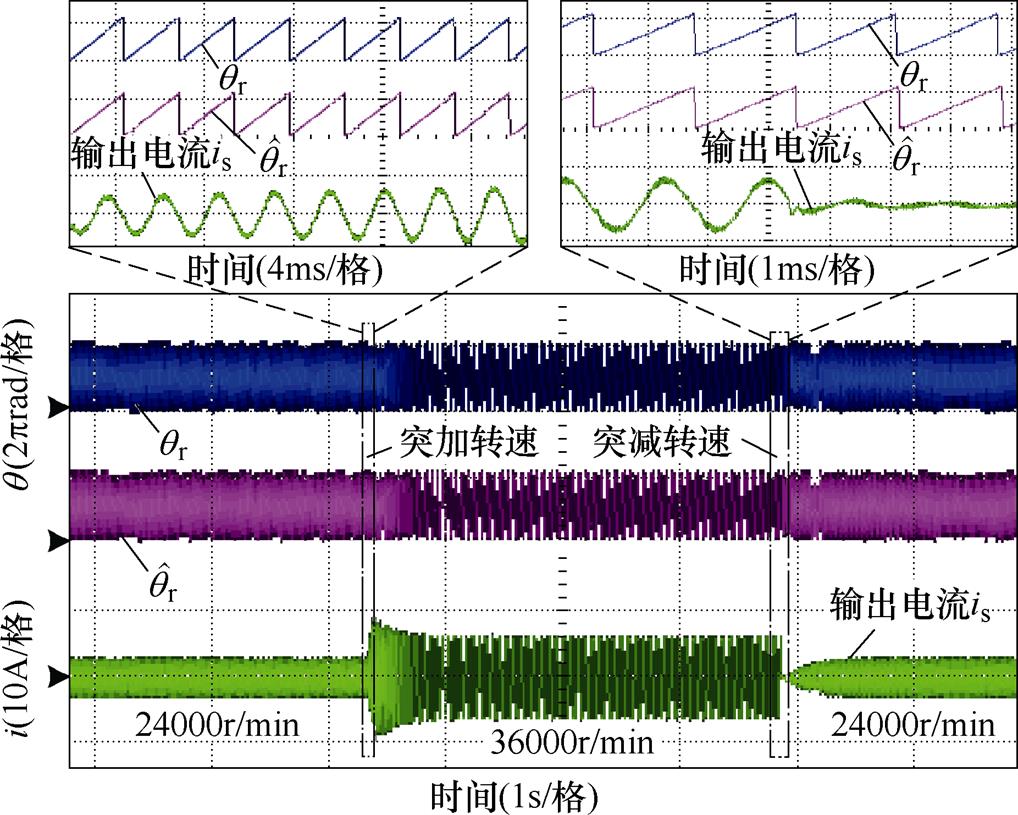
图21 自适应基准锁相环动态性能实验结果
Fig.21 The experimental results of the dynamic performance based on the PLL with adaptive phase-locked reference
综上所述,本文通过较为全面的仿真和实验结果对比分析,验证了所提出的自适应基准锁相环的有效性。
本文提出了一种适用于高速永磁同步电机的转子位置估算误差全补偿方法,能够实现对环路滤波器和电感参数偏差所造成误差的补偿,所提出方法的优势在于:
1)无需对位置估算误差准确定量,即可实现对位置估算误差的全补偿。
2)补偿算法中未引入敏感参数,具有一定的鲁棒性。
3)该方法与转子磁链观测器相配合,在电感参数误差为100%的情况下,能够准确地估计转子位置,提高了转子磁链观测器的适用性和鲁棒性。最后,通过仿真和实验,验证了本文所提出方法的有 效性。
参考文献
[1] Hong D K, Woo B C, Lee J Y, et al. Ultra high speed motor supported by air foil bearings for air blower cooling fuel cells[J]. IEEE Transactions on Mag- netics, 2012, 48(2): 871-874.
[2] 孙权贵, 邓智泉, 张忠明. 基于齿槽效应的高速永磁电机转子涡流损耗解析计算[J]. 电工技术学报, 2018, 33(9): 1994-2004.
Sun Quangui, Deng Zhiquan, Zhang Zhongming. Analytical calculation of rotor eddy current losses in high speed permanent magnet machines accountiing for influence of slot opening[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1994- 2004.
[3] 张凤阁, 杜光辉, 王天煜, 等. 高速电机发展与设计综述[J]. 电工技术学报, 2016, 31(7): 1-18.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18.
[4] 戴兴建, 姜新建, 王秋楠, 等. 1MW/60MJ飞轮储能系统设计与实验研究[J]. 电工技术学报, 2017, 32(21): 169-175.
Dai Xingjian, Jiang Xinjian, Wang Qiunan, et al. Design and experimental study of 1MW/60MJ flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 169- 175.
[5] 戈宝军, 罗前通, 王立坤, 等. 高速永磁同步电动机铁耗分析[J]. 电机与控制学报, 2020, 24(4): 32-39.
Ge Baojun, Luo Qiantong, Wang Likun. Analysis of iron losses of high speed permanent magnet syn- chronous motor[J]. Electric Machines and Control, 2020, 24(4): 32-39.
[6] 刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017, 32(16): 76-88.
Liu Jilong, Xiao Fei, Shen Yang, et al. Review of sensorless control technology of permanent magnet synchronous motor[J]. Transactions of China Electro- technical Society, 2017, 32(16): 76-88.
[7] 谷善茂, 何凤有, 谭国俊, 等. 永磁同步电动机无传感器控制技术现状与发展[J]. 电工技术学报, 2009, 24(11): 15-20.
Gu Shanmao, He Fengyou, Tan Guojun, et al. A review of sensorless control technology of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2009, 24(11): 15-20.
[8] 李永东, 朱昊. 永磁同步电机无速度传感器控制综述[J]. 电气传动, 2009, 39(9): 3-10.
Li Yongdong, Zhu Hao. Overview of sensorless control of permanent magnet synchronous motors[J]. Electric Drive, 2009, 39(9): 3-10.
[9] Wu Chao, Sun Xiangdong, Wang Jianyuan. A rotor flux observer of permanent magnet synchronous motors with adaptive flux compensation[J]. IEEE Transactions on Energy Conversion, 2019, 34(99): 2106-2117.
[10] 王子辉. 永磁同步电机全速度范围无位置传感器控制策略研究[D]. 杭州: 浙江大学, 2012.
[11] 钟臻峰, 金孟加, 沈建新. 基于分段PI调节器的模型参考自适应永磁同步电动机全转速范围无传感器控制[J]. 中国电机工程学报, 2018, 38(4): 1203- 1211.
Zhong Zhenfeng, Jin Mengjia, Shen Jianxin. Full speed range sensorless control of permanent magnet synchronous motor with phased PI regulator-based model reference adaptive system[J]. Proceedings of the CSEE, 2018, 38(4): 1203-1211.
[12] Kim H, Son J B, Lee J Y. A high-speed sliding-mode observer for the sensor-less speed control of PMSM[J]. IEEE Transactions on Industry Electronics, 2011, 47(3): 1337-1343.
[13] 尹忠刚, 张瑞峰, 钟彦儒, 等. 基于抗差扩展卡尔曼滤波器的永磁同步电机转速估计策略[J]. 控制理论与应用, 2012, 29(7): 921-927.
Yin Zhonggang, Zhang Ruifeng, Zhong Yanru, et al. Speed estimation for permanent magnet synchronous motor based on robust extended Kalman filter[J]. Control Theory & Applications, 2012, 29(7): 921- 927.
[14] 薛哗, 魏佳丹, 周波. 三级式同步电机低速阶段无位置传感器起动控制高频信号注入法的对比[J]. 电工技术学报, 2018, 33(12): 2703-2712.
Xu Hua, Wei Jiadan, Zhou Bo. Comparative investigation on sensorless control of three-stage synchronous motor based on high-frequency injection method at low speed[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2703-2712.
[15] 刘颖, 周波, 冯瑛, 等. 永磁同步电机低速无传感器控制及位置估计误差补偿[J]. 电工技术学报, 2012, 27(11): 38-45.
Liu Ying, Zhou Bo, Feng Ying, et al. Sensorless control of SPMSM based on high frequency current signal injection in the direct axis at low and zero speed[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 38-45.
[16] 王辉, 潘文丽, 吴轩. 一种自适应滤波的永磁同步电机转子位置估算方法[J]. 电机与控制学报, 2019, 23(11): 51-59.
Wang Hui, Pan Wenli, Wu Xuan. Position estimation method of permanent magnet synchronous motor based on adaptive filter[J]. Electric Machines and Control, 2019, 23(11): 51-59.
[17] 李旭春, 张鹏, 严乐阳, 等. 具有参数辨识的永磁同步电机无位置传感器控制[J]. 电工技术学报, 2016, 31(14): 139-147.
Li Xuchun, Zhang Peng, Yan Leyang, et al. Sensor- less control of permanent magnet synchronous motor with online parameter identification[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 139- 147.
[18] Song Xinda, Fang Jiancheng, Han Bangcheng, et al. Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1438-1449.
[19] 年珩, 李嘉文, 万中奇. 基于参数在线辨识的永磁风力发电机无位置传感器控制技术[J]. 中国电机工程学报, 2012, 32(12): 146-154.
Nian Heng, Li Jiawen, Wan Zhongqi. Sensorless control technique of PMSG for wind power appli- cation based on on-line parameter identification[J]. Proceedings of the CSEE, 2012, 32(12): 146-154.
[20] 黄科元, 高丽真, 黄守道. 基于电流环误差修正的高速永磁同步电机转子位置校正方法[J]. 中国电机工程学报, 2017, 37(8): 241-249.
Huang Keyuan, Gao Lizhen, Huang Shoudao. A correction method of rotor positions for high speed permanent magnet synchronous motor based on the error correction of the current loop[J]. Proceedings of CSEE, 2017, 37(8): 241-249.
[21] 顾聪, 王晓琳, 邓智泉. 一种基于双重锁相环的高速永磁同步电机转子位置估计误差全补偿方法[J]. 中国电机工程学报, 2020, 40(3): 962-970.
Gu Cong, Wang Xiaolin, Dang Zhiquan. A rotor position estimated error correction method for high- speed permanent magnet synchronous motor Based on dual-phase-locked-loop[J]. Proceedings of the CSEE, 2020, 40(3): 962-970.
[22] 施晓青, 王晓琳, 徐同兴, 等. 高速无刷直流电机自寻优换相校正策略[J]. 电工技术学报, 2019, 34(19): 3997-4005.
Shi Xiaoqing, Wang Xiaolin, Xu Tongxing, et al. Self-optimization commutation correction strategy for high-speed brushless DC motor[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3997-4005.
[23] Gu Cong, Wang Xiaolin, Zhang Feilong, et al. Correction of rotor position estimation error for high- speed permanent magnet synchronous motor sensor- less drive system based on minimum-current-tracking method[J]. IEEE Transactions on Industrial Electro- nics, 2020, 67(10): 8271-8280.
A Rotor Position Error Compensation Algorithm for High-Speed Permanent Magnet Motor Based on Phase-Locked Loop with Adaptive Reference
Abstract The accuracy of rotor position information affects the performance of high-speed permanent magnet synchronous motor (HSPMSM). The rotor position estimation is vulnerable to some non-ideal factors at high speed, such as the filters and the deviations of motor parameters. In this paper, a phase-locked loop with adaptive phase-locked reference is proposed to eliminate the rotor position error. The main idea of the proposed method is that the position error related to the fundamental frequency is compensated by reconstructing the position error with phase-locked loop (PLL). The reference of phase-locked loop is adjusted adaptively to minimize the current and compensate the position error of non-fundamental frequency. In this way, the position error is fully compensated. The proposed method has the advantages of simple implementation, low parameter-dependence and strong robustness. Finally, simulations and experiments were conducted on a HSPMSM, and the results verified the effectiveness of the proposed method.
keywords:High-speed permanent magnet synchronous motor(HSPMSM), rotor flux observer, position estimated error, phase-locked loop
DOI: 10.19595/j.cnki.1000-6753.tces.200658
中图分类号:TM351
王晓琳 男,1976年生,教授,研究方向为永磁电机、无轴承电机,高速电机的驱动和控制。E-mail: wangxl@nuaa.edu.cn(通信作者)
刘思豪 男,1994年生,硕士研究生,研究方向为高速永磁电机控制。E-mail: 1354489565@qq.com
收稿日期2020-06-16
改稿日期 2020-08-01
国家自然科学基金(5217070613)和江苏省自然科学基金(BK20201297)资助项目。
(编辑 崔文静)