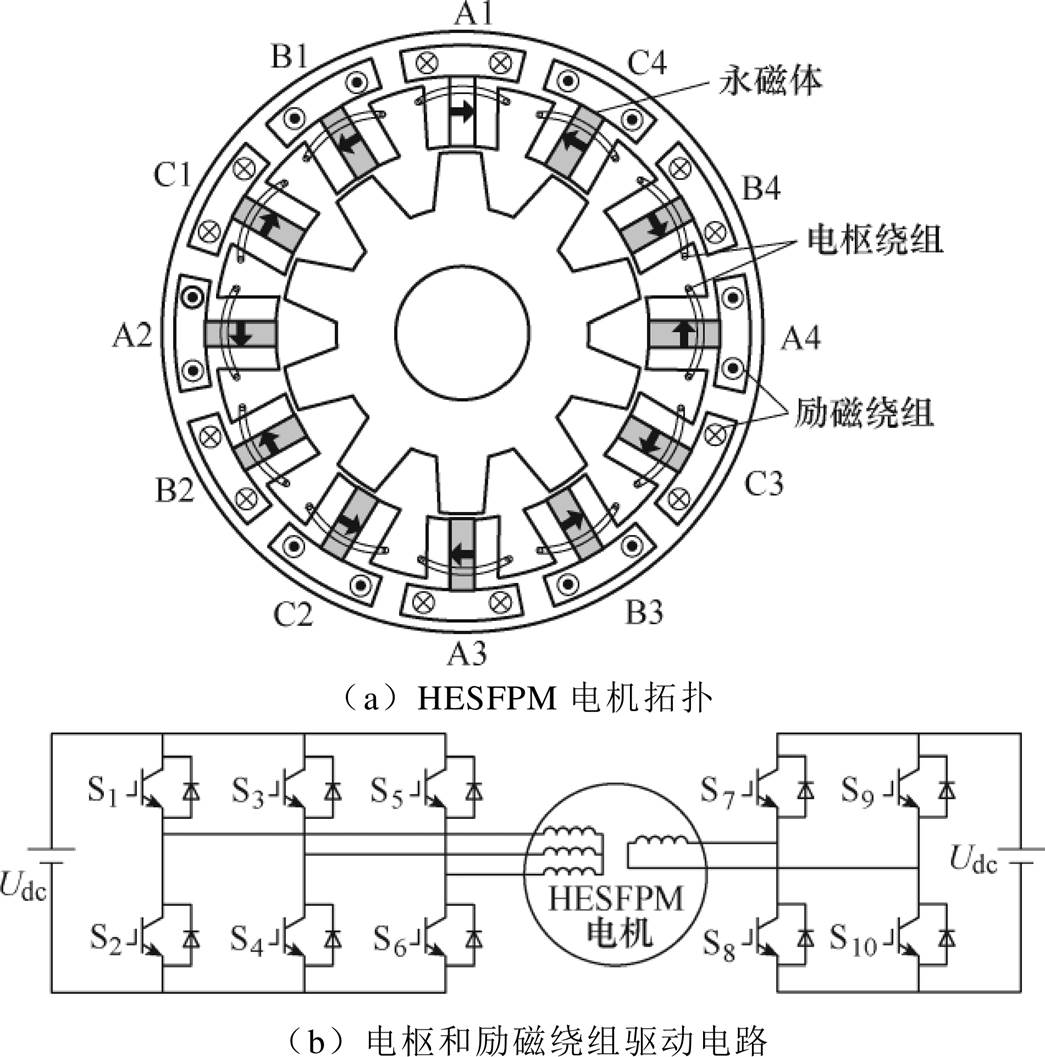
图1 HESFPM电机的拓扑及其驱动电路
Fig.1 Topology of HESFPM machine andits drive circuit
摘要 传统的零速或低速位置估计方法是将高频信号注入到永磁同步电机（PMSMs）的电枢绕组中，但该方法应用于具有低凸极比的混合励磁开关磁链永磁（HESFPM）电机时，位置检测精度较低。因此，该文提出将高频脉冲信号注入励磁绕组的转子位置估计方法。由于HESFPM电机中励磁绕组产生的磁链在d轴上，因此，励磁绕组中注入的高频脉冲信号可以在d轴上感应出高频电流信号。通过检测q轴高频电流信号，即当q轴高频电流信号为零时，判断转子的实际位置。为了验证所提出的位置估计方法，在一台HESFPM实验样机上进行实验验证。结果表明，所提出的HESFPM电机位置估计方法在稳态与动态响应方面均具有较高的精度。
关键词：混合励磁开关磁链永磁电机 位置估计 无传感器控制 高频信号注入
永磁同步电机（Permanent Magnet Synchronous Machines, PMSMs）因其具有高转矩密度和高效率的特点而得到广泛的应用[1-3]。混合励磁开关磁链永磁（Hybrid Excited Switched Flux Permanent Magnet, HESFPM）电机继承了PMSMs的优点，其d轴磁链可以通过改变励磁电流或电枢电流进行调节，且具有更宽的调速范围和更高的效率。因此，该类电机在电动汽车、航天航空等[4-6]领域具有应用潜力。通常情况下，HESFPM电机转子位置可以通过编码器、旋转变压器或霍尔传感器来检测，但这会增加成本并降低整个系统的可靠性，采用无位置传感器控制可以有效解决以上问题[7-10]。
在PMSMs中，通常利用反电动势来估计中高速时的转子位置。然而，在相对低速甚至零速时，由于反电动势较低，利用反电动势进行位置估计会出现较大的误差。在这种情况下，高频信号注入法成为获取低速时电机转子位置的有效方法。例如，旋转正弦高频信号[11-14]、脉振正弦高频信号[12]或方波高频信号[13-14]均可用于转子位置估计。高频信号注入法可分为两类，即在ab 坐标系或dq坐标系注入高频信号。与在ab 坐标系注入高频信号相比，在旋转dq坐标系注入高频信号的方法可以在不增大转矩脉动的情况下实现精确的位置估计[15-21]。
然而，无论是在ab 坐标系还是dq坐标系注入高频信号，转子位置的估计精度在很大程度上都取决于永磁电机的凸极比。当转子凸极比降低时，将出现转子位置误差增大甚至无法运行的情况。由于HESFPM电机具有较低的凸极比或磁饱和凸极比，将高频信号注入ab 坐标系或dq坐标系的位置估计方法无法获得高精度的转子位置估计。为了解决这一问题，本文提出一种将高频脉冲信号注入励磁绕组的位置估计方法。该方法以励磁绕组产生的磁链与d轴磁链方向相同为前提，当q轴的感应电流信号为零时，估计的转子位置与实际转子位置相同。该方法利用励磁绕组与电枢绕组间的互感获得转子位置，不依赖转子的凸极特性。
本文首先介绍HESFPM电机的数学模型和高频模型；然后提出基于励磁绕组高频脉冲注入的位置估计方法；接着分析系统参数对位置估计精度的影响；最后通过基于励磁绕组高频信号注入的位置估计方法的实验结果，验证所提方法的有效性。
图1为12/10 HESFPM电机的拓扑和置于定子中的电枢绕组和励磁绕组的驱动电路。如图1a所示，励磁绕组和永磁体产生的磁通为并联。通过增大励磁电流，可以增大气隙磁通密度。因此，可以通过励磁电流来调节励磁磁场。如图1b所示，通过一个H桥电路控制励磁电流。
图1 HESFPM电机的拓扑及其驱动电路
Fig.1 Topology of HESFPM machine andits drive circuit
图2为忽略铁损和磁饱和时HESFPM电机的低频等效电路模型，图中，s为微分算子。因此，dq轴电压和励磁绕组电压可以表示为
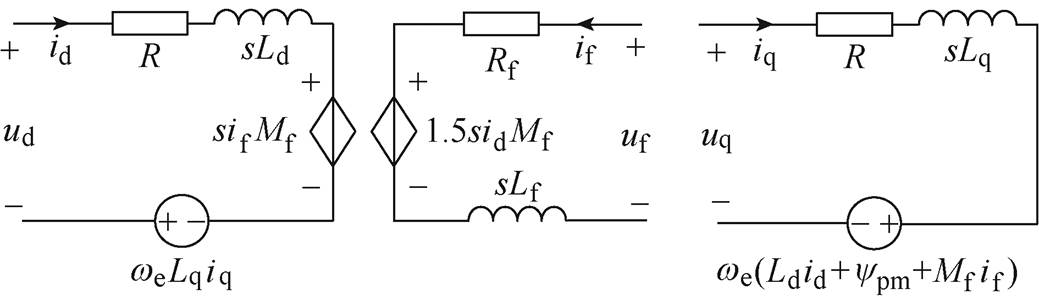
图2 HESFPM电机的低频等效电路
Fig.2 Equivalent circuit of HESFPM machine at low frequency
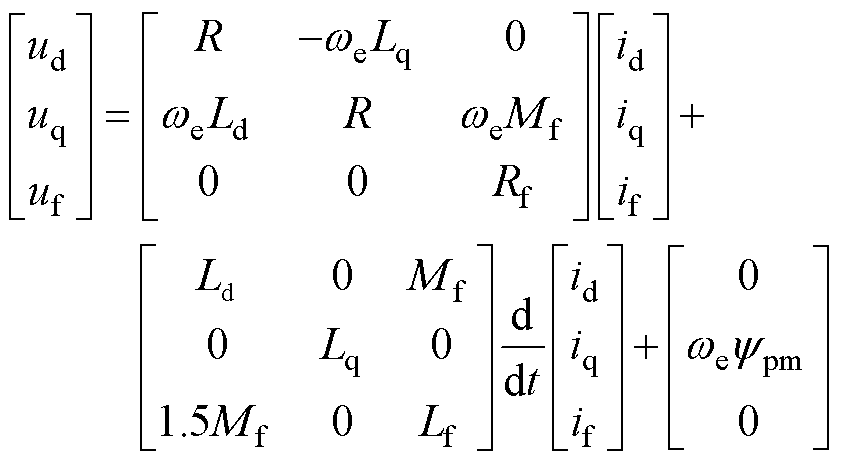（1）式中，ud、uq、id、iq、Ld、Lq分别为d轴和q轴上的电压、电流和电感；Lf、Mf分别为励磁绕组的自感、励磁绕组与电枢绕组的互感；ypm为永磁磁链；uf、if分别为励磁绕组电压和电流；R、Rf分别为电枢绕组电阻和励磁绕组电阻；we为转子电角速度。可知，由于电枢绕组和励磁绕组之间存在互感，励磁绕组的电流变化会引起电枢绕组产生同频率的电流脉动。
通过第1节分析可知，励磁绕组的电流变化会在电枢绕组中产生电流脉动。在低速或零速时，忽略转子电角速度we，高频电流所产生的电感压降远高于电阻压降。因此，简化HESFPM电机的高频数学模型，并忽略电阻压降，可得HESFPM电机高频等效模型，如图3所示。dq轴的高频电压和励磁绕组的高频电压为
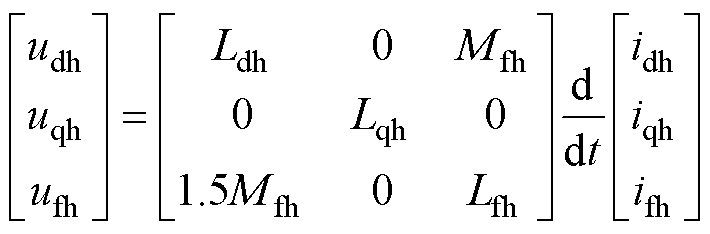（2） 式中，udh、uqh、idh、iqh、Ldh、Lqh分别为d轴和q轴上的高频电压、高频电流和高频电感；Lfh、Mfh分别为励磁绕组的高频自感、励磁绕组与电枢绕组的高频互感；ufh、ifh分别为励磁绕组高频电压和高频电流。
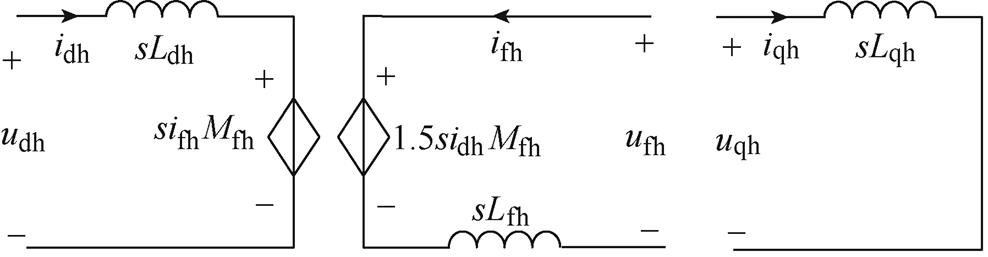
图3 HESFPM电机的简化高频等效电路模型
Fig.3 Simplified equivalent circuit of HESFPM machine at high frequency
定义Dqe为估计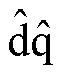
坐标系和实际dq坐标系之间的角度差，两个坐标轴之间的变换矩阵可以表示为
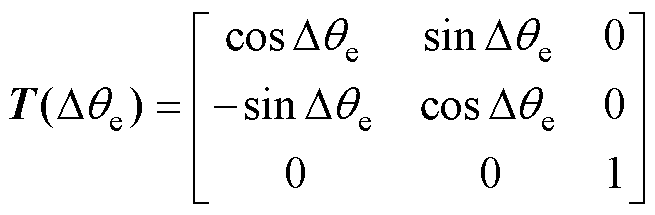（3）从式（2）可知，当高频电压脉冲仅注入励磁绕组中时，d轴和q轴上的感应电流分别为
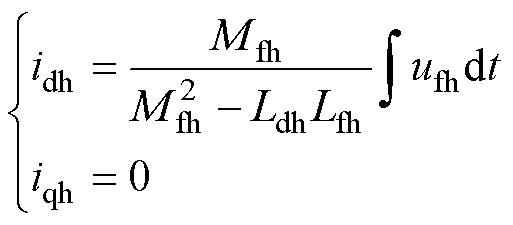（4）
因此，估计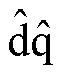坐标系的电流可以表示为
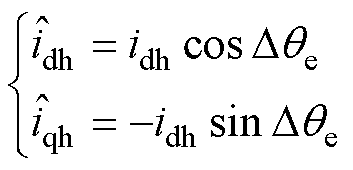（5）根据式（5）可知，由于励磁绕组产生的磁链在d轴上，因此，励磁绕组的高频电压脉冲在实际d轴上会产生相同频率的高频电流。当估计的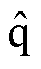
轴电流等于零时，估计的
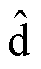轴与实际d轴重合，因而可得转子的实际位置。
图4分析了注入励磁绕组中的高频电压信号与高频电流响应的关系。如图4a所示，向励磁绕组中注入方波信号，高频励磁绕组端电压激励出的励磁电流波形如图4b所示。如图4c和图4d所示，由于励磁和电枢绕组之间存在互感，因此，在估计的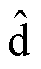轴和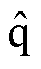轴上会产生相同频率的感应电流。当估计的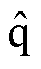轴电流为零时，估计的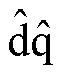坐标系和实际的dq坐标系之间的角度差等于零。
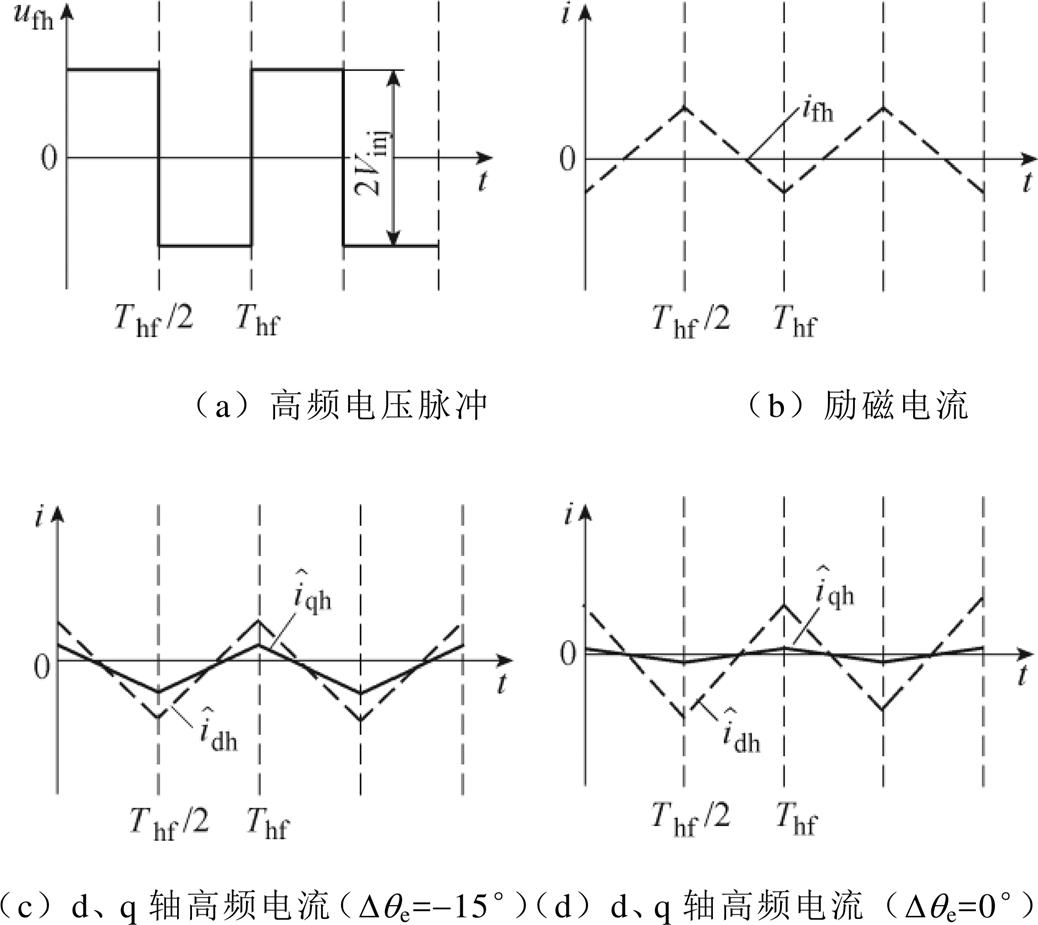
图4 不同估计位置误差下的注入高频电流响应
Fig.4 HF pulse currents in field and armature windings at different position estimation errors
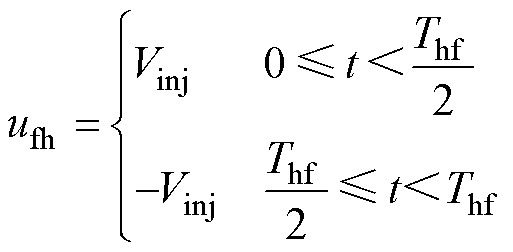（6）式中，Vinj为注入电压信号幅值；Thf为注入高频方波信号的周期。
为了估计零速时HESFPM电机的初始转子位置，打开三相桥中的开关S2、S4和S6，使电枢绕组短路。当高频电压脉冲注入励磁绕组时，通过电流传感器对电枢绕组中的感应电流进行采样。为了得到估计的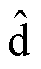轴和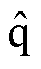轴上电流变化的幅值，在每个周期的0和Thf/2时刻对电枢电流进行采样。因此，电流采样频率是注入高频电压脉冲的两倍。
传统d轴高频信号注入检测转子初始位置的方法，需要进行磁极极性判断，本文提出的基于励磁绕组高频信号注入方法无需进行磁极极性判断，具体分析如下：
基于d轴高频信号注入方法中，采样的q轴高频电流与转子位置估计误差Dqe的关系可表示为
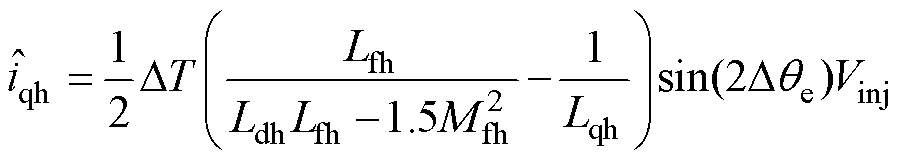（7）式中，DT为离散的时间间隔。
由式（7）可知，位置观测器角度误差与解耦后的误差函数关系如图5所示，误差函数在Dqe∈(-180°, 180°)区间内，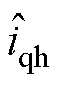
(Dqe)=0有4个解，分别为-90°、0°、90°和180°。经过位置观测器收敛，位置估计误差最终可收敛在0°和180°两个位置，-90°和90°为不稳定点。
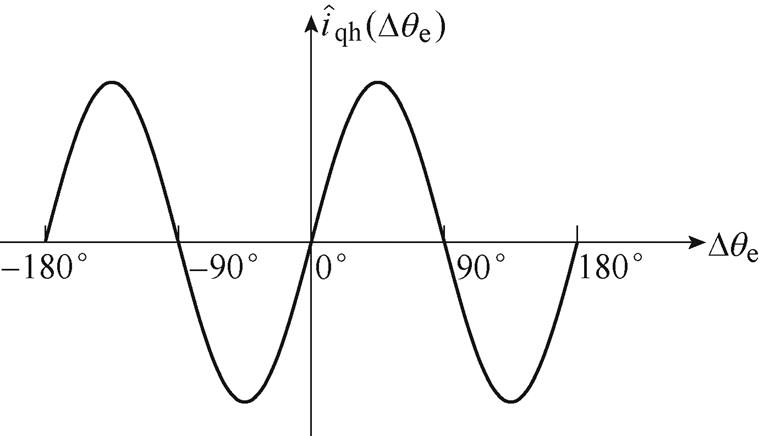
图5 基于d轴高频信号注入时q轴高频电流
Fig.5 q-axis high frequency current against estimated position error based on d-axis high-frequency signal injection
基于励磁绕组高频信号注入的方法中，采样的q轴高频电流与转子位置估计误差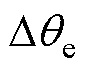
的关系可表示为
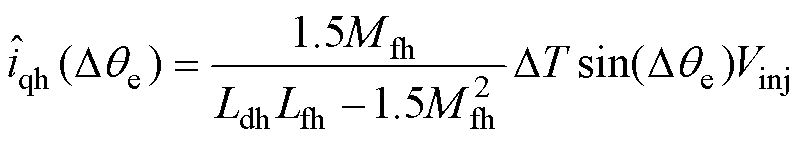（8）位置估计误差与解耦后的q轴高频电流差值关系如图6所示，估计角度误差函数在Dqe∈(-180°, 180°)区间内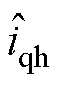，(Dqe)=0仅有两个解，分别为0°和180°。与基于d轴高频信号注入方法相比，减少了两组解。同基于d轴信号注入方法原理相同，最终估计角度误差经PI位置观测器唯一收敛到0°位置。因此，该方法不需要磁极极性判断的步骤。
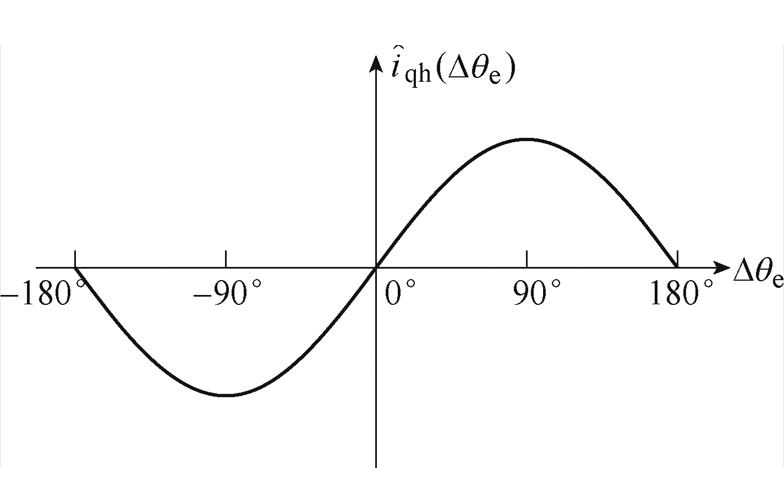
图6 基于励磁绕组高频信号注入时q轴高频电流
Fig.6 q-axis high frequency current against estimated position error based on field winding high frequency signal injection
图7为HESFPM电机初始位置估计控制框图。估计的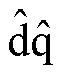坐标系中q轴电流变化量为零，采用闭环控制进行位置估计。在稳态时，当反馈的q轴电流变化幅值为零时，得到估计位置。
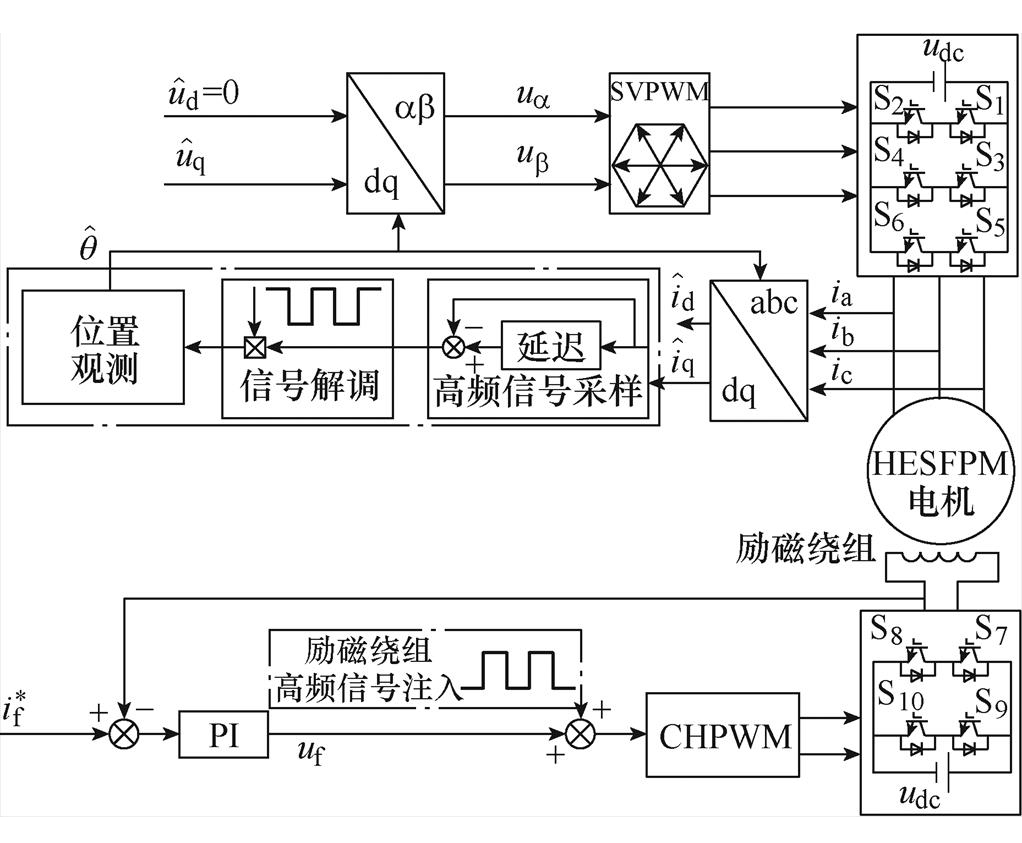
图7 初始位置估计控制框图
Fig.7 Control diagram for the initial position estimation
低速时不同转子位置估计误差下的励磁和电枢绕组高频电压脉冲及其电流如图8所示。如图8a和图8b所示，与零速时的初始位置估计不同，低速时励磁电流和电枢电流的平均值不为零。如图8c和图8d所示，为了简化控制，使用d轴电流等于零控制，电磁转矩由q轴电流控制。因此，在图8c和图8d中可以观察到q轴电流产生了直流偏置。
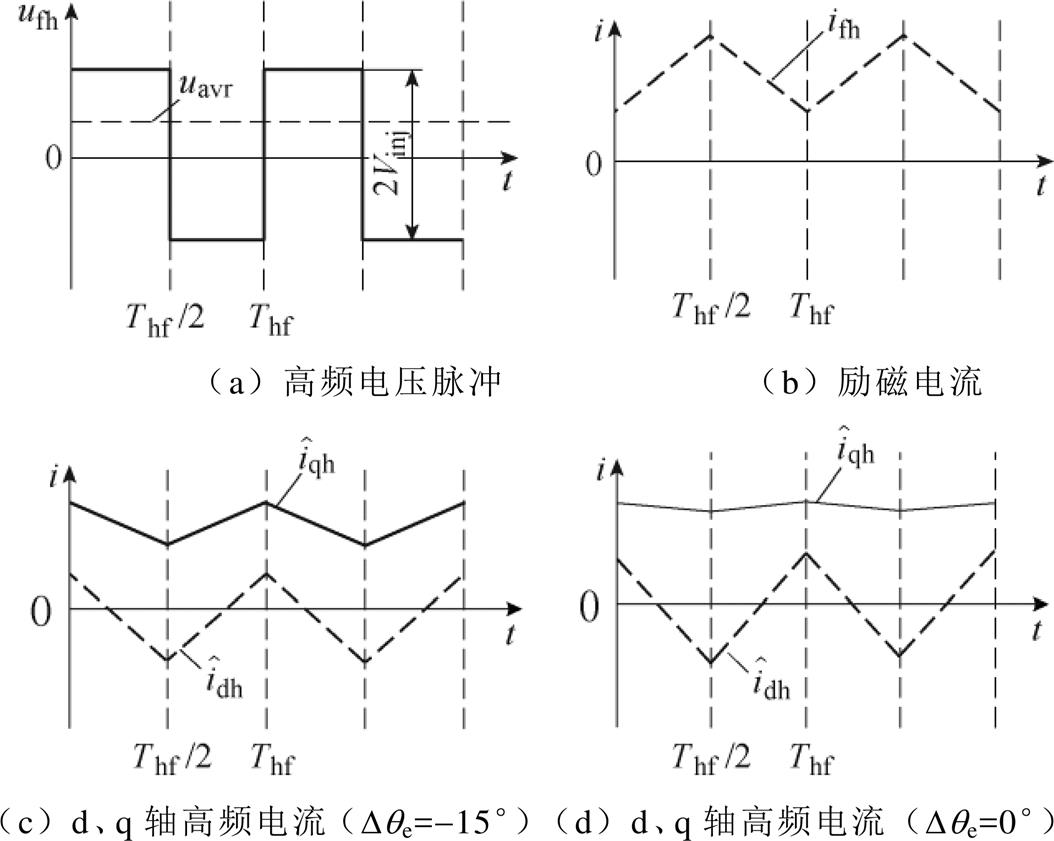
图8 低速时不同转子位置估计误差下的励磁和电枢绕组高频电压脉冲及其电流
Fig.8 HF voltage pulse and corresponding currents in field and armature windings at low speed with different rotor position errors
采用高通滤波器提取估计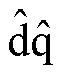坐标系中的感应电流。在每个周期的0和Thf/2时刻，通过对相电流采样，可以得到励磁绕组中注入高频脉冲引起的感应电流变化幅值。如图8c和图8d所示，与初始位置估计类似，如果估计的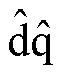坐标系和实际的dq坐标系之间的角度差不等于零，则估计的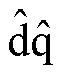坐标系中的高频q轴电流变化的幅值也不为零。当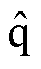轴电流变化量为零时，估计位置估计误差最小。如图9所示为HESFPM电机低速区无位置控制框图。通过采样估计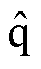轴电流，经过位置观测器模块识别转子的位置和转速信息。
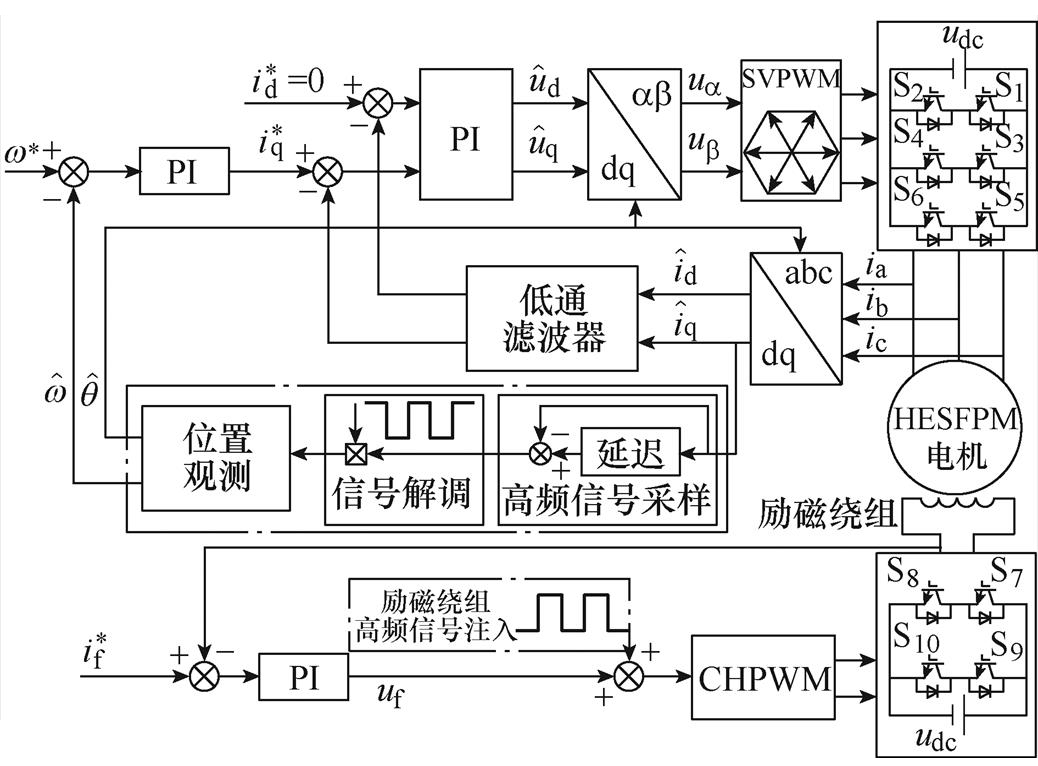
图9 低速时位置估计方法的控制框图
Fig.9 Control diagram for the position estimation method at low speed
注入高频电压的频率需要远高于基波电流的频率，并低于逆变器开关频率。通常，注入的高频信号频率可选取几百到几千Hz，具体的频率需要根据系统状态选取。采用带通滤波器提取高频电流信号时，基波相电流经过带通滤波器会产生一定的幅值衰减。为了降低相电流基波幅值的衰减，需要提高注入高频电压与基波相电流频率的比值。典型带通滤波器的传递函数可表示为
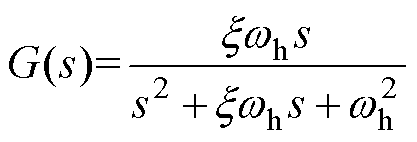（9）式中，x 为带通滤波器的阻尼系数；wh为注入高频信号角速度。定义注入高频信号的频率与基波相电流的频率比为khb，表示为
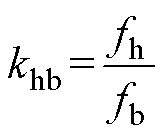（10）
式中，fh为注入高频信号频率；fb为三相基波电流频率。
由式（10）可得基波相电流经过带通滤波器的幅值衰减倍数可表示为
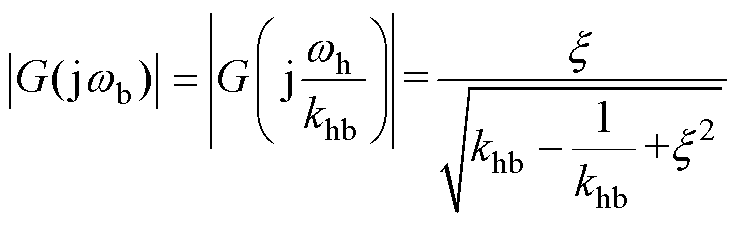（11）通过式（11）可知，基波电流信号经过带通滤波器后幅值衰减倍数随khb增大而减小。在基波频率不变的条件下，注入高频电压信号频率越高，越利于高频信号的提取。
当注入信号频率过高时，受开关频率影响，采样的高频电流中将包含其他谐波成分，注入高频信号频率fh应小于逆变器的开关频率fs。定义两者的比例关系为
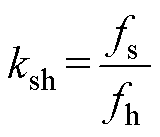（12）式中，fs为开关频率。
注入的电流波形与ksh有关，当ksh越大，注入的高频电流波形畸变程度越低。因此，注入高频信号的频率不能太高。综合上述因素，本文选取高频信号注入频率为2kHz。
利用励磁绕组与电枢绕组间互感，通过检测q轴电流实现转子位置的估计。为了获得良好的估计性能，需要高频励磁电流具有一定的幅值（励磁电流大于1.5A）。
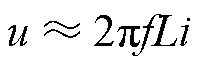（13）式中，励磁电感为0.163mH，当注入信号频率为2kHz时，获得1.5A的励磁电流所需的电压幅值可表示为
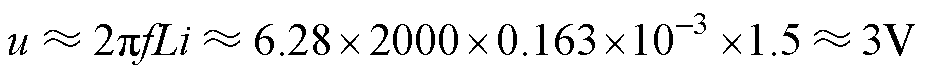（14）因此，选取注入高频信号频率为2kHz，幅值为3V。
由于高频电压脉冲信号注入励磁绕组中，而位置是由电枢电流中的电流采样来估计的，因此，电枢绕组和励磁绕组之间的互感值对转子位置的估计至关重要。电枢和励磁绕组之间的互感较小时，需要增大高频电压脉冲的幅值才能估计出准确的转子位置。
图10为当估计的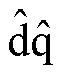轴与实际的dq轴重合的情况下，注入高频电压脉冲幅值与励磁绕组和电枢绕组间互感的关系。可以看出，当d轴电流变化相同时，随着互感值增大，注入的高频电压脉冲信号幅值减小。因此，为了获得准确的估计位置，应合理地选取高频电压脉冲的幅值。
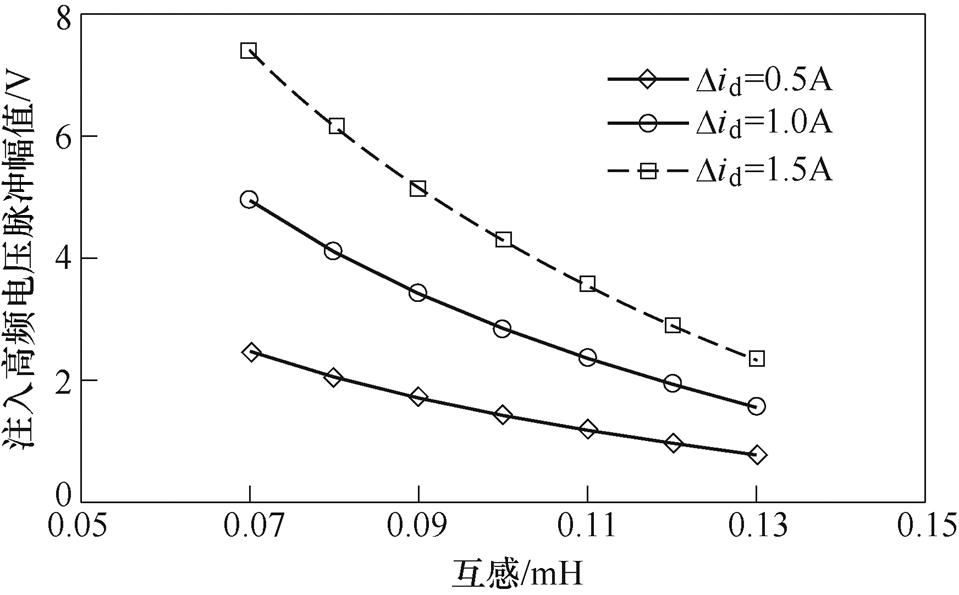
图10 在2kHz高频脉冲信号频率下，d轴感应电流变化量不同时，高频脉冲信号幅值与互感的关系
Fig.10 Amplitude of HF pulse signal against mutual inductance with different introduced d-axis current variation at the frequency of HF pulse signal of 2kHz
此外，高频电压脉冲信号的频率也是影响位置估计精度的另一个重要参数。当注入高频信号频率过高或过低时，采样电流可能会受到由磁饱和与开关频率引起的电流谐波干扰，因此，选取适当的高频电压脉冲频率有助于提高位置估计的精度。图11为在d轴感应电流变化量为1A的情况下，不同互感值对应的注入高频信号的幅值与频率之间的关系。可以看出，在互感值相同时，随着高频电压脉冲频率的增加，对应注入信号幅值也需要增大。
图11 不同互感值对应的高频脉冲信号幅值与频率之间的关系（d轴感应电流变化量为1A）
Fig.11 Amplitude of HF pulse signal against the frequency of HF pulse signal with different mutual inductance at introduced d-axis current variation of 1A
为了验证基于励磁绕组高频电压脉冲注入的位置估计方法，搭建了基于dSPACE平台的HESFPM电机驱动系统。HESFPM电机的主要参数见表1。在实验平台中，12/10 HESFPM电机的电枢绕组和磁场绕组分别由三相桥和H桥驱动，通过磁滞测功机调整样机的负载，如图12a所示。图12b和图12c分别为样机的定子与转子。三相逆变器和H桥的开关频率均设置为20kHz，直流母线电压为24V。
表1 HESFPM电机的主要参数
Tab.1 Main parameters of HESFPM machine
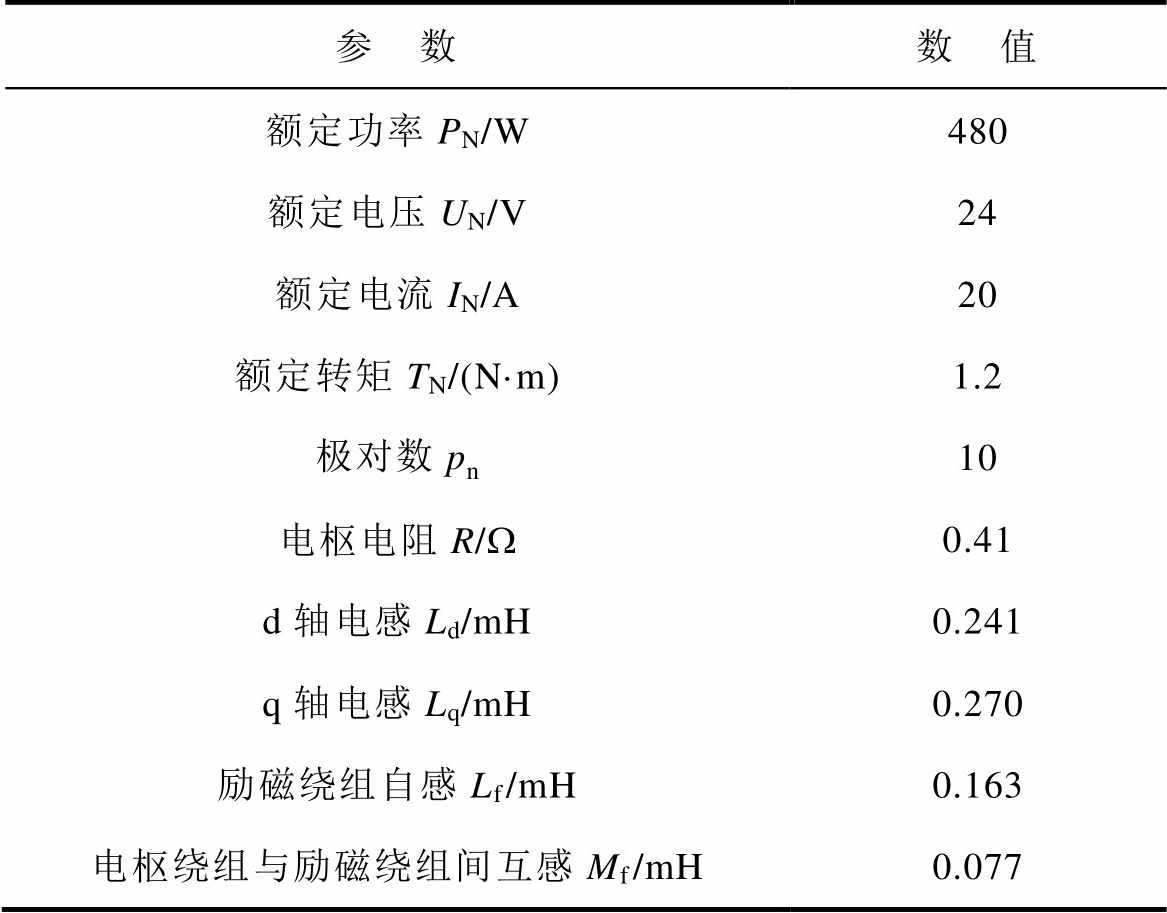
参 数数 值 额定功率PN/W480 额定电压UN/V24 额定电流IN/A20 额定转矩TN/(N·m)1.2 极对数pn10 电枢电阻R/W0.41 d轴电感Ld/mH0.241 q轴电感Lq/mH0.270 励磁绕组自感Lf/mH0.163 电枢绕组与励磁绕组间互感Mf/mH0.077
根据第3节介绍的控制方法，每0.25ms（4kHz采样频率）对q轴电流进行采样，注入的高频电压脉冲的频率设置为2kHz。
通过编码器测量实际位置，然后将高频电压脉冲注入励磁绕组中，并令转子以零速固定在随机位置。同时，通过接通下桥臂开关管使相绕组短路。电枢电流采样频率为4kHz。图13为零速时基于励磁绕组高频电压脉冲注入的初始位置估计，高频电压脉冲的幅值为3V。
图12 实验平台与HESFPM样机
Fig.12 Experimental platform and HESFPM machine
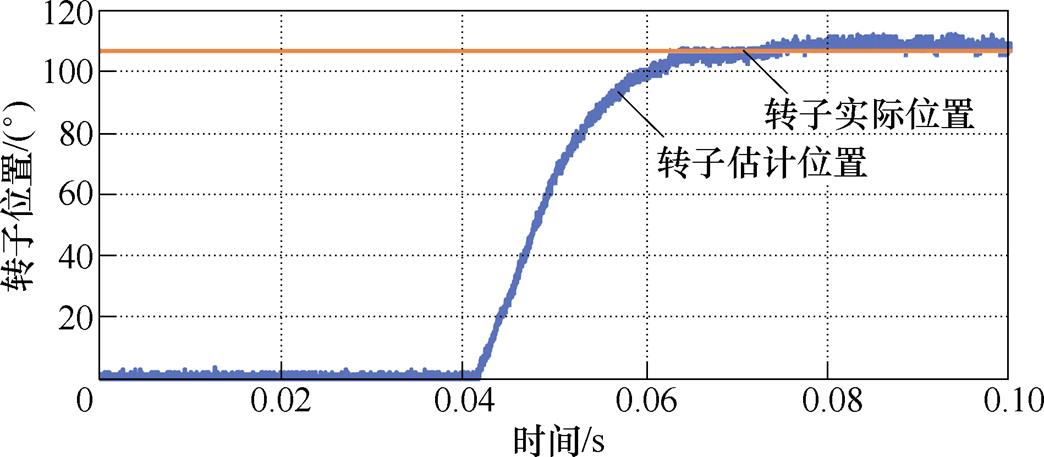
图13 初始位置估计的实验结果（Vinj=3V，finj=2kHz）
Fig.13 Test results of initial position estimation at Vinj=3V and finj=2kHz
首先，通过实验验证了传统d轴高频信号注入方法在HESFPM电机的无位置控制性能。图14a为转速为200r/min、负载为0.24N·m（即额定负载的20%）条件下，HESFPM电机测量的转子实际位置与估计位置。实际位置与估计位置之间的误差如图14b所示，最大估计位置误差约为0.24rad。实验结果表明，由于该电机转子饱和凸极性较差，导致位置估计误差较大。图14c为三相电枢电流的波形，由于电枢d轴中注入了高频电压脉冲，在三相电枢绕组中激励出较大的高频电流。
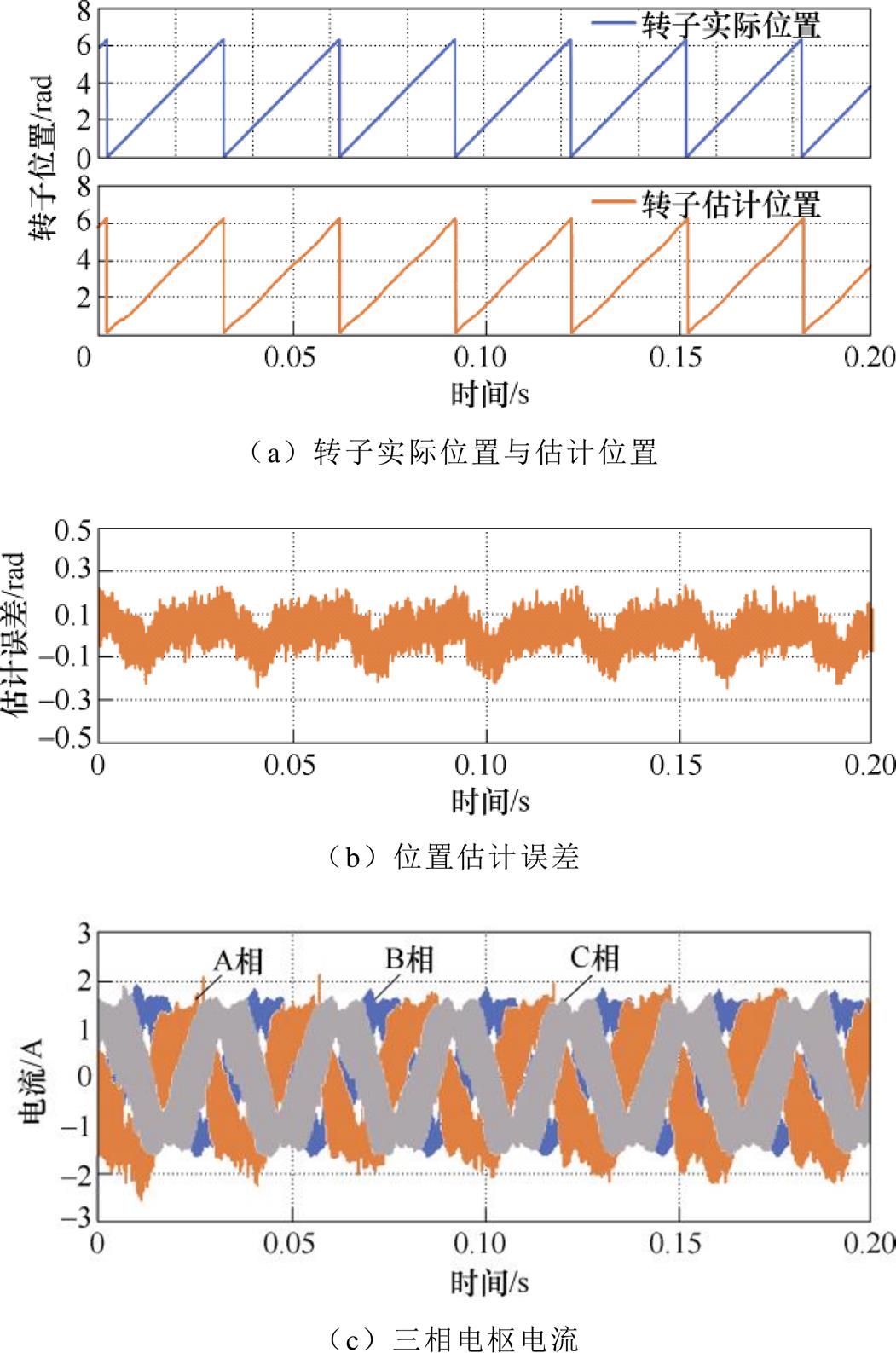
图14 基于d轴高频信号注入方法的无位置控制性能
Fig.14 Performance of sensorless control based on d-axis high frequency signal injection method
为了验证提出的位置估计方法，首先进行转速为200r/min时的空载稳态实验。为简化控制，采用d轴电流等于零控制。图15a为转速为200r/min时HESFPM电机测量的转子实际位置与估计位置。实际位置与估计位置之间的误差如图15b所示，最大估计位置误差约为0.2rad。图15c为励磁电流与三相电枢电流的波形。可以看出，由于励磁绕组中注入了高频电压脉冲，在励磁电流中可以观察到高频电流纹波，同时电枢绕组中也产生了电流纹波。
图16a为HESFPM电机在转速为200r/min、负载为0.24N·m（即额定负载的20%）条件下带载情况下的转子估计位置和实际位置。如图16b所示，最大估计误差约为0.16rad，略低于空载时的误差，励磁电流与三相电枢电流如图16c所示。
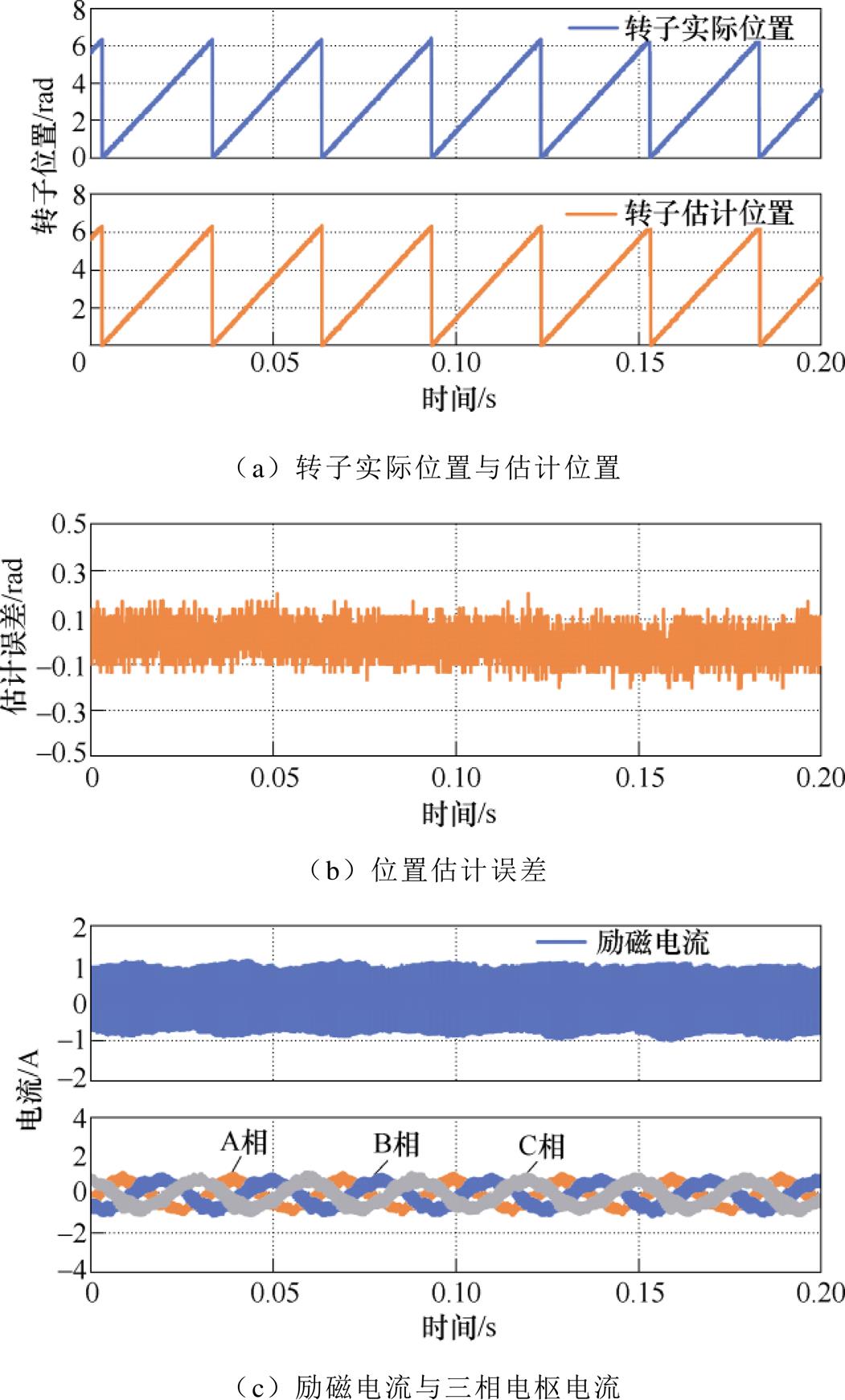
图15 空载条件下转速为200r/min时HESFPM电机实际和估计位置、估计误差和电流（Vinj=3V，finj=2kHz）
Fig.15 Actual and estimated position, estimation error and currents in HESFPM machine at 200r/min without load, Vinj=3V, finj=2kHz
上述实验中，HESFPM电机工作在空载和轻载条件下，励磁电流始终为零。然而在HESFPM电机中，励磁绕组起着调节气隙磁场的作用，在低速区运行时通过正向增大励磁电流，实现增磁，从而增大电磁转矩。图17a～图17c分别为当控制系统中励磁电流为1A、转速为200r/min、负载为0.24N·m（即额定负载的20%）条件下，转子实际位置和估计位置、转子位置估计误差、励磁电流和三相电枢电流波形，此时的最大估计位置误差与励磁电流为0A时的最大位置误差相近。从电机稳态实验结果可以看出，在不考虑负载和励磁电流的情况下，提出的位置估计方法具有良好的稳态性能。
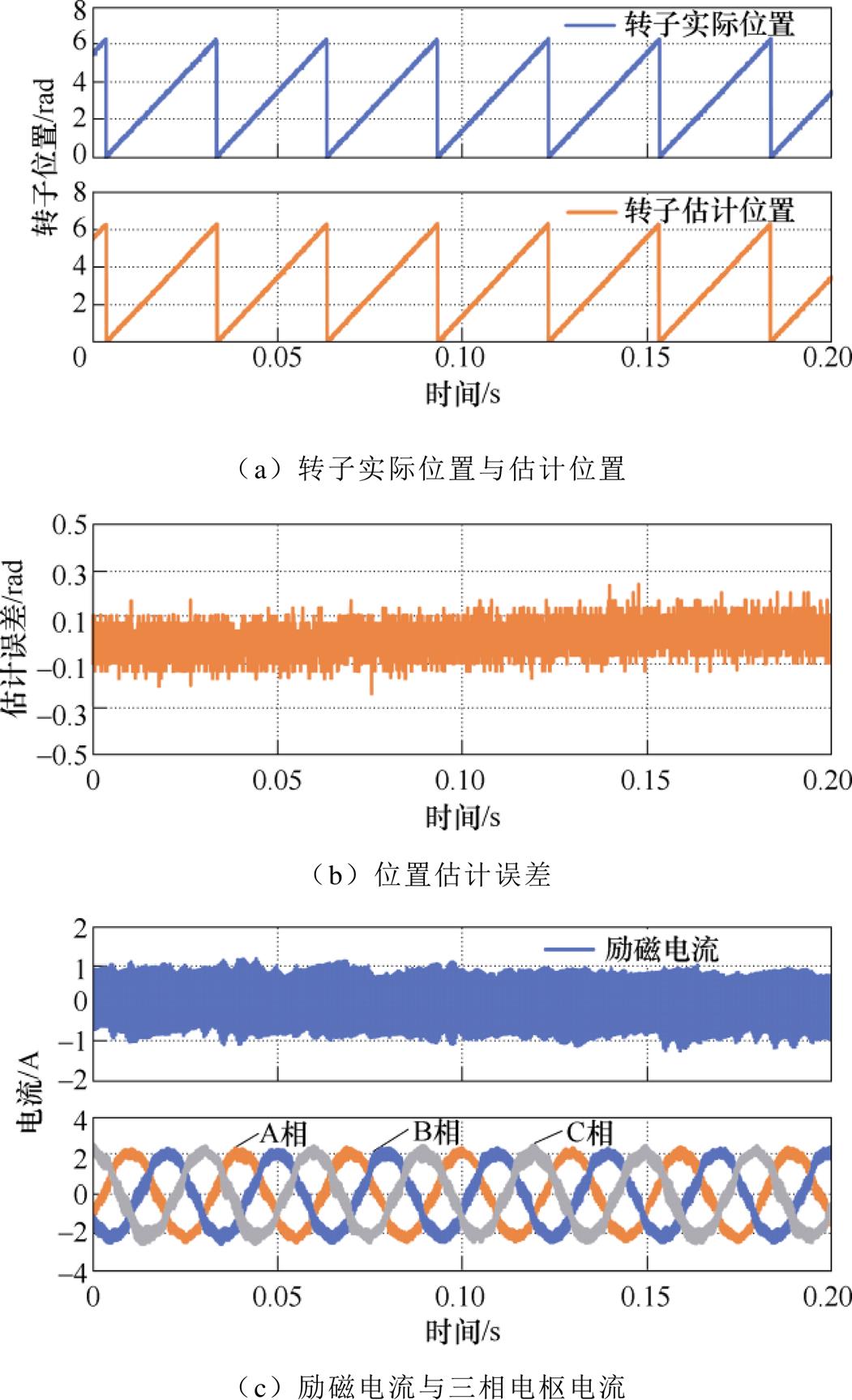
图16 带载条件下转速为200r/min时HESFPM电机转子实际位置和估计位置，估计误差以及电流波形（Vinj=3V，finj=2kHz）
Fig.16 Actual and estimated position, estimation error and current waveforms in HESFPM machine at 200r/min with load, Vinj=3V, finj=2kHz
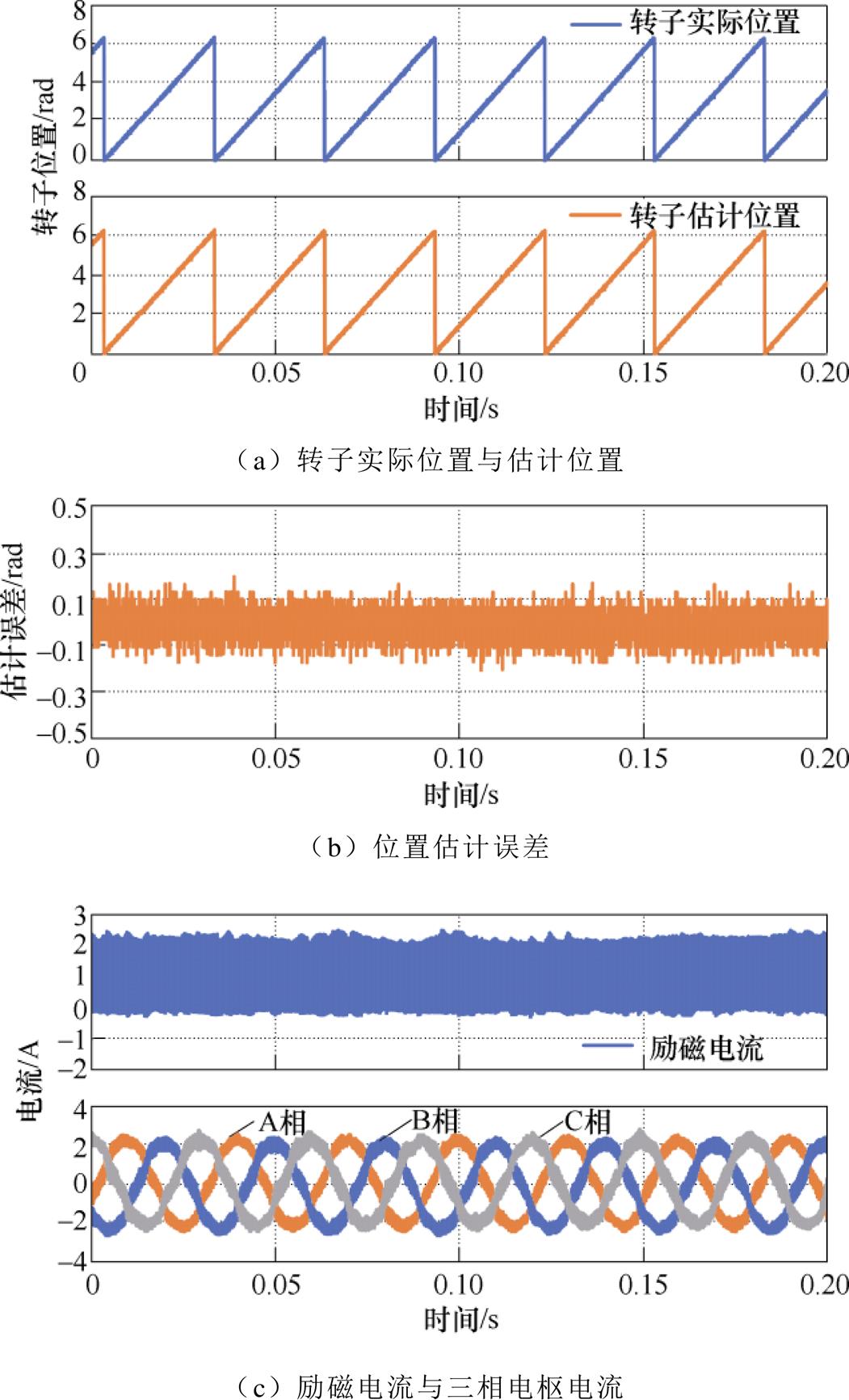
图17 负载条件下转速为200r/min时HESFPM电机的转子实际位置和估计位置，转子位置估计误差以及电流波形（Vinj=3V，finj=2kHz，if =1A）
Fig.17 Actual and estimated position, estimation error and current waveforms in HESFPM machine at 200r/min with load, Vinj=3V, finj=2kHz, if =1A
为了研究高频电压脉冲的频率对位置估计方法精度的影响，在1kHz高频电压脉冲下进行了转速为200r/min、负载为0.24N·m（即额定负载的20%）条件下的带载位置估计实验如图18所示。从图18b可以看出，随着高频电压脉冲频率从2kHz减小到1kHz，位置估计误差增大，最大位置估计误差约为0.23rad。图18c为HESFPM电机的励磁电流与三相电枢电流波形。与图16c中2kHz高频电压脉冲的实验结果相比，图18c中的励磁电流纹波增大。
图19为HESFPM电机在不同速度给定时的动态响应。从实验结果可以看到，在速度变化时估计的位置误差和速度误差与稳态误差相比较大。
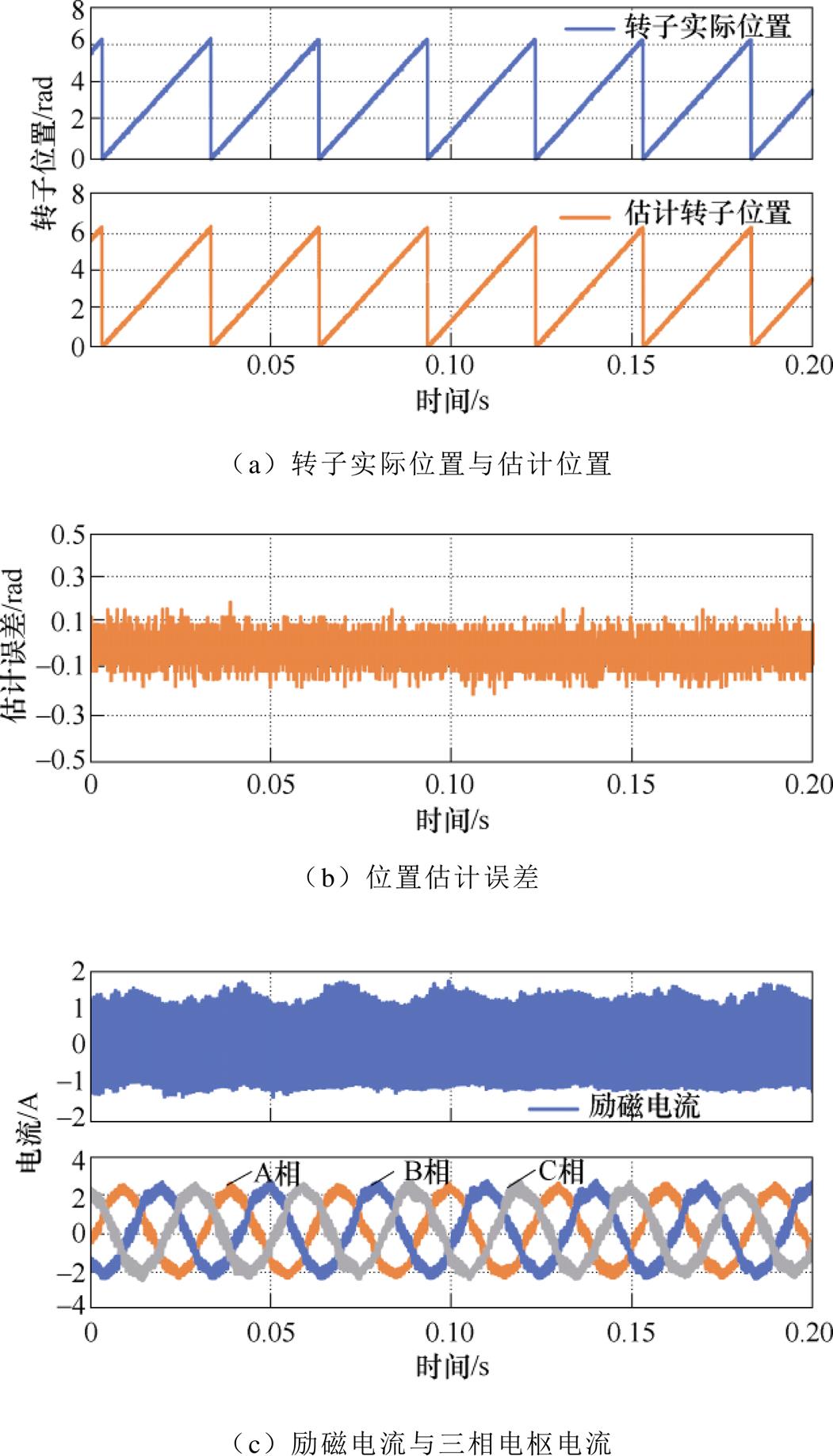
图18 负载条件下转速为200r/min时HESFPM电机转子实际位置和估计位置，位置估计误差以及电流波形（Vinj=3V，finj=1kHz）
Fig.18 Actual and estimated position, estimation error and current waveforms in HESFPM machine at 200r/min with load, Vinj=3V, finj=1kHz
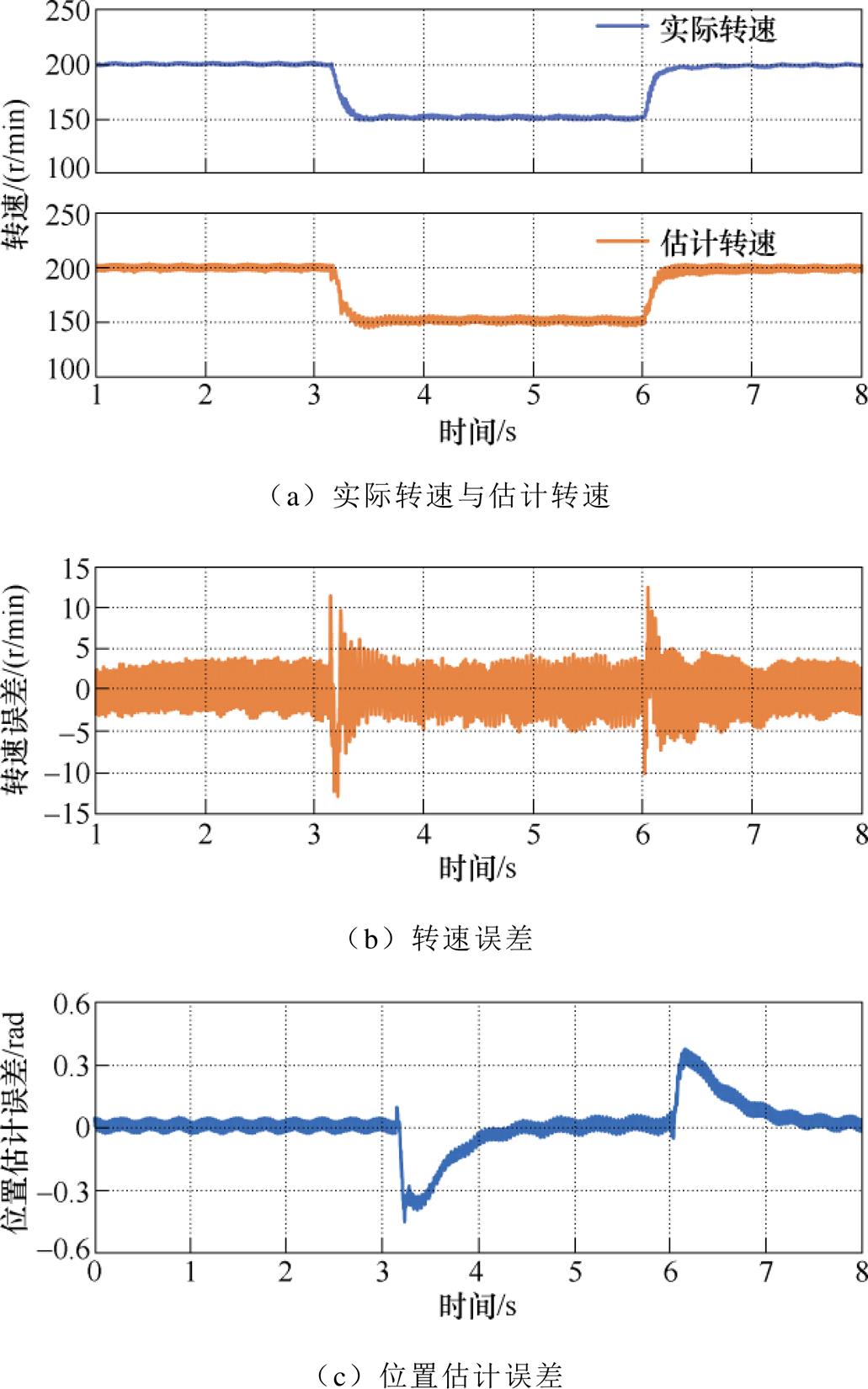
图19 负载为0.22N·m时HESFPM电机实际转速与估计转速、转速估计误差（Vinj=3V，finj=2kHz，if =1A）
Fig.19 Actual and estimated rotor speed, estimation error, Vinj=3V, finj=2kHz, if =1A with load of 0.22N·m
针对具有低凸极比的HESFPM电机在无位置传感器控制时的转子位置检测，提出一种基于励磁绕组高频电压脉冲注入来估计转子位置的方法。由于HESFPM电机中励磁绕组产生的磁链在d轴上，且励磁绕组与电枢绕组之间存在互感，因此，励磁绕组中注入的高频电压脉冲信号会在实际的d轴上感应出高频电流。当q轴上的高频电流信号收敛到零时，估计的转子位置与实际转子位置重合。
为了验证所提出的位置估计方法，制作了一台12/10 HESFPM样机并进行实验研究。实验结果表明，所提出的基于励磁绕组高频电压脉冲注入的位置估计方法在稳态和转速阶跃过程中都能很精确地估计出HESFPM电机的转子位置。
参考文献
[1] Tian Mengmeng, Zhao Wenliang, Wang Xiuhe, et al. Analysis on a novel flux adjustable permanent magnet coupler with a double- layer permanent magnet rotor[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[2] Yang Y P, Peng M T. A surface-mounted permanent- magnet motor with sinusoidal pulsewidth-modulation- shaped magnets[J]. IEEE Transactions on Magnetics, 2019, 55(1): 1-8.
[3] Lu Chao, Ferrari S, Pellegrino G. Two design pro- cedures for PM synchronous machines for electric power-trains[J]. IEEE Transactions on Transportation Electrification, 2017, 3(1): 98-107.
[4] Xu Dianguo, Wang Bo, Zhang Guoqiang, et al. A review of sensorless control methods for AC motor drives[J]. CES Transactions on Electrical Machines & Systems, 2018, 2(1): 104-115.
[5] Wang Zheng, Zheng Yang, Zou Zhixiang, et al. Position sensorless control of interleaved CSI fed PMSM drive with extended kalman filter[J]. IEEE Transactions on Magnetics, 2012, 48(11): 3688-3691.
[6] Xu Peilin, Zhu Ziqiang. Novel square-wave signal injection method using zero-sequence voltage for sensorless control of PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7444-7454.
[7] 李浩源, 张兴, 杨淑英, 等. 基于高频信号注入的永磁同步机无传感器控制技术综述[J]. 电工技术学报, 2018, 33(12): 2653-2664.
Li Haoyuan, Zhang Xing, Yang Shuying, et al. Review on sensorless control of permanent magnet synchronous motor based on high-frequency signal injection[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2653-2664.
[8] Zhang Guoqiang, Wang Gaolin, Yuan Bihe, et al. Active disturbance rejection control strategy for signal injection-based sensorless IPMSM drives[J]. IEEE Transactions on Transportation Electrification, 2018, 4(1): 330-339.
[9] Lin Tzuchi, Zhu Ziqiang. Sensorless operation capability of surface-mounted permanent-magnet machine based on high-frequency signal injection methods[J]. IEEE Transactions on Industry Appli- cations, 2015, 51(3): 2161-2171.
[10] 刘兵, 周波. 脉振高频电压注入SPMSM无位置传感器控制的估计误差分析与抑制方法[J]. 中国电机工程学报, 2018, 38(14): 4232-4241, 4329.
Liu Bing, Zhou Bo. Analysis and compensation of position estimation error in SPMSM sensor-less control based on high frequency pulsating voltage injection[J]. Proceedings of the CSEE, 2018, 38(14): 4232-4241, 4329.
[11] Yu Chenyen, Tamura J, Reigosa D D, et al. Position self-sensing evaluation of a FI-IPMSM based on high-frequency signal injection methods[J]. IEEE Transactions on Industry Applications, 2013, 49(2): 880-888.
[12] Luo Xin, Tang Qipeng, Shen Anwen, et al. PMSM sensorless control by injecting HF pulsating carrier signal into estimated fixed-frequency rotating refer- ence frame[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2294-2303.
[13] Hwang C E, Lee Y, Sul S K. Analysis on position estimation error in position-sensorless operation of IPMSM using pulsating square wave signal injection[J]. IEEE Transactions on Industry Appli- cations, 2019, 55(1): 458-470.
[14] 杨健, 杨淑英, 李浩源, 等. 基于旋转高频电压注入的永磁同步电机转子初始位置辨识方法[J]. 电工技术学报, 2018, 33(15): 3547-3555.
Yang Jian, Yang Shuying, Li Haoyuan, et al. Initial rotor position estimation for IPMSM based on high frequency rotating voltage injection[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3547-3555.
[15] Xu P, Zhu Ziqiang. Analysis of parasitic effects in carrier signal injection methods for sensorless control of PM synchronous machines[J]. IET Electric Power Appli- cations, 2018, 12(2): 203-212.
[16] 王爽, 曹栋逸, 杨影, 等. 正负高频脉冲电压注入的永磁同步电机无位置传感器控制[J]. 电工技术学报, 2020, 35(增刊1): 164-171.
Wang Shuang, Cao Dongyi, Yang Ying, et al. Sensor- less control of PMSM with positive and negative high frequency pulse voltage signal injection[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S1): 164-171.
[17] Zhang Xing, Li Haoyuan, Yang Shuying, et al. Improved initial rotor position estimation for PMSM drives based on HF pulsating voltage signal injection[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4702-4713.
[18] 张志锋, 刘晓东. 基于高频信号注入的永磁同步电动机的无传感器控制及位置估计误差补偿[J]. 电气技术, 2017, 18(5): 12-18.
Zhang Zhifeng, Liu Xiaodong. Sensorless control of permanent magnet synchronous motor based on high frequency signal injection and estimated rotor position error compensation[J]. Electrical Techno- logy, 2017, 18(5): 12-18.
[19] 杜博超, 崔淑梅, 宋立伟, 等. 一种基于变频电流信号的IPMSM无位置传感器高频注入电流噪声抑制方法[J]. 电工技术学报, 2020, 35(18): 3830- 3837.
Du Bochao, Cui Shumei, Song Liwei, et al. A variable frequency current injection sensorless control strategy of IPMSM for audible noise reduction[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(18): 3830-3837.
[20] 于安博, 刘利, 阚志忠, 等. 高频脉振信号注入永磁同步电机无滤波器初始位置辨识方法[J]. 电工技术学报, 2021, 36(4): 801-809.
Yu Anbo, Liu Li, Kan Zhizhong, et al. Initial position identification of PMSM with filterless high frequency pulse signal injection method[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 801- 809.
[21] Lin T C, Gong Liming, Liu Jiaming, et al. Investi- gation of saliency in a switched-flux permanent-magnet machine using high-frequency signal injection[J]. IEEE Transactions on Industrial Electronics, 2014, 61(9): 5094-5104.
Position Estimation for Hybrid Excited Switched Flux PM Machine by Injecting High-Frequency Pulse into the Field Winding
Abstract Due to the low saliency ratio in the hybrid excited switched flux permanent magnet (HESFPM) machines, the conventional position estimation methods, which use high-frequency signal injection into the armature windings for the permanent magnet synchronous machines at zero or low speed, may not have appropriate estimated accuracy for the sensorless control of the HESFPM machine. Therefore, in the paper, the method of injecting high-frequency (HF) pulse signals into the field winding is developed. In the HESFPM machines, since the flux-linkage produced by the field excitation is always aligned with the d-axis, the injected HF pulse signal in the field winding can only induce the HF current signal in the actual d-axis. Based on this principle, the estimated rotor position can be obtained once the HF current signal in the estimated q-axis equals zero. To verify the proposed position estimation method, an experiment on a HESFPM prototype was carried out. The results show that the proposed position estimation method for the HESFPM machines exhibits high accuracy in both steady-state and dynamic response.
keywords：Hybrid excited switched flux permanent magnet machine, position estimation, sensorless control, high frequency signal injection
DOI: 10.19595/j.cnki.1000-6753.tces.200602
中图分类号：TM351
刘 旭 男，1984年生，教授，博士生导师，研究方向为电机及其控制。E-mail: liuxu@hebut.edu.cn（通信作者）
牛大强 男，1994年生，硕士研究生，研究方向为电机及其控制。E-mail: niudaqiang@163.com
收稿日期2020-06-09
改稿日期 2020-07-12
国家自然科学基金（51507045）、河北省“杰出青年”基金（E2018202252）和河北省人社厅（E2016100004）资助项目。
（编辑 崔文静）