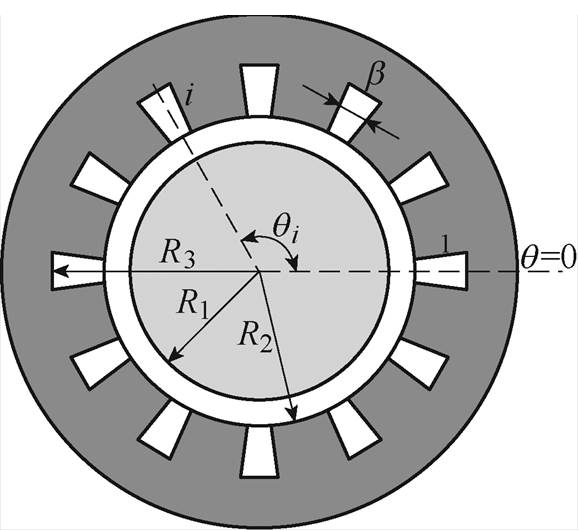
图1 实心转子感应电机横截面
Fig.1 Cross section of solid rotor induction machine
摘要 子域分析技术作为一种简捷高效的磁场解析方法,已在电机恒定磁场解析领域获得广泛应用。该文以实心转子感应电机为例,将子域分析技术拓展到电机磁准静态场解析领域。在二维极坐标平面内,将实心转子感应电机求解区域划分为定子槽子域、气隙子域和实心转子子域,从而在复频域建立考虑定子开槽影响的实心转子感应电机精确子域解析模型。该解析模型着重求解实心转子子域的偏微分方程,根据运行方式的不同,分别给出同步运行和异步运行两种工况下的解析表达式。在解析计算结果的基础上,根据磁链法计算实心转子感应电机的运算电感。最后,通过二维时谐有限元分析验证了解析模型的准确性。
关键词:实心转子感应电机 精确子域模型 磁场解析 定子开槽 运算电感
实心转子感应电机的研究可以追溯到19世纪末,因其具备结构简单、机械可靠性高、热稳定性优良和起动性能好等特点,非常适合于重载起动等频繁起停和空气压缩机等高速运行领域[1-2]。与常规笼型感应电机不同,实心转子感应电机的转子铁心是一个连续的整体,既作为电机磁路的一部分,又是转子的电流通路。实心转子里的涡流分布与定子电流频率、转子电阻率及转差率都相关,其磁场是一个典型的磁准静态场,因此其研究方法需要借助电机电磁场理论。
光滑表面实心转子是实心转子感应电机的最基本结构,国内外学者对此进行了大量的磁场解析研究工作[3-10]。在文献[3]中,首先忽略定子开槽,以分布于定子和气隙交界面的正弦电流片表示定子绕组电流,建立了直角坐标系下的经典二维解析模型,然而该经典模型的激励中仅包含占主导地位的基波空间分量。不考虑定子的开槽,学者们在极坐标下分别解析求解了实心转子感应电机的电磁功率与转矩[4]、等效电路参数[5]以及运算电抗与励磁电抗[6]等问题。不同于文献[3-6]中解析模型的电磁场场量传递表达方式,文献[7-10]基于分层阻抗理论推导实心转子感应电机的电磁场问题,其特点在于用表面阻抗表达求解域内各子层的方程解析解,然而其定子磁动势仍采用正弦分布于定子内表面的电流片,无法计及定子开槽的影响。
各式各样新型电机的提出以及电机工程中新问题的出现,带动了电机电磁场解析法的发展。近年来,以分离变量法为基础的子域解析模型[11]在预测电机电磁性能上获得了媲美有限元的精度,其中,在永磁电机方面获得了丰富的技术成果,主要有表贴式永磁同步电机[12-17]、磁性齿轮[18-19]、表面埋入式永磁电机[20]、双定子交替极永磁电机[21]和直线式永磁电机[22]等多种电磁装置。然而,以上子域解析模型的应用主要体现为恒定磁场问题,在运动导体中感应产生的时变涡流等磁准静态场的解析计算领域[23-25]还有待发展和完善。文献[23]以无槽型表面埋入式永磁电机为研究对象,在极坐标下建立了永磁体涡流损耗的精确子域解析模型,然而其定子激励为附着于定子内表面槽开口处的电流片,无法处理定子开槽的结构。文献[24]建立了一个带有转子屏蔽套的开口槽表贴式永磁电机精确子域模型,分析了屏蔽套感应涡流对电磁转矩的影响,但该模型的槽子域通解存在明显缺陷,不能在复频域内统一求解复相量形式的谐波系数方程。文献[25]尽管建立了一个实心转子感应电机的精确子域模型,但该模型仅能处理异步运行工况,且实心转子和转轴子域的解析解中复传播常数未考虑磁场谐波阶数的影响。
本文以开口槽实心转子感应电机为研究对象,在二维极坐标平面内将电机求解区域划分为定子槽、气隙和实心转子三类子域,从而在复频域建立了实心转子感应电机的精确子域解析模型。该模型中源量和场量既是空间又是时间的函数,能够更好地揭示电机运行的物理本质。对于实心转子子域,详细推导了由于源量交变和转子旋转引起的导体感应涡流扩散方程的产生,将电机同步和异步运行状态统一在方程中表达。利用子域解析模型固有的谐波分解特点,以一台整数槽实心转子感应电机为例,从磁场角度阐述了三相旋转磁动势产生的谐波,最后用二维时谐有限元验证了解析模型计算气隙磁场和运算电感的准确性。
本文以一个开口槽结构的实心转子感应电机进行推导和分析,其横截面如图1所示。为了便于子域模型的解析计算,需要进行如下基本假设:

图1 实心转子感应电机横截面
Fig.1 Cross section of solid rotor induction machine
(1)定子铁心为无穷大的磁导率。
(2)实心转子为各向同性均匀介质,磁导率为mR,电导率为sR。
(3)解析区域在二维极坐标(r, q)平面内,忽略端部效应。
(4)定子槽为径向开口槽,本例是一个单层绕组,其结构如图2所示。
取定子坐标系为解析模型参考系,且以第1槽的中心作为周向0位置。定子槽宽角为b,定子槽数为Q,则第i槽的中心位置角为
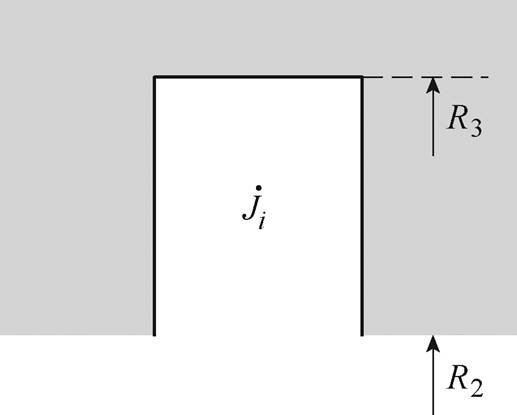
图2 定子槽
Fig.2 Stator slot
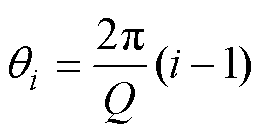 (1)
(1)为了便于各子域谐波系数的求解,本文采用文献[16]定义的两个函数,有
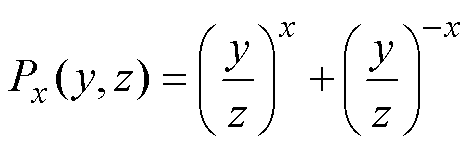 (2)
(2)
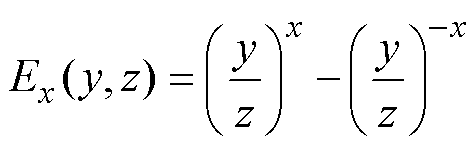 (3)
(3)实心转子感应电机结构模型可划分为三类子域:定子槽、气隙和实心转子。以矢量磁位A作为电磁场方程的求解变量,则在二维极坐标平面仅存在z轴分量。时变磁场同时是空间变量r、q 和时间变量t的函数,且是正弦交变的,有
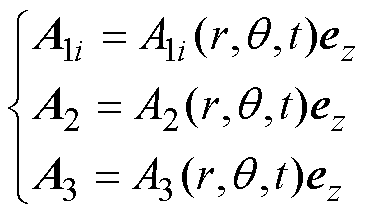 (4)
(4)
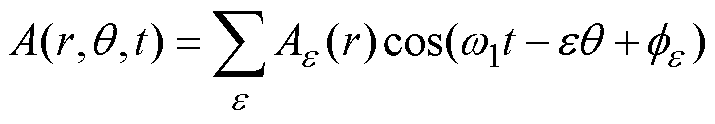 (5)
(5)式中,e 为各类子域的磁场谐波阶数;w1为时谐磁场的交变角频率;fe 为对应e 阶次谐波磁场的相位。因此,复频域矢量磁位可归结为包含时间因子的复相量表示形式,有
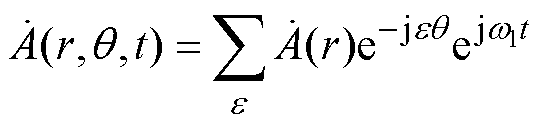 (6)
(6)
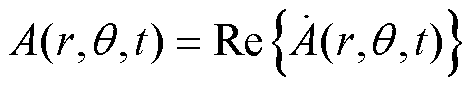 (7)
(7)该解析模型中,实心转子感应电机的定子绕组通有三相对称的正弦交变电流,因此,定子槽子域(i=1~Q)是源量区,满足泊松方程,有
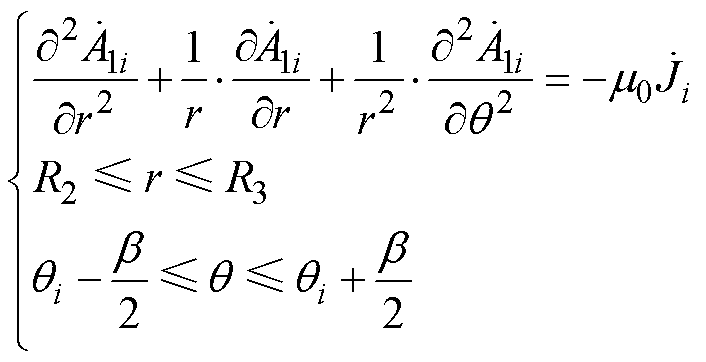 (8)
(8)式中,R2为定子内表面半径;R3为定子槽底面半径;Ji为第i槽电流密度,是一个包含时间因子的复相量,其相位根据ABC相序不同而错开120°,有
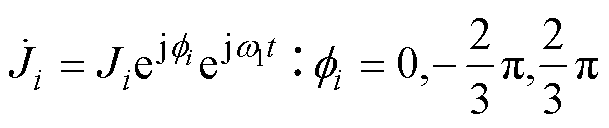 (9)
(9)
式中,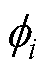 为第i槽因不同相对应的相位。
为第i槽因不同相对应的相位。
根据图1和图2,第i个定子槽子域在r、q 方向的边界条件分别为
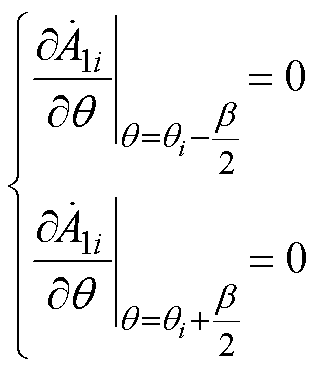 (10)
(10)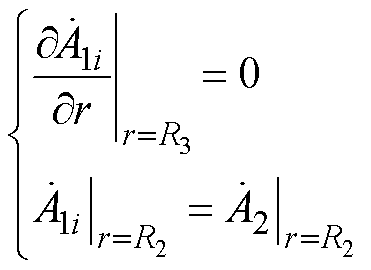 (11)
(11)
由分离变量法[11, 13]可得满足以上边界条件的第i个定子槽子域的解为
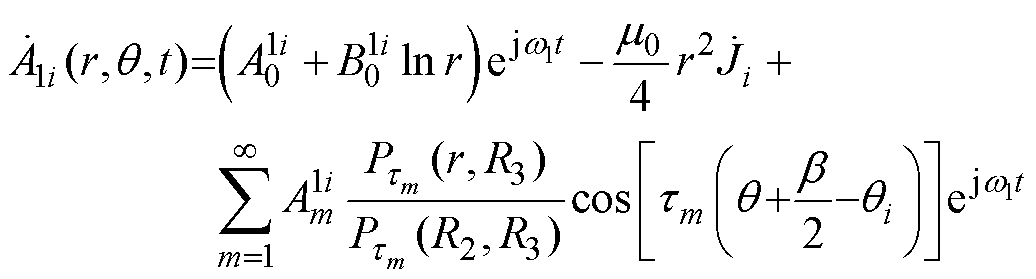 (12)
(12)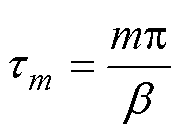 (13)
(13)
式中,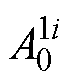 、
、 和
和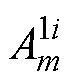 为第i个定子槽子域待求的各阶次复谐波系数;tm为定子槽子域磁场谐波阶数。
为第i个定子槽子域待求的各阶次复谐波系数;tm为定子槽子域磁场谐波阶数。
由式(11)中槽底面半径r=R3处的铁磁边界条件可知
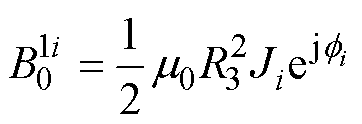 (14)
(14)气隙子域为无源区,满足拉普拉斯方程,转子外表面半径为R1,有
 (15)
(15)其边界条件为
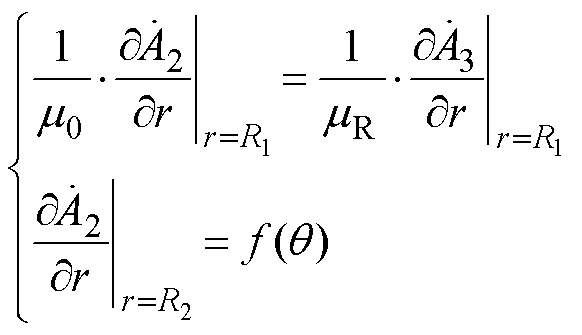 (16)
(16)
其中
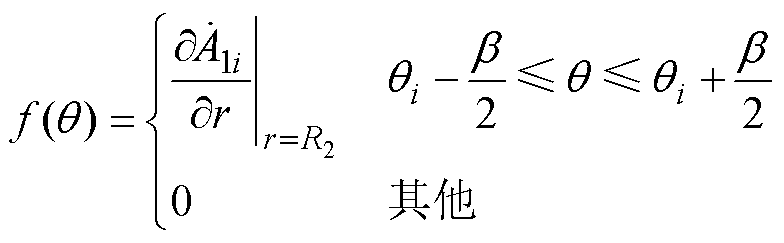 (17)
(17)求解拉普拉斯方程,气隙子域通解[13]为
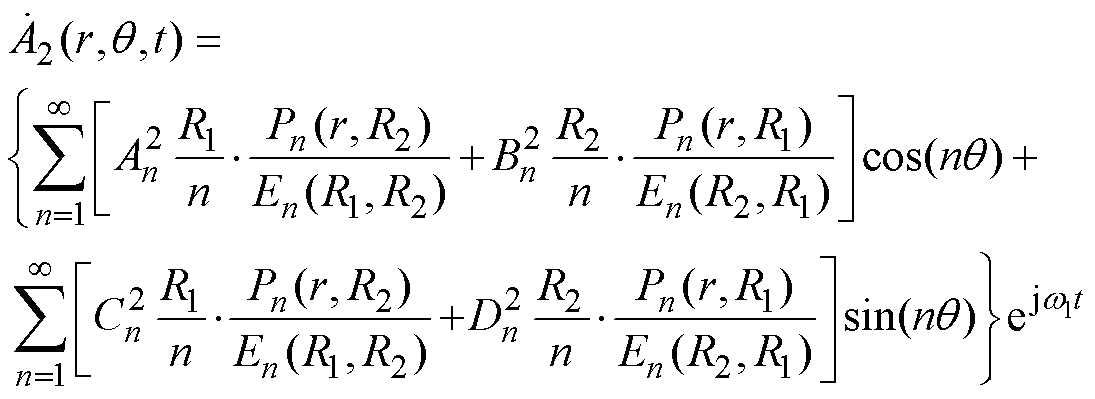 (18)
(18)
式中,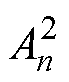 、
、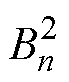 、
、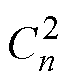 、
、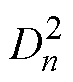 为未知的各阶次复谐波系数;n为气隙子域磁场谐波阶数。
为未知的各阶次复谐波系数;n为气隙子域磁场谐波阶数。
根据感应电机运行原理,实心转子中由于三相定子磁动势交变和转子旋转会产生感应涡流。首先推导实心转子感应电机异步运行的工况,此时该子域满足亥姆霍兹方程,有
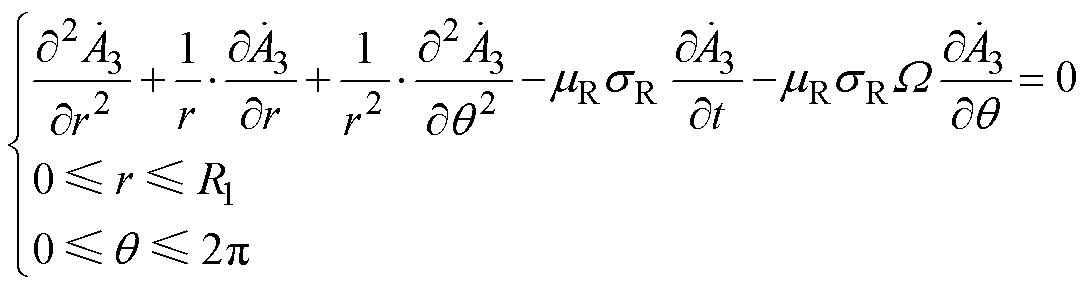 (19)
(19)其边界条件为
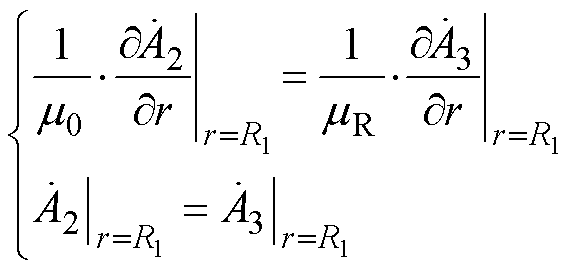 (20)
(20)
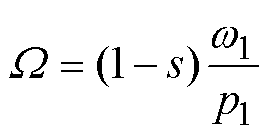 (21)
(21)式中,W 为转子旋转机械角速度;s为感应电机运行转差率;p1为电机极对数。根据解析模型基本假设,整理式(19)可得
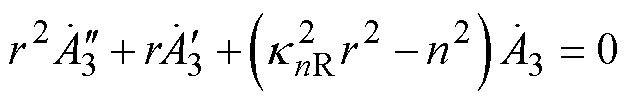 (22)
(22)
其中
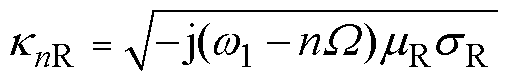 (23)
(23)式中,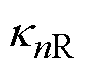 为一个与实心转子子域磁场谐波阶数n相关的复传播常数。求解式(22),得到实心转子子域的通解为
为一个与实心转子子域磁场谐波阶数n相关的复传播常数。求解式(22),得到实心转子子域的通解为
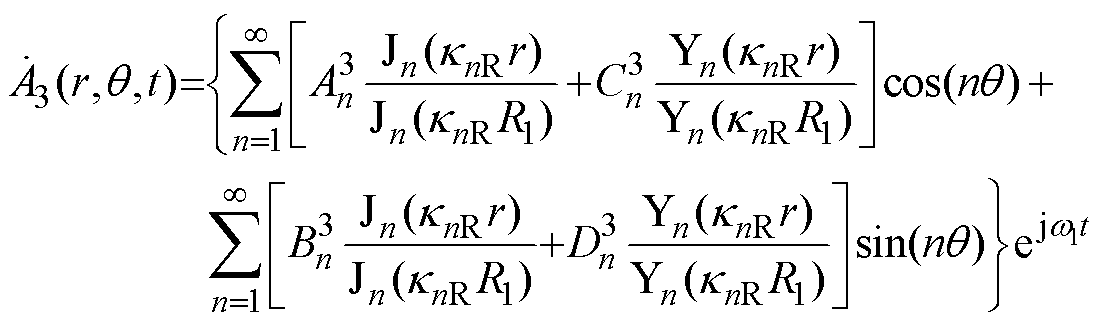 (24)
(24)
式中,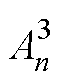 、
、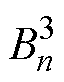 、
、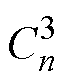 、
、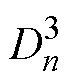 为未知的各阶次复谐波系数;
为未知的各阶次复谐波系数;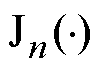 和
和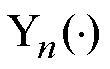 分别为n阶第一类和第二类贝塞尔函数。考虑到r=0处矢量磁位为有限值,结合第二类n阶贝塞尔函数Yn(0)为无穷大的特点,实心转子子域的通解可简化为
分别为n阶第一类和第二类贝塞尔函数。考虑到r=0处矢量磁位为有限值,结合第二类n阶贝塞尔函数Yn(0)为无穷大的特点,实心转子子域的通解可简化为
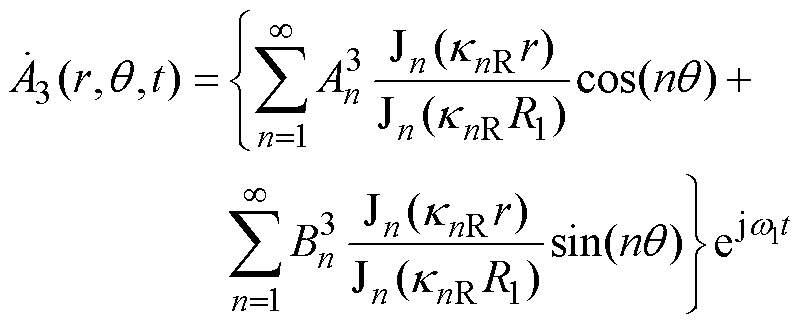 (25)
(25)感应电机运行于同步速时,根据电机学原理,定子旋转磁动势基波磁场与转子转速保持相对静止,且忽略定子旋转磁动势高次谐波,则式(19)无需考虑定子磁动势交变和转子旋转的影响,即实心转子子域中无感应涡流,此时亥姆霍兹方程退化为拉普拉斯方程,有
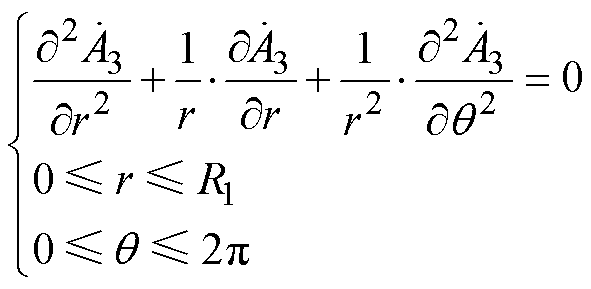 (26)
(26)
根据分离变量法,可得同步运行时实心转子子域的通解为
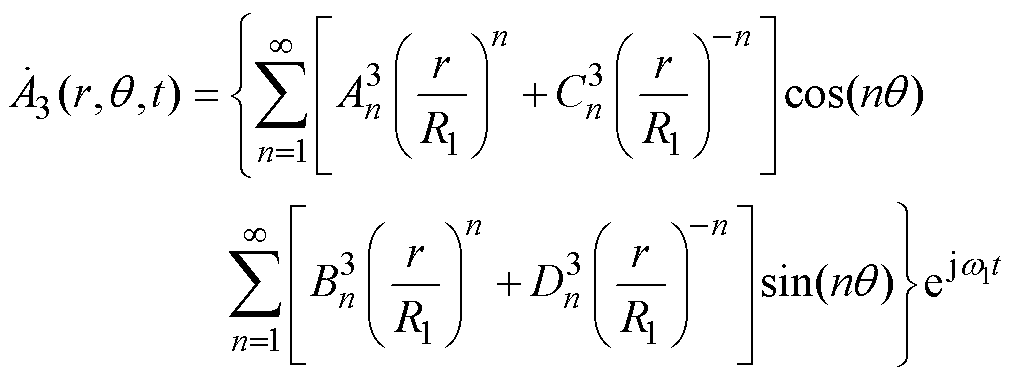 (27)
(27)同样地,考虑到r=0处矢量磁位为有限值,式(27)可简化为
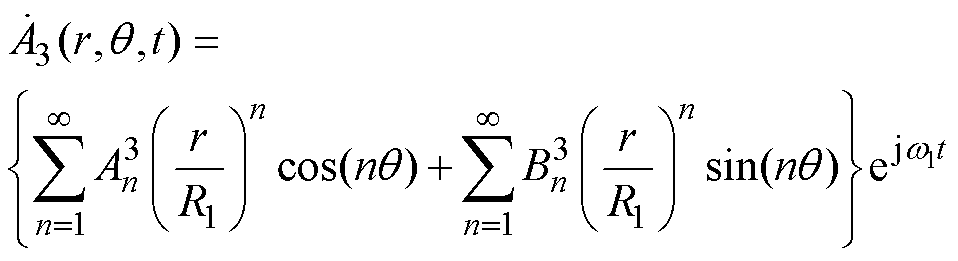 (28)
(28)
在求解出三类子域复频域内通解的基础上,需要在r方向交界面上根据法向磁通密度相等和切向磁场强度相等求解各阶次复谐波系数。为了简化表达,本节各子域复矢量磁位采用隐去时间因子的形式,有
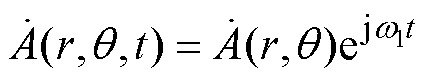 (29)
(29)在r=R2处,根据式(11)中定子槽与气隙两类子域法向磁通密度相等,有
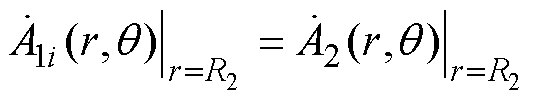 (30)
(30)结合式(12)定子槽通解,根据傅里叶级数展开式可得谐波系数数学关系为
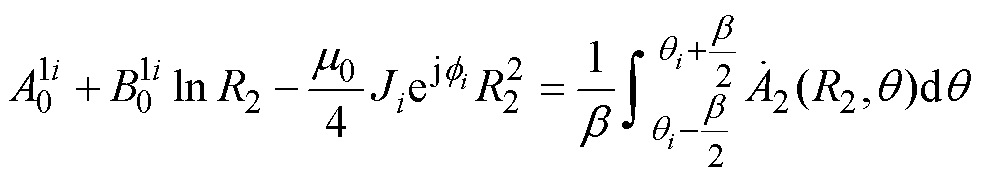 (31)
(31)
 (32)
(32)在r=R2处,根据式(16)中定子槽与气隙两类子域切向磁场强度相等,有
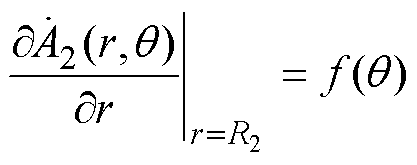 (33)
(33)
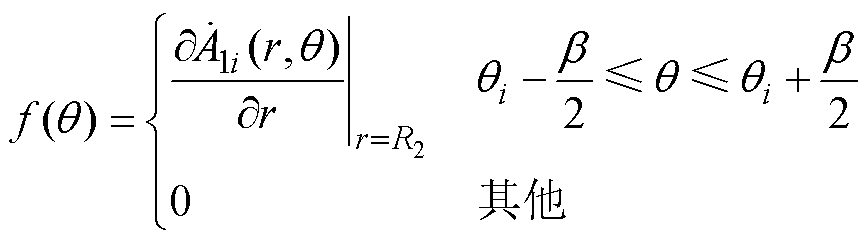 (34)
(34)结合式(18)气隙子域通解,根据傅里叶级数展开式可得谐波系数数学关系为
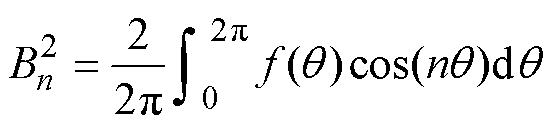 (35)
(35)
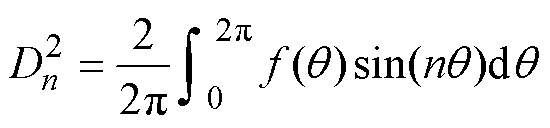 (36)
(36)在r=R1处,根据气隙与实心转子两类子域法向磁通密度相等,有
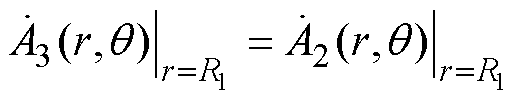 (37)
(37)结合式(25)、式(28)实心转子子域通解,根据傅里叶级数展开式可得谐波系数数学关系为
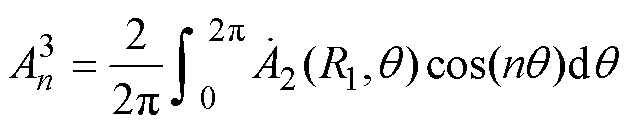 (38)
(38)
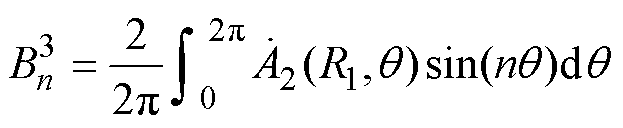 (39)
(39)在r=R1处,根据气隙与实心转子两类子域切向磁场强度相等,有
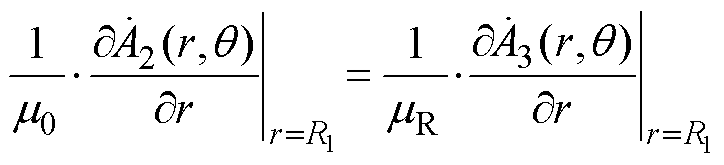 (40)
(40)
结合式(18)气隙子槽通解,根据傅里叶级数展开式可得谐波系数数学关系为
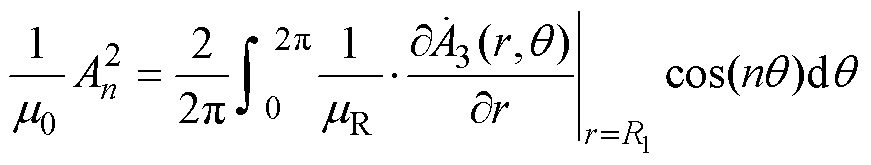 (41)
(41)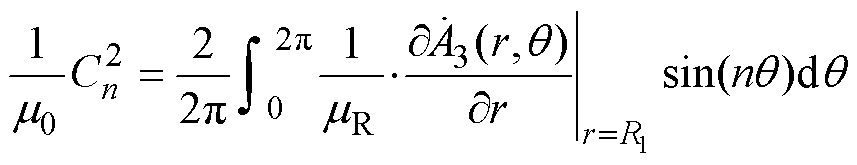 (42)
(42)
以上三类子域各阶次复谐波系数的数学关系展开过程和求解方法见附录。
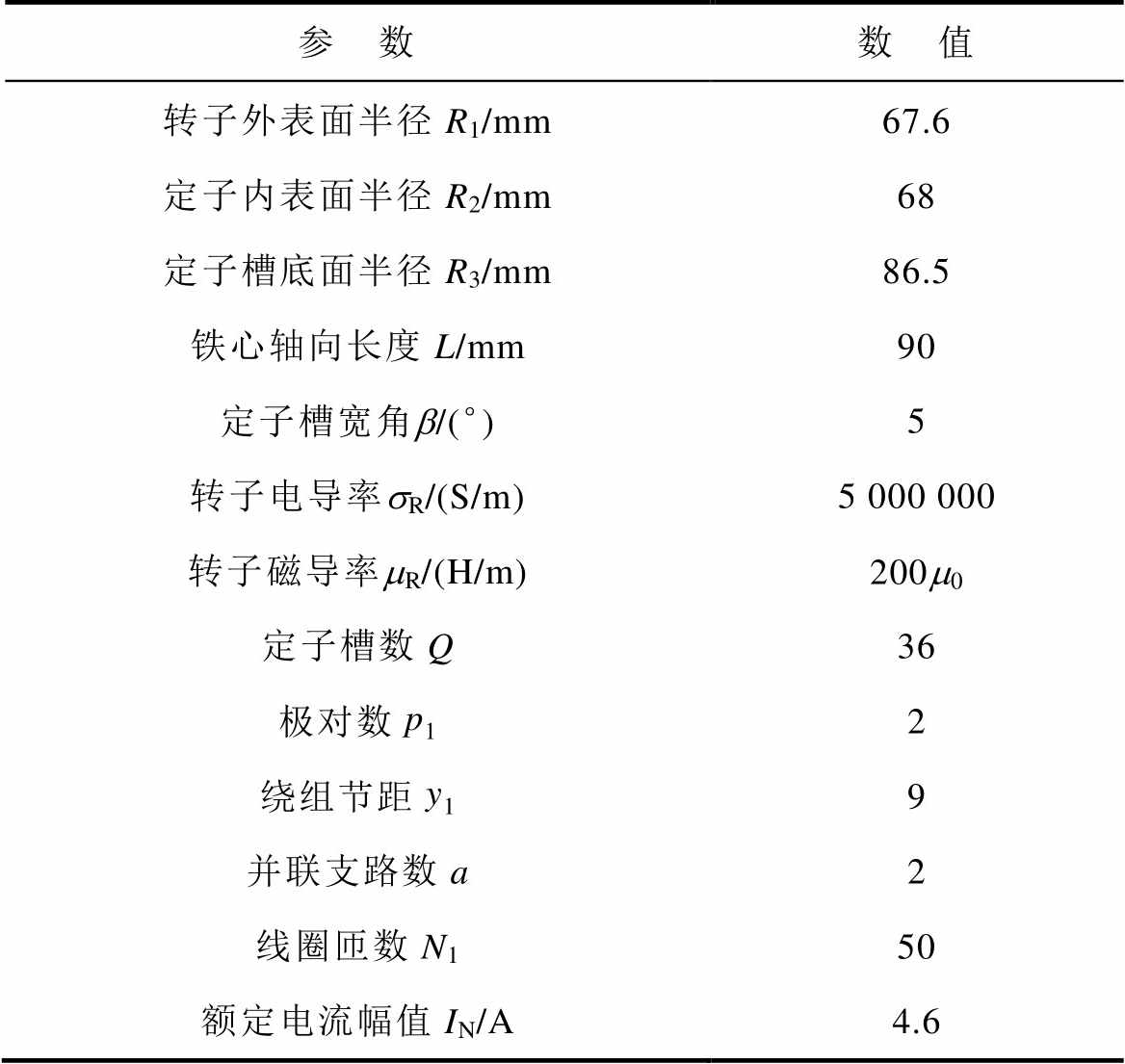
本文以一台实心转子感应电机为例进行磁场计算分析,实心转子感应电机参数见表1,定子绕组分布如图3所示。该样机由2对极组成,图3是电机一个极下的绕组分布,每极每相槽数q=3。
表1 实心转子感应电机参数
Tab.1 Parameters of solid rotor induction machine
参 数数 值 转子外表面半径R1/mm67.6 定子内表面半径R2/mm68 定子槽底面半径R3/mm86.5 铁心轴向长度L/mm90 定子槽宽角b/(°)5 转子电导率sR/(S/m)5 000 000 转子磁导率mR/(H/m)200m0 定子槽数Q36 极对数p12 绕组节距y19 并联支路数a2 线圈匝数N150 额定电流幅值IN/A4.6
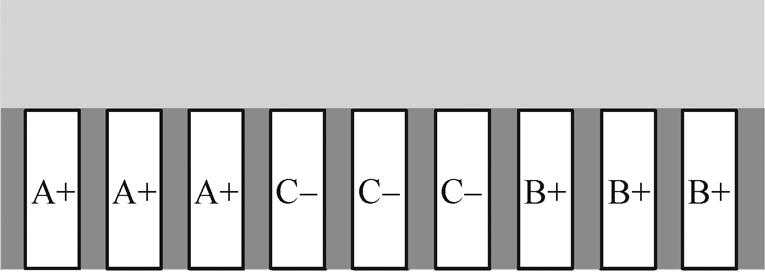
图3 定子绕组分布
Fig.3 Stator winding configurations
时变的磁场在导体中感应出涡流的电磁场问题可通过二维时谐有限元进行仿真分析,要求所有电磁量均具有相同的交变频率。本文中的实心转子感应电机采用电流源作为激励,模拟同步运行工况时将忽略转子电导率。图4为二维时谐有限元得出的t =0时刻的磁场分布,可见,磁力线由定子轭穿过气隙经转子形成闭合回路,是一个典型的4极磁场,符合三相交流绕组建立的磁动势分布。
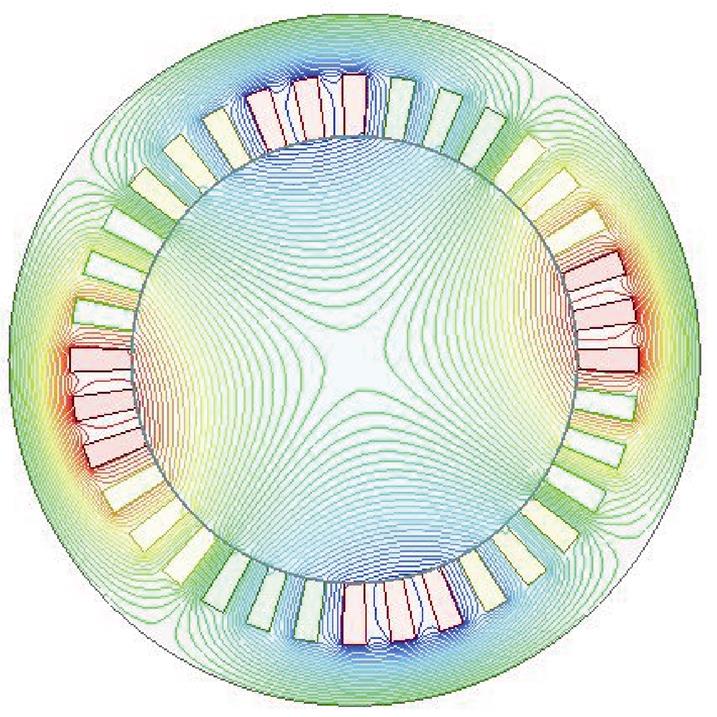
图4 同步运行工况下t =0时刻的磁场分布
Fig.4 Magnetic field distribution at t =0 under synchronous operating condition
从实际运行来讲,感应电机不能运行于同步工况,即对应s=0的空载状态。然而,虚拟的同步运行工况对于分析气隙磁通密度有重要意义。本文建立的子域解析模型同时考虑了时间和空间分量,气隙子域中任意时刻和位置的磁感应强度的径向与切向分量可表示为
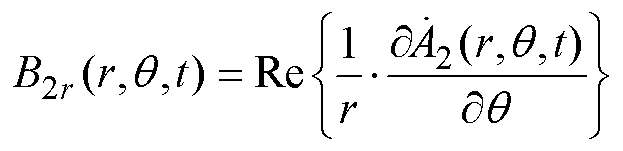 (43)
(43)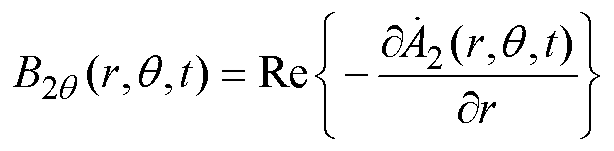 (44)
(44)
图5为实心转子感应电机同步运行工况下t=0时刻的rg=(R2+R3)/2处径向和切向磁感应强度计算结果对比。可得,解析解与有限元解的整体趋势较为吻合。不同之处在于,有限元解在定子开槽处的径向磁通密度“凹陷”更深、切向磁通密度“凸起”更高,即整体上有限元解在气隙磁导显著变化的区域突变更剧烈,这一现象与前人工作相同[14, 20]。原因在于,有限元法计算的场量在跨越不同介质边界的剖分网格处,其连续性相比解析解要相对偏弱。
将式(18)代入式(43),可得气隙磁通密度径向分量为
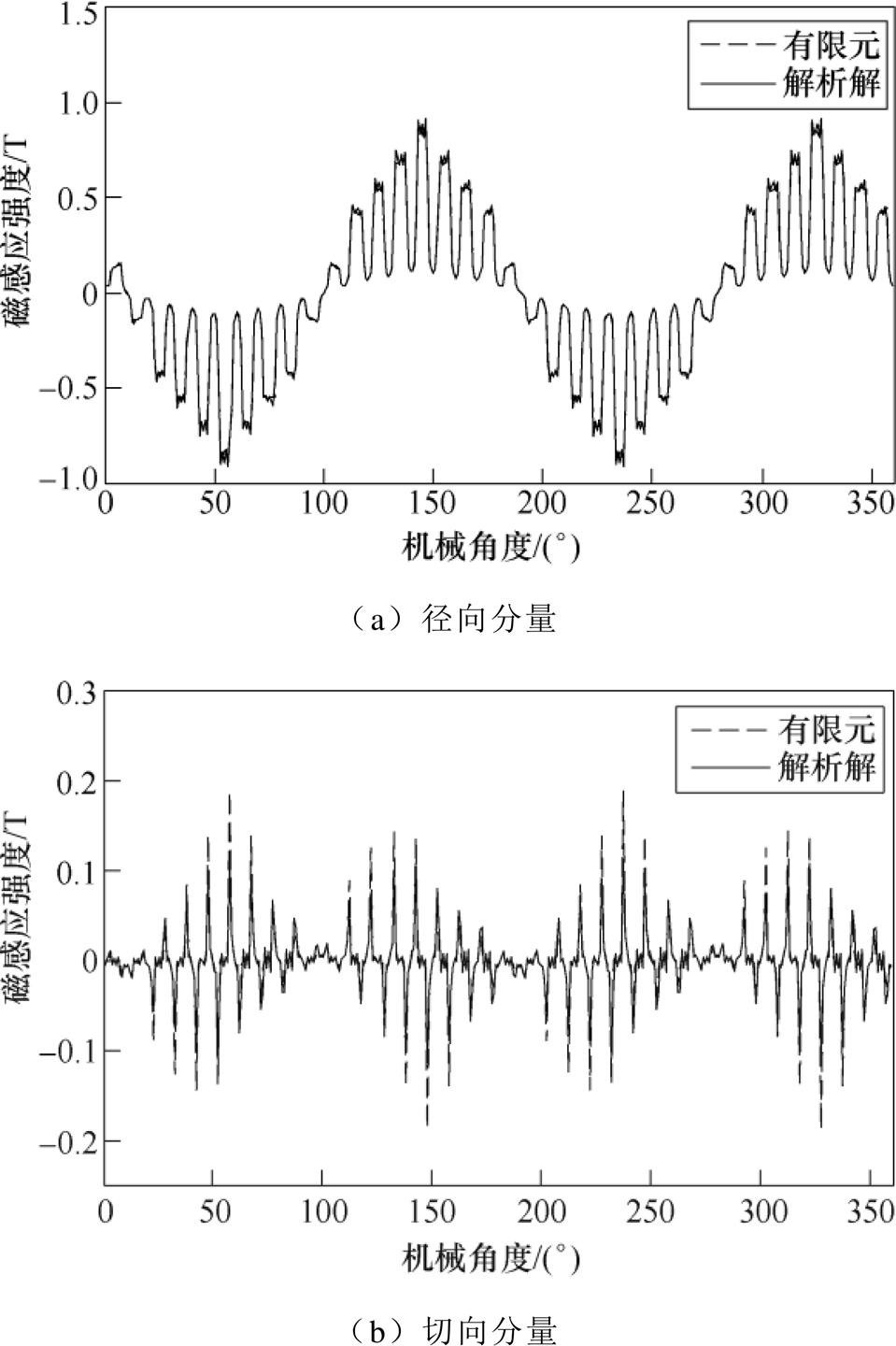
图5 同步运行工况下t =0时刻的径向和切向磁感应强度
Fig.5 Radial and tangential components of magnetic flux density at t =0 under synchronous operating condition
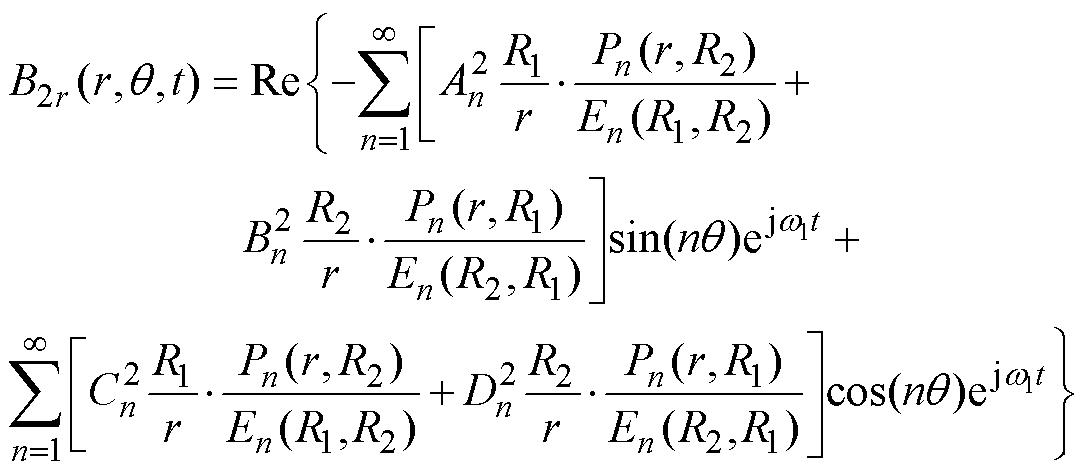 (45)
(45)由式(45)可知,气隙磁通密度径向分量是一个傅里叶级数叠加的形式,在已知各阶次复谐波系数时,可方便绘制气隙子域磁场谐波阶数n与谐波幅值的关系如图6所示,对气隙磁通密度影响最大的是一阶齿谐波n=(Q/p1±1)p1。根据电机绕组理论,整数槽绕组的空间谐波阶次主要是1±6l(l=0,1, 2,…),其在子域解析模型中对应的谐波阶数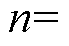
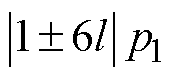 ,这与图6子域解析模型的结果相符合。除n=p1是电机基波磁场外,图6中主要的谐波分量包括n 阶齿谐波n=(nQ/p1±1)p1、正向n=7p1及反向n= 5p1旋转谐波,其空间分布分别如图7a~图7c所示。
,这与图6子域解析模型的结果相符合。除n=p1是电机基波磁场外,图6中主要的谐波分量包括n 阶齿谐波n=(nQ/p1±1)p1、正向n=7p1及反向n= 5p1旋转谐波,其空间分布分别如图7a~图7c所示。
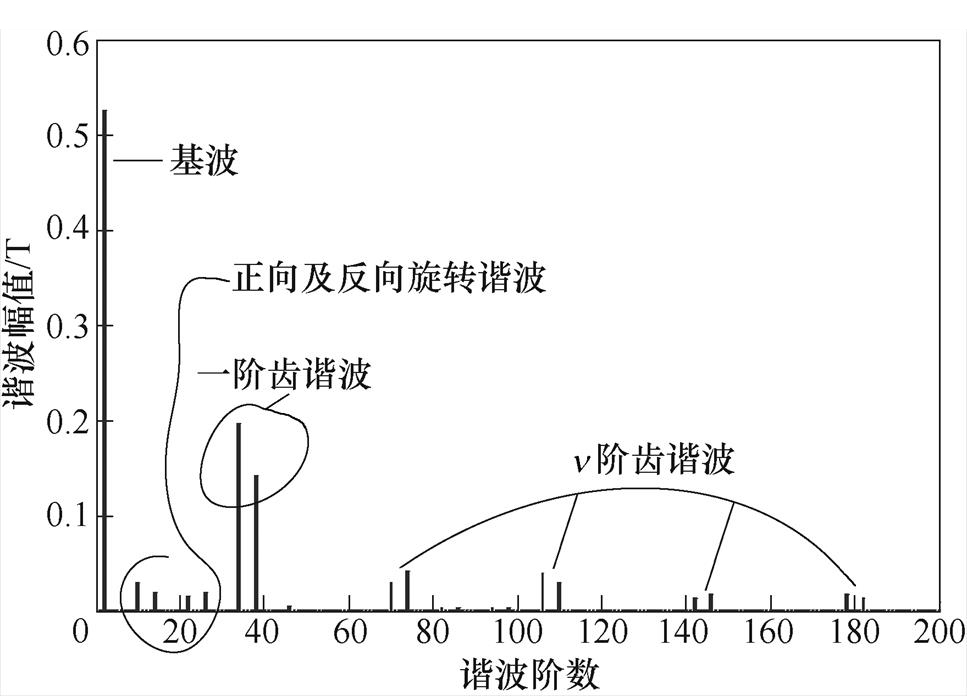
图6 n阶气隙子域谐波磁场的幅值
Fig.6 n-th order harmonic magnetic field amplitude of airgap subdomain
当实心转子感应电机运行于s=0.03的异步工况,需要将二维时谐有限元模型的实心转子区域进行频率折算,以保证电机整个求解域具有相同的交变频率。图8为异步运行工况下t =0时刻的磁场分布,可见定子绕组磁动势在实心转子中产生感应涡流,在转子表面有较明显的趋肤效应,实心转子中是一个感应产生的4极磁场。
图9为实心转子感应电机s=0.03异步工况下t = 0时刻的rg处径向和切向气隙磁通密度求解结果对比,可见,解析解与有限元解两者的磁通密度波形较为一致,再次表明,基于复频域的子域解析模型能够较好地预测磁场分布。
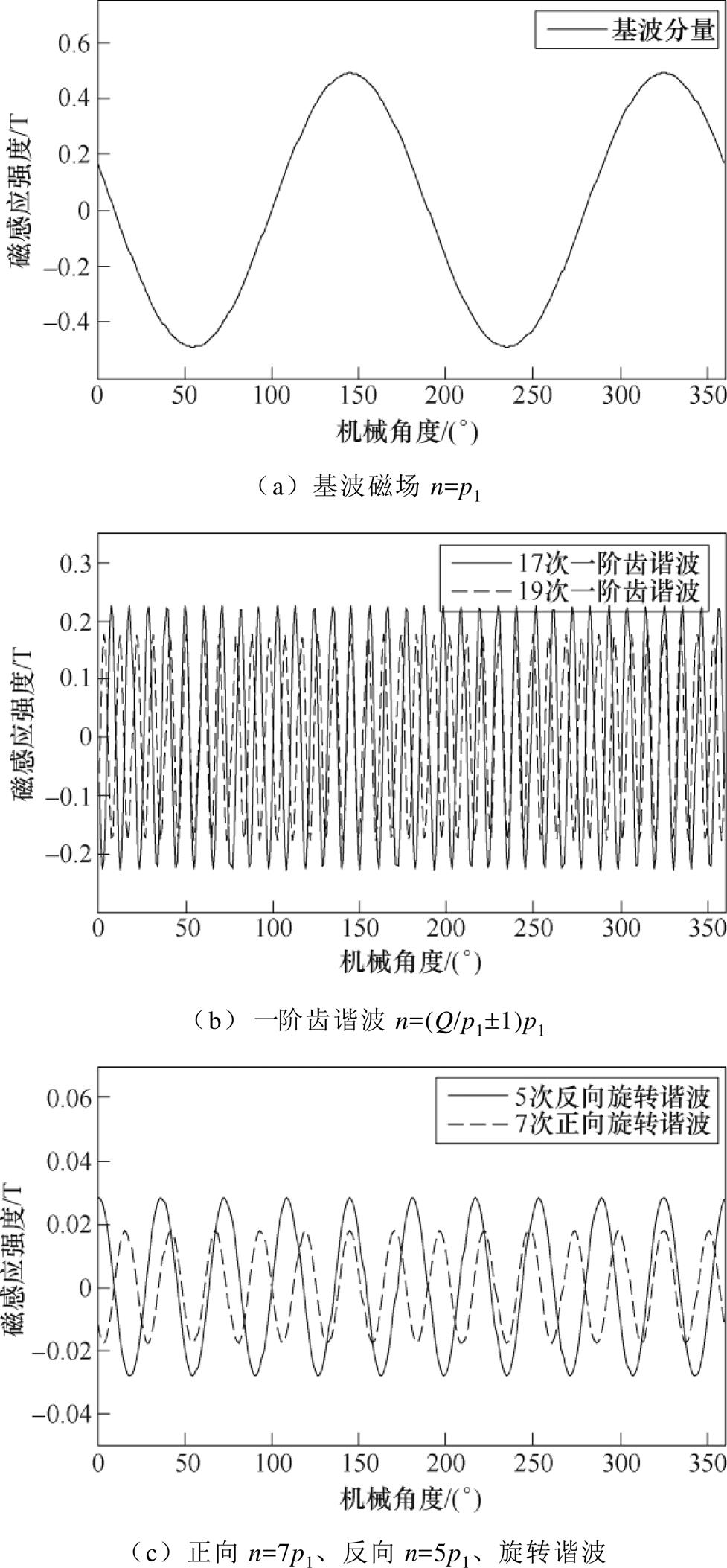
图7 同步运行工况下气隙磁通密度径向分量的谐波分析
Fig.7 Harmonic analysis of the radial component of airgap magnetic density under synchronous operating condition
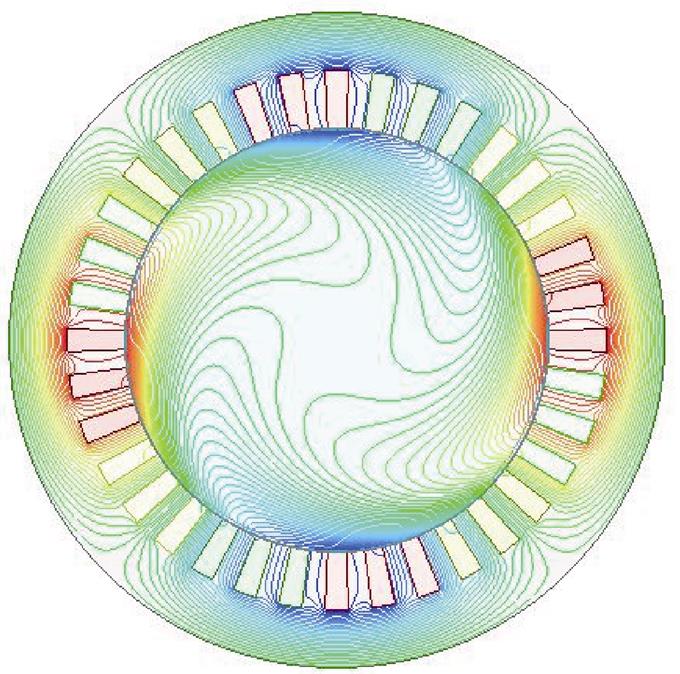
图8 异步运行工况下t =0时刻的磁场分布
Fig.8 Magnetic field distribution at t =0 under asynchronous operating condition
感应型电动机的电气制动主要包括能耗制动、反接制动和回馈制动等。在制动工况下,感应电机的转子转向与旋转磁场方向相反,电磁转矩表现为制动转矩,即转子转速nr<0,转差率s>1。假设实心转子感应电机运行于s=0.03的异步工况,此时将电源任意两相的相序反接,则电机的旋转磁场将发生反转。因机械惯性转子转向不变,则电磁转矩与转速方向相反,从而进入制动工况下的转差率sb= 1.97的制动状态。
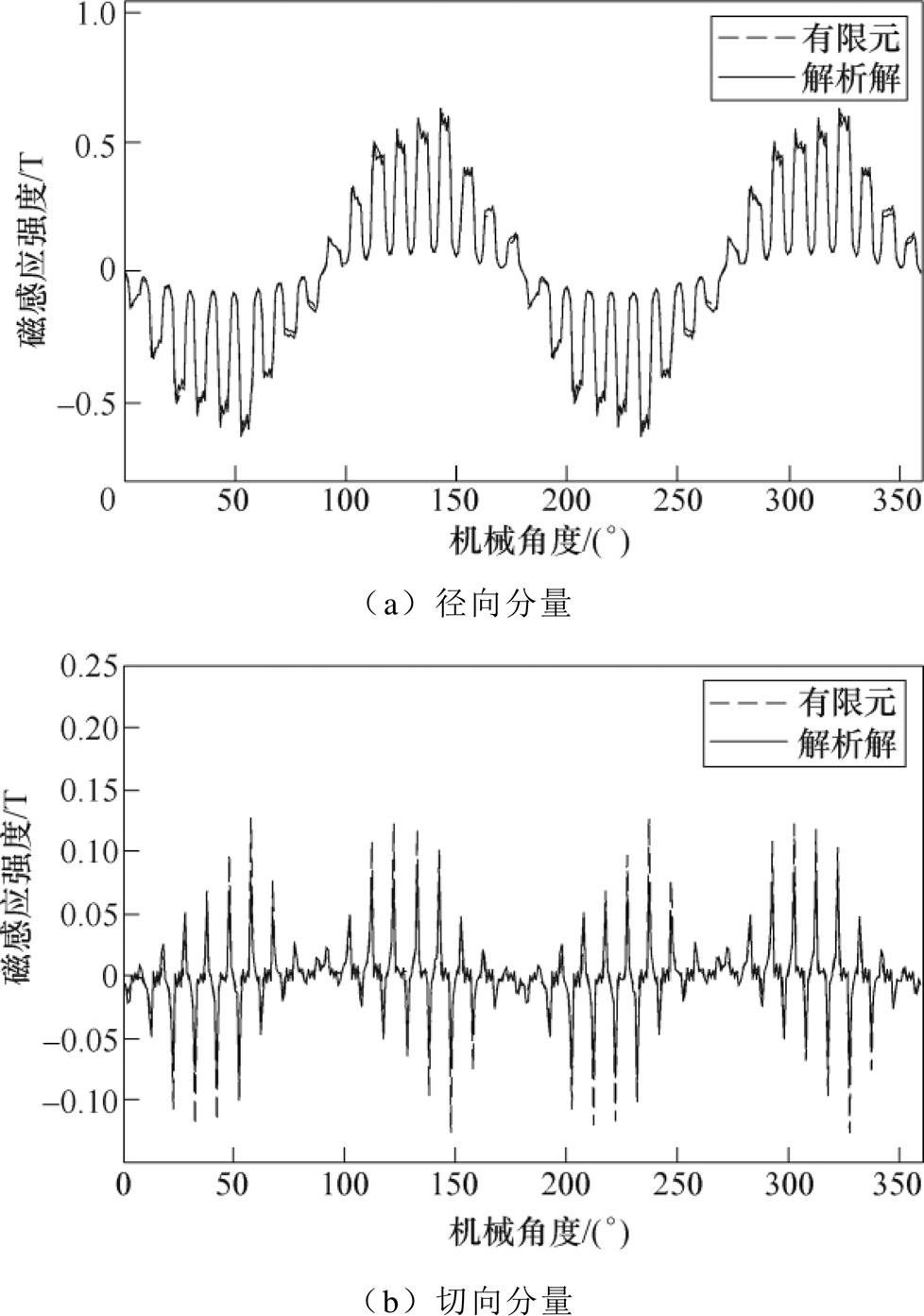
图9 异步运行工况下t =0时刻的径向和切向磁感应强度
Fig.9 Radial and tangential components of magnetic flux density at t =0 under asynchronous operating condition
图10为实心转子感应电机sb=1.97制动工况下气隙磁通密度计算结果对比,表明本文的解析模型在制动工况下能够较好地预测气隙磁场分布。
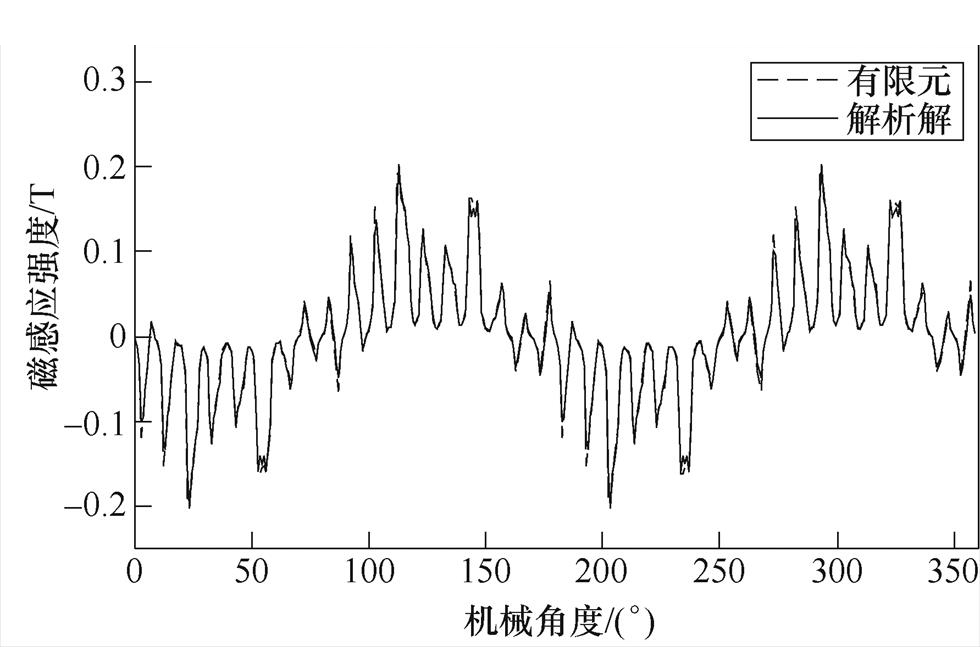
(a)径向分量
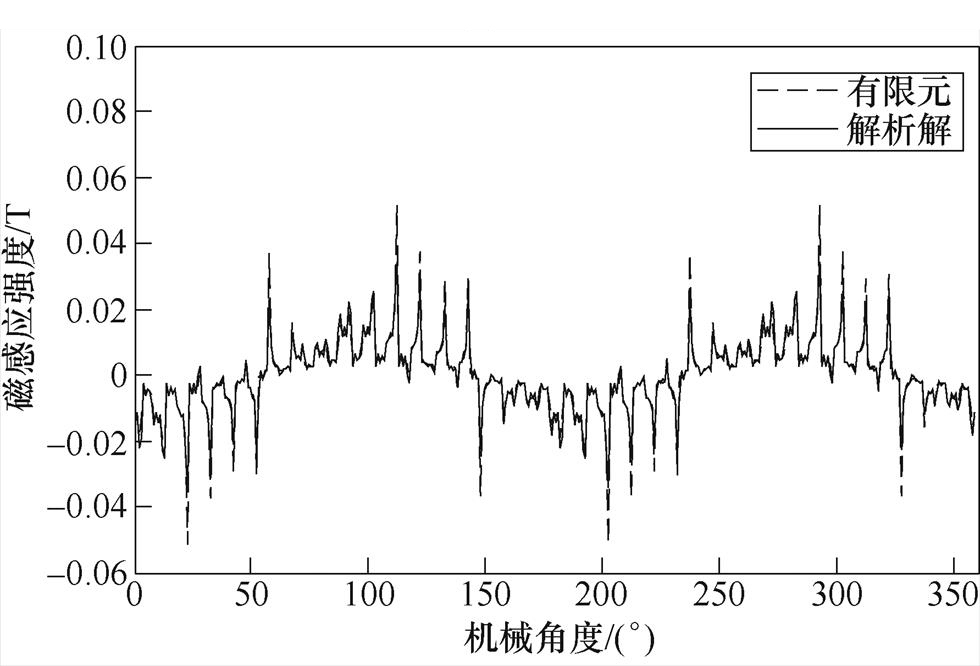
(b)切向分量
图10 制动工况下t =0时刻的径向和切向磁感应强度
Fig.10 Radial and tangential components of magnetic flux density at t =0 under braking
在B. Adkins所著《交流电机统一理论》[26]中,将微分算子p与拉氏算子p合为一体,即在时域内把p作为一个普通代数量进行运算,而在频域内是一个代数复变量。本文采用文献[26]中的规范,对于实心转子感应电机的运算电感L(p),当p=jw 时表示运算电感的频率特性L(jw)。
L(jw)是一个反映电机磁链和电流关系的传递函数,当实心转子感应电机定子中注入w=sw1、三相脉振磁动势时,三相电流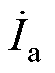 、
、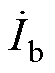 、
、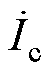 分别为
分别为
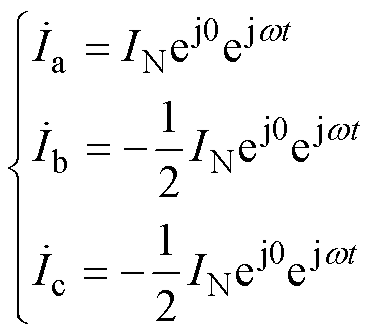 (46)
(46)根据子域解析法的定子槽子域复矢量磁位,实心转子感应电机的运算电感可表示为
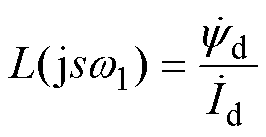 (47)
(47)
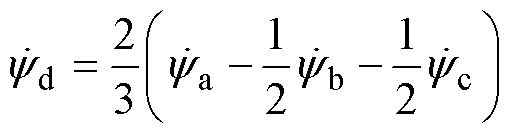 (48)
(48)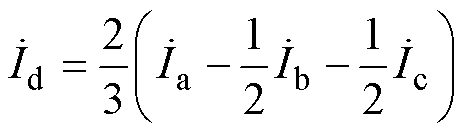 (49)
(49)
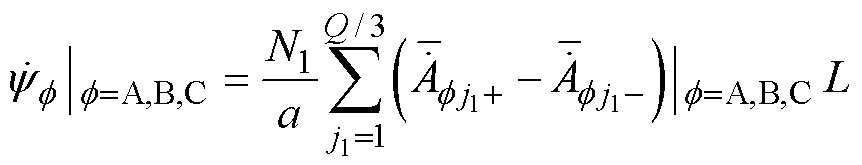 (50)
(50)
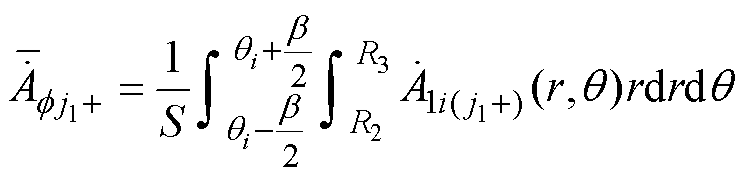 (51)
(51)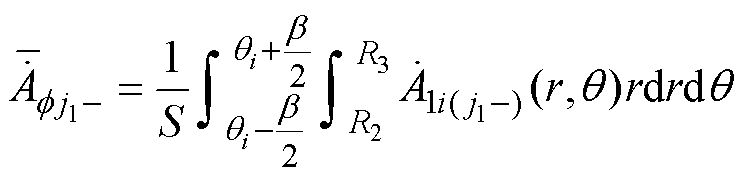 (52)
(52)
其中
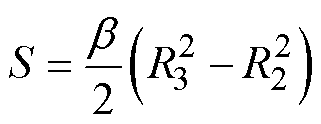 (53)
(53)式中,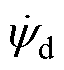 为d轴磁链;
为d轴磁链;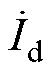 为d轴电流;
为d轴电流;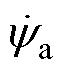 、
、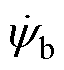 、
、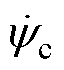 分别为A、B、C三相磁链;S为槽面积;
分别为A、B、C三相磁链;S为槽面积;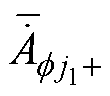 和
和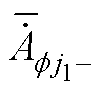 别为第f 相第j1个线圈电流流入端和流出端(分别对应一个定子槽子域)的平均复矢量磁位。
别为第f 相第j1个线圈电流流入端和流出端(分别对应一个定子槽子域)的平均复矢量磁位。
对于表1中的实心转子感应电机样机,图11所示为不同转子转差率下的运算电感计算结果对比。可见,解析解与有限元解结果相当吻合,包括运算电感实部(见图11a)和虚部(见图11b)。此时解析模型中考虑定子开槽影响,经二维时谐有限元分析验证获得了极高的计算精度。
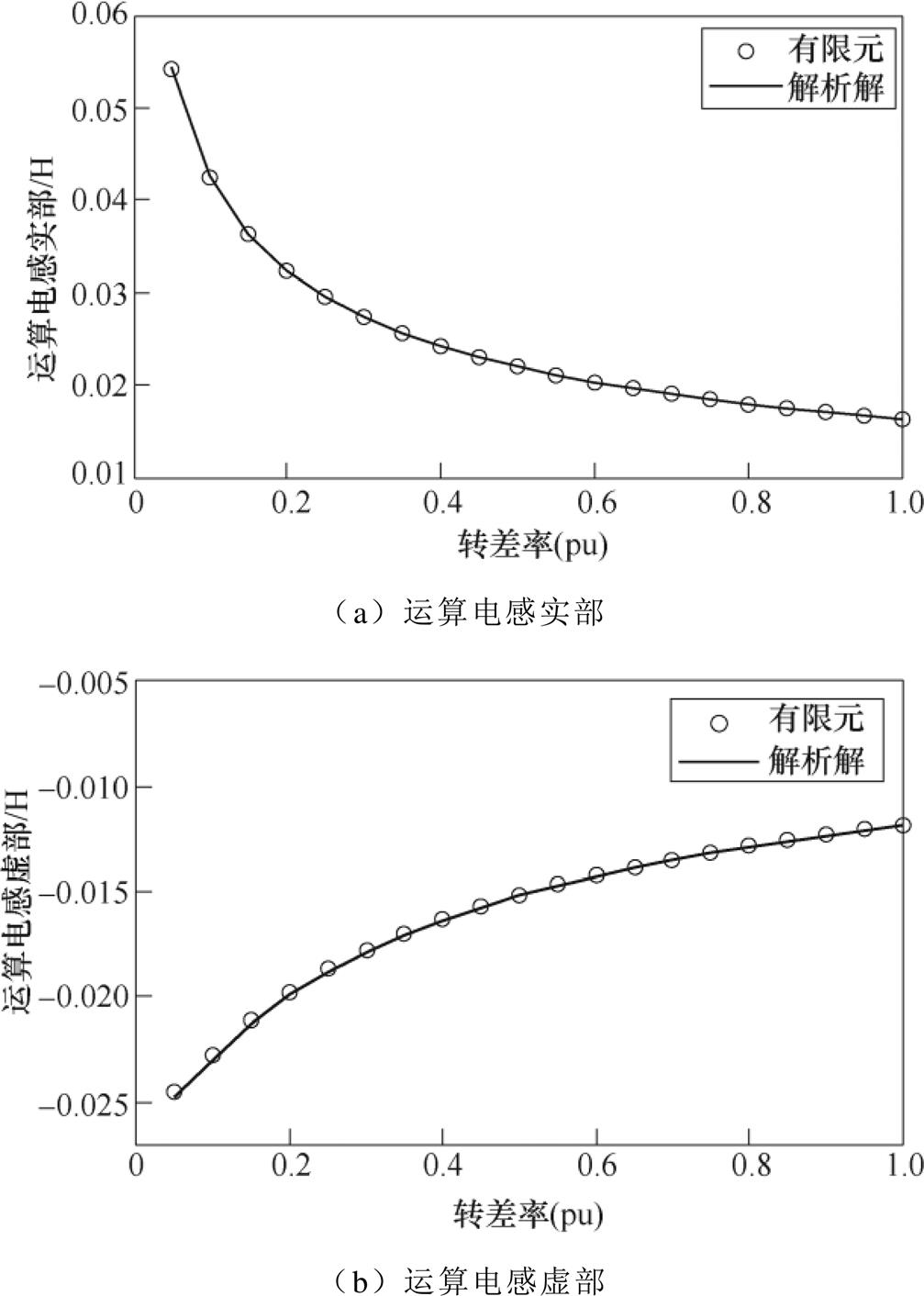
图11 异步运行工况下运算电感计算对比
Fig.11 Comparative results of operational inductanceunder asynchronous operating condition
本文以实心转子感应电机为研究对象,在二维极坐标平面内,建立了一个典型磁准静态场问题的精确子域解析模型。该解析模型包括定子槽、气隙和实心转子三类子域,各电磁量均为包含空间和时间变量的复相量形式,从而将子域模型求解从恒定磁场拓展到磁准静态场解析领域。该模型考虑了实心转子感应电机同步运行和异步运行两种工况,为三相对称交流绕组建立的气隙磁场提供了一种准确高效的分析方法。最后,以一台样机在两种运行工况下的气隙磁通密度波形以及异步运行下的运算电感计算,经解析法和二维时谐有限元结果对比,两者的一致性验证了该解析模型的有效性。
附 录
以下推导过程中各子域复矢量磁位采用隐去时间因子的形式,同第2节。
将式(18)代入式(31)、式(32),有
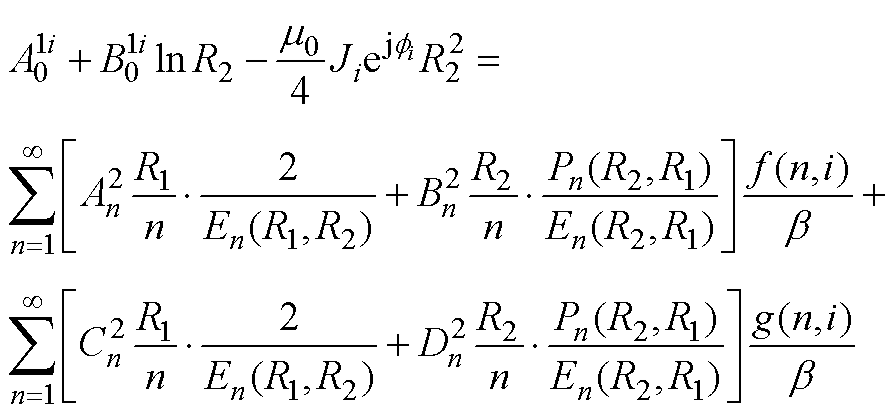 (A1)
(A1)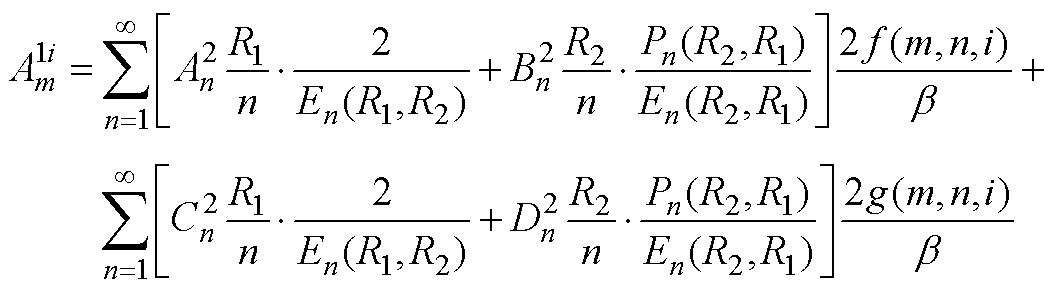 (A2)
(A2)
其中
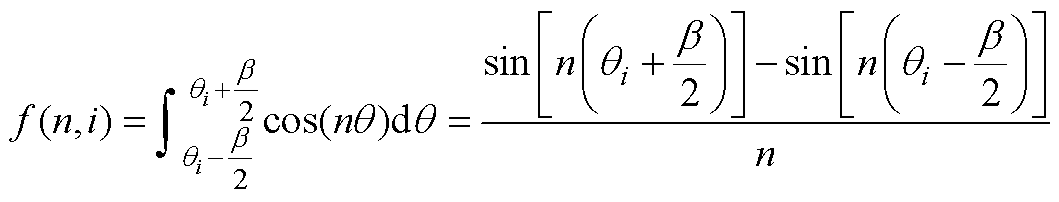 (A3)
(A3)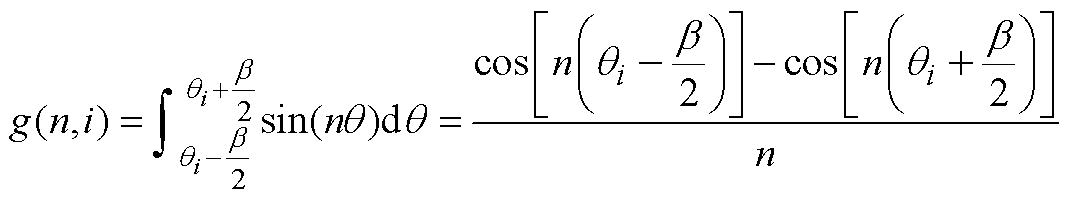 (A4)
(A4)
当tm¹n时,有
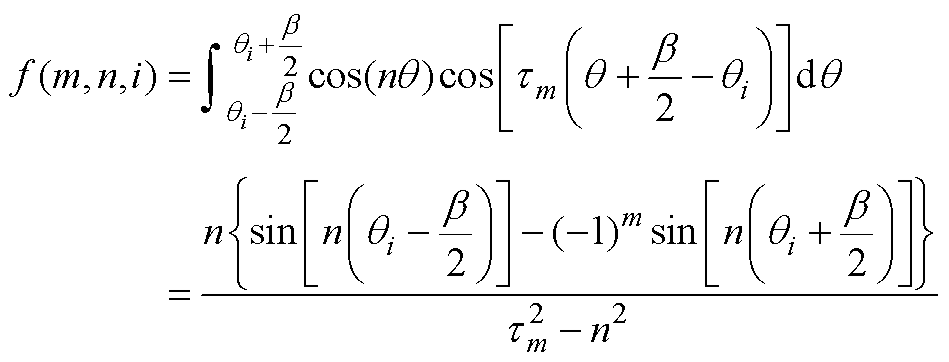 (A5)
(A5)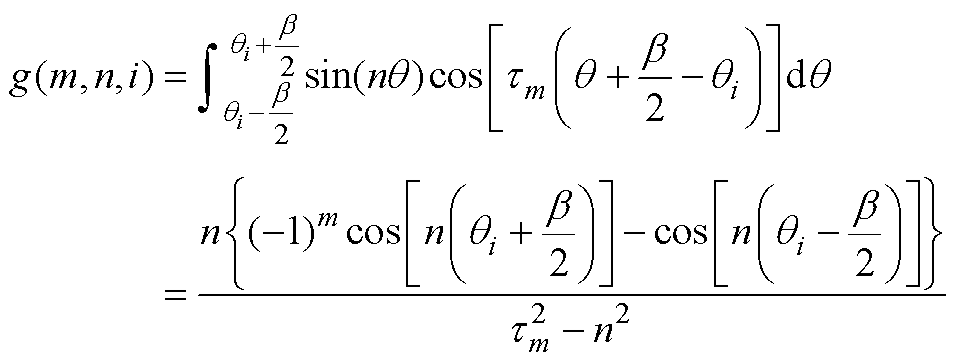 (A6)
(A6)
当tm=n时,有
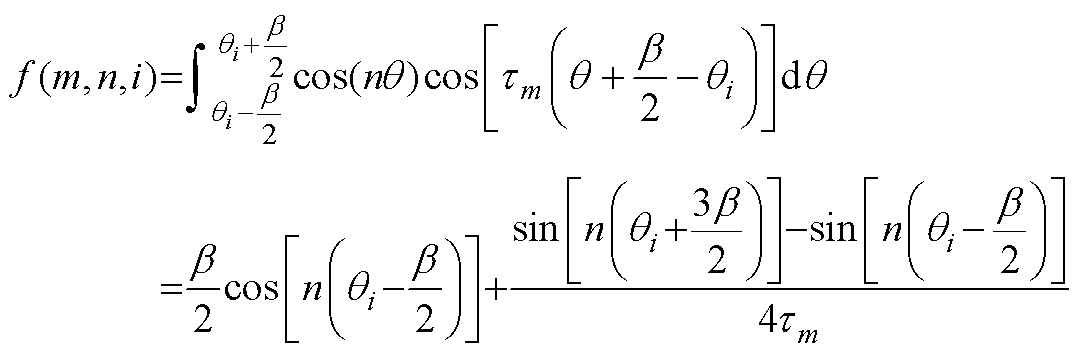 (A7)
(A7)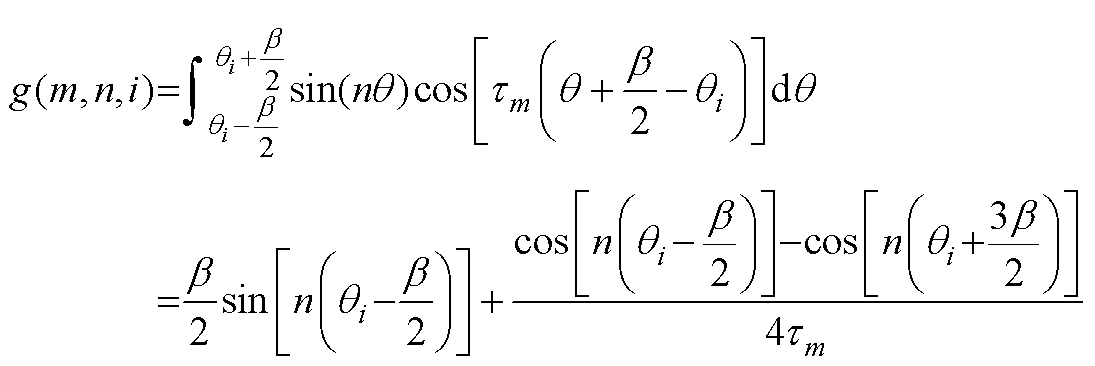 (A8)
(A8)
将式(12)代入式(35)、式(36),有
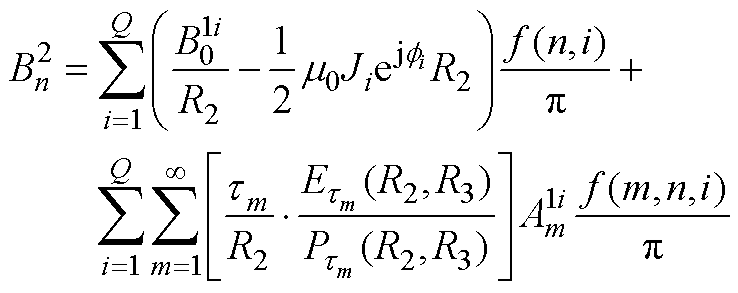 (A9)
(A9)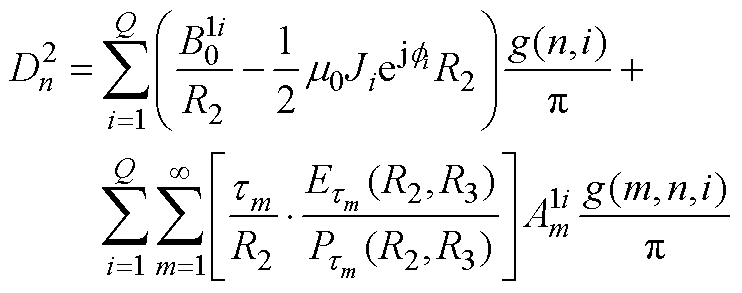 (A10)
(A10)
将式(18)代入式(38)、式(39),有
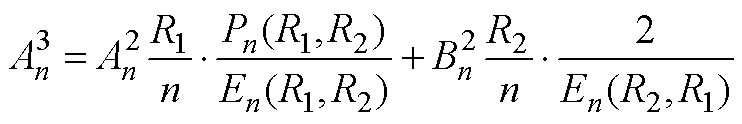 (A11)
(A11)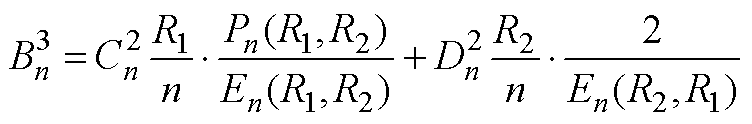 (A12)
(A12)
将式(25)代入式(41)、式(42),对应实心转子感应电机异步运行工况,有
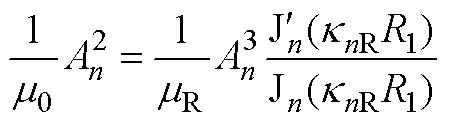 (A13)
(A13)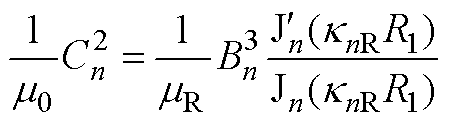 (A14)
(A14)
将式(28)代入式(41)、式(42),对应实心转子感应电机同步运行工况,有
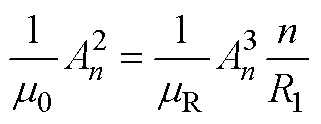 (A15)
(A15)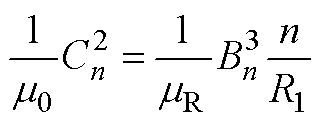 (A16)
(A16)
将定子槽子域、气隙子域、实心转子子域通解中的傅里叶级数取为有限阶次M和N,并将式(14)、式(A1)、式(A2)、式(A9)、式(A10)、式(A11)、式(A12)、式(A13)/式(A15)、式(A14)/式(A16)改写为矩阵形式,可通过矩阵运算得到每个子域未知的各阶次复谐波系数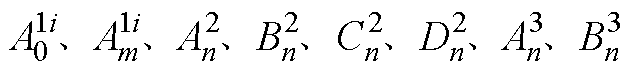 。
。
参考文献
[1] 王培欣, 司纪凯, 封海潮, 等. 实心转子感应电机研究与发展概况(上)[J]. 微特电机, 2017, 45(8): 77-82.
Wang Peixin, Si Jikai, Feng Haichao, et al. Research and development profile of solid rotor induction motor (part I)[J]. Micro Motor, 2017, 45(8): 77-82.
[2] 王培欣, 司纪凯, 封海潮, 等. 实心转子感应电机研究与发展概况(下)[J]. 微特电机, 2017, 45(9): 82-86.
Wang Peixin, Si Jikai, Feng Haichao, et al. Research and development profile of solid rotor induction motor (part II)[J]. Micro Motor, 2017, 45(9): 82-86.
[3] 唐孝镐. 实心转子异步电机及其应用[M]. 北京: 机械工业出版社, 1991.
[4] Miroslav M, Yves P. An analytical solution for the torque and power of a solid-rotor induction motor[C]// IEEE International Electric Machines and Drives Conference (IEMDC), Niagara Falls, Canada, 2011: 1053-1057.
[5] Guo Siyuan, Zhou Libing, Yang Tong. An analytical method for determining circuit parameter of a solid rotor induction motor[C]//IEEE International Confer- ence of Economy and Management Sciences, Sapporo, Japan, 2012: 1-6.
[6] 郭立炜. 实心转子感应电机的运算电抗及激磁电抗[J]. 河北机电学院学报, 1991, 8(4): 18-24.
Guo Liwei. Operational impedance and magnetizing impedance of induction machines with solid rotor[J]. Journal of Hebei Institute of Mechano-Electric Engineering, 1991, 8(4): 18-24.
[7] Gieras J F. Analysis of multilayer rotor induction motor with higher space harmonics taken into account[J]. IEE Proceedings-B, 1991, 138(2): 59-67.
[8] 童钟良. 双层实心转子感应电机的分层阻抗理论[J]. 电工技术学报, 1993, 8(2): 18-20.
Tong Zhongliang. The sublayer impedance theory for analysing double-layer solid rotor induction machines[J]. Transactions of China Electrotechnical Society, 1993, 8(3): 18-20.
[9] 童钟良. 实心转子感应电机的两层传输线比拟分析[J]. 电工技术学报, 1995, 10(1): 28-33.
Tong Zhongliang. Two-region analysis based on a transmission-line analogy in solid rotor induction machines[J]. Transactions of China Electrotechnical Society, 1995, 10(1): 28-33.
[10] Gieras J F, Saari J. Performance calculation for a high-speed solid-rotor induction motor[J]. IEEE Transactions on Industrial Electronics, 2012, 59(6): 2689-2700.
[11] Gysen B, Meessen K, Paulides J, et al. General formulation of the electromagnetic field distribution in machines and devices using Fourier analysis[J]. IEEE Transactions on Magnetics, 2010, 46(1): 39-52.
[12] Zhu Ziqiang, Wu Lijian, Xia Zhenping. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2010, 46(4): 1100- 1115.
[13] Lubin T, Mezani S, Rezzoug A. 2-D exact analytical model for surface-mounted permanent-magnet motors with semi-closed slots[J]. IEEE Transactions on Magnetics, 2011, 47(2): 479-492.
[14] 李节宝, 井立兵, 周晓燕, 等. 表贴式永磁无刷电机直接解析计算方法[J]. 电工技术学报, 2012, 27(11): 83-88.
Li Jiebao, Jing Libing, Zhou Xiaoyan, et al. Exact analytical method for surface-mounted permanent- magnet brushless motors[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 83-88.
[15] 张守首, 郭思源. 考虑分段斜极和磁性槽楔的永磁同步电机磁场解析方法[J]. 电工技术学报, 2019, 34(1): 11-22.
Zhang Shoushou, Guo Siyuan. Analytical magnetic field method of permanent magnet synchronous machine considering step-skewed magnets and magnetic slot wedge[J]. Transactions of China Elec- trotechnical Society, 2019, 34(1): 11-22.
[16] 倪有源, 王磊, 王群京. 凸形不等厚磁极永磁电机建模与分析[J]. 电工技术学报, 2020, 35(11): 2406-2414.
Ni Youyuan, Wang Lei, Wang Qunjing. Modeling and analysis of permanent magnet machines with salient shape unequal thickness magnets[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(11): 2406-2414.
[17] 高锋阳, 齐晓东, 李晓峰, 等. 部分分段Halbach永磁同步电机优化设计[J]. 电工技术学报, 2021, 36(4): 787-800.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Optimization design of partially-segmented Halbach permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(4): 787-800.
[18] 井立兵, 章跃进. 同心式磁力齿轮磁场及转矩全局解析法分析[J]. 中国电机工程学报, 2012, 32(30): 139-146.
Jing Libing, Zhang Yuejin. An exact analytical method for magnetic field computation and elec- tromagnetic torque in a concentric magnetic gear[J]. Proceedings of the CSEE, 2012, 32(30): 139-146.
[19] 井立兵, 龚俊, 章跃进, 等. Halbach阵列磁力变速永磁无刷电机解析计算与设计[J]. 电工技术学报, 2020, 35(5): 954-962.
Jing Libing, Gong Jun, Zhang Yuejin, et al. Analytical calculation and design of magnetic variable speed permanent magnet brushless machine with Halbach arrays[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 954-962.
[20] Rahideh A, Korakianitis T. Analytical magnetic field calculation of slotted brushless permanent-magnet machines with surface inset magnets[J]. IEEE Transactions on Magnetics, 2012, 48(10): 2633- 2649.
[21] Zhu Minchen, Wu Lijian, Fang Youtong, et al. Subdomain model for predicting armature reaction field of dual-stator consequent-pole PM machines accounting for tooth-tips[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2019, 3(2): 143-150.
[22] 王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 942-953.
Wang Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 942- 953.
[23] Dubas F, Rahideh A. Two-dimensional analytical permanent magnet eddy-current loss calculations in slotless PMSM equipped with surface-inset magnets[J]. IEEE Transactions on Magnetics, 2014, 50(3): 6300320.
[24] Hannon B, Sergeant P, Dupré L. 2-D analytical subdomain model of a slotted PMSM with shielding cylinder[J]. IEEE Transactions on Magnetics, 2014, 50(7): 8101410.
[25] Boughrara K, Dubas F, Ibtiouen R. 2-D analytical prediction of eddy currents, circuit model parameters, and steady-state performances in solid rotor induction motors[J]. IEEE Transactions on Magnetics, 2014, 50(12): 7028214.
[26] Adkins B, Harley R G. The general theory of alternating current machines: application to practical problems[M]. London: Chapman & Hall, 1975.
Analytical Solution of Magnetic Field in Solid Rotor Induction Machine Based on Subdomain Model
Abstract As a simple and efficient method of magnetic field analysis, subdomain techniques have been widely used in the analytical calculation of constant magnetic field analysis for electrical machines. Taking the solid rotor induction machine as an example, the subdomain technique is extended to the field of magnetic quasi-static field analysis in this paper. The solver region of the solid rotor induction machine is divided into the stator slot domain, the air-gap domain and the solid rotor domain in the two-dimensional polar coordinate plane, thereby establishing an accurate subdomain model of the solid rotor induction machine considering the stator slotting effect in the complex frequency domain. The analytical model focuses on solving the partial differential equations of the solid rotor subdomain. According to the different operating modes, the analytical expressions for synchronous operation and asynchronous operation are given. Then, the operational inductance of the solid rotor induction machine is calculated by the flux linkage method. Finally, the accuracy of the analytical model is verified by two-dimensional harmonic finite element analysis.
keywords:Solid rotor induction machine, accurate subdomain model, analytical solution of magnetic field, stator slotting, operational inductance
DOI: 10.19595/j.cnki.1000-6753.tces.210492
中图分类号:TM351
张守首 女,1987年生,博士,讲师,研究方向为电磁场及电磁波理论、信号处理技术等。E-mail: sszhang@whu.edu.cn(通信作者)
郭思源 男,1986年生,博士,高级工程师,研究方向为发电机励磁系统及其控制、电机电磁场等。E-mail: siyuanguo2001@163.com
收稿日期 2021-04-11
改稿日期 2021-06-06
湖南省自然科学基金资助项目(2020JJ5988)。
(编辑 崔文静)