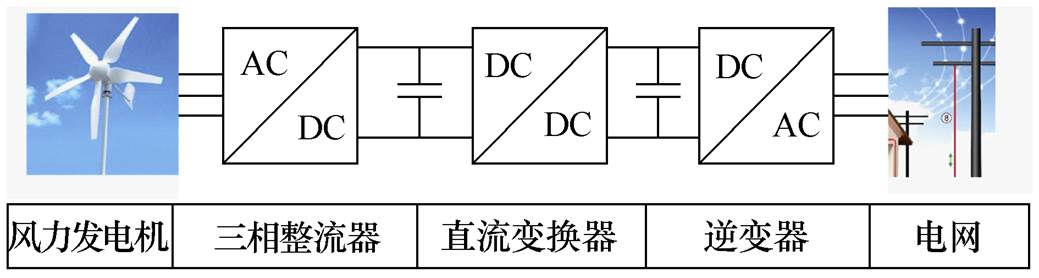
图1 并网型风力发电系统结构
Fig.1 Grid-connected wind power generation system structure
摘要 该文提出一种可变结构的多谐振软开关直流变换器。此变换器采用双变压器结构,运用两个互补导通的辅助开关管进行变换器拓扑结构的转换。相互变换的工作模态有三种,能够满足不同工况对高电压增益或高变换效率的要求。此外,该文通过合理设置谐振频率和增益点的方式对变换器的谐振参数进行设计。随后,针对额定条件下变换器同时传递基波和3次谐波能量的工况,构建同时考虑基波和3次谐波的损耗模型,对变换器的损耗分布进行详细估算。最后,为验证理论分析的可靠性,基于一台实验样机对所述变换器进行功率实验验证,在输入电压80~600V变化范围内,输出电压始终稳定在400V,在获得较宽电压增益范围的同时实现了全增益范围内的高效率变换,变换器最高效率达97.6%。
关键词:变拓扑结构 多谐振 直流变换器 软开关 损耗分析
小型风力发电是新能源发电的重要形式,具有能源可再生、清洁无污染的优点[1-3]。根据并网形式,小型风力发电系统可分为离网型和并网型。离网型风力发电系统可将获得的能量经电力电子装置直接供给负载或储能单元,结构简单、供电可靠性强,但其供电形式单一,不具广泛适用性;相较之下,并网型风力发电系统能够将捕获的能量经电力电子变换装置输送入电网,供多种形式负载使用,有效地拓宽了应用范围。典型的小型并网型风力发电系统由整流器、直流变换器和逆变器组成,详细结构如图1所示。但大部分风场具有风速小、风速波动大、系统收集能量较少的特点,使得前级整流器输出电压难以满足后级逆变器并网要求。因此,研究具有较高升压能力的中间级直流变换器具有重要 意义。

图1 并网型风力发电系统结构
Fig.1 Grid-connected wind power generation system structure
图1中,采用升压型直流变换器,主要用于将直流输出侧电压变换为后级逆变器输入侧所需电压等级,是风力发电单元中的重要一环。根据是否提供电气隔离,直流变换器可分为非隔离型和隔离型,后者在安全性上更具优势,但效率问题却是限制其应用的一大瓶颈。
在隔离型变换器中,谐振型直流变换器不仅能够提高系统的安全性,还具有易高频化、低电磁干扰、高效率变换等优点,是一种较为理想的直流变换器。该变换器根据谐振元件的数量、结构不同,可表现出不同的变换效果。
相较于传统两元件LC结构,LLC谐振直流变换器克服了轻载下电压范围难以调节及效率低下的问题。此外,其能够在全负载范围内实现零电压开通(Zero Voltage Switching, ZVS),具有结构简单、成本低廉等优点,受到了相关学者的广泛关注[4-10]。文献[11]提出了一种基于LLC结构的峰值增益配置的优化设计方法,减少谐振电容的同时采用搜寻法进行参数优化设计,在满足变换器电压增益前提下,使变换器导通损耗最小化。文献[12]研究了一种复合式全桥三电平LLC谐振变换器。该变换器集合了复合式全桥三电平(Hybrid full Bridge Three-Level, FBTL)变换器和LLC谐振变换器的优点,降低了开关管及二极管的电压应力,在全负载范围内实现ZVS,适合于宽输入电压范围的应用场合。但是,受传统LLC自身结构的固有限制,电压范围和变换效率间仍然存在较大矛盾。
多谐振软开关直流变换器因含有多个谐振点而拥有多种谐振特性,在不同频段可满足不同变换需求。因其谐振元件种类、数量、连接方式的不同,衍生拓扑众多。根据谐振元件的数量,多谐振软开关直流变换器可分为四元件结构、五元件结构、双变压器结构和拓扑变换结构。文献[13]研究了四元件CLCL谐振直流变换器,在全负载范围内实现了ZVS和准零电流关断(Zero Current Switching, ZCS),降低了功率损耗,提高了变换效率。文献[14]提出了一种五元件LLC-LC结构的变换器,基于LLC结构,在变压器二次侧增加了陷波滤波器,实现了电压增益从零可调的范围,有效地解决了起动和过电流保护的问题。文献[15]研究了一种双变压器结构的多谐振直流变换器,在CLCL拓扑结构上引入了高频变压器,实现了开关管和整流管的ZVS和准ZCS,将导通损耗最小化,提升效率。虽然上述结构都在提高电压增益和效率、缩小频率范围等方面做了详尽的研究,但由于电路形式固定、灵活性有限,电压增益范围有待进一步拓宽。
在可变结构型多谐振直流变换器的谐振腔中增加了功率开关器件,可通过控制功率开关器件的通断改变拓扑结构,经过合理的参数设计使变换器满足不同工况的应用需求。文献[16]提出了一种集成全桥变换器和半桥变换器的可变结构型直流变换器。其降低了续流状态下的传导损耗,改善了传统全桥变换器ZVS范围窄的缺点。文献[17]研究了一种双变压器谐振变换器拓扑变换结构。此拓扑应用条件自适应地改变谐振模式,实现了一次侧开关ZVS及两个谐振模式的二次侧二极管ZCS,在额定点处实现了环流能量最小化。上述拓扑改进变换方案在提高效率及拓宽增益范围方面有极大改善,但寻找宽增益、高效率、窄频段的优化结合方面仍是谐振型直流变换器的研究热点,且具有较大的研究价值。
本文提出了一种可变结构型多谐振软开关直流变换器,基于双变压器结构,通过控制辅助开关管的通断来灵活调整谐振腔电路结构,使得电路可适应多种工况。为满足应用需求,所述拓扑在输入电压较低时,可获得相对较高的电压增益,拓宽了电压范围,进而维持输出电压400V稳定的运行性能;在额定点时,变换器能同时传递1次和3次谐波,减小环流,降低了导通损耗;在输入电压较高时可工作在降压模式,理论上可提供从零可调的电压增益。因此变换器拥有升压、降压两种工况,在较窄的频率范围内可实现0.66~5倍的宽电压增益范围。最后,本文基于一台实验样机验证了理论分析的可靠性,最高效率达97.6%。
图2给出了可变结构型多谐振软开关直流变换器结构,整体上分为三个模块:左侧逆变模块由4个MOSFET管Q1~Q4组成,主要将给定的直流输入电压变为方波形式。中间的谐振腔单元包含两对电感、电容元件和两个变压器,其中,谐振元件Cs1、Ls1串联,Cp2和Lp2并联接入电路;变压器Tx2二次侧则连接由两个相对串联的MOSFET组成的辅助开关管Qa和Qb,通过控制开关管的通断可实现谐振腔结构的转换,进而满足不同模态的应用需求。谐振腔模块的主要作用是滤除方波信号的高次谐波,保留基波交流信号。右侧4个二极管VD1~VD4构成了整流模块,负责将交流电变换为直流电供负载使用。
本文所述可变结构型变换器变换结构主要分为CLTCL模式和LCLCL模式。CLTCL模式时,谐振腔内Qa关断、Qb导通,变压器Tx2完整地参与变换工作,此时两个变压器串联共同向负载输送能量;LCLCL模式时,Qa导通、Qb关断,变压器Tx2二次侧未接入电路,可将一次侧的漏感Lk2并入Lp2,然后再与励磁电感Lm2相串联等效为一个电感元件Leq2,此模式只有变压器Tx1完成能量传输的任务。
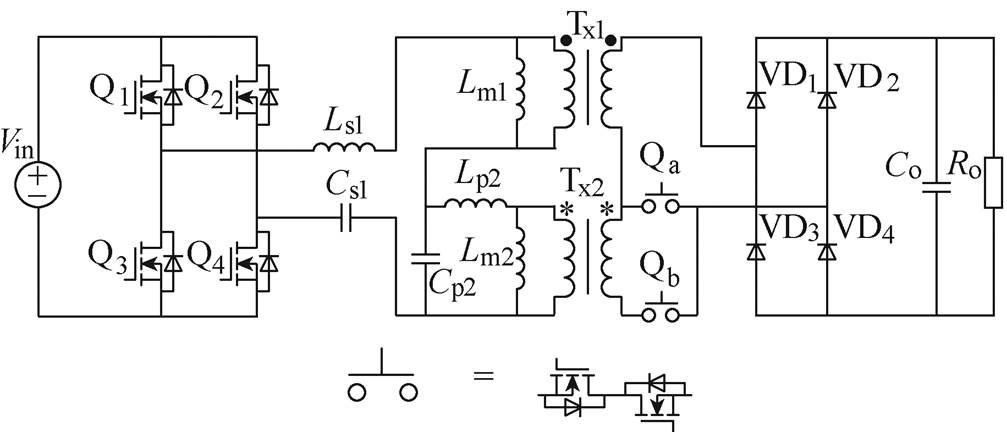
图2 可变结构型多谐振软开关直流变换器结构
Fig.2 Variable topology multi-resonant soft switching DC converter structure
图3给出了CLTCL型多谐振软开关直流变换器结构。谐振腔中两个高频变压器相串联共同传递能量。此变换器共含3个谐振点fC1、fC2和fC3,fC2为谐振零点。fC2处电压增益恒为0,且不随负载变化而变化。谐振零点的引入理论上实现了电压增益从零可调的较宽范围,同时还使电路具有了过电流保护功能,为电路的良好运行提供一定保障。此外,两个变压器的漏感分别并入谐振电感Ls1和Lp2中,参与谐振变换过程,充分利用了变压器固有寄生参数,削弱了其给电路造成的不利影响。
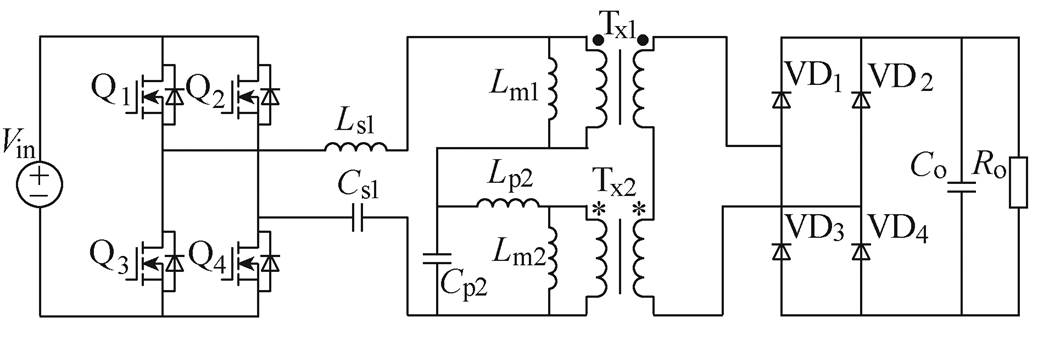
图3 CLTCL型多谐振软开关直流变换器结构
Fig.3 CLTCL multi-resonant soft switching DC-DC converter
本文利用基波等效分析法对CLTCL电路进行了建模分析,应用基尔霍夫电压、电流定律(KVL、KCL)列写方程,并对所列方程组进行简化求解,最终获得了CLTCL拓扑结构的电压增益VgainFC为
 (1)
(1)其中
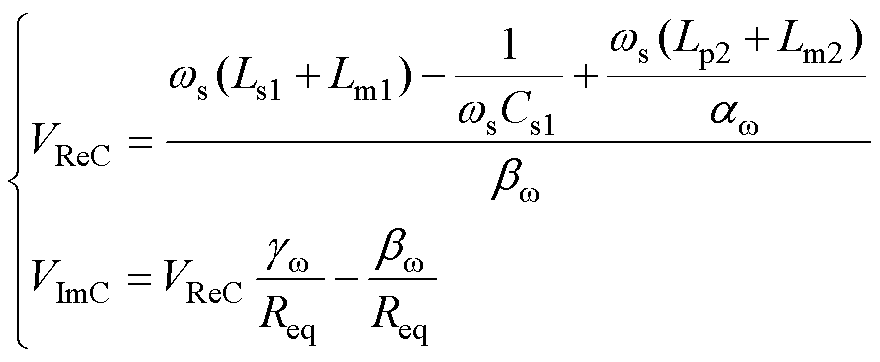 (2)
(2)
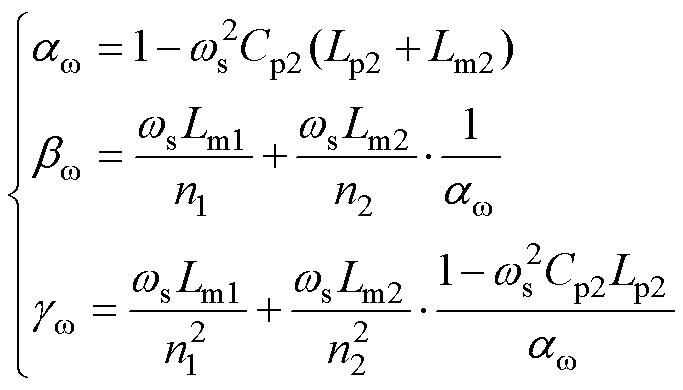 (3)
(3)式中,VReC、VImC分别为电压增益VgainFC分母的实部、虚部;Cs1、Ls1分别为变换器串联谐振电容和电感;Cp2、Lp2分别为变换器并联谐振电容和电感;Lm1和n1分别为变压器Tx1的励磁电感及匝比;Lm1、Lm2和n1、n2分别为变压器Tx1、Tx2的励磁电感和匝比;ws为开关操作频率fs的角频率,ws=2pfs;Req为负载电阻;aw、bw 和gw 均为中间变量。因文章篇幅有限,详细推导过程不再赘述。
根据式(1)~式(3),令VgainFC虚部VImC=0,可推导出fC1和fC3的表达式分别为
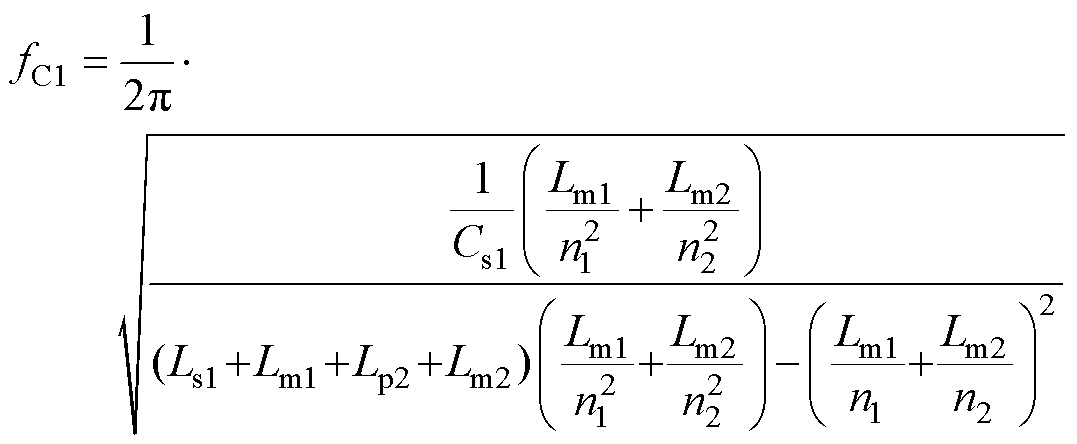 (4)
(4)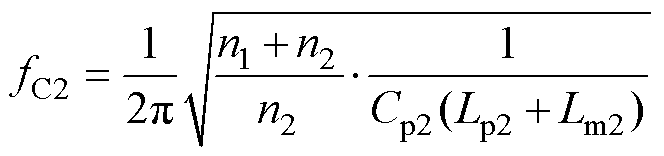 (5)
(5)
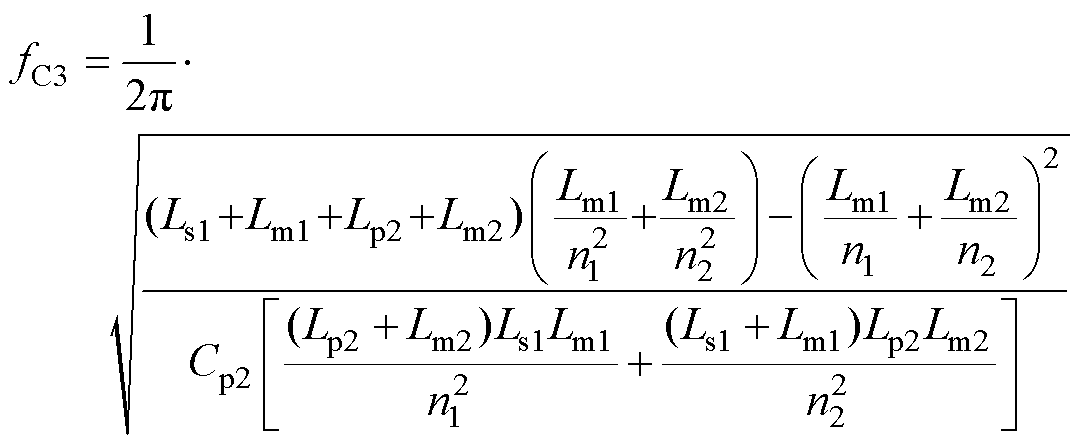 (6)
(6)
令中间变量bw=0,可解得fC2的表达式。基于式(4)~式(6)可绘出电压增益曲线。通过合理设计参数,变换器谐振腔的输入阻抗角接近于零,实现了电路中逆变单元开关管和整流单元二极管开关过程的软开关或准软开关性能,使变换器开通损耗最小化。
图4为LCLCL型多谐振软开关直流变换器结构。谐振腔单元为五元件多谐振结构,包括两对电感、电容及一个高频变压器。此变换器同样包含3个谐振点fL1、fL2和fL3。其中,fL2是谐振零点,由Lp2和Cp2并联结构引入,其对应的电压增益独立于负载,恒保持0。类比CLTCL建模方法,利用基波等效法对电路列写KVL、KCL方程,通过求解方程组获得了LCLCL电路电压增益VgainFL为
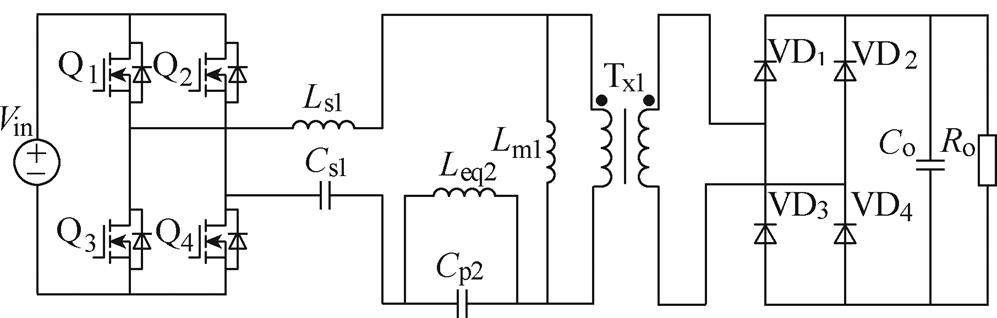
图4 LCLCL型多谐振软开关直流变换器结构
Fig.4 LCLCL multi-resonant soft switching DC-DC converter
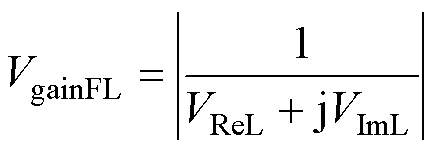 (7)
(7)其中
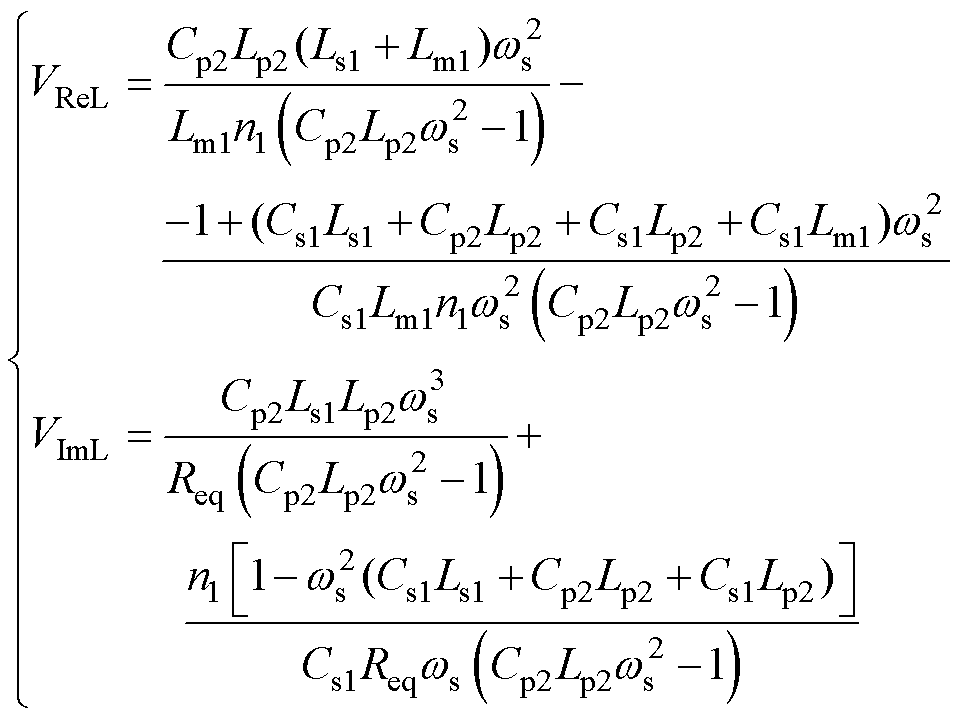 (8)
(8)
式中,VReL、VImL分别为电压增益VgainFL分母的实部、虚部。基于式(7)、式(8),令VgainFL的虚部VImL=0,可解得LCLCL拓扑结构谐振频率fL1、fL3,fL2为谐振腔中Cp2、Leq2并联引入的谐振零点,fL1~fL3的表达式分别为
 (9)
(9)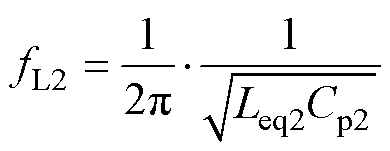 (10)
(10)
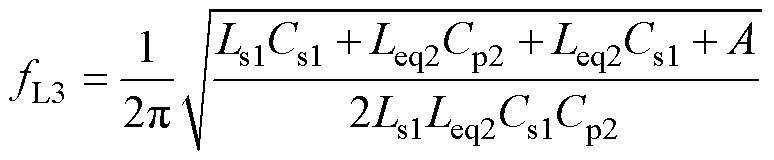 (11)
(11)
其中
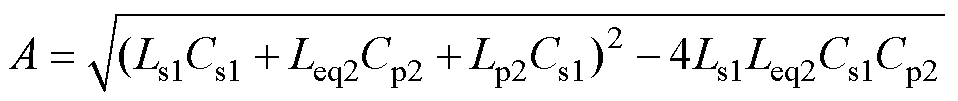 (12)
(12)式中,Leq2为电感Lp2和Tx2励磁电感Lm2串联构成的等效电感,Leq2=Lp2+Lm2。
根据式(9)~式(12)可描绘其电压增益曲线。通过合理配置fL1和fL3的关系,变换器能同时传递1次、2次谐波,3次谐波传递有功功率可减小谐振腔内环流能量,降低导通损耗,有助于提高变换器效率。
基于上述对CLTCL和LCLCL拓扑的描述分析,本文根据两种拓扑类型的相通点,合理控制辅助开关管的通断,实现了可变结构的多谐振软开关直流变换器在两种拓扑间的灵活转换,可变结构型多谐振直流变换器工作模态如图5所示。根据控制方式的不同,所述变换器有三种工作模态。
模态1:此模态下逆变单元采用全桥逆变电路,辅助开关管Qa恒关断,Qb恒导通,构成了全桥CLTCL(Full Bridge-CLTCL, FB-CLTCL)模态。两个高频变压器Tx1与Tx2相串联共同向谐振腔输出侧传递能量。合理进行参数设计,使得此模态电压增益最高点VgainFC( fC1)为整个谐振变换器的电压增益最大值处。当控制频率在电压增益最大值附近时,可实现较窄调频范围内宽电压增益可调的良好性能。
模态2:逆变单元工作模式采用全桥逆变状态,辅助开关管Qa恒导通,Qb恒关断,电路进入全桥LCLCL(FB-LCLCL)模态。此模态下变压器Tx2二次侧不参与变换工作,其漏感Lk2并入Lp2,与励磁电感Lm2相串联等效为一个电感元件Leq2,进而与电容Cp2构成并联结构。通过合理配置fL1和fL3的比例关系,此模态下3次谐波也能传递有功功率,充分利用3次谐波能量的同时减小了环流能量,降低了谐振腔内的损耗,提高了变换器的运行效率。
模态3:辅助开关管Qa和Qb运行状态与模态2一致,逆变单元采用半桥逆变电路,变换器进入半桥LCLCL(Half Bridge-LCLCL, HB-LCLCL)模态。此模态下电压增益曲线为FB-LCLCL模态的一半,满足了变换器降压工况的需求。同时变换器仍可传递1次和3次谐波,同样实现了高效率的良好性能。
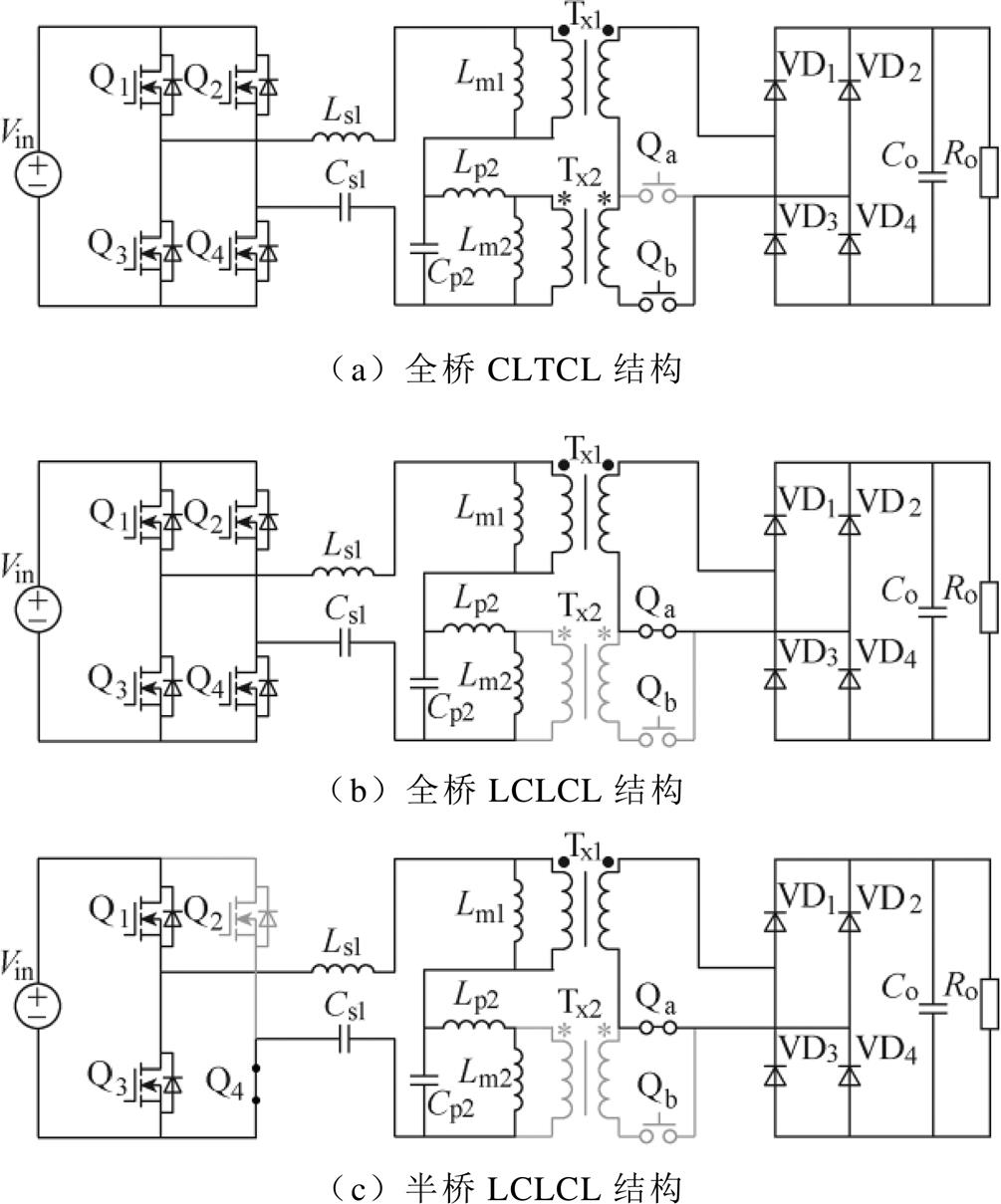
图5 可变结构型多谐振直流变换器工作模态
Fig.5 Variable topology multi-resonant DC-DC converter mode of operation
LCLCL变换器的设计目的主要是通过合理配置谐振频率关系,实现变换器同时传递1次和3次谐波功率的特点,降低环流损耗、提高变换效率。
本文设定额定频率fL1=100kHz,且3个谐振点频率关系为
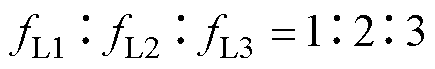 (13)
(13)当控制频率fs=100kHz时,变换器电压增益式(7)虚部为零。此处设定fL1、fL3为1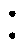 3,主要是为了3次谐波能同基波一样传递有功功率。谐振零点fL2设置在fL1、fL3之间。考虑如果fL2距离fL1较远,变换器则必须不断提高控制频率才能获得较高的降压电压比,此时高频损耗会有所增加,因而增加了磁性元件的设计难度。如果fL2距fL1过近,会使得工作频率点偏离额定工作点过快,增加谐振腔环流,降低效率。因此,综合考虑双方因素,设置LCLCL变换器3个谐振点的位置如式(13)所示。fL2位于fL1、fL3中点也可平衡谐振零点对基波和3次谐波的影响。
3,主要是为了3次谐波能同基波一样传递有功功率。谐振零点fL2设置在fL1、fL3之间。考虑如果fL2距离fL1较远,变换器则必须不断提高控制频率才能获得较高的降压电压比,此时高频损耗会有所增加,因而增加了磁性元件的设计难度。如果fL2距fL1过近,会使得工作频率点偏离额定工作点过快,增加谐振腔环流,降低效率。因此,综合考虑双方因素,设置LCLCL变换器3个谐振点的位置如式(13)所示。fL2位于fL1、fL3中点也可平衡谐振零点对基波和3次谐波的影响。
LCLCL变换器在谐振腔输入阻抗角为零时,电压增益取最大值,此处设置电压增益最大值点的谐振频率为fLmax。利用电路KCL、KVL可解得输入阻抗角jLin表达式为
 (14)
(14)全桥、半桥LCLCL模态下变换器工作范围通常为fLmax~fL1的较窄区域,进而可合理缩短操作频率调节范围。本文配置fLmax、fL1关系如式(15)所示,使得操作频率工作在0~fL1/3的频率范围内,满足设计要求。
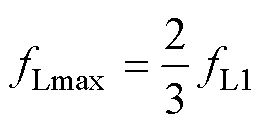 (15)
(15)
本文中,最大增益点VgainFL( fLmax)及额定增益点VgainFL( fL1)关系为
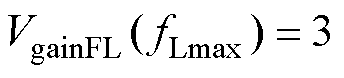 (16)
(16) (17)
(17)
CLTCL结构设计目标为追求较高电压增益。设置变换器在FB-CLTCL模态时可获得最大增益,其相应频率点在fC1处,对应的最大增益为VgainFC( fC1)。
为满足低输入电压条件下获得较高输出电压的需求,应尽量提高变换器的升压比,即获得较高的电压增益最大值VgainFC( fC1)。但电压增益增加的同时升压变压器Tx2电压比也会随之上升,导致变压器Tx2二次侧辅助开关管两端电压应力随之增大,增加了功率器件的选择及设计的难度。
通过列写KCL、KVL方程,本文推导了变换器工作在CLTCL模式时辅助开关管Qa及工作在LCLCL模式时Qb的电压应力VQa、VQb表达式分别为
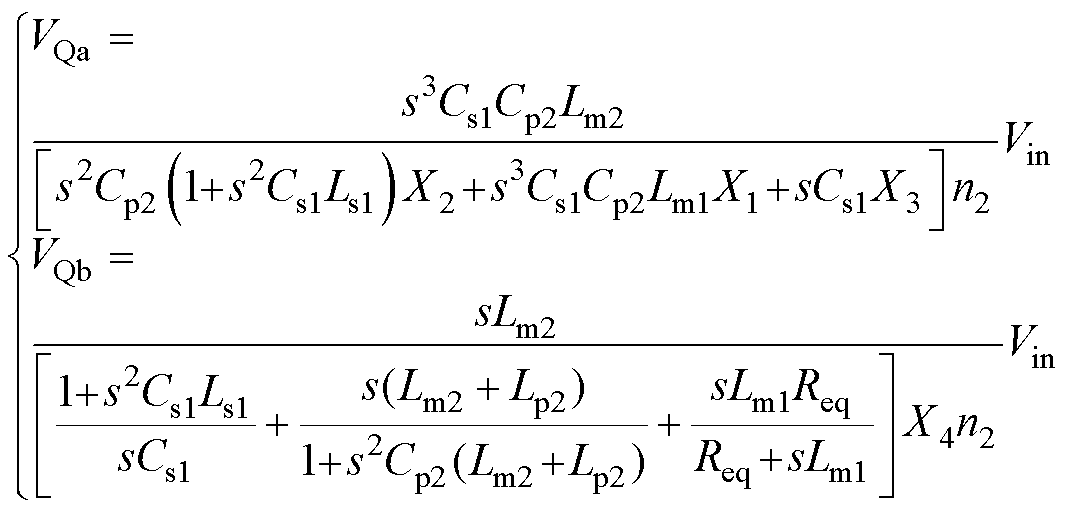 (18)
(18)其中
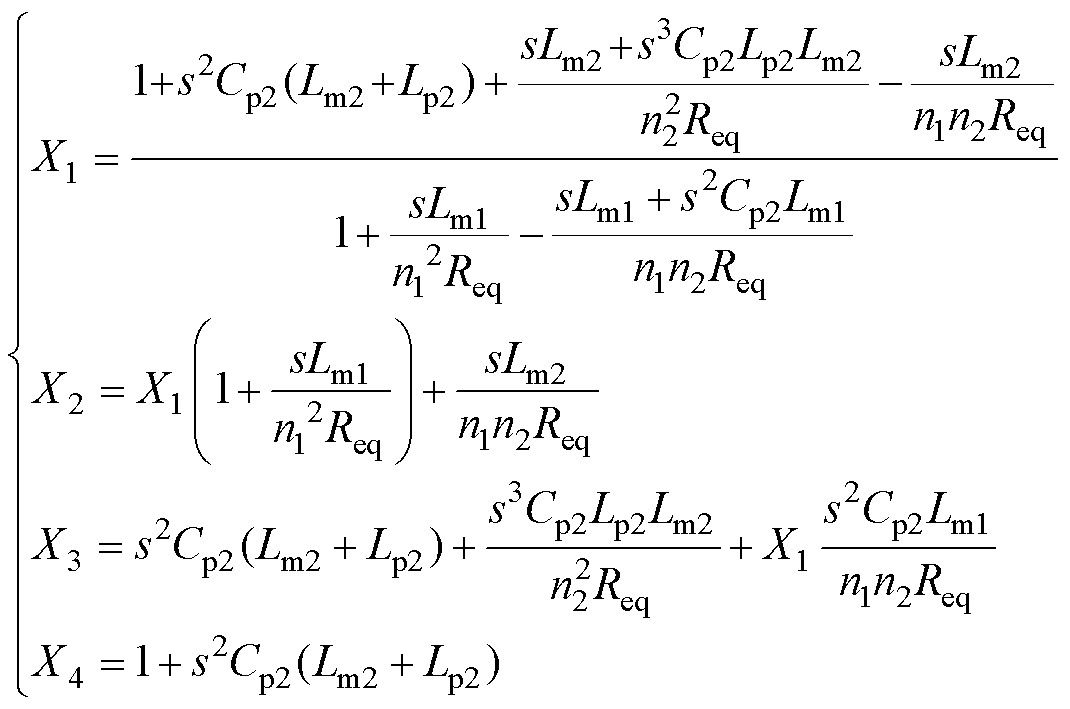 (19)
(19)
通过合理地分析观察可知,变换器辅助开关管电压应力与整个变拓扑结构变换器的最大增益值及高频变压器Tx2匝比n2间存在密切联系。变压器Tx2匝比n2越大,变换器最大电压增益值VgainFC( fC1)越大,由此造成辅助开关管Qa和Qb在各自的工作模态下电压应力相应升高。
图6给出了变换器最高电压增益值与辅助开关管电压应力间的关系。为满足并网需求,该直流变换器为输出电压恒定400V,故而其输入电压为输出电压与电压增益的比。通过观察分析可知,当电压增益大于6时,虽然满足了高增益的需求,但两个辅助开关管在各自工作模态下的电压应力均大于1 500V,这对开关管的耐压特性及功率器件的选择提出了较高要求,提高了设计成本。当电压增益小于4时,虽然降低了辅助开关管的电压应力,但电压增益较低与变换器高增益的设计目标相悖。综合考虑高增益和低电压应力的双重因素,本文取电压增益最大值为5,即
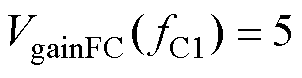 (20)
(20)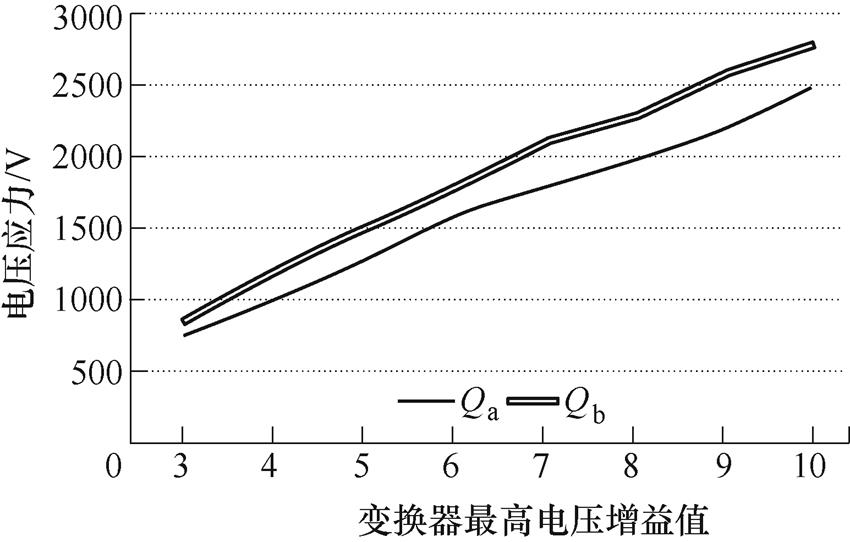
图6 变换器最高电压增益值与辅助开关管电压应力的对应关系
Fig.6 The corresponding relation between the maximum voltage gain of converter and voltage stress of auxiliary switches
为了减少磁性元件数量,利用Tx2的漏感代替Lp2,根据工程经验,Lp2的取值估计为
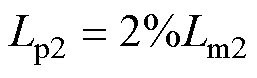 (21)
(21)结合式(1)~式(21),求解出变换器各谐振元件参数,见表1。
图7为可变结构型多谐振软开关直流变换器电压增益曲线。图中给出了三种工作模态FB-CLTCL、FB-LCLCL、HB-LCLCL下相应的增益曲线。经分析,可变结构型多谐振软开关直流变换器的增益曲线是三种模态下增益曲线中各取一段组成的,如图7中箭头走向曲线所示。
表1 谐振元件参数
Tab.1 Resonance elements parameter

参 数数 值 变压器Tx1励磁电感Lm1/mH395 变压器Tx1匝比n11.5 变压器Tx2励磁电感Lm2/mH92 变压器Tx2匝比n27.5 电感Ls1/mH100 电感Lp2/mH2.7 电容Cs1/nF11 电容Cp2/nF6.7
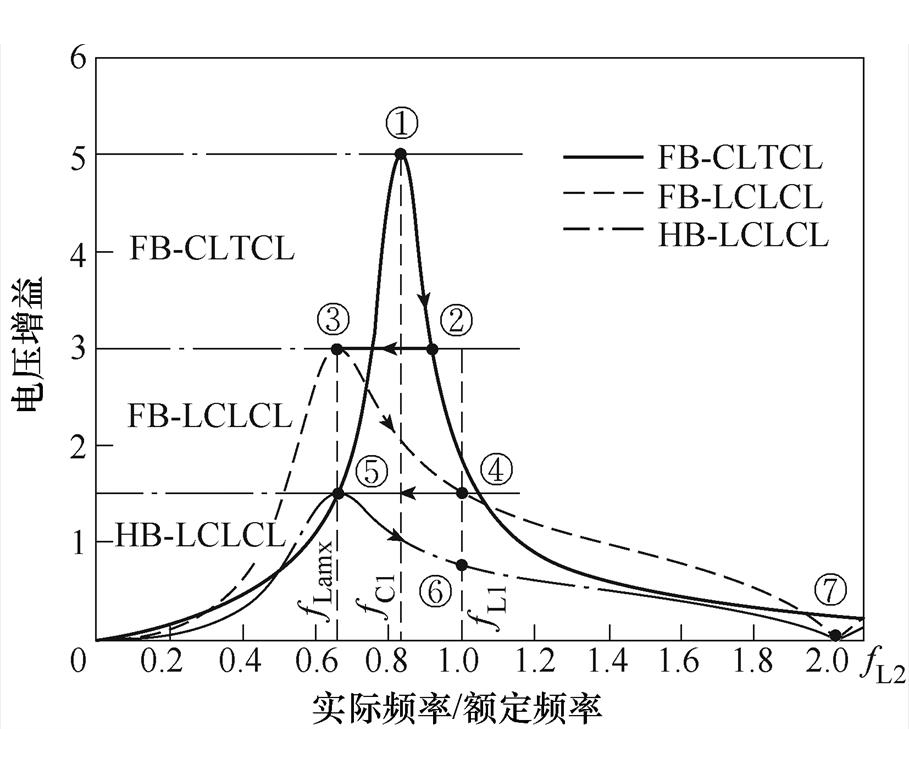
图7 可变结构型多谐振直流变换器电压增益曲线
Fig.7 Variable topology multi-resonant DC converter voltage gain curves
当输入电压较低时,调节变换器工作在FB- CLTCL模式。当控制频率fs=fC1时,变换器获得最高电压增益VgainFC( fC1)=5(见图7中点①);随输入电压增加,fs逐渐上升,电压增益随之下降,当电压增益降为3时(见图7中点②),切换变换器工作模态,此时进入到FB-LCLCL模式(见图7中点③),此时输入电压继续升高,控制频率从fLmax重新出发,电压增益继续下降,直至降低至1.5时(见图7中点④),再次切换变换器工作模态,此时进入HB-LCLCL模式(见图7中点⑤),输入电压仍保持增加,控制频率再次回归到fLmax重新出发,直至电压增益降为0(理论上可降低至0),实现了高降压比的设计要求。在整个操作工程中,控制频率主要在fLmax~fL1的较窄区间内变化,实现了较窄频段内调节宽电压增益范围的效果。
针对上述分析,本节以额定点处的工作状态为例对变换器损耗分布情况进行了建模分析。额定频率为100kHz,工作状态为FB-LCLCL模态。额定条件下,变换器可同时传递基波和3次谐波分量,因此,本节构建的损耗模型不仅包括了基波传递的影响,也考虑了3次谐波对变换器损耗的影响。令J表示通用变量,下文中的J1st和J3rd分别为基波和3次谐波的相应变量。
额定点fL1=100kHz处,变换器实现了ZVS,故开关管MOSFET的主要损耗有关断损耗、导通损耗和驱动损耗。关断损耗Poff_Q1可推算为
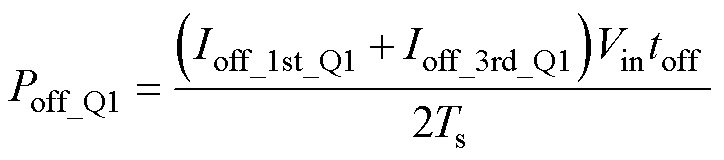 (22)
(22)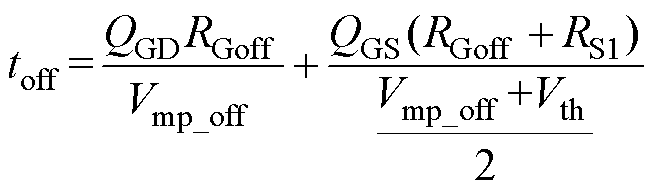 (23)
(23)
式中,Ioff_Q1为一个开关周期的关断电流;QGD为门极和漏极储存的电荷;QGS为门极和源极储存的电荷;RGoff为等效的门极电阻;RS1为等效的源极电阻;Vth为开关管门极阈值电压;Vmp_off为米勒平面电压值;Ts为开关周期。
导通损耗可推算为
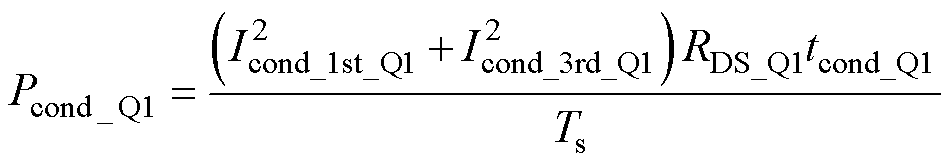 (24)
(24)式中,Icond_Q1为导通期间流过Q1的电流;RDS_Q1为导通电阻;tcond_Q1为一个开关周期的导通时间。
驱动损耗可计算为
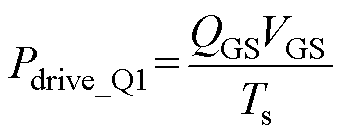 (25)
(25)式中,QGS和VGS分别为驱动电荷和驱动电压。
综上可得,单个开关管的总损耗为
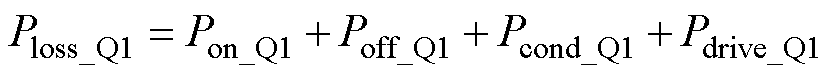 (26)
(26)式中,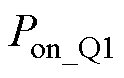 为开通损耗。
为开通损耗。
本文中辅助开关管共有Qa和Qb两个,分别由两个相对串联的MOSFET构成。辅助开关管的作用主要是通过控制其互补导通来实现变换器拓扑的切换,其只有常开或常闭两种工作状态,故辅助开关管的损耗与逆变单元开关管相比只计其导通损耗。由式(24)可得,辅助开关管导通损耗为
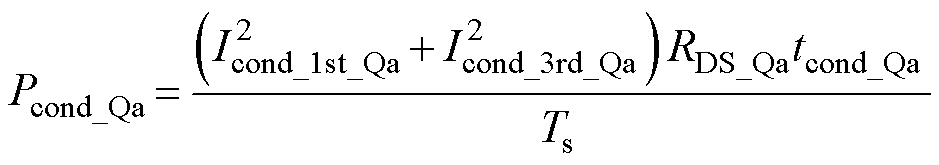 (27)
(27)二极管VD1导通损耗Pcond_VD1可推导为
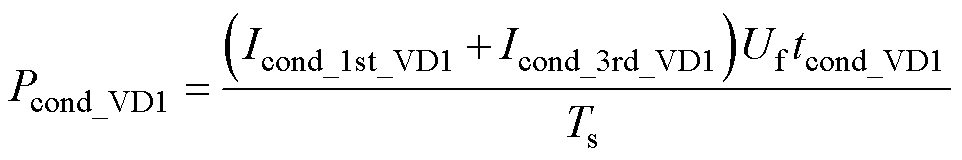 (28)
(28)式中,Uf为正向电压。
开通损耗Pon_VD1可表示为
 (29)
(29)式中,Ion_VD1为二极管开通电流;Ud为二极管上的电压;tr_VD1为上升时间。
关断损耗Poff_VD1为
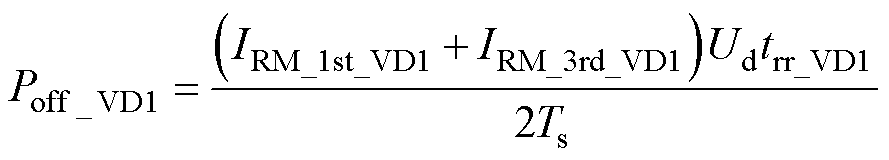 (30)
(30)式中,IRM_VD1为二极管峰值反向电流;trr_VD1为反向恢复时间。
FB-LCLCL模态中只有Tx1一个变压器接入电路中,是拓扑实现高效率变换的重要一环。变压器损耗包括绕组损耗和磁心损耗。
传统变压器的一次侧、二次侧直流阻抗Rdc_pri_Tx1和Rdc_sec_Tx1可由其几何绕组形式分别直接计算为
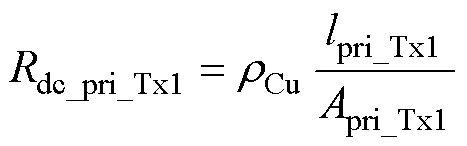 (31)
(31)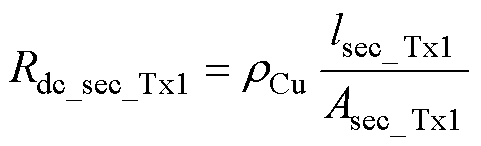 (32)
(32)
式中,rCu为铜的电阻率(W/m);Apri_Tx1和Asec_Tx1分别为变压器的一次侧、二次侧缠绕导线的等效截面积(m2);lpri_Tx1和lsec_Tx1分别为变压器的一次侧、二次侧绕线长度(m)。
n次谐波的趋肤深度可表示为
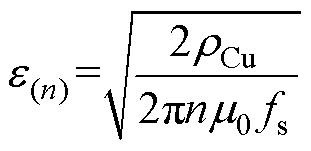 (33)
(33)式中,m0为磁导率。
n次谐波的交直流阻抗比为
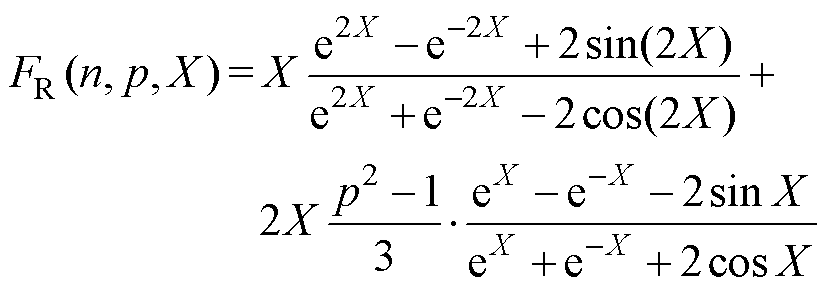 (34)
(34)当X和p满足式(35)和式(36)时,根据式(34)可计算出n次谐波的变压器一次侧交直流阻抗比FR_pri(n),其中
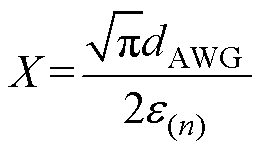 (35)
(35)
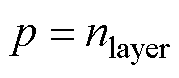 (36)
(36)式中,dAWG为绕线直径;p为绕线层数;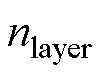 为变压器一次侧绕线的层数。
为变压器一次侧绕线的层数。
变压器二次绕组损耗计算方法与一次侧相同,本文不再赘述。
变压器一次、二次绕组损耗分别为
 (37)
(37)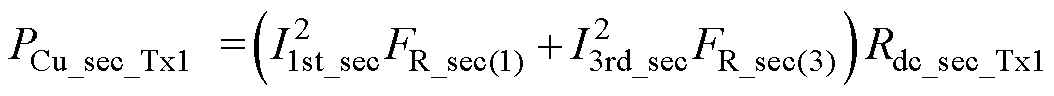 (38)
(38)
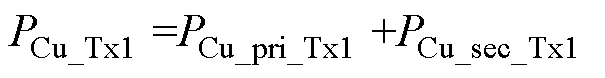 (39)
(39)
式中,In_pri和In_sec分别为流过变压器一次侧、二次侧的n次谐波电流有效值。
一个开关周期内变压器峰值磁通密度为
 (40)
(40)式中,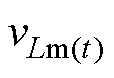 为变压器的一次电压。
为变压器的一次电压。
利用经典的Steinmetz公式可得变压器的磁心损耗为
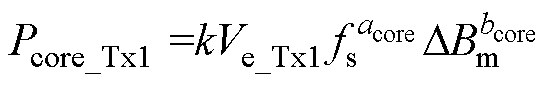 (41)
(41)式中,k、acore、bcore均为斯坦梅茨系数;Ae_Tx1为变压器Tx1的有效截面积;Ve_Tx1为变压器Tx1的磁心体积;DBm=Bmax_Tx1/2;以上参数均为变压器固有参数,可通过查阅数据手册得知。
进而可得,变压器Tx1的总损耗为
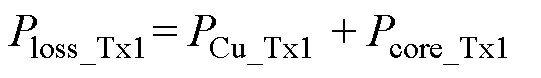 (42)
(42)电感损耗计算方法与变压器损耗计算方法类似,其主要包括绕组损耗和磁心损耗。电感Ls1的直流阻抗可根据其几何结构推导为
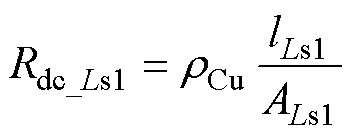 (43)
(43)当X和p满足式(44)和式(45)时,可由式(34)得到Ls1的n次谐波交直流阻抗比FR_Ls1(n),即
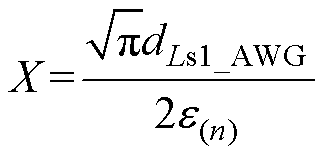 (44)
(44)
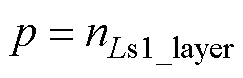 (45)
(45)进而得到Ls1的绕组损耗为
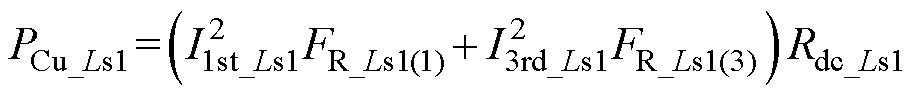 (46)
(46)
类比变压器磁心损耗计算方法,Ls1磁心损耗可推算为
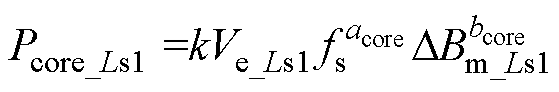 (47)
(47)综上可得,电感Ls1的损耗为
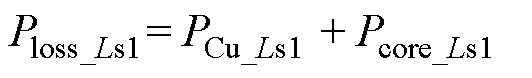 (48)
(48)
电感Leq2=Lp2+Lm2,其损耗计算方法与Ls1类似,本文不再赘述。
电路中的电容按其作用可分为输入电容、输出电容和谐振电容。
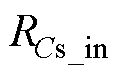 为输入电容等效电阻,Irip_in为电容纹波电流,则输入电容损耗可表示为
为输入电容等效电阻,Irip_in为电容纹波电流,则输入电容损耗可表示为
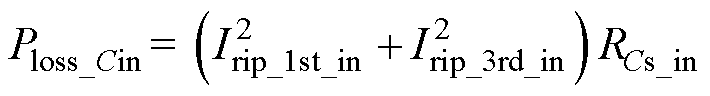 (49)
(49)谐振电容Cs1等值电阻RESR_Cs1与损耗因数tand关系为
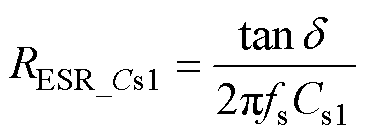 (50)
(50)
则其损耗可表示为
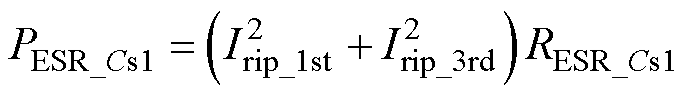 (51)
(51)输出电容损耗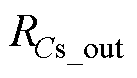 计算方法与输入电容类似,谐振电容Cp2损耗PESR_Cp2计算可类比Cs1计算方法,不再赘述。
计算方法与输入电容类似,谐振电容Cp2损耗PESR_Cp2计算可类比Cs1计算方法,不再赘述。
图8给出了额定工作点的损耗分布。此工作模态下,变换器的损耗主要包括开关管损耗、二极管损耗及磁性元件的损耗。因开关管实现了ZVS,故其损耗不包含开通损耗,主要包括关断损耗和导通损耗;磁性元件的损耗主要包括变压器损耗及两个电感的损耗。辅助开关管工作处于恒通或恒断的状态,所以其损耗只包含导通损耗;电容损耗占比较低。随着磁集成技术的深入发展及功率器件研究的不断创新,有望减小变换器的开关管损耗及磁性元件的损耗;采用性能优化的二极管器件或同步整流技术有望减小二极管损耗,进而提升变换器的运行效率。
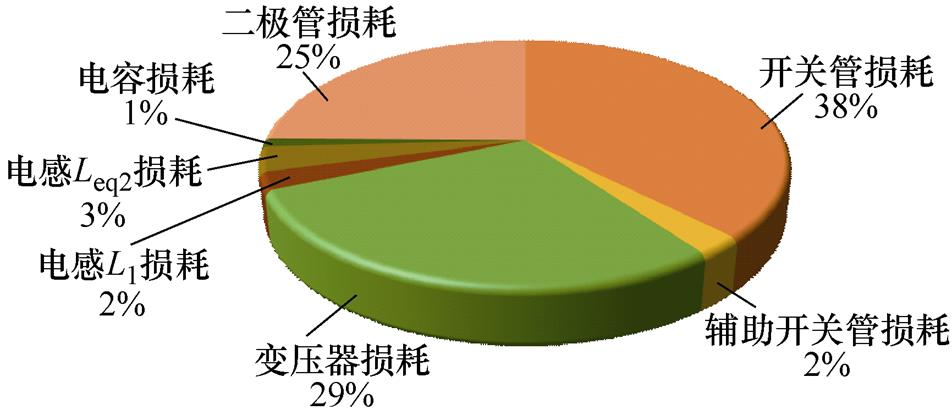
图8 额定工作点的损耗分布
Fig.8 Loss distribution of the rated point
为验证理论分析的可靠性,本文基于一台200W实验样机进行了实验验证。图9给出了实验样机的照片。样机器件的相应型号见表2。
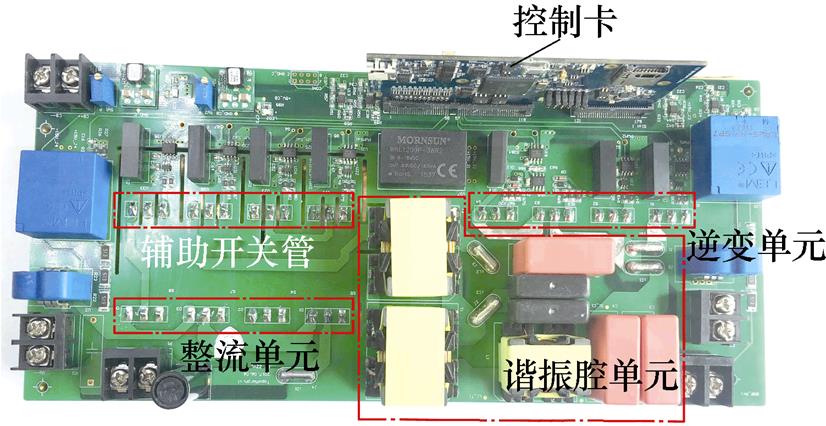
图9 样机照片
Fig.9 The picture of prototype
表2 器件型号
Tab.2 Components model

名 称型 号 开关管Q1~Q4C3M0065090D 辅助开关管Qa, QbC2M0045170D 二极管VD1~VD4C3D30065D 变压器Tx1PQ3230 PC95 变压器Tx2PQ3535 PC95
图10给出了电压增益曲线上点①处的实验波形。此处电压增益为最大值点,变换器工作在FB- CLTCL模态。图中,vQ1、iQ1分别为逆变单元中开关管Q1的电压、电流;vo为输出电压;iVD1为流过整流二极管VD1的电流。分析图10可知,当输入电压为77.5V时,输出电压为400.1V,电压增益为5.16。此外,谐振腔输入阻抗角近乎为零,由iQ1和iVD1波形可知,开关管Q1和二极管VD1的开、关电流均近似为零,变换器实现了ZVS和准ZCS,具有良好的软开关效果,有效地提高了效率。
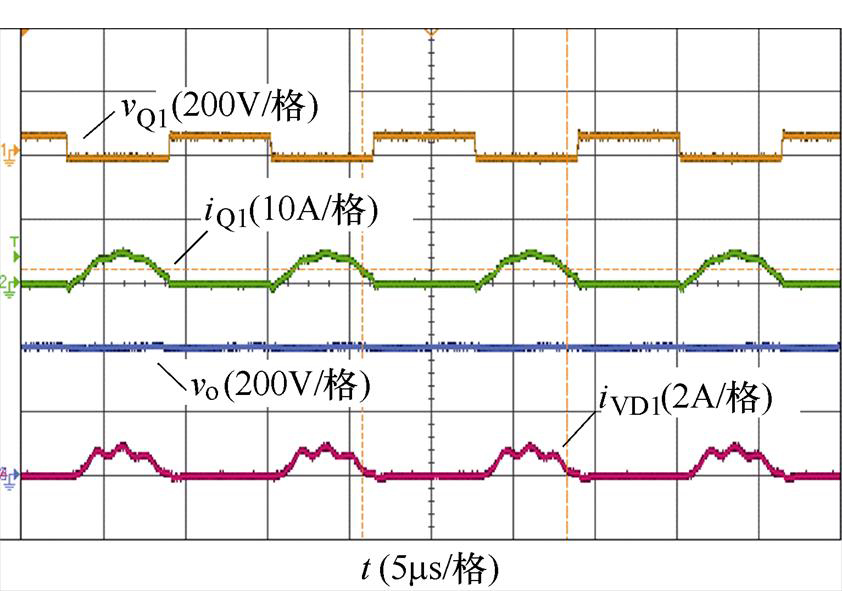
图10 FB-CLTCL电路①点实验波形
Fig.10 FB-CLTCL circuit ① point experimental waveforms
图11给出了总电压增益曲线上点④处的实验波形。此处为额定工作点,变换器工作在FB-LCLCL模态。图中各变量含义与图10类似。分析图11可知,当输入电压为266.7V时,输出电压为400.2V,此时电压增益为1.5,与设计相符。图中开关管Q1的电流iQ1呈现马鞍波状,说明电路中含大量的基波和3次谐波;同时二极管VD1的电流iVD1也呈马鞍波状,说明变换器成功传递了基波和3次谐波。此处充分利用3次谐波传递有功功率,减小了谐振腔内的环流能量,实现了变换器的高效率变换。额定点处的效率达97.6%。HB-LCLCL模态工作情况只是电压增益降低了一半,其余情况近乎无差,本文不再赘述。
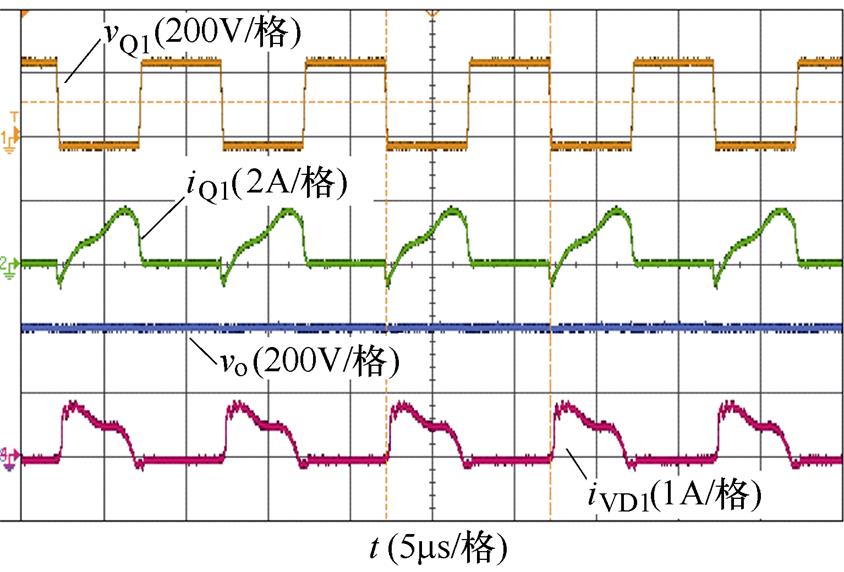
图11 FB-LCLCL电路④点实验波形
Fig.11 FB-LCLCL circuit ④ point experimental waveforms
图12给出了FB-CLTCL模态向FB-LCLCL模态切换变化过程。图中,vgs-Q4、vgs-Qb分别为逆变单元开关管Q4及谐振腔内辅助开关管Qb的驱动信号。vin、vo分别为变换器输入、输出电压。当输入电压为65V时,输出电压为335V;随后vin上升至80V左右时,vo增加至400V;此后vo钳位在400V,不再发生变化。此模态内vgs-Q4说明逆变单元工作在全桥模式,vgs-Qb说明辅助开关管Qb恒导通,变换器处于FB-CLTCL模态。当vin逐渐增加至133.3V左右时,vo仍保持在400V左右,变换器电压增益近乎为3,此时进行变换器模态的切换,Q4工作模式保持不变,Qb驱动信号置零,变换器进入FB-LCLCL模态,此后在增加至200V的过程中,输出电压始终保持在400V不变。
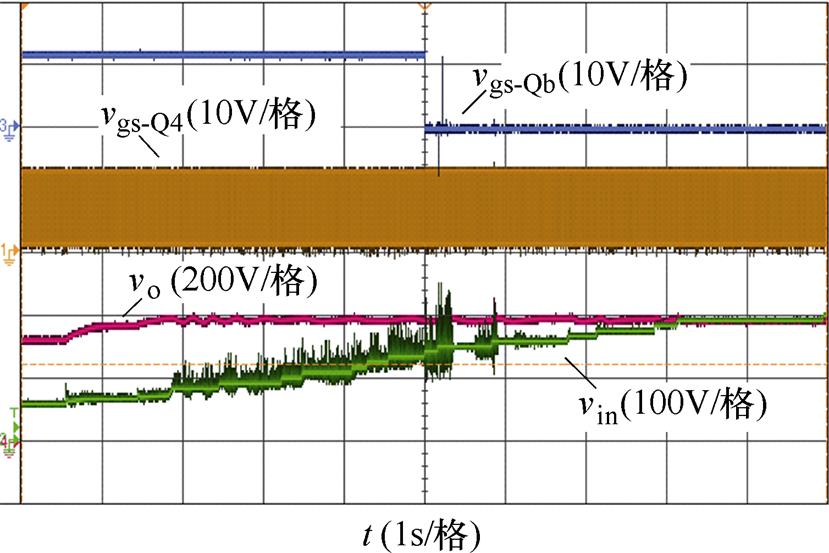
图12 FB-CLTCL模态向FB-LCLCL模态切换整体变化过程
Fig.12 Switching the whole process from the FB-CLTCL mode to the FB-LCLCL mode
图13给出了FB-LCLCL模态向HB-LCLCL模态切换变化过程。输入电压从180V增加至600V的过程中,输出电压始终保持在400V左右。当输入电压增加至266.7V左右时,电压增益为1.5左右,此时进行变换器模态的切换。Qb驱动信号始终为零,表明谐振腔仍为LCLCL结构,Q4驱动信号从持续开断工作变为恒置高状态,说明逆变单元由全桥模式转变为半桥模式,此后变换器进入HB-LCLCL模态。
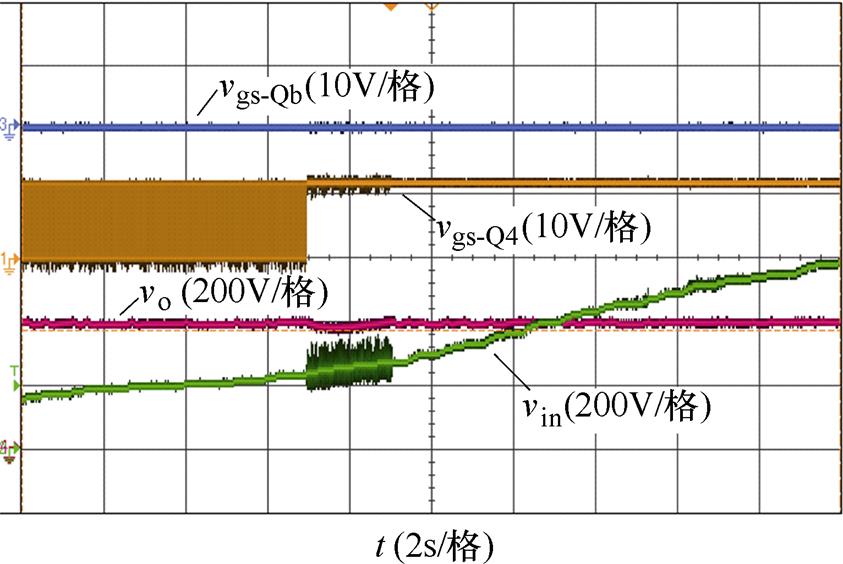
图13 FB-LCLCL模态向HB-LCLCL模态切换整体变化过程
Fig.13 Switching the whole process from the FB-LCLCL mode to the HB-LCLCL mode
图14给出了本文变换器在不同模态下的满载效率曲线。图中,虚线表示理论计算值,实线表示实验实测值。变换器共有三种工作模态,分别对应三段效率曲线。各阶段效率曲线均为在不同的电压增益区间测量的。
由图14可知,在各个工作模态下,变换器效率计算值和实测值误差在可接受范围内,说明本文构建的同时考虑基波和3次谐波改进型损耗模型的准确性和有效性。此外,实测条件下,变换器在FB- LCLCL模态下获得97.6%的最高变换效率;当电压增益小于2、变换器工作在HB-LCLCL模态时,变换器效率维持在97.55%左右;当电压增益大于3、变换器工作在FB-CLTCL模态时,变换器效率较前两种模态普遍偏低,主要因为高增益工况下,谐振腔内电流较大,由此造成的功率器件的导通损耗和磁性损耗较大,降低了变换效率。但即使这样,变换器仍能保持96.8%左右的较高效率,进一步说明了本文所述变换器的效率优势。
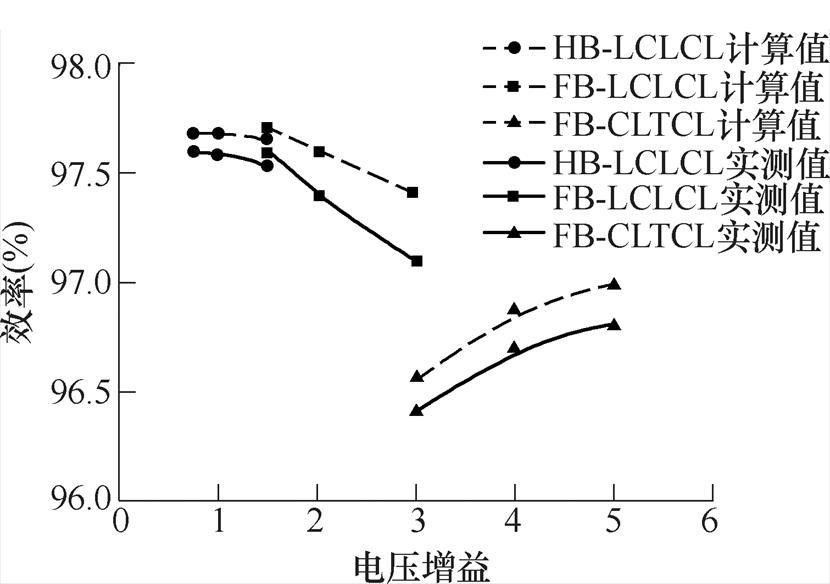
图14 不同模态下的效率曲线
Fig.14 Efficiency curves in different modes
本文提出了一种可变结构型多谐振软开关直流变换器。通过控制辅助开关管的通断,变换器可工作在FB-CLTCL、FB-LCLCL和HB-LCLCL三种模态下。CLTCL变换器的设计目的在于获取高电压增益,而LCLCL变换器则要充分利用3次谐波传递有功功率,实现高效率变换。此变换器可在较窄频率范围内实现宽电压增益可调的有益效果,同时获得较高变换效率。此外,本文通过构建同时考虑基波和3次谐波的损耗模型,对变换器额定条件下的损耗进行了详细估算和分析。最后,基于一台实验样机验证了理论分析的可靠性,最高电压增益值达5倍左右,最高变换效率达97.6%。
参考文献
[1] 许利通, 程明, 魏新迟, 等. 考虑损耗的无刷双馈风力发电系统功率反馈法最大功率点跟踪控制[J]. 电工技术学报, 2020, 35(3): 472-480.
Xu Litong, Cheng Ming, Wei Xinchi, et al. Power signal feedback control of maximum power point tracking control for brushless doubly-fed wind power generation system considering loss[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 472- 480.
[2] 王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3): 455-471.
Wang Tao, Zhu Ziqiang, Nian Heng. Review of operation technology of doubly-fed induction generator- based wind power system under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 455-471.
[3] 颜湘武, 宋子君, 崔森, 等. 基于变功率点跟踪和超级电容器储能协调控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2020, 35(3): 82-93.
Yan Xiangwu, Song Zijun, Cui Sen, et al. Primary frequency regulation strategy of doubly-fed wind turbine based on variable power point tracking and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 82-93.
[4] Yang Bo, Chen Rengang, Lee F C. Integrated mag- netic for LLC resonant converter[C]//IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 2002: 346-351.
[5] Yang Bo, Lee F C, Concannon M. Over current protection methods for LLC resonant converter[C]// IEEE Applied Power Electronics Conference and Exposition, Miami Beach, FL, USA, 2003: 605-609.
[6] Raju G S N, Doradla S. An LCL resonant converter with PWM control-analysis, simulation, and imple- mentation[J]. IEEE Transactions on Power Electro- nics, 2002, 10(2): 164-174.
[7] 汤欣喜, 邢岩, 吴红飞, 等. 兼顾稳态效率和暂态升压能力的LLC变换器[J]. 电工技术学报, 2020, 35(4): 93-100.
Tang Xinxi, Xing Yan, Wu Hongfei, et al. An improved LLC converter considering steady-state efficiency and transient boost capability[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(4): 93-100.
[8] Canales F, Barbosa P, Aguilar C, et al. A high- power-density DC/DC converter for high-power distributed power systems[C]//IEEE Power Electronics Specialist Conference, Acapulco, Mexico, 2003: 11-18.
[9] 杨东江, 段彬, 丁文龙, 等. 一种带辅助双向开关单元的宽输入电压范围LLC谐振变换器[J]. 电工技术学报, 2020, 35(4): 775-785.
Yang Dongjiang, Duan Bin, Ding Wenlong, et al. An improved LLC resonant converter with auxiliary bi-directional switch for wide-input-voltage range applications[J]. Transactions of China Electrotech- nical Society, 2020, 35(4): 775-785.
[10] Yu R, Ho G K Y, Pong B M H, et al. Computer-aided design and optimization of high-efficiency LLC series resonant converter[J]. IEEE Transactions on Power Electronics, 2012, 27(7): 3243-3256.
[11] 胡海兵, 王万宝, 孙文进, 等. LLC谐振变换器效率优化设计[J]. 中国电机工程学报, 2013, 33(18): 48-56.
Hu Haibing, Wang Wanbao, Sun Wenjin, et al. Optimal efficiency design of LLC resonant con- verters[J]. Proceedings of the CSEE, 2013, 33(18): 48-56.
[12] 金科, 阮新波. 复合式全桥三电平LLC谐振变换器[J]. 中国电机工程学报, 2006, 26(3): 53-58.
Jin Ke, Ruan Xinbo. Hybrid full bridge three-level LLC resonant converter[J]. Proceedings of the CSEE, 2006, 26(3): 53-58.
[13] Wang Yijie, Guan Yueshi, Xu Dianguo, et al. A CLCL resonant DC/DC converter for two-stage LED driver system[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 2883-2891.
[14] Wu Hongfei, Jin Xiang, Hu Haibing, et al. Multiele- ment resonant converters with a notch filter on secondary side[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 3999-4004.
[15] Wang Chengshan, Yang Liang, Wang Yifeng, et al. A 1kW CLTCL resonant DC-DC converter with restricted switching loss and broadened voltage range[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4190-4203.
[16] Lin Bor Ren. Analysis and implementation of wide zero-voltage switching dual full-bridge converters[J]. IET Power Electronics, 2016, 9(4): 751-760.
[17] Liang Zhigang, Guo Rong, Li Jun, et al. A high- efficiency PV module-integrated DC/DC converter for PV energy harvest in FREEDM systems[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 897- 909.
A Variable Topology Multi-Resonant Soft-Switching DC-DC Converter with High Efficiency and Wide Gain
Abstract A variable topology multi-resonant soft-switching DC-DC converter is proposed in this paper. Applying the double transformer structure, this converter can transform the topological structure through two complementary turn-on auxiliary switches. There are three working modes, which can meet the requirements of high voltage gain or high efficiency under different working conditions. In addition, resonant parameters of the converter are designed by setting the resonant frequency and gain point reasonably. Subsequently, according to the condition that the converter transmits the fundamental and third harmonic energy simultaneously under rated conditions, a loss model considering both the fundamental wave and the third harmonic is constructed, and the loss distribution of the converter is estimated in detail. Finally, in order to verify the reliability of the theoretical analysis, this paper conducted a power experiment on the converter based on an experimental prototype. Within the input voltage range of 80~600V, the output voltage is always stable at 400V, and a wide voltage gain range is obtained. At the same time, high efficiency conversion within the full gain range is achieved, and the maximum efficiency of the converter is 97.6%.
keywords:Variable topology, multi-resonant, DC-DC converter, soft switching, loss analysis
DOI: 10.19595/j.cnki.1000-6753.tces.L90293
中图分类号:TM46
陈梦颖 女,1993年生,博士研究生,研究方向为谐振型软开关直流变换器及其控制。E-mail: cmying@tju.edu.cn
王议锋 男,1981年生,副教授,硕士生导师,研究方向为先进电力电子技术在电网中的应用。E-mail: wayif@tju.edu.cn(通信作者)
收稿日期 2020-07-09
改稿日期 2020-10-28
国家重点研发计划资助项目(2018YFB0904700)。
(编辑 陈 诚)