
图1 桥臂结构中的等效电路
Fig.1 The equivalent circuit in the phase-leg configuration
摘要 目前碳化硅(SiC)MOSFET大多沿用Si MOSFET和IGBT的驱动设计方法。然而,由于SiC MOSFET相比Si器件具有更高的开关速度,因而栅极内阻、驱动回路电感和功率回路电感导致的栅源电压干扰情况也值得探索。该文分析栅源电压干扰产生的过程,进而归纳提炼出一种基于干扰动态响应机理的SiC MOSFET驱动参数标幺化设计方法。从开关结电容的等效电路出发,推导出功率回路和驱动回路的传递函数,基于驱动和功率双回路传递函数,研究揭示栅源电压的干扰动态响应机理。进而,引入标幺化的参数表达形式,以标准量化驱动参数对于栅源电压干扰传导路径的影响,提出基于干扰动态响应机理的SiC MOSFET驱动设计原则。最后,搭建双脉冲实验平台,验证该驱动设计原则的合理性。
关键词:SiC MOSFET 驱动设计 栅源电压干扰 动态响应
以碳化硅(SiC)、氮化镓(GaN)为代表的宽禁带半导体器件为电力电子领域的技术革新提供了契机[1-6]。由于宽禁带材料的使用,功率半导体器件可以工作在更高电压、更快频率下[7-12]。然而,在实际应用中,更高的开关速度造成桥臂结构中的两个器件之间相互干扰,引发的栅源电压干扰问题不可忽视[13-16]。
桥臂结构电路的两个SiC器件之间相互作用,在开关瞬态过程中,SiC器件的米勒电容被迫再次充放电,产生位移电流,影响栅极电压稳定性,栅源电压受到干扰,产生正向尖峰和负向尖峰。栅极电压正向尖峰过高将引发误导通现象[17],其中不完全的误导通将增大开关损耗[18],而完全的误导通将造成桥臂短路并引起器件过电流损坏[19];栅极电压的负向尖峰过高将影响器件寿命[20-22],甚至造成栅极过电压击穿导致器件失效[23]。高速率开关的器件引起的栅源电压干扰现象更为显著,若无法提供足够稳定的栅极电压将导致系统降频工作,限制变换器系统的进一步高频化和小型化。为从驱动设计的角度有效防治栅源电压干扰,首先需要探索掌握其产生机理,因此,国内外学者从数学建模的角度入手,对栅源电压干扰的机理进行了深入探讨。
文献[24]着眼于确定开关速度的关键限制因素,进而依据电压变化率、驱动电阻和结电容等效电路估算因干扰引起的栅源电压最大变化值。文献 [25]详细介绍了10kV SiC MOSFET在开关瞬态时的表征,进而在极端情况下,即假设通过器件的米勒电容的所有电流都对其栅源电容进行充电时,通过结电容等效电路估算最大栅源电压变化幅度。这些机理模型分析刻画和描述了干扰对栅源电压的影响结果,为深入分析栅源电压干扰的产生机理并精确描述打下了坚实基础。然而,这些较为简单的机理模型并未深入阐述产生振荡的机理,仅考虑干扰引发的干扰尖峰,未考虑关键的栅极内阻、驱动回路电感和功率回路电感影响,以至于不能全面认识高速开关动作对栅源电压干扰的动态特性。文献[26]首先建立了考虑高压增强型GaN器件的非线性I-V和C-V特性模型,然后将器件特性与各种电路参数相结合,建立了电路级模型,最后将分段切换过程模型和PSpice仿真相比较,证明该模型获得了更精确的分析结果。文献[27]考虑所有的电路寄生参数,分析并建立数学模型,对栅源电压干扰造成的误导通现象进行了全面的定量分析,为工程实践中的MOSFET选型、PCB设计和调试提供了准确的参考,可用来评估、判断误导通问题的发生。文献[19]基于MOSFET等效结电容模型、戴维南定理和叠加原理,并考虑MOSFET体二极管反向恢复、漏源电压变化的非线性以及驱动回路电感的影响,研究提出了一种栅源电压干扰分析模型,由变换器的寄生参数明确对应表示。然而,这些复杂的机理模型考虑的电路杂散参数过多,引入过多非主导参数,无法明确关键杂散参数,因此也就无法避免繁杂的计算过程,不能有效地直接面向工程应用指导驱动设计。目前SiC MOSFET大都沿用Si MOSFET和IGBT的驱动设计方法。由于SiC MOSFET相比Si器件具有更高的开关速度,因而栅极内阻、驱动回路电感和功率回路电感导致的栅源电压干扰情况,也值得探索。
本文研究揭示栅源电压的干扰动态响应机理,进而引入标幺化的系统参数表达形式以标准量化驱动参数对于栅源电压干扰传导路径的影响,提出基于干扰动态响应机理的SiC MOSFET驱动设计原则。
图1为桥臂结构中的等效电路。桥臂下管QL采用器件的结电容等效电路代替,用于分析暂态过程中的栅源电压受到上管QH开关切换时的干扰情况。为方便起见,QH干扰到桥臂下管(本文简称为主动管);QL受到桥臂上管干扰(本文简称为被动管)。桥臂结构负载电流IL正方向由桥臂中点流出,回到直流母线中点。

图1 桥臂结构中的等效电路
Fig.1 The equivalent circuit in the phase-leg configuration
图1中,驱动芯片输出的驱动信号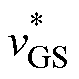 ,经过驱动电阻R,连接到栅极,为了防止过大的干扰尖峰电压,在栅极和源极上并联辅助电容Ca。常见的三引脚分立MOSFET封装具有三个端子作为引脚,栅极(G)、漏极(D)、源极(S)引脚杂散电感分别为Lg、Ld、Ls,Rg为栅极内电阻。为了分析暂态特性,引入常用的结电容等效电路,Cgs、Cgd、Cds为MOSFET内部结电容,按照工业界使用习惯,记Ciss=Cgd+Cgs、Coss=Cgd+Cds、Crss=Cgd。id为MOSFET的沟道电流,VDds为寄生体二极管。考虑功率回路寄生参数,为简便起见,Ls 为连接线、PCB过孔上的杂散电感;Rs 为功率回路杂散电阻,包括上管的导通电阻、连接线、解耦电容内电阻。一般情况下,SiC MOSFET在工作时存在较高的dv/dt,该漏源极的脉冲电压即为栅源电压干扰的主要干扰源,下面针对脉冲电压干扰源进行分析。
,经过驱动电阻R,连接到栅极,为了防止过大的干扰尖峰电压,在栅极和源极上并联辅助电容Ca。常见的三引脚分立MOSFET封装具有三个端子作为引脚,栅极(G)、漏极(D)、源极(S)引脚杂散电感分别为Lg、Ld、Ls,Rg为栅极内电阻。为了分析暂态特性,引入常用的结电容等效电路,Cgs、Cgd、Cds为MOSFET内部结电容,按照工业界使用习惯,记Ciss=Cgd+Cgs、Coss=Cgd+Cds、Crss=Cgd。id为MOSFET的沟道电流,VDds为寄生体二极管。考虑功率回路寄生参数,为简便起见,Ls 为连接线、PCB过孔上的杂散电感;Rs 为功率回路杂散电阻,包括上管的导通电阻、连接线、解耦电容内电阻。一般情况下,SiC MOSFET在工作时存在较高的dv/dt,该漏源极的脉冲电压即为栅源电压干扰的主要干扰源,下面针对脉冲电压干扰源进行分析。
图2展示了图1所示桥臂结构中SiC MOSFET栅源电压干扰产生的示意图。为简便起见,本文仅针对电力电子变换器中常见的桥臂结构电路,展开动态过程分析,IL为负载电流,流出桥臂中点为正方向。从t0时刻开始,主动管QH的漏源电压开始上升,vDS开始下降,QH干扰被动管QL栅源电压vGS的过程如下所述。
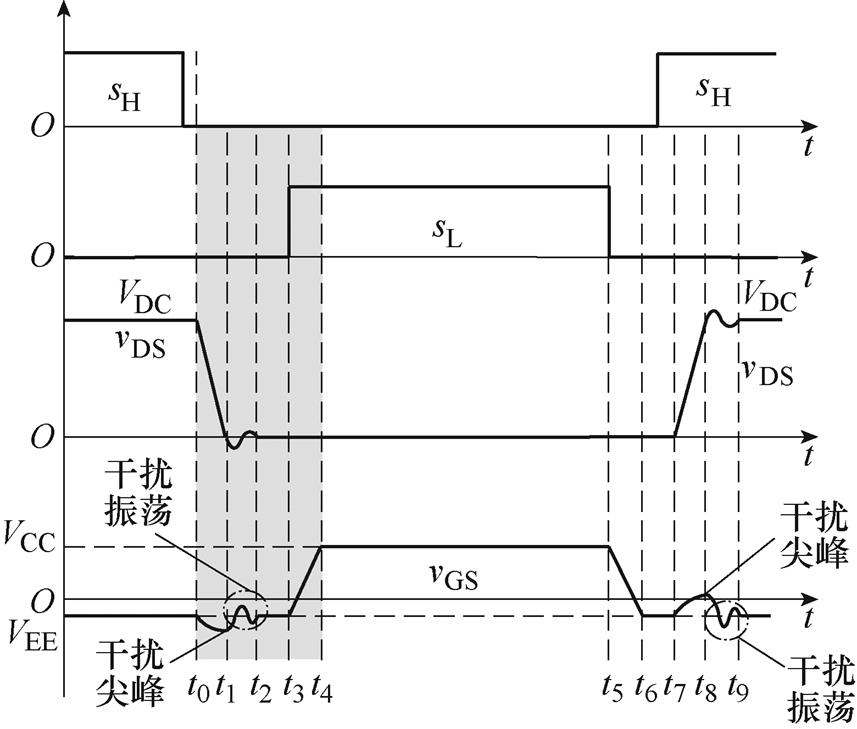
图2 桥臂结构中的栅源电压干扰
Fig.2 The gate-source voltage interference in the phase-leg configuration
模态1[t0, t1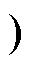 :t0时刻开始,下管QL的漏源极电压vDS从VDC减小到0。vDS下降到一定程度,当QL的寄生体二极管满足导通条件时,该模态结束。在这一阶段,QL的栅源电压vGS扰动由漏源极电压vDS的降低引起。下降的vDS可以视为斜坡信号,栅源电压vGS受到该斜坡信号干扰的激励,从关断偏置电压VEE开始降低。到t1时刻,vDS斜坡下降结束。t1时刻后vDS呈现明显的振荡现象,其影响vGS的机理与斜坡信号的不同。为简便起见,本文将t1时刻的vGS简称为负向干扰尖峰,以区别于此后vDS振荡所引发的栅源极电压干扰振荡。
:t0时刻开始,下管QL的漏源极电压vDS从VDC减小到0。vDS下降到一定程度,当QL的寄生体二极管满足导通条件时,该模态结束。在这一阶段,QL的栅源电压vGS扰动由漏源极电压vDS的降低引起。下降的vDS可以视为斜坡信号,栅源电压vGS受到该斜坡信号干扰的激励,从关断偏置电压VEE开始降低。到t1时刻,vDS斜坡下降结束。t1时刻后vDS呈现明显的振荡现象,其影响vGS的机理与斜坡信号的不同。为简便起见,本文将t1时刻的vGS简称为负向干扰尖峰,以区别于此后vDS振荡所引发的栅源极电压干扰振荡。
模态2[t1, t2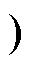 :t1时刻,QL漏源电压vDS降低到0附近(导通压降)。在这一阶段,vDS的高频振荡将激励QL栅源电压vGS产生高频振荡,振荡持续到t2时刻,QL栅源电压vGS返回到关断偏置电压VEE。
:t1时刻,QL漏源电压vDS降低到0附近(导通压降)。在这一阶段,vDS的高频振荡将激励QL栅源电压vGS产生高频振荡,振荡持续到t2时刻,QL栅源电压vGS返回到关断偏置电压VEE。
模态3[t2, t3 :由于仍然处于上下管的死区时间之内,因此,QL栅源电压vGS保持在负向关断偏置电压VEE不变,直到下管QL的PWM信号sL由低电平变为高电平。
:由于仍然处于上下管的死区时间之内,因此,QL栅源电压vGS保持在负向关断偏置电压VEE不变,直到下管QL的PWM信号sL由低电平变为高电平。
模态4[t3, t4 :t3时刻,下管QL的PWM信号sL由低电平变为高电平。驱动电压通过驱动电阻为下管QL的输入电容Ciss充电,栅源电压vGS从负向关断偏置电压VEE上升到正向导通偏置电压VCC。高于阈值电压后,QL的沟道具有低阻抗,负载电流流过MOSFET的沟道。
:t3时刻,下管QL的PWM信号sL由低电平变为高电平。驱动电压通过驱动电阻为下管QL的输入电容Ciss充电,栅源电压vGS从负向关断偏置电压VEE上升到正向导通偏置电压VCC。高于阈值电压后,QL的沟道具有低阻抗,负载电流流过MOSFET的沟道。
模态5[t4, t5 :下管QL的栅源电压vGS维持在正向导通偏置电压VCC,QL的沟道继续流通负载电流。
:下管QL的栅源电压vGS维持在正向导通偏置电压VCC,QL的沟道继续流通负载电流。
模态6[t5, t6 :t5时刻,下管QL的PWM信号sL由高电平变为低电平。驱动电压通过驱动电阻为下管QL的输入电容Ciss放电,栅源电压vGS从正向导通偏置电压VCC开始下降,到t6时刻,vGS降低到负向关断偏置电压VEE,vGS低于阈值电压后,QL的沟道具有高阻抗,电流流过QL的寄生体二极管VDds,漏源极电压vDS保持在0附近(导通压降)。vGS降低到负向关断偏置电压VEE的时刻,该模态结束。
:t5时刻,下管QL的PWM信号sL由高电平变为低电平。驱动电压通过驱动电阻为下管QL的输入电容Ciss放电,栅源电压vGS从正向导通偏置电压VCC开始下降,到t6时刻,vGS降低到负向关断偏置电压VEE,vGS低于阈值电压后,QL的沟道具有高阻抗,电流流过QL的寄生体二极管VDds,漏源极电压vDS保持在0附近(导通压降)。vGS降低到负向关断偏置电压VEE的时刻,该模态结束。
模态7[t6, t7 :由于仍然处于上下管的死区时间之内,因此,QL栅源电压vGS保持在负向关断偏置电压VEE不变,MOSFET的沟道已经关断,负载电流通过寄生体二极管续流,直到上管QH开始导通。上管QH的PWM信号sH由低电平变为高电平后,为QH的输入电容充电,当栅源电压上升到阈值后,QH的沟道电流开始上升并完成换流过程。
:由于仍然处于上下管的死区时间之内,因此,QL栅源电压vGS保持在负向关断偏置电压VEE不变,MOSFET的沟道已经关断,负载电流通过寄生体二极管续流,直到上管QH开始导通。上管QH的PWM信号sH由低电平变为高电平后,为QH的输入电容充电,当栅源电压上升到阈值后,QH的沟道电流开始上升并完成换流过程。
模态8[t7, t8 :t7时刻,QL的漏源极电压vDS从0增大到VDC。在这一阶段,上升的vDS可以视为斜坡信号,栅源电压vGS受到该斜坡信号的激励,从关断偏置电压VEE开始上升。到t8时刻,vDS斜坡上升结束。t8时刻后,vDS呈现明显的振荡现象,其影响vGS的机理与斜坡信号的影响不同。为简便起见,本文将t8时刻的vGS简称为正向干扰尖峰,以区别于此后vDS振荡所引发的栅源极电压干扰振荡。
:t7时刻,QL的漏源极电压vDS从0增大到VDC。在这一阶段,上升的vDS可以视为斜坡信号,栅源电压vGS受到该斜坡信号的激励,从关断偏置电压VEE开始上升。到t8时刻,vDS斜坡上升结束。t8时刻后,vDS呈现明显的振荡现象,其影响vGS的机理与斜坡信号的影响不同。为简便起见,本文将t8时刻的vGS简称为正向干扰尖峰,以区别于此后vDS振荡所引发的栅源极电压干扰振荡。
模态9[t8, t9]:t8时刻,QL漏源电压vDS升高到VDC。在这一阶段,vDS的高频振荡将激励QL栅源电压vGS产生高频振荡,振荡持续到t9时刻,QL栅源电压vGS返回到负向关断偏置电压VEE。进入新的稳态过程,直到下一周期开始。
由上述分析可知,栅源电压干扰出现于动态过程中,主要由漏源电压vDS变化引起,动态过程大致可以分为两个阶段:第一阶段出现典型的干扰引发的栅源电压尖峰,包括[t0, t1 和[t7, t8
和[t7, t8 ;第二阶段是栅源电压的高频振荡,包括[t1, t2
;第二阶段是栅源电压的高频振荡,包括[t1, t2 和[t8, t9]。
和[t8, t9]。
下面将分别建立功率回路模型和驱动回路模型,描述栅源电压响应高速开关干扰源的动态过程,揭示栅源电压的干扰动态响应机理。
考虑高于开关频率的高频干扰分量,建立用于被动管栅源电压干扰分析的数学模型,预测计算栅源电压响应高频干扰的动态分量。为此,在驱动信号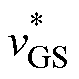 置零的前提下,进一步简化图1,单独研究干扰源vdis到栅源电压vGS的干扰路径,得到等效简化电路,如图3所示。图中,vdis为脉冲电压干扰源。功率回路电感Lo包括MOS引脚、引线电感(Ld、Ls)及杂散电感Ls(直流解耦电容与桥臂组成的回路),因此,Lo=Ls+Ld+Ls。Ro为功率回路总的等效电阻,包括PCB引线电阻、MOSFET的导通电阻。驱动回路电感Li包括栅极引脚寄生电感Lg以及源极引脚上的驱动回路电感Ls,记为Li=Lg+Ls。为突出主要矛盾,着重分析被动管栅源电压干扰成因,本节分析过程中采用分段线性化处理,近似认为Cgs、Cgd、Cds恒定不变;且忽略寄生体二极管的反向恢复影响。
置零的前提下,进一步简化图1,单独研究干扰源vdis到栅源电压vGS的干扰路径,得到等效简化电路,如图3所示。图中,vdis为脉冲电压干扰源。功率回路电感Lo包括MOS引脚、引线电感(Ld、Ls)及杂散电感Ls(直流解耦电容与桥臂组成的回路),因此,Lo=Ls+Ld+Ls。Ro为功率回路总的等效电阻,包括PCB引线电阻、MOSFET的导通电阻。驱动回路电感Li包括栅极引脚寄生电感Lg以及源极引脚上的驱动回路电感Ls,记为Li=Lg+Ls。为突出主要矛盾,着重分析被动管栅源电压干扰成因,本节分析过程中采用分段线性化处理,近似认为Cgs、Cgd、Cds恒定不变;且忽略寄生体二极管的反向恢复影响。
图3 等效简化电路
Fig.3 Simplified equivalent circuit
vds为Cds上的电压(角标为小写,与之相区分,引脚两端的漏源电压的角标为大写,即vDS);vm为Cgd与Cgs中间点的电压。数值上,有vm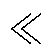 vds,且功率回路具有相对较大的电流流通,因此,从vdis到vds的部分可以近似认为与驱动回路的阻抗Zm无关,从图3a可得等效简化电路图3b,将功率回路与驱动回路等效拆解分别分析。进而可以得到
vds,且功率回路具有相对较大的电流流通,因此,从vdis到vds的部分可以近似认为与驱动回路的阻抗Zm无关,从图3a可得等效简化电路图3b,将功率回路与驱动回路等效拆解分别分析。进而可以得到
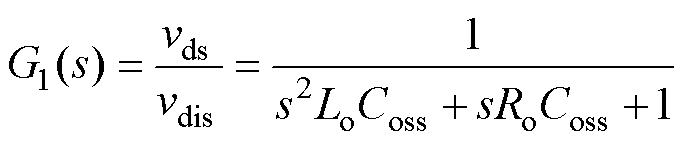 (1)
(1)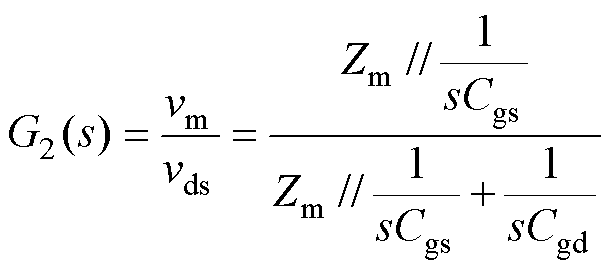 (2)
(2)
式中,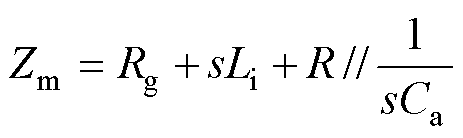 。为计算获得受到干扰的(引脚两端)栅源电压vGS,取栅源极外部并联阻抗
。为计算获得受到干扰的(引脚两端)栅源电压vGS,取栅源极外部并联阻抗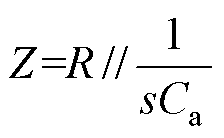 ,则有
,则有
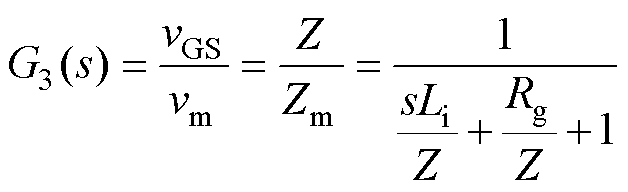 (3)
(3)设Gi(s)为驱动回路传递函数,Go(s)为功率回路传递函数,则有
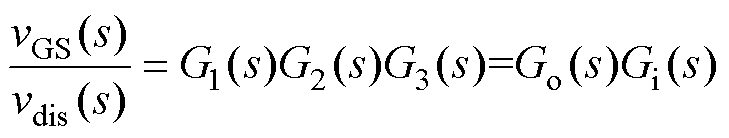 (4)
(4)
其中
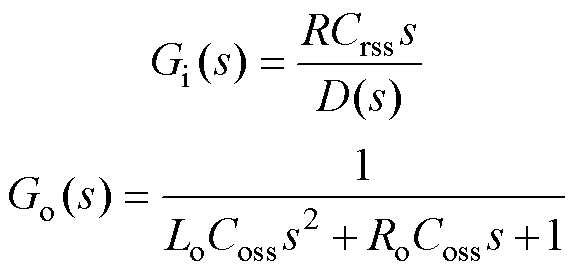
省略高阶无穷小系数后的特征多项式为
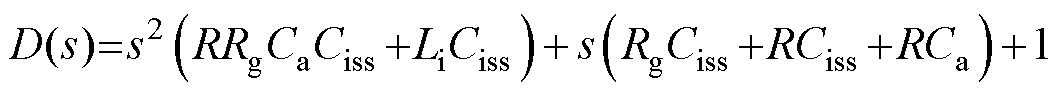 (5)
(5)
式(4)即为栅源电压干扰动态模型的解析表达式。采用不同器件,无需重新独立构造干扰路径传递函数的特征多项式。仅需要根据器件数据手册提供的暂态特性参数,在式(4)的特征多项式中代入具体数值,即可获得干扰路径传递函数的特征多项式。为了便于分析功率回路、驱动回路不同参数的作用,有针对性地优化PCB设计和布局,栅源电压干扰的等效电路如图4所示,即获得描述栅源电压对干扰的动态响应的等效电路。图中,vGS为器件引脚两端的栅源电压,vgs为器件结电容电容Cgs的电压。
在获得驱动回路和功率回路传递函数的基础上,本节将继续归纳总结该传递函数的特性。干扰路径的特性可以用其传递函数的特征多项式D(s)描述,为方便研究,描述栅源电压干扰的标准二阶系统为
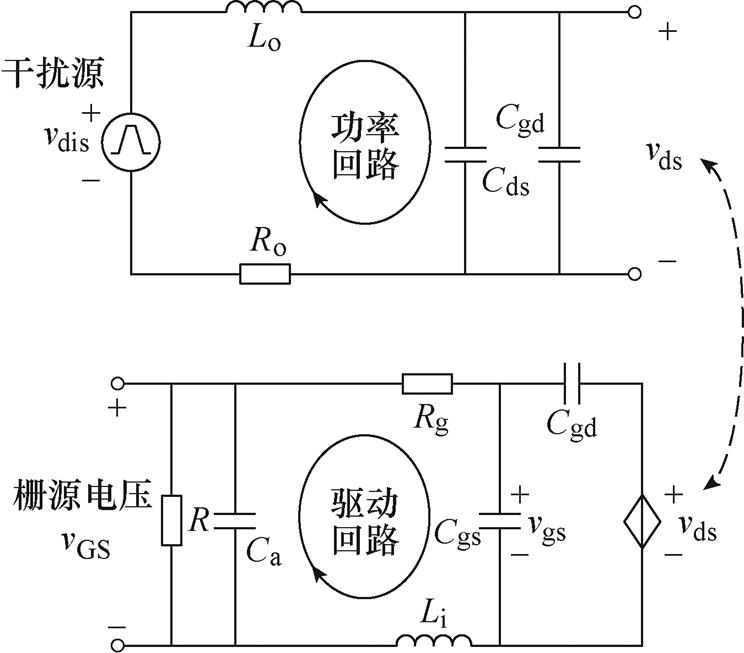
图4 栅源电压干扰的等效电路
Fig.4 The equivalent circuit for gate-source voltage interference
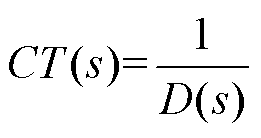 (6)
(6)CT(s)的阻尼比为
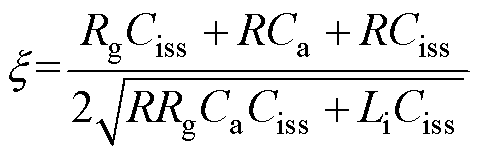 (7)
(7)
CT(s)的无阻尼自振频率为
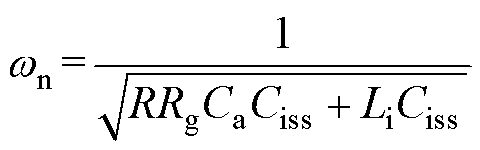 (8)
(8)具有较高的漏源电压斜率是SiC MOSFET工作频率提高时的重要特征之一。实际上,漏源电压是具有一定斜率的周期脉冲电压,其影响可以近似用驱动回路传递函数Gi(s)对斜率为K=±VDC/tr(±代表脉冲电压干扰的上升沿和下降沿)的斜坡信号响应描述。需要说明的是,SiC MOSFET的运行过程中,tr与驱动回路的参数相关,然而,为了突出主要矛盾,在分析时将斜率K近似视为固定值。估算斜率K时,根据调试经验,推荐取外部驱动电阻R在数值上等于栅极内电阻Rg时,器件电压上升下降时间的平均值为tr。驱动回路传递函数Gi(s)对斜坡信号的响应为
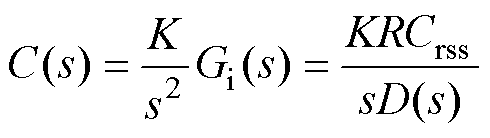 (9)
(9)
由终值定理可知,响应的终值c(∞)为
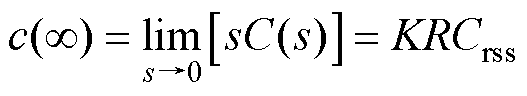 (10)
(10)如第1.1节所述,模态1和模态8期间,vDS以斜坡信号的形式干扰vGS。vDS斜坡变化阶段结束后,vDS呈现明显的振荡现象,其影响vGS的机理与斜坡信号的影响不同。为简便起见,本文将vDS斜坡变化结束时刻的vGS简称为干扰尖峰,以区别于此后振荡所引发的尖峰,并以驱动回路传递函数Gi(s)对斜坡信号的响应终值c(∞)量化。由式(10)可知,斜坡信号干扰引起的尖峰值与驱动电阻R成正比,因此,较小的驱动电阻R可以降低响应终值,一定程度上抑制干扰尖峰。然而,由式(8)可知,过小的驱动电阻R,导致无阻尼自振频率wn过大,CT(s)对于高频段的抑制能力降低,导致驱动回路对主功率回路谐振的抑制不足,有可能引发过大的栅源电压振荡。因此,驱动参数的选取极为重要。
为了标准量化驱动参数对于栅源电压干扰传导路径的影响,本文借鉴工程计算中常用的数值标记方法,引入标幺化的系统参数表达形式,以参数实际值与选定基准值的比值来表示各系统参数。取SiC MOSFET的输入电容Ciss和栅极内电阻Rg为基准值,具体来讲Ciss作为杂散电感和结电容的基准值,Rg作为驱动电阻的基准值。标幺化后的栅源极并联辅助电容 =Ca/Ciss,驱动回路杂散电感
=Ca/Ciss,驱动回路杂散电感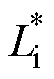 =Li/Ciss,驱动电阻R*=R/Rg。则以标幺值表示的标准二阶系统CT(s)的阻尼比和无阻尼自振频率分别为
=Li/Ciss,驱动电阻R*=R/Rg。则以标幺值表示的标准二阶系统CT(s)的阻尼比和无阻尼自振频率分别为
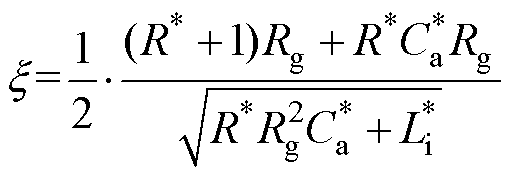 (11)
(11)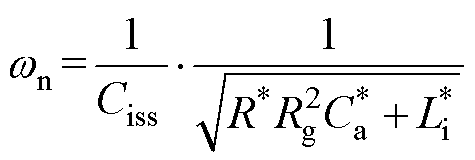 (12)
(12)
式(11)和式(12)描述栅源电压干扰的标准二阶系统CT(s)的动态特性,且以标幺化形式表示。类似地,式(10)也可以进行标幺化处理得
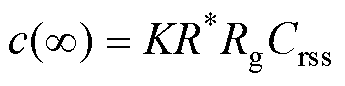 (13)
(13)对于不同的SiC MOSFET,根据数据手册提供的暂态特性参数,可获得栅源电压干扰的标准二阶系统CT(s),其阻尼比和无阻尼自振频率描述了干扰的动态特性。需要说明的是,不同的SiC MOSFET具有不同的基准值,然而基准值的改变不会影响栅源电压干扰的传导路径。因此,标幺化的形式弱化了采用不同SiC MOSFET时,栅源电压干扰在参数数值上的差别,便于直观和迅速地判断系统元件参数的合理性,并能简化计算,为后续优化设计提供理论依据。
为有效控制SiC MOSFET栅源电压干扰,并保证驱动回路具有适度的过渡过程,根据前述分析可知,SiC MOSFET驱动参数的优化设计,需遵循以下三个步骤的方法:(1)验证驱动回路杂散电感标幺值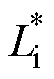 是否足够小,以保证标准二阶系统CT(s)具有足够的阻尼比;(2)设计辅助并联电容标幺值
是否足够小,以保证标准二阶系统CT(s)具有足够的阻尼比;(2)设计辅助并联电容标幺值 ,标准二阶系统在具备充足的阻尼比前提下,获得适度的、持续时间较短的过渡过程;(3)设计驱动电阻标幺值R*,均衡抑制栅源电压的干扰尖峰和干扰振荡。详细设计过程分析如下:
,标准二阶系统在具备充足的阻尼比前提下,获得适度的、持续时间较短的过渡过程;(3)设计驱动电阻标幺值R*,均衡抑制栅源电压的干扰尖峰和干扰振荡。详细设计过程分析如下:
(1)验证驱动回路杂散电感标幺值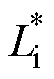 是否足够小,以保证标准二阶系统CT(s)具有足够的阻尼比。根据自动控制原理,为了让驱动回路具有良好的动态特性,避免出现剧烈的暂态振荡,一般希望CT(s)的阻尼比大于0.4[28]。考虑极端情况下,驱动电阻趋近于零(即R*→0)的时候,保守估计驱动回路杂散电感是否满足要求,根据式(11)可知,阻尼比需要满足
是否足够小,以保证标准二阶系统CT(s)具有足够的阻尼比。根据自动控制原理,为了让驱动回路具有良好的动态特性,避免出现剧烈的暂态振荡,一般希望CT(s)的阻尼比大于0.4[28]。考虑极端情况下,驱动电阻趋近于零(即R*→0)的时候,保守估计驱动回路杂散电感是否满足要求,根据式(11)可知,阻尼比需要满足
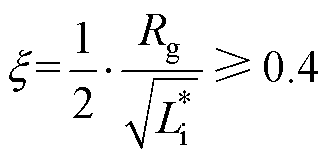 (14)
(14)整理可得
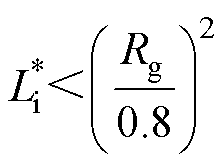 (15)
(15)
式(15)是驱动回路杂散电感的设计参考,Rg为SiC MOSFET的栅极内电阻。式(15)限定了驱动回路杂散电感的最大值,当驱动回路电感过大,超过该范围时,设计人员需调整PCB布局,缩短驱动芯片与SiC MOSFET栅源极之间的回路引线长度,以降低驱动回路的杂散电感,避免引入过大干扰。需要注意的是,式(15)的要求较为严苛,是在驱动电阻为零的极端情况下,保守估计获得的设计范围。实际应用中,可以根据工程应用环境加以修正。然而,不论如何修正,新取得的参数范围,应当与式(15)的推荐范围具有相同的数量级。
(2)设计辅助并联电容标幺值 ,标准二阶系统在具备充足的阻尼比前提下,获得适度的、持续时间较短的过渡过程,确保辅助并联电容不会过度影响开关速度。在SiC MOSFET的驱动回路杂散电感满足条件1)时,驱动回路杂散电感足够小,可以认为
,标准二阶系统在具备充足的阻尼比前提下,获得适度的、持续时间较短的过渡过程,确保辅助并联电容不会过度影响开关速度。在SiC MOSFET的驱动回路杂散电感满足条件1)时,驱动回路杂散电感足够小,可以认为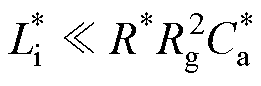 。因此,式(11)可进一步简化为
。因此,式(11)可进一步简化为
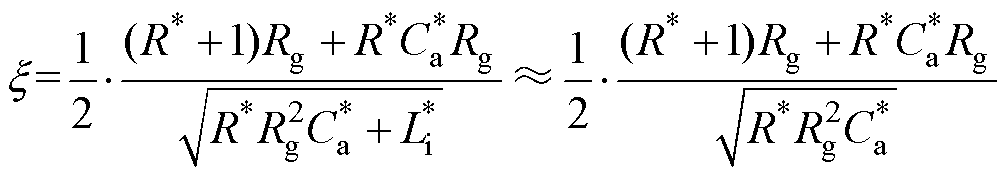
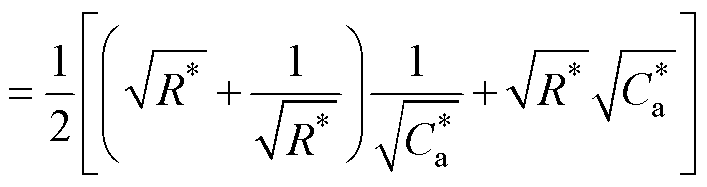 (16)
(16)
由式(16)可知,阻尼比x 为栅源极并联辅助电容标幺值 的函数,然而并非单调函数,因此需要分情况讨论。首先,当并联辅助电容很小的时候,
的函数,然而并非单调函数,因此需要分情况讨论。首先,当并联辅助电容很小的时候,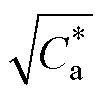 →0且
→0且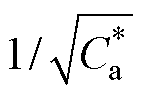 →∞,因此有
→∞,因此有
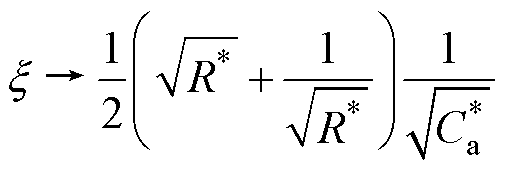 (17)
(17)当并联辅助电容很小时,阻尼比x 是栅源极并联辅助电容标幺值 的单调减函数。
的单调减函数。
类似地,当并联辅助电容很大时,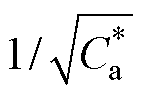 →0且
→0且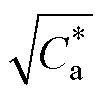 →∞,因此有
→∞,因此有
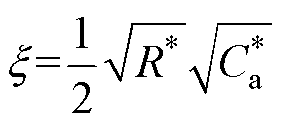 (18)
(18)当并联辅助电容很大时,阻尼比x 为 的单调增函数。综上两种情况,随着
的单调增函数。综上两种情况,随着 的增大,阻尼比x 先减小后增大,其存在极小值。极值点出现于偏导数为零的点,因此由
的增大,阻尼比x 先减小后增大,其存在极小值。极值点出现于偏导数为零的点,因此由
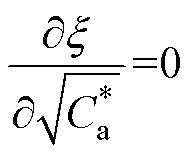 (19)
(19)
可得阻尼比x 最小的时候,并联辅助电容标幺值为
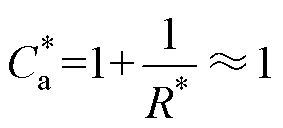 (20)
(20)因此,在SiC MOSFET的驱动回路杂散电感满足步骤(1)下,驱动回路标准二阶系统CT(s)的阻尼比为
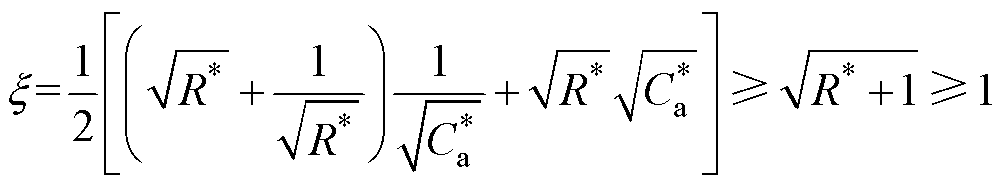 (21)
(21)
驱动回路标准二阶系统CT(s)将一直处于过阻尼状态,具备充足的阻尼比,不至于引发振荡。然而,需要注意的是,过阻尼状态下,阻尼比过大,将导致系统的过渡时间过长,驱动回路的动态过程过缓。为了让驱动回路获得持续时间适度的过渡过程,在具备充足的阻尼比不至于振荡的前提条件下,阻尼比应当尽量小,本文对 的设计遵循式(20),使得阻尼比x 处于最小值。
的设计遵循式(20),使得阻尼比x 处于最小值。
(3)设计驱动电阻标幺值R*,均衡抑制栅源电压的干扰尖峰和干扰振荡,并防止因为驱动回路截止频率过低导致栅源电压变化过缓增大开关损耗。经过步骤(1)和步骤(2)的设计,驱动回路将获得平滑无振荡且过渡时间适度的动态过程。以此为基础,依据式(11)和式(12),进一步确定驱动电阻标幺值R*的取值范围,研究驱动电阻的设计方法。为保证足够的谐振抑制比,并防止因为驱动回路截止频率过低导致栅源电压变化过缓,进而造成电压变化率dv/dt、电流变化率di/dt过小,增大开关损耗,设计时应保证wn<0.2wro[28],wro为功率回路谐振角频率,采用标幺化表示为
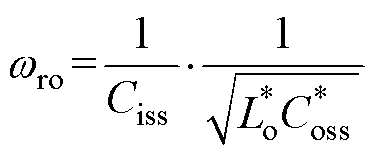 (22)
(22)式中,标幺化后的SiC MOSFET输出电容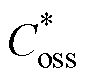 = Coss/Ciss;标幺化后的功率回路杂散电感
= Coss/Ciss;标幺化后的功率回路杂散电感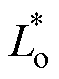 =Lo/Ciss。由式(12)可知,wn与驱动电阻标幺值R*成反比。在设计
=Lo/Ciss。由式(12)可知,wn与驱动电阻标幺值R*成反比。在设计 =1的前提下,可得驱动电阻标幺值R*的取值下限,即
=1的前提下,可得驱动电阻标幺值R*的取值下限,即
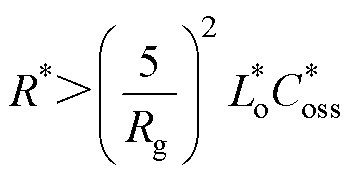 (23)
(23)
由式(13)可知,干扰尖峰值与驱动电阻标幺值R*成正比。因此,较小的驱动电阻可以降低响应终值,一定程度上抑制干扰尖峰。为了不让干扰电压尖峰过大,响应的终值|c(∞)|应当小于0.5(Vth-VGS,min),Vth为SiC MOSFET的导通阈值电压,VGS,min为栅极电压的额定最小值。简便起见,本文推荐响应的终值|c(∞)|<|VEE|,VEE为SiC MOSFET的关断偏置电压。由此可得驱动电阻标幺值R*的取值上限,即
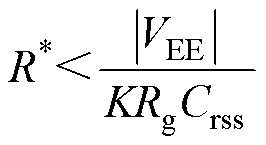 (24)
(24)综上,本文推荐驱动电阻R*的设计取值范围为
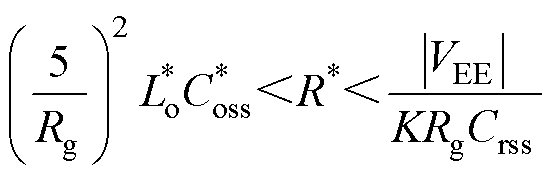 (25)
(25)
杂散电感、辅助并联电容和驱动电阻三个参数在驱动设计时,由设计者自由选取,互不干扰、相互独立。在SiC MOSFET确定后,这三个参数是驱动设计中的重要自由变量,很大程度上主导着开关暂态过程,是SiC MOSFET设计中需要着重关心的参数。综合考虑设计步骤(1)~步骤(3),为有效控制SiC MOSFET栅源电压干扰,并保证驱动回路具有适度的过渡过程。驱动参数标幺化设计流程如图5所示,本文采用SiC MOSFET驱动参数设计时,根据式(15)~式(25),分别依次设计驱动回路杂散电感标幺值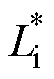 、辅助并联电容标幺值
、辅助并联电容标幺值 、驱动电阻标幺值R*。采用解析公式的标幺化参数设计方法,在实际应用中可以作为设计参考,直接使用,避免了繁杂、重复的计算过程。需要注意的是,按照本文设计方法得到的设计值,是在工程设计经验基础上提炼和归纳的,并非严格数学意义上的最优值。
、驱动电阻标幺值R*。采用解析公式的标幺化参数设计方法,在实际应用中可以作为设计参考,直接使用,避免了繁杂、重复的计算过程。需要注意的是,按照本文设计方法得到的设计值,是在工程设计经验基础上提炼和归纳的,并非严格数学意义上的最优值。
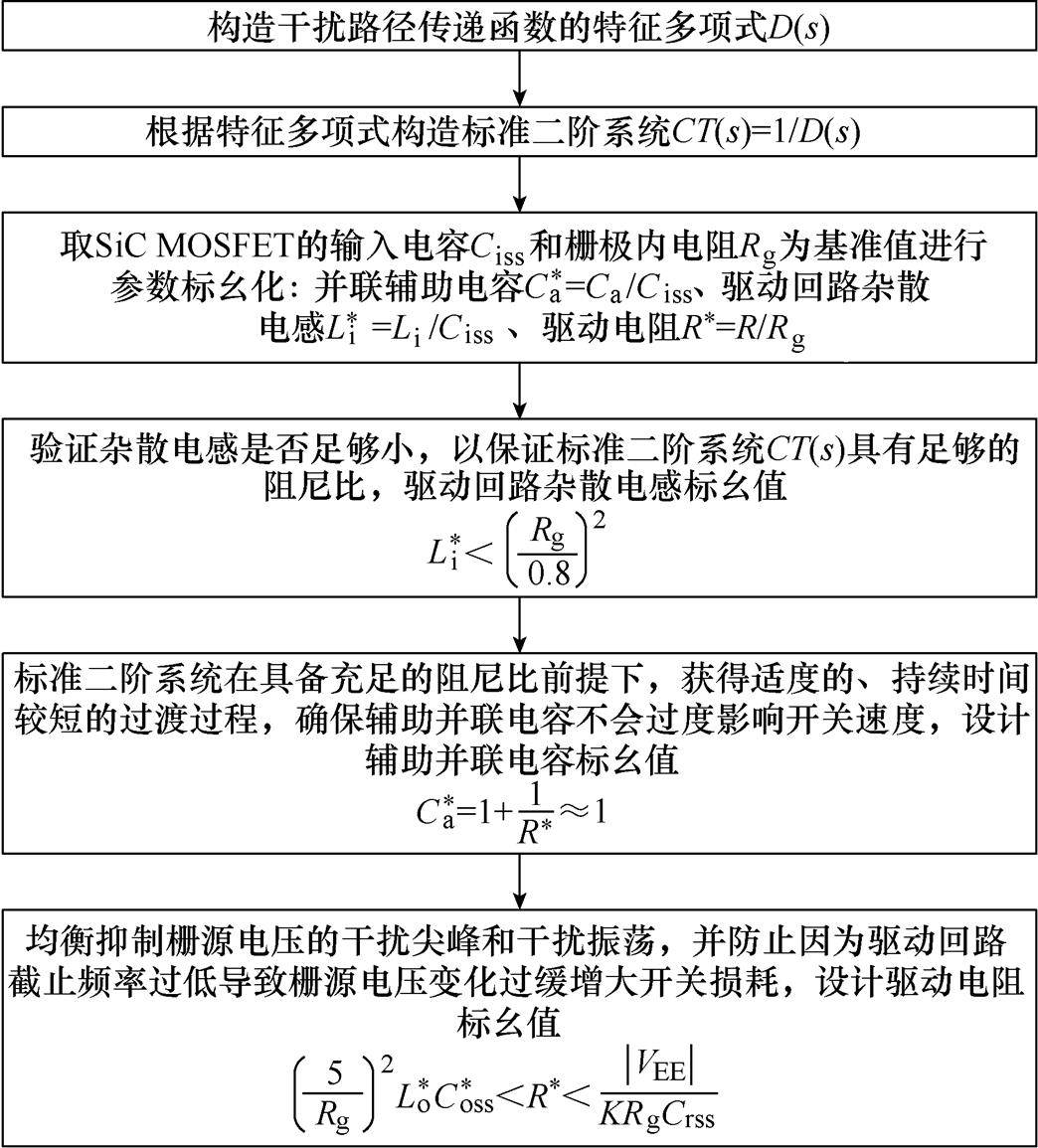
图5 驱动参数标幺化设计流程
Fig.5 Per-united design process of the driver parameters
为了进一步验证采用解耦原理降低SiC MOSFET栅极干扰的可行性,按照图1所示桥臂电路搭建双脉冲实验平台,对SiC MOSFET栅源电压进行测试,实验平台照片如图6所示。

图6 实验平台照片
Fig.6 Picture of the experimental platform
双脉冲实验中,QH为主动管,QL为被动管。QL始终处于关断状态,用于续流。通过测量QL的栅极电压信号,来反映主动管QH开通与关断动作对被动管QL栅源电压的影响。器件采用泰科天润产品SiC MOSFET G1M080120B(1 200V/40A/80mW)。为简便起见,忽略数值上较小的脉冲电流干扰,以脉冲电压干扰的下降沿为例,记外部驱动电阻在数值上等于栅极内电阻时,器件电压上升下降时间的平均值取tr≈40ns。额定直流电压VDC=800V,典型参数Rg=5.7W、Ciss=1 816pF、Crss=24pF、Coss=142pF(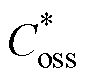 =0.078)、Li=30nH(
=0.078)、Li=30nH(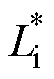 =16.52)、Lo=50nH(
=16.52)、Lo=50nH(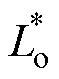 =27.53)、VEE=-5V。
=27.53)、VEE=-5V。
双脉冲实验电路设计时,驱动回路的连线距离尽可能最小,以保证驱动回路杂散电感的标幺值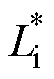 足够小。为保证标准二阶系统CT(s)具有足够的阻尼比,驱动回路杂散电感的标幺值
足够小。为保证标准二阶系统CT(s)具有足够的阻尼比,驱动回路杂散电感的标幺值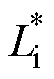 满足式(15)的约束。
满足式(15)的约束。
根据式(20)设计辅助并联电容标幺值 =1,即Ca=1 816pF=1.816nF。实际工程中可取整,采用Ca=2nF。使得标准二阶系统CT(s)在具备充足的阻尼比前提下,获得适度的、持续时间较短的过渡过程。在此基础上,通过实验验证驱动电阻标幺值R*的选取原则,以均衡抑制栅源电压的干扰尖峰和干扰振荡。
=1,即Ca=1 816pF=1.816nF。实际工程中可取整,采用Ca=2nF。使得标准二阶系统CT(s)在具备充足的阻尼比前提下,获得适度的、持续时间较短的过渡过程。在此基础上,通过实验验证驱动电阻标幺值R*的选取原则,以均衡抑制栅源电压的干扰尖峰和干扰振荡。
在VDC=800V的条件下,研究栅源电压vGS响应漏源电压vDS暂态过程波形。驱动电阻R=2W、10W、15W 时的实验波形分别如图7~图9所示,图中,vDSH、idH分别为主动管QH的漏源电压和漏极电流。双脉冲电路的主动管QH导通持续时间为1ms,以折算到占空比为50%的周期方波为例,对应开关周期为2ms、开关频率为500kHz。分别工作于驱动电阻R=2W、10W、15W,相应的驱动电阻标幺值分别为R*=0.351、1.754、2.632。由式(25)可得,驱动电
阻标幺值的最小值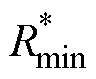 =1.657、最大值
=1.657、最大值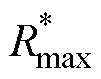 =1.828。根据驱动电阻标幺值R*的定义,得到驱动电阻9.45W<R<10.42W。
=1.828。根据驱动电阻标幺值R*的定义,得到驱动电阻9.45W<R<10.42W。
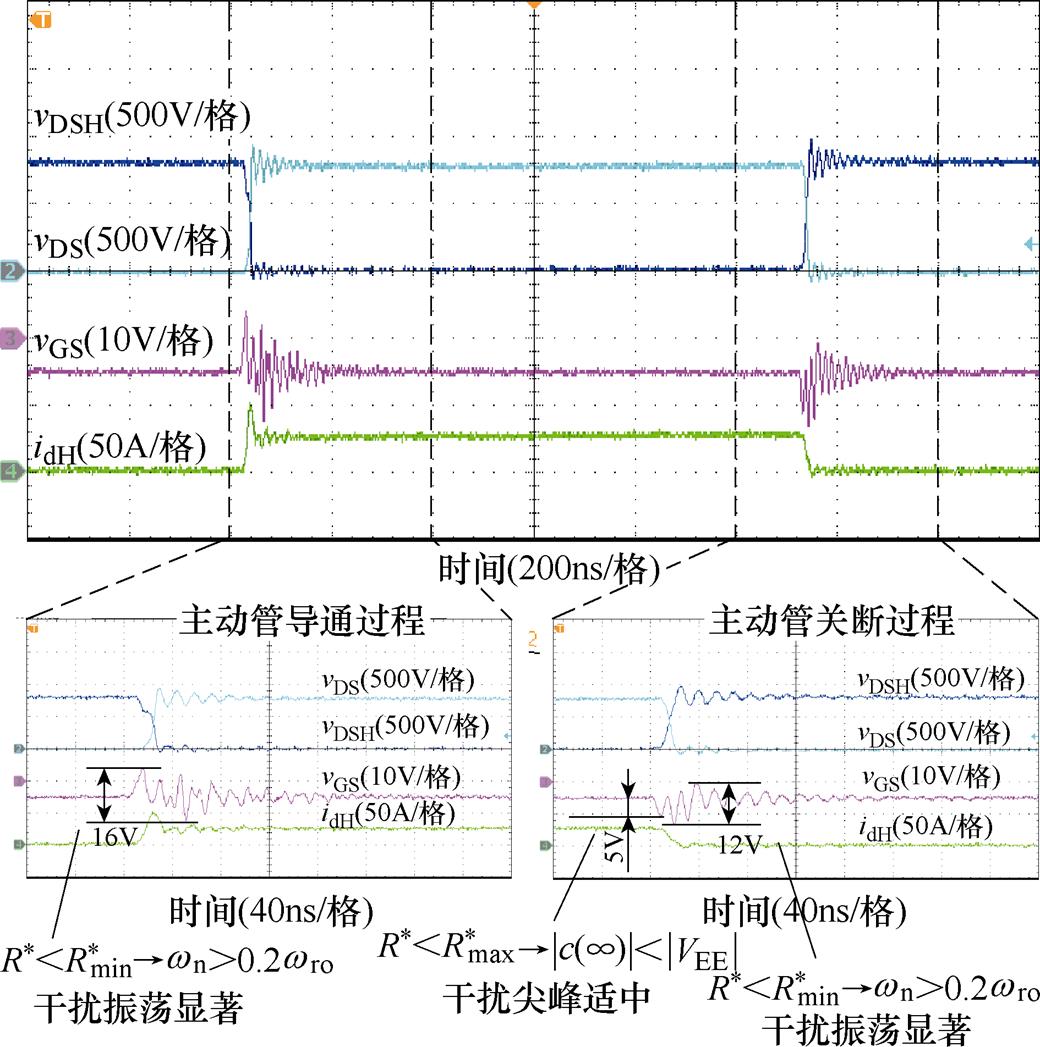
图7 驱动电阻R=2W(R*=0.351)时的实验波形
Fig.7 Experimental waveforms when driver resistance R=2W (R*=0.351)

图8 驱动电阻R=10W(R*=1.754)时的实验波形
Fig.8 Experimental waveforms when driver resistance R=10W (R*=1.754)

图9 驱动电阻R=15W(R*=2.632)时的实验波形
Fig.9 Experimental waveforms when driver resistance R=15W (R*=2.632)
图7主动管关断过程中,被动管栅源电压vGS的负向干扰尖峰约5V;其后,栅源电压vGS干扰振荡期间,有多个振荡波峰,峰峰值达到12V;由于干扰振荡显著,干扰振荡主导的第二尖峰大于vDS斜坡下降主导的第一尖峰,干扰振荡的影响大于干扰尖峰影响。图7主动管导通过程中,干扰振荡十分剧烈,贯穿了整改暂态过程,使得干扰尖峰和干扰振荡时段混杂在一起,振荡最高峰值与最低谷值之差高达16V。
图8主动管关断过程中,被动管栅源电压vGS的负向干扰尖峰达到6V;而栅源电压vGS干扰振荡期间,振荡峰峰值约8V,较图7主动管关断过程中的振荡峰峰值降低30%。图8主动管导通过程中,振荡最高峰值与最低谷值之差约3.5V,较图7主动管导通过程的振荡有较大程度缓和。
图9主动管关断过程中,被动管栅源电压vGS的负向干扰尖峰达到7V,比图8主动管关断过程中的尖峰增大约16%;栅源电压vGS干扰振荡期间,振荡峰峰值进一步降低至约5.2V,较图8主动管关断过程的振荡幅度降低35%。图9主动管导通过程中,干扰振荡最高峰值与最低谷值之差约3V,与图8主动管导通过程的振荡幅度基本持平,均较图7主动管导通过程的振荡有较大程度缓和。
分析图7~图9所示实测栅源电压波形可知:当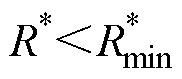 时,wn>0.2wro,栅源电压干扰振荡明显;而当
时,wn>0.2wro,栅源电压干扰振荡明显;而当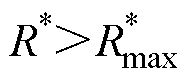 时,|c(∞)|>|VEE|,栅源电压干扰尖峰明显。从这一趋势来讲,本文建议驱动电阻设计时遵循式(25)是合理的。实际使用中,还需要根据开关速度、损耗、散热、电磁干扰等应用情况,对处于
时,|c(∞)|>|VEE|,栅源电压干扰尖峰明显。从这一趋势来讲,本文建议驱动电阻设计时遵循式(25)是合理的。实际使用中,还需要根据开关速度、损耗、散热、电磁干扰等应用情况,对处于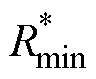 与
与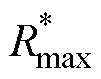 之间值进行取舍。
之间值进行取舍。
图10为针对图7~图9对应的不同驱动电阻,在图1中VDC=800V时,不同负载电流IL下QH的开关损耗。随着负载电流的增加,开关损耗也随之增加。驱动电阻R=2W(R*=0.351)时,QH在不同负载电流IL下均具有最低的开关损耗;R=15W(R*= 2.632)时,QH在不同负载电流IL下均具有最高的开关损耗;而R=10W(R*=1.754)时,QH在不同负载电流IL下均具有比R=15W(R*=2.632)时更低的开关损耗。
综合分析图7~图10所示实测波形和数据可知,栅源电压波形的变化特征符合理论计算的趋势,采用本文所揭示的SiC MOSFET驱动参数设计方法,进行驱动参数设计,一定程度上避免了过大栅源电压干扰的出现,且具有相对低的开关损耗,具有一定合理性。
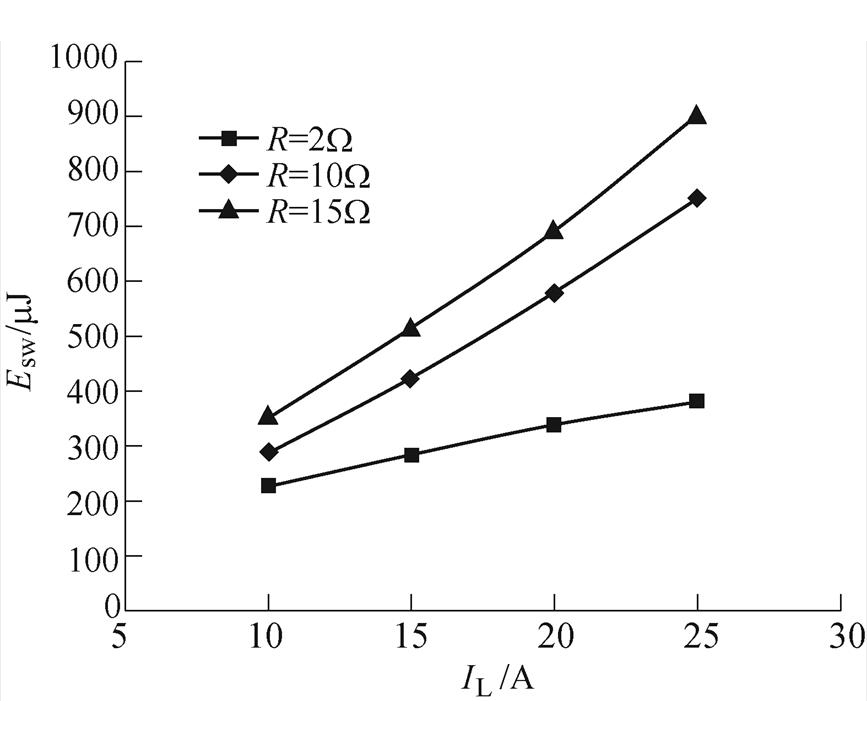
图10 不同驱动电阻(R)条件下的开关损耗(Esw)
Fig.10 Switching loss (Esw) under different driver resistance (R)
本文揭示了SiC MOSFET栅源电压的干扰动态响应机理,进而引入标幺化的系统参数表达形式以标准量化驱动参数对于栅源电压干扰传导路径的影响,提出基于干扰动态响应机理的SiC MOSFET驱动设计原则。
对于特定的SiC MOSFET,根据数据手册提供的暂态特性参数,可获得栅源电压干扰的标准二阶系统CT(s),其阻尼比和无阻尼自振频率描述了干扰的动态特性,便于直观和迅速地判断系统元件参数的合理性,并能大量简化计算。
采用解析公式的标幺化参数设计方法,在实际应用中可以作为设计参考,避免了重复的建模工作和繁杂的计算过程。经过理论分析和实验验证,提出了SiC MOSFET驱动参数解析优化设计方法。通过实测波形分析可知,栅源电压波形的变化特征符合理论分析的趋势,采用本文所揭示的SiC MOSFET驱动参数设计方法,进行驱动参数设计,一定程度上避免了过大栅源电压干扰的出现,具有一定合理性。
参考文献
[1] 曾正, 邵伟华, 胡博容, 等. SiC器件在光伏逆变器中的应用与挑战[J]. 中国电机工程学报, 2017, 37(1): 221-232.
Zeng Zheng, Shao Weihua, Hu Borong, et al. Chances and challenges of photovoltaic inverters with silicon carbide devices[J]. Proceedings of the CSEE, 2017, 37(1): 221-232.
[2] 李艳, 张雅静, 黄波, 等. Cascode型GaN HEMT输出伏安特性及其在单相逆变器中的应用研究[J]. 电工技术学报, 2015, 30(14): 295-303.
Li Yan, Zhang Yajing, Huang Bo, et al. Research on output volt-ampere characteristics of Cascode GaN HEMT and its application in single-phase inverter[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 295-303.
[3] 钱照明, 张军明, 盛况. 电力电子器件及其应用的现状和发展[J]. 中国电机工程学报, 2014, 34(29): 5149-5161.
Qian Zhaoming, Zhang Junming, Sheng Kuang. Status and development of power semiconductor devices and its applications[J]. Proceedings of the CSEE, 2014, 34(29): 5149-5161.
[4] 王旭东, 朱义诚, 赵争鸣, 等. 驱动回路参数对碳化硅MOSFET开关瞬态过程的影响[J]. 电工技术学报, 2017, 32(13): 23-30.
Wang Xudong, Zhu Yicheng, Zhao Zhengming, et al. Impact of gate-loop parameters on the switching behavior of SiC MOSFETs[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 23-30.
[5] 盛况, 任娜, 徐弘毅. 碳化硅功率器件技术综述与展望[J]. 中国电机工程学报, 2020, 40(6): 1741- 1752.
Sheng Kuang, Ren Na, Xu Hongyi. A recent review on silicon carbide power devices technologies[J]. Proceedings of the CSEE, 2020, 40(6): 1741-1752.
[6] 王莉娜, 邓洁, 杨军一, 等. Si和SiC功率器件结温提取技术现状及展望[J]. 电工技术学报, 2019, 34(4): 71-84.
Wang Lina, Deng Jie, Yang Junyi, et al. Junction temperature extraction methods for Si and SiC power devices-a review and possible alternatives[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(4): 71-84.
[7] Chen Jian, Du Xiong, Luo Quanming, et al. A review of switching oscillations of wide bandgap semi- conductor devices[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13182-13199.
[8] Zhang Boyi, Wang Shuo. A survey of EMI research in power electronics systems with wide-bandgap semi- conductor devices[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 626-643.
[9] Xue Peng, Luca Maresca, Michele Riccio, et al. Analysis on the self-sustained oscillation of SiC MOSFET body diode[J]. IEEE Transactions on Elec- tron Devices, 2019, 66(10): 4287-4295.
[10] 蒋烨, 赵争鸣, 施博辰, 等. 功率开关器件多时间尺度瞬态模型(II)——应用分析与模型互联[J]. 电工技术学报, 2017, 32(12): 25-32.
Jiang Ye, Zhao Zhengming, Shi Bochen, et al. Multi- time scale transient models for power semiconductor devices (part II: applications analysis and model connection)[J]. Transactions of China Electrotech- nical Society, 2017, 32(12): 25-32.
[11] 施博辰, 赵争鸣, 蒋烨, 等. 功率开关器件多时间尺度瞬态模型(I)——开关特性与瞬态建模[J]. 电工技术学报, 2017, 32(12): 16-24.
Shi Bochen, Zhao Zhengming, Jiang Ye, et al. Multi- time scale transient models for power semiconductor devices (part I: switching characteristics and transient modeling)[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 16-24.
[12] 何杰, 刘钰山, 毕大强, 等. 电压探头对宽禁带器件高频暂态电压精确测量的影响[J]. 电工技术学报, 2021, 36(2): 362-372.
He Jie, Liu Yushan, Bi Daqiang, et al. Impacts of voltage probes for accurate measurement of high- frequency transient voltage of wide-bandgap devices[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 362-372.
[13] 巴腾飞, 李艳, 梁美. 寄生参数对SiC MOSFET栅源极电压影响的研究[J]. 电工技术学报, 2016, 31(13): 64-73.
Ba Tengfei, Li Yan, Liang Mei. The effect of parasitic parameters on gate-source voltage of SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 64-73.
[14] Zhang Zheyu, Guo Ben, Wang Fei Fred, et al. Methodology for wide band-gap device dynamic characterization[J]. IEEE Transactions on Power Electronics, 2017, 32(12): 9307-9318.
[15] Wang Fred, Zhang Zheyu. Overview of silicon carbide technology: device, converter, system, and application[J]. CPSS Transactions on Power Electro- nics and Applications, 2016, 1(1): 13-32.
[16] 段卓琳, 张栋, 范涛. SiC电机驱动系统传导电磁干扰建模及预测[J]. 电工技术学报, 2020, 35(22): 4726-4738.
Duan Zhuolin, Zhang Dong, Fan Tao. Modeling and prediction of electromagnetic interference in SiC motor drive systems[J]. Transactions of China Electro- technical Society, 2020, 35(22): 4726-4738.
[17] Klaus Sobe, Thomas Basler, Blaz Klobucar. Characterization of the parasitic turn-on behavior of discrete CoolSiCTM MOSFETs[C]//International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management (PCIM Europe 2019), Nuremberg, Germany, 2019: 7-9.
[18] Zhang Zheyu, Guo Ben, Wang Fei. Evaluation of switching loss contributed by parasitic ringing for fast switching wide band-gap devices[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(9): 9082-9094.
[19] Li Ruqi, Zhu Qiuhua, Xie Manjing. A new analytical model for predicting dv/dt-induced low-side MOSFET false turn-on in synchronous Buck converters[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5500-5512.
[20] Thomas Aichinger, Gerald Rescher, Gregor Pobegen. Threshold voltage peculiarities and bias temperature instabilities of SiC MOSFETs[J]. Microelectronics Reliability, 2018, 80: 68-78.
[21] Dethard Peters, Thomas Aichinger, Thomas Basler, et al. Investigation of threshold voltage stability of SiC MOSFETs[C]//2018 IEEE 30th International Symposium on Power Semiconductor Devices and ICs (ISPSD), Chicago, USA, 2018: 13-17.
[22] Infineon Technologies AN-2018-09. Guidelines for CoolSiC™ MOSFET gate drive voltage window[EB/OL].Available online at https://www.infineon.com (accessed on 1 September, 2020).
[23] 李晓玲, 曾正, 陈昊, 等. SiC、Si、混合功率模块封装对比评估与失效分析[J]. 中国电机工程学报, 2018, 38(16): 4823-4835.
Li Xiaoling, Zeng Zheng, Chen Hao, et al. Com- parative package evaluation and failure mode analysis of SiC, Si, and hybrid power modules[J]. Proceedings of the CSEE, 2018, 38(16): 4823-4835.
[24] Zhang Zheyu, Zhang Weimin, Wang Fred, et al. Analysis of the switching speed limitation of wide band-gap devices in a phase-leg configuration[C]// 2012 IEEE Energy Conversion Congress and Expo- sition (ECCE), Raleigh, USA, 2012: 15-20.
[25] Ji Shiqi, Zheng Sheng, Wang Fei, et al. Temperature- dependent characterization, modeling, and switching speed-limitation analysis of third-generation 10kV SiC MOSFET[J]. IEEE Transactions on Power Elec- tronics, 2018, 33(5): 4317-4327.
[26] Xie Ruiliang, Wang Hanxing, Tang Gaofei, et al. An analytical model for false turn-on evaluation of high-voltage enhancement-mode GaN transistor in bridge-leg configuration[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 6416-6433.
[27] Zhu Tianhua, Zhuo Fang, Zhao Fangzhou, et al. Quantitative model-based false turn-on evaluation and suppression for cascode GaN devices in half-bridge applications[J]. IEEE Transactions on Power Electro- nics, 2019, 34(10): 10166-10179.
[28] 鄢景华. 自动控制原理[M]. 哈尔滨: 哈尔滨工业大学出版社, 2006.
SiC MOSFET Gate Driver Design Based on Interference Dynamic Response Mechanism
Abstract Currently, the gate driver design method of SiC MOSFET is mostly inherited from the Si MOSFET and IGBT. However, since SiC MOSFETs have higher switching speed than Si devices, it is also worth exploring the gate-source voltage interference caused by gate internal resistance, gate driver inductance and power circuit inductance. In this paper, the process of gate-source voltage interference is analyzed, and then the method of driver parameter per-united design based on interference dynamic response mechanism is summarized and extracted. This paper deduces the transfer functions of the power loop and the driver loop according to the equivalent circuit of the junction capacitance. Then, the interference dynamic response mechanism is revealed. Furthermore, a per-united parameter expression form is introduced to quantify the influence of gate driver parameters on the interference conduction path of gate-source voltage. The SiC MOSFET gate driver design principle is proposed based on the interference dynamic response mechanism. Finally, a double-pulse experimental platform was built to verify the rationality of the driver design principle.
keywords:SiC MOSFET, gate driver design, gate-source voltage interference, dynamic response
DOI: 10.19595/j.cnki.1000-6753.tces.210260
中图分类号:TM402
邵天骢 男,1990年生,博士,讲师,研究方向为宽禁带半导体功率器件驱动与保护、新能源变流器运行控制。E-mail: tcshao@bjtu.edu.cn(通信作者)
郑琼林 男,1964年生,教授,博士生导师,研究方向为轨道交通牵引供电与交流传动、高性能低损耗电力电子系统、光伏发电并网与控制、电力有源滤波与电能质量。E-mail: tqzheng@bjtu.edu.cn
收稿日期 2021-03-01
改稿日期 2021-04-27
(编辑 陈 诚)