针对GaN器件的非对称双路同步谐振栅极驱动电路
高珊珊 王懿杰 刘怡宁 徐殿国
(哈尔滨工业大学电气工程系 哈尔滨 150001)
摘要 近年来,氮化镓(GaN)器件凭借其开关速度快、导通电阻小等优点被广泛应用于电力电子变换器中,与此同时,谐振栅极驱动电路也受到广泛的关注,特别是在高开关频率、小功率的应用场合中,用以降低驱动电路的损耗。然而,与硅器件不同的是,GaN器件的开通阈值电压相对较低,且没有体二极管,反向导通压降较大,因此传统的谐振栅极驱动电路不适使用GaN器件。该文针对高频应用场合中寄生参数易引起驱动信号振荡的问题,结合GaN器件特点,提出一种非对称电压的谐振栅极驱动电路。此外,对于需要两个同步开关的应用场合,如开关电感变换器等,采用具有两个二次侧的变压器实现两路隔离同相驱动信号的输出。该文介绍了谐振栅极驱动电路的工作原理,并以效率最优的原则设计电路参数,设计一台开关频率为1MHz的驱动电路样机,并进行实验验证,实验结果与理论分析结果吻合较好。
关键词:氮化镓 谐振驱动电路 谐振电感 损耗分析
0 引言
高频率及高功率密度变换器凭借体积小、成本低、动态响应快等优点成为电力电子变换器的发展趋势。在高频率、低功率的应用场合,例如,几百瓦及以下,开关管驱动电路的驱动损耗对整个变换器有显著影响[1]。然而,传统的电压源型驱动电路(Conventional Gate Driver, CGD)的损耗随着开关频率的增加而不断增加。因此,谐振型驱动电路(Resonant Gate Driver, RGD)在高频应用中备受关注[2-4]。
在RGD中,通过设计LC谐振网络来恢复存储在功率MOSFET栅源极电容中的能量。RGD的另一个优点是具有快速充放电能力,根据初始电感电流,RGD可分为零初始电流拓扑结构和非零初始电流拓扑结构[5]两种类型。
近年来,GaN器件由于具有开关速度快、导通电阻小等优点被广泛应用于高频电力电子变换器中[6-10]。就器件本身而言,GaN器件的开通阈值电压比Si器件低,以GaN Systems公司生产的GS61008为例,其开通阈值仅为1.1V。虽然GaN器件本身不需要负压偏置来保证关断,但在高频条件下,电路中寄生参数引起的振荡很容易造成误动作,因此在高频应用中,负压偏置是必不可少的。同时,GaN器件不存在体二极管,反向导通损耗随关断电压的增大而增大。因此,传统的对称式电压驱动电路不适合GaN器件。
同时,随着光伏系统等应用场合对高电压增益DC-DC变换器的需求不断增长,级联变换器、开关电容、开关电感、耦合电感[11-14]等新技术逐渐成为研究热点。其中,开关电感变换器中有两个具有同步驱动信号的开关管。对于这些变换器,通常需要两套驱动电路,增加了驱动电路的体积、成本和 损耗。
因此,针对上述应用场合,以GaN Systems公司的GaN器件为例,官方推荐的驱动电压为6V或6.5V,同时为保证可靠关断,应具有一定的负电压。对驱动电路而言,需具有较快的开通、关断速度;具有谐振网络,以保证系统效率;并且能够输出两路同相的隔离驱动信号。
针对高频应用场合中寄生参数易引起驱动信号振荡的问题,结合GaN器件特点,本文提出了一种非对称电压的谐振栅极驱动电路。此外,对于需要两个同步开关的应用场合,如开关电感变换器等,采用具有两个二次侧的变压器实现两路隔离同相驱动信号的输出。本文首先详细介绍了所提驱动电路
的工作原理;其次介绍了谐振电感的设计方法,并分析谐振电感参数对电路损耗的影响;最后给出了实验结果及结论。
1 工作原理
针对引言中对驱动电路的要求,设计了基于变压器的谐振栅极驱动电路如图1所示,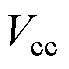 =3.3V,变压器有两个二次侧,一次、二次侧匝比为1
=3.3V,变压器有两个二次侧,一次、二次侧匝比为1 1
1 1。图中,Lr为变压器二次侧漏感,电容C1、C2,电阻R1、R2以及二极管VDL为增加的电平移位电路,Cg为待驱动开关管Q的寄生电容,Rg为待驱动开关管Q的导通电阻。S1~S4为驱动电路所需的开关管,VD1~VD4为S1~S4的体二极管。变压器可实现一次、二次侧的隔离以及两路同步信号的输出。相比于传统方案,减少了一组全桥电路,电路结构更加简单同时损耗也相应减小。通过变压器二次侧的漏感Lr与开关管的寄生电容Cg谐振,取消了抑制振荡的栅极电阻,可提升开关速度并且降低损耗。同时增加电平移位电路以调节驱动电压偏置,使驱动信号的电压满足开关器件的要求。
1。图中,Lr为变压器二次侧漏感,电容C1、C2,电阻R1、R2以及二极管VDL为增加的电平移位电路,Cg为待驱动开关管Q的寄生电容,Rg为待驱动开关管Q的导通电阻。S1~S4为驱动电路所需的开关管,VD1~VD4为S1~S4的体二极管。变压器可实现一次、二次侧的隔离以及两路同步信号的输出。相比于传统方案,减少了一组全桥电路,电路结构更加简单同时损耗也相应减小。通过变压器二次侧的漏感Lr与开关管的寄生电容Cg谐振,取消了抑制振荡的栅极电阻,可提升开关速度并且降低损耗。同时增加电平移位电路以调节驱动电压偏置,使驱动信号的电压满足开关器件的要求。
在一个工作周期内,该驱动电路有6个工作模态,图2为谐振驱动电路工作模态,图3为RGD主要电压和电流波形。开关管S2、S4在开通时可实现零电压开通(Zero Voltage Switching, ZVS),S1、S3在关断时可实现零电流关断(Zero Current Switching, ZCS)。该驱动电路可有效降低开关损耗,提升系统效率。模态分析如下:
模态1 [t0, t1 :由于变压器一次侧电感续流,开关
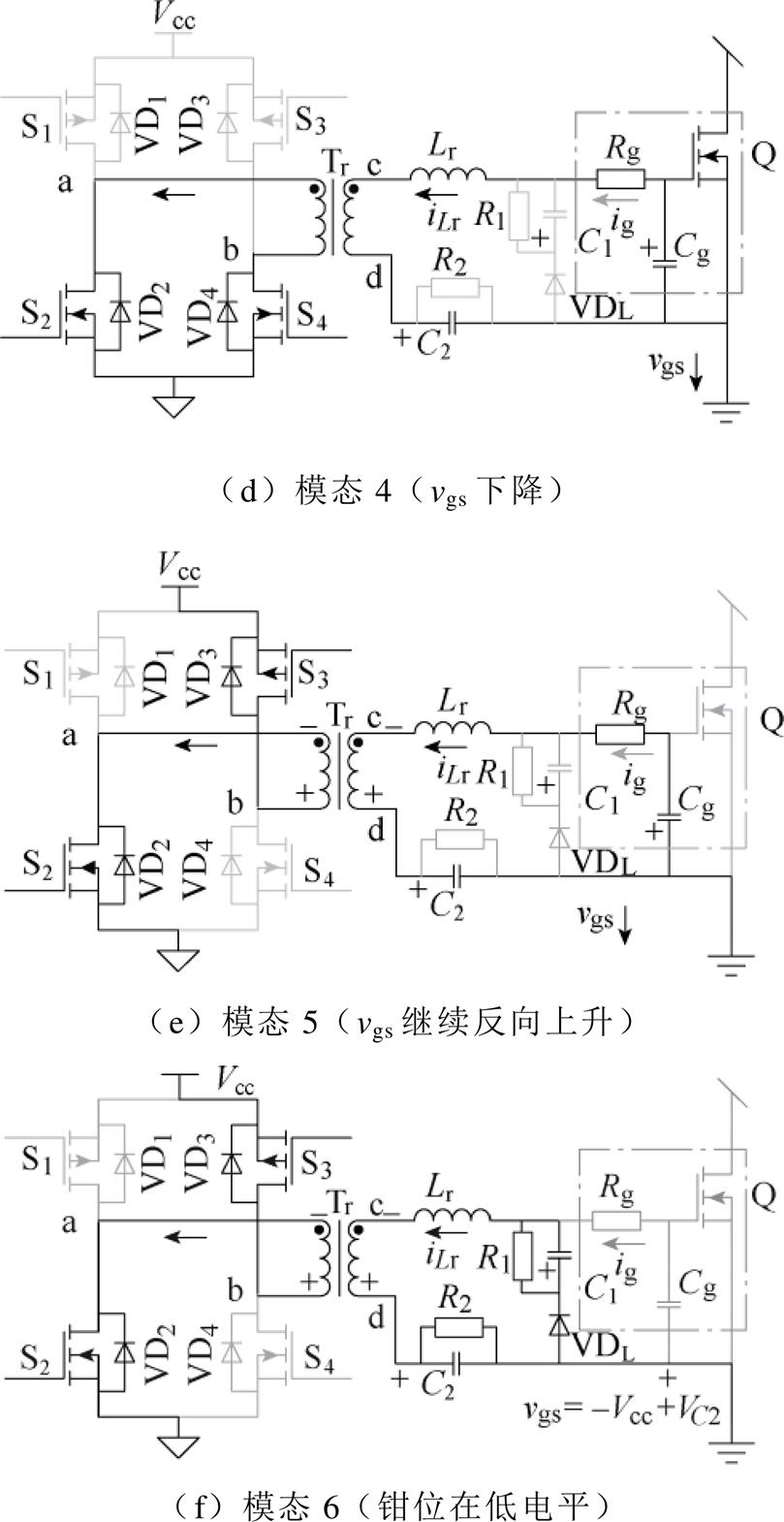
:由于变压器一次侧电感续流,开关 实现ZVS,变压器一次电压近似为零,相应地,二次电压也近似为零。开关管栅源极电容Cg与变压器漏感Lr谐振,谐振电流ig先增大后减小。令电流ig谐振为零时,模态1结束,则开关S1在模态2中可实现ZCS。此时栅源极电压vgs达到最大值,但由于电路中存在寄生电阻,vgs无法达到理想值
实现ZVS,变压器一次电压近似为零,相应地,二次电压也近似为零。开关管栅源极电容Cg与变压器漏感Lr谐振,谐振电流ig先增大后减小。令电流ig谐振为零时,模态1结束,则开关S1在模态2中可实现ZCS。此时栅源极电压vgs达到最大值,但由于电路中存在寄生电阻,vgs无法达到理想值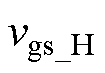 。在模态2中,Vcc将继续对栅源极电容Cg充电。
。在模态2中,Vcc将继续对栅源极电容Cg充电。
模态2 [t1, t2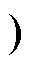 :在t1时刻,开关S4实现ZCS,开关S1、S4导通,变压器漏感Lr与电容Cg继续谐振,栅源极电压达到理想值
:在t1时刻,开关S4实现ZCS,开关S1、S4导通,变压器漏感Lr与电容Cg继续谐振,栅源极电压达到理想值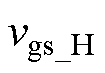 ,其表达式为
,其表达式为
其中
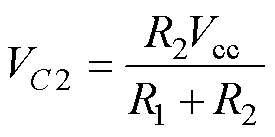
模态3 [t2, t3 :该阶段中,开关管Q的栅源极电压保持为高电平
:该阶段中,开关管Q的栅源极电压保持为高电平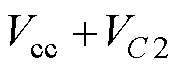 ,栅源极充电电流始终为零。
,栅源极充电电流始终为零。
模态4 [t3, t4 :t3时刻,开关S1关断,变压器一次电流方向改变,开关S2的体二极管VD2续流,S2实现ZVS。变压器一次电压及二次电压再次为零。电容Cg与漏感Lr谐振放电,电感电流
:t3时刻,开关S1关断,变压器一次电流方向改变,开关S2的体二极管VD2续流,S2实现ZVS。变压器一次电压及二次电压再次为零。电容Cg与漏感Lr谐振放电,电感电流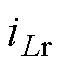 方向改变,二极管VDL仍然截止。当谐振电流
方向改变,二极管VDL仍然截止。当谐振电流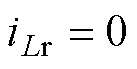 时,进入模态5。
时,进入模态5。
模态5 [t4, t5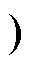 :t4时刻,开关
:t4时刻,开关 实现ZCS,开关
实现ZCS,开关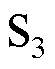 实现ZVS,变压器一次电压方向发生改变,
实现ZVS,变压器一次电压方向发生改变,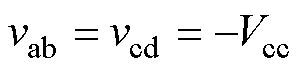 。此时电容Cg电压反向增大,直至满足二极管VDL的导通条件。开关管Q的关断电压可表示为
。此时电容Cg电压反向增大,直至满足二极管VDL的导通条件。开关管Q的关断电压可表示为
模态6 [t5, 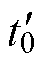 ]:当栅源极电容
]:当栅源极电容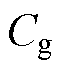 完成放电后,
完成放电后,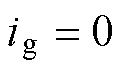 ,栅源极电压保持
,栅源极电压保持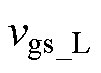 不变。谐振电感
不变。谐振电感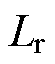 通过
通过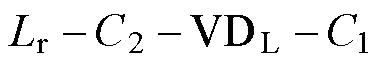 续流,直至开关S4的驱动信号到来。
续流,直至开关S4的驱动信号到来。
2 谐振电感设计
谐振电感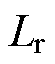 的大小直接决定着驱动电路的充电电流和开关速度。在第1节工作模态的分析中,谐振电感处于一个临界值,即充电电流ig谐振至0时,模态1结束。但实际上谐振电感的大小会影响谐振网络的工作状态和S1~S4的软开关情况,进一步影响驱动电路的损耗。因此,在满足谐振条件的情况下,谐振电感的选择应综合考虑开关速度、系统损耗等问题。
的大小直接决定着驱动电路的充电电流和开关速度。在第1节工作模态的分析中,谐振电感处于一个临界值,即充电电流ig谐振至0时,模态1结束。但实际上谐振电感的大小会影响谐振网络的工作状态和S1~S4的软开关情况,进一步影响驱动电路的损耗。因此,在满足谐振条件的情况下,谐振电感的选择应综合考虑开关速度、系统损耗等问题。
2.1 谐振条件
考虑变压器阻抗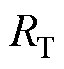 、四个开关管的导通电阻
、四个开关管的导通电阻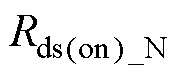 、
、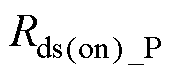 和开关管Q寄生电阻Rg,将谐振回路等效为RLC谐振,即其电压电流波形为非标准正弦波。谐振回路中等效电阻为
和开关管Q寄生电阻Rg,将谐振回路等效为RLC谐振,即其电压电流波形为非标准正弦波。谐振回路中等效电阻为
谐振回路需处于欠阻尼状态,谐振电感最小值可表示为
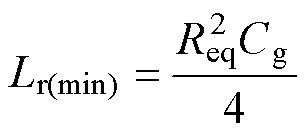 (4)
(4)
式中,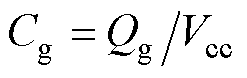 ,
,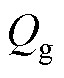 为栅源极总电荷。
为栅源极总电荷。
2.2 临界电感
定义当充电电流ig谐振为0时,开关管栅源极电压vgs谐振至最大值的电感值为临界电感,此时开关S1、S3可以实现ZCS。设计栅极电压的上升/下降时间占整个周期的2%,即
式中,Td为固有振荡周期;Ts为开关周期。
根据式(5),即可求得谐振电感的临界值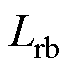 。
。
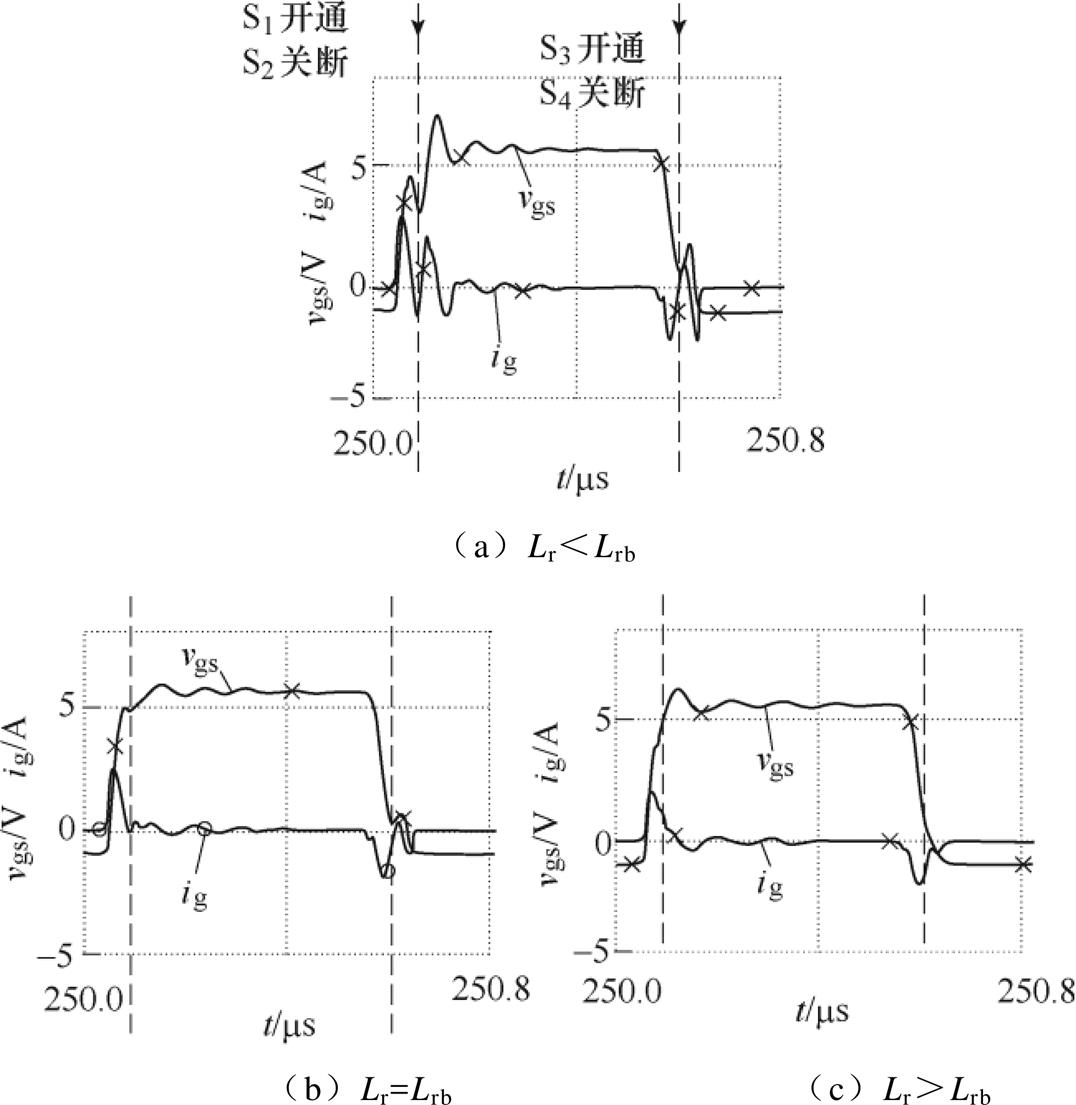
图4所示为不同谐振电感下驱动电压电流波形。以开通过程为例,当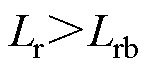 时,模态1结束时
时,模态1结束时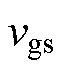 还未升至最大值,此时
还未升至最大值,此时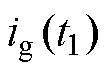 为正,开关管S1硬开通;当
为正,开关管S1硬开通;当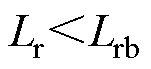 时,
时,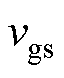 在模态1结束之前已达到最大值,模态1结束时电流
在模态1结束之前已达到最大值,模态1结束时电流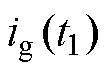 方向发生改变,开关管S1的体二极管在死区时间内续流,开关管S1实现ZVS。考虑驱动电路的效率,尽可能使更多的开关管工作于软开关状态,谐振电感的取值范围为
方向发生改变,开关管S1的体二极管在死区时间内续流,开关管S1实现ZVS。考虑驱动电路的效率,尽可能使更多的开关管工作于软开关状态,谐振电感的取值范围为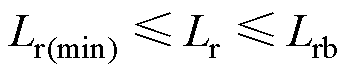 。
。
2.3 防止误动作条件
由图4a可知,当谐振电感过小时,在关断过程中,开关S3无法在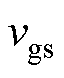 谐振降至最小值之前开通,此时
谐振降至最小值之前开通,此时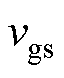 继续上升,若超过开关管的开通阈值
继续上升,若超过开关管的开通阈值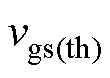 ,将导致误导通;同样,过小的谐振电感在开通过程中也会导致开关误关断。为避免上述现象的出现,在t1、t4时刻栅源极电压需分别满足
,将导致误导通;同样,过小的谐振电感在开通过程中也会导致开关误关断。为避免上述现象的出现,在t1、t4时刻栅源极电压需分别满足
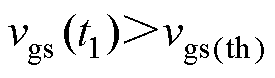 (7)
(7)
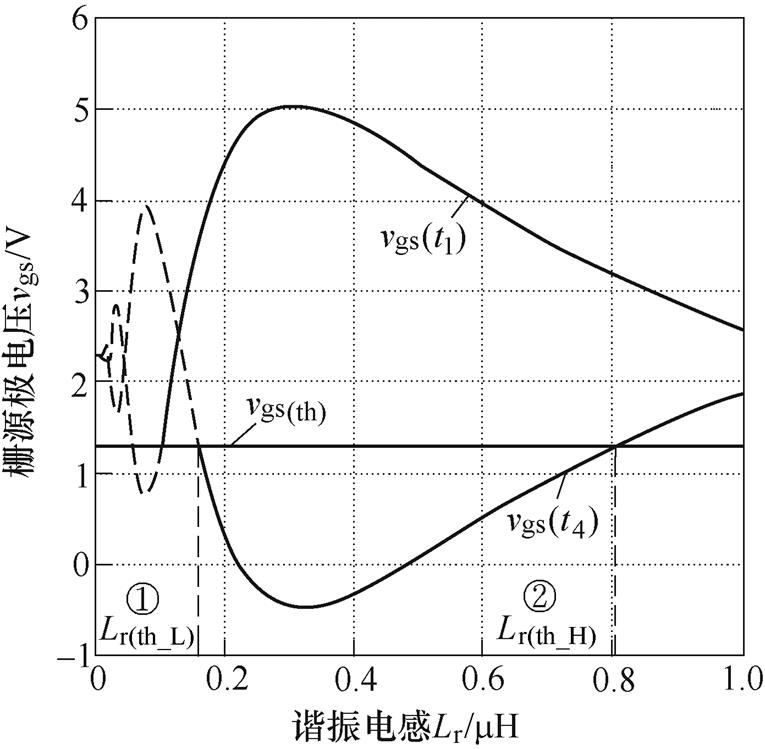
图5为t1、t4时刻栅源极电压与谐振电感的关系曲线。图中,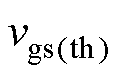 为待驱动开关管的开通阈值电压,
为待驱动开关管的开通阈值电压,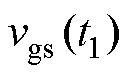 为t1时刻,即开通过程曲线,
为t1时刻,即开通过程曲线,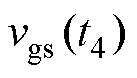 为t4时刻,即关断过程曲线。对比t1、t4时刻栅源极电压与开关管的开通阈值,实线部分表示可以正常开通/关断。由图可知,t4时刻,为防止误导通,则对电感值的要求更高,定义满足
为t4时刻,即关断过程曲线。对比t1、t4时刻栅源极电压与开关管的开通阈值,实线部分表示可以正常开通/关断。由图可知,t4时刻,为防止误导通,则对电感值的要求更高,定义满足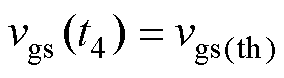 的两个谐振电感值分别为
的两个谐振电感值分别为 和
和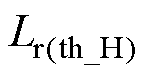 。由此,综合考虑开通和关断两个阶段,谐振电感需满足
。由此,综合考虑开通和关断两个阶段,谐振电感需满足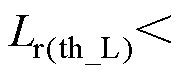
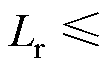
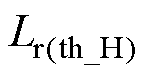 。
。
综合上述分析,谐振电感的大小需满足谐振条件、临界电感条件及防止误动作条件三个条件。当开关频率为1MHz时,选用驱动电路元器件参数见表1,临界电感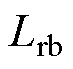 =0.28mH,谐振电感需满足
=0.28mH,谐振电感需满足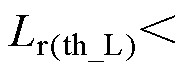
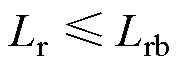 。在高频条件下,电路中的寄生参数特别是谐振电感会直接影响驱动电路工作状态,使设计的谐振网络偏离临界工作状态,造成额外的损耗。因此在PCB布局时需要注意减小Lr支路以及地线上的寄生电感。
。在高频条件下,电路中的寄生参数特别是谐振电感会直接影响驱动电路工作状态,使设计的谐振网络偏离临界工作状态,造成额外的损耗。因此在PCB布局时需要注意减小Lr支路以及地线上的寄生电感。
表1 驱动电路元器件参数
Tab.1 The parameters of the proposed RGD

参 数数值(型号) S1~S4DMC3016LSD QGS66108T R1/kW12 R2/kW100 C1, C2/mF4.7
3 驱动电路损耗分析
本文所提出的谐振式栅极驱动电路的损耗主要包含传导损耗、开关损耗、栅极驱动损耗、输出电容损耗和移位电路损耗五个部分。
(1)传导损耗。由2.1节分析可知,栅极充放电回路工作于欠阻尼状态,在模态1结束时栅源极电压无法达到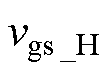 ,在模态2中
,在模态2中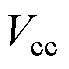 继续为栅极电容充电,使栅源极电压达到理论值。由于本文设计的驱动电路有两组二次侧,开通和关断过程中的传导损耗
继续为栅极电容充电,使栅源极电压达到理论值。由于本文设计的驱动电路有两组二次侧,开通和关断过程中的传导损耗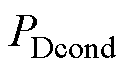 可表示为
可表示为
式中,fs为开关频率;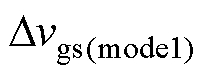 为t1时刻栅源极实际电压与理论值
为t1时刻栅源极实际电压与理论值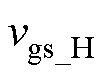 的差值;
的差值; 为t4时刻栅源极实际电压与理论值
为t4时刻栅源极实际电压与理论值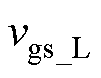 差值。具体表达式见附录式(A3)和式(A4)。
差值。具体表达式见附录式(A3)和式(A4)。
(2)开关损耗。本文设计的谐振驱动电路,由于变压器的存在,可近似视开关管开通/关断时一次侧流过的电流为零;由2.2节分析可知,当谐振电感为临界值时,电路中所有开关管均工作于软开关状态,开关损耗近似为零;当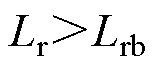 时,S2、S4硬关断,S1、S3硬开通;当
时,S2、S4硬关断,S1、S3硬开通;当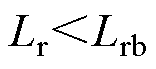 时,S1、S3实现ZVS,S2、S4仍然硬关断。因此,当
时,S1、S3实现ZVS,S2、S4仍然硬关断。因此,当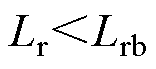 及
及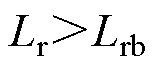 时,开关损耗可表示为
时,开关损耗可表示为
式中,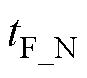 和
和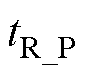 分别为S1的关断时间及S2的开通时间;
分别为S1的关断时间及S2的开通时间;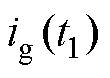 为t1时刻的栅极充电电流,有
为t1时刻的栅极充电电流,有
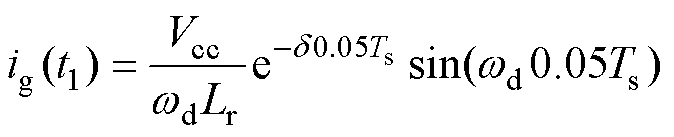 (10)
(10)
式中,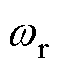 为谐振角频率,
为谐振角频率,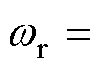
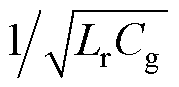 ;
;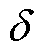 为衰减系数,
为衰减系数,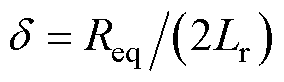 ;
;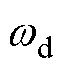 为固有振荡角频率,
为固有振荡角频率,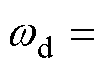
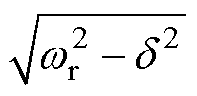 。
。
(3)S1~S4栅极驱动损耗。开关管S1~S4的驱动信号由DSP提供,驱动电压为Vcc。驱动损耗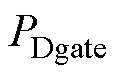 可表示为
可表示为
式中,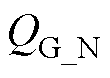 、
、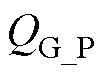 分别为S1和S2的栅极电荷。
分别为S1和S2的栅极电荷。
(4)输出电容损耗。开关管S1~S4存在漏源极寄生电容Coss,充放电过程中会产生相应的损耗,其表达式为
式中,Coss_N和Coss_P分别为S1及S2的寄生电容。
(5)移位电路损耗。为了使驱动电路的开通、关断电压与所驱动开关管相匹配,增加了电平移位电路。移位电阻R1、R2上的损耗可表示为
由于R1、R2电阻为kW 级,相比于以上四种损耗,这部分损耗可近似忽略。综合上述损耗分析,该谐振栅极驱动电路的总损耗可表示为
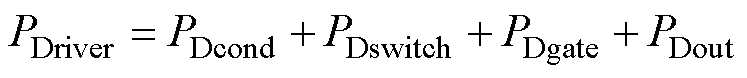 (14)
(14)
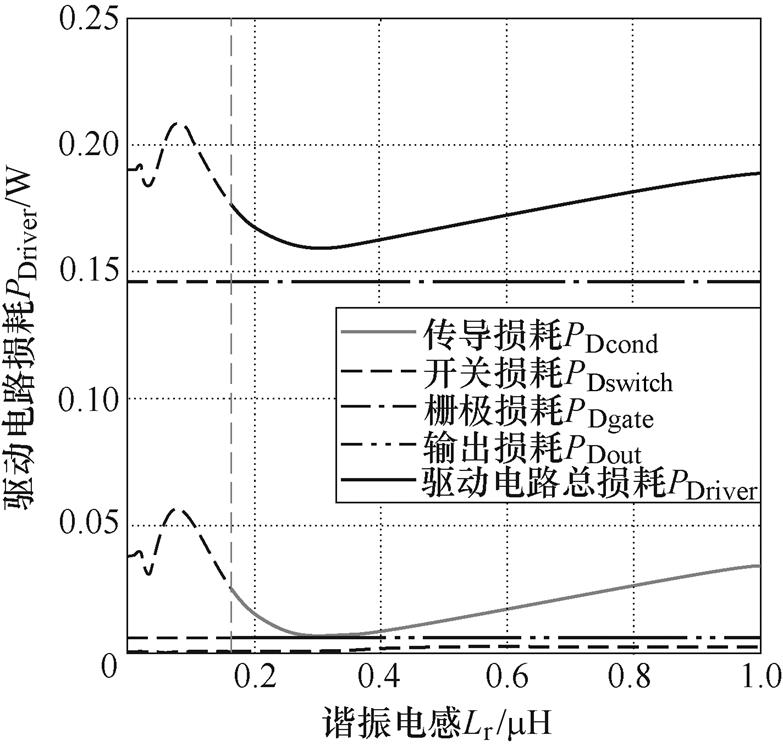
图6所示为驱动电路各部分损耗及总损耗与谐振电感的关系曲线。由图可知,开关管S1~S4的栅极损耗远大于其他各部分损耗,因此,相比于采用两个独立的驱动电路驱动两个开关管,本文设计的方案有效地降低了系统损耗。选用临界值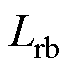 作为谐振电感,此时驱动电路损耗最小,为0.16W。
作为谐振电感,此时驱动电路损耗最小,为0.16W。
相比之下,考虑Si8271芯片的损耗及栅极电阻的损耗,基于驱动芯片的硬驱动电路损耗[15]可表示为
 (15)
(15)
式中,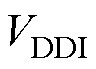 为芯片输入侧供电电压;
为芯片输入侧供电电压;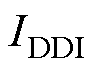 为输入侧的最大偏置电流;
为输入侧的最大偏置电流;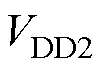 为输出侧驱动电压最大值与最小值之差;
为输出侧驱动电压最大值与最小值之差;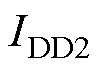 为输出侧的最大偏置电流;
为输出侧的最大偏置电流;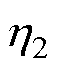 为隔离电源B0509XT的效率;
为隔离电源B0509XT的效率;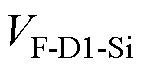 为驱动电路快速恢复二极管VD1-Si的正向压降;
为驱动电路快速恢复二极管VD1-Si的正向压降;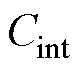 为芯片内部寄生电容。以隔离型驱动芯片Si8271为例,系统中两个开关管所需驱动电路的总损耗为
为芯片内部寄生电容。以隔离型驱动芯片Si8271为例,系统中两个开关管所需驱动电路的总损耗为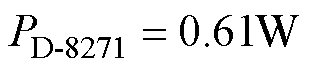 。相比于基于驱动芯片的硬驱动电路,本文所提出谐振型驱动电路损耗可减小73.8%。同时由于不存在栅极电阻,可以提高开关速度,进而减小开关器件的开关损耗,从而进一步提高变换器的效率。
。相比于基于驱动芯片的硬驱动电路,本文所提出谐振型驱动电路损耗可减小73.8%。同时由于不存在栅极电阻,可以提高开关速度,进而减小开关器件的开关损耗,从而进一步提高变换器的效率。
4 实验结果
基于上述分析,本文设计了针对GaN器件具有非对称电压及两组同步驱动信号的1MHz谐振驱动电路,用以驱动文献[14]中提出的高电压增益非耦合电感Sepic变换器。实验测得驱动电路损耗为0.18W。
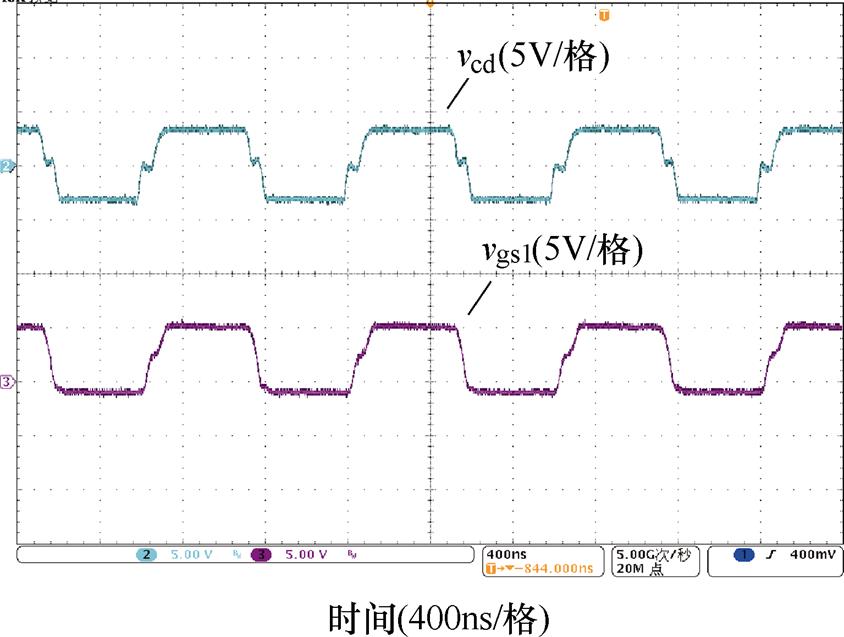
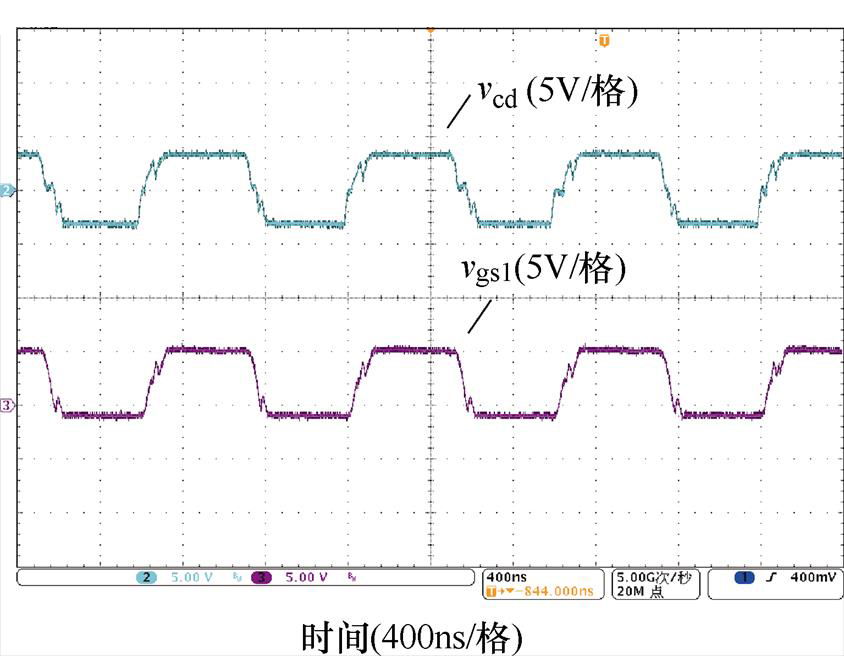
图7所示为开关管S1、S4的驱动电压信号,二者间的死区时间决定了模态1的时间。在不同工作状态下,S1~S4的驱动信号不会发生变化。图8~图10分别为Lr=Lrb、Lr<Lrb、Lr>Lrb三种不同情况下c、d两点间电压信号及一路输出驱动信号。利用电平移位电路,开通电压和关断电压分别为+5.3V和-1.3V。实验结果与仿真结果相一致。
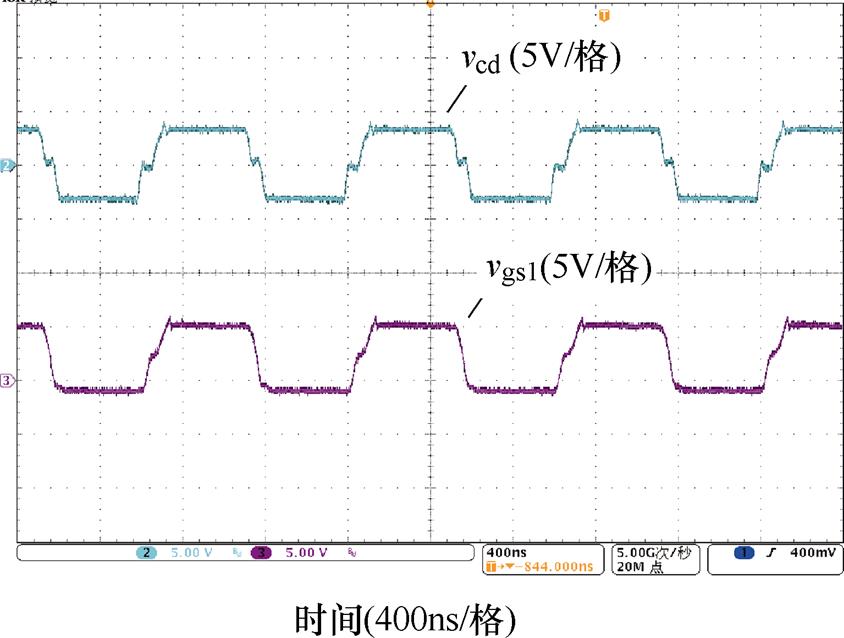
图11所示为GaN驱动信号及其相应的漏源极电压信号。由图可知,当开关管连接到主功率电路时,在关断过程中会产生高频振荡,由于关断电压为负电平,振荡的最大值被抑制到1V以下,有效地避免了误导通。
图12所示为驱动电路样机照片,PCB面积为5cm×2.6cm。
5 结论
本文针对GaN器件提出了一种具有非对称电压和两个同步驱动信号的谐振栅极驱动电路。本文在传统的谐振驱动电路的基础上,增加负电压以确保可靠关断,并采用较小的关断电压以降低损耗。此外,采用具有两组二次侧的变压器来产生两个同步驱动信号,可应用于如开关电感变换器等场合。通过优化谐振电感参数,在1MHz开关频率下,所提出的谐振驱动电路损耗相比于基于驱动芯片的硬驱动电路损耗可减小73.8%。
附 录
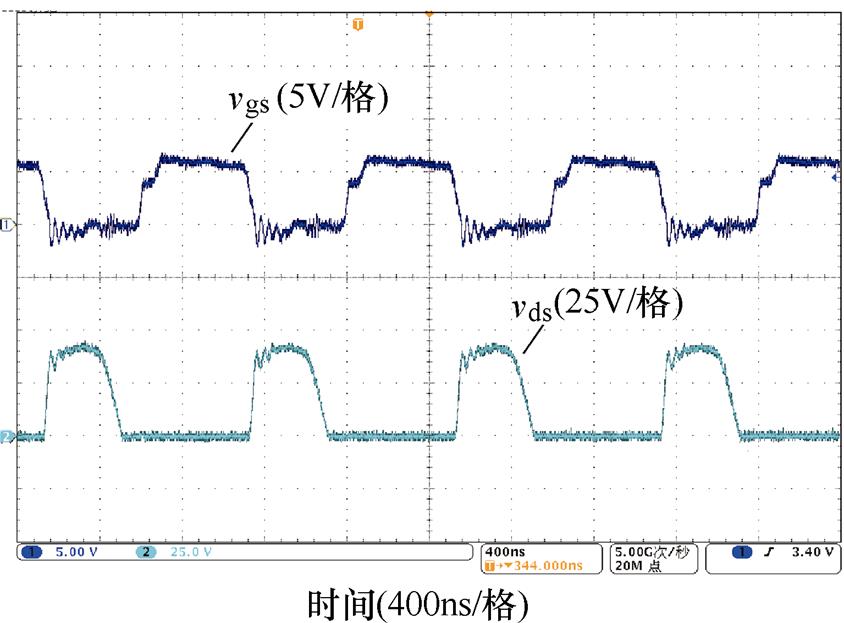
由于谐振回路当中寄生电阻的存在,谐振回路可以近似简化为RLC谐振,其电压电流波形不是标准的正弦波。以充电过程为例,可以将充电回路简化为驱动电路充电过程等效回路如附图1所示。
附图1 驱动电路充电过程等效回路
Fig.App.1 Equivalent circuit of the drive circuit during charing process
欠阻尼振荡条件如式(4)所示,由此可解得模态1和模态4中栅极电压随时间变化的表达式分别为
在栅极充电电流ig谐振至零时,栅源极电压vgs恰好谐振至最大值,即
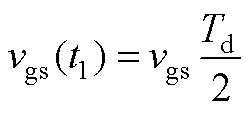 (A2)
(A2)
由于栅极充放电回路中寄生电阻的存在,t1时刻电压无法达到vgs_H,t4时刻电压无法达到vgs_L。定义t1和t4时刻栅源极实际的电压与vgs_H和vgs_L的差值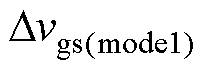 和
和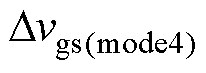 分别为
分别为
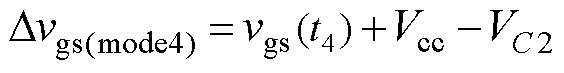 (A4)
(A4)
参考文献
[1] Wu Qunfang, Wang Qin, Zhu Jinyi, et al. Dual- channel push-pull isolated resonant gate driver for high-frequency ZVS full-bridge converters[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4019- 4024.
[2] 赵清林, 崔少威, 袁精, 等. 低压氮化镓器件谐振驱动技术及其反向导通特性[J]. 电工技术学报, 2019, 34(增刊1): 133-140.
Zhao Qinglin, Cui Shaowei, Yuan Jing, et al. Resonant drive technology and reverse conduction characteri- stics of low voltage GaN devices[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 133- 140.
[3] 张建忠, 吴海富, 张雅倩, 等. 一种SiC MOSFET谐振门极驱动电路[J]. 电工技术学报, 2020, 35(16): 3453-3459.
Zhang Jianzhong, Wu Haifu, Zhang Yaqian, et al. A resonant gate driver for SiC MOSFET[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(16): 3453-3459.
[4] 刘教民, 李建文, 崔玉龙, 等, 高频谐振逆变器的功率MOSFET管驱动电路[J]. 电工技术学报, 2011, 26(5): 113-118.
Liu Jiaomin, Li Jianwen, Cui Yulong, et al. Power MOSFET gate driver of the high frequency resonant inverter[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 113-118.
[5] Sun Bainan, Zhang Zhe, Andersen M A E. A com- parison review of the resonant gate driver in the silicon MOSFET and the GaN transistor application[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7776-7786.
[6] 高珊珊, 王懿杰, 徐殿国. 一种高频高升压比改进型Sepic变换器[J]. 电工技术学报, 2019, 34(16): 3366-3372.
Gao Shanshan, Wang Yijie, Xu Dianguo. A high frequency high voltage gain modified Sepic con- verter[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3366-3372.
[7] 刘佳斌, 肖曦, 梅红伟. 基于GaN-HEMT器件的双有源桥DC-DC变换器的软开关分析[J]. 电工技术学报, 2019, 34(增刊2): 534-542.
Liu Jiabin, Xiao Xi, Mei Hongwei. Soft switching analysis of dual active bridge DC-DC converter based on GaN-HEMT device[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 534-542.
[8] 李舒成, 刘邦银, 姜庆, 等. 基于同步PWM控制的双向CLLLC谐振型直流变换器运行特性分析[J]. 电工技术学报, 2019, 34(增刊2): 543-552.
Li Shucheng, Liu Bangyin, Jiang Qing, et al. Per- formance analysis of bidirectional CLLLC resonant converter with synchronous PWM control strategy[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 543-552.
[9] 肖龙, 伍梁, 李新, 等. 高频LLC变换器平面磁集成矩阵变压器的优化设计[J]. 电工技术学报, 2020, 35(4): 758-766.
Xiao Long, Wu Liang, Li Xin, et al. Optimal design of planar magnetic integrated matrix transformer for high frequency LLC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 758- 766.
[10] 管乐诗, 施震宇, 王懿杰, 等. 基于Class E谐振电路的隔离型高频DC-DC变换器[J].电工技术学报, 2020, 35(22): 4750-4760.
Guan Yueshi, Shi Zhenyu, Wang Yijie, et al. An isolated high frequency DC-DC converter based on Class E resonant circuit[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4750-4760.
[11] 金林, 张波. 一种开关电感型准开关升压变换器[J].电源学报, 2019, 17(2): 63-71.
Jin Lin, Zhang Bo. Quasi-switched boost converter with switched-inductor[J]. Journal of Power Supply, 2019, 17(2): 63-71.
[12] 侯世英, 冯斌, 颜文森, 等. 基于有源开关电感网络和DCM单元组的DC-DC升压变换器[J]. 电机与控制学报, 2017, 21(7): 20-28.
Hou Shiying, Feng Bin, Yan Wensen, et al. Step-up DC-DC converter based on active switched-inductor network and diode-capacitor multipliers[J]. Electric Machines and Control, 2017, 21(7): 20-28.
[13] 苏冰, 王玉斌, 王璠, 等. 基于耦合电感的多相交错并联双向DC-DC变换器及其均流控制[J]. 电工技术学报, 2020, 35(20): 4336-4349.
Su Bing, Wang Yubin, Wang Fan, et al. Multi-phase interleaved bidirectional DC-DC converter with coupled inductors and current sharing control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4336-4349.
[14] Ansari S A, Moghani J S. A novel high voltage gain noncoupled inductor SEPIC converter[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(9): 7099- 7108.
[15] https://www.silabs.com/documents/public/data-sheets/ Si827x.pdf[Z].
Resonant Gate Driver with Asymmetrical Voltage and Two Synchronous Drive Signals for GaN Switches
Gao Shanshan Wang Yijie Liu Yining Xu Dianguo
(Department of Electrical Engineering Harbin Institute of Technology Harbin 150001 China)
Abstract Commercial gallium nitride (GaN) switches are widely used in power electronic converters recently years due to their advantages such as fast switching speed and low turn-on resistance. Accordingly, resonant gate drivers are adopted to reduce drive loss in high frequency and low power applications. However, different from Si switches, the turn-on threshold voltage of GaN switches is quite low and GaN switches have no body diode, which causes large reverse voltage drop. Therefore, traditional resonant gate drivers are not suitable for GaN switches. In order to solve the drive signal oscillation caused by parasitic parameters in high frequency applications, a resonant gate driver with asymmetrical voltage is proposed in this paper. Besides, for applications that require two synchronous switches, such as switch inductor converters, a transformer with two groups of secondary sides is added. The working principles are presented and parameters are optimized for lower loss. A 1MHz prototype is designed for experimental verification. The experimental results are in good agreement with the theoretical analysis.
keywords:GaN, resonant gate driver, resonant inductor, loss analysis
DOI: 10.19595/j.cnki.1000-6753.tces.L90138
中图分类号:TM46
作者简介
高珊珊 女,1992年生,博士研究生,研究方向为高频功率变换器。E-mail: gaoshanshanhit@163.com
王懿杰 男,1982年生,教授,博士生导师,研究方向为高频、超高频功率变换器及无线电能传输技术。E-mail: wangyijie@hit.edu.cn(通信作者)
收稿日期 2020-06-30
改稿日期 2021-01-20
国家自然科学基金资助项目(51777038)。
(编辑 陈 诚)
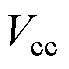 =3.3V,变压器有两个二次侧,一次、二次侧匝比为1
=3.3V,变压器有两个二次侧,一次、二次侧匝比为1 1
1 1。图中,Lr为变压器二次侧漏感,电容C1、C2,电阻R1、R2以及二极管VDL为增加的电平移位电路,Cg为待驱动开关管Q的寄生电容,Rg为待驱动开关管Q的导通电阻。S1~S4为驱动电路所需的开关管,VD1~VD4为S1~S4的体二极管。变压器可实现一次、二次侧的隔离以及两路同步信号的输出。相比于传统方案,减少了一组全桥电路,电路结构更加简单同时损耗也相应减小。通过变压器二次侧的漏感Lr与开关管的寄生电容Cg谐振,取消了抑制振荡的栅极电阻,可提升开关速度并且降低损耗。同时增加电平移位电路以调节驱动电压偏置,使驱动信号的电压满足开关器件的要求。
1。图中,Lr为变压器二次侧漏感,电容C1、C2,电阻R1、R2以及二极管VDL为增加的电平移位电路,Cg为待驱动开关管Q的寄生电容,Rg为待驱动开关管Q的导通电阻。S1~S4为驱动电路所需的开关管,VD1~VD4为S1~S4的体二极管。变压器可实现一次、二次侧的隔离以及两路同步信号的输出。相比于传统方案,减少了一组全桥电路,电路结构更加简单同时损耗也相应减小。通过变压器二次侧的漏感Lr与开关管的寄生电容Cg谐振,取消了抑制振荡的栅极电阻,可提升开关速度并且降低损耗。同时增加电平移位电路以调节驱动电压偏置,使驱动信号的电压满足开关器件的要求。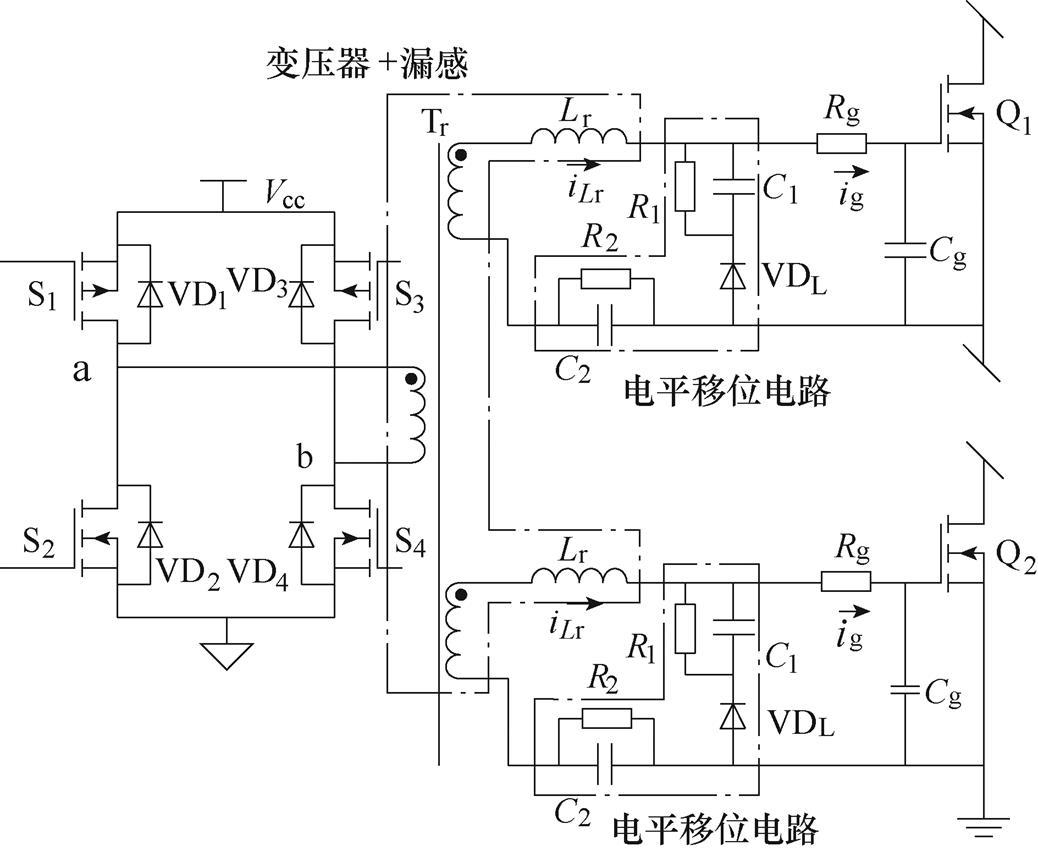
 :由于变压器一次侧电感续流,开关
:由于变压器一次侧电感续流,开关 实现ZVS,变压器一次电压近似为零,相应地,二次电压也近似为零。开关管栅源极电容C
实现ZVS,变压器一次电压近似为零,相应地,二次电压也近似为零。开关管栅源极电容C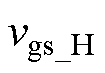 。在模态2中,V
。在模态2中,V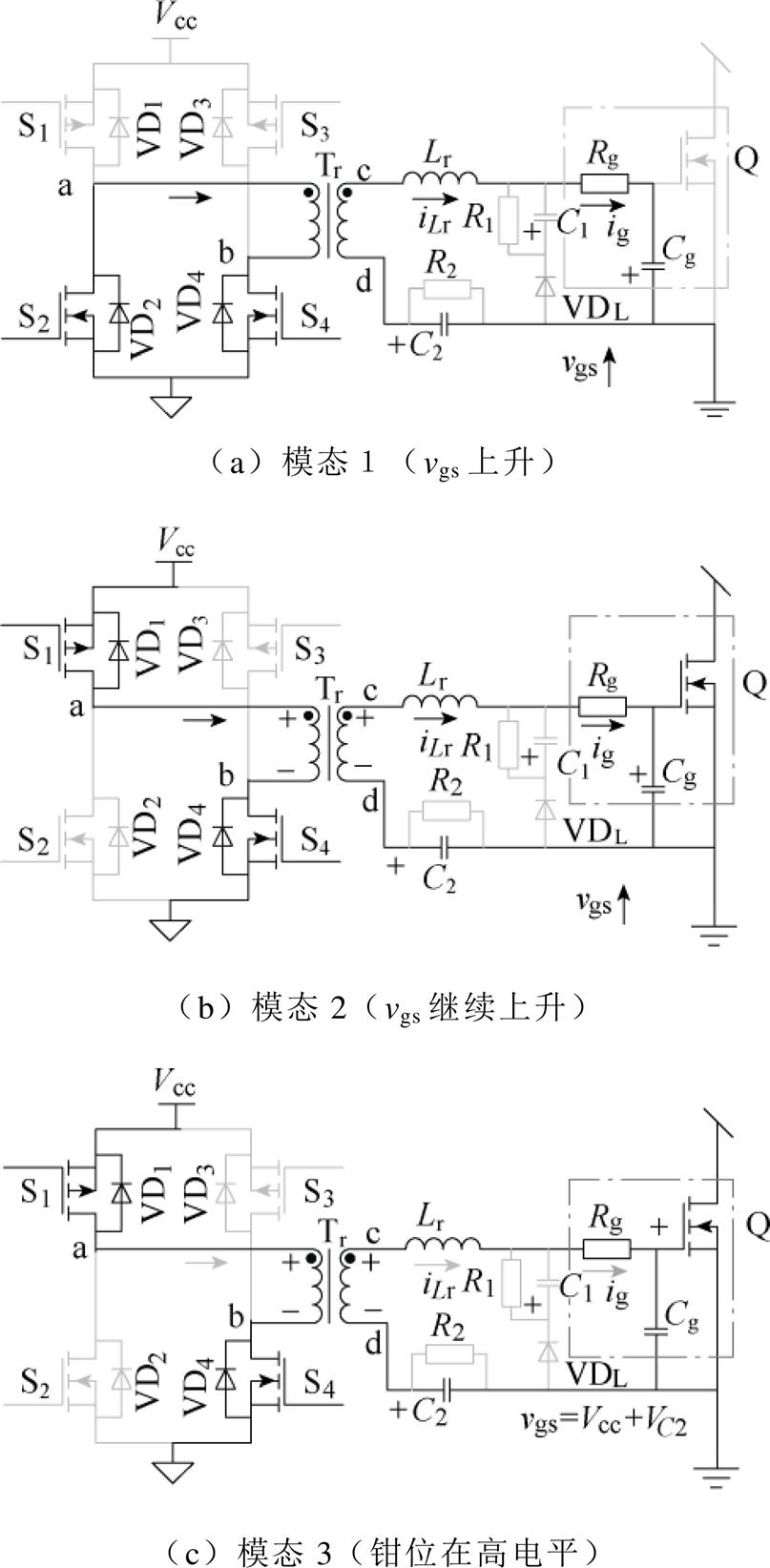

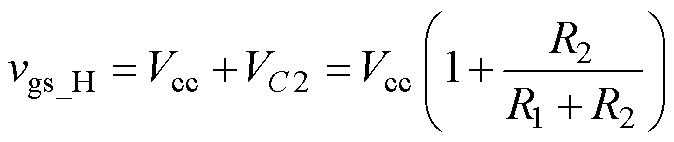 (1)
(1)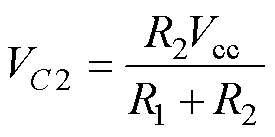
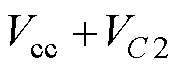 ,栅源极充电电流始终为零。
,栅源极充电电流始终为零。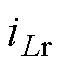 方向改变,二极管VD
方向改变,二极管VD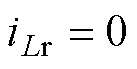 时,进入模态5。
时,进入模态5。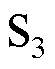 实现ZVS,变压器一次电压方向发生改变,
实现ZVS,变压器一次电压方向发生改变,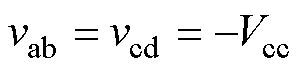 。此时电容C
。此时电容C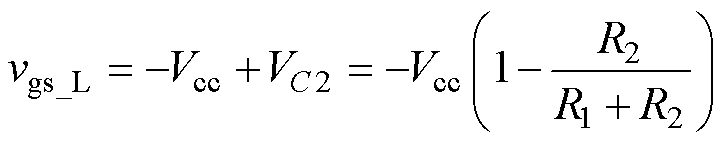 (2)
(2)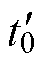 ]:当栅源极电容
]:当栅源极电容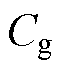 完成放电后,
完成放电后,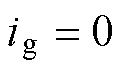 ,栅源极电压保持
,栅源极电压保持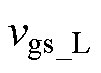 不变。谐振电感
不变。谐振电感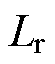 通过
通过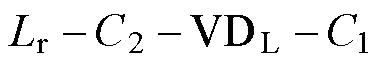 续流,直至开关S
续流,直至开关S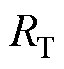 、四个开关管的导通电阻
、四个开关管的导通电阻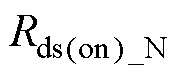 、
、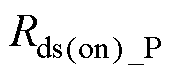 和开关管Q寄生电阻R
和开关管Q寄生电阻R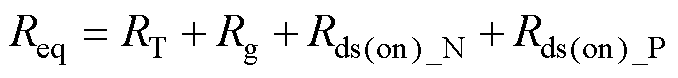 (3)
(3)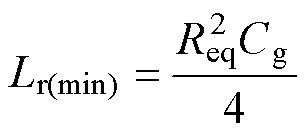 (4)
(4)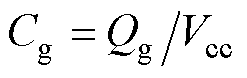 ,
,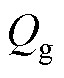 为栅源极总电荷。
为栅源极总电荷。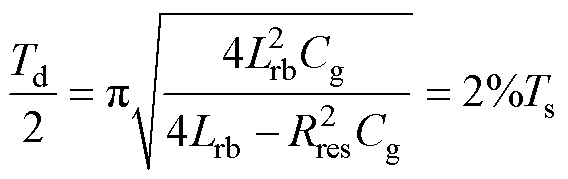 (5)
(5)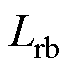 。
。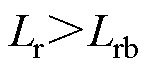 时,模态1结束时
时,模态1结束时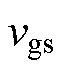 还未升至最大值,此时
还未升至最大值,此时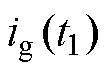 为正,开关管S
为正,开关管S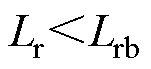 时,
时,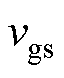 在模态1结束之前已达到最大值,模态1结束时电流
在模态1结束之前已达到最大值,模态1结束时电流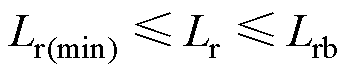 。
。
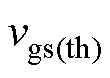 ,将导致误导通;同样,过小的谐振电感在开通过程中也会导致开关误关断。为避免上述现象的出现,在t
,将导致误导通;同样,过小的谐振电感在开通过程中也会导致开关误关断。为避免上述现象的出现,在t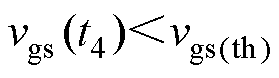 (6)
(6)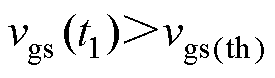 (7)
(7)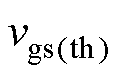 为待驱动开关管的开通阈值电压,
为待驱动开关管的开通阈值电压,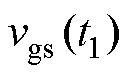 为t
为t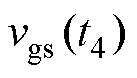 为t
为t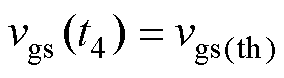 的两个谐振电感值分别为
的两个谐振电感值分别为 和
和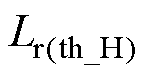 。由此,综合考虑开通和关断两个阶段,谐振电感需满足
。由此,综合考虑开通和关断两个阶段,谐振电感需满足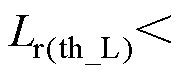
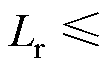
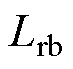 =0.28
=0.28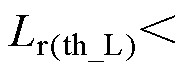
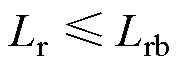 。在高频条件下,电路中的寄生参数特别是谐振电感会直接影响驱动电路工作状态,使设计的谐振网络偏离临界工作状态,造成额外的损耗。因此在PCB布局时需要注意减小L
。在高频条件下,电路中的寄生参数特别是谐振电感会直接影响驱动电路工作状态,使设计的谐振网络偏离临界工作状态,造成额外的损耗。因此在PCB布局时需要注意减小L
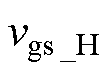 ,在模态2中
,在模态2中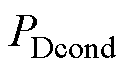 可表示为
可表示为 (8)
(8)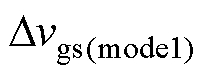 为t
为t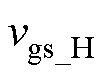 的差值;
的差值; 为t
为t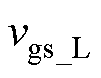 差值。具体表达式见附录式(A3)和式(A4)。
差值。具体表达式见附录式(A3)和式(A4)。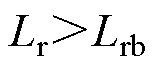 时,S
时,S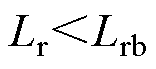 时,S
时,S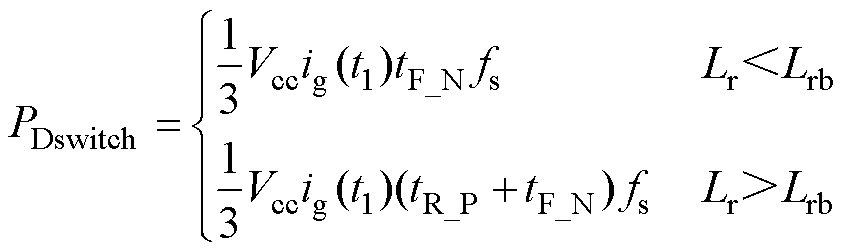 (9)
(9)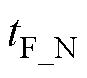 和
和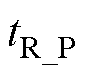 分别为S
分别为S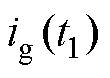 为t
为t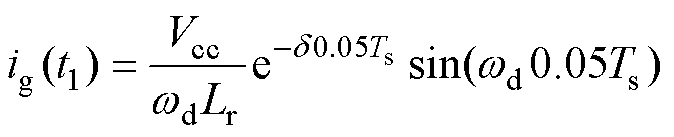 (10)
(10)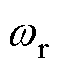 为谐振角频率,
为谐振角频率,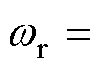
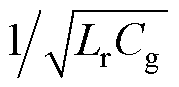 ;
;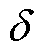 为衰减系数,
为衰减系数,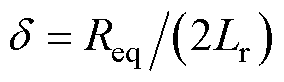 ;
;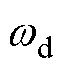 为固有振荡角频率,
为固有振荡角频率,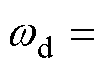
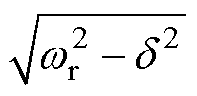 。
。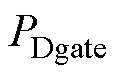 可表示为
可表示为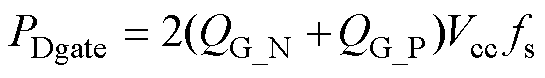 (11)
(11)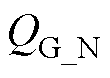 、
、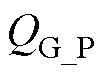 分别为S
分别为S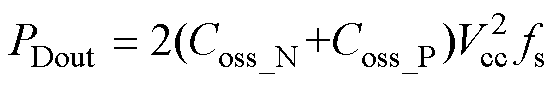 (12)
(12)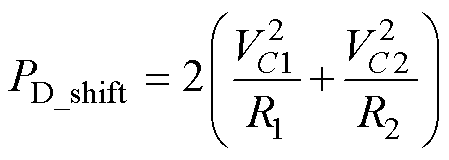 (13)
(13)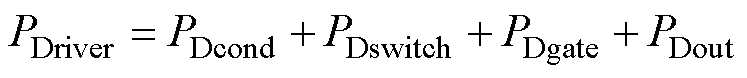 (14)
(14)
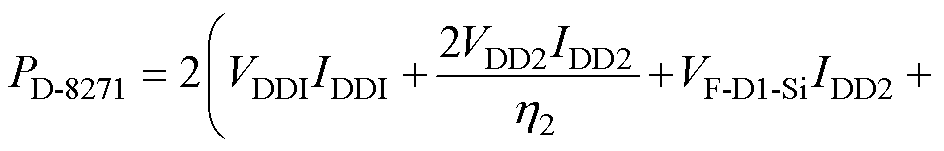
 (15)
(15)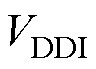 为芯片输入侧供电电压;
为芯片输入侧供电电压;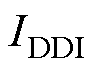 为输入侧的最大偏置电流;
为输入侧的最大偏置电流;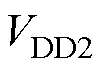 为输出侧驱动电压最大值与最小值之差;
为输出侧驱动电压最大值与最小值之差;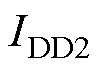 为输出侧的最大偏置电流;
为输出侧的最大偏置电流;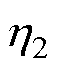 为隔离电源B0509XT的效率;
为隔离电源B0509XT的效率;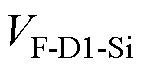 为驱动电路快速恢复二极管VD
为驱动电路快速恢复二极管VD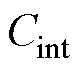 为芯片内部寄生电容。以隔离型驱动芯片Si8271为例,系统中两个开关管所需驱动电路的总损耗为
为芯片内部寄生电容。以隔离型驱动芯片Si8271为例,系统中两个开关管所需驱动电路的总损耗为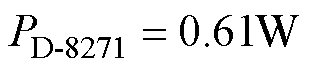 。相比于基于驱动芯片的硬驱动电路,本文所提出谐振型驱动电路损耗可减小73.8%。同时由于不存在栅极电阻,可以提高开关速度,进而减小开关器件的开关损耗,从而进一步提高变换器的效率。
。相比于基于驱动芯片的硬驱动电路,本文所提出谐振型驱动电路损耗可减小73.8%。同时由于不存在栅极电阻,可以提高开关速度,进而减小开关器件的开关损耗,从而进一步提高变换器的效率。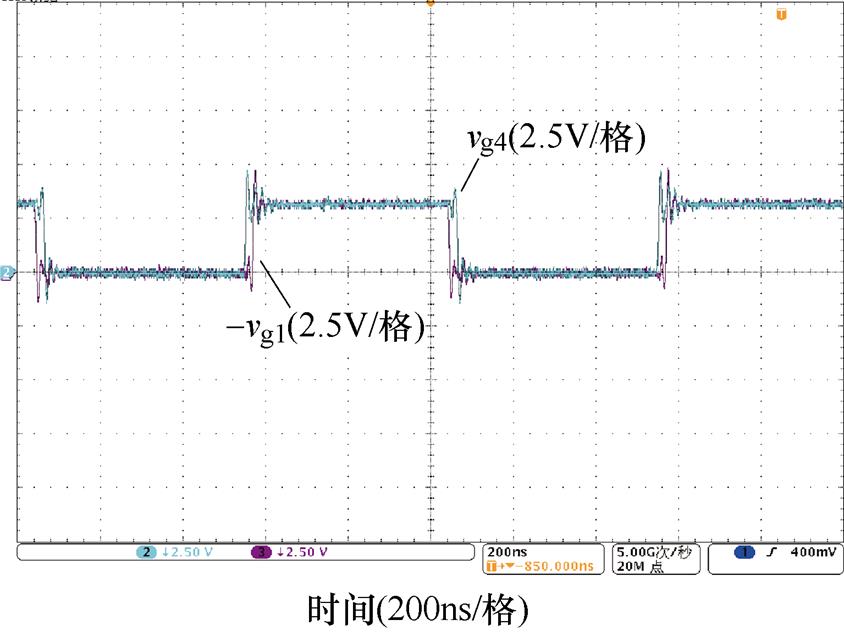
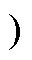

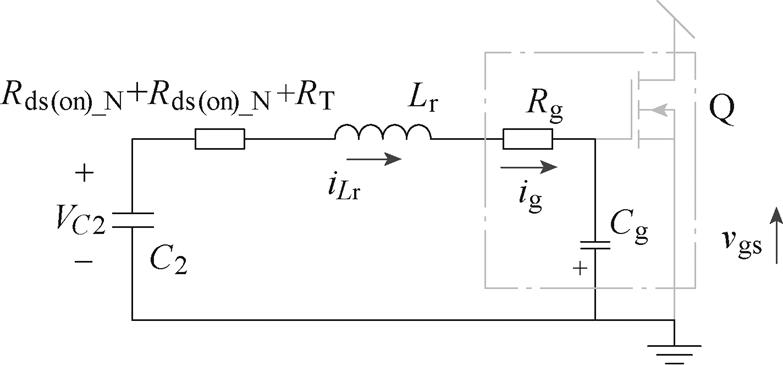
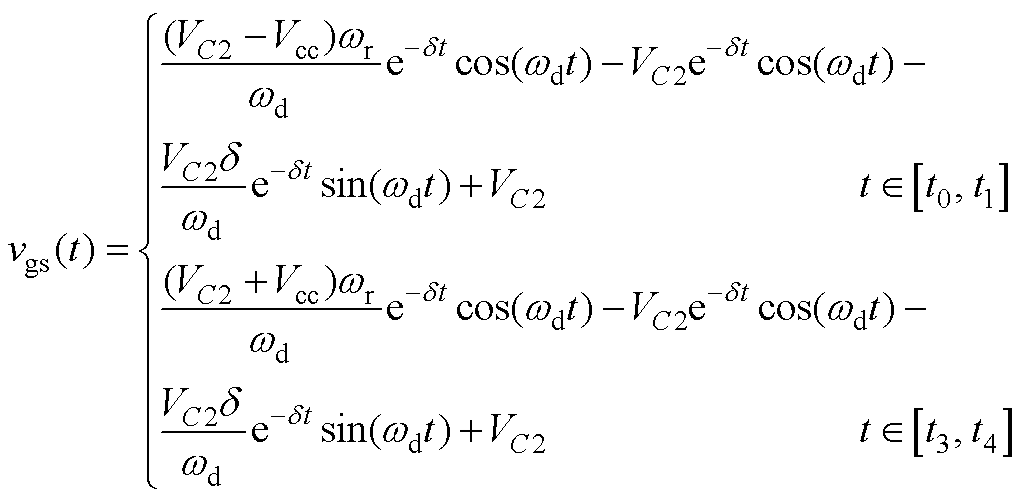 (A1)
(A1)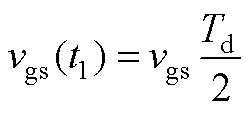 (A2)
(A2)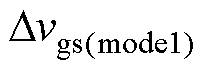 和
和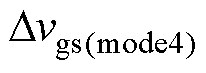 分别为
分别为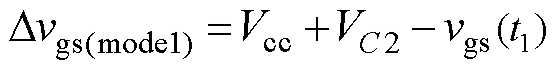 (A3)
(A3)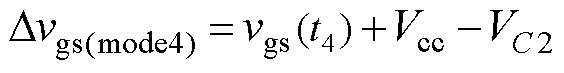 (A4)
(A4)