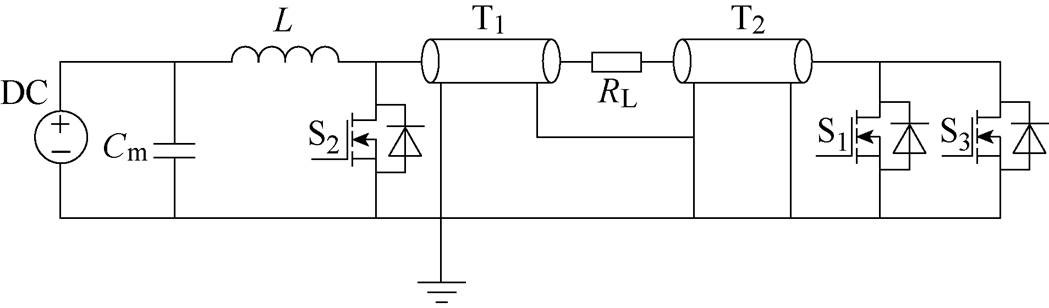
图1 脉冲发生器电路拓扑结构
Fig.1 Topology of Pulse generator circuit
摘要 随着脉冲功率技术在新型粒子加速器、生物细胞实验仪器等领域拓展应用,对脉冲功率发生器高重复频率、短脉冲、脉冲参数灵活可调提出更高的要求。该文研究了一种新型的功率变换模块电路拓扑。这种电路拓扑由LC振荡升压单元和Blumlein形成线单元组成,利用多开关时序逻辑控制实现对输出波形参数的调整,相对于传统Blumlein线在保留其短脉冲成形优点的同时,能获得输出脉冲频率数倍于开关频率,输出电压幅值数倍于直流充电电压,输出脉冲的极性及间隔时间的灵活调整。同时,通过动态电路的时域分析和传输线波过程分析阐述该电路的工作原理,并通过电路仿真加以验证。此外,采用射频MOSFET开关和同轴电缆搭建一台原理样机,在负载匹配时,实现了在开关频率500kHz时输出脉冲频率1MHz、输出脉冲电压幅值4倍于直流电源电压20ns的短脉冲。
关键词:纳秒脉冲发生器 LC振荡电路 Blumlein脉冲形成线 半导体开关
长期以来,热核聚变研究、强光光源、电磁成形[1-2]等大型科学工程应用是推动脉冲功率技术发展的主要因素。这些大型装置往往追求瞬态的高温、高压力、强电场和强磁场等极端物理环境。因此,驱动这种大型装置的脉冲功率电源一直追求更高的输出功率。而近年来,随着脉冲功率技术应用领域的拓展,特别是在新型粒子加速器[3-4]、生物细胞研究科学仪器[5]等领域,仅仅要求脉冲功率电源输出适当的功率,而对短脉冲、输出极性、高重复频率等波形特征参数有着更高的要求。
例如,在新型加速器应用领域,由于感应式回旋加速器具有高能量和高流强的优势,正逐步取代传统的射频回旋加速器[6]。在感应式回旋加速器工作中,为了让粒子束每次通过感应腔时都能加速,外部脉冲加速电场必须与粒子回旋频率同步,这就要求脉冲发生器的重复频率达到MHz级;并且感应式回旋加速器中的加速和聚束是由不同的脉冲调制器来完成,加速电压为稳定的单极性脉冲,聚束电压为双极性电压,所以要求脉冲发生器还具有可调极性的功能。此外,为了提高束流品质,往往要求注入器脉冲电源只能输出数纳秒的短脉冲[7]。
而在生物细胞试验研究中,MHz级重复频率的数纳秒脉冲发生器也有着重要作用。研究表明,脉冲重复频率、极性以及脉冲宽度对细胞的电渗透过程产生重要影响[8-10]。K. Matej等利用Blumlein形成线和全桥结构相结合实现最高重频1.1MHz、电压峰值±200V的脉冲输出[11],发现在高重频纳秒脉冲的作用下,可以实现细胞膜的透化并且减小了细胞质膜损伤。R. Lea等进一步研究发现,纳秒级短脉冲具有透膜效应,能量更加集中在细胞核膜而不是细胞外膜[12]。
随着半导体开关器件的发展,利用半导体开关在脉冲源中可输出更高重复频率脉冲。基于全固态半导体开关研制出来的高压脉冲源主要为形成线脉冲源、Marx发生器、直线型变压器驱动源(Linear Transformer Driver, LTD)等[13-16]。但是全固态Marx发生器受到开关驱动能力限制,形成脉宽难以低到几十纳秒[17]。全固态LTD虽然十分有助于快前沿短脉冲的形成[18],但是在高重频工作条件下,对于磁心材料的要求非常高,因为在多个脉冲连续工作后,磁心的等效电感量会减少,为了不影响其输出电压,还需要在脉冲间隔进行磁心复位操作,这增加了装置的成本和复杂性。而形成线产生的脉冲宽度是由其长度决定的,有利于在高重频下产生短脉冲。S. Romeo等利用微带传输线产生了最短脉宽10ns、幅值800V的短脉冲[19],但是直流充电电压需要达到1 000V,效率较低。为了克服单级Blumlein形成线产生短脉冲的低效率问题,Mi Yan等利用Blumlein形成线和传输线变压器(Transmission Line Trans- former, TLT)相结合的拓扑[20],使多级Blumlein线产生的脉冲进行叠加,能输出2.5kV、脉宽为20ns的短脉冲,但是随着级数的增加,更多的电压波馈入TLT次级线路,导致TLT电压叠加效率逐渐下降。
本文提出了一种利用LC振荡充电与Blumlein形成线相结合的新型拓扑结构,具有数倍的升压功能,并且只使用了3个半导体开关就能在500kHz的开关频率下实现重频1MHz的双极性、同极性输出以及脉冲串内延迟时间灵活可调。
本文所提出的LC振荡充电与Blumlein线结合的可调极性纳秒脉冲发生器电路拓扑如图1所示。图中,L为充电电感,Cm为稳压电容,T1与T2为两段传输线,DC为高压直流电源,RL为负载电阻,S1、S2和S3为MOSFET开关。
首先通过该电路的动态时域分析阐述脉冲发生器的LC振荡升压充电原理。其脉冲发生器工作工程主要分为:①开关闭合时,传输线放电形成脉冲并且直流电源对电感L充电;②开关断开时,电源与电感L、传输线等效电容C和负载RL形成阻尼振荡,在极短时间内提高传输线的端电压。由于传输线是等效为电容和电感组成的分布参数电路,需要考虑电磁波传输的时间。从图1中可以看出,开关S1/S3和S2在闭合对电感充电时等效电路有所不同。

图1 脉冲发生器电路拓扑结构
Fig.1 Topology of Pulse generator circuit
(1)首先分析开关S1/S3闭合时的充电过程,其等效电路如图2所示。由于前端LC振荡周期远大于传输线波长,所以Blumlein形成线可以等效为电容器C1和C2。
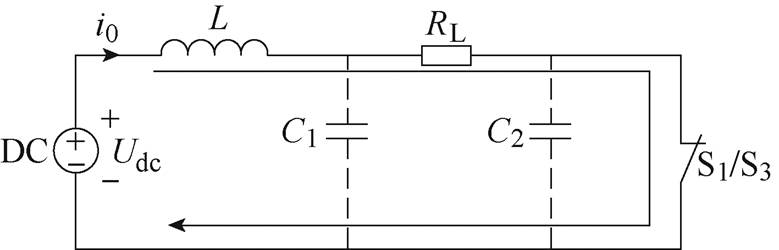
图2 开关S1/S3闭合时等效电路
Fig.2 Equivalent circuit when the S1/S3 is closed
可以根据该等效电路计算出流过电感L的电流i(t)为
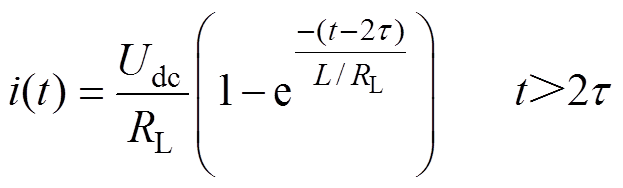 (1)
(1)式中,Udc为充电电压;t 为电磁波在每段传输线传播的时间。当已知开关的导通时间ton时,代入式(1)就能求出当开关断开时的电感初始电流i0。
(2)然后分析开关S2闭合时充电过程,没有经过传输线和负载,其充电等效电路如图3所示。
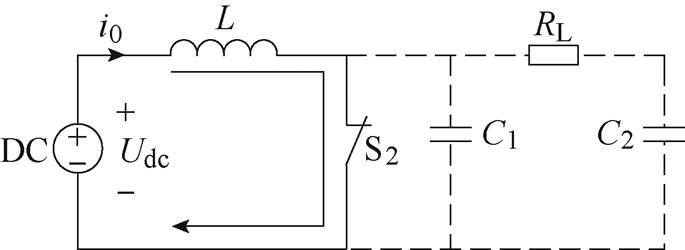
图3 开关S2闭合时等效电路
Fig.3 Equivalent circuit when the S2 is closed
根据等效电路得到i(t)为
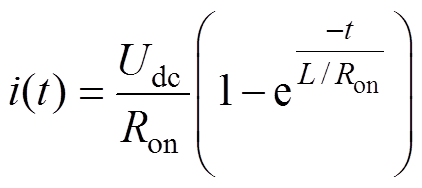 (2)
(2)式中,Ron为开关的导通电阻。经过计算,当时间t足够小(ms级及以下)时,式(2)和不带2t 延时时间的式(1)计算结果基本相同。由于S2闭合给电感L充电时没有2t 的延时时间,为了使正负极性脉冲幅值相等,应增加S1导通时间、减小S2导通时间,保证正负极性脉冲能量相等。
(3)开关S1、S2、S3断开时的等效电路相同,开关S1断开时等效电路如图4所示。由于两段传输线中的电容C1和C2可以认为是并联,所以图中取等效电容C=C1+C2。
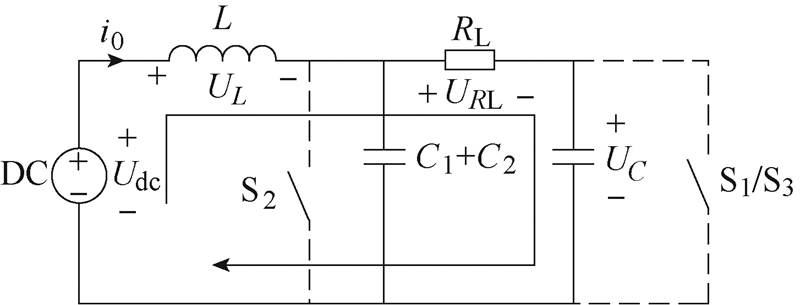
图4 开关S1断开时等效电路
Fig.4 Equivalent circuit when the S1 is disconnected
根据图4电路结构,可以知道,当开关断开时电路为全响应过程。根据基尔霍夫电压定律(Kirchhoff's Voltage Law, KVL)可得到
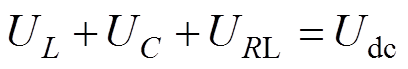 (3)
(3)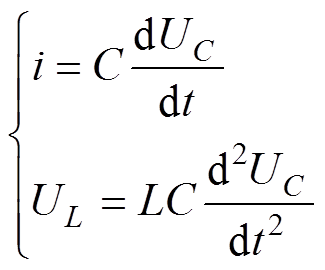 (4)
(4)
把式(4)代入式(3)可得
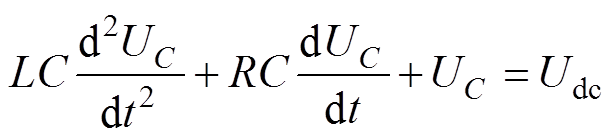 (5)
(5)由于该电路状态为全响应过程,所以解分为通解和特解。
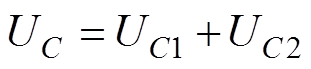 (6)
(6)
可以看出,当时间无穷大时,UC =Udc。所以其特解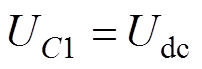 。其通解求解过程为
。其通解求解过程为
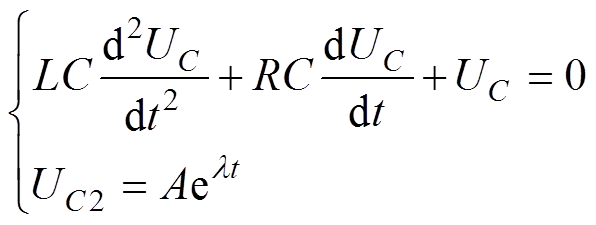 (7)
(7)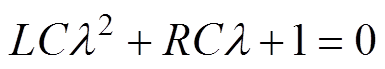 (8)
(8)
当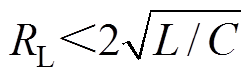 时,得到UC2和UC分别为
时,得到UC2和UC分别为
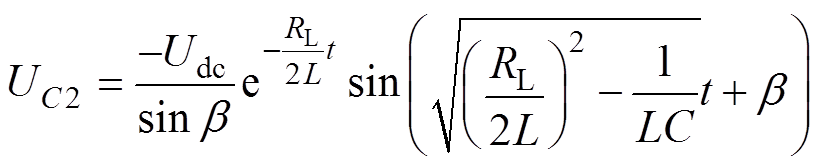 (9)
(9)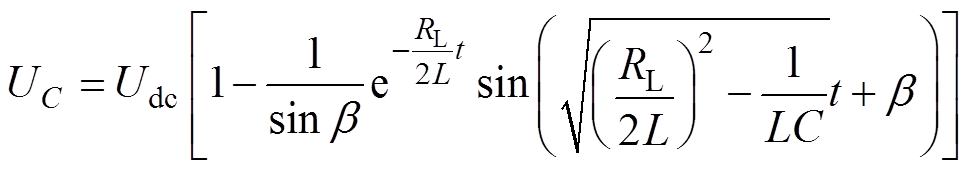 (10)
(10)
式中,b 为振荡电压的初始相位,可以根据初始条件it=0=i0(i0为开关断开时电感L的初始电流),计算出其表达式为
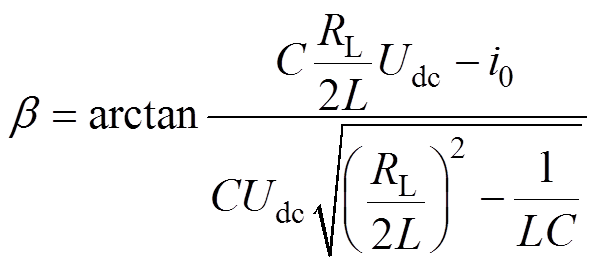 (11)
(11)其中
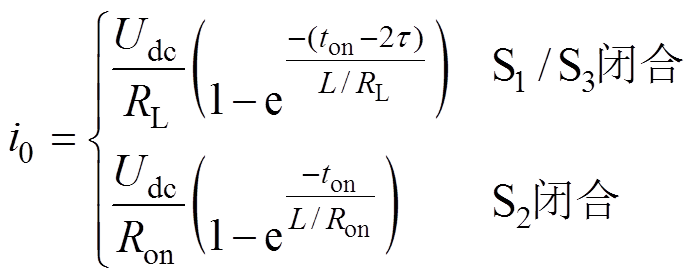 (12)
(12)
感抗的表达式为
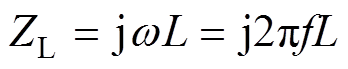 (13)
(13)可以看出,电感在高频下呈高阻抗特性,能量表达式为
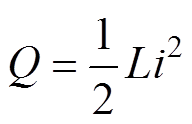 (14)
(14)
可以看出,在高频条件下,电感不仅能起到有效隔离作用,并且电感的积累能量即发热量远小于传统Blumlein脉冲发生器中的充电电阻。
该脉冲发生器除了能单极性输出外,还可以进行双极性和同极性的多模式输出。图5和图6分别为双极性和同极性的工作模式示意图。
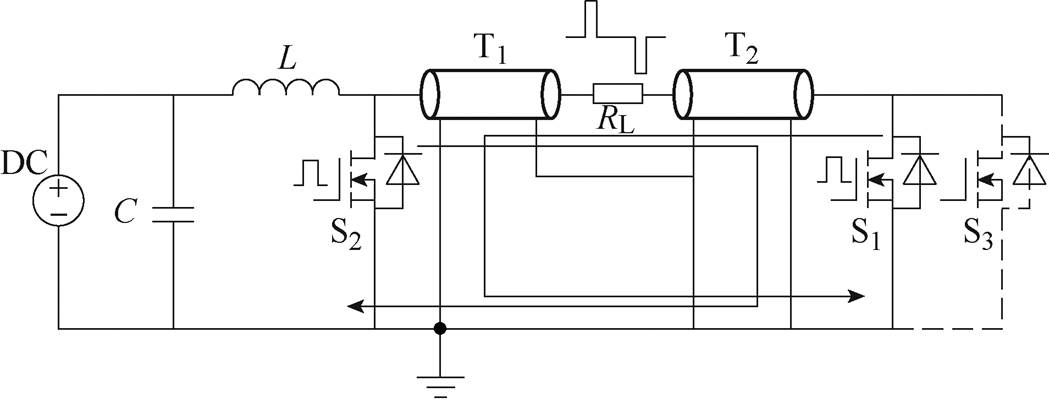
图5 双极性脉冲输出
Fig.5 The bipolar polarity pulse output
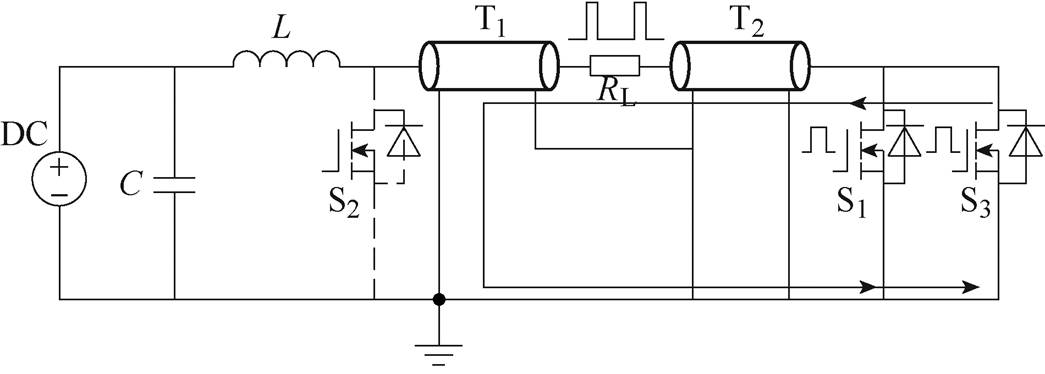
图6 同极性脉冲输出
Fig.6 The same polarity pulse output
当开关S1和开关S2交替动作,S3为关断状态时,就能在负载上实现双极性脉冲输出;而当开关S1和开关S3交替动作,S2为关断状态时,就能在负载上实现同极性脉冲输出。其具体原理需对开关动作时的波过程进行分析。以双极性脉冲输出为例,假设在所有开关关断时,传输线端电压已经通过LC振荡充电为U0。这时开关S1闭合,开关S2保持关断状态,其波过程形成如图7所示。
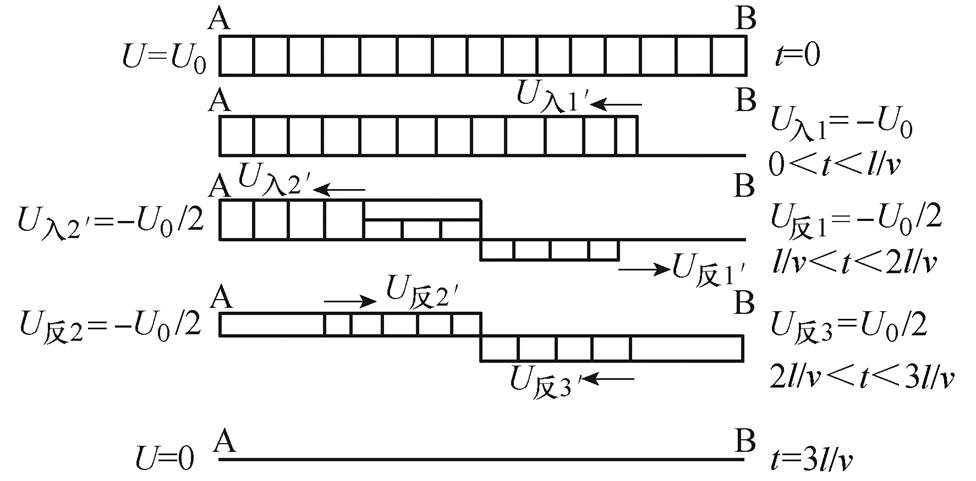
图7 开关S1闭合时波过程形成
Fig.7 Schematic diagram of wave process when switch S1 is closed
(1)开关S1闭合后,强迫B端接地。在0<t<l/v时,电压入射波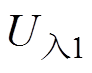 =-U0。l为每段传输线长度,v为波速。
=-U0。l为每段传输线长度,v为波速。
(2)当t =l/v时,电压入射波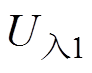 达到负载处,在负载上产生电压URL,并且一部分发生反射,产生反射波
达到负载处,在负载上产生电压URL,并且一部分发生反射,产生反射波 ,另一部分继续入射,成为
,另一部分继续入射,成为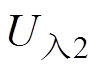 。其值可通过彼得森等效电路进行计算,其关系式为
。其值可通过彼得森等效电路进行计算,其关系式为
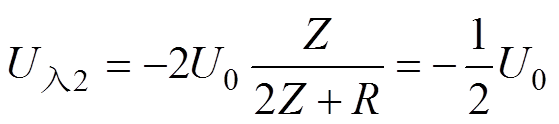 (15)
(15)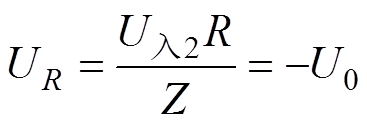 (16)
(16)
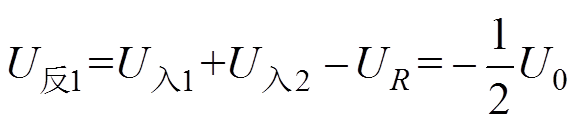 (17)
(17)
式中,Z为传输线波阻抗,阻抗匹配时满足R=2Z。
(3)当t =2l/v时,反射波 达到短路点B,形成符号相反的反射波
达到短路点B,形成符号相反的反射波 =1/2U0,入射波
=1/2U0,入射波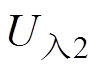 达到开路点A,形成符号相同的反射波
达到开路点A,形成符号相同的反射波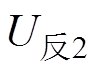 =-U0/2。
=-U0/2。
(4)当t =3l/v时,反射波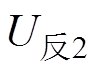 和反射波
和反射波 达到负载处,传输线电压和负载电压变为0,完成放电过程,在负载上形成一个幅值为U0及脉宽为2l/v的脉冲。
达到负载处,传输线电压和负载电压变为0,完成放电过程,在负载上形成一个幅值为U0及脉宽为2l/v的脉冲。
而当开关S1关断,S2闭合时,A点短路,B点开路,波过程传播方向是从A点到B点,由于方向反向,在负载上会形成与上一个脉冲极性相反、幅值与脉宽相同的脉冲。
相同地,在同极性脉冲输出时,开关S1关断、S3闭合时形成的波过程与S1闭合时形成的波过程完全相同,所以会在负载上形成两个极性、幅值以及脉宽一样的脉冲。
为了让该纳秒脉冲发生器能够有效地可调极性输出,需要对开关S1、S2和S3的动作时序进行协调控制,开关控制时序及负载波形如图8所示。可以看出,无论是双极性还是同极性输出,都巧妙地利用了两个开关在一个周期内同时处于关断状态时,给前端LC振荡充电提供了充足的时间,所以可以用更少的开关数量和更低的开关动作频率实现脉冲的可调极性和2倍频输出,并且当改变一个开关周期内两个开关闭合的延时(即改变两个脉冲之间的延迟时间)时,只需要通过改变两个开关的导通时间,就能形成幅值相同、延迟时间可调的双极性或同极性脉冲,这对于加速器的调制是非常重要的。在后文的仿真与实验中有所详述。
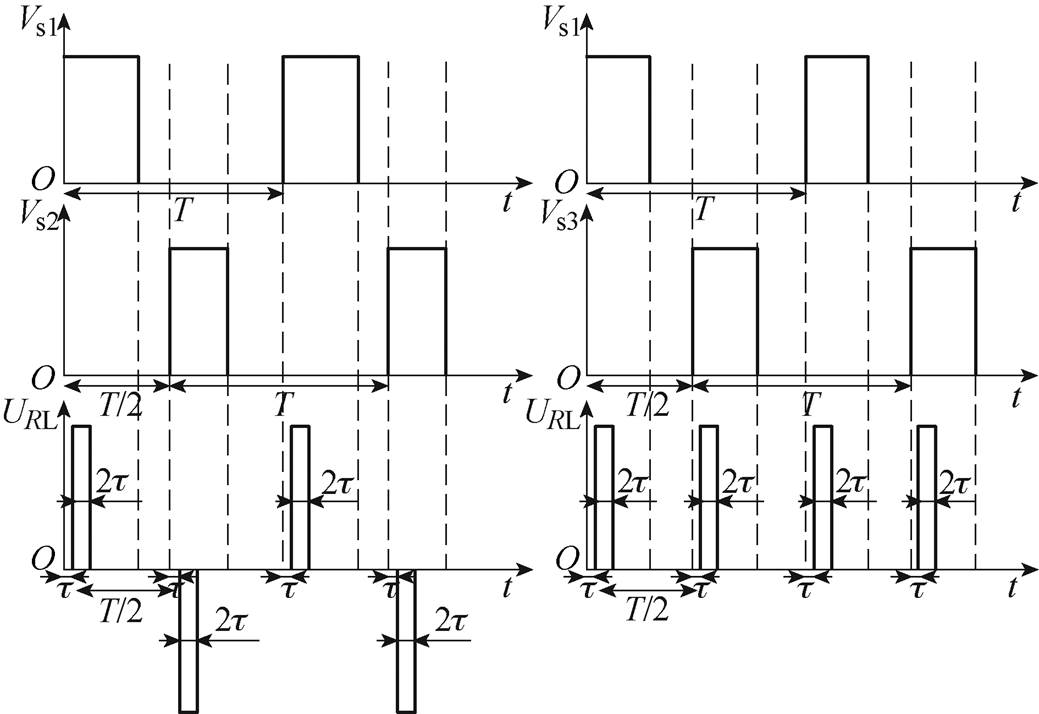
图8 开关控制时序及负载波形
Fig.8 Timing consequence of swatches and waveforms of load
本节为了验证第1节理论推导的正确性,利用PSpise仿真软件搭建电路仿真模型。内容主要分为两部分:①电路主要参数的选取;②控制开关导通占空比改变LC振荡升压比以及脉冲的可调极性倍频输出。
该脉冲发生器的主要参数有传输线、负载电阻、充电电感和直流充电电压。
2.1.1 传输线参数
为了精确地拟合实际的实验测试,传输线的各项基本参数与市场上同轴电缆设置相同,传输线采用有电容电感组合的分布参数模型。同轴电缆的单位电容cr=100pF/m,单位电感lr=250nH/m。波阻抗Z为
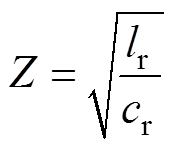 (18)
(18)计算得到波阻抗Z=50W。同轴电缆的单位延时时间t =5ns/m。根据脉宽tw=2t,传输线长度取值2m才能使脉冲宽度为20ns。
2.1.2 负载电阻
该脉冲发生器为使脉冲波形达到最优化,设计为负载匹配。匹配公式为
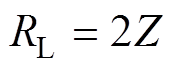 (19)
(19)计算得到负载电阻RL=100W。
2.1.3 充电电感
Blumlein线在形成脉冲时,在电感L处要基本等效为开路,这就要求L的等效阻抗ZL绝对值远大于传输线波阻Z,一般为10倍数量级以上。并且当控制开关动作周期大于1/2固有振荡周期时,才能通过改变开关导通占空比有效调节和提升脉冲电压幅值。可以得到
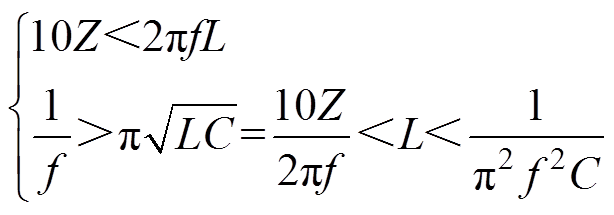 (20)
(20)式中,f为开关工作频率;C为传输线等效电容。通过计算选取电感L的值为1.6mH。
2.1.4 直流充电电压
该脉冲发生器依靠前端LC振荡电路具有数倍于直流充电电压的能力,实际中的同轴线耐压为1 000V,为了保留耐压裕度,设定直流充电电压为200V。仿真电路模型的各元器件参数见表1。
表1 仿真各元器件参数
Tab.1 Each device parameters of simulation

参 数数 值 传输线波阻抗Z/W50 传输线等效电容C/pF200 传输线等效电感L/nH500 传输线延时t/ns10 直流充电电压/V200 稳压电容Cm/mF10 充电电感Lm/mH1.6 负载电阻RL/W100
2.2.1 LC振荡升压仿真
图9给出了当设定开关S2及S3处于断开状态,S1的动作周期为1s,不同导通时间ton时的传输线端电压U0的变化曲线。
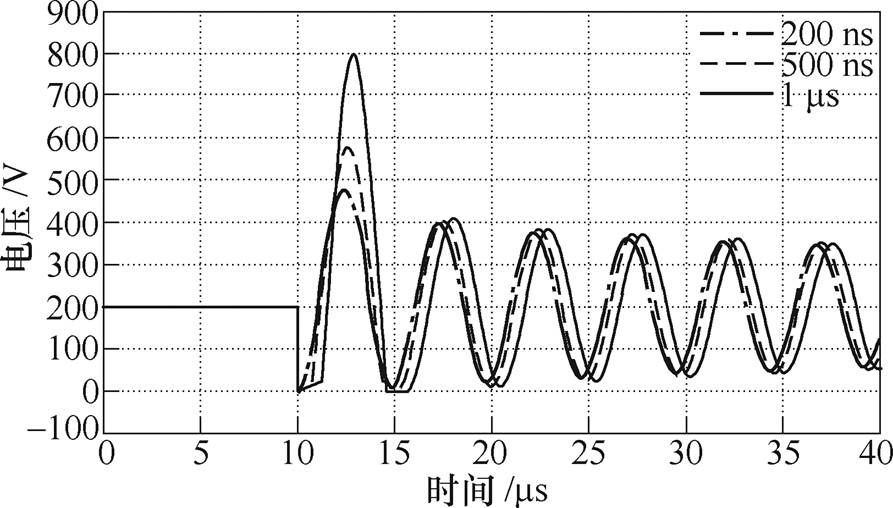
图9 传输线端电压仿真波形
Fig.9 Waveforms of transmission line terminal voltage simulation
可以看出,当开关的导通时间ton变大时,其端电压振荡幅值有所增加,造成这种现象的原因是由于ton的增加,当开关闭合时,直流电源通过负载RL为电感L充电的时间增加,电感L积累的磁场能量越大,而当开关断开进行LC振荡充电时,电感L中转换为电场能量越大,所以就导致振荡电压幅值越高。
图10给出了当开关S1动作频率为500kHz,导通时间ton分别为200ns、500ns以及1ms时的传输线端电压和负载电压仿真波形。可以看出,随着导通时间的增加,端电压和负载脉冲输出电压峰值增大。当开关导通时间为1ms时,脉冲电压峰值达到800V,为直流充电电压的4倍。说明该脉冲发生器可以通过调节开关动作占空比来调节脉冲电压峰值,更加智能化。

图10 不同开关导通时间的端电压和负载电压仿真波形
Fig.10 Terminal voltage and load voltage simulation waveforms for different switch on-time
图11给出了当设置开关导通时间500ns,动作频率500kHz时的单个负载脉冲仿真波形,可以看出,该波形为脉宽为20ns,上升沿时间为4ns,峰值为560V的方波脉冲。
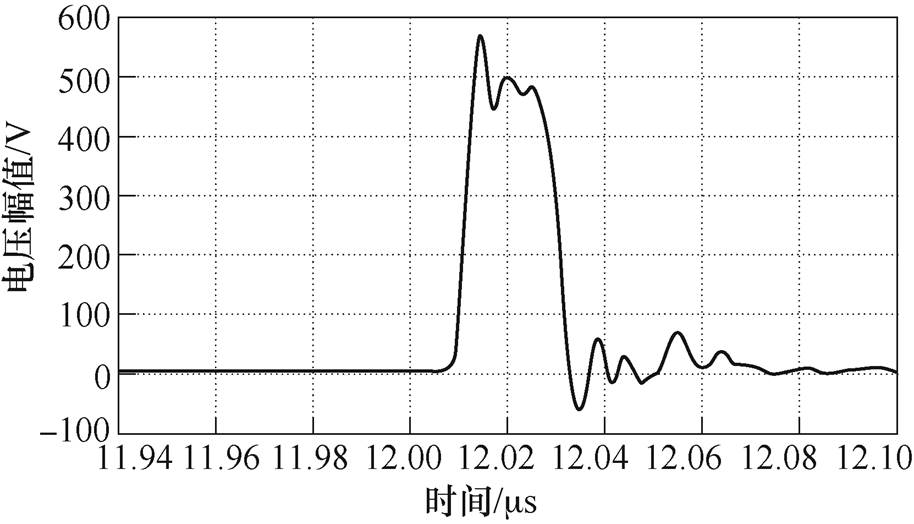
图11 负载脉冲仿真波形
Fig.11 Simulation waveform load pulse
2.2.2 可调极性倍频输出仿真
在可调极性脉冲输出的仿真中,同样保持直流充电电压为200V不变,并且维持脉冲峰值为±600V的基础上,验证可调极性脉冲的2倍频(1MHz)输出和脉冲之间的延迟时间灵活可调。
图12给出了当开关动作频率为500kHz,开关S1与S2/S3的导通延时时间为1ms时的双极性和同极性端电压及负载脉冲仿真波形,其脉冲频率为1MHz,验证了倍频功能。与单极性相比,可以看出,无论是双极性或是同极性,脉冲重复频率提升为两倍。

图12 可调极性脉冲仿真波形
Fig.12 Simulation waveforms of adjustable polarity pulse
该脉冲发生器不仅可调极性脉冲输出,并且脉冲间的延迟时间可通过控制开关的动作时序进行灵活调节。以双极性脉冲为例,图13分别给出了延迟时间为600ns和1.4ms的端电压和负载脉冲仿真波形。

图13 不同延迟时间双极性脉冲仿真波形
Fig.13 Simulation waveforms of bipolar pulse with different relaxation times
当脉冲间的延时时间改变时,需要通过调节相应的开关S1、S2和S3的导通占空比,使得电磁场能量转换动态平衡后,保证开关动作周期内的两个脉冲(双极性或同极性)幅值相等。
该纳秒脉冲发生器主要由开关驱动电路和脉冲形成主电路构成。为了减小主电路和驱动电路的杂散信号干扰和高低压隔离,采用光电转换电路把信号发生器产生的逻辑门电路(Transistor-Transistor Logic, TTL)信号进行一次电光-光电转换,然后送到开关栅级以有效驱动开关动作。在印制电路板(Printed Circuit Board, PCB)的设计中,尽量减小放电回路中的杂散电感,有利于脉冲快前沿的形成。相关主要元器件参数见表2。
表2 脉冲发生器主要元器件
Tab.2 Main components of pulse generator

器件型号主要参数 同轴线RG174/U波阻抗Z=50W, 长度l=2m 固态开关(MOSFET)IXZ631DF12N100VDSS=1kV, IDM=72A,tr=3ns, tf =2ns 储能电容CDE1 200V, 1mF 光纤接收发器FT/R50MHIR数据率50Mbit/s
主电路中的充电电感采用1.6mH的绕线电感,负载电阻采用最大功率100W、阻值100W 的无感电阻。
图14给出了该纳秒脉冲发生器的实验测试平台。由于该发生器的工作重复频率达到1MHz,即使采用倍频输出,单个开关的工作频率也达到了500kHz。在高频工作条件下,开关的热损耗非常严重,所以采用散热片对开关进行散热处理,防止过高的温度对开关动作产生影响甚至损坏。在实验样机测试时,考虑到该纳秒脉冲发生器内存在的损耗和在高重频情况下对直流电源功率的要求,本实验选用东文生产的型号为DW-P102-5000ACC2的高压电源模块作为脉冲发生器的直流电源,该电源输出电压1 000V、电流5A,最大输出功率达到5kW。信号发生器采用Stanford Research Systems超低抖动数字延时触发器DG645。示波器选用Lecroy WavePro760Zi-A,其采样率和带宽分别为10GS/s及6GHz。高压测量探头为Lecroy PPE6kV,带宽400MHz。

图14 纳秒脉冲发生器实物
Fig.14 The total view of the nanosecond pulse generator
(1)在单极性输出实验中,图15为设置开关S1动作周期1ms以及导通时间分别为200ns、500ns和1ms的传输线端电压波形。
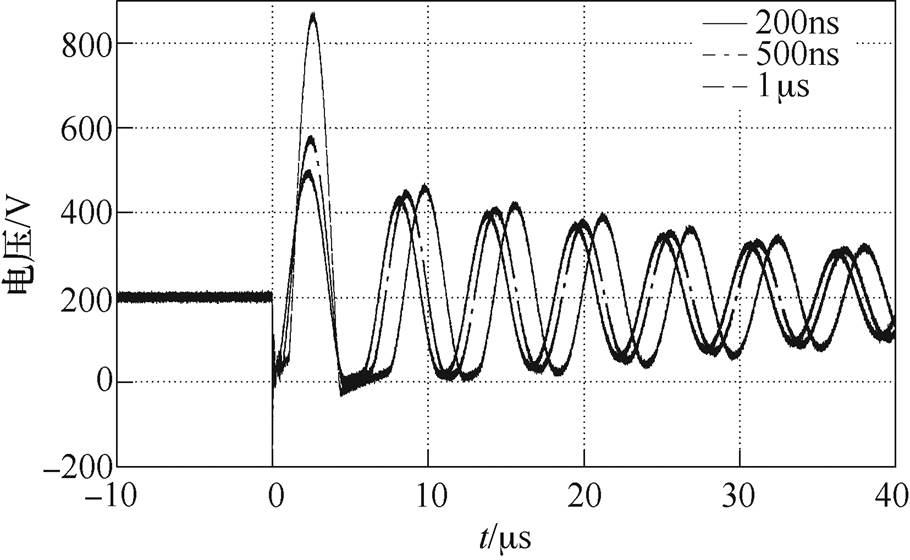
图15 实测端电压波形
Fig.15 Measured waveforms of terminal voltage
可以看出,该测试电压就是恒定周期的正弦衰减振荡波形,与第1节理论推导和第2节仿真相互验证。其中在第一个振荡周期时电压降到零电位以下时,由于开关的反向二极管的钳位作用,维持在二极管的导通电压下。
然后使脉冲发生器在500kHz重复频率下连续运行,图16分别给出在充电电压200V,开关S1导通时间为200ns、500ns和1ms的传输线端口电压U0和负载脉冲输出波形URL。实验证明了该发生器的升压性能和调制开关占空比来调节脉冲峰值的功能。

图16 不同开关导通时间的实测端电压和负载脉冲波形
Fig.16 Measured terminal voltage and load pulse waveforms for different switch on-time
图17为在开关导通时间为500ns时的测试波形时间轴进行缩短,测试的单个脉冲输出波形。可以看出,该电压波形为峰值为600V,上升时间和下降时间分别为3.1ns和6.3ns,半高宽为20ns的方波脉冲。由于在负载回路中不可避免存在一些杂散电感,所以产生脉冲后会有局部振荡。
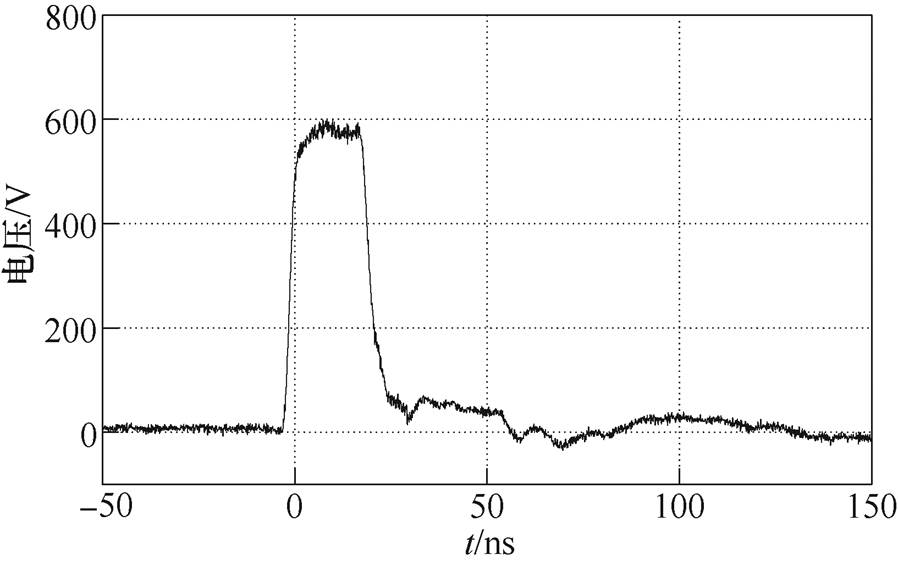
图17 单个脉冲实测波形
Fig.17 Measured waveform of single pulse
(2)控制开关S1的导通时间220ns,开关S2和S3的导通时间180ns,对该脉冲发生器的可调极性脉冲输出进行测试。图18给出脉冲间延时为1ms的双极性脉冲和同极性脉冲的传输线端口电压U0以及负载脉冲输出波形URL,其脉冲峰值为±600V,重复频率1MHz。可以看出,当重复频率达到1MHz时,脉冲之间会存在一个20V左右的直流分量,原因是前端充电电感1MHz下没有及时放完电,可以考虑适当减小充电电感以抑制直流分量。实验结果验证了该脉冲发生器利用更少的开关实现更高频率的可调极性脉冲输出。
最后以双极性脉冲输出为例,对正负极性脉冲的延迟时间可调进行实验验证。图19分别给出了延迟时间为600ns和1.4ms的双极性端电压U0和脉冲波形URL。可以看出,正负极性脉冲幅值基本相等。实验结果验证了该纳秒脉冲发生器可以通过控制开关时序来对脉冲间的时延进行灵活调制的功能。

图18 可调极性脉冲测试波形
Fig.18 Measured waveforms of multi-polar pulse
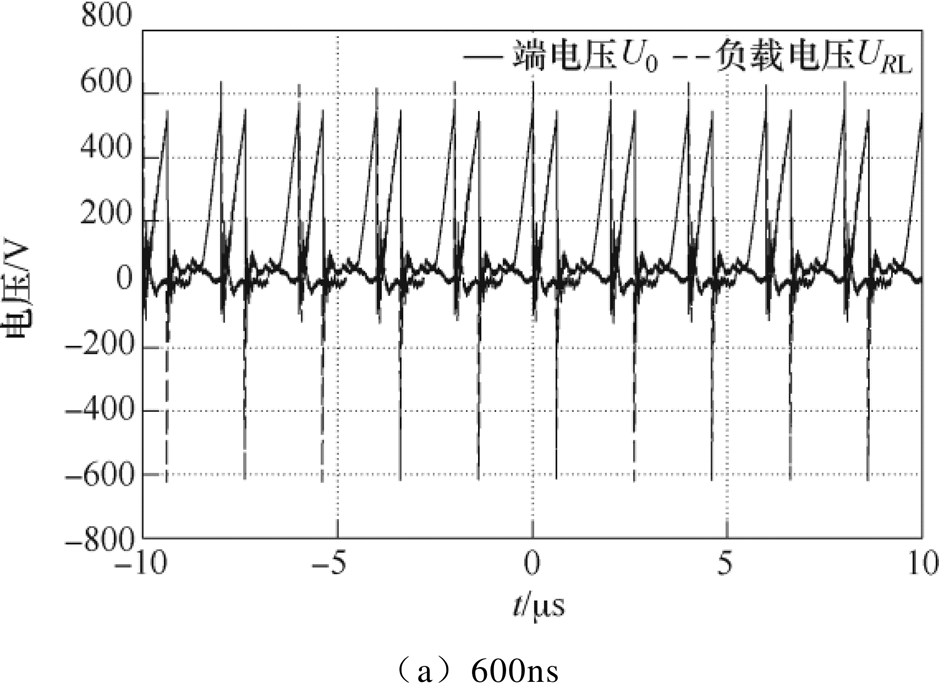
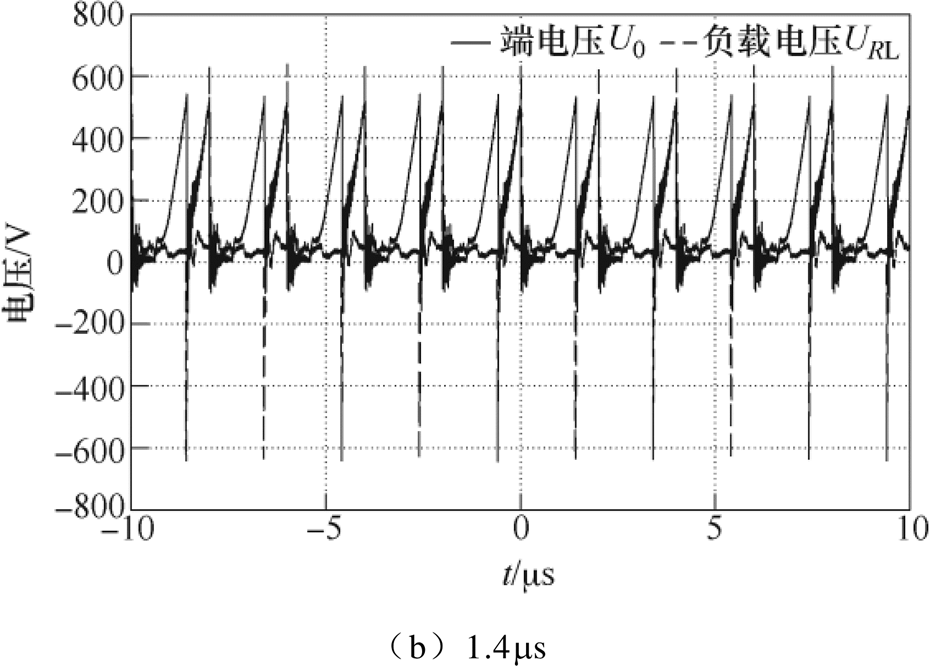
图19 不同延迟时间双极性脉冲测试波形
Fig.19 Measured waveforms of bipolar pulse with different relaxation time
本文提出了一种升压模式的可调极性高频Blumlein脉冲形成线脉冲发生器。通过理论推导、仿真分析和初步的样机实验得到如下结论:
1)该脉冲发生器利用LC振荡充电,配合开关的动作频率能在单级电路下实现最高脉冲电压幅值4倍于直流充电电压,降低对直流电源的供电需求,并且可通过控制开关导通占空比实现脉冲电压幅值的灵活调节。
2)该电路方法可利用多个开关的延时控制,实现脉冲的可调极性输出和倍频功能,不仅能有效降低单个开关损耗,相对于传统的Blumlein线在输出波形灵活性方面更具优势。尽管,初步的实验样机仅能达到数千瓦的功率输出,其主要受限于半导体开关的功率容量,然而本文中的模块可以通过模块化的叠加路线得以实现[20]。
因此,本文所提的电路方法对研制高重频、电压增益、纳秒级短脉冲、可控双极性脉冲功率发生器提供了新的思路。
参考文献
[1] 张永民, 邱爱慈, 黄建军, 等. 几项新技术在“闪光二号”加速器上的应用[J]. 强激光与粒子束, 2008, 20(5): 876-880.
Zhang Yongmin, Qiu Aici, Huang Jianjun, et al. Application of several new technologies in flash 2 accelerator[J]. High Power Laser and Particle Beams, 2008, 20(5): 876-880.
[2] Zhou Yan, Tan Jianwen, Yao Chenguo, et al. Finite- element simulation and experiments on plastic heating in the process of electromagnetic pulse forming[J]. IEEE Transactions on Plasma Science, 2018, 46(10): 3427-3437.
[3] Takayama K, Kishiro J. Induction synchrotron[J]. Nuclear Instruments & Methods in Physics Research, Section A-Accelerators, Spectrometers, Detectors and Associated Equipment, 2000, 451(1): 304-317.
[4] Takayama K, Arakida Y, Dixit T, et al. Experimental demonstration of theinduction synchrotron[J]. Physi- cal Review Letters, 2007, 98(5): 054801.
[5] 郭飞, 李成祥, 唐贤伦, 等. 冲激辐射天线实现皮秒脉冲电场在人体大脑模型中聚焦的研究[J]. 电工技术学报, 2016, 31(3): 195-202.
Guo Fei, Li Chengxiang, Tang Xianlun, et al. Focusing of picosecond pulsed electric fields electric fields in human brain model with impulse radiating antenna[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 195-202.
[6] Kakad A, Kakad B, Omura Y, et al. Modulation of electromagnetic ion cyclotron waves by Pc5 ULF waves and energetic ring current ions[J]. Journal of Geophysical Research-Space Physics, 2019, 124(3): 1992-2009.
[7] Archana S, Naresh P, Ranjeet K, et al. Sub- nanosecond pulse generator and electron beam source for nToF application[C]//IEEE International Power Modulator and High Voltage Conference, Santa Fe, New Mexico, 2014: 73-75.
[8] Kolb J F, Kono S, Schoenbach K H. Nanosecond pulsed electric field generators for the study of subcellular effects[J]. Bioelectromagnetics, 2006, 27(3): 172-187.
[9] Pakhomov A G, Shevin R, White J A, et al. Membrane permeabilization and cell damage by ultrashort electric field shocks[J]. Archives of Biochemistry and Biophysics, 2007, 465(1): 109-118.
[10] Vernier P T, Ziegler M J. Nanosecond field alignment of head group and water dipoles in electroporating phospholipid bilayers[J]. The Journal of Physical Chemistry B, 2007, 111: 12993-12996.
[11] Matej R, Matej K, Denis P, et al. Blumlein con- figuration for high-repetition-rate pulse generation of variable duration and polarity using synchronized switch control[J]. IEEE Transactions on Biomedical Engineering, 2009, 56(11): 2642-2648.
[12] Lea R, Gorazd P, Damijan M. Electroporation of intracellular liposomes using nanosecond electric pulses-a theoretical study[J]. IEEE Transactions on Biomedical Engineering, 2013, 60(9): 2624-2635.
[13] 乔中兴, 刘凯, 董寅. 铁氧体同轴传输线脉冲锐化特性的研究[J]. 电工技术学报, 2015, 30(2): 21-25.
Qiao Zhongxing, Liu Kai, Dong Yin. Investigation of ferrite-filled coaxial transmission lines for pulse sharpening[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 21-25.
[14] 李江涛, 赵政, 钟旭, 等. 基于模块化Marx电路和传输线变压器的重频纳秒脉冲源设计[J]. 电工技术学报, 2017, 32(8): 121-128.
Li Jiangtao, Zhao Zheng, Zhong Xu, et al. Design of repetitive nanosecond pulse generator based on modularized Marx circuit and transmission line trans- former[J]. Transactions of China Electrotechnical Society, 2017, 32(8): 121-128.
[15] Redondo L M, Kandratsyeu A, Barnes M J. Marx generator prototype for kicker magnets based on SiC MOSFETs[J]. IEEE Transactions on Plasma Science, 2018, 46(10): 3334-3339.
[16] Sugai T, Tokuchi A, Jiang Weihua. Effects of pulsed power control on plasma water treatment using ltd[J]. IEEE Transactions on Plasma Science, 2018, 46(10): 3566-3573.
[17] Shi Haozheng, Lu Yuanda, Gu Tianyu, et al. High- voltage pulse waveform modulator based on solid- state Marx generator[J]. IEEE Transactions on Diele- ctrics & Electrical Insulation, 2015, 22(4): 1983-1990.
[18] Kazemi M R, Sugai T, Tokuchi A, et al. Waveform control of pulsed-power generator based on solid- state ltd[J]. IEEE Transactions on Plasma Science, 2017, 45(2): 247-251.
[19] Romeo S, D'avino C, Zeni O. A Blumlein-type, nanosecond pulse generator with interchangeable transmission lines for bioelectrical applications[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2013, 20(4): 1224-1230.
[20] Mi Yan, Bian Changhao, Wan Jialun, et al. A modular solid-state nanosecond pulsed generator based on Blumlein-line and transmission line transformer with microstrip line[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2016, 24(4): 2196-2202.
An Adjustable Polarity High Frequency Blumlein Pulse Forming Line Power Modulation Module with Boost Mode
Abstract With the development of pulse power technology in new particle accelerators, biological cell experimental instruments and other fields, higher requirements are put forward for pulse power generators with high repetition frequency, short pulse and flexible adjustment of pulse parameters. This paper studies a new power conversion module circuit topology composed of an LC oscillating boost unit and a Blumlein line unit. The multi-switch timing logic is used to adjust the output waveform parameters. Compared with the traditional Blumlein line, it can obtain output pulse frequency several times the switching frequency while retaining the advantages of short pulse forming. In addition, the output voltage amplitude is several times the DC source voltage, and the polarity and interval time of the output pulse are flexibly adjusted. At the same time, the working principle of the circuit is explained by the time domain analysis of the dynamic circuit and the analysis of the transmission line wave process, and is verified by circuit simulation. Moreover, a principle prototype is built using RF MOSFET switch and coaxial cable. When the load is matched, the output pulse frequency is 1MHz at the switching frequency of 500kHz, and the output pulse voltage amplitude is 4 times the DC supply voltage with 20ns pulse width.
keywords:Nanosecond pulse generator, LC oscillation circuit, Blumlein pulse forming line, semiconductor switch
中图分类号:TM832
DOI: 10.19595/j.cnki.1000-6753.tces.191425
国家自然科学基金(51907011)、重庆市基金(cstc2019jcyj-msxm0368)和中央高校基本科研业务费(2019CDXYDQ0010)资助项目。
收稿日期 2019-11-02
改稿日期 2019-12-17
何映江 男,1995年生,硕士研究生,研究方向为脉冲功率技术及其应用。E-mail: heyingjiang@cqu.edu.cn
余 亮 男,1986年生,讲师,硕士生导师,研究方向为脉冲功率技术及其应用、大功率半导体器件应用。E-mail: yu_liang@cqu.edu.cn(通信作者)
(编辑 崔文静)