n的高频变压器提供了所需的电气隔离和两条直流母线之间的电压匹配。功率主电路中两个H桥的交流侧电压分别为vab(t)和vcd(t)，Leq为变压器漏感和外部串联电感之和，Req为开关导通电阻、变压器绕组电阻以及线路电阻总和，Co为输出电容，RC为输出电容的等效串联电阻，fs为主电路的开关频率。摘要 针对双有源全桥（DAB）DC-DC变换器传统离散迭代模型的缺陷和不足，该文提出DAB变换器的全状态离散迭代模型，并基于此对不同参数和工况条件下的输出电压纹波进行分析。目前，国际上广泛采用的DAB变换器离散迭代模型是基于一个开关周期内不同子区间逐个迭代的，经过分析可以发现，传统离散迭代模型会遗漏状态变量的许多关键信息，并不能反映出变量的真实状态。通过深入分析DAB变换器的工作原理，提出的全状态离散迭代模型则包含了变换器在一个开关周期内所有关键时刻的状态变量信息。以输出电压为例，全状态离散迭代模型可以反映出工作子区间切换时刻的输出电压信息，因而其输出电压纹波分析结果更加真实，在此基础上的参数优化设计更有利于抑制输出电压纹波和提高系统可靠性。最后，通过仿真和搭建的实验平台验证了模型和理论分析结果的正确性。
关键词：双有源全桥（DAB）变换器 离散时间模型 输出电压纹波 参数设计
双有源全桥（Dual Active Bridge, DAB）变换器是一种隔离的双向升降压DC-DC变换器，可以同时实现功率的双向流动。由于具有高电压传输比、高功率密度、易于实现软开关等优点，DAB变换器一直是隔离型双向DC-DC变换器的研究热点[1-2]。随着近年来分布式发电以及储能技术的快速发展和广泛应用，DAB变换器作为关键的接口装置[3-4]受到了行业的广泛关注。作为传统大功率DC-DC变换器的替代品，DAB变换器目前广泛用于大功率固态变压器[5-6]、智能电网[7]、电动汽车[8]等领域。
经过多年研究，目前已有多种DAB变换器的建模方法被提出，主要分为平均模型与离散模型两类。DAB变换器平均模型包括降阶平均模型[9]、输出电流平均模型[10]和广义状态空间平均模型。为了避开电感电流的交流变量，降阶平均模型和输出电流平均模型都是根据电流平均值进行建模的，这两种模型本质上是一致的。由于将电流变量进行平均化处理，上述两种模型忽略了很多电感电流的状态信息。广义平均模型[11]的建模思路是利用状态变量的傅里叶展开式系数作为新的系统状态变量。但是为了达到理想的模型精度，需要保留很高阶数的交流分量，因此会不可避免地提高模型阶数。离散模型主要包括离散小信号模型[12]和离散迭代模型[13-14]。离散小信号模型是在稳态波形上施加小扰动，然后根据扰动的演化规律得到相应的传递函数。该方法在推导过程中需要进行线性化近似并忽略线路阻抗，因此模型的准确度会有所降低。而离散迭代模型则根据变换器在一个开关周期内不同开关区间的状态特性和状态转移关系，得到某一开关周期初始时刻与下一个开关周期初始时刻状态变量之间的映射关系，进而得到系统的离散迭代模型。
DAB变换器的输出电压纹波建模与分析一直是困扰着设计人员的一大难题，特别是一些对输出电压纹波要求较高的场合。DAB变换器平均模型[9-11]的一系列加权平均过程使其难以直观准确地进行输出电压的纹波分析。而离散迭代模型[12-15]保留了系统从低频次到开关频次的所有信息，因此具有较高的准确度，十分适合输出电压纹波的建模和分析。目前广泛应用的离散迭代模型是建立在每个开关周期中不同工作子区间的离散迭代基础上的。但随着DAB变换器的广泛应用，许多工程设计人员发现这种方法分析得到的输出纹波与实验结果相比较始终存在一定的误差。甚至在某些参数下，实验波形与理论分析结果相差极大。因此基于传统离散迭代模型输出电压纹波分析的参数设计，经常会产生难以预测的输出纹波，进而造成输出滤波电容失效率的大幅提高并降低了系统的可靠性[16]。此外，为了消除输出电压纹波，一些新的DC-DC变换器拓扑结构[17-18]，以及非隔离变换器在不同电流导通模式下的输出纹波分析方法[19-21]被提出。但是这些方法的应用对象具有较大局限性，而且无法详细描述DAB变换器的输出电压纹波特性及其本质。
本文提出的DAB变换器全状态离散迭代模型充分描述了系统状态变量的所有关键时刻信息，详细刻画了不同系统参数下输出电压纹波的形态，进而指出了传统离散迭代模型无法精确分析输出电压纹波的原因。此外，基于全状态离散迭代模型的参数分析也为DAB变换器的参数设计和输出电压纹波抑制提供了指导。
数字控制DAB变换器如图1所示，数字控制DAB变换器主要由功率主电路和控制电路构成，其中主电路由双有源H桥通过中间的高频变压器连接而成，变压器电压比为1n的高频变压器提供了所需的电气隔离和两条直流母线之间的电压匹配。功率主电路中两个H桥的交流侧电压分别为vab(t)和vcd(t)，Leq为变压器漏感和外部串联电感之和，Req为开关导通电阻、变压器绕组电阻以及线路电阻总和，Co为输出电容，RC为输出电容的等效串联电阻，fs为主电路的开关频率。
移相控制是广泛应用于DAB变换器的控制方法，同一桥臂上的两个开关管180°互补导通。在单移相调制策略中，S1与S4、S2与S3开关状态分别互补，并且每个开关管的占空比均为50%。以V1侧H桥为例，通过控制V1侧四个开关管的开通与关断，可以在变压器一次侧形成两电平交流方波电压vab(t)。同理，控制V2侧四个开关管，可以在变压器二次侧形成同样的两电平交流方波电压vcd(t)。为了便于阐明本文提出的建模方法以及简化分析过程，本文以单移相调制策略为例进行数字控制DAB变换器的全状态离散建模与输出电压纹波分析。两方波之间的移相角若大于0，即vab(t)超前vcd(t)，就可以实现功率从V1侧到V2侧的流动；移相角若小于0，即vab(t)滞后vcd(t)，则功率从V2侧流向V1侧。本文只以功率由V1侧流向V2侧为例进行分析，因此定义V1为输入直流电压，V2为输出直流电压。
图1 数字控制DAB变换器
Fig.1 Digitally controlled DAB converter
1.2.1 DAB变换器不同工作状态区间的离散迭代关系
单移相控制DAB变换器在一个开关周期中有四种不同的电路状态，分别对应于图2所示的DAB变换器状态区间1～4的等效电路。其中不同的工作状态区间所对应的开关状态和时间段分别为：
状态区间1：开关S1、S4、S6、S7导通，S2、S3、S5、S8关断，对应时间为Tn1。
状态区间2：开关S1、S4、S5、S8导通，S2、S3、S6、S7关断，对应时间为Tn2。
状态区间3：开关S2、S3、S5、S8导通，S1、S4、S6、S7关断，对应时间为Tn3。
状态区间4：开关S2、S3、S6、S7导通，S1、S4、S5、S8关断，对应时间为Tn4。
要建立DAB变换器的离散迭代模型，首先要求得到其在各个不同状态区间对应的状态方程。选取电感电流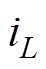
和电容电压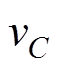
为电路状态变量，按照图2所示的状态变量参考方向，根据电路的KCL和KVL可得四个不同状态区间的主电路状态方程。每个状态方程的表达式为
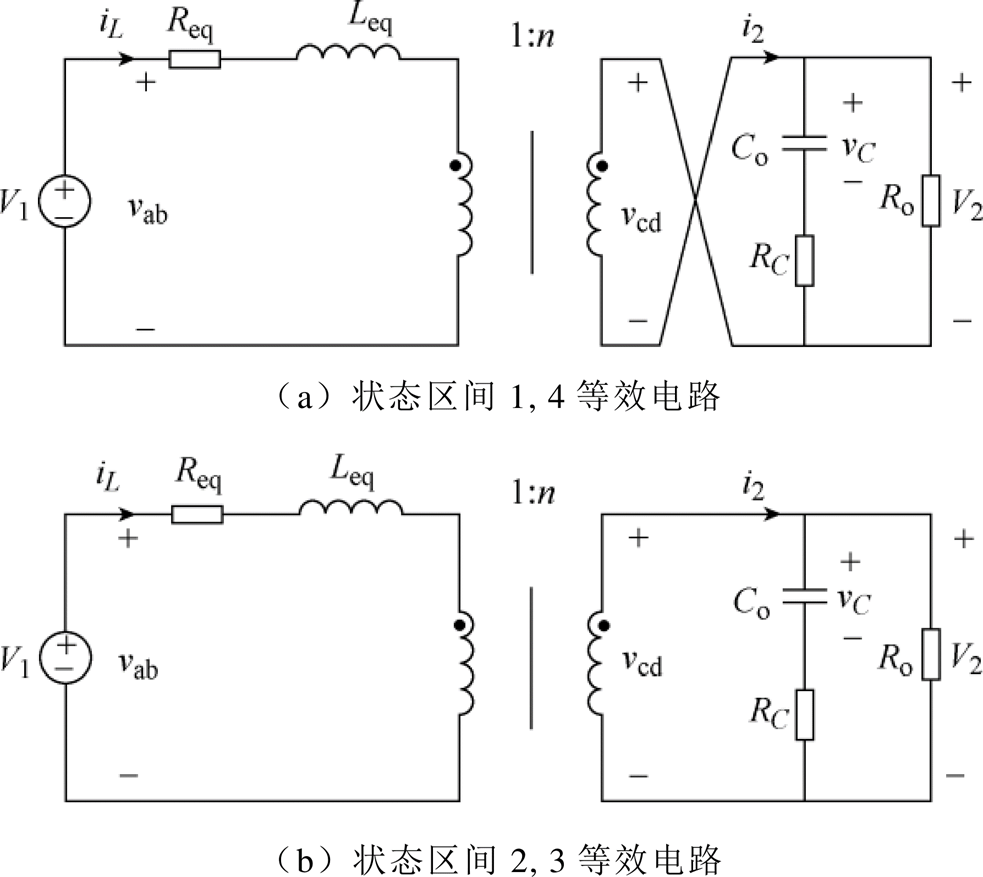
图2 DAB变换器状态区间1～4的等效电路
Fig.2 The equivalent circuits of the DAB converter in different state intervals
（1）式中，
为DAB变换器输入电压；
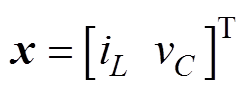为系统状态向量；
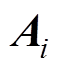和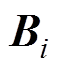
分别为系统矩阵和输入矩阵，
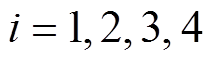对应图2所示的四个状态区间。不同状态区间的系统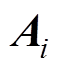矩阵和输入矩阵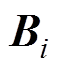的表达式分别为
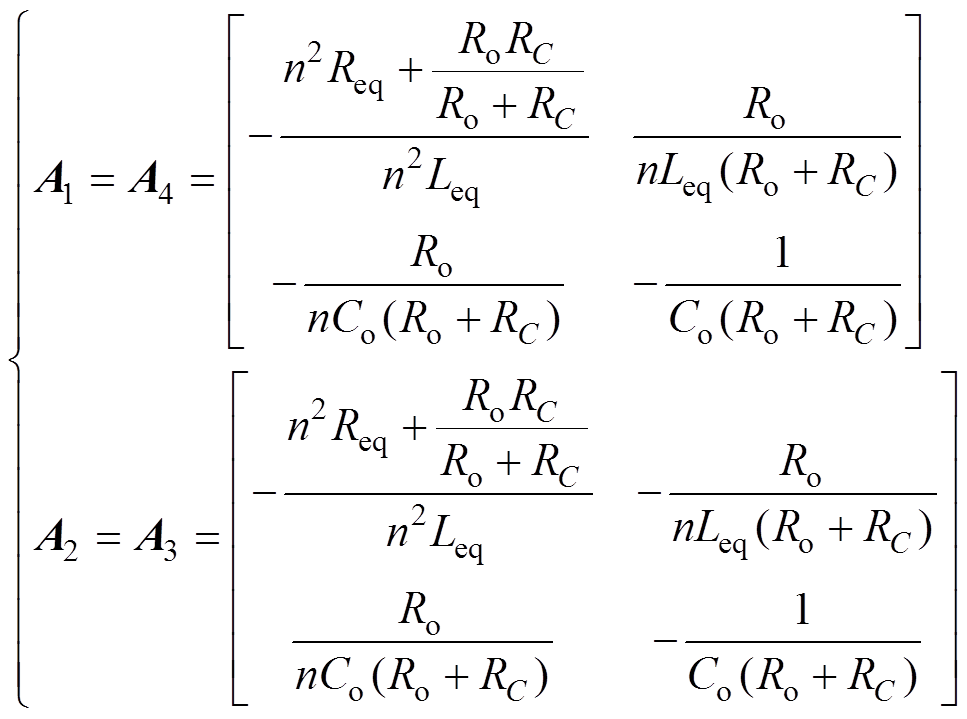（2）
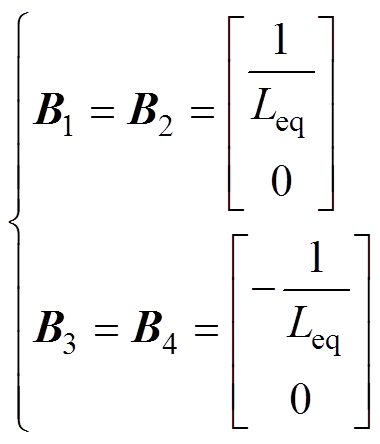（3）
DAB变换器在一个开关周期内有四个电路状态，将第n个开关周期和第n+1个开关周期初始时刻对应的状态变量x和输出电压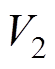
分别定义为
、
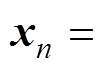
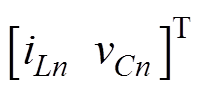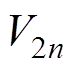和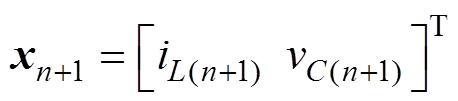
、
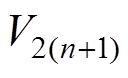。在一个开关周期内，电路状态区间1结束时刻的状态变量x和输出电压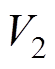可以定义为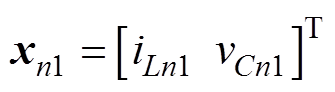
、
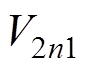。同理，电路状态区间2和电路状态区间3结束时刻的状态变量x和输出电压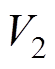可以定义为
、
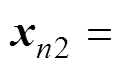
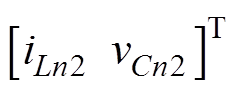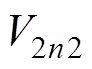和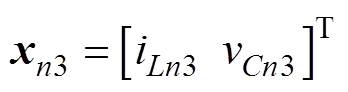
、
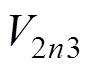。可得系统状态变量的离散迭代关系如图3所示。
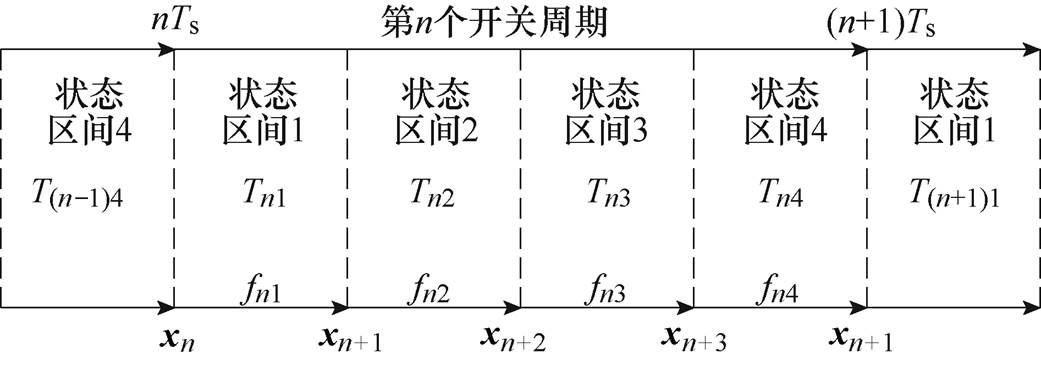
图3 状态变量的离散迭代关系
Fig.3 The diagram of the state variables iteration
在一个开关周期内，每个状态区间的末状态变量值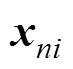
都可以作为下一状态区间的初始值进行离散迭代，进而可以得到下一状态区间的末状态变量值xn(i+1)。对式（1）进行积分运算[22]可以得到每个区间的状态变量在t时刻的值为
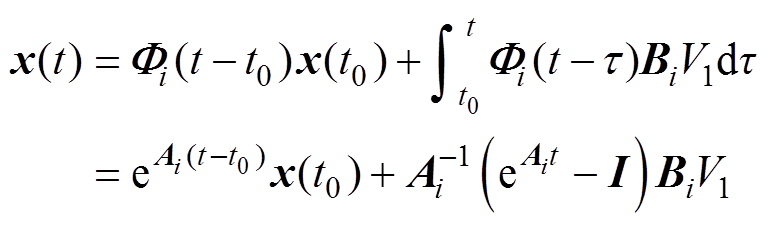（4）根据式（4）可得各个状态变量的迭代表达式为
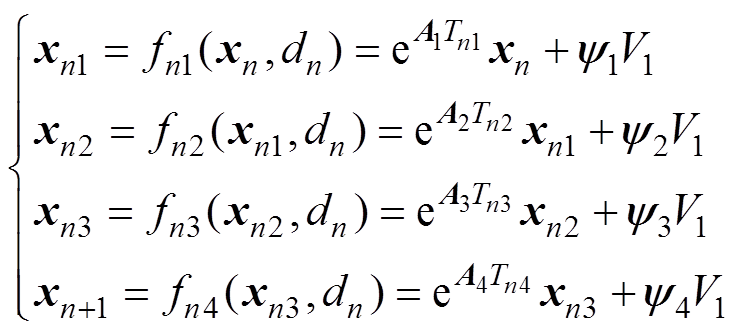（5）
其中
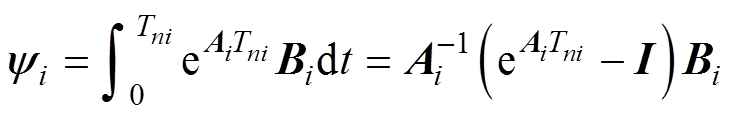（6）式中，fni为各子区间的迭代函数。联立式（5）中的各子区间迭代表达式即可得到相邻两个开关周期状态变量之间的离散迭代关系。同时，一个开关周期内每个状态区间的末状态变量值xni可用于准确地分析系统各个状态变量的纹波信息。
1.2.2 DAB变换器全状态离散迭代建模
DAB变换器的电感电流与输出电压波形示意图如图4所示（实际状态变量波形会随着输入电压、输出电压的变化而略有不同）。图中圆圈表示通过传统离散迭代模型[13]分析得到的状态变量值，即传统离散迭代模型在一个开关周期内考虑的电感电流状态分别为
、
、
、
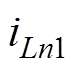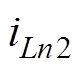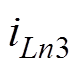，相应的输出电压状态分别为
、
、
、
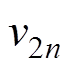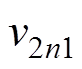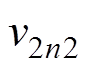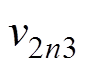。但实际仿真与实验得到的输出电压波形与传统离散迭代模型的分析结果相比会有很大的不同。通过仿真实验可以发现，输出电压在一个开关周期中实际有6个状态点，即除了传统分析方法中的四个状态外还应包括图中的
、
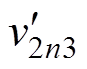。通过图2所示的DAB变换器在一个开关周期不同子区间的等效电路，可以进一步分析传统离散迭代模型缺失输出电压状态、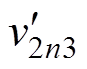的根本原因。在状态区间1与状态区间2的切换时刻
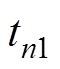以及状态区间3与状态区间4的切换时刻
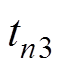，电路结构会发生突变。此时输出电流突然反向，输出电压也会相应地发生跳变。而传统离散迭代模型逐区间迭代的缺陷，使其只能考虑状态区间1和3的结束时刻，而无法灵活纳入状态区间2和4的起始时刻，因此也就丢失了开关状态2和4的起始时刻状态变量信息。实际上开关状态2和4起始时刻的状态变量值对于输出电压纹波分析是至关重要的。
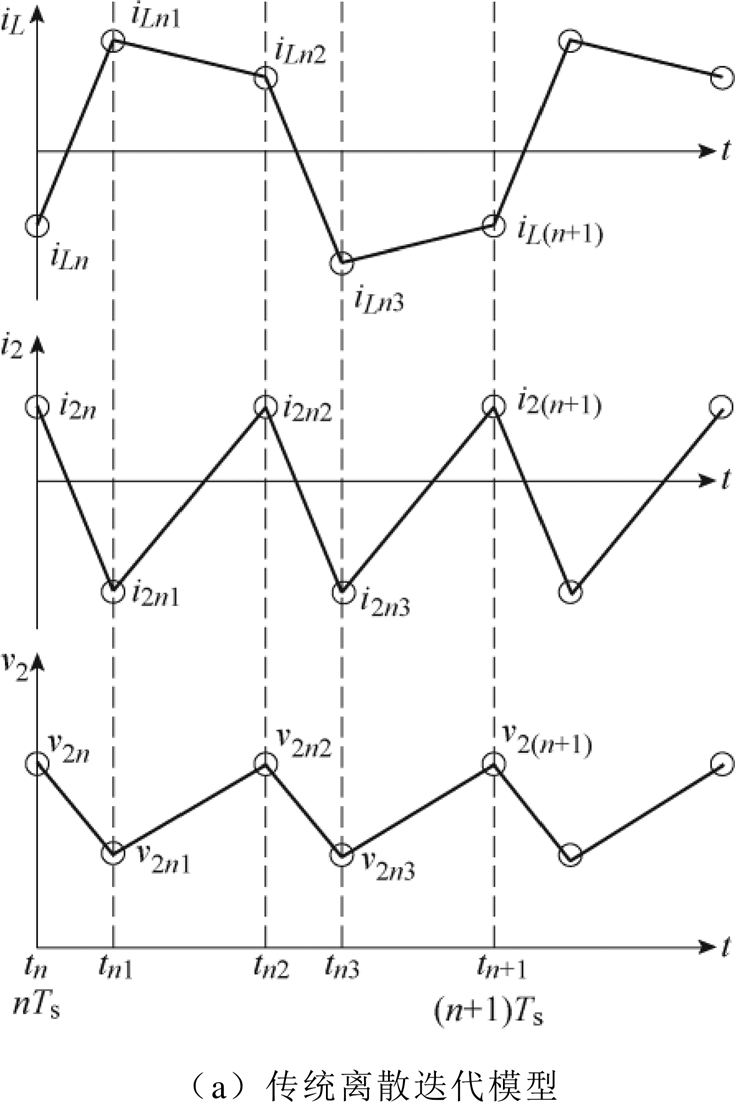
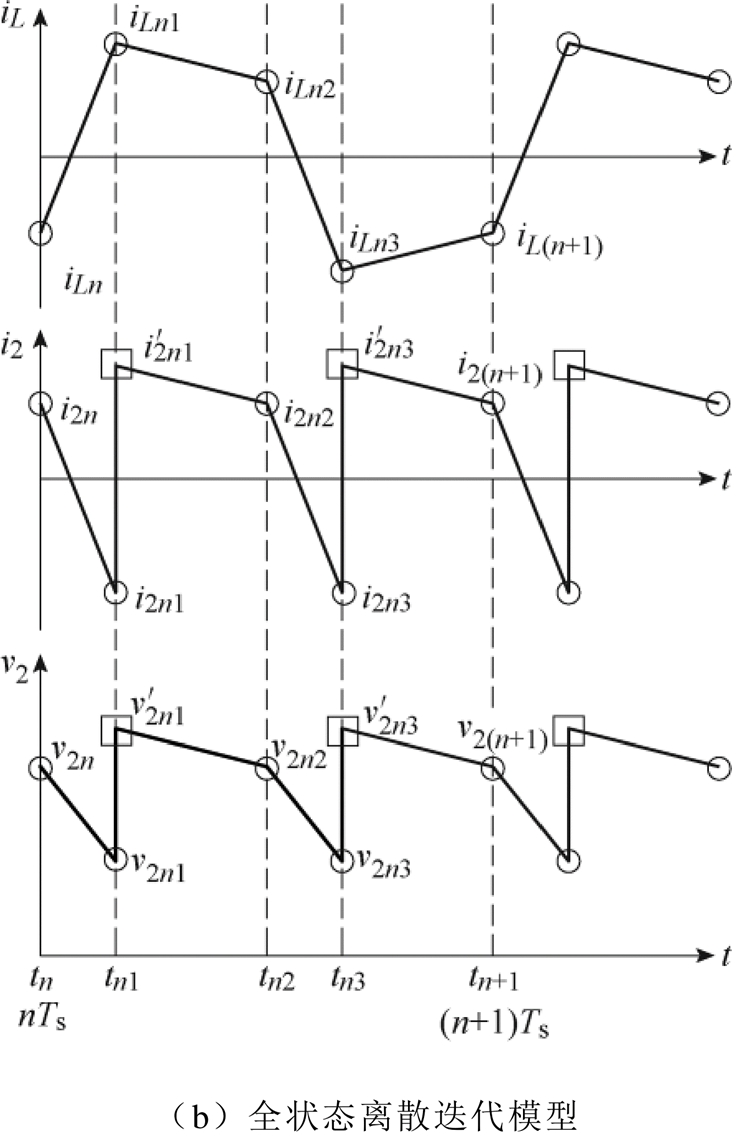
图4 DAB变换器电感电流与输出电压波形
Fig.4 The inductor current and output voltage waveforms of the DAB converter
因此，传统的基于子区间迭代的四状态离散迭代模型并不能完全反映出输出电压的真实特性。若要对DAB变换器的输出电压纹波特性进行深入分析，离散迭代模型就应当包含全面的输出电压状态。因此在建立DAB变换器的离散迭代模型时，应当将新发现的状态变量、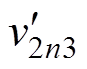考虑进去，进而可以建立更加精确的全状态离散迭代模型。
为了使输出电压离散迭代模型可包含状态点、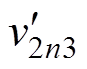的信息，应当对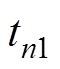、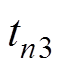时刻的电路状态进行分析。根据图2的等效电路，以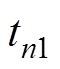时刻为例，此时图2a的电路结构会瞬间切换至图2b所示的电路结构。切换时刻电流
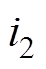会突然反向，此时电流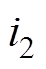的数值为
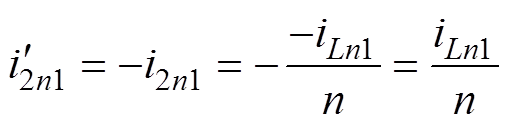（7）由电路的KCL和KVL可知，输出电压与电感电流和输出电容电压的关系为
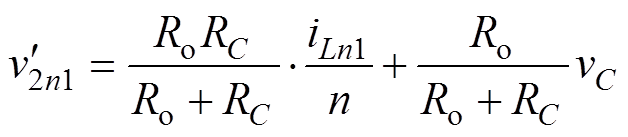（8）
将式（7）的电感电流代入式（8），可得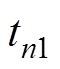时刻的输出电压的值为
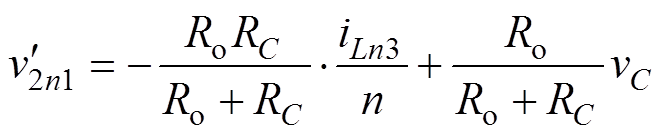（9）同理，可以求得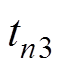时刻的输出电压状态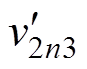为
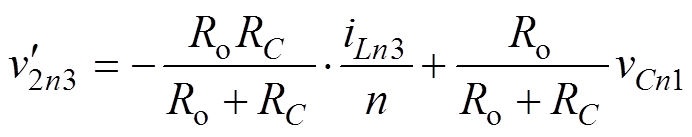（10）
由式（8）可知，一个开关周期内不同子区间的输出电压状态点可以由相应的电感电流和电容电压值得到。因此联立式（5）和式（8）即可得到输出电压的4个状态点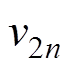、、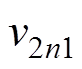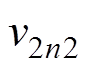和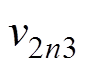。结合式（9）、式（10）所得到的另外两个子区间切换时刻的输出电压状态、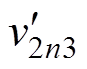，可以得到DAB变换器的输出电压全状态离散迭代模型为
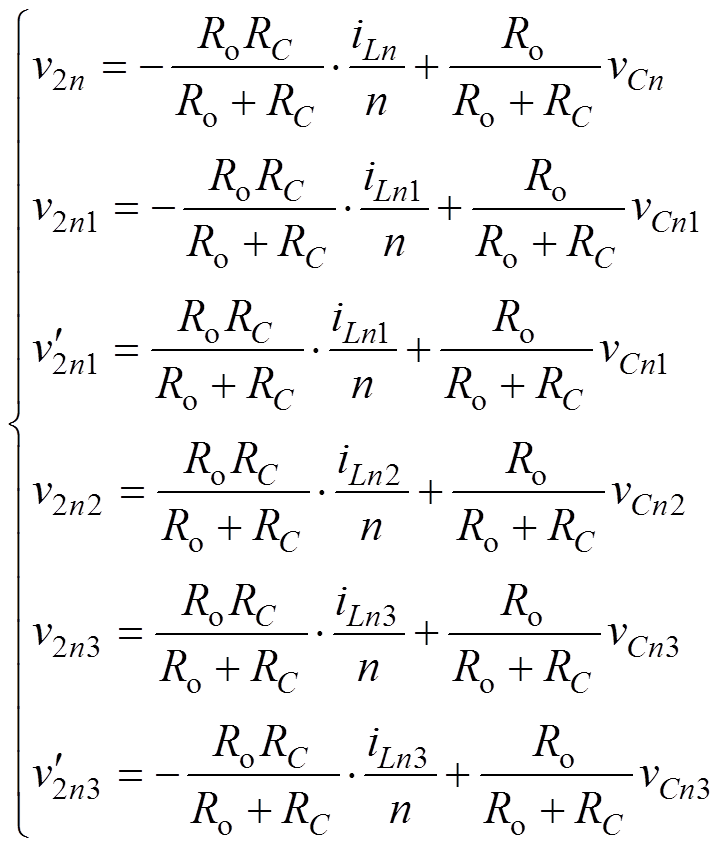（11）DAB变换器在一个开关周期内输出电压的6个状态点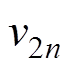、、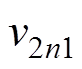、、、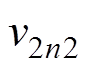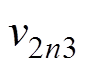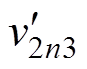便可以全部求出。这6个状态点分别为四个工作子区间的输出电压状态以及两个子区间切换时刻的状态。
在实际应用中，不同的工况和系统参数都会对DAB变换器的输出电压纹波造成很大的影响。由于DAB变换器的全状态离散迭代模型可以精确详细地揭示其输出电压的纹波信息，因此会给不同参数条件下的输出电压纹波分析带来很大的帮助。
在不同的输入电压范围内，DAB变换器的输出电压纹波形状和幅值都会有很大的差异。借助于DAB变换器的全状态离散迭代模型，下面将对这些特性进行详细的分析。
根据表1所示的系统参数，首先研究输出电压恒定时，输入电压连续变化对输出电压纹波形状和幅值的影响。图5所示为输出电压纹波随输入电压变化的曲线。由DAB变换器的全状态离散迭代模型可知，DAB变换器在一个开关周期内有6个电压状态。而输出电压波形在一个开关周期内又是相互对称的。因此一个开关周期内三组峰谷值中的最大值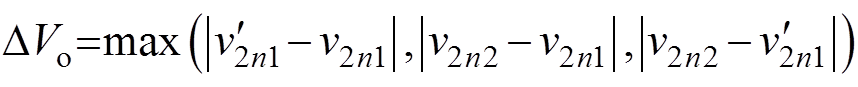
，即为DAB变换器的输出电压纹波值。输出电压纹波随输入电压变化的曲线如图5所示。图5a为三组峰谷值随输入电压变化的曲线。可以发现，三组峰谷值随输入电压的变化规律不尽相同，而且分别会在不同的输入电压区间产生最主要的影响。随着输入电压的变化，选取三组峰谷值中的最大值即可得到图5b所示的DAB变换器的三个纹波区间。每个纹波区间对应不同的峰谷值，同时也对应不同的输出电压纹波形状，不同输入电压区间输出电压波形如图6所示。在纹波区间1，输出电压的纹波形状如图6a所示，相应的DAB变换器输出电压纹波值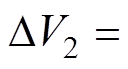
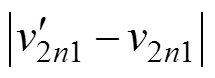。纹波区间2的输出电压纹波形状如图6b所示，对应的输出电压纹波值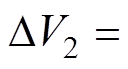
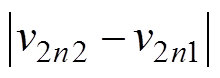。而纹波区间3对应的输出电压纹波形状如图6c所示，相应的输出电压纹波值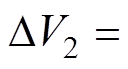
。
表1 系统参数
Tab.1 System parameters
参 数数 值 参考电压Vref/V30 等效电感Leq/mH38.26 等效电阻Req/W0.38 输出电容Co/mF500 输出电阻Ro/W20 开关频率fs/kHz20 变压器变压器电压比n1 等效串联电阻RC/W0.05
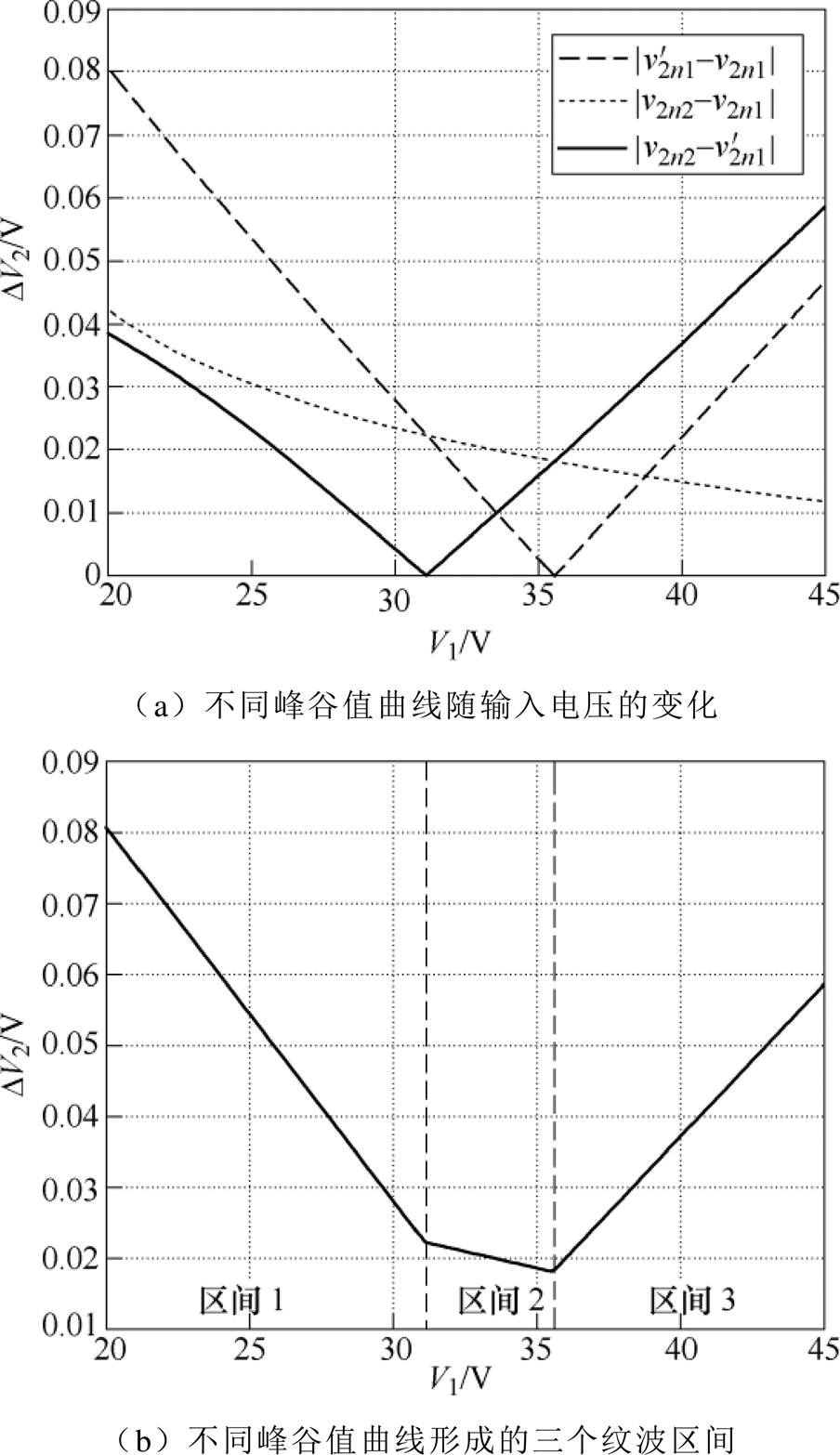
图5 输出电压纹波随输入电压变化的曲线
Fig.5 The output voltage ripple with respect to the input voltage
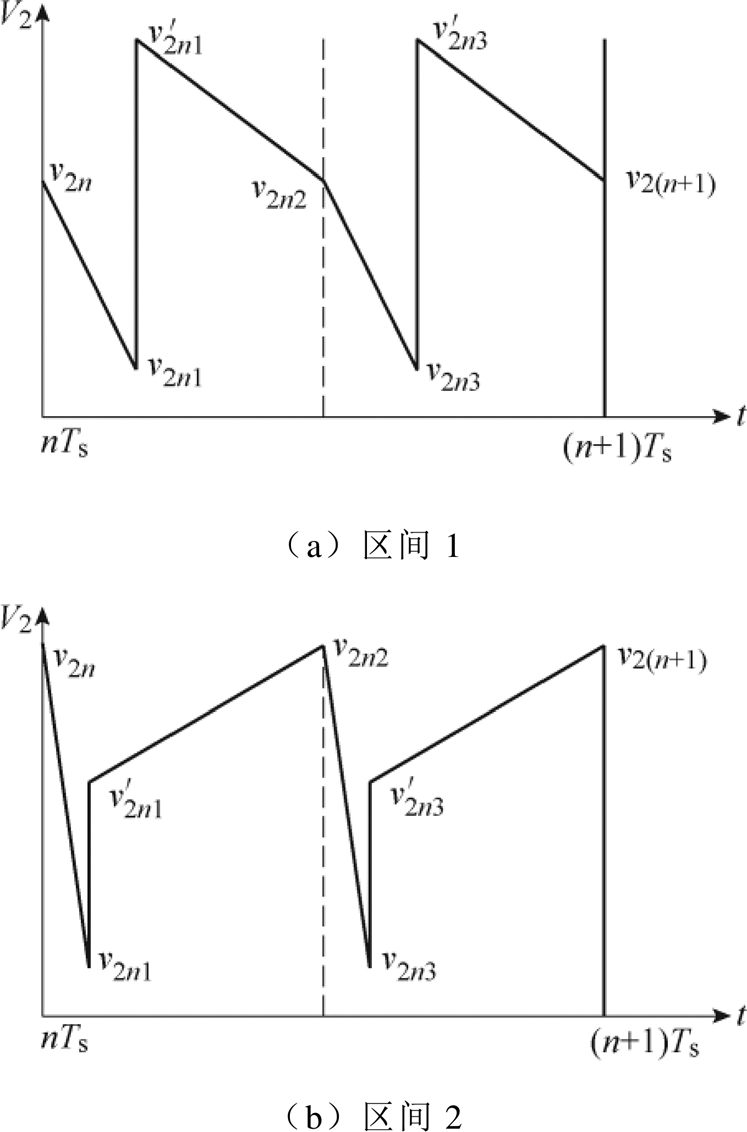
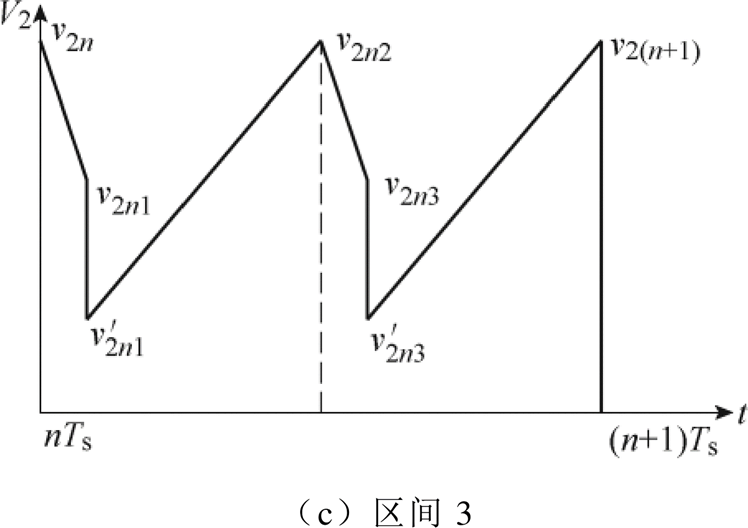
图6 不同输入电压区间输出电压波形
Fig.6 The output voltage waveforms of different range of input voltage
通过上述不同输入电压范围下的输出电压纹波特性分析可知，输入电压对输出电压纹波的形状和幅值都有很大的影响。其中，输入电压区间2对应的输出电压纹波是最小的。当输入电压落入区间1时，随着输入电压的减小，输出电压纹波会急剧增大。类似地，当输入电压落入区间3时，输出电压纹波则会随着输入电压的增大而不断增大。因此在设计DAB变换器的电压传输比时，当输出电压为恒定值时，应尽量避免输入电压位于区间1、3，以起到抑制输出电压纹波的作用。
在实际工作运行中，DAB变换器的不同工况也会对输出电压纹波造成很大的影响。以DAB变换器的不同输出电压为例，根据表2给出的输出电压变化时的系统参数，详细分析不同输出电压工况下的输出电压纹波特性。
表2 输出电压变化时的系统参数
Tab.2 System parameters when input voltage varies
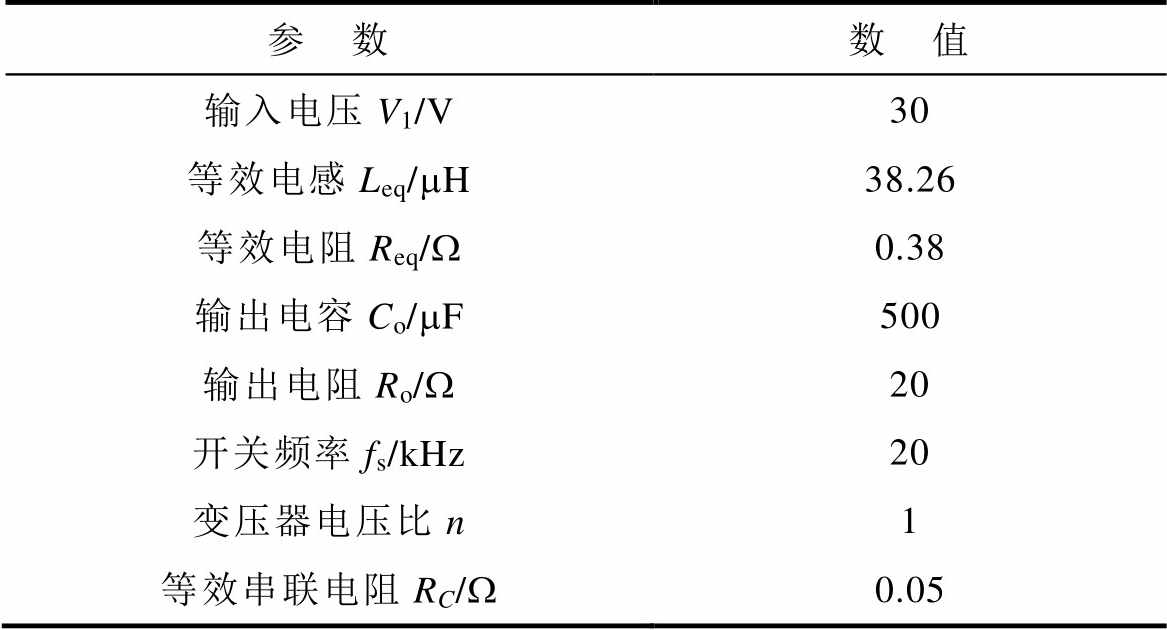
参 数数 值 输入电压V1/V30 等效电感Leq/mH38.26 等效电阻Req/W0.38 输出电容Co/mF500 输出电阻Ro/W20 开关频率fs/kHz20 变压器电压比n1 等效串联电阻RC/W0.05
输出电压纹波随输出电压变化的曲线如图7所示。根据全状态离散迭代模型，图7a给出了一个开关周期内输出电压三组峰谷值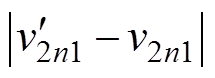
、
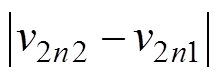和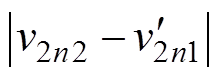
随输出参考电压变化的曲线。取各个区间上三组峰谷值的最大值，最终可得图7b所示的输出电压纹波随输出参考电压变化的曲线。
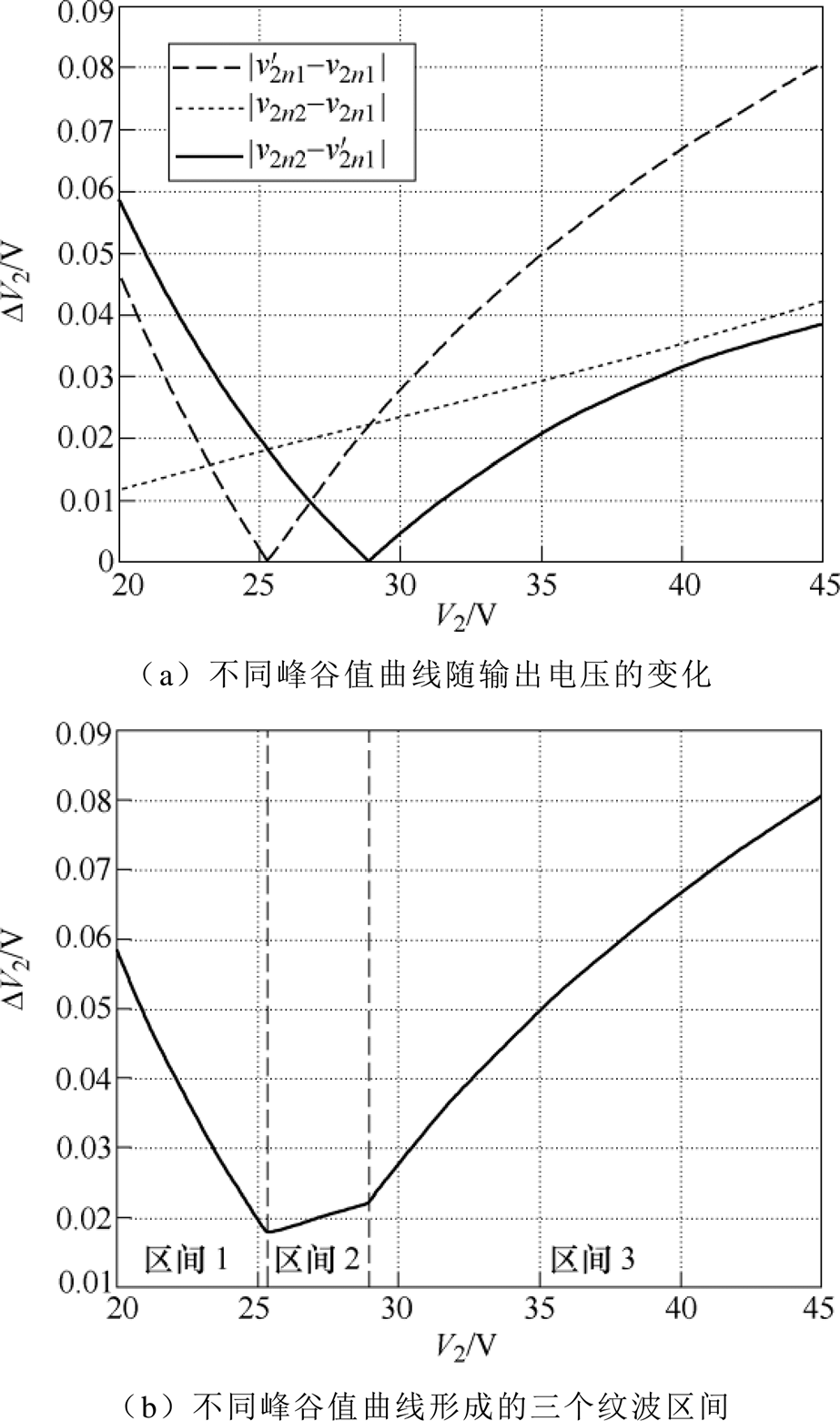
图7 输出电压纹波随输出电压变化的曲线
Fig.7 The output voltage ripple with respect to the output voltage
由图7可知，当输出电压参考值位于不同的区间时，电压纹波对应的表达式也会不同。不同输出电压区间输出电压波形如图8所示。其中输出电压区间1对应的电压波形如图8a所示，电压纹波的表达式
。而输出电压区间2和3对应的输出电压波形如图8b和图8c所示，其纹波表达式分别为
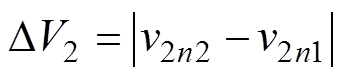和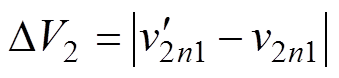
。
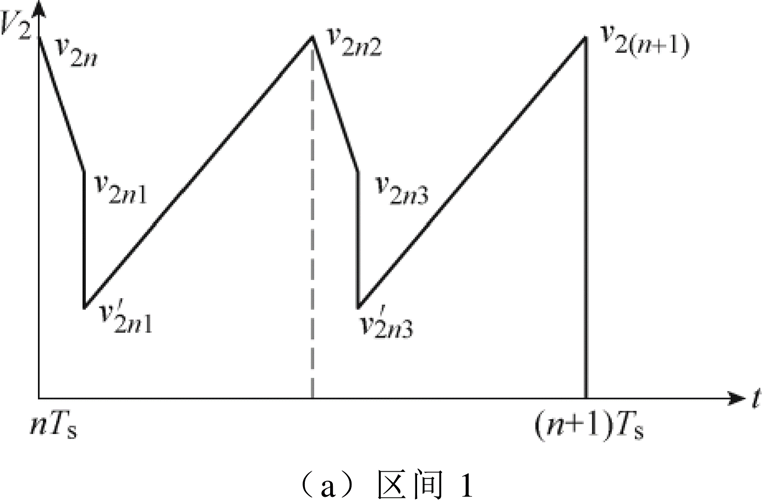
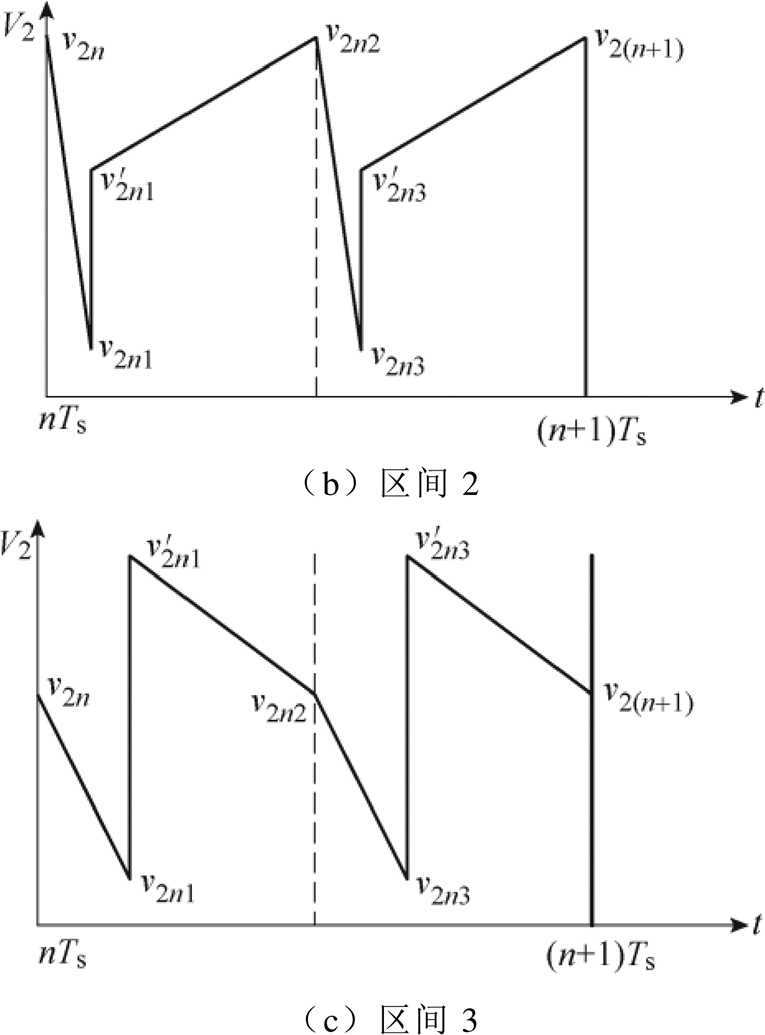
图8 不同输出电压区间输出电压波形
Fig.8 The output voltage ripple in different range of output voltage
通过以上对输出电压纹波的分析可知，当输出电压位于区间2时，输出电压的纹波是最小的。而当输出电压落入区间1和3时，输出电压纹波分别随着输出电压的减小和增大而逐渐增加。因此在DAB变换器的参数设计中，应当首先考虑区间1和3的最坏输出电压纹波工况，并通过综合的参数设计来使输出纹波控制在规定的范围内。同时，仔细对比输入电压变化与输出参考电压变化下的输出电压纹波值与纹波区间划分，可以发现两者是近似左右对称的。这也再次证明了DAB变换器作为广泛应用的接口装置，具有对称的拓扑结构。此外，以上基于全状态离散迭代模型的纹波区间划分方法和纹波特性分析同样适用于输出负载变化等其他工况下的状态变量纹波特性分析。
通过前面的分析可知，DAB变换器的不同系统参数和工况都可能会给输出电压状态带来很大的影响。在实际参数设计中，需要综合分析各系统参数和工况的影响以实现最优的设计效果。下面以输入电压和负载阻值为例，研究二者在一定范围内变化时输出电压纹波的变化现象和规律。根据前面得到的DAB变换器的全状态离散迭代模型和输出纹波分析方法，可以得到如图9所示的输出电压纹波与输入电压和负载阻值之间的关系。以图中A点和C点所对应的区域为例，当输入电压设计与负载阻值不匹配时，会造成输出电压纹波的大幅上升。因此，根据DAB变换器的负载阻值不同等工作状况，应合理设计输入电压等系统参数来避免输出电压纹波较大的情况。
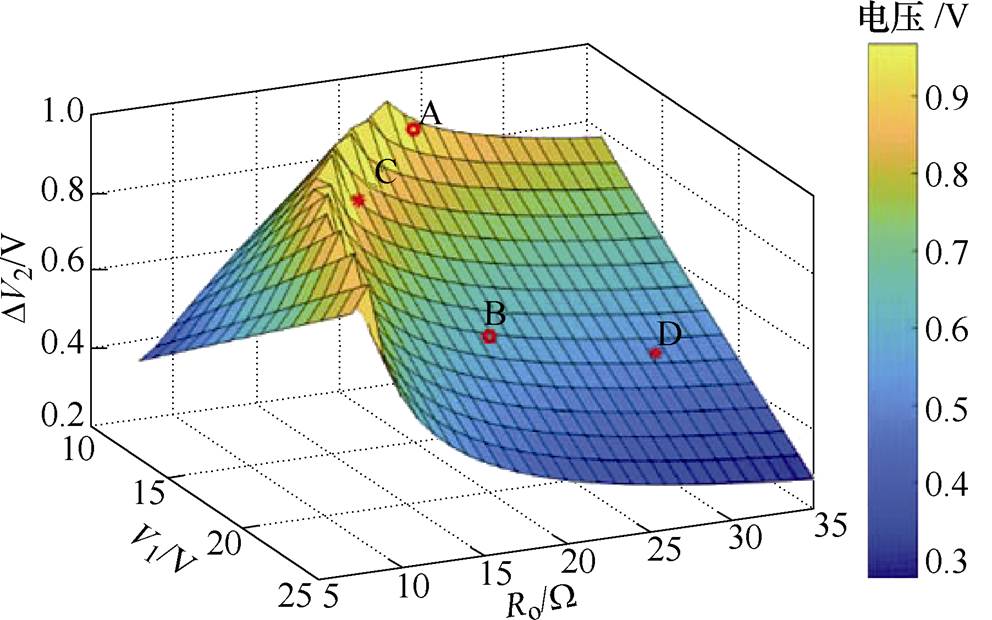
图9 输出电压纹波与输入电压和负载阻值的关系
Fig.9 The influence of the input voltage and output load resistance to the output voltage ripple
当DAB变换器的负载阻值为20Ω，输入电压分别为15V和20V时，其输出电压纹波分别对应于图9中的A点和B点。相应的传统离散迭代模型与全状态离散迭代模型的输出电压波形如图10所示。与图4的分析结果相一致，传统离散迭代模型由于在一个开关周期内丢失了两个关键的状态信息，其分析得到的输出电压纹波与实际值有很大的误差。以输入电压20V的工况为例，传统离散迭代模型计算得到的输出电压纹波与真实值相比有高达50%的误差，在此基础上的参数设计会给系统可靠性带来很大的影响。
在实际应用中，DAB变换器的负载阻值会经常发生变化。而在某些负载参数下，DAB变换器的输出电压纹波可能会非常大。图11所示为传统离散迭代模型与全状态离散迭代模型在负载阻值为10Ω和30Ω时的输出电压波形，其分别对应于图9中C点和D点。可以发现，随着负载阻值的增大，传统离散迭代模型与全状态离散迭代模型分析得到的输出电压纹波差距越来越大。这就意味着传统离散迭代模型分析得到的输出电压纹波与真实值相比，在某些参数和工况下会有极大的误差。因此，按照传统离散迭代模型分析设计的参数，在实际应用中可能会产生难以预料的输出电压纹波，进而造成输出滤波电容失效率的大幅提高和系统可靠性的降低。
图10 传统与全状态离散迭代模型在不同输入电压下的输出电压波形
Fig.10 The output voltage waveforms of the traditional and full-state iterative model under different input voltage
图11 传统与全状态离散迭代模型在不同负载阻值下的输出电压波形
Fig.11 The output voltage waveforms of the traditional and full-state iterative model under different load resistance
本文的数字控制DAB变换器实验平台如图12所示。其电路参数与表1和表2相一致。其中电压采样电路和电流采样电路会采集每个开关周期的电感电流和输出电压，然后由DSP数字控制器计算出下一周期开始时刻的移相角。
为了验证本文所提出的DAB变换器全状态离散迭代模型的有效性以及图9和图10的仿真结果，不同输入电压下的电感电流和输出电压实验波形如图13所示。为了更直观地表明全状态离散模型的准确性，图10中传统离散迭代模型与全状态离散迭代模型分析得到的输出电压纹波值和实验结果的对比见表3。可以发现，全状态离散迭代模型的分析计算结果与实验结果吻合度非常高，而传统离散迭代模型分析计算结果与实验结果却存在很大的误差。
图12 实验平台
Fig.12 Experimental prototype
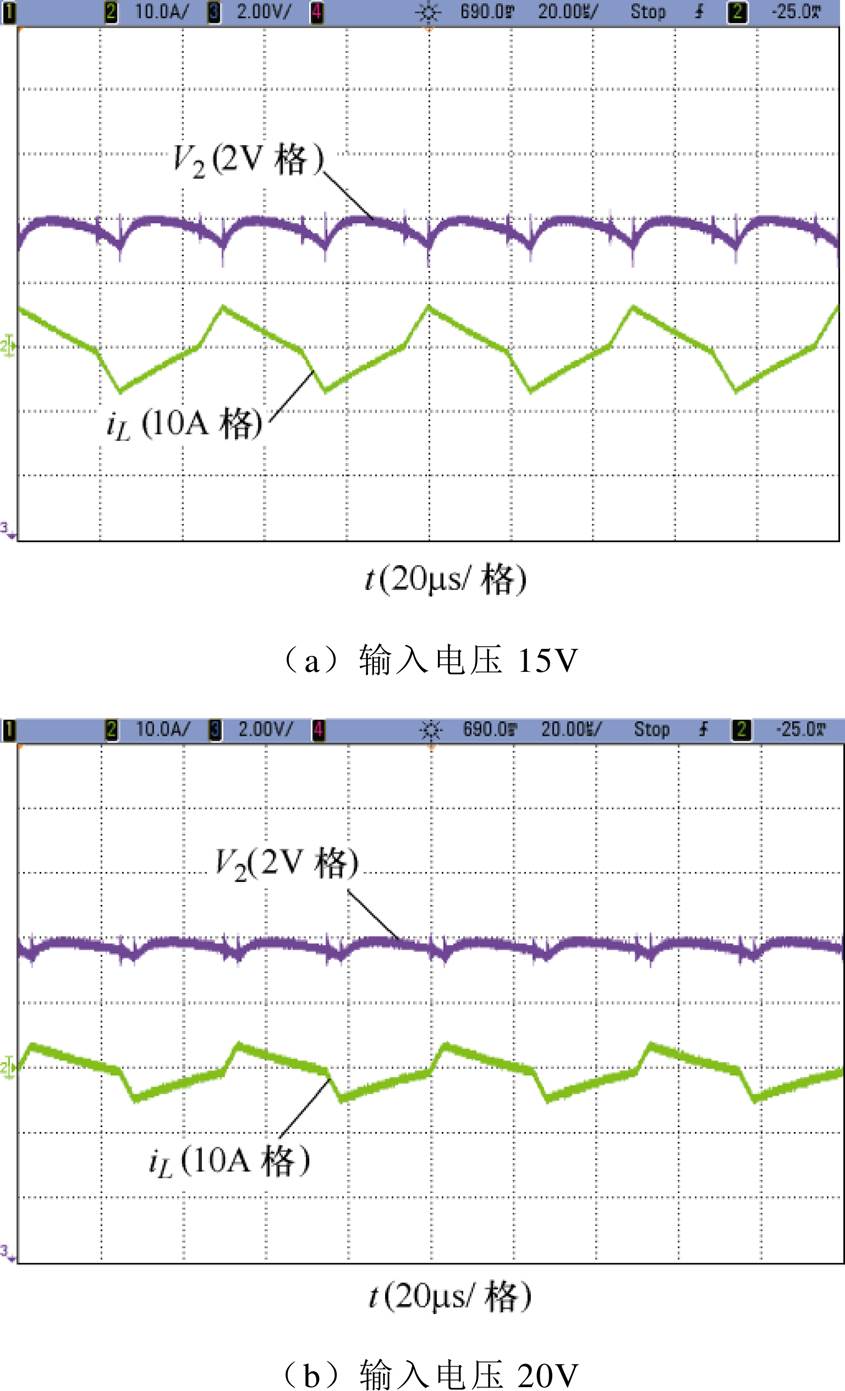
图13 不同输入电压下的电感电流与输出电压波形
Fig.13 The waveforms of the inductor current and output voltage under different input voltage
同样为了验证图11所示的两种离散迭代模型在不同负载阻值下的纹波分析结果，不同负载下的电感电流与输出电压实验波形如图14所示。实验和仿真得到的具体电压纹波值对比见表4。实验结果再次验证了全状态离散迭代模型的准确性和有效性。
表3 输入电压变化时的输出电压纹波
Tab.3 The voltage ripple under different input voltage
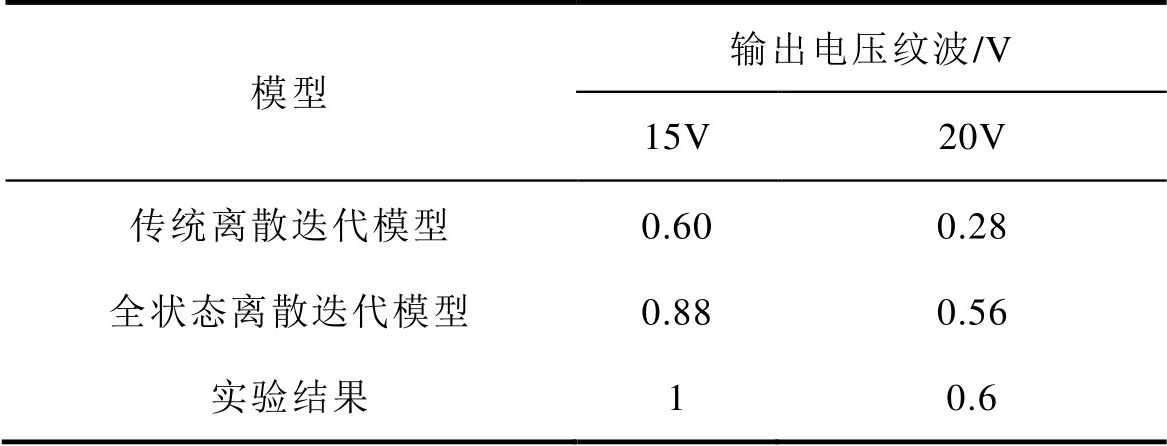
模型输出电压纹波/V 15V20V 传统离散迭代模型0.600.28 全状态离散迭代模型0.880.56 实验结果10.6
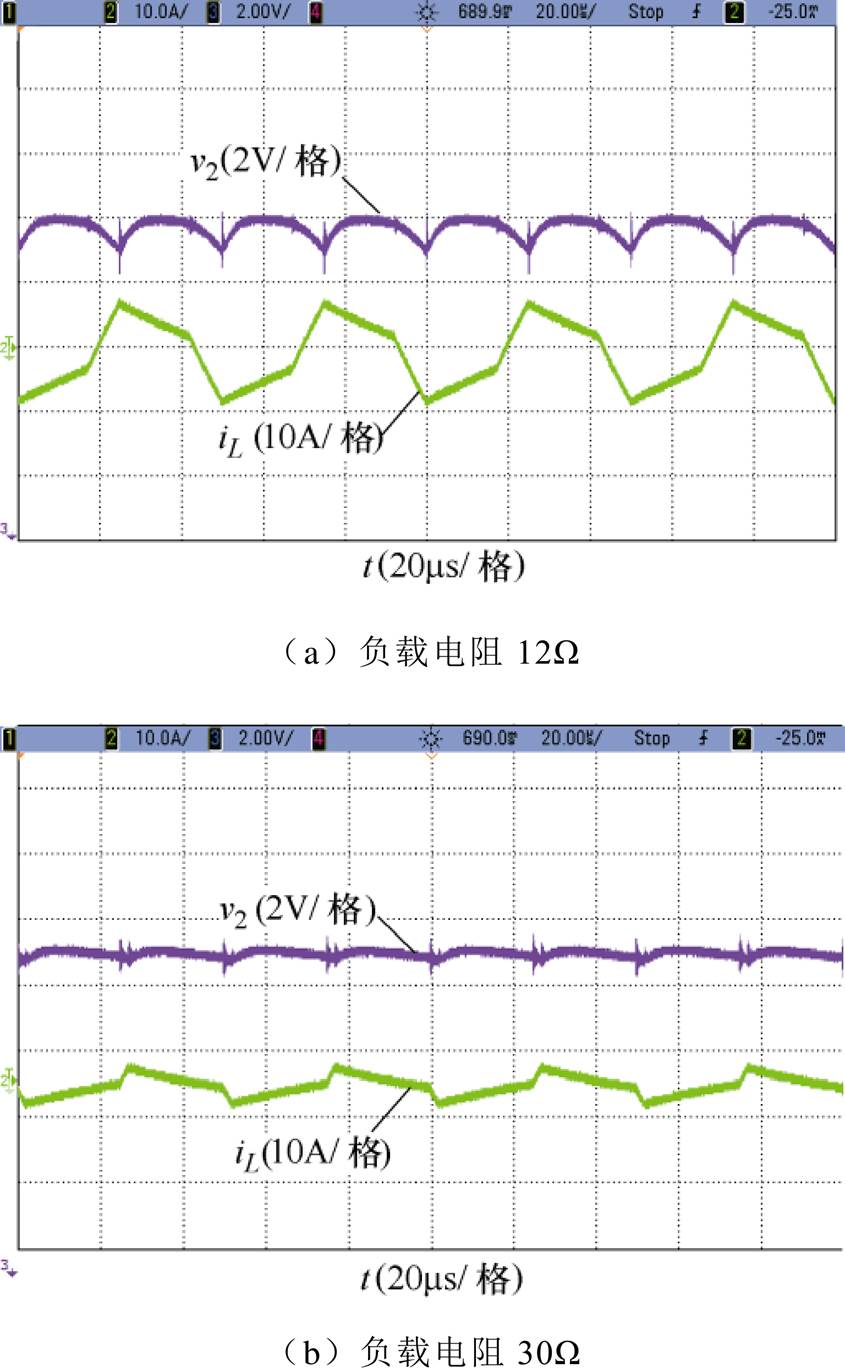
图14 不同负载电阻下的电感电流与输出电压波形
Fig.14 The waveforms of the inductor current and output voltage under different load resistance
表4 负载变化时的输出电压纹波
Tab.4 The voltage ripple under different load
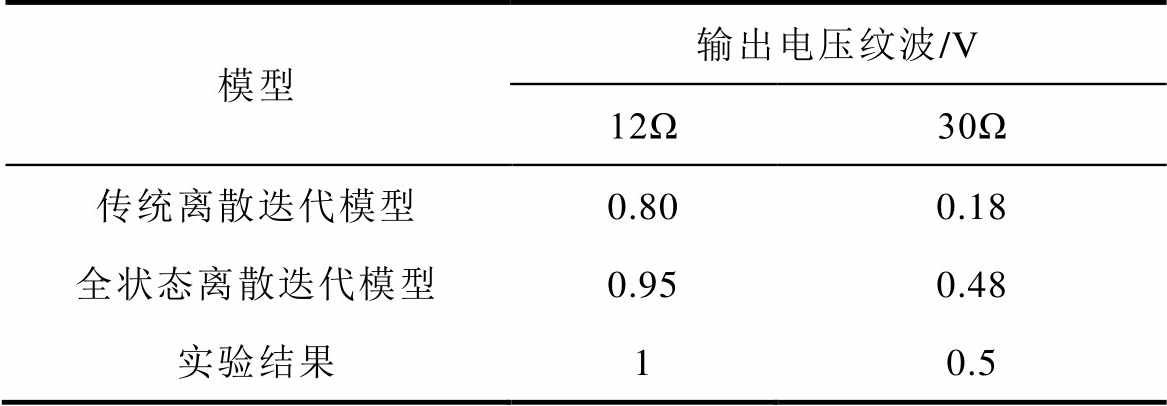
模型输出电压纹波/V 12Ω30Ω 传统离散迭代模型0.800.18 全状态离散迭代模型0.950.48 实验结果10.5
本文通过分析DAB变换器的电路结构和工作原理，揭示了传统离散迭代建模方法在DAB变换器输出电压纹波分析中的局限性。基于DAB变换器在一个开关周期中不同工作区间的状态变量分析，本文提出了DAB变换器的全状态离散迭代模型。与传统离散迭代模型相比，全状态离散迭代模型揭示了DAB变换器纹波分析中所必需的全部状态信息，因此具有更高的分析精度。
同时本文基于全状态离散迭代模型分析了DAB变换器在不同参数和工况下的输出电压纹波特征，并通过实验进行了验证。此外，本文通过综合分析不同系统参数和工况下的输出电压纹波特性，为系统参数优化设计提供了方向，同时该方法具有推广并应用到其他类型变换器离散迭代建模和纹波分析的潜力。
参考文献
[1] Zhao Biao, Song Qiang, Liu Wenhua, et al. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4091-4106.
[2] Kheraluwala M N, Gascoigne R W, Divan D M, et al. Performance characterization of a high-power dual active bridge DC-to-DC converter[J]. IEEE Transa- ctions on Industry Applications, 1992, 28(6): 1294- 1301.
[3] 苗璐, 林卫星, 姚良忠, 等. 多端口背靠背式直流-直流换流系统[J]. 中国电机工程学报, 2015, 35(5): 1024-1031.
Miao Lu, Lin Weixing, Yao Liangzhong, et al. Multiport back-to-back DC-DC converting systems[J]. Proceedings of the CSEE, 2015, 35(5): 1024-1031.
[4] 沙广林, 王聪, 程红, 等. 移相控制的双有源桥DC-DC变换器统一相量分析法[J]. 电工技术学报, 2017, 32(18): 175-185.
Sha Guanglin, Wang Cong, Cheng Hong, et al. Unified phasor analysis method for dual active bridge DC-DC converters with phase shift control[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(18): 175-185.
[5] 张明锐, 刘金辉, 金鑫. 应用于智能微网的SVPWM固态变压器研究[J]. 电工技术学报, 2012, 27(1): 90-97.
Zhang Mingrui, Liu Jinhui, Jin Xin. Research on the SVPWM solid state transformer applied in smart micro-grid[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 90-97.
[6] 张雪垠, 徐永海, 肖湘宁. 适用于中高压配电网的高功率密度谐振型级联 H 桥固态变压器[J]. 电工技术学报, 2018, 32(2): 310-321.
Zhang Xueyin, Xu Yonghai, Xiao Xiangning. A high power density resonance cascaded H-bridge solid-
state transformer for medium and high voltage distribution network[J]. Transactions of China Elec- trotechnical Society, 2018, 32(2): 310-321.
[7] Rico Secades M, García Llera D, López Corominas E R, et al. Designing dual-active bridge (DAB) converterfor energy storage/recovery systems in a lighting smart grid context[J]. Workrooms Journal, 2014, 2: 1-20.
[8] 肖智明, 陈启宏, 张立炎. 电动汽车双向DC-DC变换器约束模型预测控制研究[J]. 电工技术学报, 2018, 33(增刊2): 239-248.
Xiao Zhiming, Chen Qihong, Zhang Liyan. Con- strained model predictive control for bidirectional DC-DC converter of electric vehicles[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(S2): 239-248.
[9] Bai Hua, Mi Chunting, Wang Chongwu, et al. The dynamic model and hybrid phase-shift control of a dual-active-bridge converter[C]//Conference of the IEEE Industrial Electronics Society, Orlando, United States, 2008: 2840-2845.
[10] Guacaneme J, Garcera G, Figueres E, et al. Dynamic modeling of a dual active bridge DC to DC converter with average current control and load-current feed-forward[J]. International Journal of Circuit Theory & Applications, 2015, 43(10): 1311-1332.
[11] Hengsi Q, Kimball J W. Generalized average modeling of dual active bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 2078-2084.
[12] Costinett D, Zane R, Maksimovic D. Discrete-time small-signal modeling of a 1MHz efficiency- optimized dual active bridge converter with varying load[C]//13th Workshop on Control and Modeling for Power Electronics (COMPEL), Doshisha University, Kyoto, 2012: 1-7.
[13] Shi Ling, Lei Wanjun, Li Zhuoqiang, et al. Bilinear discrete-time modeling and stability analysis of the digitally controlled dual active bridge converter[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8787-8799.
[14] Costinett D. Reduced order discrete time modeling of ZVS transition dynamics in the dual active bridge converter[C]//2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, 2015: 365-370.
[15] 童安平, 杭丽君, 李国杰, 等. 基于离散迭代模型的DAB变换器等效电路研究[J]. 中国电机工程学报, 2019, 39 (4): 1138-1149.
Tong Anping, Hang Lijun, Li Guojie, et al. A discrete- time model based equivalent circuit of dab converter[J]. Proceedings of the CSEE, 2019, 39(4): 1138-1149.
[16] Dhople S V, Davoudi A, Domínguez-García A D, et al. A unified approach to reliability assessment of multiphase DC-DC converters in photovoltaic energy conversion systems[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 739-751.
[17] Liu J C P, Poon N K, Pong B M H, et al. Low output ripple DC-DC converter based on an overlapping dual asymmetric half-bridge topology[J]. IEEE Transa- ctions on Power Electronics, 2007, 22(5): 1956-1963.
[18] Chiu H, Chen C, Tsai M, et al. A novel isolated buck converter with output voltage ripple reduction by a complementary square-wave scheme[C]//2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 2011: 1786-1790.
[19] Babaei E, Mahmoodieh M E S, Mahery H M. Operational modes and output-voltage-ripple analysis and design considerations of Buck-Boost DC-DC converters[J]. IEEE Transactions on Industrial Elec- tronics, 2012, 59(1): 381-391.
[20] Babaei E, Mahmoodieh M E S. Calculation of output voltage ripple and design considerations of SEPIC converter[J]. IEEE Transactions on Industrial Elec- tronics, 2014, 61(3): 1213-1222.
[21] Liu Shulin, Li Yan, Liu Li. Analysis of output voltage ripple of Buck DC-DC converter and its design[C]//2009 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, China, 2009: 112-115.
[22] 刘豹. 现代控制理论[M]. 2版. 北京: 机械工业出版社, 2004.
Full-State Discrete-Time Model and the Output-Voltage-Ripple Analysis of the Dual Active Bridge Converter
Abstract By analyzing the drawbacks of the conventional discrete-time model of the dual active bridge (DAB) converter, the full-state discrete-time model of the DAB converter is proposed, and the output-voltage-ripple analysis under different system parameters and working condition is conducted. The conventional discrete-time model of the DAB converter is based on the interval-by-interval iteration, which will miss many essential information of the state variables and cannot reflect the actual working condition of the converter. By analyzing the working principle of the converter, the proposed full-state discrete-time model can reveal all the crucial information of the state variables. Taking the output voltage as an example, the full-state discrete-time model can reveal the output-voltage information at the subinterval switching moment. Therefore, the output-voltage-ripple analysis is more accurate and conducive to improving system reliability. The experimental results also verify the proposed model and the analysis results.
keywords：Dual active bridge converter, discrete-time model, output voltage ripple, parameter design
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.191643
广东电网有限责任公司科技资助项目（031300KK52170068）。
收稿日期2019-11-26
改稿日期2020-02-13
高国庆 男，1993年生，硕士研究生，研究方向为电力电子变换器建模与设计等。E-mail: gaoguoqing@stu.xjtu.edu.cn
雷万钧 男，1976年生，博士，副教授，研究方向为电能质量控制技术、无线充电等。E-mail: leiwanjun@xjtu.edu.cn（通信作者）
（编辑 陈 诚）