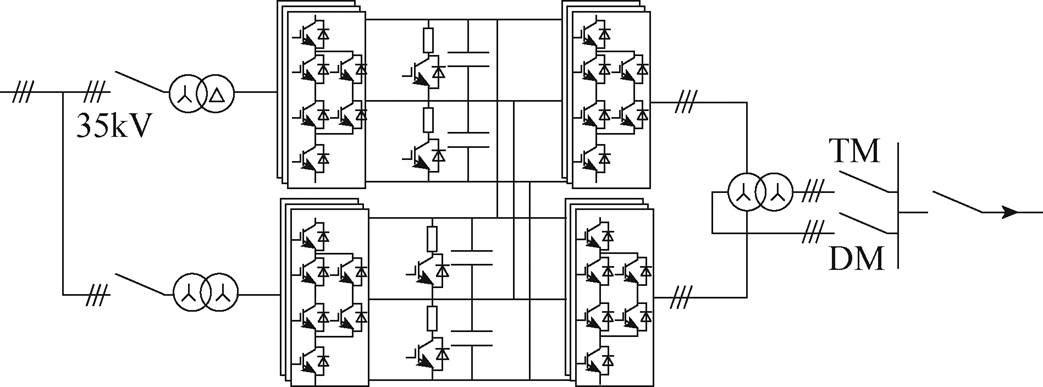
图1 磁悬浮列车牵引变流器系统框图
Fig.1 Diagram of traction converter of maglev
摘要 高速磁悬浮列车采用长定子直线同步电机驱动，在运行过程中采用分段供电的方式，当磁悬浮列车从一个定子段过渡到另一个定子段时，列车一侧的定子会经历电流降为零再增大的换步过程。对于高速磁悬浮系统中三相PWM整流器而言，负载在换步过程中变化剧烈，对直流侧输出电压产生了严重的影响。为了抑制负载扰动对直流侧电压的影响，提出一种结合自抗扰和负载功率前馈的电压、电流双闭环控制策略。通过硬件在环实验验证了该策略对负载变化具有较强的鲁棒性，降低了定子段换步过程中的直流母线电压波动，提高了PWM整流器的抗负载扰动能力和系统动态性能。
关键词：高速磁悬浮列车 PWM整流器 换步 负载功率前馈 自抗扰控制
“十三五”国家科技创新规划提出要加强高速（600km/h）磁悬浮的关键技术与装备研发，三相PWM整流器具有功率因数可控、能量双向流动、输入电流谐波含量低等优点，在交流传动领域取得了广泛的应用[1-3]，高速磁悬浮系统也采用三相PWM整流器。高速磁悬浮列车的牵引变流器系统框图如图1所示，容量为24MV·A，由输入变压器、整流器、斩波器、逆变器和输出变压器构成[4]。为满足高速磁悬浮列车运行要求，采用了两套背靠背三电平有源中点钳位（Active Neutral-Point-Clamped, ANPC）变流器共用直流母线的拓扑结构，输入变压器由两台Yy和Yd11的变压器并联，降低输入电流谐波；逆变器输出有两种输出模式，即直接模式（Direct Mode, DM）和变压器模式（Transformer Mode, TM）。牵引变流器把35kV公共电网的电能经输入降压变压器变成3 000V的交流电，整流器将此交流电变换成5 000V的直流电，逆变器则将直流电逆变成所需频率和幅值的电压，并通过馈电电缆向长定子直线电机供电。
图1 磁悬浮列车牵引变流器系统框图
Fig.1 Diagram of traction converter of maglev
与传统的交流传动不同，高速磁悬浮列车采用长定子直线同步电机驱动，磁悬浮列车运行过程中采用分段供电的方式，当磁悬浮列车从一个定子段过渡到另一个定子段时，列车一侧的定子会经历电流降为零再增大的换步过程[5]。对于高速磁悬浮系统中三相电压型PWM整流器而言，负载在换步过程中变化剧烈，对直流侧输出电压产生了严重的影响，引起较大的母线电压超调，不仅影响磁悬浮列车的稳定运行，而且还会对高速磁悬浮系统中的功率开关器件的安全造成威胁。因此如何抑制换步过程中的直流母线电压波动成为亟待解决的问题。从目前所查阅的文献看，PWM整流器主要有电压、电流双闭环的矢量控制（Vector Control, VC）、直接功率控制（Direct Power Control, DPC）以及基于现代控制理论的一些新控制策略。
电压型PWM整流器多采用电压、电流双闭环的矢量控制策略[6]，传统的基于PI的控制策略，由于交流侧电感存在差异，前馈解耦效果不好，此外电压外环的非线性也使得PI控制器的性能受到限制，在负载突变时会导致母线电压超调[7]。针对母线电压受负载扰动影响大的问题，文献[8-10]采用直流侧电容储能作为外环，并将负载功率估计后进行前馈的控制策略。文献[11]采用直流侧电容电压二次方作为控制变量，实现了稳态时直流母线电压二次方与电流有功分量的线性关系。文献[12]根据负载扰动瞬间的功率关系，把补偿电流与负载电流一起作为有功电流的补偿进行前馈控制。上述文献在一定程度上改善了负载变化时系统的动态响应，但均采用了传统的PI控制，因控制器参数是在稳态下设计的，动态变化过程中效果不佳。
直接功率控制是另一种常用的PWM整流器控制策略[13-17]，能够直接实现网侧有功和无功功率的控制，控制结构简单、灵活，响应速度快。但该策略对有功和无功功率的控制精度较差，而且谐波电流依赖直流侧电压大小，分布在很宽的频带范围内，不利于设计单一的滤波器实现滤波作用。
自抗扰控制器（Active Disturbance Rejection Control, ADRC）是一种对系统内扰和外扰鲁棒的控制器，不依赖数学模型[18]。文献[19-21]提出了基于自抗扰的PWM整流器控制策略，通过扩张状态观测器（Extended State Observer, ESO），对PWM整流器内部的扰动以及负载变化引起的外部扰动进行估计和补偿，改善了系统控制性能，在抵抗电网电压扰动和负载扰动方面具有优越性。但对高速磁悬浮系统中MW级三相电压型PWM整流器而言，负载在换步过程中变化剧烈，上述基于自抗扰的控制策略仅仅通过ESO进行观测存在滞后以及带宽受限的问题，无法及时观测出扰动并进行补偿，容易导致母线电压出现较大超调和引起过大的冲击电流。
本文针对高速磁悬浮系统中PWM整流器换步过程中母线波动大的问题，提出一种基于自抗扰的PWM整流器控制策略，并对传统自抗扰控制策略进行改进，根据负载扰动瞬间的功率关系，把负载功率进行前馈控制，提高了响应速度，降低了母线电压波动，最后通过基于RT-LAB的高速磁悬浮半实物系统硬件在环实验，验证了所提算法的正确性。
高速磁悬浮系统为了提高供电的可靠性以及降低输入电流谐波，采用两台PWM整流器经两台Yy和Yd11输入变压器并联的方式。为保证网侧电压和电流单位功率因数运行，Yd11变压器所连接的PWM整流器用于坐标变换的角度，需要在网侧电网锁相角的基础上增加30°，除此之外两台整流器控制策略基本一致，因此下面的分析均以单台PWM整流器为例。三电平有源中点钳位PWM整流器拓扑如图2所示。
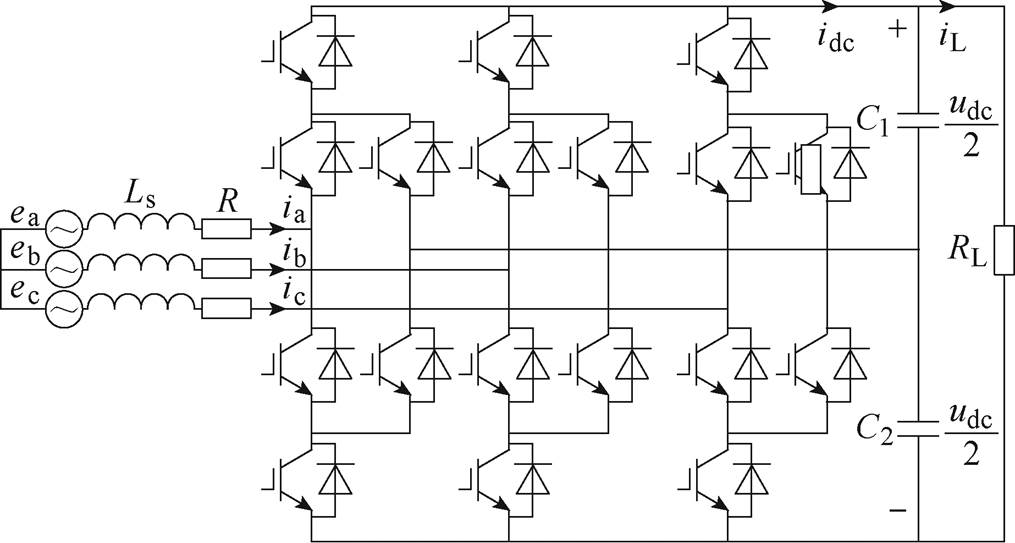
图2 三电平有源中点钳位PWM整流器拓扑
Fig.2 Topology of ANPC voltage source PWM rectifier
图2中，ea、eb、ec为电网电压；ia、ib、ic为整流器输入电流；Ls为网侧等效电感；R为内阻，通常较小；C1、C2为两个直流母线电容，容值相等为C/2；udc为直流母线电压；idc为直流母线电流；iL为负载电流；RL为负载电阻。
采用基尔霍夫电压、电流定律，通过坐标变换可以建立三电平PWM整流器在两相旋转坐标系中的状态空间方程为
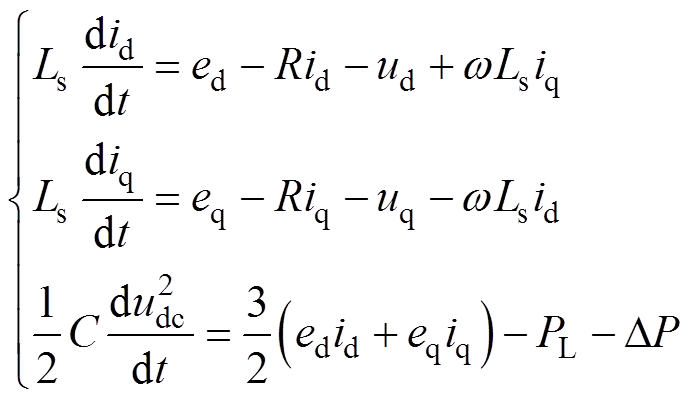（1）式中，ed、eq分别为d、q坐标下的网侧电压；id、iq分别为d、q坐标下的整流器输入电流；ud、uq分别为d、q坐标下的整流器交流侧电压；PL为负载功率；DP为整流器损耗功率，包括滤波电感和器件损耗。
从式（1）可以看出，由于耦合项的存在，dq轴电流存在耦合，通常采用前馈解耦的策略来消除。采用PI调节器作为电流内环和电压外环的控制器，可以得到
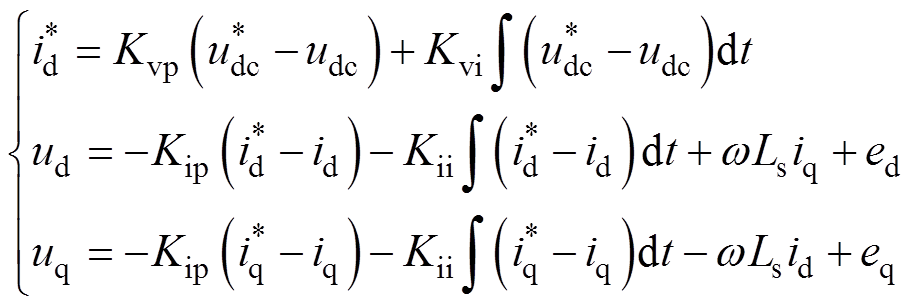（2）式中，Kvp、Kvi分别为电压外环PI调节器的比例系数和积分系数；Kip、Kii分别为电流内环PI调节器的比例系数和积分系数；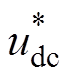
为给定母线直流电压；
、
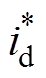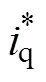分别为d轴和q轴给定电流。
三电平整流器电压、电流双闭环控制策略的控制框图如图3所示。
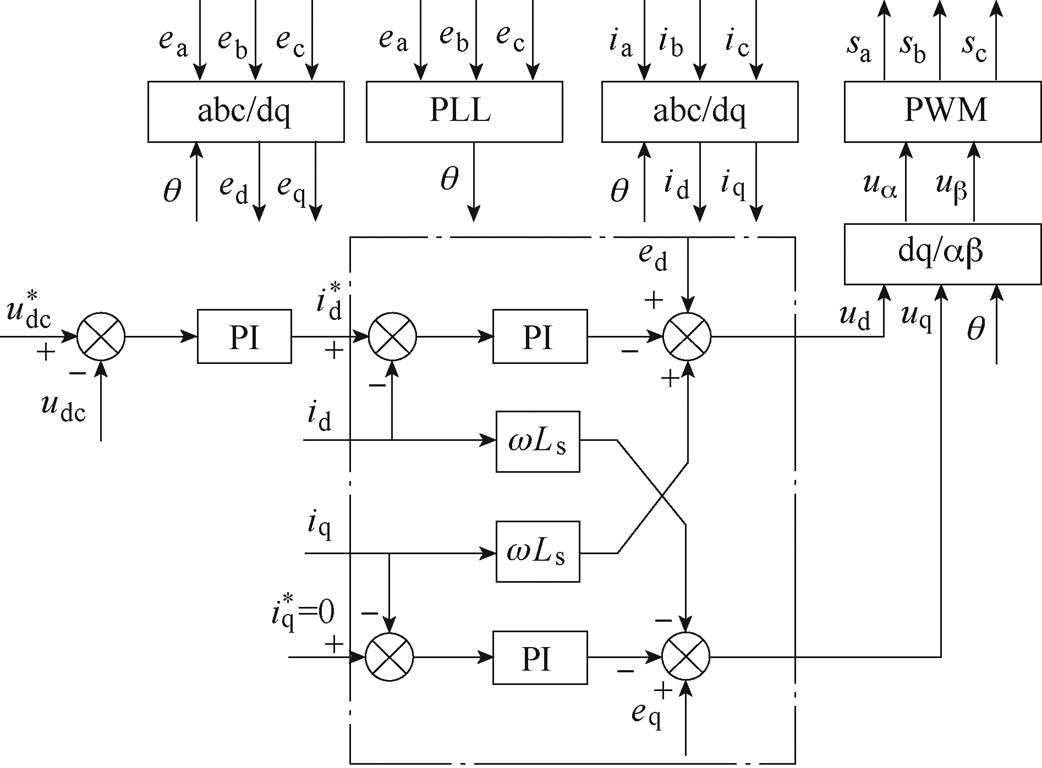
图3 基于PI的三相PWM整流器控制框图
Fig.3 The control diagram of PWM rectifier based PI
从式（2）可以看出，采用前馈解耦的策略需要准确的交流侧电感，而交流侧电感估计值与实际值存在差异，导致解耦不准确，此外电压外环的非线性也使得PI控制器的性能受到限制。
经典的一阶自抗扰控制原理如图4所示[22]，包括跟踪微分器（Tracking Differentiator, TD）、扩张状态观测器、非线性状态误差反馈控制律（Nonlinear State Error Feedback, NLSEF）。图中，r为给定信号，v1为安排过渡过程后的给定信号，z1、z2分别为输出和总扰动的观测值，b0为估算控制增益，u0为控制器输出，u为扰动补偿后的输入。
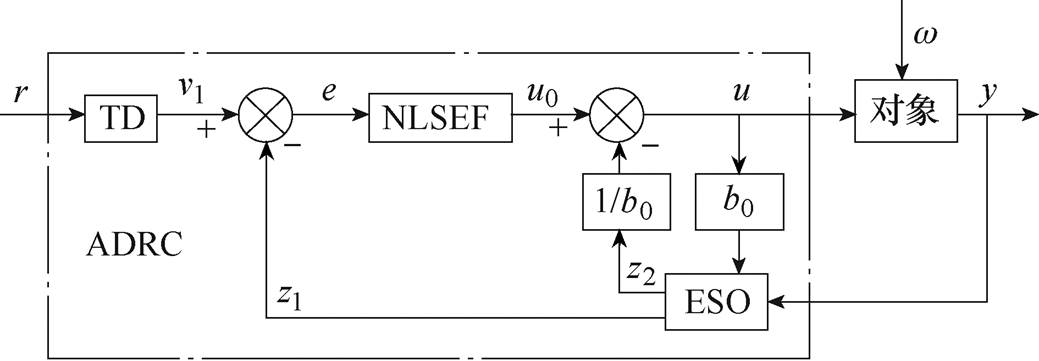
图4 自抗扰控制原理
Fig.4 Schematic diagram of ADRC
自抗扰控制的原理：首先通过TD依据被控对象的特性，安排合适的过渡过程，快速跟踪输入信号，并获得广义微分信号；然后通过ESO实时估计系统的状态信息以及总扰动信息，并对扰动进行前馈补偿；最后通过NLSEF用状态反馈规律把非线性系统变成积分串联型线性系统。ADRC通过引入ESO对总扰动进行实时观测和补偿，不依赖对象的具体数学模型，在改善系统的动态性能、鲁棒性等方面都有显著的效果。通过选择不同的TD、ESO、NLSEF函数，可以得到多种类型的自抗扰控制器。
从图4可以看出，经典的自抗扰控制器需要改变系统结构，文献[23]提出了基于误差的通用自抗扰控制器，便于工业应用。PWM整流器内环和外环均为一阶系统，因此本文在文献[23]基础上推导了一阶系统的基于误差的自抗扰控制器。采用二阶线性ESO，取消了TD环节，NLSEF选择了比例反馈控制律，将经典算法重构，选取误差信号e与扰动信号f作为状态变量，则一阶系统表示为
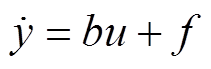（3）式中，u为控制输入；y为系统输出；f为总扰动；b为控制增益。
误差信号e=r-y，r为输入给定值，代入式（3）中得
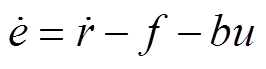（4）选取状态变量x1=e,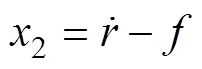 
，则式（4）所示的系统变成
（5）
对式（5）构造二阶线性ESO，可得
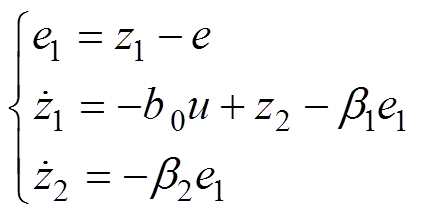（6）式中，b1、b2为扩张状态观测器系数；z1为误差信号e的观测值；z2为总扰动x2的观测值。由于观测器带宽受限，观测值有相位滞后，因此控制器选择原始的误差信号e作为输入，同时选择比例反馈控制律，可得
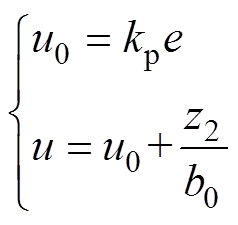（7）
式中，kp为比例增益。
在观测器带宽内，可认为z2≈x2，代入式（7）中得
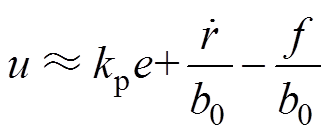（8）从式（8）可以看出，改进的控制律结合了反馈控制、输入微分前馈以及扰动补偿，具有良好的控制性能。将式（7）代入式（6）中，进行拉普拉斯变换后，得到控制器的传递函数为
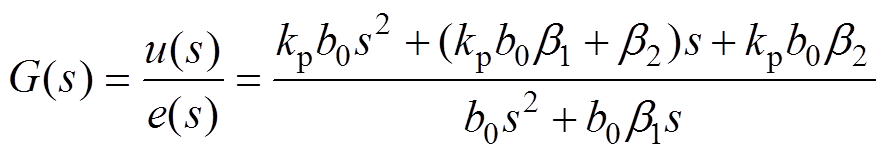（9）
通过上述推导，可得基于误差的自抗扰控制原理如图5所示。相较于经典的自抗扰控制器，ESO在观测扰动的同时观测了给定信号的微分，在观测器带宽内，可以同时实现扰动补偿和输入微分前馈，提高响应速度；控制器的输入变成了误差信号，便于与前馈控制策略结合。
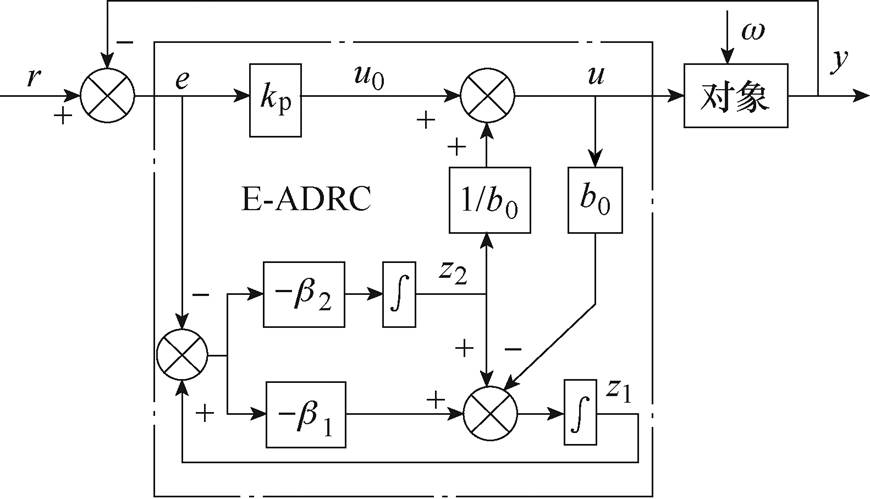
图5 基于误差的自抗扰控制原理
Fig.5 Schematic diagram of ADRC based on error
从式（9）可以看出，ADRC中有4个参数b1、b0、b0、kp需要整定。参数b1、b2按照线性ESO带宽的概念进行整定[24]，选取b1=2w0、b2=
，w0为观测器带宽，w0越大，对扰动的抑制效果越好，但会放大高频噪声。当系统实际控制增益b已知时，选择b0=b，可以得到良好的控制效果。kp按照从小到大的规律调节，参数整定简单。
式（1）经过变换可以得到
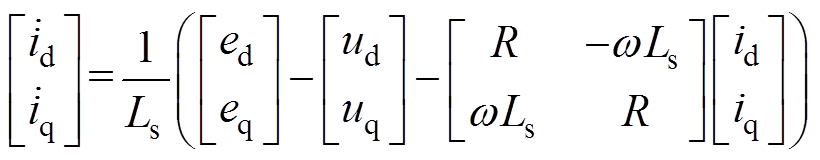（10）可以看出三电平整流器的电流内环dq轴电流为一阶微分方程。令
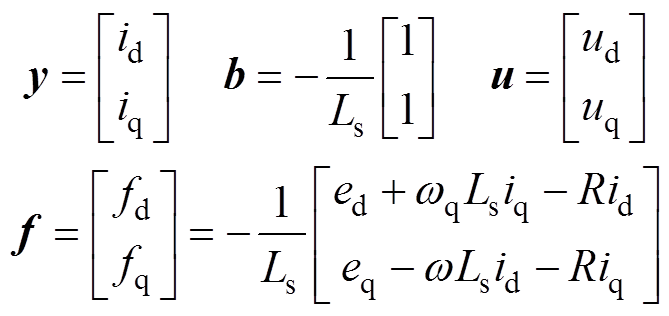
代入式（10）可得
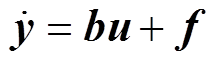（11）由式（11）可以看出，自抗扰控制器将整流器数学模型中dq轴电流的耦合项以及它们自身参数不确定项当作系统的内部扰动，将网侧电压在dq轴的分量当作外部扰动，从而构成了系统的总扰动f，然后通过ESO进行实时估计总扰动，并给予补偿，从而达到对电流内环的解耦以及抗扰的目的。电流内环的自抗扰控制器设计过程按照2.1节介绍的方法即可，将式（9）的传递函数离散后就能用程序实现。
整流器采用电压定向控制策略，单位功率因素运行，即iq=0，式（1）中的第三行经过变换可以得到
（12）令
，代入式（12）可得
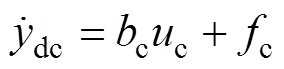（13）从式（13）可以看出，电压环自抗扰控制器把整流器数学模型中的参数变化以及忽略未建模的部分当作系统的内部扰动，把负载功率的变化当作外部扰动，从而构成了系统的总扰动fc，然后通过ESO进行实时估计总扰动量，并给予补偿，从而有效地抑制了负载变化带来的扰动量。
但对高速磁悬浮系统中MW级三相电压型PWM整流器而言，负载在换步过程中变化剧烈，如果仅仅通过ESO进行观测，总扰动存在滞后，无法及时观测并进行补偿，容易导致母线电压出现较大超调和引起过大的冲击电流。因此本文提出负载功率前馈结合扰动观测的方法，实时计算负载的功率，计算的误差以及其余扰动通过ESO观测，进行补偿，抑制负载变化对母线电压的冲击。高速磁悬浮系统中整流器负载为逆变器驱动的长定子直线电机，因此需要实时计算电机的功率。
高速磁悬浮列车牵引供电系统框图如图6所示，位于轨道两端的变电站，通过馈电电缆向长定子绕组供电，实际运行中有单端供电模式（轨道一端的变电站单独供电）和双端供电模式（相邻两个变电站通过馈电电缆同时供电）[25]两种。
根据文献[25]建立磁悬浮列车所用的长定子直线电机在双端供电模式时dq坐标系下的数学模型为
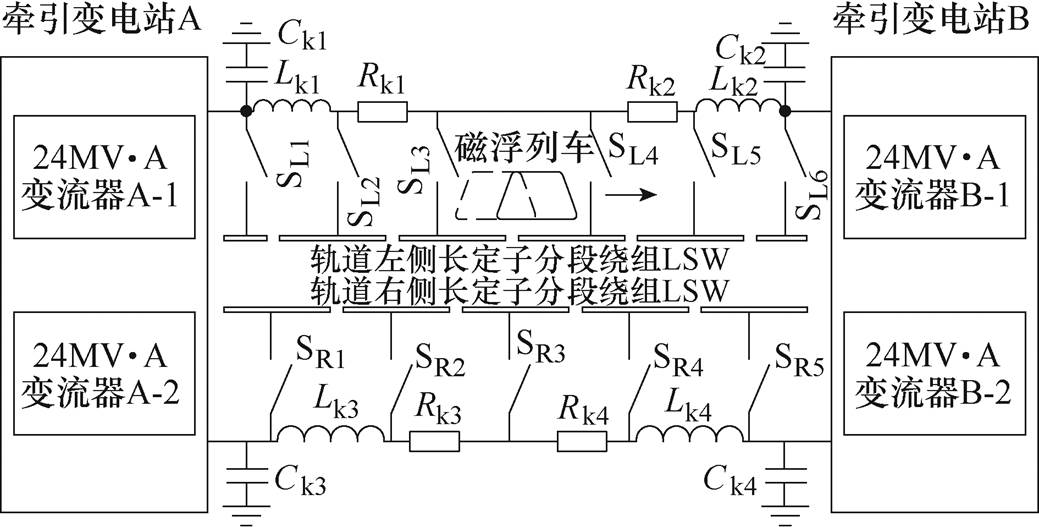
图6 磁悬浮列车牵引供电系统框图
Fig.6 Diagram of power supply system of maglev
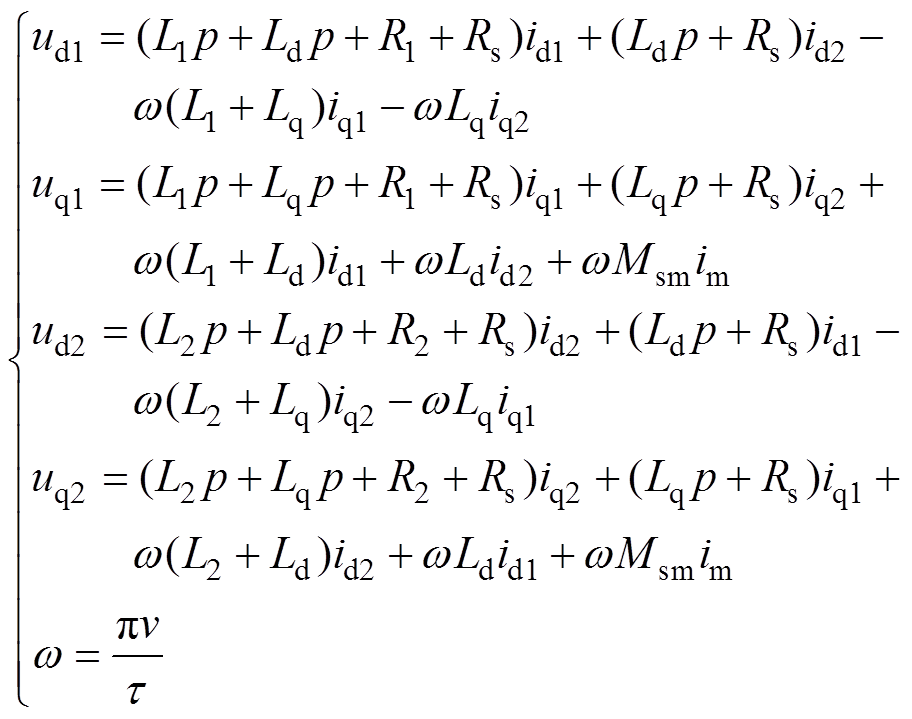（14）式中，ud1、uq1和id1、iq1为第一台24MV·A变流器输出电压和输出电流在d、q坐标系下的分量；ud2、uq2和id2、iq2为第二台24MV·A变流器输出电压和输出电流在d、q坐标系下的分量；Ld、Lq为定子绕组在d、q坐标系下的电感；Rs为定子电阻；Msm为定子与转子间的互感；im为励磁电流；v为列车速度；t 为极距；w 为动子角速度；R1、R2、L1、L2为两侧馈电电缆参数；p为微分算子。
对于整个电机调速系统，其输入的瞬时功率等于变流器输出的三相瞬时功率，由双端供电方式下牵引控制系统的电压方程式（14），可以得到电机和变流器之间能量交换的有功功率，单侧电机总的有功功率为
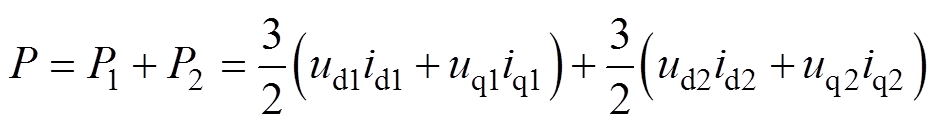（15）采用转子磁场定向控制策略，即id1=0、id2=0，与此同时由于两端的变流器采用均流控制，iq1=iq2= 0.5iq，iq为电机侧q轴电流。将式（14）代入式（15）可以得到
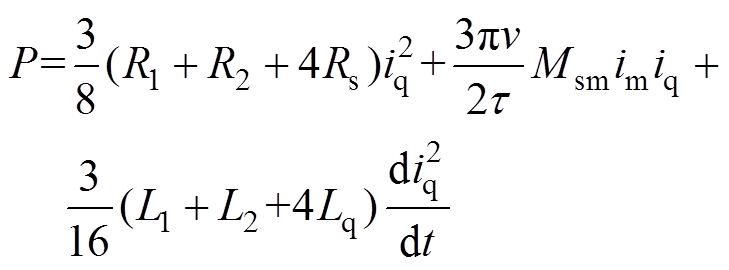（16）
根据能量传递规律，可以得到单台三相PWM整流器瞬时负载有功功率关系为
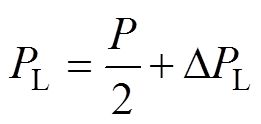（17）式中，DPL由电机有功功率估算误差、逆变器损耗以及电机损耗组成。将式（17）代入式（12）中，可得
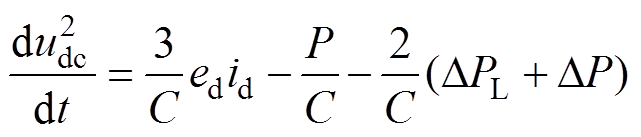（18）
按照电压定向规则，将电机负载功率P/2除以3ed/2后可以得到电流内环的d轴电流前馈值为
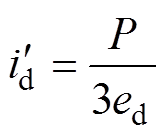（19）通过负载功率前馈后，令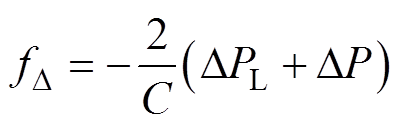
，可以得到
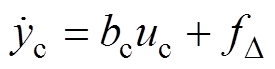（20）
相比于经典的自抗扰控制方法，将前馈控制与自抗扰相结合，实时计算电机功率前馈，把变流器损耗以及未建模的部分当作系统的内部扰动，把负载功率估算误差当作外部扰动，从而构成了系统的总扰动，大大降低了观测器负担，有效抑制负载变化对母线电压的冲击。
通过以上分析可以得到基于ADRC的三相PWM整流器控制框图如图7所示，图中，ADRC的具体闭环传递函数为式（9）所推导的结果。
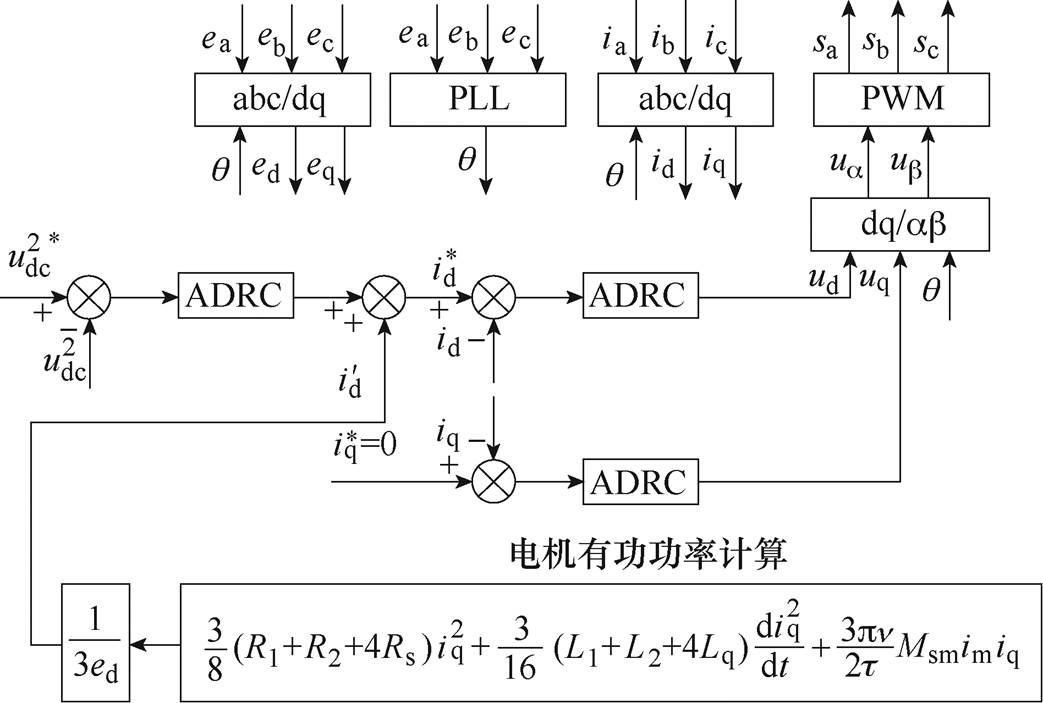
图7 基于ADRC的三相PWM整流器控制框图
Fig.7 The control diagram of PWM rectifier based ADRC
为了在实验室环境下验证本文所提控制策略的有效性，本文搭建了基于RT-LAB的高速磁悬浮半实物系统如图8所示，由RT-LAB测试系统和牵引控制系统组成。RT-LAB测试系统包括四套24MV·A高功率变流器仿真子系统和一套直线电机仿真子系统，其中每台FPGA仿真机对应一套高功率变流器仿真子系统。表1给出了硬件在环（Hardware In the Loop, HIL）实验主要参数。实验中控制器参数见表2。
图8 高速磁悬浮牵引半实物系统
Fig.8 Semi-physical traction system of high-speed maglev
表1 硬件在环实验主要参数
Tab.1 Parameters of HIL experiment
参 数数 值 PWM整流器网侧线电压有效值ea/V3 000 网侧等效电感Ls/mH0.717 直流侧电容C/mF32.4 直流母线电压udc/V5 000 开关频率f/Hz400 电机定子电阻Rs/W0.43 d轴电感Ld/mH3.061 q轴电感Lq/mH2.611 动子与定子间的互感Msm/mH165 极距t/m0.258 列车质量M/kg306 900 列车节数N5 励磁电流im/A27
表2 控制器参数
Tab.2 Parameters of controller
参数ADRCPI b1b2kb0kpki d轴1002 50021 40012 q轴1002 50021 40012 电压环609003300 00011
按照表1的参数，在高速磁悬浮牵引半实物系统上进行了硬件在环实验，按照最高时速为600km/h的运行条件，速度曲线如图9所示。实验过程中定子段长度为1.2km，定子换步方式采用两步法换步。
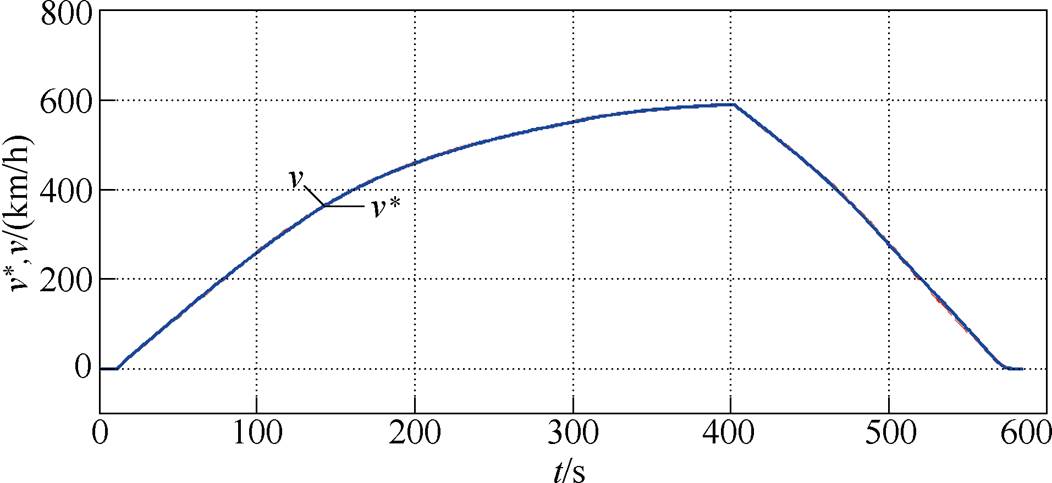
图9 磁悬浮列车速度曲线
Fig.9 The speed curves of high-speed maglev
图10和图11分别为基于PI和基于ADRC控制策略的实验波形。其中，udc、ea、ia、ia1、ia2分别是直流母线电压、网侧a相电压、变压器一次侧a相电流、第一台整流器a相电流、第二台整流器a相电流。从图中可以看出，稳态运行情况下，两种控制策略均能控制母线电压稳定在给定值（5 000V）不变，电流ia2相位超前ia1 30°，在电机加减速过程中都实现了网侧单位功率因数运行。与此同时，可以明显看出，采用基于PI的控制策略，稳态时候母线电压纹波较大，而采用基于ADRC的控制策略，母线电压波动不超过50V。
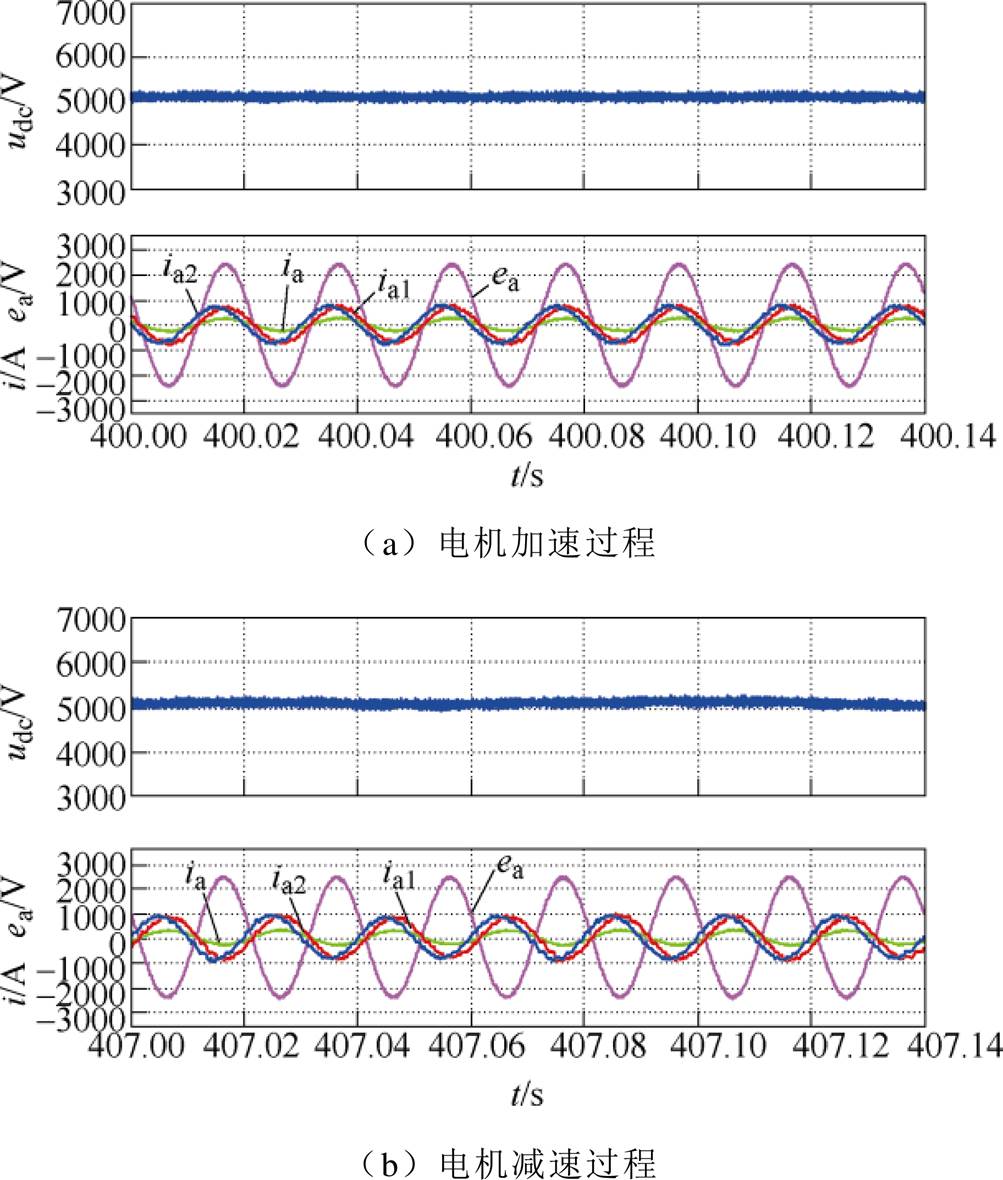
图10 基于PI控制策略的实验波形
Fig.10 The experimental waveforms based on PI control strategy
对于磁悬浮系统中三相PWM整流器而言，定子段换步过程中由满功率运行降为空载运行，换步结束后再恢复运行，负载在换步过程中波动剧烈。图12选取了磁悬浮列车高速运行阶段的母线电压波形。图12a为电压外环采用PI控制器的波形，可以看出，在换步时刻对母线电压造成了巨大的冲击，母线电压严重超调；图12b为电压外环采用PI加功率前馈的波形，采用负载功率前馈后，系统的动态性能得到改善，但由于估算的功率与实际值有所偏差，母线电压还是超调较大；图12c为电压外环采用ADRC的波形，将负载变化视为扰动，通过ESO来观测扰动并进行补偿，有效地降低了母线电压波动，然而由于观测器带宽的限制，并不能观测出所有的扰动，系统性能提升有限；图12d为采用ADRC结合电机功率前馈控制策略的波形，通过实时计算电机负载功率，进行前馈补偿，显著地降低了观测器的负担，只需观测功率计算误差以及整流器内部的扰动。稳态和动态过程中，母线电压都能很好地跟踪给定值，换步过程中最大超调量也低于4%，有效地抑制了负载扰动。
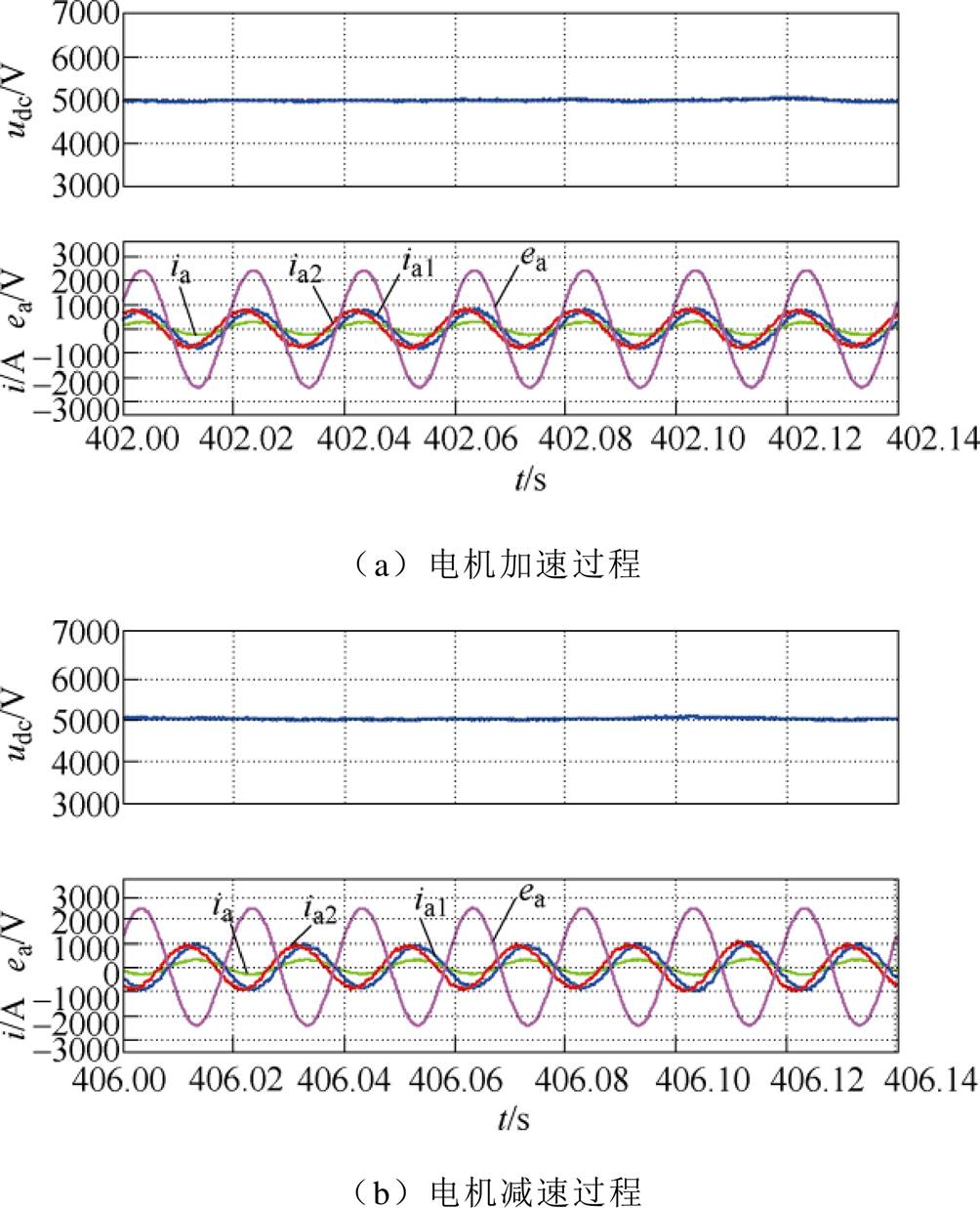
图11 基于ADRC控制策略的实验波形
Fig.11 The experimental waveforms based on ADRC control strategy
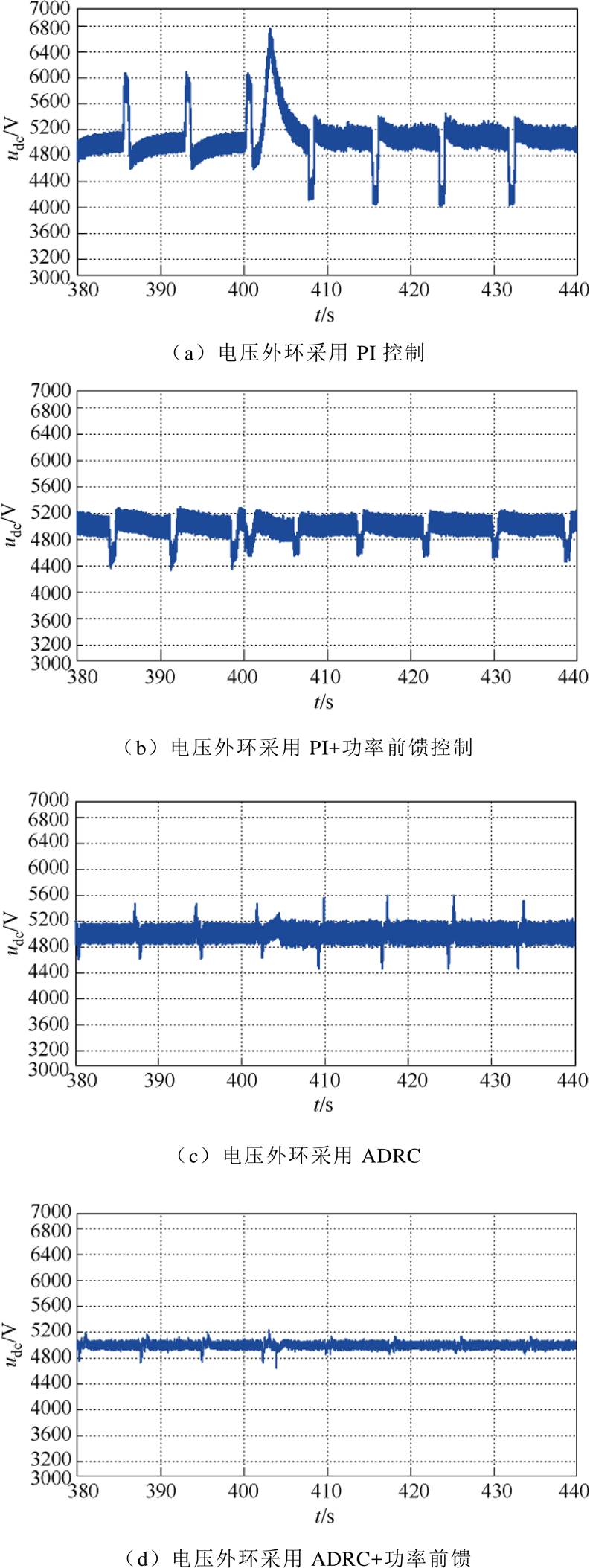
图12 负载变化过程中母线电压波形
Fig.12 The DC voltage waveforms of load change
图13给出了磁悬浮列车减速前、后一段时间，PWM整流器的d轴电流曲线，其中，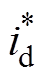
、id1、id2分别为d轴电流给定值、第一台整流器d轴电流和第二台整流器d轴电流。采用前馈解耦的策略需要准确的交流侧电感，而交流侧电感估计值与实际值存在差异，解耦补偿不能抵消实际的耦合量导致解耦不准确，电流跟踪不好，而基于自抗扰控制策略，在实现dq轴电流解耦的同时，补偿了其他因素引起的扰动，有效地提高了系统的动态响应速度和抗干扰性能，电流跟踪良好。
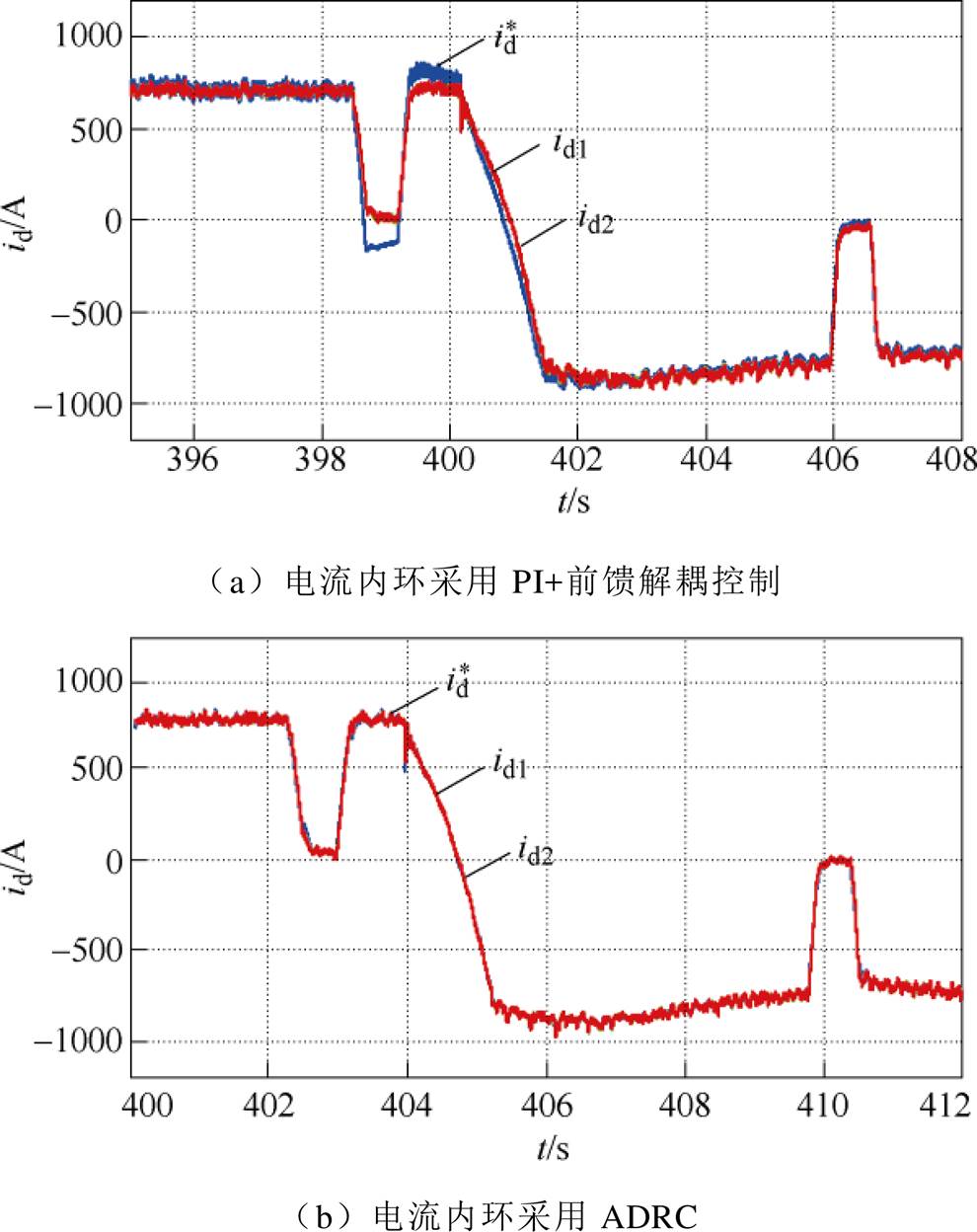
图13 d轴电流波形
Fig.13 The current waveforms of d axis
综上所述，采用自抗扰加负载功率前馈的控制策略，有效地观测出整流器内部扰动包括dq轴电流耦合项和负载变化引起的外部扰动，并加以补偿，硬件在环实验表明，该控制策略具有良好的动静态性能，既可实现直流母线电压快速调节和交流侧单位功率因数控制，同时还具有很强的抗扰动能力。
磁悬浮列车采用三相PWM整流器在换步过程中负载变化剧烈，对母线电压产生了严重的冲击，影响磁悬浮列车的稳定运行，而基于PI的控制策略抗负载扰动性能差。因此本文在传统自抗扰控制策略的基础上，提出了自抗扰加负载功率前馈的整流器控制策略，文中给出了这种功率前馈的理论依据和设计方法，该策略易于实现，对负载变化具有良好的鲁棒性，降低了换步过程中直流电压的周期性波动，改善了系统的动态性能和稳态性能。通过硬件在环实验验证了本文所提策略的有效性，该策略适用于高速磁悬浮系统中PWM整流器的控制，对进一步在实际线路上进行验证具有重要的意义。
参考文献
[1] Singh B, Singh B N, Chandra A, et al. A review of three-phase improved power quality AC-DC con- verters[J]. IEEE Transactions on Industrial Electro- nics, 2004, 51(3): 641-660.
[2] 兰志明, 李崇坚, 李耀华, 等. 基于IGCT的大功率三电平双PWM变流器的研制[J]. 电工技术学报, 2011, 26(增刊1): 36-40.
Lan Zhiming, Li Chongjian, Li Yaohua, et al. Deve- lopment of IGCT-based large power three-level dual- PWM converter[J]. Transactions of China Electro- technical Society, 2011, 26(S1): 36-40.
[3] 张颖超, 赵争鸣, 冯博, 等. 三电平双PWM变频器综合控制策略[J]. 电工技术学报, 2011, 26(11): 25-31.
Zhang Yingchao, Zhao Zhengming, Feng Bo, et al. Integrated control scheme for three-level NPC based dual-PWM converter[J]. Transactions of China Electrotechnical Society, 2011, 26(11): 25-31.
[4] 吴祥明. 磁浮列车[M]. 上海: 上海科学技术出版社, 2003.
[5] 孙鹏琨, 葛琼璇, 王晓新, 等. 磁悬浮列车在双端供电模式下的无速度传感器控制[J]. 电工技术学报, 2018, 33(18): 4249-4256.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Research on speed sensorless control of maglev with double-end power supply[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4249-4256.
[6] Blasko V, Kaura V. A new mathematical model and control of a three-phase AC-DC voltage source converter[J]. IEEE Transactions on Power Elec- tronics, 1997, 12(1): 116-123.
[7] 刘博, 贲洪奇, 白银龙. 一种抑制PWM整流器起动冲击电流的缓给定方法[J]. 电工技术学报, 2018, 33(12): 2758-2766.
Liu Bo, Ben Hongqi, Bai Yinlong. A slow given method to suppress the start-up inrush current of PWM rectifier[J]. Transactions of China Electro- technical Society, 2018, 33(12): 2758-2766.
[8] 姜卫东, 李王敏, 佘阳阳, 等. 直流电容储能反馈和负载功率前馈的PWM整流器控制策略[J]. 电工技术学报, 2015, 30(8): 151-158.
Jiang Weidong, Li Wangmin, She Yangyang, et al. Control strategy for PWM rectifier based on feedback of the energy stored in capacitor and load power feed-forward[J]. Transactions of China Electro- technical Society, 2015, 30(8): 151-158.
[9] 姜卫东, 汪磊, 赵德勇, 等. 外环采用电容储能反馈内环采用改进无差拍控制的PWM整流器的控制方法[J]. 中国电机工程学报, 2016, 36(14): 3899- 3909.
Jiang Weidong, Wang Lei, Zhao Deyong, et al. A control method based on outer loop adopting the feedback of capacitor energy storage and internal loop adopting improved deadbeat control for PWM rectifier[J]. Proceedings of the CSEE, 2016, 36(14): 3899-3909.
[10] 倪双舞, 苏建徽. 以电容储能作为外环反馈变量的双闭环多电平整流器控制策略[J]. 电工技术学报, 2016, 31(9): 92-100.
Ni Shuangwu, Su Jianhui. A dual closed loop control strategy of the multi-level rectifier using capacitor energy as the outer loop variable[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 92- 100.
[11] 王恩德, 黄声华. 三相电压型PWM整流的新型双闭环控制策略[J]. 中国电机工程学报, 2012, 32(15): 24-30.
Wang Ende, Huang Shenghua. A novel double closed loops control of the three-phase voltage-sourced PWM rectifier[J]. Proceedings of the CSEE, 2012, 32(15): 24-30.
[12] 姚绪梁, 王旭, 冯泽文. 改善三相电压型PWM整流器动态性能的研究[J]. 电工技术学报, 2016, 31(增刊1): 169-175.
Yao Xuliang, Wang Xu, Feng Zewen. Research on of improvement of the dynamic ability for PWM rectifier[J]. Transactions of China Electrotechnical Society, 2016, 31(S1): 169-175.
[13] 叶虹志, 姜燕, 黄守道, 等. 电压型PWM整流器无差拍预测直接功率控制[J]. 电工技术学报, 2015, 30(4): 121-128.
Ye Hongzhi, Jiang Yan, Huang Shoudao, et al. Deadbeat predictive direct power control for three- phase voltage source PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 121- 128.
[14] 肖雄, 张勇军, 王京, 等. 基于全响应功率补偿的电压型PWM整流器直接功率控制[J]. 电工技术学报, 2015, 30(4): 113-120.
Xiao Xiong, Zhang Yongjun, Wang Jing, et al. Direct power control under three phase boost type PWM rectifiers based on power compensation of complete response[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 113-120.
[15] 罗德荣, 周小艳, 姬小豪, 等. 基于虚拟磁链的PWM整流器模型预测直接功率控制[J]. 电力自动化设备, 2017, 37(12): 123-129.
Luo Derong, Zhou Xiaoyan, Ji Xiaohao, et al. Virtual-flux-based model predictive direct power control for PWM rectifiers[J]. Electric Power Auto- mation Equipment, 2017, 37(12): 123-129.
[16] 张辉, 李志新, 王涛, 等. 基于三矢量的三相PWM整流器低复杂性模型预测直接功率控制[J]. 电网技术, 2018, 42(3): 957-965.
Zhang Hui, Li Zhixin, Wang Tao, et al. Three vectors based low complexity model predictive direct power control for three-phase PWM rectifier[J]. Power System Technology, 2018, 42(3): 957-965.
[17] Xiao Xiong, Zhang Yongjun, Song Xian, et al. Virtual flux direct power control for PWM rectifiers based on an adaptive sliding mode observer[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5196-5205.
[18] Han Jingqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
[19] 邵立伟, 廖晓钟. 自抗扰控制器在电压型PWM整流器中的应用[J]. 北京理工大学学报, 2008, 28(1): 50-53.
Shao Liwei, Liao Xiaozhong. Active disturbance rejection controller for PWM rectifier[J]. Transa- ctions of Beijing Institute of Techonlogy, 2008, 28(1): 50-53.
[20] 郭源博, 周鑫, 张晓华, 等. 三相电压型脉宽调制整流器的自抗扰控制[J]. 电力系统自动化, 2011, 35(16): 87-93.
Guo Yuanbo, Zhou Xin, Zhang Xiaohua, et al. Active disturbance rejection control for three-phase voltage- type PWM rectifier[J]. Automation of Electric Power Systems, 2011, 35(16): 87-93.
[21] 黄庆, 黄守道, 陈泽远, 等. 不对称电压下PWM整流器的变结构自抗扰控制[J]. 电机与控制学报, 2014, 18(1): 50-55.
Huang Qing, Huang Shoudao, Chen Zeyuan, et al. Variable structure ADRC control of pulse width modu- lation rectifier under asymmetrical input voltage[J]. Electric Machines and Control, 2014, 18(1): 50-55.
[22] 韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
[23] Madonski R, Shao S, Zhang H, et al. General error-based active disturbance rejection control for swift industrial implementations[J]. Control Engin- eering Practice, 2019, 84: 218-229.
[24] 毛海杰, 李炜, 蒋栋年, 等. 基于线性扩张状态观测器的永磁同步电机状态估计与性能分析[J]. 电工技术学报, 2019, 34(10): 2155-2165.
Mao Haijie, Li Wei, Jiang Dongnian, et al. State estimation and performance analysis based on LESO for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(10): 2155-2165.
[25] 刘金鑫, 葛琼璇, 王晓新. 高速磁浮牵引控制系统半实物实验研究[J]. 电工技术学报, 2015, 30(14): 497-503.
Liu Jinxin, Ge Qiongxuan, Wang Xiaoxin, et al. Hardware-in-loop research of traction-system for high-speed maglev[J]. Transactions of China Electro- technical Society, 2015, 30(14): 497-503.
Control Strategy for PWM Rectifier of High-Speed Maglev Based on Active Disturbance Rejection Control and Load Power Feed-Forward
Abstract The high-speed maglev train is driven by long stator linear synchronous motor，which is powered by segmented power supply. When the maglev train moves from one stator section to another, the stator current will decrease to zero and then increase. For the three-phase PWM rectifier in high-speed maglev system, the load changes sharply during the process of changeover, which has a serious impact on the DC voltage. In order to suppress the influence of load disturbance on the DC voltage, a double closed-loop control strategy based on active disturbance rejection control (ADRC) and load power feed-forward estimation algorithm is proposed in this paper. The hardware-in-the-loop (HIL) experiment verifies that this strategy has strong robustness to load variation, and it can suppress the DC voltage fluctuation, improve the anti-load disturbance ability and system dynamic performance of three-phase PWM rectifier.
keywords：High-speed maglev, PWM rectifier, changeover, load power feed-forward, active disturbance rejection control
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.191572
国家重点研发计划项目（2016YFB1200602-20）和国家自然科学基金青年基金项目（51907188）资助。
收稿日期 2019-11-20
改稿日期 2020-01-03
朱进权 男，1993年生，博士研究生，研究方向为高性能电机牵引控制技术。E-mail: zhujinquan@mail.iee.ac.cn
葛琼璇 女，1967年生，研究员，博士生导师，研究方向为高压大功率变流器控制技术、高性能电机牵引控制技术。E-mail: gqx@mail.iee.ac.cn（通信作者）
（编辑 陈 诚）