功率变化环境下的四线制Vienna整流器优化联合控制方法
杨 頔 姚 钢 周荔丹
(上海交通大学电气工程系电力传输与功率变换控制教育部重点实验室 上海 200240)
摘要 在传统双闭环比例积分(PI)控制器调节下,功率的变化会造成三相四线制Vienna整流器中交流电流的过零点畸变问题。为克服这一现象,该文首先从电流工作模式,即连续与断续模式角度讨论功率变化对电流波形的影响,基于此提出PI-前馈干预-重复控制的联合控制策略,该联合控制策略中,一方面可通过占空比前馈干预使电流在过零点处不存在畸变问题;另一方面利用重复控制,进一步抑制电流谐波,提高电流跟踪精度。然后对该四线制Vienna整流控制系统进行控制器参数设计和稳定性验证。最后通过仿真和实验结果表明,上述功率变化以及占空比前馈干预对电流波形的影响,并验证了该联合控制方法在功率变化环境下工作的可行性。
关键词:Vienna整流器 占空比前馈 重复控制 PI控制器 连续电流模式
0 引言
Vienna整流器是1994年J. W. Kolar教授提出的一种三电平单向功率传输整流拓扑。该拓扑与传统两电平拓扑相比,具有功率密度高、无需考虑死区、开关应力低等特点[1-2],近年来被广泛应用于电池储能、微电网、航空电源、风力发电[3-4]等领域,尤其适合作为功率因数校正(Power Factor Correction, PFC)电路[5-6]。
然而,目前对Vienna整流器拓扑的研究多局限于三相三线制,三相四线制Vienna整流器在三相三线制拓扑的基础上多出一条中性线从而保证三相可以进行解耦,增加了控制自由度,在调制上更为灵活。但由于零序通路的存在,在建模分析时无法忽略零序电流,系统会引入3次谐波电流[7-9],因此四线制拓扑的研究工作较少。在复杂电网工况和负载频繁变化的情况下,若不采取合适的控制策略,三相四线制Vienna整流器容易出现交流电流过零点畸变、三相不对称、直流电压较大幅度波动以及功率因数下降等问题[10-13],所以需要深入研究四线制Vienna整流器拓扑,对其控制策略做进一步改进,以适应功率变化和电网扰动的场合。
文献[14]针对三相四线制Vienna整流器提出了一种比例积分(Proportional Integral, PI)控制与重复控制相结合的复合控制策略,能有效改善电流波形且对高频谐波成分有较强的抑制作用,但未考虑功率变化对电流波形的影响,复现操作时电流过零点畸变现象难以避免,且重复控制器的设计过程较为复杂。文献[15]给出三相四线制Vienna整流器的一种混合导通控制模式,详尽分析了电感电流连续导通模式(Continuous Conduction Mode, CCM)和电流断续导通模式(Discontinuous Conduction Mode, DCM)两种工作模式,但该控制方式在电网存在扰动时,会形成错误的前馈量,从而影响电流波形质量,同时需要开方运算,降低了数字处理器计算效率。文献[16]给出一种比例谐振+重复控制的控制策略,并应用在柔性直流输电当中,但理论上,重复控制已能实现无静差调节,比例谐振(Proportional Resonance, PR)调节只会增加数字化实现的复杂度。文献[17]针对四线制Vienna拓扑的电流内环,采用一种滞环比较的控制方法,也能有效抑制过零点畸变,但由此带来的问题是谐波频次不固定,不利于控制器设计和谐波治理。文献[18]从DCM的角度讨论了Vienna整流器拓扑中电感电流畸变的原因,根据不同的时间区段,计算补偿占空比,解决了轻载条件下输入电感电流不规则的问题,但并不适用于三相四线制系统,有一定局限性。文献[19]基于小功率微型逆变器讨论了宽功率范围下DCM出现的原因,提出一种临界导通模式与断续导通模式相结合的恒频控制,可以减少系统损耗,传输效率高、动态响应快,但控制方法的核心是一个可变参数电感元件,这给实际应用带来不便。
针对目前上述研究成果的不足之处,本文首先对三相四线制Vienna整流器的拓扑结构、工作原理、双闭环控制策略以及调制策略进行阐述;在此基础上分析了功率变化环境下电网电流过零点畸变产生机理,介绍占空比前馈干预的补偿原理,但仅引入占空比前馈的控制系统仍存在缺陷;为此,结合简化重复控制器,提出PI-前馈干预-重复控制的联合控制策略。该联合控制策略适用于电网扰动和功率变化的环境,可以改善交流电流波形,提高系统功率因数,加强谐波抑制,并且无需在同步旋转坐标系下进行控制,数字化实现简单,具有一定的工程应用价值,仿真与实验均验证了所提控制策略的可行性和优越性。
1 三相四线制Vienna整流器原理与控制
1.1 三相四线制Vienna整流器拓扑与工作原理
三相四线制Vienna整流器的拓扑结构如图1所示,整流桥臂采用不可控二极管,保证功率单相流动且无需考虑死区设置,三相交流侧电感出线端A、B、C与直流侧电容中点O之间是双向功率开关Sa、Sb、Sc,在图1点画的线框中给出了两种可行的结构。四线制的特点在于三相交流源的中性点N与直流侧电容中点O直接相连。图1中,usa、usb、usc为网侧三相电压,VDa1、VDa2、VDb1、VDb2、VDc1和VDc2为三相桥臂上的二极管,Lsa、Lsb和Lsc为交流侧电感,C1和C2为直流侧电容。
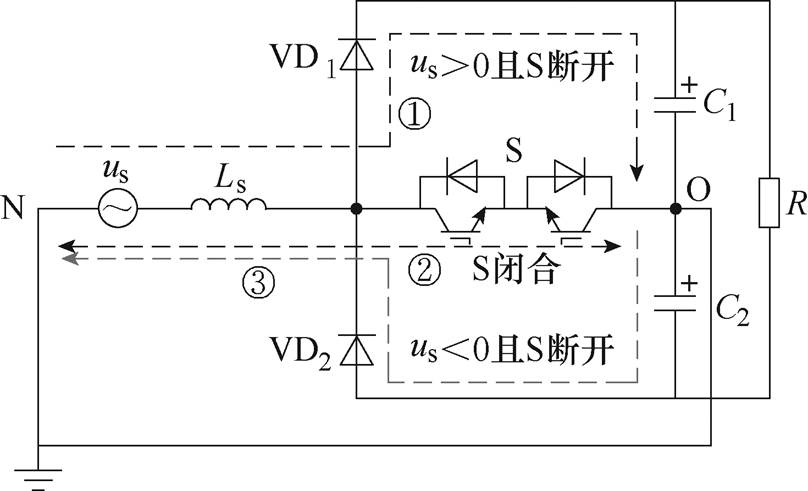
由于在四线制Vienna整流器中,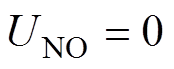 ,因此四线制拓扑可以进行解耦,三相电流可分别独立控制,解耦后的单相Vienna整流拓扑结构如图2所示。采用电阻负载R,根据开关损耗、效率和元器件数量等因素[20]综合考虑后,双向功率开关管S采用两个绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)反串联结构进行后续的理论和实验分析。此外,直流侧上下电容电压平衡也可以进行独立控制,同样体现了四线制结构控制的灵活性。S闭合时,交流电流沿图2中的路径②在N与O之间流通;S断开时,根据交流电压正负半周决定电流流经桥臂上管VD1还是下管VD2,分别如图2中的路径①和③所示,本质上可按照Boost型PFC整流电路[21]对其建模分析。
,因此四线制拓扑可以进行解耦,三相电流可分别独立控制,解耦后的单相Vienna整流拓扑结构如图2所示。采用电阻负载R,根据开关损耗、效率和元器件数量等因素[20]综合考虑后,双向功率开关管S采用两个绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)反串联结构进行后续的理论和实验分析。此外,直流侧上下电容电压平衡也可以进行独立控制,同样体现了四线制结构控制的灵活性。S闭合时,交流电流沿图2中的路径②在N与O之间流通;S断开时,根据交流电压正负半周决定电流流经桥臂上管VD1还是下管VD2,分别如图2中的路径①和③所示,本质上可按照Boost型PFC整流电路[21]对其建模分析。
1.2 三相四线制Vienna整流器传统控制方法
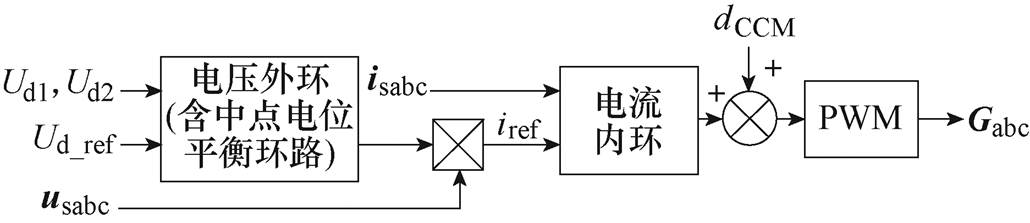
三相四线制Vienna整流器和其他常见的PFC电路一样,常用电压外环-电流内环的双闭环控制策略。图3给出了三相四线制Vienna整流器双闭环控制系统,电压外环用于控制直流侧电压稳定和中点电位平衡;电流内环控制电流波形,实现对指令电流的跟踪。图中,Ud1和Ud2为直流侧正负母线电压,Ud_ref为直流总电压参考值,usabc和isabc为网侧电压和电流,iref为内环电流参考值,Gabc为三相双向功率开关管的驱动信号。
1.3 三相四线制Vienna整流器调制方法
由于交流电网侧中性点与直流侧电容中点相连,因此三相四线制Vienna整流器存在零序电流通路,2D-空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)无法适用[22]。虽然3D-SVPWM可以对零序分量进行调制,但调制空间为一立体空间,即原先的平面调制区域会被拉伸为空间几何体,此外由于Vienna拓扑是三电平结构,在扇区的划分与判定及矢量作用时间计算上会很复杂。所以本文采用正弦脉宽调制(Sinusoidal Pulse Width Modu- lation, SPWM)产生开关管驱动信号,SPWM原理简单、容易实现。
2 功率变化对电流波形的影响及其抑制
2.1 功率变化引起电流过零点畸变现象分析
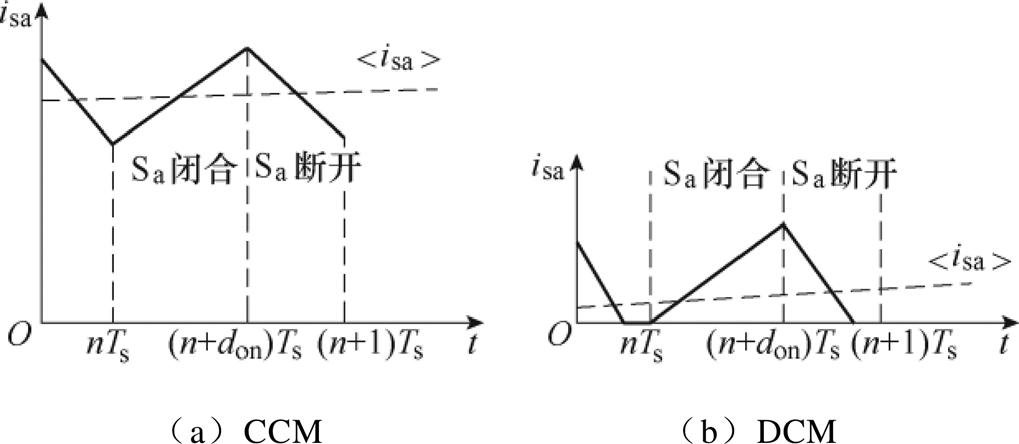
由图2可知,解耦后的单相Vienna整流器可以仿照单相Boost型PFC整流电路来进行分析[23],同样地,单相Vienna整流器也存在CCM和DCM两种工作模式,图4给出了这两种工作模式的电感电流在一个开关周期内的波形,Ts为开关周期,don为开关开通的占空比。以a相电流isa为例,图中<isa>为isa在一个开关周期内的平均值,由于Vienna整流器内环跟踪的是交流电流,故<isa>在变化趋势上并非一条平行横轴的直线。
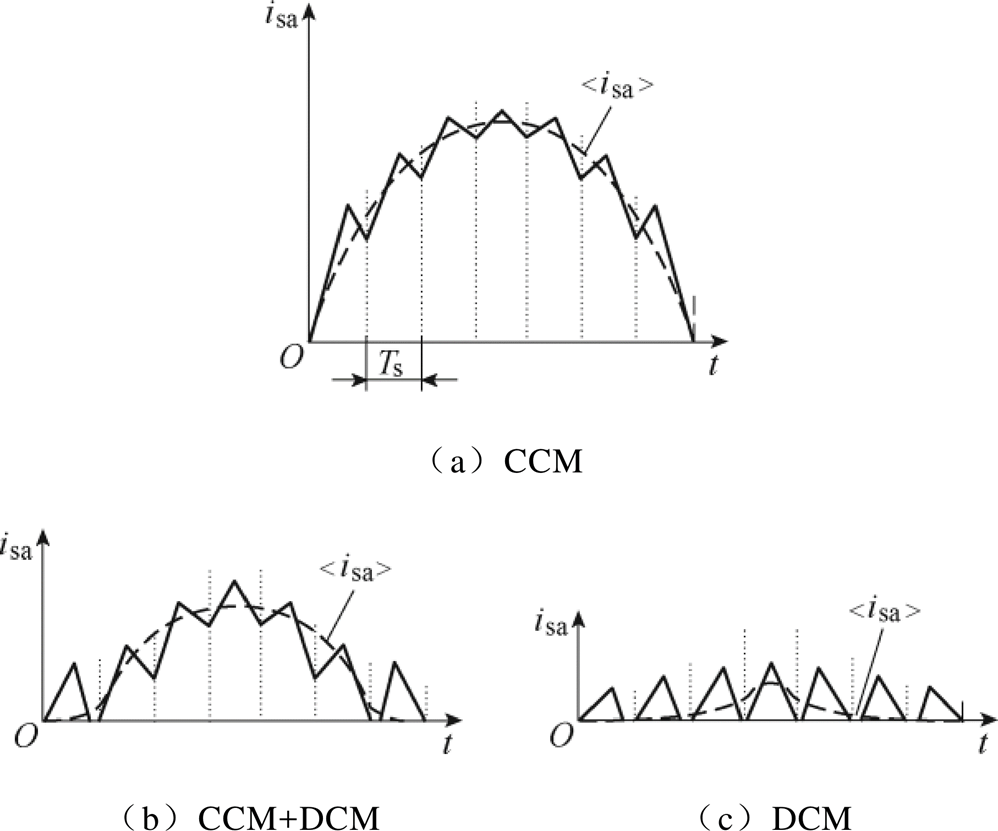
由图4不难看出,当系统功率足够大导致电感电流有效值较大或网侧滤波电感值足够大时,电感电流一直工作在CCM下。实际情况中,电感参数随着产品出厂已经设计完成,难以更改,而随着负载或电网电压的变化,系统的功率也会发生变化,进而导致电网侧的交流电流发生变化。当电流有效值下降到一定值时,使得电感电流工作在DCM下,且极易先发生在正弦电流过零点处,导致过零点畸变,不同工作模式对电感电流的影响情况如图5所示。电流下降过程由图5a至图5b再至图5c,工作模式从CCM到CCM和DCM混合再到DCM。图中,虚线表示电感电流的平均值变化趋势,显然,当系统在两种工作模式间交替改变时,过零点处会出现畸变;当完全工作在DCM时,电感电流的波形会发生更大幅度的畸变。
2.2 占空比前馈干预调节原理
占空比前馈是将电路所需要的理论占空比通过数学的方法计算后直接加入调制波或调节器的输出量上,这种方式能快速且有效地调整调制波的形状,使传统的PI或其他控制器可以只补偿实际占空比与所加入的理论占空比之间的误差,提高了系统的动态响应速度,同时,引入的占空比前馈也不会影响系统控制器参数的设计。
为了避免三相四线制Vienna整流器因受功率变化导致交流电流工作在DCM而出现过零点畸变的问题,一种思想是计算出CCM下的理论占空比,将该占空比直接作为前馈占空比叠加在调制波上,这样就使得电感电流在低功率环境下过零点处进入CCM从而解决畸变问题,当系统工作在较高的功率环境中时,电感电流一直处于CCM状态,引入的CCM前馈占空比与实际占空比误差很小,也自然不会发生电流过零点畸变现象。
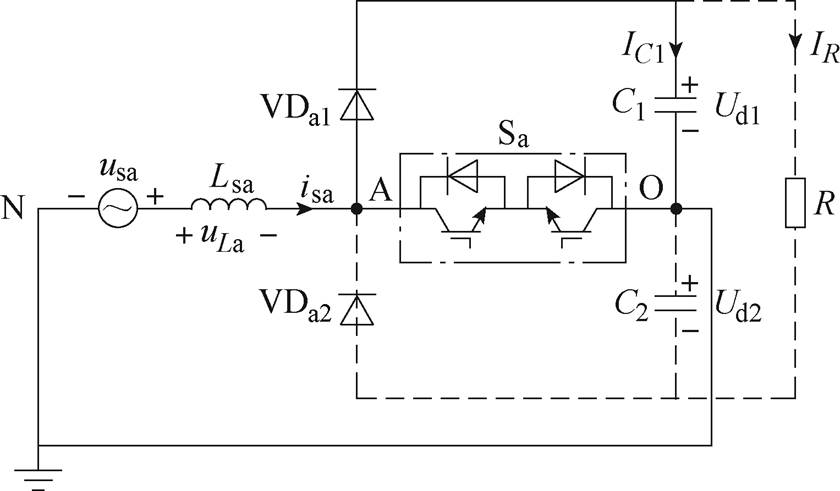
仍以解耦后的a相为例来推导上述想法所需要的CCM下的理论占空比,解耦后的a相拓扑示意图如图6所示。图6中,实线部分和Boost型PFC电路拓扑相同,uLa为a相电感上电压压降,iC1为上电容电流,IR为电阻负载电流。
忽略电感寄生电阻及二极管压降的影响,并假设在一个开关周期内直流电压维持恒定,上、下电压平衡,Ud1=Ud2=Udh。当交流网侧电压usa处于上半周期时,令D表示开关管Sa的状态,即
根据1.1节中对工作原理的介绍,并由基尔霍夫电压和电流定律,可得到
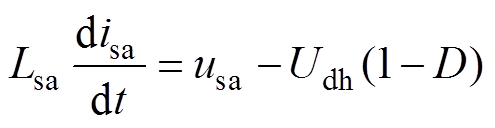 (3)
(3)
注意到式(2)、式(3)满足的前提是图6电路工作在CCM;否则,式(2)中当D=0时,将会存在电感电流减小为0而导致该等式不成立的情况。为了从式(2)、式(3)中解出CCM下的理论占空比,在此引入两个常量,分别为在一般功率条件下的额定输出电压Un和额定输出电流In,Un和In并非唯一,仅仅为后续分析引入的常量,利用Un和In对式(2)、式(3)进行整理变形,得到
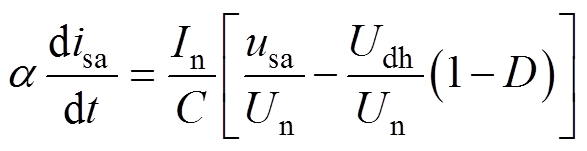 (5)
(5)
式中,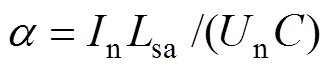 ,一般工况下,
,一般工况下,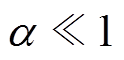 ,经上述变换后,式(4)、式(5)等式右边处于相同的数量级,利用奇异摄动理论中的快慢模型对其求解后得到
,经上述变换后,式(4)、式(5)等式右边处于相同的数量级,利用奇异摄动理论中的快慢模型对其求解后得到
从式(6)可以得知,输出直流电压的变化率远远低于输入交流电流的变化率,则式(4)为电路的慢速动态方程,式(5)为电路的快速动态方程。基于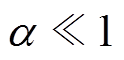 的情况,
的情况,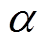 近似取0后代入式(5)得到奇异摄动理论中的退化方程,进一步求解此时的退化近似解D,该占空比即可等效为连续的占空比deq,usa处于上半周时,CCM下的理论占空比为
近似取0后代入式(5)得到奇异摄动理论中的退化方程,进一步求解此时的退化近似解D,该占空比即可等效为连续的占空比deq,usa处于上半周时,CCM下的理论占空比为
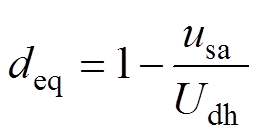 (7)
(7)
将式(7)代入式(4)得到理想情况下的慢速动态方程为
式(8)体现了电路稳态时输入、输出功率的匹配。
同理,计算出usa处于下半周时的理论占空比并与式(7)合并,可得需要叠加的前馈理论占空比为
引入CCM占空比前馈后的三相四线制Vienna整流器双闭环控制系统如图8所示。
2.3 改进联合控制策略
占空比前馈干预可以使系统在变功率环境下平滑过渡DCM工作的时间区段,进而消除电流过零点畸变,但本质上,电流内环还是仅采用PI调节器,所以2.2节所提出的控制策略在实际应用中仍存在以下缺陷:
(1)PI控制器难以实现对交流量的零稳态误差调节。
(2)当电网电压存在谐波、塌陷或其他电能质量问题时,容易引起错误的前馈量,直接导致电流呈现和电网同样的畸变趋势。
(3)对于参考电流的各频次分量跟踪效果较差,谐波抑制效果不好。
为解决上述问题,本文提出在2.2节控制策略的基础上加入重复控制。
重复控制基于内部模型原理,是一种可以稳定消除周期性累积误差的现代控制方法,达到稳态电流无静差的效果,对电流的跟踪效果更好。但由于重复控制对电流的跟踪周期比较长,因此经常与PI控制器配合来对指令电流进行跟踪[24]。本文采用PI调节器与重复控制器相并联的控制方式,其具体结构和参数设计在第3节中将详细说明。
需要注意的是,单独的PI+重复控制策略虽然在同等功率等级下对电流过零点的畸变抑制效果优于PI控制,但当运行在更低的功率场合时,电流过零点畸变现象仍旧无法避免。
综合上述讨论,本文提出改进PI-前馈干预-重复控制的联合控制如图9所示。图9中,wt为锁相环输出的相位信息;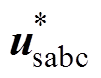 为三相单位正弦量,与电压外环输出相乘得到内环参考值;Ctrl为决定内环参考量的控制信号,即通过判断输入电压处于正半周还是负半周来决定电流内环参考电流。
为三相单位正弦量,与电压外环输出相乘得到内环参考值;Ctrl为决定内环参考量的控制信号,即通过判断输入电压处于正半周还是负半周来决定电流内环参考电流。
3 控制器参数设计
3.1 内环基本PI参数整定
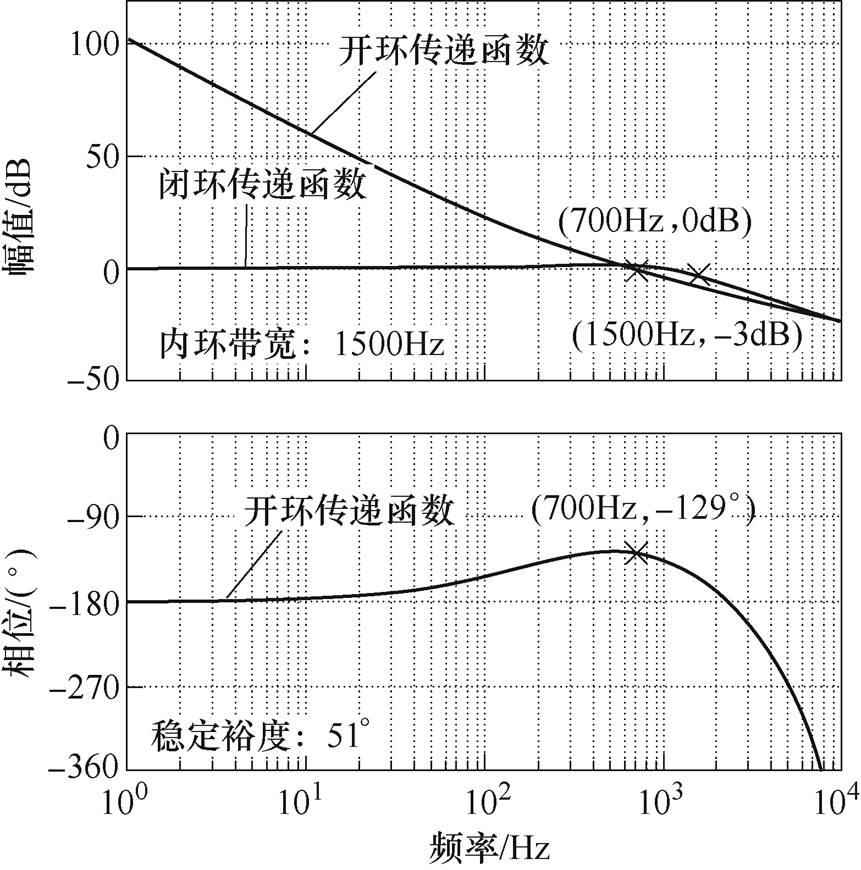
三相四线制Vienna整流器的建模方式和一般的PWM整流器类似,总体上分为电流内环和电压外环。为叙述简洁,图10直接给出了电流内环经PI调节器补偿后的系统开环及闭环伯德图,具体推导设计过程见附录,由图10可知,补偿后的系统稳定裕度为51°,带宽为1 500Hz,可以保证电流环在有PI控制时的响应速度和稳定性。
3.2 内环重复控制器参数设计
重复控制的内部模型在连续域中为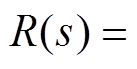
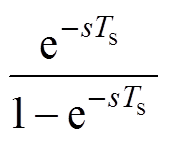 ,可将其视为一个周期函数信号发生器嵌入需要控制的闭环系统中,实现对周期为Ts的目标信号无稳态误差的跟踪。为了方便数字化实现,需要对内部模型函数进行离散化,离散化后的内部模型为
,可将其视为一个周期函数信号发生器嵌入需要控制的闭环系统中,实现对周期为Ts的目标信号无稳态误差的跟踪。为了方便数字化实现,需要对内部模型函数进行离散化,离散化后的内部模型为
式中,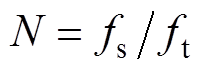 为一个跟踪信号周期内采样周期的个数,
为一个跟踪信号周期内采样周期的个数,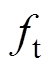 为待跟踪信号的频率。
为待跟踪信号的频率。
若仅采用上述内部模型为重复控制的基本结构,则会在控制器跟踪了若干周期后出现高频振荡的现象。为此可以在时延环节前加入低通滤波器来大幅抑制引起振荡的高频成分,同时,该重复控制器还需要一定的相位补偿以及增益以确保闭环极点位于复平面的单位圆内。图11给出修正后的简化重复控制器结构。图中,ierror为跟踪误差量,即内环输入,rep_out为重复控制器输出,Krep为重复控制器的比例系数。
图11中,一般的数字处理系统中存在1.5Ts的延时,因而取超前量l=2[25]。Q(z)可以为一个接近1的常数,也可以为一个无相位偏移的低通滤波器,如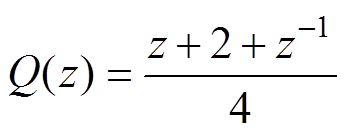 [26]。将电流内环的传递函数项用零阶保持器法转换至z域后得到如图12所示的电流内环在z域下的控制框图。图12中,
[26]。将电流内环的传递函数项用零阶保持器法转换至z域后得到如图12所示的电流内环在z域下的控制框图。图12中,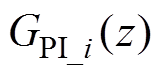 、
、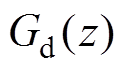 、
、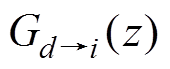 分别为z域下电流内环PI控制器、环路采样和调制延时以及占空比到交流输入电流的传递函数。重复控制部分以及电流内环总体的传递函数分别为
分别为z域下电流内环PI控制器、环路采样和调制延时以及占空比到交流输入电流的传递函数。重复控制部分以及电流内环总体的传递函数分别为
图12 电流内环在z域下的控制框图
Fig.12 Control diagram of the inner current loop in z-domain
式(12)中,由于单PI控制器的闭环系统已经完成补偿和稳定性验证,因此可以将分式项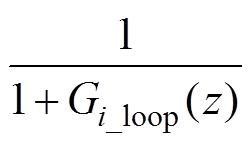 从式(12)中提取出来,仅讨论剩余项,
从式(12)中提取出来,仅讨论剩余项,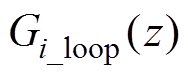 为附录中电流内环的开环传递函数的z域表达式形式,由此得到
为附录中电流内环的开环传递函数的z域表达式形式,由此得到
为方便分析,令
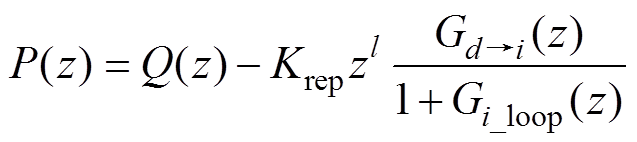 (14)
(14)
由小增益原理[27],闭环系统稳定的条件为
图13给出了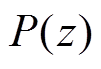 在不同Krep下的幅频特性,
在不同Krep下的幅频特性,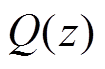 分别取0.95和
分别取0.95和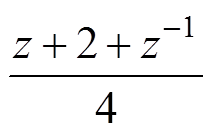 ,不难得知,当
,不难得知,当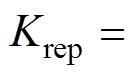
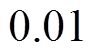 时,幅值增益小于1,式(13)的极点位于复平面单位圆内,系统保持稳定。
时,幅值增益小于1,式(13)的极点位于复平面单位圆内,系统保持稳定。
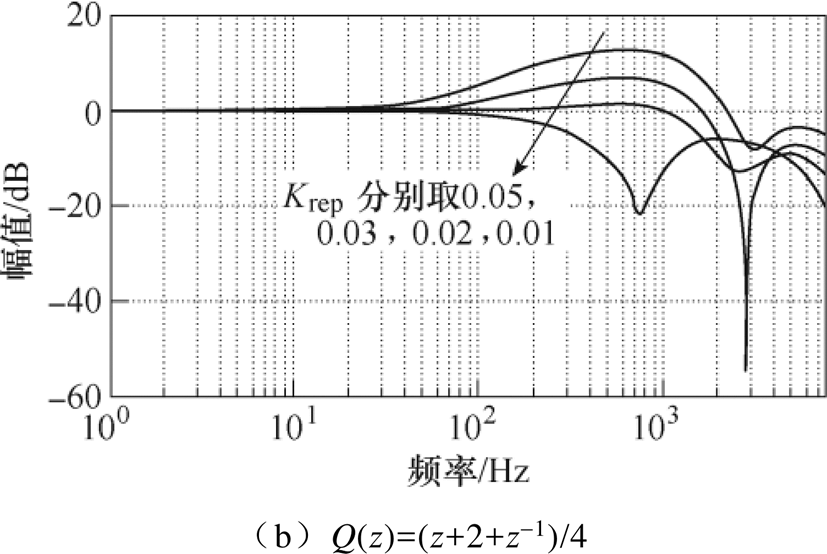
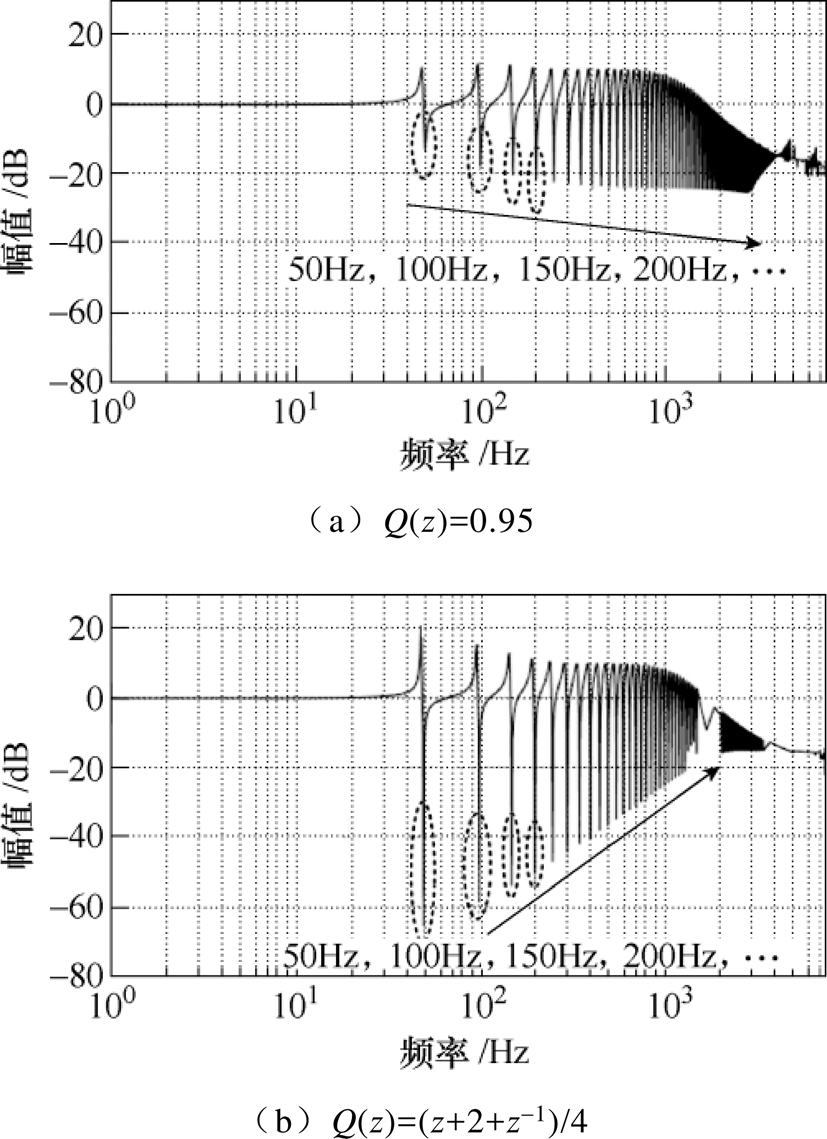
取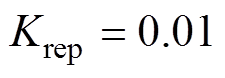 ,绘制式(13)所示不同Q(z)下的总传递函数幅频特性,如图14所示。
,绘制式(13)所示不同Q(z)下的总传递函数幅频特性,如图14所示。
由图14可知,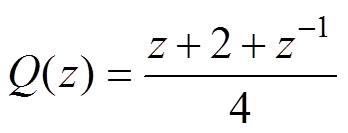 时,在50Hz倍数频次的位置处,跟踪误差的衰减更大,间接表明谐波抑制效果更佳。结合稳定性分析可知,
时,在50Hz倍数频次的位置处,跟踪误差的衰减更大,间接表明谐波抑制效果更佳。结合稳定性分析可知,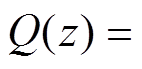
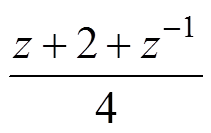 更有利于重复控制器的控制。对比图10,对于整数倍频次信号的跟踪精度,重复控制与PI并联优于单PI控制,这也验证了重复控制对谐波的抑制效果强于PI控制器。
更有利于重复控制器的控制。对比图10,对于整数倍频次信号的跟踪精度,重复控制与PI并联优于单PI控制,这也验证了重复控制对谐波的抑制效果强于PI控制器。
3.3 控制器其他部分参数设计
以上对系统建模和参数设计的过程仅适用于Vienna整流器工作在CCM下,当工作在DCM下时,占空比到电感电流的传递函数有所变化,文献[28]直接给出了其表达式为
式中,us,rms为交流电网电压的有效值。将式(16)替换到上述的讨论过程中的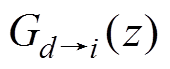 中,重新进行稳定性分析,可知上述参数在DCM下依然成立。此外,关于电压外环的设计只要将电流内环等效为增益为1的常数或者一个延时环节,控制其带宽在20Hz以下,利用上述电流环的计算方法即可完成参数的设计,本文篇幅有限,不再赘述。
中,重新进行稳定性分析,可知上述参数在DCM下依然成立。此外,关于电压外环的设计只要将电流内环等效为增益为1的常数或者一个延时环节,控制其带宽在20Hz以下,利用上述电流环的计算方法即可完成参数的设计,本文篇幅有限,不再赘述。
4 仿真研究
为了验证本文所提的控制策略,在Matlab/ Simulink中搭建了三相四线制Vienna整流器的仿真模型,仿真参数见表1,所采用的重复控制器的z域传递函数为
表1 三相四线制Vienna整流器仿真参数
Tab.1 Simulation parameters of three-phase four-wire Vienna rectifier

参 数数 值 交流网侧电压有效值us,rms/V48 交流网侧滤波电感Ls/mH300 直流侧总电压Ud/V140 直流侧负载电阻R/W10~20 直流侧电容C1, C2/mF9 000 系统功率P/kW1~2 开关频率fs/kHz15
4.1 PI+重复控制仿真
图15给出了PI+重复控制下的三相电流和直流电压波形,图15b和图15c为图15a中点画线时刻的c相电流过零点处的畸变情况。由图15a可知,电流谐波得到抑制。虽然重复控制在同一功率等级,在一定程度上会改善过零点畸变现象,但当功率进一步减小至1kW时,图15b表明,DCM依旧存在。另外,直流侧电压波动基本在±0.02V之内。
4.2 PI+占空比前馈控制仿真
图16为PI+占空比前馈控制下且运行在不同功率等级的三相交流电流和直流电压波形。图16表明,引入占空比前馈后,当系统功率运行在更低的1kW条件下时,仍能消除电流过零点畸变现象,但电流纹波相较于PI+重复控制更大,侧面验证了前述重复控制对高次谐波的抑制效果更好,但直流电压波动要比PI+重复控制的波动更剧烈。
4.3 联合控制仿真
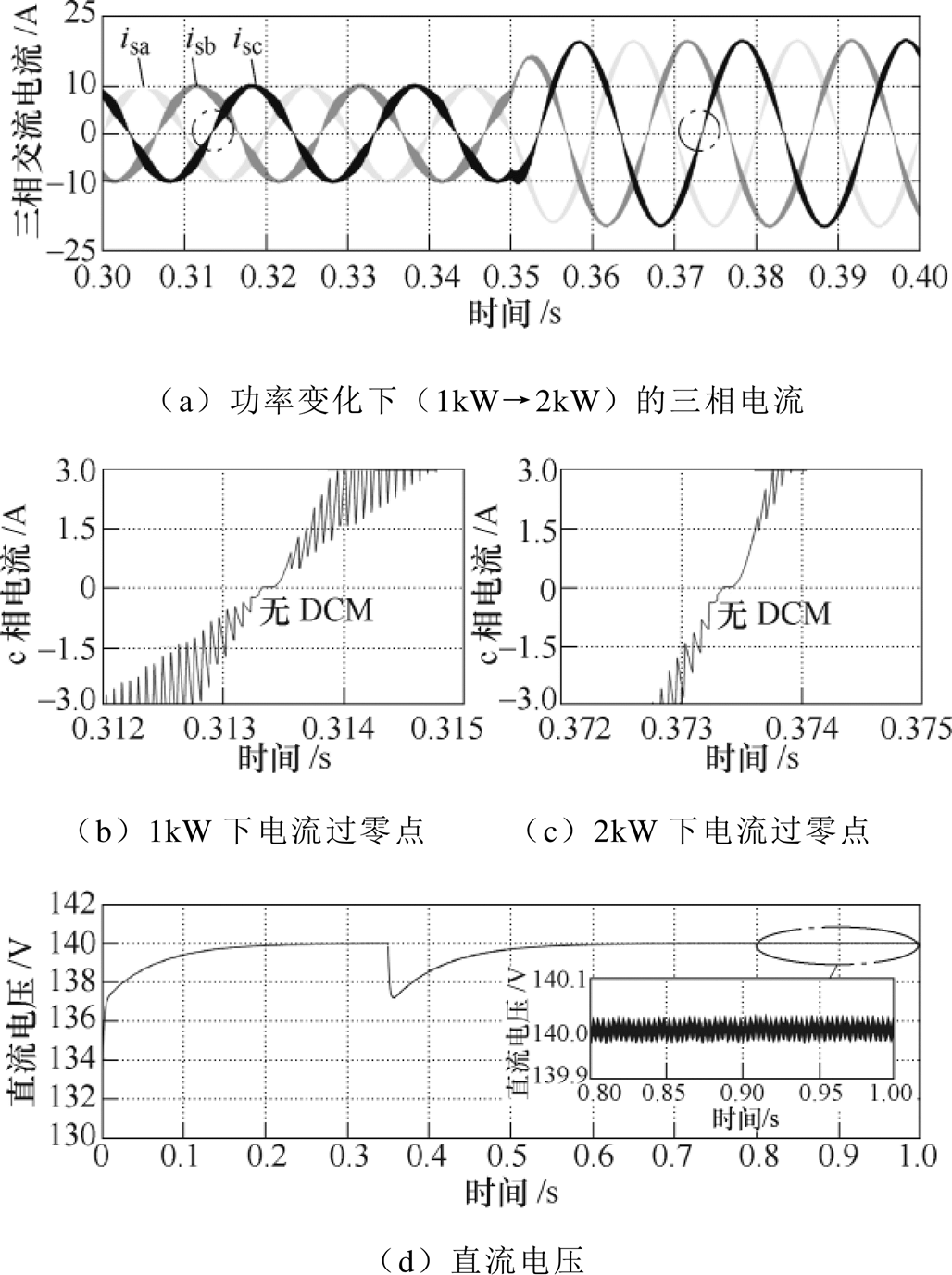
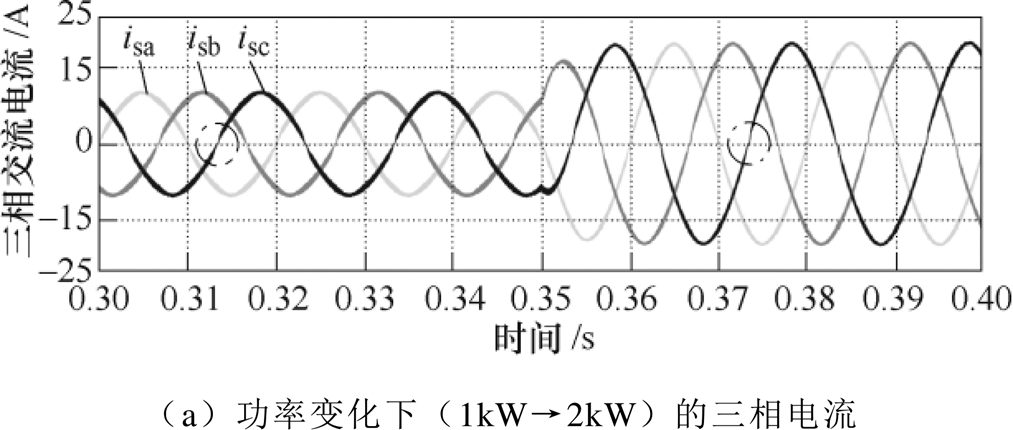
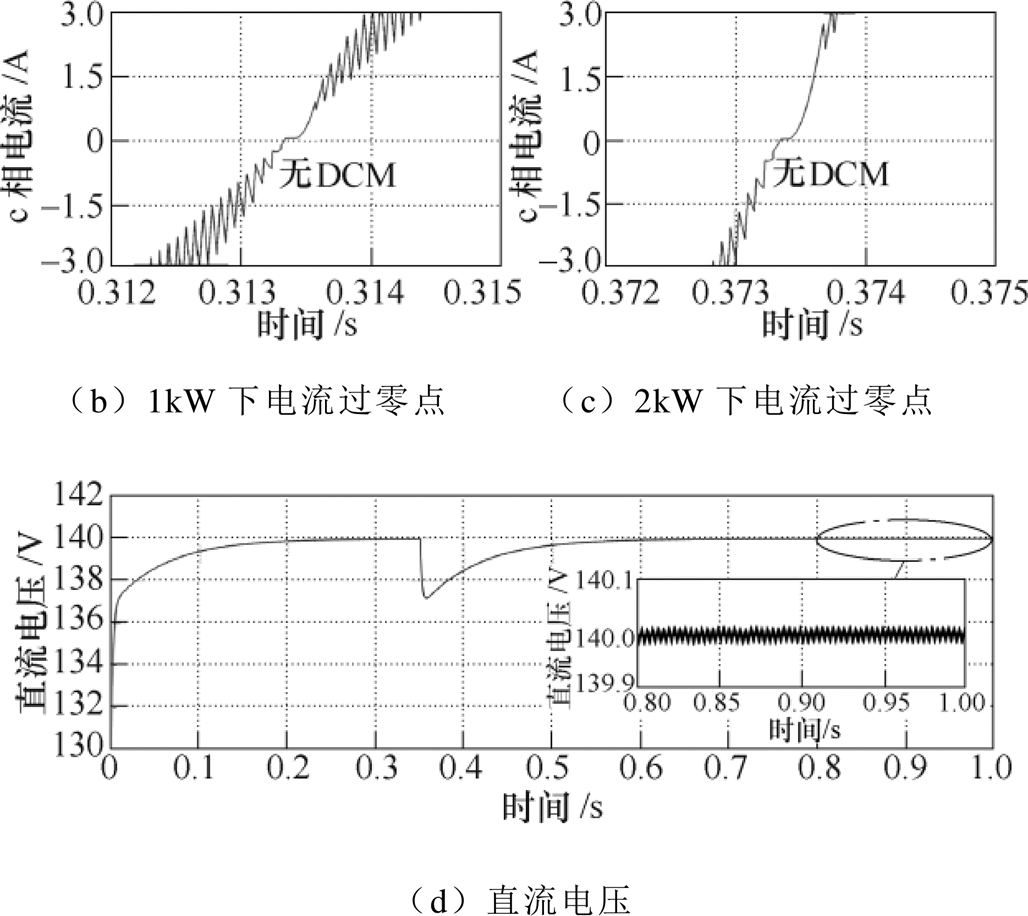
图17为综合了PI控制、占空比前馈和重复控制的改进联合控制下的三相电流波形,在保证重复控制抑制纹波效果的同时,实现了电流过零点畸变的消除。当系统功率发生变化时仍能保证在电流过零点处不会出现畸变,大大地提高了Vienna整流器在功率变化时工作的稳定性。直流电压波动也得到了大幅度的抑制,基本可以维持在±0.02V之内,整体的改善效果最佳。
4.4 其他对比分析
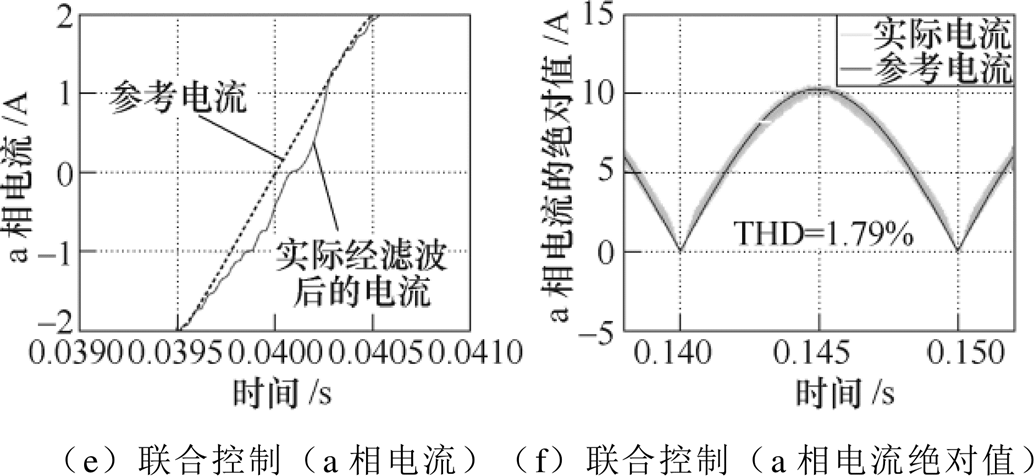
图18对上述三种控制方式得到的电流波形进行详细比对,其中,图18a、图18c、图18e为过零点附近参考电流与经滤波后的实际电流波形的对比,图18b、图18d、图18f为参考电流与实际电流的绝对值波形对比,系统功率为1kW,图18a、图18b揭示了仅重复控制会使电流在过零点处仍存在DCM,经滤波后发现该DCM状态持续时间约为0.2ms,结论与前述图5现象一致,电流总谐波畸变率(Total Harmonic Distortion, THD)较高;图18c、图18d表示仅占空比前馈干预虽能在过零点处大幅度削弱上述由DCM导致的畸变,但纹波率较高,说明对于各次谐波的抑制效果不如重复控制;图18e、图18f表明联合控制综合了占空比前馈干预与重复控制的优点,过零点处的畸变得到大幅度改善,因而可以很快地对参考电流进行跟踪,同时高频纹波也得到了进一步的抑制。
图19进一步给出了基于单周期控制、滞环控制、单PI控制与所提联合控制之间的比对。仿真条件同上,系统功率P=1kW。从图19可知,单周期控制和纯PI控制的电流波形都不理想,在过零点处有不同程度的畸变,选用2A环宽的滞环控制虽然畸变率较低,但谐波频率分布较宽,不利于控制器设计。综合来看,本文所提出的联合控制效果最好,应用性更强。
表2总结了系统在不同功率等级下,上述列举的所有控制方式的THD对比情况。可以发现,随着功率等级的提升,电流的THD逐步减小,且联合控制对电流的跟踪精度最高。
表2 几种控制方式下的电流THD
Tab.2 THD of input current under several control strategies

控制方式THD(%) 4kW2kW1kW PI4.827.8515.57 单周期控制4.227.1312.56 滞环控制1.873.647.17 PI+占空比前馈0.951.432.68 PI+重复控制3.324.918.82 联合控制0.620.871.79
图20为在三相电网电压受到扰动时,联合控制下波形效果。t =0.10s时向电网中加入5%基波含量的3、5、7次谐波。电流波形始终保持较好的正弦性,由此证明了本文所提出的联合控制在电网扰动环境下工作的有效性。
5 实验验证
为验证本文所提出的联合控制策略的有效性,搭建了一台2kW的三相四线制Vienna整流器实验样机,采用DSP与FPGA相结合完成采样和全数字化控制,DSP采用TI公司的TMS320F28335,FPGA芯片采用ALTERA公司的EP1C12Q24017N,电路参数和控制器参数与仿真情况一致,记录波形、分析电流THD和系统功率因数采用Fluke435电能质量分析仪及示波器,三相四线制Vienna整流器实验样机如图21所示。
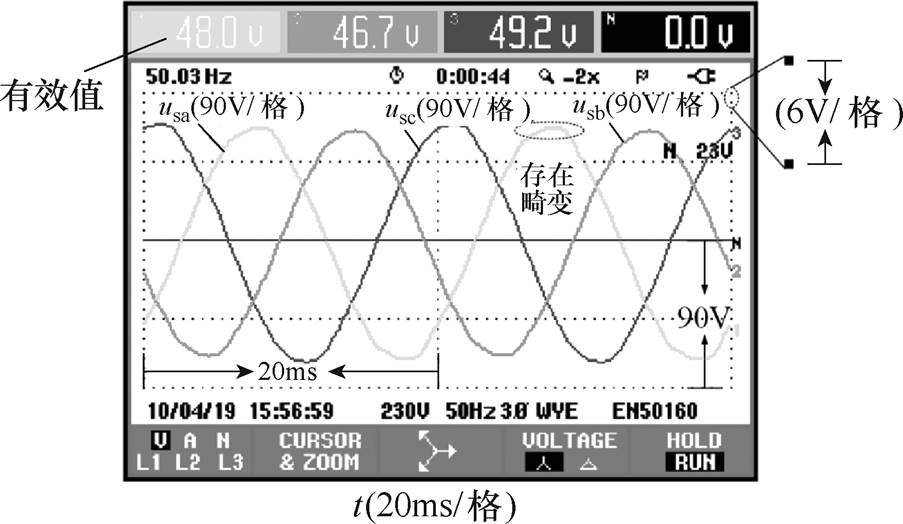
图22给出了三相电网侧交流电压波形,三相电压的有效值为48V,在峰值处可以观测到电网电压存在畸变,电压THD约为3%。由于过零点附近的DCM在低功率下更容易发生,因此图23~图26给出了实验样机在半载(P=1kW)时不同控制策略下的三相电流波形、c相电压与电流对比波形,系统功率因数和c相电流THD等电能质量信息,以证明联合控制策略的优势(如无特别说明,图23~图27中的实验刻度均按照图22所示的90V和20ms跨度,而非小格跨度)。
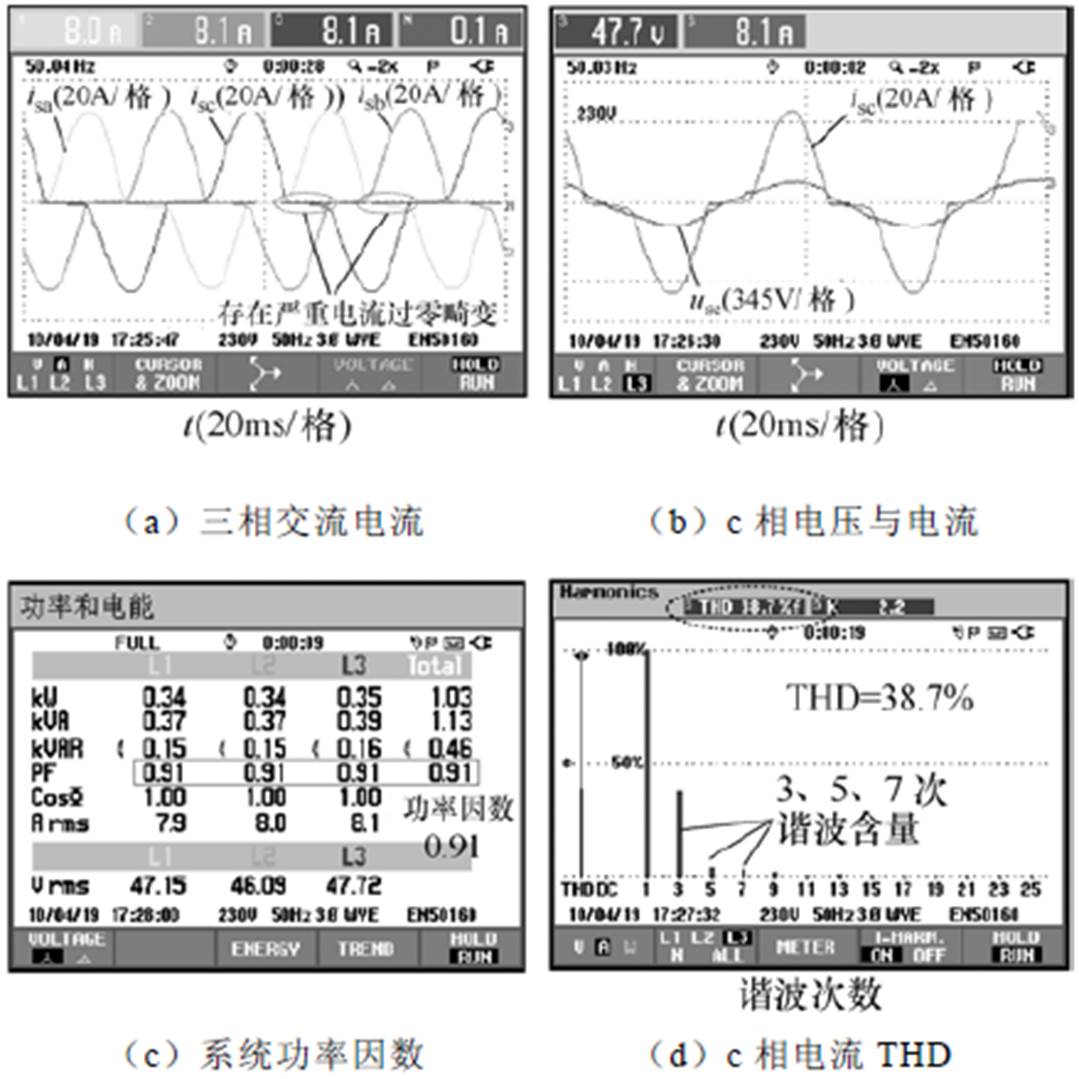
图23给出了基于PI控制的四线制Vienna整流器工作情况,可见三相电流过零点处存在较大的畸变,导致3次谐波含量很高,功率因数也仅有0.91,这是由于过零点处长时间工作在DCM造成的。
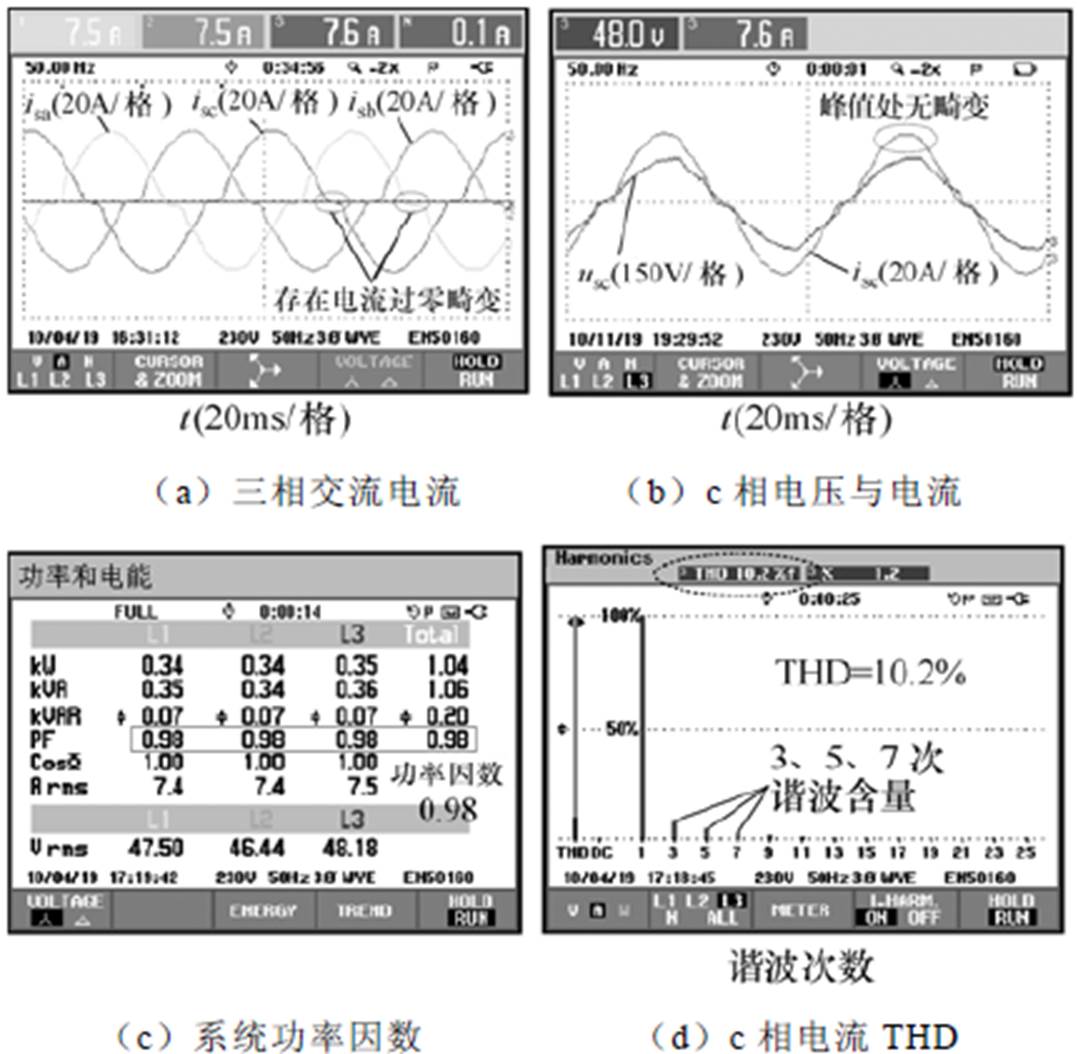
图24为引入重复控制后的三相电流波形及其他相关电能质量参数,引入了重复控制虽能改善电流波形,THD为10.2%,系统功率因数为0.98,但仍不满足谐波标准,且在低功率条件下,明显存在过零点畸变现象,另外从图24b可以观察到,在峰值处电流波形的正弦性较好,不存在畸变。
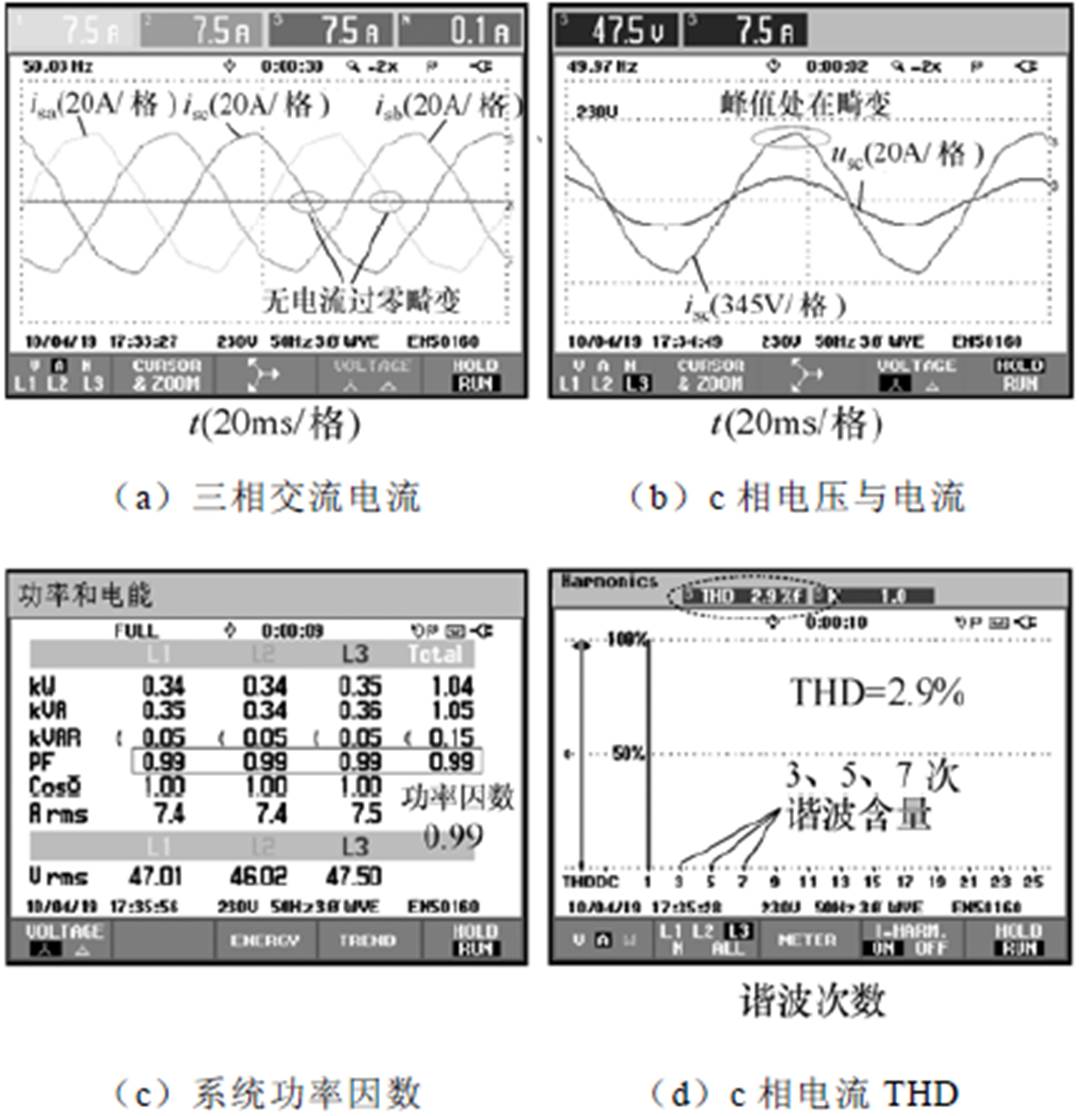
图25a为PI与占空比前馈干预配合控制的三相电流波形,过零点畸变得到了消除,由图25c、图25d可知,此时的电流THD和系统功率因数分别达到了2.9%和0.99。但从图25b中得知,电流波形的正弦性不如图24b中的重复控制,呈现和电网电压一样的畸变趋势,事实上,这是由于图22所示的电网电压在峰值处的畸变带来不正确的前馈量导致的。
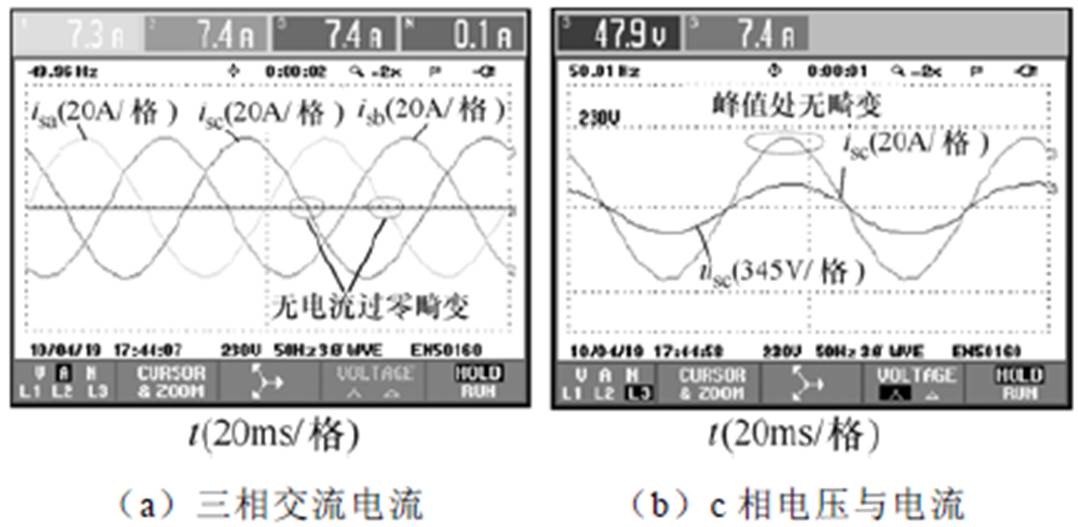
图26为改进后的PI+重复控制+占空比前馈联合控制,综合了上述各控制的优点,THD降至1.4%,正弦性很好,不存在过零点畸变现象,系统的各方面指标都得到了改进。
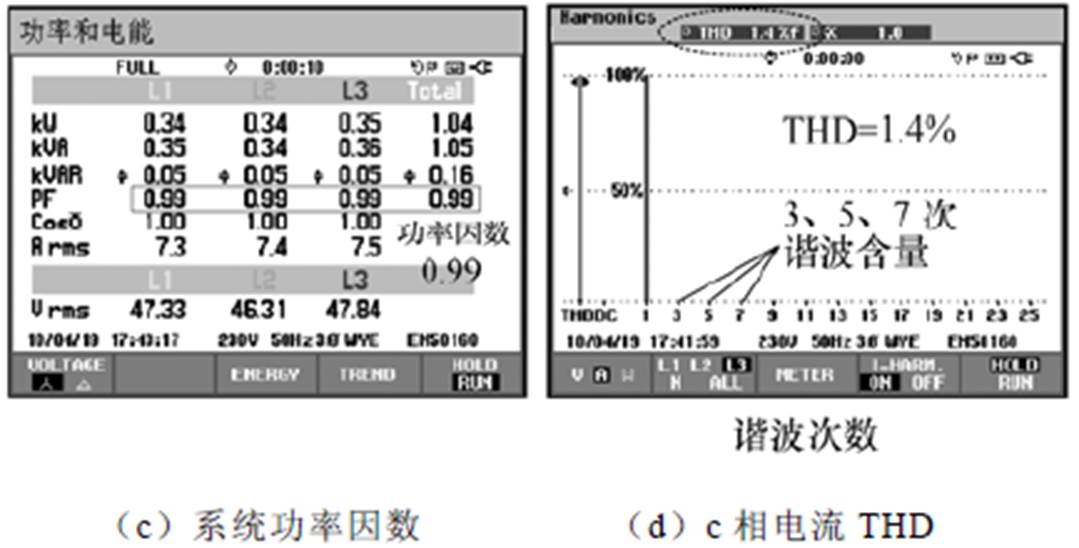
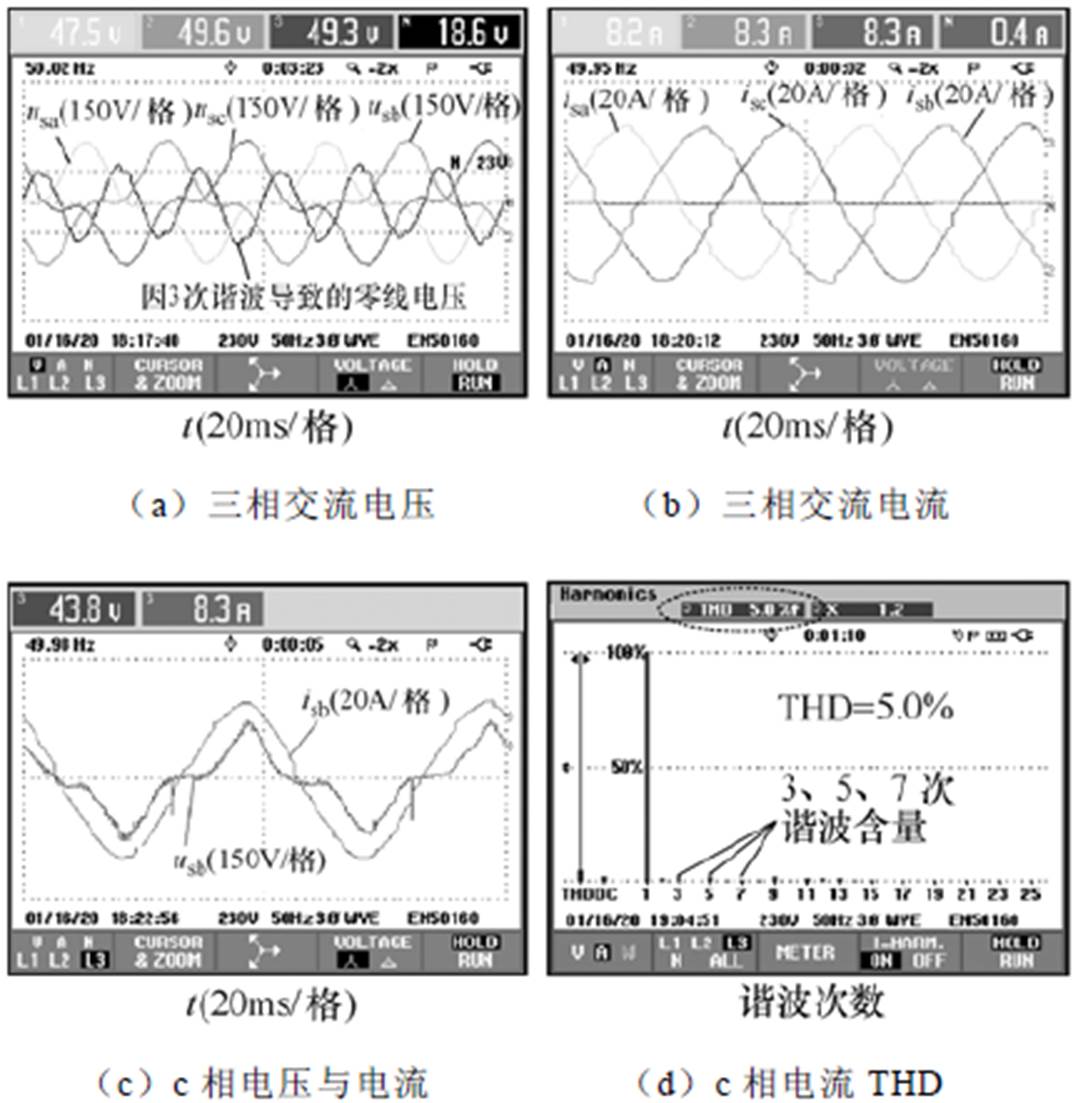
图27给出了当三相电网电压受到谐波干扰情况下联合控制的系统工作情况,图27a中电网电压畸变严重,3次谐波含量很高,在联合控制下,三相电流波形能维持较好的正弦性,THD也控制在5%之内。
表3总结了实验中不同控制策略下在满载(P= 2kW)和半载(P=1kW)时的c相电流THD以及系统的功率因数情况。由表3可知,联合控制策略可以有效地提高系统的功率因数并降低电流的谐波畸变率,控制性能最好。
表3 几种控制方式实验条件下的电流THD以及系统功率因数
Tab.3 THD of input current and system PF under experimental condition by using diffenernt control strategies
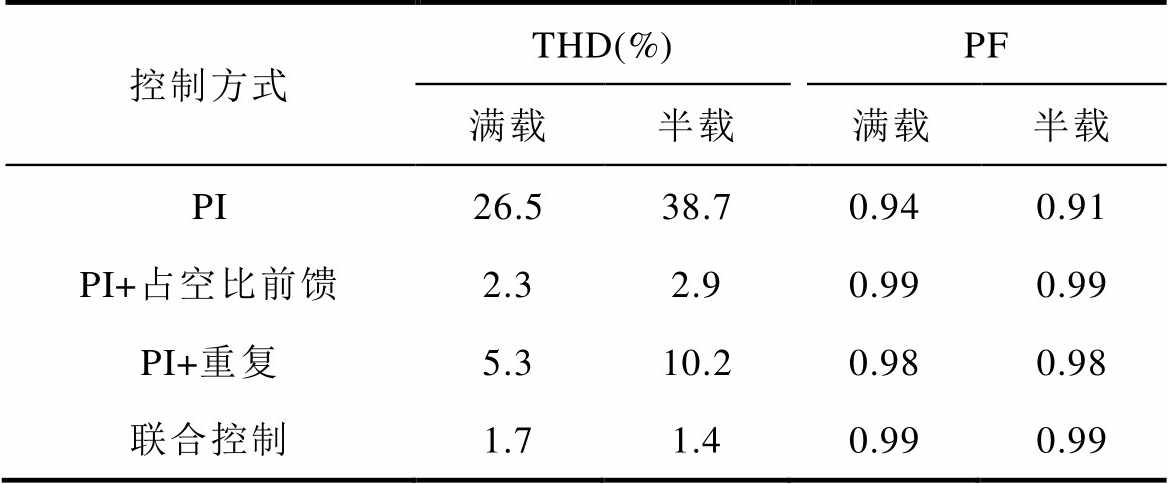
控制方式THD(%)PF 满载半载满载半载 PI26.538.70.940.91 PI+占空比前馈2.32.90.990.99 PI+重复5.310.20.980.98 联合控制1.71.40.990.99
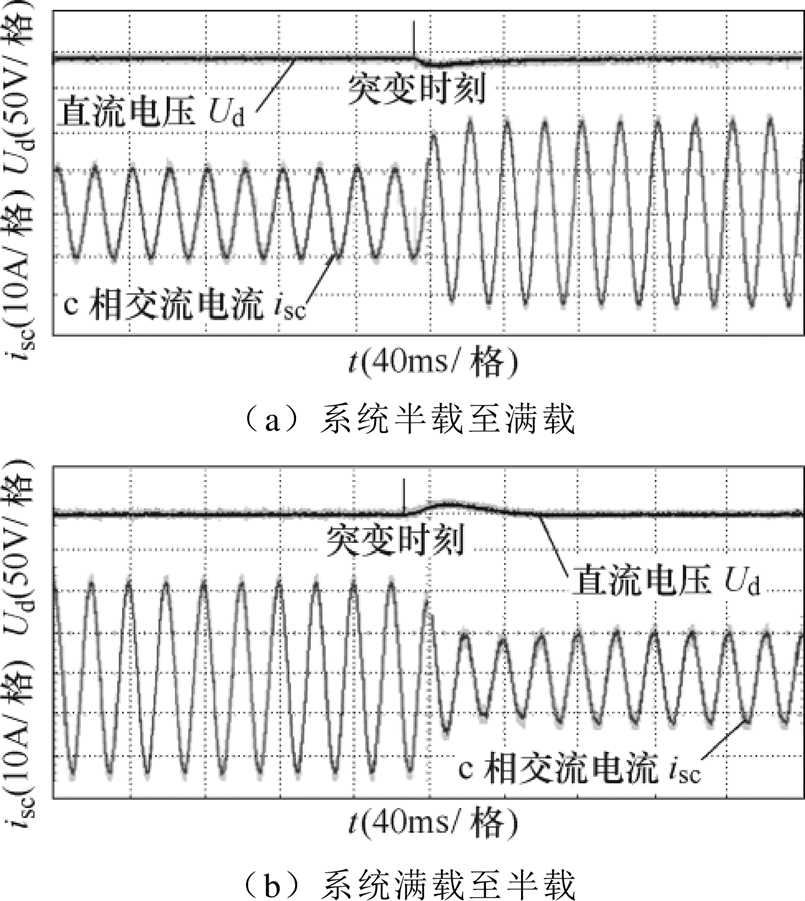
图28为负载由半载(P=1kW)突然切换至满载(P=2kW)和由满载切换至半载两种功率发生变动时的直流电压和c相电流波形。输入交流电压仍为48V,直流侧电压稳定在140V,可以看到,c相电流在联合控制下依旧保持较为理想的正弦波形,动态特性良好,不会因功率的变化而产生过零点畸变现象。另外,为了不影响电流内环的跟踪,电压外环的带宽设置较低,因而直流电压需要一定的恢复时间。
6 结论
本文基于三相四线制Vienna整流器这一典型的PFC电路,通过对输入交流电流在过零点处畸变机理的分析,得到以下结论:
1)低功率条件下,三相四线制Vienna整流器极易处于DCM,由此导致的电流过零点畸变现象会影响系统的功率因数和电流的THD。
2)占空比前馈干预可以消除电流过零点畸变现象,但无法避免电网扰动引起的错误前馈量,闭环系统的谐波抑制效果不佳,存在稳态误差。
3)重复控制能保证电流高度的正弦化,对谐波的抑制情况较好,但难以消除电流过零点畸变现象。
因此,本文提出联合控制方法,综合了上述不同控制的优点,无论是在大功率应用场合还是小功率电源环境中,该控制策略都能保证系统的高效运行,赋予系统更强的抗干扰性、更低的谐波畸变率、更稳定的直流电压,同时提高了系统的功率因数。除此之外,对电流内环中重复控制器部分给出了环路参数设计方法和稳定性验证,另外,该控制方法无需坐标变换的特性使其更容易在实际应用中操作,仿真和实验结果都表明该联合控制策略的有效性。
附 录
附图1给出了电流内环的传递函数框图。为叙述方便,以下推导中,Udh为直流侧电压的一半,Ud为直流侧总电压,Ts为一个采样周期或开关周期,Ls为交流滤波电感,忽视了其中的寄生电阻,C为直流侧电容,C1= C2=C。
附图1 电流内环s域下的传递函数框图
Fig.App.1 Transfer function diagram in s-domain of inner loop
附图1中,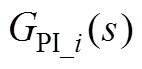 为PI调节器的传递函数,
为PI调节器的传递函数, 和
和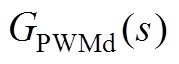 考虑了实际程序中存在的固有延时和调制延时,分别为
考虑了实际程序中存在的固有延时和调制延时,分别为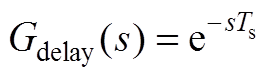 ,
,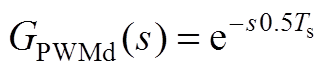 。另外,
。另外,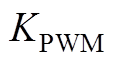 为PWM的增益系数,因载波幅值一般为1,故
为PWM的增益系数,因载波幅值一般为1,故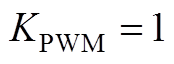 。
。 为占空比到电感电流的功率级传递函数,其表达式为
为占空比到电感电流的功率级传递函数,其表达式为 (因篇幅有限,数学模型和公式的具体推导不再展示)。
(因篇幅有限,数学模型和公式的具体推导不再展示)。
将附图1所示传递函数引入占空比前馈干预并进行延时项合并简化后的传递函数如附图2所示。
附图2 含前馈干预的简化电流内环传递函数框图
Fig.App.2 Simplified transfer function diagram in s-domain of inner current loop with duty-ratio feedforward
占空比前馈叠加项仅改变整流器系统的输入阻抗,对控制器参数设计无直接影响,在对PI参数进行整定时,为简化分析,此处可将其忽略。两个延时项合并后有 ,实际分析时可将其等效为一个一阶惯性环节,整理后,得到电流内环的开环传递函数为
,实际分析时可将其等效为一个一阶惯性环节,整理后,得到电流内环的开环传递函数为
将相关参数代入式(A1),结合二型系统参数的整定原则,可以得到如图10所示的电流内环开环及闭环传递函数伯德图。
参考文献
[1] Soeiro T B, Kolar J W. Analysis of high-efficiency three-phase two- and three-level unidirectional hybrid rectifiers[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3589-3601.
[2] 丁文龙, 刘家君, 段彬, 等. VIENNA整流器中点电位振荡抑制与平衡控制研究[J]. 中国电机工程学报, 2017, 37(24): 7284-7293, 7443.
Ding Wenlong, Liu Jiajun, Duan Bin, et al. Investi- gation of neutral-point voltage oscillation suppression and balancing control in VIENNA rectifiers[J]. Proceedings of the CSEE, 2017, 37(24): 7284-7293, 7443.
[3] Lee J S, Lee K B, Blaabjerg F. Predictive control with discrete space-vector modulation of Vienna rectifier for driving PMSG of wind turbine systems[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12368-12383.
[4] 宋卫章, 余丰, 戴智豪, 等. 带负载电流前馈的VIENNA整流器PR控制[J]. 电机与控制学报, 2019, 23(5): 76-83.
Song Weizhang, Yu Feng, Dai Zhihao, et al. Pro- portional resonant current control strategy with load current feed-forward control for VIENNA rectifier[J]. Electric Machines and Control, 2019, 23(5): 76-83.
[5] Adhikari J, Prasanna I V, Panda S K. Reduction of input current harmonic distortions and balancing of output voltages of the Vienna rectifier under supply voltage disturbances[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5802-5812.
[6] 吕征宇, 韩豪杰, 姚文熙, 等. 采用DRC-SPWM的VIENNA整流器在dq坐标系下的数学模型[J]. 电机与控制学报, 2019, 23(2): 11-18.
Lü Zhengyu, Han Haojie, Yao Wenxi, et al. Mathe- matical model of VIENNA rectifier with DRC- SPWM in dq coordinate[J]. Electric Machines and Control, 2019, 23(2): 11-18.
[7] 刘璐, 朱国荣, 陈皓, 等. 三相四线制VIENNA整流器损耗分析与热设计[J]. 电工技术学报, 2014, 29(增刊1): 282-290.
Liu Lu, Zhu Guorong, Chen Hao, et al. Power loss analysis and thermal design of three phase four wire VIENNA rectifier[J]. Transactions of China Electro- technical Society, 2014, 29(S1): 282-290.
[8] 陈杰, 赵冰, 陈新, 等. 不平衡负载条件下三相四线制并联逆变器的下垂控制[J]. 电工技术学报, 2018, 33(20): 4790-4801.
Chen Jie, Zhao Bing, Chen Xin, et al. Droop control of three-phase four-wire parallel inverters under unbalanced load condition[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4790-4801.
[9] 张国荣, 吴一鸣, 彭勃, 等. 三相四线制三电平变流器的优化调制策略[J]. 电力系统自动化, 2018, 42(22): 187-197.
Zhang Guorong, Wu Yiming, Peng Bo, et al. Optimal modulation strategy for three-phase four-wire three- level converter[J]. Automation of Electric Power Systems, 2018, 42(22): 187-197.
[10] 邹甲, 王聪, 程红, 等. 三相线电压级联VIENNA变换器调制及直流侧电压控制[J]. 电工技术学报, 2018, 33(16): 3835-3844.
Zou Jia, Wang Cong, Cheng Hong, et al. Research on modulation strategy and balance control for DC-link voltages in triple line-voltage cascaded VIENNA converter[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3835-3844.
[11] Kolar J W, Friedli T. The essence of three-phase PFC rectifier systems-part I[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 176-198.
[12] Song Weizhang, Xing Feixiong, Yan Hua, et al. A hybrid control method to suppress the three-time fundamental frequency neutral-point voltage fluctu- ation in a VIENNA rectifier[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 468-480.
[13] 朱文杰, 陈昌松, 段善旭. 一种改善Vienna整流器输入电流品质的载波钳位调制方法[J]. 电工技术学报, 2019, 34(8): 1677-1688.
Zhu Wenjie, Chen Changsong, Duan Shanxu. A carrier-based modulation method with clamped area for input current performance of Vienna rectifier[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1677-1688.
[14] 王春阳, 姚钢, 殷志柱, 等. 针对电网电压扰动的Vienna整流器复合控制方法[J]. 电测与仪表, 2017, 54(21): 49-54, 111.
Wang Chunyang, Yao Gang, Yin Zhizhu, et al. Research on new hybrid control method for Vienna rectifier under disturbed power grid voltage[J]. Electrical Measurement and Instrumentation, 2017, 54(21): 49-54, 111.
[15] 严刚, 姚文熙, 李宾, 等. 混合导通模式三相三电平VIENNA整流器控制策略[J]. 电工技术学报, 2012, 27(12): 87-93.
Yan Gang, Yao Wenxi, Li Bin, et al. Control strategy of three-phase three-level VIENNA rectifier operating in mixed conduction mode[J]. Transactions of China Electrotechnical Society, 2012, 27(12): 87-93.
[16] 徐红灿, 滕予非, 王晓茹. 基于重复和准比例谐振复合的直驱风机网侧变流器控制策略[J]. 电力系统保护与控制, 2018, 46(8): 95-102.
Xu Hongcan, Teng Yufei, Wang Xiaoru. A control strategy combining repetitive control and quasi-PR control for PMSG for grid-side converter[J]. Power System Protection and Control, 2018, 46(8): 95-102.
[17] Arvindan A N, Vela S P. Investigation for improved power quality in hysteresis current controlled three- phase four-wire VIENNA rectifier ropologies[C]// 2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 2018: 485-493.
[18] Leibl M, Kolar J W, Deuringer J. Sinusoidal input current discontinuous conduction mode control of the VIENNA rectifier[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8800-8812.
[19] 阚加荣, 吴云亚, 谢少军, 等. 宽功率范围内采用电流临界连续状态+恒频控制的光伏微逆变器[J]. 电网技术, 2017, 41(12): 3926-3933.
Kan Jiarong, Wu Yunya, Xie Shaojun, et al. PV micro-inverter with constant frequency and current BCM control strategy within wide power range[J]. Power System Technology, 2017, 41(12): 3926-3933.
[20] Thandapani T, Karpagam R, Paramasivam S. Com- parative study of VIENNA rectifier topologies[J]. International Journal of Power Electronics, 2015, 7(3/4): 147.
[21] Chen Min, Sun Jian. Feedforward current control of boost single-phase PFC converters[J]. IEEE Transa- ctions on Power Electronics, 2006, 21(2): 338-345.
[22] 唐健, 邹旭东, 佘煦, 等. 三相四线制三电平三桥臂有源滤波器中点平衡控制策略[J]. 中国电机工程学报, 2009, 29(24): 40-48.
Tang Jian, Zou Xudong, She Xu, et al. A research on neutral-point potential balancing control strategy for three-phase four-wire tri-level three-leg APFs[J]. Proceedings of the CSEE, 2009, 29(24): 40-48.
[23] Gusseme K D, Sype D M V D, Bossche A P M V D, et al. Digitally controlled boost power-factor- correction converters operating in both continuous and discontinuous conduction mode[J]. IEEE Transa- ctions on Industrial Electronics, 2005, 52(1): 88-97.
[24] 张旗, 蔡逢煌, 黄丽梅, 等. 单相程控电流源PI+重复控制[J]. 电工技术学报, 2019, 34(增刊1): 163-170.
Zhang Qi, Cai Fenghuang, Huang Limei, et al. PI+ repetitive control applied to single-phase program- mable standard power source[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 163- 170.
[25] Cho Y, Lai J S. Digital plug-in repetitive controller for single-phase bridgeless PFC converters[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 165- 175.
[26] Zhou Keliang, Wang Danwei. Digital repetitive controlled three-phase PWM rectifier[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 309-316.
[27] He Liqun, Zhang Kai, Xiong Jian, et al. A repetitive control scheme for harmonic suppression of circu- lating current in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 471-481.
[28] Chen F Z, Dragan Maksimović. Digital control for improved efficiency and reduced harmonic distortion over wide load range in Boost PFC rectifiers[J]. IEEE Transactions on Power Electronics, 2010, 25(10): 2683-2692.
An Improved Control Method of 4-Wire Vienna Rectifier Considering Power Fluctuation
Yang Di Yao Gang Zhou Lidan
(Key Laboratory of Control of Power Transmission and Conversion of Ministry of Education Department of Electrical Engineering Shanghai Jiao Tong University Shanghai 200240 China)
Abstract In most cases, power fluctuation will result in zero-crossing distortion and current ripples during the operation of three-phase four-wire Vienna rectifier under the traditional dual loop control with PI regulator. This paper discussed the influence of power fluctuation on the input current from the perspective of continuous current mode (CCM) and discontinuous current mode (DCM). Accordingly, a combination of PI controller, repetitive controller and duty-ratio feedforward control, as an improved control strategy, was proposed. On one hand, the intervention method of duty-ratio feedforward compensation can effectively eliminate the zero-crossing distortion in AC current. On the other hand, the repetitive controller gives a fiercer attenuation of AC current harmonics and has a better ability to deal with the grid voltage interruption. System modeling, parameter design and stability verification were also carried out. Finally, simulation and experiment verified the proposed control strategy.
keywords:Vienna rectifier, duty-ratio feedforward, repetitive control, PI controller, continuous current mode
中图分类号:TM461
DOI: 10.19595/j.cnki.1000-6753.tces.191681
上海市自然科学基金资助项目(18ZR1418400)。
收稿日期 2019-12-02
改稿日期 2020-02-10
作者简介
杨 頔 男,1995年生,硕士,研究方向为三相PFC整流器。E-mail: Vincent423@sjtu.edu.cn
姚 钢 男,1977年生,副研究员,硕士生导师,研究方向为电力电子在电力系统中的应用等。E-mail: yaogangth@sjtu.edu.cn(通信作者)
(编辑 陈 诚)
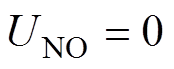 ,因此四线制拓扑可以进行解耦,三相电流可分别独立控制,解耦后的单相Vienna整流拓扑结构如图2所示。采用电阻负载R,根据开关损耗、效率和元器件数量等因素[20]综合考虑后,双向功率开关管S采用两个绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)反串联结构进行后续的理论和实验分析。此外,直流侧上下电容电压平衡也可以进行独立控制,同样体现了四线制结构控制的灵活性。S闭合时,交流电流沿图2中的路径②在N与O之间流通;S断开时,根据交流电压正负半周决定电流流经桥臂上管VD1还是下管VD2,分别如图2中的路径①和③所示,本质上可按照Boost型PFC整流电路[21]对其建模分析。
,因此四线制拓扑可以进行解耦,三相电流可分别独立控制,解耦后的单相Vienna整流拓扑结构如图2所示。采用电阻负载R,根据开关损耗、效率和元器件数量等因素[20]综合考虑后,双向功率开关管S采用两个绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)反串联结构进行后续的理论和实验分析。此外,直流侧上下电容电压平衡也可以进行独立控制,同样体现了四线制结构控制的灵活性。S闭合时,交流电流沿图2中的路径②在N与O之间流通;S断开时,根据交流电压正负半周决定电流流经桥臂上管VD1还是下管VD2,分别如图2中的路径①和③所示,本质上可按照Boost型PFC整流电路[21]对其建模分析。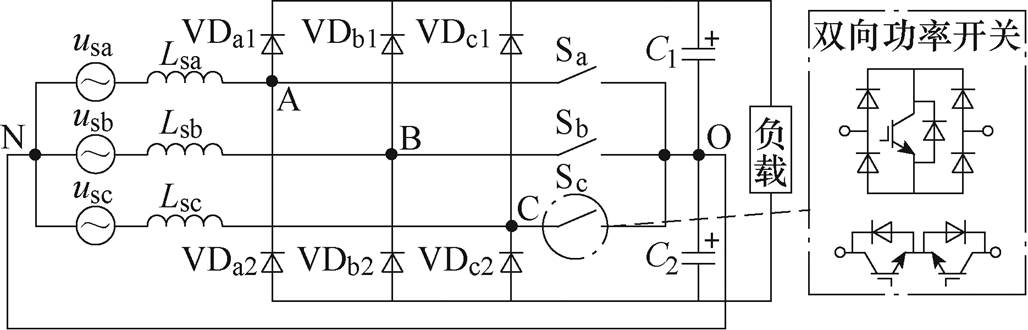

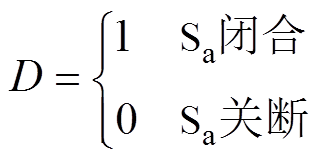 (1)
(1)
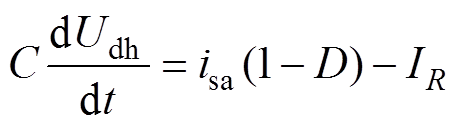 (2)
(2)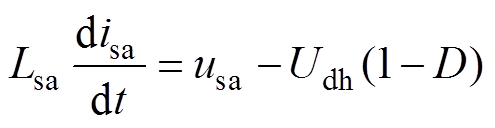 (3)
(3) (4)
(4)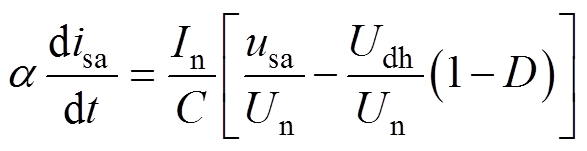 (5)
(5)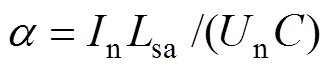 ,一般工况下,
,一般工况下,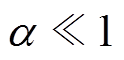 ,经上述变换后,式(4)、式(5)等式右边处于相同的数量级,利用奇异摄动理论中的快慢模型对其求解后得到
,经上述变换后,式(4)、式(5)等式右边处于相同的数量级,利用奇异摄动理论中的快慢模型对其求解后得到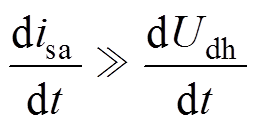 (6)
(6)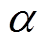 近似取0后代入式(5)得到奇异摄动理论中的退化方程,进一步求解此时的退化近似解D,该占空比即可等效为连续的占空比d
近似取0后代入式(5)得到奇异摄动理论中的退化方程,进一步求解此时的退化近似解D,该占空比即可等效为连续的占空比d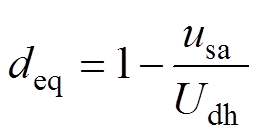 (7)
(7)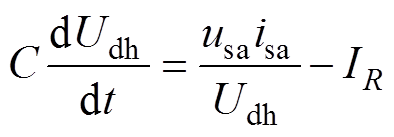 (8)
(8)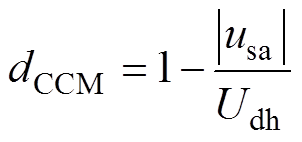 (9)
(9)
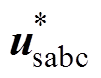 为三相单位正弦量,与电压外环输出相乘得到内环参考值;Ctrl为决定内环参考量的控制信号,即通过判断输入电压处于正半周还是负半周来决定电流内环参考电流。
为三相单位正弦量,与电压外环输出相乘得到内环参考值;Ctrl为决定内环参考量的控制信号,即通过判断输入电压处于正半周还是负半周来决定电流内环参考电流。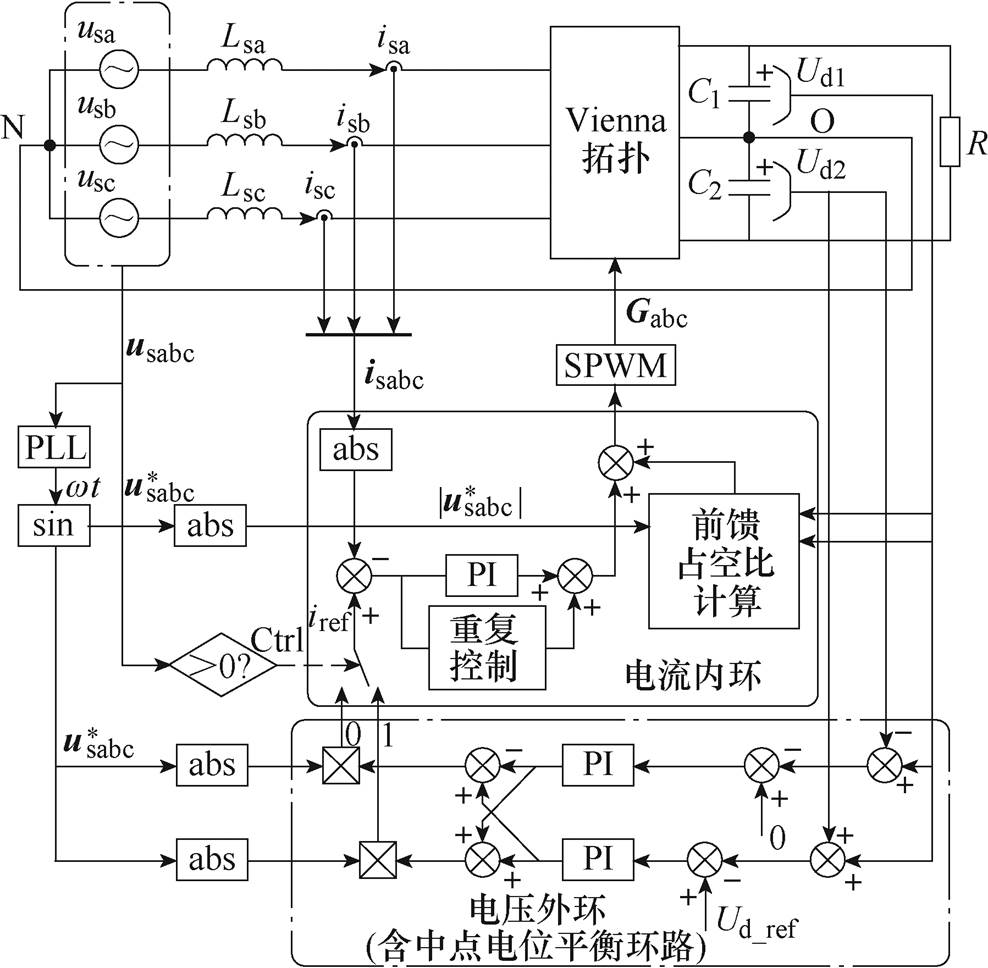
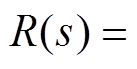
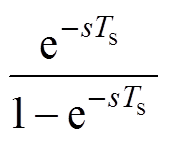 ,可将其视为一个周期函数信号发生器嵌入需要控制的闭环系统中,实现对周期为T
,可将其视为一个周期函数信号发生器嵌入需要控制的闭环系统中,实现对周期为T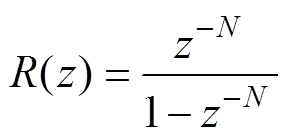 (10)
(10)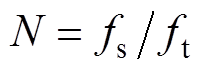 为一个跟踪信号周期内采样周期的个数,
为一个跟踪信号周期内采样周期的个数,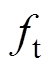 为待跟踪信号的频率。
为待跟踪信号的频率。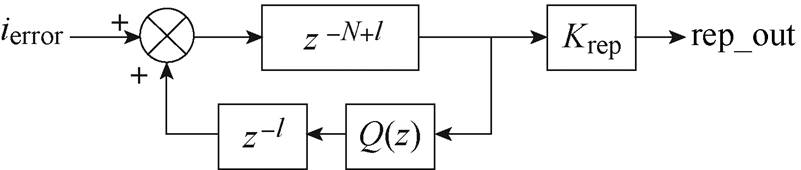
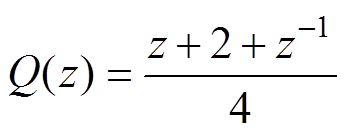
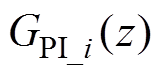 、
、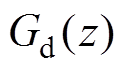 、
、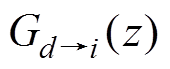 分别为z域下电流内环PI控制器、环路采样和调制延时以及占空比到交流输入电流的传递函数。重复控制部分以及电流内环总体的传递函数分别为
分别为z域下电流内环PI控制器、环路采样和调制延时以及占空比到交流输入电流的传递函数。重复控制部分以及电流内环总体的传递函数分别为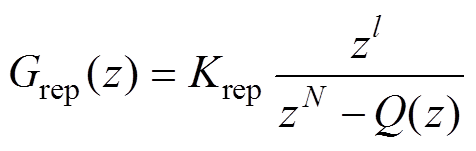 (11)
(11)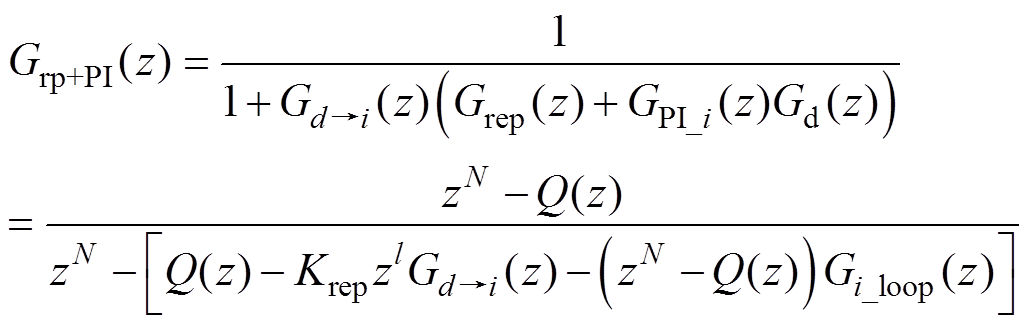 (12)
(12)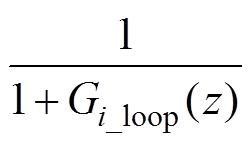 从式(12)中提取出来,仅讨论剩余项,
从式(12)中提取出来,仅讨论剩余项,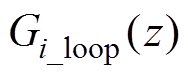 为附录中电流内环的开环传递函数的z域表达式形式,由此得到
为附录中电流内环的开环传递函数的z域表达式形式,由此得到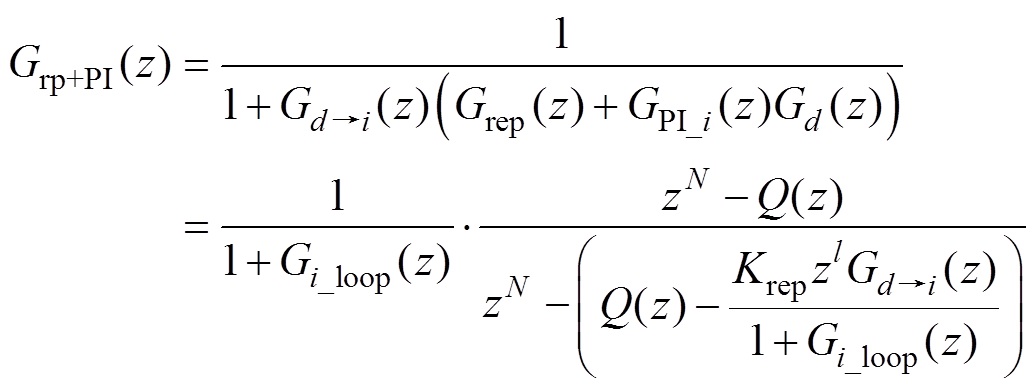 (13)
(13)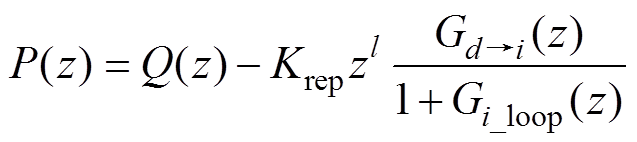 (14)
(14)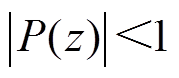 (15)
(15)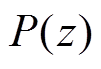 在不同K
在不同K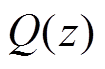 分别取0.95和
分别取0.95和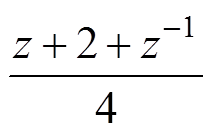 ,不难得知,当
,不难得知,当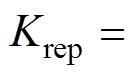
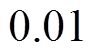 时,幅值增益小于1,式(13)的极点位于复平面单位圆内,系统保持稳定。
时,幅值增益小于1,式(13)的极点位于复平面单位圆内,系统保持稳定。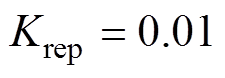 ,绘制式(13)所示不同Q(z)下的总传递函数幅频特性,如图14所示。
,绘制式(13)所示不同Q(z)下的总传递函数幅频特性,如图14所示。
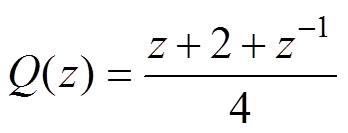 时,在50Hz倍数频次的位置处,跟踪误差的衰减更大,间接表明谐波抑制效果更佳。结合稳定性分析可知,
时,在50Hz倍数频次的位置处,跟踪误差的衰减更大,间接表明谐波抑制效果更佳。结合稳定性分析可知,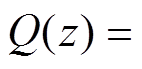
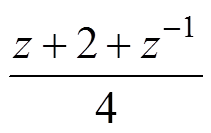 更有利于重复控制器的控制。对比图10,对于整数倍频次信号的跟踪精度,重复控制与PI并联优于单PI控制,这也验证了重复控制对谐波的抑制效果强于PI控制器。
更有利于重复控制器的控制。对比图10,对于整数倍频次信号的跟踪精度,重复控制与PI并联优于单PI控制,这也验证了重复控制对谐波的抑制效果强于PI控制器。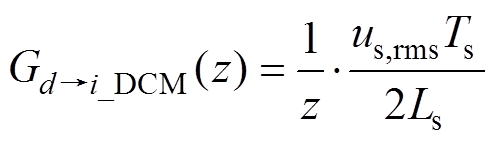 (16)
(16)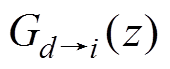 中,重新进行稳定性分析,可知上述参数在DCM下依然成立。此外,关于电压外环的设计只要将电流内环等效为增益为1的常数或者一个延时环节,控制其带宽在20Hz以下,利用上述电流环的计算方法即可完成参数的设计,本文篇幅有限,不再赘述。
中,重新进行稳定性分析,可知上述参数在DCM下依然成立。此外,关于电压外环的设计只要将电流内环等效为增益为1的常数或者一个延时环节,控制其带宽在20Hz以下,利用上述电流环的计算方法即可完成参数的设计,本文篇幅有限,不再赘述。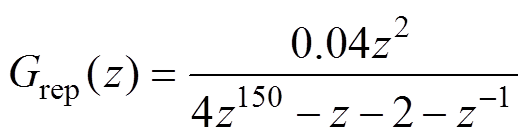 (17)
(17)








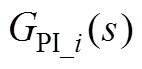 为PI调节器的传递函数,
为PI调节器的传递函数, 和
和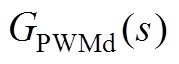 考虑了实际程序中存在的固有延时和调制延时,分别为
考虑了实际程序中存在的固有延时和调制延时,分别为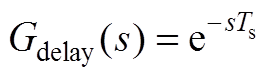 ,
,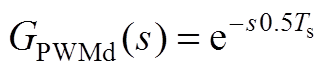 。另外,
。另外,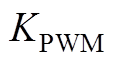 为PWM的增益系数,因载波幅值一般为1,故
为PWM的增益系数,因载波幅值一般为1,故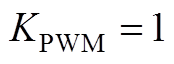 。
。 为占空比到电感电流的功率级传递函数,其表达式为
为占空比到电感电流的功率级传递函数,其表达式为 (因篇幅有限,数学模型和公式的具体推导不再展示)。
(因篇幅有限,数学模型和公式的具体推导不再展示)。
 ,实际分析时可将其等效为一个一阶惯性环节,整理后,得到电流内环的开环传递函数为
,实际分析时可将其等效为一个一阶惯性环节,整理后,得到电流内环的开环传递函数为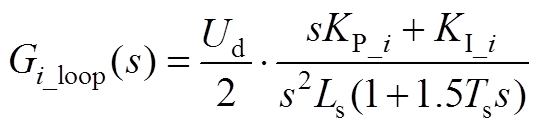 (A1)
(A1)