主动电磁轴承-刚性转子系统加速响应的鲁棒性
巩 磊1 杨 智2 祝长生1
(1. 浙江大学电气工程学院 杭州 310027 2. 中国船舶重工集团第704研究所 上海 200031)
摘要 加速响应是主动电磁轴承-刚性转子系统中一个重要的动力学特性,目前对支承在主动电磁轴承上的转子系统动力特性的研究主要以稳态特性为主,而对加速特性的研究较少。该文以主动电磁轴承-刚性转子系统为对象,分别研究PID控制和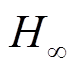 鲁棒控制时转子系统的加速特性。首先,建立主动电磁轴承-刚性转子系统在加速运动过程中的动力学方程。然后,分析加速运行过程中PID控制器和
鲁棒控制时转子系统的加速特性。首先,建立主动电磁轴承-刚性转子系统在加速运动过程中的动力学方程。然后,分析加速运行过程中PID控制器和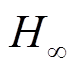 鲁棒控制器的设计原则及闭环系统的稳定性,研究PID控制参数对主动电磁轴承-刚性转子系统加速特性的影响以及
鲁棒控制器的设计原则及闭环系统的稳定性,研究PID控制参数对主动电磁轴承-刚性转子系统加速特性的影响以及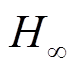 鲁棒控制器下转子系统加速特性对系统参数的不敏感性。最后,进行PID控制和
鲁棒控制器下转子系统加速特性对系统参数的不敏感性。最后,进行PID控制和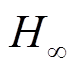 鲁棒控制条件下主动电磁轴承-刚性转子系统加速特性的仿真分析及实验。结果说明,PID控制参数变化对转子系统加速特性的影响,而
鲁棒控制条件下主动电磁轴承-刚性转子系统加速特性的仿真分析及实验。结果说明,PID控制参数变化对转子系统加速特性的影响,而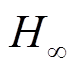 鲁棒控制下主动电磁轴承-刚性转子系统过临界的加速特性几乎不受加速度的影响,这与PID控制下传统转子系统的加速特性存在明显差异。
鲁棒控制下主动电磁轴承-刚性转子系统过临界的加速特性几乎不受加速度的影响,这与PID控制下传统转子系统的加速特性存在明显差异。
关键词:主动电磁轴承 刚性转子 加速特性 PID控制器 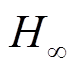 鲁棒控制器
鲁棒控制器
0 引言
主动电磁轴承(Active Magnetic Bearing, AMB)具有无摩擦、适合高速运行以及使用寿命长等优点,因此广泛应用于高速电机、涡轮分子泵、压缩机、飞轮储能等高速旋转机械[1-3]。在高速旋转机械中,旋转的转子是其核心。由于转子旋转过程中产生的振动会对整个系统产生严重影响,因此要尽最大可能地控制转子振动。对于AMB-刚性转子系统,转子的工作转速都会大于转子系统的一阶和二阶刚体临界转速,在刚体临界转速区转子会出现明显的振动,所以如何保证转子系统安全平稳地越过刚体临界转速就成为一个重点的研究内容。
传统轴承(滚动轴承及滑动轴承)支承的刚性转子系统在加速通过刚体临界转速区时,转子的最大振动随加速度的增大而减小[4]。王美令等分析了转子系统的不平衡瞬态响应,并得知加速过刚体临界转速区可有效降低瞬态响应的幅值[5]。白保东等通过有限元法计算了电磁屏蔽槽楔对高频电磁场的屏蔽效能以及轴承电流短路环的工作原理[6],通过减小电流波动可抑制转子振动。为了减小刚性转子系统在刚体临界转速区的振动,R. Boris等研究了参数优化和相位控制方法[7]。J. Sena等研究了混合磁轴承鼓风机的刚性模态振动控制[8]。S. Wang等针对转子以恒定加速度通过临界转速时产生的最大振动幅值超过间隙引起摩擦的问题,采用相位调制的方法来控制临界加速度[9-10]。然而,由于电磁轴承支承的刚性转子系统的刚体模态特征与传统轴承支承下刚体转子的刚体模态特征有所不同,所以这些研究成果并不一定适用于AMB-刚性转子系统中。
目前,在AMB-刚性转子系统中,大多数研究以考虑不平衡激励时的稳态振动为主。B. Shafai等提出了自适应力平衡控制方法来削弱位移信号中的同频扰动[11]。R. Herzog等采用窄带陷波器实现了定转速下的振动控制[12]。Jiang Kejian等依据采集的不平衡质量位置生成相应的控制信号,对转子不平衡进行实时补偿[13]。Yu Jie等提出了一种扰动抑制方法识别其幅值和相位,降低了自传感AMB-刚性转子系统的振动[14]。然而,AMB-刚性转子系统的动力学性能明显受到所采用的控制策略的影响,如PID[15-16]、自适应滑模控制器[17]和鲁棒控制器[18]等已被成熟应用于AMB-刚性转子系统的控制中,但其穿过刚体临界转速区时的加速特性却很少被研究。Mao Chuan等发现在带有不平衡补偿控制的AMB-刚性转子系统中,转子通过刚体临界转速区的最大振动随着转子运行加速度的增大而增大,与传统转子穿过临界转速的加速特性明显不同[19]。在AMB-刚性转子系统中,转子加速度如何影响转子系统穿过刚体临界转速区时的振动,至今仍没有一个统一的结论。
为探究AMB-刚性转子系统在加速穿过刚体临界转速时的振动特性,本文以AMB高速电机中的刚性转子系统为对象,分别选取PID控制器和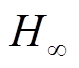 鲁棒控制器,分析了PID和强鲁棒控制条件下AMB-刚性转子系统的加速响应特性。最后通过仿真和实验对分析结果进行了验证。
鲁棒控制器,分析了PID和强鲁棒控制条件下AMB-刚性转子系统的加速响应特性。最后通过仿真和实验对分析结果进行了验证。
1 AMB-刚性转子系统在加速运动过程中的动力学模型
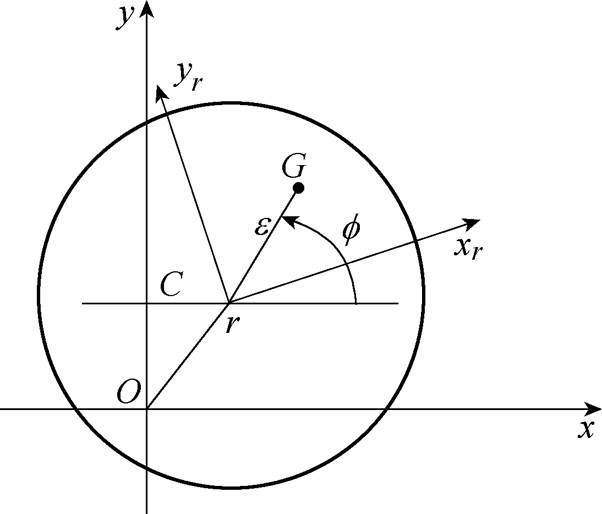
图1为本文研究的AMB-刚性转子系统结构。轴对称转子的轴向由一对永磁轴承支承,径向由两个AMB支承。为了便于描述AMB-转子系统的运动状态,在图1中定义了相关平面及坐标系。假设两端AMB-A和AMB-B的中心平面分别为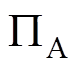 和
和 。平衡转子的质心为C,由于对称性,质心C必将位于转子几何中心线上,过
。平衡转子的质心为C,由于对称性,质心C必将位于转子几何中心线上,过 点做平行于两端AMB中心平面
点做平行于两端AMB中心平面 和
和 的平面
的平面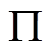 ,
,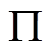 平面与定子几何中心线交于
平面与定子几何中心线交于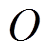 点。
点。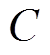 点到两端AMB中心平面
点到两端AMB中心平面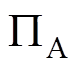 和
和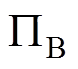 的距离分别为la和lb,平面
的距离分别为la和lb,平面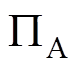 和
和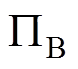 之间的距离为
之间的距离为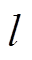 。建立
。建立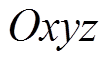 固定坐标系,其中,
固定坐标系,其中,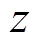 轴为旋转轴,
轴为旋转轴,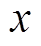 、
、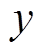 和
和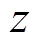 之间形成右手系。则转子的运动状态可以用转子质心在
之间形成右手系。则转子的运动状态可以用转子质心在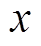 和
和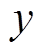 方向的平动位移(x, y)和转子绕
方向的平动位移(x, y)和转子绕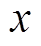 及
及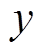 轴的角位移(
轴的角位移(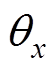 ,
,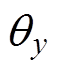 )来描述。
)来描述。
为了建立径向四自由度AMB-刚性转子系统的动力学方程,假设:①转子附加不平衡质量与转子的质量相比很小,不足以影响转子质心位置的偏移,于是不平衡转子的质心仍然在C点,不平衡转子的运动状态仍然用平衡转子质心C点的广义坐标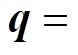
 来描述;②转子为轴对称刚性转子,转子绕x轴和绕y轴的转动惯量相同;③两端的AMB-A和AMB-B与位移传感器A和B不在同一个平面上内;④径向四个自由度的AMB结构和参数均相同;⑤忽略轴向轴承对转子径向运动的影响。
来描述;②转子为轴对称刚性转子,转子绕x轴和绕y轴的转动惯量相同;③两端的AMB-A和AMB-B与位移传感器A和B不在同一个平面上内;④径向四个自由度的AMB结构和参数均相同;⑤忽略轴向轴承对转子径向运动的影响。
对于不平衡的转子,转子的不平衡等效为由一个不在平衡转子质心C处的附加不平衡质量产生。假设该附加转子不平衡质量在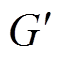 点位置,
点位置,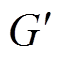 在平衡转子几何中心平面
在平衡转子几何中心平面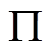 内的投影为
内的投影为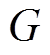 ,在
,在 轴上的投影长度为
轴上的投影长度为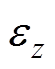 ,
,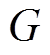 点到
点到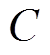 点的偏心距为
点的偏心距为 。为了便于描述
。为了便于描述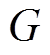 点在转子几何中心平面
点在转子几何中心平面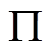 内的运动,以
内的运动,以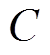 为原点,建立
为原点,建立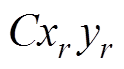 旋转坐标系,当
旋转坐标系,当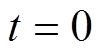 时,旋转坐标系
时,旋转坐标系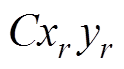 的
的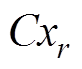 轴与
轴与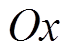 轴平行;当
轴平行;当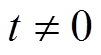 时,
时,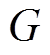 的瞬态旋转角度为
的瞬态旋转角度为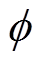 ,如图2所示。当转子稳定运行时,
,如图2所示。当转子稳定运行时,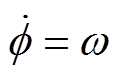 ,
,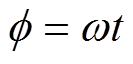 。
。
利用转子动力学理论[20],考虑转子不平衡和转子加速度的影响,可以得到AMBs-刚性转子系统在加速运行过程中的微分方程为
式中,m为转子质量;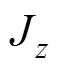 及J分别为转子绕
及J分别为转子绕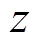 轴及绕
轴及绕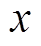 轴(
轴(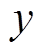 轴)的转动惯量;
轴)的转动惯量;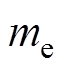 及
及 分别为不平衡质量及偏心距;
分别为不平衡质量及偏心距;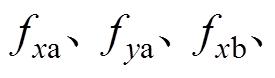
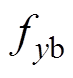 分别为两个AMB在
分别为两个AMB在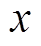 及
及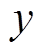 方向上的电磁力。
方向上的电磁力。
用矩阵表示为
其中,转子系统的广义质量矩阵和陀螺矩阵分别为
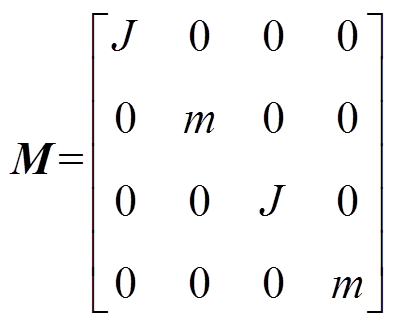
转子系统的力臂系数矩阵和系统所受广义不平衡向量分别为
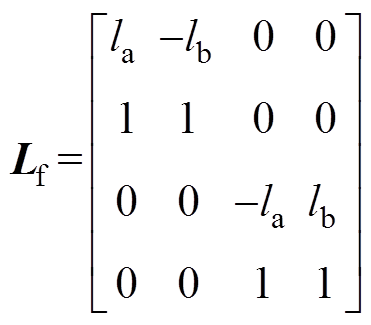
A和B端径向AMB在x和y方向上产生的电磁力向量为
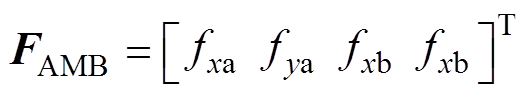
差分驱动模式下AMB线性化电磁力可表示为
其中
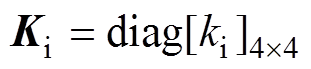
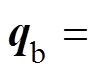
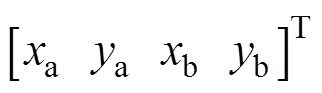
式中,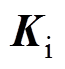 为AMB的电流刚度系数矩阵;
为AMB的电流刚度系数矩阵;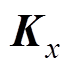 为AMB的位移刚度系数矩阵;
为AMB的位移刚度系数矩阵;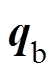 为传感器位置处的位移向量;
为传感器位置处的位移向量;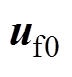 为转子处于平衡位置时的电磁力矩阵;
为转子处于平衡位置时的电磁力矩阵;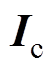 为控制电流矢量。控制电流矢量将由控制策略来决定。
为控制电流矢量。控制电流矢量将由控制策略来决定。
2 AMB-刚性转子系统的控制策略
目前,AMB-刚性转子系统的控制策略简单地分为两种:一种是传统的定参数PID控制器,最常见的就是PD、PID控制;另一种是具有强鲁棒性的变参数控制器,如滑模控制、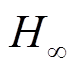 鲁棒控制器等。为了获得不同控制器条件下AMB-刚性转子系统的加速响应鲁棒特性,这里分别以PID控制和
鲁棒控制器等。为了获得不同控制器条件下AMB-刚性转子系统的加速响应鲁棒特性,这里分别以PID控制和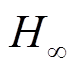 鲁棒控制为例进行分析。
鲁棒控制为例进行分析。
2.1 PD及PID控制
首先研究AMB-刚性转子系统稳定运行下的PID参数选取范围,其次研究定参数PID参数控制下的系统加速特性。
当采用PD控制,且各通道控制参数均相同时,控制电流可表示为
式中,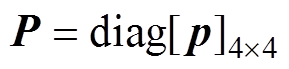 及
及 分别为AMB的比例增益系数矩阵及微分增益系数矩阵。
分别为AMB的比例增益系数矩阵及微分增益系数矩阵。
因此,PD控制下的各方向电磁力为
传感器处的位移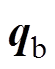 与转子几何中心C处的广义坐标
与转子几何中心C处的广义坐标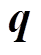 之间的关系为
之间的关系为
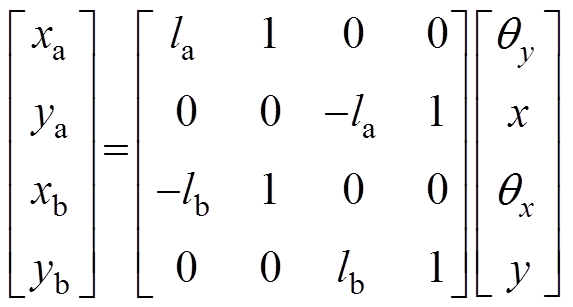 (6)
(6)
可得PD控制条件下,AMB-刚性转子系统的运动微分方程为
式中,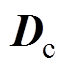 和
和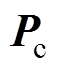 分别为PD控制器在AMB上产生的阻尼矩阵及刚度矩阵;
分别为PD控制器在AMB上产生的阻尼矩阵及刚度矩阵;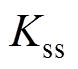 为AMB的负刚度矩阵。
为AMB的负刚度矩阵。
很显然,为了使AMB转子系统的特征根位于虚轴的左侧,刚度矩阵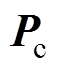 必须能够补偿系统的负刚度矩阵
必须能够补偿系统的负刚度矩阵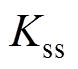 ,并且使系统具有足够的刚度保持系统稳定。而阻尼矩阵
,并且使系统具有足够的刚度保持系统稳定。而阻尼矩阵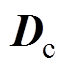 必须大于零,使系统的闭环特征根全部在复平面的左半平面,以保证系统渐进稳定。为了减小稳态误差,一般在PD控制器的基础上加入积分环节,从而实现磁悬浮转子系统的PID控制。
必须大于零,使系统的闭环特征根全部在复平面的左半平面,以保证系统渐进稳定。为了减小稳态误差,一般在PD控制器的基础上加入积分环节,从而实现磁悬浮转子系统的PID控制。
当采用PID控制,且各通道控制参数均相同时,控制电流可表示为
其中,积分增益系数矩阵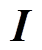 为
为
式(4)的微分方程数学模型为
在数字控制系统中,采用PID控制器作为系统的数字控制器,用向后差分变换可离散化为
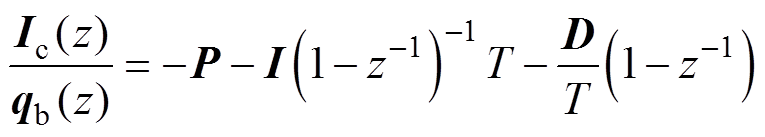 (10)
(10)
式中,T为采样周期。
可得PID数字控制器的差分方程为
式中,Ic(k)为第k时刻的控制器输出;qb(k)为第k时刻的位移信号;k为采样序号,k=1, 2, 3,…。
由式(11)可以看出,以单自由度为例,P、I及D三个参数对控制电流都会产生影响,进而影响到AMB-刚性转子系统的静动态特性和稳定性。因此,基于变参数PID控制的AMB-刚性转子系统在刚体临界转速区的加速特性是不同的,有必要探究这些参数对加速特性的影响。
AMB-刚性转子系统被控对象可表示为
结合(8)可以得到PID控制下的AMB-刚性转子系统闭环传递函数为
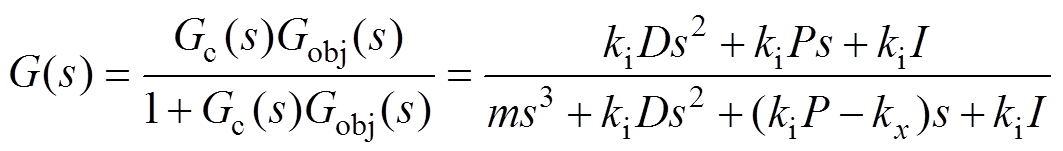 (13)
(13)
因此,得到系统的特征方程为
表1列出了PID控制器转子系统的劳斯表。
由劳斯判据可知,系统稳定的充要条件为
表1 PID控制下系统的劳斯表
Tab.1 Routh array of the system with PID control

1 0 0
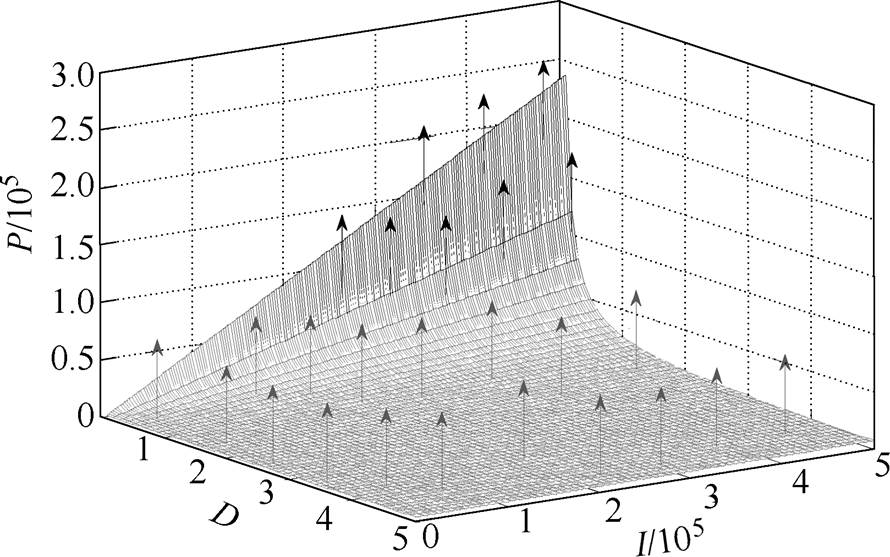
根据式(15)中不等式关系,可得到使AMB-刚性转子系统稳定的PID参数选取范围。图3给出了PID稳定控制的参数选取范围,除了需要满足稳定性条件,还需满足静动态响应要求以适应实际工况。
式(14)的解有两种形式,即三个负实极点p1、p2、p3和一个负实极点与一对复共轭极点量,z 为阻尼比。因此,式(14)的解可分解为以下两种形式,有
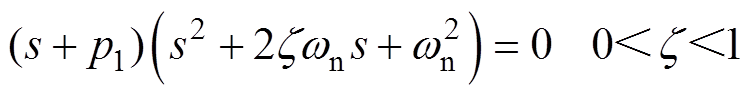 (17)
(17)
针对式(16)和式(17),其单位阶跃响应分别为
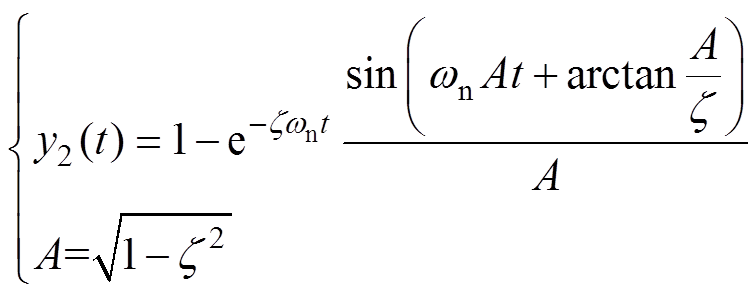 (19)
(19)
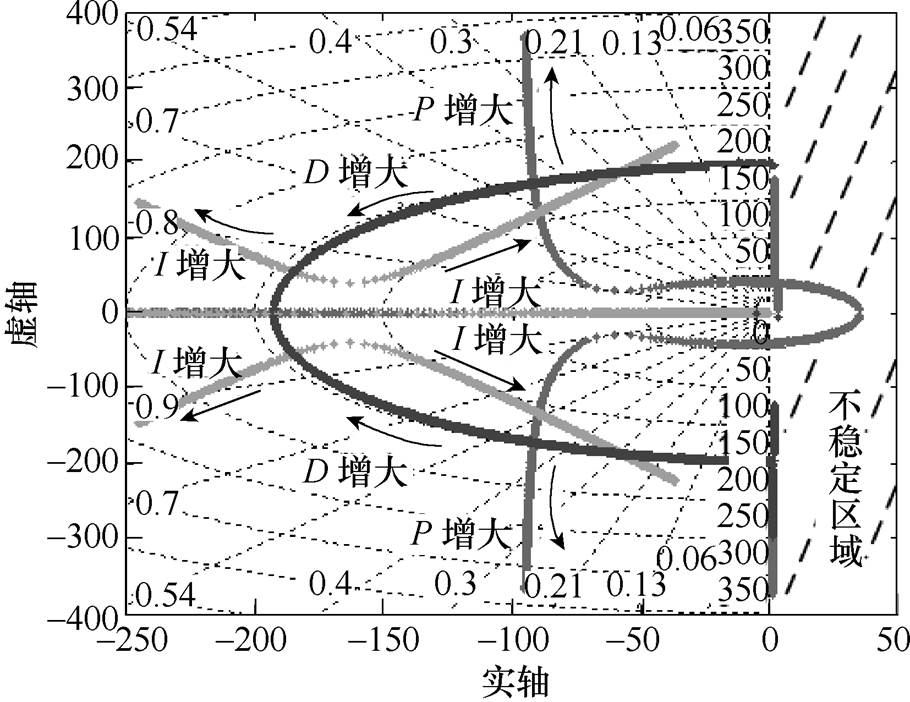
图4为AMB-刚性转子系统广义根轨迹。P较小时,阻尼比z 也较小,系统超调量很大导致共轭极点在不稳定的右半平面。随着P和z 逐渐增大,极点进入左半平面,并远离虚轴。z 越大,系统调节时间越短。同理,随着I增大,系统稳定范围内阻尼比z 逐渐减小,即系统调节时间增大。D的增大导致z 逐渐增大,极点逐渐远离虚轴。
2.2 固定PID参数控制下转子系统的加速特性
通过理论推导,可以得到频域下PID控制器的AMB广义刚度表达式为
振动理论中弹簧阻尼特性支承的广义刚度[15]为
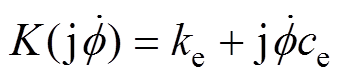 (21)
(21)
式中,ke和ce分别为弹簧阻尼特性的刚度和阻尼。要使得PID控制的AMB等效于一般弹簧阻尼支承,则需满足
由图2可知,几何中心轨迹满足
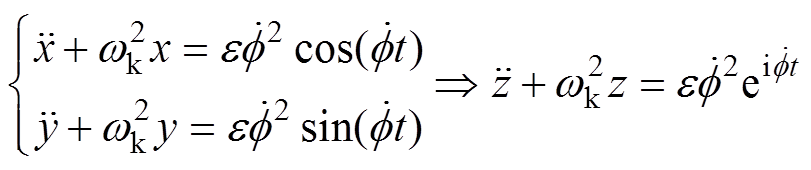 (23)
(23)
其中
得到式(23)的通解
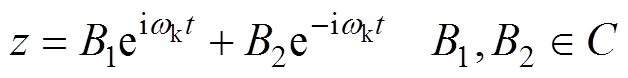 (24)
(24)
式中,B1和B2为不为零的实数;i为虚数单位;C为复数集。
假设几何中心轨迹方程特解为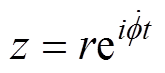 ,结合式(24)解得
,结合式(24)解得
其中
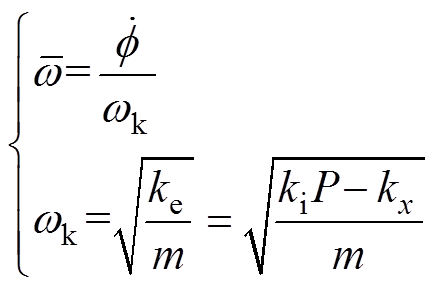
式中, 为转速比;
为转速比;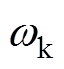 为转子系统的固有频率。
为转子系统的固有频率。
由式(25)可知,当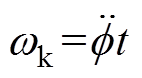 时,转子振动幅值最大。图5为在不同阻尼比z 的情况下,振幅r随频率
时,转子振动幅值最大。图5为在不同阻尼比z 的情况下,振幅r随频率 的变化曲线。
的变化曲线。
如果转子系统恒定运行在刚体临界转速下,其振动幅值可以达到理论计算的最大值。但当转子系统以较大的加速度穿过其刚体临界转速区时,转子会没有足够的时间达到理论最大振幅值,即转子振幅逼近理论最大值的过程中,转速已经超过了刚体临界转速区,这样就可能导致转子振幅不一定会达到最大值。特别是,穿过刚体临界转速区的加速度越大,转子在刚体临界转速区的实际振幅逼近理论最大值的程度越低,与理论最大值的差距越大。
2.3 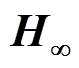 鲁棒控制
鲁棒控制
2.2节分析了固定参数的PID控制器AMB-转子系统过临界转速区的振动特性,为进一步探究变参数控制器对转子系统加速特性的影响,下面以 鲁棒控制器为例进行分析。
鲁棒控制器为例进行分析。
在多种 优化问题中,混合灵敏度问题是一种标准的
优化问题中,混合灵敏度问题是一种标准的 控制问题。利用
控制问题。利用 鲁棒控制方法设计控制系统,为保证鲁棒性和提高系统性能,通常都将设计问题转化为混合灵敏度问题进行求解。基于混合灵敏度优化的
鲁棒控制方法设计控制系统,为保证鲁棒性和提高系统性能,通常都将设计问题转化为混合灵敏度问题进行求解。基于混合灵敏度优化的 鲁棒控制下AMB-刚性转子系统的原理框图如图6所示。图中,Id为偏置电流;z1、z2、z3为评价函数;W1、W2、W3分别为磁悬浮高速电机转子系统的灵敏度加权函数、线性加权函数和补灵敏度加权函数。对于具有
鲁棒控制下AMB-刚性转子系统的原理框图如图6所示。图中,Id为偏置电流;z1、z2、z3为评价函数;W1、W2、W3分别为磁悬浮高速电机转子系统的灵敏度加权函数、线性加权函数和补灵敏度加权函数。对于具有 鲁棒控制器的AMB系统,加权函数的选择是控制器设计的关键。
鲁棒控制器的AMB系统,加权函数的选择是控制器设计的关键。
图6中,K为 鲁棒控制器,P0为标称模型,DP为模型的绝对误差。假设P为AMB-刚性转子的真实模型,则其传递函数模型可表示为
鲁棒控制器,P0为标称模型,DP为模型的绝对误差。假设P为AMB-刚性转子的真实模型,则其传递函数模型可表示为
参考输入r和干扰d分别到输出y的闭环传递函数为
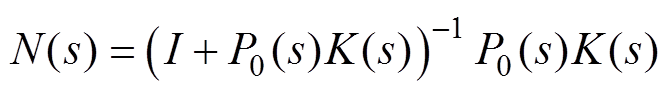 (27)
(27)
考虑到绝对误差DP的频域增益有界且小于R(s),根据最小增益定理,可知AMB-刚性转子系统鲁棒稳定的充要条件为
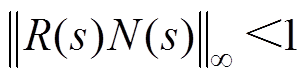 (29)
(29)
灵敏度函数M(s)体现了系统的抗扰能力。为了提高系统对外界干扰的抑制能力,引入衡量干扰大小的标量l>0,同时需设计控制器K(s),使AMB-刚性转子闭环系统满足
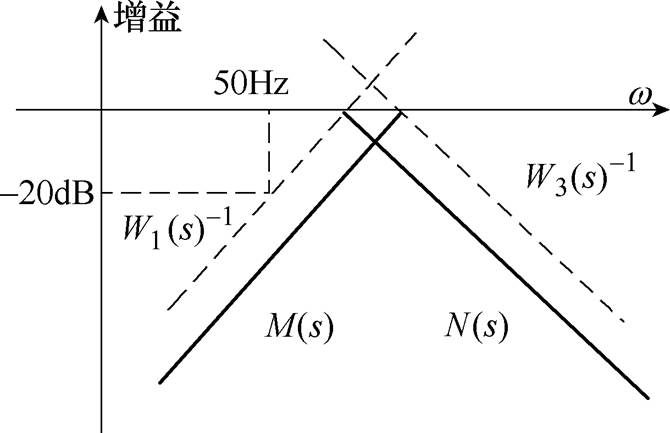
由式(27)和式(28)易知,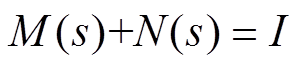 ,因此N(s)被称为补灵敏度函数。根据AMB-刚性转子系统的工程经验可知,低频段干扰主要为低于50Hz的正弦干扰,如果要抑制低频干扰的影响,需降低M(s)在低频段的增益,且干扰信号的幅值至少要衰减到-20dB。通常DP模型呈高频特性。因此,AMB-刚性转子系统的
,因此N(s)被称为补灵敏度函数。根据AMB-刚性转子系统的工程经验可知,低频段干扰主要为低于50Hz的正弦干扰,如果要抑制低频干扰的影响,需降低M(s)在低频段的增益,且干扰信号的幅值至少要衰减到-20dB。通常DP模型呈高频特性。因此,AMB-刚性转子系统的 鲁棒控制优化设计应同时降低M(s)和N(s)。根据最小增益定理和
鲁棒控制优化设计应同时降低M(s)和N(s)。根据最小增益定理和 范数条件,加权函数W1(s)、W3(s)、M(s)和N(s)需满足
范数条件,加权函数W1(s)、W3(s)、M(s)和N(s)需满足
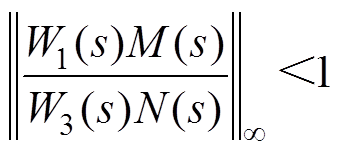 (31)
(31)
根据分析可知,频域整形图如图7所示。
W2(s)是为了描述不确定性而引入系统的一个线性加权。则输入r到z的闭环传递函数矩阵为
为了使AMB-刚性转子闭环系统稳定且鲁棒性强,需优化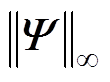 求解
求解 控制器,即K(s)要满足
控制器,即K(s)要满足
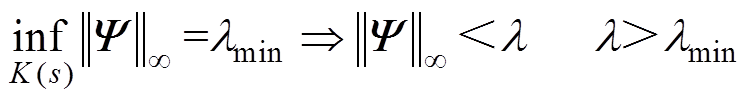 (33)
(33)
一般情况下取l=1,那么M(s)/K(s)M(s)/N(s)混合灵敏度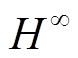 优化不等式满足
优化不等式满足
根据上述理论分析,可知灵敏度加权函数W1需具备低通滤波器特性;补灵敏度加权函数W3需具备高通滤波器特性;线性加权函数W2用来降低控制器的阶次,故分别选取为
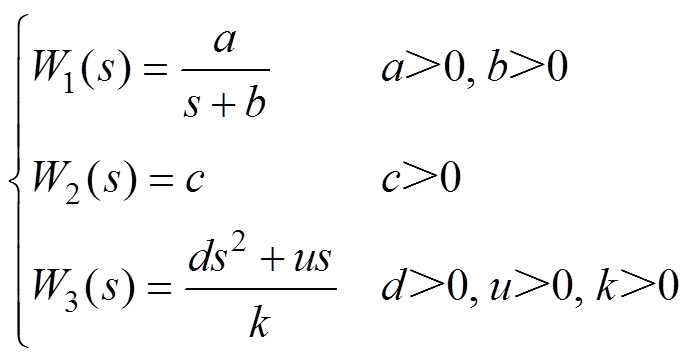 (35)
(35)
选取转子系统的状态变量为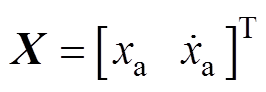 ,xa为转子A端在x方向的位移,系统输入变量为Ic,则AMB-刚性转子系统的状态空间方程的形式为
,xa为转子A端在x方向的位移,系统输入变量为Ic,则AMB-刚性转子系统的状态空间方程的形式为
AMB-刚性转子系统加权函数的选择并无特定规律可循,经过多次比较和分析,最终选择的三组加权函数分别为
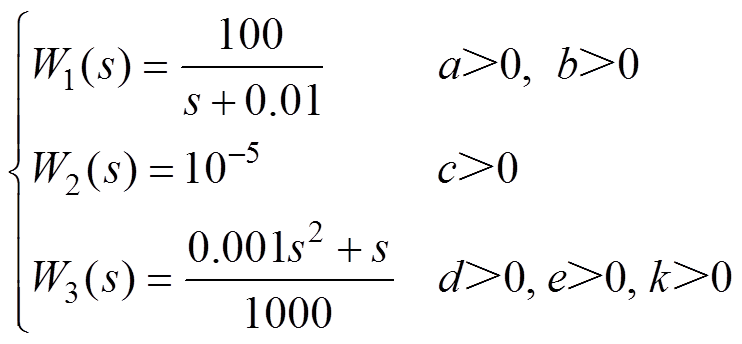 (37)
(37)
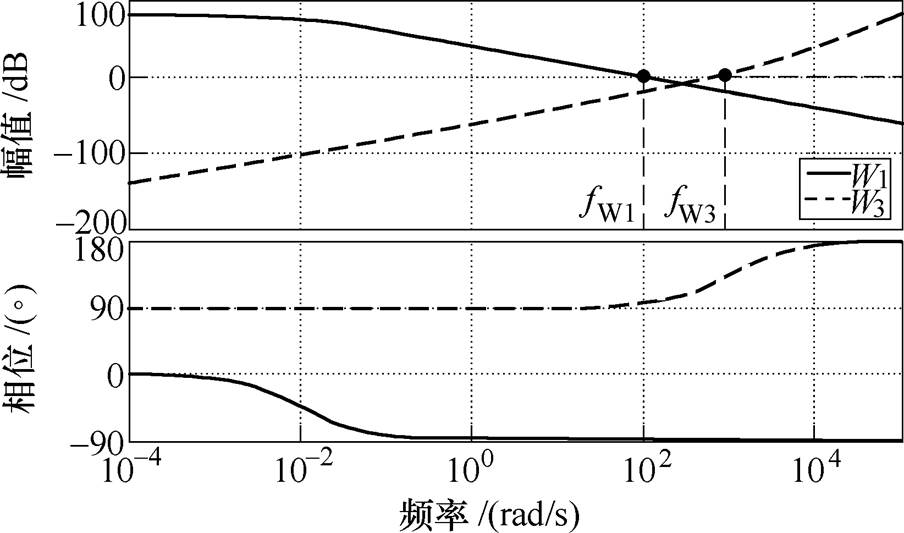
为验证选取的W1(s)和W3(s)满足加权函数的理论设计条件,绘制了相应的Bode图,如图8所示。通过Bode图可看出,W1(s)和W3(s)分别具有低通和高通特性,与理论设计一致,且W1(s)的截止频率fW1小于W3(s)的截止频率fW3。
在 鲁棒控制条件下,AMB-刚性转子系统的方法设计控制系统,为保证鲁棒性和提高系统性能,通常都是将设计问题转化为混合灵敏度问题进行求解。基于混合灵敏度优化的
鲁棒控制条件下,AMB-刚性转子系统的方法设计控制系统,为保证鲁棒性和提高系统性能,通常都是将设计问题转化为混合灵敏度问题进行求解。基于混合灵敏度优化的 鲁棒控制下AMB-刚性转子系统的原理框图如图6所示。对于具有
鲁棒控制下AMB-刚性转子系统的原理框图如图6所示。对于具有 鲁棒控制器的AMB转子系统,加权函数的选择是控制器设计的关键。
鲁棒控制器的AMB转子系统,加权函数的选择是控制器设计的关键。
3 仿真结果及分析
3.1 PID控制下转子系统的加速特性
首先,验证定参数PID控制下AMB-刚性转子系统过临界时的加速特性。仿真和实验中,AMB-刚性转子系统的各项参数见表2。
表2 AMB-转子系统的各项参数
Tab.2 Parameters of AMB-rotor system
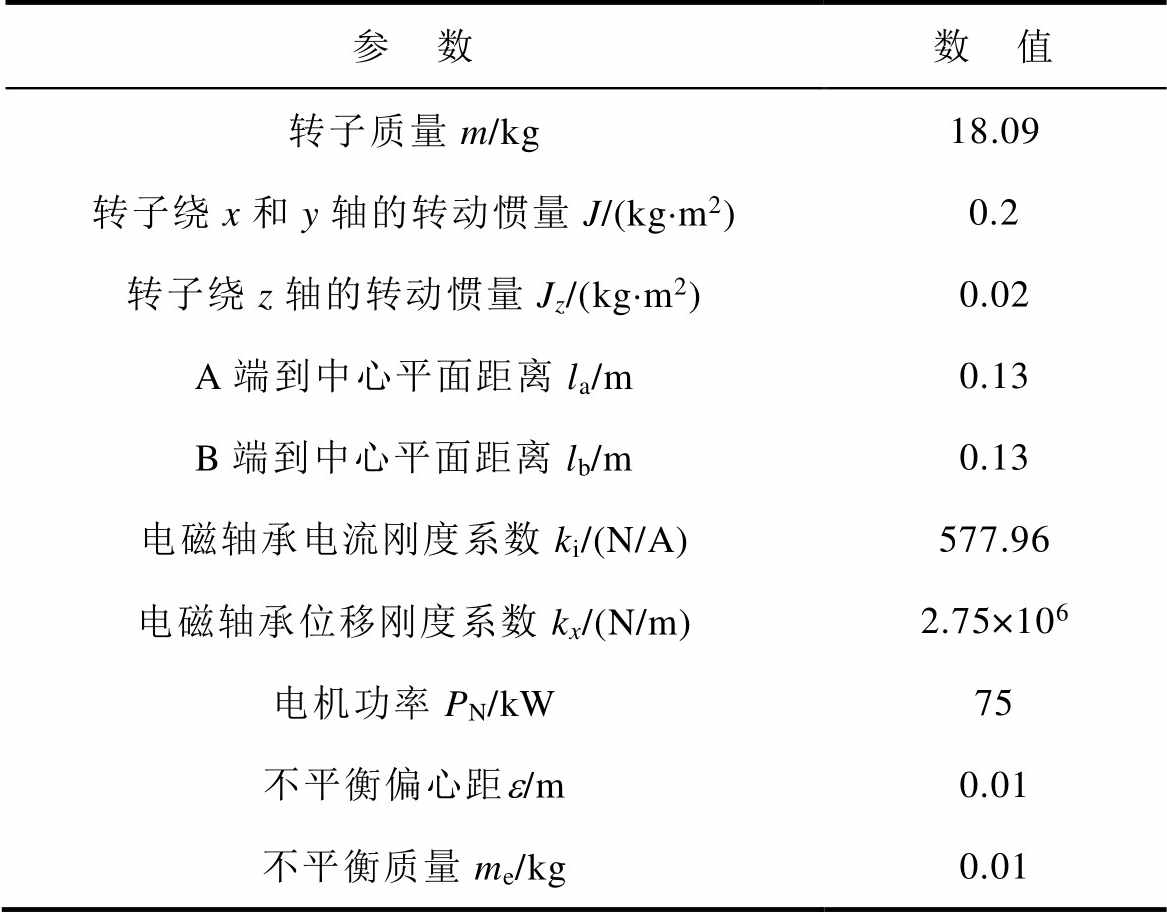
参 数数 值 转子质量m/kg18.09 转子绕x和y轴的转动惯量J/(kg×m2)0.2 转子绕z轴的转动惯量Jz/(kg×m2)0.02 A端到中心平面距离la/m0.13 B端到中心平面距离lb/m0.13 电磁轴承电流刚度系数ki/(N/A)577.96 电磁轴承位移刚度系数kx/(N/m)2.75×106 电机功率PN/kW75 不平衡偏心距e/m0.01 不平衡质量me/kg0.01
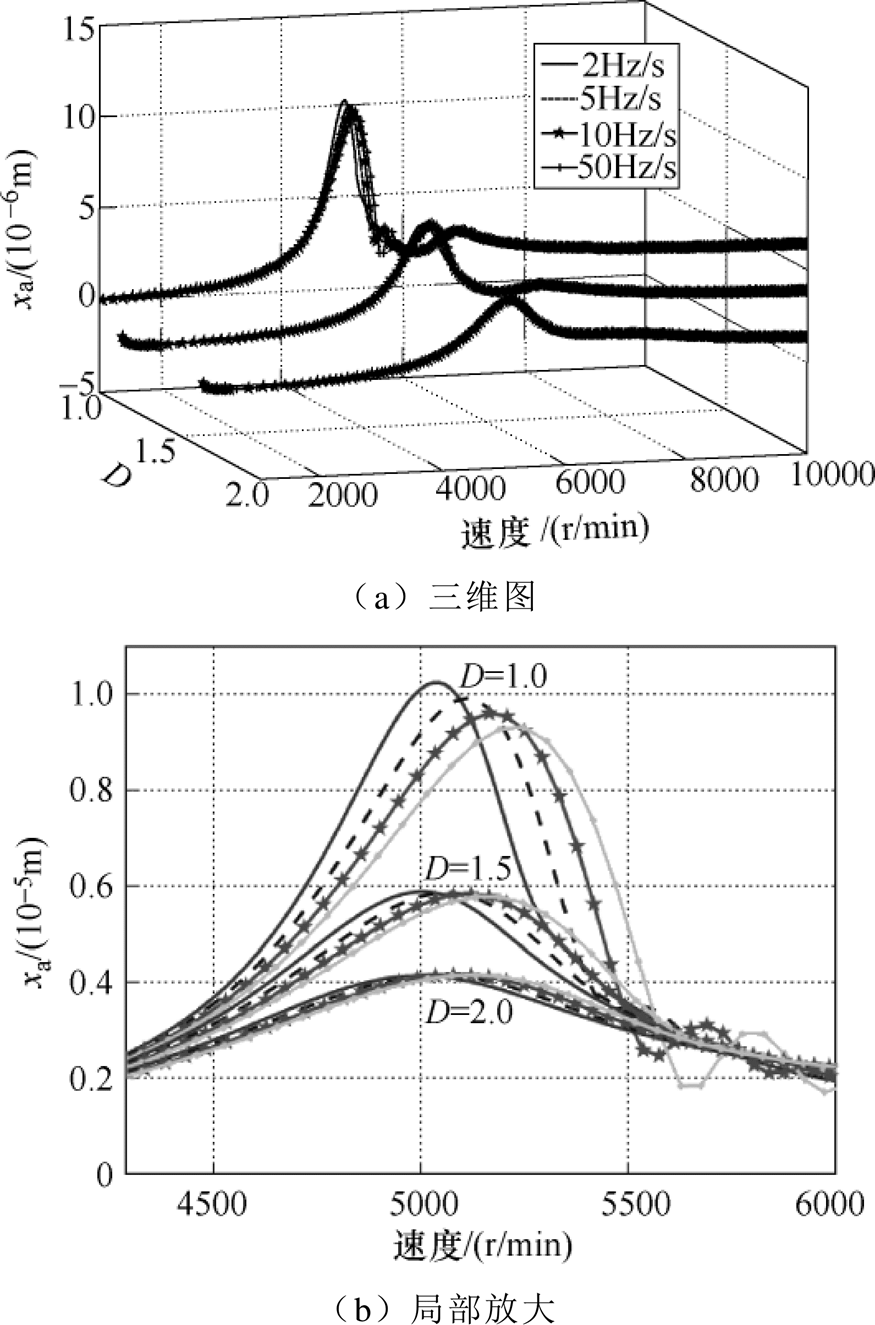
图9为PID参数分别为9 000,10 000和0.4时,转子分别以2Hz/s、5Hz/s、10Hz/s以及50Hz/s的加速度加速运行时AMB-刚性转子系统A端x和y方向上的位移响应曲线。由图9可以看出,转子加速运行过程中,由于转子平动与锥动模态的影响,转子要经历平动和锥动两个刚体临界转速,不同加速度下的加速特性有所差别,一阶及二阶刚体临界转速分别与转子的平动和锥动固有频率相对应。图10为定参数PID控制时,不同加速度下转子在刚体临界转速处的位移响应。可以看出,随着转子加速度的增大,其穿过刚体临界转速处的位移振幅逐渐减小,刚体临界转速逐渐增大,与传统轴承在刚体临界转速处的加速特性一致。
然而,PID参数不同时转子在刚体临界转速处的加速特性却有所差别。图11为D=1.0、1.5和2.0时,转子穿过刚体临界转速时A端x方向位移振幅的包络线。由图11b局部放大图可以看出,当D不变时,以D=1.0为例,随着加速度的增大,转子在临界转速处的最大位移振幅逐渐减小,临界转速稍有增大。D参数对系统的加速特性主要有两方面的影响:一方面,随着D增大,临界转速处的加速特性差异逐渐减小,仅是最大位移振幅稍有减小;另一方面,转子二阶刚体临界转速不再明显,即锥动固有频率的影响削弱,只保留第一阶平动固有频率。
图12给出了P从7 000增大到9 000时转子A端x方向位移振幅的包络线。由图12b局部放大图可以看出,P参数对系统的加速特性的影响也主要体现在两个方面:一方面,随着P参数的增大,转子的刚体临界转速明显增大,因为P影响着AMB的电流刚度矩阵Ki,所以临界转速会随着P的增大而增大;另一方面,随着P参数的增大,转子的最大位移振幅也相应地增大。
I参数在稳定范围内大幅度变化对系统的加速特性的影响很小,过临界时最大位移振幅也基本保持不变,所以此处不再展开说明。
根据以上仿真可以得到结论,PID参数不同时,AMBs-刚性转子系统过临界的加速特性是不同的。
3.2  鲁棒控制下转子系统的加速特性
鲁棒控制下转子系统的加速特性
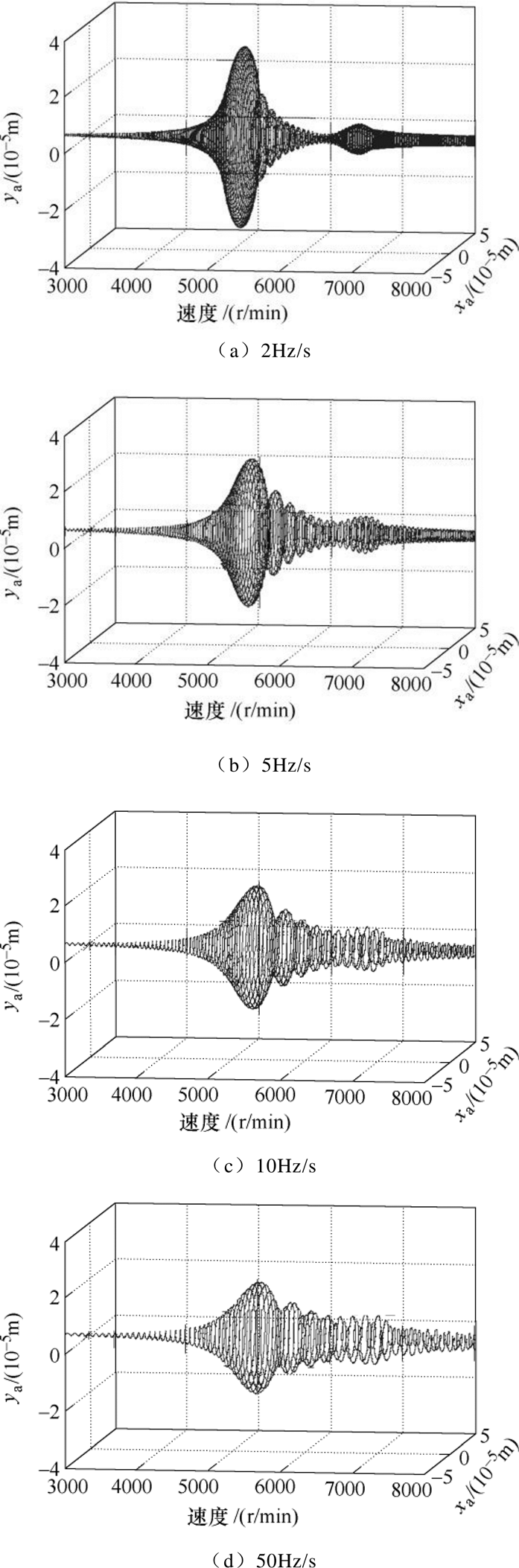
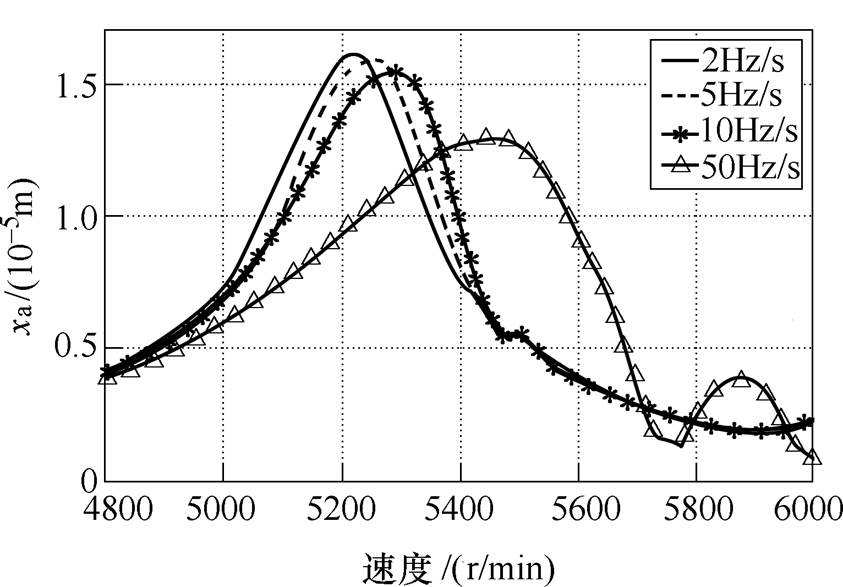
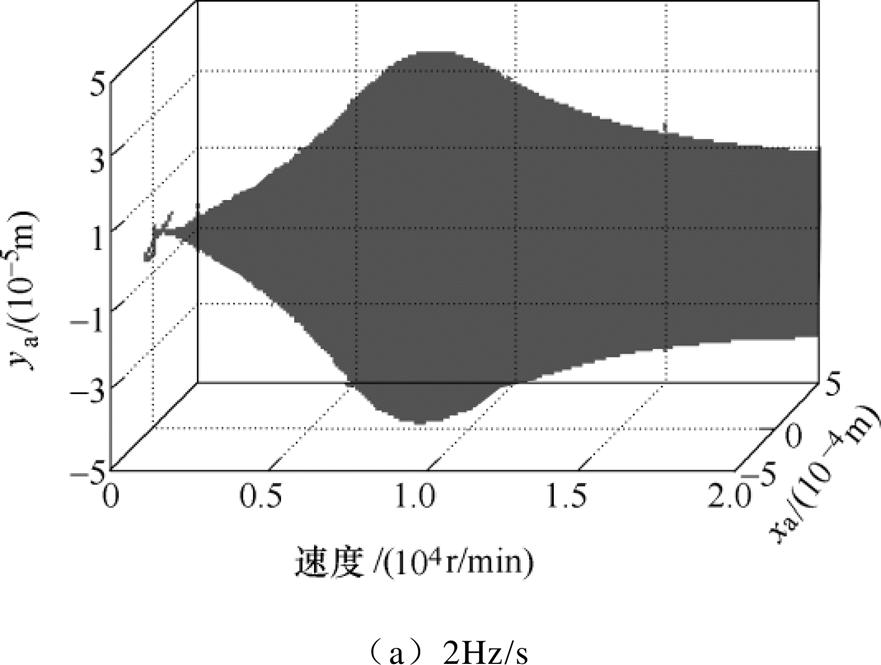
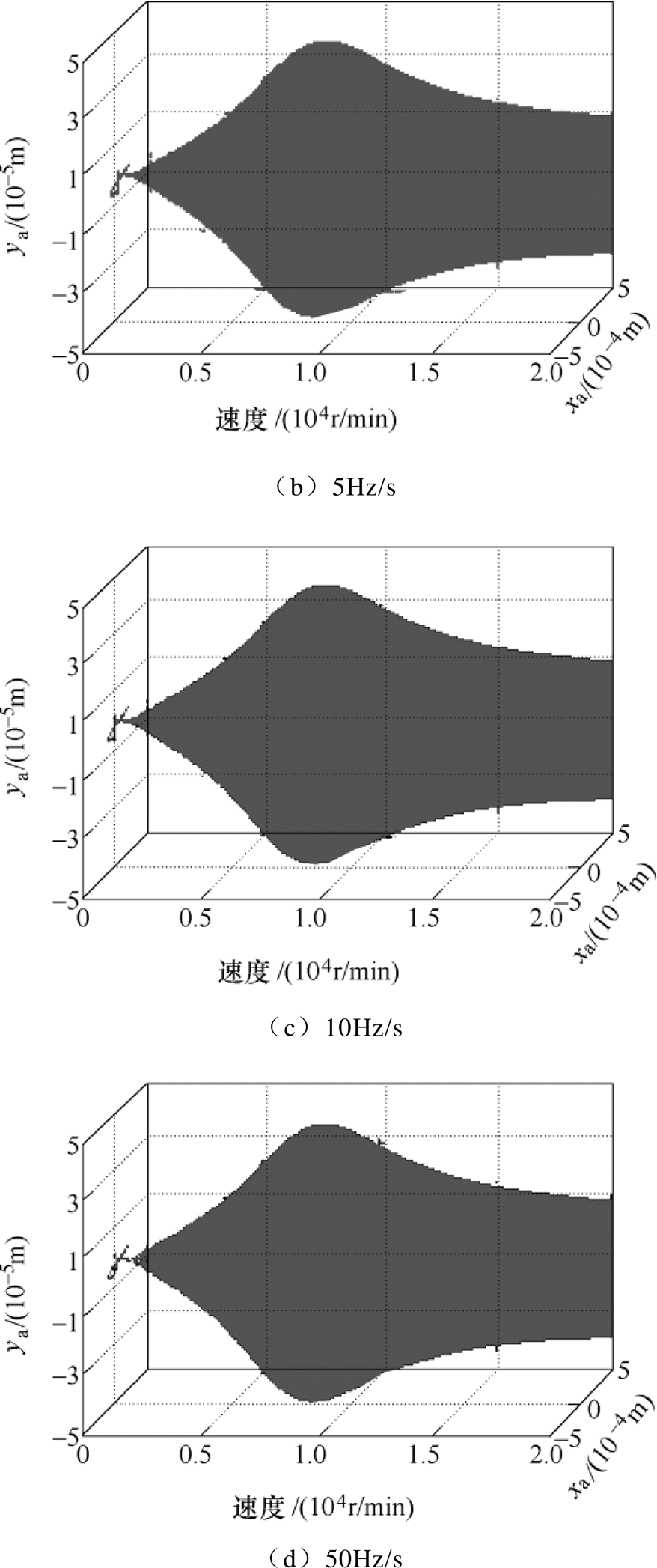
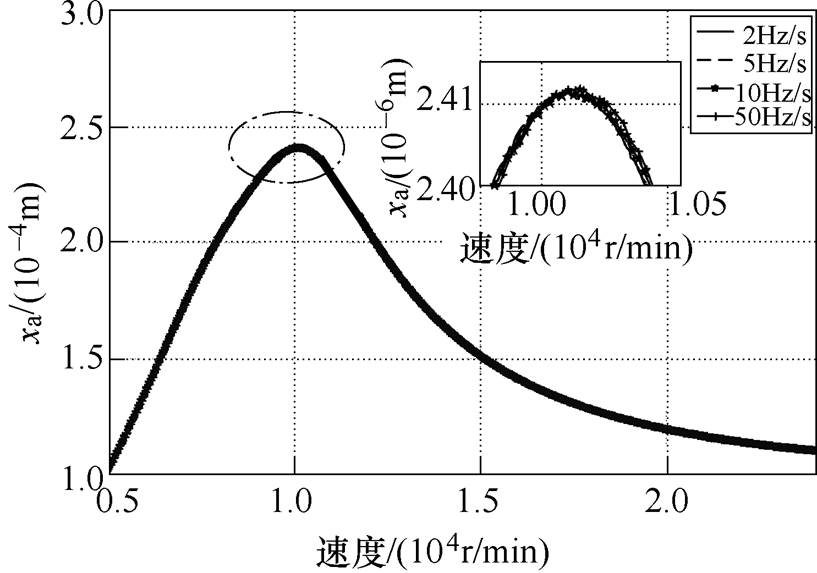
图13为 鲁棒控制器条件下,转子分别以2Hz/s、5Hz/s、10Hz/s以及50Hz/s的匀加速度运行过程中转子A端的位移响应曲线。图14为不同加速度下,A端x方向转子随转速变化的位移振动曲线。
鲁棒控制器条件下,转子分别以2Hz/s、5Hz/s、10Hz/s以及50Hz/s的匀加速度运行过程中转子A端的位移响应曲线。图14为不同加速度下,A端x方向转子随转速变化的位移振动曲线。
由图13和图14可以看出,随着加速度增大,x方向最大位移振幅几乎不变,维持在0.241mm左右,最大位移振幅处的刚体临界转速也均在10 000r/min附近。得知 鲁棒控制下转子穿过刚体临界转速时的最大振幅并不会随着加速度的增大而减小,这与定参数PID控制存在明显差别。
鲁棒控制下转子穿过刚体临界转速时的最大振幅并不会随着加速度的增大而减小,这与定参数PID控制存在明显差别。
4 实验研究
实验是在如图15所示额定功率为75kW、额定转速为24 000r/min的AMB高速电机转子系统实验平台上进行的。AMB转子系统主要由dSPACE控制平台、上位机、功放、测速模块及电涡流位移传感器等组成。由于转子在0~10 000r/min转速范围内振动比较明显,所以这里主要给出在这个区间的实验结果。
4.1 PID控制下的实验结果及分析
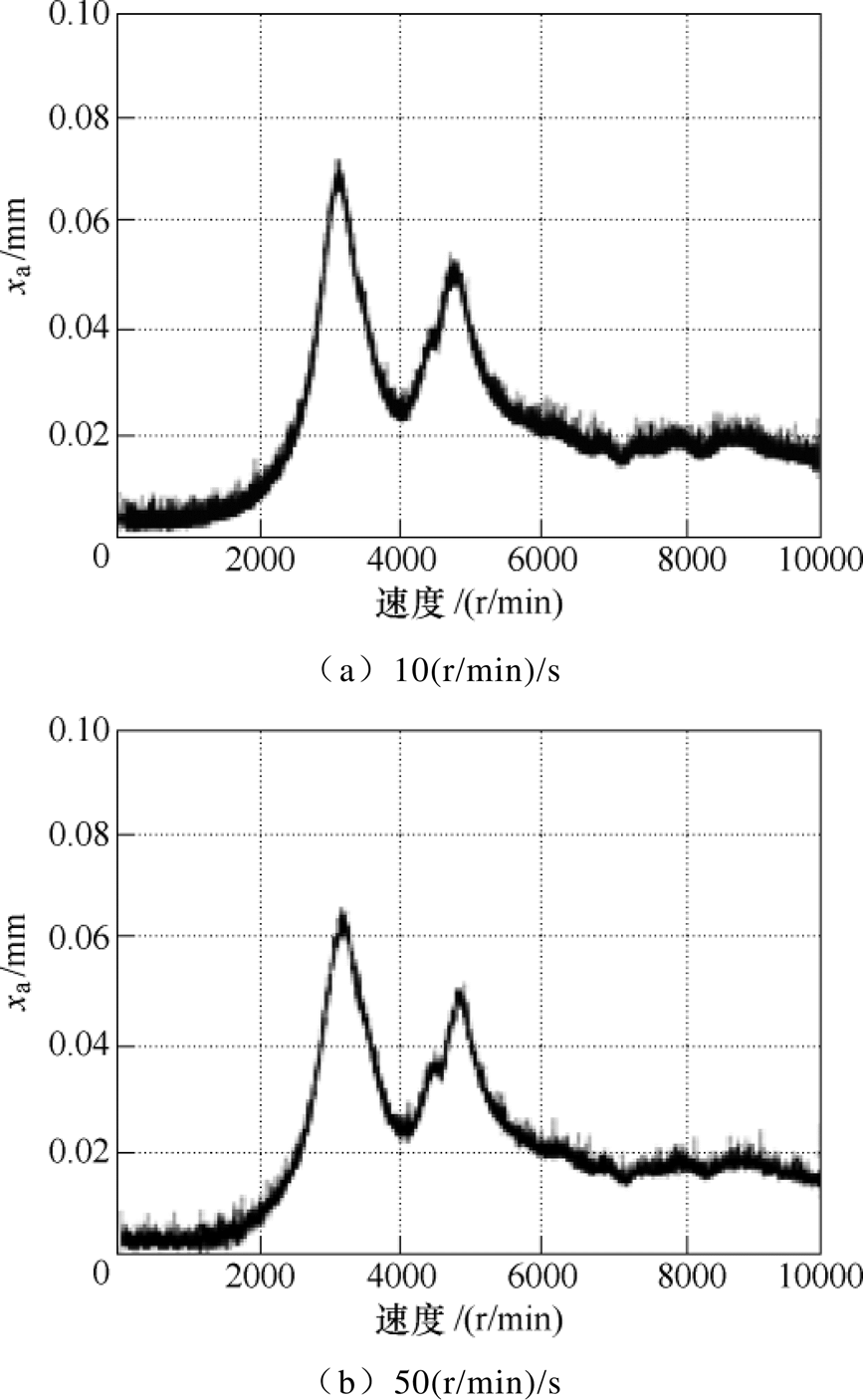
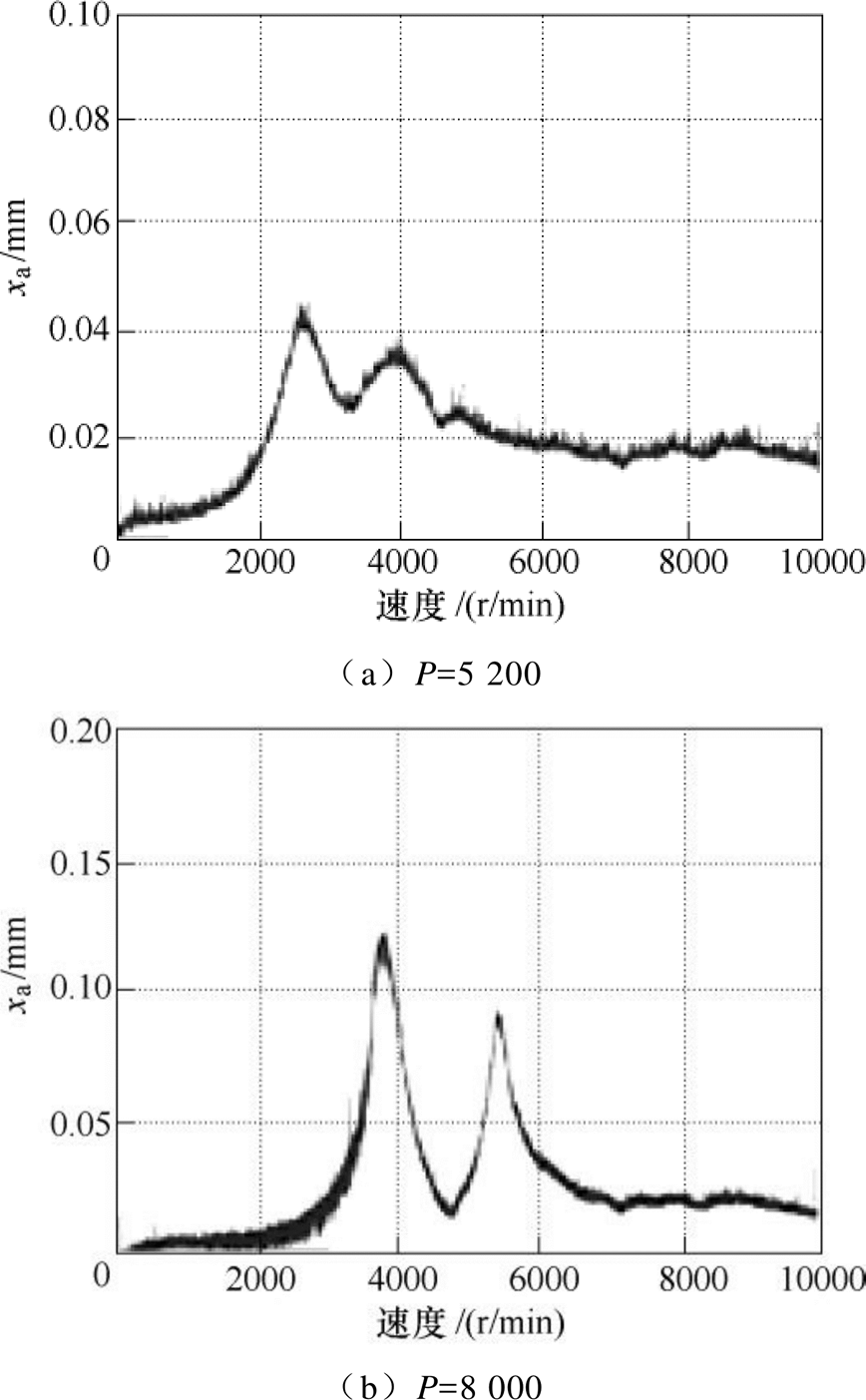
图16为不同加速度情况下AMB高速电机转子系统加速运行过程中的振动响应曲线。PID控制器参数固定不变,转子加速度分别选取10(r/min)/s、50(r/min)/s、300(r/min)/s、500(r/min)/s。
可以看出,随着加速度增大,转子在临界转速处的最大振幅逐渐减小。平动振幅由0.070mm依次减小到0.054mm,锥动振幅由0.053mm减小到0.042mm。
图17为转子以50(r/min)/s旋转时,参数P改变时磁悬浮高速电机转子的加速特性曲线,P参数分别为5 200和8 000。可以看出,随着P增大,转子的平动和锥动幅值均增大,且临界转速也逐渐增大。
图18为转子以50(r/min)/s旋转时,参数D改变时磁悬浮高速电机转子的加速特性曲线,D参数分别为6.5和8。可以看出,随着D增大,转子平动幅值减小,且锥动不再明显。
4.2  鲁棒控制下的实验结果及分析
鲁棒控制下的实验结果及分析
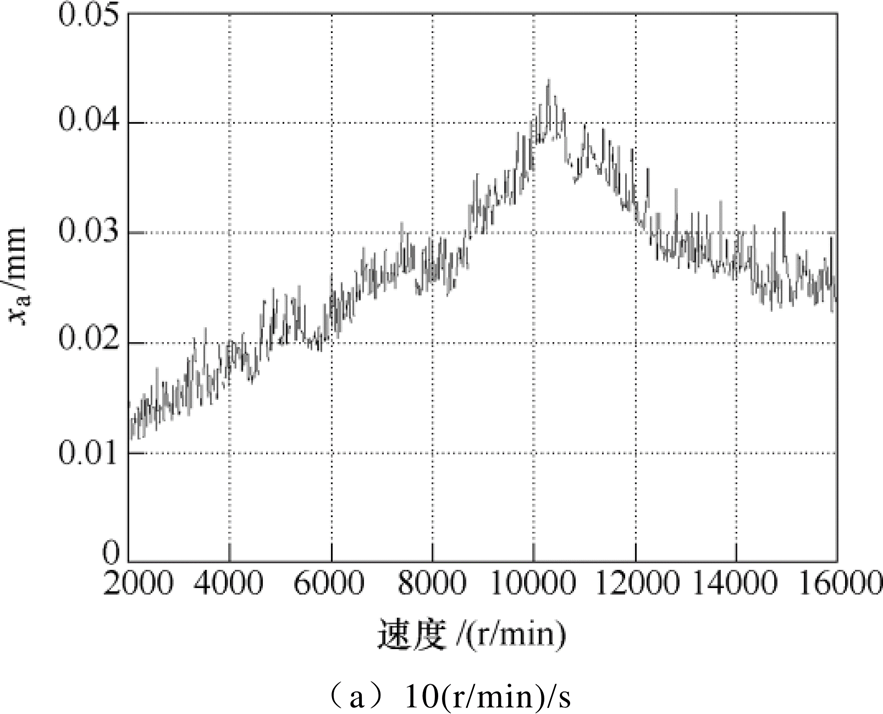
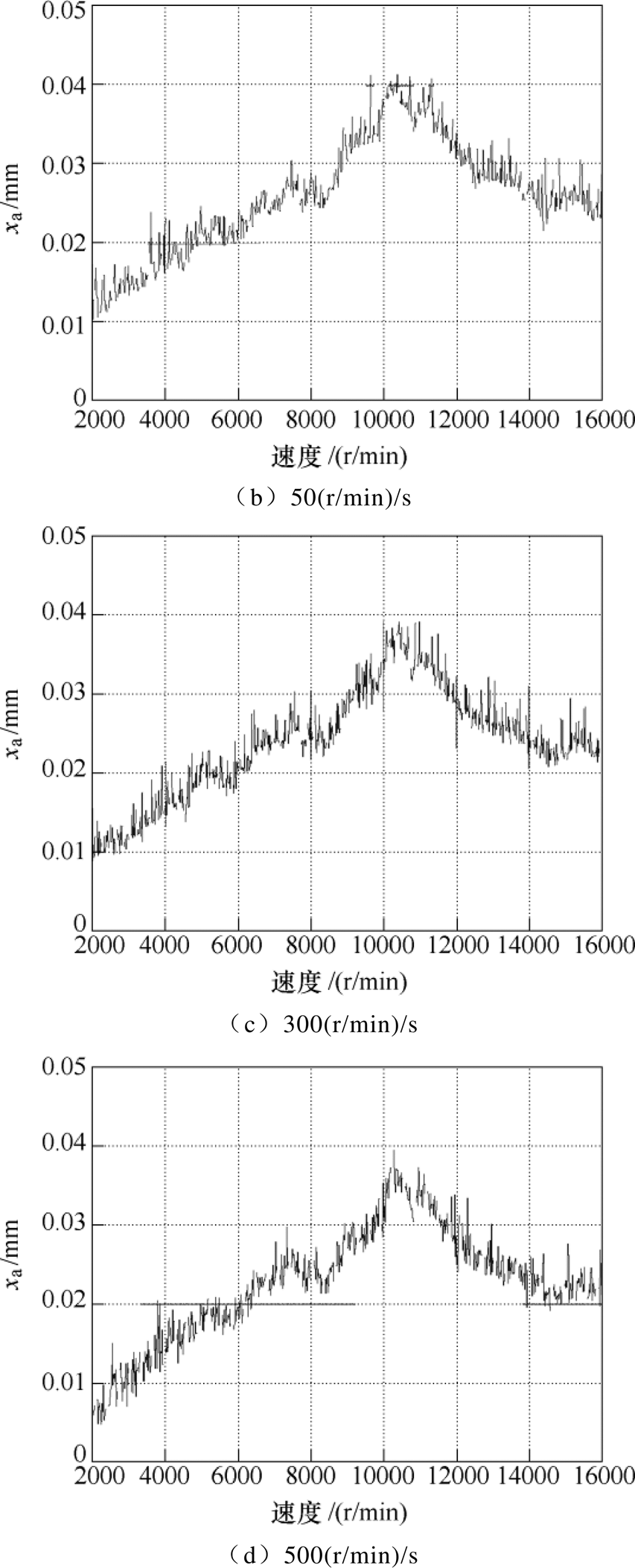
图19为转子分别以10(r/min)/s、50(r/min)/s、300(r/min)/s及500(r/min)/s的加速度加速运行过程中转子A端x方向的位移响应曲线。可以看出,不同于定参数PID控制,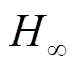 鲁棒控制下转子穿过临界转速时的最大振幅并不会随着加速度的增大而减小,且最大位移振幅和临界转速也均维持在0.04mm和10 000r/min附近。
鲁棒控制下转子穿过临界转速时的最大振幅并不会随着加速度的增大而减小,且最大位移振幅和临界转速也均维持在0.04mm和10 000r/min附近。
为了更直观地体现PID和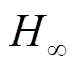 鲁棒控制下的转子穿过刚体临界区的加速特性,以及分析两种控制方法的优劣和适用情形,图20给出了不同加速度条件下的转子最大振动幅值实验结果。
鲁棒控制下的转子穿过刚体临界区的加速特性,以及分析两种控制方法的优劣和适用情形,图20给出了不同加速度条件下的转子最大振动幅值实验结果。
可以看出,当AMB-刚性转子系统所采用的控制器不同时,AMB-刚性转子系统穿过临界转速区时的加速特性也不同。在PID控制条件下,随着转子加速度的增大,转子系统在通过其刚体临界转速时的振动逐渐减小。因此,在实际转子系统的应用中,就加速特性而言,PID控制的优点是可以通过增大转子加速度进而降低转子穿越临界转速区的振动。然而PID控制的缺点是转子系统鲁棒性不强,转子的运动状态容易受外部干扰影响,但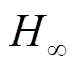 鲁棒控制可以保证转子系统的强鲁棒性。在
鲁棒控制可以保证转子系统的强鲁棒性。在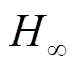 鲁棒控制条件下,随着转子穿过刚体临界转速区时加速度的增大,转子系统在刚体临界转速区的振动并没有发生明显变化。所以在
鲁棒控制条件下,随着转子穿过刚体临界转速区时加速度的增大,转子系统在刚体临界转速区的振动并没有发生明显变化。所以在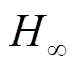 鲁棒控制的AMB-刚性转子系统中,难以通过提高转子运行加速度的方法来使转子系统通过其刚体临界转速区。
鲁棒控制的AMB-刚性转子系统中,难以通过提高转子运行加速度的方法来使转子系统通过其刚体临界转速区。
5 结论
本文以PID控制和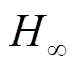 鲁棒控制为代表,研究了不同控制策略下AMB刚性转子系统穿过刚体临界转速区的振动特性,得出如下结论:
鲁棒控制为代表,研究了不同控制策略下AMB刚性转子系统穿过刚体临界转速区的振动特性,得出如下结论:
1)固定参数PID控制条件下,AMB-刚性转子系统加速特性与传统轴承转子系统的加速特性相似,也就是说,增大加速度可以降低转子系统穿过临界转速区的振动幅值。但如果PID参数发生变化,其加速特性也可能会发生相应的改变。因此,AMB-刚性转子系统穿过临界转速的加速特性依赖于PID参数。
2)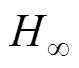 鲁棒控制条件下,AMB-刚性转子系统的加速特性与传统轴承转子系统的加速特性有明显的差异,增大加速度并不能降低转子系统穿过临界转速区的振动幅值。
鲁棒控制条件下,AMB-刚性转子系统的加速特性与传统轴承转子系统的加速特性有明显的差异,增大加速度并不能降低转子系统穿过临界转速区的振动幅值。
参考文献
[1] Schweitzer G, Maslen E. Magnetic bearing: theory, design, and application to rotating machinery[M]. New York: Springer, 2009.
[2] 李万杰, 张国民, 王新文. 飞轮储能系统用超导电磁混合磁悬浮轴承设计[J]. 电工技术学报, 2020, 35(1): 10-18.
Zhang Wanjie, Zhang Guomin, Wang Xinwen. Inte- gration design of high-temperature superconducting bearing and electromagnetic thrust bearing for fly- wheel energy storage system[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 10-18.
[3] Nikita U, Alexander S, Cheol H, et al. Design aspects of high-speed electrical machines with active magnetic bearings for compressor applications[J]. IEEE Transa- ctions on Industrial Electronics, 2017, 64(11): 8427- 8436.
[4] 顾家柳. 转子动力学[M]. 北京: 国防工业出版社, 1985.
[5] 王美令, 温保岗, 韩清凯. 弹支-刚性转子系统过共振瞬态响应特性研究[J]. 动力学与控制学报, 2018, 16(6): 533-538.
Wang Meiling, Wen Baogang, Han Qingkai. Transient response characteristic of a rigid rotor system with flexible supports across resonance[J]. Journal of Dynamics and Control, 2018, 16(6): 533-538.
[6] 白保东, 王禹, 陈志雪. 基于电磁屏蔽法变频电机轴承电流抑制研究[J]. 电工技术学报, 2016, 31(7): 33-39.
Bai Baodong, Wang Yu, Chen Zhixue. Inhibition of bearing currents in frequency variable motor based on electromagnetic shielding[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 33-39.
[7] Boris R, Lutz S, Henner D. Problems of vibration near critical speeds in rigid rotors with autobalancing devices[C]//19th Biennial Conference on Mechanical Vibration and Noise, Chicago, USA, 2003: 1-7.
[8] Sena J, Doyoung J, Yong Bin. Rigid mode vibration controland dynamic behavior of hybrid foil-magnetic bearing turbo blower[J]. Journal of Engineering for Gas Turbines and Power-Transactions of the ASME, 2017, 139(5): 1-12.
[9] Wang Shimin, Zhang Xingye. Experimental researches on reducing the critical acceleration that induces sustainable rotor rubbing[J]. Journal of Vibration and Acoustics-Transactions of the ASME, 2011, 133(6): 0610071-0610079.
[10] Wang Shuming, Lu Qishao, Twizell E H. Reducing lateral vibration of a rotor passing through critical speeds by phase modulating[J]. Journal of Engin- eering for Gas Turbines and Power-Transactions of the ASME, 2003, 125(3): 766-771.
[11] Shafai B, Beale S, Larocca P, et al. Magnetic bearing control systems and adaptive forced balancing[J]. IEEE Control Systems Magazine, 1994, 14(2): 4-13.
[12] Herzog R, Buhler P, Gahler C, et al. Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings[J]. IEEE Transactions on Control Systems Technology, 1996, 4(5): 580-586.
[13] Jiang Kejian, Zhu Changsheng, Chen Liangliang. Unbalance compensation by recursive seeking unbalance mass position in active magnetic bearing-rotor system[J]. IEEE Transactions on Industrial Electro- nics, 2015, 62(9): 5655-5664.
[14] 于洁, 祝长生, 于忠磊. 考虑涡流的自传感主动电磁轴承转子位置估计策略[J]. 电工技术学报, 2018, 33(9): 1946-1956.
Yu Jie, Zhu Changsheng, Yu Zhonglei. Rotor position estimation strategy for self-sensing active magnetic bearing considering eddy currents[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1946- 1956.
[15] 王忠博, 毛川, 祝长生. 主动电磁轴承-刚性转子系统PID控制器设计方法[J]. 中国电机工程学报, 2018, 38(20): 6154-6163.
Wang Zhongbo, Mao Chuan, Zhu Changsheng. A design method of PID controller for active magnetic bearings-rigid rotor systems[J]. Proceedings of the CSEE, 2018, 38(20): 6154-6163.
[16] 周天豪, 杨智, 祝长生. 电磁轴承高速电机转子系统的内模-PID控制[J]. 电工技术学报, 2020, 35(16): 3414-3425.
Zhou Tianhao, Yang Zhi, Zhu Changsheng. Internal model control-PID control of an active magnetic bearing high-speed motor rotor system[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(16): 3414-3425.
[17] Sheh Z, Khan T, Lazoglu I. Design and adaptive sliding-mode control of hybrid magnetic bearings[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3): 2537-2547.
[18] Noshadi A, Shi Juan, Lee W S, et al. System identi- fication and robust control of multi-input multi-output active magnetic bearing systems[J]. IEEE Transa- ctions on Control Systems Technology, 2016, 24(4): 1227-1239.
[19] Mao Chuan, Zhu Changsheng. Unbalance com- pensation for active magnetic bearing rotor system using a variable step size real-time iterative seeking algorithm[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(5): 4177-4186.
[20] 房建成, 张会娟, 刘虎. 磁悬浮刚性转子系统振动机理分析与动力学建模[J]. 控制理论与应用, 2014, 31(12): 1707-1713.
Fang Jiancheng, Zhang Huijuan, Liu Hu. Vibration mechanism analysis and dynamic model development of magnetically suspended rigid rotor system[J]. Control Theory and Applications, 2014, 31(12): 1707-1713.
Acceleration Responses Robustness of Active Magnetic Bearings-Rigid Rotor System
Gong Lei1 Yang Zhi2 Zhu Changsheng1
(1. College of Electrical Engineering Zhejiang University Hangzhou 310027 China 2. No. 704 Research Institute China Shipbuilding Industry Corporation Shanghai 200031 China)
Abstract The acceleration response is a significant dynamic characteristic of active magnetic bearings (AMBs)-rigid rotor system. Currently, the research mainly focuses on the steady state characteristics of AMBs-rigid rotor system, and there are few studies on the acceleration characteristics. In this paper, taking AMBs-rigid rotor system as the object, the acceleration characteristics caused by different imbalance mass under PID controller and 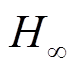 robust controller were studied. Firstly, the dynamic equation of AMBs-rigid rotor system in the process of accelerating motion was established. Then, the design principle of PID controller and
robust controller were studied. Firstly, the dynamic equation of AMBs-rigid rotor system in the process of accelerating motion was established. Then, the design principle of PID controller and 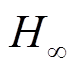 robust controller and the stability of closed loop system were analyzed. Meanwhile, the influence of PID control parameters on the acceleration characteristics of AMBs-rigid rotor system was studied. Because of strong robustness of
robust controller and the stability of closed loop system were analyzed. Meanwhile, the influence of PID control parameters on the acceleration characteristics of AMBs-rigid rotor system was studied. Because of strong robustness of 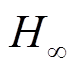 robust controller, the acceleration characteristics are not sensitive to the system parameters. Finally, simulation and experimental results verified the acceleration characteristics of AMBs-rigid rotor system under PID control and
robust controller, the acceleration characteristics are not sensitive to the system parameters. Finally, simulation and experimental results verified the acceleration characteristics of AMBs-rigid rotor system under PID control and 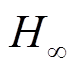 robust control. It is shown that the change of PID control parameters affects the acceleration characteristics of the rotor system, while the acceleration characteristics of the AMBs-rigid rotor system by
robust control. It is shown that the change of PID control parameters affects the acceleration characteristics of the rotor system, while the acceleration characteristics of the AMBs-rigid rotor system by 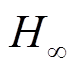 robust control are almost not affected by the acceleration, which is quite different from the acceleration characteristics of PID control and traditional rotor system.
robust control are almost not affected by the acceleration, which is quite different from the acceleration characteristics of PID control and traditional rotor system.
keywords:Active magnetic bearings, rigid rotor, acceleration characteristic, PID controller, 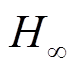 robust controller
robust controller
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.191001
国家自然科学基金项目(11632015)和国家重点研发计划(2018YF0905500)资助。
收稿日期2019-08-06
改稿日期 2019-11-12
作者简介
巩 磊 男,1993年生,博士研究生,研究方向为高速转子系统振动主动控制。E-mail: gong_lei@zju.edu.cn
祝长生 男,1963年生,教授,博士生导师,研究方向为转子系统动力学、高速电机及飞轮储能等。E-mail: zhu_zhang@zju.edu.cn(通信作者)
(编辑 崔文静)
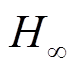 鲁棒控制时转子系统的加速特性。首先,建立主动电磁轴承-刚性转子系统在加速运动过程中的动力学方程。然后,分析加速运行过程中PID控制器和
鲁棒控制时转子系统的加速特性。首先,建立主动电磁轴承-刚性转子系统在加速运动过程中的动力学方程。然后,分析加速运行过程中PID控制器和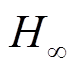 鲁棒控制器的设计原则及闭环系统的稳定性,研究PID控制参数对主动电磁轴承-刚性转子系统加速特性的影响以及
鲁棒控制器的设计原则及闭环系统的稳定性,研究PID控制参数对主动电磁轴承-刚性转子系统加速特性的影响以及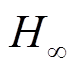 鲁棒控制器下转子系统加速特性对系统参数的不敏感性。最后,进行PID控制和
鲁棒控制器下转子系统加速特性对系统参数的不敏感性。最后,进行PID控制和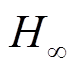 鲁棒控制条件下主动电磁轴承-刚性转子系统加速特性的仿真分析及实验。结果说明,PID控制参数变化对转子系统加速特性的影响,而
鲁棒控制条件下主动电磁轴承-刚性转子系统加速特性的仿真分析及实验。结果说明,PID控制参数变化对转子系统加速特性的影响,而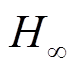 鲁棒控制下主动电磁轴承-刚性转子系统过临界的加速特性几乎不受加速度的影响,这与PID控制下传统转子系统的加速特性存在明显差异。
鲁棒控制下主动电磁轴承-刚性转子系统过临界的加速特性几乎不受加速度的影响,这与PID控制下传统转子系统的加速特性存在明显差异。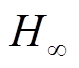 鲁棒控制器,分析了PID和强鲁棒控制条件下AMB
鲁棒控制器,分析了PID和强鲁棒控制条件下AMB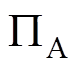 和
和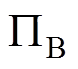 。平衡转子的质心为C,由于对称性,质心C必将位于转子几何中心线上,过
。平衡转子的质心为C,由于对称性,质心C必将位于转子几何中心线上,过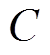 点做平行于两端AMB中心平面
点做平行于两端AMB中心平面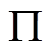 ,
,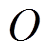 点。
点。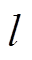 。建立
。建立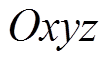 固定坐标系,其中,
固定坐标系,其中,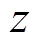 轴为旋转轴,
轴为旋转轴,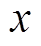 、
、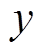 和
和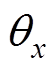 ,
, )来描述。
)来描述。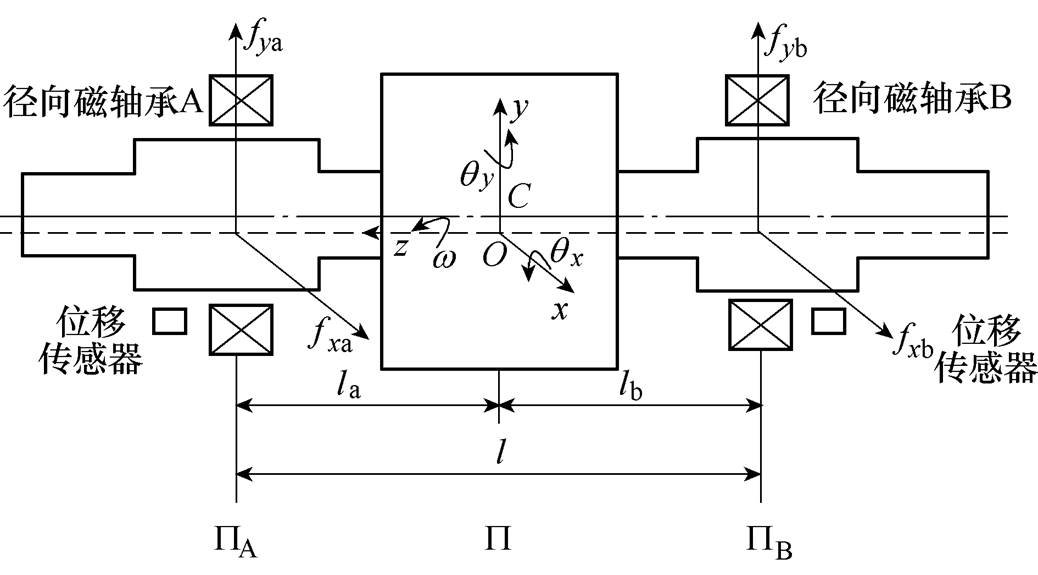
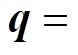
 来描述;②转子为轴对称刚性转子,转子绕x轴和绕y轴的转动惯量相同;③两端的AMB-A和AMB-B与位移传感器A和B不在同一个平面上内;④径向四个自由度的AMB结构和参数均相同;⑤忽略轴向轴承对转子径向运动的影响。
来描述;②转子为轴对称刚性转子,转子绕x轴和绕y轴的转动惯量相同;③两端的AMB-A和AMB-B与位移传感器A和B不在同一个平面上内;④径向四个自由度的AMB结构和参数均相同;⑤忽略轴向轴承对转子径向运动的影响。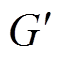 点位置,
点位置,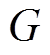 ,在
,在 轴上的投影长度为
轴上的投影长度为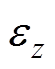 ,
, 。为了便于描述
。为了便于描述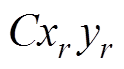 旋转坐标系,当
旋转坐标系,当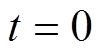 时,旋转坐标系
时,旋转坐标系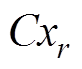 轴与
轴与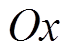 轴平行;当
轴平行;当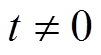 时,
时,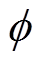 ,如图2所示。当转子稳定运行时,
,如图2所示。当转子稳定运行时,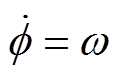 ,
,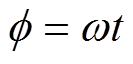 。
。
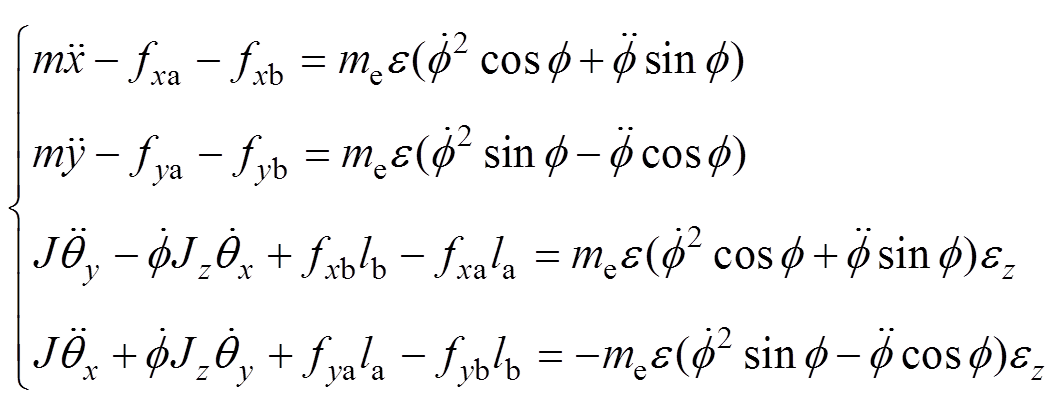 (1)
(1) 及J分别为转子绕
及J分别为转子绕 及
及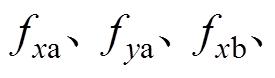
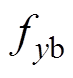 分别为两个AMB在
分别为两个AMB在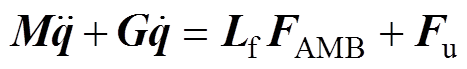 (2)
(2)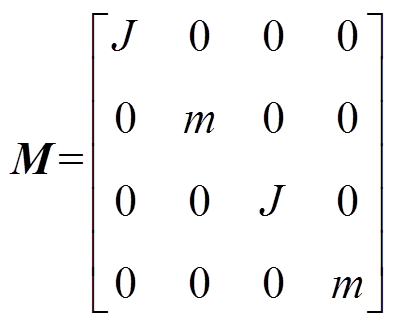
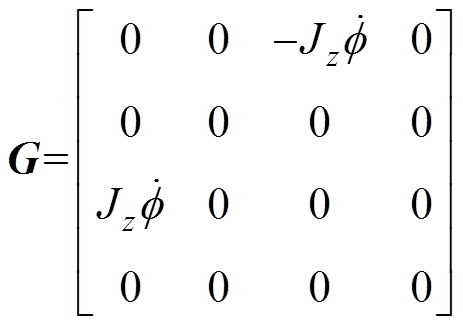
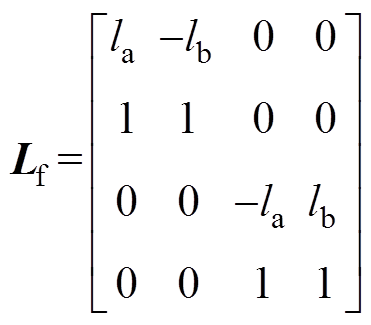
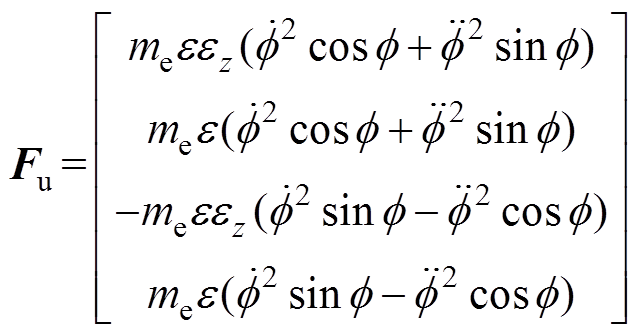
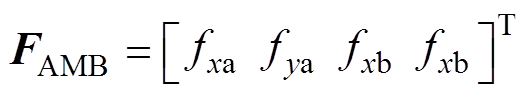
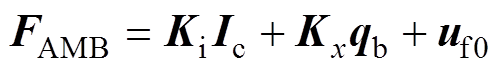 (3)
(3)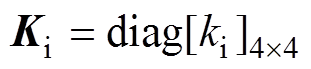
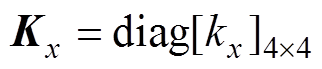
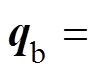
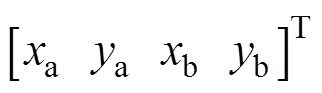
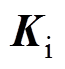 为AMB的电流刚度系数矩阵;
为AMB的电流刚度系数矩阵;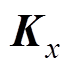 为AMB的位移刚度系数矩阵;
为AMB的位移刚度系数矩阵;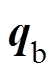 为传感器位置处的位移向量;
为传感器位置处的位移向量;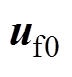 为转子处于平衡位置时的电磁力矩阵;
为转子处于平衡位置时的电磁力矩阵;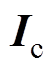 为控制电流矢量。控制电流矢量将由控制策略来决定。
为控制电流矢量。控制电流矢量将由控制策略来决定。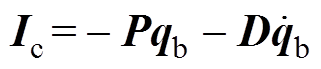 (4)
(4)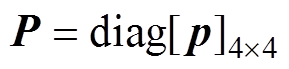 及
及 分别为AMB的比例增益系数矩阵及微分增益系数矩阵。
分别为AMB的比例增益系数矩阵及微分增益系数矩阵。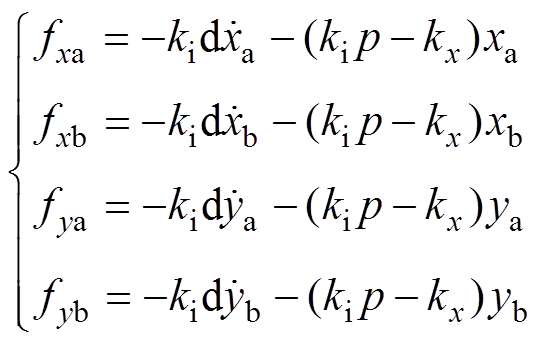 (5)
(5) 与转子几何中心C处的广义坐标
与转子几何中心C处的广义坐标 之间的关系为
之间的关系为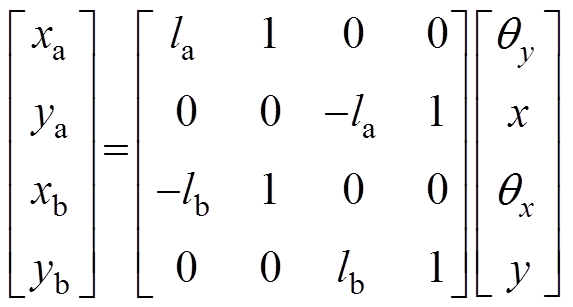 (6)
(6)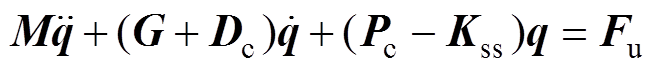 (7)
(7)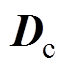 和
和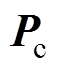 分别为PD控制器在AMB上产生的阻尼矩阵及刚度矩阵;
分别为PD控制器在AMB上产生的阻尼矩阵及刚度矩阵;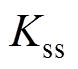 为AMB的负刚度矩阵。
为AMB的负刚度矩阵。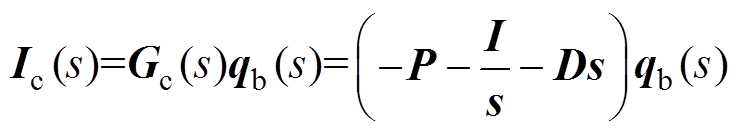 (8)
(8) 为
为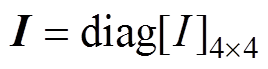
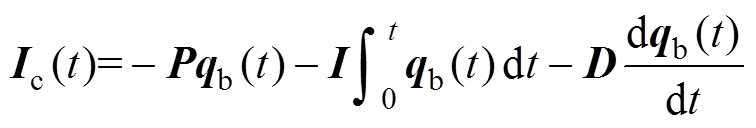 (9)
(9)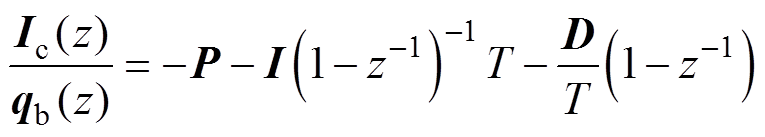 (10)
(10)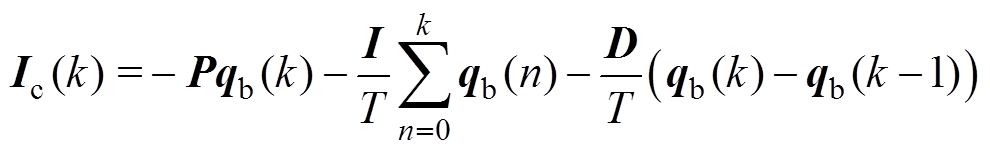 (11)
(11)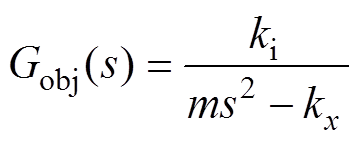 (12)
(12)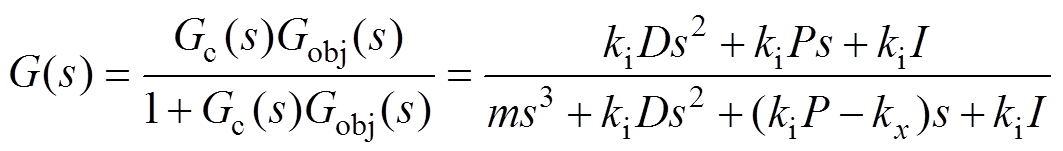 (13)
(13)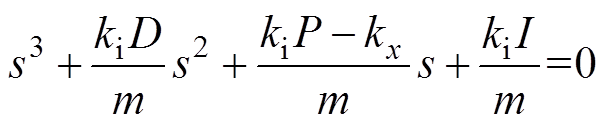 (14)
(14)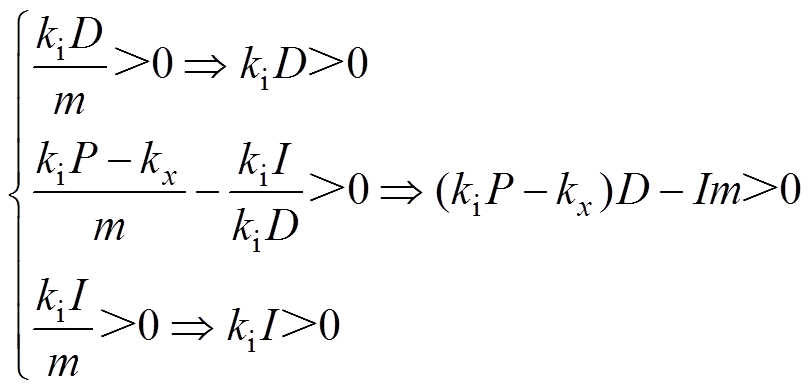 (15)
(15)
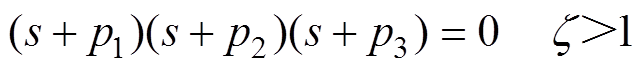 (16)
(16)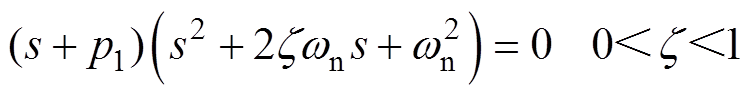 (17)
(17)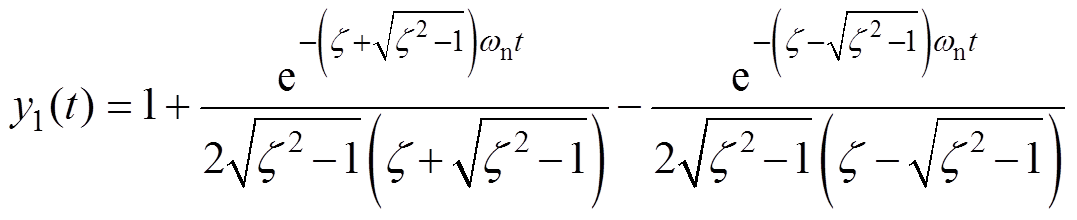 (18)
(18)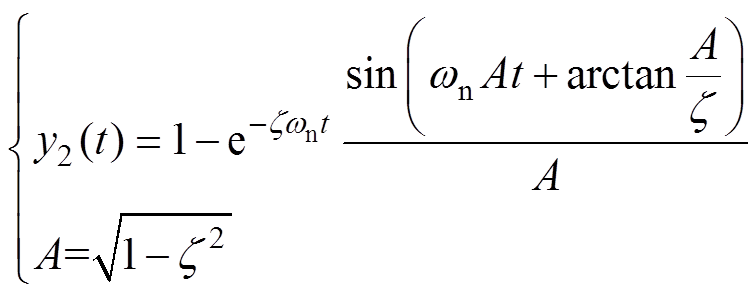 (19)
(19)
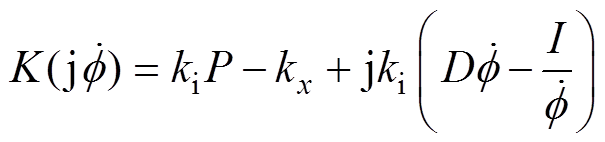 (20)
(20)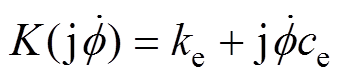 (21)
(21)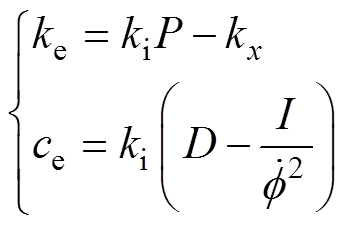 (22)
(22)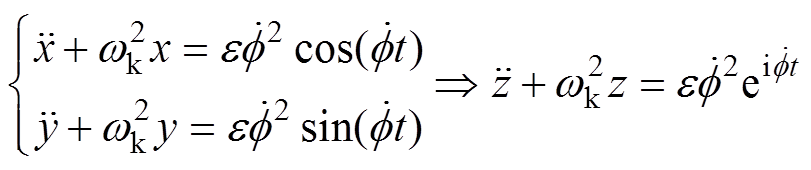 (23)
(23)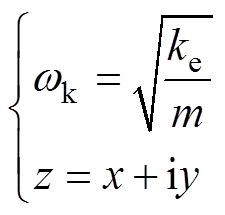
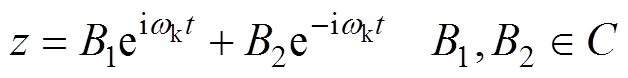 (24)
(24)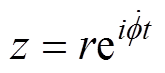 ,结合式(24)解得
,结合式(24)解得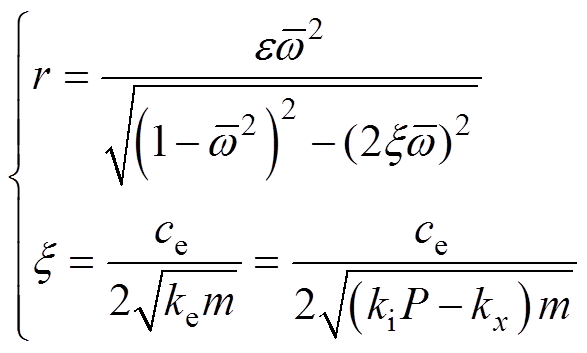 (25)
(25)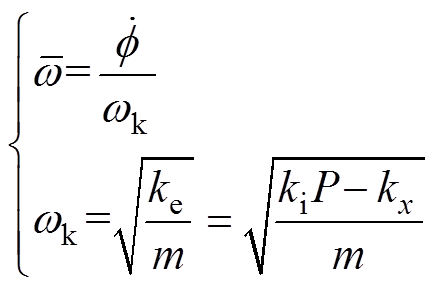
 为转速比;
为转速比;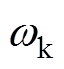 为转子系统的固有频率。
为转子系统的固有频率。 时,转子振动幅值最大。图5为在不同阻尼比
时,转子振动幅值最大。图5为在不同阻尼比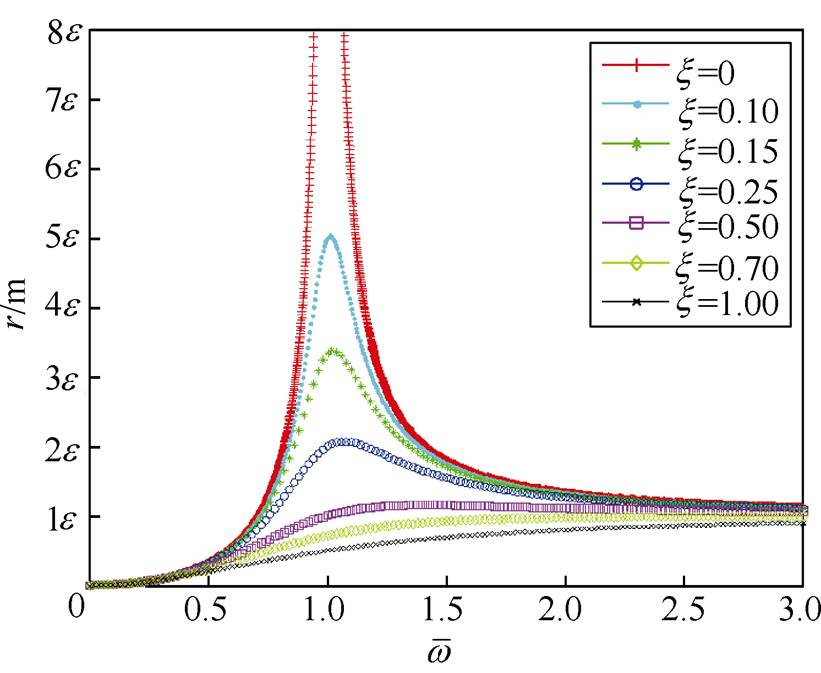
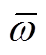 的关系
的关系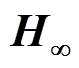 鲁棒控制
鲁棒控制 鲁棒控制器为例进行分析。
鲁棒控制器为例进行分析。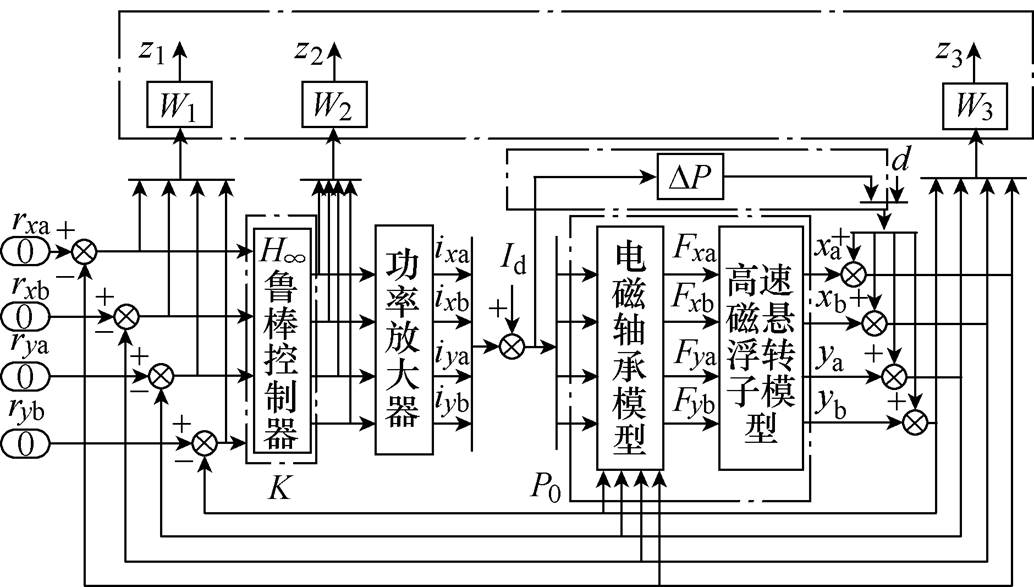
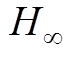 鲁棒控制系统原理框图
鲁棒控制系统原理框图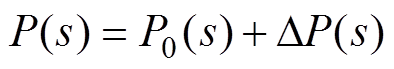 (26)
(26)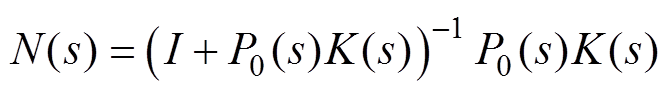 (27)
(27)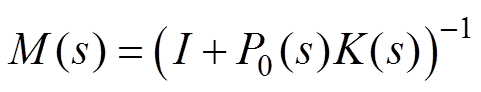 (28)
(28)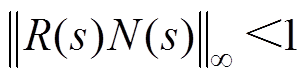 (29)
(29)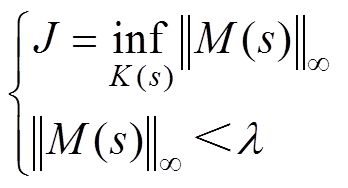 (30)
(30)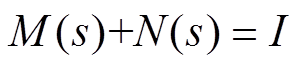 ,因此N(s)被称为补灵敏度函数。根据AMB
,因此N(s)被称为补灵敏度函数。根据AMB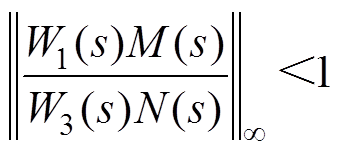 (31)
(31)
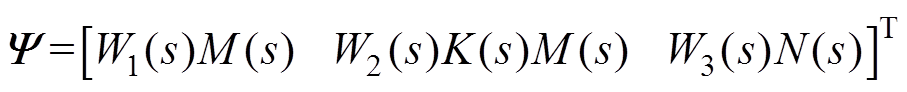 (32)
(32)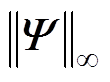 求解
求解 控制器,即K(s)要满足
控制器,即K(s)要满足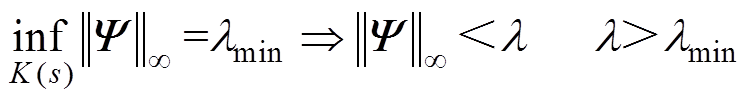 (33)
(33)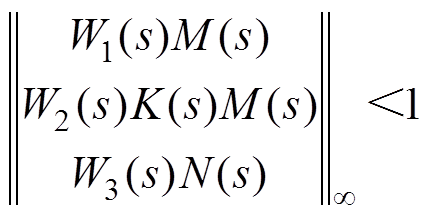 (34)
(34)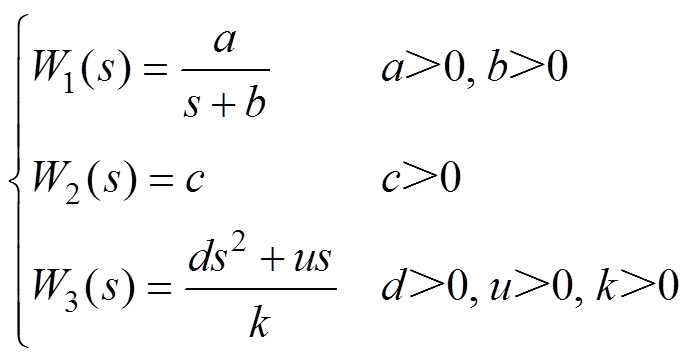 (35)
(35) ,x
,x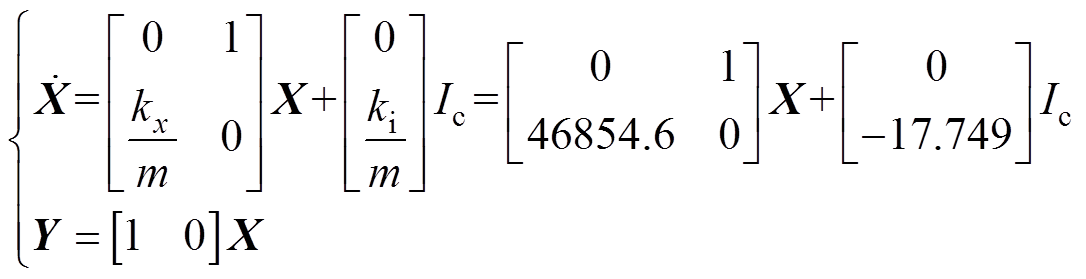 (36)
(36)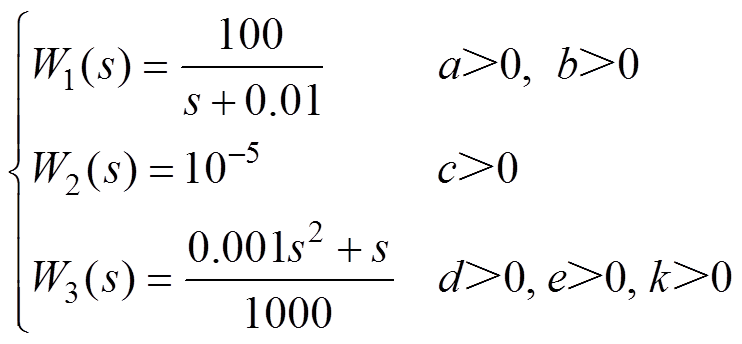 (37)
(37)




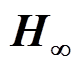 鲁棒控制下的实验结果及分析
鲁棒控制下的实验结果及分析 鲁棒控制下转子穿过临界转速时的最大振幅并不会随着加速度的增大而减小,且最大位移振幅和临界转速也均维持在0.04mm和10 000r/min附近。
鲁棒控制下转子穿过临界转速时的最大振幅并不会随着加速度的增大而减小,且最大位移振幅和临界转速也均维持在0.04mm和10 000r/min附近。
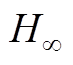 控制下的转子加速响应曲线
控制下的转子加速响应曲线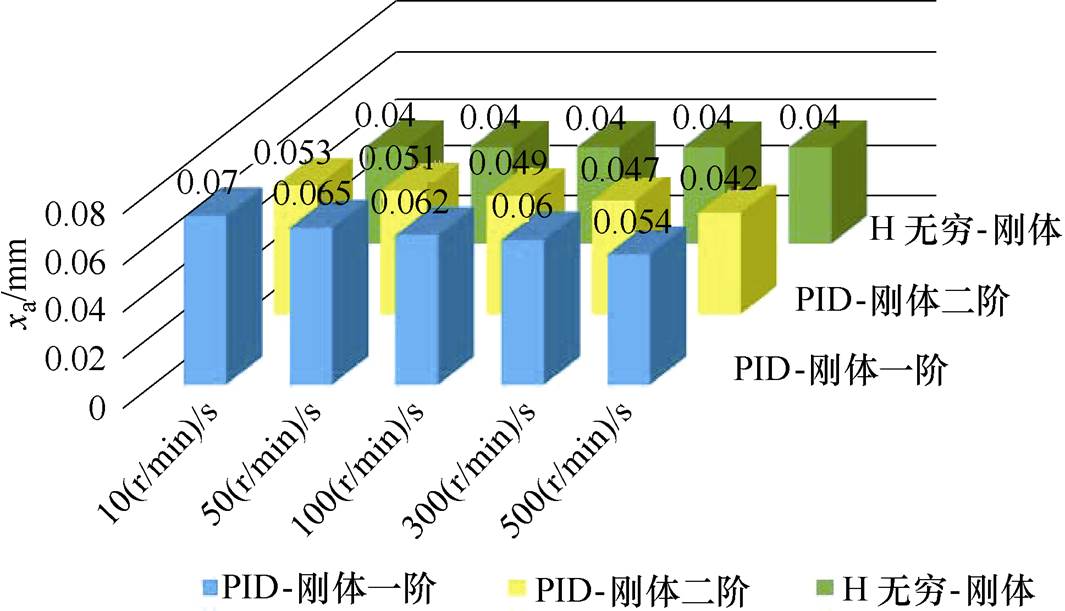
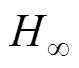 鲁棒控制条件下,AMB
鲁棒控制条件下,AMB