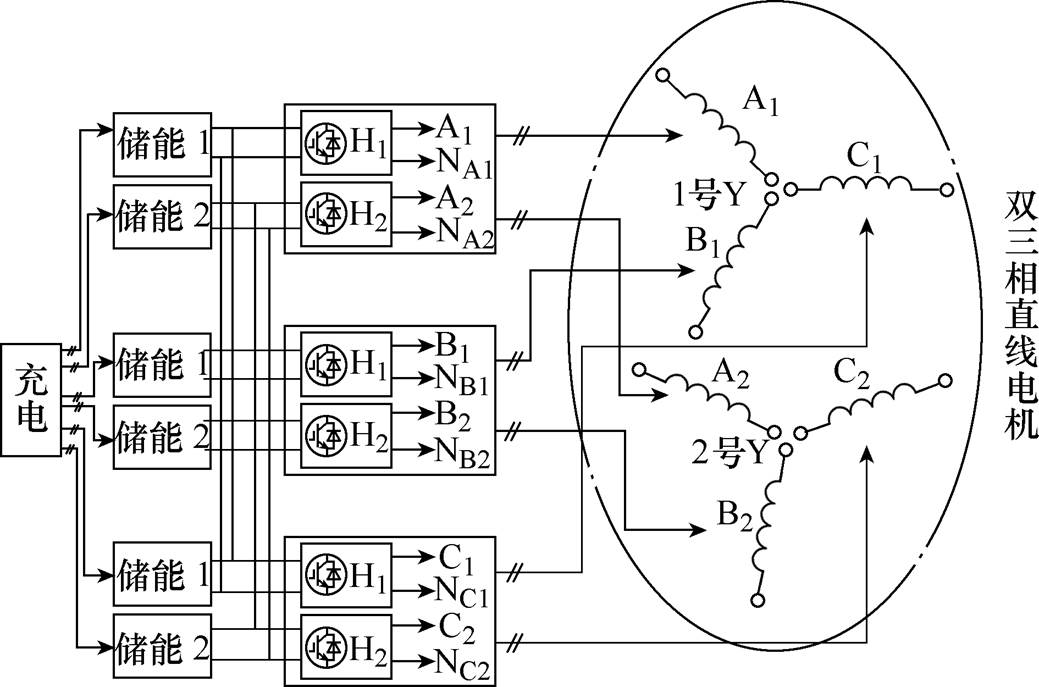
图1 双能量链直线感应电机驱动系统能量流架构
Fig.1 Energy flow architecture of dual energy chain LIM drive system
摘要 采用两条独立能量链供电,工作于非周期瞬态工况的双三相直线感应电机系统,在功率等级、功率密度、控制自由度、系统冗余度等方面具有诸多优势。该文基于考虑动态边端效应的双三相直线感应电机模型,给出了矢量控制策略。结合非周期瞬态系统的运行特性,提出一种故障模式下通过开环计算给定推力作为矢量控制输入的能量链切换控制策略。该控制策略避免了故障暂态过程中给定电流变化与输出电流尖峰的耦合,通过在考虑动态边端效应时电机在最大推力的约束下根据控制目标调整给定推力,实现了系统故障后单能量链的安全运行。仿真和实验验证了所提控制策略的正确性与可行性。
关键词:双三相直线感应电机 非周期瞬态 动态边端效应 能量链切换 最大推力
随着大功率电能变换及高能量密度脉冲储能技术的突破,利用直线电机将存储的电能瞬间转化为高速动能成为可能,促进了直线电机在电磁发射领域的应用[1]。其中,短初级直线感应电机(Linear Induction Motor, LIM)避免了采用分段供电技术带来的系统复杂、电缆压降大、可靠性低等问题,且兼顾了系统体积、质量及功率密度,具有较高的研究价值和广阔的应用前景。
直线电机与旋转电机最主要的区别在于直线电机存在边端效应,其中动态边端效应会造成气隙磁场分布不均、电机参数时变[2-3],是研究短初级直线感应电机必须考虑的重点和难点。相关研究中,较为经典且被学者和工程技术人员广泛应用的是文献 [4]提出的方法和结论,该文献通过引入无量纲系数Q,推导了励磁电感随Q变化的函数,并建立了考虑动态边端效应的直线感应电机等效电路。另一种常用的方法为基于电磁场方程及复功率守恒推导得到电机参数修正系数[3, 5-7]。相比之下,文献[4]所提方法以简单、清晰、运算量小的优点,适用于直线电机实时控制。基于考虑动态边端效应的电机模型,相关研究在旋转电机控制理论的基础上对直线感应电机的控制策略进行优化[8-10]。
为了提高直线电机系统的可靠性和安全性,可引入多能量链并联驱动技术或多相电机理论,以便于实现系统的故障容错运行。文献[11-12]以分段供电的长初级三相直线感应电机为研究对象,采用多能量链驱动多定子并联运行的模式,提出了相应的故障运行策略。而就多相电机的相关研究,大多以旋转电机为研究对象,文献[13]提出一种基于电流滞环的多相电机矢量控制策略,可推广到任意相数的多相电机控制中,方法简单易实现,但开关频率不固定,整体控制性能不高。文献[14]基于六相电机空间矢量解耦矩阵推导了电机的解耦数学模型,通过控制给定电压矢量在基波投影的子空间上的轨迹实现了磁链-转矩控制。文献[15]采用双dq变换揭示了矢量空间解耦的本质,建立了两种变换矩阵之间的联系,为六相电机的控制提供了基础。多相电机在故障后能够通过调整控制策略,实现系统的容错运行[16-21],主要方法包括:建立目标函数求解各相绕组容错电流的参考值,并采用电流滞环控制实现多相电机的容错控制;利用故障后维度不变或降维的矢量空间解耦矩阵,建立缺相电机模型并实现容错控制。
综合现有文献,有关多相直线电机系统故障容错运行的研究尚存不足。如何结合直线电机模型及其运行工况的特殊性拟定故障运行控制策略,是亟待解决的问题。
本文以工作于非周期瞬态工况,采用两条独立能量链供电的短初级双三相直线感应电机系统为研究对象,考虑动态边端效应,结合多相电机控制理论,给出电机的矢量控制策略。由于本文所述非周期瞬态系统的整个运行过程在ms级时间内完成,且全程无稳态(无匀速),因此当系统发生故障时需要用较为简单的方法控制电机继续安全完成本次运行任务,这一点与传统稳态电机的控制需求不同。基于此,本文提出一种在故障模式下开环计算给定推力并以此作为矢量控制输入的能量链切换控制策略。该控制策略能够实现系统故障后单能量链的安全运行,且实现方法简单、工程实用性强。仿真和实验验证了所提出控制策略的正确性与可行性。
采用两条独立能量链驱动的双三相直线感应电机系统的能量流架构如图1所示。

图1 双能量链直线感应电机驱动系统能量流架构
Fig.1 Energy flow architecture of dual energy chain LIM drive system
图1中,双三相直线感应电机驱动系统包含两条相互独立的能量链,分别驱动直线电机的两套绕组,即1号Y和2号Y,单条能量链包括储能环节和逆变环节,可实现独立控制。直线电机单套绕组各相间无中性点连接,即开式绕组。双三相直线感应电机的结构如图2所示。
两套互移30°的绕组布置在动子上。动子运行过程中与二次侧相互作用,在二次侧导电层上感应出涡流,使气隙平均磁场被削弱,等效励磁电感下降,电机输出推力下降。此外,感应涡流会造成附加损耗,降低电机的效率。令励磁电感和等效涡流损耗的电阻的修正系数分别为ke(v,t)和kr(v,t)[4],由于研究对象工作于非周期瞬态工况,系数的后缀表示系数随速度时变,简写为ke和kr。励磁电感和损耗电阻的表达式可写为
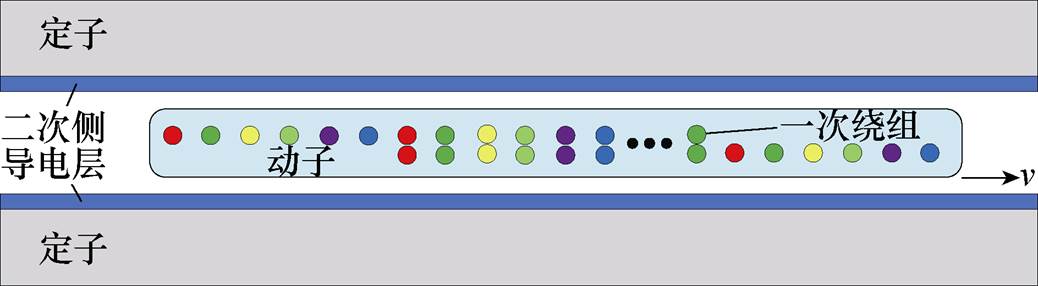
图2 双三相直线感应电机结构
Fig.2 Structure of dual three-phase LIM
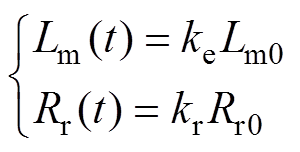 (1)
(1)其中
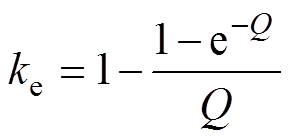
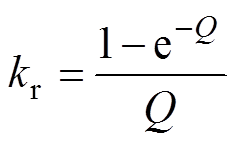
式中,Lm(t)、Rr(t)和Lm0、Rr0分别为励磁电感、损耗电阻的实时值和静态值;Q=DRr0/[v(Lm0+Llr)],D和v分别为动子长度和运行速度,Llr为二次侧漏感。根据式(1)可得考虑动态边端效应时,双三相直线感应电机dq轴等效电路如图3所示。
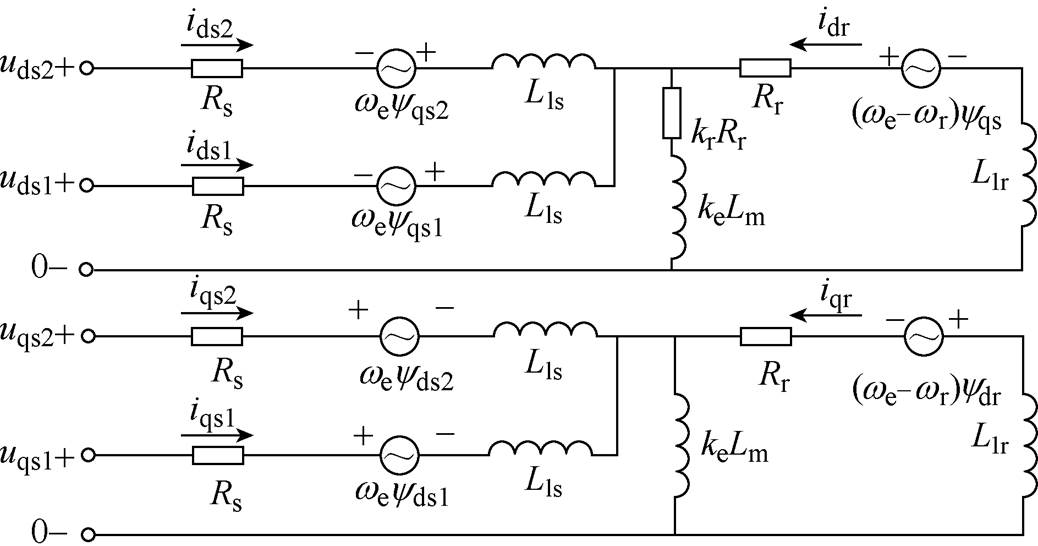
图3 双三相直线感应电机dq轴等效电路
Fig.3 dq-axis equivalent circuit of dual three-phase LIM
根据图3得到考虑动态边端效应时,双三相直线感应电机的电压、磁链方程如下。
电压方程为
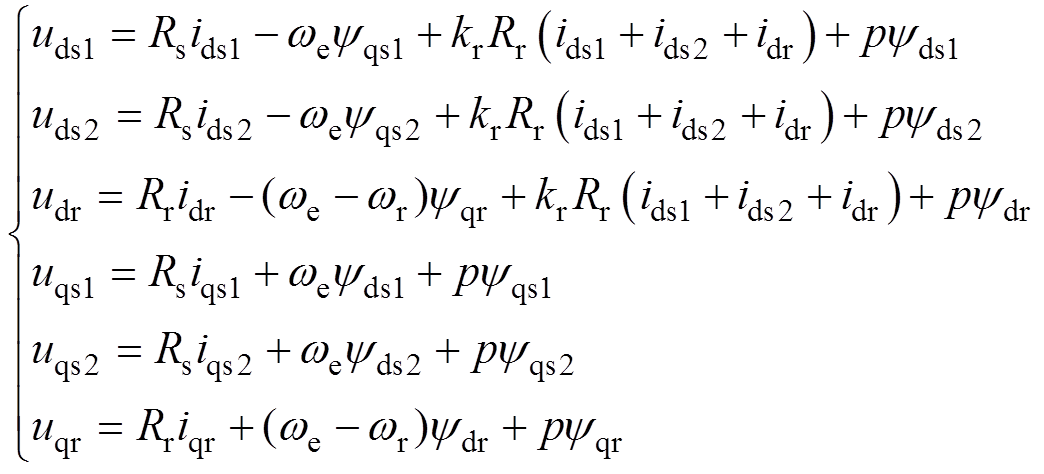 (2)
(2)磁链方程为
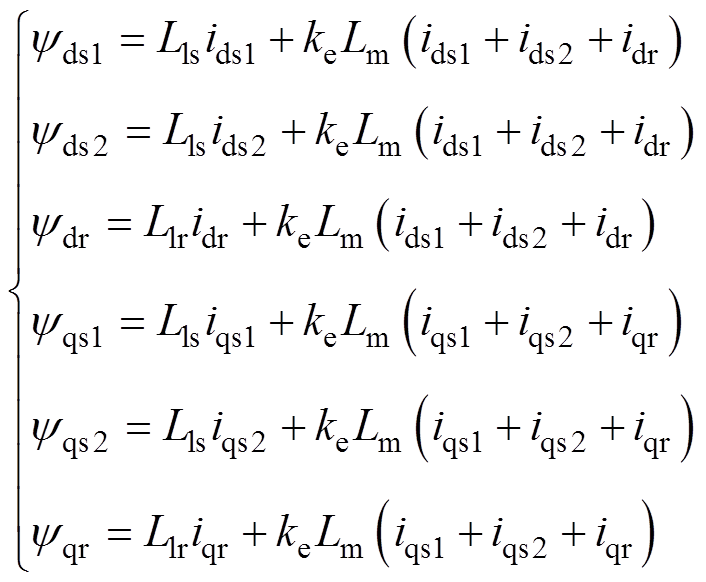 (3)
(3)
式中,udsn、udr分别为d轴一次电压和二次电压,n=1, 2表示绕组1号Y和2号Y对应的变量;uqsn、uqr分别为q轴一次电压和二次电压;Rs、Rr分别为一次侧电阻和二次侧电阻;idsn、idr分别为d轴一次电流和二次电流;iqsn、iqr分别为q轴一次电流和二次电流;ydsn、ydr分别为d轴一次侧磁链和二次侧磁链;yqsn、yqr分别为q轴一次侧磁链和二次侧磁链;Lls、Llr分别为一次侧漏感和二次侧漏感;we为同步电角度;wr为同步速度角度;p为微分算子。根据图3及式(2)可知,由于d轴等效电路的励磁支路中含有损耗电阻,导致电压方程含有一次电流与二次电流的耦合项,这一点与传统感应电机模型有明显区别。在此,将式(2)、式(3)写为矩阵的形式并利用等效变换对矩阵进行重构,重构后得到磁链方程为
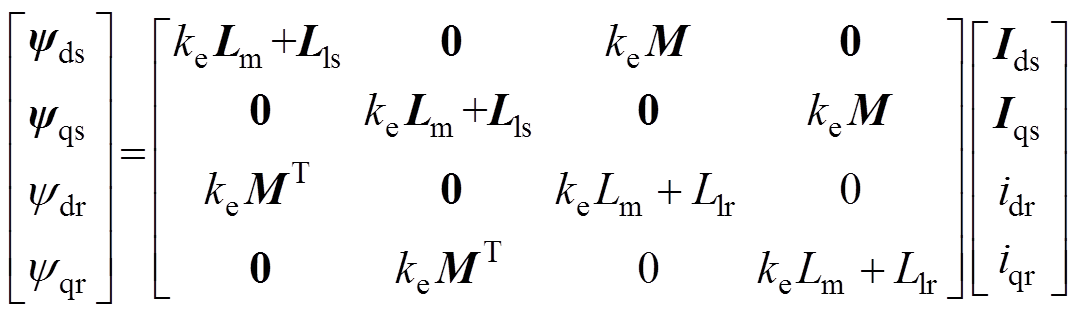 (4)
(4)其中
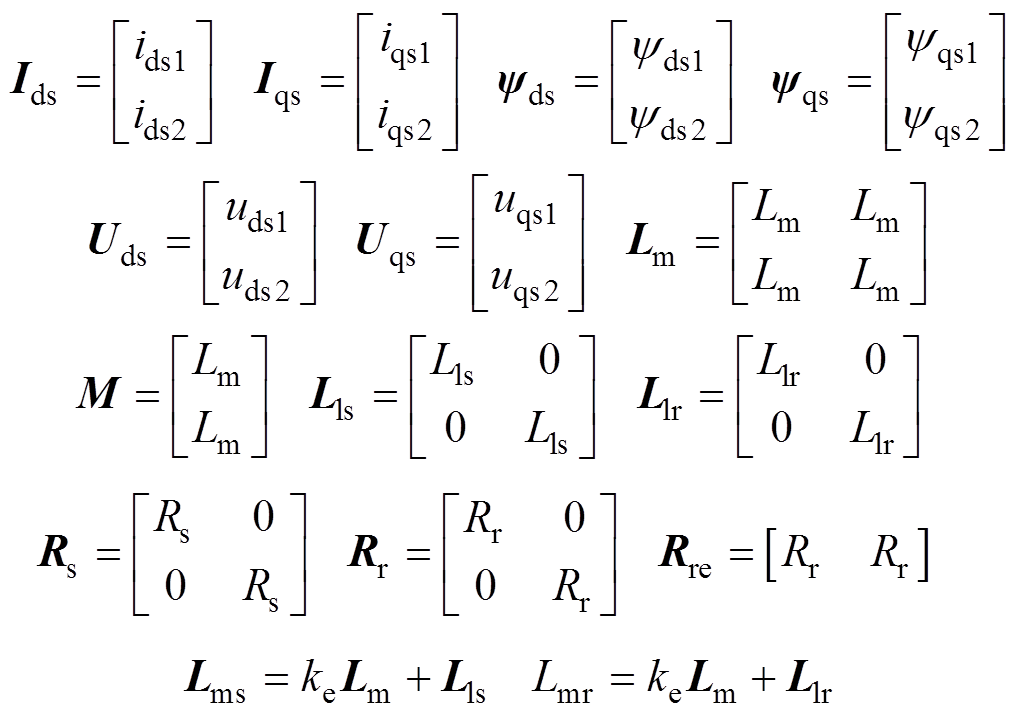
利用重构后的磁链矩阵消除转子电流和定子磁链,得到电压方程为
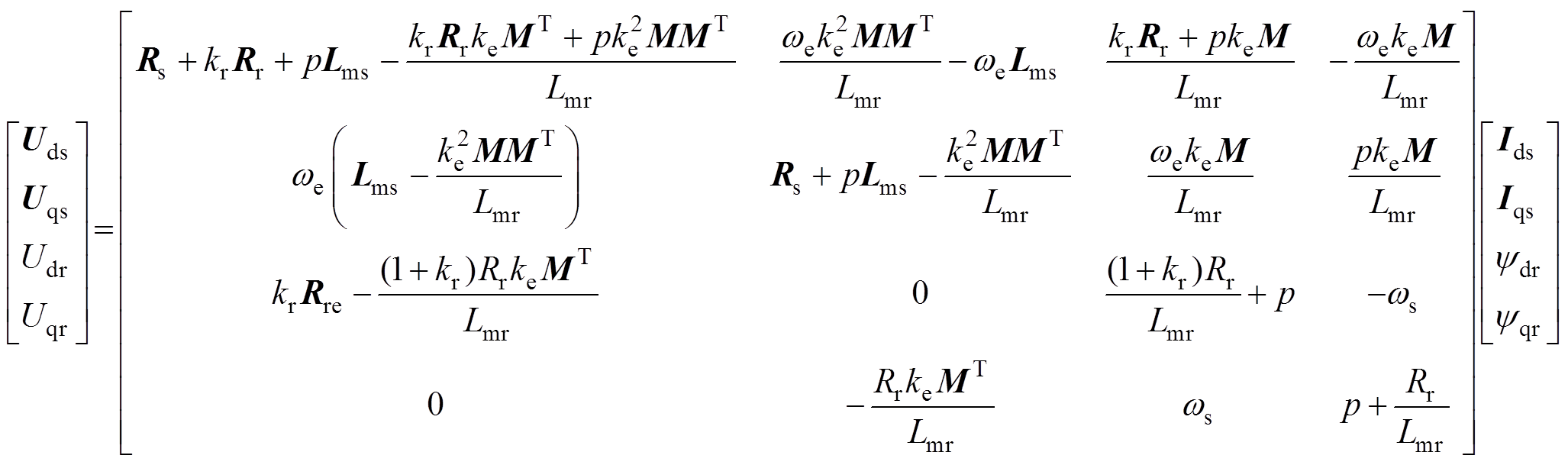 (5)
(5)电磁推力为
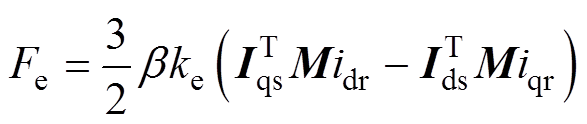 (6)
(6)
式中,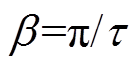 ,
,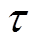 为电机极距。
为电机极距。
直线电机矢量控制理论与旋转电机相同。将d轴定向到二次侧磁链,有yqr=0,在系统运行过程中,控制二次侧磁链基本保持不变,即pydr=0,将式(5)化简并联立式(4)可推导得二次侧磁链的表达式为
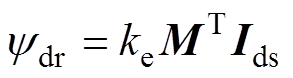 (7)
(7)联立式(4)~式(6)得推力表达式为
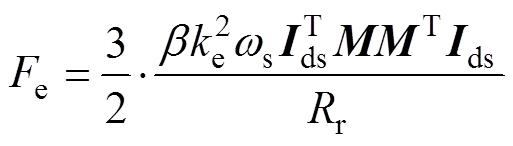 (8)
(8)
转差角频率的表达式为
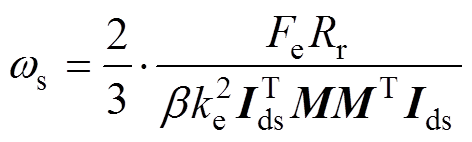 (9)
(9)q轴电流的表达式为
 (10)
(10)
利用上述推导可建立考虑动态边端效应的矢量控制模型,矢量控制框图如图4所示。瞬态直线感应电机的控制目标为动子带动负载在目标位置达到目标速度。通过图4轨迹生成模块根据控制目标生成参考加速度、参考速度及参考位置轨迹,经过位置闭环控制后乘以质量(动子与负载的质量和)即得到给定推力,作为矢量控制的输入。通过式(9)、式(10)基于考虑动态边端效应的电机数学模型进行计算,能够在线更新与速度相关的修正系数ke和kr,实时修正转差频率和q轴电流,以实现瞬态过程中的推力补偿。通过位置观测器观测及计算得到的观测位置和观测速度可计算得到供电角频率和供电角度,用于电流环中的dq变换及其反变换。矢量控制输出的给定励磁电流Id和q轴电流Iq是包含两套绕组变量的二维向量,作为电流环控制的输入,经过电流闭环控制后输出两套绕组的参考电压。
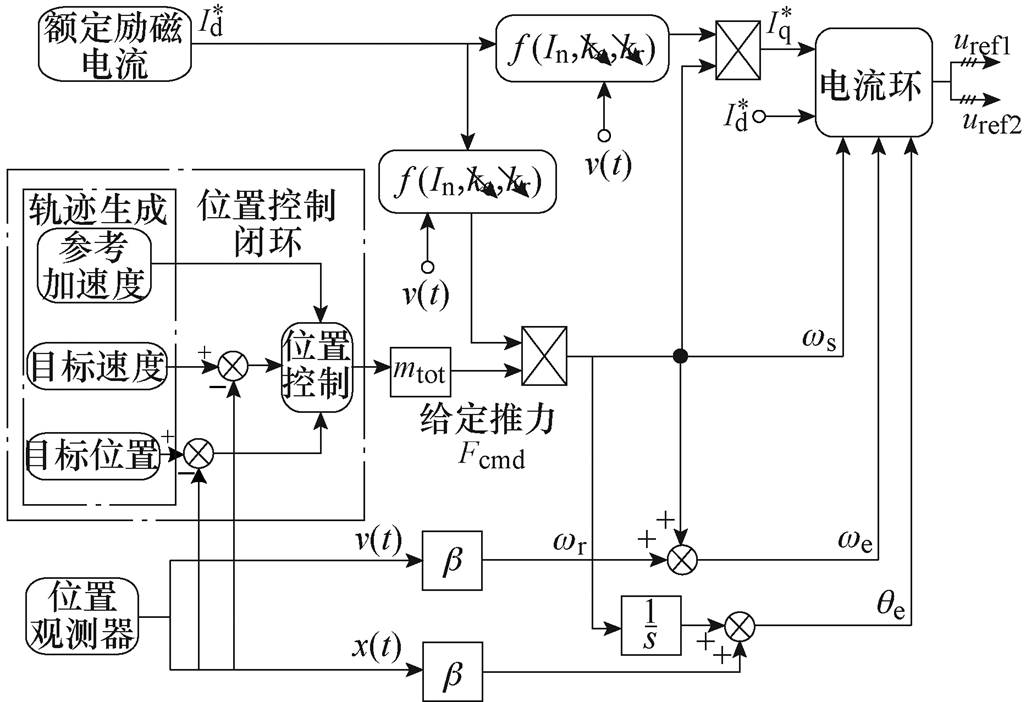
图4 矢量控制框图
Fig.4 Block diagram of vector control
系统运行过程中出现故障时,直接切除故障能量链,而非故障能量链继续运行,是一种简单有效的故障运行方法。设计能量链切换控制策略的主要原则为:①在电机运行过程中,某条能量链发生故障时,充分利用非故障能量链的最大输出能力,使动子尽可能地靠近目标速度;②保证非故障能量链能够安全、高可靠性运行。
为了保证故障后电机能够充分利用非故障能量链的最大出力能力,需要对电机的最大出力点进行设定。考虑动态边端效应时,电机的T形等效电路如图5所示。
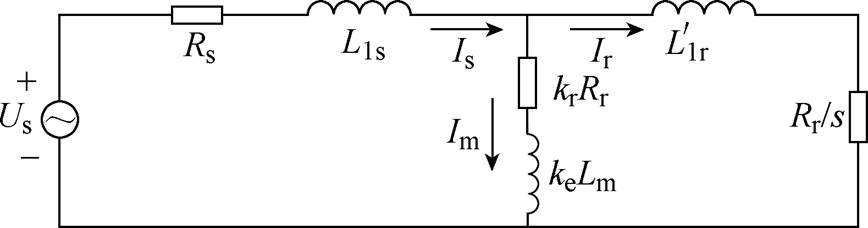
图5 T形等效电路
Fig.5 T-type equivalent circuit
考虑动态边端效应时电机的功率为
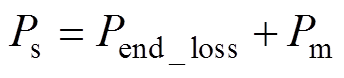 (11)
(11)其中
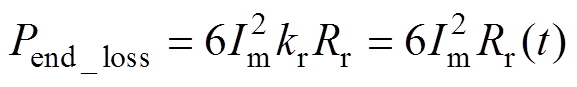 (12)
(12)
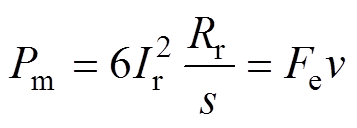 (13)
(13)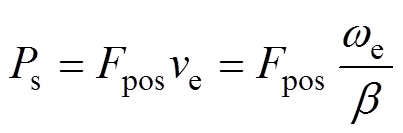 (14)
(14)
式中,s为转差率,s=ws/we。联立图5电路方程以及式(11)~式(14)可求解得到电机推力Fpos及动态边端效应造成的反向推力Fend_break表达式分 别为
 (15)
(15)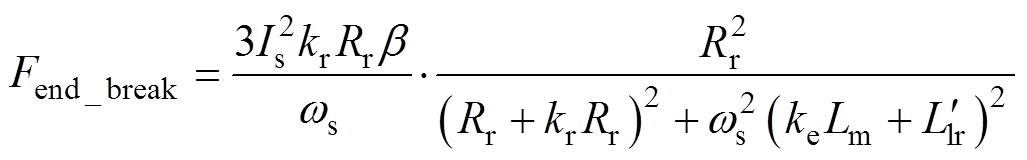 (16)
(16)
联立式(15)和式(16)可得,考虑动态边端效应后,电机的实际出力为
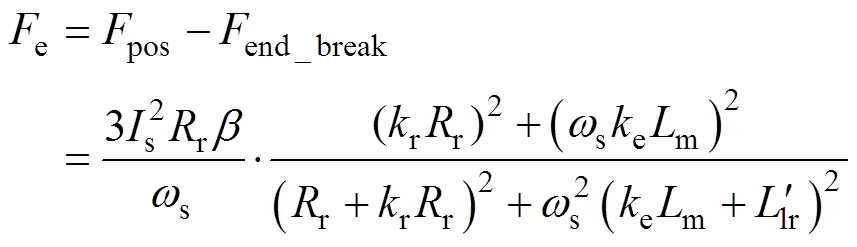 (17)
(17)将式(17)对ws求偏导并令其等于零,可得到考虑动态边端效应时电机的最大出力以及最大出力点对应的转差角频率分别为
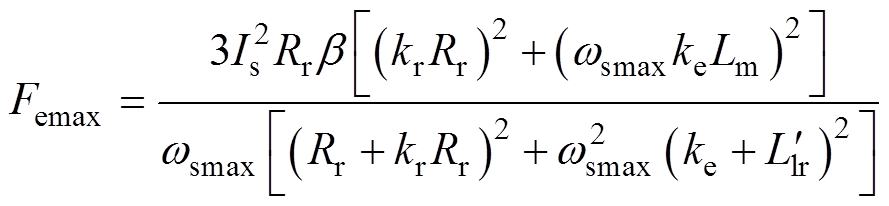 (18)
(18)
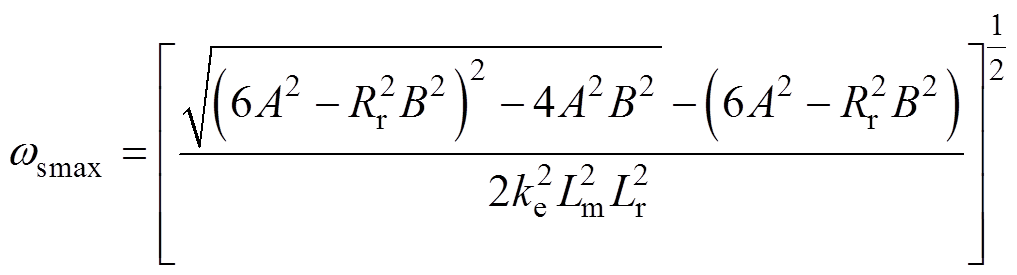 (19)
(19)式中,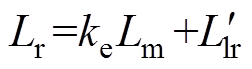 ;A=RrLmLr;B=(1+kr)keLm。从式(18)、式(19)可以看出,考虑动态边端效应时,最大推力及其对应的转差频率随速度变化。通过式(18)可知,电机推力与电流的二次方成正比,当能量链故障且逆变器输出电流不变时,电机单能量链运行的输出推力降为原来的1/4。电机单能量链运行时推力随速度及电流激励的变化规律如图6 所示。
;A=RrLmLr;B=(1+kr)keLm。从式(18)、式(19)可以看出,考虑动态边端效应时,最大推力及其对应的转差频率随速度变化。通过式(18)可知,电机推力与电流的二次方成正比,当能量链故障且逆变器输出电流不变时,电机单能量链运行的输出推力降为原来的1/4。电机单能量链运行时推力随速度及电流激励的变化规律如图6 所示。
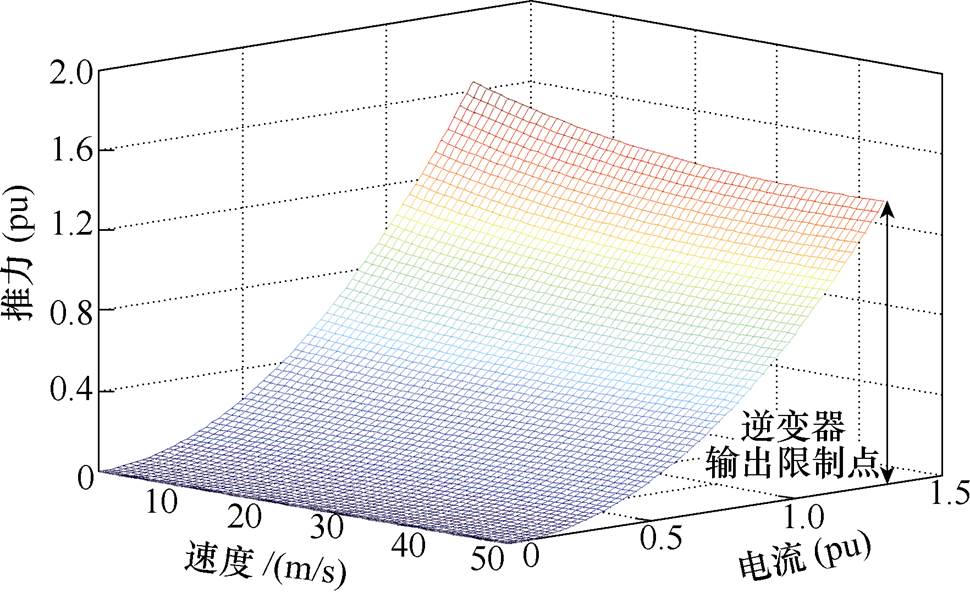
图6 电机单能量链出力随速度和电流的变化规律
Fig.6 Varation of output thrust of single energy chain with speed and current
从图6中可以看出,电机单能量链运行时最大出力随速度的增大而减小。对于电机驱动系统而言,逆变器功率等级决定了最大电流输出能力,即决定了在一定速度条件下电机的最大出力。
电机正常运行时,如图4所示,由外环前馈和反馈控制计算给定加速度并乘以动子和负载的质量和得到给定电磁力作为矢量控制环节的输入,矢量控制计算得到的给定电流作为电流内环控制的输入。当系统能量链故障,且故障能量链被切除时,电机的出力能力下降,且电机的过渡过程会导致输出电流出现尖峰。因此需要在瞬态过渡过程中保持励磁电流和q轴电流的给定值不变,以防止给定电流变化与能量链切换引起的电流尖峰耦合,产生更大的电流波动。结合2.2节的推导,本文提出一种故障模式下通过开环计算给定推力作为矢量控制输入的能量链切换控制策略,具体如下。
当其中一条能量链故障时,故障能量链的逆变器停止触发脉冲,非故障能量链继续运行,电机转入外环开环控制,给定推力降为故障前时刻推力的1/4;励磁电流和q轴电流的给定值保持在时间thold(电流尖峰的恢复时间)不变。
定义故障后电机在目标位置达到目标速度所需平均推力为Fdesire,其计算公式为
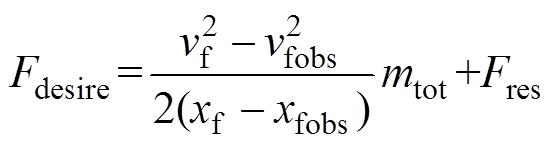 (20)
(20)式中,vf、xf分别为目标速度和目标位置;vfobs、xfobs分别为故障时刻的观测速度和观测位置;mtot为动子和负载的质量和;Fres为滑动摩擦力和空气阻力补偿。根据式(18)可计算得到电机单能量链在目标速度下的最大出力Fmaxlim,作为单能量链运行时电机的推力限幅。因此,故障模式下矢量控制输入的给定推力Ffault取Fdesire和Fmaxlim的最小值。经时间thold后,给定推力值上升至Ffault,根据式(10)可知,当推力上升时,若励磁电流不变,q轴电流会增大。为了满足单能量链的推力输出,并且防止q轴电流飙升,thold之后将给定励磁电流上升至Id_new,q轴电流的给定值随即上升,能量链切换时电机运行特性如图7所示。
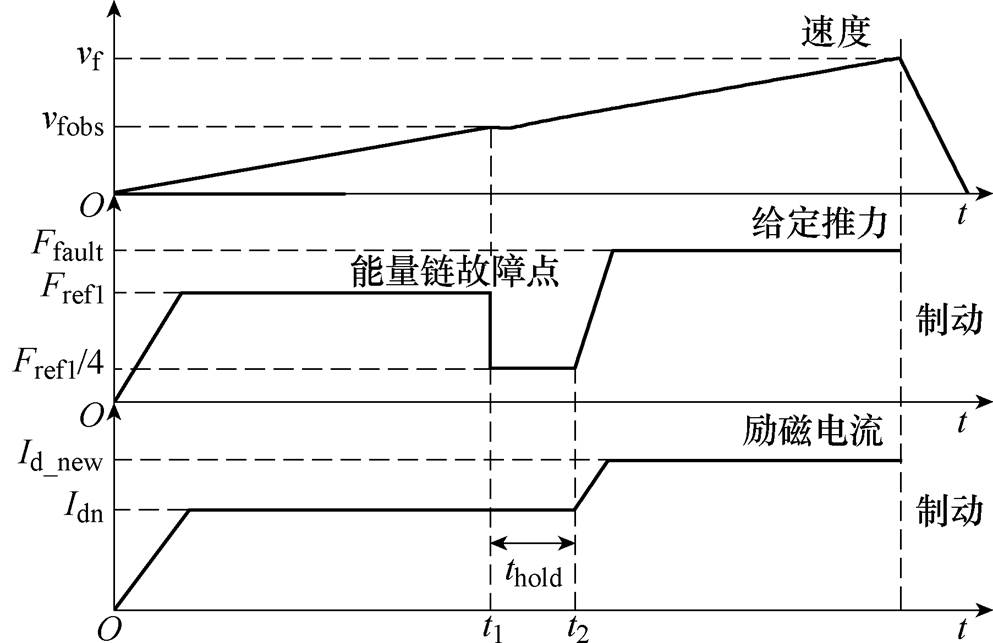
图7 能量链切换时电机运行特性
Fig.7 Operation characteristics of motor during the switching of energy chain
联立式(8)、式(18)及式(19)可计算得到Id_new。如上所述,故障后,矢量控制由图4转为故障模式下矢量控制框图如图8所示。
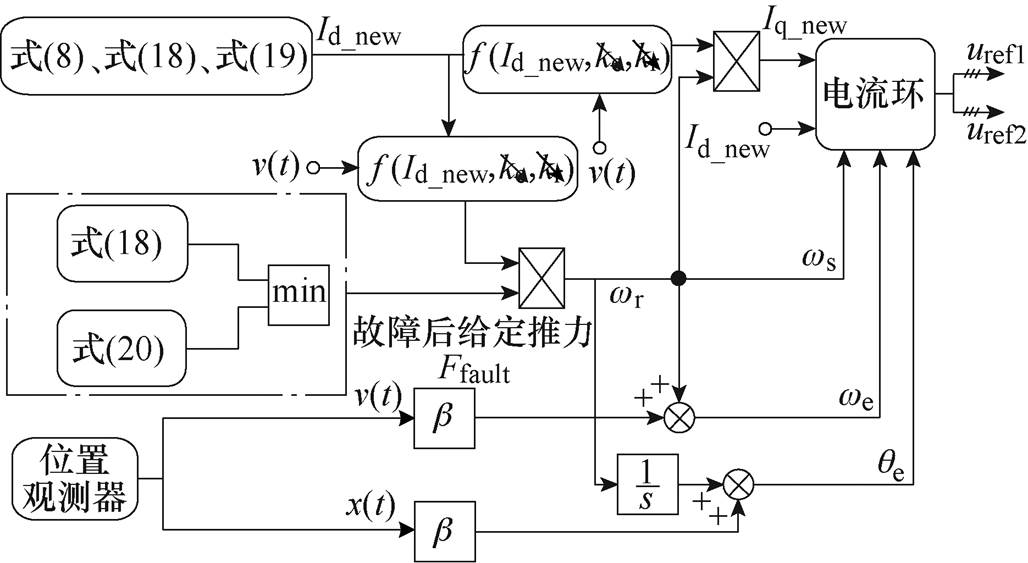
图8 故障模式下矢量控制框图
Fig.8 Block diagram of vector control in fault mode
从图8中可以看出,采用直接计算给定推力作为矢量控制输入的控制方法(外环开环),能够在系统故障且故障能量链被切除后电机的过渡过程中保持dq轴电流给定值不变,避免了给定电流变化与输出电流尖峰的耦合。同时,能量链故障后,给定推力能够在电机单能量链最大出力约束下根据系统的控制目标(目标速度和目标位置)进行调整,实现了故障模式下双能量链到单能量链的安全切换及单能量链的持续运行。
为了验证本文所述能量链切换控制策略的正确性,在Matlab/Simulink中搭建了仿真模型,仿真模型由控制模块和电机模型两部分组成,其中控制模块集成了速度观测、速度闭环、矢量控制计算、电流内环等环节,通过观测加速度和负载质量可得到电机实际的推力曲线,仿真参数见表1。
表1 仿真参数
Tab.1 The parameters of simulation

参 数数 值 励磁电感Lm/H18.3×10-5 一次侧漏感Lls/H1.1×10-5 一次绕组电阻Rs/W2.15×10-2 二次侧漏感Llr/H3.12×10-5 二次绕组电阻Rr/W3.57×10-2 动子长度D/m0.9 动子质量mshuttle/kg55 负载质量mload/kg170
仿真工况一:目标速度40m/s,模拟1号能量链故障,故障后矢量控制输入给定推力由位置闭环计算得到,工况一仿真波形如图9所示。
如图9所示,能量链故障后依然采用位置闭环计算给定推力作为矢量控制的输入,即图4的方法。在故障时刻令参考加速度降为故障前的1/4,如图9a所示,由于外环前馈与反馈的延时与误差导致给定推力无法在故障点严格的降为故障前的1/4,因此q轴电流在故障之后无法保持恒定,而出现跌落,d轴电流随即跌落,如图9b、图9c所示。从图9d输出电流波形中可以看出,在故障时刻非故障能量链的输出电流出现较大尖峰,尖峰值约为平均电流的1.35倍,若故障点恰好在输出电流的波峰处,则尖峰会很大且容易触发非故障能量链的过电流保护,严重降低了系统的安全性。

图9 工况一仿真波形
Fig.9 Simulation waveforms of Condition 1
仿真工况二:目标速度40m/s,模拟1号能量链故障,故障后矢量控制采用2.3节所述控制方法,工况二仿真波形如图10所示。
图10a~图10c中,能量链故障后采用直接计算推力作为矢量控制的输入,给定推力在故障点严格降为故障前的1/4,dq轴电流的给定值在故障后能够保持不变,持续thold时间后,给定推力上升至40m/s下单能量链最大推力值,实现了故障后单能量链的最大推力输出。与此同时,励磁电流开始上升,q轴电流随即上升,仿真波形与2.3节所述基本一致。从图10d可知,由于避免了给定电流与输出电流尖峰的耦合,故障点非故障能量链的输出电流尖峰为平均电流的1.13倍,相比工况一,电流尖峰明显减小,降低了非故障能量链过电流的风险,增加了系统的安全性。如图10e所示,观测速度最终达到了目标速度(注:仿真波形中推力基准值为10 000N,电流基准值为3 000A标幺)。
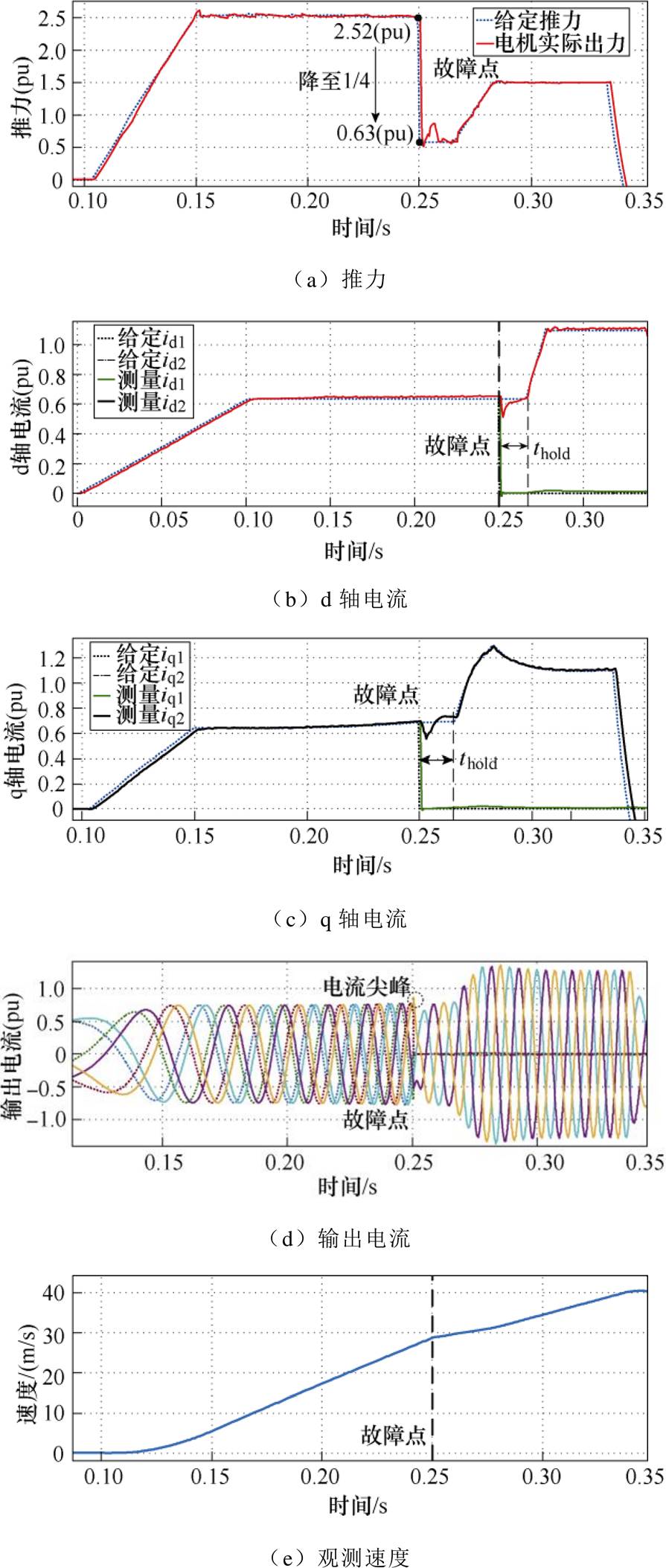
图10 工况二仿真波形
Fig.10 Simulation waveforms of Condition 2
为了验证所提出控制策略的正确性与可行性,搭建了大功率双能量链驱动的短初级双三相直线感应电机实验平台,如图11所示。通过励磁调节器控制发电机为储能单元充电,电机运行时,逆变器输出交流电驱动直线电机,将存储的电能瞬间转化为直线电机的动能。直线电机动子上安装有编码尺,定子上安装有位置传感器,可观测动子的位置,进而计算出速度和加速度。底层控制器将实时采集的数据及状态信息上传给顶层控制器,顶层控制器将采集的位置、电流等数据用于闭环控制的反馈、状态监控以及上传给上位机,上位机可在每次实验之后通过Matlab脚本解析每一次实验的数据。通过更改逆变器底层控制器程序可在固定的时间点模拟制造故障并向顶层控制器上传故障信息,顶层控制器读取到故障信号后执行能量链切换控制算法。
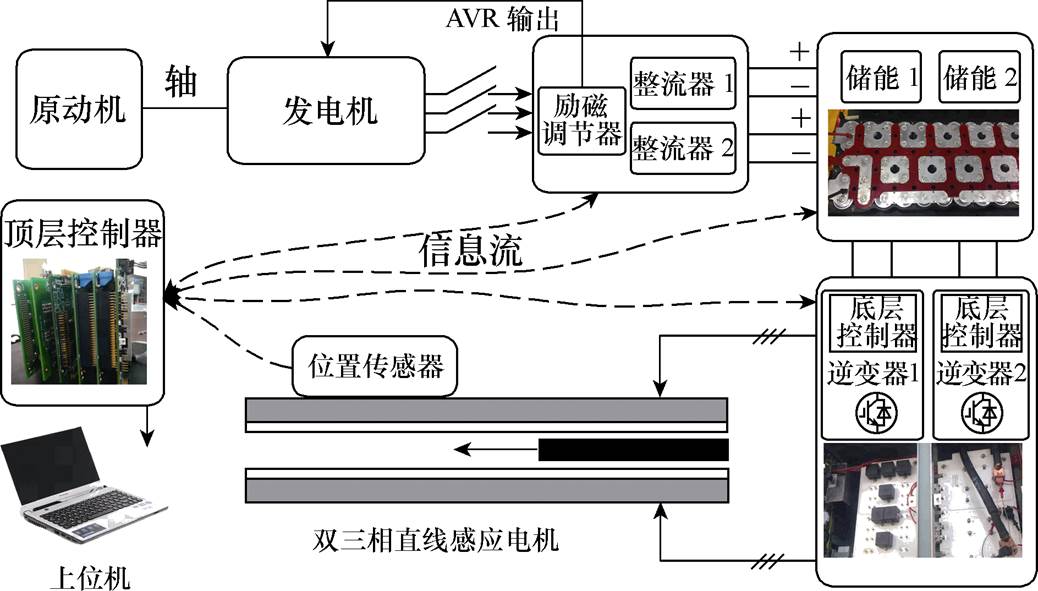
图11 实验平台
Fig.11 Experimental platform
实验工况一:目标速度40m/s,模拟1号能量链故障,故障后矢量控制输入给定推力由位置闭环计算得到,实验参数见表1,工况一实验波形如图12所示。
实验工况二:目标速度40m/s,模拟1号能量链故障,故障后转为外环开环,通过直接计算给定推力作为矢量控制的输入,实验参数见表1,工况二实验波形如图13所示。
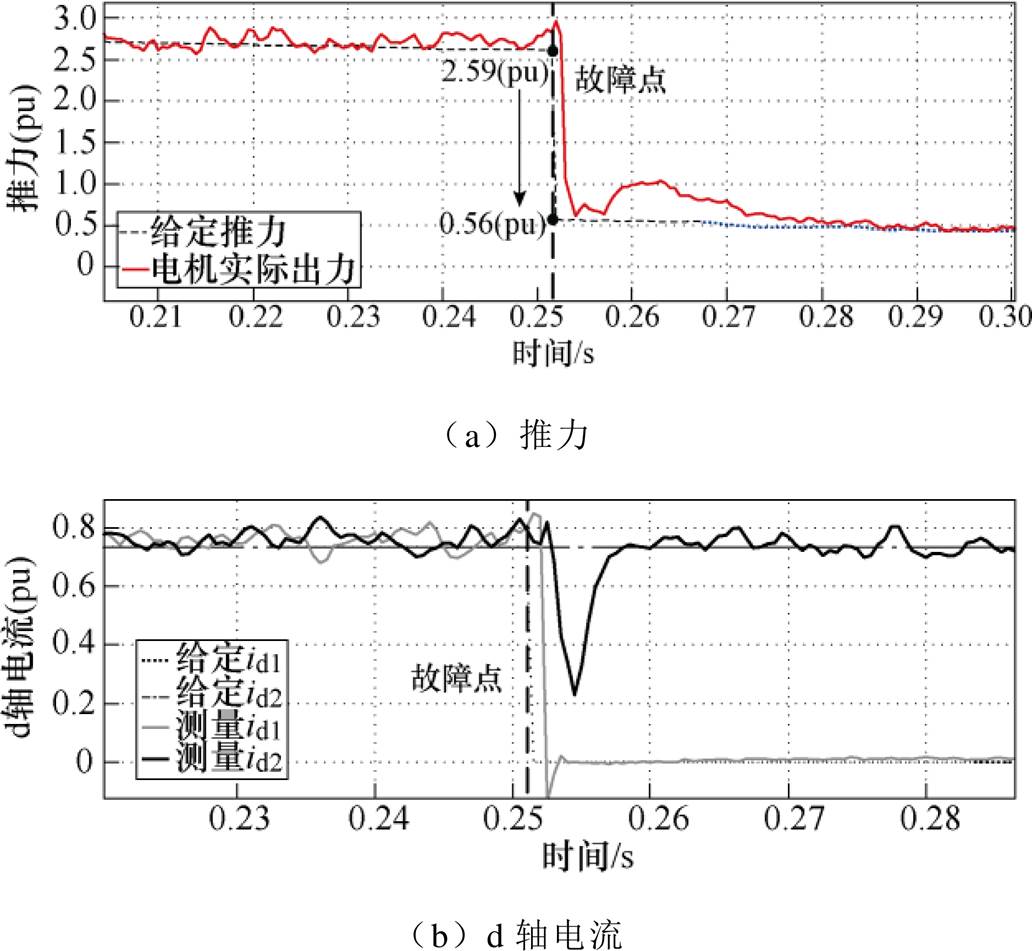
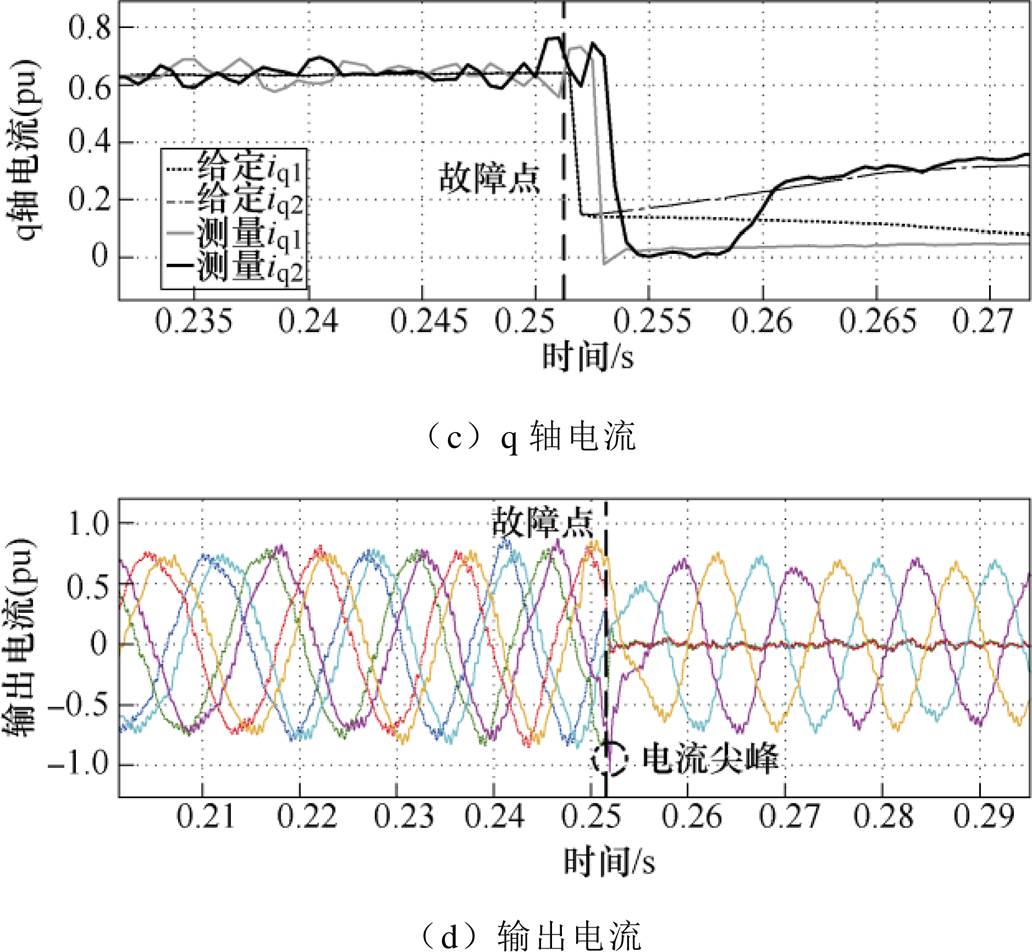
图12 工况一实验波形
Fig.12 Experimental waveforms of Condition 1
图12和图13所示实验结果与仿真相吻合,具体分析不再赘述。由于摩擦力、阻力的补偿值与实际系统相比存在误差,实验推力和输出电流大于仿真。实验结果表明,采用所提出的能量链切换控制策略,能够有效地避免给定电流突变与输出电流尖峰的耦合,相比外环闭环的控制方法,故障时刻的电流尖峰由平均电流的1.32倍降为1.07倍,并且能够在故障后充分利用逆变器的输出能力,实现单能量链的最大推力输出,使电机最终能够达到目标速度(注:实验波形中推力基准值为10 000N,电流基准值为3 000A)。
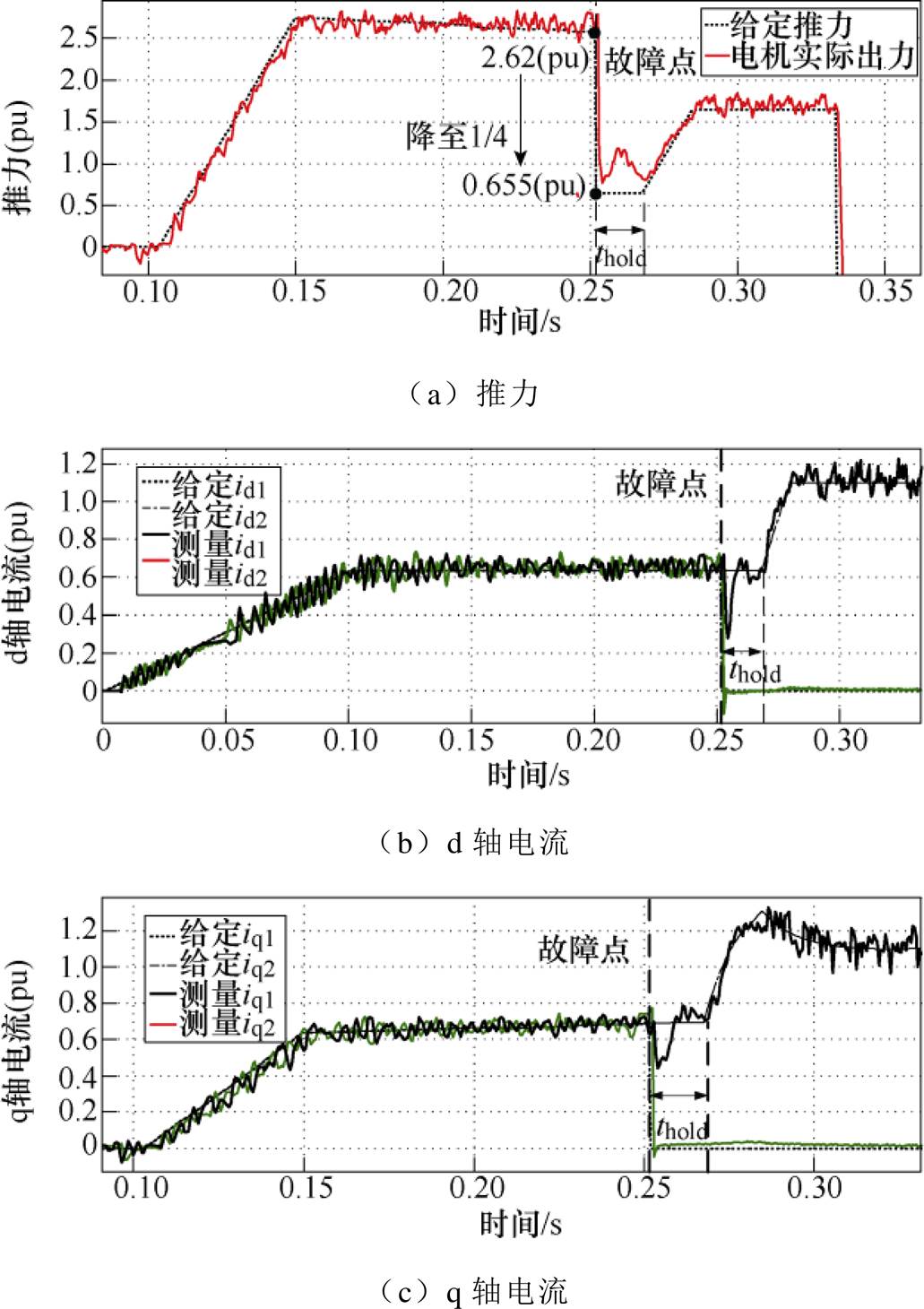
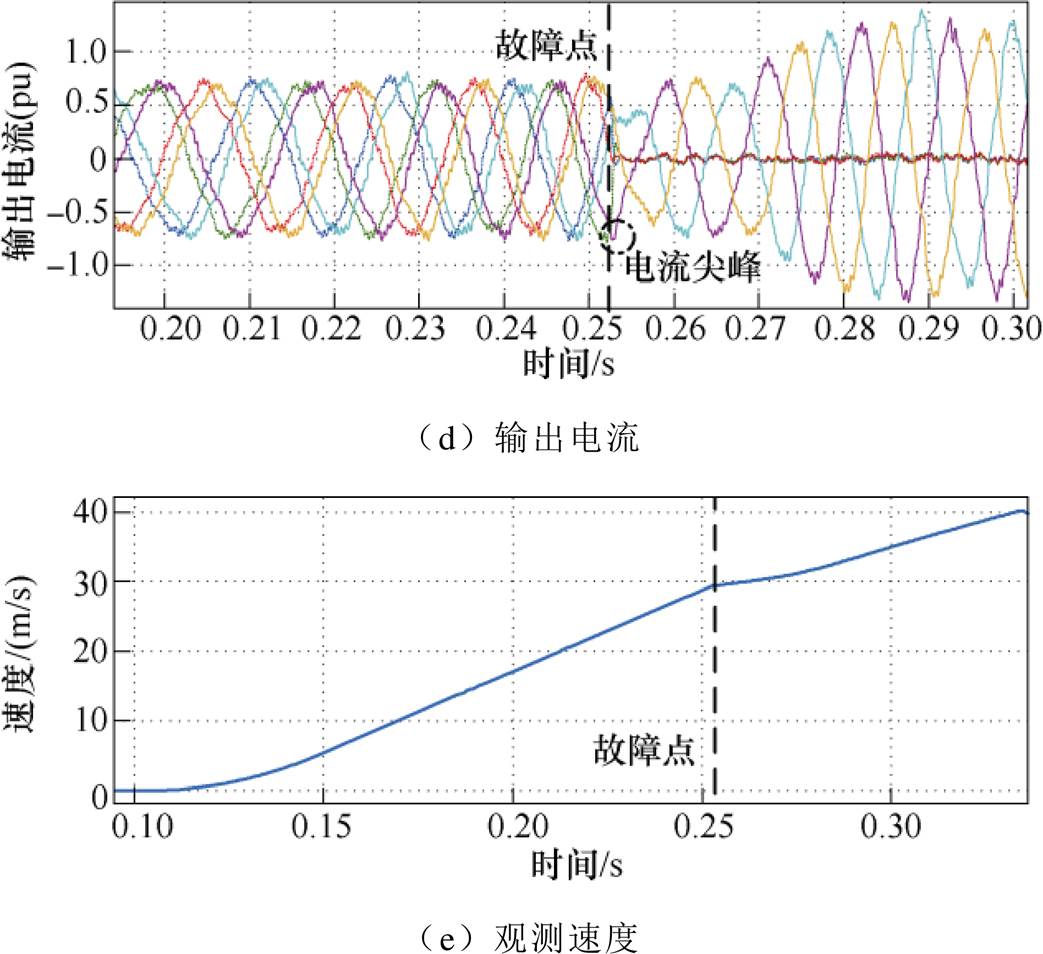
图13 工况二实验波形
Fig.13 Experimental waveforms of Condition 2
本文以考虑动态边端效应的双三相直线感应电机数学模型及矢量控制策略为基础,通过分析和推导指出,在动态边端效应影响下,电机的最大出力随速度的增大而下降,并给出了在能量链故障时电机单能量链最大推力的计算方法。基于此提出一种系统故障后通过外环开环计算给定推力作为矢量控制输入的能量链切换控制策略。仿真和实验结果表明,该控制策略能够避免能量链故障时给定电流变化与输出电流尖峰的耦合,有效地减小非故障能量链输出电流的尖峰。同时,根据控制目标和单能量链的最大推力限制计算故障后矢量控制的给定推力,实现了故障模式下单能量链的安全运行,提高了系统的可靠性。
参考文献
[1] Doyle M, Sulish G, Lebron L. The benefits of electro- magnetically launching aircraft[J]. Naval Engineering Journal, 2000, 112(3): 77-82.
[2] 叶云岳. 直线电机原理与应用[M]. 北京: 机械工业出版社, 2000.
[3] 龙遐令. 直线感应电动机的理论和电磁设计方法[M]. 北京: 科学出版社, 2006.
[4] Duncan J. Linear induction motor-equivalent circuit model[J]. IEE Proceedings, 1983, 130(1): 51-57.
[5] Xu Wei, Zhu Jianguo, Zhang Yongchang, et al. Equivalent circuits for single-sided linear induction motors[J]. IEEE Transactions on Industry Appli- cations, 2010, 6(46): 2410-2423.
[6] Xu Wei, Zhu Jianguo, Zhang Yongchang, et al. An improved equivalent circuit model of a single-sided linear induction motors[J]. IEEE Transactions on Vehicular Technology, 2010, 59(5): 2277-2289.
[7] Xu Wei, Sun Guangong, Wen Guilin. Equivalent circuit derivation and performance analysis of a single-sided linear induction motor based on the winding function theory[J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1515-1525.
[8] Hu Dong, Xu Wei, Dian Renjun, et al. Loss minimization control of linear induction motor drive for linear metros[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 6870-6880.
[9] Wang Ke, Li Yaohua, Ge Qiongxuan, et al. An improved indirect field-oriented control scheme for linear induction motor traction drives[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9928-9936.
[10] Lü Gong, Zeng Dihui, Zhou Tong. An advanced equivalent circuit model for linear induction motors[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(9): 7495-7503.
[11] 马名中, 马伟明, 王公宝, 等. 多定子直线感应电机任务交班控制策略[J]. 电机与控制学报, 2012, 16(3): 1-7.
Ma Mingzhong, Ma Weiming, Wang Gongbao, et al. Assignment alternating strategy of multiple primaries linear induction motor[J]. Electric Machines and Control, 2012, 16(3): 1-7.
[12] 马名中, 马伟明, 范慧丽, 等. 长初级直线感应电机分段供电切换暂态过程[J]. 电机与控制学报, 2015, 19(9): 1-6.
Ma Mingzhong, Ma Weiming, Fan Huili, et al. Switch transient process of section powered long- primary linear induction motor[J]. Electric Machines and Control, 2015, 19(9): 1-6.
[13] Toliyat H A, Lipo T A. Analysis of a concentrated winding induction machine for adjustable speed drive applications-motor analysis[J]. IEEE Transactions on Energy Conversion, 1991, 6(4): 679-683.
[14] Zhao Yifan, Lipo T A. Space vector PWM control of dual three-phase induction machine using vector space decomposition[J]. IEEE Transactions on Indu- stry Applications, 1995, 31: 1100-1109.
[15] Bojoi R, Lazzari M, Profumo F, et al. Digital field- oriented control for dual three-phase induction motor drives[J]. IEEE Transactions on Industry Appli- cations, 2003, 39(3): 752-760.
[16] Bojoi R, Tenconi A, Griva G, et al. Vector control of dual-three-phase induction-motor drives using two current sensors[J]. IEEE Transactions on Industry Applications, 2006, 42(5): 1284-1292.
[17] Che H S, Levi E, Jones M, et al. Current control methods for an asymmetrical six-phase induction motor drive[J]. IEEE Transactions on Power Elec- tronics, 2014, 29(1): 401-417.
[18] 吴一丰, 邓智泉, 王宇, 等. 六相永磁容错磁通切换电机及其单相故障的容错控制[J]. 电工技术学报, 2013, 28(3): 71-79.
Wu Yifeng, Deng Zhiquan, Wang Yu, et al. Six-phase fault-tolerant flux switching permanent magnet motor and control strategy for single-phase fault con- dition[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 71-79.
[19] Tani A, Marri M, Zarri L, et al. Control of multiphase induction motors with an odd number of phases under open circuit phase fault[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 565-577.
[20] Che H S, Duran M J, Levi E, et al. Postfault operation of an asymmetrical six-phase induction machine with single and two isolated neutral points[J]. IEEE Transactions on Power Electronics, 2014, 29(10): 5406-5416.
[21] Betin F, Capolino G A. Shaft positioning for six- phase induction machines with open phases using variable structure control[J]. IEEE Transactions on Industrial Electronics, 2012, 59(6): 2612-2620.
Energy Chain Switching Control of a Dual Three-Phase Linear Induction Motor Operating in Non-Periodic Transient Conditions
Abstract A dual three-phase linear induction motor operating in non-periodic transient conditions driven by two independent energy chains has advantages in power level, power density, freedom degree of control and system redundancy. In this paper, a vector control method is given based on the model of dual three-phase linear induction motor with dynamic end effect. According to the operation characteristics of the non-periodic transient system, an energy chain switching control method under the fault operation condition is proposed, which uses the open-loop calculation of the given thrust as the input of vector control. The proposed method can avoid the coupling of the given current change and the output current peak during the transient processes of system fault. Taking the maximum output thrust constraint with dynamic end effect into consideration, it adjusts the given thrust according to the control target, thereby realizing the safe operation of the single energy chain in case of system failures. Simulation and experimental results verified the correctness and feasibility of the proposed control method.
keywords:Dual three-phase linear induction motor, non-periodic transient, dynamic end effect, energy chain switching, maximum output thrust
中图分类号:TM359
DOI: 10.19595/j.cnki.1000-6753.tces.191604
国家自然科学基金资助项目(51977218)。
收稿日期 2019-11-22
改稿日期 2020-02-28
韩 一 男,1990年生,博士研究生,研究方向为直线感应电机控制技术。E-mail: frankleonhy@163.com(通信作者)
聂子玲 男,1975年生,教授,博士生导师,研究方向为大功率电能变换技术。E-mail: nieziling@163.com
(编辑 陈 诚)