0 引言
功率变换器中的变压器工作在多种励磁状态下,其等效电路模型以及非线性电感、漏感和电容参数影响了功率变换器的仿真精度。尤其在高频电力电子变换器中,变压器往往包含多个绕组,其绕制方法也复杂多样,确定多绕组高频变压器的等效电路模型及参数有一定困难。多年来国内外学者对变压器的精确建模进行了研究。T.Vu基于测量数据分析绕组的非线性特性和建模方法[1]。O.Mohammed通过对双绕组变压器实施电路——有限元的耦合分析提出了变压器模型[2]。Xianming,Deng和C.Park利用有限元方法(Finite Element Method,FEM)研究变压器的等效电路参数,并表明FEM适合分析几何特性复杂的变压器的非线性参数[3-4]。F.Starr和A.Boyajian研究了多绕组变压器等效电路的建模,他们的等效模型被称为星形等效电路[5-6]。星形电路中的元件参数可由端口测试结果确定。星形多绕组变压器模型通常含有负电感,负电感并没有物理意义。在过去的三十年中,负电感也一直被认为是引起数值振荡的原因[7]。事实上,数值振荡问题本质上是由于变压器的励磁支路并未正确连接导致的[8]。
在研究电磁瞬态问题时,BCTRAN是最常用的多绕组变压器,电力系统仿真软件EMTP中包含该模型[9]。该模型在确定参数时是基于端口测量结果计算漏磁阻抗的逆矩阵,从而避免矩阵求逆可能导致的病态矩阵问题。该模型在高频下具有良好的数值稳定性,但BCTRAN变压器模型的缺点在于没有精确考虑变压器的几何形状,且将表征磁心损耗的电阻只是简单地并联到最靠近磁心的绕组的励磁支路上[10]。
对偶模型源于电路和磁路之间的对偶关系,其本质是将回路磁通方程转换为节点电压方程,亦即实现了磁路到电路的转换[11-12]。对偶模型的拓扑较复杂,电路参数数量多,很难根据端口测量结果确定电路参数值,特别是对于包含大量磁化电感分支的多绕组变压器。因此,本文考虑利用数值方法确定电路参数。
无论是端口模型(可以通过端口测量结果反推其参数的模型,例如星形电路和BCTRAN),还是对偶模型,研究人员面临的最大的困难是如何准确地确定等效电路的参数。F.de León提出了一种新的用于低频电磁瞬态分析的多绕组变压器对偶模型[7]。在确定模型的漏感参数时,F.de León的做法是在传统的对偶模型中增加互感和漏感,以此实现利用端口测量的信息确定对偶等效电路模型中的漏感参数。由于传统的对偶模型中的漏感参数无法与多绕组变压器短路测量得到的漏感参数个数相匹配,因此F.de León提出的基于短路测量结果计算互漏感的方法可以解决此问题。然而,对于绕组采用三明治绕法且跨层的多绕组变压器,F.de León的参数确定方法不容易实现。
对于电路模型中的磁化电感,可以利用端口测量信息反推,也可利用解析公式计算,不过两种方法在磁心非线性程度明显时的计算误差会增加[13],尤其在磁心上开有气隙时精度较差。多绕组变压器对偶模型的拓扑复杂、参数多,端口测量信息及解析计算方法都不能确定模型的参数,因此本文提出利用有限元方法确定电路参数。为计算磁化电感,可在一次绕组端口施加多幅值的电流激励,分析不同电流激励下变压器内部的磁场分布,确定变压器磁路中的磁阻与通过的磁通的关系,磁阻的计算方法将在第3节中描述。根据计算的磁阻得到非线性磁化电感。为计算漏感,在所有绕组上施加低幅值激励电流,然后基于磁场能量计算漏感参数,基于电场的数值仿真计算寄生电容参数。
利用本文提出的模型和参数确定方法建立用于反激变换器中的四绕组变压器对偶模型,并将对偶电路仿真结果与多边形模型仿真结果进行比较[14]。将提出的等效电路模型应用于反激变换电路中并进行电路仿真,将电路仿真结果与实验结果进行比较以验证模型的准确性。
1 对偶模型的建立
基于对偶原理建立的电路模型中的电路元件与变压器绕组和磁心有对应的物理关系[12]。在建立对偶模型时,首先需要描绘变压器的集总磁路模型,用集总磁路中的各部分磁阻来表征磁心、绕组和空气中流过的磁通。基于描绘的集总磁路,通过方程转换或者绘图法便可得到电路模型。因此,电路模型中的参数与物理结构一一对应。
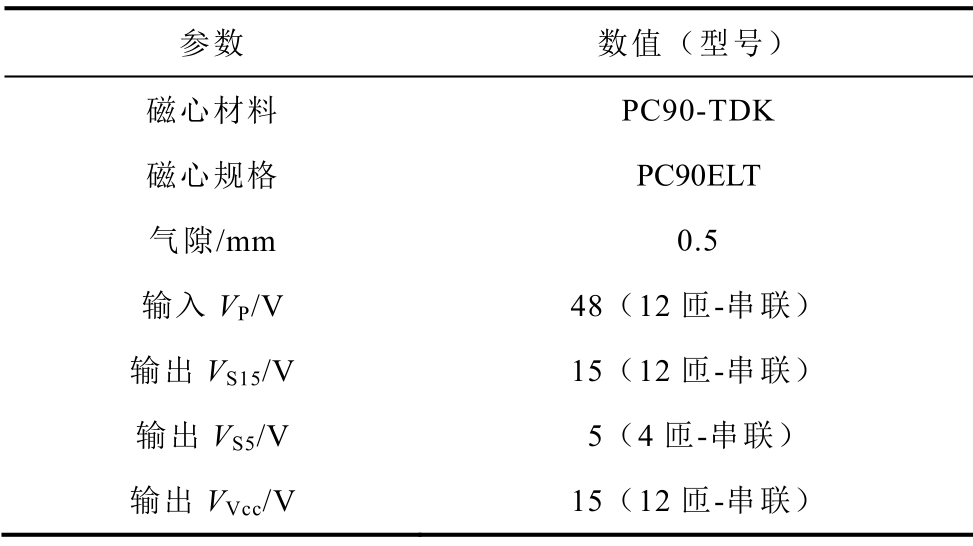
本文以反激变换器中的四绕组变压器为例,阐述等效电路模型的建立方法。四绕组变压器的结构如图1所示,变压器选用平面磁心,以实现紧凑结构设计和工艺稳定性。一次绕组用P48表示,分为四层,采用串联连接;二次绕组用S15、S5和Vcc15表示,分别由两层线圈串联连接。表1给出了四绕组变压器的参数。磁心选用牌号为PC90的铁氧体材料,当频率小于1MHz且温度在40~280℃范围时,该材料具有相对稳定的磁导率和较低的损耗。用于反激变换器拓扑结构的变压器应具有存储能量的能力,为避免磁心饱和,布置0.5mm的气隙。绕组印制在印制电路板(Printed Circuit Board,PCB)中,以提高变换器的功率密度。

图1 四绕组反激变压器模型与结构
Fig.1 Prototype and model of a four-winding fly-back transformer
表1 四绕组变压器参数
Tab.1 Specifications of the four-winding transformer
多绕组变压器的磁路拓扑如图2所示。其中,流经磁心柱的磁通路径用Rm表示,流经铁轭的磁通路径用Rmu和Rmd表示;流经气隙的磁通路径由Rmair表示;漏磁通路径由R1~R8表示。由于中间两层绕组是串联连接,可忽略它们之间的漏磁通。由磁路转换为电路时,在每个磁阻上设置电感,并在磁路的每个网格中设置节点[12],进而得到如图3所示的对偶电路模型。其中,磁化电感用Lm表示,漏感用L表示。将绕组之间的寄生电容加到相应的绕组间。
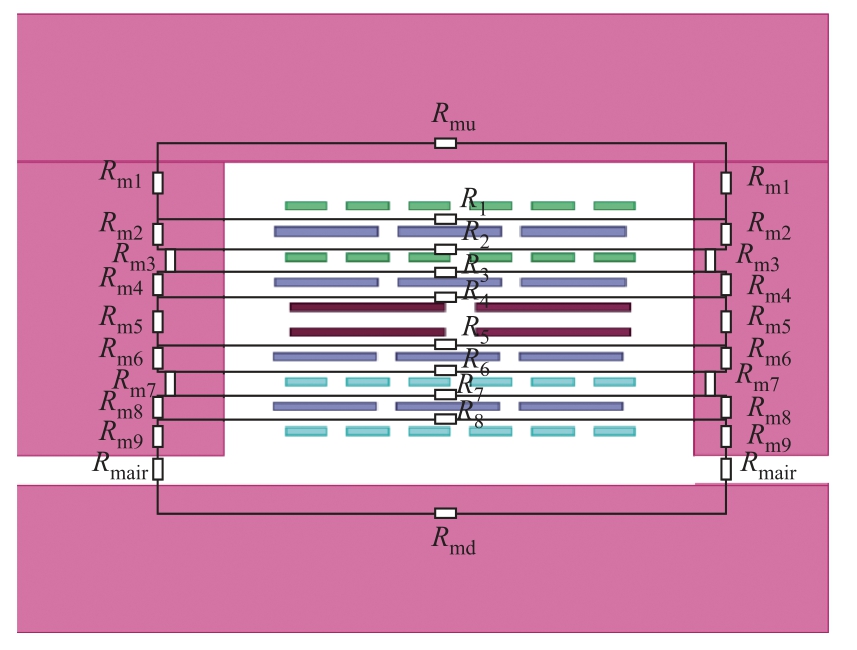
图2 多绕组变压器磁路拓扑
Fig.2 Reluctance circuit for the multi-winding transformer
2 模型参数确定
得到图3所示的电路模型后,需要确定模型参数,包括磁化电感、漏感、电容参数。磁心损耗不是本文研究的重点,故在图3中并未给出表征磁心损耗的电阻。对于考虑磁心损耗的情况,将表征磁心损耗的电阻与各磁化电感并联即可。考虑利用有限元数值方法分析平面变压器的磁场和电场,基于磁场的分布确定图3中所示的磁化电感和漏感,基于电场分布确定分布电容参数。
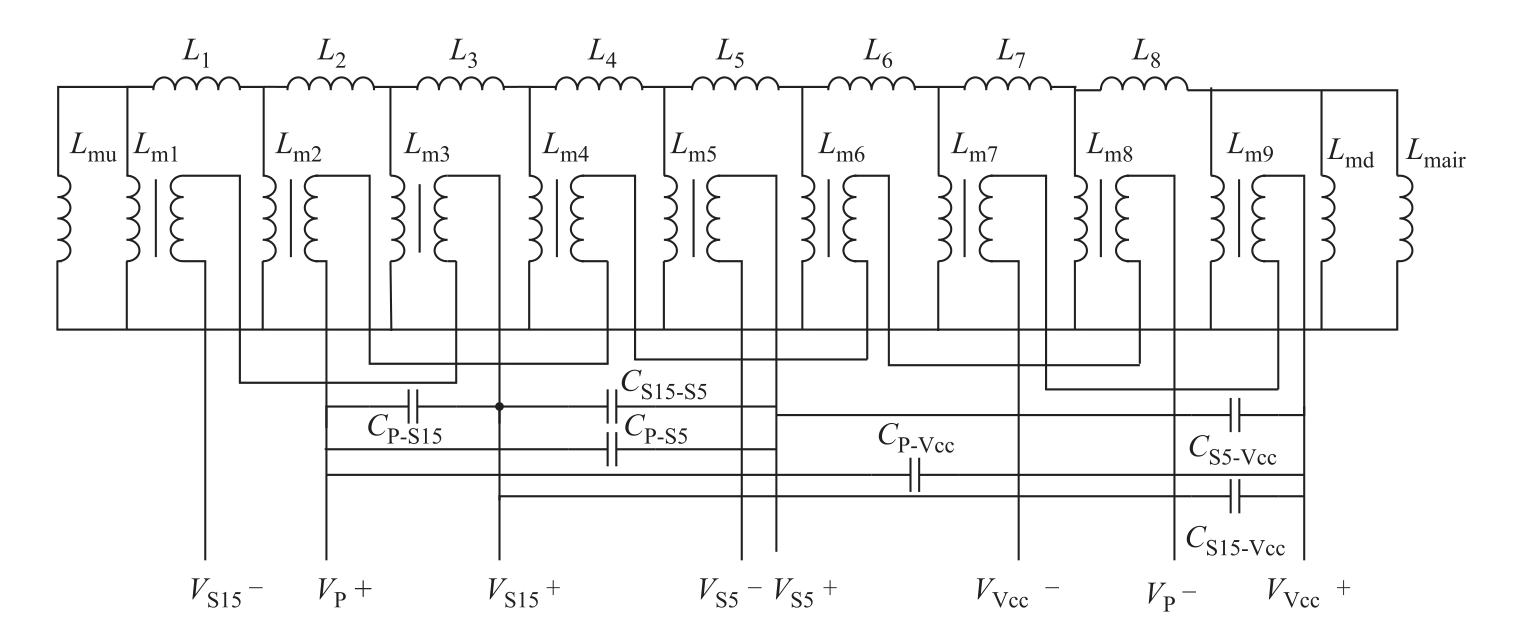
图3 基于对偶关系的电路模型
Fig.3 Equivalent electric circuit based on the principle of duality
2.1 磁化电感参数的确定
由于端口的测量信息不足以确定多个磁化电感,因此考虑先确定各个磁阻值,再转换得到电感值。在确定磁阻参数时,可利用有限元数值计算的磁场分布结果计算磁阻。
建立三维变压器模型,设置磁心材料时选择温度为100°C时的单极磁化曲线。在初级绕组端口施加电流激励。得到的磁场能量密度如图4所示,磁感应强度如图5所示。图4中,变压器磁心被分成多个部分,同时各部分磁阻的磁通积分面如图5所示。利用各部分磁阻内部的磁场能量W和流过磁阻的磁通Φ计算磁阻值为
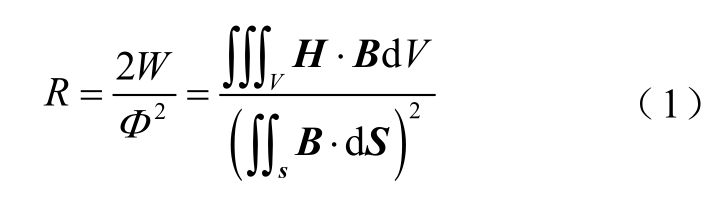

图4 四绕组变压器内部的磁场能量密度
Fig.4 Magnetic energy density of the four-winding transformer

图5 磁感应强度的分布
Fig.5 Distribution of the magnetic flux density
在式(1)中,通过对磁心各部分的能量进行积分计算磁场能量W,通过对磁心各部分中间横截面的磁感应强度进行积分近似计算流经磁阻的磁通Φ。
表2所示为激励电流等于4A时磁心各部分磁阻Rmi的磁场能量Wmi。表3所示为在此激励下流经各部分磁阻的磁通Φmi。此激励下各个磁阻的Rmi值见表4。相应的磁化电感Lmi计算式为
表2 各部分磁阻的能量
Tab.2 Energy of each section

表3 积分截面的磁通
Tab.3 Flux of the integral surface

表4 多绕组变压器的磁阻
Tab.4 Reluctance of the multi-winding transformer


式中,N为已转换为一次绕组的匝数,计算的磁化电感见表5。
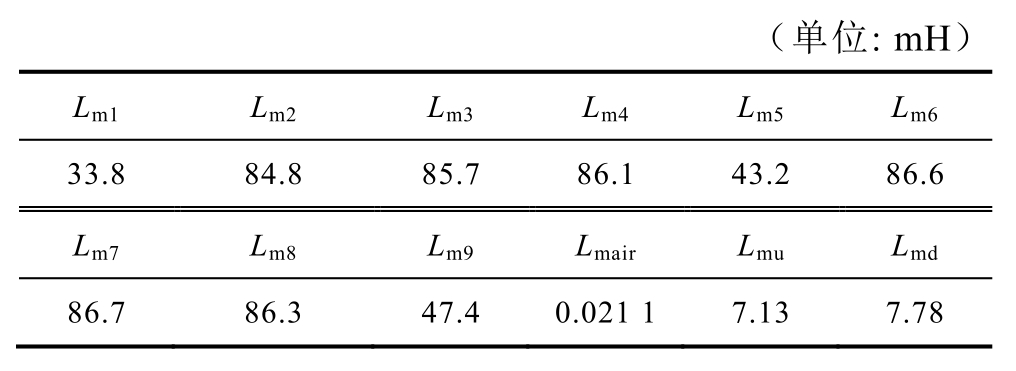
表5 额定电流下变压器的电感
Tab.5 Magnetizing inductance of the multi-winding transformer when applying rated current
由于磁心的非线性特性,当励磁电流变化时,磁阻的值随磁通量变化。因此,假如端口施加不同的激励电流,就可得到磁阻和磁通之间的非线性关系。非线性磁阻可以用以磁通为自变量的函数来表示,然后,经过转换可得到以电流为自变量的非线性磁化电感。图6给出了几个典型的非线性电感。非线性电感可由Φ和i之间的关系表示。本质上,本文在确定变压器等效电路参数的非线性曲线时,使用的是“打点法”,即每施加一个幅值一定的直流电流进行静态场分析,可得到“非线性曲线上的一个点”。通过分析多个幅值下的磁场获得多个点,进而描述非线性曲线。静态场的单点分析可保证较高的精度。
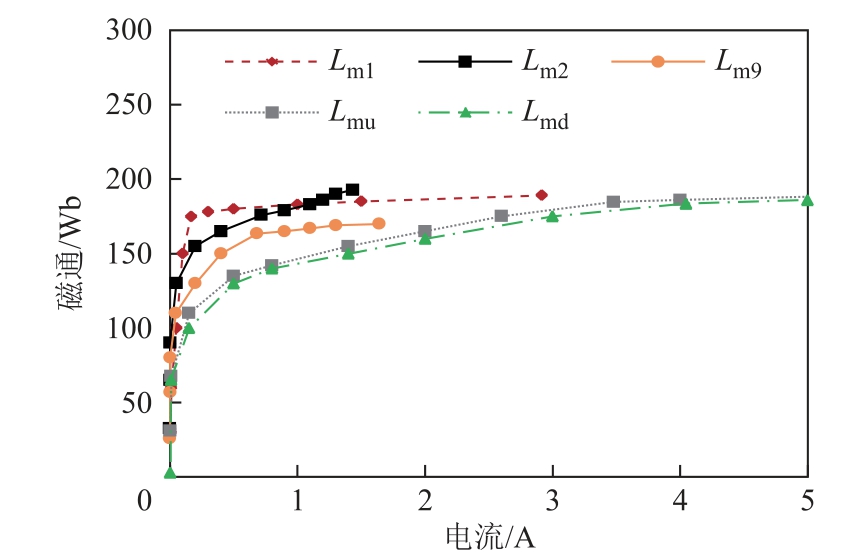
图6 典型电感的非线性曲线
Fig.6 Nonlinear curves for several typical inductances
本文提出的确定参数的方法没有在激励方式中体现频率对模型参数的影响,但在数值仿真的材料设置时体现了频率的影响。频率对参数的影响体现在对磁心和导线的影响。磁心的磁化曲线和损耗曲线都随着频率变化,本文在用数值仿真确定参数时,设置的磁心材料曲线为表6所示的非线性曲线(频率为100kHz),以提高参数在高频时的准确性。
表6 磁心磁化曲线的典型数据
Tab.6 Typical data of magnetization curve of the core

2.2 漏感参数的确定
对于传统的变压器,漏感通常通过变压器端口的短路测试获得。对于含有N个绕组的变压器,存在N(N-1)/2对不同的短路情况。对于四绕组变压器,通过短路测试可获得六个漏电感,见表7。然而,绕组之间的这六个漏电感不能直接与图3中所示的八个漏感匹配。为了解决这个问题,可使用耦合电感将测得的漏电感与对偶模型中的漏电感匹配[7]。然而,漏感的这种表示方法并不适用于包含跨层绕组结构的变压器。
表7 短路测量的绕组间漏感
Tab.7 Leakage inductances between windings obtained by short-circuit tests

本文考虑利用数值计算确定变压器模型的漏感参数。在一次绕组和二次绕组同时施加激励电流,保持一次绕组和二次绕组的磁通势相同。设置一次绕组的励磁电流为3A,二次绕组S15、S5和Vcc的励磁电流分别为1A、3A和1A。变压器中的漏磁能量分布如图7所示,同时漏磁能量值Wi在表8中给出。由于层间绝缘介质的磁阻远大于铁氧体磁心,因此可认为磁通势全部集中在绝缘介质的磁阻上。基于漏磁能量和磁通势,可以得到层间的漏电感。将层间漏感Li转换到一次侧,其值见表9。

图7 漏磁能量分布
Fig.7 Distribution of the leakage energy
表8 漏磁部分的能量
Tab.8 Energy of each leakage region

表9 层间漏感
Tab.9 Leakage inductance between layers

得到磁化电感和层间漏感后,可对图3所示的等效电路进行电路仿真。对几个绕组的端口分别设置短路,利用电路仿真可以模拟端口试验,据此可以得出绕组之间的漏电感。例如,如果对一次绕组P施加电压激励并使绕组S15短路,同时保持绕组S5和绕组Vcc断开,则可以获得绕组P和绕组S15之间的漏电感。变压器中有四个绕组,最终可在绕组之间获得6个漏电感,见表10中第三行所示。将变压器端子上的短路测试结果列于表10第二行。比较发现,模拟和测试的结果之间的差异低于7%。通过这种方式,也验证了数值计算确定的漏感值的准确性。
表10 四绕组之间的漏感
Tab.10 Leakage inductances between 4 windings

2.3 分布电容参数的确定
多绕组变压器的分布电容包括接地磁心和绕组之间的电容、绕组之间的电容及同一绕组各层之间的电容。确定电容参数时可用能量法,即根据变压器中的电场能量计算寄生电容参数。利用三维有限元法仿真分析变压器内部的电场,电场能量分布的情况如图8所示,进而确定四绕组之间分布电容参数,见表11。
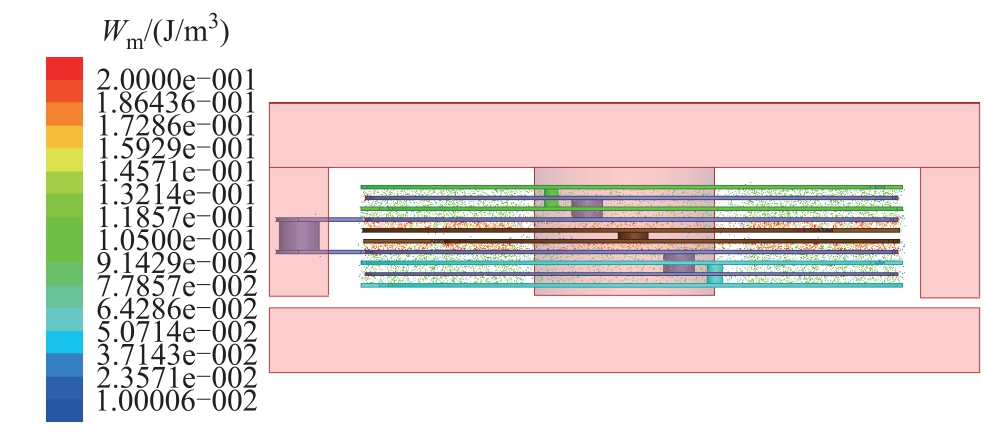
图8 四绕组变压器内部的电场能量密度
Fig.8 Electric energy density of the four-winding transformer
表11 绕组间电容
Tab.11 Capacitances between windings

3 模型的验证
3.1 对偶电路仿真与场路耦合仿真的比较
由于在场路耦合分析时,变压器的瞬态场数值计算中不能考虑内部的寄生电容,所以为了保持一致性,在利用场路耦合的分析结果验证电路模型时,电路仿真并未考虑图3中的各个电容分支。利用场路耦合分析的结果仅可验证对偶等效电路中电感参数的准确性。
仿真时,变压器的一次侧由脉冲电压源(100kHz,15V)供电。图9所示为场路耦合和对偶模型得到的输出波形,匹配良好的前沿波形说明了等效电路中励磁电感和漏电感具有较好的精度。
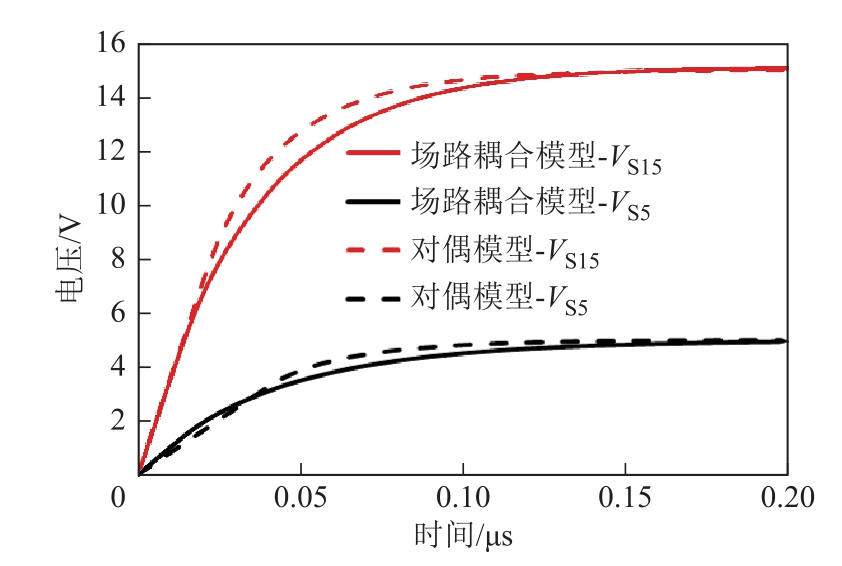
图9 场路耦合模型和对偶模型仿真得到的输出波形
Fig.9 Output waveforms obtained by the field-circuit coupled analysis and the duality model simulations
3.2 对偶电路仿真与多边形模型仿真的比较
图10中所示为四绕组变压器的多边形模型,利用端口的测试结果可确定多边形模型中的电感值,电容值可直接采用有限元分析得到的分布电容值[15-17]。如图10中所示,多边形模型的电感参数存在负值,这是由端口结果反推产生的,没有物理意义,负电感在一些情况下会导致复杂电路仿真发生振荡。
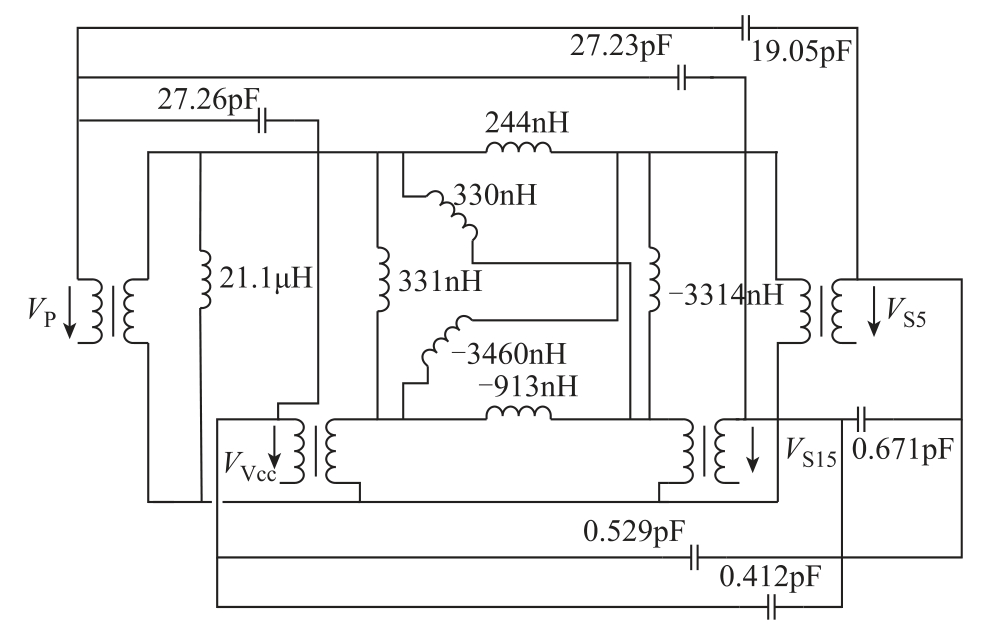
图10 四绕组变压器的多边形模型
Fig.10 Polygon model for the four-winding transformer
在变压器的一次侧设置脉冲电压源(100kHz,15V),比较包含电容的对偶模型的电路仿真结果与多边形模型的仿真结果。图11所示为两种模型的输出波形,波形的过冲匹配良好。由于漏感和寄生电容是影响过冲的关键参数[18-19],因此匹配良好的过冲波形验证了等效电路中的漏感和电容参数的精度。
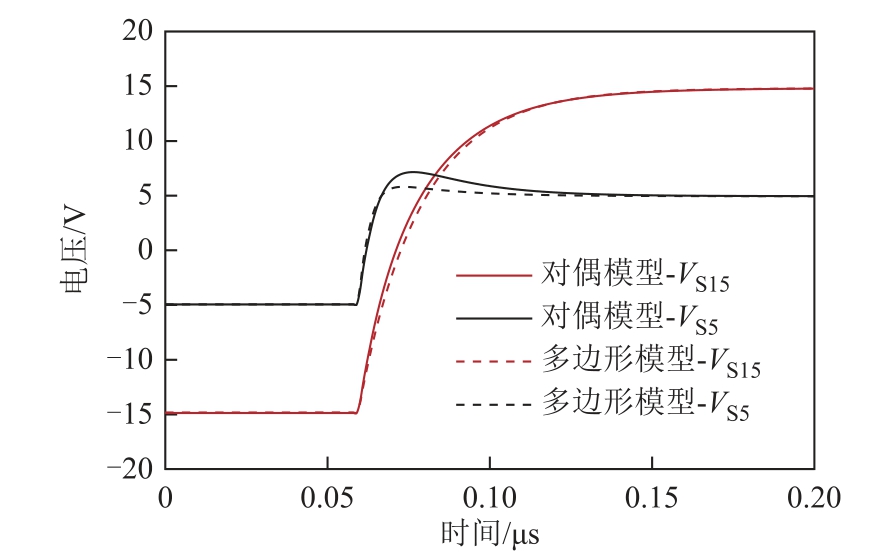
图11 多边形和对偶模型仿真得到的输出波形
Fig.11 Output waveforms obtained by the polygon model and the duality model simulations
3.3 对偶模型在反激变换器中的应用
本文搭建了一个反激变换器以验证对偶模型的适用性。反激变换器的电路拓扑如图12所示。激励源是输出为48V的直流电源。剩余电流装置(Residual Current Device,RCD)吸收电路中的电容为1nF,吸收电阻为500Ω。变换器设置在非连续导通模式(Discontinuous Conduotion Mode,DCM)下工作,占空比设置为0.26。三个二次绕组的负载设置分别为RS5=10Ω,RS15=19Ω,RVcc=19Ω。图13给出部分试验结果,包括MOSFET的漏极和源极之间的电压Vds和一次电流iP。图14是等效电路拓扑的仿真结果,其与测量结果的一致性好。
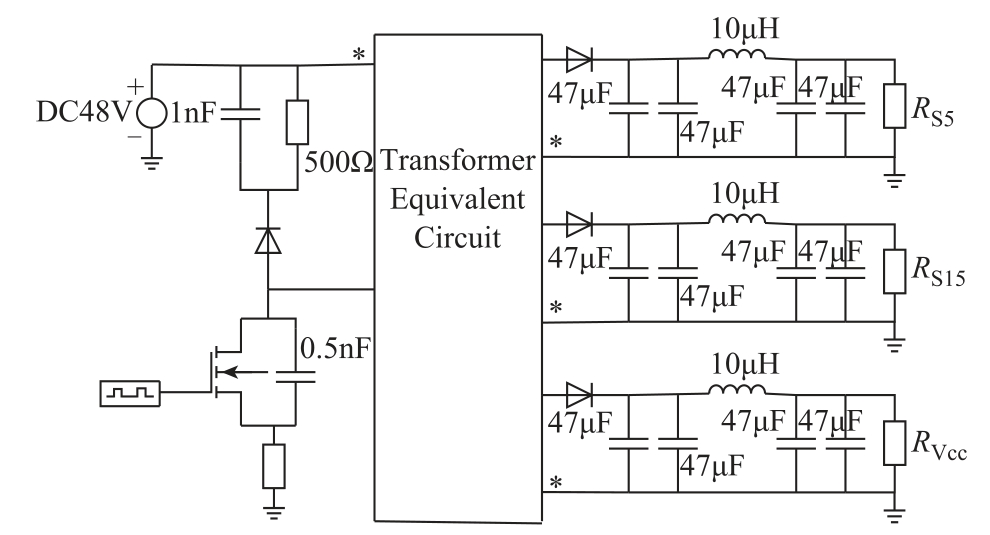
图12 验证对偶模型的反激变换电路
Fig.12 Circuit prototype of a fly-back converter for verification of the duality model
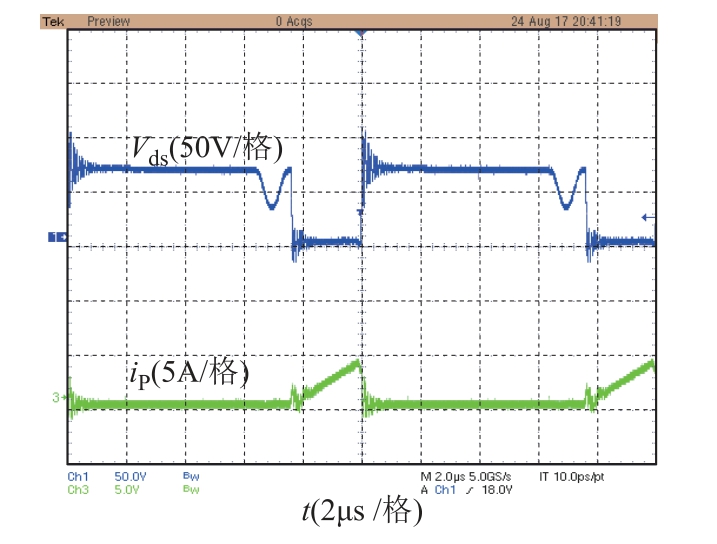
图13 DCM状态下测量的电压Vds
Fig.13 Measured voltage Vds under DCM
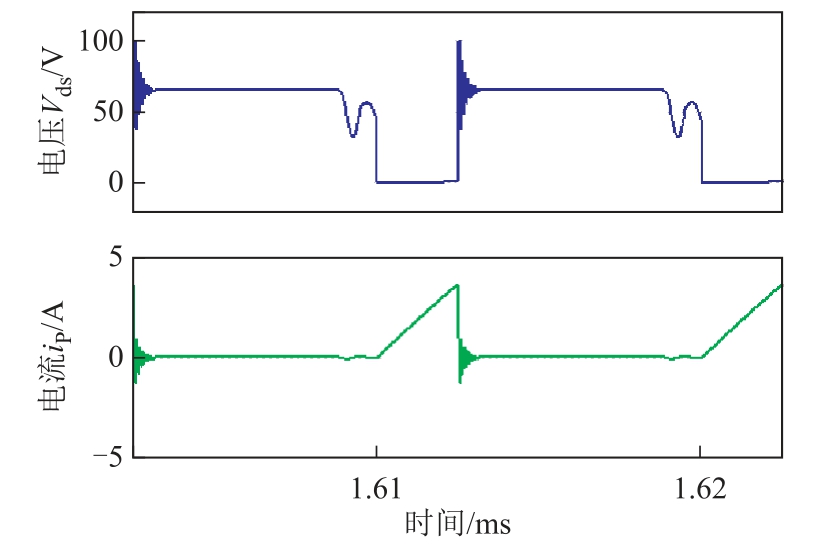
图14 DCM状态下电路仿真得到的电压Vds
Fig.14 Simulated voltage Vds under DCM
当MOSFET关断时,流过漏感的电流不会突然改变,电流的变化将产生感应电动势。如测量和仿真结果所示,当MOSFET关断时,由于感应电动势和二次反射电压,Vds远大于48V的输入电压。存储在漏感中的能量将通过RCD吸收电路释放[20]。图15比较了MOSFET关断时Vds前沿波形的过冲和振荡。关断MOSFET时,Vds的过冲和振荡与漏感和寄生电容参数密切相关。因此,比较测量和仿真得到的Vds的过冲波形,可以验证对偶变压器等效电路的有效性。观察到测量和模拟结果在幅度和振荡周期中匹配得较好,电路仿真波形振荡时间比测量波形略短,其振荡的阶数比测量结果略低。提出的高阶等效电路模型及参数确定方法在分析高频问题时可保证较好的准确性。

图15 测量结果和仿真结果的比较
Fig.15 Comparison of measured and simulated waveforms
此外,在MOSFET导通之前,二次电流已降至零,Vds大于输入电压。它使MOSFET的结电容和磁化电感产生共振。从图13和图14中可以看出,在MOSFET导通之前Vds波形在衰减系数和频率方面略有不同。这是因为未能精确地估计MOSFET的漏极-源极电容和引线电感。
4 结论
本文提出了应用于功率变换器中的多绕组且含跨层绕组结构时高频变压器的等效电路模型,并提出了利用有限元场分布结果确定非线性电感、漏感及电容参数的方法。提出的方法很好地解决了跨层绕组的参数确定问题。通过与多边形模型仿真及试验分析结果的比较验证了多绕组高频变压器等效电路的准确性。本文为对偶模型在多绕组高频变压器的应用提供了方法基础。
[1] Vu T,Driscoll S,Ringwood J.Nonlinear dynamic transformer time-domain identification for power converter application[J].IEEE Transactions on Power Electronics,2014,29(1):318-327.
[2] Mohammed O,Liu Z,Liu S.Finite-element-based nonlinear physical model of iron-core transformers for dynamic simulations[J].IEEE Transactions on Magnetics,2006,42(4):1027-1030.
[3] Deng Xianming,Cheng En,Liu Na.A novel transformer with adjustable leakage inductance[J].International Journal of Applied Electromagnetics and Mechanics,2017,55(S1):1-14.
[4] Park C,Lee H,Lee B.A study on the design parameters of inductive power transformers[J].International Journal of Applied Electromagnetics and Mechanics,2012,39(4):809-815.
[5] Starr F.Equivalent circuits—I[J].Transactions of the American Institute of Electrical Engineers,1932,51(2):287-298.
[6] Boyajian A.Theory of three-circuit transformers[J].Transactions of the American Institute of Electrical Engineers,1924,23:508-529.
[7] Álvarez-Mariño C,de León F,López-Fernández X M.Equivalent circuit for the leakage inductance of multiwinding transformers:unification of terminal and duality models[J].IEEE Transactions on Power Delivery,2012,27(1):353-361.
[8] Jazebi S,Zirka S E,Lambert M,et al.Duality derived transformer models for low-frequency electromagnetic transients part I:topological models[J].IEEE Transactions on Power Delivery,2016,31(5):2410-2419.
[9] Brandwajn V,Dommel H W,Dommel I I.Matrix representation of three-phase N-winding transformers for steady-state and transient studies[J].IEEE Transactions on Power Apparatus and Systems,1982,101(6):1369-1378.
[10] 陈彬,李琳,赵志斌.双向全桥DC-DC 变换器中大容量高频变压器绕组与磁心损耗计算[J].电工技术学报,2017,32(22):123-133.
Chen Bin,Li Lin,Zhao Zhibin.Calculation of highpower high-frequency transformer's copper loss and magnetic core loss in dual-active-bridge DC-DC converter[J].Transactions of China Electrotechnical Society,2017,32(22):123-133.
[11] Cherry E C.The duality between interlinked electric and magnetic circuits and the formation of transformer equivalent circuits[J].Proceedings of Physics Society,1949,62(2):101-111.
[12] Slemon G R.Equivalent circuits for transformers and machines including nonlinear effects[J].Proceedings of the IEE-Part IV:Institution Monographs,1953,100(5):129-143.
[13] Pedra J,Corcoles F,Sainz L,et al.Harmonic nonlinear transformer modeling[J].IEEE Transactions on Power Delivery,2004,19(2):884-890.
[14] Blume L F,Boyajian A,Camilli G,et al.Transformer Engineering[M].NewYork:Wiley,1951.
[15] Starr F.An equivalent circuit for the four-winding transformer[J].General Electric Review,1933,36(3):150-152.
[16] Aicher L C.A useful equivalent circuit for a fivewinding transformer[J].Electrical Engineering 1943,62(2):66-70.
[17] de León F,Martinez-Velasco J A.Dual three-winding transformer equivalent circuit matching leakage measurements[J].IEEE Transactions on Power Delivery,2009,24(1):160-168.
[18] 高志刚,冬雷,李永东,等.基于高频变压器的背靠级联 H桥型变换器[J].电工技术学报,2013,28(6):122-128.
Gao Zhigang,Dong Lei,Li Yongdong,et al.Research on back to back cascaded H-bridge converter based on high frequency transformer[J].Transactions of China Electrotechnical Society,2013,28(6):133-138.
[19] 刘树林,曹剑,胡传义,等.正-反激组合变换器的能量传输模式及输出纹波电压分析[J].电工技术学报,2019,34(8):1648-1656.
Liu Shulin,Cao Jian,Hu Chuanyi,et al.Energy transmission modes and output ripple voltage of forward-flyback converter[J].Transactions of China Electrotechnical Society,2019,34(8):1648-1656.
[20] 黄阳强,许建平,殷刚,等.准谐振软开关双管反激变换器[J].电工技术学报,2018,33(18):4314-4322.
Huang Yangqiang,Xu Jianping,Yin Gang,et al.Quasi-resonant soft-switched two-switch flyback converter[J].Transactions of China Electrotechnical Society,2018,33(18):4314-4322.