0 引言
随着高压直流输电系统容量的不断提升，换流变压器的安全稳定运行就显得十分重要。不同于交流变压器，换流变压器正常工作时绕组中将有高次谐波电流流过，因此其负载损耗的计算将更加复杂[1]。其中安装于铁心主柱叠片最外层起到承重作用的拉板，其表面漏磁将远大于油箱、夹件等结构件，因此虽然拉板损耗占总的负载损耗比例并不大，但由于高入射磁通密度和较差的冷却条件，局部温升会非常高[2]。如果不能精确地计算换流变压器负载电流中各次谐波电流造成的拉板损耗，就可能导致对热点温升的低估，进而引起拉板附近的绝缘材料老化[3]，严重影响换流变压器的寿命和使用。
目前针对变压器拉板损耗的最新研究比较少。文献[4]假设低压绕组内表面的磁场强度沿着拉板高度的方向在空间中呈周期性正弦变化，结合试验数据给出了拉板损耗的解析公式。为了更加精确地计算拉板损耗并对拉板开槽的影响进行分析，文献[5]运用2D/3D有限元法，量化了不同因素对拉板损耗的影响，并对不同材料、不同开槽的数量、宽度下涡流的路径进行了深入的分析。文献[6]则在文献[5]的基础上以降低拉板损耗为目的，对拉板的结构进行了优化设计。文献[7]针对换流变压器拉板开槽的特殊性，分析了拉板开全槽和半槽对其损耗计算结果的影响。然而上述研究都是针对拉板基波损耗，没有考虑换流变压器中高次谐波电流对拉板损耗的影响。
换流变压器额定负载电流中含有大量谐波成分，如果知道损耗与电流频率的关系，就可以依据基波损耗快速计算出总的谐波损耗。文献[8-11]最早提及换流变压器损耗频率特性，通过实测数据的分析，其分别认为换流变压器结构件损耗的频率指数为0.9、1、1.4和1.5。2017年，IEEE—60076—57—129标准中制定了HVDC换流变压器负载损耗的计算方法，该标准假设换流变压器中结构件杂散损耗与电流的二次方成正比，与频率的0.8次方成正比。文献[12]则基于Problem21系列基准模型，以实验的形式分别研究了换流变压器油箱、夹件、拉板等结构件各自的谐波损耗频率特性，文献[12]认为拉板损耗的频率指数为1.5。文献[13]对比研究了谐波电流对导磁和非导磁结构件杂散损耗的影响。但上述研究不是没有专门针对拉板损耗进行研究，就是没有理论依据。
因此本文结合拉板表面磁场分布的特点，简化磁场方程，推导了拉板损耗的计算公式。通过公式分析，得到不同拉板开槽情况下，其损耗频率指数变化规律和范围大小。为了验证理论分析的正确性并进一步确定实际拉板损耗计算的频率指数数值，针对一台800kV特高压换流变压器拉板损耗进行了有限元仿真计算。结果表明，拉板开槽在减小基波损耗的同时还会增加高次谐波损耗，导致其损耗频率指数的大幅增加。实际计算中可取数值1.5，远大于不开槽时的数值0.6。该结论可为快速准确地计算换流变压器负载情况下拉板损耗提供理论依据。
1 拉板涡流损耗模型
换流变压器拉板安装在铁心主柱叠片最外层，面向网侧绕组的内表面。漏磁通从网侧绕组端部径向离开，近似垂直地射入拉板中，因此拉板的涡流损耗主要集中在与绕组端部平齐的位置，且沿着拉板宽度方向的中心轴左右对称分布。换流变压器拉板为不锈钢材料，磁导率远小于铁心硅钢片，再加上其厚度很薄，所以可以假设磁场垂直穿透拉板进入铁心。基于实验数据，拉板表面的磁场强度沿着它的长度方向在空间中呈正弦变化[4]，在磁场最大值附近可认为其为二次函数分布。图1为简化的拉板涡流损耗分析模型，x、y、z分别为拉板厚度、长度、宽度方向，b为拉板宽度数值的一半。
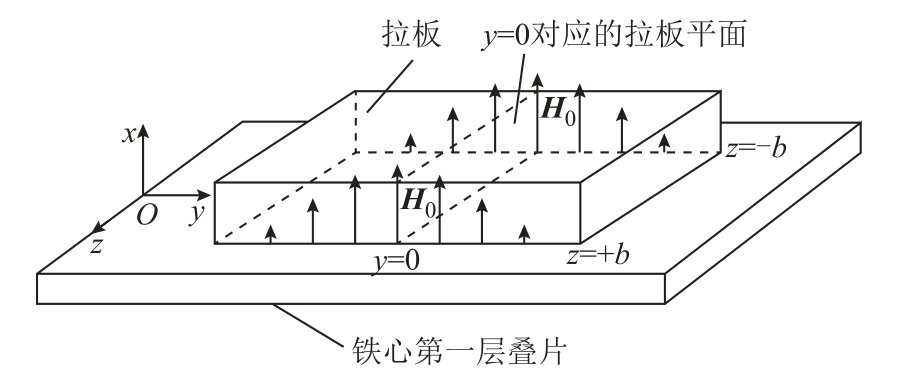
图1 拉板涡流损耗分析模型
Fig.1 Eddy current loss analysis model of flitch plate
准静态电磁场方程为
式中，μ、σ 分别为拉板的磁导率和电导率，均为常数；H为磁场强度的向量形式。假设正弦变化的拉板表面磁场强度H只有x方向，且仅为y、z方向的函数。式（1）可化简为
式中，j为虚数单位；ω为角频率。因为x方向磁场强度Hx沿着y轴长度方向呈二次函数分布，所以其二阶导数为常数，假设Hx对y的二阶导数在z方向随着磁场强度Hx线性变化。磁场强度在y方向最大值位置（低压绕组端部水平对应的拉板左右两侧，y= 0，z=±b）的峰值为H0。此时式（2）可进一步化简为
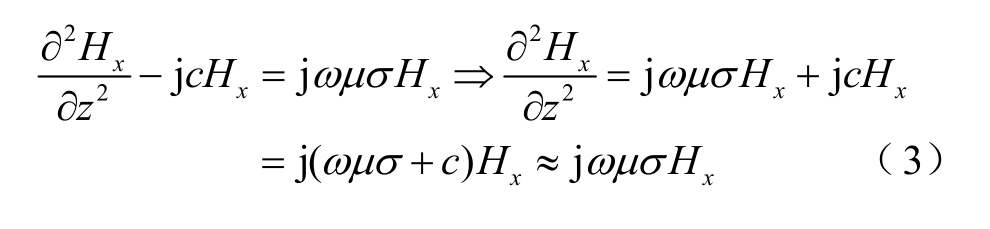
式中，c为正常数，由于拉板的长度远大于趋肤深度，因此在数值上，ωμσ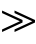
c，即忽略磁场强度Hx在y方向变化的影响。此时方程变成一元二阶微分方程，形式上与绕组的涡流损耗方程一致[14-15]。结合边界条件：y=0,z=±b时 Hx=H0，可解得Hx为
式中，δ为趋肤深度，
。
因为在y方向上Hx呈正弦变化，变化率很小且与频率无关，因此拉板的总损耗频率特性和y=0对应的拉板平面的损耗频率特性一致。所以只需分析计算y=0拉板平面单位厚度上的损耗 Ps即可。
将式（6）代入到式（5），化简可得
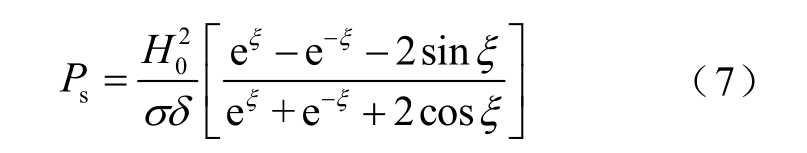
式中，ξ为归一化拉板宽度，ξ= 2b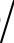
δ。
2 拉板损耗频率特性理论分析
IEEE标准中推荐使用式（8）计算换流变压器结构件损耗。
式中，PSE为结构件损耗；PSE1r为基频测量损耗；I1r为基频测试电流；f1为基波频率；h为谐波次数。Ih、fh 分别为对应谐波的电流和频率。使用该公式可以快速计算任意负载电流频谱下的换流变压器结构件损耗。对于拉板损耗而言，由于磁场强度与电流数值成正比，由式（7）可知拉板损耗电流指数为2，这与式（8）中给出的数值一致。但该公式中给出的损耗频率指数为0.8，是综合考虑了换流变压器中各个结构件得到的。因此该频率指数是否适用于拉板损耗是值得分析的。
当2b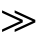
δ时，ξ
1，式（7）可化简为
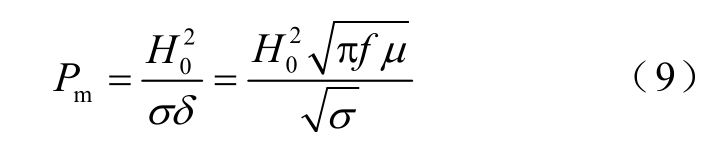
式中，Pm为拉板宽度远大于趋肤深度时的损耗值。将拉板损耗Ps归算到Pm，可得归一化后的拉板损耗曲线如图2所示。
图2 拉板涡流损耗与宽度关系图
Fig.2 Relation diagram of eddy current loss and width of flitch plate
由图2可知，拉板的损耗和拉板归一化宽度之间的变化趋势可分为三个阶段。在第一阶段，即归一化拉板宽度ξ＜2.4时，拉板损耗随着拉板归一化宽度的增加急剧增大；之后进入一个短暂的渐稳状态，即第二阶段；当其数值达到临界值6时，拉板损耗基本维持在一个恒定值 Pm，进入稳定的第三阶段。换流变压器的拉板宽度大约在300～400mm之间，其材料为不锈钢。50Hz时趋肤深度为67mm，对应的归一化拉板宽度范围约为4.5～6。因此当拉板不开槽时各个谐波频率下，拉板损耗可直接由式（9）计算，此时拉板的损耗频率指数取值为0.5。
为了降低拉板损耗，实际换流变压器拉板会开槽，且为全槽。假设开槽数为n，此时拉板的总损耗为n+1个宽度约为原来1
(n+1)的小拉板组成。由图2可知，电流频率为基波50Hz时，由于小拉板宽度的大幅减小导致其损耗关系曲线进入到第一阶段，造成损耗数值的急剧减小，使得最终n+1个小拉板相加损耗仍然小于不开槽时的数值。但是对于高频的谐波而言，其趋肤深度远小于基波时的数值，因此拉板开槽并不会导致每个小拉板的归一化拉板宽度小于临界数值6，其损耗曲线一直稳定在第三阶段，造成总的损耗的增加。因此换流变压器拉板开槽时基波损耗会减小，但随着电流频率的增加该效果会越来越弱，当频率达到一定数值时损耗不降反升。当频率足够大时，开槽后每个小拉板的损耗等于没开槽时整个拉板的损耗，所以开槽后的拉板总损耗将会是不开槽时的n+1倍。因此对于实际拉板开槽的换流变压器而言，其拉板的谐波损耗与基波损耗换算的损耗频率指数将远大于不开槽时的理论数值0.5。
3 有限元模型
3.1 换流变压器拉板有限元模型的搭建
为了验证理论分析的正确性，运用有限元仿真软件COMSOL，针对一台800kV换流变压器的铁心主柱拉板损耗进行了仿真计算。该换流变压器为单相四柱式结构，套在中间两主柱上的对应绕组之间并联连接，网侧绕组在内，阀侧绕组在外，两者的电流流向相反。铁心主柱上的拉板均匀开两槽，与交流变压器开半槽不同的是，换流变压器拉板为全槽。具体尺寸：拉板宽度为400mm，长度为3 600mm，厚度为25mm，开槽宽度为10mm；铁心长6.58m，宽1.132m，高3.92m；铁心主柱截面积为1.17m2。换流变压器额定参数和材料参数见表1和表2。上述数据均为生产厂家提供。
表1 换流变压器参数
Tab.1 Converter transformer parameters
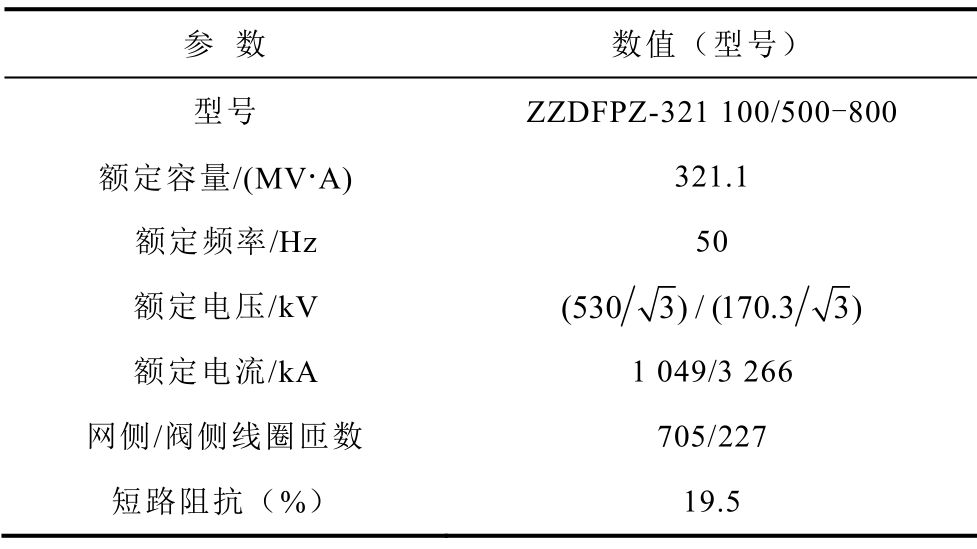
表2 材料参数
Tab.2 material parameter
图3为换流变压器八分之一有限元模型。在建模过程中进行了以下简化和考虑：①对铁心进行整体建模，不考虑铁心叠片结构；②忽略铁心和绕组的涡流损耗；③对拉板进行充分的网格剖分，尤其是在拉板宽度的左右两侧，保证在一个趋肤深度内至少有五个单元；④由于换流变压器具有对称结构，为了减小计算量，只构建其八分之一模型，对应的边界条件为：XZ平面和YZ平面设置为磁力线垂直边界条件，其余四个外边界设置为磁力线平行边界条件；⑤模型激励为直接在网侧和阀侧绕组横截面施加方向相反的电流激励。
图3 换流变压器八分之一有限元模型
Fig.3 One-eighth finite element model of converter transformer
3.2 Problem21a模型的验证
由于无法将换流变压器拉板损耗从测量的总损耗中分离出来，因此不能通过实验的形式直接验证3.1节有限元模型的正确性。TEAM Problem 21基准族是为了解决变压器结构件损耗计算而提出的一系列标准模型，其中Problem21a-2模型是以变压器铁心拉板开两槽为背景。因此可以通过使用3.1节的建模方式搭建Problem21a-2模型，再将仿真得到的数值与标准模型提供的实测数据进行比较，以此来间接地验证3.1模型的正确性。图4为Problem21a-2模型详细结构尺寸。图5为其四分之一有限元模型。文中模型的尺寸数据与实测的各种数值来源于最新版本的TEAM Problem 21 Family（V.2 009）。
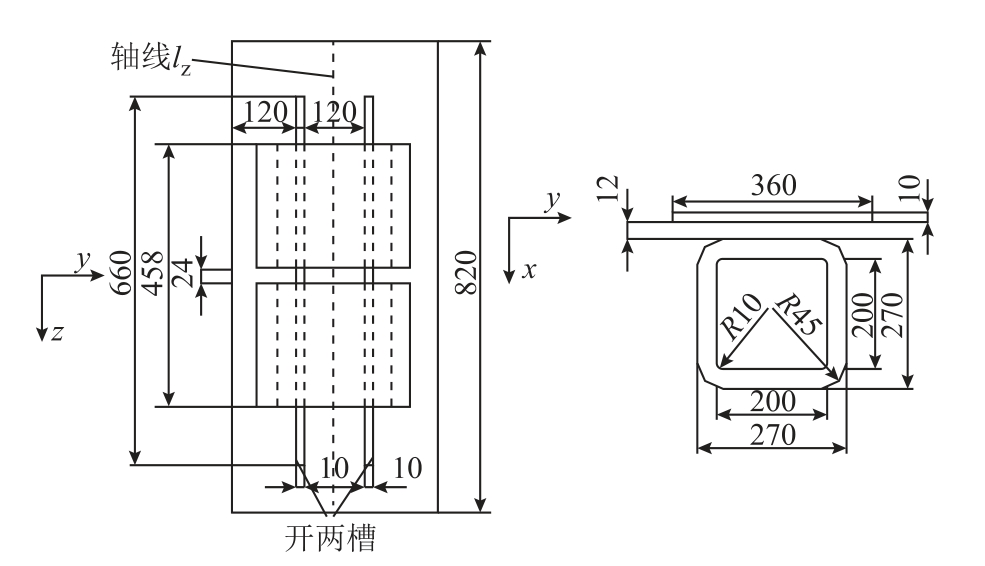
图4 Problem21a-2模型结构尺寸
Fig.4 Problem21a-2 model structural dimensions
图5 Problem21a-2四分之一有限元模型
Fig.5 Quarter finite element model of Problem21a-2
绕组中施加的电流有效值为10A，频率为50Hz。拉板的材料为不锈钢，绕组为铜。仿真得到的拉板损耗数值为1.69W，而实测数值为1.68W，两者的误差仅有0.6%。表3为Problem21a-2模型中沿拉板表面轴线lz分布的径向磁通密度 Bx的仿真值和测量值。
表3 Problem21a-2拉板表面磁感应强度Bx
Tab.3 Flitch plate surface Bx of Problem21a-2
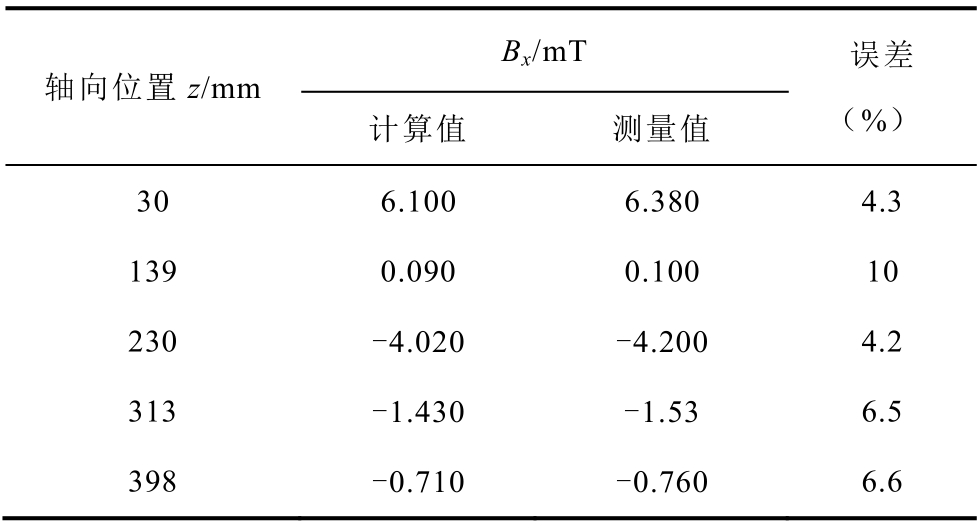
通过表3和拉板损耗数值的对比可以看出，仿真与实测数值之间误差很小。因此3.1小节建立的换流变压器拉板有限元模型是正确的。
4 仿真分析
图6为本文所使用的换流变压器阀侧额定负载电流频谱图。从图6中可以看出，谐波含量随着频率的增加呈指数下降，而拉板损耗与电流数值的二次方成正比，所以高频谐波造成的损耗与基波损耗相比很小。又因为其谐波含量主要由6n±1次谐波组成，n为正整数[17-18]，相邻两次谐波频率相差很小。因此仿真只计算了电流频率为50Hz、250Hz、550Hz、850Hz和2 450Hz下拉板不开槽和开两全槽时的损耗。由于该换流变压器采用的是两主柱上绕组并联连接的方式，因此3.1节有限元模型中绕组中通入的电流为额定电流的一半。
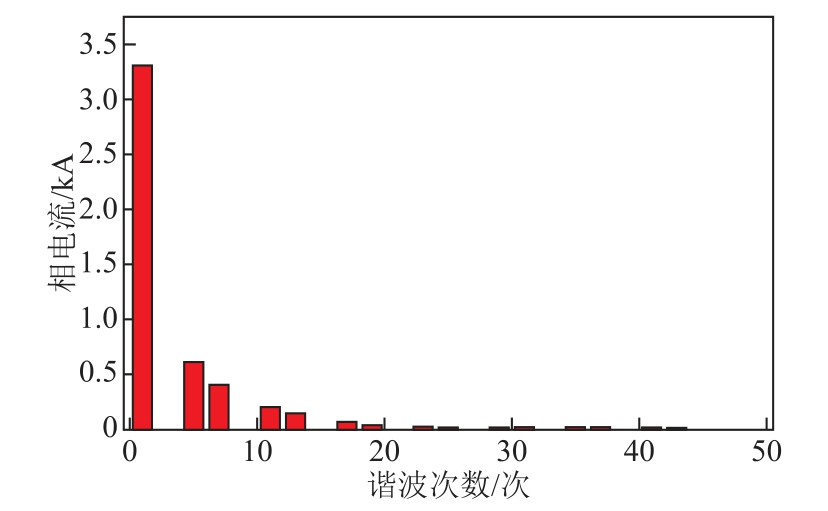
图6 换流变压器额定负载电流频谱
Fig.6 Rated load current spectrum of converter transformer
4.1 拉板表面涡流和磁场分布结果分析
图7a、图7b分别为拉板不开槽和开两全槽时，电流频率50Hz下拉板正表面和侧表面的涡流密度分布局部图，图中拉板侧表面与正表面的长度尺寸关系为虚线框所示。从图7a中可以看出拉板不开槽时，涡流基本沿着拉板的长度方向（y轴方向）流动，且在厚度方向（x轴方向）上涡流密度均匀分布。在宽度方向（z轴方向）上，涡流沿着拉板中心轴左右对称分布，主要集中在拉板的两侧，且涡流损耗最大值位置与绕组端部等高。这与文献[5]中图6a和图6c得到的涡流密度分布图基本一致。对比图7b可以发现，拉板开全槽并不会改变涡流在每一个小拉板上的流向。
图7 拉板表面涡流分布
Fig.7 Eddy current distribution on flitch plate surface
图8a、图8b分别为拉板不开槽和开两全槽时，基波电流和17次谐波电流下拉板正表面x轴方向磁场强度Hx分布图。从图8a可以清楚地看到，随着电流频率的增加，磁场强度的趋肤现象越来越明显。当电流频率为850Hz即17次谐波时，可以认为拉板在宽度方向上除了两侧表面，内部没有磁场强度分布。由于拉板没有开槽，其宽度远大于基波趋肤深度，因此基波磁场强度仍只存在拉板两侧，拉板中部并没有磁场强度分布。当拉板开槽时，由图8b可知，磁场强度在每一个小拉板上的分布情况除数值大小外其余完全一样。电流频率为基频时，磁场强度在每一个小拉板正表面上与不开槽时相比分布得很均匀。但是对于17次谐波而言，拉板开槽后每个小拉板的宽度仍远大于其趋肤深度，因此磁场强度分布规律与不开槽时相同，都是在拉板的两侧，拉板中部并没有磁场强度分布。
图8 拉板表面磁场Hx分布
Fig.8 Magnetic fieldHxon flitch plate surface
综上所述，拉板表面涡流和磁场强度分布的计算结果与第1、2节理论分析的结论一致，这也证明了本文所建立的有限元仿真模型的正确性。
4.2 拉板损耗频率特性分析
为了方便分析电流频率对拉板损耗的影响规律，并确定频率指数，假设谐波电流在数值上与基波一样，因为拉板损耗与电流的二次平方成正比，此时对应的谐波损耗为计算得到的数值乘上系数kh，kh为电流I1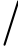 
Ih的二次方，h为谐波次数。
4.2.1 拉板不开槽
表4为拉板不开槽时计算得到的各个频率下的损耗数值Ph，该数值是利用仿真结束后COMSOL自带的后处理器计算得到的。具体过程为：对拉板上每一个节点的体损耗密度在一个周期内取平均值，然后对其在整个拉板上进行体积分。表中的频率指数Ch计算式则为
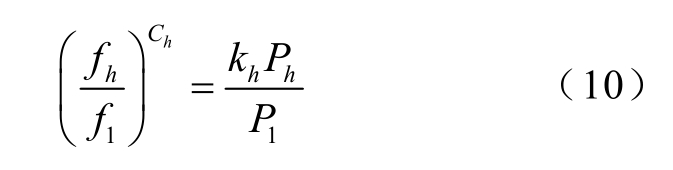
表4 换流变压器拉板不开槽涡流损耗
Tab.4 Eddy current loss of flitch plate on converter transformer
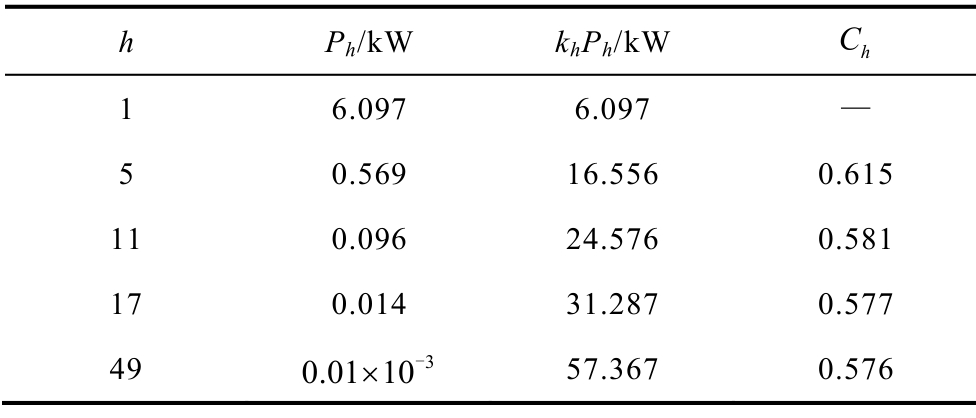
从表4中可以看出当拉板不开槽时，对于实际的换流变压器负载电流频谱而言，高次谐波损耗与基波损耗相比很小，17次谐波损耗仅为基波损耗的0.23%，49次谐波损耗则更小，几乎可以忽略。而其频率指数随着电流频率的增加逐渐减小，但变化的范围很小，基本上在0.58上下浮动。这与第2小节的理论推导结果0.5基本一致，两者之间的误差是由于没有考虑拉板表面z轴方向磁场强度造成的少量涡流损耗导致的。综上所述，当换流变压器拉板由于某些特殊需要选择不开槽时，使用式（8）计算换流变压器负载情况下的拉板损耗时，其总损耗频率指数可靠近低次谐波频率指数取值，本文中的换流变压器取值为0.6。
4.2.2 拉板开两全槽
表5为拉板开两全槽时计算得到的各个频率下的损耗数值Ph和对应的频率指数Ch。与表4对比可以发现，换流变压器拉板开槽之后，50Hz基波电流造成的涡流损耗大幅减小，约为不开槽时的20%，减小了4/5。但是随着电流频率的增大，两者之间的损耗差值逐渐减小，当谐波次数大于5时，对应频率下的拉板损耗则会大于不开槽时的数值，且之后随着频率的增加，两者之间的损耗差值逐渐增大。对于17次谐波损耗而言，其为基波损耗的1.85%，而不开槽时仅为0.23%。当谐波次数达到规定范围内的最大值49次时，其造成的拉板损耗为不开槽时的3.4倍，这与第2节理论部分给出的造成的损耗为不开槽时3倍的结论基本吻合。上述结果的分析验证了理论推导的正确性：换流变压器拉板开槽会导致基波损耗的减小，但同时也会增加高次谐波损耗。所以拉板采用不锈钢材料的换流变压器，其开槽数并不是越多越好，实际中开2～3槽较为合适。而对于特殊情况下拉板采用磁钢材料的换流变压器，由于材料趋肤深度的大幅减小，拉板开槽对拉板损耗的影响很小。
表5 换流变压器拉板涡流损耗
Tab.5 Eddy current loss of flitch plate on converter transformer
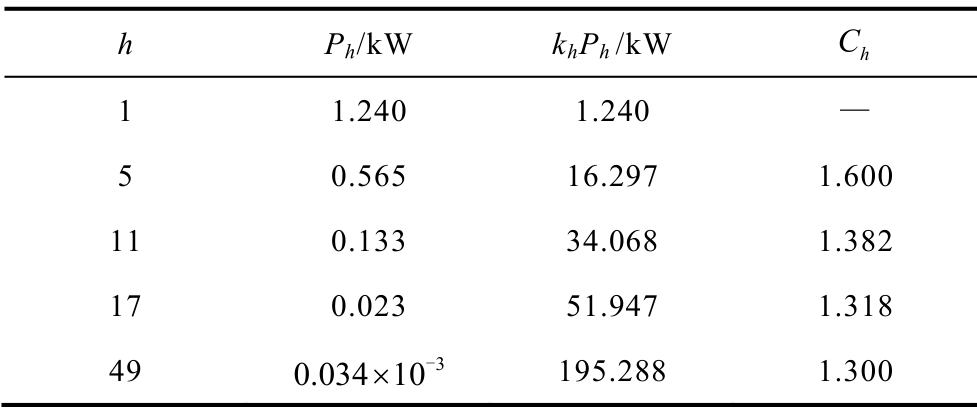
由于拉板开槽导致谐波损耗占基波损耗的比重激增，因此其对应的频率指数也会大幅增大。电流频率为250Hz时，其频率指数为1.6，是不开槽时的2.46倍，之后随着电流频率的增加逐渐减小。虽然开槽使得高次谐波的比重增加了，但其数值与总的损耗相比依旧很小，因此使用式（8）计算换流变压器负载情况下拉板总损耗时，其总的频率指数仍然可以选取的靠近低次谐波，本文中可取数值1.5。该数值也与文献[12]中实验得到的数值一致。由此可见，若不考虑拉板开槽的影响，依旧使用不开槽时的指数0.6，将会对拉板总损耗的计算造成较大的误差。
5 结论
本文通过对换流变压器拉板表面磁场分布进行简化，推导得到了拉板损耗的近似表达式，结合有限元仿真计算，研究了不同拉板开槽情况下，电流频率对拉板涡流损耗数值和损耗频率指数的影响。主要结论如下：
1）换流变压器拉板开槽虽然会使基波损耗大幅减小，但同时也会增加高次谐波损耗，因此拉板采用不锈钢材料的换流变压器，其开槽数并不是越多越好，实际中开2或3槽较为合适。而对于特殊情况下拉板采用磁钢材料的换流变压器，拉板开槽对拉板损耗的影响则很小。
2）换流变压器拉板损耗的频率指数受拉板开槽数量和电流频率影响：拉板开槽数量越多频率指数越大；电流频率越大频率指数越小。对于800kV特高压换流变压器，拉板采用不锈钢材料的情况下，拉板损耗计算中不开槽时频率指数可取0.6，开两槽时可取1.5。
[1] 潘超,王格万,蔡国伟,等.交直流混杂模式下变压器励磁电流谐波与箱体损耗映射研究[J].电工技术学报,2019,34(13):2830-2838.
Pan Chao,Wang Gewan,Cai Guowei,et al.Research on maping from excitation current harmonic to tank loss for AC-DC hybrid operation of transformer[J].Transactions of China Electrotechnical Society,2019,34(13):2830-2838.
[2] 赵庆波,张正陵,白建华,等.基于特高压输电技术的电力规划理论创新及实践[J].中国电机工程学报,2014,34(16):2523-2532.
Zhao Qinbo,Zhang Zhengling,Bai Jianhua,et al.Theoretical innovation and practice of power planning based on UHV transmission technology[J].Proceedings of the CSEE,2014,34(16):2523-2532.
[3] 杜伯学,朱闻博,李进,等.换流变压器阀侧套管油纸绝缘研究现状[J].电工技术学报,2019,34(6):1300-1309.
Du Boxue,Zhu Wenbo,Li Jin,et al.Research status of oil-paper insulation for valve side bushing of converter transformer[J].Transactions of China Electrotechnical Society,2019,34(6):1300-1309.
[4] Kerenyi D.Approximate formula for the eddy current losses induced in rectangular metal blocks magnetic fields[J].GANZ Electric Review,1987,16(1):13-22.
[5] Koppikar D A,Kulkarni S V,Srinivas P N,et al.Evaluation of flitch plate losses in power transformers[J].IEEE Transactions on Power Delivery,2002,14(3):996-1001.
[6] 张志刚,胡明方,杜仕祥,等.电力变压器拉板结构、材质与其涡流损耗关系的数值优化[J].变压器,2015,52(12):12-15.
Zhang Zhigang,Hu Mingfang,Du Shixiang,et al.Numerical optimization of the relationship between structure,material and eddy current loss of power transformer flitch plate[J].Transformer,2015,52(12):12-15.
[7] 刘连光,潘尧,王泽忠.特高压换流变压器支撑件的直流偏磁损耗计算[J].电网与清洁能源,2018,34(3):1-6.
Liu,Lianguang,Pan Yao,Wang Zezhong.Eddy current loss calculation of supporting parts of UHV converter transformer under DC bias[J].Power System and Clean Energy,2018,34(3):1-6.
[8] Emanuel A E,Wang Xiaoming.Estimation of loss of life of power transformers supplying nonlinear loads[J].IEEE Transactions on Power Apparatus &Systems,1985,104(3):628-636.
[9] Forrest J A C.Harmonic load losses in HVDC converter transformers[J].IEEE Transactions on Power Delivery,1991,6(1):153-157.
[10] Karasev V V.The dependence of losses in transformer tanks upon current,frequency and temperature[J].All-Union Electrotech.Inst,1969,79(3):129-148.
[11] Ram B S,Forrest J A C.Effects of harmonics on converter transformer load losses[J].IEEE Transactions on Power Delivery,1988,3(3):1059-1066.
[12] Liu Yaqing,Zhang Dandan,Li Zhenbiao,et al.Study of the stray losses calculation in structural parts for HVDC converter transformers based on the TEAM problem 21 family[J].IEEE Transactions on Power Delivery,2016,31(2):605-612.
[13] 赵小军,王佳雯,刘洋,等.谐波激励下变压器结构件杂散损耗的模拟与验证[J].中国电机工程学报,2020,40(2):652-663.
Zhao Xiaojun,Wang Jiawen,Liu Yang,et al.Simulation and verification of stray loss of transformer structure under harmonic excitation[J].Proceedings of the CSEE,2020,40(2):652-663.
[14] Liu Yaqing,Zhang Dandan,Li Zhenbiao,et al.Calculation method of winding eddy-current losses forhigh-voltage direct current converter transformers[J].IET Electric Power Applications,2016,10(6):488-497.
[15] 李亚丽,凌跃胜,刘宏勋,等.高频变压器涡流损耗公式的推导及有限元方法的验证[J].电工技术学报,2015,30(增刊2):82-87.
Li Yali,Ling Yuesheng,Liu Hongxun,et al.The derivation of eddy current loss formula and validation by using FEM in high frequency transformer[J].Transactions of China Electrotechnical Society,2015,30(S2):82-87.
[16] Kulkarni S V,Khaparde S A.Transformer engineering:design,technology,and diagnostics [M].2nd Ed.Los Angeles:CRC Press,2012.
[17] Hu LiHua,Yacamini R.Harmonic transfer through converters and HVDC links[J].IEEE Transactions on Power Electronics,1992,7(3):514-525.
[18] 黄天超,王泽忠.地磁暴对直流输电逆变侧换相角及谐波的影响机理分析[J].电工技术学报,2020,35(16):3377-3384.
Huang Tianchao,Wang Zezhong.Mechanism analysis of geomagnetic storm on commutation angle and harmonic of inverter side of HVDC transmission[J].Transactions of China Electrotechnical Society,2020,35(16):3377-3384.