0 引言
直流配电网具有电能质量好、无需无功补偿、便于电源和负载接入等优势,受到了广泛关注和推广。21世纪以来,美国、日本、欧洲、中国和韩国相继建设了直流配电网研究基地,在拓扑结构、优化调度、功率变换及控制和通信等方面均展开了研究[1-2]。由于直流电流不存在电流过零点,在开断电磁炉、暖风机等功率相对较大的负载时容易产生难以熄灭的直流电弧。现有交流开关、插头无法安全快速地无弧开断直流电流,另外,接头接触不良、导线绝缘破损、接头松动等原因也容易引起电弧故障,均会严重影响配电网的安全稳定运行,制约直流配用电的发展。因此,研究直流电弧的稳定燃弧条件对抑制电弧的发生有重要意义[3-4]。
现有对直流系统的电弧故障研究多针对电弧特性建模或直流断路器的设计等,但缺乏对感性负载条件下稳定燃弧条件的研究,以及对直流电弧的稳定燃弧条件的理论推导。
文献[5-10]涉及电弧的起弧条件和熄灭的影响因素研究,部分文献也表明电感对电弧的产生、维持与熄灭均有影响,但仅从实验结果的角度进行说明,未进行深入的探讨。文献[5]研究了接触直径、分离速度、电流换相路径中的电缆电感等参数对无弧换相阈值电流的影响,结果表明:零电压开关(Zero Voltage Switch,ZVS)中较大的接触直径、较慢的分离速度和较小的电感有利于减小无弧换相的阈值电流。文献[7]表明,常用的触头材料的最小生弧电压约12~16V,最小生弧电流约为数百毫安。文献[8]针对航空270V直流接触器电弧,采用栅片和磁吹系统相结合的直流接触器进行实验,表明感性负载情况下电弧开断难度最大,且随着回路电感值的增大,燃弧时间和电弧熄灭时产生的过电压峰值增加,但未分析电感对直流系统燃弧的影响。关于直流电弧特性[11-19]的研究,W.B.Nottingham在Ayrton公式的基础上提出电弧静态伏安特性的一般经验公式[11-12],在电弧长度恒定的条件下,电弧电压和电弧电流是非线性关系,并通过铜电极和碳电极实验证明了公式的正确性。文献[13]通过电弧实验和数值分析获得不同条件下串联型故障电弧数学模型参数,建立了预测串联型故障电弧数学模型参数的黑箱模型,可以实现对不同电路和环境条件下电弧模型参数的预测。文献[18]分析了电弧的能量变化过程,建立了链式电弧模型,结合实验结果可以表明利用能量平衡的计算方法能更准确地计算燃弧时间,且对有风情况下的燃弧时间更为适用。西安交通大学王其平[20]对电器电弧的物理特性和物理过程以及交流、直流电路中电弧的开断和熄灭方法等的基本理论做出了较为全面的介绍,但电弧理论在很多方面还不完善,有待进一步的研究和发展。
课题组已搭建直流电弧模拟实验平台,通过实验明确了电源电压对能否产生稳定电弧有直接影响[21]。在W.B.Nottingham和课题组研究工作的基础上,本文深入研究直流电弧特性和稳定燃弧条件,并关注电感性负载的影响。根据GBT 35727—2017中低压直流配电电压导则,直流配电网低压直流配电系统的标称电压一般小于1kV,而民用负荷配电侧电压更低。常见直流负荷往往带有一定的感性负载,但负荷运行时不易测得其等效电阻和电感,因此,本文研究最大等效负荷(电阻280Ω、电感30mH)下的稳定燃弧阈值电压,该值可基本涵盖大部分民用直流电器。
1 直流电弧发生实验
1.1 实验平台
搭建如图1所示的低压直流母线与负荷模拟实验平台,串入课题组[21]已有的直流电弧发生装置。

图1 实验电路示意图
Fig.1 Schematic diagram of experimental circuit
实验所用的调节电阻为高频无感电阻(电感约0.2μH,可以忽略不计);电感为铁心磁导率较高(不易磁饱和)的绕制电感,并用RLC测试仪精确测试其电感值;电源为IDRC CDP系列可程式直流稳压电源,电压输出为0~380V可调,最大输出电流为60A,输出电压精确度为±0.05%,可以满足实验所需的精度要求。实验过程中电弧电压、电流均采用R&S(罗德与施瓦茨)RTB2004数字示波器采集,采样率152kS/s。
1.2 实验方法及信号采集
实验中采用拉开式起弧方式产生电弧,电极采用单心铜电极。记录直流稳压电源电压、回路电流、电阻阻值、电感值及拉开间距等数据,为了提高数据可靠性,取起弧后2~3s电弧电压和电流的平均值作为实测值。
实验采集电弧电压和电弧电流信号如图2所示。电弧发生后,电弧电压从0开始增大,回路电流减小,约1s后到达稳定状态。此时电弧电压和电流基本维持稳定,电弧可持续稳定燃烧。

图2 电弧电压和电弧电流信号
Fig.2 Arc voltage and arc current signal
2 直流电弧工作特性分析
为了解释实验数据的规律性并获得稳定燃弧的最低电压值,本节首先分析电弧的工作特性。
2.1 电弧的伏安特性
电弧的伏安特性是电弧电压与电流之间的关系,对于小功率(电压低于1kV,电流低于100A)和短间隙(小于12mm)的直流电弧,其静态伏安特性[5-6]可由经验公式表示为

式中,ua为电弧电压,V;ia为电弧电流,A;a、b、n为常数。根据式(3)可绘制出如图3中的凹形曲线A。
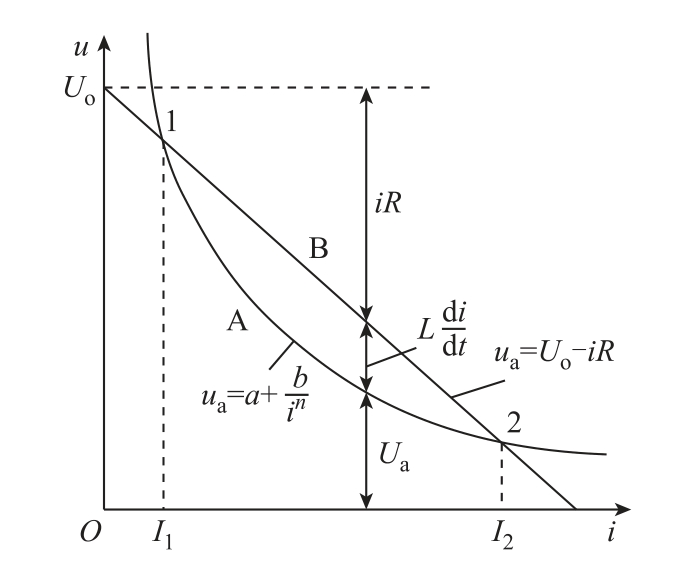
图3 直流电弧的伏安特性
Fig.3 Volt ampere characteristics of DC arc
2.2 电弧的稳定性
在直流系统中,电火花对系统安全影响较小,电弧若能持续稳定燃烧,产生的高温对系统的威胁极大,甚至导致电气火灾。
2.2.1 电弧稳定燃烧和熄灭条件
对于如图1中由直流电压源、电阻、电感和电弧发生装置所串联组成的直流回路,可列写电压平衡方程式,即
式中,Uo为电压源电压,V,视为恒定值;R为回路电阻,Ω;L为回路电感,H;i为回路电流,A。在串联回路中,电弧电流ia等于回路电流i。若由于某种原因导致电流波动量为Δi,此时电弧电压波动量 Δu a = dua/diΔi,式(2)变为

将式(2)和式(3)求差,然后积分,可得
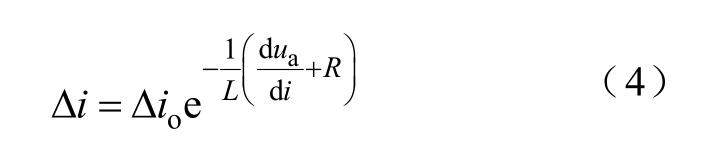
在式(4)中,若dua /di +R>0,Δi将减小,电流最终回到原来的位置,因此电弧是稳定的;若d ua/di +R<0,Δi将无限增大,电弧不能稳定燃烧。因此,将dua /di +R>0作为电弧稳定的条件。
电弧伏安特性曲线 ua = a +b/ 和纯阻性负载特性线( u = U o−IR)分别如图3中的曲线A、B所示,两曲线相交于1、2两点。在点1左侧和点2右侧 U o−ua−IR<0,则 Ldi /dt <0;在点1、2两点之间,Ldi /dt >0;在1、2两点上,Ldi /dt = 0。当电弧电流在点2附近出现一个扰动,若电流大于I2,则 Ldi /d t <0,电路中电流减小;若电流小于I2,则Ldi /dt >0,回路电流会增大,因此,点2为电弧的稳定燃烧点。在点1处,dua /di +R<0,电弧不能稳定燃烧。
和纯阻性负载特性线( u = U o−IR)分别如图3中的曲线A、B所示,两曲线相交于1、2两点。在点1左侧和点2右侧 U o−ua−IR<0,则 Ldi /dt <0;在点1、2两点之间,Ldi /dt >0;在1、2两点上,Ldi /dt = 0。当电弧电流在点2附近出现一个扰动,若电流大于I2,则 Ldi /d t <0,电路中电流减小;若电流小于I2,则Ldi /dt >0,回路电流会增大,因此,点2为电弧的稳定燃烧点。在点1处,dua /di +R<0,电弧不能稳定燃烧。
2.2.2 负载电阻对稳定燃烧点的影响
负载电阻R的大小变化体现为纯阻性负载特性线( u = U o−IR)斜率的改变。如图4所示,增大电阻R可使起弧前电流减小,同时稳定燃弧电流也会减小,对应的稳定燃弧电压会相应提高。纯阻性负载特性线的斜率增大使得与电弧伏安特性曲线交叉状态变为相切或无交点,从而使得电弧熄灭对应的电弧间距减小,更有利于电弧熄灭。

图4 负载电阻对电弧稳定燃烧点的影响
Fig.4 Influence of load resistance on stable burning point of arc
2.3 电弧的燃炽时间和电弧能量
从理论上确定电弧燃炽时间比较困难,因为它与电极材料与间距、介质属性、湿度等环境参数有关。但在上述参数恒定的条件下,可用数学分析方法求解电弧燃炽时间。在电弧电压 ua =a +b/ 为常数的情况下,将式(2)积分,可得电流表达式为
为常数的情况下,将式(2)积分,可得电流表达式为

式中, τc为时间常数,τc = L/R 。令i=0,可得
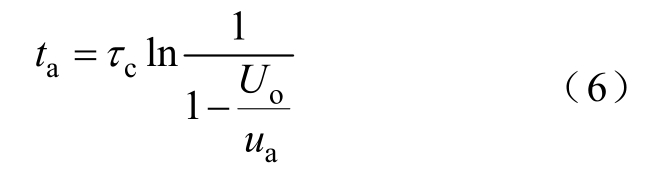
式中,ta为电弧的燃炽时间。在电弧燃炽期间,直流电弧的能量为
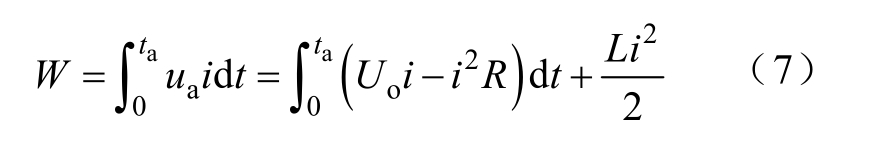
式(7)中,第一项为电弧在燃烧过程中从电源处获得的能量,第二项是电感中所储存的能量,且在电弧开断过程中,电感中的能量全部消耗在电弧上。由此可见,电路中电感越大,电路中储存的能量越多,电弧越难熄灭,电弧的燃炽时间也越长。
3 实验结果分析
3.1 电弧的伏安特性及负载对燃弧的影响
采用图1所示的实验平台进行电弧实验,测试电弧的伏安特性曲线。实验中电源工作在恒流源模式,回路中不串入电感,分别缓缓拉开电极至间距为2mm、4mm和5mm(易于判断电弧是否为自持放电)。实验过程中电源输出电流以0.1A为步长增大,并调整回路电阻阻值,使电弧能够发生,每个间距下采集42个测试点,分别逐点绘制不同间距下电弧的伏安特性如图5所示。当恒压源Uo=200V,负载电阻分别为200Ω、100Ω和50Ω时,在图中分别绘制 u= U o−IR特性直线,参照2.2节的理论分析,进一步明确其燃弧条件。

图5 不同间距下的电弧伏安特性曲线
Fig.5 Volt ampere characteristic curve of arc under different electrode spacing
如图5所示,电弧电压随着电弧电流的增加逐渐减小,且电流大于3A以后电弧电压趋于平稳;电弧间距的增大会导致伏安特性曲线的上移,且电弧电压随着间距的增大而增大。图5中的8个坐标点是三条 u= U o−IR特性线和电弧伏安特性曲线的交点。其中,黑色标注数据表示可直接起弧;灰色标注为无感电阻条件下不起弧,仅当回路中串入电感后可产生稳定电弧。其原因在2.2.1节中有理论分析,进一步解释为:当电阻和间距较小时,回路电流较大,可以产生稳定电弧;当电阻及间距增大时,电弧电阻也增大,电流减小,纯阻性负载不能产生稳定电弧,在回路中串入电感后,可以产生稳定燃烧电弧。实验结果表明,在原本不能稳定燃弧的纯阻性回路中串入适量电感后可产生稳定燃炽的直流电弧,因此,电感有利于电弧的稳定燃炽,但电感仅对起弧过程有影响,不会影响稳定燃弧后的电弧电压、电流值。
由图5可得,燃弧的电弧电流和电压均在两曲线的右下方交点附近,从实验的角度证明了电弧的稳定燃烧点为2.2节图2中的点2。实验中电弧间距过大,不易产生稳定电弧,间距过小易熔弧,且不易控制和观察,考虑到5mm间距下电弧电压较低,与实际电路中由于触头接触不良导致的电弧更为相似,因此,后文中的实验均固定5mm间距不变,开展研究。
3.2 稳定燃弧条件
将电弧建立稳定燃弧条件所需的最小电源电压与回路电流称为燃弧电压和电流。电弧燃烧会受电极间距、负载电阻、电感及环境因素等诸多因素的影响,本节首先通过实验探究电极燃弧电压、电流与负载电阻、电感的关系。
在尽量保证实验条件及环境因素(温度22~25℃、相对湿度50%~60%、无风条件)不发生变化的前提下,测试回路分为无电感及串入0.05mH、0.1mH、0.15mH、0.3mH、0.8mH、1.4mH、5mH、10mH、20mH、30mH电感,同时增大回路中电阻阻值,调整电压源输出电压至可以产生稳定燃烧的电弧,分别记录不同阻感性负载的燃弧电压。为了保证实验的可重复性,在每一实验条件下均进行三次拉弧操作,缓缓拉开电极并产生电弧,若有一次电弧能稳定燃烧5s及以上实验记录为可稳定燃弧,否则继续小幅增大电源电压,重复实验。每组电感下测试电阻均从1.25Ω增大到280Ω,并从中分别取46个电阻值测试燃弧电压,用描点法绘制各电感影响下的燃弧电压值如图6所示。当电阻较小时,数据点较为密集,不同电感下对应的稳定燃弧电压基本一致,分别列出电感为10mH,电阻为10~70Ω,电弧可以稳定燃炽所对应的电源电压及电弧电压值,并计算电弧电压占电源电压的比重见表1。

图6 阻感性负载下的燃弧阈值电压曲线
Fig.6 Arc voltage curve under resistance and inductance load
表1 小电阻回路电弧电压占电源电压的比重
Tab.1 Proportion of arc voltage in small resistance circuit to power supply voltage

图6a表示不同电感影响下随着电阻的增大燃弧电压的变化情况。图例表示起弧前的回路电流值,可以看出对于阻感负载电阻越大,燃弧电压越高;在同一电阻情况下,电感越大,燃弧电压越低。由表1可知,当电阻较小时,电弧电压占电源电压的比例均在60%以上,且随着电阻增大,电弧电压所占比重有减少的趋势。图6a中电阻小于70Ω时,数据点较为密集,表明电感对燃弧电压基本没有影响,原因可能为电弧电压占据了大部分的电源电压,必须增大回路电流使电弧电压降低才能产生稳定电弧,电感对维持电弧稳定无能为力;当电阻大于70Ω时,随着电阻的增大,电感可有效降低燃弧电压;当电阻为280Ω时,回路中串入20mH电感,可降低燃弧电压约100V。对于燃弧电流,随着电阻增大,电流从20A迅速降低至2A以下,并基本保持稳定。图6b表示不同电阻影响下,随着电感的增大燃弧电压的变化情况。当电阻较小时,燃弧电压随电阻变化曲线近似为一条直线,同样表明小电阻下电感对电弧产生影响较小;电阻增大后,随着回路中电感的增大,燃弧电压迅速下降,且电阻越大,电感对燃弧电压的影响越大,但当电感大于20mH后,再增大电感对燃弧电压的降低不再明显。
为了使实验结果更具直观性,将图6中燃弧电压、燃弧电流随阻感负载的变化情况绘制三维曲面图分别如图7a、图7b所示。图7a、图7b中图例分别表示燃弧电压和电流值。从图7b中可以发现电感对燃弧影响不大,原因为电阻较小时电源电压差异较小,导致电流基本一致。而电阻大于160Ω时,燃弧的最小电流值降至1A以下。电阻对燃弧电流影响明显,电阻小于50Ω时,随着电阻增大,燃弧电流以指数规律迅速降低,且在电阻大于50Ω后降至4A以下并趋于平缓。

图7 电弧稳定燃弧条件曲面图
Fig.7 Arc stable condition 3D surface
4 数据分析与模型建立
为了探究可以发生稳定电弧的最小电源电压(燃弧阈值电压)与等效负荷(电阻280Ω、电感30mH)之间的关系,结合实验数据及电弧特性,建立稳定燃弧阈值电压数学模型。
4.1 电弧伏安特性
结合式(1)对5mm电弧伏安特性曲线进行数值拟合,可得系数 a = 23.51,b = 68.24,n= 0.57,即电弧的伏安特性可用公式表示为

评定拟合效果的主要参数有RMSE(方均根误差)和R-square(相关系数),计算公式如式(9)和式(10)所示,其中,RMSE越接近于0,R-square越接近于1,拟合效果越好。经计算,式(8)数值拟合中RMSE=1.294 9,R-square=0.993 0,表明数值拟合效果较好,后文均采用此公式作为电弧静态伏安特性。
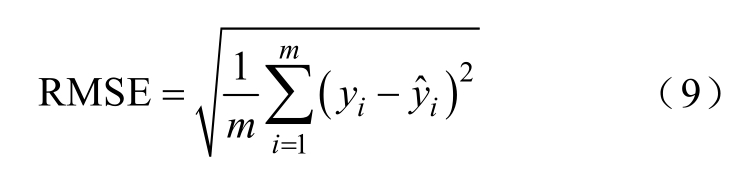

式中,yi为原始数据;![]() 为预测数据;
为预测数据;![]() 为原始数据均值;m为总数据量。
为原始数据均值;m为总数据量。
4.2 阻感性负载对燃弧电压的影响
从图6可以看出,无感情况下稳定电弧所需的电源电压最大,为了明确阻感负载中电阻和电感对燃弧电压阈值的影响,绘制阻感负载对燃弧阈值电压影响的曲线如图8所示。

图8 阻感性负载对燃弧阈值电压的影响
Fig.8 Influence of inductive load on arc threshold voltage
图8a、图8b横坐标分别为回路电阻和电感,纵坐标为回路中串入同一电阻时无感和有电感情况下燃弧电压的差值,记为ΔUk。图8a表明电阻越大,电感对ΔUk的影响越明显;且电感越大,影响越大。从图8b可以看出随着电感增大,电阻较小时电感对ΔU k的影响微弱;而当电阻较大时,电感对ΔUk的影响明显,但电感大于15mH后走势趋于平缓,随着电感的增大,ΔUk基本维持不变,说明电感对燃弧阈值电压的影响存在饱和值。电感大于15mH后再增大,电感值将不会降低燃弧阈值电压。
4.3 稳定燃弧阈值电压模型
为了得到串联回路中电阻、电感对燃弧电压的影响程度,从数学模型的角度说明稳定燃弧条件,建立电弧的稳定燃弧电压阈值模型。
如图2所示,电弧发生后电弧电压有轻微的波动,但整体趋于稳定,因此假设电弧燃烧时电弧电压为常数[22]。为了探究燃弧阈值电压U0与负载电阻R及电感L的关系,对式(2)积分可得

式中,M为常数,可由边界条件确定。
由此确定电弧燃炽时间ta,当t=ta时电弧熄灭,此时电弧电流i=0。将t=ta,i=0代入式(11)得
式(12)表明了回路中电阻和电感一定时,在一定间距下电弧稳定燃烧ta所需要的最小电源电压。
当负载变化时,电弧电压ua也随之变化,由式(4)可知,电弧能够发生的临界条件为dua/di=R,为了明确可以产生电弧的最大电弧电压,将式(1)对电流i求导数可得
由式(13)可得电弧发生的临界条件,如图9点P处的临界电弧电流 和临界电弧电压
和临界电弧电压 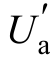 。
。

图9 直流电弧静态伏安特性曲线
Fig.9 Static volt ampere characteristics of DC arc

对于不同阻感负载的回路,发生电弧后的电弧电压不同,即图9中曲线A、B的交点2会发生移动,对于相同电阻不同电感的回路,电感越大,维持电弧所需的电流越小,电弧电压越大,ΔU = −Ua 也越小。
−Ua 也越小。
为了获取不同回路中电感和电阻对ΔU的影响,联立式(1)和 u = U o−IR特性线B对应的公式 ua = U o−IR,结合实验采集的数据点,求解每一回路中ΔU和电阻、电感的关系并绘制曲线如图10所示。

图10 不同阻感负载回路对ΔU的影响
Fig.10 Influence of different inductive loads on ΔU
图10a表示不同电感值下随着电阻增大ΔU的变化趋势。当电感小于0.15mH时,随着电阻增大,ΔU 不断增大;但当电感大于0.15mH时,ΔU先减小后增大。如图10b所示,随着电感的增大,临界电弧电压和实际电弧电压的差值快速减小最后趋于平缓,且不同的电阻对应的稳定点不同,但稳定值均在10V以内,可以忽略不计;在电阻为0~200Ω范围内,电阻越大,稳定点处的ΔU越小,最后趋近于0。因此,拟采用指数函数的形式描述电感的影响。拟采用如下公式描述阻感性负载对ΔU的影响。
式中,d、g、f、k均为常系数。结合式(12)可得直流串联回路中最低电源电压、电阻、电感及燃弧时间之间的关系为
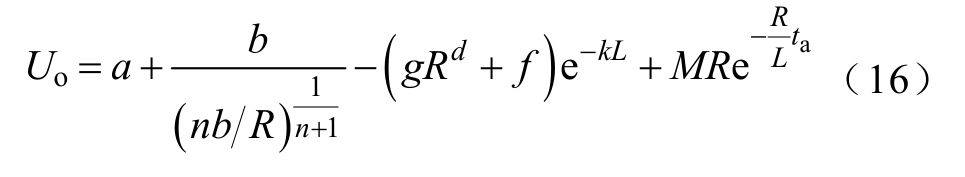
式中,系数M可以由边界条件t=0时刻开始建立稳定燃弧条件,此时i=ia,且t=ta时,电弧熄灭,此时回路中电流为0。将上述边界条件代入式(11)中,并结合电弧电压公式可得
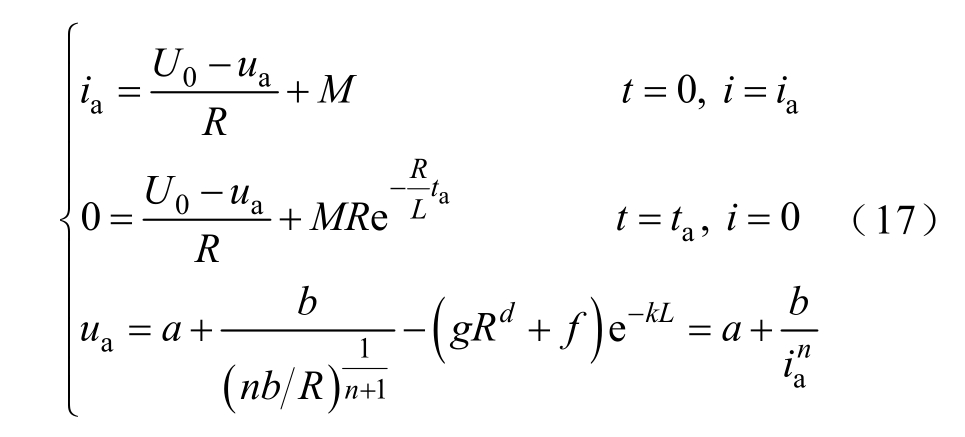
计算可得系数M为
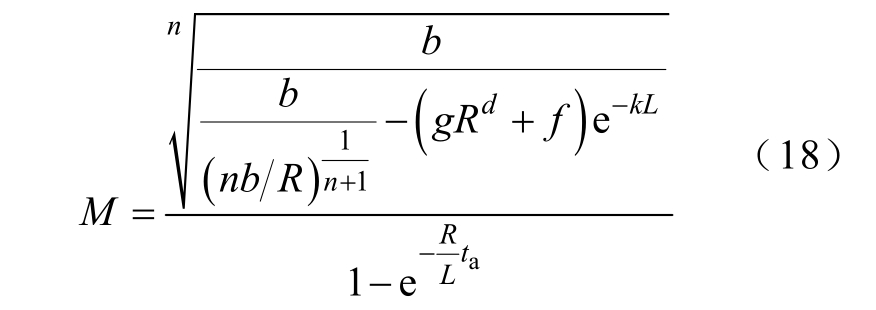
结合式(16)和式(18)可得阻感性负载下燃弧电压、电阻、电感及电弧燃炽时间之间的关系。实验过程中将电弧燃炽时间控制在5s以上,因此将电弧燃炽时间视为大于5的常数,可获得关于电阻、电感以及可以产生稳定电弧的最小电源电压的关系,从而建立直流系统中串联电弧稳定燃弧阈值电压模型。
5 稳定燃弧阈值电压模型验证与讨论
式(16)为阻感性负载回路中直流电弧燃弧阈值模型。为了获得相关系数,结合实验数据通过Matlab进行数值拟合,获取模型中未知的常系数,对比分析阈值模型数据分别为 d = 1.43,f =−12.61,g =−0 .02,k = 4167.32,t a= 7.50。拟合效果如图11所示。
图11a表明了阻感负载下稳定燃弧的最小电压变化趋势,并辅以等高线以50V为步长标注在图中。图例表示可以产生稳定燃烧电弧的最小电压值,图中的点为实测数据点,可以看出电阻越大,燃弧阈值电压越高,回路中电感增大可在一定程度上减小燃弧电压,但电感大于0.8mH后对燃弧阈值电压影响不再明显。图11b为实验数据和拟合数据的残差图,结果表明,对于实验数据和燃弧阈值模型拟合数据相似度较高,最大误差不超过15V。
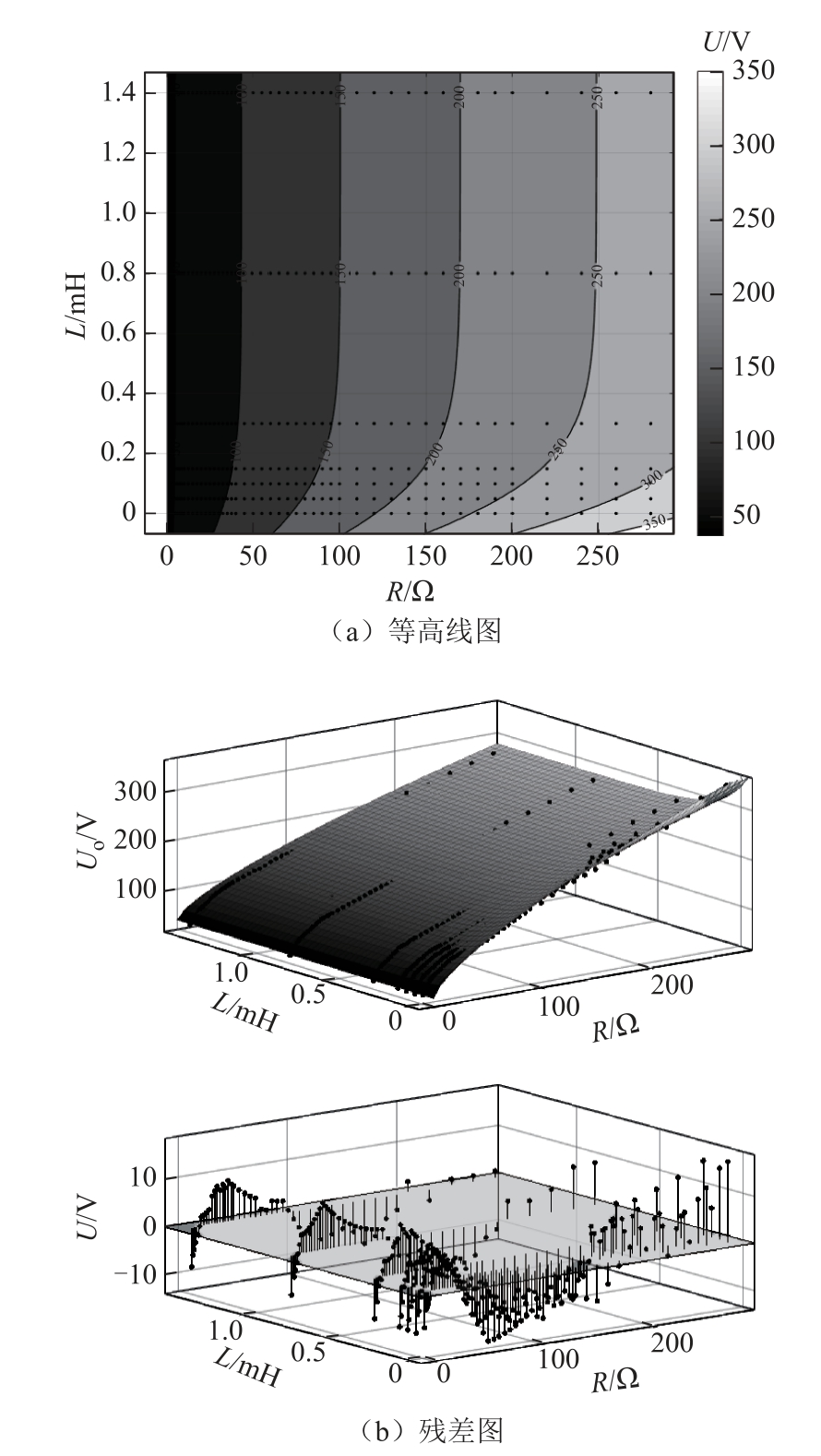
图11 燃弧阈值模型数值拟合效果图
Fig.11 Effect chart of numerical fitting of arc threshold model
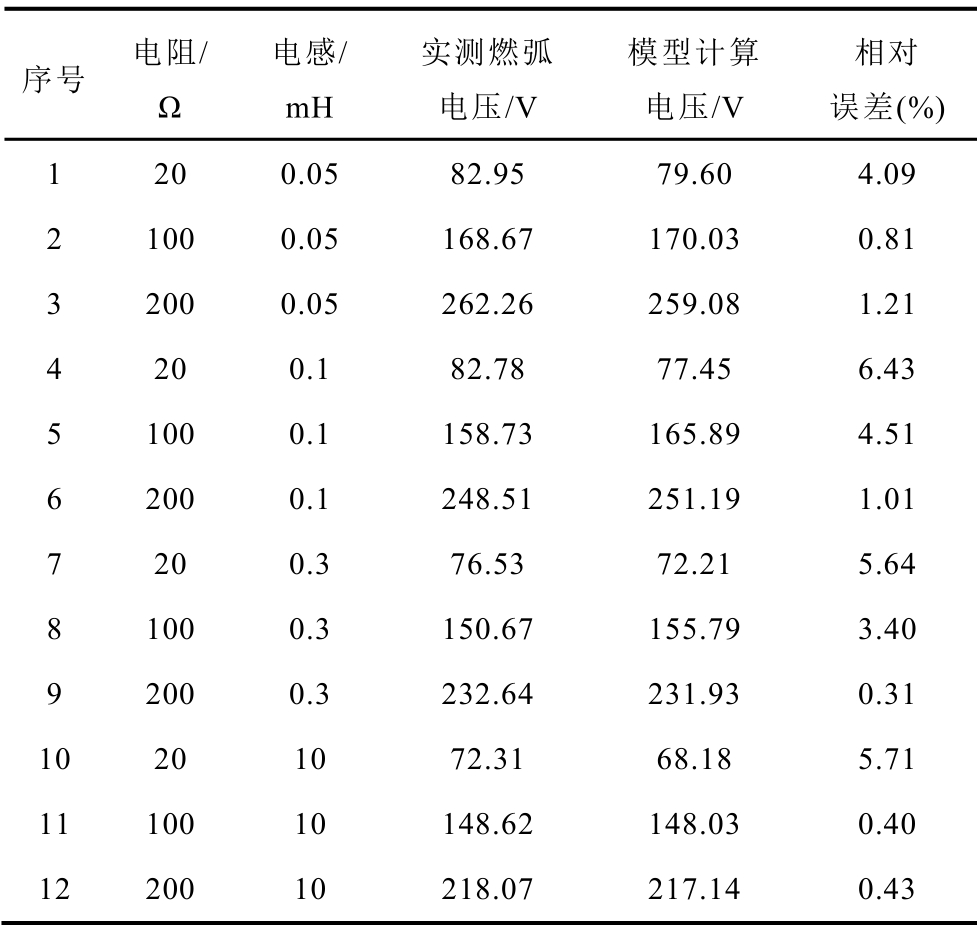
为了探究直流电弧稳定燃弧阈值电压模型的准确性,随机取不同负载参数,对比实测燃弧电压与模型计算电压,并进行误差分析,燃弧阈值模型误差计算表2。结果表明,与实测值相比,相对最小误差仅为0.31%,最大误差为6.43%,实测燃弧电压与模型计算电压值相近。经计算,得所建立模型计算的燃弧电压相较于实验数据的方均根误差(RMSE)为6.151 1V,相关系数(R-square)为0.992 4。表明拟合效果较好,阈值模型分析数据接近于实验数据值。
表2 燃弧阈值模型误差计算
Tab.2 Error calculation of arcing threshold model
根据GBT 35727—2017中低压直流配电电压导则,常用低压配用电母线标称电压值220V(±110V)。在此电压范围内,以150V、200V、250V为例,在该供电电压下不能稳定燃弧的最小阻感分界线分别为图11a中的对应电压的等高线。例如,对于150V供电电压,分界线左侧为可稳定燃弧的负载范围,分界线右侧为不可产生稳定电弧的负载范围。可知不产生稳定燃烧电弧的最小电阻约为65Ω,即电阻大于65Ω时,无感条件下不能产生稳定电弧;若电感大于0.8mH,不产生稳定燃烧电弧的最小电阻上升为100Ω。由此可得,对于200V和250V电源电压,有感条件下不产生稳定燃烧电弧的最小电阻分别为160Ω、250Ω。因此,研究结果可明确不同供电电压下抑制电弧发生的最大负载;同时,为直流配电网的母线标称电压选取提供了参考依据。
6 结论
本文通过实验探究阻感性负载(R<280Ω,L<30mH)直流电弧的稳定燃弧条件及影响因素。从理论和实验两个角度表明电感可以在一定程度上降低稳定燃弧阈值电压,但不会影响稳定后的电弧特性;同时,负载电阻越小(重载),负载电感越大,越易稳定燃弧。
基于实验数据与电弧燃炽理论,建立了电弧的稳定燃弧阈值电压模型,确立了含阻感性负载的稳定燃弧条件,即最低电源电压。基本涵盖直流配电网低压配电侧一般负荷的等效电阻和电感范围,工作条件接近于重载情况下的直流配电系统,为直流配用电标称电压的选取提供一定的参考依据。本文所做工作对直流电弧的稳定燃弧条件分析具有一定的指导意义,为研究低压直流开断特性及保护措施提供了工程参考。
[1] Murari K,Padhy N P.Graph theoretic-based approach for solving load flow problem of AC-DC radial distribution network with distributed generations[J].IET Generation Transmission &Distribution,2020,14(22):5327-5346.
[2] Achlerkar P D,Nougain V,Ketan P B.Backstepping technique-based customer-end voltage control strategy of DC distribution network[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2021,9(1):666-676.
[3] 翟国富,薄凯,周学,等.直流大功率继电器电弧研究综述[J].电工技术学报,2017,32(22):251-263.
Zhai Guofu,Bo Kai,Zhou Xue,et al.Investigation on breaking arc in DC high-power relays:a review[J].Transactions of China Electrotechnical Society,2017,32(22):251-263.
[4] Shekhar A,Ramirez-Elizondo L,Bandyopadhyay S,et al.Detection of series arcs using load side voltage drop for protection of low voltage DC systems[J].IEEE Transactions on Smart Grid,2018,9(6):6288-6297.
[5] Chen Mo,Nakayama K,Zen S,et al.Threshold current of arc-less current commutation in a hybrid DC switch[J].IEEE Transactions on Components Packaging and Manufacturing Technology,2019,9(6):1029-1037.
[6] Cui Xinglei,Zhou Xue,Zhai Guofu,et al.Electrical lifespan prediction of HVDC relay based on the accumulated arc erosion mass[J].IEEE Transactions on Components Packaging and Manufacturing Technology,2018,8(3):356-363.
[7] Sekikawa J,Kubono T.An experimental equation for dependence of duration of breaking arcs on supply voltage with constant circuit resistance[J].IEICE Transactions on Electronics,2005,E88C(8):1584-1589.
[8] 贾博文,武建文,刘俊堂,等.270V直流开断特性研究与耗散功率变化的Mayr模型仿真分析[J].中国电机工程学报,2019,39(5):1334-1342.
Jia Bowen,Wu Jianwen,Liu Juntang,et al.Research on DC breaking characteristics of 270V DC system and simulation analysis of the mayr model with variable dissipation power[J].Proceedings of the CSEE,2019,39(5):1334-1342.
[9] Li Shimin,Geng Yingsan,Liu Zhiyuan,et al.Influence of arc-melted cathode layer depth on vacuum insulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2017,24(6):3327-3332.
[10] 陈博博,屈卫锋,杨宏宇,等.小电流接地系统单相接地综合电弧模型与选线方法的研究[J].电力系统保护与控制,2016,44(16):1-7.
Chen Bobo,Qu Weifeng,Yang Hongyu,et al.Research on single phase grounding arc model and line selection for neutral ineffectively grounding system[J].Power System Protection and Control,2016,44(16):1-7.
[11] Duddell W.On the resistance and electromotive forces of the electric arc[J].Philosophical Transactions of the Royal Society of London,1904,203(1):305-342.
[12] Nottingham W B.A new equation for the static characteristic of the normal electric arc[J].Journal of the American Institute of Electrical Engineers,2013,42(1):12-19.
[13] 刘艳丽,郭凤仪,李磊,等.一种串联型故障电弧数学模型[J].电工技术学报,2019,34(14):2901-2912.
Liu Yanli,Guo Fengyi,Li Lei,et al.A kind of series fault arc mathematical model[J].Transactions of China Electrotechnical Society,2019,34(14):2901-2912.
[14] Bessis B,Messaad M,Khorie H.Study of electron emission at the cathode in an arc discharge[J].Electrical Engineering,2018,100(4):2737-2742.
[15] 李建南,张慧媛,王鲜花,等.中压电缆网接地故障的电弧建模及仿真研究[J].电力系统保护与控制,2016,44(24):105-109.
Li Jiannan,Zhang Huiyuan,Wang Xianhua,et al.Arc modeling and simulation of the ground faults of the middle voltage cable network[J].Power System Protection and Control,2016,44(24):105-109.
[16] Moon W,Kim J,Jo A,et al.Ignition characteristics of residential series arc faults in 220V HIV wires[J].IEEE Transactions on Industry Applications,2015,51(3):2054-2059.
[17] Georgijevic N L,Jankovic M V,Srdic S,et al.The detection of series arc fault in photovoltaic systems based on the arc current entropy[J].IEEE Transactions on Power Electronics,2016,31(8):5917-5930.
[18] 丛浩熹,李庆民,行晋源,等.基于能量平衡的潜供电弧燃弧时间计算方法[J].中国电机工程学报,2015,35(13):3450-3458.
Cong Haoxi,Li Qingmin,Xing Jinyuan,et al.Computation method of arcing time of the secondary arcs based on energy balance[J].Proceedings of the CSEE,2015,35(13):3450-3458.
[19] 高杨,王莉,张瑶佳,等.简化的Schavemaker交流电弧模型参数的计算方法研究[J].电力系统保护与控制,2019,47(8):96-105.
Gao Yang,Wang Li,Zhang Yaojia,et al.Research on the calculation method for the parameters of the simplified schavemaker AC arc model[J].Power System Protection and Control,2019,47(8):96-105.
[20] 王其平.电器电弧理论[M].北京:机械工业出版社,1992.
[21] 熊兰,曾泽宇,杨军,等.小电流直流故障电弧的数学模型及其特性[J].电工技术学报,2019,34(13):2820-2829.
Xiong Lan,Zeng Zeyu,Yang Jun,et al.Mathematical model and characteristics of low current DC fault arc[J].Transactions of China Electrotechnical Society,2019,34(13):2820-2829.