0 引言
目前，我国6～60kV中压配电系统广泛采用中性点非有效接地方式，而单相接地故障约占所有故障类型的80%[1]，简单接地故障问题已基本得到解决，选线正确率达到90%以上[2]。高阻接地时，系统故障信号相对微弱，使得故障特征的辨析难度加大[3-6]，易导致现有选线方法失效，由此需要一种选线方法，不仅能有效可靠地解决简单故障问题，还能够适应更多的复杂接地故障。
传统的选线法往往利用零序稳态量进行故障选线[7]，系统接地方式和运行方式很容易影响选线结果[8-9]，再加上目前系统对故障电流补偿方式的灵活多变[10]，此类选线方法已不再适应当前系统；而暂态行波选线法则不易受到上述问题的影响[11]，且高频故障行波信号具有一定耐过渡电阻性能[12]。先前的行波法选线策略对行波初始波头依赖较大，存在严重的选线死区[13-15]。后来随着行波积分比值思想的出现[16-17]，文献[18]提出单相反、正向行波积分比值法（Reverse and Forward Traveling Wave integral ratio，RFTW）进行故障选线，大大降低了行波选线的死区问题，也为后文构造判据提供了有力的借鉴。但该方法易受到行波全反射的影响，且高阻接地时的故障选线效果不理想，现场选线灵敏度和准确性较差。文献[19]提出利用零序暂态初始能量法选线，利用能量守恒的思想提高了高阻接地选线的正确率，为本文提供了有效思路。
暂态行波因携带丰富的故障信息，且行波在传输过程中满足能量守恒，因此提出方向行波能量法（Directional Traveling Wave Energy,DTWE），用以解决现有行波选线法针对特殊接地故障下灵敏度不高、准确度较低的问题。
1 方向行波法的理论分析
1.1 现有行波选线法的理论分析
故障后的网络可以当作故障前的负荷网络和故障分量网络的叠加[12]。图1为N条支路系统的故障分量网络图，发生B相接地故障，Ubf、ibf分别为故障点B相电压、电流初始行波，而UbF为故障点附加电压源电压，Rf为过渡电阻，各量关系为
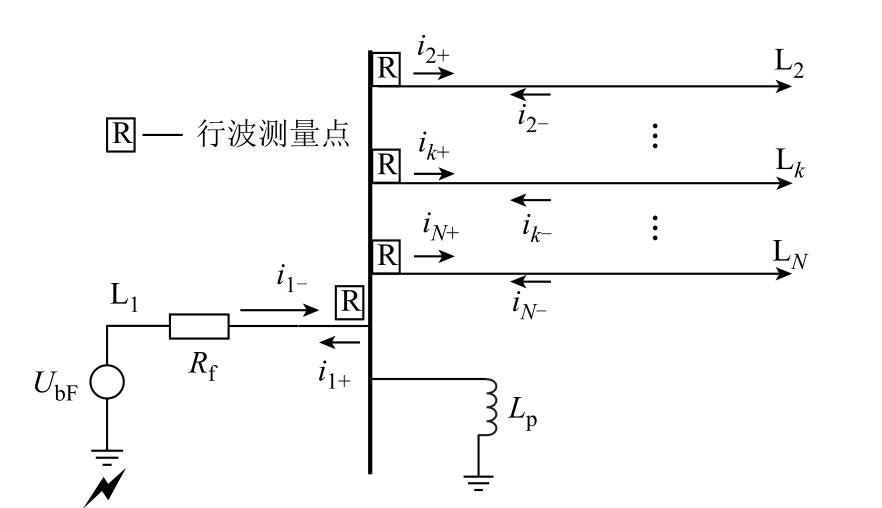
图1 N条支路配电系统故障分量网络图
Fig.1 Fault component network diagram of distribution system of N lines
由于故障初始行波为高频分量，只需要将故障信号滤去以工频和自振频率为主的信号及更高频噪声信号[20]，就可以得到仅由故障点处附加电源传来的初始行波。
设支路L1波阻抗为Z1，L2～LN的并联波阻抗设为Z∑，而消弧线圈Lp对高频故障行波近乎开路，故忽略其影响。电流行波沿支路L1在母线处反射系数 β1的计算公式为
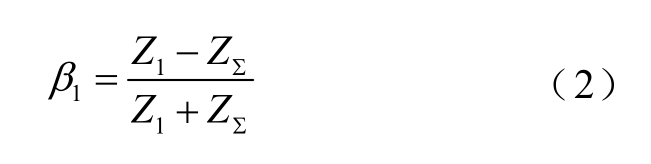
支路L1故障后，UbF产生故障初始行波并沿着支路L1向母线方向传播，在母线处发生折、反射。其反射行波沿L1原路返回；折射行波则沿着健全线路传播，到达末端或者不连续点后再发生折、反射。本文定义行波由母线向支路方向传播为正方向。
传统选线法利用相电流初始波头幅值和极性进行故障选线[14（]Initial Wave Head Method,IWHM），但方法严重依赖初始波头，如图2a所示，而初始波头持续时间极短，且易被噪声等因素影响导致波形不稳定，从而利用IWHM法故障识别较为困难。而RFTW法利用仅含正向行波和仅含反向行波的信号量进行积分比值，延长判据有效时间，提高了选线可靠性。
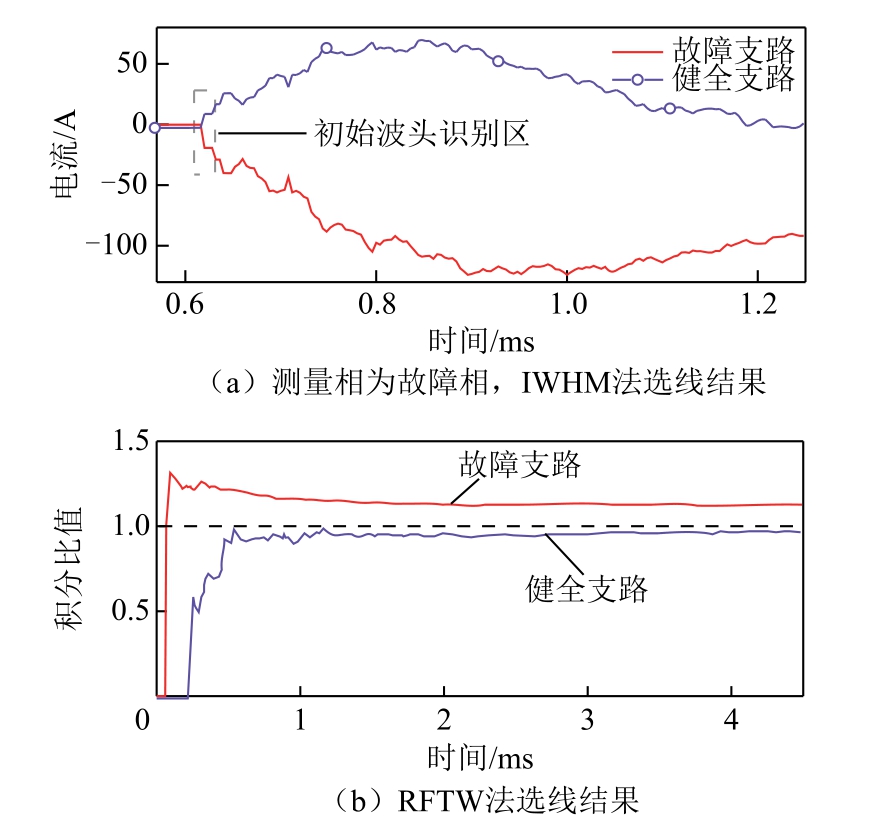
图2 现有行波选线方法选线结果
Fig.2 Line selection results of existing traveling wave line selection methods
RFTW选线方法利用电流反射系数绝对值小于1的原理，得知故障支路反、正向行波积分比值大于1，而健全支路反、正向行波积分比值小于1，该方法的选线判据波形如图2b所示。
由于我国配电网络普遍为架空-电缆混合网络，架空线路波阻抗一般为电缆线路波阻抗的十几倍，且故障频发线路多为架空线路，可知多数情况下Z1远大于Z∑，β1很接近1，从而RFTW法对故障线路的比值判据非常接近于1，灵敏度较低，文献[18]中的仿真也证明这种情况的存在。在这种情况下，根据行波能量守恒，还可以得知只有极少部分故障行波能量由故障线路透射到健全线路。
从图2b中可以看到，由于大部分电流行波在健全线路末端近乎全反射，使得判据值很接近于1。可知健全线路和故障线路的选线判据均易出现灵敏度较低的现象，故障难以准确识别，而且噪声更容易模糊判据所反映的故障特征。
架空线路高阻接地时，由式（1）可知，故障线路初始行波受到削弱，而透射到各个健全线路的故障行波能量更是微乎其微，利用RFTW法测量相为健全相时，健全线路信号所携带的故障特征将更加不明显，如图3所示。这导致对健全线路发生误判概率增加，增加了供电系统的不稳定性。
图3 故障线路与健全线路的故障初始行波
Fig.3 Faulty initial traveling waves of faulty branches and sound branches
综上所知，RFTW法虽解决了传统选线方法对初始波头的过度依赖，但针对特殊故障难以选线，判据需要做到对故障信息的全局把握。
1.2 零模电流方向行波的构建
故障线路上任一点测得的暂态电流都是正向行波和反向行波的叠加[21]，设ZC为故障线路波阻抗，电流正向行波和反向行波分别为
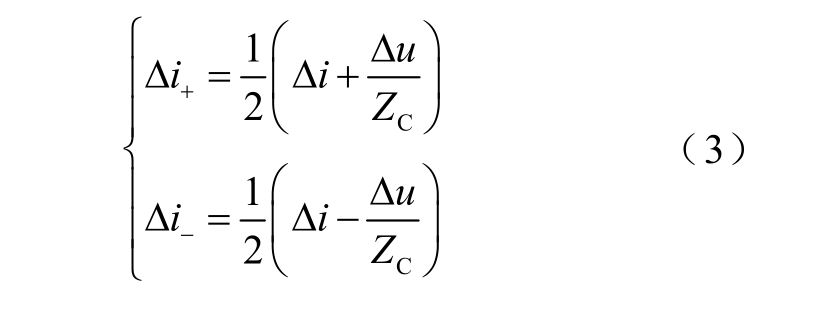
式中，Δu和Δi分别为各线路测量设备测量到的电压和电流故障分量，且仅与故障分量网络有关。
利用凯伦贝尔变换矩阵得到互为独立的零模、线模电流行波[22]。为了避开三相耦合的影响，使得判据更加稳定，利用独立零模量构造方向行波表达式，故障后各出线路零模正、反向电流行波为
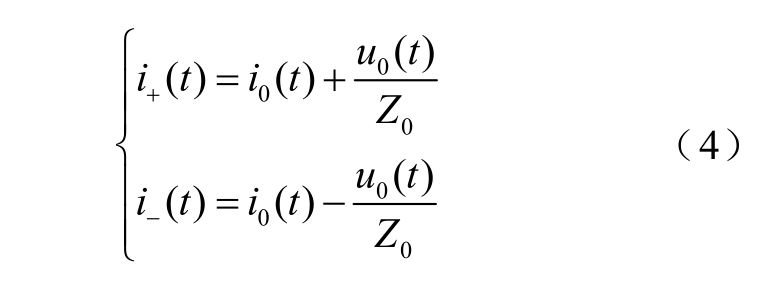
式中，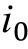
为各线路零模电流；u0为母线零模电压，u0=(uA+uB+uC)/3；
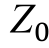为该线路零模等值波阻抗。
2 方向行波能量法
2.1 零模电流方向行波能量表达式的构建
由于电流行波的折射系数0＜α＜2，且架空线路和电缆线路波阻抗相差较大，理论上折射电流行波的初始波头有可能大于入射行波的初始波头，显然无法利用能量守恒的概念。于是引入波阻抗，构造行波能量[23]，计算公式为
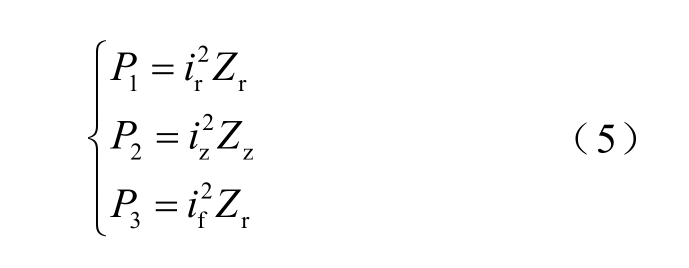
式中，P1为不连续点入射行波能量；P2为折射行波能量；P3为反射行波能量，根据能量守恒。显然有P1=P2+P3，且P1＞P2。
如图1，图中的电流下标“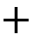
”表示各线路的零模正向电流行波，下标“
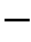”表示各线路零模反向电流行波。线路L1发生故障后（第2节理论公式全部基于L1故障推导），设p1
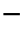(t)和p1
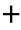(t)分别为线路L1的反向初始行波能量和正向初始行波能量，而在母线折射到健全线路的正向初始行波总能量设为p∑+(t)，能量值均为对时间t的积分，方便后文利用积分比值构建判据。各量满足关系为
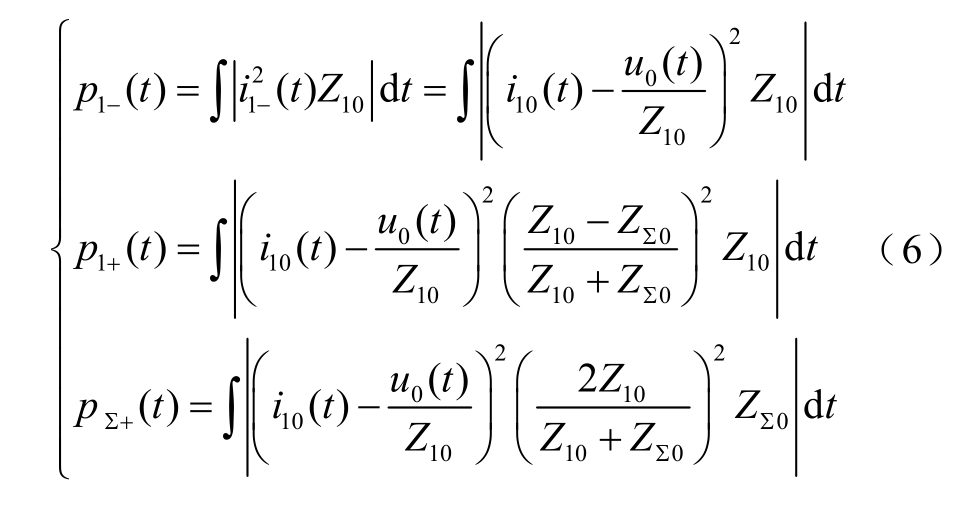
式中，ZΣ0为所有健全线路并联零模波阻抗；Z10为L1的零模波阻抗。与式（5）大小关系相同，式（6）中的各量满足 p1−(t)＞ p ∑+(t)。
对于任意一个健全支路k，k≠1，设Zk0为该健全支路k的零模等效波阻抗，则健全支路k正向行波能量为
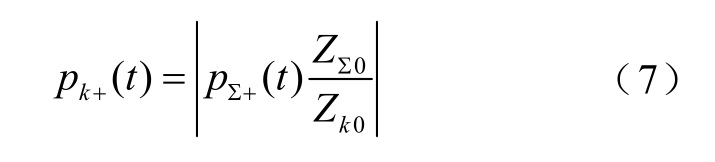
2.2 对于故障支路的判据分析
将故障支路L1的反向行波能量与所有支路正向行波能量的1/2的比值设为B1，因为 p1−(t)＞p∑+(t)，显然可以满足
当架空-电缆混合配电系统发生架空支路故障，行波在母线处反射系数绝对值|β1|近乎为1，此时p1−(t)远大于 p∑+(t)，比值B1的值趋向于2，若根据B1大于1为故障支路，显然判据较灵敏。若|β1|趋向于0，B1则更趋向于1，比值判据灵敏度降低，此时设任意一条健全支路的 pk +(t)减去 pk −(t)的差值为
，由于行波传输过程总是存在能量耗散，故
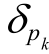＞0，则所有健全支路的反向初始行波能量之和p∑−(t)为
显然有 p∑−(t)＜ p ∑+(t)，于是故障支路的选线判据变为
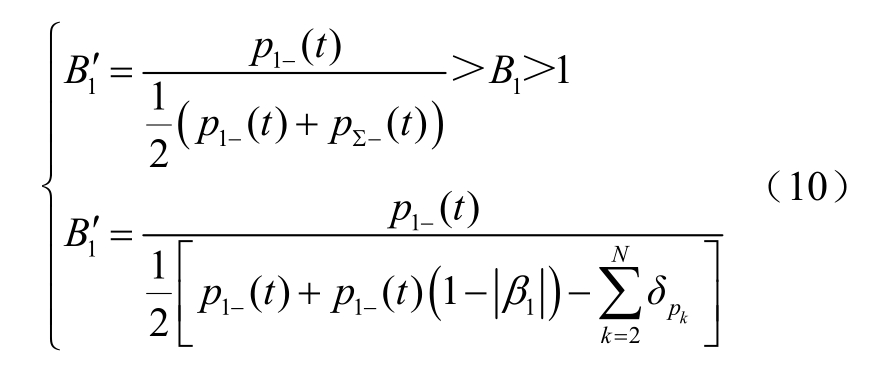
可知选线灵敏度又经过了提升。分析可知，故障支路的B1受到|β1|的影响较大，B1的值和|β1|的关系如图4所示，1/|β1|即为故障支路L1的p1
(t)和p1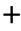
(t)的比值，其中，0＜|β1|＜1。由于所有健全支路的反、正向行波能量差值之和较大，故在|β1|取值范围内，故障支路的比值判据均能满足大于1。
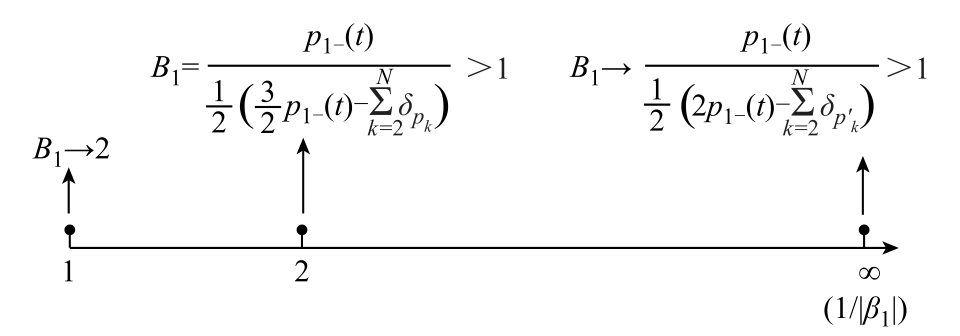
图4 B1和|β1|的关系
Fig.4 The relationship between B1 and |β1|
2.3 对于健全支路的判据分析
对于任意健全支路k的比值判据Bk，k≠1，得到
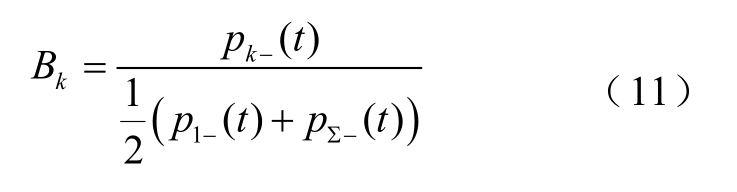
因为某健全支路k的 pk −(t)是所有健全支路总能量 p∑−(t)的一部分，显然 pk −(t)＜ p ∑−(t)，且 p∑−(t)又是 p1−(t)能量中的一部分。当健全支路末端发生近乎全反射时，即反射系数很接近于1，则 pk−(t)非常接近于 pk +(t)，且 pk −(t)＜ pk+(t)，这时显然满足关系：pk −(t)＜ pk +(t)＜ p ∑−(t)＜(p1−(t)+p∑−(t))/2，若 利 用RFTW法的选线判据约为
由以上分析可知，发生全反射时的Bk非常接近于1，选线灵敏度较差，另外，高阻接地后健全支路的故障信号极其微弱，即pk
(t)和pk+(t)幅值极小，此时RFTW法得出的比值Bk所反映的故障特征将更加不可靠。而基于本文，选线判据为
显然
，也较RFTW选线方法在灵敏度上有了较大提升，避免了行波全反射时判据不灵敏的情况。
2.4 基于反向行波能量构造判据
令 p−(t)= p1−(t)+p∑−(t)为所有支路的反向初始行波总能量，pi −(t)为第i条支路的反向初始行波能量。行波能量由积分计算所得，目的也是为了避免对行波初始波头的依赖，对比值判据的有效性有一个保持作用，提高选线的可靠性，判据为
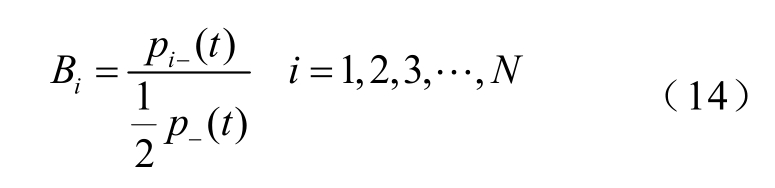
当Bi＞1，则第i条支路为故障支路；当Bi＜1，则第i条支路为健全支路。
由2.2节和2.3节的公式推导可知，在保证故障支路比值判据大于1、健全支路比值判据小于1的前提下，判据可对整体故障信息充分把握，增加了故障支路的辨识度。
2.5 对于母线故障的判据分析
为了区别母线故障和支路故障，利用现有测量数据，令所有支路的正向行波能量之和与所有支路的反向行波能量之和的比值Bm为
2.5.1 支路故障
当支路L1发生单相接地故障时，且不忽略消弧线圈极少部分故障行波能量的流入及母线上行波能量的微量散射，有以下关系成立：
可知当支路故障时判据Bm＜1，即
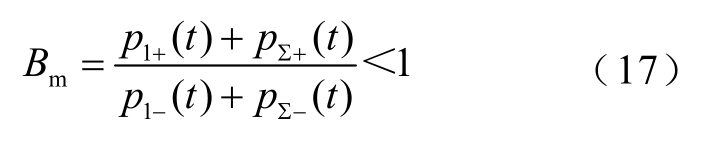
因为是最先捕获到 p1−(t)、p1+(t)和 p∑+(t)的值，所以判据从一开始就满足小于1，随着反向行波的到来，比值逐渐减小并趋于一个更小于1的稳定值。
2.5.2 母线故障
母线接地故障时，由于任意支路的正向行波能量都大于反向行波能量，于是Bm＞1，即
且p+(t)最先被捕获，此时求出的比值Bm为无穷大，且保持到测量设备测量到第一个反向行波能量值后才开始衰减，本文将Bm在此时间段的波形特征称为“无穷大时间”。
3 DTWE选线方法应用性分析
3.1 行波能量传输过程中的衰减问题
零模行波分量相对线模量衰减较快，且行波频率越高衰减越快[24-25]，而零模行波传输速度也受到很多因素的影响[26-27]。
针对故障支路，由于配电支路送电距离一般较短，为6～20km，行波到达母线出线处的测量点所需时间极短，零模行波衰减的量也较少。行波在健全支路发生末端反射时，在支路上进行了往返路径，因此测到的反向行波能量衰减程度相比故障支路一般较大，由式（8）～式（15）推导和图4可知，这会使得δpk增大，B1的值将更趋向于2，而所有健全支路
的值将更加小于2-B1，可见这有利于选线灵敏性。
3.2 高频故障信号的有效传变问题分析
实际工程中，故障行波频率多集中在8～200kHz，而电流互感器（CT）可对几百kHz的电流行波信号进行有效传变。针对电压互感器（PT），实际中存在两种PT：电容式和电磁式。电容式PT分压电容两端抽取测得的突变电压信号上升速度慢，传变截止频率低。电磁式PT磁化电抗相对高频电流行波开路，且感性线圈传变突变电压信号时上升速度极快，故可以准确、实时地为二次系统传变行波有效数据。文献[28]指出电磁式PT容量不同时，对高频故障电压行波都有几百kHz的良好传变性能。
根据配网现有电磁式PT参数（均已经归算至一次侧）：一、二次线圈等效漏感之和L=24mH，一、二次侧等效杂散电容：C1=500pF，C2=5pF，得到PT截止频率为318kHz。
3.3 选线方法DTWE的多数据化判别依据
系统发生接地故障后，故障支路和健全支路的零模正、反向电流波形如图5所示。可知故障支路的正、反向初始行波和健全支路的正向初始行波几乎同时到达测量点，而健全支路反向初始行波滞后正向初始行波一定时间到达测量点。
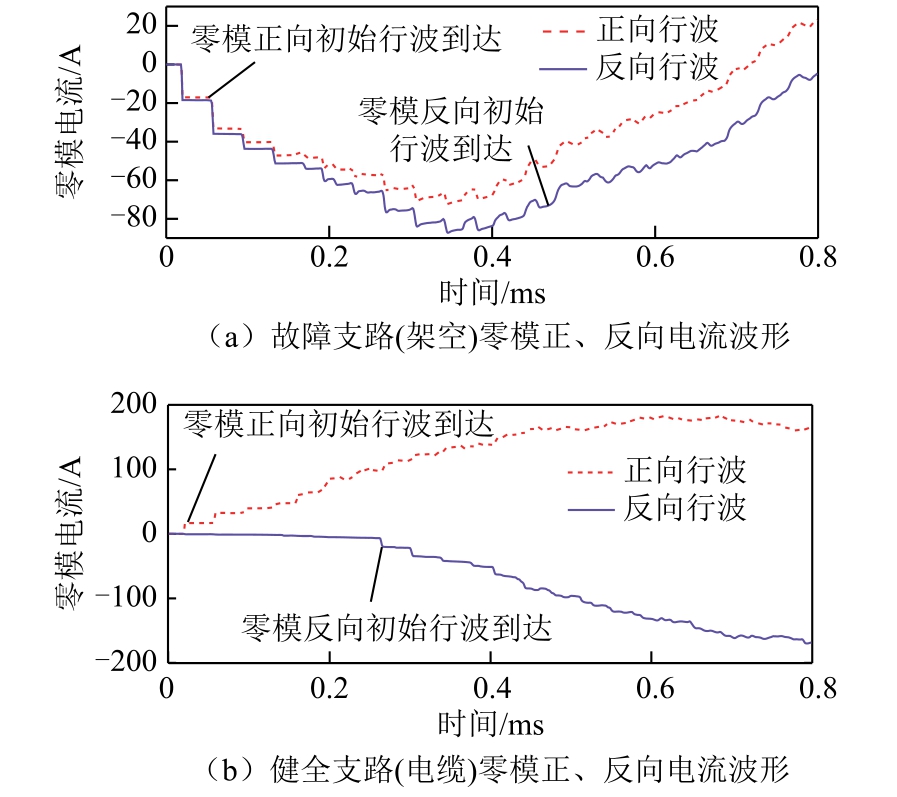
图5 故障支路和健全支路的正、反向行波到达时间
Fig.5 Forward and reverse initial travelling wave arrival times of faulty and healthy branches
由DTWE法的判据比值表达式可知，检测点最先检测到故障支路的反向行波能量，此时比值为2，且一直保持到健全支路反向行波到达检测点之后才有所下降，而此期间健全支路的比值判据为0。DTWE法在此时选线灵敏度达到最高，本文将该波形特点称为“最灵敏时间”，该特点反映了“故障反行波在故障支路和健全支路到达检测点的时间不同”的故障特征。
DTWE法利用故障信息的整体性，究其根本其实就是利用故障支路的初始行波能量大于任意健全支路的关系来构造选线判据，因此比值判据也是故障支路的最大，以此作为选线判据，也可以选出故障支路。本文定义选线DTWE法的这个判别依据为“故障支路能量最大”。
由此可知DTWE法仅仅在比值判据上具有选线自具性（自具性：仅利用本支路故障特征进行故障选线，不与其他支路相比较），然而利用的却是所有支路故障信息。针对一般的简单故障，可利用单支路零模反、正向行波能量积分比值法（Zero-mode reverse and forward traveling wave energy integral ratio method，Z-RFTW）选出正确的故障支路，积分比值大于1为故障支路，小于1为健全支路，若所有支路比值均小于1则母线故障。且该方法检测量也是零模方向行波能量，可直接利用DTWE法所得数据即可选线，以此又为DTWE法提供了一条选线判定依据。
4 故障行波的滤波工具
本文对高频故障行波的滤波工具为小波变换，其处理含有奇异突变信号具有非常敏感的特性[29]，可将信号进行多尺度变换，为本文所提选线方法提供可靠有效的数据支持。而二进离散小波不仅简化了计算量还保留了故障行波的细节特性，也为现场硬件的配置降低难度。二进离散小波表达式为[30]
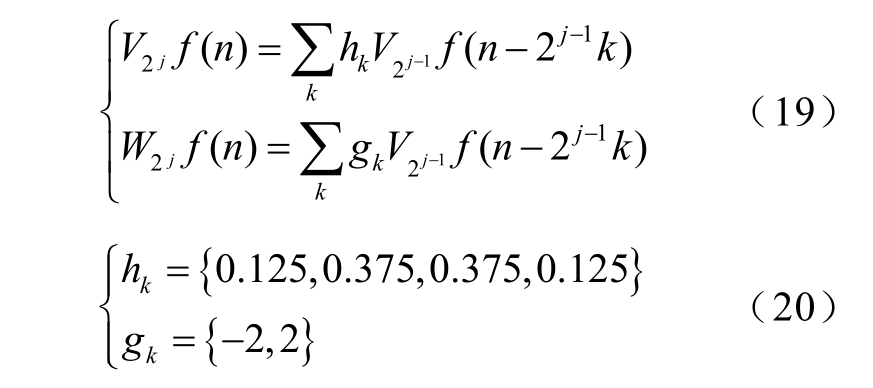
式中，n为采样序号；j为小波变换尺度；hk和gk为由小波函数决定的小波系数；k=-1,0,1,2。
5 选线系统实施方案
本文行波能量法故障选线策略是基于前人理论及实验方案的基础上推出，因此，选线策略具有一定的可行性基础[31-32]。本文给出选线方法实施方案，如图6所示。
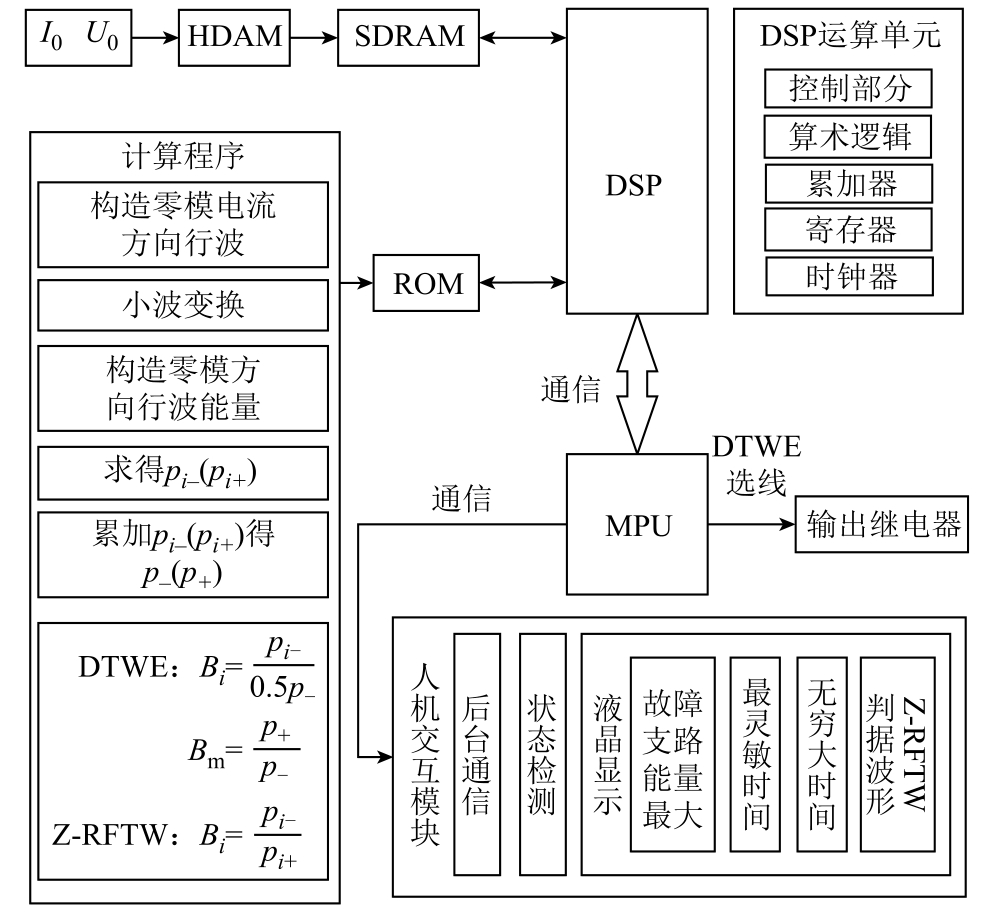
图6 选线系统构成图
Fig.6 Line selection system composition diagram
图6中，HDAM（high-speed data acquisition module）为高速数据采集模块；DSP为信号处理芯片，具有多个运算单元；SDRAM为储存录波数据以供DSP调用；ROM为储存核心算法程序以供DSP调用；MPU（micro processor unit）为具有逻辑判断功能的微处理器。
6 仿真验证
6.1 仿真模型及步骤
实际仿真电路如图7所示，系统为五条支路，利用仿真软件Matlab中的Simulink模块建立10kV配电系统，架空线路和电缆线路参数[19]见表1。
图7 系统仿真模型
Fig.7 System simulation model diagram
表1 线路参数
Tab.1 Line parameters
具体仿真步骤如下：
1）采样设备采样率为500kHz，采样步长为2μs。
2）测出母线零模电压
和各支路出线零模电流，利用式（4）计算得出各支路零模电流正、反向行波录波数据。
3）将步骤2）所得数据进行二进离散小波变换，分解得到以下频带的小波系数：125～250kHz，62.5～125kHz，31.25～62.5kHz，15.625～31.25kHz，将频带62.5～125kHz和频带31.25～62.5kHz的小波系数叠加，利用式（6）将所得一系列叠加值与波阻抗组合，从而构建方向行波能量表达式，并进行后续比值计算。
4）为对比选线法的判据灵敏度，本文设置选线装置动作的灵敏度系数为Ksen=1.1，对应于后文判据比值波形图中的非灵敏区，落在非灵敏区的比值取值范围为0.9＜Bi＜1.1，在此区域保护装置的误动概率最大，需要指出选线判据灵敏度和选线装置动作灵敏度（Ksen）的指代含义不同。合理的Ksen在继电保护中的作用是既使得选线判据能被装置可靠识别，同时要降低保护装置的误动概率。
5）当支路L1发生B相接地故障后，接地电阻为10Ω，求出各线路的比值判据，选出故障支路。
图8a为各支路测量点首次测量到的零模方向行波波头能量绝对值大小，图中δp为L1反、正向行波能量差值，其大小和所有健全线路波头能量之和相接近，考虑到行波能量在健全线路上的耗散，验证了行波传输过程中满足能量守恒。
图8b为DTWE法选线结果。随着暂态能量的衰减，比值波形也逐渐稳定至某一个值，判据满足故障支路大于1、健全支路小于1，灵敏度较高，且波形符合“故障支路能量最大”特点。如图8c，因为最先测量到的是故障支路的反行波能量，故B1的值最先到达2，符合“最灵敏时间”波形特征。
Z-RFTW法的选线结果如图8d所示。可见选线具有自具性，只有健全支路L4和L5的判据不太灵敏。当RFTW法对具有三角形接法的母线补偿电容的系统进行判别故障时，线模电流在母线处被过滤，可知健全线路只有零模电流，健全线路比值判据和本次仿真效果相同。
图8 仿真结果
Fig.8 Simulation results
图8e为RFTW法的选线结果，测量相为A相，其他接地条件不变。故障支路L1是波阻抗较大的架空线，故障行波在母线处的电流反射系数较为接近1，可知故障行波接近全反射，B1值为1.124（取其波形稳定值，后文同），接近于非灵敏区。健全支路L4的B4触及非灵敏区，行波近乎全反射，而支路L2、L3、L5的比值判据为0.805、0.794、0.913。可知RFTW法受到行波全反射影响较大，总体选线灵敏度不高。而对比DTWE法的选线结果，则避开了该问题，具有较好的选线灵敏性，与前文理论分析相符。
对于母线故障问题的区分，根据式（15），通过仿真得出图9所示的波形图，母线故障接地电阻同为10Ω。暂态过程结束后，波形趋于稳定，此时，母线故障积分比值为1.58，支路故障积分比值为0.64，满足判据。且与前文DTWE法具有“无穷大时间”的结论相符。
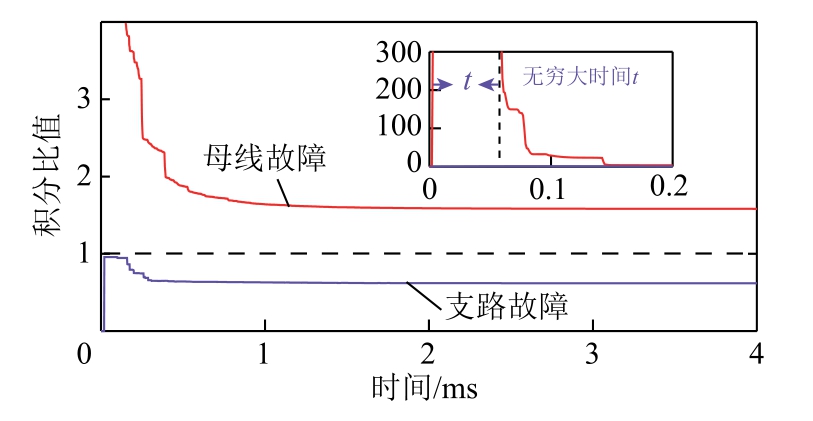
图9 母线故障和支路故障的判别结果
Fig.9 Discrimination results of bus faults and branch faults
6.2 低采样率下的选线效果
IWHM法当测量相为健全相时，在零模到达后，线、零模混叠后近乎为零，电流各模量行波波形如图10所示。
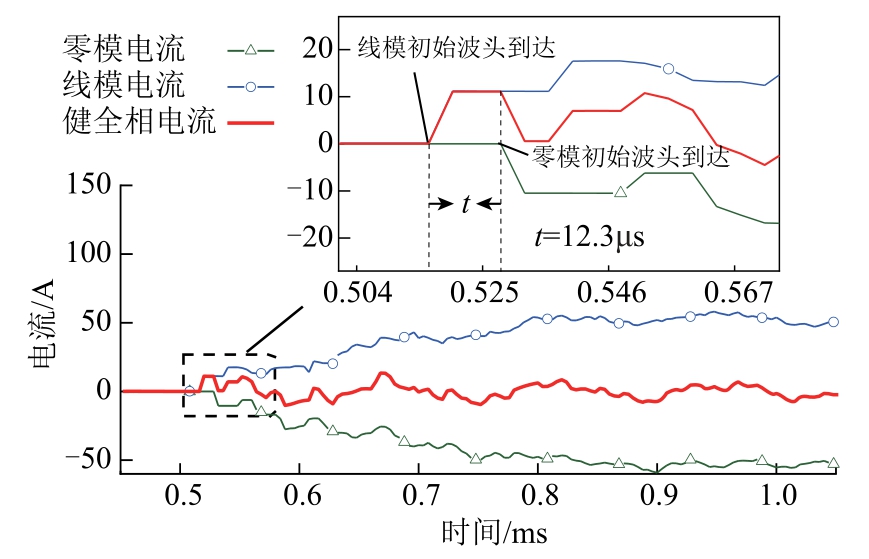
图10 健全相电流各模量行波波形
Fig.10 Traveling wave waveform diagram of each modulus of sound phase current
这使得相电流初始波头持续时间更加短暂，可知，IWHM法还要在零模行波到达之前完成故障甄别。图10中线、零模电流到达时刻仅相差12.3μs，可知若采样时间间隔超过该值，IWHM法将失效，然而故障点距离测量点较近时，线、零模电流到达时间差将更加短暂，IWHM法更将难以选线。而RFTW法检测量为健全相电流时，方向行波量的幅值也会受到零模量削弱，甚至填平，使得检测信号的故障行波含量减少，仅提高采样率并不能有效解决该问题。
DTWE法不仅在更长的时间窗具有选线效果，且采样数据为独立的零模行波信号，从采样原理上讲相比以往选线法更加准确可靠。本次仿真线路L1故障，故障点距离检测点3km，接地电阻100Ω，故障电压初相角10°，本节将采样率降为25.6kHz，采样步长为39.6μs。取RFTW法和DTWE法的积分比值稳定值进行灵敏度比较，见表2。
表2 低采样率下两种选线方法的判据灵敏度比较
Tab.2 Comparison of criteria sensitivity of two line selection methods at low sampling rate
6.3 高阻接地下的选线准确率与灵敏度分析
本次仿真设置L1支路B相接地故障，故障时间为0s，接地电阻为1kΩ，模拟实际系统中存在的轻微噪声，加入信噪比150∶1的均匀分布伪随机数，信噪比为信号幅值与噪声幅值之比。选线结果为：RFTW法下的支路L5发生误判，选线失败；DTWE法所有支路判别正确，且选线灵敏度较高，选线成功。两种方法下支路L1、L5选线结果如图11所示，方法RFTW的测量相为健全相A相。
图11 接地电阻1500Ω时，方法RFTW和DTWE选线结果对比
Fig.11 Comparison of RFTW and DTWE line selection results when ground resistance is 1500Ω
保持噪声信噪比不变，DTWE法的其他选线结果见表3，表中Rf为过渡电阻，l为测量点距离故障点的距离，φ为故障相初始角。由表3可以看出，DTWE法对各种故障接地条件都具有良好的选线准确度，无论简单低阻接地还是复杂高阻接地，故障支路的判据和健全支路的判据选线灵敏度较高，与前文理论推导相符合。且符合DTWE法“故障支路能量最大”的特征。
表3 其他接地条件下方法DTWE的仿真结果
Tab.3 Simulation results of method DTWE under other grounding conditions
注：表3中的数据根据仿真波形图稳定后所取，并按照四舍五入取其近似值，保留精确值至小数点后2位。线路L4故障距离大于6m的，表示故障位置在它的分支线路上。
表4为不同支路故障，分别对应的故障支路零模反、正向行波能量积分比值，比值在无噪声下测得。该比值由行波在故障线路上到达母线处的反射系数绝对值|β|决定，且比值等于1/|β|。结合表3、表4数据分析可知，|β|不同时DTWE法选线均具有良好的选线效果。
表4 故障支路不同，方法Z-RFTW下的故障支路比值
Tab.4 When the faulty branch is different,the ratio of the faulty branch under the method Z-RFTW
6.4 选线方法的抗噪性分析
在实际配电系统中，信号获取过程中往往存在噪声干扰。本次模拟噪声的方法是在电流和电压采集通道同时叠加均匀分布伪随机数和平坦的白噪声数据，信噪比为30:1。故障支路L1线路总长度改为23km，故障距离设置为20km，B相接地，接地电阻设为1 500Ω，RFTW法的测量相为故障相B相。两种方法下支路L1、L3选线的结果如图12所示。
由图12可见RFTW法对故障支路和健全支路均已误判，如果测量相为健全相时，故障行波所携带的故障信号将更加微弱，更难以选线。DTWE法下所有支路均符合正确的选线判据，为方便表述，其余支路波形不再显示，故障支路比值虽然有下降趋势，但在6ms时间窗内仍具有良好的选线灵敏性，且6ms时比值约为1.375，可知其他支路判据比值必然小于0.625，符合健全支路比值小于1。
图12 信噪比为30时DTWE法和RFTW法的选线结果对比
Fig.12 Comparison of line selection results between DTWE and RFTW at 30 SNR
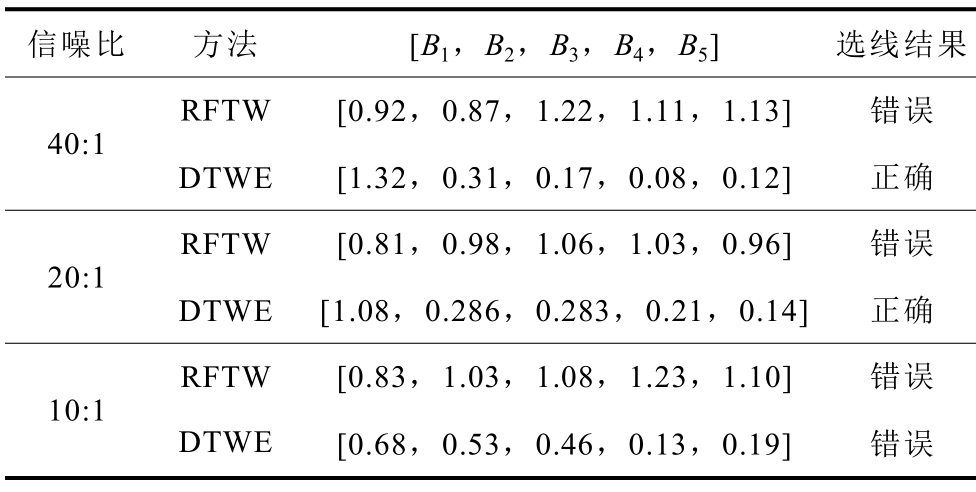
接地条件不变，改变信噪比后其他选线结果见表5。因为噪声一直存在，两种方法的判据比值波形无法稳定在某一个值，但3ms时间窗后波形波动逐渐减小，取故障时间窗6ms时的波形值作为选线结果。可以看出，在信噪比小于等于40时，RFTW法均不具有有效性。当信噪比为10时，强噪声背景下，两种选线方法均已失效。而DTWE法可利用判据“故障支路能量最大”的故障特征选出故障线路。
表5 其他信噪比时两种选线方法的选线结果
Tab.5 Line selection results of two line selection methods with different signal to noise ratios
7 选线方法DTWE的现场实际故障验证
现场实验的方式是通过调取某市变电站近三年多次单相接地故障数据，进行一系列数据处理和计算。
实际选线波形如图13所示，采样率为21kHz。图13a为某次一般简单型单相接地故障，图13b为架空线发生的电弧接地故障波形。
针对两种不同的接地故障，图13a、图13b波形均满足故障线路判据大于1，健全线路判据小于1，与理论推导相符。其他两组故障选线结果见表6，其中支路编号（1）、（5）、（6）为架空线路，②为架空-电缆混合线路，3代表电缆线路。
表6 其他两组信号的选线结果
Tab.6 Line selection results of the other two sets of signals
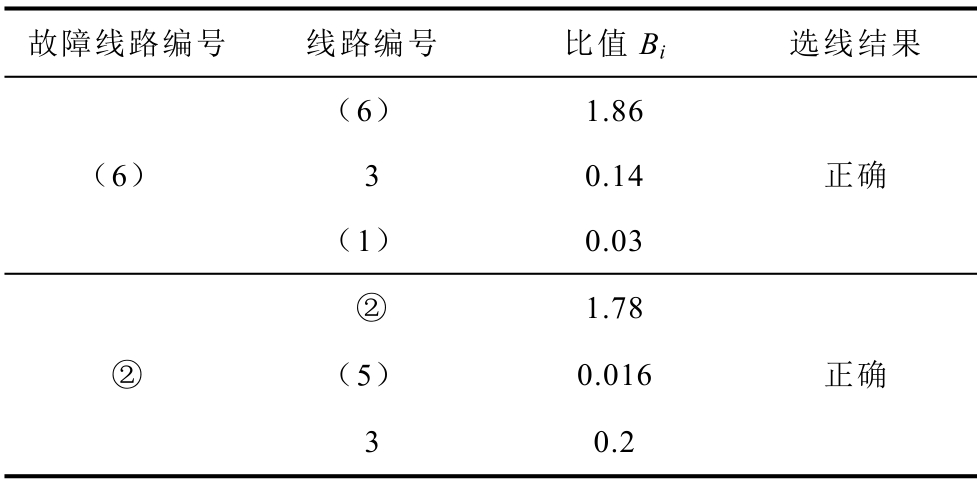
图13 现场实际数据选线结果
Fig.13 Line selection results of actual data on site
8 结论
方向行波能量选线的方法分别从信号选择、判据的构造及故障的判定方面对选线灵敏度和准确度有一个较大的提升。
1）信号选择：行波选线不受系统接地方式和运行状态的影响，本身适应性强。选用独立的零模行波信号，在保证有效性的前提下避开相间耦合影响，且不需要判别故障相，判据更稳定。本文所提选线策略并不需要更换测量设备的连接方式，便可同时为DTWE法和Z-RFTW法提供数据来源，也为未来行波选线法的智能融合、多数据化判别依据提供便利和可行性。
2）判据的构造：DTWE法选线判据简单明了，且仅对选线判据来说，不需要与其他线路做比较。分析可知DTWE法从判据上避开了行波全反射问题，最大化放大选线灵敏度，对复杂单相接地故障问题具有良好选线效果。
3）故障的判定：DTWE法充分把握故障信息，在选线比值判据“故障支路大于1，健全支路小于1”的前提下，判据波形具有“最灵敏时间”和“故障支路能量最大”特征，且在判别母线故障时，判据波形又具有“无穷大时间”特征。这些多数据化判别依据较为完整地反映了故障特征，为检修人员提供更多的故障辨别视角，从功能上更具有实用性。
仿真和实验证明，该方法使得行波法适应范围更加广泛。
[1] 郭丽伟,薛永端,徐丙垠,等.中性点接地方式对供电可靠性的影响分析[J].电网技术,2015,39(8):2340-2345.
Guo Liwei,Xue Yongduan,Xu Bingyin,et al.Research on effects of neutral grounding modes on power supply reliability in distribution networks[J].Power System Technology,2015,39(8):2340-2345.
[2] 徐丙垠,薛永端,冯光,等.配电网接地故障保护若干问题的探讨[J].电力系统自动化,2019,43(20):1-7.
Xu Bingyin,Xue Yongduan,Feng Guang,et al.Discussion on several problems of earthing fault protection in distribution network[J].Automation of Electric Power Systems,2019,43(20):1-7.
[3] 刘健,张志华,李云阁,等.基于故障相接地的配电网单相接地故障自动处理[J].电力系统自动化,2020,44(12):169-177.
Liu Jian,Zhang Zhihua,Li Yunge,et al.Automatic processing of single-phase grounding fault in distribution network based on fault phase grounding[J].Automation of Electric Power Systems,2020,44(12):169-177.
[4] 龙毅,欧阳金鑫,熊小伏,等.基于零序功率变化量的配电网单相高阻接地保护[J].电工技术学报,2019,34(17):3687-3695.
Long Yi,Ouyang Jinxin,Xiong Xiaofu,et al.Protection principle of single-phase high resistance fault for distribution network based on zero-sequence power variation[J]. Transactions of China Electrotechnical Society,2019,34(17):3687-3695.
[5] Ghaderi A,Mohammadpour H A,Ginn H L,et al.Highimpedance fault detection in the distribution network using the time-frequency-based algorithm[J].IEEE Transactions on Power Delivery,2015,30(3):1260-1268.
[6] 董俊,李一凡,束洪春,等.配电网馈出线路单相永久性接地故障性质辨识方法[J].电工技术学报,2020,35(21):4576-4585.
Dong Jun,Li Yifan,Shu Hongchun,et al.Study on identification method of single phase permanent ground fault in distribution network feedout line[J].Transactions of China Electrotechnical Society,2020,35(21):4576-4585.
[7] 林湘宁,高艳,刘沛,等.基于零序补偿导纳的小电流接地系统单相故障保护新方法[J].中国电机工程学报,2006,26(10):45-49.
Lin Xiangning,Gao Yan,Liu Pei,et al.A novel method to identify the single phase-to-earth fault in the neutral un-effectual grounded system using the zero modulus compensated admittance[J].Proceedings of the CSEE,2006,26(10):45-49.
[8] 金涛,褚福亮.基于暂态非工频零序电流的含DG新型配电网的接地选线方法[J].电工技术学报,2015,30(17):96-105.
Jin Tao,Chu Fuliang.A fault line-selection method in new distribution network with DG based on transient non-power frequency zero sequence current[J].Transactions of China Electrotechnical Society,2015,30(17):96-105.
[9] 刘渝根,王建南,米宏伟,等.10kV配电网中性点接地方式的优化研究[J].高电压技术,2015,41(10):3355-3362.
Liu Yugen,Wang Jiannan,Mi Hongwei,et al.Optimization research on neutral grounding mode of 10kV distribution networks[J].High Voltage Engineering,2015,41(10):3355-3362.
[10] 周兴达,陆帅.一种基于消弧线圈和静止同步补偿器协同作用的配电网消弧结构与方法[J].电工技术学报,2019,34(6):1251-1262.
Zhou Xingda,Lu Shuai.An arc-suppression method based on the coordinated operation of the petersen coil and the static synchronous compensator in distribution networks[J].Transactions of China Electrotechnical Society,2019,34(16):1251-1262.
[11] 董新洲,毕见广.配电线路暂态行波的分析和接地选线研究[J].中国电机工程学报,2005,25(4):3-8.
Dong Xinzhou,Bi Jianguang.Analysis on transient traveling wave and study on fault line selection for distribution lines[J].Proceedings of the CSEE,2005,25(4):3-8.
[12] 郑玉平,司鑫尧,吴通华,等.特高压半波长交流输电线路的行波保护[J].电力系统自动化,2020,44(18):124-131.
Zheng Yuping,Si Xinyao,Wu Tonghua,et al.Travelling wave protection of UHV half-wavelength AC transmission lines[J].Automation of Electric Power Systems,2020,44(18):124-131.
[13] 董新洲,周双喜.单相接地故障行波分析[J].电力系统自动化,2005,29(23):29-32.
Dong Xinzhou,Zhou Shuangxi.Analysis of single-phaseto-ground fault generated traveling waves[J].Automation of Electric Power Systems,2005,29(23):29-32.
[14] 施慎行,董新洲.基于单相电流行波的故障选线原理研究[J].电力系统保护与控制,2008,36(14):13-16.
Shi Shenxing,Dong Xinzhou.Study of fault line selection using single-phase current traveling waves[J].Power System Protection and Control,2008,36(14):13-16.
[15] 毕见广,董新洲,周双喜.基于两相电流行波的接地选线方法[J].电力系统自动化,2005,29(3):17-20.
Bi Jianguang,Dong Xinzhou,Zhou Shuangxi.Fault line selection based on two-phase current traveling wave[J].Automation of Electric Power Systems,2005,29(3):17-20.
[16] 张帆,潘贞存,张慧芬,等.基于方向行波的小电流接地系统故障选线[J].中国电机工程学报,2007,27(34):70-75.
Zhang Fan,Pan Zhencun,Zhang Huifen,et al.Fault line selection in non-solidly earthed network based on direction traveling wave[J].Proceedings of the CSEE,2007,27(34):70-75.
[17] Zou G B,Gao H L.Fast pilot protection method based on waveform integral of traveling wave[J].International Journal of Electrical Power &Energy Systems,2013,50(1):1-8.
[18] 姜博,董新洲,施慎行.基于单相电流行波的配电线路单相接地故障选线方法[J].中国电机工程学报,2014,34(34):6216-6227.
Jiang Bo,Dong Xinzhou,Shi Shenxing.A method of single phase to ground fault feeder selection based on single phase current traveling wave for distribution lines[J].Proceedings of the CSEE,2014,34(34):6216-6227.
[19] 方毅,薛永端,宋华茂,等.谐振接地系统高阻接地故障暂态能量分析与选线[J].中国电机工程学报,2018,38(19):5636-5645.
Fang Yi,Xue Yongduan,Song Huamao,et al.Transient energy analysis and faulty feeder identification method of high impedance fault in the resonant grounding system[J].Proceedings of the CSEE,2018,38(19):5636-5645.
[20] 要焕年,曹梅月.电力系统谐振接地[M].北京:中国电力出版社,2000.
[21] 邬林勇,何正友,钱清泉.一种提取行波自然频率的单端故障测距方法[J].中国电机工程学报,2008,28(10):69-75.
Wu Linyong,He Zhengyou,Qian Qingquan.A single ended fault location method using traveling wave natural frequency[J].Proceedings of the CSEE,2008,28(10):69-75.
[22] 葛耀中.新型继电保护与故障测距原理与技术[M].西安:西安交通大学出版社,1996.
[23] 汪梅,朱亮,张国强,等.基于小波能量谱的T型线路故障定位新算法[J].振动•测试与诊断,2018,38(3):479-485.
Wang Mei,Zhu Liang,Zhang Guoqiang,et al.A new T-line fault location algorithm based on wavelet energy spectrum[J].Journal of Vibration,Measurement&Diagnosis,2018,38(3):479-485.
[24] Jia Huibin,Ruben S.An improved traveling-wavebased fault location method with compensating the dispersion effect of traveling wave in wavelet domain[J].Mathematical Problems in Engineering,2017,2017(Article ID 1019591):1-11.
[25] 陈乐,彭咏泉,林湘宁,等.面向接地故障辨识的半波长线路测距式超高速就地主保护新原理研究[J].电工技术学报,2019,34(24):5234-5243.
Chen Le,Peng Yongquan,Lin Xiangning,et al.New ultra high speed local measurement-based protection principle for half-wave transmission line ground fault identification[J].Transactions of China Electrotechnical Society,2019,34(24):5234-5243.
[26] 李学生,盛洪江.基于波速影响的零模行波研究[J].电力自动化设备,2011,31(6):93-97.
Li Xuesheng,Sheng Hongjiang.Study of zero-mode traveling wave based on influence of wave velocity[J].Electric Power Automation Equipment,2011,31(6):93-97.
[27] 熊列彬,吴高华,王志洋.基于IHHT的多测点行波法故障测距在全并联AT牵引网中的研究[J].电工技术学报,2019,34(15):3244-3252.
Xiong Liebin,Wu Gaohua,Wang Zhiyang.Study on fault location of multi measuring points traveling wave method based on IHHT in all parallel AT traction network[J]. Transactions of China Electrotechnical Society,2019,34(15):3244-3252.
[28] 季涛.利用电磁式电压互感器实现小电流接地系统行波故障定位和选相[J].电工技术学报,2012,27(8):172-178.
Ji Tao.Study of the fault location and fault phase position selection based on traveling waves using electromagnetic voltage transformer in neutral noneffective grounding system[J].Transactions of China Electrotechnical Society,2012,27(8):172-178.
[29] 王楠,律方成.基于小波奇异性检测的在线监测数据处理[J].电工技术学报,2003,18(4):61-64.
Wang Nan,Lü Fangcheng.On-line monitoring data processing based on wavelet singularity detection[J].Transactions of China Electrotechnical Society,2003,18(4):61-64.
[30] 董新洲,王世勇,施慎行.极化电流行波方向继电器[J].电力系统自动化,2011,35(21):78-83.
Dong Xinzhou,Wang Shiyong,Shi Shenxing.Polarized current travelling-wave based directional relay[J].Automation of Electric Power Systems,2011,35(21):78-83.
[31] 王世勇,董新洲,施慎行.极化电流行波方向继电器的实现方案[J].电力系统自动化,2011,35(23):76-81.
Wang Shiyong,Dong Xinzhou,Shi Shenxing.Realization scheme of polarized current travelingwave based directional relay[J].Automation of Electric Power Systems,2011,35(23):76-81.
[32] 王珺,董新洲,施慎行.配电线路单相接地行波保护的实现与试验[J].中国电机工程学报,2013,33(13):172-178.
Wang jun,Dong Xinzhou,Shi Shenxing.Scheme and test of traveling-waves based single-phase-to-ground protection for distribution lines[J].Proceedings of the CSEE,2013,33(13):172-178.