0 引言
传统的同步相量测量装置（Phasor Measurement Unit,PMU）未考虑电信号的幅值、频率和相位波动，认为电信号是恒定正弦波，通常采用离散傅里叶变换（Discrete Fourier Transform,DFT）及各类改进技术进行相关参数估计[1-2]。实际电力系统中的电压电流信号的幅值、相位和频率通常存在一定波动，传统的基于DFT的同步相量测量技术在电参量存在波动的情况下难以实现对信号同步相量的精确估计。为了实现动态同步相量测量，学者们提出了一系列动态估计算法。
文献[3]提出一种由插值DFT(Interpolated DFT,IpDFT）与希尔伯特变换（Hilbert Transform,HT）相结合得到的动态同步相量估计算法，并通过稳态和动态测试分析了所提出算法的性能。文献[4]提出一种高精度相量测量方法，可用于PMU的测试与校准。文献[5-6]提出了一种用于电力系统振荡情况下的同步相量测量方法，由于该方法采用泰勒展开公式，因此称之为泰勒傅里叶变换（Taylor-Fourier Transform,TFT）。TFT打破了传统DFT只能分析稳态正弦信号的限制，能够在幅值、相位波动时精确估计待分析信号的动态同步相量。此外，TFT还能够得到信号的实时频率和频率变化率（Rate of Change of Frequency,ROCOF）。在此基础上，学者们又对TFT做了进一步的改进及拓展应用[7-15]。文献[7-8]通过设计最大平坦滤波器实现动态同步相量和频率的测量，在一定程度上增加了所设计的最大平坦滤波器的带宽，其本质是借助窗函数对TFT进行加权处理，使得分析误差降低、带宽增大。TFT的计算过程中需要进行矩阵的求逆、乘法等操作，运算量较大。针对运算量问题，文献[9]提出一种基于多项式实现的方法，能够针对某次特定谐波进行参数估计，大大减小了TFT的计算量。文献[10]将TFT和卡尔曼滤波算法相结合，得到一种运算量小、实时检测性能强的泰勒卡尔曼滤波器（Taylor-Kalman Filter,TKF）动态谐波测量算法。文献[11]在TKF的基础上对其进行了进一步优化，得到一种动态性能更好、测量精度更高、稳定性更好的加强版TKF。文献[12]利用TFT的动态信号检测能力，将其用于动态谐波分析，在完成同步相量测量的同时，实现了对各次谐波的动态同步相量的测量。同步相量测量中，间谐波干扰信号会导致TFT算法性能的严重下降，文献[13-14]将压缩感知（Compressive Sensing,CS）算法和TFT相结合，提出一种能够分析多频率信号的压缩感知TFT多频模型（Compressive Sensing TFT Multifrequency model,CSTFM），并研究了针对所提出算法减小运算量的方法。文献[15-16]指出TFT在存在频偏的情况下，其谐波同步相量的分析精度会下降，且谐波次数越高误差越大。文献[15]提出一种基于SINC插值函数的动态同步相量测量算法，其谐波分析带宽相对于TFT有所增加，但是基波带宽并未改变。文献[16]将DFT和TFT相结合，通过查表法实现了宽频带同步相量测量，但是计算过程相对复杂，且计算量较大。
随着动态同步相量测量技术的发展，IEEE关于同步相量测量的相关标准也在逐步完善，从早期未考虑动态变化情况的版本[17]发展到如今考虑动态同步相量[18-19]。根据IEEE标准，电力系统同步相量测量中的最大频偏可以达到5Hz。所以动态同步相量测量算法需要有较大的带宽，TFT算法是目前动态同步相量分析中很热门的研究，但是大多数文献并未在模型中考虑频率偏差，算法带宽并不能达到5Hz，有的文献能够达到这一带宽，但是算法实现较复杂，计算量较大。
本文提出一种考虑频率偏差的宽频TFT动态同步相量估计器（Wide Band Taylor-Fourior Transform,WB-TFT），即使频偏达到5Hz也能保持对同步相量的精确估计，并且与TFT相比较，WB-TFT的在线计算量并未增加。WB-TFT在标称频率的两侧以固定的频率间隔生成多个离散频率点，然后根据实际标称频率和虚拟标称频率，利用TFT的方法生成多个动态滤波器，将其保存到存储器，便于后续查表使用。在线计算时，需要检测待分析信号的频偏。为了最大可能降低算法复杂度和运算量，WB-TFT不借助锁相环、DFT等其他频率检测手段，而是使用TFT自身计算得到的频率，以递推的方式进行频偏估计。根据估计频率选择与之最接近的离散频率点对应的滤波器进行同步相量测量。最后，在各种典型的频率偏差条件下，通过仿真信号和实际信号测试了WB-TFT的性能。测试结果表明，该方法能够在IEEE标准规定的频率偏差条件下对动态同步相量进行精确估计。
1 考虑频偏的动态同步相量估计器
根据IEEE标准C37.118.1[18]及其最新修订版C37.118.1a[19]，电力系统中实际信号的基波频率偏离系统标称频率值的最大值可以达到5Hz，因此，同步相量测量装置必须具有足够的带宽。本文提出一种考虑频率偏差的动态同步相量估计算法，该算法能够在最大频偏达到5Hz的条件下正常工作，并且，与现有的TFT算法相比，在相同的频偏条件下该算法能够取得更高的分析精度。
1.1 同步相量估计器数学模型
根据文献[18-19]，电力系统信号的同步相量可以表示为
式中，Xm(t)为信号的瞬时幅值；Δf为实际信号频率与系统标称频率之间的偏差；ϕ(t)为信号随时间变化的初相角。由同步相量可以得到信号的时域模型为
式中，f0为系统标称频率；f为信号的实际频率。
相关文献介绍的基于TFT的动态同步相量测量算法通常对式（2）做了简化处理，在分析中忽略了系统频偏，即默认Δf为零。这样处理使得问题得到了简化，并且TFT具有最大平坦滤波器性能，在频偏较小时TFT的分析精度受影响较小[7-8]。但是，随着频偏的增大，TFT的分析误差迅速增大，所以简化模型不能在频偏较大时对电参量进行精确估计。WB-TFT在模型中考虑了Δf，并将式（2）通过欧拉公式变换为
式中，p(t)为输入信号的动态同步相量，
为p(t)的共轭；ω为实际角频率，ω=2πf。注意，与TFT模型不同，这里使用的是实际信号频率。动态同步相量p(t)包含了幅值、初相角信息，根据泰勒公式，可以将其在一段观察时间T内进行K阶泰勒展开。
假设采样周期为Ts，在观察窗口时间内，t=0的两侧各有Nh个采样点，总共 N =2 N h+1个采样点。结合式（3）、式（4），并对其进行离散化，可以得到矩阵表达式为
式中，X为在一个观察窗口内输入信号的采样点构成 的 列向量，X= [x(−N h)… x(0)… x(Nh)]T ；MK为N×K的矩阵，
为其共轭，其中的列向量可以表示为
−N h ≤ n ≤ Nh；PK为同步相量p(t)在t=0时刻的各阶导数构成的列向量，PK = [p(0)… p ( k)(0)… p(K)(0)]T，
为其共轭。
综上所述，同步相量在中心点处的各阶导数可以通过最小二乘法得到。
式中，M∗为M的伪逆矩阵。
至此，通过式（4）、式（6）可以得到同步相量的最小二乘解。必须指出，在上述推导中，矩阵 M∗使用的不是标称频率，而是实际频率f，因此，必须首先对信号频率进行检测。
1.2 频率离散化处理
在TFT计算中，伪逆矩阵 M∗的行向量相当于最大平坦滤波器的系数。求解伪逆矩阵需要耗费大量的时间，所以，需要提前求解伪逆矩阵，并将其保存到存储器中，通过使用查表法，这样可以大幅度缩减在线运算量。需要指出的是，在考虑频偏时，伪逆矩阵 M∗的求解过程需要输入信号的实际频率信息。也就是说，要想对伪逆矩阵进行线下求解，前提是先估计出信号实际频率。根据IEEE标准，最大频偏可以达到5Hz，因此本文引入离散频率常数df 对标称频率两侧5Hz以内的频率进行离散化，得到离散频率值fz为
式中，Mf=round(5/df)，round()表示四舍五入取整运算符，2Mf+1表示总的离散频率数量。通过选择合理的df值，实际信号频率f和距离它最近的离散频率
之间的差值可以忽略，因此可以用离散频率代替实际频率，利用式（5）和式（6）分别生成各个离散频率点fz对应的伪逆矩阵，并将其保存在存储器中。上述工作可以离线完成，大大降低在线求解同步相量的运算负担。在线运行时，首先需要检测信号的频率f，并根据这个频率选择与之最接近的离散频率
为
1.3 信号频率估计及WB-TFT的实现流程
常用的频率检测方法很多，比如FFT[20]、锁相环[21-22]等，但是使用这些技术手段必然会额外增加计算量和算法复杂度。TFT在估计同步相量的同时，还可以估计频率，因此，本文采用TFT本身进行频率检测，其具体实现原理详述如下。
算法启动时，默认信号频率为系统标称频率，并采用TFT对分析窗口内的信号进行频率估计，用该估计值作为下一分析窗口的频率估计值
。之后，在每个观察窗中，将上一个观察窗中TFT的频率估计值作为下一个观察窗的频率预测值。然后，通过式（8）求出与之最接近的离散频率
，通过查表法选择与其对应的伪逆矩阵。采用式（4）、式（6）可以求得动态同步相量p(t)及其在窗口中心处的各阶导数。进而，输入信号在窗口中心点处的幅值、相位及其各阶导数可表示为（本文以二阶泰勒展式为例）
式中，abs(·)表示计算幅值；angle(·)表示计算相位；real(·)表示取实部；imag(·)表示取虚部。
根据泰勒公式可以得到幅值、相位及其导数的时域函数表达式为
进一步可以求得频率和频率变化率为
需要指出的是，在频率检测环节，每次使用的频率预测值是TFT上一个观察窗口的频率估计值，所以该预测频率存在一个观察窗口的延迟。本文后面的频率爬坡和系统振荡仿真证明，该延迟并不会对WB-TFT的分析精度造成很大影响。综上所述，本文提出的考虑频偏的同步相量估计器的实现流程如图1所示。synchrophasor estimator considering frequency deviation
图1 考虑频偏的同步相量估计器的实现流程
Fig.1 Implementation flowchart of the dynamic
具体实现流程主要包括离线计算和在线计算两部分，详述如下：
离线计算部分：
1）选择合适的离散频率常数df，生成对应离散频率fz。
2）根据fz 生成对应的伪逆矩阵 M∗，并将其保存到存储器中。
在线计算部分：
1）将TFT上一个观察窗估计得到的频率值作为本次观察窗中信号频率的预测值，并找到与之最接近的离散频率fz 。
2）根据离散频率选择相应的伪逆矩阵进行计算，估计出待分析信号的同步相量、频率和频率变化率。该频率估计结果将作为下一个观察窗的频率预测值，转到步骤1）。
2 离散频率常数选取
本文所提出的估计器模型引入了离散频率常数df，本部分通过仿真分析离散常数选择对WB-TFT性能的影响。总矢量误差（Total Vector Error,TVE）、频率误差（Frequency Error,FE）和频率变化率误差（Rate of change of Frequency Error,RFE）是IEEE标准中规定的同步相量测量误差衡量指标，因此在接下来的分析中，误差分析均根据这些指标进行。
本文采用六个基波周期长度观察窗，将采样频率、TFT阶数K、采样点数N分别设置为3kHz、2、360。离散常数df为0.5Hz、0.2Hz时，最大TVE、FE和RFE的仿真结果如图2～图4所示。因为45～55Hz频率段关于50Hz对称，所以只给出50～55Hz部分。
图2 不同df取值对应的最大TVE
Fig.2 Max TVE at different df values
图3 不同df取值对应的最大FE
Fig.3 Max FE at different df values
图4 不同df取值对应的最大RFE
Fig.4 Max RFE at different df values
从仿真结果可以看出，随着df的减小，TVE、FE和RFE的值大幅度减小。df越小，离散频率点越多，需要存储的伪逆矩阵数量越多，但算法精度越高；反之亦然。通过仿真结果可以发现，当df取不同的值时，各个指标的最大误差总是出现在两个相邻离散频率点的中心处。比如，由式（7）可得，df=0.5Hz时的离散频率点集合为{45Hz,45.5Hz,46Hz,…,54Hz,54.5Hz,55Hz}，则出现最大误差的频率点集合为{45.25Hz,45.75Hz,…,54.25Hz,54.75Hz}。
当df取值为0.54Hz、0.2Hz时频率预测误差分别小于0.25mHz、0.02mHz，频率分析精度完全能够满足WB-TFT对信号实际频率预测的需求。在本文接下来的分析测试中，将df的值选取为0.2Hz。
3 运算量和延迟分析
本文提出的WB-TFT主要包括两部分内容，即伪逆矩阵的离线计算和同步相量的在线估计。离散频率常数df越小，离散频率点越多，对应的伪逆矩阵数量越多。伪逆矩阵系数相当于滤波器，将其离线计算之后保存到存储器中。如果模型阶数为K，采样点数为N，则每个伪逆矩阵需要3(K+1)行、N列的复数空间进行保存。离线计算不影响在线运算量，所以该算法的主要运算量是由同步相量估计造成的。同步相量估计的计算主要来自式（4）、式（6）、式（10）和式（11），主要的加减和乘除运算量见表1。
表1 WB-TFT的运算量统计
Tab.1 WB-TFT calculation statistics
本文将采样频率fs、观察窗采样数N、模型参数K和df的值分别设置为3kHz，360、2和0.2Hz。由df可以得到在45～55Hz范围内的离散频率点数为51，需要离线计算并存储的伪逆矩阵数量为51个，每个矩阵需要9行、360列的复数空间。按照每个复数占用8个字节计算，总共需要26KB存储空间。对于实时同步相量估计，由于每次复数运算可以拆分为两次实数运算，所以需要10 080次实数乘法和10 068次实数加法，即总共20 148次浮点运算。德州仪器（TI）提供的C6000系列浮点处理器TMS320C6712D的时钟频率为150MHz，支持256M Byte的存储空间，并可以执行900 MFLOPS。如果用于计算，则总计算时间将在0.03ms以内，说明WB-TFT的计算量很小。WB-TFT的观察窗口时间参考点在窗口中心，所以延迟时间为半个窗口长度，即三个基波周期，所以WB-TFT的总延迟时间在60.03ms之内。IEEE标准规定报告率为50帧/s的P类和M类PMU的最大延迟时间分别为40ms和100ms，WB-TFT可以满足M类PMU的要求，但不满足P类PMU的要求。
4 综合性能测试
为了验证本文WB-TFT算法的综合性能，本部分进行各种典型工况下算法的性能测试。因为WBTFT是在TFT模型的基础上考虑了频偏得到的，下面的测试中用TFT和WB-TFT进行对比。值得注意的是，TFT只能在频偏很小的时候才有良好的工作性能，当频偏较大时，TFT性能迅速恶化，WB-TFT能够工作在频偏较大的情况下。因此，在以下测试中，使TFT工作在频偏1Hz以内，WB-TFT工作的最大频偏达到5Hz。对两种算法的测试结果进行比较，并与IEEE最新标准要求进行对比，分析WBTFT的综合性能。IEEE标准将PMU分为两类：P类和M类。P类PMU要求的响应时间短，而M类PMU要求的测量精度高。在对下面的测试结果进行对比时选择最严厉的方式，即将测量精度与M类装置比较，响应时间与P类装置比较。
4.1 频率爬坡测试
实际电力系统中，系统频率并非恒定不变，在一定条件下存在频率爬坡的情况。IEEE标准针对频率变化情况通常采用频率线性爬坡的测试方法，即让系统频率从标称频率开始以某一固定的频率变化率线性爬坡。频率爬坡测试信号的表达式为
式中，Rf为频率爬坡率，根据IEEE标准取为1Hz/s。测试中，TFT从50Hz爬坡到51Hz，WB-TFT从50Hz爬坡到55Hz。两种算法测试得到的TVE、FE和RFE分别如图5～图7所示。
图5 频率爬坡工况下的TVE
Fig.5 TVE under frequency ramp condition
图6 频率爬坡工况下的FE
Fig.6 FE under frequency ramp condition
图7 频率爬坡工况下的RFE
Fig.7 RFE under frequency ramp condition
在TFT的爬坡测试中，经过1s时间后，频率从50Hz爬坡到51Hz，测试得到的TVE、FE和RFE随着频率偏差的增大而迅速增大。TVE在t=1.5s左右达到1%，FE在t=1s左右时达到0.015Hz，RFE在t=2s左右时接近0.2Hz/s。
在WB-TFT的爬坡测试中，经过5s时间，频率从50Hz爬坡到55Hz，频率偏差最大达到5Hz，但是TVE、FE和RFE分别保持在0.1%、0.002Hz和0.03Hz/s以下，远低于TFT的测试结果。
IEEE标准规定的频率爬坡工况下TVE、FE和RFE的约束值分别为1%、0.01Hz和0.2Hz/s。可以看出，WB-TFT的测试结果远优于TFT，并且能够满足标准规定的误差要求。
4.2 系统振荡测试
电力系统中的信号不仅存在频率爬坡，还可能出现频率和幅值振荡的情况。IEEE标准通常采用幅值调制和相位调制信号来模拟系统振荡情况并进行测试，本测试采用的信号为
式中，kt为幅值调制因数，kt = 1 +kx c os(2πfm t)；φt为相位调制因数，φt = ka cos(2πfmt)；fm为调制频率，fm=2Hz；kx和ka为相关系数，kx=ka=0.1；f为包含频偏的信号频率，f = f0 +Δf。部分频率下测试得到的误差结果统计见表2。
表2 TFT和WB-TFT系统振荡工况测试结果
Tab.2 Test results of TFT and WB-TFT under system oscillation condition
（续）
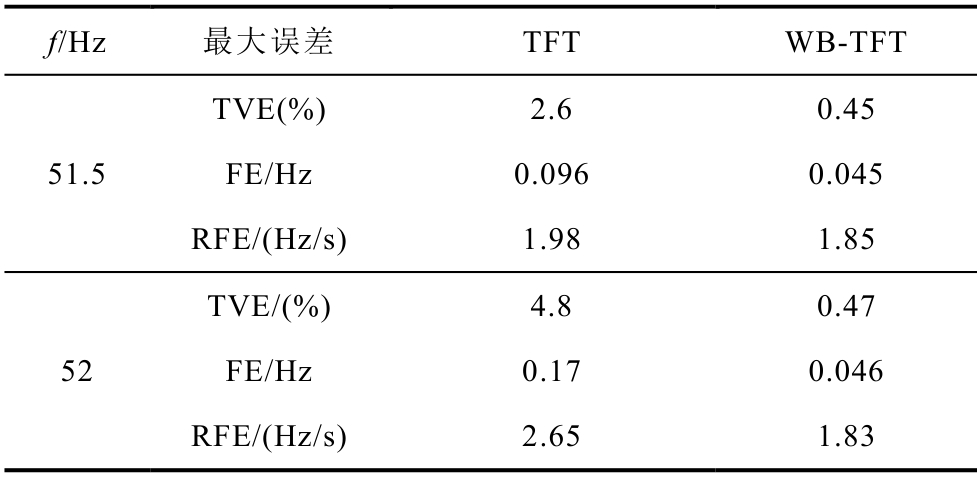
IEEE标准中，M类设备在系统振荡工况下的TVE、FE、RFE限值分别为3%、0.06Hz和2Hz/s。从表2中数据可以看出，随着频率的增大，TFT的各项误差迅速增大，并且在51Hz时FE达到标准限值，到52Hz时各项误差指标均超出标准限值。但WB-TFT的误差并未随着频率增大而出现明显变化，且TVE、FE、RFE均远远小于标准要求值。
在50～55Hz范围内对TFT和WB-TFT测试得到的TVE、FE、RFE结果如图8所示。显然，随着频偏增大，TFT的分析误差迅速增大。在51Hz附近，最大RFE接近标准规定限值，说明在该测试条件下TFT的工作带宽约为1Hz。WB-TFT的测试误差波动不大，各误差值远小于标准规定限值，其工作带宽可达到5Hz，即WB-TFT在45～55Hz范围内的性能能够满足标准要求。
图8 系统振荡时的TVE、FE、RFE
Fig.8 TVE、FE、RFE under system oscillation
4.3 谐波和噪声干扰测试
电力系统中电压电流信号通常不是纯净的正弦波，而是包含一定谐波分量。根据国家标准GB/T 26862—2011，同步相量测量中通常考虑13次谐波，因此本测试采用的谐波干扰测试信号为
式中，ah为谐波幅值，其取值见表3。IEEE标准对于汇报率Fs＞20时TVE和FE的限值为1.3%和0.025Hz，最新的标准取消了对RFE的要求。频率f= 50Hz 时，WB-TFT的TVE、FE的测试结果如图9所示。从测试结果可以看出，WB-TFT能够满足标准要求。
表3 各次谐波的幅值
Tab.3 Amplitude of every harmonic
图9 谐波干扰下WB-TFT的TVE、FE
Fig.9 TVE、FE of WB-TFT under harmonic disturbance
存在频偏情况下的TFT和WB-TFT的测试结果见表4。可以看出，随着频率偏差的增大，TFT和WB-TFT的误差均有所增大。51Hz时两种算法的结果相差不大，当频率增大到54Hz时，TFT的结果已经完全失去意义，WB-TFT的误差并未有明显增大，说明WB-TFT能够在较大频偏工况下工作。
表4 存在频偏时谐波干扰工况测试结果
Tab.4 Test results of harmonic interference in the presence of frequency deviation
4.4 实际信号测试
由于较难采集到频率偏差较大的实际信号，此处使用某光伏电站采集到的稳态电流数据进行WB-TFT的性能测试。实际电流波形如图10所示，采集时使用的采样频率为10kHz。
图10 实际电流波形
Fig.10 Actual current waveform
文献[15]提出一种类似于TFT的估计器（简称DHSE），并对两者做了对比。DHSE的具体介绍见附录。本文所提出的思想同样可以应用于DHSE，以下将基于DHSE改进得到的考虑频偏的同步相量估计器简称为WB-DHSE。接下来的测试中，使用TFT、WB-TFT和WB-DHSE三种算法对所采集的电流信号进行分析，并对三种算法的分析结果通过作图的方法加以对比。采样率都设置为10kHz，采样点数取1 201，df取0.2Hz，得到的幅值和频率估计结果如图11所示。理论上来讲，信号频率偏差较小时TFT和WB-TFT的分析结果应该非常相似。图11中两种算法在分析实际电流信号时得到的结果几乎完全重合，符合理论分析。TFT、WB-TFT和WB-DHSE的幅值分析结果与实际波形幅值基本一致，三者的频率仿真结果也很接近，说明本文所提出的考虑频偏的估计器模型可以用于实际信号的电参数估计。
图11 电流信号幅值和频率的估计结果
Fig.11 Amplitude and frequency estimate results of the current signal
5 结论
本文在TFT动态同步相量估计器的基础上，提出一种考虑频率偏差的动态同步相量估计器WBTFT。WB-TFT在TFT的基础上增加频率离散化和信号频率在线检测两个部分。WB-TFT引入了一个离散频率常数df，对基波频带进行离散化，并根据离散频率fz离线计算出对应的伪逆矩阵 M∗，将其保存到存储器中。在线计算时，通过TFT完成信号频率估计，并根据频率估计值找出与之最接近的离散频率，进而选择对应的伪逆矩阵完成同步相量、频率和频率变化率的计算。
文章分析了离散频率常数的选择对于WB-TFT分析结果的影响，通过仿真对比发现，df取值越小，则需要的存储空间越大，WB-TFT的计算精度越高，反之亦然。考虑到运算量和模型的复杂度，本文未采用锁相环、DFT等其他频率检测手段，而是直接采用TFT的频率估计值作为信号的频率预测值。所提出的模型极大地增加了泰勒傅里叶的带宽，但没使用任何外部频率检测工具，没有增加计算负担。最后，通过各类典型仿真信号和实际采样数据对WB-TFT的综合性能进行了测试。测试结果表明WB-TFT能够在较大频偏情况下实现同步相量、频率和频率变化率的精确分析。
附 录
根据IEEE相关标准[18-19]，电信号的同步相量可以表示为
式中，Xm(t)为信号的瞬时幅值；Δf为实际信号频率与系统标称频率之间的偏差；ϕ(t)为信号随时间变化的初相角。由同步相量可以得到信号的时域模型为
式中，f0为系统标称频率；f为信号的实际频率。对式（A2）进行欧拉公式变换可以得到
式中，p(t)为输入信号的动态同步相量，p(t)= X m(t)e jϕ(t)；ω= 2πf为实际角频率。动态同步相量p(t)包含了幅值、初相角信息，可以将其在一段观察时间T内展开为[15]
式中，B0为大于p(t)的最大频率的一个频率值；pk为p(t)在 t=k /(2 B0)时刻以2B0采样率得到的采样点，pk =p[k /(2B 0)]；K为p(0)两边的采样数。观察窗口的长度需要满足T＜K/B0。
假设采样周期为Ts，在观察窗口时间内，时间0点两侧各有Nh个采样点，总共 N =2 N h +1个采样点。可以得到输入信号的离散表达式为
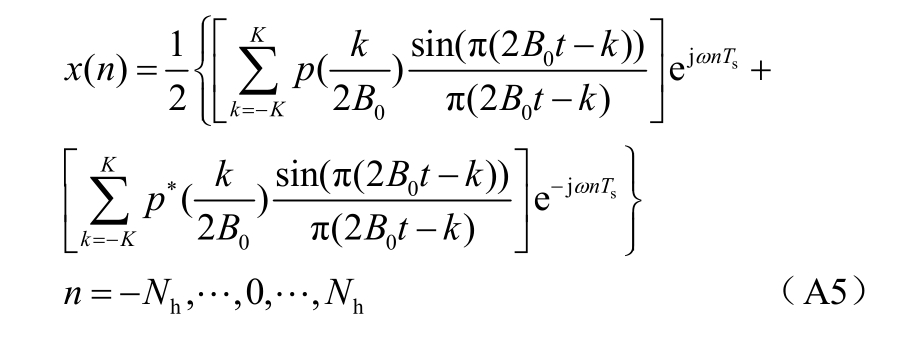
进一步可以将其转换为矩阵表达式，即
式中，M∗为M的伪逆矩阵。
令K=2，得到p(t)在观察窗中心点处的各阶导数为
结合式（A8）和式（A4）就可以计算出同步相量p(t)。
令 D0=p K(0),D1=pK(1)(0)，D2=p K (2)(0)，可以得到频率和频率变化率的表达式为
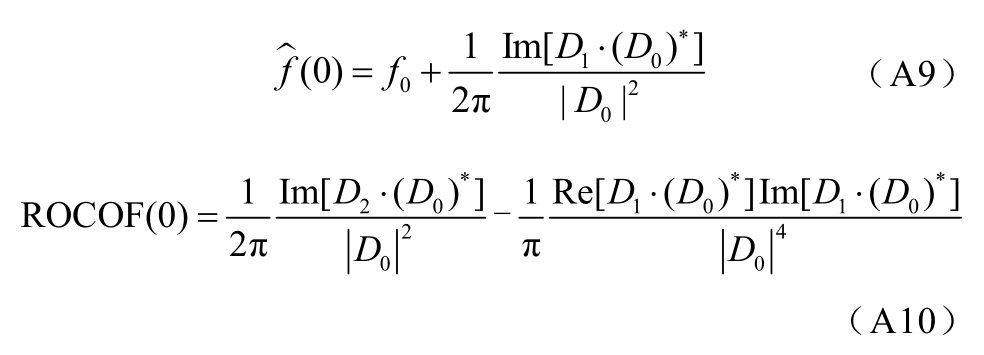
和WB-TFT一样，在上述推导中，伪逆矩阵 M∗的计算中使用的不是标称频率，而是实际频率f，因此，需要对信号频率进行检测。
[1] Wang M,Sun Y.A practical,precise method for frequency tracking and phasor estimation[J].IEEE Transactions on Power Delivery,2004,19(4):1547-1552.
[2] 金涛,陈毅阳,段小华,等.基于改进DFT的电力系统同步相量测量算法研究[J].电工技术学报,2017,32(17):1-10.
Jin Tao,Chen Yiyang,Duan Xiaohua,et al.Research on synchronous phasor measurement algorithm of power system based on improved DFT[J].Transactions of China Electrotechnical Society,2017,32(17):1-10.
[3] Frigo G,Dervikadi A,Paolone M.Reduced leakage synchrophasor estimation:hilbert transform plus interpolated DFT[J]. IEEE Transactions on Instrumentation and Measurement,2019,68(10):3468-3483.
[4] 许苏迪,刘灏,毕天姝,等.一种适用于同步相量测量装置校准器的高精度相量测量方法[J].电工技术学报,2020,35(2):372-382.
Xu Sudi,Liu Hao,Bi Tianshu,et al.A high accuracy phasor estimation algorithm for phasor measurement units calibrator [J]. Transactions of China Electrotechnical Society,2020,35(2):372-382.
[5] Serna J A de la O.Dynamic phasor estimates for power system oscillations and transient detection[C]//Power Engineering Society General Meeting,Montreal,QC,2007:7.
[6] Serna J A de la O.Dynamic phasor estimates for power system oscillations[J].IEEE Transactions on Instrumentation &Measurement,2007,56(5):1648-1657.
[7] Garza M A P,Antonio D L O S J.Dynamic phasor estimates through maximally flat differentiators[C]//2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century,Pittsburgh,PA,2008:1-8.
[8] Garza M A P,Serna J A de la O.Dynamic phasor and frequency estimates through maximally flat differentiators[J].IEEE Transactions on Instrumentation &Measurement,2010,59(7):1803-1811.
[9] Garza M A P,Serna J A de la O.Polynomial implementation of the taylor-fourier transform for harmonic analysis[J]. IEEE Transactions on Instrumentation &Measurement,2014,63(12):2846-2854.
[10] 刘洁波，黄纯，江亚群，等.基于强跟踪泰勒-卡尔曼滤波器的动态相量估计算法[J].电工技术学报,2018,33(2):433-441.
Liu Jiebo,Huang Chun,Jiang Yaqun,et al.Dynamic phasor estimator based on strong tracking Taylor-Kalman filter[J]. Transactions of China Electrotechnical Society,2018,33(2):433-441.
[11] Garza M A P,Serna J A de la O.Dynamic harmonic analysis through taylor-fourier transform[J].IEEE Transactions on Instrumentation &Measurement,2011,60(3):804-813.
[12] Kusljevic M D,Tomic J J.Multiple-resonator-based power system Taylor-fourier harmonic analysis[J].IEEE Transactions on Instrumentation &Measurement,2015,64(2):554-563.
[13] Bertocco M,Frigo G,Narduzzi C,et al.Compressive sensing of a Taylor-fourier multifrequency model for synchrophasor estimation[J].IEEE Transactions on Instrumentation &Measurement,2015,64(12):3274-3283.
[14] Narduzzi C,Bertocco M,Frigo G,et al.Fast-TFMmultifrequency phasor measurement for distribution networks[J].IEEE Transactions on Instrumentation and Measurement,2018,67(8):1825-1835.
[15] Lei Chen,Wei Zhao,Qing Wang,et al.Dynamic harmonic synchrophasor estimator based on sinc interpolation functions[J].IEEE Transactions on Instrumentation and Measurement,2019,68(9):3054-3065.
[16] Fu Ling,Zhang Jiayi,Xiong Siyu,et al.A Modified dynamic synchrophasor estimation algorithm considering frequency deviation[J].IEEE Transactions on Smart Grid,2017,8(2):640-650.
[17] IEEE.Synchrophasors for power systems:C37.118—2005 [S].2006,doi:10.1109/IEEESTD.2006.99376.
[18] IEEE.Synchrophasor measurements for power systems:C37.118.1—2011[S].2011,doi:10.1109/IEEESTD.2011.6111219.
[19] IEEE.Synchrophasor measurements for power systems—amendment 1:modification of selected performance requirements:C37.118.1a-2014[S].2014,doi:10.1109/IEEESTD.2014.6804630.
[20] 卿柏元,滕召胜,高云鹏,等.基于Nuttall窗双谱线插值FFT的电力谐波分析方法[J].中国电机工程学报,2008,28(25):153-158.
Qing Baiyuan,Teng Zhaosheng,Gao Yunpeng,et al.An approach for electrical harmonic analysis based on nuttall window double-spectrum-line interpolation FFT[J].Proceedings of the CSEE,2008,28(25):153-158.
[21] 杨才伟,王剑,游小杰,等.二阶广义积分器锁频环数字实现准确性对比[J].电工技术学报,2019,34(12):2584-2596.
Yang Caiwei,Wang Jian,You Xiaojie,et al.Accuracy comparison of digital implementation on the secondorder generalized integrator frequency-locked loop[J].Transactions of China Electrotechnical Society,2019,34(12):2584-2596.
[22] Golestan S,Guerrero Ge J M,Vasquez J,et al.Modeling,tuning,and performance comparison of second-order-generalized-integrator-based FLLs[J].IEEE Transactions on Power Electronics,2018,33(12):10229-10239.