0 引言
随着电力电子应用高功率、高电压方向的发展，对半导体开关器件的耐压等级及可靠性的要求也随之升高。相比于碳化硅（SiC）、氮化镓（GaN）等新兴宽禁带半导体器件，传统硅（Si）基IGBT在耐压等级、成本及技术成熟性等方面仍具有较大的优势，并仍广泛应用于高压直流输电、列车牵引变流器及大规模风力发电系统中[1-4]。然而，这些场合通常需要数百kV甚至上千kV的高电压[2]，单只IGBT无法满足承压需求，串联IGBT的应用成为解决该问题的一种选择，串联IGBT应用过程中各IGBT间电压平衡也成为近年来研究的热点。针对该问题，文献[5-15]给出了不同的解决方案，根据其作用方式的不同，主要分为以下三类：
（1）无源缓冲电路[5-8]。该方法主要通过在IGBT集射极或集栅极间并联无源器件以实现先关断器件过电压能量的吸收，进而实现保护及均压功能。该方法成本低、可靠性高。但缓冲电路自身的损耗限制了该方法在高频高效率场合的应用，即使采用文献[7-8]所述的带有能量反馈功能的缓冲电路结构，开关瞬态时间的延长所引起的IGBT自身损耗的增加仍不能被忽视。
（2）电容耦合驱动[9-11]。该方法仅采用单只驱动电路结合耦合电容便可实现串联器件整体通断控制。由于上部IGBT驱动电量来源于下部IGBT集电极电位变化所引起的耦合电容充放电，因而驱动时间差异不可避免，虽然通过适当的电容值选取可以削弱该时间差异的影响，但该驱动方式对串联器件数量及开关占空比仍有一定的限制[10]。另外，驱动电压的不同造成部分IGBT长时间工作于有源区，开关损耗的增加也会影响其使用寿命。
（3）有源门极驱动[12-15]。该方法通过实时控制IGBT门极驱动电压、电流以改变其开关瞬态特性，配合相应控制算法实现各IGBT间的承压均衡。文献[12]以集栅极间钳位电路作用时间为依据实时调节驱动信号发出时刻，在实现过电压保护的同时完成电压平衡控制。文献[13]通过阻容分压及高速光耦实现承压采样并据此调节驱动信号发出时刻。上述两种方式均需要控制级与驱动级间额外的隔离单元，增加了电路的复杂性及共模干扰[16]。此外，相应的平衡算法增加了变流器主控器负担，对主控器频率及存储提出了更高的要求。文献[14]提出了一种基于参考电压跟随的闭环驱动电路。然而，为确保控制的精确性，电路参数选取要求较高，不当的阈值选取会影响控制的稳定性与可靠性。文献[15]提出了一种基于额外电流源的有源驱动方式，通过检测IGBT所处开关阶段的时长，逐步改变门极电流的大小以实现均压控制。然而，该方法监测变量较多，开关瞬态时长的检测对驱动核心控制芯片及AD-DA转换芯片带宽要求较高，增加了电路的成本与复杂度。
为实现串联IGBT间电压均衡的同时避免上述方法存在的问题，本文提出了一种基于门极电量补偿的有源驱动电路。该电路具有如下优点：
（1）通过在传统电压驱动基础上附加辅助电路实现均压控制，无需额外的电源与信号隔离。
（2）辅助电路控制周期与开关周期相同。因此，低成本低频控制芯片（如51单片机）即可满足要求，降低了电路成本。
（3）辅助电路不会降低IGBT开关速度，避免了器件损耗的增加。
（4）驱动电路间彼此独立，没有串联数量限制。
本文在介绍该驱动电路工作原理的同时给出详细的参数设计原则，并基于仿真与实验验证了该驱动在串联IGBT电压平衡控制上的有效性与适用性。
1 电路结构与原理
本文所提出的有源驱动电路框图如图1所示，其通过在传统驱动电路基础上附加辅助电路以实现均压控制。其中传统驱动电路由驱动IC及门电阻RG构成，依据开关信号实现通断控制。辅助电路由电流吸收电路、触发电路及控制采样电路三部分构成。其各自功能如下：
电流吸收电路于IGBT关断瞬态对其输入电容Ciss产生额外吸收电量Qsink，进而调节IGBT关断瞬态特性。Qsink的大小由触发电路输出Vctrl决定。
触发电路依据驱动IC输出电压Vdout的下降沿来确定Qsink生成时刻。同时，发出信号VST触发控制采样电路对IGBT实时承压VCE进行采样，并将其生成的控制量VDAout于IGBT关断瞬态以脉冲Vctrl的形式传递给电流吸收电路。
图1 有源驱动电路框图
Fig.1 Block diagram of the proposed active gate drive
控制采样电路根据采样得到的VCE值判断IGBT是否过电压，并依据VCE的大小生成相应的控制量VDAout以实现一个开关周期内的均压调节。各部分电路的实现形式及其工作过程如下所述。
1.1 电流吸收电路
图2所示为基于Wilson电流镜结构的电流吸收电路。Vctrl为输入电压，其值由辅助电路另外两部分决定。高速运算放大器OP与三极管VQ1～VQ4构成镜像电流源，其输出电流Isink用以产生额外吸收电量Qsink，对于固定的电路元件，Isink的大小由Vctrl的值决定，其关系满足
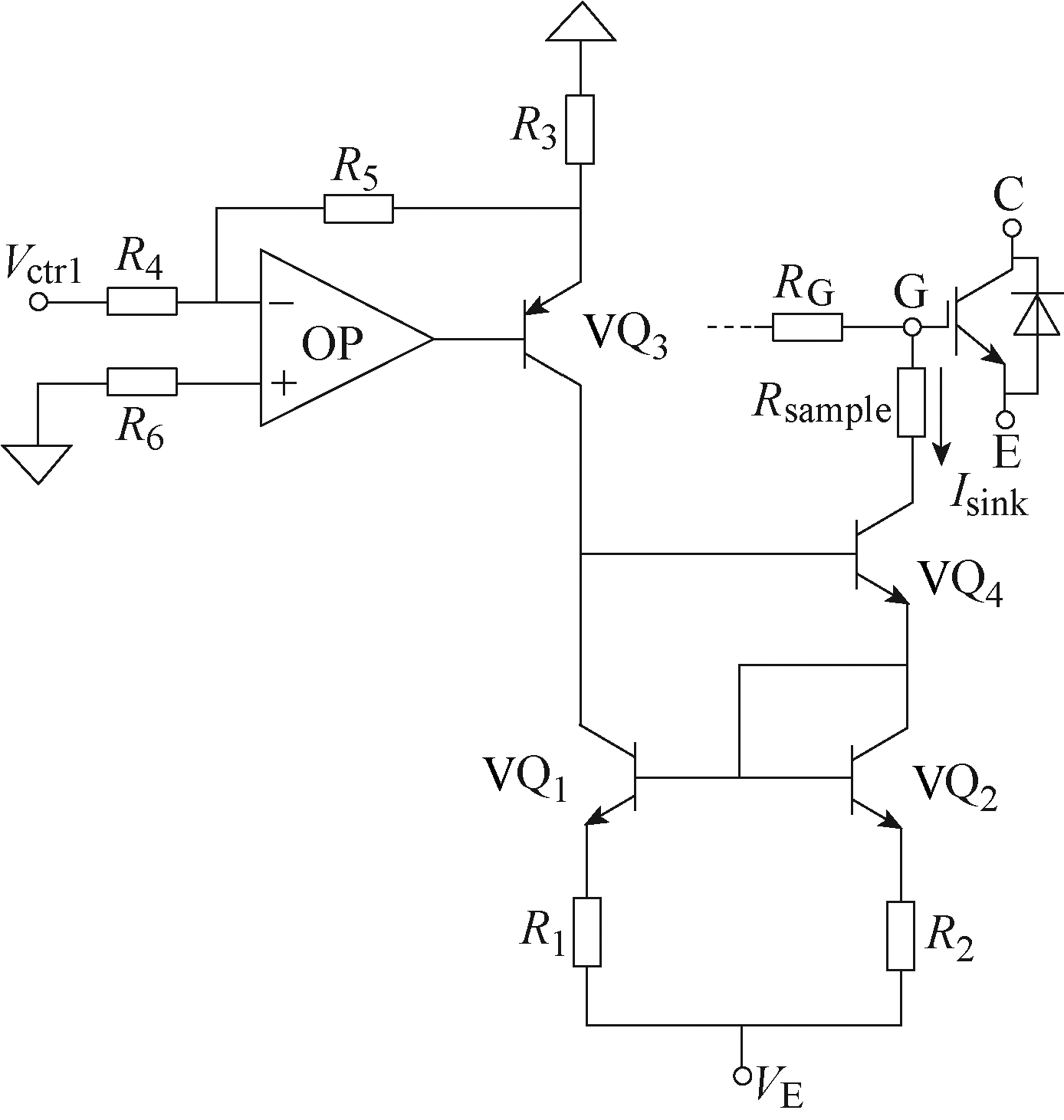
图2 电流吸收电路
Fig.2 The schematic circuit of the current sink
设Vctrl作用时间为tctrl，则该时段内电流吸收电路电源VE吸收的电量Qsink为
为说明电流吸收电路对串联IGBT关断承压的影响，本文给出其作用下的两只IGBT串联测试电路如图3所示，其中RL、L及续流二极管VD构成阻感负载，VT1与VT2为串联的两只IGBT且参数完全一致，Cp1与Cp2为驱动IC及其供电电源内部寄生电容[16]，IG1与IG2为VT1与VT2门极放电电流，IG为驱动IC吸收电流，VDC为直流母线电压源，RG为栅极外部电阻。根据关断过程电压电流状态，电流吸收电路影响下串联IGBT关断过程从t0～t4可分为四个阶段，如图4所示。其过程分析如下：
图3 基于两只IGBT串联的测试电路
Fig.3 Test circuit based on two series-connected IGBTs
图4 电流吸收电路影响下串联IGBT关断波形
Fig.4 Turn-off waveforms of series-connected IGBTs with the current sink circuit
1）t0～t1b。t0时刻，驱动输入脉冲宽度调制 （Pulse Width Modulation, PWM）信号由高至低，而此时驱动输出电压不会马上降低，这是因为驱动IC均存在一定的传输延迟，对于不同种类驱动IC其延迟由数十ns至数百ns不等。同时，由于制造工艺的不同，即使相同型号驱动IC其延迟时间也存在一定差异，设VT1驱动延迟小于VT2驱动延迟且相差为tdelay，则门极电压VGE1较VGE2提前降低，VT1输入电容Ciss1首先开始放电。
2）t1b～t2b。t1b时刻，VT2门极电压VGE2也开始下降，同时电流吸收电路控制电压Vctrl由0上升至VDAout，电流吸收电路开始工作并产生额外放电量Qsink1。此阶段Ciss1与Ciss2的放电量QGE1与QGE2分别为
式中，Qdelay为上一阶段关断延迟tdelay在这一阶段显现出的门极放电偏差，其值为
式中，Vmiller为米勒平台电压；VDD为正驱动电压。同时tdelay满足
额外的放电量Qsink1将加快VT2输入电容Ciss2的放电速率，虽然VGE2晚于VGE1开始下降，但在Qsink1的作用下其将与VGE1同时降至Vmiller。
3）t2b～t3。t2b时刻，VT1与VT2集射极电压VCE1与VCE2开始上升，而VCE2的上升将引起VT1门极对地电位的快速升高，进而为VT1门极对地寄生电容Cp1充电，其充电量为
式中，VEE为负驱动电压；VCEsat为IGBT开通饱和压降。同时，VT2门极对地电容Cp2充电量为
令Cp1=Cp2=Cp，由式（6）与式（7）可得，Qcp1与Qcp2的差值Qcp为
若驱动IC所吸收的电量相同，则Qcp在该阶段将引起Ciss1与Ciss2放电量的偏差。在电流吸收电路作用下，该阶段Ciss1与Ciss2的放电量QGC1与QGC2分别为
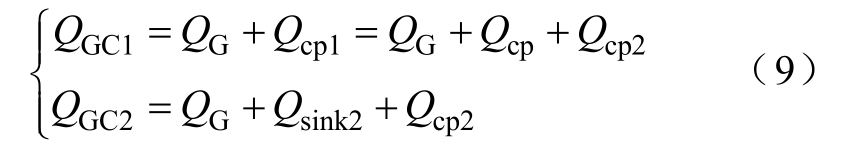
式中，QG为驱动IC吸收电量；Qsink2为电流吸收电路在这一阶段额外吸收电量。
4）t3～t4。该阶段VT1与VT2承压已达到关断稳态值，Vctrl重新降为0，电流吸收电路不再工作。集电极电流IC开始下降，由于主回路及器件杂散电感的存在，感生电压在VCE上形成幅值为Vos的电压尖峰[15, 17]，其值满足
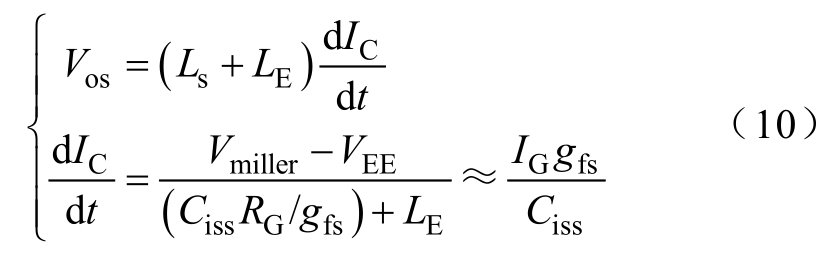
式中，Ls与LE分别为主回路杂散电感与IGBT射极寄生电感；gfs为器件跨导。由式（10）可知，Vos的大小与关断瞬态IC下降速率有关，而IC下降速率与IG正相关，由于此阶段内电流吸收电路不再作用，故其不会影响关断尖峰电压值。此阶段门极电压从阈值降至VEE，串联IGBT关断完成。
由IGBT开关过程输入电容充放电定义可知，IGBT关断过程中所需关断电量QGoff[18]为
由式（3）、式（9）、式（11）可知，若满足
则有
即VT1与VT2关断过程输入电容放电量QGoff1与QGoff2满足
由文献[17]分析可知，对于特性完全相同的串联IGBT，关断过程中输入电容的放电量影响其关断瞬态特性及稳态承压。因此，关断瞬态输入电容放电量的一致性是确保其关断承压均衡的重要因素。据式（12），若使电流吸收电路额外吸收电量Qsink等于驱动输出延迟及驱动寄生电容所引起的放电偏差Qdelay与Qcp之和，则可实现电压平衡。
为验证门极放电量对串联IGBT关断承压的影响及电流吸收电路的均压作用，本文给出基于LTSpice的两只IGBT串联仿真结果如图5所示，其仿真电路结构与图3一致，仿真元器件及其参数见表1及表2。
由图5a可以看出，没有电流吸收电路作用时，10ns的关断延时所造成的串联IGBT门极放电偏差Qdelay将引起798V的承压差。由于该情况下，下管VT2承压VCE2非常小，据式（8）可知，此时寄生电容Cp所引起放电偏差Qcp也如图5a所示，其值很小不足以影响关断瞬态特性。
图5b所示为电流吸收电路作用下串联IGBT关断瞬态相关波形。可以看出，Vctrl控制下的吸收电 流Isink所生成电量Qsink用以补偿放电偏差Qdelay及Qcp。在其作用下，VCE1与VCE2在关断稳态时幅值基本一致，电压平衡得以实现。需要注意的是，与图5a相比，该情况下Qcp的值随着VCE2的升高而增大，与前文理论分析一致。
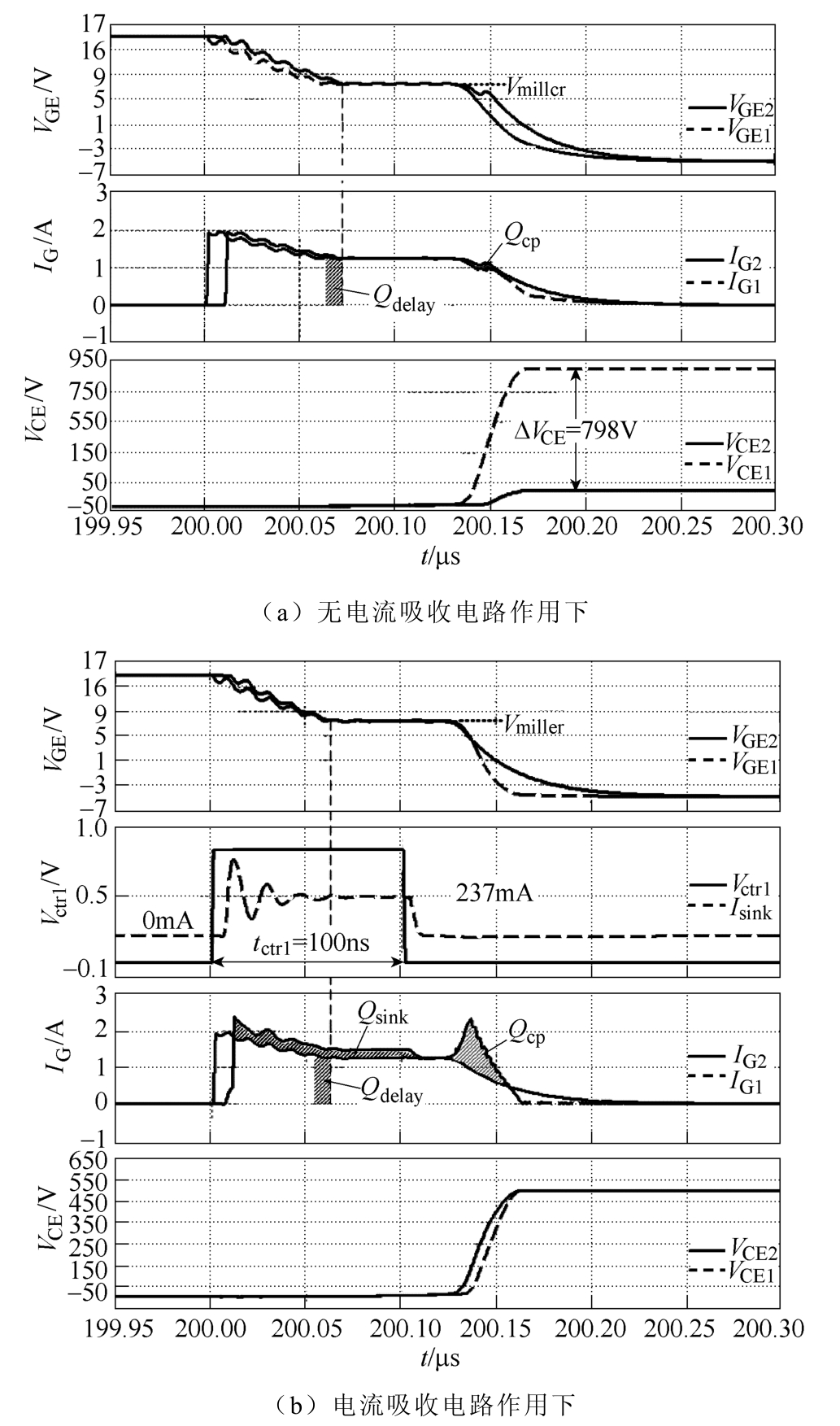
图5 串联IGBT关断瞬态仿真波形
Fig.5 Simulation waveforms of the series-connected IGBTs during a turn-off transient
表1 主功率回路仿真参数 Tab.1 The simulation parameters of power circuit
参 数 数值(型号) 母线电压VDC/V 1 000 RL/Ω 100 负载 L/μH 25 IGBT FGL40N120AND(1200V/40A) 续流二极管VD C4D40120D(1200V/40A) 驱动电压VDD/VEE/V/V +15/−5 门电阻RG/Ω 10 寄生电容Cp1, Cp2/pF 50 驱动延时tdelay/ns 10
表2 电流吸收电路仿真参数
Tab.2 The simulation parameters of current sink circuit
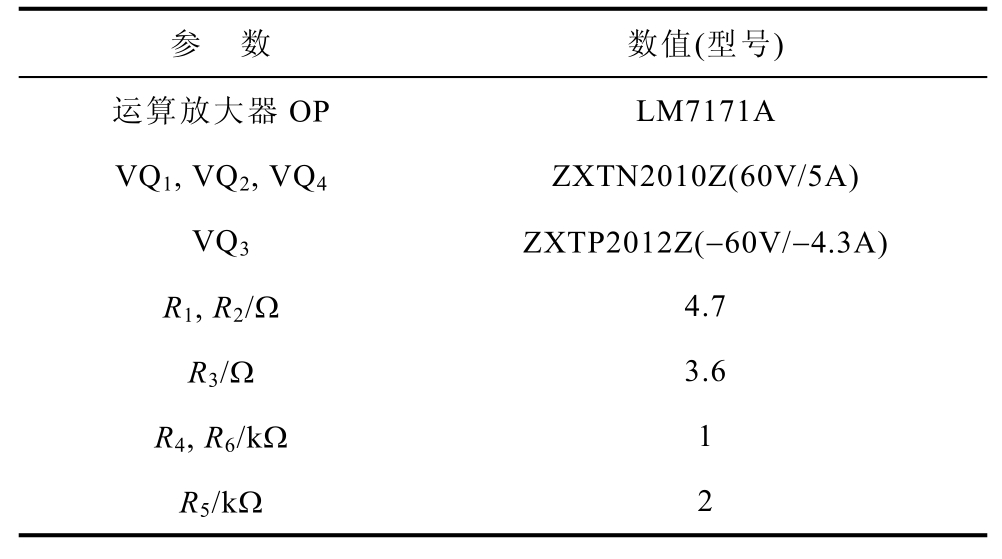
参 数 数值(型号) 运算放大器OP LM7171A VQ1, VQ2, VQ4 ZXTN2010Z(60V/5A) VQ3 ZXTP2012Z(−60V/−4.3A) R1, R2/Ω 4.7 R3/Ω 3.6 R4, R6/kΩ 1 R5/kΩ 2
1.2 触发电路
触发电路及其工作原理如图6所示。图6a为本文所提出的触发电路，其由阻容分压电路及脉冲发生电路组成。其中分压电路通过合适的阻容搭配将驱动IC输出电压Vdout转化为TTL电平信号并传输给脉冲发生电路。脉冲发生电路由两只下降沿触发单稳态触发器U1、U2及一只模拟开关组成，其中U1产生一时长为TST脉冲信号VST用以触发采样。而U2产生一时长为tctrl脉冲信号VCT用以控制模拟开关，在脉冲时间tctrl内，将控制采样电路输出信号VDAout与电流吸收电路输入级Vctrl相连，实时改变Vctrl的值。各信号时序如图6b所示，其中，Ts为开关周期，D为占空比，TD为控制采样电路输出延迟。
触发电路的响应时间影响整个辅助电路的控制精确性与有效性，因此，触发电路各元件应具有高带宽频率及响应速度。本文采用TI公司单稳态触发器SN74LVC1G123及模拟开关TS5A63157，其在5V电源电压下最大响应时间分别为7.6ns及5ns。合适的阻容搭配下分压电路延迟时间基本可以忽略，因此整个触发电路最大响应时间为12.6ns。
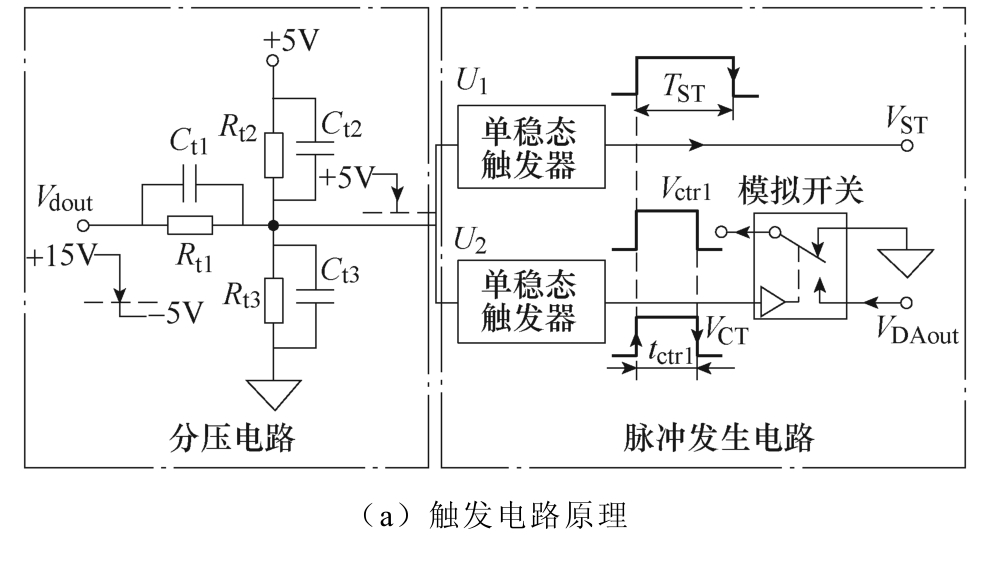
图6 触发电路及其工作原理
Fig.6 The schematic and sequence diagrams of the trigger circuit
1.3 控制采样电路
由图1与图6b可知，控制采样电路的功能是在触发信号VST的作用下依据每个关断周期IGBT静态承压来产生下一周期Vctrl对应的幅值VDAout。进而实现整个驱动电路的闭环均压控制。
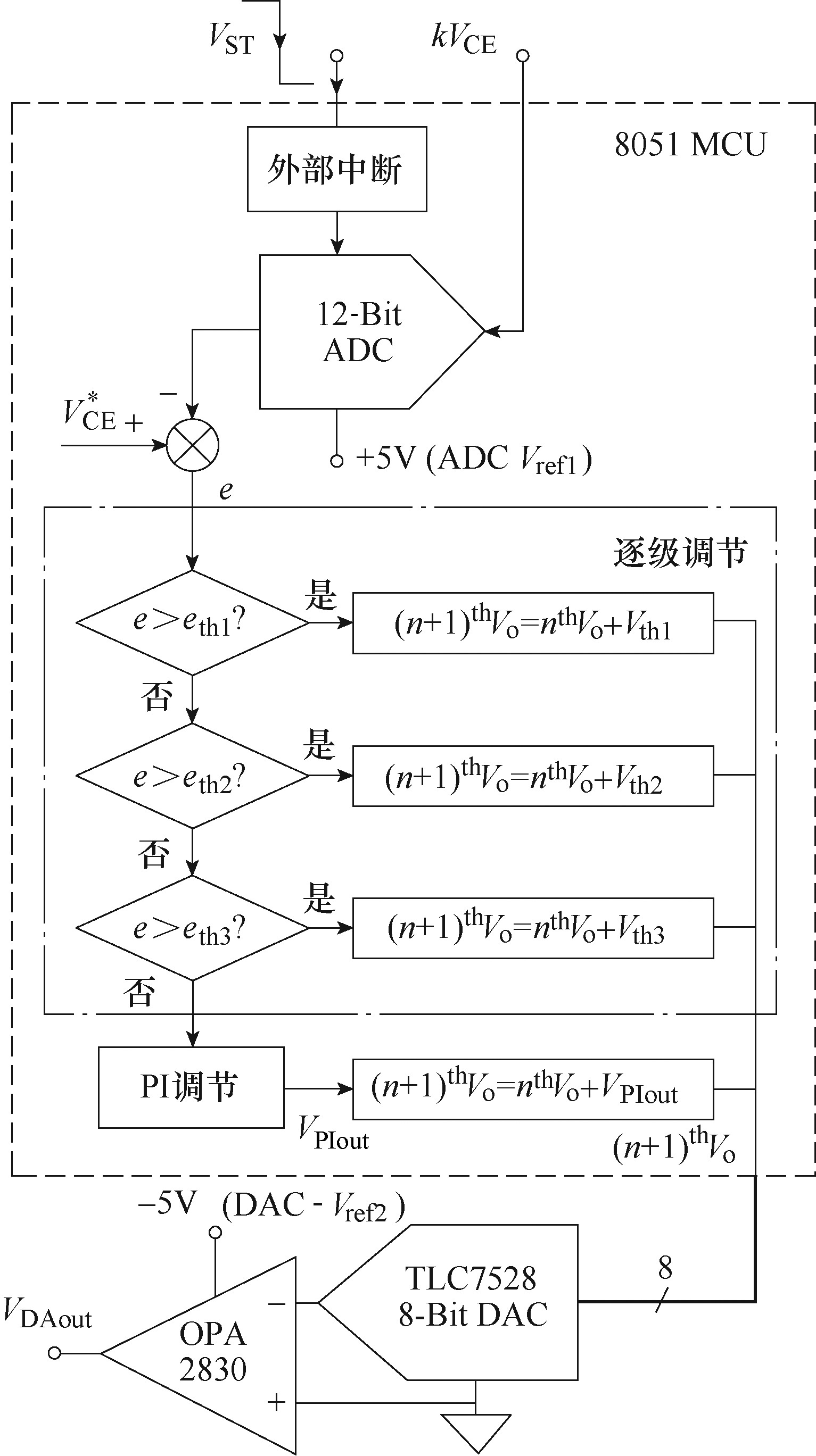
图7 控制采样电路原理框图
Fig.7 Schematic diagram of control and sampling circuit
为实现上述功能，本文提出如图7所示的控制采样电路。为降低驱动电路成本，主控芯片采用1T 内核8051单片机STC8A8K64S4A12（宏晶），其自身集成采样率800Ksps模数转换器（ADC）。主控芯片输出信号通过TLC7528实现数模（DA）转换，并由OPA2830缓冲输出。
本文均压调节控制算法采用逐级调节与PI调节相结合的形式。IGBT静态承压VCE经阻容分压后作为ADC的输入。MCU检测到触发电路输出信号VST下降沿后开启AD转换，采样值与理论平均承压 值
相比较，若其值小于
，则二者差值记为e。 e依次与预设阈值eth1、eth2及eth3相比较，若e大于预设阈值ethx（x=1, 2, 3），则相应的增量Vthx（x=1, 2, 3）将被叠加于这一周期输出nthVo，并将其和作为下一周期的输出(n+1)thVo，直至数个周期后e小于最小阈值eth3时，PI调节替代逐级调节将输出稳定于较小范围内。采用逐级调节的目的在于迅速界定辅助电路输出电压范围，确保控制的快速性，采用PI调节的目的在于输出范围界定后利用较大的积分系数避免输出的波动，确保控制的稳定性。
2 设计方法
在分析了本文所提出的有源驱动电路工作原理后，本文给出实际应用过程中各子电路参数设计原则。其实验给定条件为：直流母线电压VDC=1kV，最大负载电流10A，两只串联IGBT型号为IHW20N120R3（1 200V/20A，英飞凌）。
2.1 电压驱动电路设计
本文采用安华高ACPL-W341光耦作为基本驱动芯片，其驱动电压设为+15V/−5V，辅助电路IC为+5V供电，电流吸收电路电源电压VE设为−15V，输入级放大器OP供电电压为±15V。根据所需电压等级，±15V电压由DC-DC模块电源WRE0515S- 3WR2（金升阳）提供，±5V电压分别由位于模块电源后级的线性稳压芯片MC78L05与MC79L05（安森美）提供。
2.2 辅助电路设计
由1.1节的分析可知，辅助电路的目的在于补偿关断瞬态驱动延迟差异及门极对地寄生电容所引起的串联IGBT输入电容放电偏差。因此，最大理论放电偏差是确定电路元件参数的重要因素之一。对于Qdelay的理论最大值可由式（4）求得。其中，tdelay为ACPL-W341最大输出延迟差异，tdelay= 100ns，Vmiller[19]可以估算为 式中，Vth为IGBT门极阈值电压，Vth=5.8V；gfs= 16.3S。依据实验条件可以求得Vmiller=6.4V。代入式（4）解得Qdelay最大值为86nC。
寄生电容Cp由隔离电源及驱动芯片隔离寄生电容组成，通过数据手册可知，DC-DC电源隔离电容最大值为50pF，ACPL-W341输入输出间寄生电容为0.6pF，因此Cp的值约为50.6pF。当承压均衡时，VCE2=500V，IGBT饱和压降约为2V。代入式（8）可得，Qcp最大值为25.2nC。由式（12）可知， Qsink的最大值为111.2nC。
由IHW20N120R3数据手册可知，其关断所需时间由关断延迟时间td(off)及电流下降时间tf组成，其值分别为387ns及25ns。根据1.1节所述电流吸收电路工作原理可知，tctrl的大小在满足补偿所需时间的同时应不大于td(off)，以避免加快电流下降速率进而增大关断电压尖峰，本文取tctrl的值为210ns。
电流吸收电路中运放OP及三极管VQ1～VQ4的选型与表2一致，其中，R3影响电流吸收电路最大输出，其选取原则如下：由于LM7171A最大负输出摆幅为−10.5V，且ZXTP2012Z饱和压降为−950mV，因此R3两端最大压差VR3(max)为−9.55V。考虑到tctrl时段内电流吸收电路需能提供Qsink的最大值，由式（2）可得，最大吸收电流Isink(max)=530mA，因此由
可知，R3=18.02Ω，此处取常用阻值18Ω。
触发电路在提供时长为tctrl的控制信号VCT的同时还需提供时长为TST的采样延迟信号VST。由图6b可知，一方面，TST要足够长以确保采样时刻VCE关断尖峰电压已消失且达到稳态值；另一方面，TST不能大于单开关周期内IGBT关断时长(1−D)Ts，以避免在其开通期间采样。因此，TST的大小需满足
式中，Dmax为最大开关占空比；fs(max)为IGBT最大开关频率。令fs(max)=5kHz，Dmax=0.9，代入式（17）解得412ns≤TST≤20μs，此处取TST=1μs。
图8所示为应用上述器件构成的有源驱动电路结构，其中，控制采样电路为独立可插拔结构，便于更换其他型号MCU及DAC以适应不同应用需求。从图8可以看出，该驱动电路不需要额外电源或信号隔离单元，在降低成本的同时减小了寄生参数及电磁干扰对IGBT开关特性的影响。
图8 有源驱动电路结构
Fig.8 Outlook of the active driving circuit board
控制采样电路参考电压
满足
式中，n为串联单元数量；m为单只IGBT允许承压 误差，通常取5%[20]。根据实验条件可得
=550V。 阈值eth1～eth3的选取决定了控制的准确性与快速性，其关系应满足
根据式（19）结合实验条件及测试验证，本文逐级控制算法相关参数及PI控制系数（Kp, Ki）见表3。
表3 控制算法相关参数
Tab.3 The parameters of the control algorithm
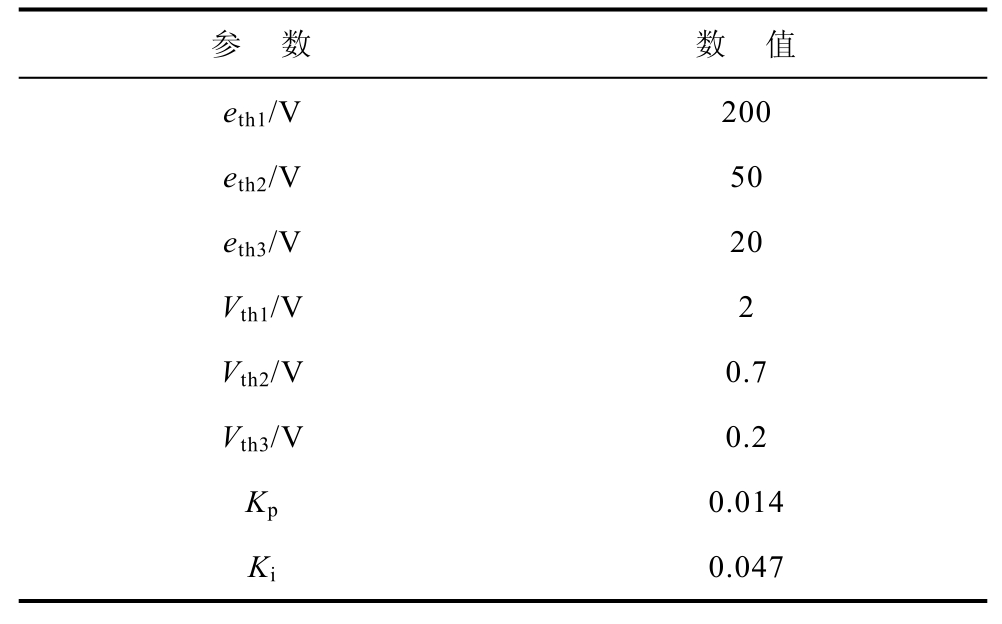
参 数 数 值 eth1/V 200 eth2/V 50 eth3/V 20 Vth1/V 2 Vth2/V 0.7 Vth3/V 0.2 Kp 0.014 Ki 0.047
3 实验验证
为验证所提出的有源驱动电路均压作用，本文依据图3搭建了如图9所示的两只IGBT串联实验平台。其中直流母线电压为1kV，负载采用100Ω线绕电阻，其等效电感为25μH。串联IGBT型号如第2节所述为IHW20N120R3（1 200V/20A），主回路续流二极管采用3只G3S06510A（650V/10A）串联结构。电压波形由泰克四通道隔离示波器TPS2024B配合无源探头P2220（200MHz/300V）及UT−P20（250MHz/1.5kV）完成采集，驱动信号由CPLD（5M240ZT100C5N）产生。
图9 主电路及测试平台
Fig.9 The testing board and platform setup in this paper
3.1 仅使用传统驱动时串联实验波形
为对比有源驱动电路均压效果，本文首先给出传统驱动电路作用下串联IGBT电压波形。图10给出了tdelay=100ns时串联IGBT电压波形。由于缺少高压差分探头，上管VT1承压波形通过对两只IGBT集电极电压相减的方式显示于MATH通道。可以看出，下管VT2的延迟关断使上管VT1在关断瞬态几乎承受了整个母线电压1kV，尽管在静态均压电阻作用下二者承压趋于平衡，但随着母线电压的升高VT1将有过电压损坏的风险。
图10 传统驱动电路作用下串联IGBT电压波形
Fig.10 Experimental waveforms of series-connected IGBTs with conventional gate drivers
3.2 有源驱动作用下串联实验波形
图11所示为有源驱动电路作用下串联IGBT电压波形。与图10相比可以看出，虽然VGE2晚于VGE1开始下降，但在电流吸收电路的作用下，更快的下降速率使其与VGE1几乎同时进入米勒平台。VCE1与VCE2上升时间基本一致，电压平衡得以实现。
图11 有源驱动电路作用下串联IGBT电压波形
Fig.11 Experimental waveforms of series-connected IGBTs with proposed active gate drivers
图12给出了电流吸收电路作用时Vctrl与Isink的波形。可以看出，在检测到VGE2的下降沿后，Vctrl由零变为控制采样电路输出VDAout。由于运放LM7171的输出延迟及三极管开通延迟的存在，Isink滞后于Vctrl约30ns。然而，如2.2节所述，电流吸收电路作用时间tctrl（210ns）仍处于IGBT关断延迟时间387ns内，故其在关断瞬态提供的放电补偿量不变，不影响电压平衡控制效果。
图12 Vctrl与Isink实验波形
Fig.12 Experimental waveforms of Vctrl and Isink
3.3 控制算法的验证
首先，为了验证控制采样电路的性能，图13给出了调节过程中触发信号VST与控制采样电路输出VDAout的波形。可以看出，在VST下降沿到来时，VCE2已达到稳态值。经过5μs的AD采样、算法处理及DA输出延迟TD后，VDAout的值得以更新并在下一个开关周期作为电流吸收电路的输入。
图14给出了初始12个开关周期内串联IGBT电压及控制采样电路输出VDAout波形。据图14可以 看出，在第一个开关周期内，由于辅助电路尚未作用，两只IGBT承压呈现出极大的不平衡，VDAout依据逐级控制算法阈值设置上升Vth1（2V）。在下一个开关周期，虽然电压不平衡仍然存在，但2V的Vctrl已使其不平衡度大幅降低。因此，VDAout上升增量降低为Vth2（0.7V），在其作用下，电压不平衡程度进一步降低。经过4个开关周期后，两只IGBT承压基本一致，PI控制取代逐级控制方式并将VDAout的值稳定在较小区间内，均压调节完成。
图13 控制采样电路输出电压时序波形
Fig.13 Time sequence among the relevant voltage signals of the control and sampling circuit
图14 有源驱动电路作用下电压调节过程
Fig.14 The voltage regulating process with the proposed active gate drive
3.4 有源驱动电路适用性验证
为进一步验证该有源驱动电路在串联IGBT电压平衡调节中的作用，图15给出了不同开关频率时该有源驱动电路作用下串联IGBT承压波形。由于辅助电路仅于关断瞬态激活，因此开关频率不是影响其工作特性的因素。不同开关频率下有源驱动电路均压效果如图15所示，当开关频率fs分别为2kHz与10kHz，且tdelay=100ns时，该驱动电路作用下串联IGBT仍可实现电压平衡。
图15 不同开关频率下有源驱动电路均压效果
Fig.15 Voltage waveforms of the series-connected IGBTs at different switching frequencies
图16与图17分别给出了开关占空比为50%与80%且驱动信号间延迟tdelay=100ns时，传统驱动电路与有源驱动电路作用下各IGBT承压波形。可以看出，不同开关占空比下，该有源驱动电路仍可实现同样的均压效果。
图16 占空比为50%时有源驱动电路承压波形
Fig.16 The voltage waveforms of the series-connected IGBTs when the duty cycle is 50%
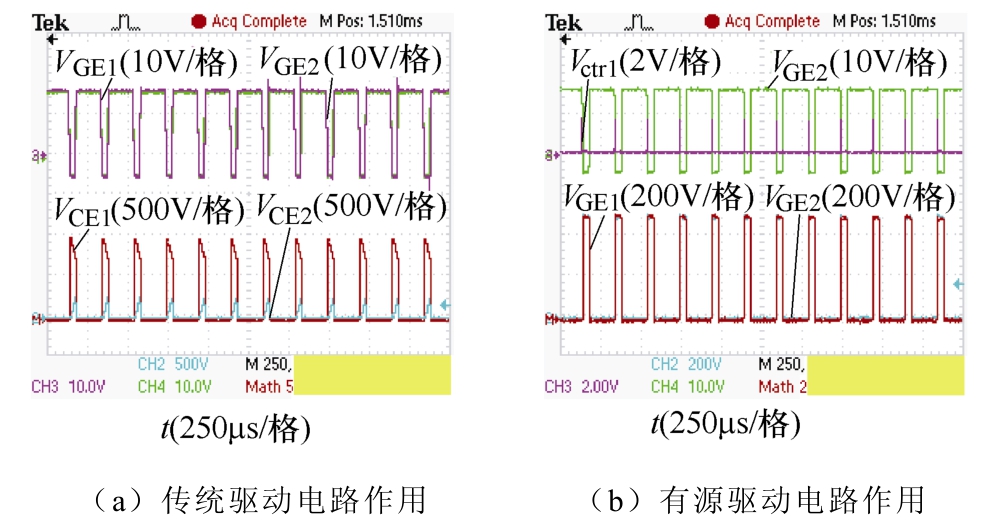
图17 占空比为80%时有源驱动电路承压波形
Fig.17 The voltage waveforms of the series-connected IGBTs when the duty cycle is 80%
图18给出了母线电压降低至800V与600V时，tdelay=100ns条件下两只IGBT承压波形。从图18可以看出，不同母线电压下，应用该有源驱动电路的串联IGBT仍可实现电压平衡。
图18 不同母线电压时有源驱动电路承压波形
Fig.18 The voltage waveforms of the series-connected IGBTs under different DC bus voltages
4 结论
本文提出了一种旨在补偿串联IGBT关断瞬态门极放电偏差的有源驱动均压电路，与目前应用的有源驱动均压电路相比，该方法在实现电压平衡控制的同时还具备以下优点：
1）辅助电路仅使用现有驱动IC输出信号下降沿作为触发信号，易于与传统驱动相集成。
2）仅将IGBT静态承压作为采样对象及闭环控制输入，降低了采样难度，提升了稳定性。
3）控制采样频率与变流器开关频率一致。因此，低成本控制器（如51单片机）即可满足要求，降低了电路成本。
4）无需引入额外的隔离控制与反馈信号，在减小了门极对地寄生电容Cp的同时减小了信号间的共模干扰[16]。
该有源驱动均压电路在实际应用中仍存在改进的空间，未来的工作将在以下两个方面予以优化：
1）虽然该驱动电路可应用于不同母线电压，但 当其值变化时，参考值
也需要重新设置。因此， 在母线电压变化较大的场合，需要在驱动电路中集成VDC监测功能。
2）根据3.3节的实验结果可以看出，由于闭环控制滞后一个开关周期，起动过程中至少有一个开关周期辅助电路是无法起到均压作用的。文献[13]所述的电压斜率抑制电路可以应用于各串联单元以避免控制初期的过电压风险。
[1] 苏见燊, 郭敬东, 金涛. 柔性直流电网中直流故障特性分析及线路故障重启策略[J]. 电工技术学报, 2019, 34(增刊1): 352-359.
Su Jianshen, Gou Jingdong, Jin Tao. DC fault characteristics and line fault recovery strategy in flexible DC power network[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 352-359.
[2] 张志文, 雷诗婕, 翟承达, 等. 高压直流输电系统吸收与并联电容换相换流器特性分析[J]. 电工技术学报, 2019, 34(2): 684-691.
Zhang Zhiwen, Lei Shijie, Zhai Chengda, et al. The characteristic analysis of HVDC system with absorption and shunt capacitance commutated converter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 684-691.
[3] 刘建强, 刘传铎, 王轶欧, 等. 单相PWM整流器IGBT及直流侧电容故障诊断方法[J]. 电工技术学报, 2019, 34(增刊1): 244-257.
Liu Jianqiang, Liu Chuanduo, Wang Yiou, et al. Fault diagnosis method for IGBT and DC-link capacitor of single-phase PWM rectifier[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 244-257.
[4] 贾英杰, 罗毅飞, 肖飞, 等. 一种符合欧姆定律的IGBT等效电阻模型[J]. 电工技术学报, 2020, 35(2): 310-317.
Jia Yingjie, Luo Yifei, Xiao Fei, et al. An equivalent electrical resistance model of IGBT suitable for Ohm’s law[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 310-317.
[5] Zhang Xiangyu, Yu Zhanqing, Chen Zhengyu, et al. Modular design methodology of DC breaker based on discrete metal oxide varistors with series power electronic devices for HVDC application[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7653-7662.
[6] Guerrero A F, Ustariz-Farfan A J, Tacca H E, et al. IGBT series connection with soft switching and power recovery in driver power supply[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11679-11691.
[7] Zarghani M, Mohsenzade S, Kaboli S. A series stacked IGBT switch based on a concentrated clamp mode snubber for pulsed power applications[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 9573-9584.
[8] Mohsenzade S, Zarghani M, Kaboli S. A high-voltage series-stacked IGBT switch with active energy recovery feature for pulsed power applications[J]. IEEE Transactions on Industrial Electronics, 2020, 67(5): 3650-3661.
[9] 宋慧敏, 田苗, 吴俊锋, 等. 均压驱动耦合型单驱动IGBT串联电路设计[J]. 高压电器, 2019, 55(5): 144-153.
Song Huimin, Tian Miao, Wu Junfeng, et al. Design of voltage-sharing driving coupled single driving IGBT series circuit[J]. High Voltage Apparatus, 2019, 55(5): 144-153.
[10] Bagheri A, Iman-Eini H, Farhangi S. A gate driver circuit for series-connected IGBTs based on quasi- active gate control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(2): 791-799.
[11] Teerakawanich N, Johnson C. Design optimization of quasi-active gate control for series-connected power devices[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 2705-2714.
[12] Ji Shiqi, Wang Fei, Tolbert L M, et al. An FPGA- based voltage balancing control for multi-HV-IGBTs in series connection[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4640-4649.
[13] 周野, 王旭, 鲜亮, 等. 基于多级钳位与门信号调节相结合的IGBT串联均压电路研究[J]. 中国电机工程学报, 2020, 40(13): 4277-4290.
Zhou Ye, Wang Xu, Xian Liang, et al. Voltage balancing circuit for series-connected IGBTs based on multi-level clamp topology and gate drive signal adjustment[J]. Proceedings of the CSEE, 2020, 40(13): 4277-4290.
[14] Yang Xin, Yuan Ye, Zhang Xueqiang, et al. Shaping high-power IGBT switching transitions by active voltage control for reduced EMI generation[J]. IEEE Transactions on Industry Applications, 2015, 51(2): 1669-1677.
[15] Zhang Fan, Yang Xu, Ren Yen, et al. A hybrid active gate drive for switching loss reduction and voltage balancing of series-connected IGBTs[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(10): 7469-7481.
[16] Nguyen V, Kerachev L, Lefranc P, et al. Characteri- zation and analysis of an innovative gate driver and power supplies architecture for HF power devices with high dv/dt[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 6079-6090.
[17] Baraia I, Barrena J, Abad G, et al. An experimentally verified active gate control method for the series connection of IGBT/diodes[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 1025-1038.
[18] Baliga B J. Fundamentals of power semiconductor devices[M]. Switzerland: Springer, 2019.
[19] Ren Yu, Yang Xu, Zhang Fan, et al. A compact gate control and voltage-balancing circuit for series- connected SiC MOSFETs and its application in a DC breaker[J]. IEEE Transactions on Industrial Electro- nics, 2017, 64(10): 8299-8309.
[20] Lu Ting, Zhao Zhengming, Yu Hualong, et al. Parameter design of a three-level converter based on series-connected HV-IGBTs[J]. IEEE Transactions on Industry Applications, 2014, 50(6): 3943-3954.