0 引言
交流变频电机是工业中应用广泛的动力驱动部件,其运行状态将直接影响设备运行的安全性及稳定性。转子断条作为最常见的故障形式,在早期故障检测中具有识别难、隐含性强的特点,致使工业检测中识别率较低[1]。尽管利用振动信号检测电机故障已开展了众多研究[2-3],但振动信号在强电磁干扰环境下往往成分复杂,早期故障特征信息易被噪声等不相干成分淹没。而电流信号具有信噪比高、非侵入式检测的优点,能直接反映电机的内部动态机械与电气特性[4]。因此,本文将利用电流信号检测交流变频电机早期转子断条故障作为研究的关键。
目前,电流信号检测技术(Motor Current Signature Analysis, MCSA)以信号基频及旁瓣分量为分析特征已被应用于电机故障监测中[5]。但对于交流变频电机来说,由于受工作特性的限制,电机在低速状态下的转子断条故障初期阶段,(1±2s)fs(s为转差率,fs为电流基频)特征频率分量相对微弱,且s和fs较低,导致特征频率旁瓣分量容易与基频混叠,难以识别[6]。这一问题已引起一些学者的重点关注。就提高电流信号频谱分辨率研究方面,G. Singh等[1]利用多重信号分类(Multiple Signal Classification, MUSIC)算法来提高电流二次方伪谱的分辨率,以提高转子断条故障检测的灵敏度。在此基础上,孙丽玲等[7]提出一种MUSIC与模拟退火算法相结合的电机转子断条故障检测方法,以实现对转子断条故障特征频率幅值和相位的准确估计。T. R. J. Romero等[8]将完全集成经验模态分解与MUSIC算法相结合,实现了基于瞬态电流和稳态电流的转子断条故障的检测。在抑制基频分量增强故障频率特征研究方面,贾朱植等[9]通过对定子三相电流Park矢量模二次方信号进行离散小波变换来抑制基频分量,同时突出转子断条故障特征信息。刘新正等[10]提出基于最小方均误差自适应滤波的转子断条故障诊断方法,同样达到了滤除电流信号基频分量,突出故障特征信息的目的。另外,为实现电流信号与故障信息的解耦,在电流信号解调研究方面,M. B. Abd-El-Malek等[11]通过对电流信号进行Hilbert解调,以包络信号标准差的波动值作为故障特征,已实现不同负载下转子断条故障的定量分析。赵妍等[12]提出以谱峭度法为基础结合Hilbert包络解调的转子断条电机故障检测新方法。目前,一些增强电流信号故障特征信息的检测方法也在进一步完善[13-17],以上相关研究都为电机故障诊断方法提供了良好的理论借鉴。
上述研究中多以提取与增强电流信号中的故障频率作为出发点,而弱化了电流基频与高次谐波分量的分离。在电机故障早期,转差率低容易造成高次谐波分量与基频混叠,致使频谱分辨率低、故障难以识别,同时会给转子断条故障特征频率和转差率的计算带来误差。变分模态分解(Variational Mode Decomposition, VMD)通过迭代搜寻变分模型最优解来确定每个分量的频率中心和带宽,从而自适应地将原信号分解为预设分解个数的多个单分量信 号[18]。因此,本文以电机电流信号高次谐波分量与基频分量的分离为目标,研究基于VMD的交流变频电机转子断条故障识别方法。通过设定VMD分解个数和初始化各模态分量的中心频率分布,以适应交流变频电机定子电流信号的频率分布特性。针对惩罚参数的获取,研究利用萤火虫群优化算法(Firefly Algorithm, FA)实现对惩罚参数的寻优,以增强VMD对电流信号的自适应分解能力。并在此基础上,结合Park变换,利用电流信号相位关系实现转子断条故障调制频率的提取,以避免MCSA分析中基频谱泄漏对旁瓣分量的影响,实现交流变频电机在低速状态下转子断条早期故障的识别。本研究将有助于提高以电流信号为基础的交流变频电机早期转子断条故障的检测能力。
1 转子断条故障在定子电流中的表现形式
正常交流变频电机中转子导条均匀分布,供电电流通过定子时分别形成频率为fs和sfs对称分布的定子、转子旋转磁场,不存在逆序分量。当转子导条断裂时,转子磁场的对称性将会被破坏,产生与原磁场旋转方向相反,频率为−sfs的逆序分量。该逆序分量将在定子电流中感应出频率为(1−2s)fs的电流分量,此电流分量产生的旋转磁场又与原气隙磁场相互作用,导致电磁转矩和转速以2sfs的频率波动,使电机传动系统最终达到动态平衡,即
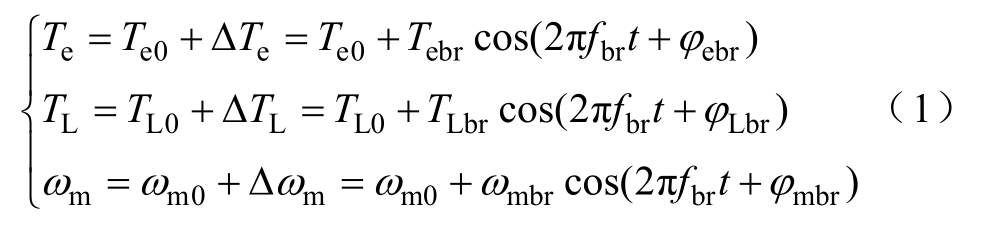
式中,Te、TL、ωm分别为电磁转矩、负载转矩、电机角速度;Te0、TL0、ωm0和ΔTe、ΔTL、Δωm分别为相应均值及波动值;ϕebr、ϕLbr、ϕmbr为相应初始相位;fbr=2sfs为故障特征调制频率。
根据矢量控制中的转矩方程,转子发生断条故障将以频率fbr对定子三相电流进行幅值和频率调制。此时电机电流信号相位θ 为
式中,θ0为初始相位;a为频率调制系数。
通过变频器低速驱动电机时,脉冲宽度调制(Pulse Width Modulation, PWM)将输出一个关于1/4周期对称的奇函数方波,其傅里叶级数只包括基频奇次谐波分量,从而影响以低速电流为检测对象的电机故障识别。而fbr同样会对基频的奇次谐波分量进行调制,因此转子断条交流电机定子三相电流可表达为

式中,al、bl分别为频率调制系数和幅值调制系数;il为电流信号基频2l+1次谐波分量对应幅值;β1l、β2l为初始相位;l =0, 1, 2, 3,…。
以上为变频电机转子断条故障在电流信号中的基本表达,直接反映了定子电流与故障频率之间的关系。
2 基于参数优化变分模态分解和Park变换的转子断条故障识别方法
2.1 VMD分解原理
VMD是以维纳滤波、Hilbert变换和频率混合为基础,通过寻找约束变分模型最优解,将复杂调制信号分解为K个预设尺度的单分量函数的信号自适应分解方法。
在VMD中,对于每一个内禀模态函数(Band- limited Intrinsic Mode Function, BIMF)uk可利用Hilbert变换得到其解析函数为
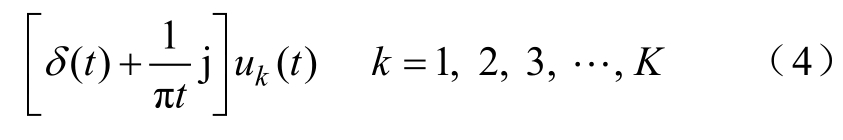
式中,δ (t)为单位脉冲函数;uk(t)为内禀模态函数;j为虚数标识。
通过指数项将各模态频谱调制到相应基频带上,利用高斯平滑度来估算各模态中心频率ωk的带宽,从而得到一个受约束的变分问题为
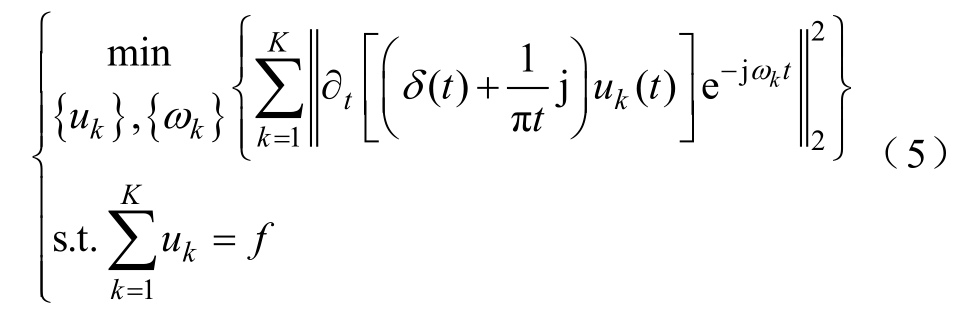
式中,f为输入信号;{ωk}={ω1, ω2,…, ωK}。
最后引入二次惩罚参数α 及Lagrange乘子λ(t)将上述问题转变成无约束变分问题,扩展拉格朗日表达式为
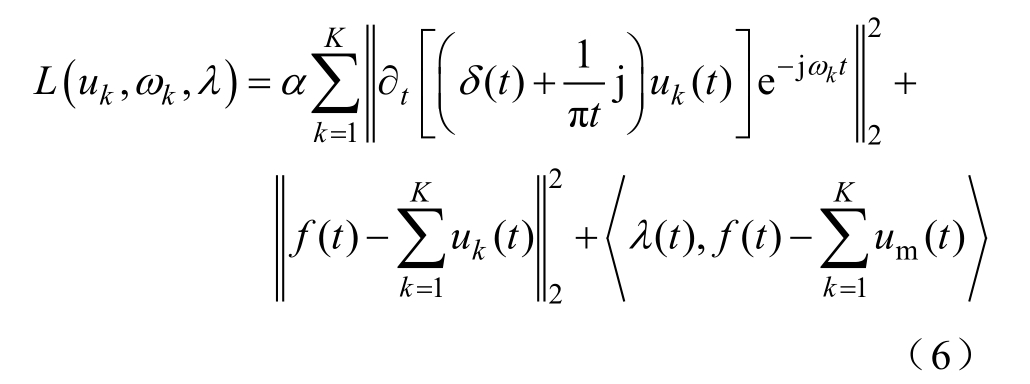
利用交替方向乘子算法得到上述扩展拉格朗日函数的鞍点,即最优解,从而实现对复杂调制信号自适应分解,得到K个单分量函数。
2.2 VMD分解个数及中心频率分布初始化
利用VMD算法对信号进行自适应分解时,需要预先设定分解个数K和惩罚参数α,并初始化各模态分量中心频率分布ωk(k=1, 2,…, K)。K. Dragomiretskiy[19]给出了三种中心频率初始化方案,如下:
(1)中心频率均匀分布
式中,F为采样频率。
(2)中心频率随机分布
(3)中心频率都初始化为0
由于交流电机定子电流信号表现为电流基频及其奇次谐波分量的叠加形式,本文根据这一特性设定VMD分解个数和初始化中心频率分布。首先根据香农采样定理,只有最高频率小于采样频率F一半才不会产生频谱混叠,设定分解个数为K,有
基于式(10)可以将采集到的小于采频一半的电流基频及其奇次谐波分量个数准确估计出来。
而K个模态分量的中心频率可依次初始化为
式中,各中心频率ωk分别对应电流基频及2k−1次谐波频率,从而进一步减少VMD分解迭代次数,加强其针对变频电机定子电流信号的自适应分解效率。
2.3 VMD分解惩罚参数设定方法
惩罚参数α 对VMD分解结果也有较大影响,α越大,则各BIMF分量带宽越小;α 越小,则各BIMF分量带宽越大。由于实测信号成分复杂,而惩罚参数α 的选取大多又依赖于经验。如何确定惩罚参数α,便是利用VMD分解处理交流电机定子电流信号的关键。FA算法能够同时搜索多模态函数的多个最优解,非常适合处理复杂的局部优化问题。因此本文基于FA算法对惩罚参数α 进行优化,筛选出最优参数,以避免人为主观因素的干扰。
基于FA算法优化惩罚参数α,需要设定适应度函数,并通过对比适应度值对萤火虫位置进行更新。针对交流变频电机定子电流信号,VMD理论分解结果为中心频率从低到高的K个BIMF分量,并且其中心频率分别为基频及其3, 5,…, 2K−1奇次倍频,与式(3)中交流变频电机定子电流表现形式相对应。因此,相邻BIMF分量中心频率间隔fi(i=1,2,…,K−1)理论上为基频的2倍频,定义适应度函数为
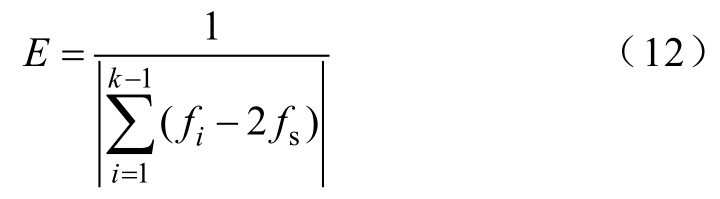
在上述定义下,适应度值越大代表各模态分量中心频率分布与理论值越接近,VMD分解效果也越好。基于FA算法的惩罚参数α 优化方法具体步骤如下:
在可行解空间中随机生成n个具有相同荧光素值和邻域范围的萤火虫。设定传感半径rs、荧光素增长因子γ、荧光素衰减因子ρ、邻域决策范围rd、萤火虫移动步长s、最大迭代次数titer、增益常量κ和期望邻居数nt。
依据萤火虫位置的变化更新其荧光素值,有
式中,li(t)和xi(t+1)分别为第i个萤火虫在第t次和第t+1次迭代时的荧光素值和位置。
萤火虫在其邻域内搜索荧光素值比自身高的个体作为邻居,有
式中,Ni(t)和disio(t)分别为第i个萤火虫在第t次迭代时的邻居数和与第o个萤火虫间的欧式距离。
确定萤火虫移动方向,有
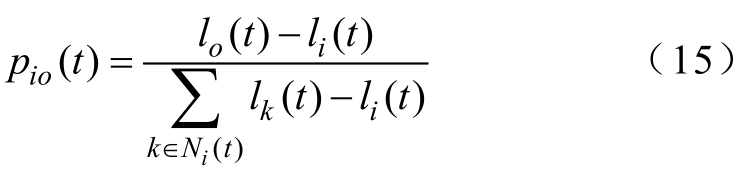
式中,pio(t)为第i个萤火虫在第t次迭代时向邻居o移动的概率。
分别对萤火虫位置和邻域范围进行更新,有
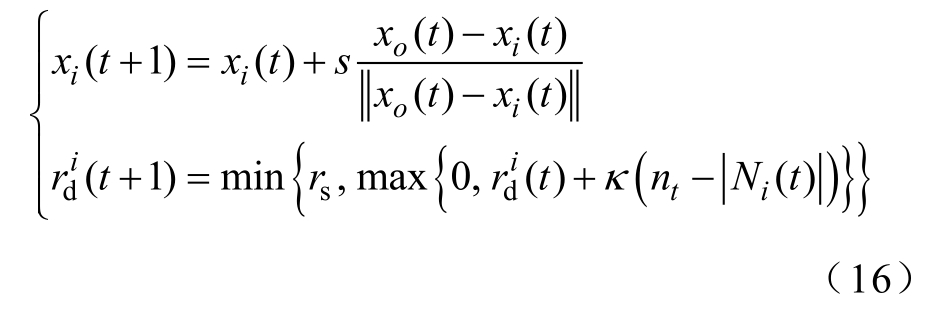
判断t≤titer,是则t =t+1并更新萤火虫荧光素值重复上述过程;否则终止算法,退出循环。
基于FA算法的惩罚参数α 优化方法具体流程如图1所示。
2.4 基于Park变换的故障特征调制频率检测方法
Park变化能够将三相电流等效转换为两相信息,从而快速构造解析信号来检测故障特征调制频率。通过VMD对定子三相电流进行分解后,分别取其基频分量的调制信号即BIMF1构成新的待处理信号iu、iv、iw,有


图1 惩罚参数优化流程
Fig.1 Flow chart of penalty parameter optimization
式中,a、b分别为频率调制系数和幅值调制系数;im为电流基频分量幅值;β1、β2为初始相位。
对式(17)进行Park变换获得两相电流id、iq分别为
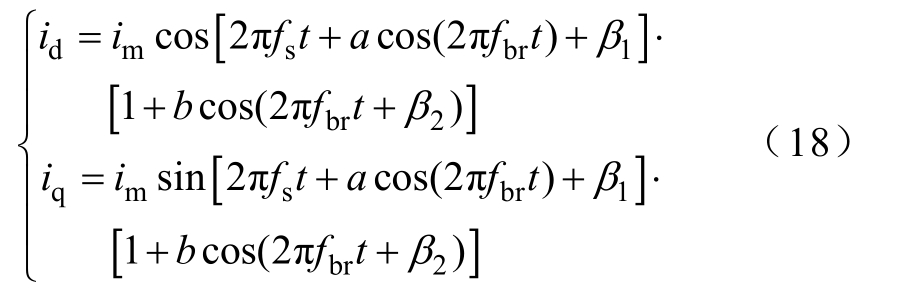
iq为id的90°相移信号,基于id和iq分量构造解析信号iz为
对解析信号iz求模和幅角就可以获得电流信号iu的幅值信息A(t)和相位信息ϕ (t)分别为
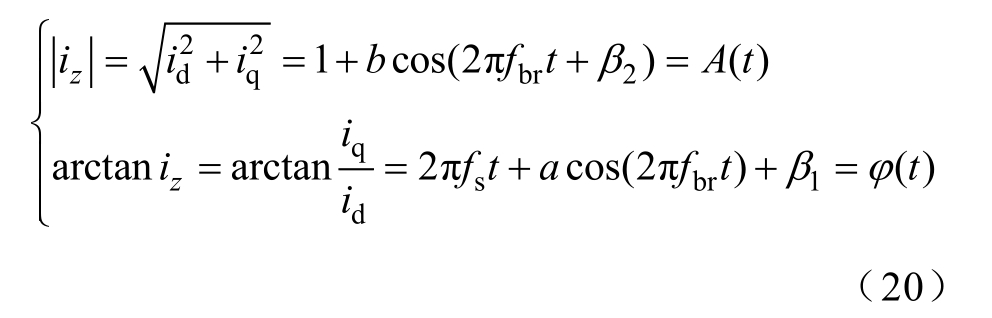
然后基于具有二阶精度的求导公式对解卷相位进行数值微分,计算瞬时频率ω (t)为
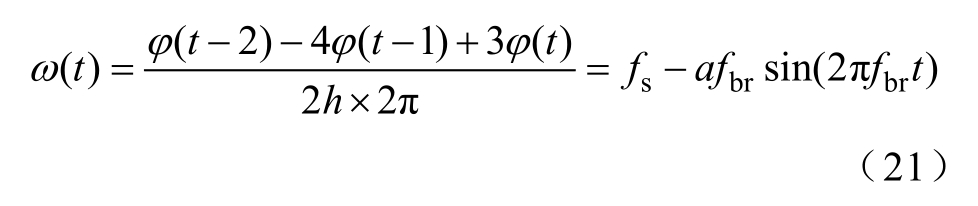
式中,h为采样间隔。
对瞬时幅值A(t)和瞬时频率ω (t)进行频谱分析就可以直接在低频段对转子断条故障特征调制频率fbr进行检测。相比于传统Hilbert变换解调,本方法不需要事先确定中心频率和带宽,更适合交流电机定子电流信号。
3 转子断条故障识别方法流程
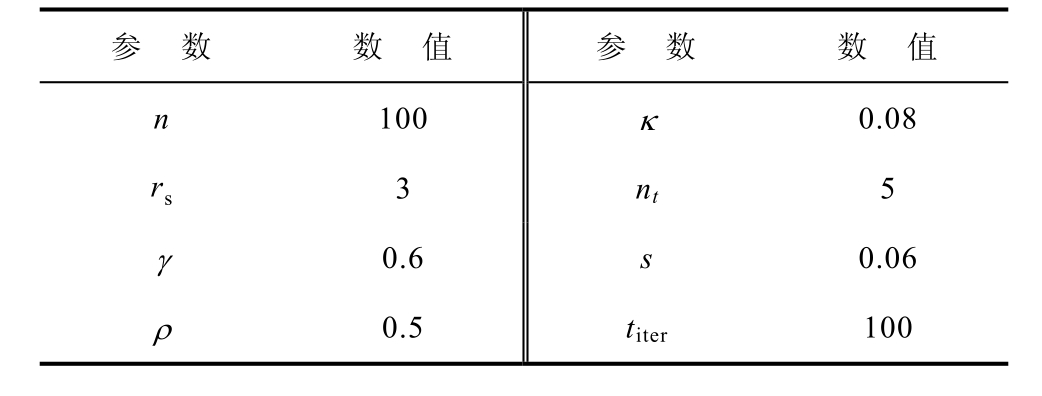
针对交流变频电机早期故障在电流信号中难识别的问题。本文将VMD分解引入到电机定子电流信号的分析处理中,首先基于交流变频电机定子电流信号自身特点设定VMD分解个数并初始化各模态分量中心频率分布,随后利用FA优化惩罚参数α,由此提出适应于交流变频电机定子电流信号的VMD分解参数设定方法,其中,FA的各项参数初始化见表1。在此基础上,基于VMD分解并结合Park变换提出低速状态下交流变频电机早期转子断条故障的特征调制频率识别方法。图2为转子断条故障识别方法流程。
表1 FA算法参数初始化
Tab.1 Initialization parameters of FA algorithm
参 数 数 值 参 数 数 值 n 100 κ 0.08 rs 3 nt 5 γ 0.6 s 0.06 ρ 0.5 titer 100

图2 转子断条故障识别方法流程
Fig.2 Flow chart of broken rotor bars fault recognition method
4 仿真信号分析
为验证本文方法的有效性,转子断条故障交流变频电机定子三相电流仿真信号设置为
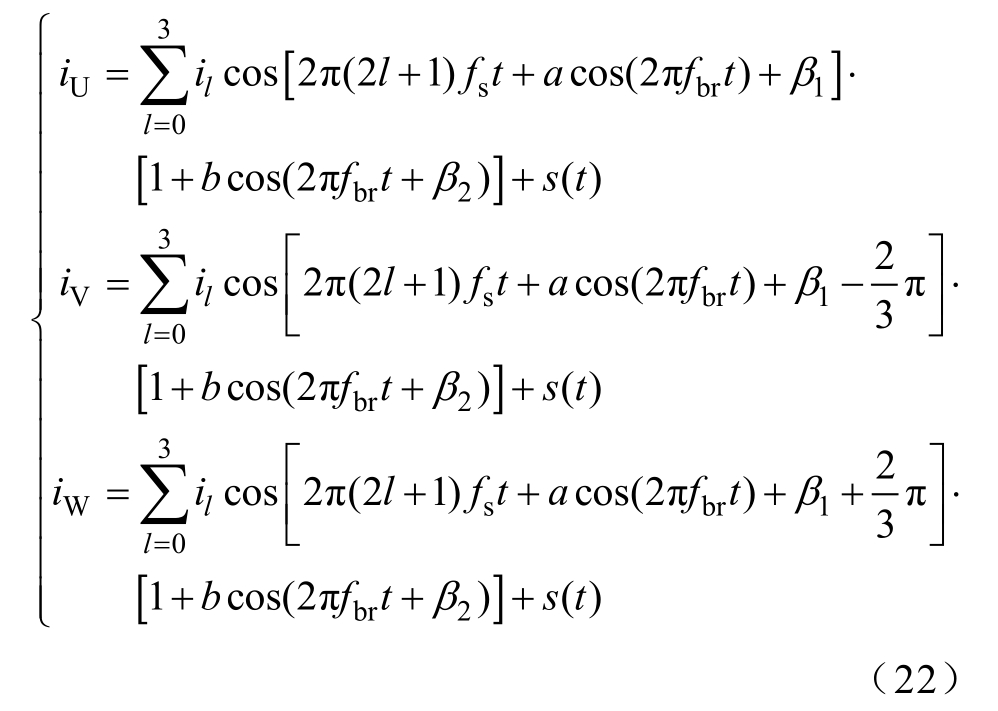
式中,仿真信号包含电流基频(fs=25Hz)及其3、5、7次谐波分量;幅值il分别设置为1、0.01、0.01、0.01;a、b分别为频率调制系数和幅值调制系数,设置为0.05和0.1;β1、β2为初始相位,设置为0;fbr为转子断条故障特征调制频率,且fbr=2sfs=2Hz,转差率s=4%;由于电流信号信噪比高,因此s(t)设为−40dBW的高斯白噪声;仿真信号参数设置与实测低速交流变频转子断条电机定子电流信号相符。采样频率F=500Hz。仿真信号iU分量波形及对数谱如图3所示。

图3 仿真信号
Fig.3 Simulation signal
首先根据式(10)设定VMD分解个数K=5,随后分别基于2.2节中的方案1、方案2、方案3和本文方法初始化各模态分量中心频率分布,相对应的VMD分解效率对比见表2。可见,通过本文方法对中心频率初始分布方式进行改进可以有效提高VMD分解对于交流变频电机定子电流信号的分解效率,减少迭代次数。
表2 VMD分解效率对比
Tab.1 Comparison of VMD decomposition efficiency

初始化方案 迭代次数 方案1 31 方案2 68 方案3 85 本文方法 8
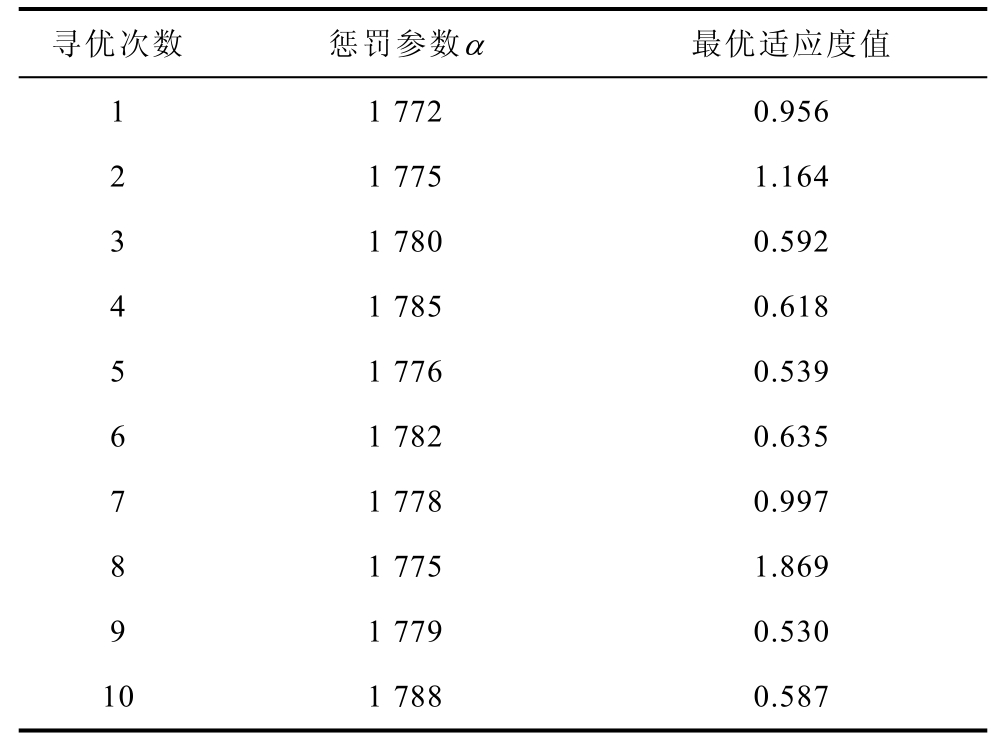
按表1初始化FA参数,并在可行解区间[200, 3 000]内对上述仿真信号进行惩罚参数α 寻优。独立计算10次,惩罚参数寻优结果见表3。在10次寻优结果中,当惩罚参数α =1 775时,最优适应度值最大。因此,设定惩罚参数α =1 775,iU分量VMD分解结果如图4所示。
表3 惩罚参数寻优结果
Tab.3 Results of penalty parameter optimization
寻优次数 惩罚参数α 最优适应度值 1 1 772 0.956 2 1 775 1.164 3 1 780 0.592 4 1 785 0.618 5 1 776 0.539 6 1 782 0.635 7 1 778 0.997 8 1 775 1.869 9 1 779 0.530 10 1 788 0.587
可以看到,通过VMD可以准确将电流iU分解为从低频到高频5个单分量调制信号。其中,BIMF1~ BIMF4分别对应电流信号iU中的基频及3、5、7次谐波的单分量调制信号,并且其幅值与预先设定值相等。BIMF5为高频残余分量。最后分别提取三相电流VMD分解后的BIMF1分量并基于Park变换检测故障特征调制频率,结果如图5所示。在瞬时幅值频谱和瞬时频率频谱的理论位置处均可以清晰检测到转子断条故障特征调制频率fbr,且fbr频率分量幅值分别等于理论计算值b=0.1和afbr=0.1。从而 避免了如图4b中直接对BIMF1分量进行频谱分析产生的频谱混叠、故障特征频率难以识别的问题。

图4 VMD分解结果
Fig.4 Results of VMD
为体现本文方法分解交流变频电机电流信号的准确性,利用经验模态分解(Empirical Mode Decomposition, EMD)对上述仿真信号进行自适应分解并与本文方法进行对比[20],iU分量EMD分解 结果如图6所示。EMD将iU分量分解为从高频到低频两个模态函数IMF1、IMF2和一个残余分量RES。

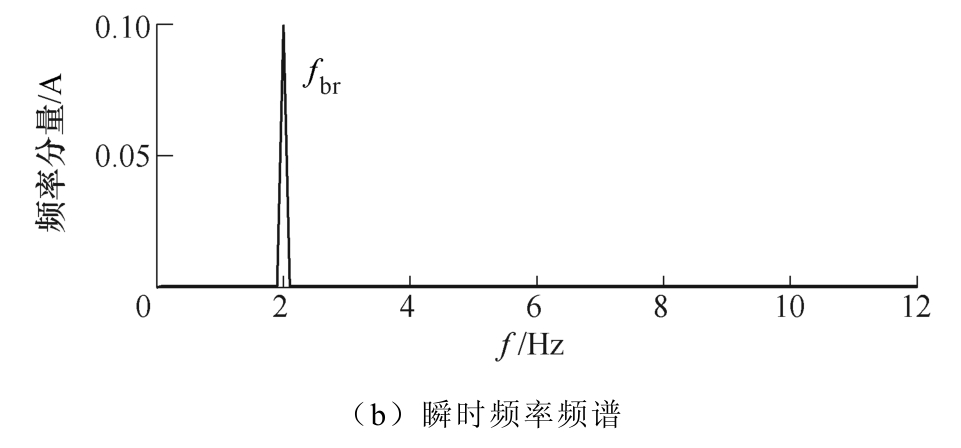
图5 故障特征频率检测结果
Fig.5 Detection results of characteristic frequencies
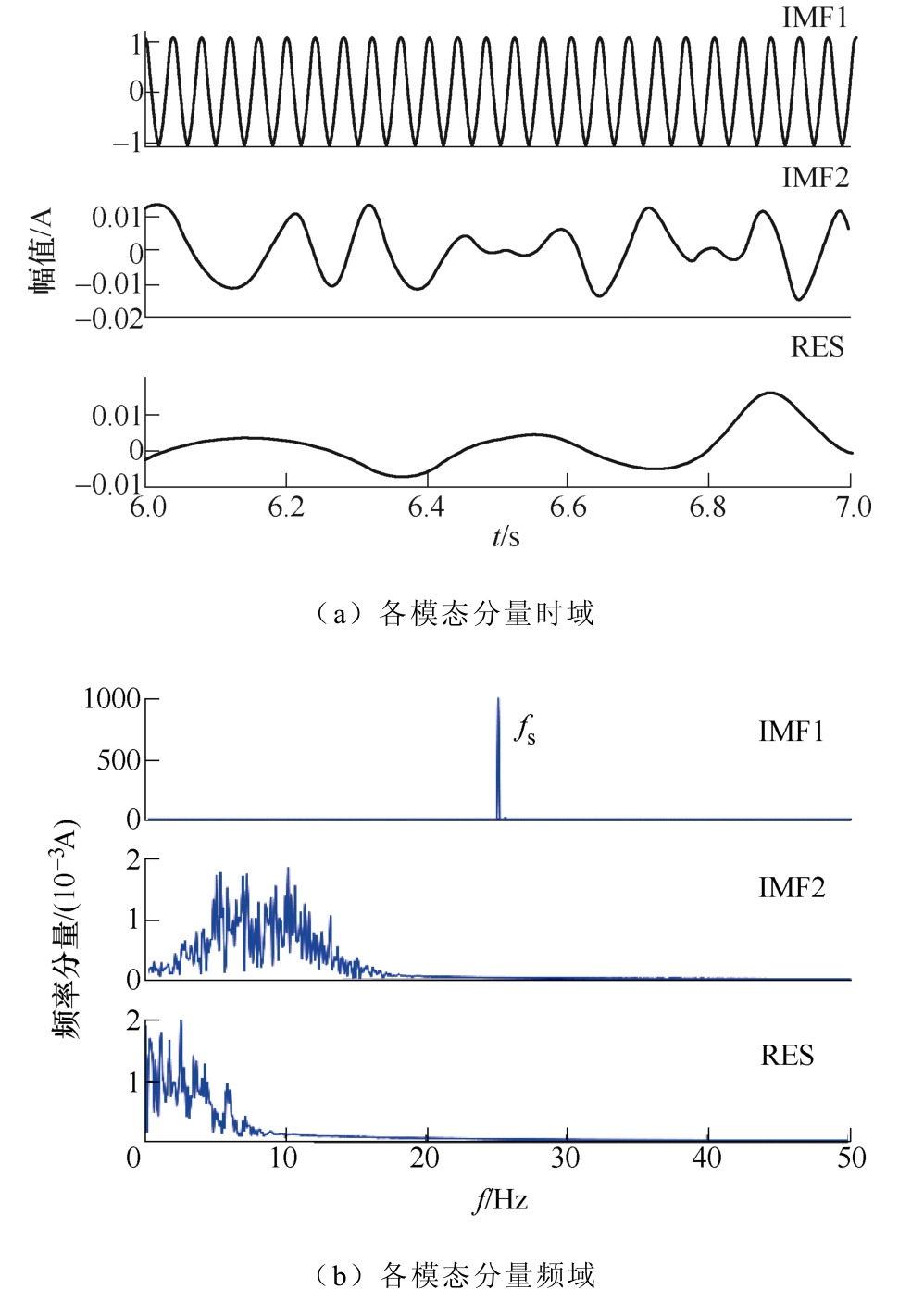
图6 EMD分解结果
Fig.6 Results with EMD
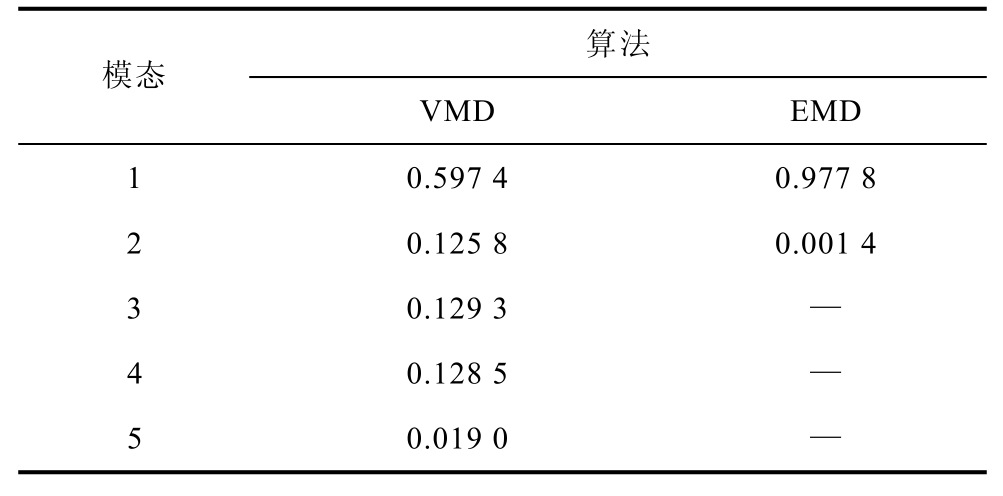
相比于各模态与原信号间的相关系数,互信息能更好地识别虚假分量,因此本文以互信息为指标来评价VMD和EMD的分解效果。各模态互信息计算结果见表4。可见,VMD分解各模态的互信息能够准确反映各分量之间的关系。而EMD分解后IMF1分量几乎包含了电流信号iU的所有信息,模态混叠严重。IMF2互信息值接近于0,产生虚假模态,完全没有将电流基频及其高次谐波分量分开。
表4 各模态互信息
Tab.4 Mutual information of each mode
算法 模态 VMD EMD 1 0.597 4 0.977 8 2 0.125 8 0.001 4 3 0.129 3 — 4 0.128 5 — 5 0.019 0 —
5 实验及结果验证
5.1 实验装置及数据采集
本文基于Spectra Quest的机械故障模拟器(Machinery Fault Simulator, MFS)搭建实验测试平台,如图7所示。该实验测试平台包括电源系统、电机拖动负载和数据采集系统三部分。电源系统由交流电机和变频器组成,通过变频器改变电机基频使电机在不同转速下运转,配备的转速计可以实时对电机转速进行测量和显示;电机拖动负载包括由联轴器连接的转子、传动带和负载齿轮箱三部分;数据采集系统由灵敏度为100mV/A的FLUKE电流钳、4通道NI9234采集卡和个人计算机构成。实验用电机为额定功率为0.56kW、额定转速为2 850r/min、极对数为1内置1根转子断条故障交流变频电机。实验过程中,首先通过变频器设置电流基频为25Hz并通过负载齿轮箱使电机在额定负载下稳定运行。设定采样频率为500Hz、获取时间长度为10s的定子三相电流信号,并对数据进行离线分析。

图7 实验测试平台
Fig.7 Test bench and instruments
5.2 实验分析结果
同步采集的转子断条故障交流变频电机定子三相电流中iU分量波形及对数谱如图8所示,可见,电流信号中包含了电流基频及其3、5、7、9次谐波分量。
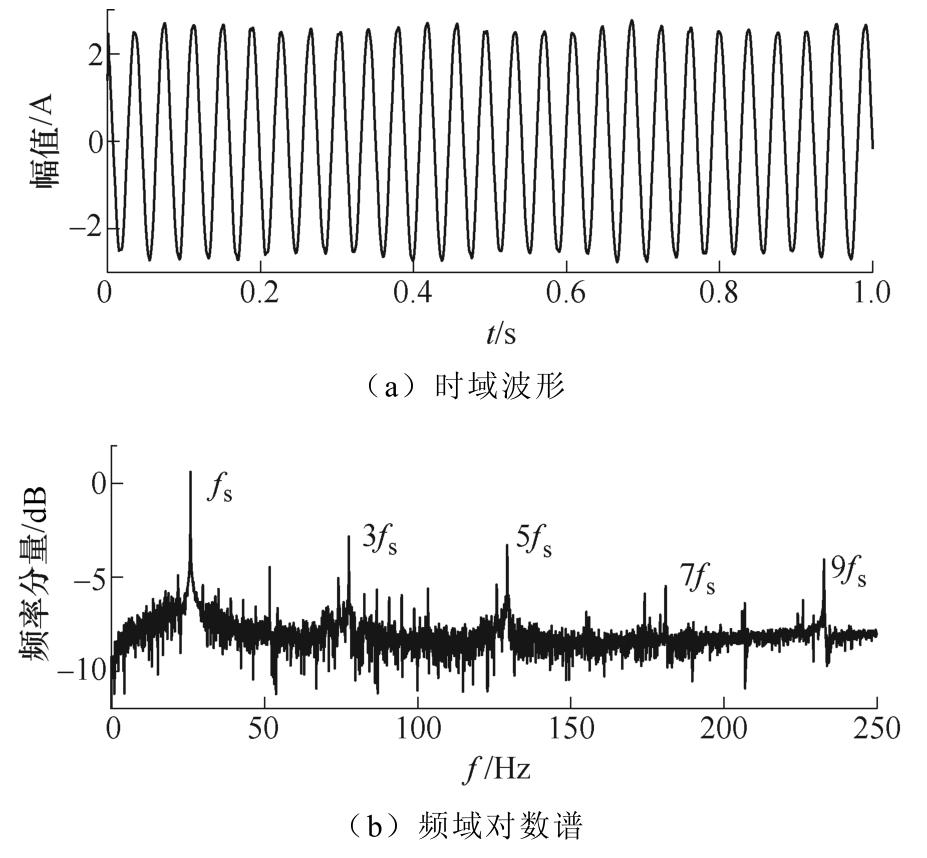
图8 实测电流信号
Fig.8 Test signal of current
首先根据式(10)设定VMD分解个数K=5,并初始化各模态中心频率为fs、3fs、5fs、7fs、9fs。按表1初始化FA参数,并在区间[200, 3 000]内对上述信号对惩罚参数α 寻优。独立计算10次,实测信号惩罚参数寻优结果见表5。可见,在10次寻优结果中当惩罚参数α =880时,最优适应度值最大。因此,设定惩罚参数α =880,iU分量VMD分解结果如图9所示。
表5 实测信号惩罚参数寻优结果
Tab.3 Penalty parameter optimized result of test signal
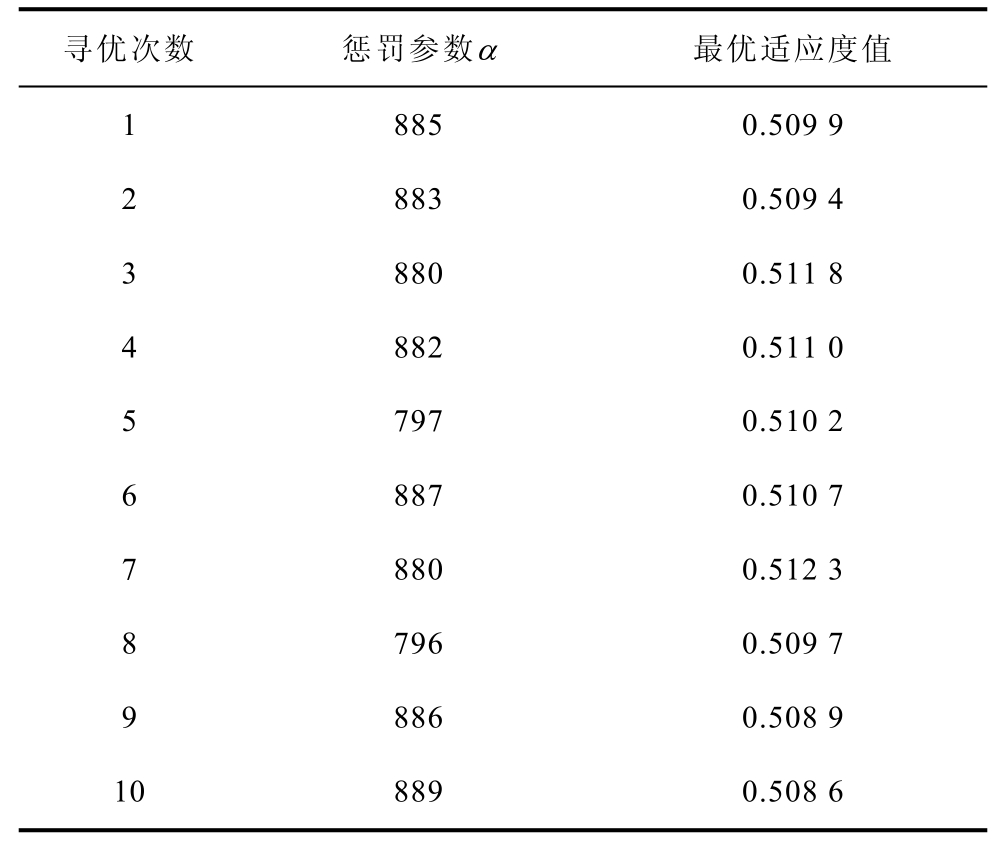
寻优次数 惩罚参数α 最优适应度值 1 885 0.509 9 2 883 0.509 4 3 880 0.511 8 4 882 0.511 0 5 797 0.510 2 6 887 0.510 7 7 880 0.512 3 8 796 0.509 7 9 886 0.508 9 10 889 0.508 6
可以看到,通过VMD方法可以准确将电流iU分解为从低频到高频5个单分量调制信号,且BIMF1~BIMF5分别对应iU中的基频及3、5、7、9次谐波的单分量调制信号。但是,在基频分量即BIMF1频谱中,转子断条故障特征频率被基频分量掩盖难以识别。

图9 实测信号VMD分解结果
Fig.9 Results of test signal with VMD
最后分别提取三相电流的BIMF1分量并基于Park变换检测故障特征调制频率,如图10所示。在瞬时幅值频谱和瞬时频率频谱的理论位置处均可以清晰地检测到转子断条故障特征调制频率fbr,从而对转子断条故障进行识别。
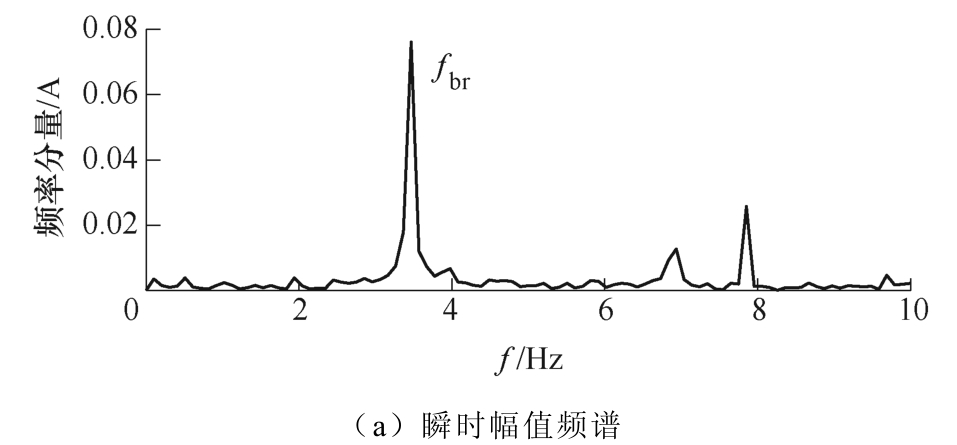
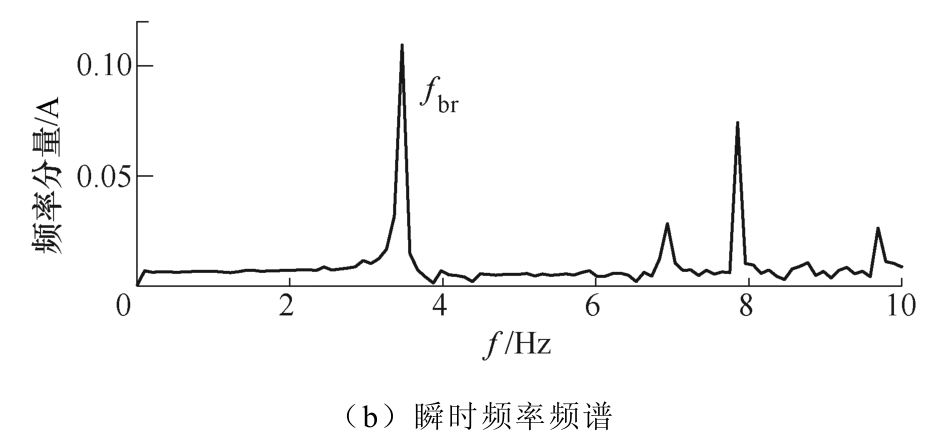
图10 实测信号故障特征调制频率检测结果
Fig.10 Fault characteristic modulation frequency of test signal
同样,为体现VMD分解结果的准确性,利用 EMD方法对iU信号进行自适应分解,与本文方法进行对比,EMD分解结果如图11所示。
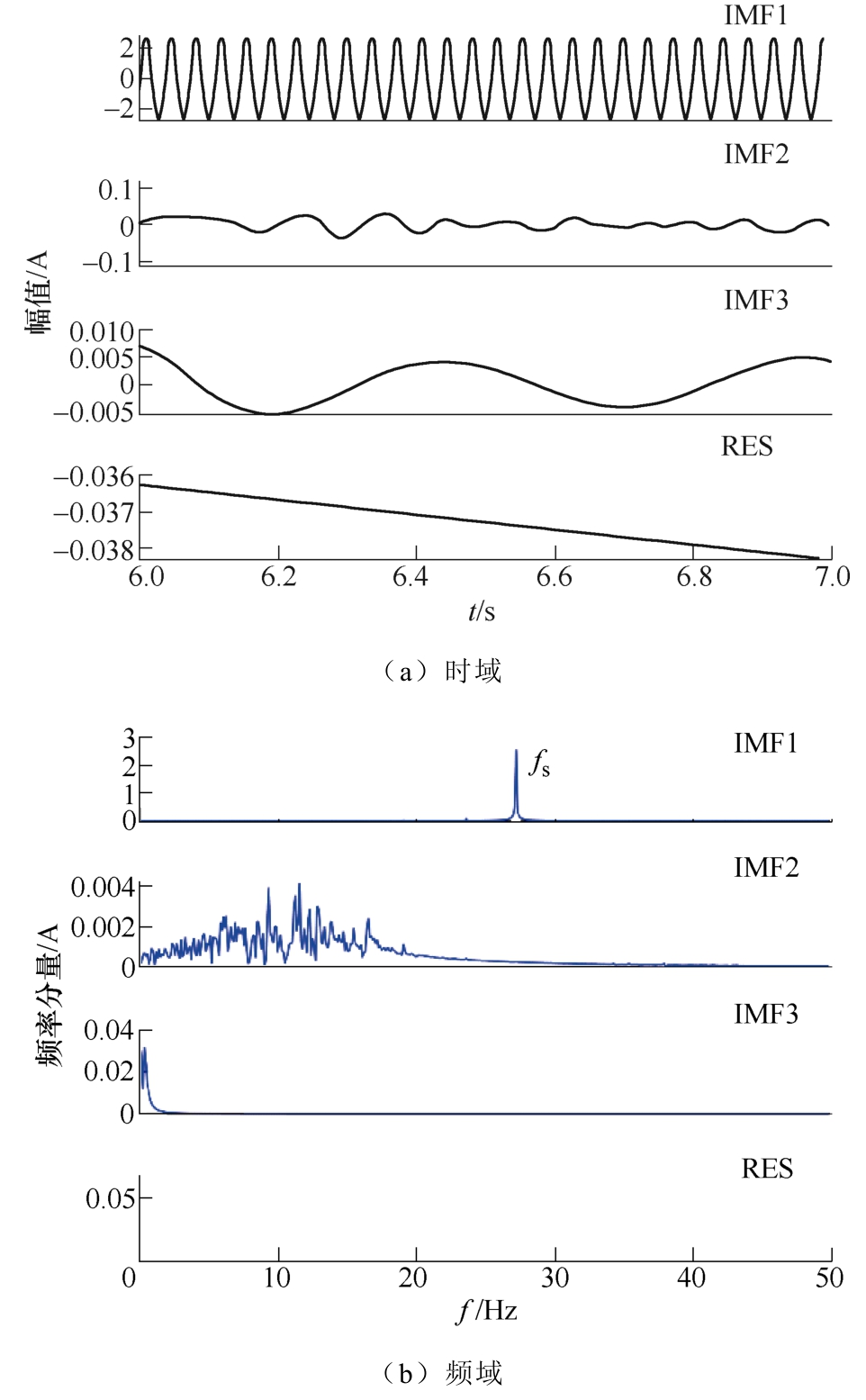
图11 实测信号EMD分解结果
Fig.11 Results of test signal with EMD
EMD将iU信号分解为从高频到低频3个模态分量IMF1~IMF3和一个残余分量RES。
两种分解方法得到的各模态分量与原始信号iU的互信息见表6。可见,VMD分解后各模态分量的互信息能够准确反映各分量之间的关系。而EMD分解后IMF1分量几乎包含了iU的所有信息,模态混叠严重。IMF2、IMF3互信息值接近于0,产生虚假模态,并没有将基频分量与其高次谐波分量分开。
表6 实测信号各模态互信息
Tab.6 Mutual information of each mode of test signal

算法 模态 VMD EMD 1 0.597 4 0.941 8 2 0.114 5 0.036 0 3 0.108 7 0.017 7 4 0.096 2 — 5 0.083 2 —
为进一步验证本文方法对于低速状态下交流变频电机转子断条故障的识别能力,通过变频器使故障电机分别在基频为10Hz、15Hz和20Hz条件下稳定运行,相对应的定子电流瞬时幅值频谱和瞬时频率频谱分别如图12和图13所示。可见,通过本文方法可以在低频段清晰检测到故障特征调制频率fbr,并且随着基频的变大,在频谱图中也能够检测到fbr的倍频2fbr、3fbr。

图12 不同基频下瞬时幅值频谱
Fig.12 Spectrum of instantaneous amplitude at different supply frequencies

图13 不同基频下瞬时频率频谱
Fig.13 Spectrum of instantaneous frequency at different supply frequencies
6 结论
针对低速状态下交流变频电机早期转子断条故障在电流信号中难识别的问题,本文提出基于参数优化变分模态分解和Park变换的故障识别方法。理论和实验表明:
1)基于交流变频电机定子电流信号自身特点和FA寻优算法可以有效设定VMD分解参数,提高了VMD的分解效率,进一步强化了其针对电流信号的自适应分解能力。
2)通过VMD分解可以实现电流基频分量与其高次谐波分量的分离,从而避免高次谐波干扰产生的转差率和故障特征频率估计误差问题。并通过与EMD方法进行对比验证了本文方法分解电流信号的准确性。
3)在此基础上综合利用定子三相电流间的相位关系并基于Park变换成功在低频段检测到转子断条故障特征调制频率,从而避免了传统MCSA分析时基频谱泄漏的影响,实现了转子断条故障特征频率的早期定位。
[1] Singh G, Naikan V N A. Detection of half broken rotor bar fault in VFD driven induction motor drive using motor square current MUSIC analysis[J]. Mechanical Systems and Signal Processing, 2018, 110: 333-348.
[2] Gangsar P, Tiwari R. Signal based condition moni- toring techniques for fault detection and diagnosis of induction motors: a state-of-the-art review[J]. Mecha- nical Systems and Signal Processing, 2020, 144: 106908-106944.
[3] Joung B G, Lee W J, Huang Aihua, et al. Develop- ment and application of a method for real time motor fault detection[J]. Procedia Manufacturing, 2020, 49: 94-98.
[4] 杨明, 董传洋, 徐殿国. 基于电机驱动系统的齿轮故障诊断方法综述[J]. 电工技术学报, 2016, 31(4): 58-63.
Yang Ming, Dong Chuanyang, Xu Dianguo. Review of gear fault diagnosis methods based on motor drive system[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 58-63.
[5] 宋向金, 王卓, 胡静涛, 等. Hilbert解调制方法诊断异步电机轴承故障[J]. 电工技术学报, 2018, 33(21): 4941-4948.
Song Xiangjin, Wang Zhuo, Hu Jingtao, et al. Diagnosis of bearing fault in induction motors using Hilbert demodulation approach[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4941- 4948.
[6] 王臻, 李承, 许允之, 等. a-b坐标系下瞬时无功功率的笼型异步电机转子故障诊断[J]. 电工技术学报, 2015, 30(10): 179-186.
Wang Zhen, Li Cheng, Xu Yunzhi, et al. Rotor fault diagnosis of squirrel cage asynchronous motor based on instantaneous reactive power in a-b coordinates[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 179-186.
[7] 孙丽玲, 许伯强, 李志远. 基于MUSIC与SAA的笼型异步电动机转子断条故障检测[J]. 电工技术学报, 2012, 27(12): 205-212.
Sun Liling, Xu Boqiang, Li Zhiyuan. A MUSIC-SAA based detection method for broken rotor bar fault in induction motors[J]. Transactions of China Electro- technical Society, 2012, 27(12): 205-212.
[8] Romero T R J, Garcia P A, Morinigo S D, et al. Rotor unbalance and broken rotor bar detection in inverter- fed induction motors at start-up and steady-state regimes by high-resolution spectral analysis[J]. Electric Power Systems Research, 2016, 133: 142- 148.
[9] 贾朱植, 祝洪宇, 杨理践, 等. 鼠笼电机起动暂态转子断条Wigner-Ville分布诊断方法[J]. 电机与控制学报, 2018, 22(7): 69-77.
Jia Zhuzhi, Zhu Hongyu, Yang Lijian, et al. Diagnosis of broken rotor bars in squirrel cage induction motor during start-up transient based on Wigner-Ville distribution[J]. Electric Machines and Control, 2018, 22(7): 69-77.
[10] 刘新正, 何升华, 高琳, 等. LMS滤波法在笼型异步电机转子断条诊断中的特征[J]. 电机与控制学报, 2017, 21(5): 1-7.
Liu Xinzheng, He Shenghua, Gao Lin, et al. The features of LMS adaptive filter in rotor bar broken diagnosis[J]. Electric Machines and Control, 2017, 21(5): 1-7.
[11] Abd-El-Malek M B, Abdelsalam A K, Hassan O E. Novel approach using Hilbert transform for multiple broken rotor bars fault location detection for three phase induction motor[J]. ISA Transactions, 2018, 80: 439-457.
[12] 赵妍, 李志民, 李天云. 一种基于谱峭度的异步电机故障诊断方法[J]. 电工技术学报, 2014, 29(5): 189-196.
Zhao Yan, Li Zhimin, Li Tianyun. A method for fault diagnosis of induction motors based on spectral kurtosis[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 189-196.
[13] Corne B, Vervisch B, Derammelaere S, et al. The reflection of evolving bearing faults in the stator current's extended park vector approach for induction machines[J]. Mechanical Systems and Signal Pro- cessing, 2018, 107: 168-182.
[14] Chen Xiaowang, Feng Zhipeng. Induction motor stator current analysis for planetary gearbox fault diagnosis under time-varying speed conditions[J]. Mechanical Systems and Signal Processing, 2020, 140: 106691.
[15] 李永刚, 王罗, 李俊卿, 等. 基于多源信息融合的同步发电机转子绕组匝间短路故障识别[J]. 电力系统自动化, 2019, 43(16): 162-170, 191.
Li Yonggang, Wang Luo, Li Junqing, et al. Identifi- cation of inter-turn short-circuit fault in rotor windings of synchronous generator based on multi- source information fusion[J]. Automation of Electric Power System, 2019, 43(16): 162-170, 191.
[16] Niu Jiahao, Wang Xiaoxian, Lu Siliang, et al. Motor bearing fault diagnosis based on frequency con- version estimation and order analysis[J]. Procedia Manufacturing, 2020, 49: 160-165.
[17] 陈勇, 梁洪, 王成栋, 等. 基于改进小波包变换和信号融合的永磁同步电机匝间短路故障检测[J]. 电工技术学报, 2020, 35(增刊1): 228-234.
Chen Yong, Liang Hong, Wang Chengdong, et al. Detection of stator inter-turn short-circuit fault in PMSM based on improved wavelet packet transform and signal fusion[J]. Transactions of China Electro- technical Society, 2020, 35(S1): 228-234.
[18] Li Hua, Liu Tao, Wu Xing, et al. An optimized VMD method and its applications in bearing fault diagnosis[J]. Measurement, 2020, 166: 108185.
[19] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transaction on Signal Processing, 2014, 62(3): 531-544.
[20] 蒋海峰, 张曼, 赵斌炎, 等. 基于改进Hilbert- Huang变换的电网故障诊断[J]. 电工技术学报, 2019, 34(增刊1): 336-342, 351.
Jiang Haifeng, Zhang Man, Zhao Binyan, et al. Fault diagnosis of power grid based on improved Hilbert- Huang transform[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 336-342, 351.