0 引言
可变磁通磁阻电机(Variable Flux Reluctance Machine, VFRM)是一种定子励磁的无刷同步电机[1],其转子上没有绕组或永磁体。VFRM的散热性能良好,调速范围宽,性能稳定,成本低[2-3],具有良好的应用前景。在VFRM中使用集成励磁绕组和电枢绕组,绕组中注入含有交流和直流分量的定子电流。定子电流的交流分量作为电枢电流,直流分量作为励磁电流[4]。根据零序分量的定义[5-11],定子电流的直流分量是零序电流。为了给零序电流提供回路,在VFRM的控制系统中使用共直流母线的双逆变器结构[12-13]。
VFRM的反电动势幅值与转速成正比,因此在额定负载下,当电机的速度超过基速时,逆变器的输出电压将无法满足需求[14]。为了拓宽调速范围,需要通过弱磁控制将d轴电流调节为负值,从而削弱反电动势[15]。弱磁控制通常分为基于反馈的方法或基于前馈的方法[16-25]。在基于反馈的方法中,通常通过电流环的输出电压与最大电压之间的偏差来调制d轴电流。在基于前馈的方法中,通常通过等转矩曲线,电流或电压极限圆的交点来计算弱磁区中的工作点。在基于前馈的方法中,为了简化电流参考值的计算,通常忽略电阻压降。文献[26]分析了忽略电阻压降对弱磁控制的影响:当忽略绕组电阻压降时,参考电流将高于电机的实际需求,使得电流环饱和,从而导致逆变器饱和,这不仅增加了电流谐波,还将使电机失控甚至损坏。考虑电阻压降后计算出的电流参考值可以使电机在弱磁区域内沿着最佳的电流轨迹稳定运行。文献[27-28]提出基于插值的参考电流计算方法,该方法考虑了弱磁区域的dq轴上的电阻压降。文献[29]分析了绕组和逆变器中的电阻压降,并用来补偿q轴电压,从而使电机沿着最佳电流轨迹运行。文献[30]提出一种基于牛顿拉夫逊算法的参考电流在线计算的方法。然而,上述研究针对的都是永磁同步电机中dq轴(电枢绕组)上的电阻压降。与永磁同步电机相比,VFRM除了电枢绕组上的电阻压降外,还有零序回路中的电阻压降,如果要准确计算弱磁区中的参考电流,需要同时考虑电枢和零序回路上的电阻压降。
为了解决上述问题,本文对VFRM在弱磁区内考虑电阻压降的电流参考值计算进行分析。基于电压和电流的约束方程,采用拉格朗日乘数法计算出弱磁区中VFRM的最优参考电流方程,并用牛顿拉夫逊算法进行迭代求解。首先介绍VFRM的拓扑和数学模型;然后分析了考虑电阻压降的最优工作点轨迹的计算方法;最后将该方法在一台6/4VFRM上实现,通过实验结果对该方法进行验证。
1 VFRM的模型
图1为使用零序电流励磁的6/4V FRM的拓扑结构。VFRM的电枢绕组和励磁绕组并联。在VFRM的绕组中,定子电流含有交流和直流分量。定子电流的交流分量充当电枢电流,而直流分量充当励磁电流。为了给零序电流提供回路,采用公共直流母线的双逆变器结构。三相电流的表达式为
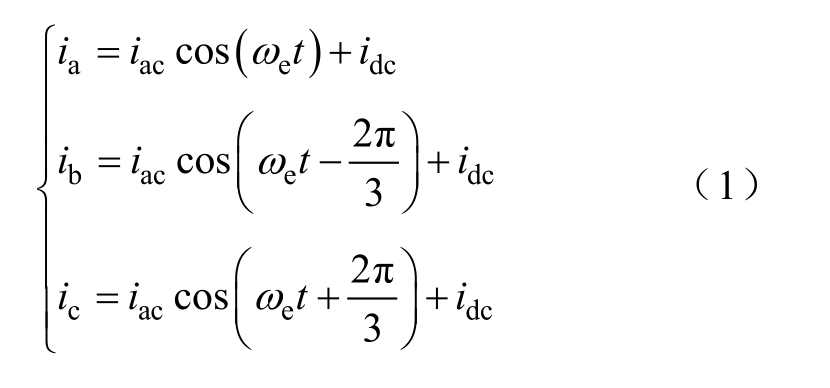
式中,ia、ib、ic为三相电流;iac为相电流的交流分量幅值;idc为相电流的直流分量(在后文中用i0表示);ωe为电角速度。

图1 使用零序电流励磁的6/4 VFRM的拓扑结构
Fig.1 Topology of zero-sequence current excited 6/4 VFRM
VFRM在dq0坐标系的电压方程如式(2)所示,其中,3次谐波分量为静止坐标系中的2次谐波在dq0平面上的映射[31]。

式中,ud、uq和u0分别为dq0轴电压分量;id、iq、i0分别为dq0轴电流分量;Rs为绕组的电阻;Ls为定子电感的恒定分量;Lδ 为定子电感的变化分量;θe为电角度。
由式(2)可知,在正弦电流条件下,反电动势中含有谐波,而基波电流环只能输出正弦电压,不能补偿这些谐波,在实际控制中会造成电流畸变。畸变的电流不利于弱磁区中的电流控制,还会降低控制系统的稳定性,增加电机的损耗。因此,在本文中,通过谐波电流环对基波电压进行补偿,从而抑制电流的畸变[24]。通过谐波电流环,一方面对反电动势中的谐波进行补偿,抑制了谐波电流;另一方面,可以将定子电压分离为基波分量和谐波分量,有利于弱磁区中参考电流的计算。在使用谐波电流环对电压进行补偿后,在弱磁控制中推导参考电流时,可以只使用电压方程的基频分量。这时,将电压方程式(2)中的3次分量忽略,得到VFRM的简化电压方程为
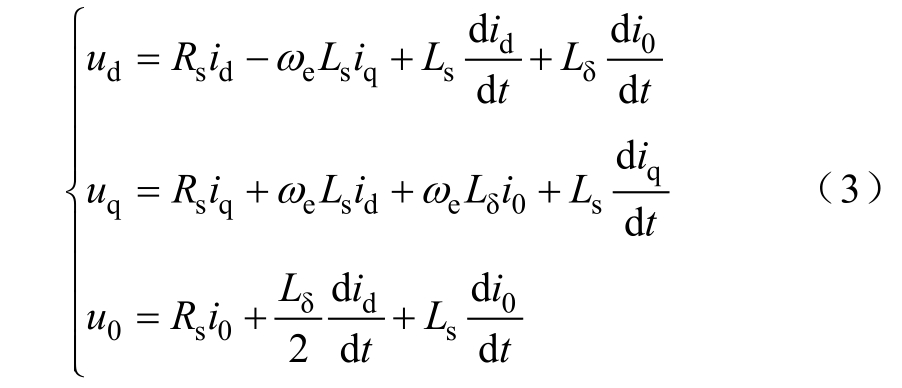
VFRM的瞬时转矩为
式中,Nr为转子极数;β 为超前电流角。
弱磁控制中参考电流的计算仅涉及平均转矩。因此,仅使用电磁转矩方程式的平均转矩表达式。平均转矩是式(4)中的恒定分量,即
2 弱磁区控制方法
2.1 电流和电压约束
基于逆变器或电机的温度限制,可以确定最大定子电流imax [32]。参考电流应满足
最大电压umax由直流母线电压和脉冲宽度调制(Pulse Width Modulation, PWM)策略决定[32]。在VFRM中,反电动势中的谐波会降低直流母线电压的利用率[4]。相电压的峰值大于基波幅值。因此,当相电压的峰值达到Udc时,相应的基波分量幅值被确定为最大电压,从而避免逆变器饱和。考虑零序电压后,电压约束关系为
将式(3)代入式(7)并忽略dq轴上的电阻性电压降,可以将电压约束重写为
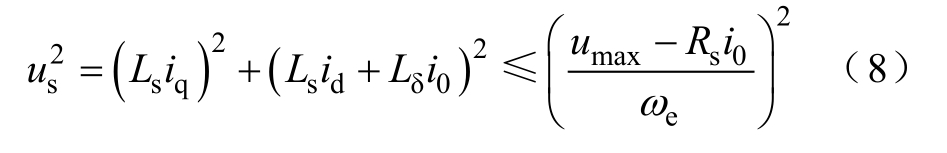
2.2 最优电流工作点的计算
在弱磁区中,VFRM有3个电流分量需要控制。为了计算最优的电流参考值,采用拉格朗日乘子法计算id、iq和i0。为求转矩的极大值,根据转矩公式,设目标函数为
使用电压和电流限制方程作为约束条件。得到拉格朗日函数FL为

式中,λ1和λ2为拉格朗日乘子。
对拉格朗日函数中变量id、iq和i0以及λ1、λ2求偏微分可得

在方程组式(11)中,消去λ1和λ2,则得到以下方程组。该方程组的根即考虑电阻压降后弱磁区内的最优id、iq、i0值。

id和iq可以用i0表示。利用式(12)第二个等式可以得到id的表达式为
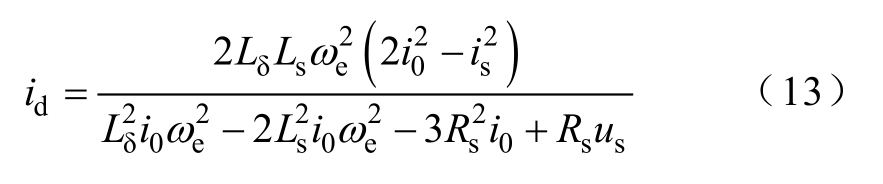
利用式(12)第三个等式和式(13)可以得到iq为

由式(12)第一个等式,设函数N 0()f i为
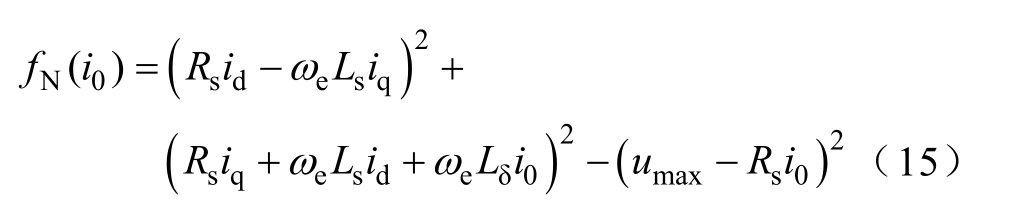
函数N 0()f i中id和iq可由式(13)和式(14)表示。对于i0,可以通过牛顿拉夫逊算法,对N 0()f i= 0迭代求解得出。函数N 0()f i的导数为N 0()f i′ 。每次迭代后的根为i0(k+1)。当相邻两次迭代结果的差满足精度要求时,将完成迭代。迭代过程为
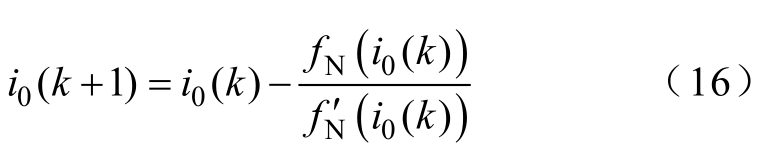
设置初始值为1,当所需精度为0.01A时,可以用多次迭代来完成计算。求得i0的给定值后,通过式(13)和式(14)可以求得id和iq的给定值。
dq平面中的电压极限圆方程为
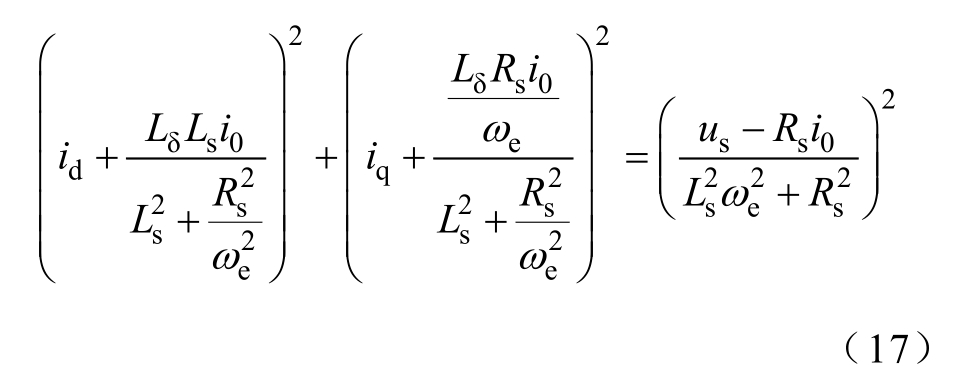
电压极限圆的中心坐标为
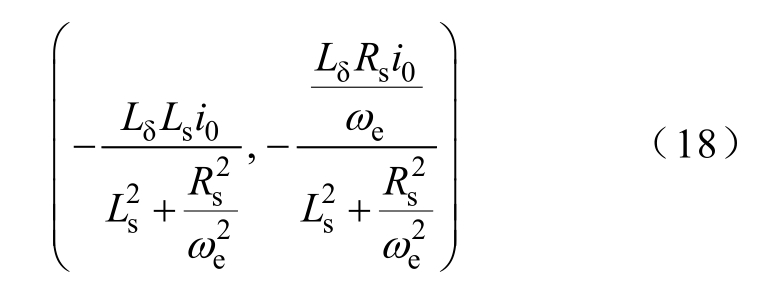
忽略电阻压降时,将Rs设置为0。电压极限圆心的坐标为

图2为忽略Rs时,电压和电流极限圆随转速升高的变化情况。从式(19)可以看出,电压极限圆的圆心始终在d轴上。随着速度的增加,电压极限圆缩小。为了保持在弱磁区输出最大功率,根据式(12),i0将随速度增加。并且,电压极限圆的圆心向d轴的负方向移动。此外,根据式(6),随着i0的增加,电流极限圆的半径减小。电压极限圆与电流极限圆的交点即为当前工作点。

图2 忽略电阻压降的电流轨迹
Fig.2 Current trajectory with zero-sequence resistive voltage drop neglected
图3为考虑电阻压降时电压和电流的极限圆随速度的增加而变化的示意图。电机从零开始加速,负载增加到定子电流达到最大值。在此过程中,电机在A点处工作。当转速为基速时,电机运行到达恒定转矩区域的边界。如果转速继续上升,需要进行弱磁控制。在弱磁区,工作点将移动到dq电流平面的第二象限,其轨迹为AB,如图3所示。与A和B所在电压圆对应的圆心分别为O1和O3。

图3 考虑电阻压降的电流轨迹
Fig.3 Current trajectory with zero-sequence resistive voltage drop considered
图4为当转速达到恒定转矩区域的边界时考虑和忽略电阻压降的工作点分析。图4中的电压圆1和2分别是忽略和考虑电阻压降的情况。A点是实际工作点。如果忽略电阻压降,根据电压圆1,电机尚在恒转矩区域,而根据电压圆2,则达到了逆变器的最大输出电压。如果转速继续升高,在忽略电阻压降时,由于控制系统认为电机仍在恒转矩区,所以仍将根据恒定转矩区域的规则计算参考电流。由于电压和电流的限制,电机电流将无法跟踪该参考电流值,在这种情况下,电流调节器会饱和,从而导致电机失去控制。为了使电机稳定运行,工作点保持在电压极限圆内,必须减小负载。这样,输出功率将降低。相应地,考虑电阻压降后,可以准确获取电机工作所需的电流参考值。

图4 恒转矩区边界时工作点情况
Fig.4 Operating point at the boundary of constant torque region
2.3 最大电压计算
根据第2.2节分析可知,VFRM的定子电压获取对判断是否进入弱磁区和参考电流的计算非常重要。然而,定子电压的峰值与基波分量的幅值不一致,这给电压约束计算带来了困难。因此本节将对最大电压进行分析。

图5 相电压波形及其谐波分析
Fig.5 Phase voltage waveforms and corresponding harmonic analysis
根据电压方程式(2)可知,VFRM的dq轴电压中含有3次谐波变化分量。这部分3次谐波变化分量是相电压的2次谐波在dq平面中的映射[27]。在转速400r/min、iq为2A、id=0A的条件下,根据式(2)计算出dq轴电压的波形后通过Park反变换,可以得到相电压的波形,如图5所示[33]。为了抑制相电流中的谐波,本文使用了指定谐波次数抑制 法[31]。在指定谐波次数抑制法中,需要抑制的谐波电流都有对应的谐波电流环。
以2次谐波电流为例。为了抑制2次谐波电流,构建了2次谐波电流环,并将参考值设为零。2次谐波的旋转坐标变换矩阵为
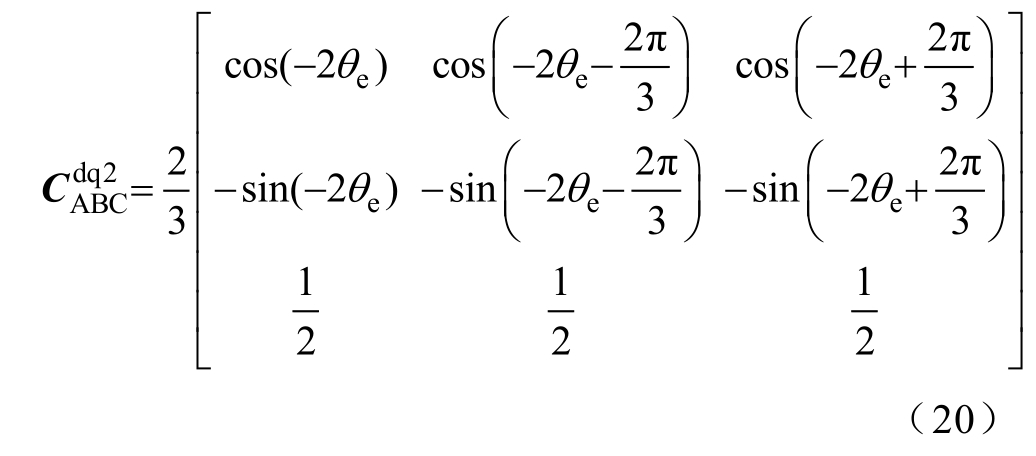
稳态下,特定次数的谐波在相应次数下的dq分量是恒定值,但是其他次数谐波在本次数dq坐标系中的映射是交流分量。例如,基波在2次dq坐标系下表现为3次谐波,其变换矩阵为
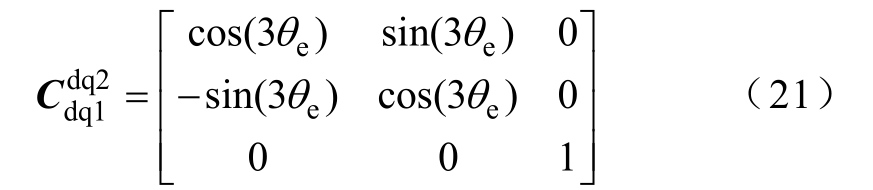
因此,可以通过截止频率低于基频的低通滤波器来提取对应次数的dq分量。2次谐波电流环如图6所示。通过2次dq变换和低通滤波,可以获得2次谐波的dq轴分量。将调制后的二阶αβ 轴电压叠加在基频上,可以达到抑制2次谐波电流的目的。图6中,带“*”的变量代表该变量是给定值。本文后面“*”的含义也相同。

图6 2次谐波电流环框图
Fig.6 Scheme of second harmonic current loop
通过谐波电流环,一方面对反电动势中的谐波进行补偿,抑制了谐波电流;另一方面,将相电压分为了基波分量和2次谐波分量。对于弱磁控制,需要基波的电压幅值,这样,基波相电压的dq轴分量被分离出,更容易求取定子电压的基波分量。
从图5a可知,式(2)计算出的相电压波形与真实值比较接近。因此可以推测相电压峰值为
式中,ud和uq采用式(2)进行计算。
最大电压umax=36V情况下,根据式(22)计算出的定子电压在转速0~2 000r/min范围内峰值的最大值约为62V。考虑5%的电压裕度后,65V的直流母线电压可以使电机的最大基波定子电压为36V。

图7 弱磁控制系统框图
Fig.7 Drive scheme with flux-weakening control
整个弱磁控制系统框图如图7所示。参考电流 由最大转矩电流比(Maximum Torque Per Ampere, MTPA)和弱磁模块计算。共直流母线的双逆变器用来为零序电流提供回路。电压补偿模块用于对反电动势中特定次数的谐波进行补偿。另外,通过使用有限元法生成的电感表来考虑不同工作条件下的电感变化[34]。如图8所示为电感随电流变化的有限元仿真结果。电流的变化范围是id(−1.2~0A),iq(1~2A),i0为1A, 2A。可见,电感随电流变化的范围很小,可以认为电机没有进入饱和区。

图8 电感随电流变化的情况
Fig.8 Inductance variation according to currents
3 实验分析
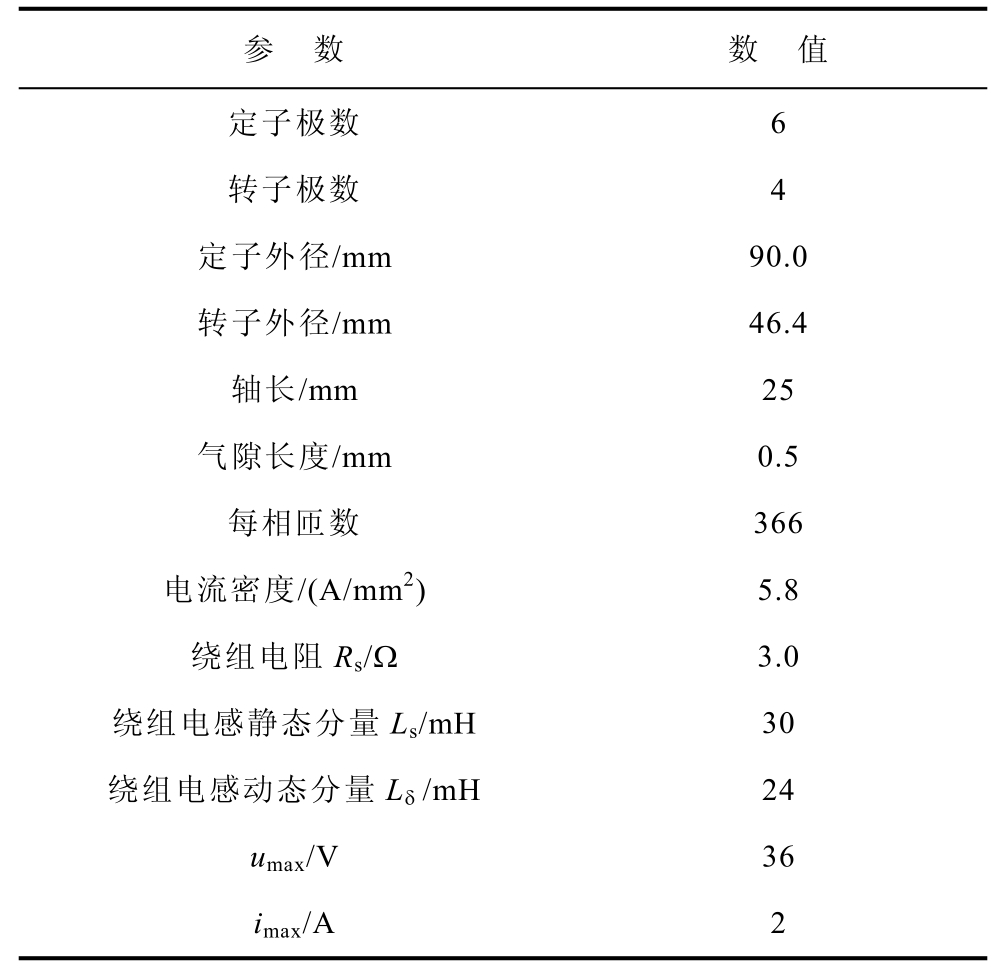
为了验证考虑电阻压降的弱磁控制方法,搭建了基于6/4 VFRM的双逆变器控制系统。表1是实验中使用电机的参数。实验平台如图9所示。实验中使用的控制器为dSPACE;VFRM由双逆变器驱动;IGBT的开关频率设置为10kHz;电机的输出转矩由奇石乐4 502A传感器测量;本实验使用的示波器为横河DL850W;功率、效率和功率因数等参数的测量采用横河WT3000E功率分析仪。
表1 VFRM参数
Tab.1 Parameters of VFRM
参 数 数 值 定子极数 6 转子极数 4 定子外径/mm 90.0 转子外径/mm 46.4 轴长/mm 25 气隙长度/mm 0.5 每相匝数 366 电流密度/(A/mm2) 5.8 绕组电阻Rs/Ω 3.0 绕组电感静态分量Ls/mH 30 绕组电感动态分量Lδ /mH 24 umax/V 36 imax/A 2

图9 实验平台
Fig.9 Picture of the experimental setup
当转速为100r/min时,增加负载转矩使定子电流达到最大值。然后,增加转速并记录电流、速度、转矩等变量。图10为在稳态下测得的dq0轴电流以 及A相电流的波形。此时的转速为1 500r/min,转矩为0.32N·m。VFRM这时处于弱磁区,id为负值。图11为随着转速的增加,测得的id、iq、i0的变化。在0~930r/min阶段,电机处于恒转矩区,负载转矩约为0.41N·m,其中,id=0,iq和i0保持固定比例。在930~2 000r/min阶段,电机处于弱磁区,负载转矩随着速度的增加而减小。当电阻压降被忽略并且定子电压被低估时,参考电流将继续根据恒转矩区的规则进行计算。但是,由于电压和电流的限制,电机在转速提高后会无法跟踪参考电流。为了使VFRM可控,必须降低输出转矩。考虑电阻压降后,VFRM可以沿着弱磁区的最佳电流轨迹运行。图12为考虑和忽略电阻压降时的转矩-转速曲线。由于忽略了电阻压降,所以电机在弱磁区中无法跟随参考电流,这限制了电机在高速时功率的输出。

图10 稳态电流波形(1 500r/min)
Fig.10 Current waveforms at steady state (speed at 1 500r/min)

图11 VFRM在弱磁区内dq0轴电流随转速的变化
Fig.11 Currents of the VFRM varies with speed in flux-weakening region

图12 转矩-转速曲线
Fig.12 Torque-speed curves
如图13所示为实验测得的考虑和忽略电阻压降时的功率-转速曲线。采用文中控制后,可变磁通磁阻电机可以准确判断并进入弱磁区。因此,采用考虑电阻压降的弱磁控制后,样机可以在弱磁区内沿着最优电流轨迹运行,并输出最大功率。而忽略电阻压降时,对于本实验中使用的样机,由于控制系统不能准确判断其进入弱磁控制的时刻,因此在高速时的输出功率下降。

图13 功率-转速曲线
Fig.13 Power-speed curves
图14为实验测得的采用文中方法前后的电机效率。不考虑电阻压降,电机在高速时定子电流幅值减小,因此铜耗也减小。在输入输出功率均减小的情况下,其效率反而比考虑电阻压降时的高。但是在其输出功率减小的情况下,效率高没有意义。

图14 效率-转速曲线
Fig.14 Efficiency-speed curves
图15为实验测得的不同转速下功率因数变化情况。在恒转矩区中,有功功率中的铜耗较大,因此功率因数在低速区很高。随着转速的升高,无功功率上升,铜耗占比减小,功率因数也逐渐减小。在弱磁区中,考虑电阻压降控制下,由于样机能沿着最优电流轨迹运行,电流和电压的有效值均不变,因此视在功率不变。在这种情况下,功率因数与有功功率的趋势有关。电流有效值不变时,铜耗相对变化较小。因此功率因数在弱磁区中与输出功率的变化趋势一致,均是先增加后趋于平稳。而在未考虑电阻压降控制下,高速时电机的输入输出功率均减小。
图16为在0~2 000r/min的过程中转速、转矩和电流的变化情况。当给出转速指令时,为了使电机加速,控制系统会增加iq和i0,以使电机的输出转矩迅速增加,达到升速的目的。同时,在速度增加到基速后,电机进入弱磁区。为了削弱反电动势,id被调节为负值。在速度达到2 000r/min后,电机重新恢复稳定状态。
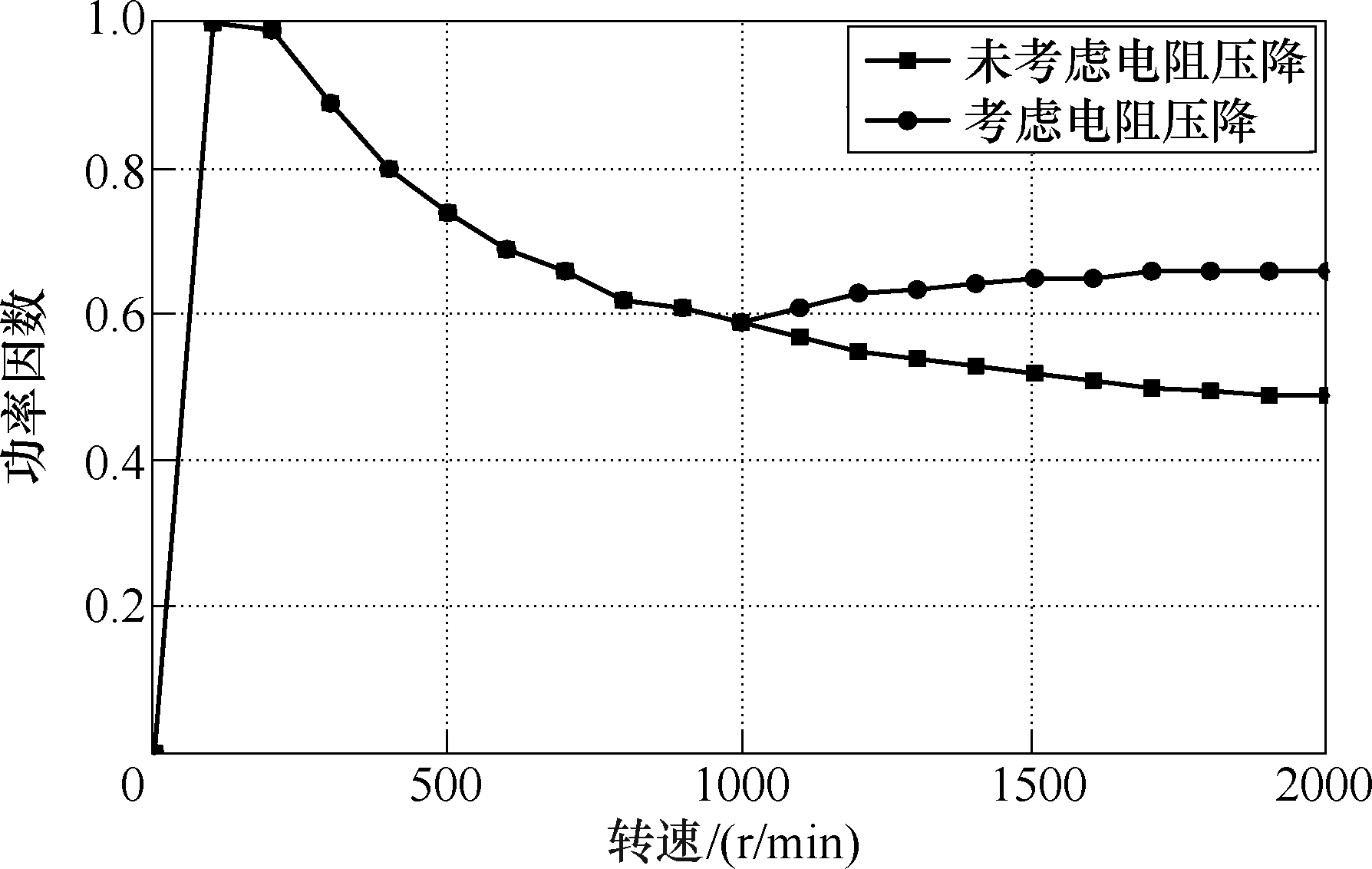
图15 功率因数-转速曲线
Fig.15 Power factor-speed curves

图16 电机升速(0~2 000r/min)时的实验结果
Fig.16 The experimental results while the speed increases from 0r/min to 2 000r/min
4 结论
本文提出考虑电阻压降的VFRM的弱磁控制策略。基于电机的电压方程和电压、电流约束,使用拉格朗日乘数法和牛顿拉夫逊法来计算考虑电枢和零序回路电阻压降的最优参考电流。另外,分析了定子电压最大值的计算。最后在一台6/4 VFRM上实现了本文的控制策略并验证了其有效性。实验结果表明,如果忽略电枢和零序回路上的电阻压降,则弱磁区中电流参考值的计算会受到影响。在这种情况下,逆变器将会饱和,电机中的电流将不能跟随给定值。因此,忽略电阻压降会造成电机在弱磁区的输出功率下降。而考虑了电枢和零序回路电阻压降后,VFRM可以在弱磁区沿着最优电流轨迹稳定运行并保持最大功率输出。
[1] Zhu Ziqiang, Liu Xu. Novel stator electrically field excited synchronous machines without rare-earth magnet[C]//Ninth International Conference on Ecolo- gical Vehicles & Renewable Energies, Monte-Carlo, Monaco, 2014: 1-13.
[2] Liu Xu, Zhu Ziqiang, Wu Di. Evaluation of efficiency optimized variable flux reluctance machine for EVs/ HEVs by comparing with interior PM machine[C]// International Conference on Electrical Machines & Systems, Hangzhou, China, 2014: 2648-2654.
[3] Liu Xu, Zhu Ziqiang. Comparative study of novel variable flux reluctance machines with doubly fed doubly salient machines[J]. IEEE Transactions on Magnetics, 2013, 49(7): 3838-3841.
[4] Zhu Ziqiang, Lee B, Liu Xu. Integrated field and armature current control strategy for variable flux reluctance machine using open winding[J]. IEEE Transactions on Industry Applications, 2016, 52(2): 1519-1529.
[5] 陈轶涵, 郭鸿浩, 陈杰, 等. 中频三相四桥臂逆变器控制策略不平衡负载状态相量模型分析[J]. 电工技术学报, 2019, 34(9): 1912-1923.
Chen Yihan, Guo Honghao, Chen Jie, et al. Analysis on control strategies for unsymmetrical state of medium frequency three phase four leg inverter based on vector model[J]. Transactions of China Electro- technical Society, 2019, 34(9): 1912-1923.
[6] 翁汉琍, 刘雷, 林湘宁, 等. 涌流引起换流变压器零序过电流保护误动的机理分析及对策[J]. 电力系统自动化, 2019, 43(9): 171-182.
Weng Hanli, Liu Lei, Lin Xiangning, et al. Mechanism and countermeasures of mal-operation of converter transformer zero-sequence overcurrent protection caused by inrush current[J]. Automation of Electric Power Systems, 2019, 43(9): 171-182.
[7] 郭倩雯, 莫文雄, 郑方晴, 等. 高压内置型变压器空投导致零序电流保护误动分析及对策[J]. 电力系统保护与控制, 2018, 46(22): 170-176.
Guo Qianwen, Mo Wenxiong, Zheng Fangqing, et al. Analysis and measures of zero sequence current protection malfunction caused by no-load high- voltage built-in transformer[J]. Power System Protection and Control, 2018, 46(22): 170-176.
[8] 林志超, 刘鑫星, 王英民, 等. 基于零序电流比较的小电阻接地系统接地故障保护[J]. 电力系统保护与控制, 2018, 46(22): 21-27.
Lin Zhichao, Liu Xinxing, Wang Yingmin, et al. Grounding fault protection based on zero-sequence current comparison in low resistance grounding system[J]. Power System Protection and Control, 2018, 46(22): 21-27.
[9] 桂林, 李岩军, 詹荣荣, 等. 大型调相机内部故障特征及纵向零序电压保护性能分析[J]. 电力系统自动化, 2019, 43(8): 145-149.
Gui Lin, Li Yanjun, Zhan Rongrong, et al. Analysis of internal fault characteristics and longitudinal zero- sequence overvoltage protection performance of large-scale condenser[J]. Automation of Electric Power Systems, 2019, 43(8): 145-149.
[10] 张广儒, 杨勇, 刘丽娟, 等. 光伏电站送出线路零序保护异常动作分析[J]. 电气技术, 2019, 20(1): 93-96.
Zhang Guangru, Yang Yong, Liu Lijuan, et al. Analysis of zero sequence protection action abnor- mally for photovoltaic power station transmission line[J]. Electrical Engineering, 2019, 20(1): 93-96.
[11] 叶吉亮, 李岚, 刘海霞, 等. 电网电压不平衡及谐波状态下的并网逆变器控制策略[J]. 电力系统保护与控制, 2018, 46(6): 113-119.
Ye Jiliang, Li Lan, Liu Haixia, et al. Control strategy of grid-connected inverter under unbalanced and harmonic voltage condition[J]. Power System Pro- tection and Control, 2018, 46(6): 113-119.
[12] Shivakumar E G, Gopakumar K, Sinha S K, et al. Ranganathan, space vector PWM control of dual inverter fed open-end winding induction motor drive[C]//Applied Power Electronics Conference (APEC), Anaheim, CA, USA, 2001: 9-18.
[13] 袁渊, 朱孝勇, 左月飞, 等. 共直流母线开绕组电机的移相解耦控制策略[J]. 电工技术学报, 2019, 34(22): 4670-4677.
Yuan Yuan, Zhu Xiaoyong, Zuo Yuefei, et al. Decoupled SVPWM control strategy for open winding permanent magnet synchronous motor with common DC bus[J]. Transactions of China Electro- technical Society, 2019, 34(22): 4670-4677.
[14] 莫为, 汪梅, 莫会成. 不同转子结构对永磁交流伺服电机弱磁特性影响[J]. 电工技术学报, 2018, 33(增刊1): 89-98.
Mo Wei, Wang Mei, Mo Huicheng. Influence of different rotor structure on flux-weakening properties of permanent magnet AC servo motor[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(S1): 89-98.
[15] 朱永彬, 林珍. 电动汽车用永磁同步电动机弱磁研究综述[J]. 电气技术, 2015, 16(10): 1-7.
Zhu Yongbin, Lin Zhen. Summarization for flux- weakening performance of permanent magnet synchronous motors applied in electric vehicle[J]. Electrical Engineering, 2015, 16(10): 1-7.
[16] Kwon Y C, Kim S, Sul S K. Voltage feedback current control scheme for improved transient performance of permanent magnet synchronous machine drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(9): 3373-3382.
[17] 张梓绥, 王琛琛, 游小杰, 等. 基于单Q轴电流调节器的永磁同步电机电流轨迹控制[J]. 电工技术学报, 2018, 33(24): 5779-5788.
Zhang Zisui, Wang Chenchen, You Xiaojie, et al. Current locus control of permanent magnet synchronous motor based on single Q-axis current regulator flux- weakening method[J]. Transactions of China Electro- technical Society, 2018, 33(24): 5779-5788.
[18] 李华, 方晓春, 林飞, 等. 异步牵引电机方波单电流闭环控制策略及其参数鲁棒性分析[J]. 电工技术学报, 2018, 33(9): 2034-2043.
Li Hua, Fang Xiaochun, Lin Fei, et al. Singles current loop control strategy of induction traction motor in square wave mode and its parameter robustness analysis[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2034-2043.
[19] 李雪, 迟颂, 刘聪, 等. 基于虚拟电阻的永磁同步电机单电流调节器弱磁控制[J]. 电工技术学报, 2020, 35(5): 1046-1054.
Li Xue, Chi Song, Liu Cong, et al. Flux-weakening control with single current regulator of permanent magnet synchronous motor based on virtual resistor[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1046-1054.
[20] 李生民, 张泽灵, 郭思语, 等. 混合励磁同步电机反馈线性化控制[J]. 电工技术学报, 2019, 34(增刊1): 39-51.
Li Shengmin, Zhang Zeling, Guo Siyu, et al. Feedback linearization control of hybrid excitation synchronous motor[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 39-51.
[21] 郭栋, 张波, 王巍, 等. 混合励磁同步电机弱磁控制[J]. 电机与控制学报, 2020, 24(5): 135-142.
Guo Dong, Zhang Bo, Wang Wei, et al. Flux- weakening control of hybrid excitation synchronous machines[J]. Electric Machines and Control, 2020, 24(5): 135-142.
[22] 甘志伟, 王云冲, 缪冬敏, 等. 宽转速范围永磁同步发电机电流矢量控制[J]. 电机与控制学报, 2020, 24(1): 1-9.
Gan Zhiwei, Wang Yunchong, Miao Dongmin, et al. Current vector control of permanent magnet syn- chronous generator for wide-speed-range operation[J]. Electric Machine and Control, 2020, 24(1): 1-9.
[23] Kwon T S, Sul S K. Novel antiwindup of a current regulator of a surface-mounted permanent-magnet motor for flux-weakening control[J]. IEEE Transa- ctions on Industry Applications, 2006, 42(5): 1293- 1300.
[24] Preindl M, Bolognani S. Model predictive direct torque control with finite control set for PMSM drive systems, part 2: field weakening operation[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 1912-1921.
[25] Pan C T, Liaw J H. A robust field-weakening control strategy for surface-mounted permanent-magnet motor drives[J]. IEEE Transactions on Energy Con- version, 2005, 20(5): 701-709.
[26] Chen Yu, Zhu Ziqiang, Howe D. Influence of inaccuracies in machine parameters on field- weakening performance of PM brushless AC drives[C]//IEEE International Conference of Elec- tronics Machine Drives, Seattle, WA, USA, 1999: 691-693.
[27] Tursini M, Chiricozzi E, Petrella R. Feedforward flux-weakening control of surface-mounted permanent- magnet synchronous motors accounting for resistive voltage drop[J]. IEEE Transactions on Industrial Electronics, 2010, 57(1): 440-448.
[28] Tursini M, Chiricozzi E, Petrella R. Flux-weakening control of surface mounted PM synchronous motors accounting for resistive voltage drop[C]//Inter- national. Conference of Electronics Machines, Vilamoura, Portugal, 2008: 1-6.
[29] Liu Hesong, Zhu Ziqiang, Mohamed E, et al. Flux- weakening control of nonsalient pole PMSM having large winding inductance, accounting for resistive voltage drop and inverter nonlinearities[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 942-952.
[30] Wang Shuo, Kang Jinsong, Degano M, et al. An accurate wide-speed range control method of IPMSM considering resistive voltage drop and magnetic saturation[J]. IEEE Transactions on Industrial Electronics, 2020, 67(4): 2630-2641.
[31] 李帅, 孙立志, 刘兴亚, 等. 永磁同步电机电流谐波抑制策略[J]. 电工技术学报, 2019, 34(增刊1): 87-96.
Li Shuai, Sun Lizhi, Liu Xingya, et al. Current harmonics suppression strategies of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 87-96.
[32] Sul S. Control of electric machine drive systems[M]. Piscataway: Wiley-IEEE Press, 2011.
[33] Liu Xu, Bi Jiaxuan, Zhu Ziqiang. Prediction of torque-speed characteristics of 6/4 variable flux reluctance machine considering high-order Harmonics of Flux-linkage[C]//22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-6.
[34] Zheng Junqiang, Zhao Wenxiang, Lee C H, et al. Improvement torque performance of interior permanent- magnet machines[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 12-18.