0 引言
锂离子电池由于在能量密度、耐用性和环境保护方面的优势而在汽车和轨道交通领域中越来越受欢迎。在实际应用中,锂离子电池通常与DC-DC变换器连接来控制能量流动,这就会产生高频噪声和电流纹波,使电池在工作时受到高频激励。因此,需要开发一种新的模型,能够更好地描述电池的高频行为,有利于优化电力电子电路的控制策略以及无源元件的设计。
常见的电池模型主要有黑箱模型、电化学模型(Electrochemical Model, EM)和等效电路模型(Equivalent Circuit Model, ECM)。黑箱模型基于机器学习方法,需要大量的实验数据进行训练,但没有设计明确的模型结构来模拟电池内部的反应[1]。电化学模型是基于电化学原理建立的,可以从本质上反映电池外部特性与内部参数之间的关系。尽管电化学模型具有较高的精度,但这些模型存在明显的缺点:模型结构复杂、参数识别困难以及运算速度低。因此,电化学模型应用于实际车辆的电池管理系统(Battery Management System, BMS)中,使用效果并不理想[2-3]。而由理想电气元件组成的等效电路模型已成功地应用于荷电状态(State of Charge, SOC)、健康状态(State of Health, SOH)和能量状态(State of Energy, SOE)的估计[4-6]。
但是,整数阶等效电路模型不能准确地描述电池的动态过程,阶数会影响其准确性。具体来说,低阶模型精度较低但是计算量小,高阶模型精度较高但是计算量大,在实际使用中通常根据应用领域和需求的不同来选择使用低阶模型还是高阶模型。文献[7]对常用的整数阶模型进行了深入的比较和讨论。近年来,随着分数阶微积分应用的推广,越来越多的学者将分数阶等效模型用于电池的研究。使用分数阶阻抗元件,如恒相位元件(Constant Phase Element, CPE)(通常记为Q)和Walberg阻抗可以更准确地描述锂离子电池的电化学过程,如电荷转移、双电层效应、物质转移和扩散等,既提高了精度,又有效地解决了模块过多引起的计算复杂问题。文献[8]使用包含一个CPE的分数阶模型模拟不同条件下的电压曲线,结果表明,它的精度要高于不同阶次的整数阶模型。文献[9]对几种不同结构的分数阶模型进行比较研究,分析了计算准确性和计算负担与模型结构之间的关系。
然而,很少有研究者去专门关注锂离子电池的高频响应,等效电路中的高频部分通常由电感L代替[10],甚至被忽略[11]。也有研究者进行了高频激励的阻抗分析,并提出了与欧姆电阻并联的电感作为等效电路模型中的高频部分[12-13],在这些文献中为了便于进行基于等效电路的仿真使用了整数阶模型,更加关注锂离子电池在高频范围内不同条件下的行为或电流在模型内不同支路中的分布,对于模型的精度没有较高的要求。同样,文献[14]使用多个RL和RC串联来建立高频模型,在时域和频域的响应上都有着较高的精度,但是模型较为复杂、计算量大。也有相关研究者将典型分数阶模型中的整数阶电感L替换为分数阶元件,在更高频率的阻抗响应上有着较高的精度[15],但是没有在时域响应上进行验证,无法在实际中使用。此外,文献[16-17]通过建立复杂传输线模型或包含趋肤效应的模型来研究电磁干扰对电池的影响,其频率远高于电力电子设备的典型开关频率,本文不再赘述。
本文基于电化学阻抗谱(Electrochemical Impe- dance Spectroscopy, EIS)建立了几种高频模型,通过使用分数阶模型,在保证模型精度的同时降低了模型的复杂度。然后对几种模型在时域上进行参数辨识,通过比较其响应精度和计算量,给研究人员提供参考,为锂离子电池选择合适的高频模型。同时研究发现,根据EIS拟合得到的最优模型并不一定在时域拟合中也是最优。
1 分数阶模型
1.1 电化学阻抗谱
EIS是研究电池电化学性能的重要手段,通过测量不同频率响应信号与扰动信号的比值,来获得相应频率下的阻抗值。EIS具有以下三个特点:①电化学系统受到小幅值正弦信号的扰动,因此电动势与电流之间存在线性关系,简化了测量结果的数学处理;②阳极和阴极的反应过程在电极上交替发生,即使测量时间较长,也不会积累极化,是一种“准稳态方法”;③EIS是一种频域测试方法,可以测量较宽的频率范围,从而可以获得比传统电化学方法更多的动力学信息和电极界面信息[18]。
一种典型锂离子电池EIS及其等效电路模型如图1所示,该图可分为低频直线、中频半椭圆和高频感性部分三段。一般认为,低频直线与正负极锂离子扩散动力学有关,通常用Walberg阻抗(见图1中ZW)表示;中频半椭圆与电荷转移反应和双电层电容有关,通常用电阻与CPE(见图1中CQ)并联表示;高频感性部分代表电池的电感特性以及测试电缆和连接装置带来的感性构成,通常用电感元件表示[19]。此外,图中与实轴相交的部分代表锂离子电池的欧姆内阻。

图1 一种典型锂离子电池EIS及其等效电路模型
Fig.1 A typical EIS of lithium-ion battery and its equivalent circuit model
通常根据EIS建立的模型是不唯一的,通过对EIS进行拟合来获得模型中每个参数,并验证模型的准确性。本文采用自适应差分进化算法进行拟合,具有较好的全局收敛性,具体的算法过程如下[20]:
(1)初始化个体数目NP、变量维数D、最大进化代数G、初始变异算子0F、交叉算子CR和阈值T。
(2)产生初始种群![]() ,计算个体目标函数;对第K代的种群
,计算个体目标函数;对第K代的种群 ![]() ,执行步 骤(3)~步骤(6),来产生第K+1代的种群。
,执行步 骤(3)~步骤(6),来产生第K+1代的种群。
(3)根据式(1)生成变异种群iv,即
其中
式中,r、u、v为1~NP中随机选取的相异整数;F为自适应变异算子。
(4)将在步骤(3)中生成的iv和当前的种群K ix进行交叉生成交叉种群iu,即

式中,rand为[0, 1]之间的随机数。
(5)对边界条件采用在可行域中随机产生参数向量的方式进行处理。
(6)计算步骤(4)中生成的ui的目标函数f (ui ),与原种群![]() 的目标函数
的目标函数![]() 进行“一对一”选择操作,若
进行“一对一”选择操作,若![]() ,则ui将代替
,则ui将代替![]() ;否则,将
;否则,将 ![]() 保留到下一代,即
保留到下一代,即
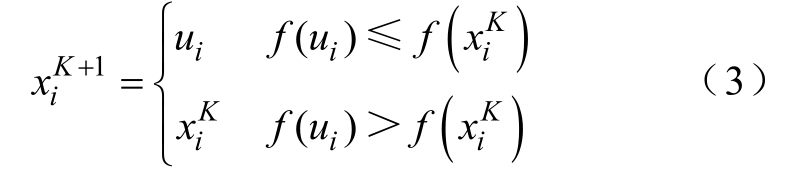
(7)判断是否满足终止条件:若满足,则结束搜索过程,输出优化值;若不满足,则继续进行迭代优化。
用于EIS拟合的目标函数[11]为

其中

式中,wgt为对数距离函数,表示某一频率下计算数据与实验数据的复合偏差;Zcal和Zexp分别为计算阻抗和测量阻抗;a和b分别为对数运算后结果的实部和虚部;w为拟合过程中相位的权重大小,默认值为2.2;N为实验数据的长度;Pk为模型中的第k个参数。在拟合过程中的目标是使总误差E最小。与线性加权相比,运用对数距离函数可以更好地适应参数未知的大范围变化,对数的缩放操作也保证了不同量级参数的权重相差不大。
本文研究内容为锂离子电池高频模型,因此忽略低频部分,测量了1Hz~20kHz的中高频EIS,EIS实测值和拟合结果如图2所示。针对高频部分实部增加的现象选择了三种拟合结果较好的高频模型,如图3所示。模型a~模型c简称FOM1~FOM3。图3中,UOCV为开路电压,LQ为分数阶电感,L1、L2为整数阶电感,RL为电感支路并联阻抗,R0为欧姆内阻,Rct为电荷转移阻抗,CQ为双电层电容。对三种模型采用上述方法进行拟合后,结果显示在图2内,目标函数值分别为EFOM1=0.002 2,EFOM2=0.002 2,EFOM3=0.002。可以看出,三种模型拟合误差都很小,其中FOM3拟合结果最好,FOM1和FOM2拟合结果几乎没有区别。
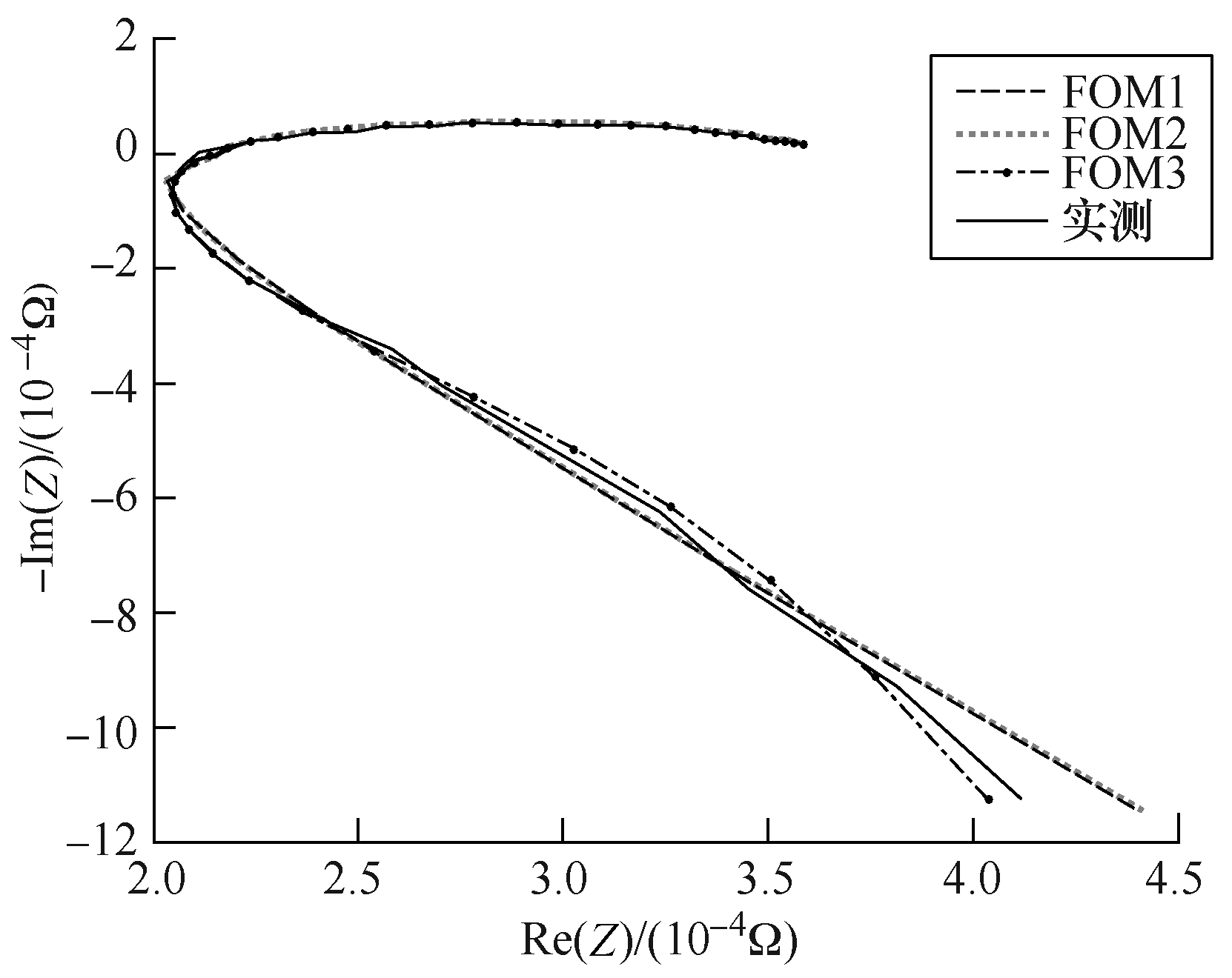
图2 EIS实测值和拟合结果
Fig.2 EIS measured value and fitting results

图3 高频等效模型
Fig.3 High frequency equivalent model
1.2 分数阶模型的数值计算方法
莱布尼兹在1695年就提出了分数微积分算法,然而直到最近才被研究人员应用于工程控制系统、建模和状态估计中。由于分数阶算法更适用于模拟包括传质、扩散动力学和记忆滞后在内的物理化学系统,因此被用在了锂离子电池系统的建模中[21]。分数阶微积分的连续微分积分算子定义为
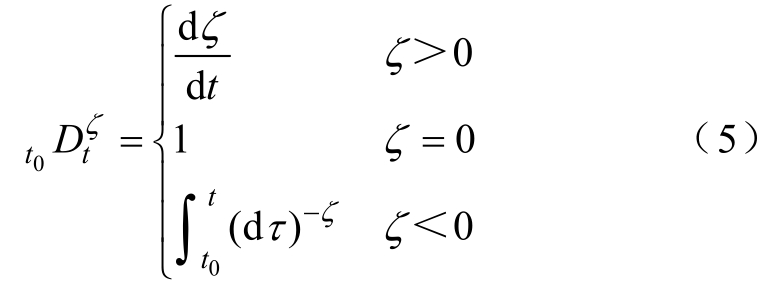
式中,ζ为分数阶微积分的阶数;0t和t为积分的下限和上限;τ为积分变量。在分数阶算法的众多定义中,有三种是最常用的,分别为Caputo定义、Riemann-Liouville定义和G-L(Grunwald-Letnikov)定义。G-L定义描述了如何直接离散化连续分数阶方程,更适合于数值计算,给定函数()f t的ζ阶导数的G-L定义为
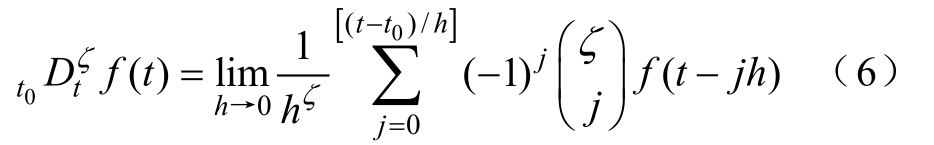
式中,h为采样周期;![]() 的整数部分;
的整数部分;![]() 为牛顿二项式系数。
为牛顿二项式系数。
以图3a为例,介绍分数阶模型的数值计算,电路中分数阶元件LQ、CQ的阻抗表达式分别为

如果电池阻抗可以类似地作为系统传递函数处理,输入为电流、输出为开路电压和端电压之差,则在拉普拉斯域的表达式为
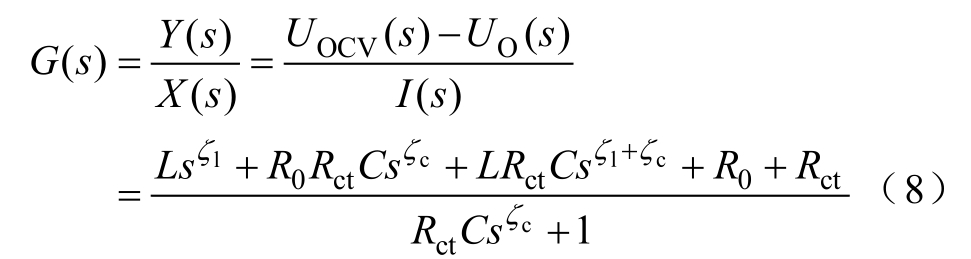
式中,UO为端电压。
将式(8)转换到时域中可以得到,系统的分数阶微分方程为

首先定义四个多维变量α、p、β、q分别为
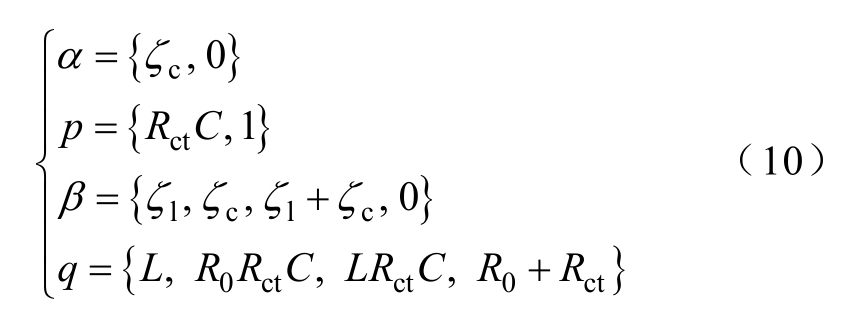
则式(9)可写成

在本例中,n=1,m=3。计算顺序如图4所示,为了计算方便引入了中间变量()u t,然后,根据式(6)可以得到离散化后模型输出()y t的数值解的一般表达式[22],即
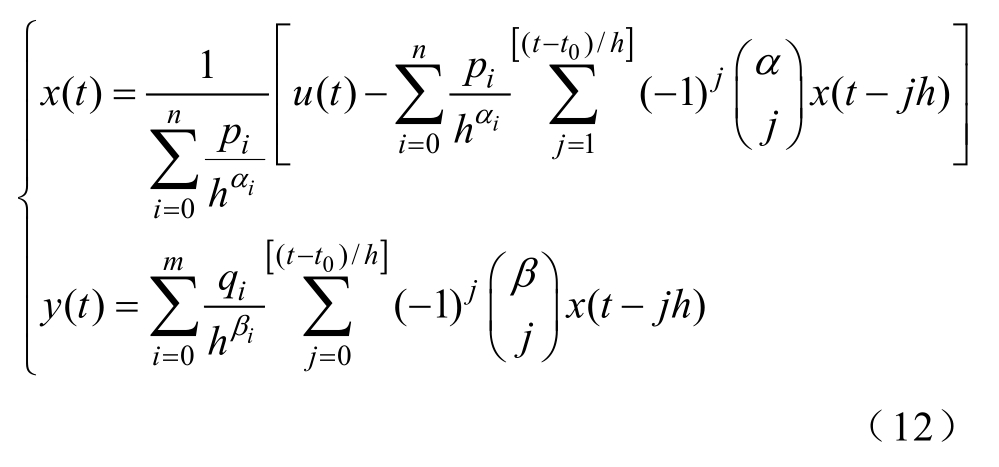

图4 计算顺序
Fig.4 Calculation order
2 实验验证
2.1 实验方案
在本文中,选择了标称容量为25A·h的钛酸锂离子电池作为实验对象,锂离子电池规格见表1。搭建电池测试平台如图5所示,实验设备包括充电机(DC-DC)、dSPACE、工控机(包括PC主机)。其中,dSPACE只用作DC-DC的闭环控制,工控机由于其扩展性高,可以插入不同功能的板卡,具有很强的抗干扰能力,所以用作高频数据采集,同时兼顾主机功能。为了更精确地观察电池电压电流变化的细节,工控机的采样频率选择250kHz。
表1 锂离子电池规格
Tab.1 Lithium-ion battery specifications

参 数 数 值 额定容量/(A·h) 25 额定电压/V 2.35 充电截止电压/V 2.8 放电截止电压/V 1.5
为了模型的参数识别,在25℃的环境温度下测量了不同频率纹波电流下的电压响应。电池的初始SOC为80%,充放电平均电流为1C,分别在1kHz(纹波幅值为±1C)、2kHz(纹波幅值为±0.5C)和4kHz(纹波幅值为±0.25C)的频率下进行一次20%~ 80%SOC的充放电循环,由于要观察不同频率、相同幅值下的电压响应,在更换DC-DC的电感后再进行一次10kHz(纹波幅值为±1C)的充放电循环。

图5 电池测试平台
Fig.5 Battery test platform
2.2 参数辨识结果
模型参数辨识方法框图如图6所示,根据电池的实验数据和仿真数据,利用误差最小原理进行辨 识[23]。实验数据包括电池在充放电过程中的电流以及所产生的电压响应,仿真数据为通过输入电流值得到的模型输出的电压,通过自适应差分进化算法得到最优的模型参数。
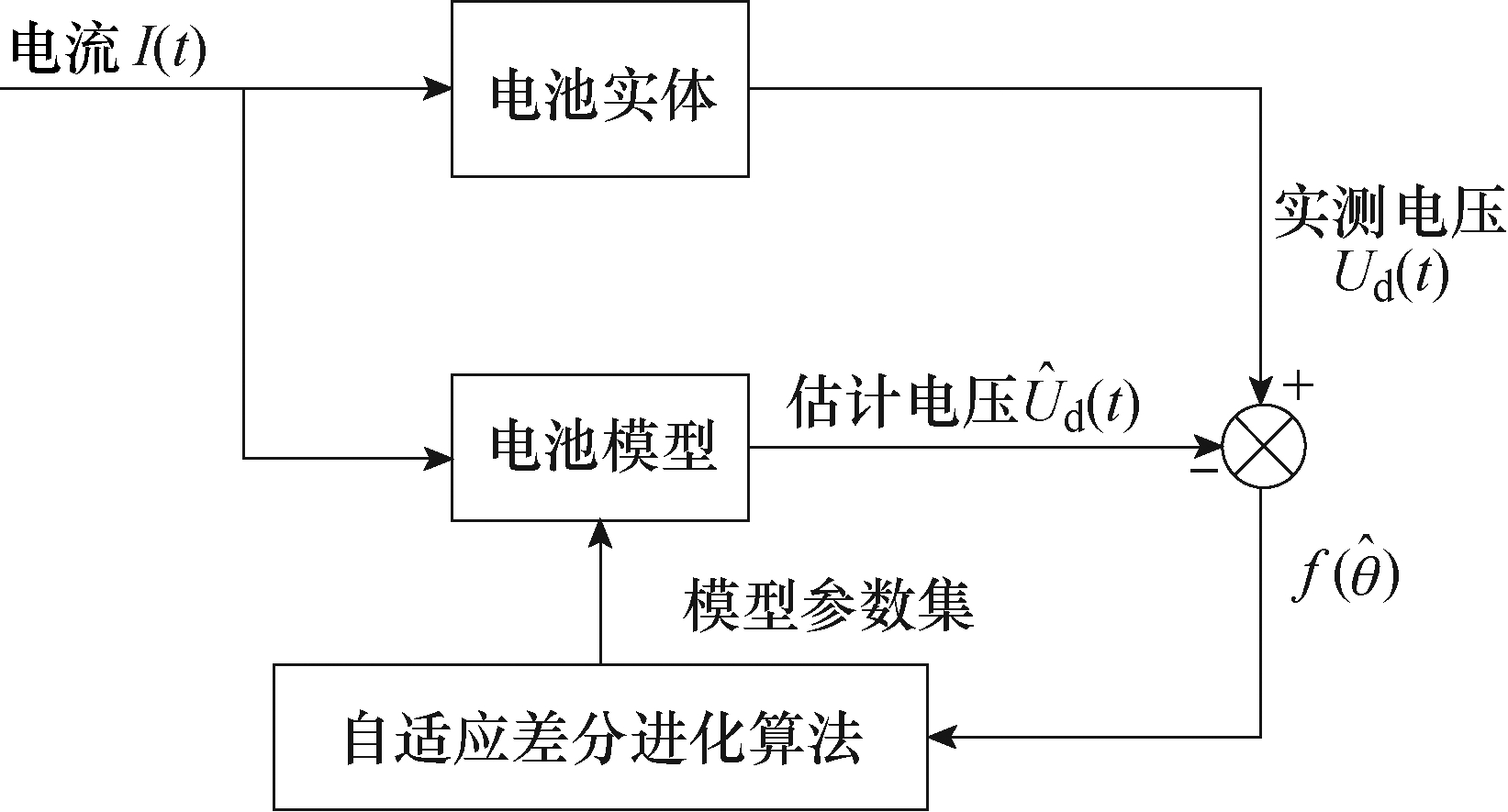
图6 参数辨识方法框图
Fig.6 Block diagram of parameter identification method
用于分数阶模型参数辨识的目标函数为

式中,![]() 为适应度函数;
为适应度函数;![]() 为模型中需要识别的 参数集;Ud( j)为电池第j个采样点的电压数据。给定输入电流Ij和模型参数
为模型中需要识别的 参数集;Ud( j)为电池第j个采样点的电压数据。给定输入电流Ij和模型参数![]() ,从分数阶模型得到电 池的估计电压为
,从分数阶模型得到电 池的估计电压为![]() 。参数辨识的目的就是使适应度函数的值最小来找到模型中各个参数的值。
。参数辨识的目的就是使适应度函数的值最小来找到模型中各个参数的值。
三种模型在不同频率下进行参数辨识后,不同频率拟合结果如图7所示。可以看出,在电流换向时,电池电压会产生突变,这体现了电池在高频电流下的电感特性,然后电压变化变缓则与电池内阻有关。从拟合结果来看,FOM2最接近实测值,FOM1和FOM3在电压缓慢变化阶段不能较好地跟随。

图7 不同频率拟合结果
Fig.7 Fitting results of different frequencies
此外,在参数辨识过程中发现FOM2中的分数阶元件LQ的阶数大于0.95,在部分频率下甚至大于0.99,非常接近整数阶元件。因此,将FOM2中的LQ元件替换为整数阶元件L,得到另一种模型(LR)R(RCQ),简称FOM4,如图8所示。在不同频率下对FOM4重新进行参数辨识,以1kHz为例,FOM2和FOM4在1kHz下的拟合结果如图9所示。可以看出,FOM2与FOM4的拟合结果非常接近,同时说明为了准确拟合EIS高频部分而使用的分数阶电感元件并没有对时域上的拟合精度有较大地提升,这一点在第3节会进一步论述。
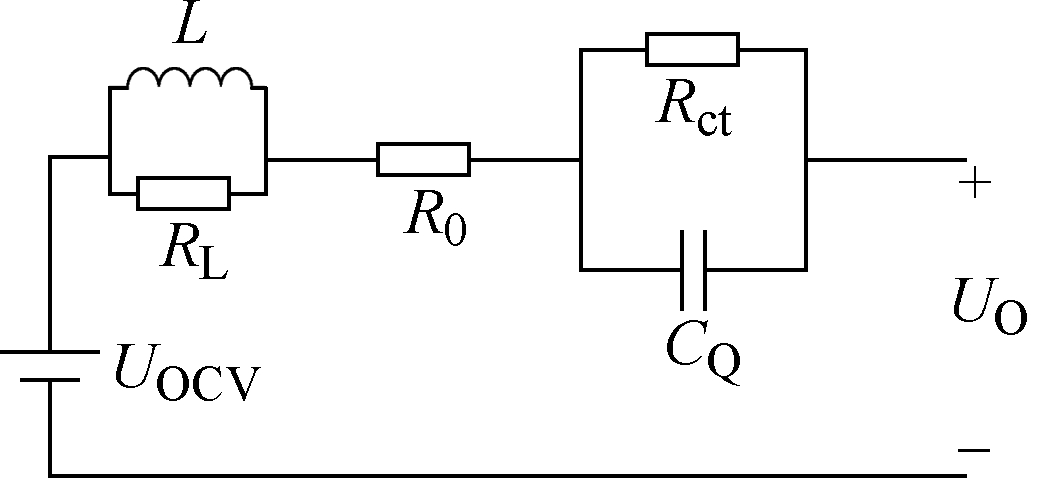
图8 (LR)R(RCQ)模型
Fig.8 (LR)R(RCQ) model

图9 FOM2和FOM4在1kHz下的拟合结果
Fig.9 Fitting results of FOM2 and FOM4 under 1kHz
3 模型比较
3.1 误差比较
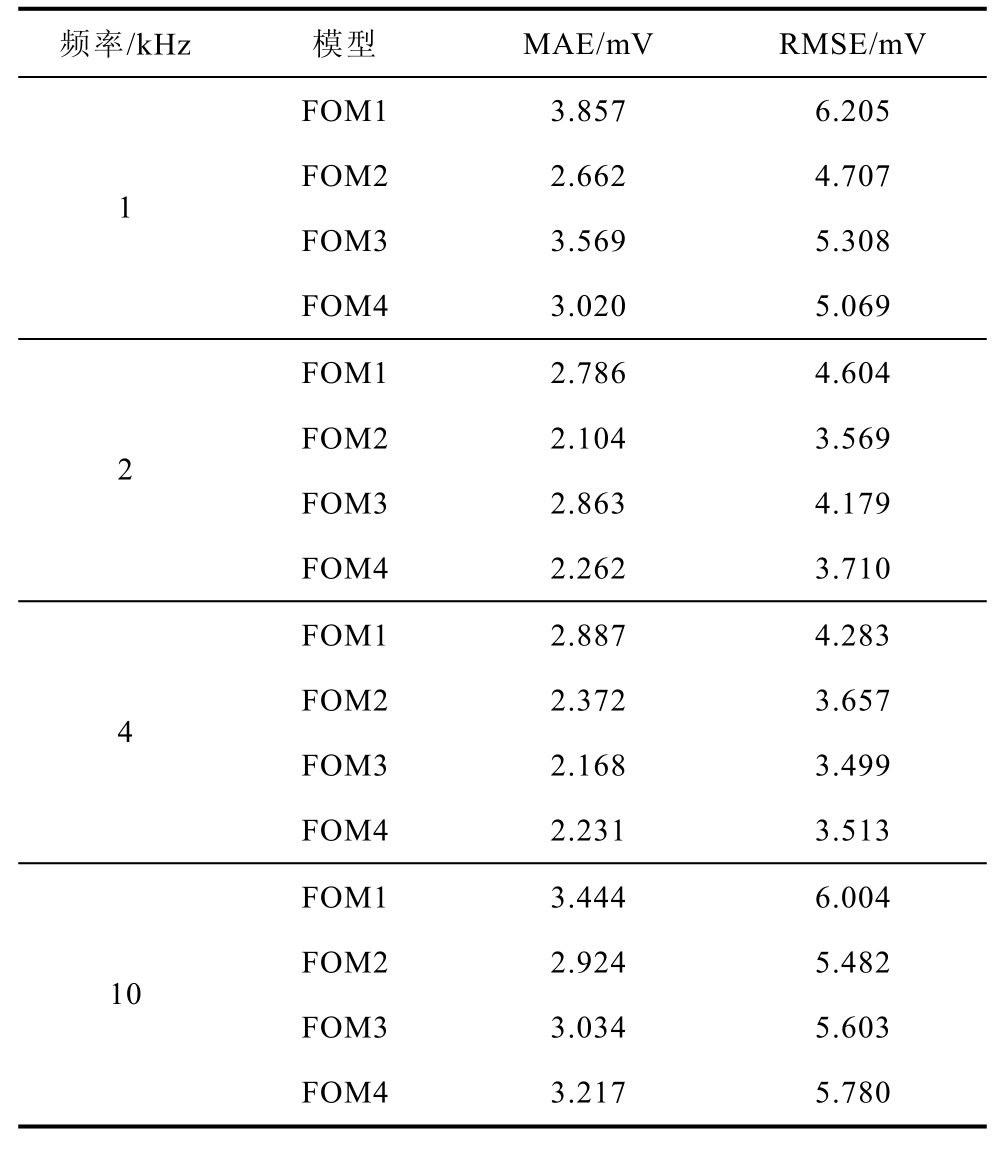
不同模型的误差见表2。在表2中比较了这三种模型的方均根误差(Root Mean Square Error, RMSE)和平均绝对误差(Mean Absolute Error, MAE)。RMSE是一种常用的度量,用于评估模型预测值与观测值之间的差异,RMSE越小,预测结果越准确。MAE表示预测值和观测值之间绝对误差的平均值,可以更好地反映预测值误差的实际情况,MAE越小,预测结果越好。从表2中可以得出,FOM2相较于FOM1、FOM3和FOM4,在1kHz下MAE降低了31%、25%和12%,RMSE降低了24%、11%和7%;在2kHz下MAE降低了24%、27%和7%,RMSE降低了22%、15%和4%;在4kHz下MAE降低了18%、−9%和−6%,RMSE降低了15%、−5%和−4%;在10kHz下MAE降低了15%、4%和9%,RMSE降低了9%、2%和5%。可以看出,除了4kHz外,FOM2在四种模型中误差是最小的,即使在4kHz,FOM2的误差也只是略大于FOM3和FOM4。
表2 不同模型的误差
Tab.2 Errors of different models
频率/kHz 模型 MAE/mV RMSE/mV FOM1 3.857 6.205 FOM2 2.662 4.707 FOM3 3.569 5.308 1 FOM4 3.020 5.069 FOM1 2.786 4.604 FOM2 2.104 3.569 FOM3 2.863 4.179 2 FOM4 2.262 3.710 FOM1 2.887 4.283 FOM2 2.372 3.657 FOM3 2.168 3.499 4 FOM4 2.231 3.513 FOM1 3.444 6.004 FOM2 2.924 5.482 FOM3 3.034 5.603 10 FOM4 3.217 5.780
3.2 计算量比较
分数阶模型的计算量很大程度上取决于传递函数中分数阶导数的数量,即与分数阶元件的数量和位置有关。表3为不同模型的计算量。可以看出,FOM2和FOM3分数阶导数个数最多,计算量最大,但由于总元件数不同,导致FOM3需要辨识的参数更多,计算量更大。同样,FOM1与FOM4相比,FOM4计算量更大。四种模型的计算量从小到大依次为FOM1、FOM4、FOM2、FOM3,与实际仿真得到的结果相一致。
表3 不同模型的计算量
Tab.3 Computational load of different models

模型 分数阶元件个数 分数阶导数个数 所有元件个数FOM1 2 4 4 FOM2 2 6 5 FOM3 1 6 7 FOM4 1 4 5
3.3 结果分析
从比较结果可以看出,根据应用领域的不同可以选择不同的高频模型,如果对模型精度要求较高时可以选择FOM2,如果对运算速度要求较高时可以选择FOM1。此外,从FOM2和FOM4的误差比较中可以看出,二者的时域拟合结果相差并不大,但是EIS的拟合结果却有较大差异,用FOM4对[1Hz, 20kHz]的EIS进行拟合后,拟合结果如图10a所示,EFOM2=0.002 2,EFOM4=0.007 8。因此,在时域上对电池进行分数阶建模时,不能忽略EIS与日常使用之间的差异。如果将EIS的测量频率范围增加到100kHz,则这种差异将变得更加明显,四种模型的拟合结果如图10b所示,EFOM1=0.005 5,EFOM2= 0.005 6,EFOM3=0.002 6,EFOM4=0.015 8。可以看出,只有FOM3拟合结果较好,其他三种模型都不能较好地跟随阻抗的变化,这与第2节时域拟合的结果不同。因此,适用于EIS拟合的复杂模型并不一定在时域拟合中也是最优,在针对高频部分进行建模时需要注意这种差异性。

图10 不同频率范围EIS拟合结果
Fig.10 EIS fitting results in different frequency ranges
4 结论
本文根据EIS的拟合结果选择了三种分数阶等效电路模型来模拟锂离子电池在高频纹波电流下的电压响应,并由此设计了实验,采集了锂离子电池在不同频率电流下的电压响应。然后根据实验数据对几种模型进行了参数辨识,并根据辨识结果简化了FOM2,提出了FOM4。最后从响应精度和计算量两方面对几种模型进行比较,其中FOM2的精度最高但是计算量较大,FOM1的计算量最小但是精度较低,根据应用领域和使用场景的不同可以进行不同的选择。此外,从FOM2和FOM4的比较结果中还引申出另一个结论,即根据EIS拟合得到的复杂分数阶模型并不一定在时域拟合中也能得到最优的结果。
本文只选择了一种类型的电池进行了实验,可以基于不同材料和类型的电池数据来扩展比较。此外,本文仅在短时间尺度下对模型进行了拟合验证,将来可以对整个充放电循环进行验证,并且估计锂离子电池在高频应力下的荷电状态。
[1] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[2] Xiong Rui, Li Linlin, Li Zhirun, et al. An electro- chemical model based degradation state identification method of lithium-ion battery for all-climate electric vehicles application[J]. Applied Energy, 2018, 219: 264-275.
[3] He Hongwen, Xiong Rui, Guo Hongqiang, et al. Comparison study on the battery models used for the energy management of batteries in electric vehicles[J]. Energy Conversion and Management, 2012, 64: 113- 121.
[4] 张振宇, 汪光森, 聂世雄, 等. 脉冲大倍率放电条件下磷酸铁锂离子电池荷电状态估计[J]. 电工技术学报, 2019, 34(8): 1769-1779.
Zhang Zhenyu, Wang Guangsen, Nie Shixiong, et al. State of charge estimation of LiFePO4 battery under the condition of high rate pulsed discharge[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(8): 1769-1779.
[5] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948.
Yan Xiangwu, Deng Haoran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Electro- technical Society, 2019, 34(18): 3937-3948.
[6] 刘伟龙, 王丽芳, 王立业. 基于电动汽车工况识别预测的锂离子电池SOE估计[J]. 电工技术学报, 2018, 33(1): 17-25.
Liu Weilong, Wang Lifang, Wang Liye. Estimation of state-of-energy for electric vehicles based on the identification and prediction of driving condition[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 17-25.
[7] Hu Xiaosong, Li Shengbo, Peng Huei. A comparative study of equivalent circuit models for li-ion batteries[J]. Journal of Power Sources, 2012, 198: 359-367.
[8] Zou Yuan, Li Shengbo, Shao Bing, et al. State-space model with non-integer order derivatives for lithium- ion battery[J]. Applied Energy, 2016, 161: 330-336.
[9] Xiong Rui, Tian Jinpeng. A comparative study on fractional order models for voltage simulation of lithium ion batteries[C]//IEEE 89th Vehicular Tech- nology Conference, Kuala Lumpur, 2019: 1-5.
[10] Andre D, Meiler M, Steiner K, et al. Characterization of high-power lithium-ion batteries by electro- chemical impedance spectroscopy. II: modelling[J]. Journal of Power Sources, 2011, 196(12): 5349-5356.
[11] Hu Minghui, Li Yunxiao, Li Shuxian, et al. Lithium- ion battery modeling and parameter identification based on fractional theory[J]. Energy, 2018, 165: 153-163.
[12] Uno M, Tanaka K. Influence of high-frequency charge-discharge cycling induced by cell voltage equalizers on the life performance of lithium-ion cells[J]. IEEE Transactions on Vehicular Technology, 2011, 60(4): 1505-1515.
[13] Rahmoun A, Armstorfer A, Helguero J, et al. Mathematical modeling and dynamic behavior of a lithium-ion battery system for microgrid appli- cation[C]//2016 IEEE International Energy Conference (ENERGYCON), Leuven, 2016: 1-6.
[14] Ferraz P K P, Schmidt R, Kober D, et al. A high frequency model for predicting the behavior of lithium-ion batteries connected to fast switching power electronics[J]. Journal of Energy Storage, 2018, 18: 40-49.
[15] Sun Bingxiang, Bian Jingji, Ruan Haijun, et al. Modeling study for li-ion batteries considering high-frequency inductance characteristics based on electrochemical impedance spectroscopy[C]//2018 International Conference on Energy, Ecology and Environment, Melbourne, 2018: 1-7.
[16] Jeschke S, Maarleveld M, Baerenfaenger J, et al. Development of a passive impedance network for modeling electric vehicle traction batteries for EMI measurements[C]//2017 International Symposium on Electromagnetic Compatibility-EMC EUROPE, Angers, 2017: 1-6.
[17] Yang Yongming, Yao Mo, Wang Quandi. Research on high frequency model of hybrid vehicle battery[J]. Research Journal of Applied Sciences, Engineering and Technology, 2013, 6(14): 2601-2606.
[18] 曹楚南, 张鉴清. 电化学阻抗谱导论[M]. 北京: 科学出版社, 2002.
[19] Jossen A. Fundamentals of battery dynamics[J]. Journal of Power Sources, 2006, 154(2): 530-538.
[20] 方红伟, 宋如楠, 冯郁竹, 等. 基于差分进化的波浪能转换装置阵列优化[J]. 电工技术学报, 2019, 34(12): 2597-2605.
Fang Hongwei, Song Runan, Feng Yuzhu, et al. Array optimization of wave energy converters by differ- ential evolution algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2597-2605.
[21] Ma Chengbin, Hori Y. Fractional-order control: theory and applications in motion control[J]. IEEE Industrial Electronics Magazine, 2007, 1(4): 6-16.
[22] 薛定宇. 分数阶微积分学与分数阶控制[M]. 北京: 科学出版社, 2018.
[23] 吴红杰, 袁世斐, 谢旺. 基于分数阶理论的锂离子电池动态模型及其参数辨识方法[J]. 新型工业化, 2013, 3(9): 106-112.
Wu Hongjie, Yuan Shifei, Xie Wang. Lithium-ion battery dynamic model and its parameters identifa- cation based on fractional theory[J]. The Journal of New Industrialization, 2013, 3(9): 106-112.