0 引言
电磁成形(Electromagnetic Forming, EMF)是一种在线圈中通以脉冲大电流产生脉冲强磁场,进而在金属工件中感应涡流,磁场和涡流共同作用产生洛伦兹力,从而驱动材料发生塑性变形的高速率成形技术[1]。其具有高效率、低损耗等优势,可广泛应用于航天航空、船舶以及汽车等领域[2-4],但由于成形线圈在EMF过程中产生大量焦耳热引起线圈温升过高[5],使线圈使用寿命大大缩短,造成EMF设备使用寿命有限,使该技术无法满足工业生产大规模长时间持续运行的要求,严重限制了EMF技术的发展。
目前,国内外学者针对成形线圈的研究主要从线圈材料、绕制工艺、结构设计[6-7]和安装位置[8-9]这四个方面展开。其中,成形线圈的结构设计研究最为丰富,不仅包括各式各样的线圈整体结构设 计[10-11],还有线圈的局部结构优化[12-13]。但遗憾的是,绝大部分关于成形线圈的结构研究,是为了改善电磁成形效果,实现工件成形要求,而对于线圈在EMF过程中的温升研究极少,仅有邱磊[14]与刘良云[15]以抑制线圈温升为目的,探讨了单层平板线圈匝间距与高度对线圈温升的影响,验证了优化线圈结构能有效抑制线圈温升。线圈温升作为影响其使用寿命的重要因素之一,是学者研究的重要方向。关于这一瓶颈,还有Cao Quanliang等[16]和Qiu Li等[17]分别利用放电电路中的续流回路、晶闸管开关改变放电电流波形,抑制电流振荡衰减,减小线圈焦耳热,降低线圈温升。Qiu Li等[18]通过在驱动线圈旁放置额外的散热线圈,以耦合散热的方法减少驱动线圈温升。上述研究虽已为线圈温升抑制提供了方向,但秉承温升越低越好的原则,解决方法还不够多。虽有学者验证了优化单层平板线圈部分结构参数可抑制线圈温升,但仅针对单层平板线圈,且仅考虑了两个结构参数对线圈温升的影响,不够全面与详细。故可通过详细研究线圈结构参数对线圈温升的影响情况,优化线圈结构,抑制线圈温升,延缓线圈因温升而加速老化,避免线圈绝缘破坏甚至烧毁,延长线圈使用寿命,促进EMF技术更广泛地应用于工业化生产。
鉴于此,本文将围绕线圈温升展开研究,以螺线管线圈为研究对象,针对线圈绕制工艺的特点,详细探讨线圈结构对线圈温升的影响,总结线圈高度、宽度、层数、匝数、匝间距和层间距这六种结 构参数对线圈温升的影响规律,并简要讨论线圈结构优化对成形效果的影响,继而综合考虑线圈温升与成形效果以比较各结构参数的影响程度,为优化线圈结构设计提供参考建议。
1 仿真模型
EMF过程中电磁场、温度场以及机械结构场不断变化且相互影响,本文根据EMF过程中多物理场耦合关系,考虑电流趋肤效应、管件位移及速度对放电电流与磁场的影响以及线圈温升对其电导率的影响,建立基于COMSOL软件的电磁场-机械结构场-温度场耦合模型[16],为研究线圈结构对线圈温升的影响提供依据。
本文通过COMSOL软件,选取“全局常微分和微分代数方程”、“磁场”、“固体力学”、“固体传热”以及“动网格”这5个模块,利用前4个模块分别计算等效电路、电磁场、机械结构场、温度场模型,将“全局常微分和微分代数方程”计算的电流作为激励施加于“磁场”的线圈,将“磁场”计算的线圈电压代入“全局常微分和微分代数方程”,再将“磁场”计算的电磁损耗和洛伦兹力分别作为“固体传热”的热源和“固体力学”的体载荷。同时,将“固体力学”计算的工件位移速度用于“磁场”的洛伦兹项以计算动生电动势,将“固体传热”计算的材料温度用于计算“磁场”的材料线性电导率。最后,利用“动网格”按照物理场变化情况更新网格,最终实现EMF多物理场耦合。整个模型具体求解流程如图1所示。

图1 模型求解流程
Fig.1 Solution flow chart of model
仿真时,为减小计算量且不影响计算误差,本文根据实际情况构造二维轴对称的几何结构,划分合适单元大小的网格,设定合理的计算域与约束条件。其中,仿真时管件EMF系统几何结构示意图如图2所示,所用的材料参数见表1[15],结构参数与电气参数见表2。同时,表2不仅提供了仿真时所用的初始线圈结构参数,还给出了后文所需线圈结构参数的选取范围。由于本文的目标是为线圈设计提供宏观上的指导性建议,因此在参数范围的选取上做了大胆的假设,既考虑现有的实际工艺,也考虑了未来可能的工艺发展,预留了一定的范围,以期通过更广泛的参数值总结更为准确的变化规律。

图2 仿真时管件EMF系统几何结构示意图
Fig.2 Schematic diagram of the geometric structure of the tube EMF system during simulation
表1 EMF系统的材料参数
Tab.1 Material parameters of EMF system
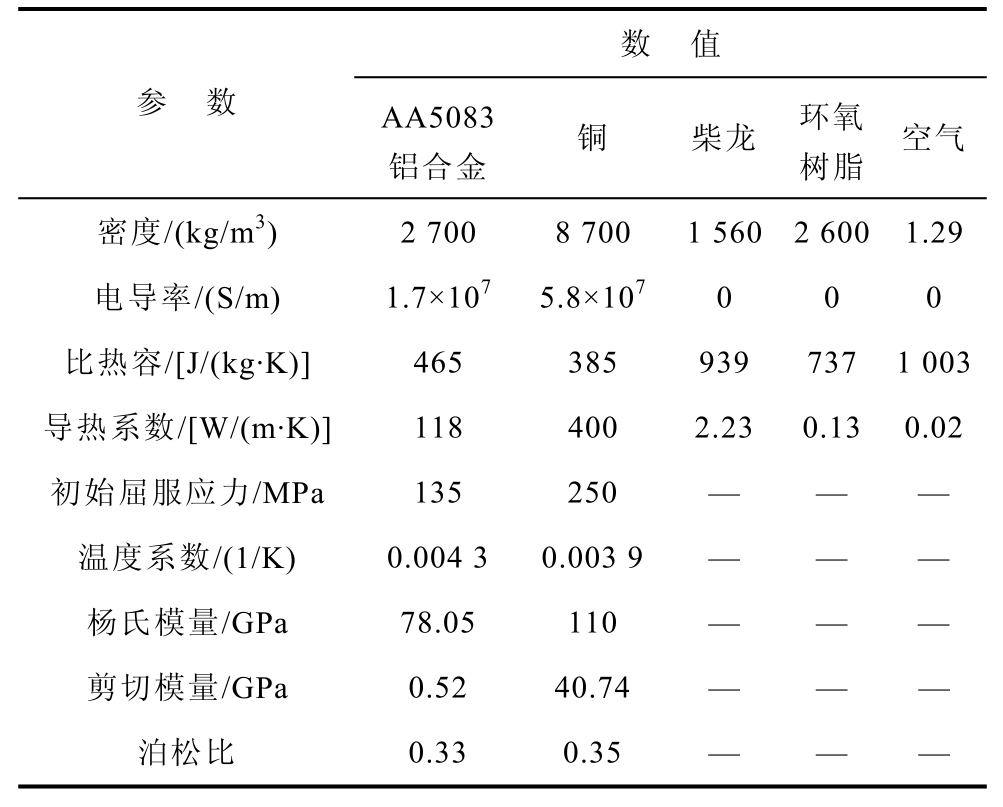
数 值 参 数 AA5083 铝合金 铜 柴龙 环氧树脂 空气密度/(kg/m3) 2 700 8 700 1 560 2 600 1.29电导率/(S/m) 1.7×107 5.8×107 0 0 0 比热容/[J/(kg·K)] 465 385 939 737 1 003导热系数/[W/(m·K)] 118 400 2.23 0.13 0.02初始屈服应力/MPa 135 250 — — — 温度系数/(1/K) 0.004 3 0.003 9 — — — 杨氏模量/GPa 78.05 110 — — — 剪切模量/GPa 0.52 40.74 — — — 泊松比 0.33 0.35 — — —
另外,网格尺寸会影响仿真模型的求解精度,但过细的网格划分将会增大模型求解的计算量,增加求解时间。图3为采用表1、表2的参数值所建立的不同精度网格的模型,其模型计算结果中,极细化单元大小的网格(最大单元3.6mm,最小单元0.007 2mm,平均单元质量0.920 3,单元数22 418)和常规单元大小的网格(最大单元24.1mm,最小单元0.108mm,平均单元质量0.778 7,单元数2 836) 对于最高温升的计算仅相差0.48%,对于平均温升的计算也仅相差1.36%,不同精度网格下模型的计算结果对比如图4所示。但采用常规单元大小的网格对应的单元数可减少87.35%,这在保证足够计算精度的同时大大缩减了计算量,因此本文的模型均采用常规单元大小的网格进行计算。
表2 系统的结构参数与电气参数
Tab.2 Structure and electrical parameters of system
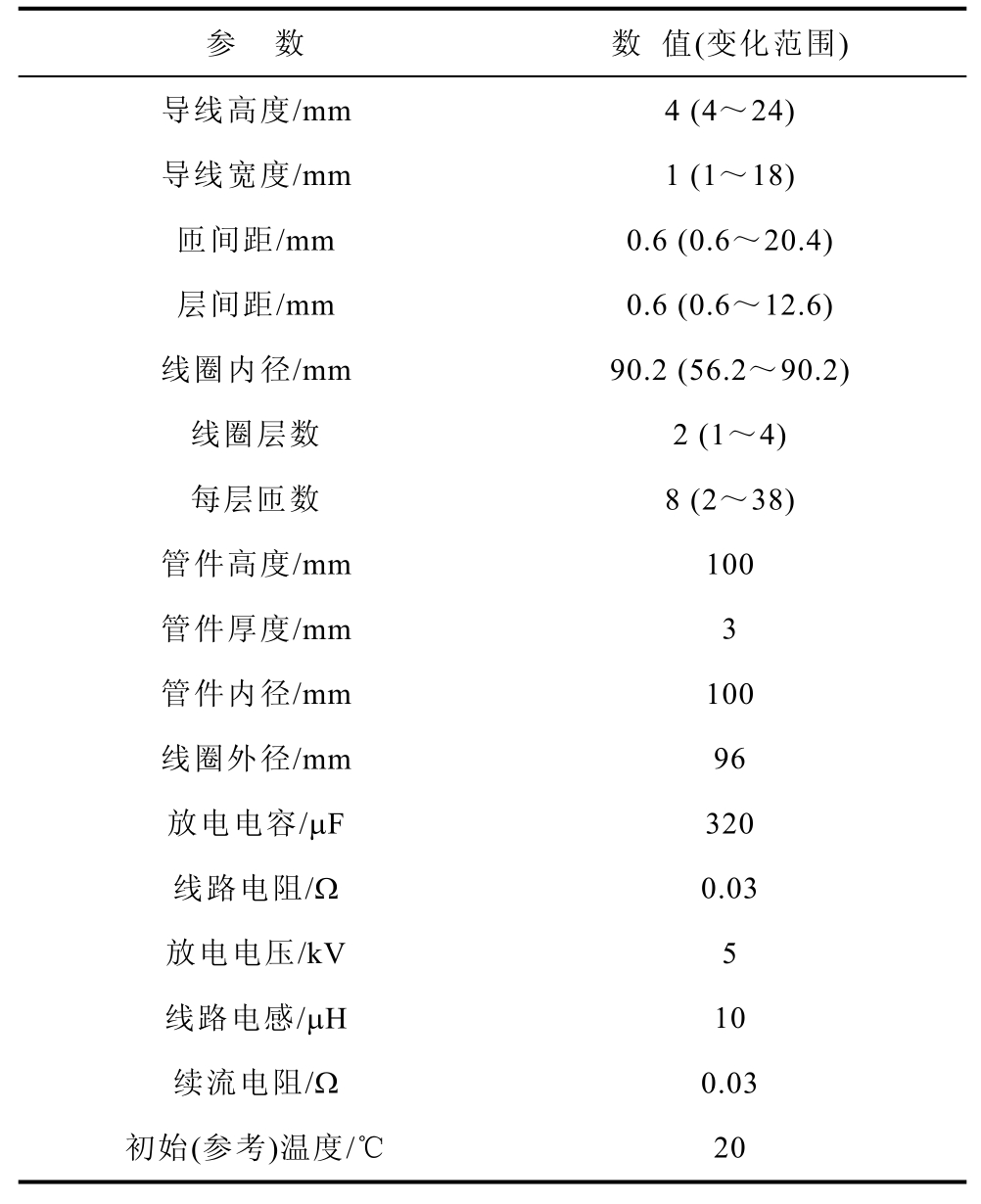
参 数 数 值(变化范围) 导线高度/mm 4 (4~24) 导线宽度/mm 1 (1~18) 匝间距/mm 0.6 (0.6~20.4) 层间距/mm 0.6 (0.6~12.6) 线圈内径/mm 90.2 (56.2~90.2) 线圈层数 2 (1~4) 每层匝数 8 (2~38) 管件高度/mm 100 管件厚度/mm 3 管件内径/mm 100 线圈外径/mm 96 放电电容/μF 320 线路电阻/Ω 0.03 放电电压/kV 5 线路电感/μH 10 续流电阻/Ω 0.03 初始(参考)温度/℃ 20

图3 不同精度网格的模型
Fig.3 Models of different precision grids
1.1 等效电路模型
本文选用带有续流回路的放电电路,该EMF系统等效电路如图5所示。
根据基尔霍夫电压定律、基尔霍夫电流定律以及元器件特性,得到该等效电路模型为
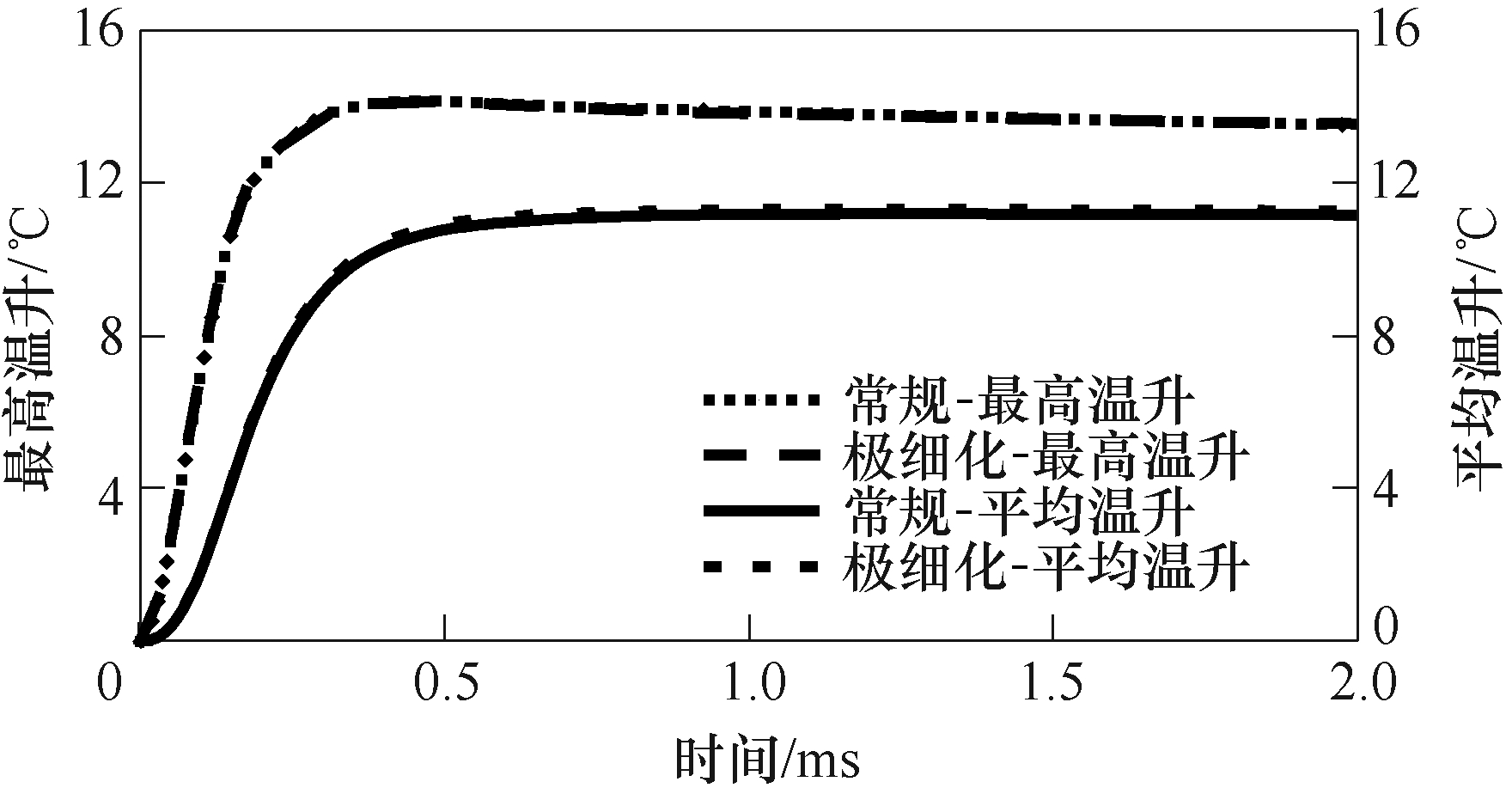
图4 不同精度网格下模型的计算结果对比
Fig.4 Comparison of calculation results of models under different precision grids
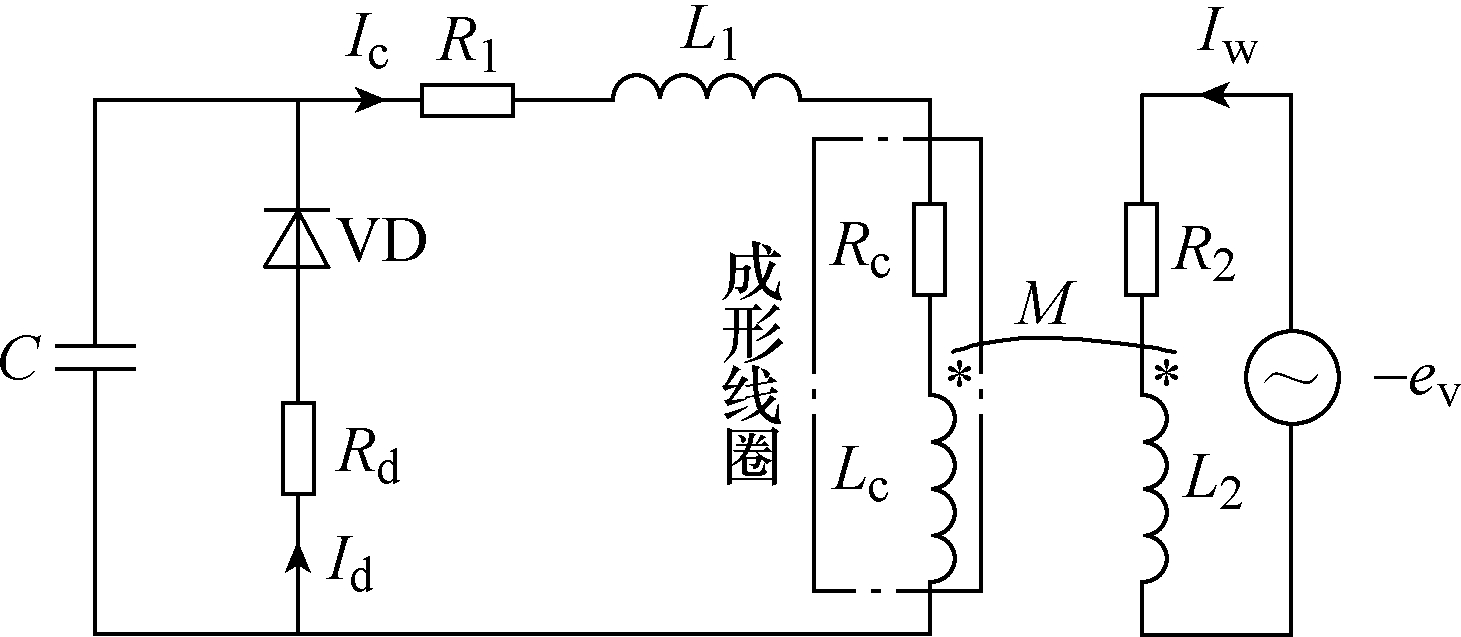
图5 等效电路
Fig.5 equivalent circuit diagram
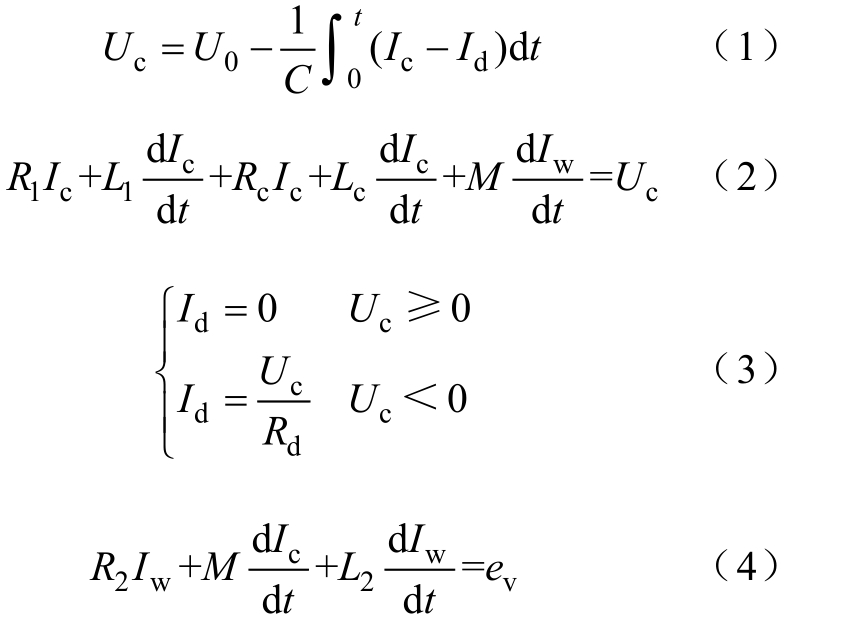
式中,0U电容器初始电压;cU为放电电压;C为电容值;L1、R1分别为线圈电感与电阻;cI为流过成形线圈的放电电流;Lc、Rc分别为成形线圈的等效电感与等效电阻;wI为管件的感应电流;M为成形线圈与管件的互感系数;ve为管件位移产生的动生电动势;R2、L2分别为管件的等效电阻、等效电 感;Rd为续流电阻;dI为流过续流回路的电流。
考虑电流趋肤效应与邻近效应,成形线圈横截面电流分布不均匀,电流密度处处不相等,则线圈电流密度为
式中,phiJ为线圈电流密度;s为线圈截面积。
1.2 电磁场模型
为研究EMF过程中电磁场变化情况,建立电磁场模型。根据麦克斯韦方程组,可得管件成形的电磁场数值模型,同时将矢量磁动势Α作为计算变量以便于求解该模型,模型具体表示为
式中,ϕ为标量电位;μ为磁导率;γ为电导率;v为管件运动速度。对于管件和空气,γϕ−∇=0;对于成形线圈, γϕ−∇ 为外部电源供给成形线圈的电 流密度phiJ。
通过式(6)可求出计算变量A,从而求得管件感应电流密度和管件受到的电磁力密度分别为
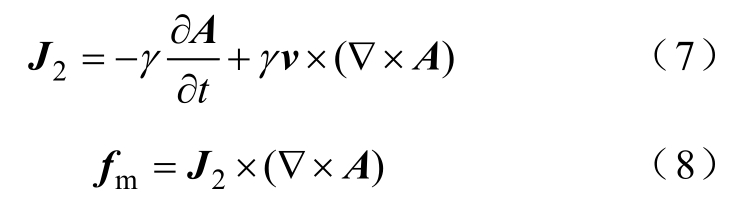
式中,2J为管件感应电流密度;mf为管件电磁力密度。
仿真时,本文通过“磁场”模块搭建电磁场模型,选取线圈、管件、加固层、环氧层以及一大片空气区域作为电磁场的计算域。
1.3 机械结构场模型
管件受到电磁力的作用将发生机械结构变形,为研究管件变形过程,建立机械结构场模型,具体模型为
式中,ρ为管件材料密度;u为管件位移量;σ为应力张量。
本文选用铝合金AA5083作为管件材料,根据文献[16]对AA5083材料准静态应力-应变曲线拟合的结果,获取表达式为

式中,qsσ为准静态应力;ε为弹性应变;E为杨氏模量,E=78.05GPa;εp为塑性应变,εp=ε−σqs /E ;![]() 为初始屈服应力,qs0σ=135MPa;a=539.2MPa;b=0.491 4。
为初始屈服应力,qs0σ=135MPa;a=539.2MPa;b=0.491 4。
为有效反映EMF过程中高塑性应变率的影响,采用Cowper-Symonds模型描述材料的应力应变关系,材料的本构方程为
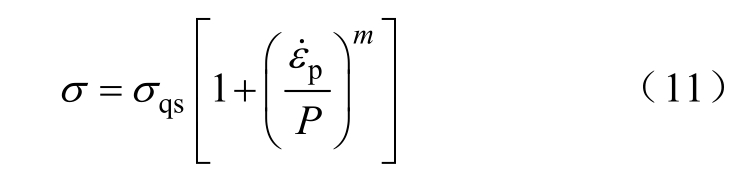
式中,![]() 为塑性应变率;P和m为体现材料应变率效应的常数,铝合金AA5083的P和m分别为6 500s−1 和0.25[19]。
为塑性应变率;P和m为体现材料应变率效应的常数,铝合金AA5083的P和m分别为6 500s−1 和0.25[19]。
仿真时,本文通过“固体力学”模块搭建机械结构场模型,选取管件作为机械结构场的计算域。同时,为约束管件整体移动,实验时常常将管件两端固定,故指定管件两端边界的径向位移为0,并考虑到管件局部变形较大,设定管件为大塑性应变。
1.4 温度场模型
电流流过线圈产生焦耳热,焦耳热作为热源向周围导体传递热能,造成介质材料温度升高。为研究材料温度升高情况,建立温度场模型,通过热传递方程计算材料温度分布情况。温度场模型为
式中,mρ为材料密度;T为材料温度;Cm为材料热容;km为材料热传递系数;Q为热源。
在EMF过程中,热源主要来自线圈、管件、线路电阻以及续流电阻产生的焦耳热。由于本文的研究对象为成形线圈,故将重点关注线圈产生的焦耳热,其焦耳热表示为
式中,mσ为线圈电导率。
仿真时,本文通过“固体传热”模块搭建温度场模型,选取线圈、管件、加固层、环氧层以及较小的空气区域作为温度场的计算域,并假定边界没有热交换。
2 仿真结果与分析
为详细研究线圈结构对线圈温升的影响,本文选取了六种线圈结构参数,它们均是线圈绕制过程中可控的工艺参数,其线圈层数与匝数反映线圈设计,宽度与高度反映导线截面,匝间距与层间距反映绝缘层和加固层厚度。继而利用上述多物理场耦合模型,模拟不同层数、匝数、宽度、高度、匝间距以及层间距的线圈在EMF过程中温升情况,分析其仿真结果,总结线圈结构对线圈温升的影响规律。本文在研究某一结构参数对线圈温升的影响时仅改变该结构参数,保持其他结构参数不变,同时,保证在相同初始储能下研究六种结构参数对线圈温升的影响,以便于后续分析对比各结构参数对线圈温升和成形效果的影响,更好地为线圈结构优化提供参考建议。仿真所用参数具体见表1和表2。
2.1 线圈层数对线圈温升的影响
图6为不同层数线圈的最高温升随时间变化曲线,可以看出,线圈最高温升随层数增加而减少,且每增一层,其最高温升大约降低26.60%。这是由于线圈层数增加使其电阻与电感增大,从而线圈电流及放电频率减小(文中所提的放电频率均指放电电流等效频率,可通过1/(4Tp)简要估算,Tp为放电电流到达第一个脉冲峰值的时间),同时线圈的导线截面积不变,故电流密度减小,线圈最高温升降低。又由于增加线圈层数不仅减少电流还降低放电频率,使电流分布更加均匀,电流密度更小,从而使线圈温度更低且分布更均匀,故线圈最高温升曲线随层数增加愈发平缓,曲线凸起部分越来越小。
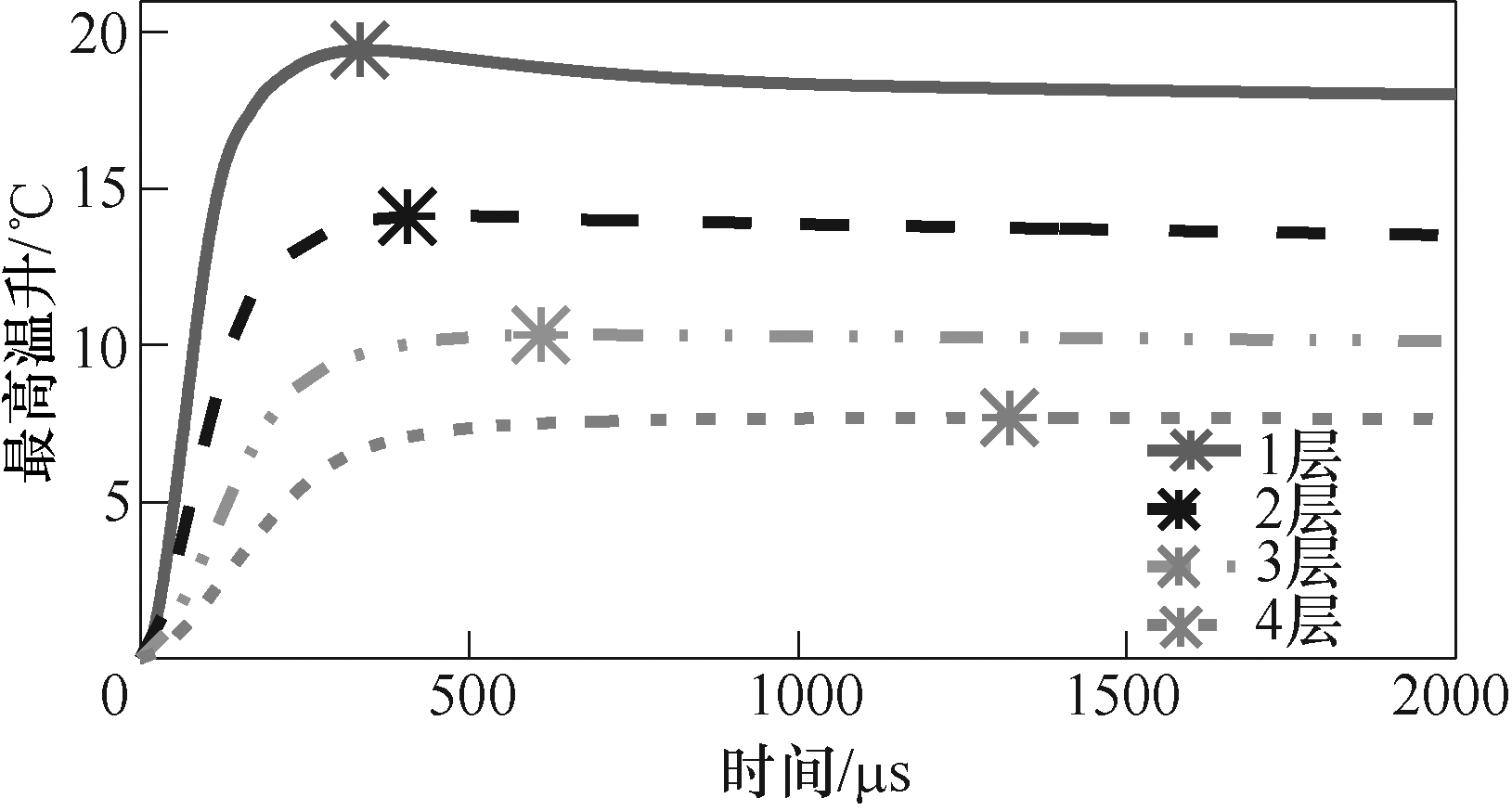
图6 不同层数线圈的最高温升随时间变化曲线
Fig.6 Time-varying curves of maximum temperature rise of coils with different layers
图7为不同层数线圈的平均温升随时间变化曲线,可以看出,当线圈由外向内,由1层开始逐层增加层数时,线圈平均温升不断降低,其降低率由28.50%减为25.65%再减至25.21%。平均温升也随层数增加而减小,且降低率逐渐减小。这由于当线圈层数较少时,增加层数使放电电流减小,线圈电阻及放电时间增加,根据焦耳热公式可知,线圈焦耳热难以减少,但线圈总质量因层数增加而大幅提升,故线圈平均温升逐步降低。当层数较多时,增加线圈层数会使电流减小程度大于电阻及放电时间 增大程度,线圈焦耳热将减少,从而平均温升还将降低。同时,随线圈层数增加,增加的线圈半径变小,线圈受热面积的增量减小,故线圈平均温升降低幅度随层数增加而减小。

图7 不同层数线圈的平均温升随时间变化曲线
Fig.7 Time-varying curves of average temperature rise of coils with different layers
2.2 线圈匝数对线圈温升的影响
图8为不同匝数的线圈最高温升随时间变化曲线,可以看出,当线圈每层增2匝时,最高温升最大降低率可达19.38%,最小降低率也有13.29%。随匝数增加,线圈最高温升逐渐降低,且降低率变小。这是由于增加线圈匝数使线圈电感与电阻增大,线圈电流减小,而流经电流的线圈截面积不变,故电流密度减小,线圈最高温升降低。又由于匝数增加使线圈与管件间耦合关系更加紧密,系统总电感增大幅度减小,从而电流降低幅度减小,线圈电流密度降低幅度减小,故线圈最高温升降低速度逐渐变慢。同时,线圈匝数增加引起的电感增大使放电频率持续减小,趋肤效应减弱,线圈电流分布变均匀,所以线圈最高温升随时间变化曲线愈发平缓。

图8 不同匝数的线圈最高温升随时间变化曲线
Fig.8 Time-varying curves of maximum temperature rise of coils with different turns
图9为不同匝数的线圈焦耳热及平均温升曲线,可明显看出,线圈平均温升随匝数增加而降低,线圈每增加2匝,平均温升约降低7.36%,但从线圈焦耳热的角度分析,增加匝数使焦耳热呈增大趋势,所以增加线圈匝数可有效抑制线圈平均温升,但无法有效减少线圈承受的热负荷。这是由于增加线圈匝数,使放电电流减小,放电时间延长,线圈电阻增大,根据焦耳热计算公式可知,线圈产生的焦耳热将难以减少,但由于线圈质量随匝数增加而大大提高,故线圈平均温升随匝数增加而稳步降低。
综合图8分析可知,当线圈每层分别为2匝、8匝及20匝时,线圈最大温差(最高温升峰值与平均温升的差值)分别为5.179℃、2.963℃和0.672℃。随线圈匝数增加,线圈最高温度与平均温度之间的温差明显减小。增加匝数可增大线圈受热面积,使 其发热更均匀。在优化线圈结构设计时,不仅需考虑线圈长期允许工作温度,还需考虑最高允许工作温度,故可通过增加线圈匝数,降低温升,减少线圈内部温差,使其各部分热损耗趋于一致,延长其使用寿命。

图9 不同匝数的线圈焦耳热及平均温升曲线
Fig.9 Curves of Joule heat and average temperature rise of coils with different turns
2.3 线圈宽度对线圈温升的影响
图10描述不同导线宽度的线圈最高温升随时间变化情况,可以看出,当导线宽度由1mm增至4mm时,线圈最高温升降低61.80%。当导线宽度由4mm增至16mm时,温升仅降低9.36%。当导线宽度较窄时,增大导线宽度能使线圈最高温升急剧降低,在此基础上继续增大宽度虽能抑制线圈最高温升,但影响较小。这是由于当导线宽度较窄时,增加导线宽度使系统总电感减小,放电电流及频率增大,但导线截面积增大,其增大程度大于电流增大程度,故电流密度减小,线圈最高温升降低。当导线较宽时,放电频率很高,趋肤效应和邻近效应明显,电流更趋于线圈表面且偏向于管件侧分布,此时增大导线宽度难以使电流因截面积增大而均匀分布,从而难以减小电流密度,故线圈最高温升降低速度减小。
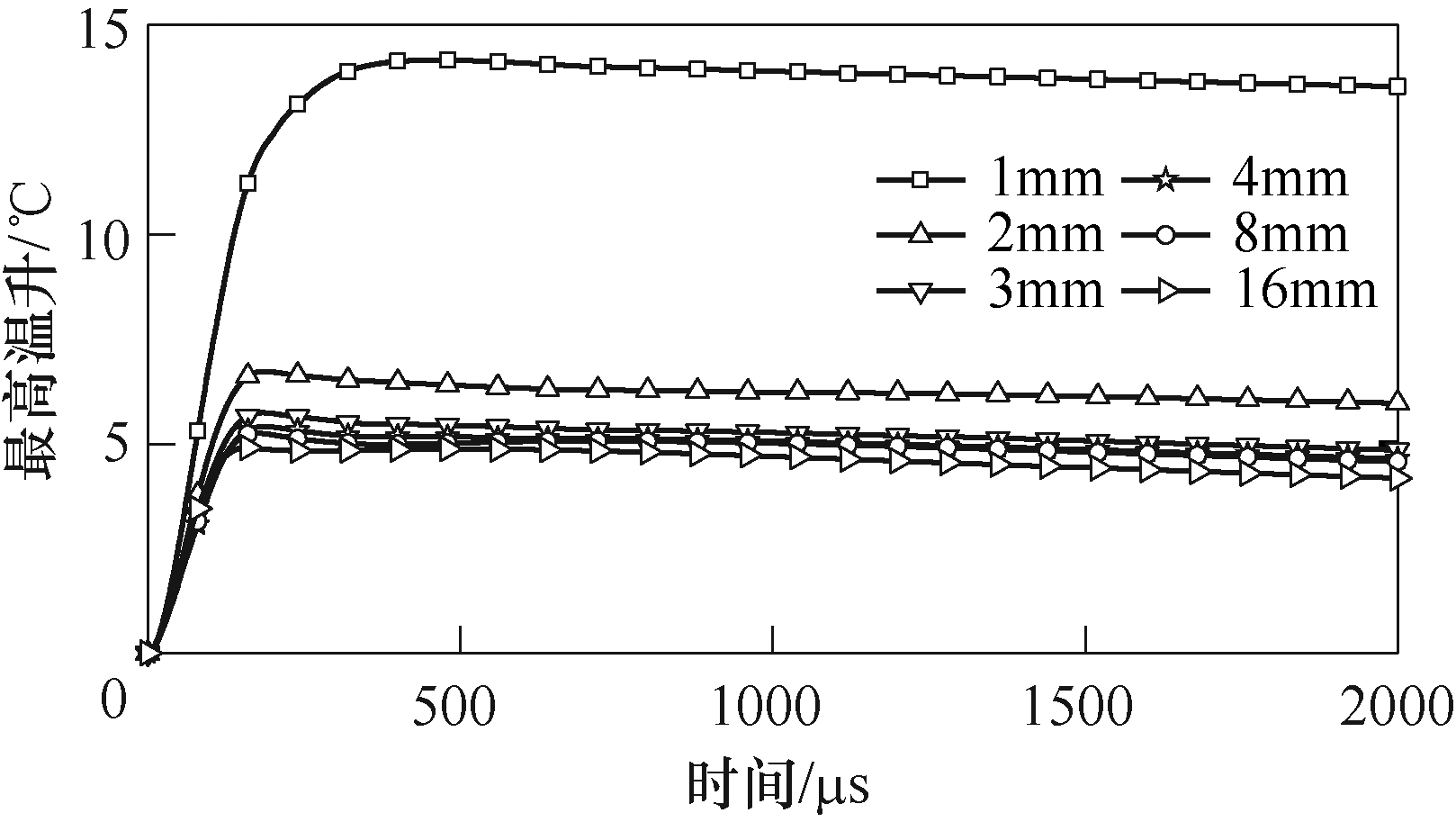
图10 不同导线宽度的线圈最高温升随时间变化曲线
Fig.10 Time-varying curves of maximum temperature rise of coils with different wire widths
可以预见,当导线非常宽时,电流集中分布在导线两端,且靠近线圈中心轴侧电流密度将大于靠近管件侧电流密度,在此基础上增大导线宽度将促进电流向中心轴分布,电流密度增大,从而线圈最高温升增加。但该情况电流流通的有效面积小,成形量极小,能量利用率极低,故不予考虑。
图11为线圈焦耳热与平均温升随导线宽度变化情况,可以看出,当导线宽度由1mm增至16mm时,线圈焦耳热的降低率66.75%小于平均温升的降低率97.54%。同时,相比于最高温升的降低率,增大导线宽度更能有效降低线圈平均温升。同样地,增大导线宽度能降低线圈焦耳热和平均温升,但其降低率随导线加宽而越来越小。这是由于导线宽度较窄时,增大导线宽度使系统总电感与线圈电阻减小,放电时间缩短,放电电流增大,且放电电流增大程度小于电阻减小程度,线圈产生的热量减少,同时导线加宽会提高线圈质量,根据热传递公式可知,线圈平均温升必将降低且降低程度大于焦耳热。但线圈平均温升的降低率随导线加宽而减小,这是由于放电频率随导线加宽而增大,电流分布愈不均匀,使线圈电阻减小幅度逐渐变小所导致的。总之,增大线圈宽度不仅能有效抑制线圈温升,还能减轻线圈承受的热负荷,提高电磁成形效率。
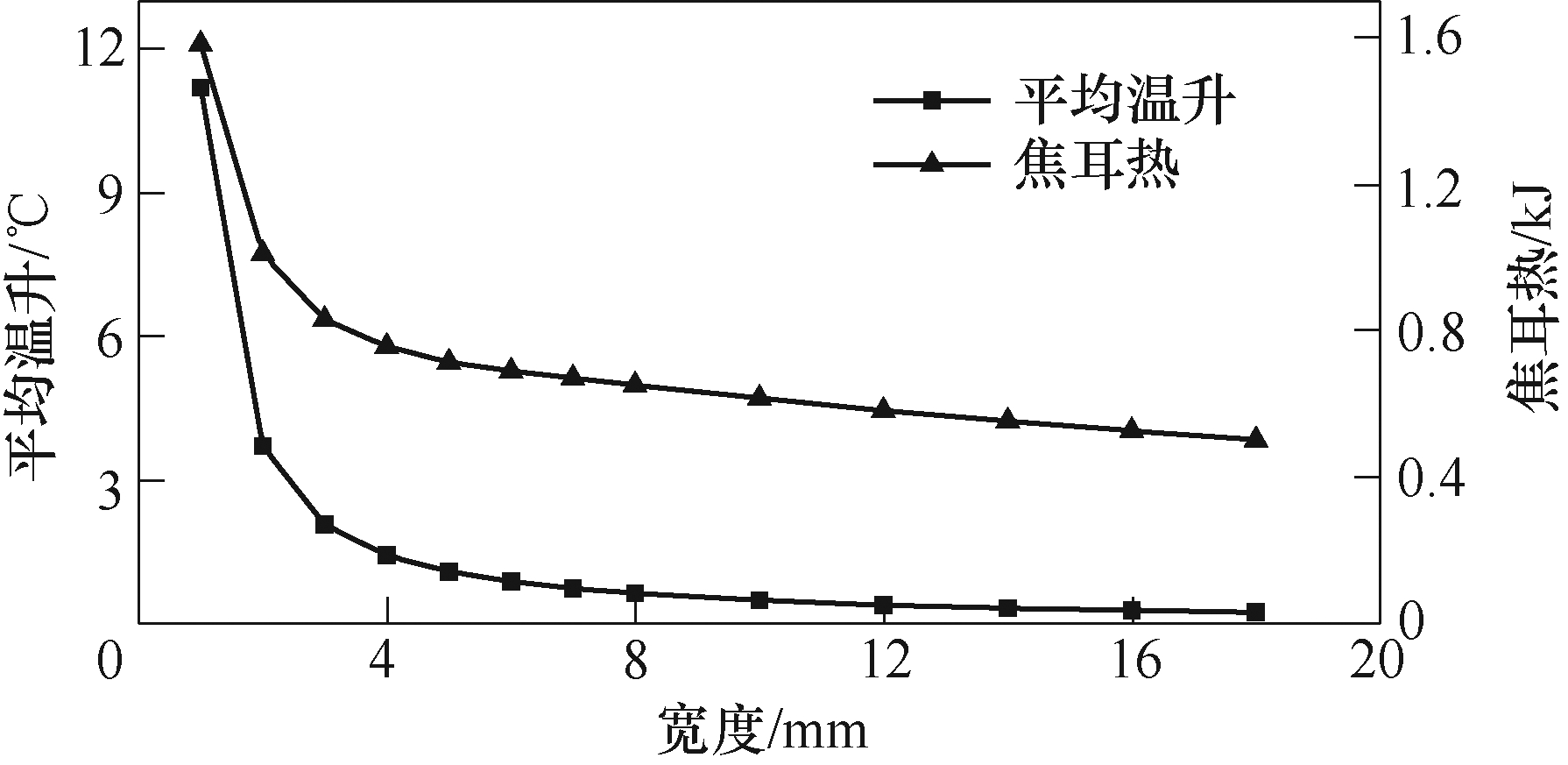
图11 线圈焦耳热与平均温升随导线宽度变化情况
Fig.11 Coil Joule heat and average temperature rise change with wire width
2.4 线圈高度对线圈温升的影响
图12为不同导线高度的线圈最高温升随时间变化曲线,可以看出,在管件长度范围内,增大导线高度以抑制线圈最高温升的效果较为稳定,每增加1mm导线高度,线圈最高温升平均降低15.25%。这是由于增大导线高度可使线圈电感与电阻减小,进而放电电流增大,但同时导线截面积大幅增加,故电流密度减小,线圈最高温升降低。然而,当线圈高度超过管件时,最高温升将随导线增高而增大。这是由于邻近效应使管件感应电流与线圈电流相互吸引,在此情况下增大导线高度使电流分布更集中,从而电流密度变大,线圈最高温升增大。而线圈高度大于管件时成形量极小(关于线圈高度对成形效果的影响将在后文集中分析),成形效率极低,且目前电磁管件胀形实验使用的线圈高度常常小于管件,故一般仅考虑线圈高度小于管件高度的情况,线圈最高温升随导线增高而降低。

图12 不同导线高度的线圈最高温升随时间变化曲线
Fig.12 Time-varying curves of maximum temperature rise of coils with different wire heights
结合图10可知,在初始导线宽度基础上增加2mm时,线圈最高温升减小59.49%。而在初始导线高度基础上增加2mm时,其最高温升仅减小34.33%。但随着导线高度或宽度加大,当上述参数分别增加6mm后,导线高度参数对应的线圈的最高温升幅度降低,将大于宽度参数对应的线圈的最高温升幅度降低。由此可见,当导线初始截面较小时,在一定范围内增加等长的导线宽度或高度,导线高度对线圈温升的影响较小。当初始截面较大或较大幅度改变导线截面时,改变导线高度使线圈最高温升降低率更高。这说明在优化线圈结构时应考虑其导线初始尺寸,合理调整导线宽度或高度,以更有效的方式降低线圈最高温升。
图13为线圈焦耳热与平均温升随导线高度变化曲线,可明显看出,增大导线高度可降低线圈平均温升,且温升降低率随导线增高而逐渐减小,同时线圈焦耳热呈减少趋势。当导线高度由4mm增至16mm时,线圈平均温升降低90.67%,而焦耳热只减少62.96%,可见焦耳热减少速度较平均温升慢。这是由于增大导线高度使线圈电感减小,放电电流增大,放电时间缩短,线圈电阻大幅减小,从而线圈产生的焦耳热逐渐减少,又因线圈质量随导线变高而增加,故线圈平均温升大幅降低,且温升降低率高于焦耳热减少率。
结合图11可知,当导线初始截面较小时,在较小范围内增加导线宽度使线圈平均温升降低幅度较大,而超出某一范围,平均温升随导线宽度变化十分缓慢,此时增加导线高度使线圈平均温升降低较快。当导线初始截面较大时,增加导线高度对线圈 平均温升的抑制更高效。由此可见,无论是抑制线圈平均温升还是最高温升,都应根据线圈初始尺寸选择合适的导线截面优化方案,延长线圈使用寿命。

图13 线圈焦耳热与平均温升随导线高度变化曲线
Fig.13 Curves of Joule heat and average temperature rise of coil with wire height
2.5 线圈匝间距对线圈温升的影响
图14描述了不同匝间距的线圈最高温升曲线,可明显看出,随线圈匝间距增大,线圈最高温升先降后升。这是因为,当线圈匝间距较小时,增大匝间距使线圈与管件耦合关系变紧密,系统总电感略有减小,放电电流及频率增大。虽然导线截面积不变,放电电流增大本该引起电流密度增大,但增大匝间距还使邻近效应减弱,从而使导线中电流分布更均匀,故在放电电流提升程度不大的情况下,线圈电流密度因邻近效应而减小,最高温升降低。然而,随匝间距逐渐增大,电流增大程度将强于邻近效应的影响,线圈最高温升将逐渐增大。当匝间距增大至某一长度后,线圈高度大于管件高度,在此基础上增大匝间距使线圈与管件间耦合关系变弱,系统总电感变大,放电频率变慢,电流逐渐减小,但此时电流分布很不均匀,线圈最高温升依旧增大。然而,继续增大匝间距,线圈电流减小程度变大,线圈最高温升将减小。可以预知,当线圈高度远大于管件高度时,离管件较远的部分线圈与管件间耦合关系很弱,线圈匝间距对线圈最高温升的影响相当于在管件高度范围内的部分线圈改变匝间距对线圈最高温升的影响,所以此后线圈最高温升随匝间距增大呈先减后增再减的交替变化,但总体呈增大趋势。总之,改变线圈匝间距对线圈最高温升有影响,但影响较小,在匝间距变化过程中,线圈最高温升最大降低率仅为13.55%。
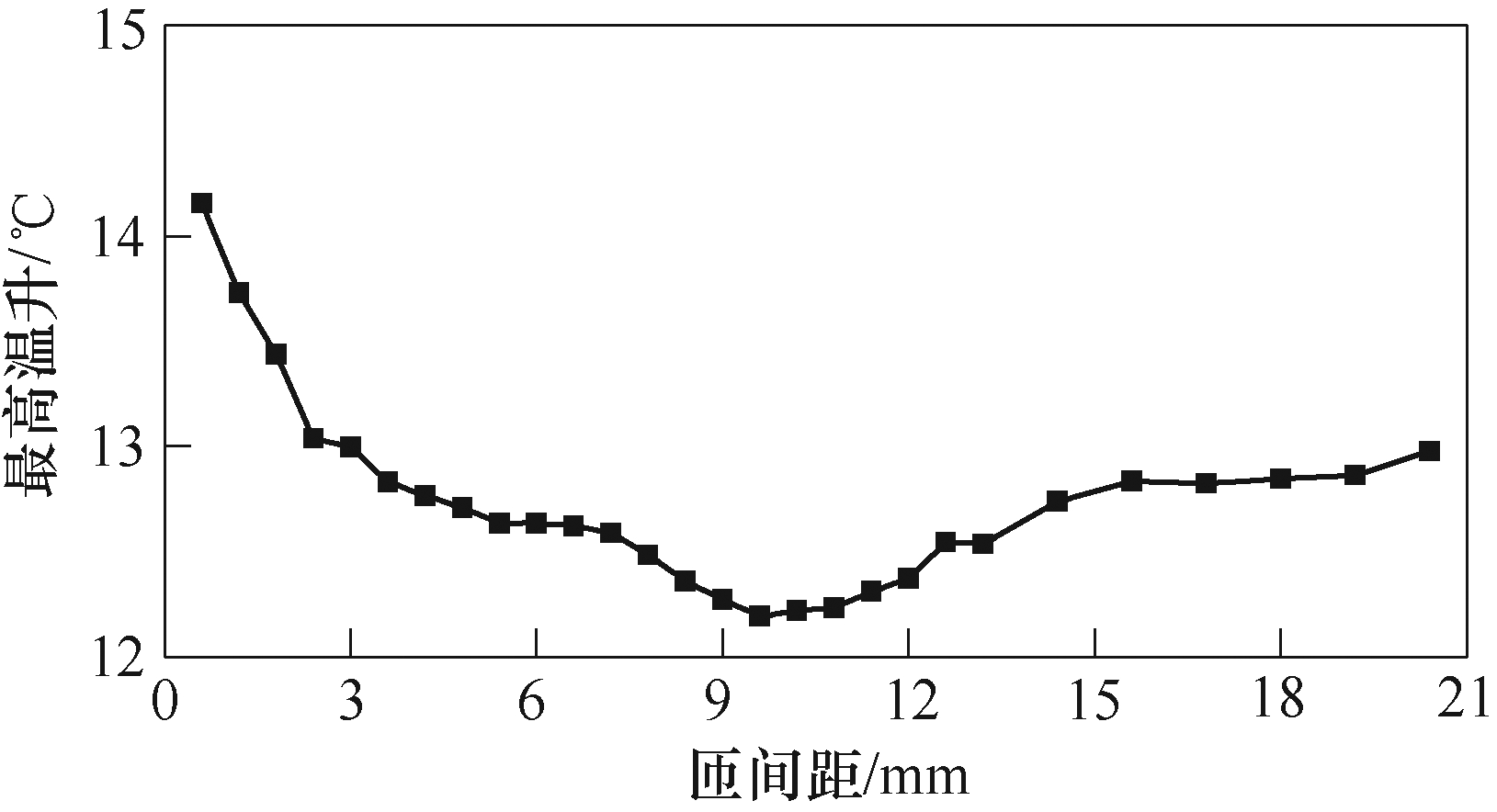
图14 不同匝间距的线圈最高温升曲线
Fig.14 Maximum temperature rise curve of coil with different turn spacing
图15为不同匝间距的线圈平均温升情况,可以看出,在匝间距增大过程中,线圈平均温升有波动,但总体趋势呈先降后升,最大降低率仅为4.29%。这是由于当匝间距较小时,增大匝间距使系统总电 感减小,邻近效应减弱,线圈电阻减小,放电电流增大,放电时间缩短,而此时匝间距变化引起邻近效应减弱较明显,电感变化较小,放电电流增大程度小于放电时间和电阻减小程度,线圈焦耳热减少,平均温升降低。当匝间距进一步增大时,放电电流增大更明显,线圈焦耳热将增多,平均温升将增大。当匝间距很宽时,增大匝间距引起电感增大,放电电流减小,放电时间延长,线圈焦耳热继续增加,平均温升持续增加。虽然焦耳热及平均温升变化情况难以预测,但其变化范围很小。
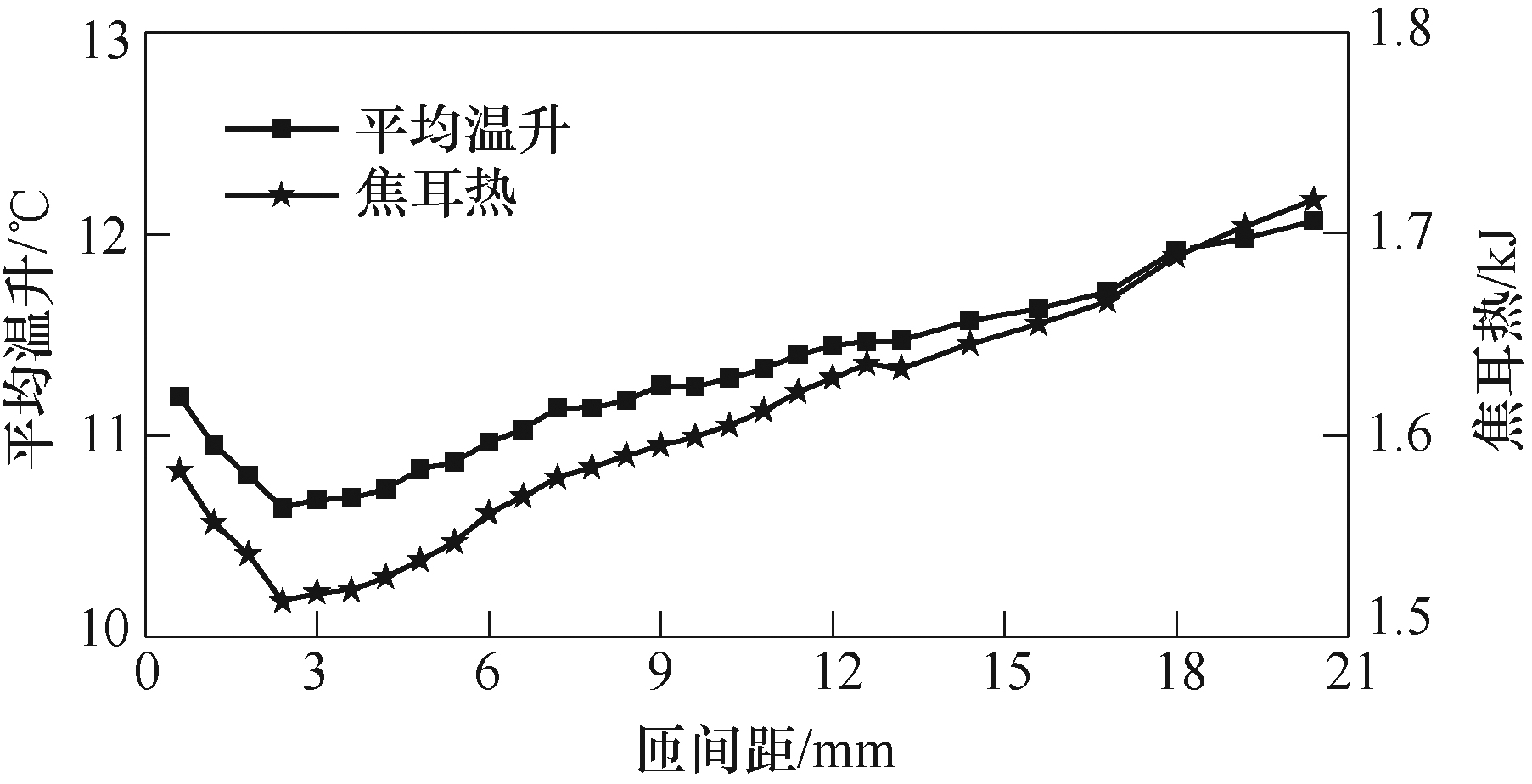
图15 不同匝间距的线圈平均温升情况
Fig.15 Average temperature rise of coils with different turn spacing
综合图14分析可知,线圈平均温升和最高温升均受匝间距影响较小,适当的匝间距可使线圈焦耳热最少,过宽的匝间距不仅使线圈绕制难度大且成形效果差,还可能增加线圈热负荷及温升。在优化线圈设计时,需权衡线圈绕制难度、热负荷、成形效率等多方面,合理优化匝间距。
2.6 线圈层间距对线圈温升的影响
图16为线圈最高温升随层间距变化曲线,可以看出,在层间距增大过程中,线圈最高温升先减后增。这是由于当线圈的导线较窄且层间距较小时,层间距增大引起线圈电感与电阻略微减小,而电阻减小程度小于电感减小程度,从而电流阻尼系数变大,放电时间缩短,线圈电流减小,而导线截面积不变,故电流密度减小,线圈最高温升降低。当层间距较大时,增大层间距使线圈电感与电阻减小程度较大,从而线圈电流增大,但此时邻近效应明显减弱,导线中电流分布更均匀,这使电流密度减小,线圈最高温升降低。当导线较宽或层数较多或层间距非常大时,增大层间距引起线圈电感与电阻大大减小,线圈电流大幅提升,同时邻近效应的影响已不明显,故最终线圈电流密度增大,最高温升增加。虽然改变层间距可降低线圈最高温升,但降低幅度很小,在层间距变化过程中线圈最高温升最大降低率仅为7.09%,层间距对线圈最高温升的影响很小。
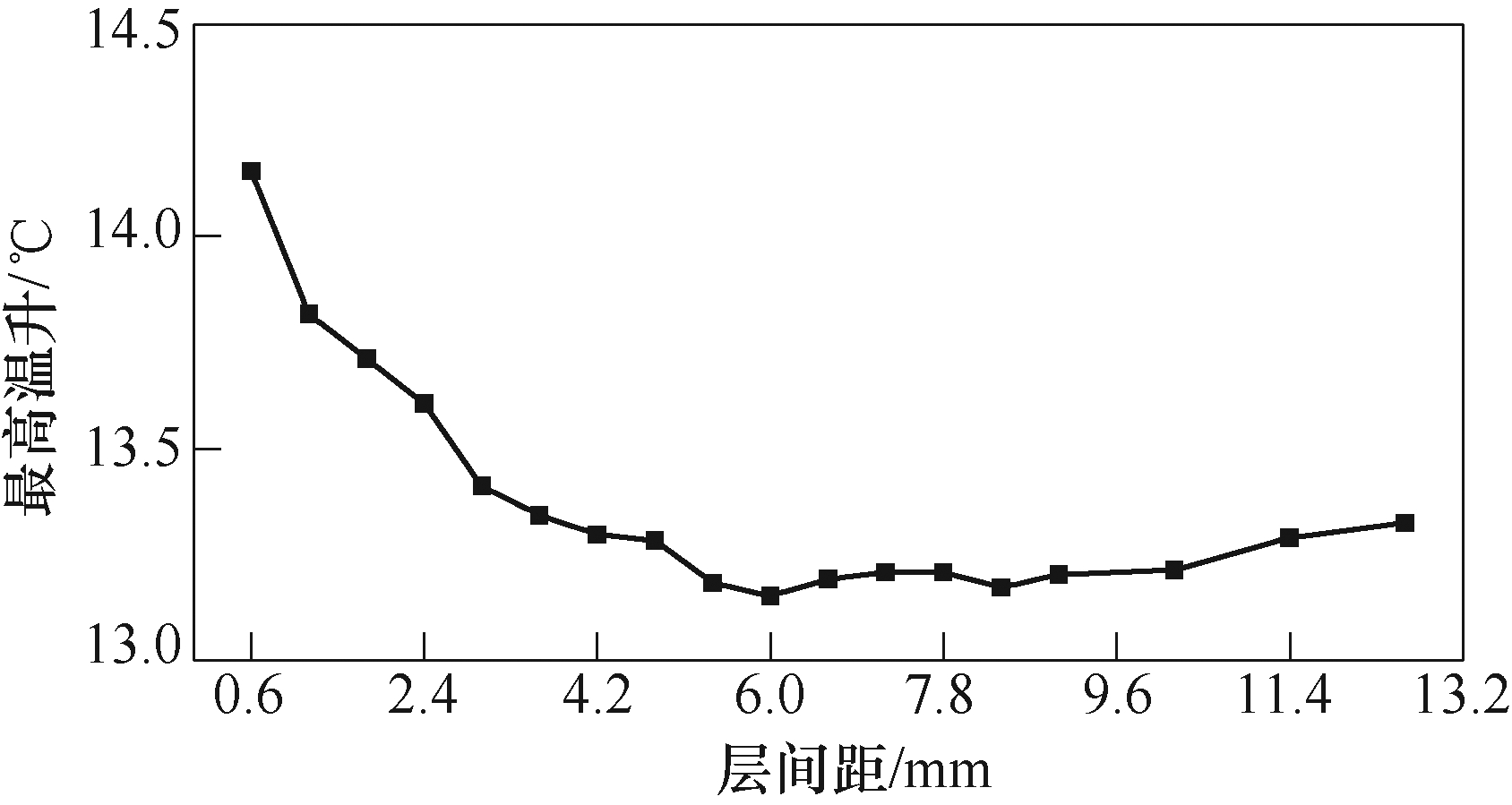
图16 线圈最高温升随层间距变化曲线
Fig.16 Curve of coil maximum temperature rise with layer spacing
图17为不同层间距的线圈焦耳热与平均温升情况,可以看出,当线圈层间距增大时,线圈平均温升和焦耳热不断上下波动,但整体变化趋势为先降后增。这是因为当线圈初始层间距较小时,增大层间距使线圈电阻及电感略微减小,放电电流及时间均减少,从而使线圈产生的焦耳热减少,平均温升降低。当层间距达到一定程度时,增大层间距使线圈电阻与电感变化较大,放电电流增大,放电时间减小,但由于电流增大程度小于电阻减小程度,此时线圈焦耳热依旧减少,平均温升降低。在此基础上继续增大层间距,电流增大程度变大,焦耳热减少速度变小,而这时增大层间距使线圈质量减小程度相对较大,故线圈平均温升增大。当层间距较大时,增大层间距使放电电流大大增加,其增加程度大于电阻和放电时间减小程度,故线圈焦耳热增多,平均温升增加。当层间距非常大时,增大层间距使电阻和放电时间均减少,其减小程度大于电流增大程度,焦耳热减少,但线圈质量大大减少,故线圈温升依旧增大。同样地,在关于层间距对线圈温升的影响研究中,线圈平均温升最大降低率仅为4.02%,层间距对平均温升抑制效果依然很小。由此可见,改变层间距仅降低小于10%的线圈温升,而这需要成倍增加层间距。显然,线圈层间距对线圈温升的影响较小,平均温升与最高温升均随层间距增大呈先降后升趋势,改变层间距只能略微降低线圈温升。
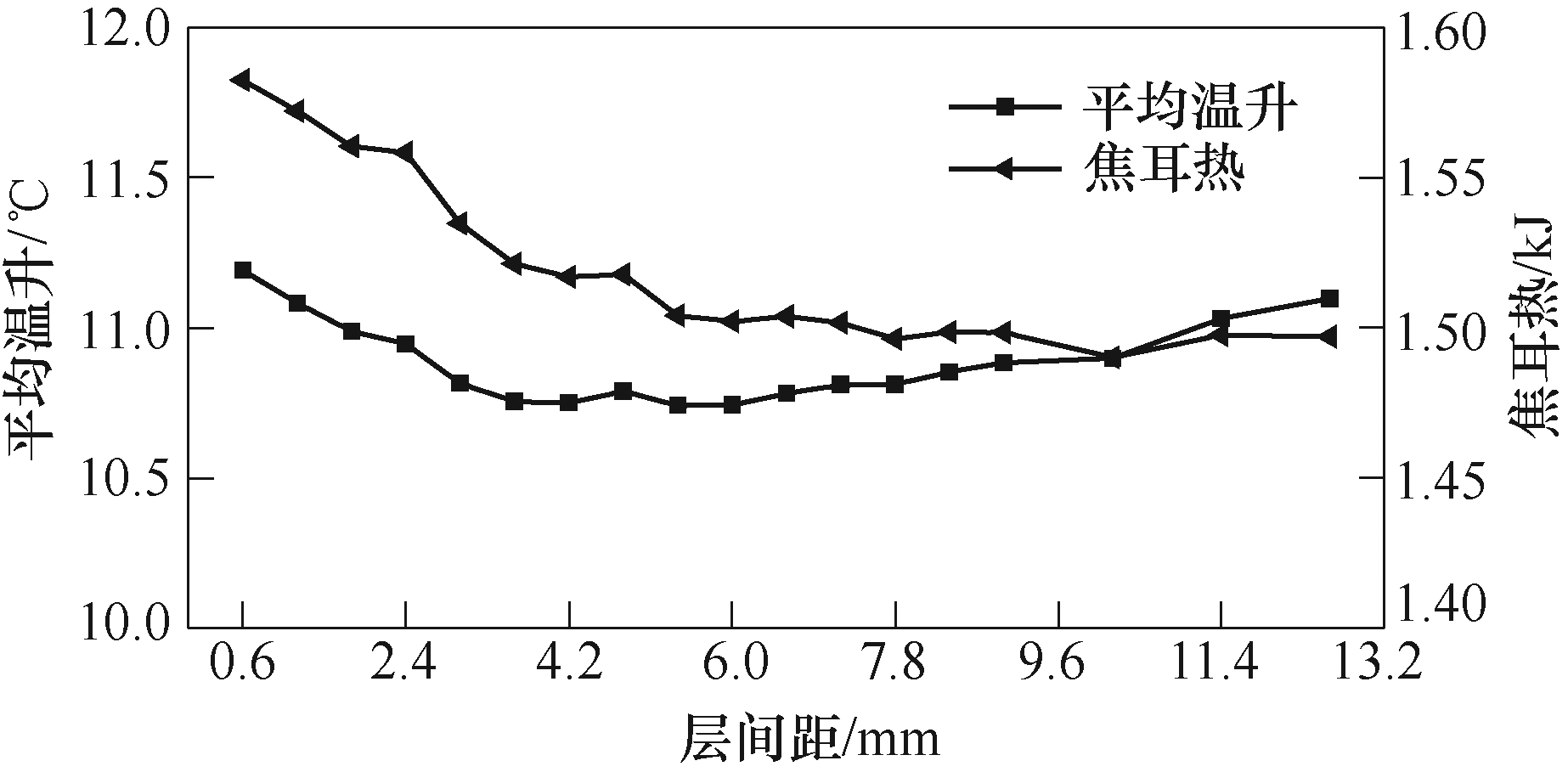
图17 不同层间距的线圈焦耳热与平均温升情况
Fig.17 Joule heat and average temperature rise of coils with different layer spacing
2.7 不同线圈结构的成形效果对比分析
由上述分析可知,线圈结构对线圈温升有影响,且不同结构参数对线圈温升的影响不同。然而,线圈结构不仅影响线圈温升还影响成形效果。本文为提供更有价值的线圈结构设计建议,将对比分析线圈各结构参数对管件变形效果的影响,以总结既能抑制线圈温升,延长线圈寿命,又能保持甚至提升成形效果的优化方案。
由于线圈匝数和高度相较于其他结构参数对管件变形效果影响较大,所以本文仅展示如图18所示的两个参数的管件变形情况。

图18 不同线圈高度或匝数时管件变形情况
Fig.18 Deformation of tube with different coil heights or turns
由图18可知,在不同结构参数下管件变形轮廓形状相似,都近似为半球形,故本文在管件变形轮廓相似的情况下选取管件中点处的最大位移量作为度量管件变形效果的指标,线圈各结构参数变化引起管件最大位移量变化曲线如图19所示。由于目前大多数EMF实验所用的线圈层间距、匝间距以及导线截面积均较小,故本文在线圈初始结构较小的情况下进行结果分析,以提供优化线圈结构设计的新思路。

图19 采用不同结构参数线圈的管件变形效果对比
Fig.19 Comparison of the effects of tube deformation with coils of different structural parameters
由图19可知,随线圈层数或匝数增多,管件最大位移量先增后减,而线圈平均温升与最高温升均降低,故可选取合适的线圈层数和匝数,实现较低的线圈温升与较好的成形效果。从图中还可看出,随线圈的导线宽度、高度、匝间距以及层间距增加,管件最大成形量持续减少。同时,不同结构参数对成形量降低幅度也是不同,据估算,大约每降低1℃平均温升,各线圈结构参数的管件最大位移量降低率由小到大依次为宽度、高度、匝间距、层间距,具体降低率见表3。
表3 各线圈结构参数的管件最大位移量平均降低率
Tab.3 The average reduction rate of the maximum displacement of the tube under different coil parameter

线圈结构参数 管件位移平均降低率(%) 宽度 0.99 高度 1.13 匝间距 14.03 层间距 16.83
通过以上分析可知,选取合适的层数与匝数可使工件成形效果较好且线圈温升较低。在一般情况下,改变线圈的导线高度、导线宽度、匝间距、层间距以抑制线圈温升将减小管件变形效果。在进行成形线圈结构设计时,建议优先调整线圈层数及匝数,其次优化线圈的导线高度、宽度,最后考虑线圈匝间距、层间距,同时需考虑线圈绕制工艺难度、材料耗费、机械强度等因素,设计合理的线圈组建方案,使线圈温升低且成形效果好,以高效、节能的方式实现EMF。
3 结论
本文围绕EMF过程中线圈发热的问题展开研究,提出了一种以优化线圈结构来抑制线圈温升的新思路。为验证优化线圈结构能有效抑制线圈温升,本文利用电磁场—机械结构场—温度场耦合模型,详细研究了线圈六种结构参数对线圈温升的影响。仿真结果如下:
1)增加线圈层数与匝数能通过增大其受热面积的方式减小线圈温升。
2)增大线圈宽度和高度也能增大其受热面积,抑制线圈温升,且一般能减少线圈焦耳热,提高能量转化率。
3)线圈匝间距和层间距对线圈温升的影响较小,温升抑制效果较差,线圈温升随匝间距、层间距增加呈先减后增趋势。
上述结果表明,优化线圈结构可有效抑制线圈温升,且不同结构参数对线圈温升及成形效果的影响不同。基于此,本文为管件成形线圈的结构优化设计提供了建议,为提高线圈使用寿命指明了方向。
[1] 邱立, 李彦涛, 苏攀, 等. 电磁成形中电磁技术问题研究进展[J]. 电工技术学报, 2019, 34(11): 2247- 2259.
Qiu Li, Li Yantao, Su Pan, et al. Research on electromagnetic problems in electromagnetic forming process[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2247-2259.
[2] Xiong Qi, Huang Hao, Xia Liangyu, et al. A research based on advance dual-coil electromagnetic forming method on flanging of small-size tubes[J]. The Inter- national Journal of Advanced Manufacturing Tech- nology, 2019, 102(9-12): 4087-4094.
[3] 周纹霆, 董守龙, 王晓雨, 等. 电磁脉冲焊接电缆接头的装置的研制及测试[J]. 电工技术学报, 2019, 34(11): 2424-2434.
Zhou Wenting, Dong Shoulong, Wang Xiaoyu, et al. Development and test of electromagnetic pulse welding cable joint device[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2424-2434.
[4] Xiong Qi, Yang Meng, Liu Xin, et al. A dual-coil method for electromagnetic attraction forming of sheet metals[J]. IEEE Access, 2020, 8: 92708-92717.
[5] Gies S, Lobbe C, Weddeling C, et al. Thermal loads of working coils in electromagnetic sheet metal forming[J]. Journal of Materials Processing Tech- nology, 2014, 214(11): 2553-2565.
[6] Mamutov A V, Golovashchenko S F, Mamutov V S, et al. Experimental-analytical method of analyzing performance of coils for electromagnetic forming and joining operations[J]. Journal of Materials Processing Technology, 2018, 255: 86-95.
[7] Xiong Qi, Huang Hao, Deng Changzheng, et al. A method to improve forming accuracy in electro- magnetic forming of sheet metal[J]. International Journal of Applied Electromagnetics and Mechanics, 2018, 57(3): 367-375.
[8] 邱立, 杨新森, 常鹏, 等. 双线圈轴向压缩式管件电磁胀形电磁力分布规律与管件成形性能研究[J]. 电工技术学报, 2019, 34(14): 2855-2862.
Qiu Li, Yang Xinsen, Chang Peng, et al. Electro- magnetic force distribution and forming performance in electromagnetic tube expansion process with two coils[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2855-2862.
[9] 邱立, 余一杰, 聂小鹏, 等. 管件电磁胀形过程中的材料变形性能问题与电磁力加载方案[J]. 电工技术学报, 2019, 34(2): 212-218.
Qiu Li, Yu Yijie, Nie Xiaopeng, et al. Study on material deformation performance and electro- magnetic force loading in electromagnetic tube expansion process[J]. Transactions of China Electro- technical Society, 2019, 34(2): 212-218.
[10] Xiong Qi, Tang Hongtao, Wang Muxue, et al. Design and implementation of tube bulging by an attractive electromagnetic force[J]. Journal of Materials Pro- cessing Technology, 2019, 273: 116240.
[11] Paese E, Geier M, Homrich R P, et al. Sheet metal electromagnetic forming using a flat spiral coil: experiments, modeling, and validation[J]. Journal of Materials Processing Technology, 2019, 263: 408- 422.
[12] 汪志强, 黄亮, 李建军, 等. 大型铝合金曲面零件电磁渐进成形线圈结构优化设计[J]. 塑性工程学报, 2015, 22(6): 71-77.
Wang Zhiqiang, Huang Liang, Li Jianjun, et al. Structural optimization design of coil on electro- magnetic incremental forming of large aluminum alloy curved surface parts[J]. Journal of Plasticity Engineering, 2015, 22(6): 71-77.
[13] Lai Zhipeng, Cao Quanliang, Han Xiaotao, et al. Analytical optimization on geometry of uniform pressure coil in electromagnetic forming and welding[J]. Springer London, 2019, 104(5-8): 3129-3137.
[14] 邱磊. 平板成形线圈连续放电过程热负荷分析[D]. 武汉: 华中科技大学, 2017.
[15] 刘良云. 平板电磁成形线圈温度特性及优化研究[D]. 武汉: 华中科技大学, 2017.
[16] Cao Quanliang, Han Xiaotao, Lai Zhipeng, et al. Analysis and reduction of coil temperature rise in electromagnetic forming[J]. Journal of Materials Processing Technology, 2015, 225: 185-194.
[17] Qiu Li, Wang Chenglin, Abu-Siada A, et al. Coil temperature rise and workpiece forming efficiency of electromagnetic forming based on half-wave current method[J]. IEEE Access, 2020, 8: 9371-9379.
[18] Qiu Li, Deng Kui, Li Yantao, et al. Analysis of coil temperature rise in electromagnetic forming with coupled cooling method[J]. International Journal of Applied Electromagnetics and Mechanics, 2020, 63(1): 45-58.
[19] Mamalis A G, Manolakos D E, Kladas A G, et al. Electromagnetic forming and powder processing: trends and developments[J]. Applied Mechanics Reviews, 2004, 57(4): 299-324.