0 引言
近年来,电力机车正朝着小型化、轻量化、低损耗和低噪声的方向发展。为了减小电力机车上各电气设备的体积和质量,逐渐考虑将中高频变压器技术引入到电力机车用变压器设计中去,通过提高频率的方法来减小变压器的整体质量及体积[1]。铁心材料作为中高频变压器的关键部件,其性能好坏决定了变压器的运行性能。目前为止,常用的中高频铁心材料有铁氧体、非晶合金、纳米晶体等。对于铁心材料的性能研究主要是对其进行磁性能研究。铁心材料的磁性能包括损耗特性和磁致伸缩特性。
铁心损耗特性是评价变压器运行效率好坏的重要依据。现有计算铁心损耗的方法大致可以概括为三种:①损耗分离法。比较有代表性的是Bertotti损耗三项式模型[2-4],铁心损耗被看作是磁滞损耗、涡流损耗和异常损耗三者之和。②磁滞模型法。如Preisach模型、Jiles-Atherton(J-A)模型[5]。③基于斯坦梅兹方程的经验公式[6]。斯坦梅兹经验公式由于结构相对简单,便于计算,准确度高,是目前较为常用的损耗计算公式。斯坦梅兹公式是基于正弦波激励推导拟合的损耗计算公式,若要将它应用于非正弦激励,则需对其进行相应的改进。近年来,国内外学者对斯坦梅兹经验公式进行了改进。考虑到铁心的损耗除了与磁通密度的幅值B有关以外,还与磁通密度的变化率(dB/dt)有关,提出了斯坦梅兹修正公式[7-8]。之后,国外学者认为损耗不但与磁通密度的变化率有关,还与磁化周期内磁通密度的瞬时值B(t)有关,从而提出了广义的斯坦梅兹公式[9]。考虑到磁化的过程除了与磁化周期的变化率有关,还与磁化的历史有关。不同磁化过程的反转点会使一个磁化周期内磁滞回线的形状有很大区别,又提出了广义斯坦梅兹改进公式[10]。中高频变压器在非正弦激励下铁心损耗的大小与其磁化过程中的诸多因素有关。各种修正公式重点考虑了非正弦激励下磁通密度的变化率(dB/dt)、磁感应强度瞬时值B(t)和磁化历史ΔB这三种影响因素中的一到两个因素对铁心损耗所带来的影响[11],通过引入等效频率的方法修正模型精度,虽然相比于传统的斯坦梅兹公式,修正模型计算精度得到了改善,但是在不同的方波激励频率下等效频率引入的有效性问题仍有待进一步研究。
另一方面,铁心的磁致伸缩特性是指在外加磁场的作用下,铁心的体积和尺寸随着磁场强度的变 化而变化的现象。尽管单位长度的铁心材料的磁致伸缩效应仅有几微米大小,远远小于铁心材料的尺寸,但是研究表明,磁致伸缩效应会加剧铁心在某些频率的振动,而且铁心材料的磁致伸缩特性引起变压器的振动噪声占整个变压器振动噪声的50%左右[12-13]。这就意味着,磁致伸缩是产生变压器振动噪声的主要因素。因此,在进行中频变压器的设计时,需要对铁心磁致伸缩引起的振动进行认真的分析和研究。首先需要准确把握铁心材料的磁致伸缩特性。目前,对于铁心材料的磁致伸缩特性研究主要集中在工频状态下电工钢片的磁致伸缩特性研究。
本文对中频变压器铁心材料非晶合金的磁特性进行研究。首先模拟中频变压器实际工况,对方波激励下非晶合金的损耗特性进行测量,并对斯坦梅兹损耗预估模型进行优化改进,使其满足在中频非正弦激励条件下铁心损耗的计算。然后利用实验室现有的磁致伸缩激光测试仪,对非晶合金磁致伸缩特性进行测量,采用非线性压磁方程建立非晶合金磁致伸缩预估模型,并进行模型验证。非晶合金磁特性测量与模型的建立为中频变压器进一步优化设计打下基础。
1 非晶合金铁心磁特性测量
铁心材料的磁性能测量主要是针对铁心材料的损耗特性和磁致伸缩特性。实际工况下铁心材料磁性能的准确测试,是研究铁心材料磁性能的前提和基础。
1.1 非晶合金铁心材料损耗特性测量及分析
对于铁心材料的电磁特性通常是按照国际标准,在正弦交变磁化条件下测量获取的。但是由于中频变压器通常工作在方波、PWM波等非正弦波激励的电力电子电路中,为了检测铁心材料在不同频率的方波激励下磁滞特性和损耗特性,本文将利用实验室从德国购置的MPG200型磁性能测试系统,实现损耗特性测试,通过测量的数据进行方波激励下非晶合金的磁特性分析及研究。
图1给出了中频铁心磁特性测量装置与测试试样实物。被测非晶合金试样被绕制成环形,在测量前装入非铁磁性绝缘材料保护盒中,防止试样在绕线和测试过程中受力。试样上同时缠绕一次绕组和二次绕组,一次绕组的励磁电压源来自功率放大器,励磁电压的波形由上位机输出;二次绕组可测得感应电压波形,再由电磁感应定律计算出铁心试样的磁通密度波形。测试过程为闭环控制,通过调节一次绕组的激励电压实现控制输入磁通密度的波形为期望的波形形式。

图1 中频铁心磁特性测量装置与测试试样实物
Fig.1 Magnetic characteristics measuring device of medium frequency core and physical drawing of test sample
非晶合金的电磁特性如图2所示。通过对铁心样品进行测量获取的数据可以绘制出非晶铁心在频率为4kHz方波激励下的磁滞回环曲线及在方波和正弦波激励下的损耗特性曲线,如图2a所示。从图2a可以看出,随着磁通密度的增加,非晶合金铁心的剩磁和矫顽力明显增大,损耗也逐渐增大。

图2 非晶合金的电磁特性
Fig.2 Electromagnetic properties of amorphous alloys
图2b、图2c分别给出了在正弦波激励和方波激励下非晶合金铁心损耗测量结果。测量结果表明,当激励频率相同时,方波激励下的损耗略大于正弦波激励下的损耗。而对于同一种激励工况,在0.1~0.4T范围内,铁心损耗随频率增加变化不太大,但0.4T之后损耗迅速上升。在同一磁通密度下,铁心材料频率越高损耗越大。
1.2 非晶合金铁心磁致伸缩特性测量及分析
为了研究非晶合金铁心的振动噪声问题,首先需要研究铁心的磁致伸缩特性。因此,本文测量了非晶合金单片在不同频率下的磁致伸缩特性,得到非晶合金铁心的磁致伸缩特性数据。本试验采用德国磁测仪公司生产的非晶合金磁致伸缩测试仪[14]。搭建的测试系统由系统主机、测量装置、激光发射接收器三部分组成。其中,为了防止外界振动对测量结果的影响,将激光发射接收器和检测装置放置于气浮动平台上。磁路装置由两组线圈组成,一组线圈通过加载的电源信号给待测样品励磁;另一组线圈为感应线圈,检测磁路中的励磁信号。将长度为500mm、宽度为60mm待测样片水平放置在线圈绕组内部空腔中,空腔内磁场沿样片的长度方向分布。样片一端固定,另一端可以自由伸缩。激光发射接收装置用于测量样片的微小伸缩量。其中,激光器的取样频率范围最大1kHz,可检测范围500Hz,分辨率为0.3nm/m。其工作原理为通过激光测试系统来测量非晶合金单片的延展率,也就是由磁致伸缩引起的形变量。测量样片的磁致伸缩随着外施磁场的变化而变化。试验过程中用空气压缩机托起试验平台,当外部因素干扰时,该平台可以自动调平,不受环境振动的影响,保证测试数据的准确性。非晶合金磁致伸缩特性测试设备如图3所示,图3a为磁致伸缩测试仪,图3b为主机控制系统。

图3 非晶合金磁致伸缩特性测试设备
Fig.3 Equipment for testing magnetostrictive properties of amorphous alloys
基于上述测试系统,测试不同频率的正弦交变磁化下,非晶铁心的磁致伸缩特性数据。测试样品选用北京安泰科技有限公司生产的非晶合金铁心材料。图4和图5分别给出了励磁频率为50Hz与100Hz时磁致伸缩应变随着时间变化波形曲线及蝴蝶曲线。可以看出,磁致伸缩的变化周期为磁通密度变化周期的2倍,即磁致伸缩的变化频率为100Hz、200Hz。在同一频率下,随着磁通密度的增大,磁致伸缩的峰峰值λpp不断增大。其中,磁致伸缩峰峰值λpp描述了磁致伸缩回环的最大变化量,可定义为磁致伸缩回环最大值与最小值的差值,计算为
式中,maxλ和minλ分别为磁致伸缩回环的最大值和最小值。同时,两种频率下磁致伸缩回线的翅膀宽窄是不同的,由于磁畴的转动引起的磁致伸缩的变化量也不同,当磁化频率由50Hz变化到100Hz时,铁心内部磁畴的磁化时间变短,磁畴的变化周期变短,从而导致磁致伸缩值减小。

图4 磁致伸缩应变在一个时间周期内的波形
Fig.4 Magnetostrictive strain waveforms over a time period

图5 不同磁通密度下非晶合金的磁致伸缩回环
Fig.5 Magnetostriction loops under different magneticflux density values
2 非晶合金铁心材料损耗模型改进与验证
2.1 传统损耗计算模型
对于铁心损耗计算,斯坦梅兹修正公式认为,铁心的损耗除了与铁心磁化过程中磁感应强度的幅值有关,还与磁通密度的变化率有关,因此给出了损耗计算公式[7, 9]为
式中,B为磁通密度幅值;feq为等效频率;f为励磁频率;K、α 和β 为待定系数。采用式(2)对方波激励下非晶合金铁心损耗估算之前,首先要对feq、K、α 和β 进行求解计算。
首先,在一个周期内,磁通密度变化率的平均值可以被定义为
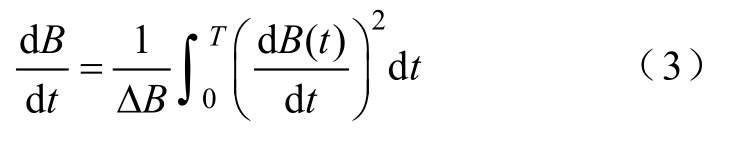
式中,ΔB为一个磁化周期内磁通密度的峰峰值;T为磁化周期。式(3)可以被归一化处理为一个正弦激励的情况,通过磁通密度的变化率,引入一个等效频率feq,表示为
因此,方波激励下的非晶合金损耗计算公式可写为

文献[8]建议式(5)的系数K=12,α =1.31,β =2.55。
采用式(5)对方波激励下非晶合金铁心损耗的估算主要是通过引入一个等效频率的概念,将加载的方波激励的磁化频率通过近似等效的方法转换成一个近似的正弦磁化频率,从而计算近似等效的正弦波信号作用在铁心上产生的损耗[15]。通过利用式(5)的计算值与测量值进行比较,比较结果如图6所示。可以看出,式(5)给出的损耗计算模型损耗预估误差较大,并且不同频率下损耗的误差值也不尽相同。究其原因主要是在不同的激励频率下,铁心材料的电磁特性不尽相同,用一组固定的系数来预估不同频率下的铁心损耗,必然会导致误差较大,通用性不强。
2.2 损耗模型改进

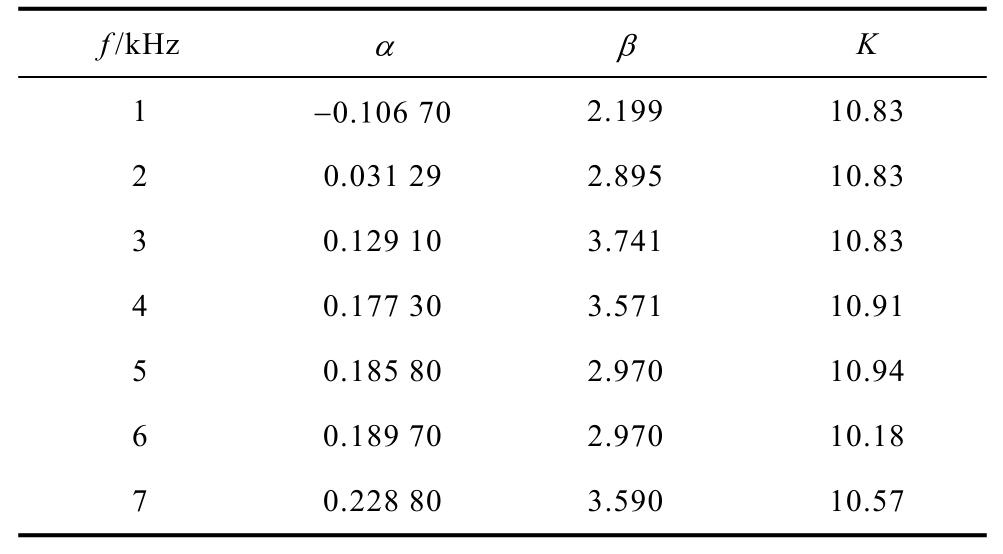
为了提高损耗计算公式在不同特征频率下的通用性,本文对模型参数K、α 和β 在不同特征频率 下的非线性特性进行研究。利用式(5)对测试结果进行数据拟合,获取在不同频率下的损耗计算公式系数,见表1。
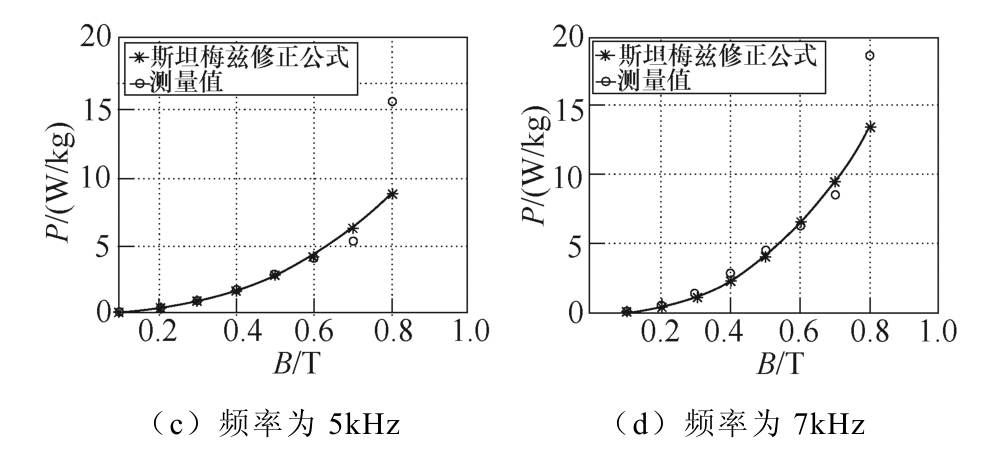
图6 方波激励下非晶合金损耗对比
Fig.6 Comparison of losses of amorphous alloys under square wave excitation
表1 不同频率下拟合的系数
Tab.1 Fitting coefficients under different frequencies
f /kHz α β K 1 −0.106 70 2.199 10.83 2 0.031 29 2.895 10.83 3 0.129 10 3.741 10.83 4 0.177 30 3.571 10.91 5 0.185 80 2.970 10.94 6 0.189 70 2.970 10.18 7 0.228 80 3.590 10.57
从表1可以看出,随着频率的增加,系数α 也相应地增大。但是系数β 和K随频率的变化较小。因此,接下来主要对系数α 随着频率的变化进行详细讨论。系数α 和频率的关系定义为
式中,A、C、b为待定系数。通过表1的数据,系数α 的函数可以得出
将式(6)代入式(4),本文给出的进一步改进的损耗计算公式为

通过测量的数据进行拟合,可以得出式(8)中系数K=10.656,β =3.146。
2.3 测试结果比较
为了验证式(8)损耗计算公式的准确性,通过建立的损耗测量系统对非晶合金环形铁心在方波激励下的损耗数据进行测量,对测量的损耗数据和预测的结果进行比较,结果如图7所示。

图7 方波激励下非晶合金损耗对比
Fig.7 Loss comparison for amorphousalloy core with square wave excitation
从图7可以看出,在不同的频率下,预测的损耗计算公式准确性更优于传统的损耗计算公式,当磁通密度为0.6T时,最大损耗预测误差由30%降低到7.5%。可见,本文建议的损耗模型考虑了励磁频率对损耗的影响,并进行准确的分析计算。
3 非晶合金铁心材料磁致伸缩模型建立及验证
3.1 磁致伸缩数据测量及分析
根据图5绘制的蝴蝶曲线,本文提取了50Hz正弦激励下的磁致伸缩单值曲线,如图8所示。从图8可以看出,随着外加磁场的增强,磁致伸缩峰峰值λpp逐渐增大。当外加磁场的磁通密度从0.5T逐渐增大到1.4T时,磁致伸缩的峰峰值λpp呈近似的线性增长,但当磁通密度达到1.4T以后,铁心材料在外磁场的作用下,磁性能趋于饱和,磁致伸缩也开始出现拐点,逐渐进入饱和区域,即磁致伸缩峰峰值λpp呈非线性的趋势。从微观角度进一步分析可知,在外加磁场的作用下,构成非晶合金铁心材料的磁畴逐渐沿外场方向平行排列,整个磁化过程均伴随着磁畴尺寸的变化。当所有磁畴形成一个单畴样品时就达到了磁化强度的饱和,磁畴的应变也趋于饱和。此时,由磁畴引起的磁致伸缩的形变也达到饱和状态,如果磁场进一步增加,磁化强度增加缓慢,而应变也仅有非常缓慢的增加。

图8 50Hz正弦激励下磁致伸缩的单值曲线
Fig.8 The single value curve of magnetostriction under 50Hz sinusoidal excitation
根据图8绘制的磁致伸缩的单值曲线,表2进一步给出了非晶合金铁心磁通密度B与磁致伸缩伸缩峰峰值λpp的对应关系。
表2 不同磁通密度下磁致伸缩峰峰值
Tab.2 Peak to peak value of magnetostriction under the differentmagnetic densitites

B/T λpp/(μm/m) 0.8 6.3 0.9 8.2 1.0 9.7 1.1 11.8 1.2 14.1 1.3 16.1 1.4 18.4 1.5 19.7
3.2 非晶合金铁心材料的磁致伸缩模型建立
磁致伸缩数学模型通常用线性压磁方程来描述,线性压磁方程包括两个公式[16]:①应变的方程。描述铁心材料在外加应力和磁场的作用下分别产生的应变之和。②磁感应强度的方程。描述外加应力和外加磁场分别引起的磁感应强度之和。对于非晶铁心,只考虑材料在单一轴向的伸缩时,线性压磁方程表示为

式中,ε 为应变;![]() 为磁场强度在某一常数时的杨氏模量;H为磁场强度;σ 为外加应力;d为压磁 系数;μσ 为应力在某一常数时的磁导率。
为磁场强度在某一常数时的杨氏模量;H为磁场强度;σ 为外加应力;d为压磁 系数;μσ 为应力在某一常数时的磁导率。
当只考虑磁场作用下的磁致伸缩效应,而不考虑外加应力对磁致伸缩的影响时,式(9)和式(10)可简化为

将式(11)和式(12)合并,并用λ 表示磁致伸缩应变,有
式中,k为磁致伸缩系数。
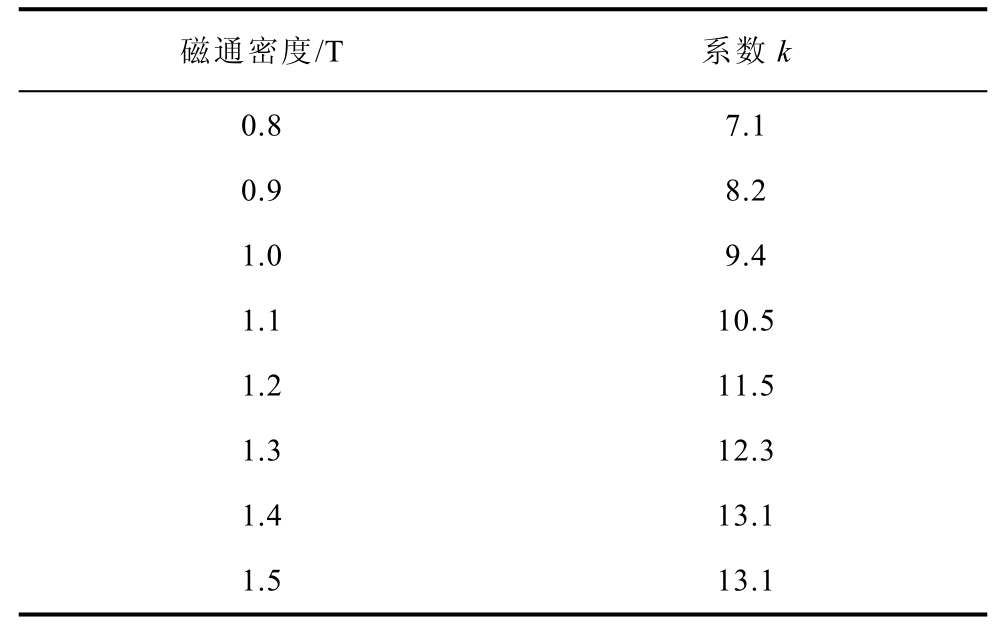
通常,通过式(13)对铁心材料进行磁致伸缩计算时,总是粗略地认为系数k为一个线性常数。但是通过图8的磁致伸缩曲线可以看出,非晶合金铁心的磁致伸缩曲线在整个磁化过程中并不是完全呈线性关系,随着铁心在外磁场的作用下逐渐达到饱和,铁心的磁致伸缩峰峰值λpp逐渐呈非线性关系。因此,简单地认为系数k为线性是不准确的。分别在工频正弦波激励下的系数进行计算可以得到在不同磁通密度时系数k的取值,见表3。通过表3可以看出,磁致伸缩系数k与外加磁场的关系是非线性的,为使磁致伸缩计算模型拟合更加精确,给出系数k随着磁通密度B变化的多项式为
表3 磁致伸缩系数k随磁通密度的变化
Tab.3 The variation of the magnetostriction coefficient k with the magnetic density
磁通密度/T 系数k 0.8 7.1 0.9 8.2 1.0 9.4 1.1 10.5 1.2 11.5 1.3 12.3 1.4 13.1 1.5 13.1
其中,系数ki见表4。
表4 系数ki
Tab.4 The value of coefficient ki

i ki 3 −6.012 2 14.19 1 −0.274 8 0 2
将式(14)代入到式(13)可得
3.3 测量结果比较
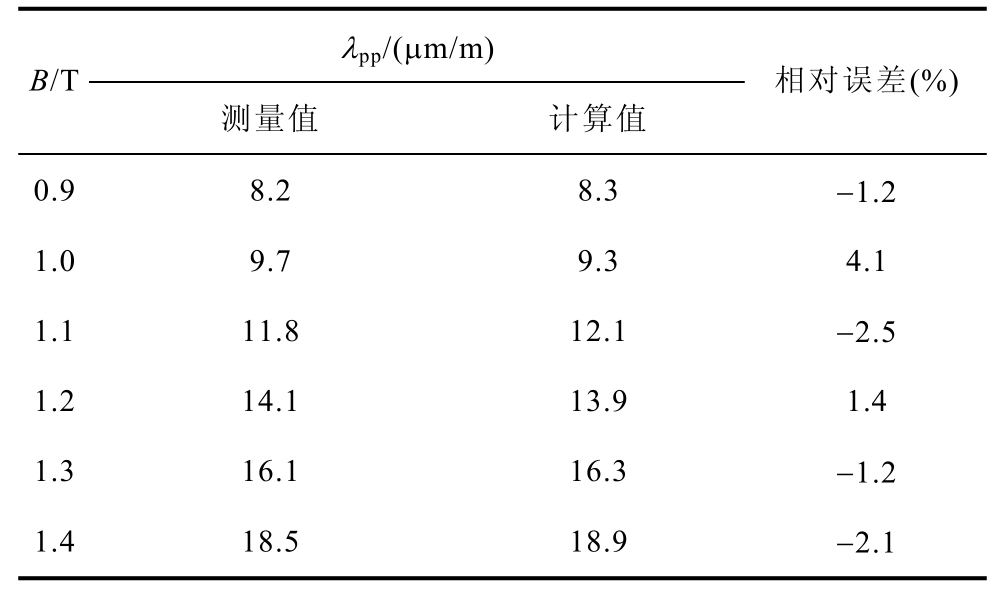
为了验证磁致伸缩计算公式的准确性,对非晶合金铁心加载正弦激励下的磁致伸缩应变进行测量,通过测量数据与改进的磁致伸缩计算公式计算值进行比较,结果见表5。可以看出,计算值与测量值吻合度较高,表明非线性磁致伸缩计算式(15)更符合材料本身的磁致伸缩特性。
表5 不同磁通密度下磁致伸缩的计算值与测量值
Tab.5 Calculated and measured values of magnetostriction under different magnetic densities
λpp/(μm/m) B/T 测量值 计算值 相对误差(%)0.9 8.2 8.3 −1.2 1.0 9.7 9.3 4.1 1.1 11.8 12.1 −2.5 1.2 14.1 13.9 1.4 1.3 16.1 16.3 −1.2 1.4 18.5 18.9 −2.1
4 结论
本文借助先进的磁性材料特性测量系统,测试并分析了非晶合金铁心材料在方波和正弦波激励条件下的损耗特性。兼顾计算精度和工程实用性,修正了传统斯坦梅兹损耗计算模型并进行了实验验证。上述研究结果为开展降低中频变压器铁心损耗、提高铁心结构优化效率等工作打下了基础。同时,对于非晶合金的磁致伸缩特性的研究,利用激光测试系统,完成了非晶合金的磁致伸缩测量,根据测量数据,对线性压磁方程系数k的非线性进行讨论,给出系数k的非线性公式,提高了线性压磁方程对于磁致伸缩计算的准确度,为后续中高频变压器振动噪声研究提供了理论依据。
[1] 周柯, 葛钦, 葛平娟, 等. 不平衡负荷下输出并联型电力电子变压器的优化控制策略[J]. 电工技术学报, 2018, 33(增刊1): 149-156.
Zhou Ke, Ge Qin, Ge Pingjuan, et al. The research on the control strategy of PET under unbalanced load[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 149-156.
[2] 迟青光, 张艳丽, 任亚军, 等. 铁心旋转损耗模型改进与局部损耗测试[J]. 电工技术学报, 2018, 33(17): 3951-3957.
Chi Qingguang, Zhang Yanli, Ren Yajun, et al. Improvement on rotational loss model and mea- surement of local loss in the iron core[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(17): 3951-3957.
[3] 谭博, 张海涛, 华志广, 等. 一种减小无刷直流电机转子涡流损耗以及铜耗的驱动方法[J]. 电工技术学报, 2018, 33(18): 4239-4248.
Tan Bo, Zhang Haitao, Hua Zhiguang, et al. A drive method of brushless DC motor to decrease rotor eddy current loss and copper loss[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4239-4248.
[4] 刘刚, 孙立鹏, 王雪刚, 等. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报, 2018, 33(21): 13-22.
Liu Gang, Sun Lipeng, Wang Xuegang, et al. Improvement of core loss calculation method and simulation application under sinusoidal and harmonic excitations[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 13-22.
[5] Du Ruoyang, Robertson P. Dynamic Jiles-Atherton model for determining the magnetic power loss at high frequency in permanent magnet machines[J]. IEEE Transactions on Magnetics, 2015, 51(6): 1-10.
[6] Muhlethaler J, Biela J, Kolar J W, et al. Core losses under the DC bias condition based on steinmetz parameters[J]. IEEE Transactions on Power Elec- tronics, 2012, 27(2): 953-963.
[7] Barg S, Ammous K, Mejbri H, et al. An improved empirical formulation for magnetic core losses estimation under non-sinusoidal induction[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2146-2154.
[8] Leite J, Silva P, Sadowski N, et al. Vector hysteresis under nonsinusoidal induction waveforms: modeling and experimentation[J]. IEEE Transactions on Mag- netics, 2008, 44(6): 906-909.
[9] Lancarotte M, Penteado A. Estimation of core losses under sinusoidal or nonsinusoidal induction by analysis of magnetization rate[J]. IEEE Power Engineering Review, 2001, 21(6): 69.
[10] Yan Zhou, Sun Aiming. Simplified ferrite core loss separation model for switched mode power con- verter[J]. IET Power Electronics, 2016, 9(3): 529- 535.
[11] 律方成, 郭云翔. 非正弦激励下中频变压器铁损计算方法对比分析[J]. 高电压技术, 2017, 43(3): 808- 813.
Lü Fangcheng, Guo Yunxiang. Comparative analysis of core loss calculation methods for medium frequ- ency transformer under non-sinusoidal excitation[J]. High Voltage Engineering, 2017, 43(3): 808-813.
[12] Mohammed O, Calvert T, Mcconnell R. Coupled magnetoelastic finite element formulation including anisotropic reluctivity tensor and magnetostriction effects for machinery applications[J]. IEEE Transac- tions on Magnetics, 2001, 37(5): 3388-3392.
[13] Belahcen A. Vibrations of rotating electrical machines due to magnetomechanical coupling and magnetostriction[J]. IEEE Transactions on Magnetics, 2006, 42(4): 971-974.
[14] 张艳丽, 王佳音, 白保东, 等. 直流偏磁磁场对硅钢片磁致伸缩特性的影响分析[J]. 中国电机工程学报, 2017, 36(15): 4299-4306.
Zhang Yanli, Wang Jiayin, Bai Baodong, et al. Influence analysis of DC biased magnetic field on magnetostrictive characteristics of silicon steel sheet[J]. Proceedings of the CSEE, 2017, 36(15): 4299-4306.
[15] 张宁, 李琳, 魏晓光. 非正弦激励下磁心损耗的计算方法及实验验证[J]. 电工技术学报, 2016, 31(17): 224-232.
Zhang Ning, Li Lin, Wei Xiaoguang. Calculation method and experimental verification of core losses under non-sinusoidal excitation[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 224- 232.
[16] 吴胜男, 唐任远, 韩雪岩, 等. 磁致伸缩引起的非晶合金铁心振动解析计算及影响因素[J]. 电工技术学报, 2016, 31(20): 73-82.
Wu Shengnan, Tang Renyuan, Han Xueyan, et al. Analytical calculation and influence factors of vibration in amorphous metal cores[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 73-82.