0 引言
稀土超磁致伸缩材料自发现以来,以其伸缩系数大、机电耦合系数高、能量密度高、响应速度快、可靠性高等优良特性[1-3]在航天航空、国防军工、机械电子、水声通信等众多领域得到广泛应用[4]。
目前,国内外在稀土超磁致伸缩材料特征参数与性能测试方面方法不尽相同,且国内正处于对磁特性测试仪器的自主研究和设计阶段[5]。以往研究发现,预应力对稀土超磁致伸缩棒材性能存在较大影响[6-8],这是由于外界应力引起棒材磁畴状态发生变化[9],从而对棒材的磁致伸缩系数、杨氏模量、磁导率等性能产生影响,预应力也是磁致伸缩换能器的重要初始偏置条件之一,但国内外文献[7, 10-12]中设计制造的平台均未考虑测试过程中由于棒材伸长导致的预应力大范围变化,且铽镝铁(TbDyFe)合金稀土超磁致伸缩材料与传统磁致伸缩材料相比,其应变是Ni的40~50倍,是Fe-Ga系材料的5倍左右,因此其预应力变化更明显,导致测试结果出现大偏差[13-14]。
综上,本文设计搭建了一套稀土超磁致伸缩棒材特性测试平台,平台包括驱动模块、测量装置、信号采集模块及保压装置四部分,可对棒材进行静态和准静态性能及参数测试,可在不同的驱动条件和负荷条件下对棒材的磁致伸缩性能、B-H曲线、杨氏模量等进行测试。
本文对平台进行以下优化:重点对平台保压装置进行设计优化与改进,采用铜块和碟簧复合组合的方式置于极头与液压机压头中部,达到良好的保压缓冲效果;对B-H曲线测试装置及方法进行优化,开发一套Labview信号采集与处理程序,搭配数据采集卡可实现B-H曲线的自动绘制,代替磁通计实现感应电压的采集和处理以得到磁感应强度,其响应速度快,数据采集处理更为自动化。
1 平台搭建与优化
稀土超磁致伸缩棒材特性测试平台主要由驱动模块、测试装置、信号采集模块以及保压装置四部分组成,其测试平台如图1所示。

图1 稀土超磁致伸缩棒材特性测试平台
Fig.1 Test platform of rare-earth gaint magnetostrictive rod characteristics
1—励磁线圈 2—霍尔探头 3—极头
4—稀土超磁致伸缩棒材 5—硅钢磁轭 6—压力传感器 7—液压油压机 8—程控直流电源 9—高斯计 10—上位机 11—电阻应变仪 12—保压装置
1.1 驱动模块
驱动模块包括程控直流电源和双励磁绕组,通过编程以实现电源直流0~20A的自动化输出,电流通过励磁绕组产生磁场。实验证明,测试棒材磁致伸缩性能和磁导率时,随着电流的增大,棒材内磁场先迅速增大,再缓慢增大,最后逐渐趋向于饱和,电流-磁场强度关系如图2所示。因此驱动电流输出步长也应逐渐增大,这样可更好地采集有效磁 场强度数据点,准确测试磁场强度和其他变量的对应关系,同时缩短大电流输出时间,减少线圈发热。
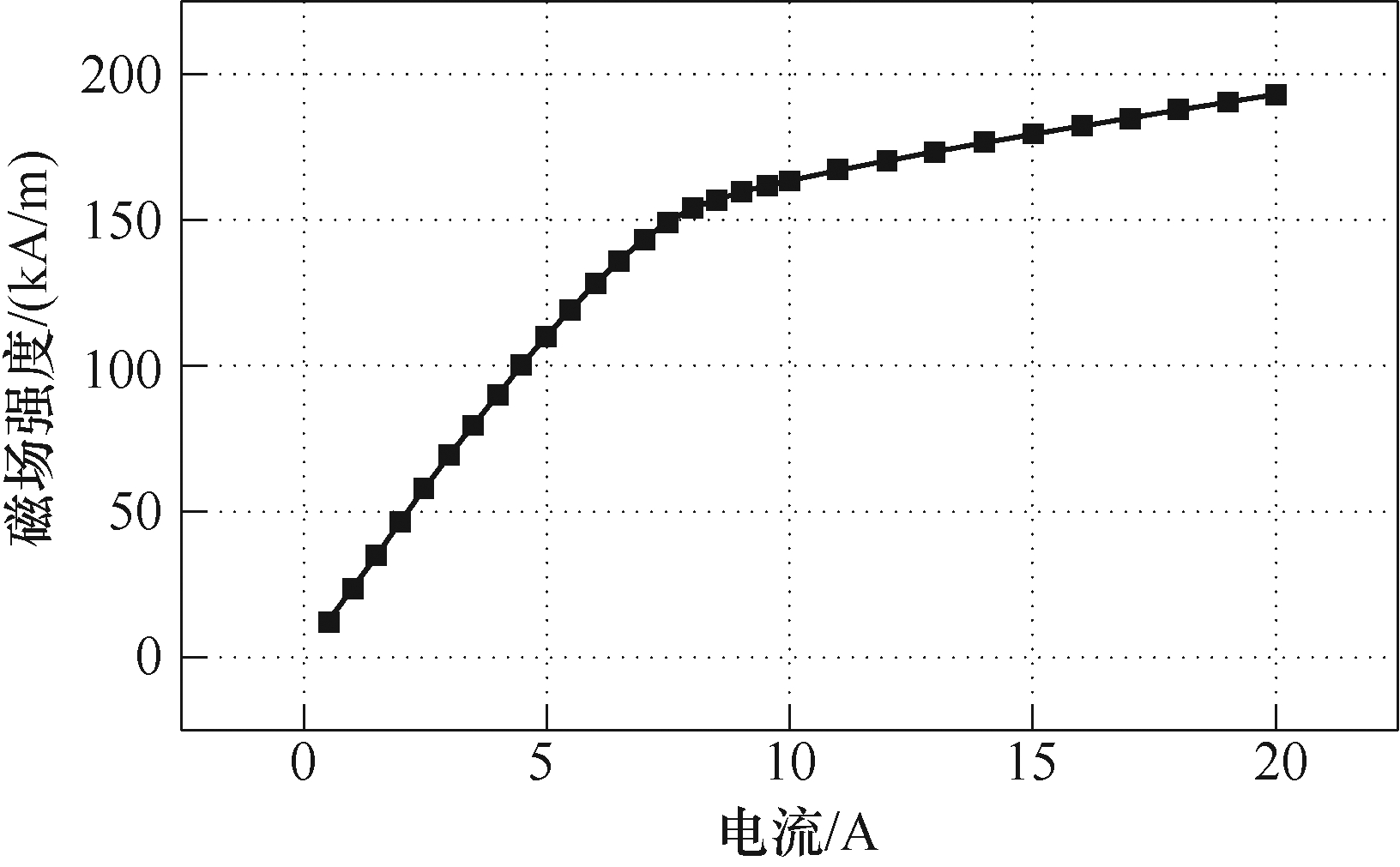
图2 电流-磁场强度关系
Fig.2 Current-magnetic field strength
1.2 测试装置
测试装置包括环形硅钢磁轭、上下极头、液压油压机、压力传感器及稀土超磁致伸缩棒材。测试装置与驱动模块组成平台核心部分——预应力可调节的双励磁绕组换能器,实现电−磁−机能量转换和参数测量。环形磁轭由0.6mm硅钢片叠成,磁场通过磁轭由两个励磁线圈汇集到中间的稀土超磁致伸缩棒材内,可增大棒材内的磁场[15-16],测试平台磁力线分布如图3所示。

图3 测试平台磁力线分布
Fig.3 Magnetic field line of test platform
上、下极头采用磁导率高且刚度大的电工纯铁,极头为圆柱形并开槽,槽的直径稍大于棒材,槽深2mm,以固定棒材。
测试对象采用未切割的稀土超磁致伸缩棒材,由于本文测试均为静态性能测试,棒材无需考虑涡流的影响,且未切割棒材可保证其力学性能的均匀一致,同时在棒材顶部和底部包裹一层特氟龙胶带[17],以实现隔振,保护边缘,防止棒材损坏的效果。
液压油压机通过压头向棒材施压,压力传感器置于压头和上极头间,可准确显示棒材所受压力。上述结构有两个优点:一是可一定程度上加强棒材内的磁场;二是便于磁场强度测试。
对比传统线圈包裹棒材的换能器测试平台形式[18-19],由于其结构存在限制,霍尔探头无法放置,棒材内磁场强度都是利用一般形式的安培环路定律简化公式计算,即
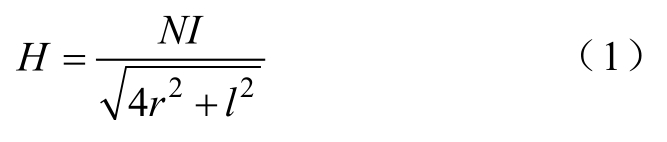
式中,H为棒材内磁场强度;N为线圈匝数;I为线圈内驱动电流;r为线圈半径;l为线圈长度。此方法未考虑损耗、漏磁及磁路等因素,与实际情况存在较大误差。本文设计平台的棒材周围为开放空间,利于放置霍尔探头,可实时测试棒材表面的磁场 强度。
1.3 信号采集模块
信号采集模块包括高斯计、横向霍尔探头、探头支架、感应线圈、数据采集卡、电阻应变仪和上位机。模块可实时采集棒材内的磁场强度H、磁感应强度B、棒材应变λ 和预应力σ,后期对采集数据进行处理可得棒材同一位置处λ-H、B-H及-σλ曲线,进而可分析棒材磁致伸缩性能、恒定应力下的 磁导率![]() 及恒定磁场下的杨氏模量
及恒定磁场下的杨氏模量![]() ,参数定义为
,参数定义为
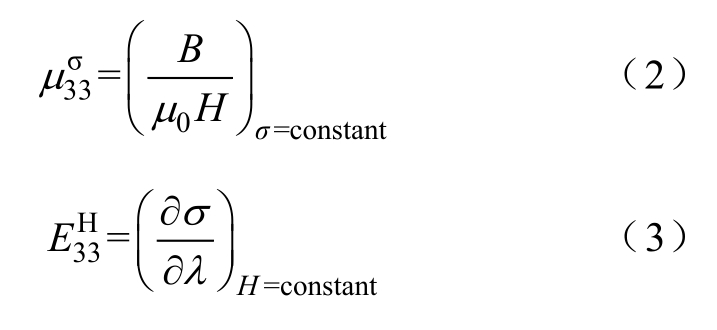
式中,μ0为真空磁导率;constant为常数。
1.3.1 磁场强度的测量
利用横向霍尔探头测试棒材表面切线方向空气域磁场强度[7, 11],设置其采样频率为2kHz,可实时反映棒材内磁场情况,理论推导如下:棒材与空气分界面应用安培环路定律如图4所示,在稀土超磁致伸缩棒材与空气的媒质分界面上,围绕一点P取一矩形回路,矩形回路高为1lΔ,并取宽度2 0lΔ→,根据安培环路定律,在磁场中,磁场强度H沿任一闭合路径的线积分等于穿过该回路所包围面积的自由电流(不包括磁化电流)的代数和[20],即
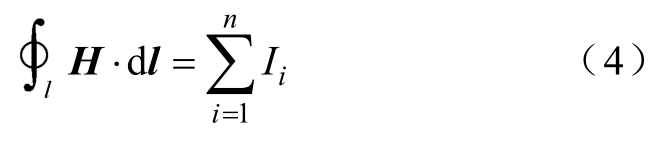
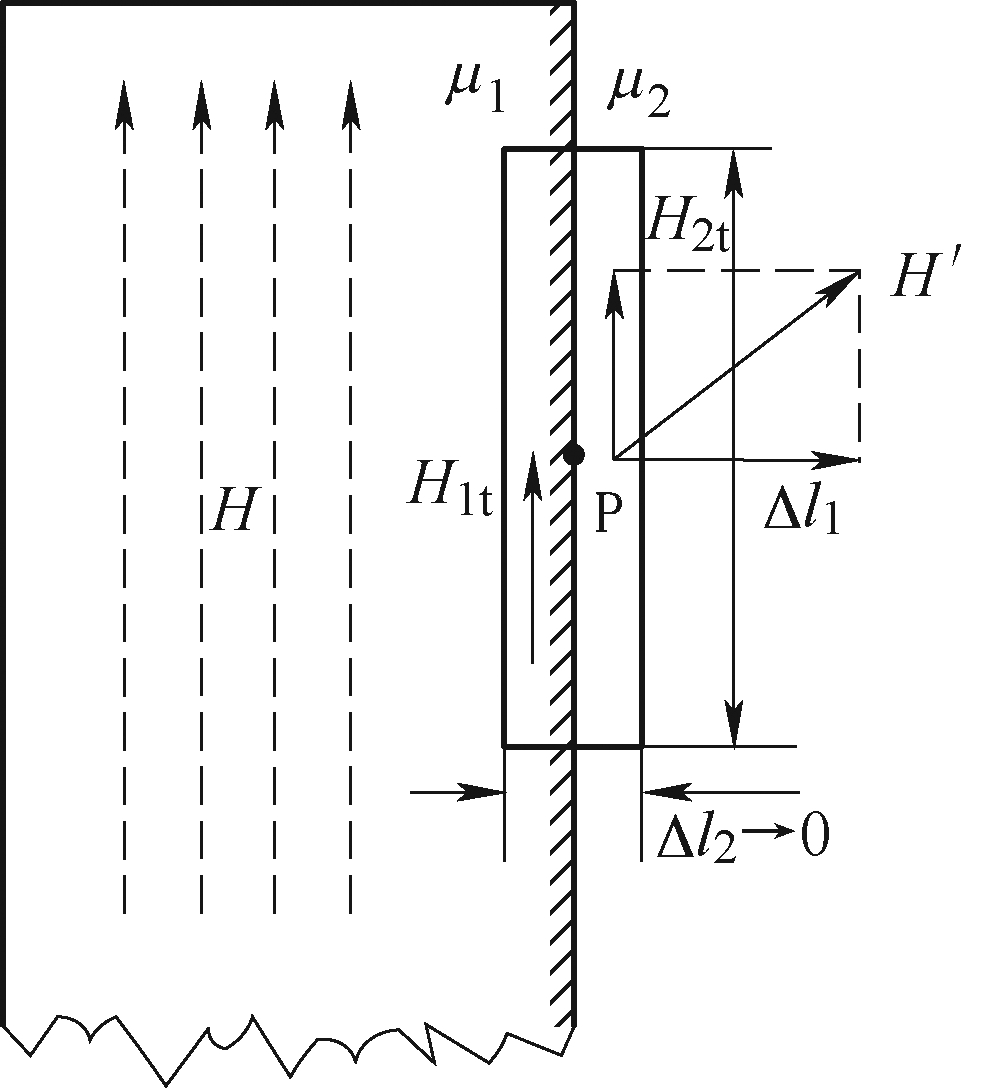
图4 棒材与空气分界面应用安培环路定律
Fig.4 Application of ampere circuital theorem to the interface between the rod and air
棒材表面不存在自由电流,又因棒材内磁场沿轴向分布,则
式中,H1t为棒材内磁场;H2t为贴近棒材表面空气域磁场,两者近似相等,为使测试结果更精确,霍尔探头探针体积要尽可能小,同时要贴紧棒材。
1.3.2 磁感应强度的测量
法拉第电磁感应定律指出:闭合回路中的感应电动势ε与穿过磁回路的磁通随时间的变化率dφm/dt成正比,数学形式为
因此,在横截面积为S的圆柱形稀土超磁致伸缩棒材表面紧密缠绕N匝感应线圈,棒材上电阻应变片和感应线圈如图5所示。当棒材内磁场产生变化时,线圈两个出线端感应出电动势,通过数据采集卡采集感应电动势信号,设置其采样频率为2kHz,在Labview中进行滤波和数学积分操作,可反推出棒材内磁感应强度[3, 7, 15, 21]大小为

图5 棒材上电阻应变片和感应线圈
Fig.5 Strain gauge and induction coil
1.3.3 应变的测量
利用电阻应变仪测量棒材应变,电阻应变片紧密贴合在棒材表面如图5所示。应变片随棒材一同伸缩,其电阻发生变化,通过应变仪半桥一对一补偿电路,反映为应变量大小,设置其采样频率为32kHz,数值可在上位机软件读取。应变片贴合时严格遵循使用规范以保证应变测试的准确性,贴合前应将棒材表面打磨光滑并用酒精擦拭干净以保证牢固。
实验前应在棒材测试位置处正反贴两片应变片,并进行快速验证实验。在一定预应力下,对棒材外加驱动磁场,若两片应变片应变数值误差在10%内,则证明棒材均匀受力,未出现弯曲情况,实验可正常进行[7, 15, 22]。
1.3.4 应力的测量
采用1 000kg量程压力传感器测试棒材所受应力大小,压力传感器置于极头与铜块之间,通过数字显示屏显示应力数值。
1.4 保压装置
本文重点对平台的保压装置进行设计改进,预应力对稀土超磁致伸缩棒材性能具有较大影响,以往文献设计的铁磁材料测试平台中,大都未考虑和解决测试过程中由于材料伸长导致的预应力变化,但通过实验发现,直接通过液压油压机对测试装置施加压力时,由于测试过程中棒材处于伸长状态,预应力不会保持在预定值,而是随着棒材的伸长逐渐增大[23]。
以往有文献在稀土超磁致伸缩棒材两端垫薄橡胶片[24]以实现隔振隔声,或垫铜片[7]以减小棒材端面所受预应力的不均匀性,防止棒材边缘损坏,有一定缓冲效果,但均效果不佳。本文采用在液压油压机压头和测试装置极头中间增加黄铜块和不同组合方式碟簧的方法,实现预应力宽范围的缓冲和保持效果。
碟簧形状为圆锥碟状,与传统弹簧不同,其负荷大,行程短,压缩行程最佳使用范围在其最大压缩行程的10%~75%之间。本文平台测试对象稀土超磁致伸缩棒材尺寸为φ 20mm×50mm,要求预应力施加范围为0~25MPa,则通过计算,棒材所受压力的范围为0~7 854N,测试装置对碟簧变形量无要求,选取C系列碟簧参数见表1[25]。
表1 碟簧参数
Tab.1 Parameters of disc spring
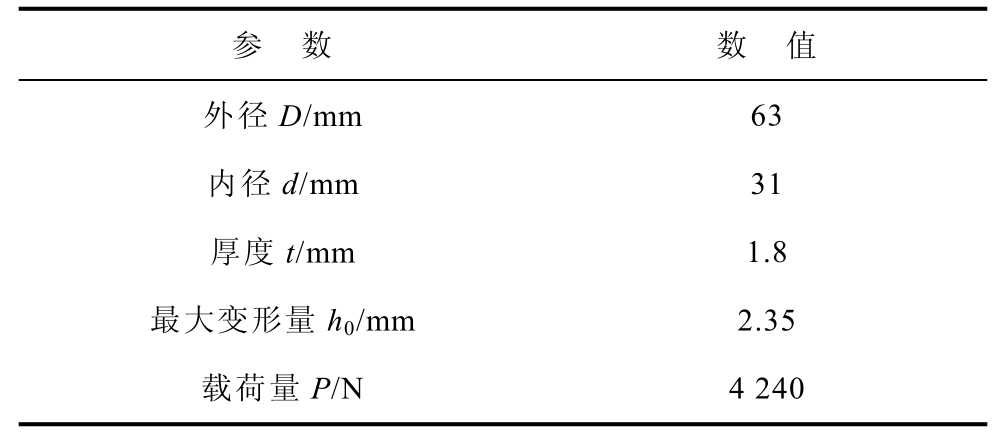
参 数 数 值 外径D/mm 63 内径d/mm 31 厚度t/mm 1.8 最大变形量h0/mm 2.35 载荷量P/N 4 240
选取16片此规格碟簧,在0~25MPa预应力范围内进行测试,力的变化范围大,由于单个碟簧载荷量存在限制,因此采用两种不同的碟簧组合方式来对应不同的负荷:
(1)在预应力小于15MPa时,采用对合组合碟簧方式,即叠合碟簧中单个碟簧片数n=1,对合碟簧中碟簧片数i=16。
(2)当预应力在15~25MPa范围时,采用复合组合碟簧,即叠合与对合的复合结构,叠合碟簧中单个碟簧片数n=2,对合碟簧中叠合碟簧组数i=8。
对于单片碟簧,其位移f与载荷P关系为

式中,直径比C=D/d=2;弹性模量E=206 000N/mm2;泊松比μ =0.3;厚度t =1.8mm;最大变形量h0= 2.35mm;K4=1。
不计摩擦力,复合组合碟簧总位移负荷关系为

式中,Ps为碟簧总负荷;fs为碟簧总位移。因此,单个、对合组合与复合组合C系列碟簧位移载荷关系如图6a所示,碟簧组合实物如图6b所示。

图6 碟簧载荷-位移关系和碟簧组合实物
Fig.6 Displacement-load relationship of disc spring and physical drawing of disc spring combination
棒材的伸长量在测试过程中最大0.05mm左右,由图6a和计算可以得到:
(1)预应力小于15MPa时采用的对合组合碟簧,最大载荷量与单个碟簧相同,棒材伸长变形时,负荷变化量是单个碟簧的1/16。
(2)预应力在15~25MPa范围时采用的复合组合碟簧,最大载荷量是单个碟簧的2倍,棒材伸长变形时,负荷变化量是单个碟簧的1/4。
综上,使用碟簧可实现预应力的缓冲和保持,在测试范围内有效地减小预应力的变化,保持测试过程中预应力恒定,使测试结果更为准确。
2 实验结果与分析
为验证本文设计保压装置及测试平台的有效性,进行以下实验,并对结果进行分析。
2.1 预应力变化对比实验
在三种方式下:方式1为无保压装置;方式2为棒材两端垫铜片保压;方式3为本文保压装置。利用程控直流电源对双励磁绕组施加0~20A驱动直流电流,利用压力传感器分别测试10MPa、15MPa、20MPa及25MPa预应力下,稀土超磁致伸缩棒材伸长导致的预应力变化情况,不同保压方式下预应力随磁场强度的变化如图7所示。

图7 不同保压方式下预应力随磁场强度的变化
Fig.7 Changes of prestress on magnetic field strength under different pressure retaining modes
可以看出,在三种不同方式下,预应力变化情况不同。方式2棒材两端垫铜片进行测试时,由于铜片不导磁,相当于磁路中存在一个较大的空隙,因此同样驱动电流下,棒材内的磁场强度相对于其他保压方式明显降低,影响磁路中磁场分布,同时保压效果不佳,故方式2不可取。因此重点对比方式1、方式3预应力变化情况,采用预应力变化率为
对结果进行分析比较,具体数据如图8所示。

图8 预应力变化率
Fig.8 Rate of prestress change
结果表明,测试稀土超磁致伸缩棒材磁致伸缩性能时,由于其在外加磁场下伸长,因此实验开始设定好的预应力会产生变化。如图7、图8所示,驱动电流0~20A时:
(1)方式1:无缓冲装置下测试,预应力不能维持一个平稳状态,应力变化明显,在10MPa下测试预应力变化率高达10.625%,会导致磁致伸缩性能等一系列测试出现偏差。
(2)方式3:本文提出的保压装置下,由图7可明显看出,预应力维持效果好,曲线平缓,变化不明显,在驱动磁场200kA/m、预应力25MPa以内,预应力变化率最高不超过1.134%。
综上可得,相比无缓冲装置,本文保压装置使得测试过程中预应力变化率由10.625%降低至1.134%以下,预应力保持良好状况,保证了在预应力前提条件基本不变下,使得测试过程及结果更为严谨有效。
2.2 磁致伸缩应变对比实验
实验前,利用实验装置对棒材施加一定的预应力,线圈通过驱动电流产生驱动磁场,在不同保压方式下,利用电阻应变仪测试棒材的磁致伸缩性能进行对比,不同保压方式下GMM棒的磁致伸缩性能如图9所示。可以看出,不同保压方式下磁致伸缩棒材应变存在差异。这是由于在测试过程中,棒材伸长导致预应力产生较大变化,而不同保压方式的预应力保持效果也不同,因此应变测试结果出现明显不同。
预应力在20MPa以下时,在低磁场强度下,方 式1、方式3下测试的磁致伸缩性能差异小,磁场强度较高,由于不同方式应力差别逐渐增大,应变开始出现较大差异;预应力20MPa以上时,不同保压方式下,棒材整个伸长过程中应变存在较大差异,方式1无保压装置相比方式3本文设置的保压装置,低磁场强度下应变更小,高磁场强度下应变更大。
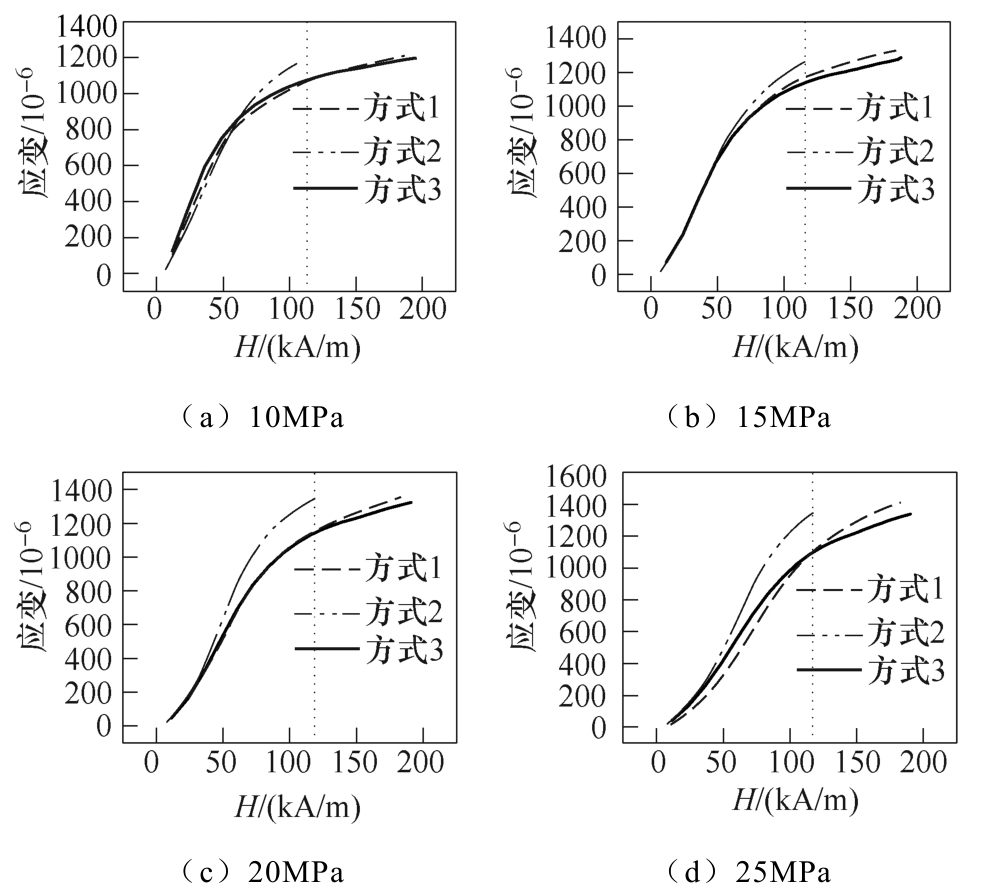
图9 不同保压方式下GMM棒的磁致伸缩性能
Fig.9 Magnetostriction of GMM rod under different pressure retaining modes
综上可得,优化后的测试平台在不同预应力条件下对磁致伸缩应变测试更加精确,这对于磁致伸缩换能器设计中初始偏置条件的选择,即预应力和偏置磁场的确定具有指导意义。
2.3 B-H曲线测试结果
棒材下半部分表面紧密缠绕50匝感应线圈,测试时采集线圈两端感应电动势,由电磁感应定律得到棒材内磁感应强度。由于本文平台中棒材内部磁场分布上下对称,因此测试磁场强度时,利用两个霍尔探头贴近棒材上半部分,测试棒材1/6、1/3两个位置,取平均值可反映整根棒材内平均磁场强度。使用数据采集卡采集B、H数据至上位机,对H进行处理取其平均值,在无预应力条件下,利用开发的Labview程序实时绘制出B-H曲线。平台施加频率为5Hz、1~2A的驱动电流,测试棒材准静态磁滞回线。通过上述测试结果进而分析计算出棒材的相对磁导率等。
磁化曲线及相对磁导率曲线如图10所示,随着棒材外加磁场强度的增大,棒材的磁导率呈先增大后减小,最后逐渐平稳的趋势。平台测试得棒材准静态磁滞回线、B-H回线(频率5Hz、驱动电流1~2A)如图11所示,可进一步分析棒材的磁学性能,如磁滞损耗等[21, 26-27]。

图10 磁化曲线及相对磁导率曲线
Fig.10 Magnetization curves and Relative permeability

图11 B-H回线(频率5Hz、驱动电流1~2A)
Fig.11 Hysteresis loop (frequency 5Hz, drive current 1~2A)
综上,利用平台测试得到棒材磁导率、磁滞回线等,可为磁致伸缩换能器有限元仿真设计提供实际准确的材料参数,使得仿真结果更具参考价值和实际意义。
2.4 杨氏模量测试结果
根据杨氏模量的定义,在不同偏置磁场下(0kA/m、40kA/m、80kA/m),通过平台对棒材施加压力,利用压力传感器测试压力大小,利用电阻应变仪测试棒材应变,利用霍尔探头测试磁场强度,记录数据并得到-σλ曲线,对曲线进行拟合,如图12所示。 对-σλ 曲线进行微分可得棒材在恒定磁场下随预应 力变化的杨氏模量![]() ,杨氏模量曲线如图13所示。
,杨氏模量曲线如图13所示。
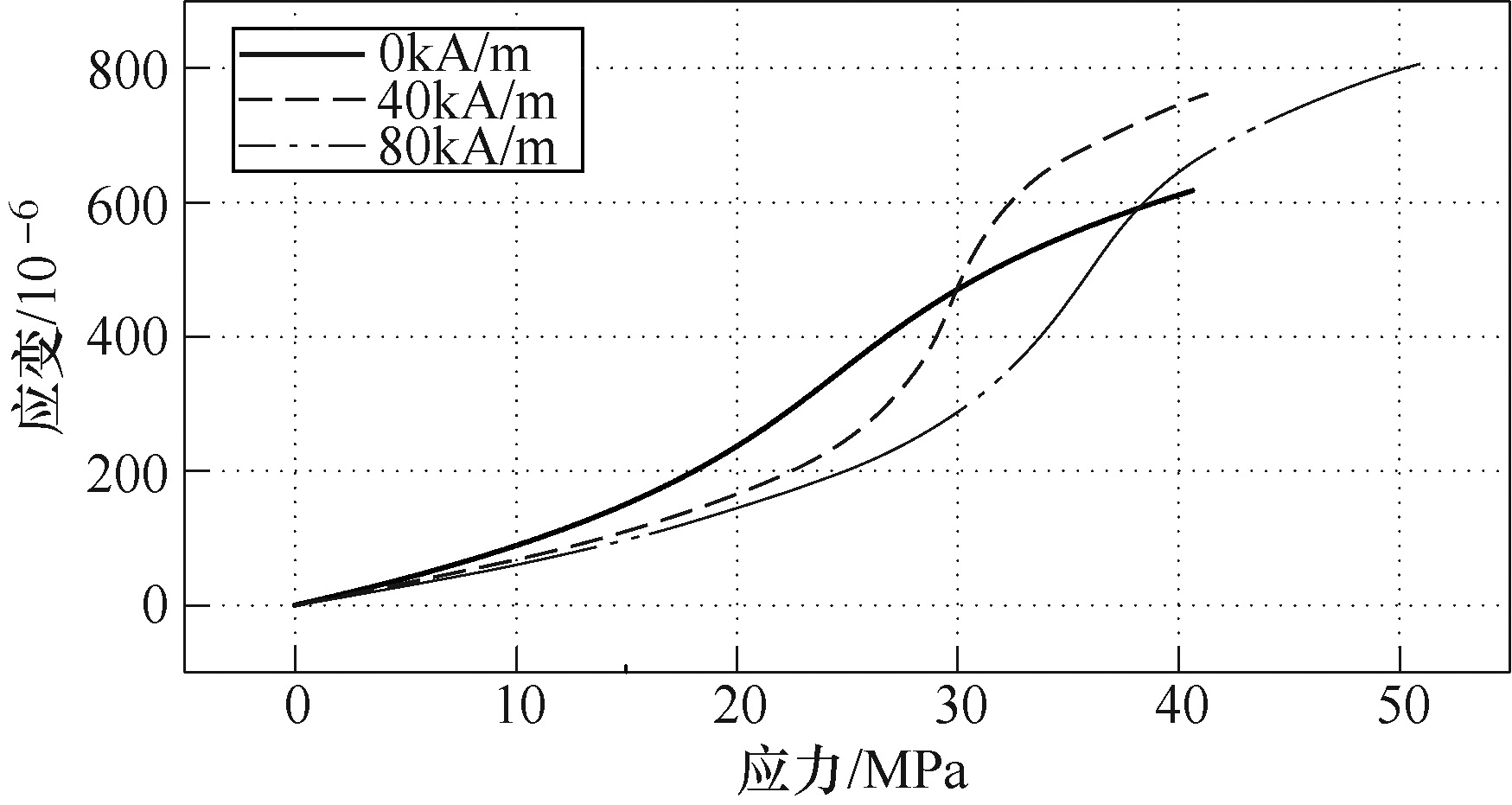
图12 应力-应变曲线(0、40kA/m、80kA/m)
Fig.12 -σλ curves (0、40kA/m、80kA/m)

图13 杨氏模量曲线
Fig.13 Young's modulus curves
由于效应,测试过程中棒材的磁化强度会产生变化。但在实际实验过程中,利用霍尔探头实时测量棒材表面磁场强度,发现磁场强度在加压过程中变化大小在1kA/m左右,因此忽略磁场变化的影响[28]。
由上述结果可以得到,随着棒材所受压力的增大,棒材恒定磁场下的杨氏模量呈先减小后缓慢增 大的趋势;随着偏置磁场的增大,棒材![]() -σ 曲线 整体向右移动。此外,实际的杨氏模量等力学参数 是认识棒材力学性能的基础,同时其为磁致伸缩换能器的有限元仿真、换能器阻抗建模提供支撑,能更好地进行换能器的设计理解。
-σ 曲线 整体向右移动。此外,实际的杨氏模量等力学参数 是认识棒材力学性能的基础,同时其为磁致伸缩换能器的有限元仿真、换能器阻抗建模提供支撑,能更好地进行换能器的设计理解。
3 结论
本文设计搭建了一套稀土超磁致伸缩棒材特性测试平台,平台包括驱动模块、测试装置、信号采集模块以及保压装置四部分,可对稀土超磁致伸缩棒材的磁致伸缩性能、B-H曲线、杨氏模量等重要性能和参数进行测量。
考虑到测试过程中磁致伸缩棒材伸长会导致预应力发生变化,本文重点对稀土超磁致伸缩棒材的保压装置进行优化,根据预应力的范围大小,利用黄铜块、两种不同组合方式的碟簧构成的可调节机械装置,实现了测试平台预应力宽范围的缓冲和保持效果。本文设置两个对比实验验证保压装置的有效性。最后,根据参数定义,利用本文平台对不同条件下棒材的λ-H、B-H和σ-λ 曲线进行测试,分析了棒材的磁致伸缩性能,得到了棒材的磁导率、磁滞回线和杨氏模量等参数。结论如下:
1)利用本文设置的碟簧保压装置,预应力变化率由10.625%降至1.134%以下,保压效果显著,利用平台测试的棒材参数结果更为精确。
2)随着棒材外加磁场强度的增大,棒材的磁导率呈先增大后减小,最后逐渐平稳的趋势。
3)随着棒材所受压力的增大,恒定磁场下棒材的杨氏模量呈先减小后增大的趋势。
以上实验和理论均证明了本平台的设计及优化为超磁致伸缩棒材参数的提取提供了一种更为可靠的测定方法。同时,本文工作及方法为磁致伸缩材料的理解使用、磁致伸缩换能器的有限元仿真设计及换能器阻抗特性建模等工作提供了实际参数支撑。
[1] 李一宁, 张培林, 何忠波, 等. 超磁致伸缩致动器的等效电路模型研究及实验分析[J]. 中国电机工程学报, 2018, 38(11): 3375-3383.
Li Yining, Zhang Peilin, He Zhongbo, et al. Research and experimental analysis on equivalent circuit models for giant magnetostrictive actuators[J]. Pro- ceedings of the CSEE, 2018, 38(11): 3375-3383.
[2] 许岳峰, 黄文美. 双线圈超磁致伸缩换能器三维磁场分析与优化[J]. 机电工程, 2019, 36(5): 544-548.
Xu Yuefeng, Huang Wenmei. Optimization of 3D magnetic field of double coil giant magnetostrictive transducer[J]. Journal of Mechanical & Electrical Engineering, 2019, 36(5): 544-548.
[3] 黄文美, 薛胤龙, 王莉, 等. 考虑动态损耗的超磁致伸缩换能器的多场耦合模型[J]. 电工技术学报, 2016, 31(7): 173-178.
Huang Wenmei, Xue Yinlong, Wang Li, et al. Multi- field coupling model considering dynamic losses for giant magnetostrictive transducers[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 173-178.
[4] 刘敬华, 张天丽, 王敬民, 等. 巨磁致伸缩材料及应用研究进展[J]. 中国材料进展, 2012, 31(4): 1-12, 25.
Liu Jinghua, Zhang Tianli, Wang Jingmin, et al. Giant magnetostrictive materials and their applications[J]. Materials China, 2012, 31(4): 1-12, 25.
[5] 翁玲, 罗柠, 张露予, 等. Fe-Ga合金磁特性测试装置的设计与实验[J]. 电工技术学报, 2015, 30(2): 237-241.
Weng Ling, Luo Ning, Zhang Luyu, et al. Design and experiment of a testing device for Fe-Ga magnetic properties[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 237-241.
[6] Wang Bowen, Huang Wenmei, Weng Ling, et al. Effect of stress and magnetic field on young’s modulus of Tb0.3Dy0.7Fe2 <110> oriented alloy[J]. Materials Science Forum, 2011, 675-677: 1159-1162.
[7] Moffett M B, Clark A E, Wun-Fogle M, et al. Characterization of Terfenol-D for magnetostrictive transducers[J]. Journal of the Acoustical Society of America, 1991, 89(3): 1448-1455.
[8] Clark A E, Savage H T. Magnetostriction of rare earth-Fe2 compounds under compressive stress[J]. Journal of Magnetism and Magnetic Materials, 1983, 31: 849-851.
[9] 冯雪. 铁磁材料本构关系的理论和实验研究[D]. 北京: 清华大学, 2002.
[10] Scheidler J J, Asnani V M, Deng Zhangxian, et al. Dynamic characterization of Galfenol[C]//SPIE Smart Structures/NDE Conference, San Diego, CA, USA, 2015, 9432: 94320J.
[11] Palumbo S, Rasilo P, Zucca M. Experimental investigation on a Fe-Ga close yoke vibrational harvester by matching magnetic and mechanical biases[J]. Journal of Magnetism and Magnetic Materials, 2019, 469: 354-363.
[12] Liang Yirui, Zheng Xiaojing. Experimental researches on magneto-thermo-mechanical characterization of Terfenol-D[J]. Acta Mechanica Solida Sinica, 2007, 20(4): 283-288.
[13] Li He, Liu Shuying, Wen Feng, et al. Study on dynamic of giant magnetostrictive material transducer with spring of nonlinear stiffness[J]. Journal of Mechanical Science and Technology, 2007, 21(6): 961-964.
[14] 蔡万宠, 冯平法, 郁鼎文. 超磁致伸缩换能器预应力优化设计方法研究[J]. 振动. 测试与诊断, 2017, 37(1): 48-52, 198. Cai Wanchong, Feng Pingfa, Yu Dingwen. Research on the optimization design method of prestress for giant magnetostrictive transducer[J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(1): 48-52, 198.
[15] 翁玲, 曹晓宁, 胡秀玉, 等. 双线圈铁镓合金换能器的输出特性[J]. 电工技术学报, 2018, 33(19): 4476-4485.
Weng Ling, Cao Xiaoning, Hu Xiuyu, et al. Output characteristics of double coil Fe-Ga alloy trans- ducer[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4476-4485.
[16] 翁玲, 梁淑智, 王博文, 等. 考虑预应力的双励磁线圈铁镓换能器输出特性[J]. 电工技术学报, 2019, 34(23): 4859-4869.
Weng Ling, Liang Shuzhi, Wang Bowen, et al. Output characteristics of double-excited coil Fe-Ga transducer considering pre-stress[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4859- 4869.
[17] Abell J S, Butler D, Greenough R D, et al. Magnetomechanical coupling in Dy0.73Tb0.27Fe2 alloys[J]. Journal of Magnetism and Magnetic Materials, 1986, 62(1): 6-14.
[18] Rafferty A, Bakir S, Brabazon D, et al. Calibration and characterisation with a new laser-based magneto- striction measurement system[J]. Materials & Design, 2009, 30(5): 1680-1684.
[19] Kvarnsjo L, Engdahl G. A set-up for dynamic measurements of magnetic and mechanical behavior of magnetostrictive materials[J]. IEEE Transactions on Magnetics, 1989, 25(5): 4195-4197.
[20] 冯慈璋, 马西奎. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000.
[21] 翁玲, 李薇娜, 曹晓宁, 等. 环形Fe-Ga合金动态磁导率和损耗分析[J]. 电工技术学报, 2019, 34(3): 459-465.
Weng Ling, Li Weina, Cao Xiaoning, et al. Analysis of dynamic permeability and energy loss of ring- shaped Fe-Ga alloy[J]. Transactions of China Electro- technical Society, 2019, 34(3): 459-465.
[22] Zhang Qian. Experimental characterization of Galfenol (FeGa) alloys[D]. Columbus: The Ohio State University, 2014.
[23] 张旭辉. 超磁致伸缩作动器优化及主动隔振控制研究[D]. 北京: 北京航空航天大学, 2008.
[24] Bai Xiabing, Jiang Chengbao. Dynamic parameters of Tb-Dy-Fe giant magnetostrictive alloy[J]. Journal of Rare Earths, 2010, 28(1): 104-108.
[25] 全国弹簧标准化技术委员会. GB 1972—2005碟形弹簧[S]. 北京: 中国标准出版社, 2005.
[26] 赵小军, 刘小娜, 肖帆, 等. 基于Preisach模型的取向硅钢片直流偏磁磁滞及损耗特性模拟[J]. 电工技术学报, 2020, 35(9): 1849-1857.
Zhao Xiaojun, Liu Xiaona, Xiao Fan, et al. Hysteretic and loss modeling of silicon steel sheet under the DC biased magnetization based on the Preisach model[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1849-1857.
[27] 翁玲, 常振, 孙英, 等. 不同磁致伸缩材料的高频磁能损耗分析与实验研究[J]. 电工技术学报, 2020, 35(10): 2079-2087.
Weng Ling, Chang Zhen, Sun Ying, et al. Analysis and experimental study on high frequency magneto- strictive energy loss of different magnetostrictive materials[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2079-2087.
[28] Su Quanmin, Morillo J, Wen Yiting, et al. Young's modulus of amorphous Terfenol-D thin films[J]. Journal of Applied Physics, 1996, 80(6): 3604-3606.