0 引言
人体组织的介电特性检测一直是医学和工程技术领域研究的焦点问题，文献[1]报导人脑的电导率分布范围约(0, 1.5)S/m，相对介电常数为(30, 60)。已经证实，正常组织和肿瘤组织的电导率和介电常数差异较大。实验研究表明，在较宽的频谱上，癌变组织与正常组织在电特性上有显著的不同，乳腺癌大于200%[2]，膀胱癌大于100%[3]。传统的介电检测法包括基于贴片电极的电阻抗成像及磁声成像等方法[4-5]，无需取出病变组织就能实施实时、在体的检测。
本文研究的磁共振介电特性成像（Magnetic Resonance Electrical Properties Tomography, MR- EPT）[6-9]，基于磁共振（Magnetic Resonance, MR）成像系统的介电特性扫描与重建方法。根据宏观、定量分析电磁场的麦克斯韦方程组，人体组织内部的电导率和介电常数分布可以由射频磁场反演计算得到。得益于磁共振成像较高的空间分辨率，与射频场映像相关的磁共振介电特性成像也具有较高的空间分辨率。另外，随着磁共振系统朝着高电场强度的方向发展，人体在更高频段上的射频耐受性也是必须要评估的[10]。磁共振介电特性成像提供的局部电导率分布信息，将有助于真实电磁波吸收比值（Specific Absorption Rate, SAR）的计算和分析[11]。
磁共振介电特性成像的核心是复介电常数的重建，而重建所需的射频（Radio Frequency, RF）磁场数据，又与扫描序列密切相关。根据磁共振成像的原理，射频磁场分为发射激励磁场和接收检测磁场，前者的分布仅由本构关系决定，而后者中增加了组织质子密度因子，在用于反演复介电常数时相关权重不易去除[12]。考虑磁共振介电特性成像的临床应用时，目前主流的体线圈发-多通道收的射频线圈结构用于结合电特性重建算法尚有一定难度，而早期的单通道鸟笼线圈，因其自发自收、正交检测的特点，使接收磁场相位等于检测信号相位的一半，较利于准确重建出组织的电导率分布[13]。在探索临床应用阶段，为完成初步的算法验证，鸟笼线圈是较合适的选择。
近年来，磁共振介电特性成像重建过程主要有基于简化Helmholtz方程和非简化Helmholtz方程两种算法[14]。前者假定成像体中不同组织界域内的介电特性均匀，从而忽略掉反演方程中电特性变化相关项。后者虽可基于多通道收发一体线圈获得求解多未知量方程所需的信息，但相关多通道线圈技术在目前1.5T和3.0T的磁体中仅做并行成像时的接收线圈使用。为了验证磁共振介电特性成像重建算法的准确性，文献[15]系统地开展了基于积分形式Helmholtz方程介电特性检测的仿真、水模以及志愿者实验研究，在1.5T系统上由发射磁场分别重建出高电导率体和低电导率体的相对介电常数分布，但所采用的自旋回波序列对磁化率不敏感，并不适合介电特性的扫描。文献[16]提出一种基于电特性梯度间接计算电特性分布的算法，利用超高场磁共振中常用的横电磁多通道收发一体线圈，结合真实偏转角成像和梯度回波序列，得到全套的各个通道的发射和接收磁场的幅值与相位分布数据，但该方法最后计算电特性时需依据先验知识提供初值点，如选取不当可能导致结果出现较大偏差。为了解决介电特性图像信噪比低的问题，文献[17]首次提出将简化Helmholtz方程算法和字典查询型机器学习相结合的磁共振介电特性成像新方法，利用传统的正交鸟笼线圈和基于梯度回波稳态自由进动序列，对4名被试进行了脑部的射频磁场扫描，结果显示，运用机器学习后的电特性重建值相比学习前，与射频场幅值的相关度从0.758上升到了0.893。以上研究中，无论是简化还是非简化Helmholtz方程，相关求解过程中二阶拉普拉斯项所引入的噪声均给电特性重建结果带来了误差。
本文在文献[17]方法的基础上，对重建算法进行改进以解决图像信噪比低的问题。在前期磁共振介电特性成像方法研究的基础上[18]，为减小磁场二阶导数计算所带来的噪声，在中心差分方程中引入整数步长因子参与电特性分布重建，以提高算法的准确性。为了验证降低拉普拉斯项噪声的有效性，首先利用Simulation4life仿真软件分析鸟笼线圈下真实人体头模型的电磁场分布，进而反演重建电特性；然后采集一例脑转移瘤被试的磁共振3D梯度回波序列头部扫描数据，进行电导率分布重建；之后通过增加步长因子，仿真和实测图像上信噪比均有明显的改善；最后通过与磁共振幅值结构像病灶区域的比较，验证了磁共振介电特性成像在肿瘤诊断方面有一定的可行性。
1 基于射频交变磁场的介电特性逆问题
生物组织的微观结构中，细胞内外溶液电解质浓度的不同决定着外加电磁场下传导电流和位移电流的大小[19]，并包含着电导率和介电常数的分布信息。在时谐场条件下，发射激励磁场作用后检测的磁共振信号SI可以表示为
式中，ρ为组织的质子密度；
为发射线圈作用磁场；
为接收线圈检测到组织内自旋体系的进动信 号。在磁共振成像中，扫描发射磁场的序列包括真实偏转角分布成像（Actual Flip-angle Imaging, AFI）和基于Bloch-Siegert Shift的梯度回波序列，但受目 前并行成像线圈结构的限制，均只能得到
的幅 值。正交类线圈，如鸟笼线圈和横电磁线圈，当在 自发自收工作模式下，检测信号相位SIφ、发射磁场相位
和接收磁场相位
满足
本文基于单通道正交线圈和稳态自由进动序列扫描射频磁场，能够满足式（2）条件，由磁共振信号开展变步长因子的介电特性重建算法研制与验证实验。在组织界域内认为匀质的条件下[20]，发射磁场与复介电常数的解析关系可以表示为
式中，ω为射频磁场角频率；μ为人体组织中的磁导率；εc为复介电常数，εc= ε0ε r −iσ/ω，ε0为真空 中的介电常数，rε为介质中的相对介电常数，σ为介质电导率，均是空间位置r的函数，为表述简洁，下文表达式中将省略r。通过分离复数的实部和虚部，根据拉普拉斯运算定义，可以推导出rε和σ的计算公式[15]为
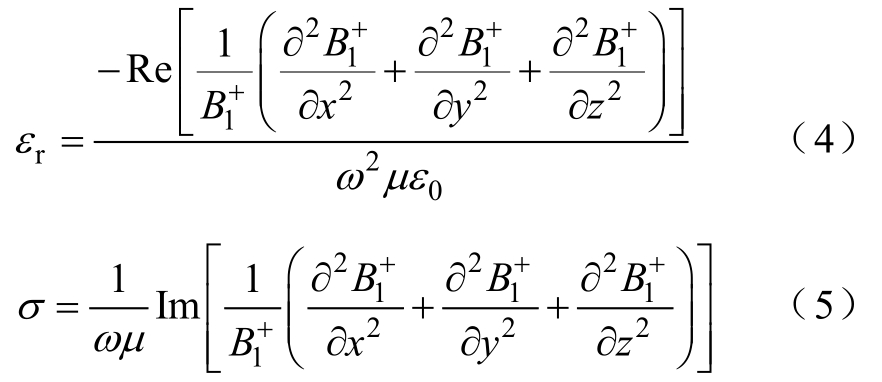
考虑到磁共振重建像素矩阵的特点，设目标点 坐标为(l ,m, n)，对式（4）和式（5）中复数磁场的二阶偏导数项进行常规的后向差分处理，有
式中，xΔ、yΔ 和zΔ分别为x、y和z方向的空间步长。
磁共振扫描得到的射频磁场中的噪声经上述拉普拉斯运算后会进一步放大，从而影响介电特性重建的准确性。本文在拉普拉斯运算中新引入步长控制因子sf，通过增加运算单元的体积，使得二阶导数项值增加而噪声水平保持不变。
介电特性扫描重建实验中有关像素大小及其控制，取决于所采用的具体射频和梯度脉冲序列。由选层梯度、射频激励带宽、频率编码梯度和相位编 码梯度等参数，可以得到( Δx, Δy ,Δz )。在电导率和介电常数的整个解析式推导过程中，各物理量均 采用国际单位制，并未做任何调整或近似，因此本文重建介电特性值将在实际范围之内。
2 逆问题仿真计算
利用电磁场有限元仿真软件Simulation4Life科研版（ZMT Zurich MedTech AG, Switzerland），对已知材料和几何参数的线圈与介质模型结构进行正问题计算求解。根据第1节逆问题分析的电特性重建算法，再由射频磁场可重建得到电导率和介电常数分布，对与模型数据的相关性进行分析，从而评估引入步长因子后重建算法的准确性。
本文以单通道鸟笼式线圈与真实人体杜克（Duke）头模型为对象进行数值仿真，磁共振介电特性成像仿真模型如图1所示，相关仿真参数见表1。
图1 磁共振介电特性成像仿真模型
Fig.1 Modeling for verifying magnetic resonance electrical properties tomography
表1 磁共振介电特性成像重建算法仿真参数
Tab.1 The parameters in algorithm simulation for magnetic resonance electrical properties tomography
参 数 数 值 共振频率f/MHz 127.728 线圈注入电流有效值Irms/A 1 电导率σ/(S/m) [0, 2.5] 相对介电常数rε [0, 90] 不同组织种类数n 7 体素体积v/mm3 8 层数s 112 层内点阵数Ar 141×122 鸟笼线圈长度L/mm 200 鸟笼线圈半径R/mm 140 鸟笼线圈导体厚度T/mm 0.5 鸟笼线圈条带数N 14
图1中，鸟笼型线圈产生垂直于轴线方向的平面内旋转磁场，即当被试处于超导磁共振磁体中时，射频磁场垂直于主磁场。
模型建立后，实际的组织相关格点数为1 541 299，Windows 10 64位系统、双核1.8GHz CPU、4.0GB内存条件下，计算时间约为90min。
首先，根据模型已知的材料介电特性数据重建得到原始的电导率和介电常数分布图像，真实人体头模型（Duke）电特性分布如图2所示。本文仿真计算中选取的目标层面序号均为39号。
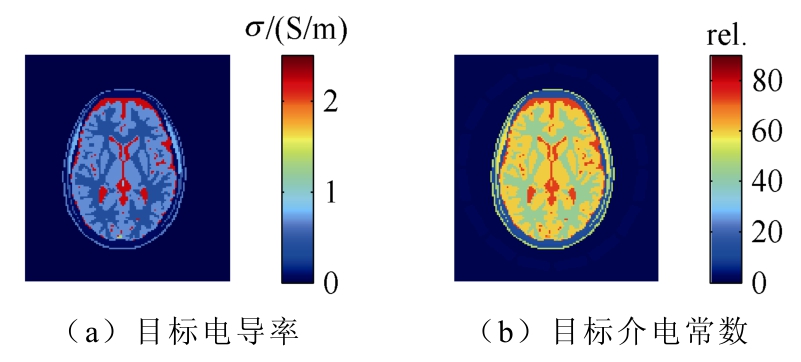
图2 真实人体头模型（Duke）电特性分布
Fig.2 Raw data distribution of electrical properties for real human body model (Duke)
图2中，脑白质、灰质、脑脊液以及头部等位置均呈现不同的电特性。
其次，由安培定律可知，物质的复介电常数与电场相互作用得到磁场的旋度，因此，如果已知电场和磁场也能够计算出复介电常数。仿真工作中，进行基于安培定律的介电特性逆问题求解，相关结果如图3所示。
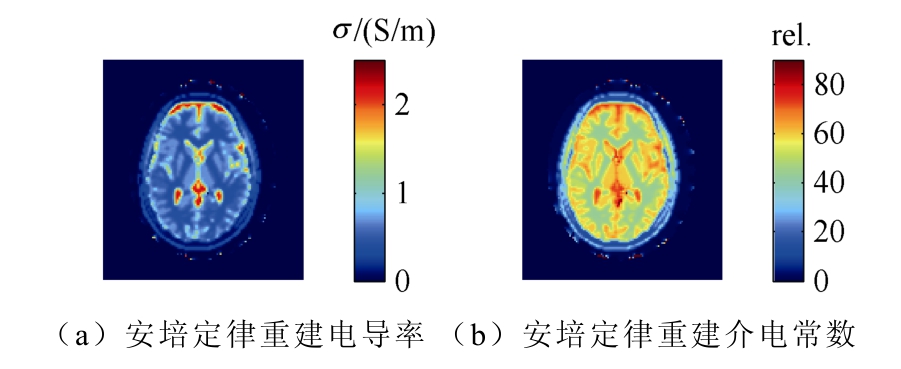
图3 由安培定律重建电导率和介电常数分布
Fig.3 Ampere-law based conductivity and permitivity reconstruction with electrical and magnetic field
可以看出，由于计算引入的噪声，相比于模型数据，该重建结果图像的信噪比有所下降。
进一步地，将注入电流产生的磁场由直角坐标 分量变换为圆极化形式
，采用新的变步长介电特 性重建算法，分别得到单位步长和2倍步长下的电导率和介电常数断层分布，如图4所示。
因组织均质假设下电导率和介电常数分别主要与射频磁场的幅值和相位相关，求解过程中二阶导 数项表达式分别代入
和cosφ+ sinφ，φ为 各 场点相位。
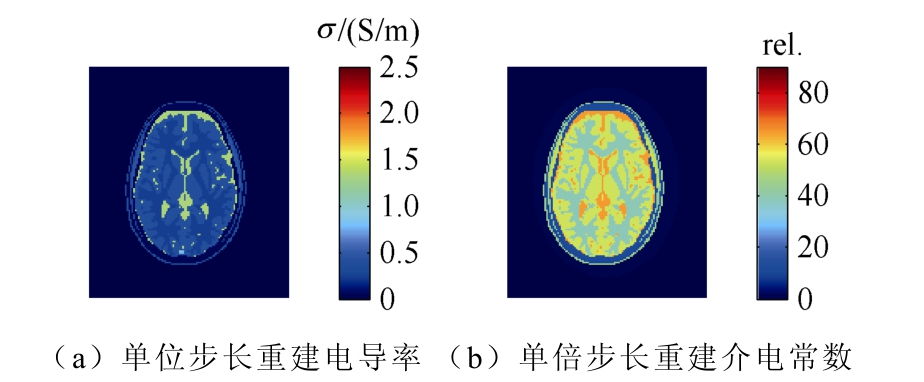
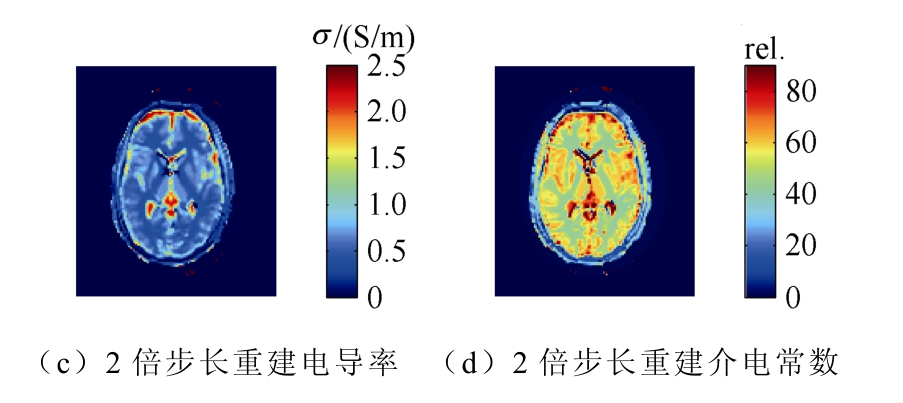
图4 变步长算法重建电导率和介电常数分布
Fig.4 Conductivity and permitivity reconstruction by step-variable algorithm
为评估不同重建算法的准确性，基于模型数据定义相对误差与相关系数为
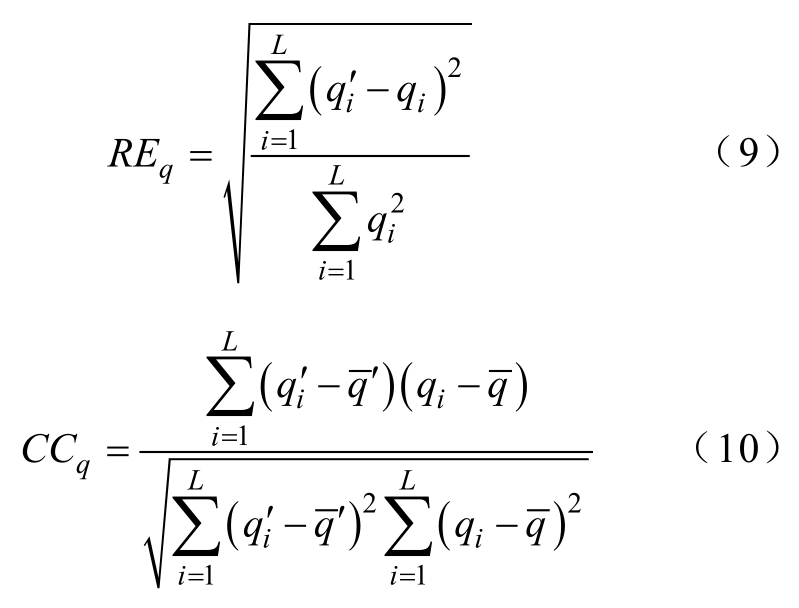
式中，q为空间分布量；q′为重建值；L为总像素数；“−”为取平均。受仿真条件的限制，上述重建 电特性图像中仅涉及了灰质、脑白质和脑脊液等七种典型组织。以电导率分布为例，计算得到采取不同重建算法结果之间的相关度见表2。
表2 电导率原始值和不同算法重建值间相关度
Tab.2 Correlations between raw conductivity and different reconstructions
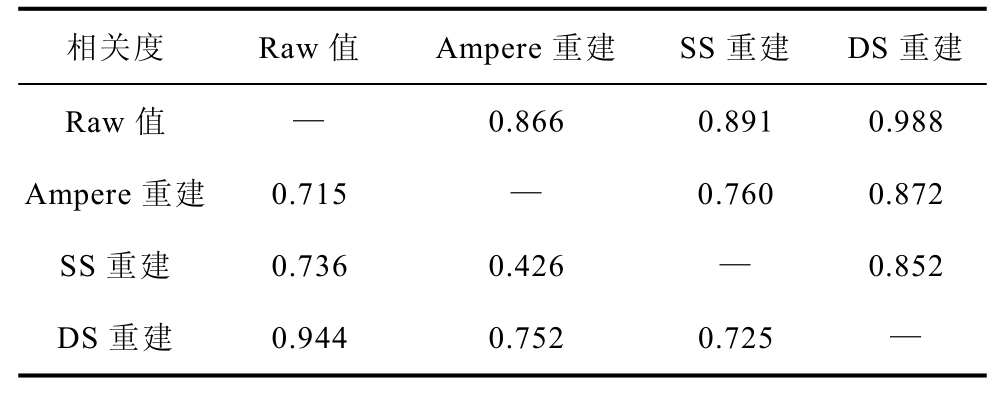
相关度 Raw值 Ampere重建 SS重建 DS重建Raw值 — 0.866 0.891 0.988 Ampere重建 0.715 — 0.760 0.872 SS重建 0.736 0.426 — 0.852 DS重建 0.944 0.752 0.725 —
表2中，SS表示单位步长Helmholtz算法，DS表示2倍步长Helmholtz算法。主对角线下方的数据反映了图1中不同算法于脑灰质区重建的平均电导率值间的相关度，而主对角线上方的数据则反映了在白质区各算法重建结果间的相关度。可见，2倍步长介电特性重建的准确度优于单倍步长算法以及基于安培定律重建算法。
3 磁共振介电特性成像实验验证
很多身体其他部位的癌症都有脑转移的情况，如肺癌、乳腺癌、黑色素瘤等，相关癌细胞从原位置扩散到了脑部。正常脑组织和肿瘤组织的介电特性差异由含水量、离子浓度等因素所引发，给磁共振介电特性成像观察到早期和治疗过程中肿瘤的演进提供了可能。
本文选取一例脑转移被试为实验研究对象，进行磁共振介电特性成像与图像重建。所用射频单通道鸟笼线圈与第2节仿真条件保持一致，采用基于梯度回波的稳态自由进动序列（Steady State Free Precession, SSFP）进行射频磁场扫描。相关实验参数为：GE 3T磁共振机Discovery MR750W，3D扫描模式，TR/TE=3.4/1.7ms, Voxel size=1mm×1mm× 1mm, 偏转角为25°，层数为76，层厚为1mm，FOV为256mm2，层内分辨率为1mm2，4次平均，总扫描时间为440s。
图5为磁共振介电特性成像原始幅值和相位参照像，由于人眼视网膜对空间相位信息捕捉敏感度低，临床诊断均采用幅值像作为依据。本文研究的电导率分布，主要与磁场的相位分量有关，且所用正交鸟笼线圈的激发和接收磁场间相位近似相等，因此进行了组织电导率的反演重建。
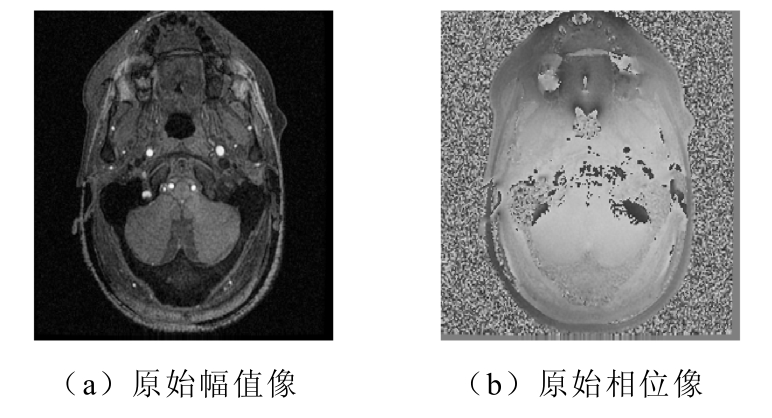
图5 磁共振介电特性成像原始幅值和相位参照像
Fig.5 Magnitude and phase images of MR for structure reference
图5中，中间区域4个亮点分别代表颈动脉、静脉、椎动脉和静脉，给图像做肿瘤诊断带来一定的干扰，未来实验中考虑结合流体衰减反转恢复序列（Fluid-Attenuated Inversion Recovery, FLAIR）以消除该问题。
进一步对原始扫描相位像数据行电导率重建算法，分别以1mm和2mm为差分步长，原始磁场相位、重建电导率和幅值加权电导率像如图6所示。
磁场相位直接由原始相位数据[−π, π]归一化而来。在单倍和2倍步长电导率重建中，利用中值滤波减小了由拉普拉斯运算引入的噪声。对比图5和 图6，所建的功能性电导率图相比于相位结构，在组织结构细节方面虽有一定的提升，但对未来为临床医生用作肿瘤诊断的影像学依据，尚有待和其他方法如正电子发射计算机断层显像（Positron Emi- ssion Tomography, PET）、磁共振增强扫描图像以及病理等结果做进一步的对比研究。
图6 原始磁场相位、重建电导率和幅值加权电导率像
Fig.6 Raw RF magnetic field phase, conductivity reconstruction and magnitude weighted reconstruction
4 结论
本文基于交变电磁场与人体组织的相互作用，给出了基于磁共振成像的介电特性重建新算法，通过变换拉普拉斯运算中的步长因子可提高图像数据的抗噪性。利用仿真计算，验证了本文所提电特性重建算法的结果与模型数据的相关度可达0.944。在临床磁共振平台上，初步探索了介电特性成像在脑转移瘤扫描中的应用，表明功能性电导率图像的结构解析力优于原始相位结构图像。本文的组织电特性分布图像，为临床医生的肿瘤确诊工作提供了新的参考信息，有望在早期发现和疗效评估中发挥作用。
[1] Foster K R, Schwan H P. Dielectric properties of tissues and biological materials: a critical review[J]. Critical Reviews in Biomedical Engineering, 1989, 17(1): 25-104.
[2] Jossinet J, Schmitt M. A review of parameters for the bioelectrical characterization of breast tissue[J]. Annals of the New York Academy of Sciences, 1999, 873(1): 30-41.
[3] Wilkinson B A, Smallwood R H, Keshtar A, et al. Electrical impedance spectroscopy and the diagnosis of bladder pathology: a pilot study[J]. The Journal of Urology, 2002, 168(1): 1563-1567.
[4] 黄欣, 刘国强, 夏慧, 等. 感应式磁声成像的脉冲磁场研究[J]. 电工技术学报, 2013, 28(2): 67-72.
Huang Xin, Liu Guoqiang, Xia Hui, et al. Study of pulsed magnetic field used in magnetioacoustic tomography with magnetic induction[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 67-72.
[5] 张帅, 李子秀, 张雪莹, 等. 基于时间反演的磁动力超声成像仿真与实验[J]. 电工技术学报, 2019, 34(16): 3303-3310.
Zhang Shuai, Li Zixiu, Zhang Xueying, et al. The simulation and experiment of magneto-motive ultrasound imaging based on time reversal method[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3303-3310.
[6] 辛学刚. 人体组织电特性磁共振断层成像(MR EPT)技术进展[J]. 中国生物医学工程学报, 2015, 34(1): 83-90.
Xin Xuegang. Technological progresses of the mag- netic resonance electrical property tomography of human tissues[J]. Chinese Journal of Biomedical Engineering, 2015, 34(1): 83-90.
[7] Vaidya M V, Collins C M, Sodickson D K, et al. Dependence of and field patterns of surface coils on the electrical properties of the sample and the MR operating frequency[J]. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering, 2016, 46(1): 25-40.
[8] 李彩莲, 李元园, 刘国强. 基于磁声电技术的肺部组织成像仿真研究[J]. 电工技术学报, 2021, 36(4): 732-737.
Li Cailian, Li Yuanyuan, Liu Guoqiang. Simulation of lung tissue imaging based on magneto-acousto- electrical technology[J]. Transactions of China Elec- trotechnical Society, 2021, 36(4): 732-737.
[9] Liao Yupeng, Oros-Peusquens A M, Lindemeyer J, et al. An MR technique for simultaneous quantitative imaging of water content, conductivity and suscepti- bility, with application to brain tumours using a 3T hybrid MR-PET scanner[J]. Scientific Reports, 2019, 9(1): 1-12.
[10] 杨文晖. 磁共振成像发展与超高场磁共振成像技术[J]. 物理, 2019, 48(4): 227-236. Yang Wenhui. The development of ultra-high field magnetic resonance imaging[J]. Physics, 2019, 48(4): 227-236.
[11] Rosenkrantz A B, Verma S, Choyke P. Prostate magnetic resonance imaging and magnetic resonance imaging targeted biopsy in patients with a prior negative biopsy: a consensus statement by AUA and SAR[J]. The Journal of Urology, 2016, 196(6): 1613- 1618.
[12] Zhang Xiaotong, de Moortele P F V, Schmitter S, et al. Complex B1 mapping and electrical properties imaging of the human brain using a 16-channel transceiver coil at 7T[J]. Magnetic Resonance in Medicine, 2013, 69(5): 1285-1296.
[13] Tha K K, Katscher U, Yamaguchi S, et al. Noninvasive electrical conductivity measurement by MRI: a test of its validity and the electrical conductivity characteristics of glioma[J]. European Radiology, 2018, 28(1): 348-355.
[14] Mori N, Tsuchiya K, Sheth D, et al. Diagnostic value of electric properties tomography (EPT) for differ- entiating benign from malignant breast lesions: comparison with standard dynamic contrast-enhanced MRI[J]. European Radiology, 2019, 29(4): 1778- 1786.
[15] Voigt T, Katscher U, Doessel O. Quantitative conductivity and permittivity imaging of the human brain using electric properties tomography[J]. Magnetic Resonance in Medicine, 2011, 66(2): 456- 466.
[16] Liu Jiaen, Zhang Xiaotong, Schmitter S, et al. Gradient-based electrical properties tomography (g EPT): a robust method for mapping electrical properties of biological tissues in vivo using magnetic resonance imaging[J]. Magnetic Resonance in Medicine, 2015, 74(3): 634- 646.
[17] Hampe N, Herrmann M, Amthor T, et al. Dictionary- based electric properties tomography[J]. Magnetic Resonance in Medicine, 2019, 81(1): 342-349.
[18] 陈海燕, 赵世龙, 李晓南, 等. 低场永磁体磁共振射频场映像[J]. 波谱学杂志, 2018, 35(4): 498-504.
Chen Haiyan, Zhao Shilong, Li Xiaonan, et al. B1 mapping on low-field permanent magnet MRI scanner[J]. Chinese Journal of Magnetic Resonance, 2018, 35(4): 498-504.
[19] 张帅, 高昕宇, 周振宇, 等. 基于GrC模型的经颅磁声电刺激对神经元放电活动的影响[J]. 电工技术学报, 2019, 34(17): 3572-3580.
Zhang Shuai, Gao Xinyu, Zhou Zhenyu, et al. Effect of transcranial magnetic-acoustic electrical stimu- lation on neuronal discharge activity based on GrC model[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3572-3580.
[20] Astrid L L, Brunner D O, Pruessmann K P, et al. B1+ phase mapping at 7T and its application for in vivo electrical conductivity mapping[J]. Magnetic Resonance in Medicine, 2012, 67(2): 552-561.