0 引言
电穿孔是一种通过脉冲电场在细胞膜上产生瞬时孔进而促进大分子进入细胞的技术。近年来，电穿孔技术已成功应用于基因转移[1-2]、药物传递[3]、肿瘤消融[4-8]等领域，并展现出良好的应用前景。
电穿孔技术的一个重要应用是促进细胞摄入并表达DNA分子。电穿孔过程中细胞膜上产生大量微孔，从而能够促进细胞摄入DNA分子，目前该方法已成为最有效的基因转移方法之一[9-11]。基因转移的有效性取决于脉冲参数，如幅值、脉宽、重复频率等[12-13]。国内外学者在这方面开展了大量实验，研究了微/毫秒级矩形脉冲对基因转移的影响，并取得了富有成效的研究成果[14-16]。
随后，研究人员通过大量的实验发现，高压短脉冲和中/低压长脉冲的组合对各种组织的基因转染十分有效[17-19]。因此，学者们开始研究双脉冲对细胞摄取DNA的影响，如文献[20]从实验角度分析了不同脉冲参数对DNA摄取的影响，证实了高压脉冲加中压脉冲在DNA摄取方面拥有较好效果；文献[21]研究了第一脉冲为交流脉冲，第二脉冲为低压直流脉冲的双脉冲对细胞摄取不同大小荧光素葡聚糖的影响，结果表明，增加第一脉冲幅值，能够促进荧光素葡聚糖分子的摄取。
上述研究从实验角度证实了脉冲电场对DNA分子摄入的促进作用，并给出了不同脉冲参数对细胞摄入DNA分子的影响规律，但这些研究并未从机理角度分析脉冲电场作用下细胞摄入DNA分子的机制，进而导致实验中脉冲参数的选择仍十分盲目，从而严重制约该方法的临床应用及推广。
目前，关于脉冲电场作用下细胞摄入DNA分子的理论研究仍较为匮乏，文献[22]通过Nernst- Planck方程，提出了细胞的DNA摄取模型；文献[23]同样基于Nernst-Planck方程，改进细胞摄取DNA模型；文献[24]在文献[23]的基础上考虑控制作用，研究了细胞对DNA的摄取。上述研究模型都是基于Nernst-Planck方程，而文献[25]则基于化学动力学方案和梯形势垒模型，研究了各种脉冲参数对DNA分子摄取的影响，其结果与文献[16]中的结论相符，说明了脉冲电场变化率在12.5V/cm/μs和50V/cm/μs之间，对DNA分子摄取影响较小。该部分的理论研究侧重解释电穿孔对DNA分子摄入的促进作用，并未从机理研究角度给出优选的脉冲参数组合，以实现最大程度的DNA分子摄入。
综上所述，本文基于电穿孔、孔径变化以及DNA迁移方程，建立了脉冲电场作用下细胞摄取DNA的数值模型，并通过计算分析典型单脉冲/双脉冲电场参数对细胞摄取DNA的影响机制。
1 数值模型
1.1 球形细胞摄入DNA分子模型
电穿孔是一种高度非线性的动力学现象。通常，由电穿孔导致的基因传递过程可分为四个阶段，即微孔形成、微孔演化、DNA摄取和微孔重新密封。脉冲电场作用下球形细胞摄入DNA分子模型如图1所示，细胞半径为10μm，细胞内外分别为细胞质和细胞外液，其DNA分子浓度分别为Ci和Co，DNA分子通过细胞膜上电穿孔产生的微孔（孔径＞10nm）进出细胞，进而改变细胞内DNA分子浓度；球形细胞上下边界代表施加脉冲电场的平板电极，且电极长度远远大于细胞尺寸，从而使球形细胞处于电场强度为E的均匀电场之中。
图1 球形细胞摄入DNA分子模型
Fig.1 The model of a spherical cell uptakes DNA molecular
1.2 孔密度方程
W. Krassocwska等[26]提出以常微分方程来描述脉冲电场作用下细胞电穿孔过程中微孔密度的变化，该方程已广泛地运用于细胞电穿孔的数值模拟仿真。微孔密度N随时间t的变化为
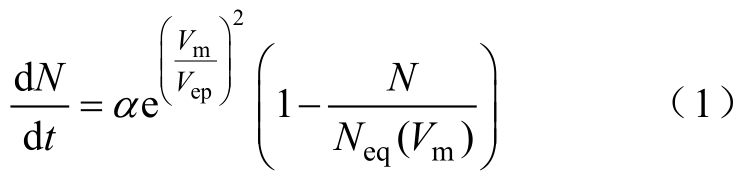
式中，Vm为跨膜电位；Vep为电穿孔的特征电压；α为产生率系数；Neq为平衡孔密度，有
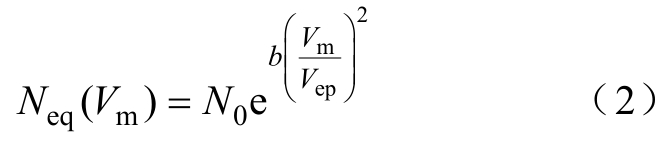
式中，N0为Vm=0时的平衡孔密度；b=(rm/r*)2，半径rm为最小能量孔径，r*为亲水孔的最小孔径；N0和b皆为常数。
1.3 孔径变化方程
假设由式（1）所产生的微孔半径为rm，其孔径变化以使脂质双分子层的能量wm最小。假如在给定的时刻，存在孔径为rn（n=1, 2,…, K）的K个孔，孔径的变化由双分子层能量确定，有
式中，D为扩散系数；k为玻耳兹曼常数；T为热力学温度；wm为双分子层能量，有
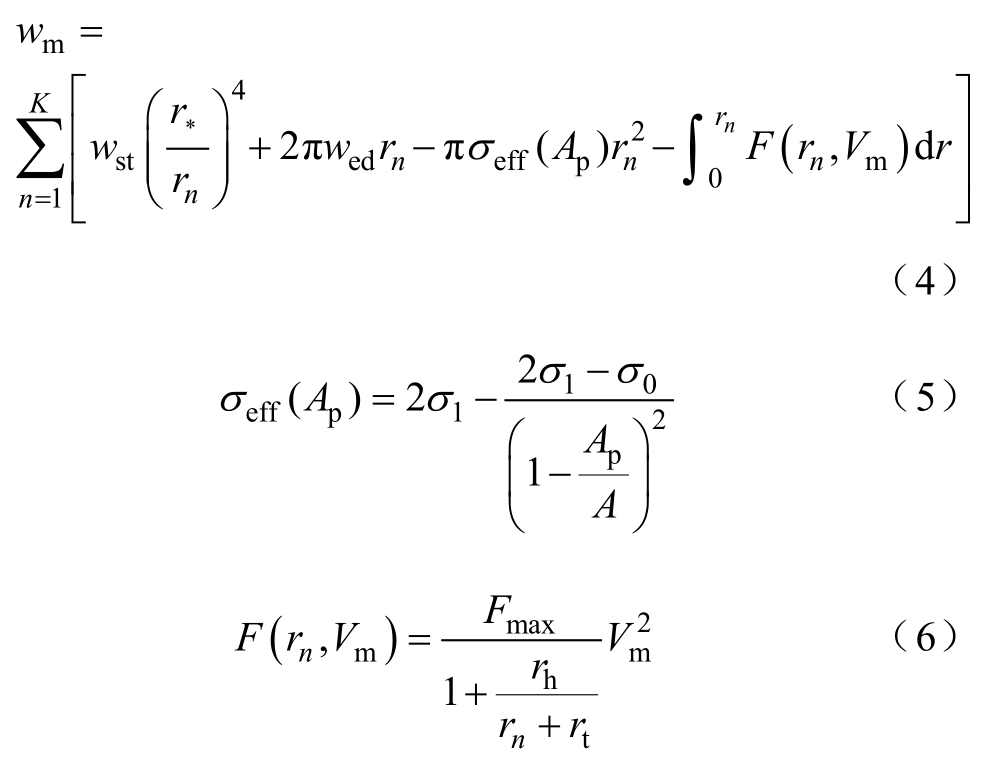
式中，wst为空间排斥能量；wed为边缘能量；σeff为膜的有效张力；σ1为碳氢-水界面张力；σ0为无 孔时膜张力；A为细胞膜面积；
为电穿 孔面积，即所有大孔的面积和；F为孔的电场力；Fmax、rh和rt为常数；Vm为跨膜电位。
1.4 DNA迁移方程
文献[22]通过Nernst-Planck方程，建立了DNA迁移模型为
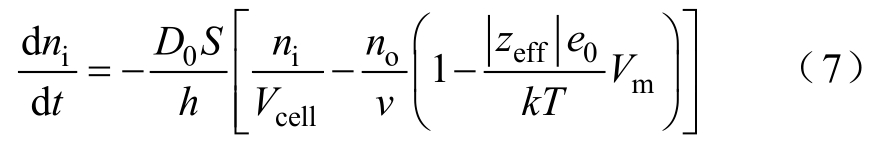
式中，ni为单个细胞内的DNA分子数；no为细胞外的DNA分子数；D0为DNA扩散系数；h为细胞膜厚度；Vcell为细胞体积；v为溶液体积；zeff为DNA分子的化合价；e0为元电荷；S为细胞电穿孔面积。
K. C. Smith等[23]对式（7）进行了修改，将其应用于每个单独的微孔，从而得到
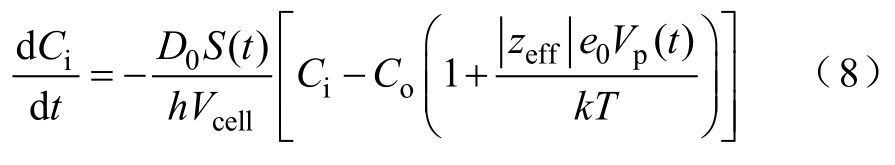
式中，S(t)为单个微孔面积；Vp(t)为电压降。二者均与时间相关。
式（7）用于整个细胞胞膜，故S是所有孔的面积和，Vm等于跨膜电位。而式（8）应用于每个单独的微孔（孔径rn＞10nm），故S(t)为单个孔的面积，Vp(t)对应于单个孔的实际电压降，有
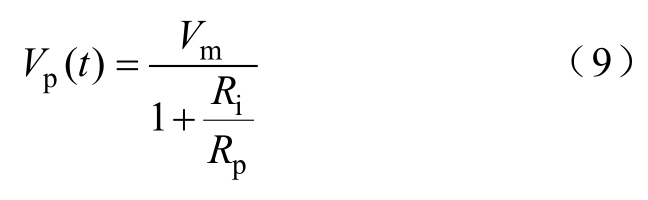
其中
式中，pR为大孔电阻；Ri为输入电阻；h为膜厚度；g为溶液电导率。
考虑到不同半径微孔摄取的DNA分子数量也不一样。因此，本文采用式（8）计算DNA浓度。
1.5 微孔恢复
当外加脉冲电场消失时，细胞膜通过微孔快速放电，导致Vm迅速下降到零，并且孔径收缩至最小能量半径rm附近，随后微孔密封进而消失，细胞恢复常态。该过程可由式（1）～式（3）表示，式（3）可预测微孔的缩小，当孔径收缩到rm时，微孔消失可由式（1）描述。
1.6 跨膜电位
脉冲电场致细胞电穿孔时，会在细胞内外两侧产生电位差，即跨膜电位；电穿孔发生时细胞膜上产生大量微孔，其中，微孔密度可由式（1）定量描述，孔径变化由式（3）定量描述，二者均影响跨膜电位的时间分布规律；此外，跨膜电位反过来会影响微孔的产生、孔径的演变以及DNA的摄取。本文将细胞膜等效为图2所示的电路模型，同时考虑大孔、小孔以及静息电位对跨膜电位的影响。
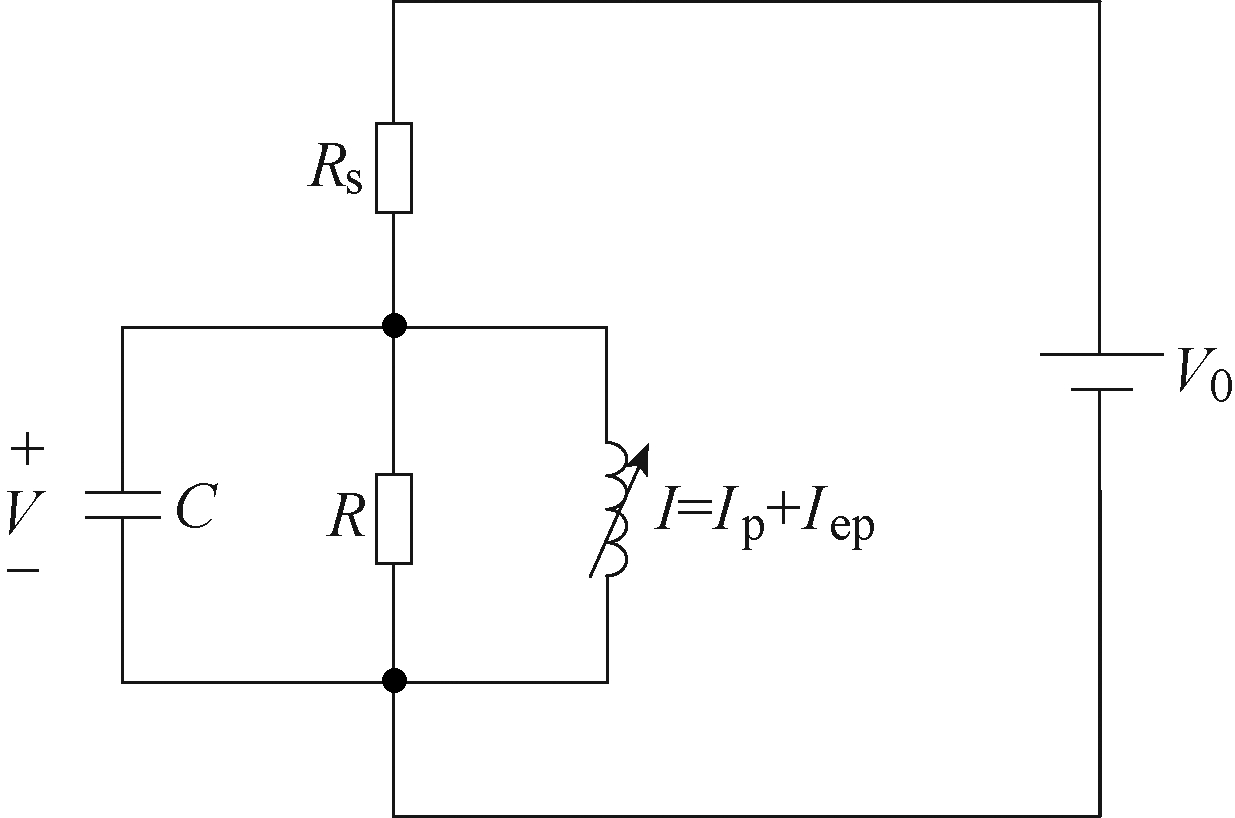
图2 细胞等效电路模型
Fig.2 Cell equivalent circuit model
电路包含通过微孔的电流I，细胞膜电容C= CmA和细胞膜电阻R=Rm/A，其中，Cm和Rm分别为膜的表面电容和表面电阻。V0为外加脉冲电场，电阻Rs为实验装置的串联电阻。因此，脉冲电场作用下细胞膜的等效电容电压V可由以下常微分方程求解，有
而跨膜电位Vm=V+Vrest。其中，Vrest为细胞膜的静息电位，而式（10）中，I=Ip+Iep为通过所有微孔 的电流。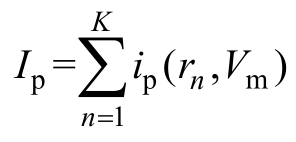
为通过所有大孔的电流，ip 为通过单个大孔的电流，有
Iep则为通过小孔的电流，有
其中
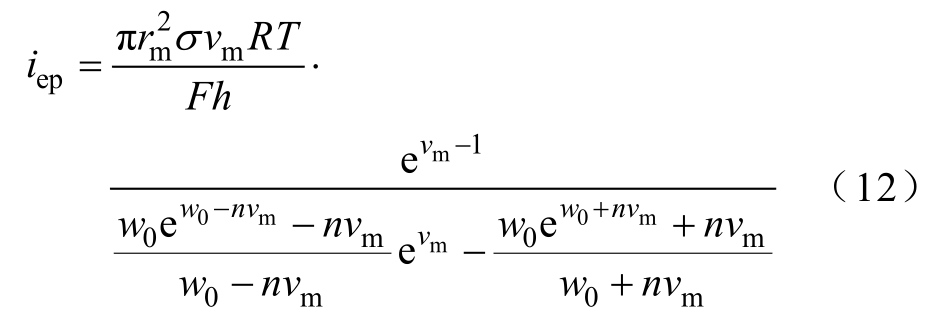
式中，iep为单个小孔的电流；σ 为填充孔的水溶液电导率；F为法拉第常数；R为通用气体常数；w0为孔内的能量势垒；n为孔的相对入口长度；vm为无量纲跨膜电势，vm=VmF/RT。
1.7 脉冲电场参数
本文中所用脉冲如图3和图4所示。图3为上升时间tr（下降时间tf =tr）、半峰值脉宽th、脉冲幅值V1的单个矩形脉冲，该脉冲为DNA电转染实验中常用的典型脉冲；图4为不同脉宽、幅值的两个矩形脉冲构成的双脉冲，tr1、tr2（tf1, tf2）分别为第一脉冲和第二脉冲的上升时间（下降时间），th1、th2分别为第一脉冲和第二脉冲的脉宽，V1、V2分别为第一脉冲的幅值和第二脉冲的幅值，tb为两个脉冲 的时间间隔，该脉冲在DNA电转染实验中具有较好的效果。具体参数如下所示，单脉冲：①电场强度1kV/cm（2V）、脉宽100μs，上升/下降时间10μs的方波脉冲；②电场强度0.5kV/cm（1V）、脉宽1ms，上升/下降时间100μs的方波脉冲；以及由上述两种单脉冲组成的两种双脉冲方案，分别为100μs脉冲+ 1ms脉冲和1ms脉冲+100μs脉冲。
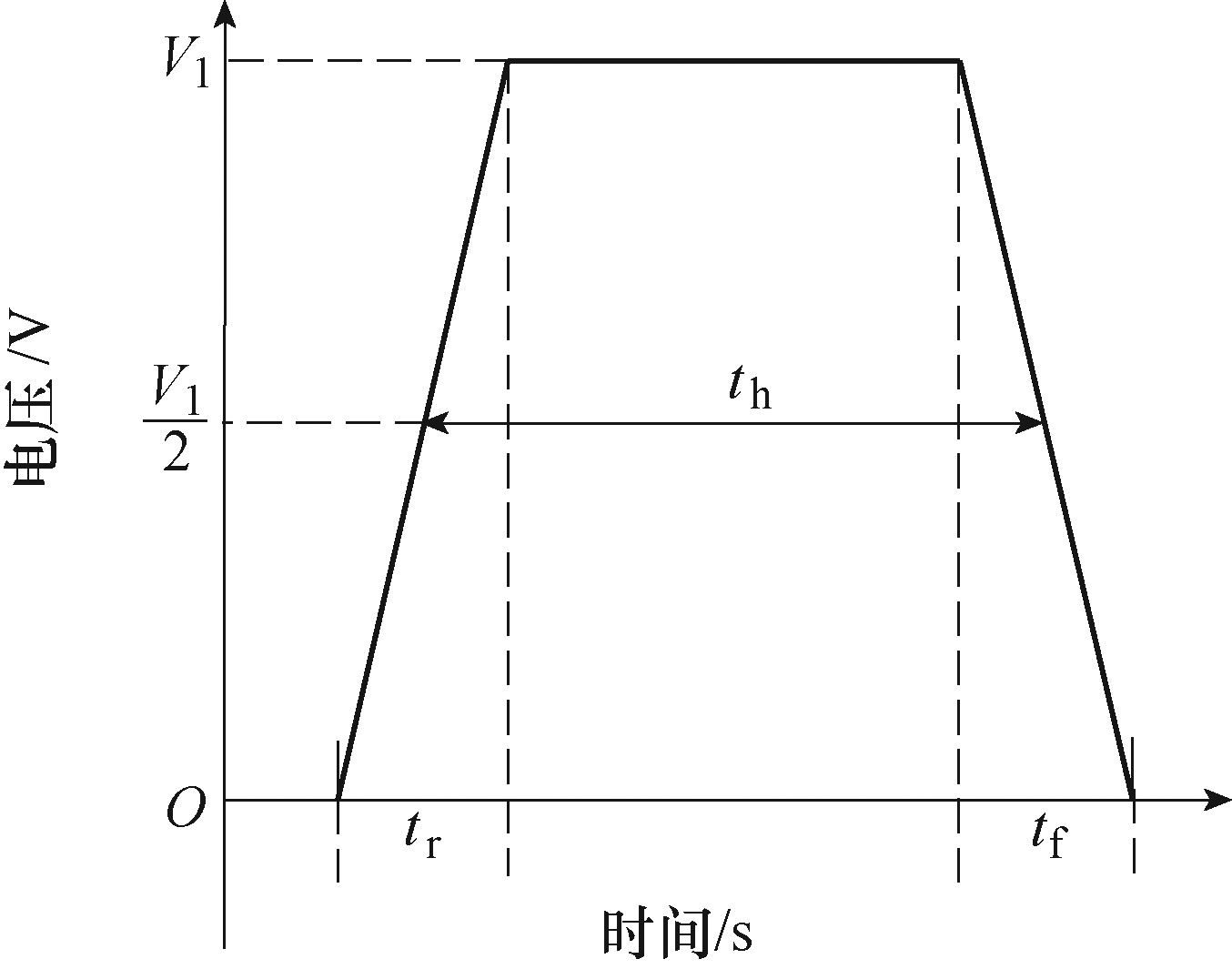
图3 单个矩形脉冲
Fig.3 Single rectangular pulse
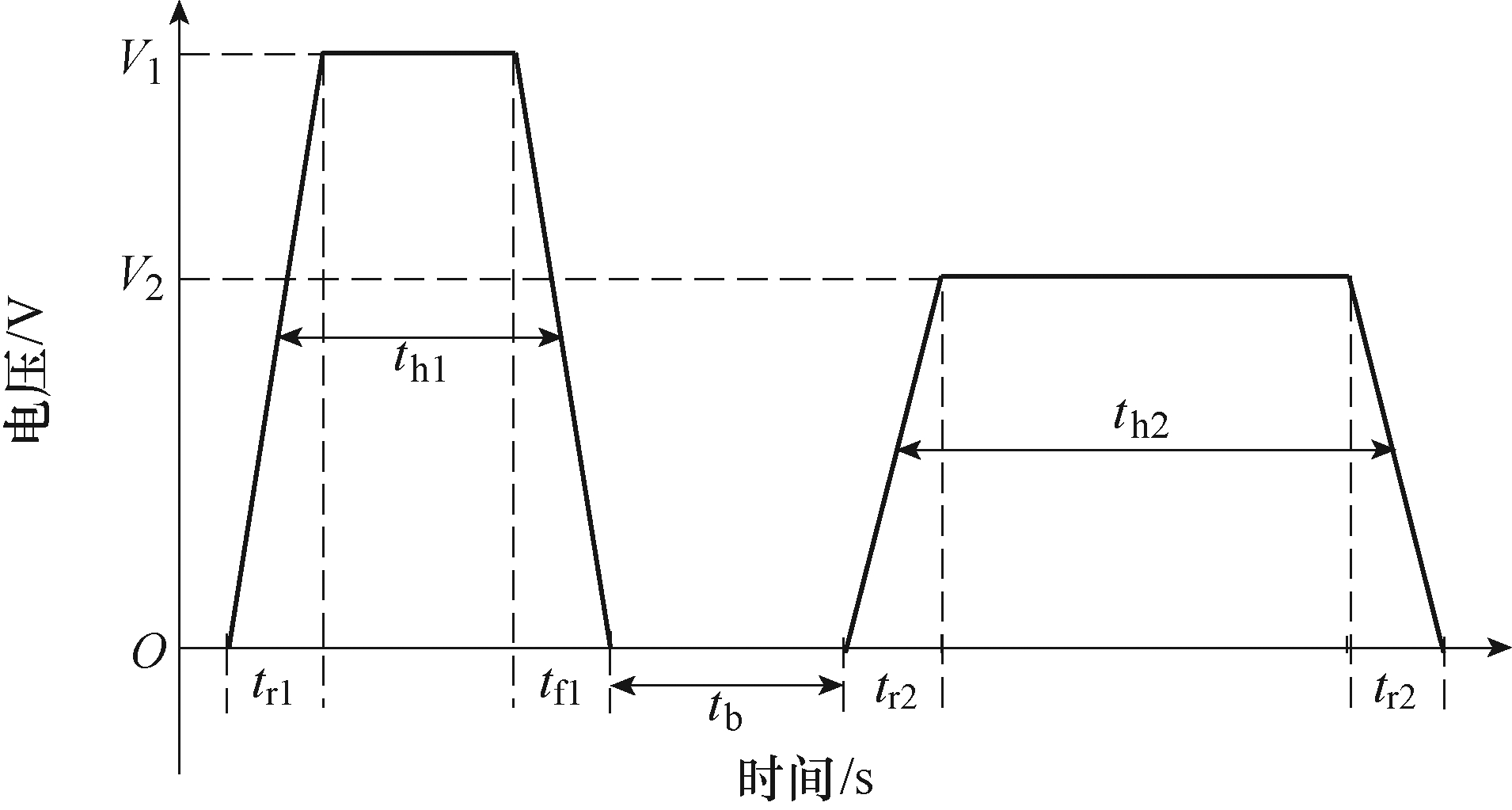
图4 不同参数组合构成的双脉冲
Fig.4 A double pulse composed of different parameter combinations
1.8 数值模型算法实现
上述模型可通过Matlab求解。模型假定存在大孔和小孔两个微孔群：由微孔密度N描述在最小能量半径rm附近聚集的小孔，并假设小孔半径为rm；以及半径大于rm的大孔，其半径变化由式（3）决定。
初始条件假定膜上有静息电位Vm(0)=−80mV，大孔数K=0，小孔密度N(0)=N0，且细胞内DNA浓度Ci=0。时间循环包含以下步骤：
（1）小孔产生。使用式（1）计算产生或消失的小孔，即孔密度N的值。
（2）大孔数量。小孔产生后其中部分小孔将变为大孔。因此，大孔增加的个数为（floor(NA)），相应地孔密度N减小相应的值（K/A）。为确保大孔半径在数值上不同，假定大孔初始半径服从均值为rm、标准偏差为0.001nm的正态分布。
（3）大孔演化。根据所有大孔的半径，计算所有大孔的面积和Ap，根据式（5）、式（6）计算有效膜张力σeff和电场力F；并根据式（3）计算每个大孔的半径。
（4）大孔转化。任何一个大孔的半径降至rm以下，则该孔转化为小孔。因此，K减少1并且N增加1/A。
（5）DNA摄取。根据式（8），计算每个孔（孔径rn＞10nm）的DNA分子浓度，将每个孔的浓度增加量相加除以2，得到整个细胞的DNA分子浓度增加量，再加上前一时刻的DNA分子浓度，得到现在DNA分子浓度。
（6）跨膜电位计算。根据式（11）和式（12）分别计算小孔和大孔的电流，再计算总电流I，并根据式（10）和Vm=V+Vrest，计算Vm的值。
式（1）、式（3）、式（8）、式（10）在每个时间循环中通过Matlab中的函数ode23t进行求解。而初始循环时间步长设为1ns，基于自适应时间步进算法模拟计算上述数学模型，即根据实际情况更改时间步长，以加快程序运算求解。本文结果为计算至脉冲降为0V的下一时刻所得结果，时间步长分别为1ns、10ns、100ns（1μs）。各参数汇总见表1。
表1 各参数汇总
Tab.1 Summary table of parameters
参 数 数 值 创造率系数α/(m2·s) 1×109 电穿孔的特征电压Vep/V 0.258 Vm=0时的孔密度N0/m2 1.5×109 亲水孔的最小半径r*/m 0.51×10−9 Vm=0时的最小能量半径rm/m 0.8×109 孔径的扩散系数D/(m2/s) 5×1014 热力学温度T/K 310 空间排斥能量wst/J 1.4×10−19 边缘能量wed/(J/m) 1.8×10−11 无孔时双分子层的张力σ0/(J/m2) 1×10−3 水-烃界面张力σ1/(J/m2) 2×10−2 膜面积A/m2 1.26×10−9 Vm=1V时的最大电力Fmax/(N/V2) 0.7×10−9 式（6）中的常数rh/m 0.97×10−9 式（6）中的常数rt/m 0.31×10−9 DNA的扩散系数D0/(m2/s) 1.3×10−12 胞外DNA浓度[DNA]0/(mol/m3) 1.3×10−6 膜的表面电容Cm/(F/m2) 9.5×10−3 膜的表面电阻Rm/(Ω·m2) 0.523 电源内阻Rs/Ω 100 膜的厚度h/m 5×10−9 溶液电导g/(S/m) 2 水溶液的电导率σ /(S/m) 0.6 孔内的能量势垒w0 2.65 孔的相对入口长度N 0.15 静息电位Vrest/V −80×10−3
2 仿真结果
2.1 模型验证
脉冲作用下各参数随时间变化趋势如图5所示。为验证本文模拟仿真算法的正确性，根据文献[23]中的模型及其参数，可重现文献中结果，如图5中虚线所示。可见，在幅值1.2V，脉宽10ms的单脉冲作用下，跨膜电位在达到1.2V后缓慢衰减至0.94V，孔数随时间增至30 500，孔径最大值和均值在达到峰值（55nm/46nm）后共同衰减至25nm，电穿孔面积比随时间增至4.8%。仿真结果与文献结果一致，说明本文数值模拟仿真程序的正确性。基于本文模型，在相同脉冲电场参数作用下电穿孔参数随时间变化趋势如图5中实线所示。跨膜电位（见图5a）在脉冲施加瞬间达到峰值约1.12V，而后迅速衰减并趋于0.93V；孔数（见图5b）则随时间单调增加，最终在10ms时增至18 300左右；孔径的最大值和均值（见图5c）均在短时间内达到峰值（120nm/72nm），随后缓慢减小，在2ms时两者几乎相等，说明所有大孔半径相近；由图5d可知，电穿孔面积比（Ap/A）在短时间内快速增加，而后缓慢增至4.2%。与文献中结果比较可得，图5中的各参数变化规律与文献中结果基本一致，但孔数和电穿孔面积比低于文献中结果，孔径最大值和均值的峰值均高于文献中结果，这是由于本文模型考虑了小孔电流以及静息电位的影响。
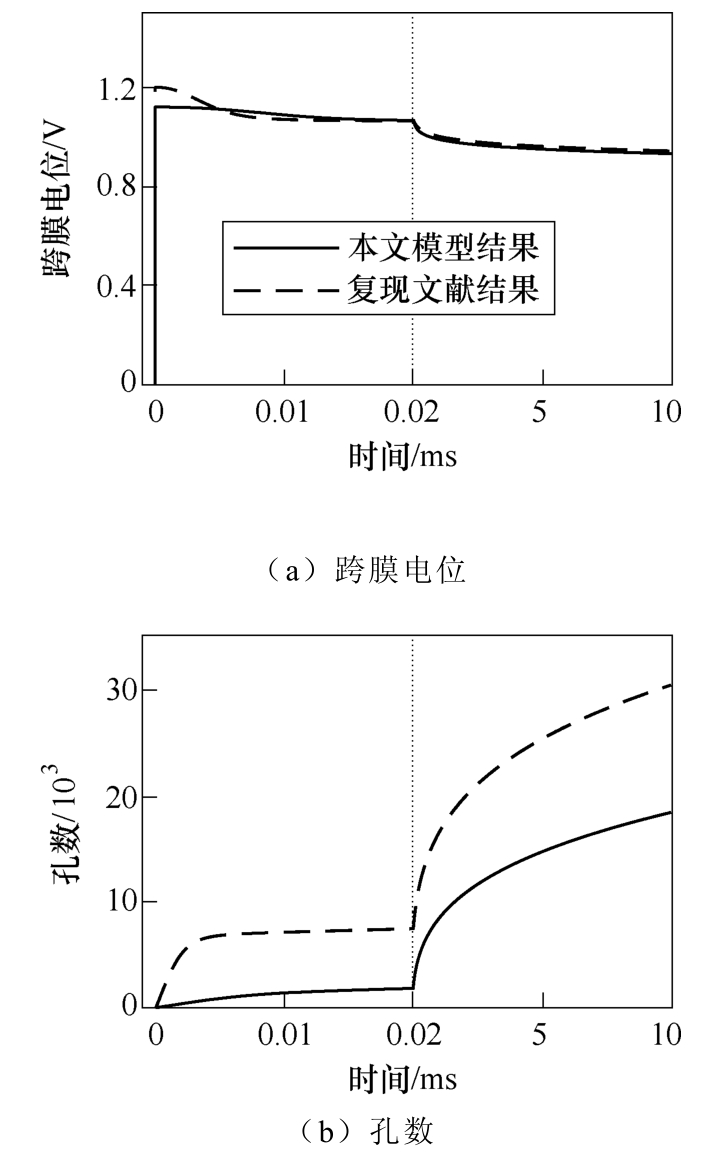
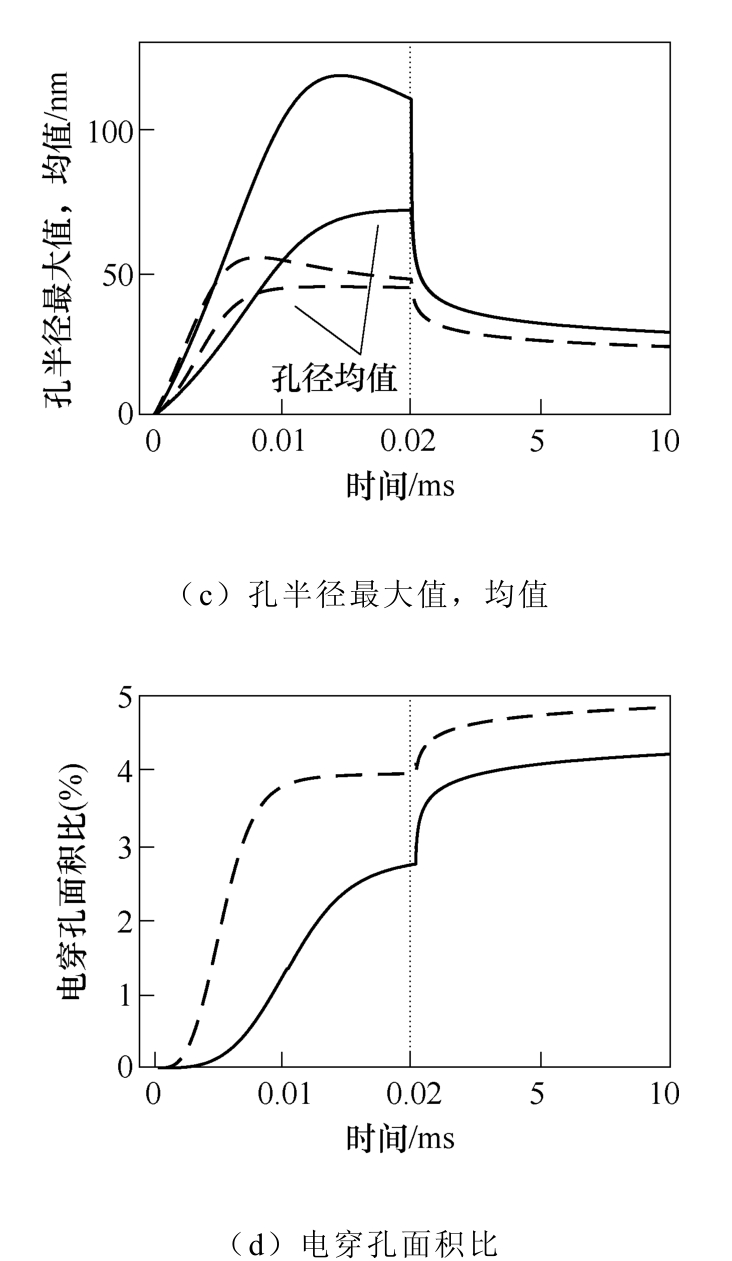
图5 脉冲作用下各参数随时间变化趋势
Fig.5 The variation trend of each parameter with time under the single pulse
2.2 单脉冲仿真结果
图6为100μs和1ms单脉冲作用下各参数随时间的变化曲线。根据图6可知，100μs脉冲作用下，跨膜电位（见图6a）从−80mV处开始上升，在上升时间结束时达到峰值约1.3V，而后平缓地下降至1.12V，在脉冲下降时间骤降为负值；进而导致孔数（见图6b）在跨膜电位上升期间急剧变化，而后变化趋势逐渐平缓，最终增至133 900左右；而孔径最大值和均值（见图6c、图6d）在上升时间内相继达到峰值（38nm/20nm）后共同下降并趋于16nm，因孔数和孔径的急剧变化，孔径均值变化曲线出现了波动。因为上升时间和幅值的差异，在1ms脉冲作用下，跨膜电位随脉冲幅值变化而变化，孔数随时间缓慢增至286（见图6b标注处）。孔径迅速扩张至800nm，而后随时间衰减至120nm。因此，两种脉冲作用下电穿孔面积比（见图6e）和DNA浓度（见图6f）出现巨大的差异，在100μs脉冲作用下，电穿孔面积比达到8.8%，DNA浓度随时间增至7.8×10−8mol/m3；而在1ms脉冲作用下，电穿孔面积比稳定在1.8%，DNA浓度缓慢增长，在脉冲结束时DNA浓度达到1.1×10−8mol/m3。
图6 100μs和1ms单脉冲作用下各参数随时间的变化曲线
Fig.6 The change curves of each parameter with time under the action of 100μs and 1ms pulse
2.3 双脉冲仿真结果
上述两种单脉冲组成的双脉冲（tb=0）作用下的仿真结果如图7所示。100μs+1ms双脉冲作用下，跨膜电位（见图7a）随外加脉冲幅值变化而变化；孔数（见图7b）在第一脉冲期间随时间急剧增加，并在第二脉冲期间稳定在136 000左右；孔径最大值和均值（见图7c、图7d）受跨膜电压和孔数的影响，在第一脉冲快速上升后共同衰减至16nm，并最终在下降时间衰减至0.8nm，而后在第二脉冲作用时孔径又迅速上升并稳定在10.6nm，并在下降时间衰减至0.8nm；电穿孔面积比（见图7e）在第一脉冲期间稳定在8.8%，在第二脉冲作用时其值下降并保持在3.8%；由图7f可得，DNA的浓度随时间的增加而增长，最终增至3.45×10−7mol/m3。
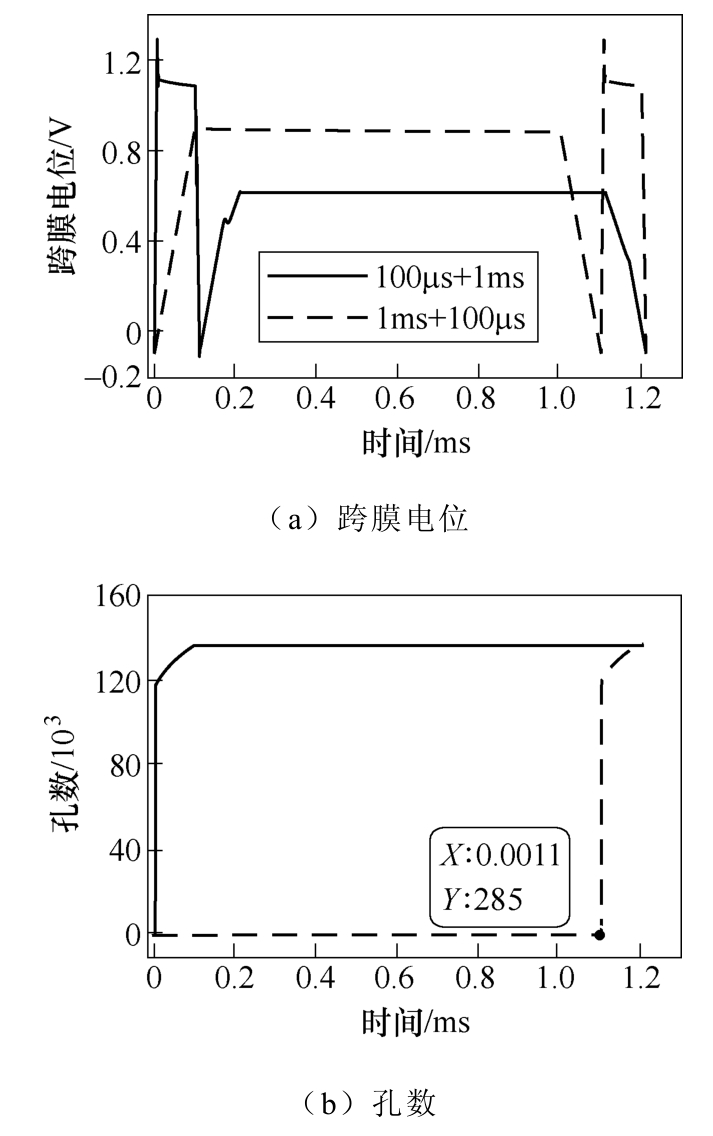
图7 双脉冲作用下各参数随时间变化趋势
Fig.7 The variation trend of parameters with time under the action of double pulses
而在双脉冲1ms+100μs的作用下，跨膜电位同样随输入电压的变化而变化；孔数在第一脉冲期间缓慢增至285（图7b标注处），随后在第二脉冲作用下急剧增长到136 000左右；孔径受孔数和跨膜电位的影响，在第一脉冲期间增长到800nm后衰减至120nm，并在第二脉冲作用时衰减至15nm；根据图7e可知，电穿孔面积比在第一脉冲期间稳定在1.7%，随后上升并保持在8.8%；DNA浓度则在第一脉冲作用下随时间缓慢增长，并在第二脉冲期间迅速增至8.9×10−8mol/m3。
2.4 时间间隔和脉冲幅值对DNA摄取的影响
改变双脉冲的时间间隔，使其在0～1s之内变化，观察DNA浓度的变化，结果如图8所示。根据图8可得，在双脉冲100μs+1ms的作用下，细胞内DNA浓度不随时间间隔的增长而变化，DNA浓度始终稳定在3.45×10−7mol/m3左右。在不同时间间隔的双脉冲1ms+100μs作用下，DNA浓度如图8中虚线所示，可见，在时间间隔小于10ms时，DNA浓度保持在8.9×10−8mol/m3，当时间间隔大于10ms 时，DNA浓度随时间间隔的增长而增加，在时间间隔增至1s时，DNA浓度达到1.68×10−7mol/m3。
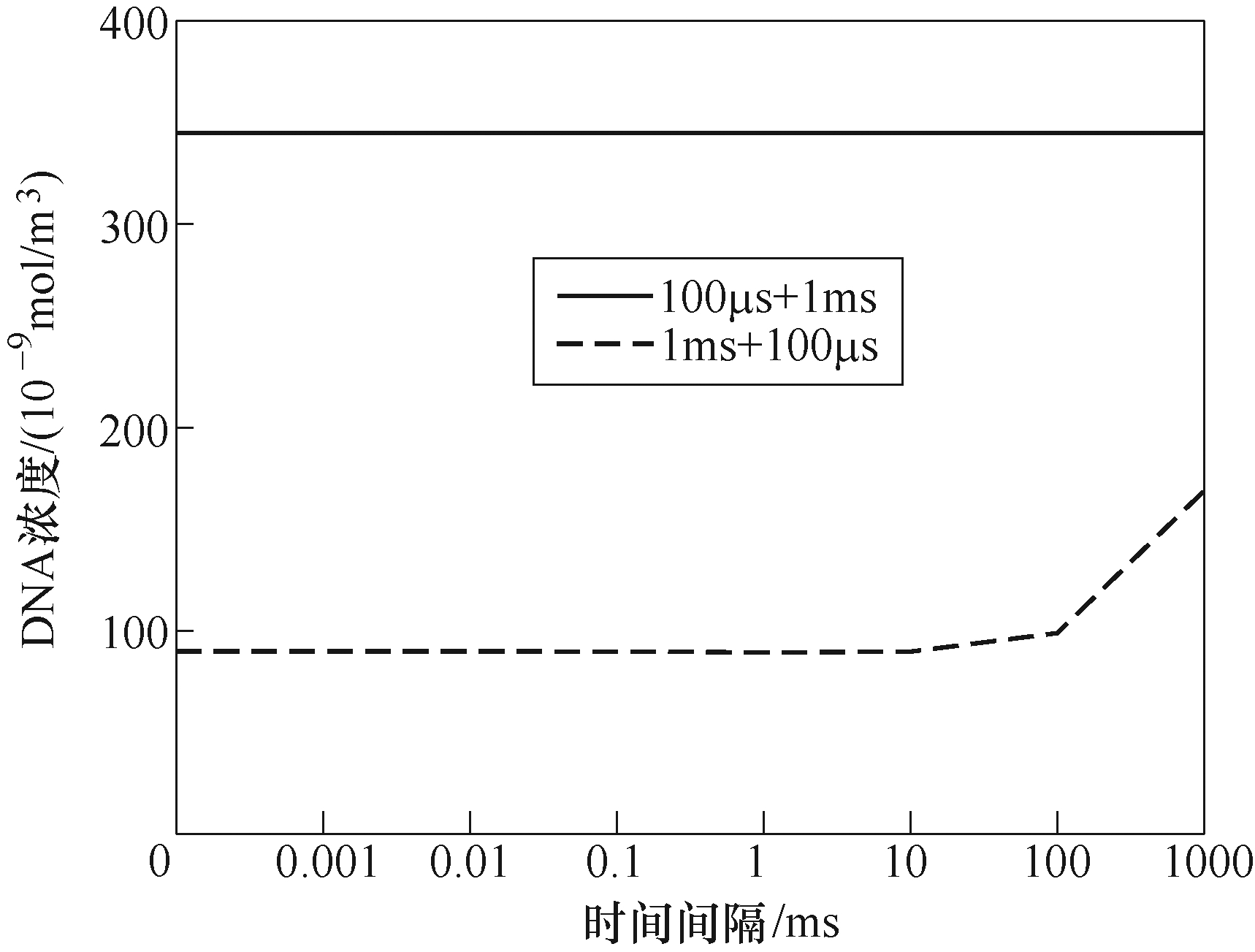
图8 时间间隔对DNA浓度的影响
Fig.8 The effect of time interval on the concentration of DNA
脉冲参数见表2。
表2 脉冲参数
Tal.2 Pulse parameter list
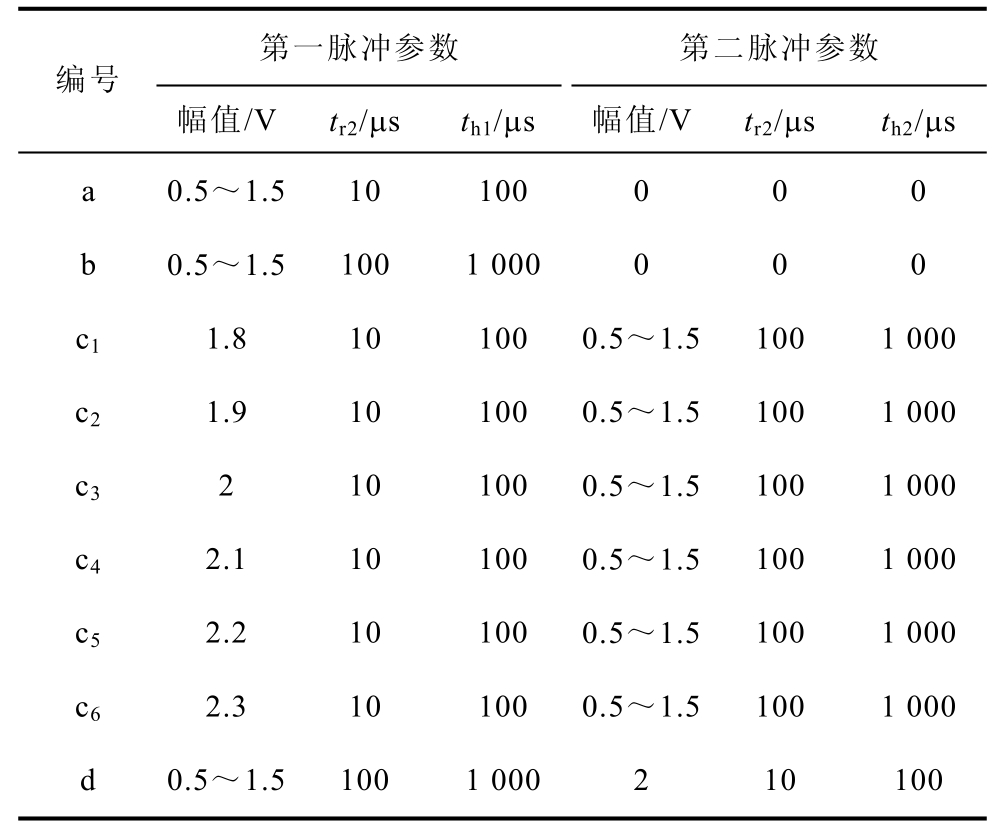
第一脉冲参数 第二脉冲参数 编号 幅值/V tr2/μs th1/μs 幅值/V tr2/μs th2/μs a 0.5～1.5 10 100 0 0 0 b 0.5～1.5 100 1 000 0 0 0 c1 1.8 10 100 0.5～1.5 100 1 000 c2 1.9 10 100 0.5～1.5 100 1 000 c3 2 10 100 0.5～1.5 100 1 000 c4 2.1 10 100 0.5～1.5 100 1 000 c5 2.2 10 100 0.5～1.5 100 1 000 c6 2.3 10 100 0.5～1.5 100 1 000 d 0.5～1.5 100 1 000 2 10 100
此外，本文研究了脉冲幅值对DNA浓度的影响。图9为表2中脉冲参数作用下DNA浓度随幅值的变化趋势。可见，单脉冲作用下，在脉冲幅值小于1V时，DNA浓度变化率较小。当幅值大于1V时，DNA浓度随幅值的增加而迅速上升，在脉冲幅值为1.5V时，100μs（1ms）脉宽的DNA浓度为4.4×10−8（3.55×10−7）mol/m3。因c3和d两种情况只是交换了脉冲施加顺序，故两者能量相等。可见，在c3的作用下，当第二脉冲幅值较低（V2＜1V）时，DNA浓度无变化，当幅值大于1V时，DNA浓度随第二脉冲幅值的增加而增加；而在d的作用下，DNA浓度在第二脉冲幅值小于1V时缓慢增长，而后随幅值的增加而快速增加。而当改变第一脉冲幅值时，DNA浓度变化曲线如图9c所示。可见，每个幅值对应的DNA浓度与第二幅值关系曲线都相似，都呈现出当第二脉冲幅值低于某值时DNA浓度都保持不变，当超过该值时DNA浓度都随第二脉冲幅值呈线性增长的变化趋势；并且当第二脉冲幅值一定时，DNA摄取量与第一脉冲的幅值正相关。
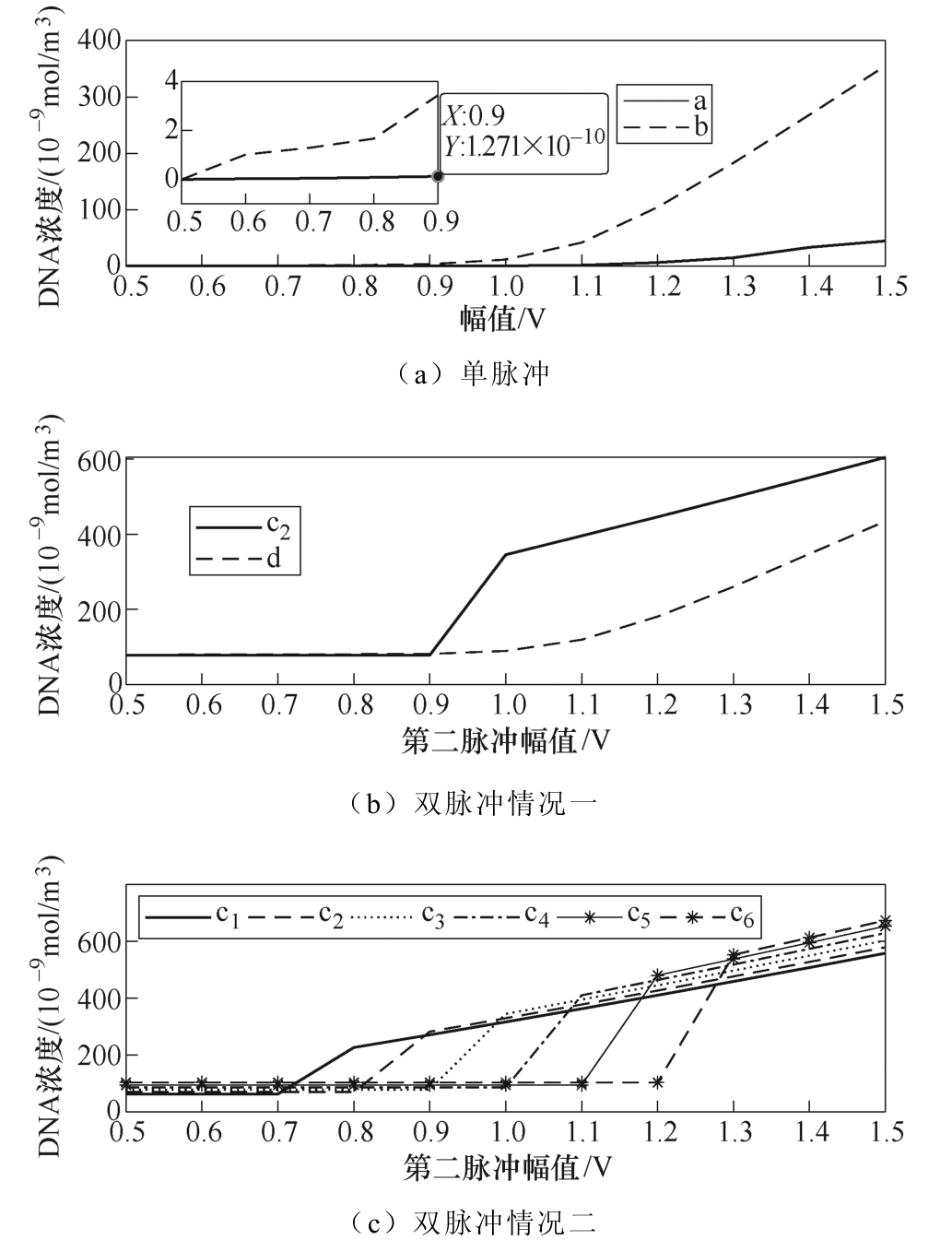
图9 幅值对DNA摄取量的影响
Fig.9 Effect of amplitude on DNA uptake
3 讨论
本文所建立的DNA电转染数值模型基于电穿孔方程、孔径变化方程以及DNA迁移方程，并将细胞膜等效为电阻和电容的组合，给出了细胞膜电穿孔动态变化过程、孔径变化过程以及DNA摄取过程。相较以前的模型，本文在跨膜电位计算时引入了小孔电流和静息电位，从而使得跨膜电位的计算更为精确。图5中的仿真结果明确表明，当引入小孔电流和静息电位时，微孔个数、孔径最大值和均值的峰值、电穿孔面积比都发生了较大的改变。图10给出在100μs和1ms单脉冲作用下小孔电流与大孔电流的比值。由图10可知，在脉冲施加时该比值迅速上升（最大时约为7%），而后迅速衰减至一个较小的值（10−7），并长期保持在该值附近。因此，小孔电流会在脉冲上升阶段对跨膜电位造成一定影响，从而在后续微孔生成和演化过程中产生影响。上述结果表明，小孔电流只在脉冲上升阶段产生一定影响，故图5中仿真结果的差异主要由静息电位的引入造成。
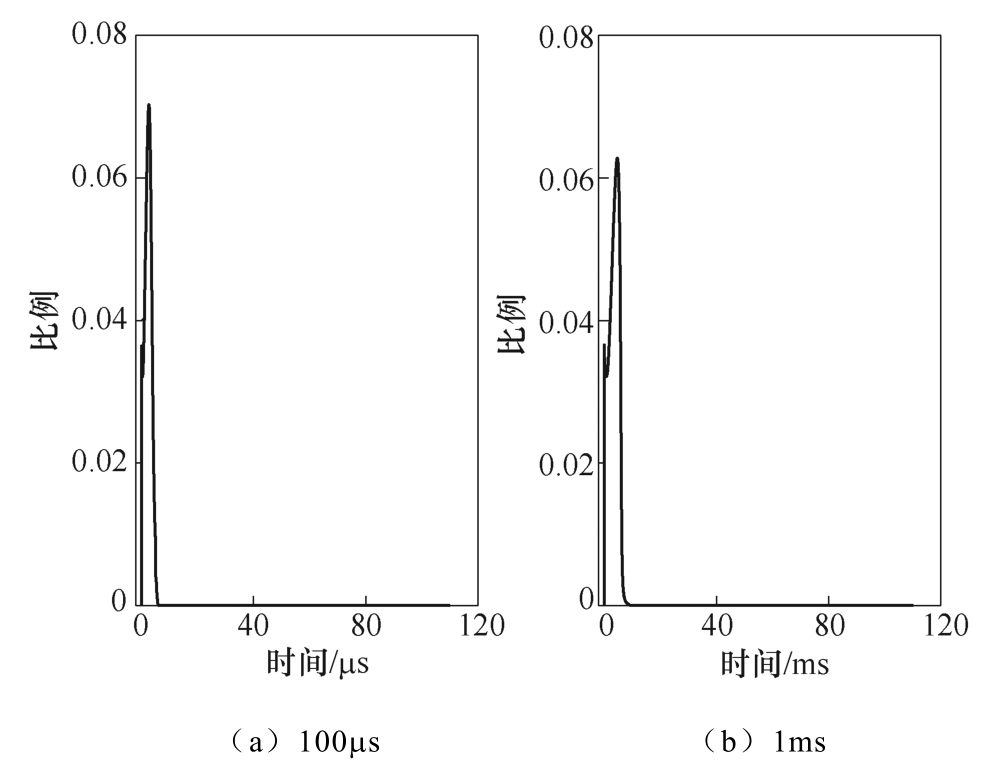
图10 100μs和1ms脉冲作用下小孔电流与 大孔电流之比
Fig.10 The ratio of small pore current to large pore current under the action of 100μs and 1ms pulse
众多学者在进行电穿孔实验时，发现了双脉冲在DNA摄取方面的独特优势。因此，本文仿真研究了双脉冲作用下胞内DNA浓度变化情况。文中由100μs和1ms单脉冲组成的双脉冲仿真结果表明，不同施加顺序对DNA摄取效果大为不同，由图6和图7可知，两种单脉冲作用下DNA摄取浓度之和与双脉冲1ms+100μs作用下的DNA摄取浓度相近，但远远小于双脉冲100μs+1ms作用下的结果，这与文献[27]的结论相吻合，双脉冲与对应高压短脉冲的DNA转染率之比如图11所示。图11中，分别从仿真（100μs+1ms）和实验（400μs+5ms）角度给出了高电压短脉冲和低电压长脉冲组成的双脉冲作用下DNA转染率相对于对应高压短脉冲的提升作用。双脉冲仿真结果和实验结果中DNA转染率分别增为各自对应单脉冲结果的4倍和14.4倍，考虑到实验与仿真脉冲参数及具体条件不同，二者基本相符，表明该脉冲组合构成的双脉冲能够显著增强DNA转染率。这是因为高压脉冲能够产生大量的大孔，而中压长脉冲能够维持孔数并使孔生长，从而摄入大量DNA分子；反之，先施加中/低压长脉冲，再施加高压短脉冲相当于单独施加两个单脉冲，两脉冲之间影响较小，故先施加高压短脉冲再施加中压长脉冲的双脉冲方案在DNA摄取方面显得更优异。
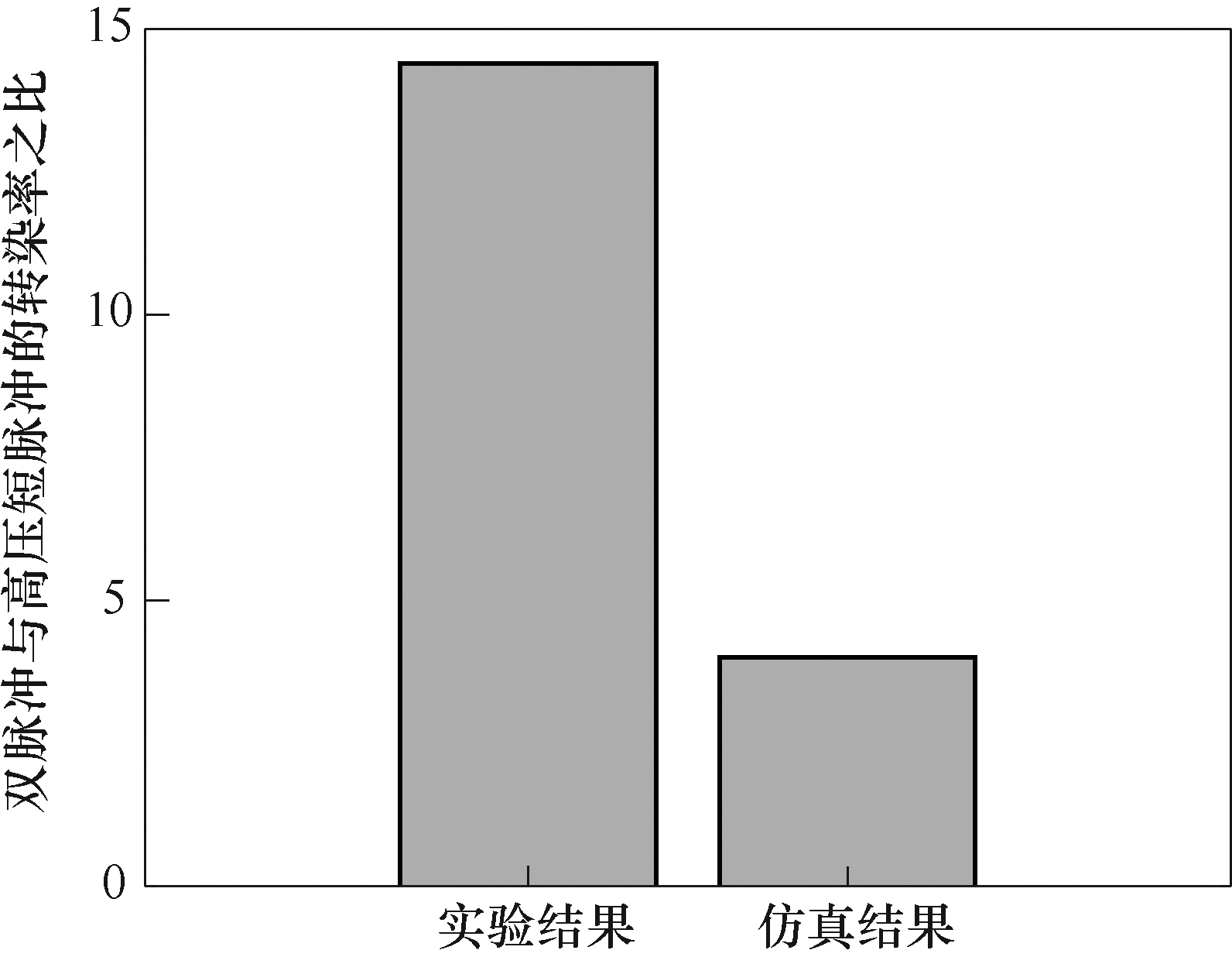
图11 双脉冲与对应高压短脉冲的DNA转染率之比
Fig.11 The ratio of DNA transfection rates between double pulses and single pulses
此外，本文也探究了双脉冲时间间隔的作用。因微孔产生后寿命为秒级，同时为了兼顾仿真时间，故本文时间间隔只计算至1s。根据结果可知，时间间隔对双脉冲100μs+1ms基本无影响，这是因为孔径在脉冲下降时间，根据式（3）收缩至0.8nm左右（见图7c、图7d），在第二脉冲施加时再次生长。故时间间隔只起到了让所有孔的孔径长时间维持在0.8nm的作用，而DNA摄取的条件是孔径大于10nm，因此，在该脉冲的作用下，时间间隔的长短不影响细胞摄取DNA。而长时间间隔（＞10ms）能提高双脉冲1ms+100μs作用时DNA的浓度，这是由于时间间隔期间孔径最大值远大于孔径均值，表明存在少数孔扩大，多数孔收缩至rm附近的现象，这与文献[23]中提到的孔径扩大现象相符；这种现象使得时间间隔的影响不可忽视，因为少量孔能摄取DNA，若时间间隔足够长，则DNA摄取量随时间而增加，故呈现图8所示的结果，在时间间隔大于10ms时，DNA浓度会随时间间隔的增长而增加。根据文献[28]可得，在生物实验中双脉冲之间的时间间隔对细胞荧光素酶（荧光素酶用来检测DNA）转染的影响如图12所示。比较图8和图12可知，在高压短脉冲和低压长脉冲的作用下，长时间间隔（＞300ms）对DNA摄取影响较小，这与仿真结果基本相符。在实际的临床应用和生物实验中，脉冲幅值的选择仍比较盲目，且不同幅值作用下细胞摄取DNA分子数有明显差异。如图9所示，在单脉冲作用时，当脉冲幅值较小（＜1V）时，幅值的增加并不能有效地提高DNA摄取量。这是因为脉冲幅值较小，跨膜电压较小，进而导致生成的孔较少，而幅值的增加并不能显著提高孔数，故DNA浓度增加较少。当幅值高于1V时，幅值的增加会导致孔数的急剧增加，进而导致DNA摄取量的显著提高。同时比较图9中的a和b可知，当脉冲幅值较小（＜1）或较大（＞1.5）时，脉宽对DNA浓度的影响较大，脉宽的增加能显著提高DNA的摄取量；反之，脉宽对DNA浓度的影响较小。这是因为脉冲幅值高，导致跨膜电压高，生成的孔数多，脉宽的作用能够通过孔数体现，而当脉冲幅值较低时，生成的孔数有限，脉宽在DNA摄取过程中占据主导地位。c3和d两者能量相等，比较这两者可知，c3的DNA摄取量远高于d，进一步说明了高压脉冲加中压脉冲在DNA摄取方面的优异。同时从图9b中可得，在d作用下，当第一脉冲幅值较低（0.5～1V）时，双脉冲作用下的DNA浓度基本等于两单脉冲作用时DNA浓度之和，在幅值大于1V时，双脉冲的DNA浓度远高于两单脉冲的DNA浓度之和。这说明当先施加中/低压脉冲再施加高压脉冲时，随着第一脉冲幅值的增加，DNA浓度快速上升，且第一脉冲幅值越高，对第二脉冲的影响越大。根据图9c可知，在具有不同幅值第一脉冲作用下，DNA浓度与第二脉冲幅值的关系曲线相似。这是因为在第一脉冲期间，细胞生成了大量孔，而当第二脉冲幅值较低时，孔数限制了孔径的增长，使孔径小于10nm，故DNA浓度没有增长。当第二脉冲的幅值能够促进孔径增长至10nm时，幅值越大，所产生孔的孔径越大，进而导致DNA摄取量线性增加。第一脉冲幅值越高，孔数越多，因此，在相同的第二脉冲作用下，DNA浓度越高。故可知，DNA浓度与幅值呈正相关。
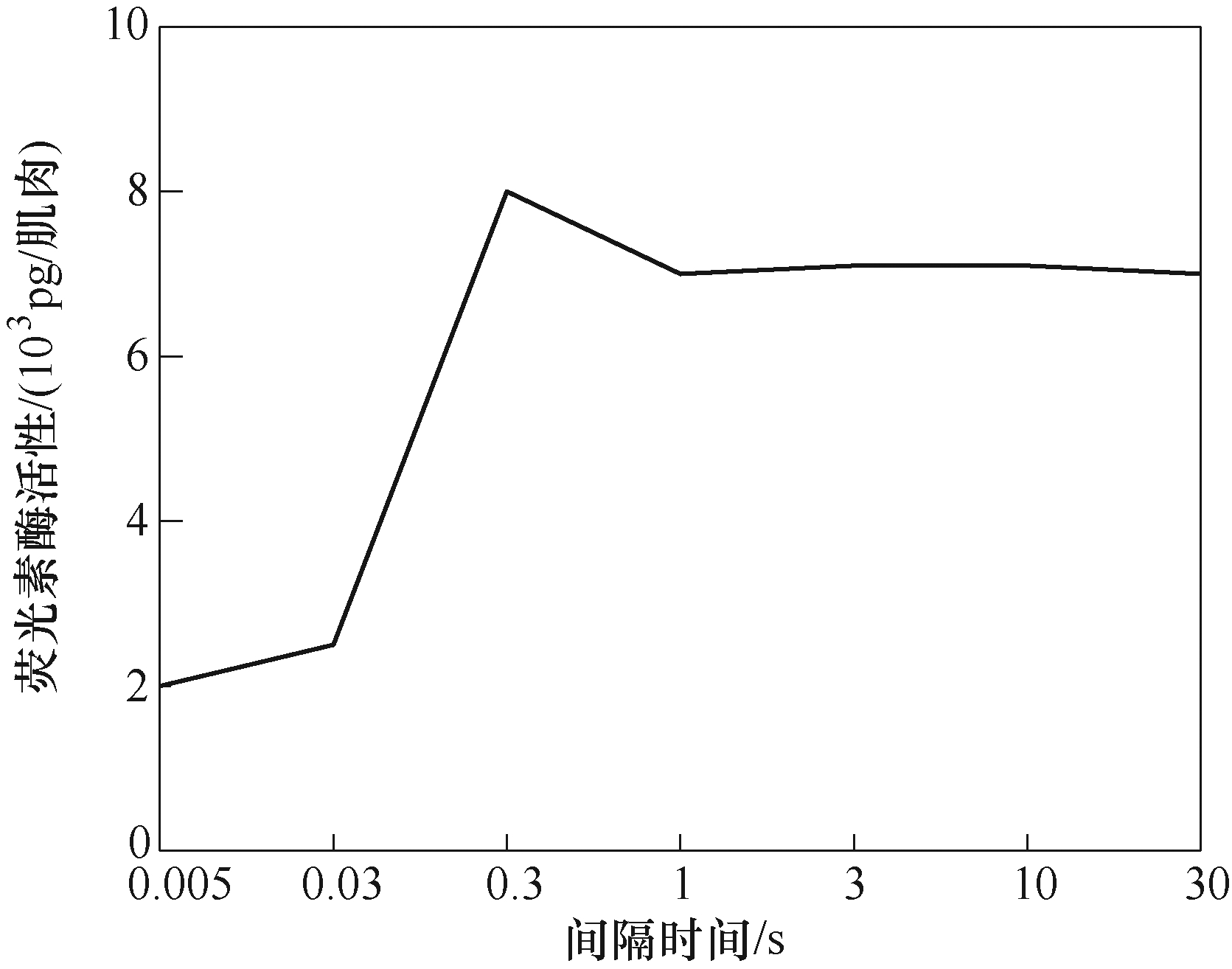
图12 双脉冲的时间间隔对肌肉细胞 转染荧光素酶的影响
Fig.12 Effects of time interval of double pulses on luciferase transfection in muscle cells
综上所述，脉冲电场作用细胞时，细胞膜的跨膜电位变化，诱导细胞膜电穿孔，导致DNA分子进出细胞，因此，DNA转移的有效性取决于脉冲参数，如幅值、脉宽、重复频率等，并且各个脉冲参数作用方式不同。本文仿真结果表明，脉冲幅值通过改变细胞膜上所产生的孔数和孔径来影响细胞摄取DNA分子数；脉宽则通过持续作用时间来增加进入细胞的DNA分子数；在一定条件下，脉冲个数会产生累积效应，促使细胞摄取DNA分子。
本文所建模型在一定程度上反映了球形细胞DNA电转染过程，但模型仍比较简单粗糙，下一步研究中将考虑建立真实细胞摄取DNA模型。
4 结论
本文基于等效电路模型，并结合电穿孔方程、孔径变化方程及DNA摄取方程，仿真了微毫秒脉冲参数作用下球形细胞DNA转染情况，得到以下结论：
1）双脉冲作用下，先施加高压短脉冲后再施加中压长脉冲更有利于DNA转染。
2）时间间隔对DNA摄取的影响与是否出现孔扩张现象有关。若出现孔扩张现象，则较长时间间隔（＞10ms）会促进细胞摄取DNA；反之，时间间隔的长短不影响细胞摄取DNA。
在一定条件下，DNA摄取量与单脉冲幅值正相关。双脉冲作用时，当第二脉冲能够促使细胞摄取DNA时，DNA摄取量与幅值呈线性关系。
[1] Spanggaard I, Dahlstroem K, Laessoee L, et al. Gene therapy for patients with advanced solid tumors: a phase I study using gene electrotransfer to muscle with the integrin inhibitor plasmid AMEP[J]. Acta Oncologica, 2017, 56(7): 909-916.
[2] Fujii M, Matano M, Nanki K, et al. Efficient genetic engineering of Human intestinal organoids using electroporation[J]. Nature Protocols, 2015, 10(10): 1474-1485.
[3] Kotnik T, Frey W, Sack M, et al. Electroporation- based applications in biotechnology[J]. Trends in Biotechnology, 2015, 33(8): 480-488.
[4] 米彦, 刘权, 李盼, 等. 低强度纳秒脉冲电场联合靶向金纳米棒对A375黑色素瘤细胞的杀伤效果研究[J]. 电工技术学报, 2020, 35(12): 2534-2544.
Mi Yan, Liu Quan, Li Pan, et al. Study of killing effects of A375 melanoma cells treated by low intensity nanosecond pulsed electric fields combined with targeted gold nanorods[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2534-2544.
[5] 刘红梅, 姚陈果, 董守龙, 等. 基于测量信号的不可逆电穿孔动态过程数值模拟及分析[J]. 电工技术学报, 2019, 34(18): 3732-3740.
Liu Hongmei, Yao Chenguo, Dong Shoulong, et al. Dynamic numerical modeling and analyzing on the process of irreversible electroparation based on measurement signal[J]. Transactions of China Electro- technical Society, 2019, 34(18): 3732-3740.
[6] 姚陈果, 郑爽, 刘红梅, 等. 面向临床多针消融肿瘤的不可逆电穿孔量效关系模型[J]. 电工技术学报, 2020, 35(11): 2491-2498.
Yao Chenguo, Zheng Shuang, Liu Hongmei, et al. Model of irreversible electroporation dose-effect relationship for clinical multi-needle ablation tumors[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2491-2498.
[7] 姚陈果, 宁郡怡, 刘红梅, 等. 微/纳秒脉冲电场靶向不同尺寸肿瘤细胞内外膜电穿孔效应研究[J]. 电工技术学报, 2020, 35(1): 115-124.
Yao Chenguo, Ning Junyi, Liu Hongmei, et al. Study of electroporation effect of different size tumor cells targeted by micro-nanosecond pulsed electric field[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 115-124.
[8] 刘红梅, 董守龙, 宁郡怡, 等. 纳秒脉冲高频透膜效应优先杀伤化疗抗性肿瘤细胞的仿真与实验研究[J]. 电工技术学报, 2019, 34(22): 4839-4848.
Liu Hongmei, Dong Shoulong, Ning Junyi, et al. Simulation and experimental study on preferential killing of chemoresistance tumor cells induced by the high-frequency permeation effect of nanosecond pulse field[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4839-4848.
[9] André F M, Gehl J, Sersa G, et al. Efficiency of high- and low-voltage pulse combinations for gene electrotransfer in muscle, liver, tumor, and skin[J]. Human Gene Therapy, 2008, 19(11): 1261-1272.
[10] Andre F M, Mir L M. Nucleic acids electrotransfer in vivo: mechanisms and practical aspects[J]. Current Gene Therapy, 2010, 10(4): 267-280.
[11] Mcmahon J M, Wells D J. Electroporation for gene transfer to skeletal muscles: current status[J]. Biodrugs, 2004, 18(3): 155-165.
[12] Escoffre J M, Portet T, Wasungu L, et al. What is (still not) known of the mechanism by which electroporation mediates gene transfer and expression in cells and tissues[J]. Molecular Biotechnology, 2009, 41(3): 286-295.
[13] Gehl J. Electroporation: theory and methods, perspectives for drug delivery, gene therapy and research[J]. Acta Physiologica Scandinavica, 2003, 177(4): 437-447.
[14] Rols M P, Teissié J. Electropermeabilization of mammalian cells. quantitative analysis of the phenomenon[J]. Biophysical Journal, 1990, 58(5): 1089-1098.
[15] Wolf H, Rols M P, Boldt E, et al. Control by pulse parameters of electric field-mediated gene transfer in mammalian cells[J]. Biophysical Journal, 1994, 66(2): 524-531.
[16] Kotnik T, Pucihar G, Reberšek M, et al. Role of pulse shape in cell membrane electropermeabilization[J]. Biochim Biophys Acta, 2003, 1614(2): 193-200.
[17] Pasquet L, Bellard E, Golzio M, et al. A double-pulse approach for electrotransfection[J]. Journal of Membrane Biology, 2014, 247(12): 1253-1258.
[18] Hassibi A, Vikalo H, Riechmann J L, et al. Real-time DNA microarray analysis[J]. Nucleic Acids Research, 2009, 37(20): e132.
[19] Sadik M M, Yu Miao, Zheng Mingde, et al. Scaling relationship and optimization of double-pulse elec- troporation[J]. Biophysical Journal, 2014, 106(4): 801-812.
[20] Orio J, Coustets M, Mauroy C, et al. Electric field orientation for gene delivery using high-voltage and low-voltage pulses[J]. Journal of Membrane Biology, 2012, 245(10): 661-666.
[21] Forjanic T, Markelc B, Marcan M, et al. Electropo- ration induced stress response and its effect on gene electrotransfer efficacy: in vivo imaging and numerical modelling[J]. IEEE Transactions on Biomedical Engineering, 2019, 68(9): 2671-2683.
[22] Neumann E, Kakorin S, Tsoneva I, et al. Calcium- mediated DNA adsorption to yeast cells and kinetics of cell transformation by electroporation[J]. Biophysical Journal, 1996, 71(2): 868-877.
[23] Smith K C, Neu J C, Krassowska W. Model of creation and evolution of stable electropores for DNA delivery[J]. Biophysical Journal, 2004, 86(5): 2813- 2826.
[24] Jiang Wen, Zhao Xiaopeng. Dynamics and control of the two-pulse protocol in electroporation: numerical exploration[J]. Mathematical Biosciences, 2011, 232(1): 24-30.
[25] Miklavcic D, Towhidi L. Numerical study of the electroporation pulse shape effect on molecular uptake of biological cells[J]. Radiology & Oncology, 2010, 44(1): 34-41.
[26] Neu J C, Krassowska W. Asymptotic model of electroporation[J]. Physical Review E, 1999, 59(3): 3471-3482.
[27] Stroh T, Erben U, Kühl A A, et al. Combined pulse electroporation−a novel strategy for highly efficient transfection of Human and mouse cells[J]. Plos One, 2010, 5(3): e9488.
[28] Satkauskas S. Mechanisms of in vivo DNA electro- transfer: respective contributions of cell electroper- meabilization and DNA electrophoresis[J]. Molecular Therapy, 2002, 5(2): 133-140.