0 引言
工程实践中的很多问题都会用到数学建模，计算模型已经成为各大领域检验各种复杂现象的有效工具[1-2]。模型的复杂性各有不同，往往存在由于各种原因引起的不确定性因素。不确定性量化（Uncertainty Quantification, UQ）是一门对模型的输入不确定性参数进行随机变量建模，进而将其转化成相应的随机问题，并对输出变化进行统计学分析的量化求解技术[3-4]。与常规的模型计算不同的是，UQ是给定每个输入参数可能的概率分布，通过模型不确定性的传播，最终得到输出的某种分布。UQ的核心是探究模型输入参数的不确定性对模型预测质量的影响，分析各个不确定性因素并尽可能降低这些不确定性带来的风险[5]。
不确定性量化方法大体分为概率框架下和非概率框架下两类。概率框架下的UQ是将计算模型的输入参数建模成随机变量并给定其变量类型，从概率论的角度用统计学的方法拟合出模型参数的概率分布类型，最后统计分析确定模型输出在某区间的分布概率。常用的概率不确定性量化方法主要有蒙特卡罗模拟（Monte Carlo Simulation, MCS）法[6]、混沌多项式展开（Polynomial Chaos Expansion, PCE）法[7]、代理模型法、降维法等。
近年来，不确定性量化越来越受到学术界的重视。在工程力学、电力电子、水文学、流体力学、核电站安全评估等方面有很多应用[8-11]。UQ在生物电磁学中也有一些应用[12-13]。2015年，有学者将MCS和PCE法用于经颅磁刺激（Transcranial Magnetic Stimulation, TMS）中，对考虑三层组织电导率的不确定性随机模型进行研究[14]。随着模型精度的提高，不确定性参数增多，PCE无法解决较多随机参数变化的不确定性问题，研究者提出采用参数化模型降阶（Parametric Model Order Reduction, PMOR）来处理高维参数的不确定性问题[15-18]。降维法是由美国爱荷兰大学S. Rahman等提出来的，主要是为了解决“维数灾难”的问题。将系统原函数分解成若干个单变元、双变元或多变元函数求和的形式，并在此基础上求其相关统计信息，进而对输出分布进行量化分析[19]。目前研究领域应用较多的是单变元降维法（Univariate Dimension Reduction Method, UDRM）[20-21]。
生物医学电阻抗成像（Electrical Impedance Tomography, EIT）是生物电磁学的一个研究内容，它是一种无创的以人体内部组织电导率分布为目标的图像重建技术[22]。EIT技术在临床上可应用于脑出血、脑水肿等颅脑疾病的检测[23]。生物组织电导率与多种因素有关[24-25]。然而在对EIT的临床研究中，不同时刻、不同状态、不同生理病理下生物组织电导率通常被假定为恒定的，这在某种程度上使图像重构结果发生变化。当利用数值计算方法对EIT正问题进行计算时，需要进行单元离散。为达到足够的计算精度，单元剖分的数目会增加，这将导致模型的不确定性增加。电导率参数的不确定性会对正问题的计算结果产生影响，进而影响逆问题的结果，因此对电导率不确定性的研究具有重要意义[26-27]。课题组前期利用蒙特卡罗模拟法和混沌多项式展开法对电导率分布的变化、对EIT正问题不确定性的影响进行了研究，结果表明，PCE在低维参数的UQ中能达到和基准方法一致的结果[28]。但随着剖分单元数目的增加，模型中不确定性参数随之增多（d＞10），PCE无法处理问题，即所谓的“维数灾难”问题，而UDRM有望解决高维参数不确定性量化的问题。
本文针对EIT技术中生物组织电学特性的特点，采用基于均值点展开的UDRM将其用于电导率的不确定性量化，并与MCS法、PCE法做对比证明了所提方法的有效性。
1 理论
1.1 蒙特卡罗模拟（MCS）法
MCS法是最简单的基于样本计算的方法，在求解不确定性问题时，需要多次样本重复进行计算，样本依赖性强[29]。MCS不确定性分析方法原理简单，重点在如何产生样本。
首先根据随机输入变量X=[X 1X2…Xd ]的分布类型，产生N个样本
（i= 1,…,N）；然后依次将xi代入Y=g(X)中求解yi（i=1,…,N）；最后对N次输出计算其相关统计信息，如均值、标准差、概率函数分布等。
MCS的均值收敛率为
，即只有当样本数足够大时才能得到精确的结果，故MCS法一般只在不确定性量化中作基准，计算量大、运行时间长限制了其发展。
1.2 混沌多项式展开（PCE）法
PCE法是近年来较为流行的一种不确定性量化方法，它对随机问题进行有限阶截断展开，用一系列确定性的系数多项式方程表示原不确定性问题，通过对多项式方程组系数的求解获得随机问题的精确解[30]。对于混沌多项式模型，输出Y=g(X)表示为
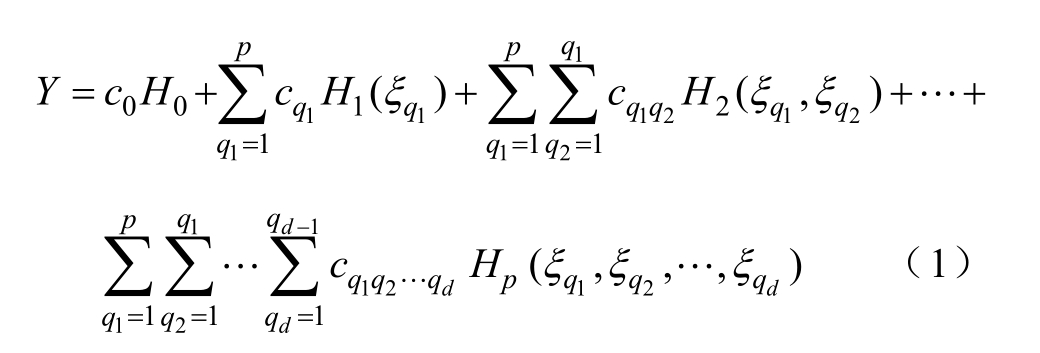
式中，p为多项式模型阶数；c0为常系数；cq1 q 2…qd =cq 为待求的第q阶多项式系数；ξ=(ξq1,ξq2,…,ξqd )为d维标准随机变量；Hp (ξ)为p阶的Hermite正交多项式。
PCE法精度高、收敛速度快，但对于复杂的模型计算问题，cq的求解过程将变得繁琐。
1.3 单变元降维法（UDRM）
基于均值点展开的UDRM以均值点作为单变元的参考点，对原函数进行分解。UDRM主要通过以下三步实现。
首先找一组参考点，将原函数g(X)在各单变元的均值点μi处近似分解表示为多个单变元函数求和的形式，有
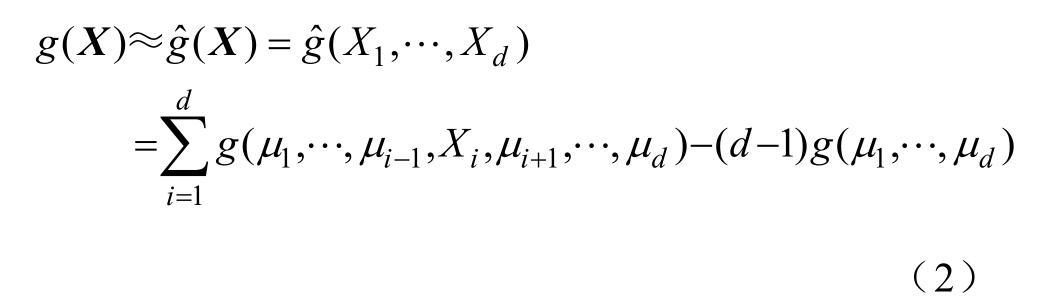
式中，d为变量维度；μi为第i维变量对应的均值；Xi为唯一变量；g(μ1,…,μi−1,Xi,μi+1,…,μd )为变量Xi函数值；g(μ1,…,μd )为g(X)在μX处的函数值。
从式（2）可以看出，等号右端的d个求和项减去d−1个常数项等于等号左端项。
在对g(X)单变元分解后，UDRM第二步为求解 
的第r阶统计矩，即直接对式（2）积分得
式中，E(⋅)为数学期望算子。
基于二项式定理展开求g(X)的r阶统计矩为
继续对式（4）利用二项式定理展开，定义
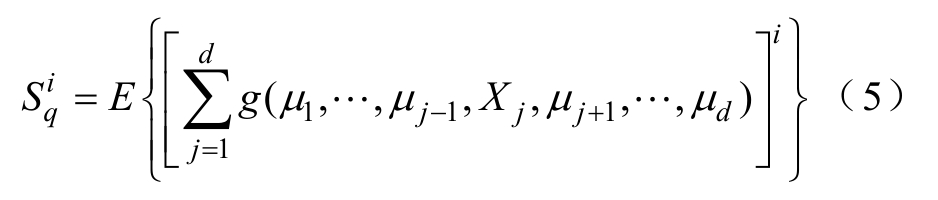
式中，q=1,…,d；i=1,…,r。
将式（5）递推展开得
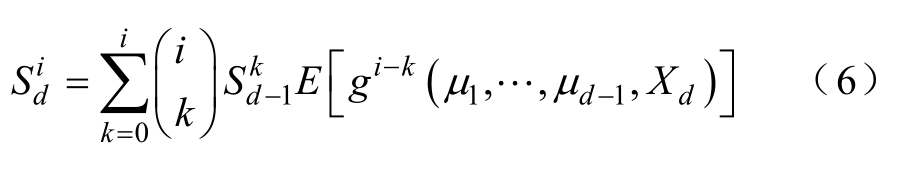
式中，i=1,…,r。
将式（6）代入式（4）得g(X)的第r阶统计矩通用表达式为
观察式（6）和式（7）中的未知项为
式中，h=i−k；f Xj (xj )为第j维变量Xj的边缘概率密度函数，可根据给定随机变量类型计算得出或已经 给出。
观察式（8），求解g(X)的第r阶统计矩转变为计算d个单变元积分。
UDRM第三步即具体求解这d个一维积分。从数学角度来看，插值型求积公式分为牛顿-科特斯和高斯型求积公式两种。两种方法使用场景不同，对于UDRM，选择计算高阶积分的高斯型插值求积公式，则式（8）为
式中，g (μ1,…,μj−1,l ji,…,μj+1,μd )为第j维变量所对 应的单变元函数值。
至此，UDRM实现了将g(X)的多元函数积分求解转变为函数中只含一个变量的一维函数积分求解。在计算基于高斯型插值求积公式时，各维选择m个对称分布的积分节点，当变量维数为d时，UDRM需调用g(X)计算次数为(m−1)d ，相对于PCE法的
（p为截断阶数），计算量大大减小。根据输入变量的分布类型得到各维随机变量所对应的节点和权值，表1给出了几种常用分布类型对应的高斯型插值求积的节点和权值。
表1 基于高斯求积的节点（αi）和权值（ωi）
Tab.1 Node (αi) and weight (ωi) based on Gaussian quadrature
分布类型 参数 概率密度函数 求积公式 αi ωi 正态分布 μ, σ ( σ＞0) 2( )2 2 1 e 2π xμ σ σ−− Gaussian-Hermite 2iσα μ+ π iω 指数分布 λ (λ＞0) e xλ λ− Gaussian-Laguerre iαλ iω 均匀分布 a, b 1 b a− Gaussian-Legendre 1 0 1 0 2 2 i μ μ μ μ α+−+2 iω
在得到各维变量的节点和权值后，依次获取d个单变元1维积分对应的节点和权值，其中，权值即各维随机变量对应的权值。根据数值积分的思想计算式（9）得到d个单变元1维积分，最后基于式（4）求g(X)的第r阶统计矩。
2 电阻抗成像正问题中的算例应用
2.1 电阻抗成像正问题的计算模型
EIT正问题是在已知目标电导率σ 分布的情况下，根据给定的边界激励条件求目标体内及边界电位分布ϕ 的情况[31]。通常将其所在场域看成稳态电流场来处理，数学模型表示为
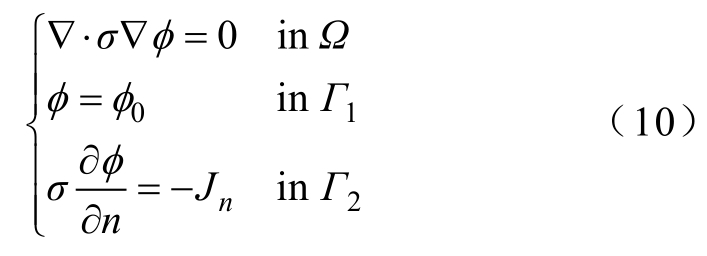
式中，Jn为注入电流密度；Ω 为目标区域； Γ1和Γ2 分别为第一类和第二类边界条件；ϕ0为边界电位。
由于求解目标大多形状不规则且不均匀，EIT正问题的求解需要采用数值解法。有限元由于在处理任意形状目标时具有优势而被广泛采用[32]。本文采用有限元法进行EIT正问题的求解。
2.2 四层同心圆头模型的仿真实验
2.2.1 四层同心圆头模型的构建
由于人头部结构近似球对称，本文在研究电阻抗的头部成像时，选用四层同心圆模型来仿真建模，该模型从里到外分别模拟大脑、脑脊液、颅骨、头皮，其各部分的相对半径及电导率值见表2，此模型在EIT正问题的其他研究中也有应用[33]。激励电流为1mA，50kHz，头皮半径为10cm，采用16个电极均匀放置于头部表面，如图1所示。
表2 四层同心圆头模型各部分的相对半径及电导率
Tab.2 The relative radius and conductivity of each part of the four-layer concentric circular head model
相对半径 电导率σ /(S/m) 大脑 0.8 0.33 脑脊液 0.85 1.0 颅骨 0.92 0.004 2 头皮 1 0.33
图1 四层同心圆头模型
Fig.1 Four-layer concentric circular head model
2.2.2 基于三种不确定性量化方法的仿真实现
分别采用基于均值点展开的UDRM、MCS法、PCE法三种UQ方法对电阻抗成像中的不确定性量化分析。以表2中σ 值为参考值，分别对当σ 服从不确定性变化率为1%、5%、10%、20%的随机均匀分布时对模型输出变化分析计算。由于头部结构的对称性，本实验部分以2号电极点为例，MCS法不确定性量化结果作为实验基准。
（1）MCS法。MCS法在不确定性量化领域一般用作方法基准。使用MCS对EIT正问题中电导率的不确定性计算时，分为以下步骤：
根据给定的σ 的分布类型，随机产生N个样本；将N个输入样本依次代入到EIT的有限元计算模型中，重复计算，求出相应的N个样本输出值；利用数理统计知识计算出边界电压的相关统计特性，如均值、标准差、概率密度分布等。
MCS的均值收敛率与N的关系如图2所示，当样本数达104时结果趋于收敛，所以在接下来的研究中实验样本选为N=105。
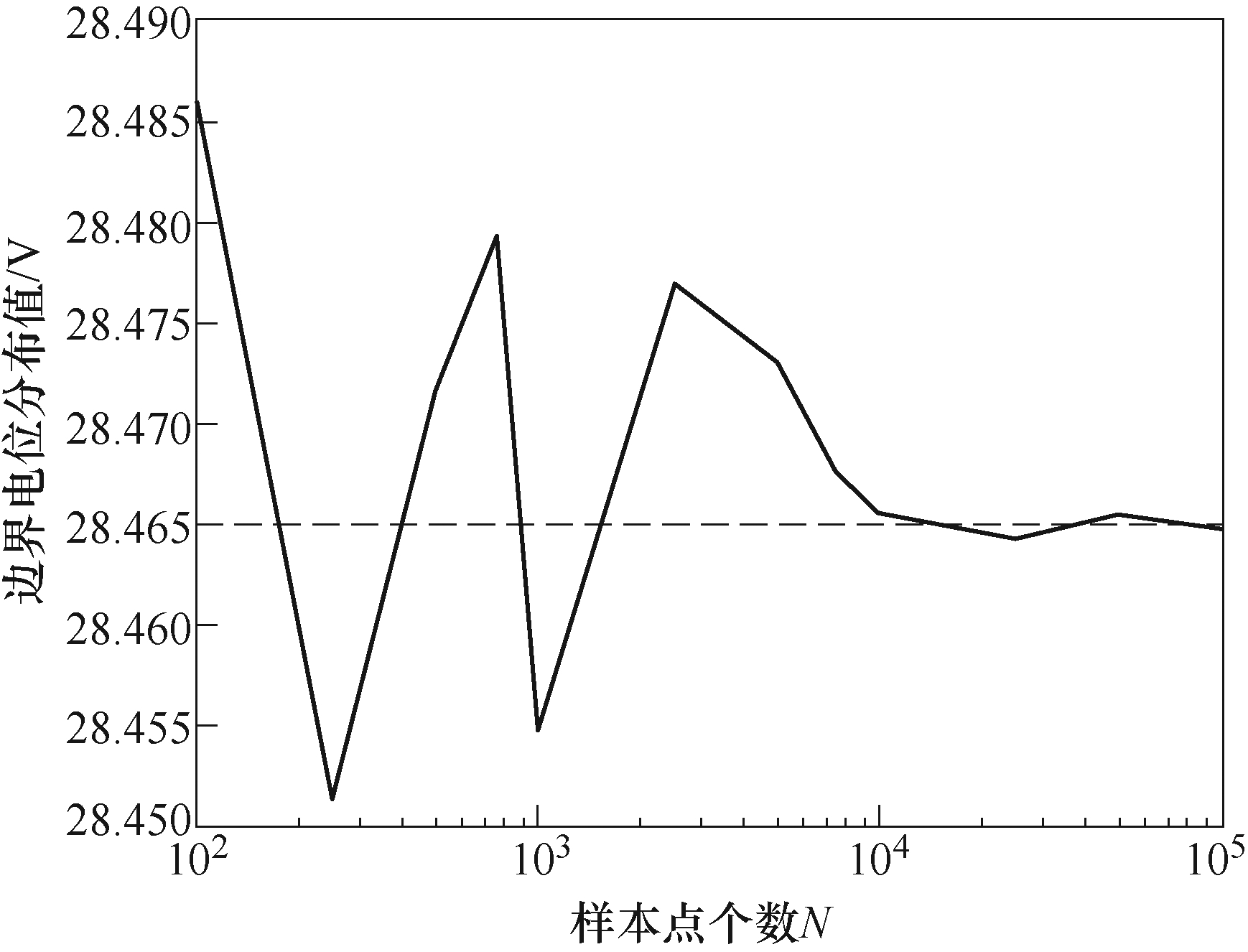
图2 MCS的均值收敛率
Fig.2 Mean convergence rate of MCS
（2）PCE法。PCE法的重点在于多项式模型的构建，然后在其模型上进行量化分析。
将EIT有限元模型表示为式（1）所示的多项式模型；在标准随机空间（ζ 空间）选取采样点数目Q并将其变换到原随机空间（X空间），选用合适的方法求PCE系数bi，通常来说Q的数量2倍于bi的个数；计算边界电压值的概率统计特性。
考虑到PCE法截断阶数可能对计算结果产生影响，分别采用2阶展开（p =2）、3阶展开（p =3）、4阶展开（p =4）的PCE法进行实验。
（3）UDRM。采用UDRM方法时，以表1中σ 参考值作为均值点，将EIT有限元模型表示为式（2）形式；确定各维随机输入变量对应的积分节点个数m；根据随机输入变量类型计算相应的1维高斯节点和权值；将给定电导率不确定性范围代入式（9）单变元计算，并计算模型输出电压的统计矩。
2.2.3 结果的量化分析
为了定量评价不确定性量化结果，通常采用均值、标准差等参数描述输出的不确定性信息[34]。
当有大量样本时，μ 是样本的算术平均数，有
标准差（Std）描述随机变量分布X相对于其均值的偏离程度，标准差越小，样本点分布越集中。
协方差（Cov）用于描述变量间的相互关系，有
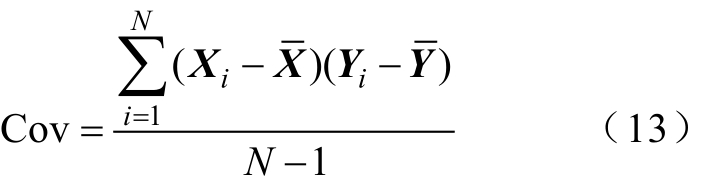
式中，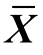
和
分别为变量X和Y的平均值。
变异系数（Cvar）衡量模型预测值的离散程度，又称“离散系数”，代表模型的稳定情况。不同的Cvar值代表不同的稳定情况，模型稳定性量化表见表3。Cvar的计算公式为
表3 模型稳定性量化表
Tab.3 Model stability quantization table
Cvar 模型稳定情况 ≤0.2 波动非常小，很稳定 ≤0.4 较小波动，基本稳定 ≤0.6 一般波动，不太稳定 ≤0.8 较大波动，不太稳定 ＞0.8 高度变化，随机性大
平均绝对误差（Mape）判别模型预测准确度情况，有
式中，N为样本数；u为实际值；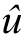
为模型预测值。
以2号电极为例，表4～表7给出了1%、5%、10%、20%变化幅度下三种UQ方法计算结果量化表；图3给出了三种UQ方法下电压的概率分布。
表4 1%不确定性时不同UQ法评价表
Tab.4 Evaluation table of different UQ methods when 1% uncertainty
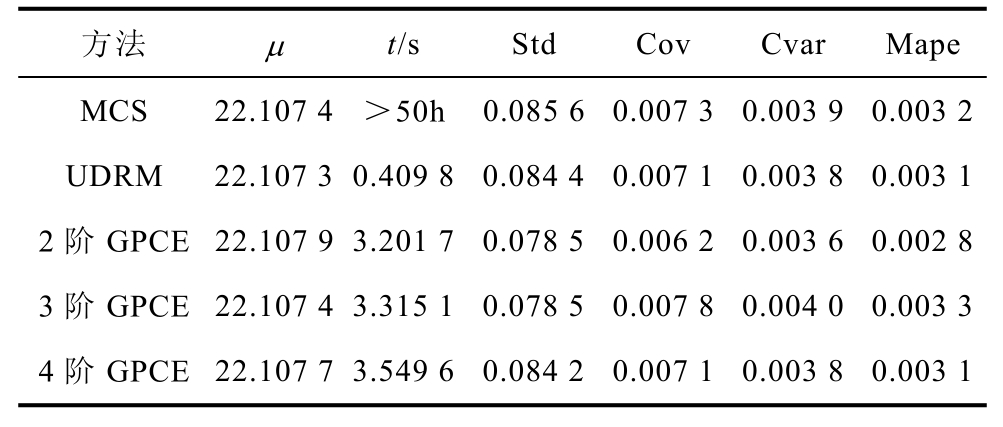
方法 μ t/s Std Cov Cvar Mape MCS 22.107 4 ＞50h 0.085 6 0.007 3 0.003 9 0.003 2 UDRM 22.107 3 0.409 8 0.084 4 0.007 1 0.003 8 0.003 1 2阶GPCE 22.107 9 3.201 7 0.078 5 0.006 2 0.003 6 0.002 8 3阶GPCE 22.107 4 3.315 1 0.078 5 0.007 8 0.004 0 0.003 3 4阶GPCE 22.107 7 3.549 6 0.084 2 0.007 1 0.003 8 0.003 1
表5 5%不确定性时不同UQ法评价表
Tab.5 Evaluation table of different UQ methods when 5% uncertainty
方法 μ t/s Std Cov Cvar Mape MCS 22.099 4 ＞50h 0.429 4 0.184 4 0.019 4 0.015 9 UDRM 22.101 1 0.422 4 0.422 6 0.178 6 0.019 1 0.015 6 2阶GPCE 22.104 3 3.140 1 0.391 6 0.153 3 0.017 7 0.014 1 3阶GPCE 22.101 7 3.268 4 0.441 6 0.195 0 0.020 0 0.016 3 4阶GPCE 22.100 1 3.599 3 0.421 4 0.177 6 0.019 1 0.015 6
表6 10%不确定性时不同UQ法评价表
Tab.6 Evaluation table of different UQ methods when 10% uncertainty
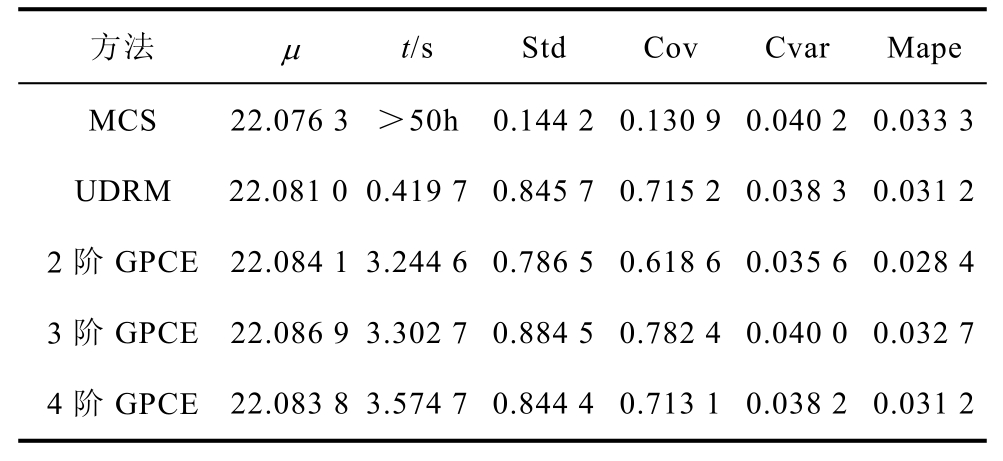
方法 μ t/s Std Cov Cvar Mape MCS 22.076 3 ＞50h 0.144 2 0.130 9 0.040 2 0.033 3 UDRM 22.081 0 0.419 7 0.845 7 0.715 2 0.038 3 0.031 2 2阶GPCE 22.084 1 3.244 6 0.786 5 0.618 6 0.035 6 0.028 4 3阶GPCE 22.086 9 3.302 7 0.884 5 0.782 4 0.040 0 0.032 7 4阶GPCE 22.083 8 3.574 7 0.844 4 0.713 1 0.038 2 0.031 2
表7 20%不确定性时不同UQ法评价表
Tab.7 Evaluation table of different UQ methods when 20% uncertainty
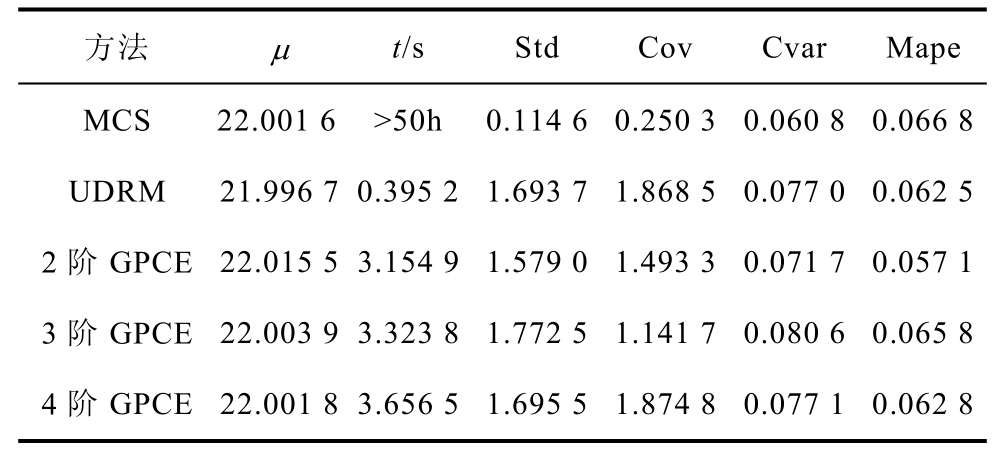
方法 μ t/s Std Cov Cvar Mape MCS 22.001 6 >50h 0.114 6 0.250 3 0.060 8 0.066 8 UDRM 21.996 7 0.395 2 1.693 7 1.868 5 0.077 0 0.062 5 2阶GPCE 22.015 5 3.154 9 1.579 0 1.493 3 0.071 7 0.057 1 3阶GPCE 22.003 9 3.323 8 1.772 5 1.141 7 0.080 6 0.065 8 4阶GPCE 22.001 8 3.656 5 1.695 5 1.874 8 0.077 1 0.062 8
从表4～表7中得，当电导率服从不同的不确定性变化范围时，MCS法、PCE法、UDRM三种方法的统计矩计算结果基本一致。图3a～图3d分别表示边界电压随着不同的电导率变化时的概率密度函数（Probability Density Function, PDF）变化曲线。图3a中电导率的不确定性为1%时，以MCS法结果做基准，UDRM和4阶展开（p =4）PCE法的概率分布基本重合，形似正态分布，但p =2的概率最高点（22.11, 4.547）明显大于MCS法的概率最高点（22.11, 4.314），p =3的概率最高点（22.11, 4.129）小于MCS法的概率分布最高点。观察图3b～图3d，边界电压的概率分布情况与图3a相同，p =2、3时的差异表明此时PCE法展开阶数达不到计算精 度，p =4展开时能达到与MCS法、UDRM一致的电压概率分布。随着不确定性范围的扩大，Cov值在不断增大，变量间的相互作用在增大，对应图3d中UDRM在（21.86, 0.212 7）处跟MCS法结果出现了偏差。
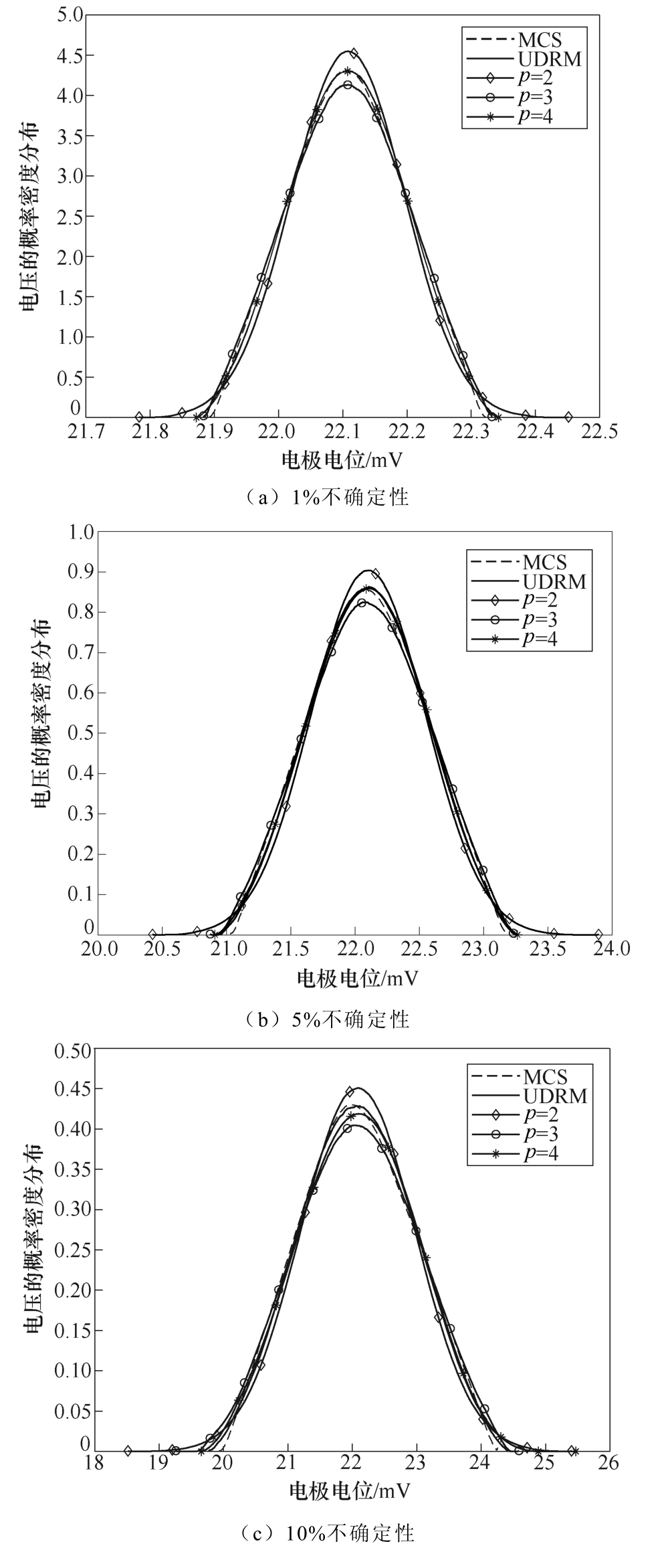
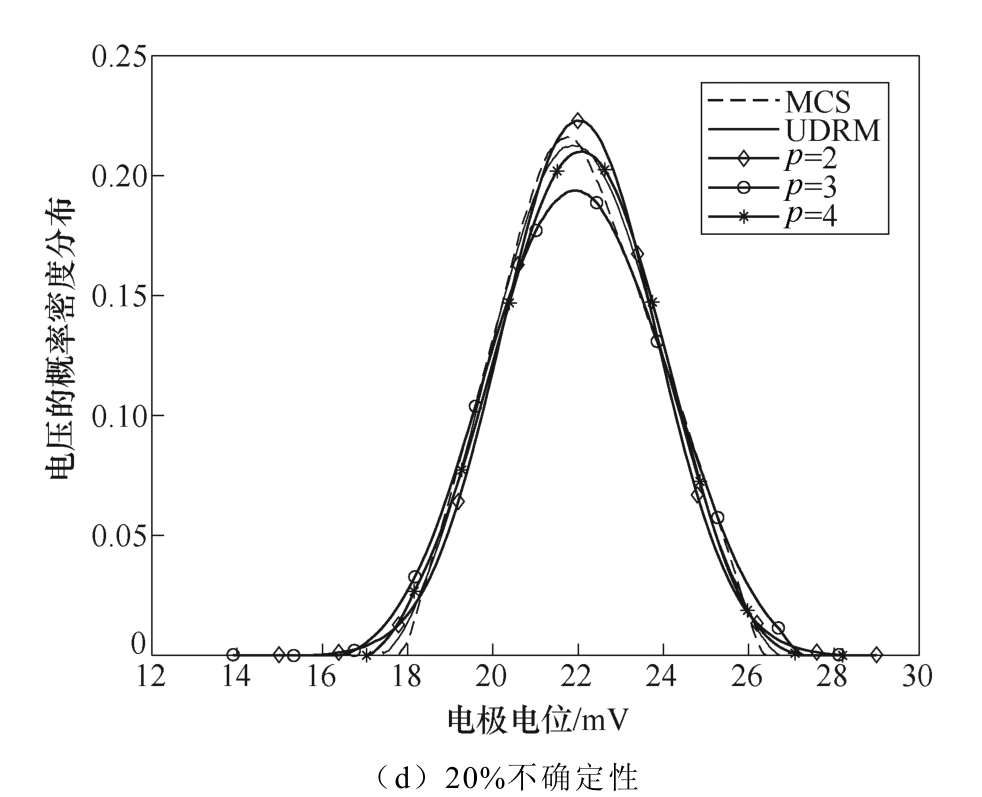
图3 四层头模型的电压PDF
Fig.3 The voltage probability density function diagram of the four-layer head model
2.3 二维圆模型的仿真实验
2.3.1 二维圆模型的构建
对于不能用分层均匀模型进行建模的问题，场域的剖分对实际成像效果有重要的影响。对于同一个目标，剖分越细，单元数越多，成像的分辨率越高。在剖分模型中，不同单元中的电导率值是变化的，所以随着剖分规模的增加，电导率分布的不确定性增加。建立一个二维圆模型来进行高维不确定性量化的仿真研究，二维圆模型中的电位分布如图4所示，在单位圆边缘均匀放置16个电极，施加50kHz，1mA的激励电流，将单位圆模型剖分成均匀的三角形单元，剖分单元数目为64个，每个单元 的电导率σ 为不确定值，所以不确定性参数个数d=64，圆外为真空（σ =0）。
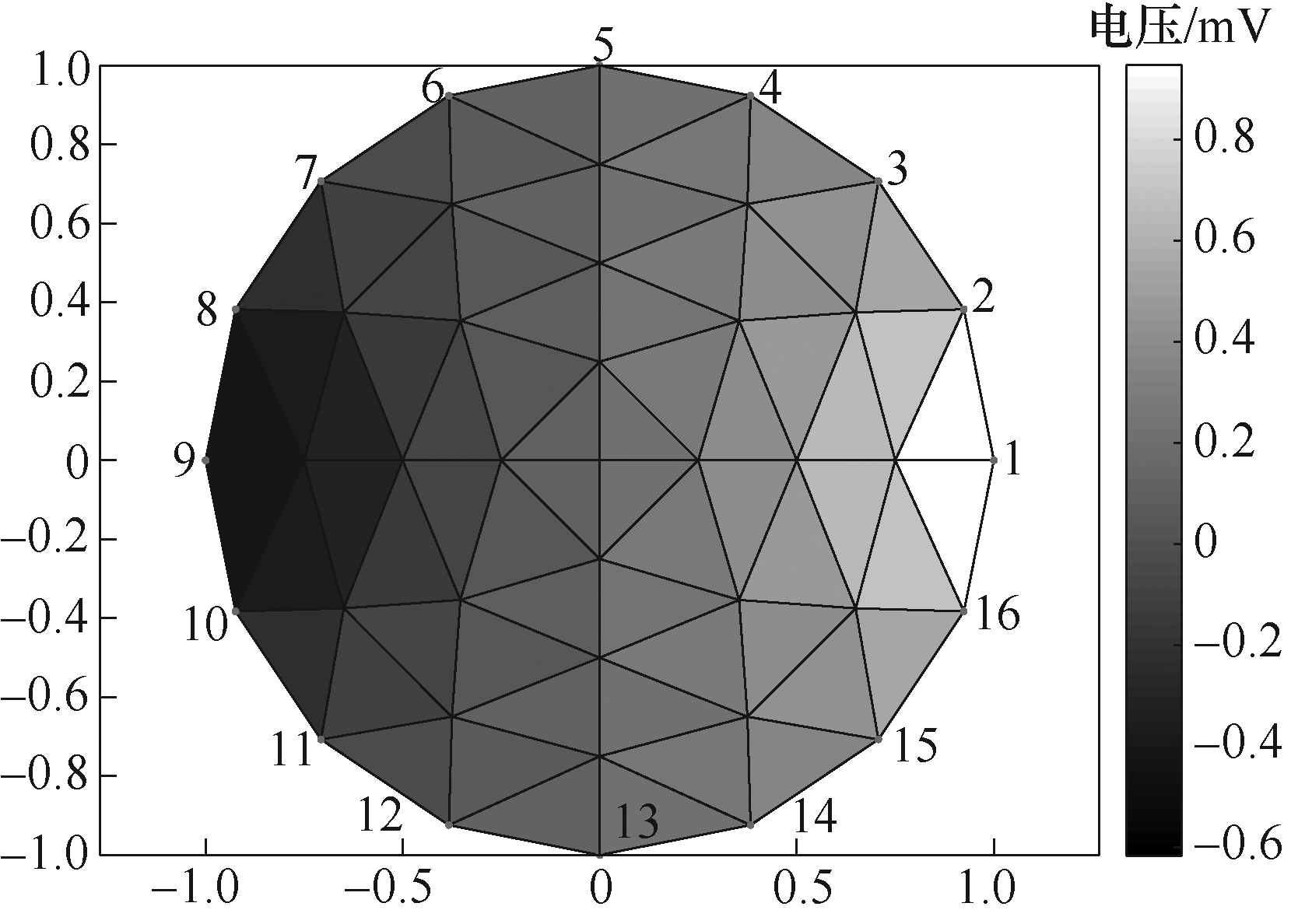
图4 二维圆模型中的电位分布
Fig.4 Potential distribution in 2D circular model
2.3.2 基于UDRM的不确定性量化方法的仿真实现
在仿真计算中，电流注入模式选择相对注入，即电流从电极1流入，从电极9流出，注入电流为50 kHz，1mA。给定电导率服从均值为1S/m，变化率为20%的随机均匀分布，即输入电导率的变化范围在0.8～1.2S/m之间。在实验中，每个单元代表一个不确定性，右侧代表电压值（mV）。分别用UDRM和MCS法在二维圆模型上进行EIT正问题计算，已知64个电导率服从随机均匀分布，样本数N=105，计算2～8、10～16号边界电极（激励电极不考虑）电压的相关统计信息，同样以MCS法结果作为实验基准。
2.3.3 结果的量化分析
表8给出了对UDRM与MCS法计算结果的评价表（由于对称性，只列出了2～8电极点的评价指标），图5给出了电极边界电压的PDF。
表8 二维圆模型下不同UQ方法评价指标
Tab.8 Evaluation index of different UQ methods under two-dimensional circle model
电极序号 方法 Cov Cvar Mape μ Std MCS 0.000 4 0.029 83 0.025 00 0.674 78 0.020 13 2 UDRM 0.000 4 0.030 34 0.027 01 0.670 53 0.020 34 MCS 0.000 21 0.033 18 0.027 51 0.439 43 0.014 58 3 UDRM 0.000 22 0.033 56 0.028 96 0.437 16 0.014 67 MCS 0.000 17 0.044 20 0.035 90 0.291 07 0.012 87 4 UDRM 0.000 16 0.043 81 0.035 75 0.290 74 0.012 74 MCS 0.000 15 0.074 19 0.059 27 0.163 97 0.012 17 5 UDRM 0.000 15 0.073 55 0.058 63 0.164 15 0.012 07 MCS 0.000 16 0.339 47 0.269 58 0.036 84 0.012 51 6 UDRM 0.000 15 0.326 45 0.266 87 0.038 04 0.012 42 MCS 0.000 19−0.124 65 0.099 03 −0.111 55 0.013 90 7 UDRM 0.000 20−0.125 64 0.099 52 −0.111 37 0.013 99 MCS 0.000 38−0.056 53 0.045 73 −0.346 91 0.019 61 8 UDRM 0.000 38−0.056 08 0.045 14 −0.346 10 0.019 41
从表8可得，电极5为Std值最小点，激励电极1到电极5间逆时针旋转，电压Std值随之减小；电极5到激励电极9间逆时针旋转，电压Std值随之增大，Std的变化说明带电导率的不确定性对电压的影响与边界电极位置有关。两种方法的Cov值表明多个不确定性参数间的相互作用很小，UDRM适用于无强相互作用的不确定性量化。Cvar值及Mape值表明，基于UDRM的不确定性模型计算电极电压结果准确。观察图5，UDRM和MCS法电极电压的概率密度分布规律基本一致趋于光滑的正态分布，两种方法PDF曲线越接近，说明UDRM在EIT多维不确定性参数量化中效果越好。
图5 二维圆模型的部分电压PDF
Fig.5 Probability density distribution of partial voltages in a two-dimensional circle model
3 分析讨论
为了研究UDRM在EIT电导率的不确定性问题中的可行性和高效性，将其与传统的MCS法、广泛流行的PCE法进行对比。对四层同心圆头模型的仿真实验结果可看出，用MCS法进行不确定性量化分析时，样本均值收敛率低，只有当N数量足够大时，才可以得到光滑的概率分布曲线，耗费很大的时间成本。PCE法结果精度高、运行速度快，且随着多项式阶数p的增大，不确定性计算结果更加准确。但随着σ 不确定性个数d的增多，由PCE法求解规模与p和d的关系式可知，PCE法的系数计算将变得十分复杂，系数无法求解。而利用UDRM量化结果与MCS法结果非常接近，精度明显要高，且计算量小，程序运行时间短，这证明基于均值点展开的单变元降维法在研究电阻抗成像正问题中电导率的不确定性是有效的，且随着不确定性个数增多，它的优势将会非常明显，可以很大程度上缓解“维数灾难”问题。
进而，以二维圆模型为例进行研究。由于当模型输入维数较高时，PCE系数求解矩阵规模较大，计算过程中会出现数值病态问题，因而将UDRM与MCS法基准结果作比较。当电导率为无相互作用的随机输入参数，UDRM能够准确快速判断出电导率的不确定性对边界电压概率分布的影响，其结果与MCS法基本一致。从离散程度、平均绝对误差等几个常用的精度检验参数来评价方法的好坏，验证了基于UDRM后的EIT模型更稳定、准确度更高，得到了更为可靠的结果。对比这三种方法，无论是从结果精度还是方法计算效率来看，UDRM都更优。
4 结论
本文采用基于均值点展开的UDRM研究了EIT中由于电导率的不确定性给正问题计算带来的影响，以同心圆头模型和二维圆模型为算例，在给定多个电导率参数服从随机均匀分布类型基础上，计算了边界电压的相关统计信息（如均值、标准差、概率分布密度图等）和精度信息（如平均绝对误差、变异系数）。对于低维不确定性问题，采用四层同心圆头模型，将UDRM与MCS法、PCE法结果做对比，发现UDRM具有计算量小、精度更高、替代模型更稳定的优势。在研究高维问题时，以二维圆模型为仿真算例，发现UDRM和MCS法的结果基本一致，UDRM可准确快速地判断电导率的不确定性对边界电压概率分布的影响，有效解决了“维数灾难”问题。
基于均值点展开的单变元降维法在EIT不确定性量化研究中具有计算量小、精度高、适用范围广的优越性。本文对EIT正问题的不确定性量化的研究为进一步实现EIT逆问题的计算优化奠定了基础。
[1] Brodland G W. How computational models can help unlock biological systems[J]. Seminars in Cell & Developmental Biology, 2015, 47(48): 62-73.
[2] 颜湘武, 徐韵, 李若瑾, 等. 基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化[J]. 电工技术学报, 2019, 34(10): 2022-2037.
Yan Xiangwu, Xu Yun, Li Ruojin, et al. Multi-time scale reactive power optimization of distribution grid based on model predictive control and including RDG regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2022-2037.
[3] 汤涛, 周涛. 不确定性量化的高精度数值方法和理论 献给林群教授80华诞[J]. 中国科学: 数学, 2015, 45(7): 891-928.
Tang Tao, Zhou Tao. Recent developments in high order numerical methods for uncertainty quanti- fication[J]. Scientia Sinica: Mathematica, 2015, 45(7): 891-928.
[4] Feinberg J, Langtangen H P. Chaospy: an open source tool for designing methods of uncertainty quanti- fication[J]. Journal of Computational Science, 2015, 11(1): 46-57.
[5] Tennoe S, Halnes G, Einevoll G T. Uncertainpy: a Python toolbox for uncertainty quantification and sensitivity analysis in computational neuroscience[J]. Frontiers in Neuroinformatics, 2018, 12(1): 49-77.
[6] 方斯顿, 程浩忠, 徐国栋, 等. 基于Nataf变换含相关性的扩展准蒙特卡洛随机潮流方法[J]. 电工技术学报, 2017, 32(2): 255-263.
Fang Sidun, Cheng Haozhong, Xu Guodong, et al. A Nataf transformation based on extended quasi Monte Carlo simulation method for solving probabilistic load flow problems with correlated random variables[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 255-263.
[7] 于全毅, 刘长英, 吴定超, 等. 基于广义混沌多项式法的多导体传输线辐射敏感度分析方法[J]. 电工技术学报, 2020, 35(17): 3591-3600.
Yu Quanyi, Liu Changying, Wu Dingchao, et al. Radiation sensitivity analysis of multiconductor trans- mission Lines based on generalized polynomial chaos method[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3591-3600.
[8] 谢仕炜, 胡志坚, 王珏莹, 等. 基于不确定随机网络理论的主动配电网多目标规划模型及其求解方法[J]. 电工技术学报, 2019, 34(5): 1038-1054.
Xie Shiwei, Hu Zhijian, Wang Yuying, et al. A multi-objective planning model of active distribution network based on uncertain random network theory and its solution algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1038-1054.
[9] 李幸芝, 韩蓓, 李国杰, 等. 考虑非高斯耦合不确定性的交直流配电网两阶段概率状态估计[J]. 电工技术学报, 2020, 35(23): 4949-4960.
Li Xingzhi, Han Bei, Li Guojie, et al. Two-stage probabilistic state estimation for AC/DC distribution network considering non-Gaussian coupling uncer- tainties[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4949-4960.
[10] Zhang Xinlei, Xiao Heng, Gomez T, et al. Evaluation of ensemble methods for quantifying uncertainties in steady-state CFD applications with small ensemble sizes[J]. Computers and Fluids, 2020, 203(1): 104530.
[11] Chen Yangli, Ma Weimin. Uncertainty quantification for trace simulation of fix-II no.5052 test[J]. Annals of Nuclear Energy, 2020, 143(1): 107490.
[12] Saturnino G B, Thielscher A, Madsen K H, et al. A principled approach to conductivity uncertainty analysis in electric field calculations[J]. Neuroimage, 2019, 188(1): 821-834.
[13] 甘源, 白锐, 张琪. 基于场-路耦合的干式空心电抗器稳态电磁场及电动力分析[J]. 电力系统保护与控制, 2019, 47(21): 144-149.
Gan Yuan, Bai Rui, Zhang Qi. Steady-state electro- magnetic field and electrodynamic analysis of dry- type air-core reactor based on field-circuit coupling[J]. Power System Protection and Control, 2019, 47(21): 144-149.
[14] Weise K, Rienzo L D, Brauer H, et al. Uncertainty analysis in transcranial magnetic stimulation using nonin- trusive polynomial chaos expansion[J]. IEEE Transactions on Magnetics, 2015, 51(7): 1-8.
[15] Codecasa L, Rienzo L D, Weise K, et al. Fast MOR-based approach to uncertainty quantification in transcranial magnetic stimulation[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.
[16] Codecasa L, Rienzo L D. MOR-based approach to uncertainty quantification in electrokinetics with correlated random material parameters[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-4.
[17] Codecasa L, Weise K, Rienzo L D, et al. MOR-based uncertainty quantification in transcranial magnetic stimulation[J]. Model Reduction of Parametrized Systems, 2017, 17(1): 421-437.
[18] Torchio R, Rienzo L D, Codecasa L. Stochastic PEEC method based on polynomial chaos expansion[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4.
[19] Rahman S, Xu Heqin. A univariate dimension- reduction method for multi-dimensional integration in stochastic mechanics[J]. Probabilistic Engineering Mechanics, 2004, 19(4): 393-408.
[20] Xu Heqin, Rahman S. A generalized dimension- reduction method for multidimensional integration in stochastic mechanics[J]. International Journal for Numerical Methods in Engineering, 2004, 61(12): 1992-2019.
[21] Xu Heqin, Rahman S. Decomposition methods for structural reliability analysis[J]. Probabilistic Engin- eering Mechanics, 2005, 20(3): 239-250.
[22] 徐灿华, 董秀珍. 生物电阻抗断层成像技术及其临床研究进[J]. 高电压技术, 2014, 40(12): 3738- 3745.
Xu Canhua, Dong Xiuzhen. Advancements in electrical impedance tomography and its clinical applications[J]. High Voltage Engineering, 2014, 40(12): 3738-3745.
[23] 周润奭, 隆云, 李尊柱, 等. 重视电阻抗成像技术在重症急性呼吸窘迫综合征患者肺部护理中的应用[J]. 中华急危重症护理杂志, 2020, 1(6): 536-539.
Zhou Runshi, Long Yun, Li Zunzhu, et al. Attention to the application of electrical impedance imaging in the pulmonary care of patients with severe acute respiratory distress syndrome[J]. Chinese Journal of Emergency and Critical Care Nursing, 2020, 1(6): 536-539.
[24] Gabriel S, Lau R W, Gabriel C. The dielectric properties of biological tissues Ⅱ: measurements in the frequency range 10Hz to 20GHz[J]. Physics in Medicine and Biology, 1996, 41(11): 2251-2269.
[25] Gabriel C, Peyman A, Grant E H. Electrical con- ductivity of tissue at frequencies below 1MHz[J]. Physics in Medicine and Biology, 2009, 54(16): 4863- 4878.
[26] 杨宁, 张杰, 代萌, 等. 具有真实颅骨分层解剖结构与电阻率分布的电阻抗成像头部物理模型构建[J]. 医疗卫生装备, 2018, 39(4): 15-19.
Yang Ning, Zhang Jie, Dai Meng, et al. Novel human-head phantom with realistic skull anatomy and resistivity distribution[J]. Chinese Medical Equipment Journal, 2018, 39(4): 15-19.
[27] Suksawang S, Niamsri K, Ouypornkochagorn T. Scalp voltage response to conductivity changes in the brain in the application of electrical impedance tomography (EIT)[C]//Proceedings of the 2018 15th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Rai, Thailand, 2018: 223-236.
[28] 李颖, 崔阳阳, 闫伟, 等. 电导率分布变化影响EIT正问题的不确定性量化方法[J]. 天津大学学报(自然科学与工程技术版), 2021, 54(1): 51-60.
Li Ying, Cui Yangyang, Yan Wei, et al. Uncertainty quantization methods of the influence of the change of conductivity distribution on the EIT forward problem[J]. Journal of Tianjin University (Science and Technology), 2021, 54(1): 51-60.
[29] 陈志国, 邓忠民, 毕司峰. 基于Monte Carlo法的结构动力学模型确认[J]. 振动与冲击, 2013, 32(16): 76-81.
Chen Zhiguo, Deng Zhongmin, Bi Sifeng. Structural dynamics model validation based on Monte Carlo method[J]. Journal of Vibration and Shock, 2013, 32(16): 76-81.
[30] Tripathy R K, Bilionis I. Deep U Q: learning deep neural network surrogate models for high dimensional uncertainty quantification[J]. Journal of Computa- tional Physics, 2018, 375(1): 565-588.
[31] 李颖. 脑电逆问题求解的数值计算方法研究[D]. 天津: 河北工业大学, 2003.
[32] Anusha V, Sudha B. Influence of skewing design for reduction of force ripples in DSL-SynRM using 3D FEA[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 397-402.
[33] 徐征, 何为, 何传红, 等. 头部电阻抗成像正问题的解析解研究[J]. 计算物理, 2010, 27(1): 107-114.
Xu Zheng, He Wei, He Chuanhong, et al. Analytical solution of forward problem in brain electrical impedance tomography[J]. Chinese Journal of Com- putational Physics, 2010, 27(1): 107-114.
[34] 熊芬芬, 杨树兴, 刘宇. 工程概率不确定性分析方法[M]. 北京: 科学出版社, 2015.