0 引言
电压源型高压直流输电(Voltage Source Converter-High Voltage Direct Current, VSC-HVDC)技术相比于传统的电流源型高压直流输电(Line Current Converter-High Voltage Direct Current, LCCHVDC)技术有着控制灵活、无换相失败等优点,它可以实现向无源网络供电及多落点受电的功能,且功率定向可控。VSC换流器灵活的控制方式更有利于形成多端交直流混联系统。当多端直流电网通过VSC换流站接入传统的交流电网后,会对交流电网的电压稳定性造成巨大的影响,且直流电网本身也存在电压稳定性的问题。因此,研究AC/VSC-MTDC混联系统的电压稳定性问题成为当前的焦点之一,其对保证交直流混联系统大电网安全可靠的运行具有极其重要的意义[1-6] 。
文献[7-9]采用灵敏度法对电压稳定性问题进行了分析研究。目前灵敏度法主要应用于纯交流系统的电压稳定性问题。该方法利用输入变量与目标变量之间的偏微分关系求得灵敏度指标,计算简单且物理概念明确;但该方法的参考价值严重依赖所选变量的偏微分灵敏度公式。在实际应用中,难以运用变量之间的偏微分灵敏度指标全面表征系统的运行情况,所以灵敏度法存在一定的局限性。
文献[10-13]采用连续潮流法(Continuation Power Flow, CPF)对交流电网进行电压稳定性分析。该方法主要用于计算纯交流系统当前运行点至电压稳定临界点之间的最大负荷裕度。文献[14]将CPF应用于VSC-MTDC交直流混联系统的电压稳定性研究中,但该方法主要通过模拟负荷增长求解电压稳定裕度,无法兼顾其他故障场景,如直流电网线路故障;也不能精确定位系统中影响电压稳定的关键节点或线路,且计算速度较慢。
文献[15-17]中将短路比指标应用于交直流系统中,但大部分短路比指标的表达式中,均有部分变量取值于系统额定运行工况。而实际运行中,系统参数是实时变化的(如直流闭锁后的紧急功率恢复过程),因此,这些指标不能及时、准确地反映系统的变化,导致其常应用于交直流混联系统的规划和设计阶段,在指导实际电力系统安全稳定运行时准确性不足。
文献[18]应用模态分析法对电压稳定性进行分析。模态分析法能够判断系统在某一运行状态下的电压稳定情况,得到系统当前运行点距电压不稳定点之间的距离,并找出影响系统电压稳定的关键节点和线路。因此,模态分析法是静态电压稳定性分析方法中常用的一种。但是,传统的模态分析法是基于降阶Q-V雅可比矩阵JR计算的,忽略了系统有功功率对电压稳定的影响[18];文献[19]虽然对传统的模态分析法进行了改进,但也只在系统PQ节点达到无功功率限制时考虑有功功率对电压稳定的影响;文献[20]对模态分析法进一步改进,基于交流系统全雅可比矩阵进行分析,提出一种新的状态-模态指标,能够量化表征系统状态对临界模态的贡献,但该文的分析对象是纯交流系统的电压稳定性;文献[21]将模态分析法应用于交直流系统,但针对的是基于LCC(line current converter)技术的交直流混联系统,且仅考虑了一条直流线路,直流比例低且未能成网。
因此,本文旨在对传统模态分析法进行改进,并提出将交直流混联系统进行解耦分析。解耦之后,交流电网基于其全雅可比矩阵而非降阶Q-V矩阵进行计算与模态分析,所以考虑了有功功率对电压稳定性的影响;而直流电网由于仅传输有功功率,改进后的模态分析法能够推广应用到直流系统的电压稳定性评估过程中。因此,本文将改进的模态分析法推广应用到AC/VSC-MTDC混联系统的静态电压稳定性评估领域。并且,本文将状态-模态指标推广应用到交直流系统中,对影响电压稳定性的关键节点和线路进行准确辨识,能够分析交流、直流系统负荷增长及线路故障对交直流混联系统电压稳定性的影响。此外,通过改变换流站的控制功率和换流站在交流电网的连接位置,能够量化分析换流站、交流电网及直流电网之间的相互影响,从而进一步量化换流站作为连接交流电网与直流电网的“桥梁”所发挥的关键作用,进而改善整个交直流混联系统的电压稳定性。
1 VSC换流站模型建立
当前许多研究在对VSC换流站建模时,没有考虑换流站的损耗或是直接省略了滤波器元件[22-23],这不符合实际,会对潮流计算结果产生一定的影响。因此,本文采用精确计及VSC换流站损耗的模型。VSC可采用两电平、三电平中点钳位或模块化多电平换流器结构。换流站直流侧采用双极接线,连接到直流母线。交流电网通过换流变压器、滤波器和换相电抗器连接在VSC换流器上。VSC换流站的结构如图1所示。
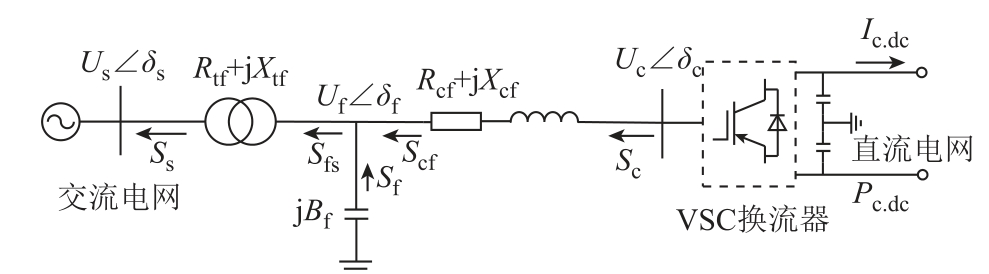
图1 VSC换流站的结构
Fig.1 Diagram for the structure of VSC station
图1 中,换流变压器的等值阻抗为Zt=Rtf+jXtf,相应的导纳1/Zt=Gtf+jBtf;电抗器阻抗为Zc=Rcf+jXcf,相应的导纳1/Zc=Gcf+jBcf;滤波器的电纳为jBf;Us∠δs表示交流节点电压;Uf∠δf表示滤波器节点的电压;Uc∠δc为VSC换流站交流侧的电压。
以图1中的功率方向为正方向,则VSC换流站注入到交流电网的有功和无功功率则可分别表示为

VSC换流站交流侧的有功和无功功率可以分别表示为

本文采用精确计及换流站损耗的模型,具体的损耗为流过换流站电流Ic的二次函数,即
式中,a、b、c为损耗系数,通常从实际工程中获取,本文采用的换流站及直流电网参数可参见文献[24]。
2 交直流系统雅可比矩阵建立
电力系统的潮流方程可分为以节点注入功率、电流和电压为网络注入量的三种类型。根据节点注入功率,可以建立一组非线性潮流方程。为了计算方便,本文将交直流混联系统的潮流模型进行统一表达,主要分为三个部分:交流电网、换流站和直流电网。进而采用牛顿拉夫逊法进行迭代求解,并取最后一次迭代收敛的雅可比矩阵用于后续的模态分析。
交流电网、换流站以及直流电网的功率失配方程如下[24]。
交流电网功率失配方程为
式中,XAC为交流电网的状态变量向量,XAC=[δT UT]T,δ为交流电网所有非平衡节点的电压相角,U为交流电网所有PQ节点电压幅值;ΔP为所有PQ节点和PV节点有功不平衡量;ΔQ为所有PQ节点的无功不平衡量。
VSC换流站功率失配方程为
式中,XVSC为换流站的状态变量向量,本文VSC换流站采用单点电压控制,故XVSC=[δT f UT f δT c UT c]T;ΔPf和ΔQf为滤波器节点的功率不平衡量;ΔPs和ΔQs为VSC换流器注入到交流电网的功率不平衡量。
直流电网的失配方程为
式中,XDC为直流电网的状态变量向量![]()
![]() 为所有直流节点的电压幅值向量;ΔPdc为直流节点的有功不平衡量。
为所有直流节点的电压幅值向量;ΔPdc为直流节点的有功不平衡量。
由上述可知,式(6)~式(8)组成了交直流系统潮流计算的非线性方程组。其中所有待求电压幅值的初值设为1.0(pu),相位初值设为0°。采用牛顿拉夫逊法,对非线性方程组式(6)~式(8)进行迭代求解,忽略泰勒展开式的高阶项,即可得到相应的修正方程式为

为了方便后续推导计算,将式(8)简记为F(X)=JΔX,其中J为交直流系统的雅可比矩阵。
3 交直流系统静态电压性稳定分析
交流电网的失配方程中不包括直流电网的变量,同样地,直流电网的失配方程也不包括交流电网的变量[24]。而交流、直流电网的失配方程同时都包含了换流站的变量。由式(9)中雅可比矩阵J的元素也可以看出,∂FAC/∂XDC=0,∂FDC/∂XAC =0,这说明交流电网中控制变量的改变不会直接引起直流电网变量的改变;反之亦然。二者之间的相互作用是通过换流站传递的。换流站通常分为整流站和逆变站,整流站从交流电网吸收有功功率,注入到直流电网;逆变站则从直流电网吸收有功功率,注入到交流电网。这两种类型的换流站对交流电网和直流电网的电压稳定性影响是完全相反的。因此,将传统的模态分析法直接套用在整个交直流系统是不可取的,必须对传统的模态分析法进行改进。因此,本文提出对交直流混联系统进行解耦。下面将证明对交直流系统进行解耦分析的可行性。
在传统的模态分析法中,若系统的降阶Q-V雅可比矩阵奇异,则判断系统电压失稳[18]。同样地,在交直流混联系统中,若交直流系统的雅可比矩阵J奇异,则整个交直流混联系统电压失稳。但是,由于不同类型的换流站对交流电网和直流电网的电压稳定性影响是完全相反的,因此,直接对交直流系统的雅可比矩阵J进行模态分析是不可取的。本文对交流分块矩阵JAC和直流分块矩阵JDC分别进行模态分析。接下来将证明JAC和JDC其中之一出现奇异,则J也会奇异[25]。
根据式(9),对矩阵J求逆,可以推导出交直流混联系统的状态变量的修正量表达式为

其中

由式(10)可以得出一些重要结论:
(1)交直流系统雅可比矩阵J的逆矩阵在很大程度上同时取决于交流分块矩阵JAC和直流分块矩阵JDC。
(2)JAC和JDC是分别代表交直流系统在交流电网和直流电网的矩阵,如果这两个矩阵中有一个矩阵奇异,则不可能求出J的逆,故J也会奇异。
上述结果说明JAC和JDC均包含了足够的信息来表征交流、直流系统的电压稳定性;而整体交直流混联系统中,一旦交流电网或直流电网任何一方失稳,都会导致整个交直流系统电压失稳,从而在理论上保证了将交直流系统解耦分析的可行性。
3.1 交流电网电压稳定性分析
将交直流系统中的交流电网修正方程展开为
与传统的模态分析法不同,本文基于整个交流分块矩阵JAC对交流电网进行静态电压稳定分析。因此,能够考虑有功功率对电压稳定性的影响。
对交流电网矩阵JAC进行模态分析,JAC为
则特征值矩阵可进一步表示为
相应地,交流电网的最小特征值可以表示为
式中,ηmin、ξmin分别为λmin对应的左右特征向量。与传统模态分析法中的参与因子指标不同,本文采用一种新的分析视角,通过对JAC进行分解,将交流电网的最小特征值λmin表示为系统状态的加权和,从而产生了状态-模态参与因子(State-in-Mode Participation Factor, SIMPF)和状态-模态灵敏度(State-in-Mode Sensitivity, SIMS)的定义[20]。SIMPF可以量化系统状态对临界模态的直接贡献,而SIMS则用于量化系统状态对临界模态的控制灵敏度。相应地,将λmin重新改写为[20]
λmin由三个部分组成,Cnet、Cinj、Cline越小,λmin就越小,系统则越趋于不稳定,现对其进行具体分析。
Cnet表示电力网络耦合强度对最小特征值的贡献,且Cnet恒为正[20],表明网络耦合对电压稳定性有积极影响,这与我们的实际经验一致[20]。因此,临界模态的形成主要取决于Cinj和Cline。Cinj量化了节点注入功率对最小特征值的贡献大小;而Cline则体现了线路传输功率对最小特征值的贡献。
将λmin对应的左右特征向量ηmin、ξmin的有功、无功部分分别记为ηmp、ηmq、ξmp、ξmq,i∈vpq和j∈vpv分别表示交流节点i、j的类型,则Cinj可具体展开为[20]
同理,可将Cline具体展开为[18]

根据式(16),定义节点i的有功功率和无功功率的SIMPF指标为
式中,SPi和SQi分别为相应的SIMS指标,将其分别展开为
一般而言,可认为Pij≈Pji,因此,根据式(17),可定义表征线路Lij之间传输功率的SIMPF指标为
Sij为线路Lij的SIMS指标,将其展开为
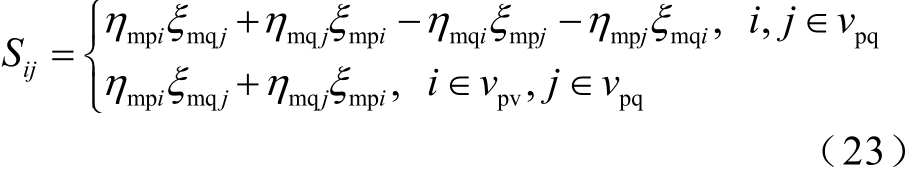
SIMPF和SIMS分别衡量系统状态对临界模态的直接贡献大小和控制灵敏度。因此,具有负SIMPF的系统状态不利于电压稳定,具有正SIMPF的系统状态有利于电压稳定。而SIMS指标的符号则指明了调整相应系统状态以改善静态电压稳定性的方向。且SIMS的绝对值越大,同样的状态调整量可产生更好的效果。
相比传统模态分析法中参与因子(Mode-in-State Participation Factor, MISPF)指标[20],本文所采用的状态-模态指标具有以下优点:
(1)MISPF是一种模态-状态指标,只能表征在临界模态下,系统节点的无功功率对该节点电压幅值的影响。而状态-模态指标将临界模态表示为系统状态的加权和,能够具体量化系统状态对临界模态形成的直接影响。
(2)MISPF指标基于纯交流系统中降阶Q-V雅可比矩阵JR进行分析,假定各节点的有功功率不变,只考虑节点的无功功率对电压稳定的影响。这一近似处理在距系统临界运行点较远时是成立的。但随着负荷加重,系统逼近临界运行点时,节点的无功功率逐渐达到其上限,此时,节点有功功率的变化无法忽略,假设ΔP=0是不符合实际的。因此,MISPF指标应用在临界运行点时存在一定局限。而状态-模态指标基于整个交流分块雅可比矩阵JAC分析,能够同时考虑节点注入有功、无功功率对电压稳定性的影响,在实际应用中更为全面、合理。
(3)状态-模态指标能够计及有功功率对电压稳定性的影响,而直流部分只传输有功功率,因此,状态-模态指标能够推广应用到直流电网,并且能够具体量化分析直流电网与交流电网之间的相互影响。
3.2 MISPF与SIMS的区别与联系
无论是运用本文方法对整个交流分块雅可比矩阵JAC进行模态分析,还是运用传统的模态分析法对纯交流系统的降阶Q-V雅可比矩阵JR进行模态分析,当系统处于临界模态时,系统的最小特征值均为0。因此有JACξmin=0和 ηT minJAC=0,其中ηmin和ξmin分别为JAC的临界特征值对应的左右特征向量;同理,也有JRξq=0和ηT q JR=0,ηq和ξq分别为JR的临界特征值对应的左右特征向量。因此,JR在临界模态时的左右特征向量ηq和ξq实际上是JAC的临界特征向量ηmin和ξmin的无功部分[20]。根据文献[18],节点i在临界模态时的MISPF指标为ηqiξqi,该指标与式(21)中的SQi成正比。所以,MISPF在数值上等于SQi/2。但传统的MISPF指标侧重于临界模态对系统状态的影响,该指标只能表征在临界模态下,系统节点的无功功率对该节点电压幅值的影响;而本文采用的SIMS指标从状态-模态的角度出发,将系统状态表示为临界模态的加权和,因此能够量化系统状态对临界模态形成的直接贡献。
3.3 直流电网电压稳定性分析
状态-模态指标SIMPF和SIMS能够计及有功功率对系统电压稳定的影响,而直流电网只传输有功功率,因此,本文将SIMPF和SIMS指标推广应用于直流电网的电压稳定性评估。
设直流部分共有ndc个直流节点,与交流部分类似,直流部分的修正方程式为
同理,将直流雅可比矩阵的最小特征值λcri用直流电网系统状态表示为
式中,ηcri和ξcri分别为直流电网最小特征值λcri对应的左、右特征向量。
同样地,将直流部分的雅可比矩阵JDC进行分解,JDC可表示为[26]
不同于交流部分的雅可比矩阵,直流雅可比矩阵JDC中元素只有∂Pdc/∂Udc, 且直流导纳矩阵Y中只有实部G而没有虚部B,因此JDC分解后只含有两部分,具体为
其中
![]() 表示直流线路之间的传输功率及耦合强度;
表示直流线路之间的传输功率及耦合强度;![]() 包含的Pdci表示直流节点注入功率的贡献。将λcri具体展开为
包含的Pdci表示直流节点注入功率的贡献。将λcri具体展开为
实际中,电力系统多为微损系统,因此JDC的不对称程度较低![]() 又由于
又由于![]() 恒为正,因此
恒为正,因此![]() 恒为正。由此可知,λcri的变小甚至变负主要由
恒为正。由此可知,λcri的变小甚至变负主要由![]() 决定,现将其展开为
决定,现将其展开为
式中,i为直流的节点,i∈ndc。
因此,直流节点i的SIMPF指标可以定义为
相应的控制灵敏度指标SIMS则为
SIMPF指标反映了节点注入有功功率对直流系统最小特征值的直接贡献,而SIMS则定位了影响直流系统电压稳定的关键节点。
4 算例
本文采用经修改的IEEE 57节点交直流混联系统[24],并在文献[24]算例的第2、3、4、7个直流节点分别增加了0.1(pu)的直流负荷,同时将2号换流站的连接位置从交流12节点更换至13节点。如图2所示,换流站分别通过1、13、16、17、15交流节点接入交流系统。

图2 改进IEEE 57节点7端VSC-MTDC系统示意图
Fig.2 Diagram for modified IEEE 57-bus system with 7-terminal VSC-MTDC
换流站的控制方式为单点电压控制,控制参数参见文献[24]。潮流计算中,交直流混联系统的基准功率设为100MV·A,直流电网的基准电压设为200kV,交流电网基准电压设为220kV,收敛的精度设为10-6。为了增强实验效果,交流电网的原始负荷被提高到1.4倍,作为本算例的基本负荷水平。
4.1 最小特征值指标的有效性验证
增加交流电网的负荷直至潮流计算结果不收敛,分别绘制交流、直流电网最小特征值指标随着交流电网负荷增加的变化趋势;而直流电网部分,由于直流电网初始的最小特征值指标λcri较大,即电压稳定裕度较高,因此,为了明确量化λcri的变化情况,直流负荷倍数需提高至很高的水平,才能使潮流计算结果不收敛。分别绘制交流、直流电网最小特征值指标随直流电网负荷增加的变化趋势,其结果如图3所示。
由图3a可知,随着交流电网负荷增加,交流电网最小特征值λmin逐渐减小,当系统潮流计算结果临界收敛时,λmin接近于0,系统极不稳定,而直流电网的最小特征值变化却不大。由图3b可知,随着直流电网负荷增加,直流电网最小特征值λcri逐渐减小,当系统潮流计算结果临界收敛时,λcri接近于0,系统的电压趋于崩溃,而交流电网最小特征值几乎不变。

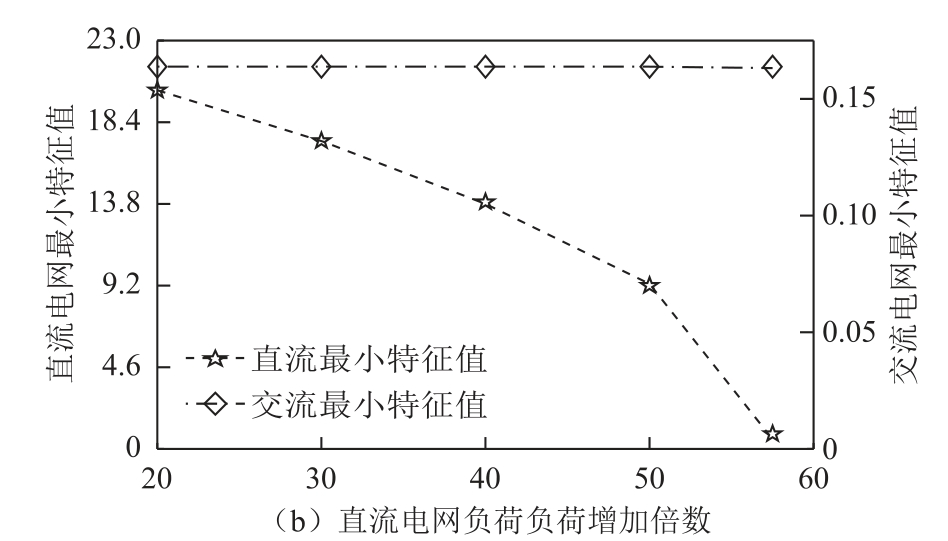
图3 交直流电网最小特征值随交直流负荷增长变化曲线
Fig.3 AC-DC minimum eigenvalue change curves with increase of AC-DC load
上述实验结果表明,将交、直流最小特征值作为表征交直流系统失稳的指标是可行的;同时也表明,在换流站控制功率不变的前提下,交流、直流系统无法传递对彼此之间的影响,二者之间的影响是间接的。这一结果也进一步验证了本文将交直流系统进行解耦分析的可行性。
4.2 交流电网电压稳定性分析
4.2.1 交流电网关键节点识别
Cinj指标能够准确定位交流电网中对电压稳定性影响较大的关键节点。表征交流节点的有功、无功功率的SIMPF和SIMS指标见表1和表2。SIMPF指标表征系统状态对最小特征值的直接贡献:若SIMPF指标为负,则说明该系统状态不利于电压稳定。而SIMS指标的符号则指明了调整相应系统状态以增强静态电压稳定性的方向,且SIMS的绝对值越大,意味着同样的状态调整量可产生更好的效果。
表1 SIMS指标排名靠前的节点注入有功率
Tab.1 Node active power injection with high SIMS ranking
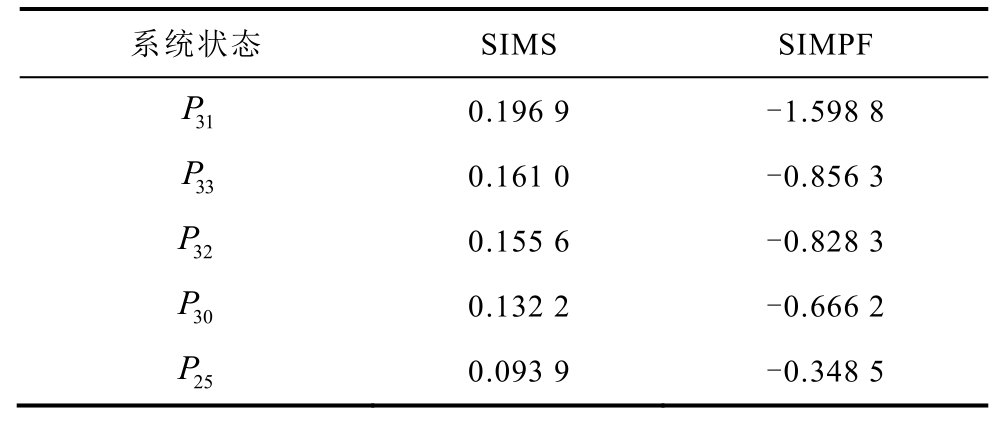
注:表1中的系统状态按其SIMS指标绝对值从大到小排列。
?
表1 、表2分别列出了SIMS绝对值取值最大的前5个系统状态。表中SIMPF指标为负,说明相应的系统状态不利于电压稳定,而SIMS指标为正,说明减小相应的系统状态能够改善系统的电压稳定性,即需要对上述的负荷节点采取相应的补偿措施。在以上节点分别通过有功储能装备额外增加该节点的有功出力10MW、通过无功补偿增加无功出力10Mvar。采取有功、无功补偿措施后,交流电网的最小特征值λmin变化如图4所示。
表2 SIMS指标排名靠前的节点注入无功功率
Tab.2 Node reactive power injection with high SIMS ranking

注:表2中的系统状态按其SIMS指标绝对值从大到小排列。
?
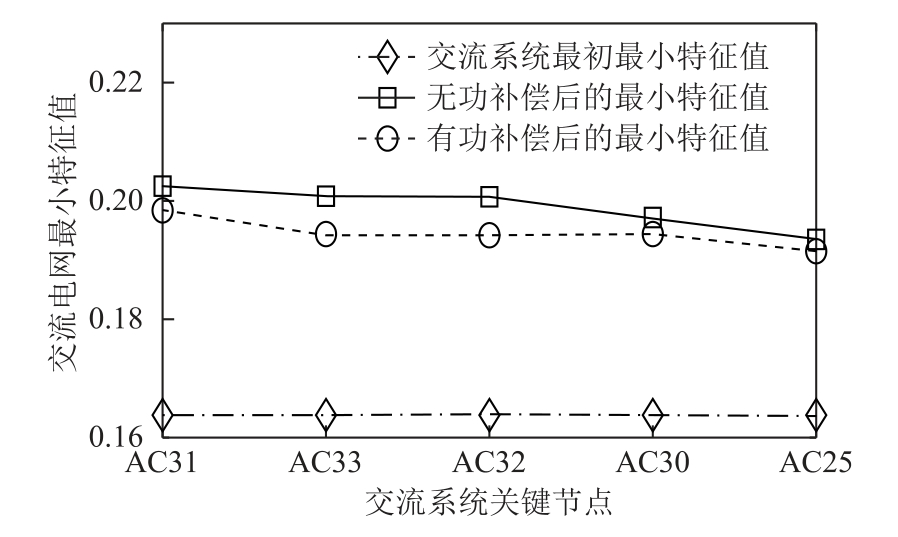
图4 交流电网最小特征值对比图
Fig.4 Comparison for the minimum eigenvalue of AC system
分别在前五个关键节点采取有功、无功补偿措施后,λmin从0.163 8增大到0.2左右,且SIMS指标越大,采取同样的补偿量,λmin增大程度越大,交流系统电压稳定性改善越好。作为对比,在表1中所涉及节点外的任一位置如44节点处增加10MW有功出力,λmin变为0.164 3;同理,在表2指标所涉及节点外的任一位置如19节点处增加10Mvar无功补偿,λmin变为0.168 7。
由图4可知,在表1、表2所示关键节点之外的其他位置采取同样的补偿之后,λmin虽有增大,但较图4中对关键节点采取补偿而言,λmin增大幅度微弱。实验结果表明,通过SIMS指标识别系统的关键节点,进而采取相应的补偿方案是有效的。
4.2.2 交流电网关键线路识别
Cline指标能够准确定位交流电网中对其电压稳定性影响较大的关键线路,表3列出了SIMS绝对值取值最大的前5个线路状态。为了验证该指标识别关键线路的准确性,分别断开上述关键的交流线路,交流电网的最小特征值λmin变化见表4。
表3 SIMS指标排名高的交流线路
Tab.3 AC lines with high SIMS ranking
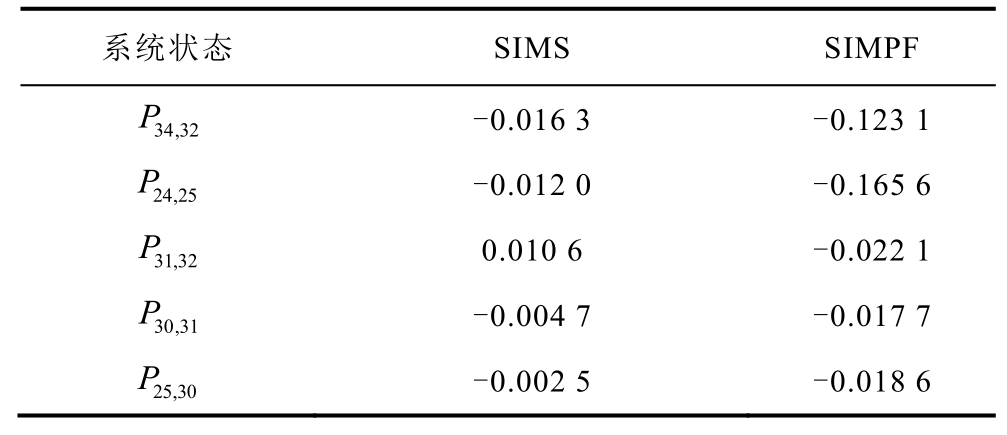
注:表3中的系统状态按其SIMS指标的绝对值从大到小排列。
?
表4 交流线路开断后的最小特征值
Tab.4 Minimum eigenvalue after tripping off AC lines

注:L24,25(1),L24,25(2)分别表示双回线L24,25的第1、2回线路。
?
若线路L34,32故障断开,此时潮流计算的结果不收敛,系统电压失稳,说明线路L34,32对维持系统电压稳定具有重要意义;而线路L24,25为双回线,若两条线都发生故障断开,此时潮流计算结果也不收敛,即系统失稳;若只有一回线路发生故障,λmin的下降程度也比其他线路大。
实验结果表明,Cline指标能够对交流电网中的关键线路进行识别,且线路SIMS指标的绝对值越大,线路发生故障后,λmin下降程度越大,说明线路对维持交流电网的电压稳定性越重要。
4.3 直流电网电压稳定分析
4.3.1 直流负荷对直流电压稳定的影响
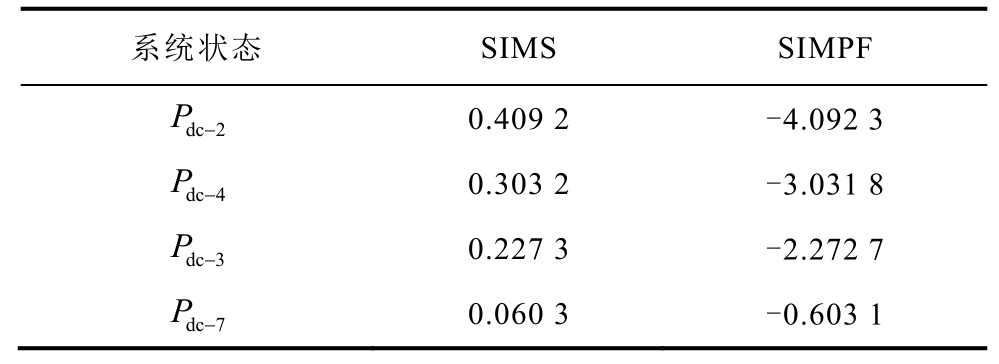
同样地,将直流节点的SIMS指标按其绝对值从大到小排列,结果见表5。
表5 直流电网节点注入有功SIMS指标
Tab.5 SIMS of node active power injection in DC Grid
?
表5 中SIMPF指标为负,说明直流节点的有功负荷不利于电压稳定,而SIMS指标为正,则说明减小节点有功负荷有利于电压稳定,即要对相应节点采取补偿措施。在以上节点位置分别额外增加有功出力10 MW,采取补偿措施后的直流系统最小特征值λcri变化趋势如图5所示。
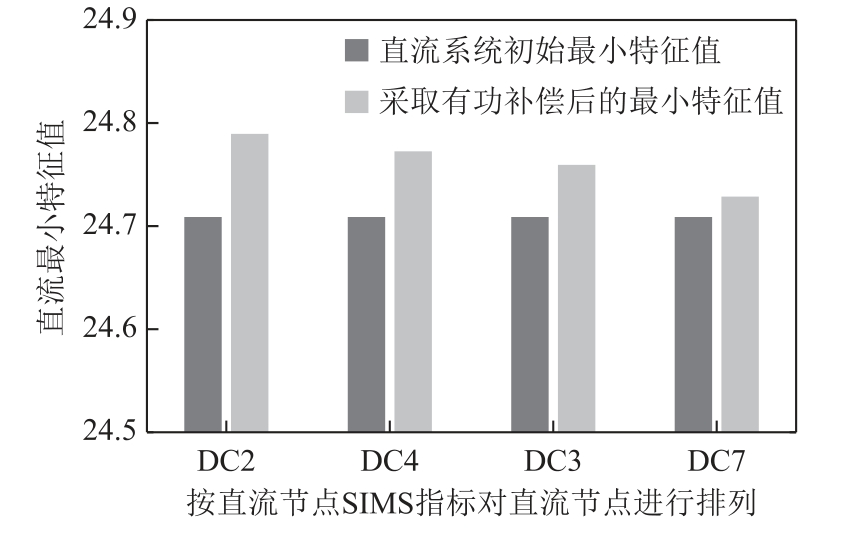
图5 采取补偿措施后直流最小特征值对比图
Fig.5 Comparison for DC minimum eigenvalue after compensation measure
由图5可知,分别在直流节点2、4、3、7处额外增加有功出力,λcri变大,直流电网电压稳定性得到改善,且SIMS指标越大,采取同样的有功补偿量,λcri的提高幅度越大。
4.3.2 直流线路对直流电压稳定的影响
由于直流雅可比矩阵中元素只有∂Pdc/∂Udc,且直流导纳矩阵Y只有实部G,所以直流系统的状态-模态指标中并没有识别关键直流线路的指标。因此,本文采取模拟直流线路故障的方式,对直流线路的关键程度进行判断。
该算例中共有7条直流线路,断开线路L17、L16和L56会使得潮流计算结果不收敛,结合图2分析可知,这三条线路中的任一条线路故障都会使交流与直流系统解列,因此这三条线路对维持交直流系统的电压稳定性至关重要。而分别断开剩余4条直流线路后,原本流过该线路的有功功率,就会被其他直流线路分担,而导致这些线路承担的传输功率比之前增加了,因此直流电网电压稳定性会下降。绘制直流电网最小特征值λcri随直流线路故障的变化如图6所示。当线路L37和L47发生故障时,λcri下降程度要比线路L24和L32大,这是由于线路L37和L47传输的有功功率比L24和L32大,因此线路L37和L47对维持直流系统电压稳定性有着更为重要的作用。总之,通过模拟直流线路故障的思路,可以对直流系统的关键线路进行识别。
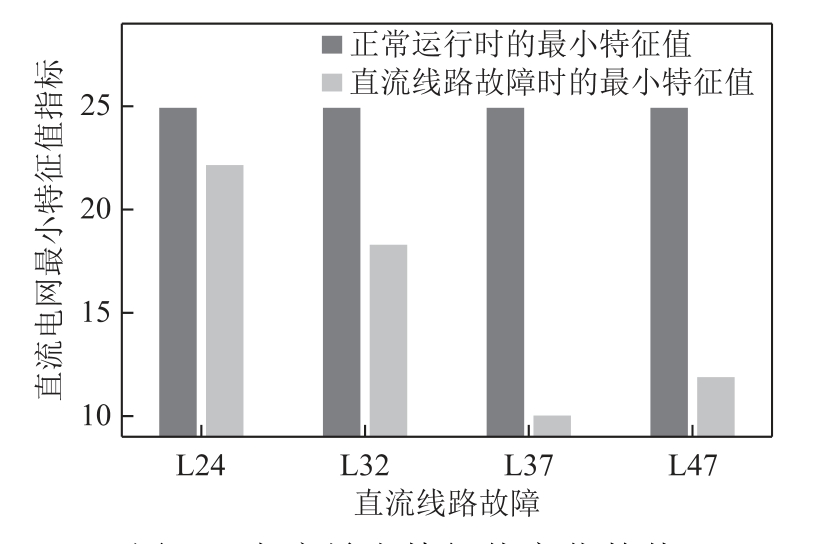
图6 直流最小特征值变化趋势
Fig.6 Trend for DC minimum eigenvalue change
4.4 换流站对交、直流电压稳定性的影响
4.4.1 换流站控制功率对交、直流电压稳定性的影响
由第3节可知,交直流混联系统中,换流站与交流、直流系统直接相连,换流站的控制功率的增大(或减小)会直接影响交流、直流系统之间的电压稳定性。分别绘制直流、交流系统最小特征值随换流站控制功率增加的趋势如图7、图8所示。
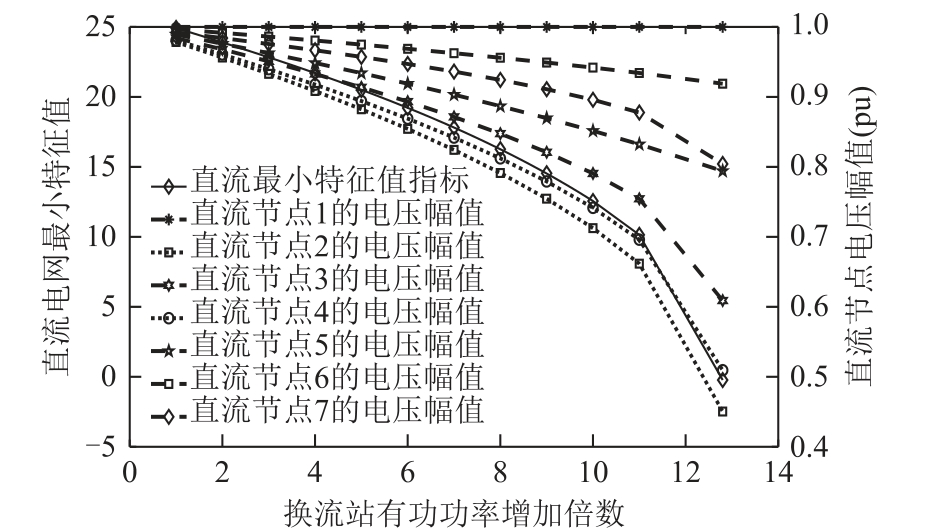
图7 直流最小特征值随换流站控制功率变化曲线Fig.7 DC minimum eigenvalue change curves with VSC control power
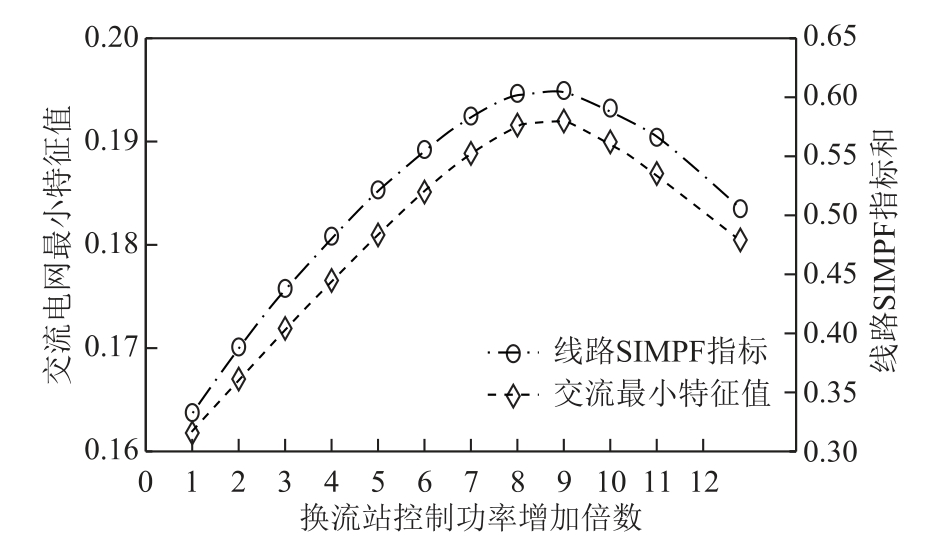
图8 交流最小特征值随换流站控制功率变化曲线
Fig.8 AC minimum eigenvalue change curves with VSC control power
由图7可知,随着换流站控制功率的增加,直流系统的最小特征值λcri逐渐减小,当换流站的有功功率增加到原来的12.6倍时,λcri变负,此时直流系统中部分节点的电压幅值已降至很低的水平,从而最终导致直流电网的电压失稳。
如图8所示,随着换流站控制功率的增加,交流系统的最小特征值λmin先增大后减小。这是由于换流站控制功率增大后,逆变站注入到与其直接相连的交流节点的有功功率也会增大,会导致与这几个交流节点直接相连的交流线路传输的有功功率的方向发生改变,从而改变了交流线路的SIMPF指标。而SIMPF反映了线路传输功率对λmin的直接影响。因此,图8中同时绘制了所有线路的SIMPF指标之和随换流站控制功率的变化趋势图。由图8可知,λmin的变化趋势与SIMPF指标的变化趋势是一致的,这说明换流站控制功率的变化通过改变交流系统线路之间的潮流分布,从而影响到交流系统的电压稳定性。尽管λmin先增大后减小,但最终都比VSC控制功率未改变时大。因此,交流系统的电压稳定性仍然得到改善。由图7、图8可知,换流站控制功率的改变,对交流、直流系统的电压稳定性的影响是完全相反的,这也进一步验证了将交直流系统进行解耦分析的正确性。
4.4.2 直流电网对交流电压稳定性的影响
直流电网与交流电网通过换流站相连,二者之间的影响是间接的。直流电网通过直接影响VSC换流站,再由换流站影响交流节点的注入功率,从而影响交流电网的电压稳定性。因此,通过改变换流站在交流电网的连接位置,可以分析直流系统对交流系统的电压稳定性影响。 换流站与交流电网最初的连接位置如图2所示,与换流站相连接的交流节点的有功SIMS与SIMPF指标见表6。
表6 与换流站连接的交流节点有功指标
Tab.6 Index for active power of AC bus connecting to the VSC

?
对交流系统而言,逆变站相当于有功电源,逆变站接入交流系统,可以改善交流系统的电压稳定性。根据表1、表2中的交流节点指标,将逆变站的位置分别更改为SIMS指标为前四的节点处,SIMS从大到小分别为交流节点31、33、32、30。绘制交流电网的最小特征值指标如图9所示。
由图9可知,根据SIMS指标改变换流站在交流电网的连接位置,交流电网的最小特征值指标λmin明显提高,均提高至0.3以上,交流电网的电压稳定性上升。作为对比,将换流站2的落点更换到除表1外的任意位置,如节点44,λmin从原来的0.163 8增加到0.194 6,提升幅度有限。
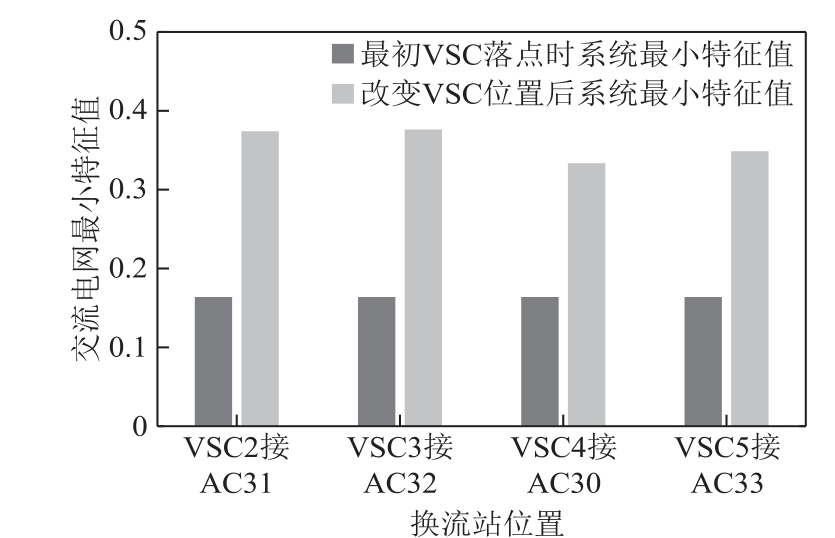
图9 改变VSC位置后交流最小特征值变化图
Fig.9 Diagram for minimum eigenvalue after relocation of VSC
该结果表明,换流站在交流电网的连接位置不同,对交流电网的电压稳定性影响也不同。根据SIMS指标,改变换流站在交流电网的连接位置,不会对直流电网的电压稳定性造成影响,但却能够将直流电网对交流电网的积极影响发挥到最大,从而改善整个交直流混联电网的电压稳定性。这一应用也可以为换流站在交流电网的落点选址提供依据。
4.4.3 交流电网对直流电压稳定性的影响
同样地,交流系统对直流系统的影响也是间接的。在实际运行中,交流电网内部功率传输的变化,会对与它相连的换流站节点处的功率提出不同的要求。也就是说,根据交流电网的不同运行情况,会对换流站的功率进行调整,而换流站的控制功率变化会进一步改变直流电网传输的有功功率,进而引起直流系电网的电压稳定性变化。因此,通过改变换流站的功率分配,可以量化交流电网对直流电网的电压稳定性的影响。
由图2可知,该算例共有五个换流站,其中1号站为整流站,其余四个为逆变站,整流站与逆变站之间满足有功功率平衡:即整流站向直流电网注入的有功功率等于四个逆变站从直流电网吸收的有功功率之和,总计200MW。在1号站总功率不变的情况下,可以根据交流电网的运行情况,将四个逆变站的控制功率进行重新分配。又因为与逆变站相连的四个直流节点的SIMPF指标全为负,因此,逆变站对直流电网的电压稳定性影响是不利的,且直流节点SIMS指标越大,该不利因素的影响越大。
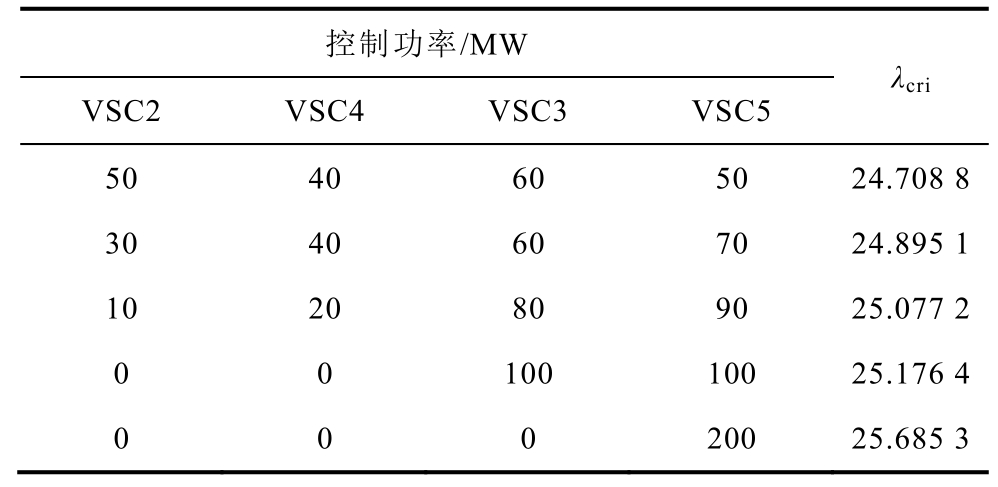
因此,在1号站总功率不变的情况下,连接节点2、3、4、5的逆变站的控制功率应该与这几个节点的SIMS指标大小成负相关进行分配;直流节点2、3、4的SIMS指标已在表4中展示,节点5的SIMS指标约为0。因此,对换流站的控制功率重新分配后,其功率大小应满足VSC2≤VSC4≤VSC3≤VSC5。改变逆变站的控制功率后,直流电网的最小特征值指标λcri见表7。
表7 换流站控制功率对λcri的影响
Tab.7 Influence of VSC control power on λcri
?
根据与换流站直接相连的直流节点的SIMS指标,改变换流站的控制功率后,直流电网最小特征值λcri变大,直流电网的电压稳定性得到改善。且VSC2的功率越小,同时VSC5处的功率越大,λcri增大幅度越明显,即直流电网的电压稳定性越好。
改变换流站的控制功率后,直流电网中,直流节点电压幅值增加的平均数量级为10-3;作为对比,交流电网中,交流节点电压幅值变化的平均值的数量级为10-4,可认为交流电网的电压稳定性基本不变。因此,该实验结果表明,改变换流站的功率分配,不会影响交流电网的电压稳定性,却能够改善直流电网的电压稳定水平,从而提升整个交直流混联系统的电压稳定性。
5 结论
本文对传统的模态分析法改进,将交直流混联系统进行解耦分析,并将模态分析法应用到VSCMTDC交直流混联系统的静态电压稳定性分析中。同时,将状态-模态指标引入并推广到交直流系统中,能够计及有功功率对电压稳定性的影响。所提方法与指标不仅可以量化交、直流负荷变化对电压稳定性的影响,还能够分析交、直流线路故障情况。
此外,本文通过改变换流站的控制功率及换流站在交流电网的连接位置,详细探讨了交流电网、VSC换流站及直流电网之间的直接、间接影响。该方法为VSC-MTDC交直流混联系统的安全稳定运行提供了有价值的参考信息,运行人员可以对交直流系统的关键节点、线路采取相应的补偿措施或者调节换流站的控制功率,从而改善整个交直流混联系统的电压稳定性。
[1] 刘英培, 解赛, 梁海平, 等. 计及换流站间电压误差的VSC-MTDC系统自适应下垂控制[J]. 电工技术学报, 2020, 35(15): 3270-3280.Liu Yingpei, Xie Sai, Liang Haiping, et al. Adaptive droop control strategy for VSC-MTDC system considering DC voltage errors among converter stations[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3270-3280.
[2] 陈鹏远, 黎灿兵, 周斌, 等. 异步互联电网VSCHVDC 紧急功率支援与动态区域控制偏差协调控制策略[J]. 电工技术学报, 2019, 34(14): 3025-3034.Chen Pengyuan, Li Canbing, Zhou Bin, et al.Coordination control strategy of emergency power support and dynamic regional control deviation for asynchronous interconnected power system VSCHVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3025-3034.
[3] 刘子文, 苗世洪, 范志华, 等. 基于自适应下垂特性的孤立直流微电网功率精确分配与电压无偏差控制策略[J]. 电工技术学报, 2019, 34(4): 795-806.Liu Ziwen, Miao Shihong, Fan Zhihua, et al. Accurate power allocation and voltage unbiased control strategy for isolated DC microgrid based on adaptive droop characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 795-806.
[4] 弓帅, 张文, 谢季平. 混合多馈入交直流混联系统中长期电压分级协调控制[J]. 电力系统自动化,2020, 44(22): 54-61.Gong Shuai, Zhang Wen, Xie Jiping. Hierarchical coordinated medium and long-term voltage control in hybrid multi-infeed AC/DC system[J]. Automation of Electric Power Systems, 2020, 44(22): 54-61.
[5] 李岩, 滕云, 冷欧阳, 等. 含多端柔性直流互联的交直流电力系统静态安全分析[J]. 电力系统自动化, 2019, 43(10): 155-163.Li Yan, Teng Yun, Leng Ouyang, et al. Static security analysis of AC/DC power system with multi-terminal flexible DC[J]. Automation of Electric Power Systems,2019, 43(10): 155-163.
[6] 董新洲, 汤涌, 卜广全, 等. 大型交直流混联电网安全运行面临的问题与挑战[J]. 中国电机工程学报, 2019, 39(11): 3107-3119.Dong Xinzhou, Tang Yong, Bu Guangquan, et al.Confronting problem and challenge of large scale ACDC hybrid power grid operation[J]. Proceedings of the CSEE, 2019, 39(11): 3107-3119.
[7] 段献忠, 袁骏, 何仰赞, 等. 电力系统电压稳定灵敏度分析方法[J]. 电力系统自动化, 1997, 21(4): 12-15.Duan Xianzhong, Yuan Jun, He Yangzan, et al.Sensitivity analysis method on voltage stability of electric power system[J]. Automation of Electric Power Systems, 1997, 21(4): 12-15.
[8] Lee B, Ajjarapu V. Invariant subspace parametric sensitivity (ISPS) of structure-preserving power system models[J]. IEEE Transactions on Power Systems, 1996, 11(2): 845-850.
[9] Flatabo N, Ognedal R, Carlsen T. Voltage stability condition in a power transmission system calculated by sensitivity methods[J]. IEEE Transactions on Power Systems, 1990, 5(4): 1286-1293.
[10] 伍利, 古婷婷, 姚李孝. 基于改进连续潮流法的静态电压稳定分析[J]. 电网技术, 2011, 35(10): 99-103.Wu Li, Gu Tingting, Yao Lixiao. Static voltage stability analysis based on improved continuation power flow[J]. Power System Technology, 2011,35(10): 99-103.
[11] 陈厚合, 黄亚磊, 姜涛, 等. 含VSC-HVDC的交直流系统电压稳定分析与控制[J]. 电网技术, 2017,41(8): 2429-2438.Chen Houhe, Huang Yalei, Jiang Tao, et al. Voltage stability analysis and control for AC/DC system with VSC-HVDC[J]. Power System Technology, 2017,41(8): 2429-2438.
[12] Canizares C A, Alvarado F L. Point of collapse and continuation methods for large AC/DC systems[J].IEEE Transactions on Power Systems, 1993, 8(1): 1-8.
[13] 王红燕, 蔡亮, 祁中建. 求取电力系统PV曲线的改进连续潮流算法[J]. 电气技术, 2011, 12(7): 28-31.Wang Hongyan, Cai Liang, Qi Zhongjian. Improved continuation power flow in tracing PV curves of power systems[J]. Electrical Engineering, 2011, 12(7):28-31.
[14] Yan Wei, Ding Chong, Ren Zhouyang, et al. A continuation power flow model of multi-area AC/DC interconnected bulk systems incorporating voltage source converter-based multi-terminal DC networks and its decoupling algorithm[J]. Energies, 2019, 12(4): 733.
[15] Xiao Hao, Li Yinhong, Shi Dongyuan, et al.Evaluation of strength measure for static voltage stability analysis of hybrid multi-infeed DC systems[J]. IEEE Transactions on Power Delivery,2019, 34(3): 879-890.
[16] 辛焕海, 章枫, 于洋, 等. 多馈入直流系统广义短路比:定义与理论分析[J]. 中国电机工程学报, 2016,36(3): 633-647.Xin Huanhai, Zhang Feng, Yu Yang, et al. Generalized short circuit ratio for multi-infeed DC systems:definition and theoretical analysis[J]. Proceedings of the CSEE, 2016, 36(3): 633-647.
[17] 潘学萍, 李乐, 黄华, 等. 综合灵敏度和静态电压稳定裕度的直流受端交流系统电压薄弱区域评估方法[J]. 电力自动化设备, 2019, 39(3): 1-8.Pan Xueping, Li Le, Huang Hua, et al. A method for evaluating the weak area of DC receiver AC systems with a combination of sensitivity and static voltage stability margin[J]. Electric Power Automation Equipment, 2019, 39(3): 1-8.
[18] Gao B, Morison G K, Kundur P. Voltage stability evaluation using modal analysis[J]. IEEE Transactions on Power Systems, 1992, 7(4): 1529-1542.
[19] 韩光, 丁晓群, 刘小波, 等. 基于模态技术和Q-U曲线的一种电压稳定性指标[J]. 继电器, 2006,34(6): 21-23.Han Guang, Ding Xiaoqun, Liu Xiaobo, et al. A voltage stability index based on modal technology and Q-U curve[J]. Relay, 2006, 34(6): 21-23.
[20] Song Yue, Hill D J, Liu Tao. State-in-mode analysis of the power flow jacobian for static voltage stability[J]. International Journal of Electrical Power and Energy Systems, 2019, 105: 671-678.
[21] 吴杰康, 张飚, 陈国通. 运用特征值法确定交直流系统电压失稳区[J]. 继电器, 2006, 34(7): 27-31.Wu Jiekang, Zhang Biao, Chen Guotong. Voltage weak stability zone calculation of AC/DC system using eigenvalue method [J]. Relay, 2006, 34(7): 27-31.
[22] 杜萍静, 杨明, 曹良晶, 等. 含电压源换流器交直流系统的仿射潮流算法[J]. 电工技术学报, 2020,35(5): 1106-1117.Du Pingjing, Yang Ming, Cao Liangjing, et al. Affine power flow algorithm for AC/DC systems with voltage source converter[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1106-1117.
[23] 邵冰冰, 赵书强, 高本锋, 等. 连接弱交流电网的VSC-HVDC失稳机理及判据研究[J]. 电工技术学报, 2019, 34(18): 3884-3896.Shao Bingbing, Zhao Shuqiang, Gao Benfeng, et al.Instability mechanism and criterion analysis of VSCHVDC connected to the weak AC power grid[J].Transactions of China Electrotechnical Society, 2019,34(18): 3884-3896.
[24] Chai Runze, Zhang Baohui, Bo Zhiqian, et al. A generalized unified power flow algorithm for AC/DC networks containing VSC-based multi-terminal DC grid[C]//2014 International Conference on Power System Technology, Chengdu, 2014: 2361-2366.
[25] Da Silva L C P, Da Costa V F, Xu W. Preliminary results on improving the modal analysis technique for voltage stability assessment[C]//2000 Power Engineering Society Summer Meeting, Seattle, 2000:1946-1950.
[26] Chai Runze, Zhang Baohui, Dou Jingming, et al.Unified power flow algorithm based on the NR method for hybrid AC/DC grids incorporating VSCs[J]. IEEE Transactions on Power Systems, 2016,31(6): 4310-4318.