0 引言
近年来，新的直线电机的拓扑结构和控制方式层出不穷[1-2]，尤其是横向磁通永磁直线电机问世后，打破了传统直线电机的设计理论和电源供电方式，为直线直驱运动系统提供了全新的解决方案。与传统永磁直线电机相比，横向磁通永磁直线电机一方面其磁力线所在的平面垂直于其运动方向，解决了齿和槽在空间上竞争同一个平面的问题，实现了电负荷与磁负荷的解耦，可以在一定范围内通过提高磁能变化率来提高出力；另一方面各相之间相互解耦，便于独立控制，且易于设计成多相结构，在多相运行时即使缺少一相也能正常工作，容错性能好，提高了电机的可靠性。因此针对横向磁通永磁直线电机（Transverse Flux Permanent Magnet Linear Machine, TFPMLM）的研究引起了国内外电机界学者的广泛关注[3-11]。
然而TFPMLM复杂的拓扑磁路结构和严重的漏磁增加了其优化设计的难度，此外，TFPMLM的优化设计研究目前主要集中在单一优化变量或者优化目标上，缺乏对电机多目标综合性能指标的优化[12]。文献[13]针对双交替极横向磁通直线电机，分别对极距、安匝数、永磁体厚度、齿宽系数和槽口尺寸进行优化，提高了该电机的推力密度，但只追求推力密度单一优化目标，未能整体提高该电机的电磁性能。目前，对电机进行优化设计的两种常用方法是试验设计（Design of Experimental, DoE）和智能算法，但是这两种方法在优化过程中要么仅针对单目标进行优化，要么其单独使用存在一定的局限性。DoE与智能算法相结合的多目标优化方法为解决上述问题提供了新思路[14-19]。多目标优化方法能最大程度地平衡电机各参数的性能指标，使得电机得到较优的综合性能，在电机的优化设计中起着重要的作用。文献[20]以永磁直线电机的推力最大值和推力波动最小值为优化目标，分别采用单一的粒子群优化算法和基于正交阵列的田口算法进行优化设计。相比于单一的粒子群优化算法，田口算法能得到更大的推力和更小的推力波动，最后通过样机实验验证了田口算法的优越性和有效性。文献[21]针对一种双边游标直线永磁电机，以推力、推力波动和功率因数为优化目标，利用表面响应法对选取的显著变量进行建模，并通过差分进化算法寻求最优解。通过有限元和样机实验验证，证明了优化后的电机可以获得更高的推力密度和功率因数，推力脉动也相应减小，提高了该电机的整体电磁性能。文献[22]采用有限元法和改进的粒子群算法相结合的多目标优化设计方法，以效率、弱磁率和价格为优化目标，对五种不同转子拓扑结构的永磁同步电动机进行多目标优化，并比较了它们的弱磁性能、效率、价格和抗退磁能力，优化后的电机具有较高的效率、转矩密度和较低的成本价格，通过样机实验验证了多目标优化设计方法的可行性和有限元分析的准确性。文献[23]提出一种电励磁双定子场调制电机，以转矩密度和转矩纹波为优化目标，通过敏感性分析对该电机的结构参数进行灵敏度分层，根据参数敏感度层次将基于遗传算法的多目标优化设计以及响应面法和单参扫描法等多种优化方法相结合，最终确定电机的最优结构。
本文针对一种新型动子三面墙聚磁式结构的TFPMLM提出表面响应法和粒子群优化（Particle Swarm Optimization, PSO）算法相结合的多目标优化设计方法，以推力密度、推力波动和功率因数为优化目标，对该电机选取的关键尺寸参数进行灵敏度分析；选取灵敏度值显著的优化变量构建响应面数学模型，得到优化目标和优化变量之间的函数关系；将粒子群算法应用于响应面模型对该电机进行多目标优化，最终确定该电机的最优结构参数，并通过三维有限元模型对比优化前后TFPMLM的定位力、电磁力等电磁性能，验证基于表面响应面法和粒子群优化算法的多目标优化设计方法的有效性。
1 横向磁通永磁直线电机的基本结构和工作原理
1.1 基本结构
本文所提出的三相聚磁式TFPMLM的结构示意图如图1所示，其定子由两个C型定子铁心组成，其内部三面墙（上、下、中）均匀设置多个间距相等的条形槽，定子上、下齿相对，中间齿分别与上下槽相对，C型定子以镜像方向分别设置于动子的两侧，结构简单；动子由永磁体、U型凸极铁心、连接板和电枢绕组组成。连接板的两端各有三个凸极铁心，每个凸极铁心有三个U型齿，U型齿凹槽内嵌切向充磁的永磁体（N-S-N）。该电机属于双边结构，抵消了法向吸力，每相分别有六个面，四支独立的磁回路，且相间解耦，具有较强的容错能力，三相对称结构，定位力较小。可用于对系统的可靠运行有较高要求的领域，特别是对系统体积及连续运行有严格要求的航空航天、军事装备等应用场合。
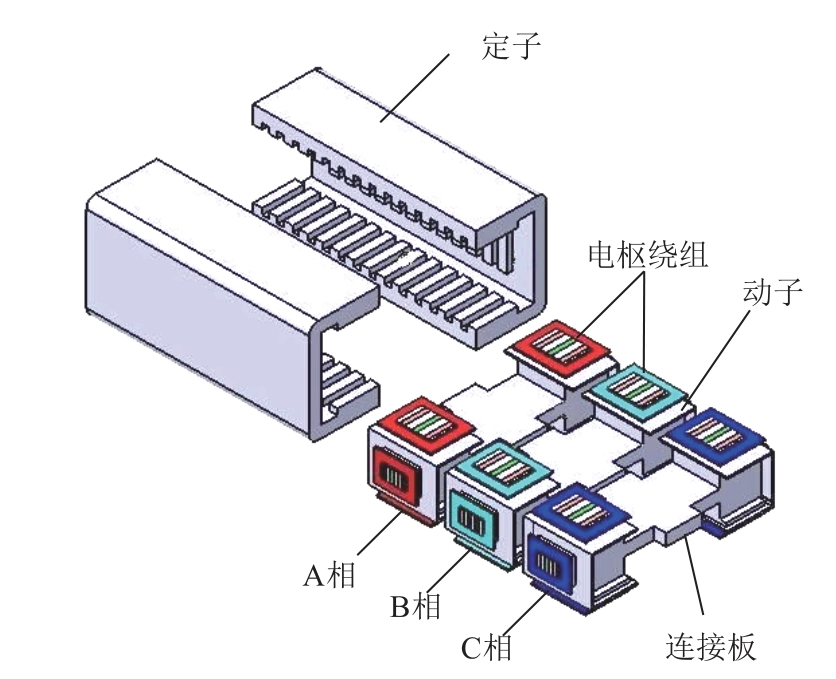
图1 横向磁通永磁直线电机三相结构示意图
Fig.1 The structure diagram of three phase TFPMLM
由凸极齿、永磁体和凹槽组成的动子凸极平面结构如图2所示。在每个凸极上有三个凹槽，相邻凹槽内放置三个永磁体。上部、中部、下部绕组均绕在凸极结构外且绕组串联，但上部绕组与中部、下部绕组的绕制方向相反。绕组的联结方式如图2d所示。
图2 动子凸极平面结构及绕组联结方式Fig.2 The salient pole plane structure and winding connection mode of the mover
1.2 工作原理
该电机单相单边磁力线走向示意图如图3所示。从图3可以看出，通过合理设计初级极距/次级极距，使得上下凸极中的永磁体发出的磁力线分别聚磁后通过连接板到达相邻的凸极铁心中的永磁体，通过第一个气隙、次级铁心、第二个气隙回到起始凸极铁心，形成上1和下2两个主磁通回路。主磁通回路1的磁力线流通回路为：上部U型凸极铁心中的永磁体产生的磁通从N极出发，向下依次经过上部、中部动子铁心到达中部U型凸极铁心中永磁体S极，再由永磁体的 N 极经过中部气隙向上经过该电机的定子、气隙回到上部U型凸极铁心永磁体S极，进而形成一个闭合的回路。由图3可以看出，TFPMLM内部磁场呈复杂的三维分布，其所在平面与电机运动方向垂直，即电机主磁通为横向磁通。该电机永磁体励磁源与电枢绕组都位于动子侧，依靠动子的永磁体励磁源与定子凸极的调制作用，使得动子绕组中的磁链发生交变，从而产生感应电势与电磁力，实现机电能量转换，属于磁场调制电机的一种。
图3 横向磁通永磁直线电机单相单边磁力线走向示意图
Fig.3 The schematic diagram of magnetic lines in single phase of TFPMLM
2 灵敏度分析
为了减少多目标优化所需的优化时间，采用灵敏度分析方法，不仅减少设计空间还可以有效地分析各个设计变量对电机性能的影响。本文首先通过对TFPMLM进行初步分析，确定合理的优化目标和优化变量取值范围。然后建立TFPMLM有限元模型，对电机的电磁性能进行初步评估。合理评价不同结构参数对优化目标的敏感度，将综合灵敏度大于0.1的优化变量作为显著变量，针对显著变量本文采用基于响应面模型（Response Surface Model,RSM）和粒子群优化算法（PSO）相结合的优化方法进行优化设计。TFPMLM的灵敏度分析流程如图4所示。
图4 灵敏度分析流程
Fig.4 Flow chart of sensitivity analysis
2.1 优化目标和优化变量的确定
本文所提出的聚磁式TFPMLM的尺寸结构示意图如图5所示，选取其中6个关键尺寸结构参数对TFPMLM进行多目标优化设计。表1给出了TFPMLM优化变量初值及变化范围。
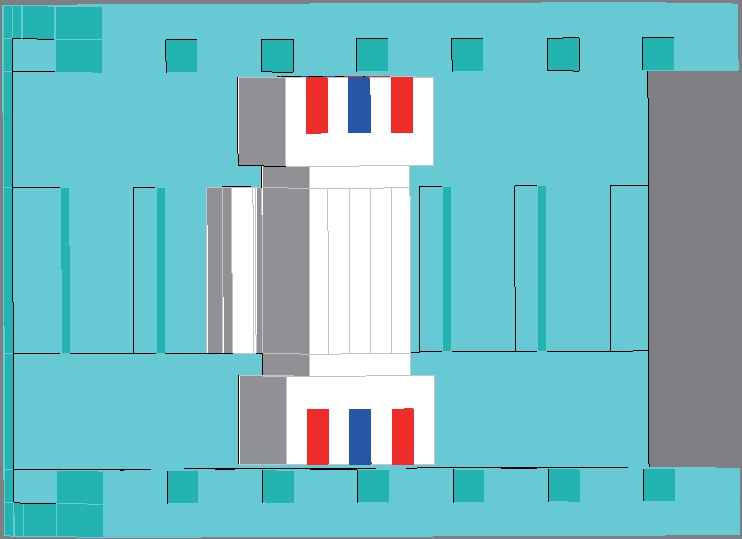
图5 横向磁通永磁直线电机的尺寸结构
Fig.5 Dimension structure of TFPMLM
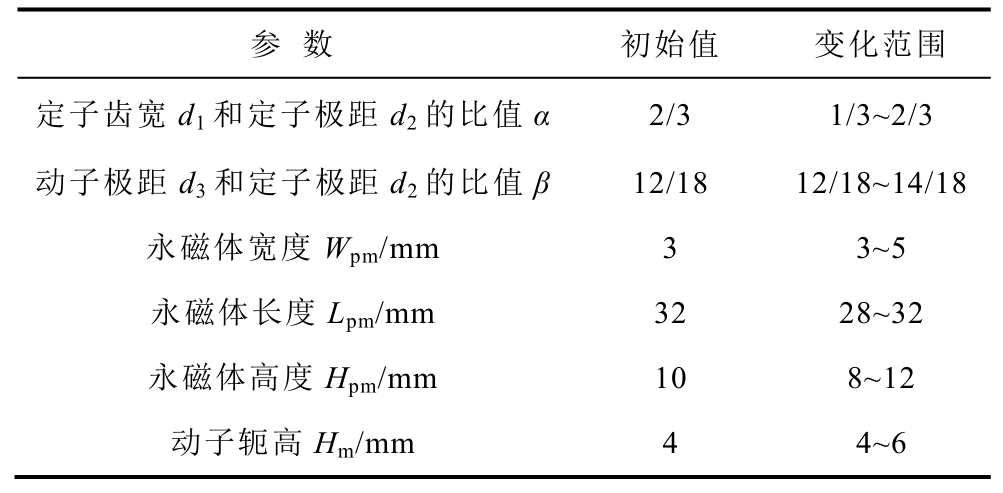
表1 电机优化变量初值及变化范围
Tab 1. Initial value and variation range of design variables of TFPMLM machine
?
为了满足优化设计要求，实现TFPMLM的最优性能，选取推力密度Davg和功率因数PF最大值、推力波动Fr最小值作为该TFPMLM多目标优化设计的优化目标。
本文TFPMLM的推力密度Davg被定义为单位永磁体体积下电机推力大小，即
式中，Favg为平均推力；Vpm为永磁体体积。
TFPMLM的推力波动Fr为
式中，Fmax和Fmin分别为推力的最大值与最小值。TFPMLM采取直轴电流为零的控制方式(id=0)。电枢绕组的电流等于交轴电流(is=iq)，交轴电感可以表示为
式中，L0为自感；Lm为每相互感的2次谐波。
TFPMLM的功率因数PF为
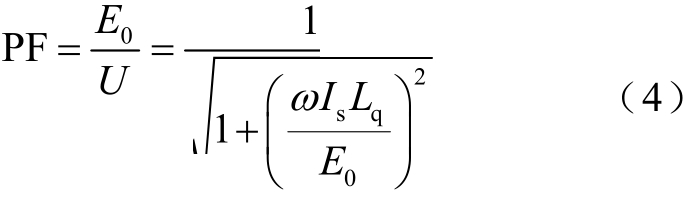
式中，E0为空载反电动势；Is为电枢电流；ω为电角频率。
因此，TFPMLM的多目标优化函数g(ni)可以表示为
式中，
和PF′分别为优化前电机推力密度、推力波动和功率因数；
为优化目标函数，分别表示ni取某一参数时，电机推力密度、推力波动和功率因数的大小；λ1、λ2、λ3分别为推力密度、推力波动和功率因数的权重系数，且满足λ1+λ2+λ3=1。TFPMLM适应于低速大推力应用场合，对电机的高推力密度要求更高，运行的稳定性也需要相对较低的推力波动。此外，功率因数作为所提出电机的关键指标也应予以考虑。因此多目标优化函数g(ni)的权重系数λ1为0.5，而λ2、λ3分别取为0.25。此外，该电机在优化过程中还需要设置一些约束条件，如线电流密度J=8A/mm2。
2.2 优化变量的灵敏度分析
首先利用三维有限元模型对该TFPMLM性能进行初步分析，并据此对各个优化变量ni进行敏感性评估，得到优化变量ni针对某一优化目标的敏感因子G(ni)，再综合分析三个优化目标，得到优化变量ni对于多目标的综合灵敏度S(ni)。敏感因子G(ni)可表示为[21]
综合考虑三个优化目标，采用权重系数法对各优化变量进行综合估算。引入了一个综合灵敏度S(ni)，可描述为
式中，GDavg、GFr、GPF分别为优化变量ni针对推力密度、推力波动和功率因数三个优化目标的敏感因子。
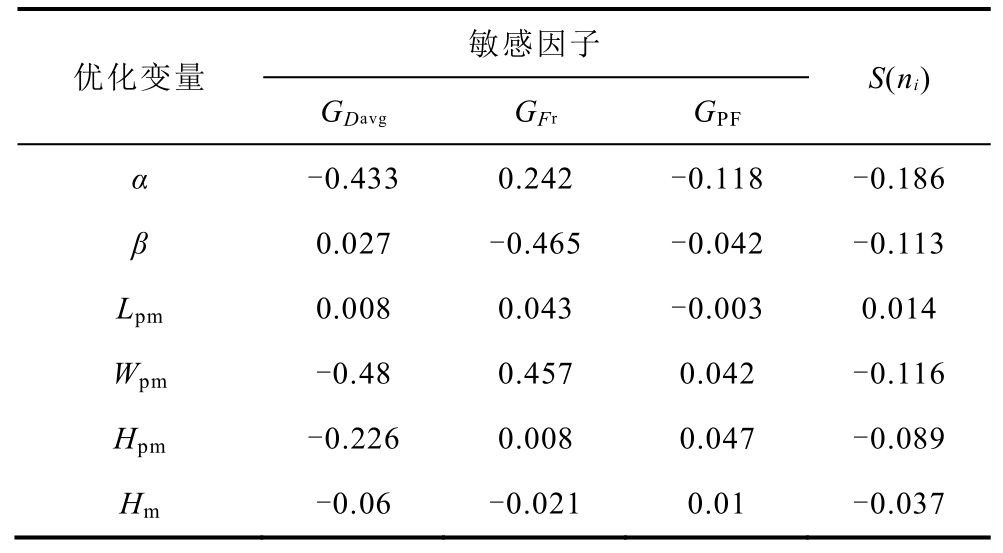
根据上述原理公式，求出各优化变量对三个优化目标的敏感因子和综合灵敏度指标，分析结果见表2。
表2 各优化变量的灵敏度分析结果
Tab.2 Sensitivity analysis results of each design variable
?
为了清楚地分析每个优化变量的灵敏度指标，表2中的数据由图6所示的直方图表示。正灵敏度指标表示优化目标随优化变量的增大而上升，而负灵敏度指标则表示优化目标随优化变量的减小而下降。敏感因子绝对值较高的优化变量意味着优化变量对优化目标的影响大于其他变量。由表2和图6可以看出，不同的优化变量对推力密度、推力波动和功率因数的影响是有差异的。在上述敏感性分析的基础上，将综合敏感度
的优化变量α、β和Wpm划为显著优化变量，其对推力密度、推力波动和功率因数存在交叉影响，且相互之间作用性较强。因此，显著优化变量应采用试验设计和智能算法相结合的优化方法，而非显著优化变量Lpm、Hpm和Hm可以采用单参数优化的方法得到最优结果。
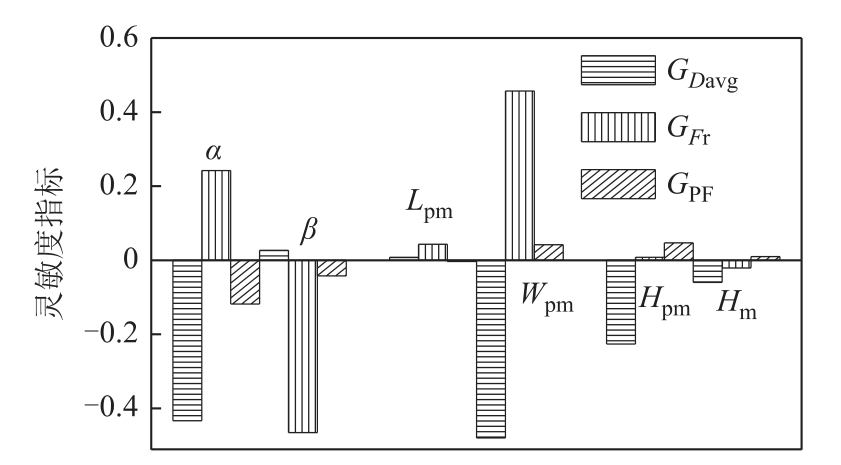
图6 优化变量的灵敏度指标
Fig.6 Sensitivity index of design variables
3 构建响应面模型
TFPMLM构建响应面数学模型的具体流程如图7所示。首先，将灵敏度分析得到的显著优化变量进行编码并确定其水平值，根据Box-Behnken Design（BBD）方法的试验设计原则，建立正交试验矩阵并通过有限元计算分别得到在各个水平下优化目标的响应值。其次，针对试验结果的响应值进行多元二次回归拟合，得到各个优化目标响应面的数学模型和三维曲面。再次，通过对三维曲面的梯度分析，证明RSM具有最佳的优化变量范围。最后，通过多重相关系数R2和预测响应值分析来验证所获得的数学模型具有较高的拟合度和精度。
图7 基于BBD方法的响应面建模流程
Fig.7 RSM optimization process based on BBD method
3.1 Box-Behnken Design数学模型
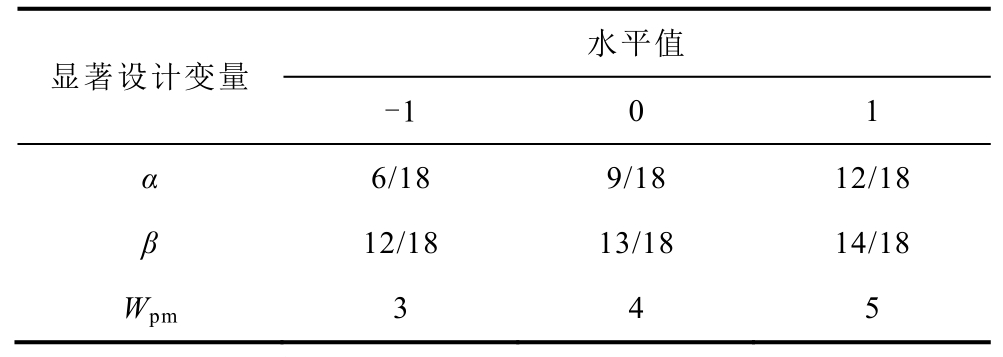
响应面模型（RSM）是一种数学建模优化和综合试验设计方法，可以有效减少试验次数，准确分析设计变量之间的相互作用。其中，BBD方法是一种经典、常用的试验设计方法，通常适合建立2～5个水平的RSM [24]。BBD方法可以保证各设计变量的灵敏度指标不受设计变量间相互作用的影响。BBD方法将每个因子的三个级别编码为-1、0和+1。其中0为中心点，+1和-1为相对高低值。表3给出了各设计变量编码及水平值。
表3 设计变量编码及水平值
Tab.3 Code and level value of design variables
?
3.2 BBD正交试验矩阵
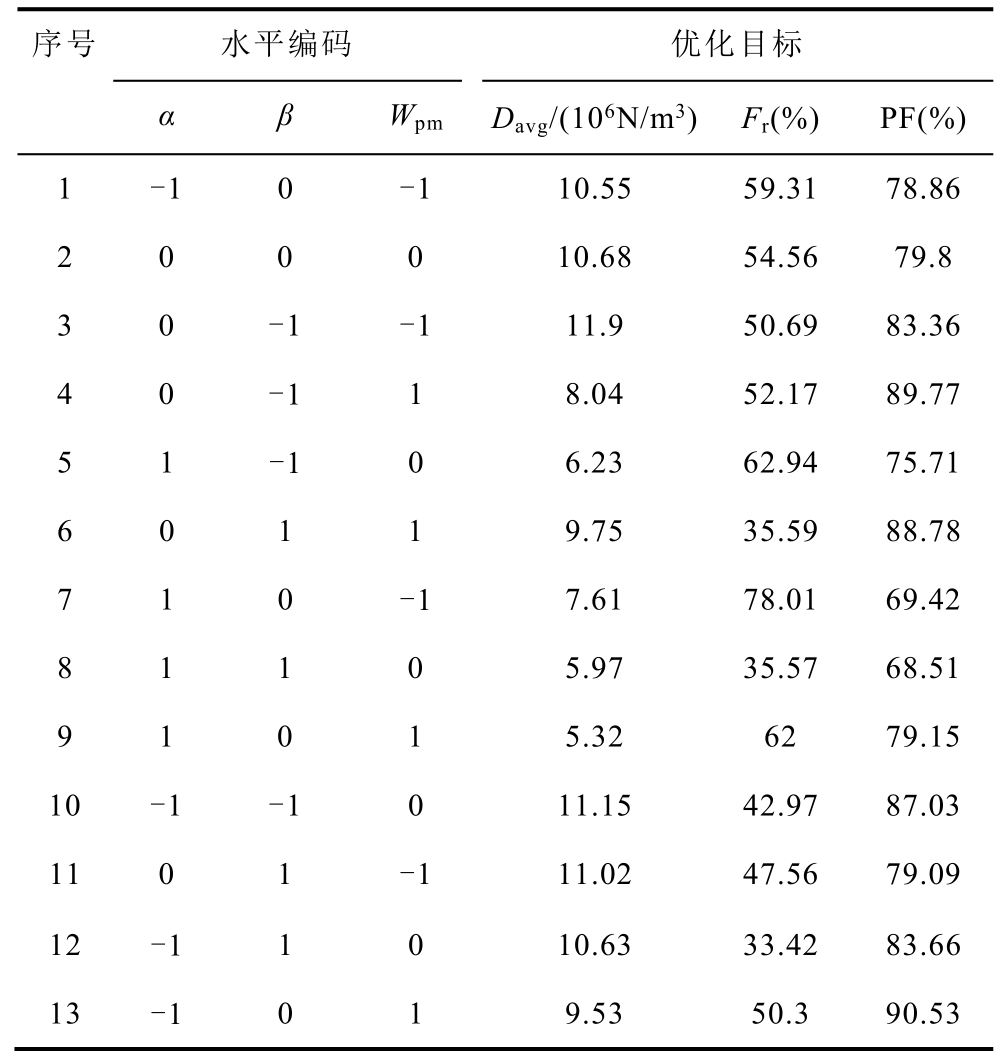
根据三水平三因素试验设计原则，建立了BBD的正交试验矩阵。可以看出，仅需计算13次试验即可。因为设计变量为三水平四因素，所以传统单参数扫描的方法需要34=81次试验。与此相比，BBD显著减少了TFPMLM优化设计的时间，节省了大量时间成本。通过试验得到了TFPMLM关于Davg、PF和Fr的响应，并据此建立表面响应模型。BBD正交试验矩阵及三个优化目标的响应结果见表4。
表4 正交试验矩阵及试验结果
Tab.4 Orthogonal experimental matrix and experimental results
?
3.3 优化目标的表面响应分析
对于三因素优化问题，二阶RSM在优化过程中具有足够的精度。RSM的二阶多项式可以表示为[21]
式中，G(t)为响应值；a0、ai 、aj为回归系数；ti、tj为两个不同的优化变量；ε为拟合误差。
在得到上述试验结果的响应值后，对数据进行多元二次回归拟合，即可得到响应面的数学模型。
TFPMLM推力密度的拟合回归方程为
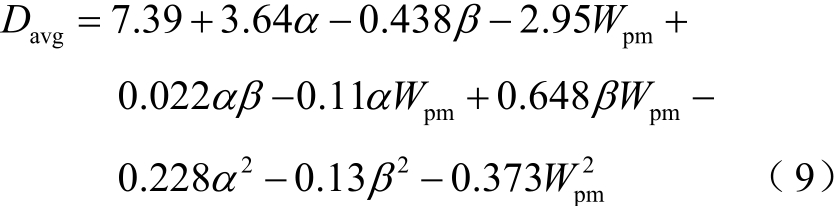
TFPMLM推力波动的拟合回归方程为
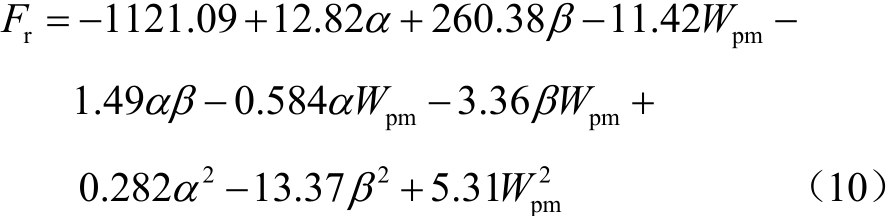
TFPMLM功率因数的拟合回归方程为
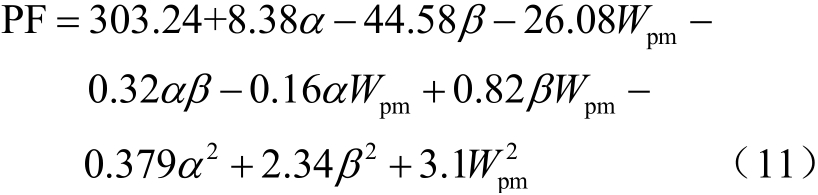
图8 ~图10分别给出了设计变量α、β和Wpm在三个优化目标上的三维响应面，通过对响应面的分析，可以看出三维曲面具有较高的梯度，证明RSM具有最佳的设计变量范围。
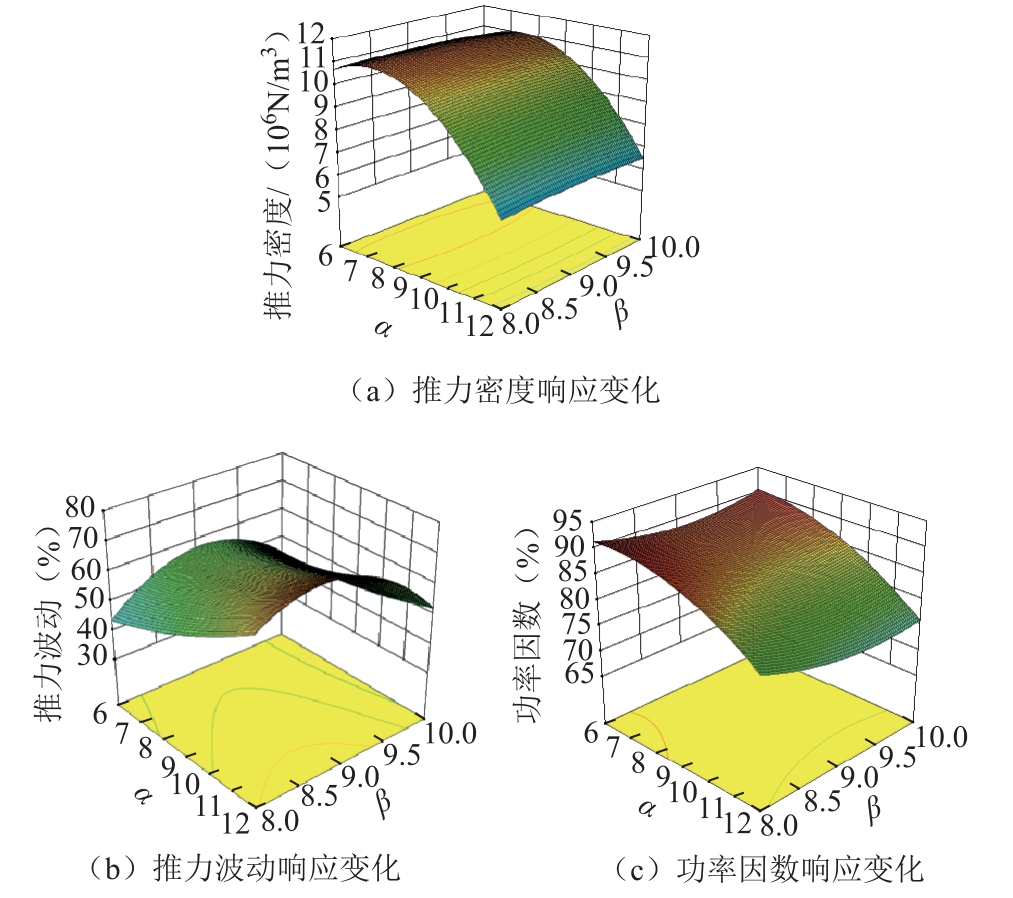
图8 三个优化目标在结构参数α和β下的响应Fig.8 Response of three optimization objectives to the structure parameters α and β
图10 三个优化目标在结构参数β和Wpm下的响应Fig.10 Response of three optimization objectives to the structure parameters β and Wpm
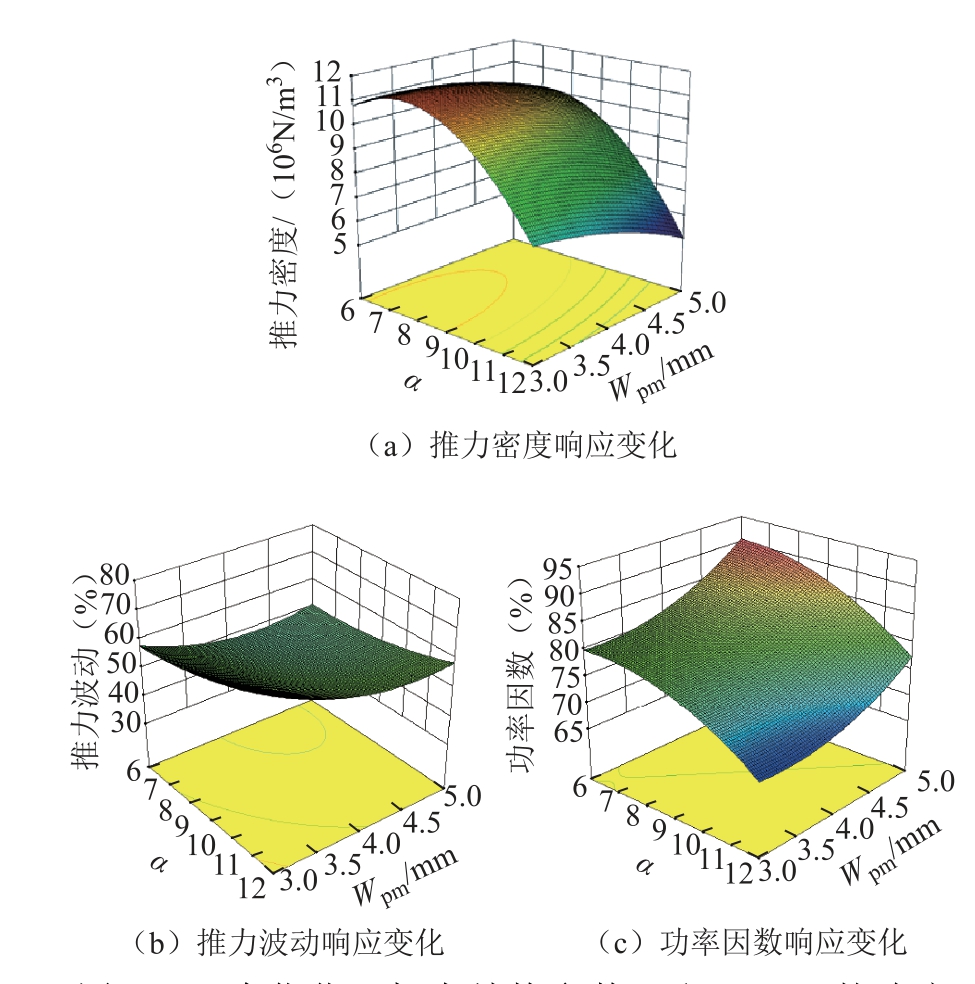
图9 三个优化目标在结构参数α和Wpm下的响应Fig.9 Response of three optimization objectives to the structure parameters α and Wpm
3.4 RSM模型的验证
试验数据的总误差程度可用偏差平方和（Total Sum of Square, SST）的概念描述。SST是全部响应值与总试验数据平均值的偏差平方和，反映全部响应值的离散情况[25]。
式中，Yu为实际响应值；
为试验数据平均值。组间离差平方和（Sum Squared Residual, SSR）包括随机误差和系统误差，反映的是随机误差和系统误差的大小。
式中，
为响应面模型预测值。
多重相关系数R2代表了二阶RSM对TFPMLM实际电磁性能的逼近程度。
R2值越接近1，二阶RSM的试验数据越符合TFPMLM的实际性能。TFPMLM三个响应的多重相关系数R2分别为推力密度Davg（97.5%）、功率因数PF（98.19%）和推力波动Fr（96.28%）。可以看出，在这个范围内，二阶回归多项式对设计变量有很好的精度。
RSM各个优化目标的实际值和预测响应值如图11所示。模型的响应值越接近45°线，响应面模型预测精度越高。通过以上分析，证明拟合回归模型具有较高的精度，RSM能较好地反映TFPMLM响应的数据规律。
图11 表面响应的预测值与实际值的交叉验证
Fig.11 Cross validation of predicted and actual surface response
4 粒子群优化算法
然而，每个响应面设计变量的最佳范围可能不相同，甚至相反。为了寻找三个优化目标的全局最优解，将粒子群优化算法引入到TFPMLM的多目标优化设计中。PSO算法具有收敛速度快、易于实现、参数调整少等优点，其有效的搜索策略使其广泛应用于解决多目标优化问题[26]。算法中的每个粒子代表问题的一个潜在解，并根据目标函数计算出每个粒子位置对应的适应值，在可解空间中，根据自身和其他粒子的运动经验，动态调整速度，实现个体最优化。PSO算法的优化流程如图12所示。
图12 粒子群算法优化流程
Fig.12 The optimization flow chart of PSO
在每次迭代过程中，粒子的位置和速度由局部和全局最优点更新。粒子群优化算法的基本方程为
式中，Vid为第i个粒子在d维空间的速度；Xid为第i个粒子在d维空间的位置；θ为惯性权重；k为当前迭代次数；d为粒子搜索空间的大小；c1和c2为加速系数；r1和r2为[0, 1]之间的随机数；P和Q分别为局部和全局最优点。
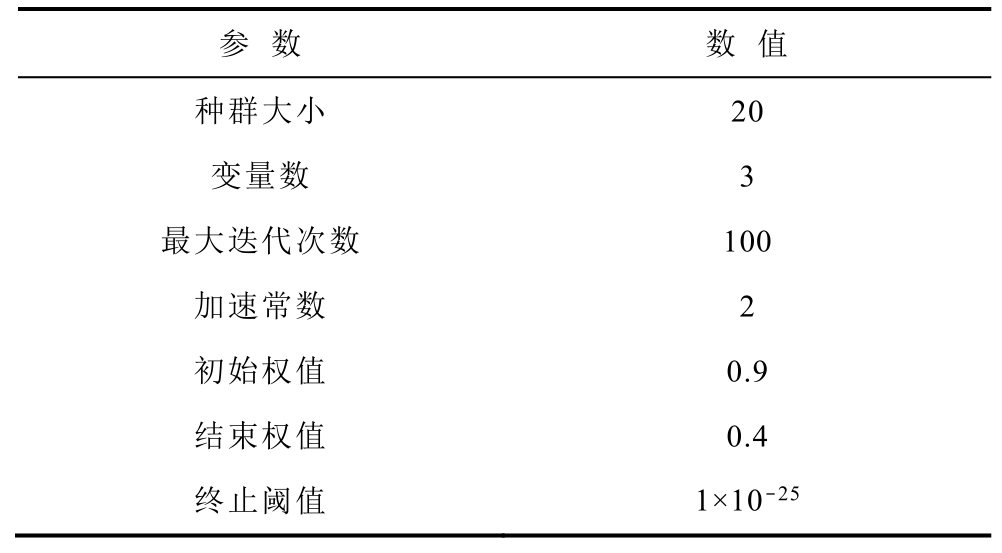
通过灵敏度分析和构建RSM数学模型，在恰当的适应度函数评估的基础上，对得到的二阶RSM数学模型采用PSO算法进行求解，以准确地表达优化变量与电机响应之间的关系。利用惯性权重平衡粒子群算法的检测能力和开发能力[27]，初始权值设定为0.9，使算法具有较高的全局搜索能力；将结束权值设置为0.4，这有利于更精确地进行局部搜索。整个优化过程仅需20s，而基于有限元求解器的单参数优化通常需要2h左右，可以节省大量的计算时间。PSO的种群规模被设置为20，最大迭代次数被设置为100。图13所示为多目标优化函数g(ni)的迭代收敛情况（优化过程中实际数据每迭代50次记录为1次迭代收敛位数），经过变量的全局寻优，实际迭代总次数为750次时，多目标优化函数 g(ni)则可稳定到最小值，约为0.483。PSO的参数设置见表5。优化前后电机的结构参数见表6。经过PSO优化后，选取最终的设计变量α=8.79/18，β=14/18，Wpm=5mm。
图13 基于粒子群算法的目标函数收敛情况Fig.13 Objective function value change based on the PSO algorithm
表5 PSO参数设置
Tab.5 Parameter setting of PSO
?
表6 优化前后电机结构参数结果对比
Tab.6 Comparison of results before and after optimization
?
5 电机优化前后性能对比
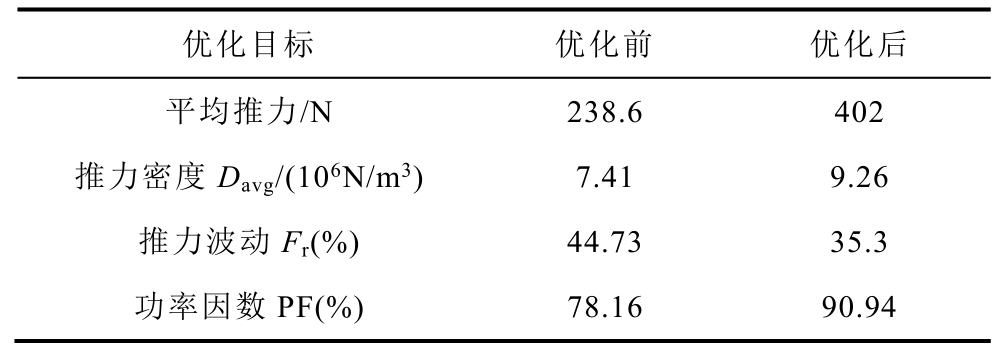
优化前后TFPMLM的定位力波形和推力波形分别如图14a和图14b所示。从图中可以看出优化前电机定位力峰峰值为21.1N。采用多目标优化方法对该电机进行优化设计后定位力峰峰值为14N，定位力峰峰值降低了33.26%。平均推力由优化前的238.6N增大到402N，平均推力提高了68.47%，推力波动从优化前的44.73%降低到优化后的35.3%。表7给出了优化前后TFPMLM电磁性能指标。经过多目标优化后，电机的推力密度提高了25%，推力波动降低了21%。此外，功率因数由初始电机的78.16%提高到优化后的90.94%，电机的功率因数提高了16.4%。优化后的电机比初始电机具有更高的推力密度和更高的功率因数，同时其推力波动相对较小。显然，本文提出的多目标优化设计方法可以有效地提高TFPMLM的整体电磁性能。
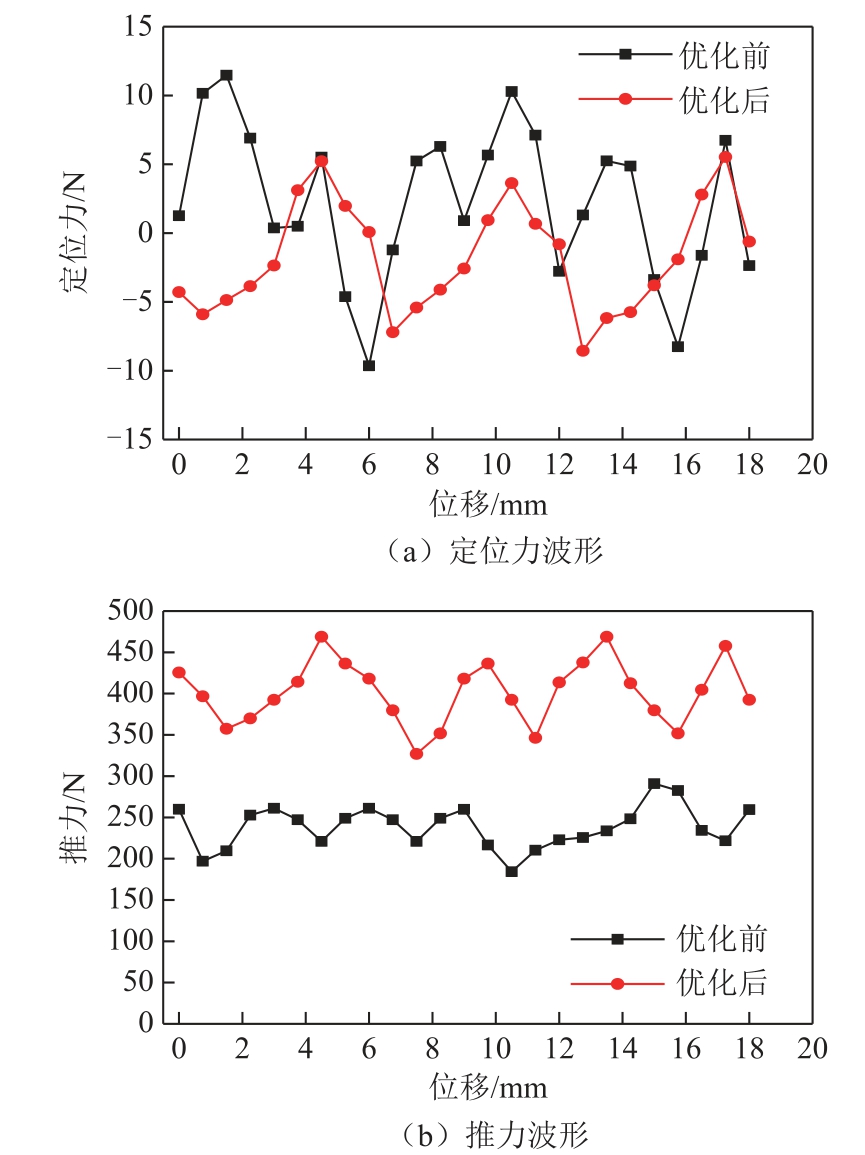
图14 优化前后电机电磁性能波形对比
Fig.14 Comparison of electromagnetic performance waveforms of machine before and after optimization
表7 优化前后TFPMLM电磁性能对比
Tab.7 Comparison of electromagnetic performance indexes of TFPMLM before and after optimization
?
6 结论
1）本文提出了一种动子三面墙聚磁式结构的横向磁通永磁直线电机，介绍了TFPMLM的结构和工作原理。
2）在对TFPMLM优化变量灵敏度分析的基础上，提出一种基于RSM和PSO相结合的TFPMLM多目标优化设计方法。该优化方法可以在保证优化设计精度的前提下，大幅度缩短优化时间。
3）采用三维有限元模型将优化后的电机与初始电机的电磁性能进行了比较。分析结果表明，优化后的TFPMLM比初始TFPMLM具有更高的推力密度和更高的功率因数，其推力波动相对较小。进一步验证了本文所提出的多目标优化方法的有效性。
[1] 曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020,35(5): 1001-1012.Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001-1012.
[2] 许孝卓, 孙震, 汪旭东, 等. Halbach交替极永磁同步直线电机特性分析[J]. 电工技术学报, 2019,34(9): 1825-1833.Xu Xiaozhuo, Sun Zhen, Wang Xudong, et al.Characteristic of a novel permanent magnet linear synchronous motor with halbach array consequentpole[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1825-1833.
[3] Zou Jibin, Zhao Mei, Wang Qian, et al. Development and analysis of tubular transverse flux machine with permanent magnet excitation[J]. IEEE Transactions on Industrial Electronics, 2012, 59(5): 2198-2207.
[4] 赵玫, 邹继斌, 王骞. 定子单元铁心轴向类分布排列的横向磁通永磁直线电机[J]. 电工技术学报,2013, 28(11): 106-111.Zhao Mei, Zou Jibin, Wang Qian. Transverse flux PMLM with class distribution of the stator core[J].Transactions of China Electrotechnical Society, 2013,28(11): 106-111.
[5] Dong Dingfeng, Huang Wenxin, Bu Feifei, et al.Modeling and optimization of a tubular permanent magnet linear motor using transverse-flux fluxreversal topology[J]. IEEE Transactions on Industry Applications, 2019, 55(2): 1382-1391.
[6] Zhao Mei, Wei Yao, Yang Hongyong, et al.Development and analysis of novel flux-switching transverse-flux permanent magnet linear machine[J].IEEE Transactions on Industrial Electronics, 2019,66(6): 4923-4933.
[7] 徐衍亮, 崔波, 张文晶, 等. 软磁复合材料-Si钢组合铁心盘式横向磁通永磁无刷电机[J]. 电工技术学报, 2020, 35(5): 983-990.Xu Yanliang, Cui Bo, Zhang Wenjing, et al. Disk transverse flux permanent magnet brushless motor based on soft magnetic composite-Si steel core[J].Transactions of China Electrotechnical Society, 2020,35(5): 983-990.
[8] 赵玫, 于帅, 张华强. 聚磁式横向磁通永磁直线电机的变磁导等效磁网络[J]. 电机与控制学报, 2020,24(4): 12-22.Zhao Mei, Yu Shuai, Zhang Huaqiang. Variable permeability equivalent magnetic circuit network of flux-concentrated transverse flux permanent magnet linear machine[J]. Electric Machines and Control,2020, 24(4): 12-22.
[9] 寇宝泉, 杨小宝, 罗俊, 等. 横向磁场磁通反向电机的特性分析[J]. 电工技术学报, 2017, 32(增刊2):18-25.Kou Baoquan, Yang Xiaobao, Luo Jun, et al.Characteristic analysis of transverse-flux flux reversal motor[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 18-25.
[10] Zhao Mei, Wei Yao, Yu Shuai, et al. Development and analysis of a novel transverse flux permanent magnet linear motor with the concentrated flux mover[J].IEEE Transactions on Applied Superconductivity,2019, 29(2): 1-6.
[11] Wei Yao, Zhao Mei, Yang Hongyong, et al.Electromagnetic characteristic of a novel linear flux switching machine with three-dimensional magnetic circuit[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(2): 1-5.
[12] 寇宝泉, 罗俊, 杨小宝, 等. 横向磁场磁通反向直线电机的设计与分析[J]. 中国电机工程学报, 2017,37(4): 1216-1225.Kou Baoquan, Luo Jun, Yang Xiaobao, et al. Design and analysis of a transverse-flux flux-reversal linear machine[J]. Proceedings of the CSEE, 2017, 37(4):1216-1225.
[13] 罗俊, 寇宝泉, 杨小宝. 双交替极横向磁通直线电机的优化与设计[J]. 电工技术学报, 2020, 35(5):991-1000.Luo Jun, Kou Baoquan, Yang Xiaobao, et al.Optimization and design of dual-consequent-pole transverse flux linear machine[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 991-1000.
[14] Liu Chunyuan, Zhu He, Dong Rui, et al. Sensitivity analysis and optimal design of a linear magnetic gear for direct-drive wave energy conversion[J]. IEEE Access, 2019, 7: 73983-73992.
[15] 张邦富, 程明, 王飒飒, 等. 基于改进型代理模型优化算法的磁通切换永磁直线电机优化设计[J].电工技术学报, 2020, 35(5): 1013-1021.Zhang Bangfu, Cheng Ming, Wang Sasa, et al.Optimal design of flux-switching permanent magnet linear machine based on improved surrogate-based optimization algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1013-1021.
[16] Xu Wei, Hu Dong, Lei Gang, et al. System-level efficiency optimization of a linear induction motor drive system[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(3): 285-291.
[17] Tsai J T, Chang C C, Chen Wenping, et al. Optimal parameter design for IC wire bonding process by using fuzzy logic and taguchi method[J]. IEEE Access, 2016,4: 3034-3045.
[18] Du Jinhua, Lu Pan, Liang Deliang. Optimal design of a linear transverse-flux machine with mutually coupled windings for force ripple reduction[J]. IET Electric Power Applications, 2018, 12(2): 271-280.
[19] Lee J H, Song J Y, Kim D W, et al. Particle swarm optimization algorithm with intelligent particle number control for optimal design of electric machines[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1791-1798.
[20] Song Juncai, Dong Fei, Zhao Jiwen, et al. Optimal design of permanent magnet linear synchronous motors based on taguchi method[J]. IET Electric Power Applications, 2017, 11(2): 41-48.
[21] Zhao Wenxiang, Ma Anqi, Ji Jinghua, et al. Multiobjective optimization of a double-side linear vernier PM motor using response surface method and differential evolution[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 80-90.
[22] Song Tengfei, Zhang Zhenyang, Liu Huijuan, et al.Multi-objective optimization design and performance comparison of permanent magnet synchronous motor for EVs based on FEA[J]. IET Electric Power Applications, 2019, 13(8): 1157-1166.
[23] 李祥林, 李金阳, 杨光勇, 等. 电励磁双定子场调制电机的多目标优化设计分析[J]. 电工技术学报,2020, 35(5): 972-982.Li Xianglin, Li Jinyang, Yang Guangyong, et al.Multi-objective optimization analysis of electricexcitation double-stator field-modulated machine[J].Transactions of China Electrotechnical Society, 2020,35(5): 972-982.
[24] Lee S, Kim Y, Lee K, et al. Multi-objective optimization design of small-scale wind power generator with outer rotor based on box-behnken design[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1-5.
[25] 李争, 张璐, 王群京, 等. 基于响应面法的永磁转子偏转式三自由度电动机结构参数的优化设计[J].电工技术学报, 2015, 30(13): 134-142.Li Zheng, Zhang Lu, Wang Qunjing, et al. Optimal design of structure parameters of three-dof deflection type PM motor based on response surface methodology[J]. Transactions of China Electrotechnical Society, 2015, 30(13): 134-142.
[26] Hasanien H M. Particle swarm design optimization of transverse flux linear motor for weight reduction and improvement of thrust force[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4048-4056.
[27] Lee J H, Song J Y, Kim D W, et al. Optimal design of permanent magnet linear synchronous motors at multispeed based on particle swarm optimization combined with SN ratio method[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1943-1954.