0 引言
锂离子电池一经问世便以其高能量密度、高输出电压、低自放电率、无记忆效应、工作范围广、零污染等显著优势被广泛应用于储能市场,如电动汽车、便携式电子设备、航空航天、潜海等领域[1-3]。然而,一方面随着循环充放电的进行,锂离子电池性能退化、寿命衰减;另一方面,由于其能量密度高、工作坏境复杂,在循环使用过程中容易发生自燃和爆炸事故。因此电池的健康管理与寿命预测(Prognostics and Health Management, PHM)研究势在必行[4]。PHM的目的在于通过对电池健康状态(State of Health, SOH)的预测来提升其安全性能、延长使用寿命。
锂离子电池的SOH反映了当前电池相对于新电池的存储和供应能量的能力。根据应用工况的不同,通常用容量和内阻来表征电池的SOH[5-7]。一般来讲,当电池的容量下降到额定值的80%~70%或内阻加倍时,电池达到寿命阈值。目前,国内外对电池SOH估计的研究方法主要分为三种[8-11]:①从定义出发,直接测量;②从电池电化学老化机理出发,建立电化学模型或基于外特性建立电路模型描述电池的SOH;③从电池的监测参数中提取能够表征电池容量退化的间接健康特征(Indirect Health Features, IHF),借助智能算法以估计电池的SOH。
K. S. Ng、C. S. Moo和ChenYiping等采用库仑计数法求得电池最大可释放容量来评估SOH[12],并引入表征放电的新指标放电深度(Depth of Discharge,DOD)联合估计SOC和SOH。Xing Yinjiao等建立OCV-SOC曲线,提供了一种考虑在温度影响下生成OCV-SOC曲线的方法[13]。这种直接测量法虽然具有较低的计算复杂度,并且结果较精确,易于在电池管理系统中实现,但是耗时长,鲁棒性较弱,估算精度很大程度上取决于测量技术,且易受噪声的影响。Zhiyong Xia通过研究交流复数阻抗与老化导致的容量衰减之间的关系来估计SOH,得出电池阻抗相位的过零频率可以反映电池的老化[14]。Wang Bojing等基于锂电池的特定物理现象开发了含16个参数的电化学模型[15],其中有10个模型参数是使用混合多粒子群优化方法从测量的电化学阻抗谱(Electrochemical Impedance Spectroscopy, EIS)数据中得到的。但是,该种方法电化学参数多且求解复杂,仅适合实验室研究。对此,许多学者建立Rint模型、Thevenin模型、PNGV模型,RC模型和复合模型等电气模型,并且结合参数辨识的方法对电池SOH进行求解[16-17],而该方法由于其参数缺乏实际的物理化学意义,难以在不同的环境和工况条件下保持较高精度。综上所述,现在更多的研究是关注与数据驱动的方法,如人工神经网络、相关向量机、模糊算法、粒子滤波、维纳过程和高斯过程回归等方法[18-22]。Duo Yang[18]将一阶等效电路模型(Equivalent Circuit Models, ECM)和荷电状态(State of Charge, SOC)参数作为反向传播神经网络的输入,SOH作为输出训练NN模型对SOH预测,但只能给出预测结果的点估计值,不能给出置信区间,而实际应用中由于噪声、测量误差和模型误差的存在,预测结果必然存在一定的不确定性。郭佩瑶等[20]提取了14个间接健康特征建立电池SOH预测的相关向量机(Relevance Vector Machine, RVM)模型,但是健康因子过多导致之间存在相互耦合的问题。此外,很多文献[24-26]直接给出间接健康特征,缺少清楚合理的提取方法,并且未考虑变温度下的健康特征提取问题。另外,在建立数据驱动的锂离子电池模型,求解SOH预测问题时,不少学者选择一些启发式算法对模型的超参数进行优化,如模拟退火[27]、粒子群滤波[28]、灰狼算法[29]、蝙蝠算法[30]等以提升模型回归预测效果。文献[28]用粒子群算法对模糊神经网络模型中的权重、偏值、隶属度函数进行优化。文献[20]提出一种改进粒子群优化(Particle Swarm Optimization, PSO)算法对RVM的核函数参数进行优化,提高算法的收敛速度和精度,但是均未避免过拟合的问题。
基于上述分析,综合考虑方法的适用性、模型的准确性及预测结果的概率性表达,本文提出了基于变温度下IHF-IGPR框架的锂离子电池SOH预测方法,从核函数及求解模型超参数两个维度进行GPR优化。首先,从电流、电压、时间曲线中构建不同温度下的IHF,以此作为输入,容量作为输出,建立电池老化的IGPR模型,并引入梯度下降法进行模型参数优化;最后在NASA提供的数据集上设计实验验证,以实现SOH的预测。
1 变温度下健康特征的构建
1.1 锂离子电池老化实验数据
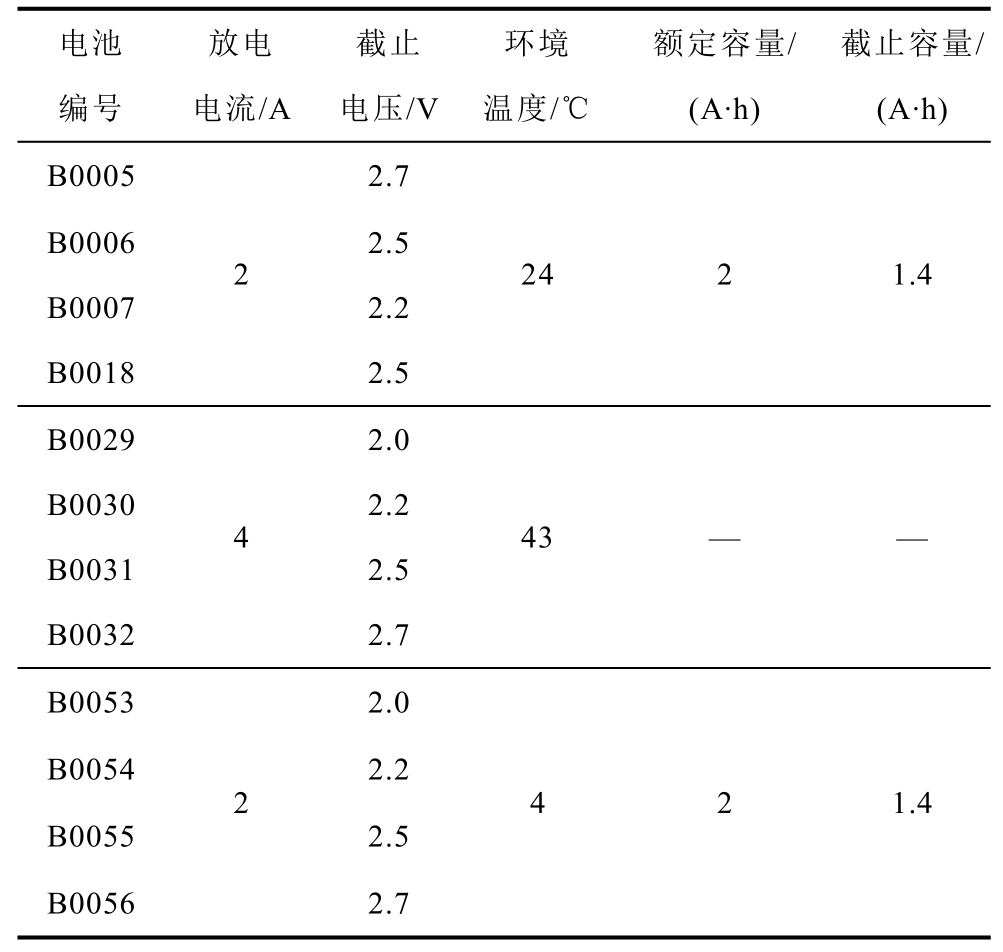
本文用于不同温度下间接健康特征构建和算法验证的锂离子电池数据来源于美国国家航空航天局(National Aeronautics and Space Administartion,NASA)艾姆斯卓越预测研究中心(Prognostics Center of Excellence, PCoE)[31]。NASA PCoE搭建锂离子电池测试平台,对额定容量为2A·h的18650型锂离子电池在不同温度、工况下进行充放电实验测试,直到电池容量下降到额定容量的30%时,认为电池失效,终止电池退化测试实验。具体循环充放电过程为:对锂离子电池进行1.5A恒流充电,当其电压达到4.2V后转为恒压充电直到充电电流下降至20mA,充电结束;在放电阶段,根据不同的负载,数据集中各电池的工况不相同,放电至截止电压,结束放电过程;实验通过EIS法对锂离子电池进行阻抗测量,扫描频率的范围为0.1Hz~5kHz。
最终,测试数据集以Matlab中标准数据文件格式保存,顶层数据结构表示充电、放电或阻抗测量等实验,下层数据保存了实验中采集的电池充放电参数,例如温度、电压、电流、时间等。本文选取了三组共12个电池的充放电循环数据,选用其中的5号、6号、7号和18号电池为室温下退化的电池;29号、30号、31号、32号电池为高温下退化的电池;53号、54号、55号、56号电池为低温下退化的电池。其电池编号及实验参数见表1。
表1 电池的实验参数
Tab.1 Experimental parameters for lithium-ion batteries
?
1.2 不同温度下间接健康特征的构建
目前,市场上大部分的锂离子电池都采用恒流-恒压充电模式[32]。由于锂电池的循环使用寿命受温度的影响很大。常温下,随着电池容量的退化,恒流充电时间会逐渐减小;高(低)温下,随着电池容量退化,恒流放电的时间出现逐渐减小的趋势,因此从恒流充放电过程的参数出发构建不同温度下锂离子电池的间接健康特征意义重大。
1.2.1 常温下间接健康特征的构建
锂离子电池在实际中通常成组使用,单体电池的不一致性使得恒压过程难以实现。本文研究了循环充放电过程中恒流充电电压随时间的变化,该现象和相关分析表明,恒流充电电压随电池容量的衰减出现下降趋势,因此构建等时间间隔的充电电压差(Charging Voltage Difference of Equal Time Span,CVD-ETS)作为常温下间接健康特征以表征循环充放电过程中容量的下降。图1所示为常温下间接健康特征提取过程。其中图1a为NASA PCoE 5、6、7、18号电池容量的退化曲线;图1b为恒流充电阶段电压的上升曲线,可以看出,随着充放电次数的增加,锂离子电池容量逐渐退化的同时,恒流充电时间呈现缩短的趋势;图1c为CVD-ETS作为间接健康特征表征常温下电池容量的衰减。

图1 常温下间接健康特征提取过程
Fig.1 The process of indirect health feature extraction at room temperature
室温下,第k个周期的等长恒流充电时间中的充电电压差 Vk _CVD_ETS 为
则k个周期的健康特征序列表示为
式中,Vk _CVD_ETS 为健康特征序列,即CVD-ETS;tmax与tmin为ETS的相应时刻; Utmax与 Utmin 分别为对应的电压值;k = 1,2,…,n。因此,常温下间接健康特征的构建步骤为:
(1)提取锂离子电池每个充放电循环的恒流充电电压、恒流充电时间等监控参数。
(2)确定恒流充电时间间隔,本文使用随机数法确定最佳的ETS。随后,使用式(1)计算ETS对应的CVD。
(3)计算与tm ax −tm in 对应的CVD,获得每个充放电循环的CVD-ETS序列,如式(2)所示。
1.2.2 高(低)温下间接健康特征的构建
NASA在43℃进行高温实验,在-4℃进行低温实验。由图2显示,高(低)温下的充电曲线中电压变化快,且变化区间狭窄,因此使用1.2.1节构建的间接健康因子难以捕获电池退化的信息,从而不能有效地表征电池容量的衰减过程。考虑到新的储能设备一开始充满电工作时间最长,但是随着充放电循环使用,工作时间越来越短。可见,放电时间与电池容量退化存在一定的关系。因此,构建等电压间隔的放电时间差(Discharging Time Difference of Equal Voltage Span, DTD-EVS)作为高(低)温下间接健康特征以表征循环充放电过程中的容量下降。图3所示为高(低)温下间接健康特征的提取过程。

图2 变温度下恒流充电电压曲线
Fig.2 Constant current charging voltage curves under variable temperature
图3 a为NASA PCoE 29、30、31、32号电池容量的退化曲线;图3b为NASA PCoE 53、54、55、56号电池容量的退化曲线;图3c和图3d分别为高(低)温下恒流放电阶段的电压下降曲线,可以看出,高(低)温下,该曲线的趋势是相同的:随着充放电次数的增加,锂离子电池容量逐渐退化的同时,恒流放电时间呈现缩短的趋势。因此,图3e构建了DTD-EVS作为间接健康特征表征高(低)温度下电池容量的衰减。


图3 高(低)温下间接健康特征的提取过程
Fig.3 Extraction process of indirect health characteristics at high (low) temperature
高(低)温下,第k个周期的DTD表示为
则k个周期的间接健康特征序列DTD-EVS表示为
式中, Tk _DTD_EVS 为高(低)温下的IHF,即DTDEVS;Umax与Umin分别为EVS的相应电压,TUmax与TUmin分别为对应的时刻。因此,高(低)温下间接健康特征的构建步骤为:
(1)在线采集锂离子电池每个充放电循环的恒流放电电压、恒流放电时间等监控参数。
(2)确定恒流放电电压压降,本文使用随机数法确定最佳的EVS。随后,使用式(3)计算EVS对应的DTD。
(3)计算与 U max −U min 对应的DTD,以获得每个充放电循环的DTD-EVS序列,如式(4)所示。
1.2.3 基于变温度下间接健康特征的分析验证
1.2.1 节及1.2.2节中虽然对间接健康特征与容量的相关程度进行了直观的表达,但是不足以对两者之间的关系进行数学的分析,因此本节采用灰色关联度分析(grey relational analysis)和皮尔逊相关系数(Pearson product-moment correlation coefficient)对构建的锂离子电池系统中的间接健康特征与容量之间的相关程度进行量化分析。
灰色关联度分析的基本思想是:通过研究不同因素的数据序列曲线的相似程度来判断因素间的关联程度[33]。即曲线的几何形状越相似,因素间的关联度越大,灰色关联度越接近1;反之,因素之间的关联度越小。首先对所提取的间接健康特征进行归一化处理,令处理后的容量序列为参考序列Y={y(k),k=1,2,…,n},令健康特征序列为比较序列Xi={xi(k),i=1,2,3; k=1,2,…,n}。第i个间接健康特征和容量之间的灰色关联系数可以表示为
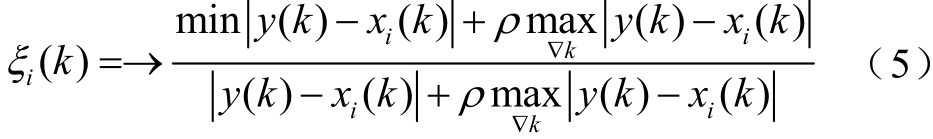
式中,ρ为分辨系数, ρ∈ [0,1],文中取值0.5;i= 1,2,3,…。关联度系数ξi为比较序列与参考序列在各个时刻的关联度,通过计算其平均值求得灰色关联度iγ。
皮尔逊相关系数用于度量两个变量X与Y之间的相关程度,其相关程度越高,绝对值越接近1。在锂离子电池系统中基本处理同上,计算公式为

采用以上两种不同的方法能够从不同的维度验证所构建的健康特征的准确性。为高斯过程回归建模提供保障。
2 基于改进高斯过程回归的锂离子电池SOH估计方法
2.1 高斯过程回归
高斯过程回归[34](Guassian Process Regression,GPR)是一种灵活的、非参数化模型,能同时给出预测值的点估计和不确定性表达,对小样本、非线性的预测问题具有很好的学习能力。
当给定训练样本集S, S = {( x i ,y)|i= 1,2,3}=(X,y),X为输入数据集![]() 输入矩阵为X∈Rn×d;对应的函数输出为
输入矩阵为X∈Rn×d;对应的函数输出为![]() 输出向量 Y ∈Rn×1。回归的目的就是根据训练样本集学习X与Y之间的映射关系( f (.):R d↦R),在新的测试点x*下,预测出最有可能的输出值f(x*)。
输出向量 Y ∈Rn×1。回归的目的就是根据训练样本集学习X与Y之间的映射关系( f (.):R d↦R),在新的测试点x*下,预测出最有可能的输出值f(x*)。
输入矩阵[x1 x2 … x n ]与对应的输出向量{f (x1 ) ,f (x2 ),…, f (xi )}构成一个随机变量的集合,f (X)中的任意有限维组合都服从联合高斯分布,它们所形成的随机过程即为高斯过程,可描述为
式中,m( x ) =E (f(x))为函数f(x)构成的均值函数;k (x i ,xj )为协方差函数,k (x i ,x j ) =E[ (f (xi)−m( xi ))(f (xi ) −m(x j))]。
在实际应用中,只能获取含有噪声的函数值,由此建立式(9)所示的高斯过程回归模型。
式中,y为输出向量, y =[y1 y2 y3 … y k]T;ε为噪声,服从0均值的高斯分布。
因此,如果f(x)为高斯过程,则y的有限观测值形成的集合为一个高斯过程,表示为可知,f(x*)与y将服从联合高斯分布,即
此时,对于一组新的样本(x*,f(x*)),由式(11)

由贝叶斯的回归方法可知,通过GPR预测的输出f(x*)服从均值![]() 和协方差cov f(x*)的高斯分布,分别用式(13)~式(15)表示。
和协方差cov f(x*)的高斯分布,分别用式(13)~式(15)表示。
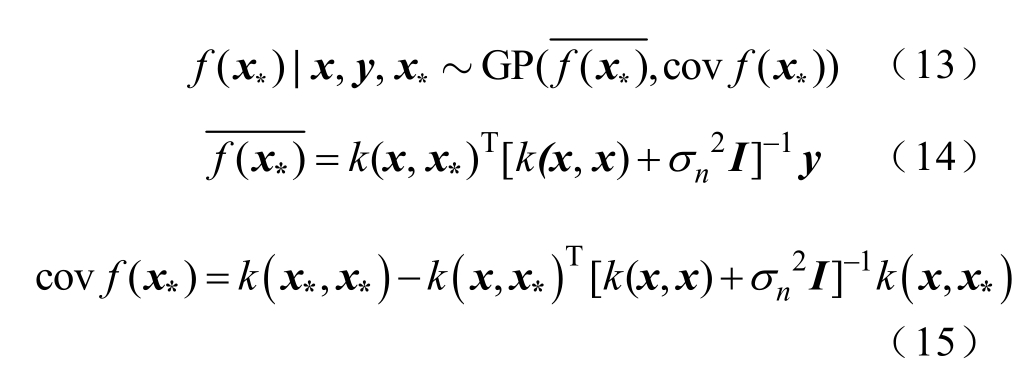
GPR模型不仅能够预测测试输出的均值,而且能够给出预测模型的置信水平或不确定性,给出更可靠的预测结果。预测输出值的置信水平由式(15)中的cov f(x*)确定,95%的置信区间为
2.2 核函数与共轭梯度算法优化GPR模型
从公式的推导过程来看,预测值可由协方差函数线性表示,因此对高斯过程回归建模的关键在于协方差函数的选择及模型中超参数的优化求解问题。锂电池系统具有复杂的非线性,且容量在退化过程中存在容量再生现象,因此文章选取以下两种常用的协方差函数进行对比对该问题进行求解。
(1)平方指数协方差
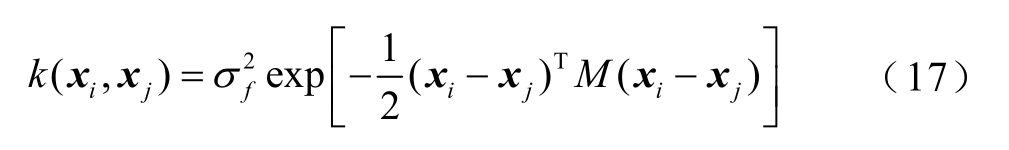
(2)有理二次协方差
式中, M =diag(λ−2);超参数 θ=(λ ,σ f,α)。可通过极大似然法获得最优解,首先,对超参数的边际似然函数取负对数,即
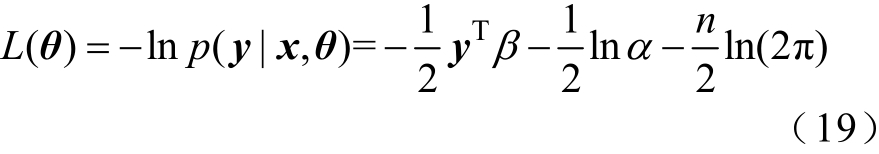
式中,![]() 再次,通过对式(19)求偏导得到超参数。
再次,通过对式(19)求偏导得到超参数。
本文提出利用共轭梯度算法优化求解GPR模型的超参数。共轭梯度法主要是在初始参数点的位置构造梯度方向,使得求解参数沿着梯度方向步步逼近,较快地收敛到目标函数的极小点[35]。
优化的目标满足式(20)时,则θ取得最优解*θ。

共轭搜索方向dk为![]()
式中,线搜索法确定搜索步长kα,其满足
搜索的新的超参数点为
使用共轭梯度法求解超参数最优值的流程如图4所示。

图4 求解超参数最优值的流程
Fig.4 Flow for solving the hyperparametric optimum
2.3 基于IGPR的锂离子电池SOH预测
本文对不同温度下锂离子动力电池SOH估计的基本思路如下:根据1.2节不同温度下间接健康特征的构建结果,分别以CVD-ETS及DTD-EVS作为输入,以容量的监测值作为输出,训练GPR预测模型,并利用共轭梯度法对模型的超参数进行优化,在新的健康因子 *x下给出预测值 *y的概率估计。最后设计单电池实验及多电池实验验证所提框架的准确性、适用性、小样本特性。
2.3.1 K折交叉检验法训练数据
本文利用K折检验法对改进GPR模型进行单电池训练及测试[36]。将锂离子电池间接健康特征集合S随机划分为k个互斥子集:S =S1 ∪S 2 ∪…∪Sk,Si ∩Sj =∅,依次选取S i,i = 1,2,…,k 为测试集,其余子集为训练集对模型进行训练。本文取k=4,经过K折交叉检验,选取k次中的最优结果作为模型的超参数解,建立GPR模型,用于新的数据点的预测,并给出置信区间。使用K折检验法,能够使模型的训练更加准确,又可避免参数过拟合的问题,鲁棒性更好。
2.3.2 基于IGPR预测锂离子电池SOH的流程
不同温度条件下基于锂离子电池间接健康特征和改进高斯过程回归模型的电池SOH预测的流程如图5所示。具体步骤如下:
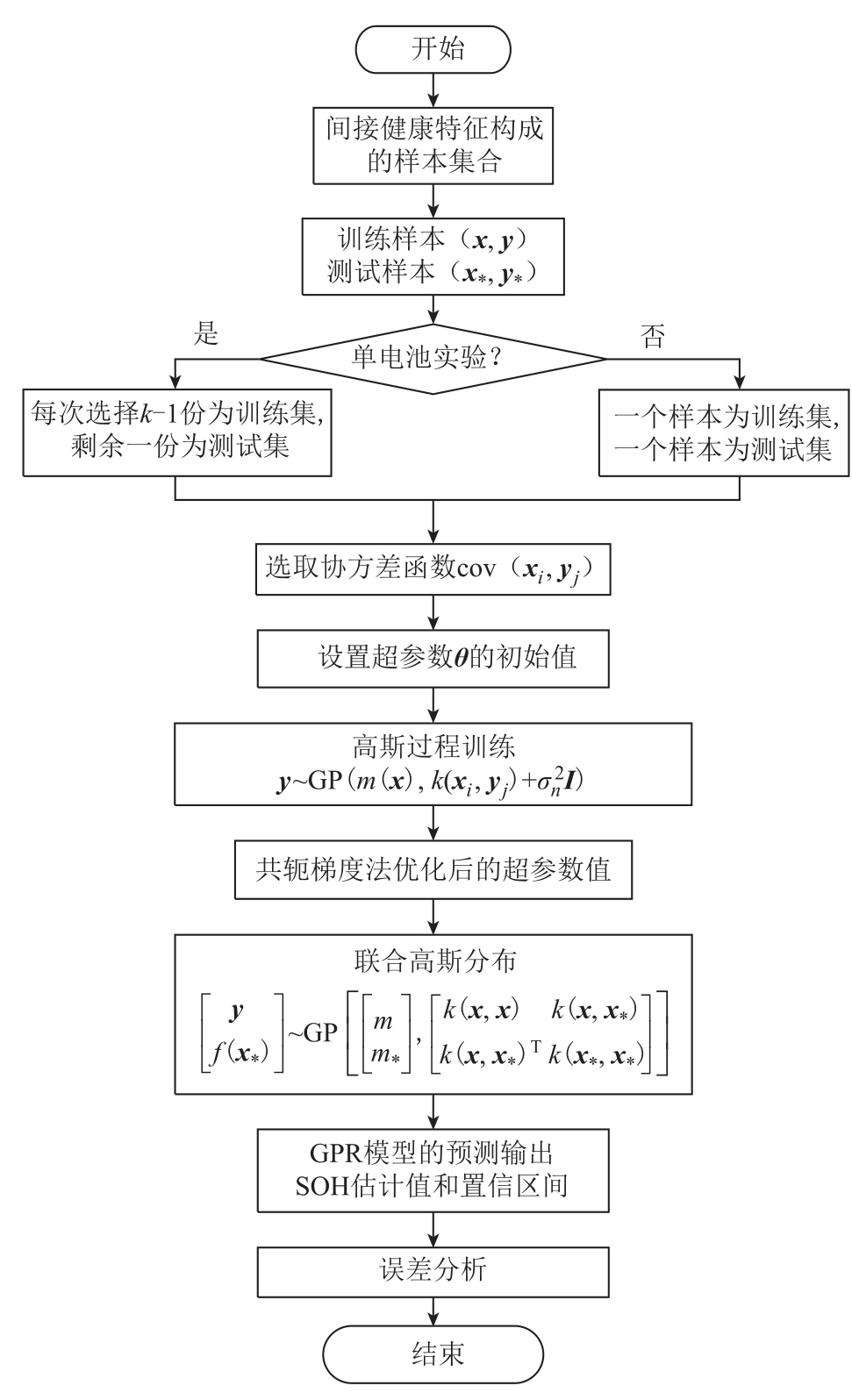
图5 不同温度下SOH的预测流程
Fig.5 Prediction flow chart for SOH at different temperatures
(1)数据集:从充放电曲线中提取锂离子电池的IHF序列:X i = {xi (k ), i = 1,2,3;k =1,2,…,n}、容量序列: Y = {y ( k ), k =1,2,…,n},二者构成样本总体(x,y)。其中,常温下的健康特征为CVD-ETS,高(低)温下的健康特征为DTD-EVS。
(2)单电池及多电池实验:根据不同的实验要求,筛选出训练样本与测试样本。单电池实验进行K折交叉验证,筛选出训练样本(x,y)和测试样本(x* ,y*);多电池实验,以前一个电池的样本数据为训练样本,后一个电池的样本数据为测试样本。
(3)模型训练:训练样本(x,y)在高斯过程的假设条件下,以x作为输入y作为输出进行模型训练,满足![]()
(4)参数优化:设置均值为0,协方差函数分别为二次方指数与有理二次协方差函数;随机初始化核函数的参数θ0=(λ ,σ f ,α);通过共轭梯度法求出初始值下L(θ)的最小值对应的θ*。此时确定的模型为最优的预测模型。
(5)预测与模型分析:预测未来时刻的容量估计值y*。以x*为输入数据,输入到优化的GPR模型中进行预测,得到具有均值和不确定性表达的输出y*并分析误差。y*与y满足联合高斯分布![]()
3 实验验证与分析
本节主要用于验证所提出的基于IHF-IGPR的锂离子电池SOH预测框架的合理性及准确性,可分为以下几部分:
(1)定性及定量分析不同温度下所构建的IHF与锂离子电池容量的相关性。以散点图直观地表示其相关程度,同时,以灰色关联度及皮尔逊系数的大小精确描述二者之间的相关性。
(2)验证不同协方差函数对模型的影响及超参数优化的必要性。
(3)设计单电池实验及多电池实验验证所提框架的合理性及准确性;单电池实验下验证改进GPR算法适应小样本训练集的回归建模。
3.1 IHF与容量退化相关性的验证分析
3.1.1 常温下相关性的验证分析
本文通过随机数法,以式(7)近似于1为目标,得到在最佳恒流充电时间间隔从1 150~3 600s时充电电压的变化作为CVD-ETS,B0006锂离子电池容量与CVD-ETS随充电周期的变化曲线如图6所示。图6a为所构建的IHF随充放电周期的变化,图6b为二者的相关程度曲线。可见,随着电池充放电的不断进行,CVD-ETS与容量呈现相同的趋势,并且所构建的IHF与容量呈现强线性关系,与预期一致。

图6 常温下电池容量与CVD-ETS随充电周期的变化
Fig.6 Variation of battery capacity and CVD-ETS with charging cycle at room temperature
用灰色关联度式(6)与皮尔逊相关系数式(7)定量描述所构建的IHF与容量的相关程度,所选常温下四个电池的容量与CVD-ETS的相关程度见表2。依据该结果,所构建各电池IHF与容量的相关程度均大于0.9。
表2 常温下电池容量与构建的IHF的相关度
Tab.2 Correlation between battery capacity and constructed indirect health characteristics at room temperature

?
3.1.2 高(低)温下相关性的验证分析
与3.1.1节同理,通过随机数法,以式(7)近似于1为目标,得到在最佳恒流放电电压间隔从4.0~3.6V时放电时间的变化作为DTD-EVS,高温43℃下B0030锂离子电池容量与DTD-EVS随充放电周期的变化曲线如图7所示。图7a为所提取的IHF随充放电周期的变化,图7b为二者的相关程度曲线。低温4℃下,B0056号电池容量与DTD-EVS随充放电周期的变化曲线如图8所示。图8a为所提取的IHF随充放电周期的变化,图8b为二者的相关程度曲线。可以直观地看到,高(低)温下所构建的IHF皆能准确地表征电池容量的退化。

图7 高温下电池容量与DTD-EVS随充电周期的变化
Fig.7 Variation of battery capacity and DTD-EVS with charging cycle at high temperature
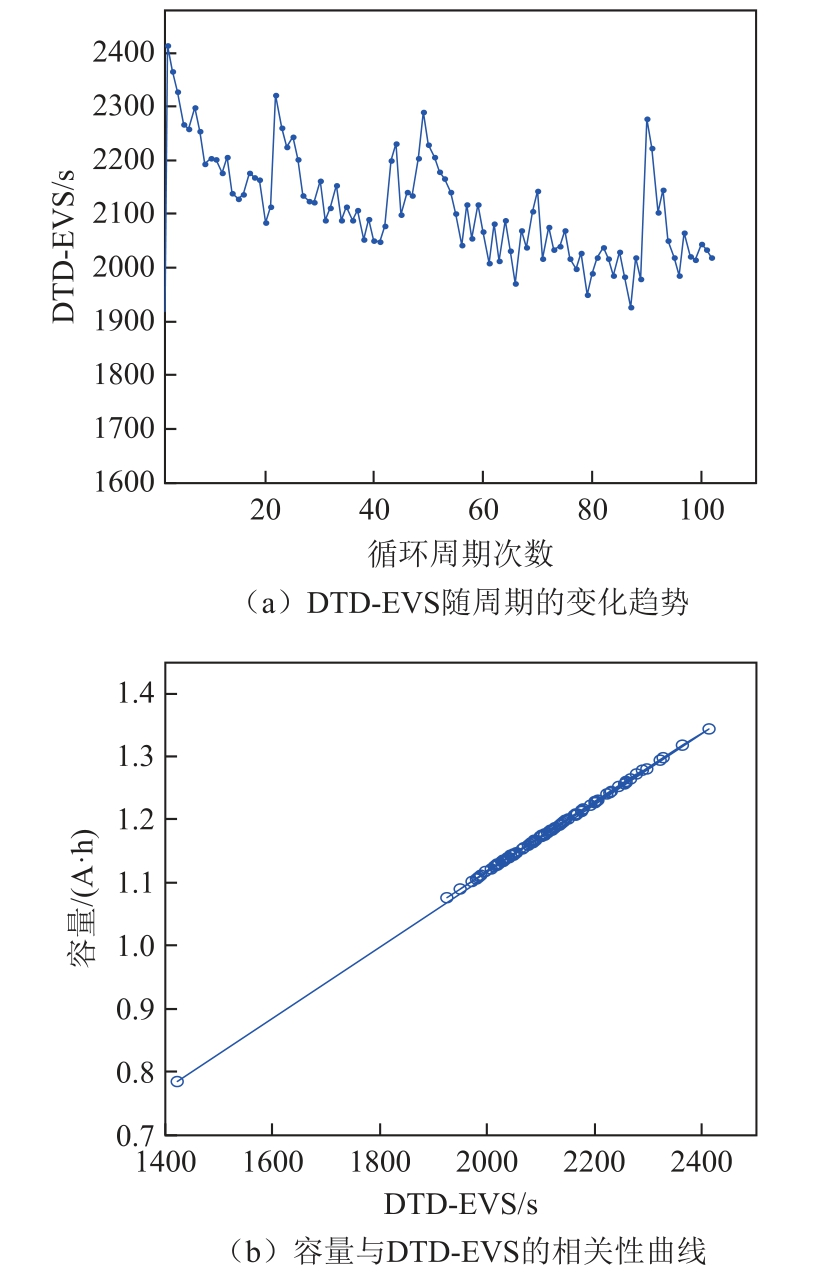
图8 低温下电池容量与DTD-EVS随充电周期的变化
Fig.8 Variation of battery capacity and DTD-EVS with charging cycle at low temperature
用灰色关联度式(6)与皮尔逊相关系数式(7)定量描述所构建的间接健康特征与容量的相关程度,所选的高(低)温下4个电池的容量与DTDEVS的相关程度见表3。与常温下的验证结果类似,除个例,构建的间接健康特征与容量之间均取得了很高的相关度。
表3 高(低)温下电池容量与构建的IHF的相关度Tab.3 Correlation between cell capacity and constructed indirect health characteristics at high (low) temperature

?
(续)

?
3.2 不同核函数及优化对比
在不同温度下选取锂离子电池分别验证二次方指数协方差及有理二次协方差对模型训练和预测效果的影响,结果如图9所示。结果显示,在不同温度下,基于有理二次协方差的GPR模型预测更为准确,能够准确刻画锂离子电池的容量再生及局部波动变化,该变化规律与电池容量真实退化曲线更相近,预测效果更好。

图9 两种协方差函数的预测结果
Fig.9 Prediction of two covariance functions
根据以上验证,以有理二次协方差函数作为GPR模型的核函数。为验证共轭梯度算法对超参数的优化效果,用常规的GPR求解问题式(19),并与共轭梯度优化下的预测曲线作对比,得到图10。

图10 是否优化核函数的预测结果对比
Fig.10 Comparison of predicted results with or without optimization of the kernel function
由图10可知,将共轭梯度法优化求解加入GPR算法中,增大了超参数寻优的速度,从而更快地求得更小的拟合误差和更高质量的超参数值,提高了GPR模型的回归性能。
3.3 单电池实验及多电池实验
为验证本文所研究的基于变温度下IHF和IGPR框架的锂离子电池SOH预测方法,选取NASA PCoE所提供的表1所示的锂离子电池的监测数据,对每组数据分别进行单电池及多电池实验。室温下的单电池实验采用4折交叉验证的方法,每次选择总样本数据的3/4作训练集,1/4为测试集,分别进行四次,以最优值作为最终结果,高(低)温下的循环周期较少,同时为验证所提方法适应于小样本回归建模,因此采用不同训练集-测试集进行单电池实验;多电池实验采用同一组电池的一对样本数据分别作为训练集与测试集进行验证。
本节以平均绝对百分比误差(MAPE)和方均根误差(RMSE)作为锂离子电池SOH的预测评价标准,计算公式如式(24)、式(25)所示。评价指标MAPE与PMSE越小,则模型的精确度越高。

3.3.1 单电池实验
根据以上验证,IGPR模型选取协方差函数为有理二次协方差,使用共轭梯度算法对其参数进行优化,各采用不同温度下一个电池(B0005,B0030, B0055)的循环充放电容量与IHF数据进行单电池实验。需要说明的是,为验证所用算法适用于小样本回归建模,分别采用30%、60%的训练集进行实验。
在室温下的4折交叉验证实验结果、高(低)温下60%训练集-40%测试集的实验结果和相对误差如下所示。图11为24℃下B0005交叉验证的过程及最优预测结果。图12为43℃下B0030健康状态的预测结果及相对误差。图13为4℃下B0055健康状态的预测结果及相对误差。表4列出了3组单电池验证实验的MAPE与RMSE。

图11 B0005 4折交叉验证结果及误差
Fig.11 4-fold cross validation results and errors for B0005
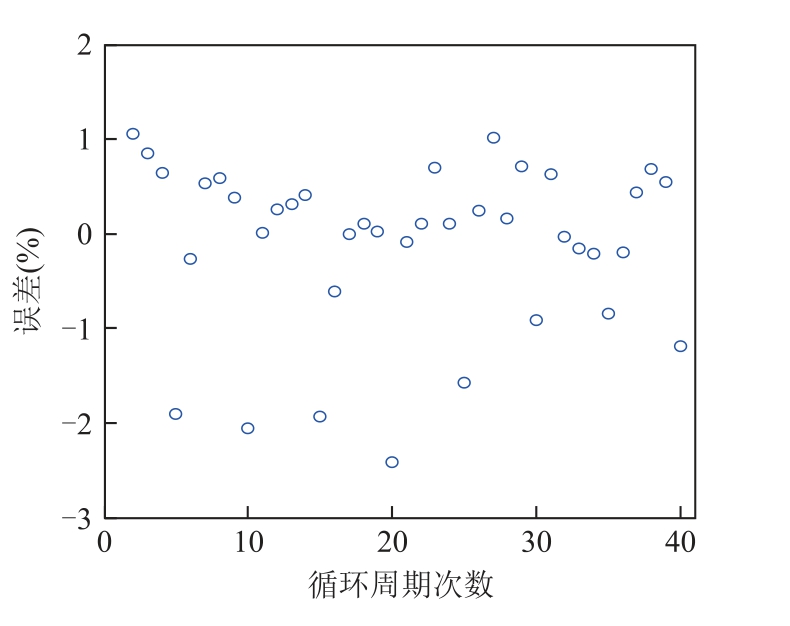
图12 B0030 SOH预测结果及误差
Fig.12 SOH prediction results and errors for B0030

图13 B0055 SOH预测结果及误差
Fig.13 SOH prediction results and errors for B0055
表4 单电池验证实验的估计误差
Tab.4 Estimated errors for single-cell verification experiments

?
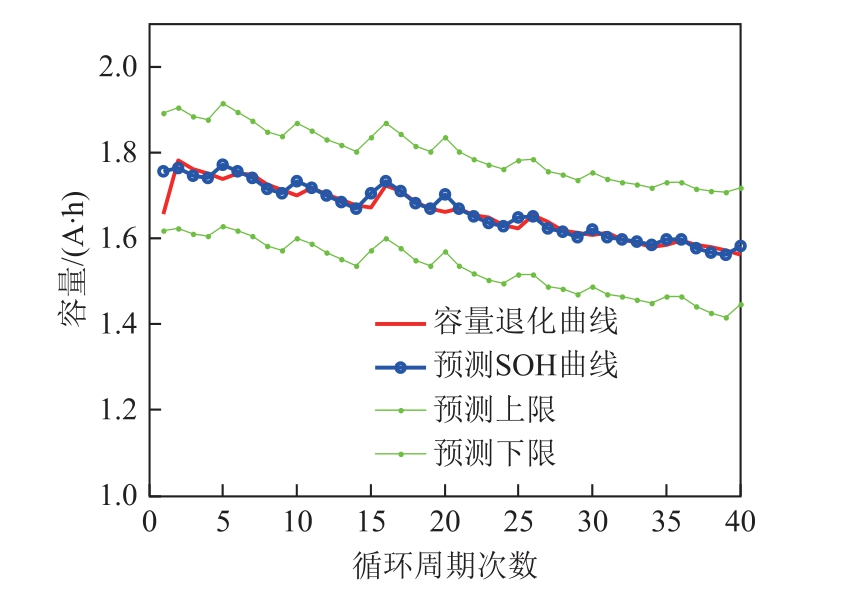
分析图11~图13可知,不同电池组中单电池实验的SOH估计误差除了个别点在3%,大部分在1.5%以内,在变温度下表现出了较高的估计精度,反映了构建的IHF的有效性和IGPR模型在锂离子电池SOH预测中良好的回归性能。对常温下循环周期较长的锂电池采用交叉验证的方法,与60%训练集-40%测试集下的实验验证取得了类似的结果,更加说明了此框架的有效性。
表4 对预测误差进行定量表示,变温度下的MAPE与RMSE均在0.1之内,表明本文所提框架具有较高的预测精度。
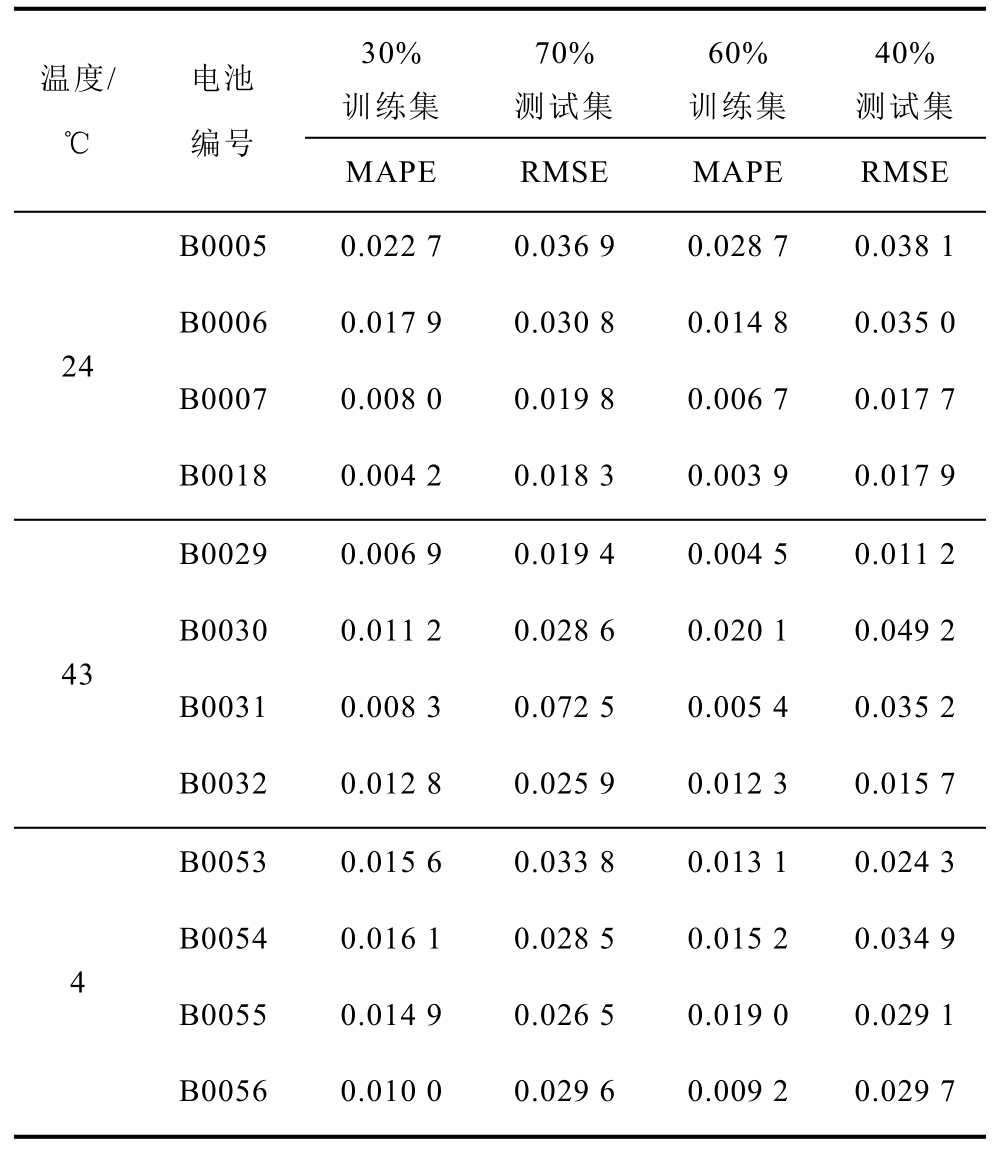
所提出的改进的GPR算法可以适应小样本训练集的回归建模,为验证本节中单电池实验的训练集的大小对所提预测框架的精度是否会产生影响,将三组中12个电池的训练集测试集分别设为30%~70%与60%~40%进行训练并且分别进行容量估计,比较它们的误差。误差的对比结果见表5,可以看出,在不同训练集的比例划分下,所有电池的误差都在同一水平,验证了所提框架适合小样本训练集。
表5 不同训练集-测试集验证实验的估计误差
Tab.5 Estimation errors for different training set-test set validation experiments
?
3.3.2 多电池实验
本节设计多电池实验以验证所提出预测方法的合理性及准确性。多电池实验采用放电工况相同的电池组的前一个样本数据进行训练模型,对后一个样本进行预测。图14~图16为在不同温度下的六组多电池实验的结果和相对误差。表6列出了六组多电池验证实验的MAPE与RMSE。

图14 常温下多电池实验预测结果
Fig.14 Predicted results of multi-cell experiments at room temperature


图16 低温下多电池实验预测结果
Fig.16 Prediction results Multi-cell experiments at low temperature
表6 多电池验证实验的估计误差
Tab.6 Estimation errors for multi-cell verification experiments

?

图15 高温下多电池实验预测结果
Fig.15 Predicted results of multi-cell experiments at high temperatures
由图14~图16可知,采用IHF-IGPR框架预测SOH的多电池实验相对误差大部分在3%以内,由于电池单体参数的差异性造成个别组数据误差较大,但是相对误差在8%以内,仍然具有较高的精度。表6对多电池实验的预测误差进行定量表示,可看出变温度下的MAPE与RMSE值均在0.1之内,表明本文所提框架具有较高的预测精度。
且多电池实验中的训练集和测试集为不同电池的数据,较为接近实际应用情况,实验在不同温度下取得的良好的估计精度,能够反映出电池的SOH参数,验证了基于改进GPR的估计方法能够适应不同的训练集,有较强的实用性和鲁棒性。需要说明的是,本文的单电池与多电池实验是基于NASA数据集而展开的;同时,也利用牛津数据集和马里兰大学的数据进行了验证。所提的SOH估算方法适用于多种阴极材料的锂离子电池,如18650 NCA三元锂离子电池、LiCoO2锂离子电池等。实验验证的基于IHF-IGPR的锂电池SOH预测方法适用于恒流或脉冲放电的工况。
4 结论
本文针对锂离子电池健康状态预测过程中样本少、预测精度低、适用性有限等问题,提出了不同温度条件下基于IHF和IGPR框架的锂离子电池SOH的预测方法。在此基础上,利用锂离子电池公开数据集进行了一系列不同温度下的单电池及多电池实验进行验证。结果表明:在训练模型阶段,不同温度下所构建的间接健康特征与容量退化有较高的相关度,所使用的随机数法对求解最优的区间提供了理论支持;在预测阶段,本文所提出的IGPR预测模型能够较准确地给出变温度下锂离子电池的SOH预测的点估计及95%的概率估计,共轭梯度优化算法的引入进一步提升了GPR的预测性能。值得一提的是,单电池及多电池实验验证了其在不同工况下的实用性及IGPR可以适用小样本训练集的回归建模,显示出本文所提的方法具有较强的鲁棒性和泛化能力。
但是,本文的研究仍然存在很多不足,未来的研究工作将从以下方面开展:①电池组中电池的状态估计及预测问题;②方法的适应性需要在更复杂多变的工况下进行验证。
[1] 闫金定. 锂离子电池发展现状及其前景分析[J]. 航空学报, 2014, 35(10): 2767-2775.Yan Jinding. Current status and development analysis of lithium-ion batteries[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(10): 2767-2775.
[2] 王鹏博, 郑俊超. 锂离子电池的发展现状及展望[J].自然杂志, 2017, 39(4): 283-289.Wang Pengbo, Zheng Junchao. The present situation and expectation of lithium-ion battery[J]. Chinese Journal of Nature, 2017, 39(4): 283-289.
[3] 刘艳莉, 戴胜, 程泽, 等. 基于有限差分扩展卡尔曼滤波的锂离子电池SOC估计[J]. 电工技术学报,2014, 29(1): 221-228.Liu Yanli, Dai Sheng, Cheng Ze, et al. Estimation of state of charge of lithium-ion battery based on finite difference extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 221-228.
[4] 刘大同, 周建宝, 郭力萌, 等. 锂离子电池健康评估和寿命预测综述[J]. 仪器仪表学报, 2015, 36(1):1-16.Liu Datong, Zhou Jianbao, Guo Limeng, et al. Survey on lithium-ion battery health assessment and cycle life estimation[J]. Chinese Journal of Scientific Instrument, 2015, 36(1): 1-16.
[5] Li Li, Liu Kailong. Data-driven health estimation and lifetime prediction of lithium-ion batteries: a review[J]. Renewable and Sustainable Energy Reviews, 2019, 113: 109254.
[6] Farmann A, Waag W, Marongiu A, et al. Critical review of on-board capacity estimation techniques for lithium-ion batteries in electric and hybrid electric vehicles[J]. Journal of Power Sources, 2015, 281: 114-130.
[7] Lu Languang, Han Xuebing, Li Jianqiu, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J]. Journal of Power Sources, 2013,226: 272-288.
[8] Hossain L M S, Hannan M A, Aini H, et al. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles:challenges and recommendations[J]. Journal of Cleaner Production, 2018, 205: 115-133.
[9] Ungurean L, Cârstoiu G, Micea M V, et al. Battery state of health estimation: a structured review of models, methods and commercial devices[J].International Journal of Energy Research, 2017, 41(2):151-181.
[10] Tian Huixin, Qin Pengliang, Li Kun, et al. A review of the state of health for lithium-ion batteries:Research status and suggestions[J]. Journal of Cleaner Production, 2020, 261: 120813.
[11] 孙丙香, 刘佳, 韩智强, 等. 不同区间衰退路径下锂离子电池的性能相关性及温度适用性分析[J].电工技术学报, 2020, 35(9): 2063-2073.Sun Bingxiang, Liu Jia, Han Zhiqiang, et al.Performance correlation and temperature applicability of lithium-ion batteries under different range degradation paths[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2063-2073.
[12] Ng K S, Moo C S, Chen Yiping, et al. Enhanced coulomb counting method for estimating state-ofcharge and state-of-health of lithium-ion batteries[J].Applied Energy, 2009, 86(9): 1506-1511.
[13] Xing Yinjiao, He Wei, Michael P, et al. State of charge estimation of lithium-ion batteries using the opencircuit voltage at various ambient temperatures[J].Applied Energy, 2014, 113(1): 106-115.
[14] Xia Zhiyong, Abu-Qahouq J A. Adaptive and fast state of health estimation method for lithium-ion batteries using online complex impedance and artificial neural network[C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA,USA, 2019: 3361-3365.
[15] Li S E, Wang Baojing, Peng Hui, et al. An electrochemistry-based impedance model for lithiumion batteries[J]. Journal of Power Sources, 2014, 258:9-18.
[16] 蒋璐, 李奇, 陈维荣, 等. 基于Nelder-Mead优化的PEMFC三阶RQ等效电路参数辨识研究[J]. 电源学报, 2019, 17(2): 12-18.Jiang Lu, Li Qi, Chen Weirong, et al. Research on parameter identification of third-order RQ equivalent circuit of PEMFC based on Nelder-Mead optimization[J]. Journal of Power Supply, 2019, 17(2):12-18.
[17] 傅祎飏, 李锐华, 胡波, 等. 一种参数化电池模拟器模型及参数辨识方法[J]. 电气技术, 2020, 21(11):7-12.Fu Yiyang, Li Ruihua, Hu Bo, et al. A parameterized battery model for battery emulator and parameter identification method[J]. Electrical Engineering, 2020,21(11): 7-12.
[18] Yang Duo, Wang Yujie, Pan Rui, et al. A neural network based on state-of-health estimation of lithium-ion battery in electric vehicles[J]. Energy Procedia, 2017, 105: 2059-2064.
[19] Xu Xiaodong, Yu Chuanqiang, Tang Shengjin, et al.State-of-health estimation for lithium-ion batteries based on wiener process with modeling the relaxation effect[J]. IEEE Access, 2019, 7: 105186-105201.
[20] Guo Peiyao, Cheng Ze, Yang Lei. A data-driven remaining capacity estimation approach for lithiumion batteries based on charging health feature extraction[J]. Journal of Power Sources, 2019, 412:442-450.
[21] 焦自权, 范兴明, 张鑫, 等. 基于改进粒子滤波算法的锂离子电池状态跟踪与剩余使用寿命预测方法[J]. 电工技术学报, 2020, 35(18): 3979-3993.Jiao Ziquan, Fan Xingming, Zhang Xin, et al. State tracking and remaining useful life predictive method of lithium-ion battery based on improved particle filter algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3979-3993.
[22] 陈琳, 陈静, 王惠民, 等. 基于小波包能量熵的电池剩余寿命预[J]. 电工技术学报, 2020, 35(8): 1827-1835.Chen Lin, Chen Jing, Wang Huiming, et al. Prediction of battery remaining useful life based on wavelet packet energy entropy[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1827-1835.
[23] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020,35(19): 4106-4119.Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106-4119.
[24] Widodo A, Shim M C, Caesarendra W, et al.Intelligent prognostics for battery health monitoring based on sample entropy[J]. Expert Systems with Applications an International Journal, 2011, 38(9):11763-11769.
[25] Li Junfu, Liu Chao, Wang Lixin, et al. Remaining capacity estimation of Li-ion batteries based on temperature sample entropy and particle filter[J].Journal of Power Sources, 2014, 268: 895-903.
[26] Liu Datong, Zhou Jianbao, Liao Haitao, et al. A health indicator extraction and optimization framework for lithium-ion battery degradation modeling and prognostics[J]. IEEE Transactions on Systems Man &Cybernetics Systems, 2015, 45(6): 915-928.
[27] 刘燕, 任航永, 张健. 模拟退化算法在飞机巡航路径问题中的应用[J]. 光电技术应用, 2019, 34(4): 39-42.Liu Yan, Ren Hangyong, Zhang Jian. Application of simulated annealing algorithm in aircraft cruise traveler problem[J]. Electro-Optic Technology Application, 2019, 34(4): 39-42.
[28] 王震, 陆金桂. 改进的 ACO-BP 神经网络在锂离子电池 SOC 估算中的应用[J]. 轻工学报, 2019,34(4): 81-86.Wang Zhen, Liu Jingui. Application of improved ACO-BP neural network in estimation of SOC of lithium ion battery[J]. Journal of Light Industry, 2019,34(4): 81-86.
[29] 王桥, 魏孟, 叶敏, 等. 基于灰狼算法优化极限学习机的锂离子电池 SOC 估计[J]. 储能科学与技术, 2021, 10(2): 744-751.Wang Qiao, Wei Meng, Ye Min, et al. SOC estimation of lithium-ion battery based on gray wolf optimizer optimized extreme learning machine[J]. Energy Storage Science and Technology, 2021, 10(2): 744-751.
[30] Tian Dongdong, Li Liwei, Yang Yuxin, et al. SOC of estimation of lithium battery based on IBA-PF[J].Energy Storage Science and Technology, 2020, 9(5):1585-1592.
[31] Saha B, Goebel K. Battery data set[Z]. NASA Ames Prognostics Data Repository, (http://ti.arc.nasa.gov/project/prognostic-data repository), NASA Ames Research Center, Moffett Field, CA. 2007.
[32] Edd.ahech A, Briat O, Vinassa J M. Determination of lithium-ion battery state-of-health based on constant-voltage charge phase[J]. Journal of Power Sources, 2014, 258: 218-227.
[33] 田民, 刘思峰, 卜志坤. 灰色关联度算法模型的研究综述[J]. 统计与决策, 2008(1): 24-27.Tian Min, Liu Sifeng, Bu Zhikun. Research review of grey relational degree algorithm model[J]. Statistics and Decision, 2008(1): 24-27.
[34] 阎述学, 李一平, 封锡盛. 一种基于高斯过程回归的AUV自适应采样方法[J]. 机器人, 2019, 41(2):232-241.Yan Shuxue, Li Yiping, Feng Xisheng. An AUV adaptive sampling method based on gaussian process regression[J]. Robot, 2019, 41(2): 232-241.
[35] 戴彧虹, 袁亚湘. 非线性共轭梯度法[M]. 上海: 上海科技出版社, 1999.
[36] 胡局新, 张功杰. 基于K折交叉验证的选择性集成分类算法[J]. 科技通报, 2013, 29(12): 115-117.Hu Juxin, Zhang Gongjie. K-fold cross-validation based selected ensemble classification algorithm[J].Bulletin of Science and Technology, 2013, 29(12):115-117.