0 引言
锂离子电池凭借高能量密度、低自放电、无污染和长寿命等优点,被广泛应用到储能、电动汽车及小型电子设备等领域[1-3]。然而,随着锂离子电池不断地循环使用,电池内部结构会发生重大改变,导致电池的性能不断退化,比如电池的可循环锂损失,SEI膜增厚或分解,电解液分解和集电极腐蚀等,进而导致电池剩余使用寿命(Remaining Useful Life, RUL)的衰减[4-5]。不同应用领域对电池性能等级要求不同,准确预测锂离子电池RUL,能够提前获知电池的剩余寿命信息,可及时对到达失效阈值的电池进行更换,保障电池安全可靠运行,避免因电池失效导致设备性能下降或者停机,甚至发生危险的事故。
目前,国内外学者广泛采用的锂离子电池RUL预测方法主要分为两类:基于模型的方法和基于数据驱动的方法。
基于模型的方法,是综合考虑电池材料属性、负载条件及失效机理等因素,构建电池性能退化模型来完成电池RUL的预测。S. N. Kong等[6]考虑了环境温度的影响,提出一种基于充放电效率的容量退化模型;G. K. Prasad等[7]考虑了电池内阻和电池正极中Li+扩散的时间,利用线性最小二乘法和自适应梯度法不断更新这两个老化参数,在一定程度上简化了电化学模型;Fan Guodong等[8]利用Galerkin投影法对模型降阶,可以有效减少粒子扩散状态的数量,简化了电化学模型。上述方法在一定程度上简化了模型的复杂性,但同时降低了模型预测的精度。He Wei等[9]采用了Dempster-Shafer 证据(D-S证据)理论和粒子滤波算法(Particle Filter, PF)方法来预测锂离子电池RUL,其中DS理论用于初始化模型参数,PF用于更新模型参数,利用电池容量值实现RUL预测;然而PF算法在迭代过程中存在粒子贫化问题,为解决此问题,Zhang Xin等[10]构建了一种在无迹粒子滤波(Unscented Particle Filter,UPF)方法中引入马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)的预测方法,利用MCMC方法解决了UPF算法中的粒子退化和贫化问题,从而准确预测电池的RUL;此外,为减少模型计算的复杂度,Ma Yan等[11]提出一种多尺度卡尔曼滤波(Multiscale Extended Kalman Filter, MEKF)方法,并利用高斯赫米特与粒子滤波(Gauss Hermite Particle Filter, GHPF)方法更新模型的参数,降低了模型的复杂度,提高了运算速度,但此类方法易受外界动态因素的影响。
基于数据驱动方法无需考虑电池内部物理化学反应过程,直接从电池历史数据中挖掘电池性能变化的隐含信息及演变规律,实现电池RUL预测。随着人工智能技术和机器学习算法的飞速发展,越来越多的研究学者将这类算法应用到锂离子电池RUL预测中,例如人工神经网络(Artificial Neural Network, ANN)[12]、高斯过程回归(Gaussian Process Regression, GPR)[13]、相关向量机(Relevance Vector Machine, RVM)[14]和支持向量机(Support Vector Machine, SVM)[15-16]等。Zhang Shuzhi等[17]利用滤波方法来平滑增量容量曲线,并利用相关分析法在增量容量曲线中提取特征值,之后利用ANN方法实现基于这些特征值的RUL预测;刘健等[18]构建了多核核函数的GPR模型,并利用粒子群优化(Particle Swarm Optimization, PSO)算法对改进的GPR模型参数进行优化,从恒流充电阶段中提取等压差充电时间特征参数,并基于此特征参数实现容量退化轨迹的预测;L. L. Li等[19]利用改进鸟群算法优化最小二乘支持向量机,从而提高锂离子电池RUL预测的准确性;Gao Dong等[20]将多项式核函数和径向基核函数进行结合,构建多核核函数的SVM模型,并利用PSO算法对多核SVM模型参数寻优,提高了锂离子电池RUL的预测精度;Liu Datong等[21]提出一种无需满足Mercer条件且具备稀疏表达能力的RVM方法,并利用增量学习动态更新算法模型,实现了RUL的在线预测,考虑到RVM方法的稀疏性,可能会造成预测结果的不稳定性。
RUL预测的核心技术是预测电池容量损失量。实际应用中电池容量损失量难以直接获取,需要利用电池在使用过程中的监测数据寻找其表征量,进而实现对电池RUL的准确预测。因此,本文从可监测的外特性参数(如电压、电流等)中提取能够表征电池性能退化的间接健康因子。此外,提出一种改进蚁狮优化算法(Improved Ant Lion Optimization,IALO)来优化支持向量回归(Support Vector Regression, SVR)模型参数,构建基于健康因子的IALO-SVR预测方法,并利用NASA提供的电池数据集对IALO-SVR方法进行验证。通过对比分析反向传播(Back Propagation, BP)神经网络法、SVR方法和ALO-SVR方法,实验结果表明,本文所提出的方法能够更加准确地预测锂离子电池RUL。
本文主要介绍IALO算法和SVR算法,并构建IALO优化SVR模型参数的预测方法;阐述了锂离子电池数据集,分析并提取间接健康因子;对所构建的方法进行实验验证。
1 IALO-SVR模型的建立
1.1 支持向量回归方法
机器学习算法中SVR方法被广泛应用于时间序列预测领域,其能够很好地处理小样本数据、非线性及时间序列等问题,且具有较强的泛化能力[22]。假设给定样本集![]() 为输入向量,xi∈Rn,y为相应的输出向量,yi∈R。SVR方法主要思想:利用非线性映射将样本集从低维空间映射到高维空间,此非线性映射可定义为
为输入向量,xi∈Rn,y为相应的输出向量,yi∈R。SVR方法主要思想:利用非线性映射将样本集从低维空间映射到高维空间,此非线性映射可定义为
式中,x为输入数据;φ(x)为非线性映射函数;ω为权重;b为截距。根据结构风险最小化原则,f(x)可等效于求解优化问题,即
式中,L为损失函数;C为惩罚因子,是调节样本回归模型的复杂性与样本拟合精度的因子,若C越大,则越重视离群点。通过引入松弛变量![]() 来纠正不规则的因子,此时可得
来纠正不规则的因子,此时可得

式中,ε为不敏感损失因子(允许的最大误差),ε>0。将回归问题转换为求取目标函数的最小化问题,利用对偶原理,同时引入拉格朗日乘法算子,可转换为
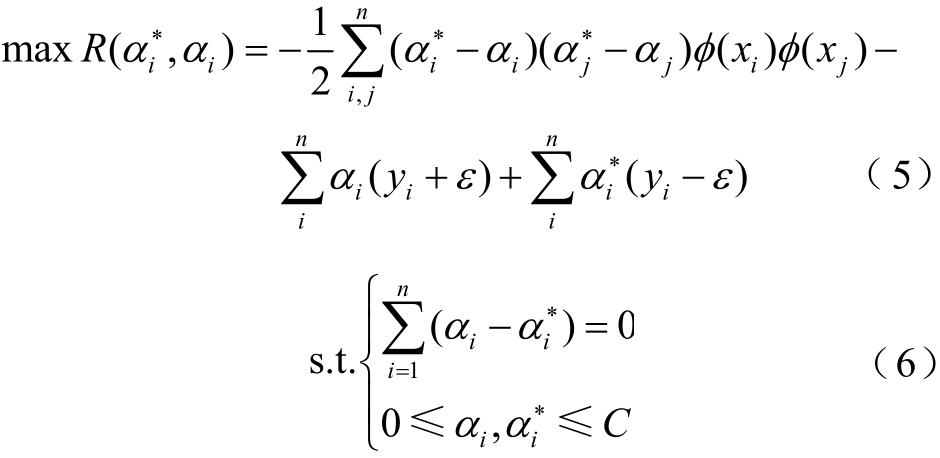
式中,iα和![]() 为拉格朗日乘数。根据Mercer定理法则,求解上述凸二次规划问题并获得非线性映射SVR表达式为
为拉格朗日乘数。根据Mercer定理法则,求解上述凸二次规划问题并获得非线性映射SVR表达式为
式中,K (xi ,x) =φ (xi )φ(xj)为核函数。径向基核函数(Radial Basis Function, RBF)用途广泛,也是被广大学者所采用的核函数,因此本文选取RBF核函数,其可定义为
式中,γ为核参数, γ=1(2σ2)。
惩罚因子C和核参数γ直接决定了SVR方法的准确性,为了提高SVR模型的预测精度,需要对这两个参数进行寻优选取。因此,选取合适的优化算法是SVR方法实现锂离子电池RUL准确预测的关键。
1.2 蚁狮优化算法
ALO算法是一种生物启发式算法,模拟自然界中蚁狮的捕猎行为进行运算,具有调节参数少、收敛精度高、鲁棒性好的优点。ALO算法的具体步骤如下[23]:
1)蚁狮构建陷阱:ALO算法根据适应度值通过轮盘赌操作随机选取蚁狮来修筑陷阱,这种方式保证了蚁狮有较大的概率捕猎到猎物。
2)蚂蚁随机游走:蚂蚁在搜索空间中随机游走,其可描述为
式中,cums用于计算累计和;t为随机游走的步长;r (t)为随机函数,其定义为
式中,rand为在[0,1]之间的随机数。
记录并保存优化期间蚂蚁的位置及适应度值,可以分别表示为

式中,MAnt为蚂蚁的位置;And是第n个蚂蚁d维的值;MOA为蚂蚁的适应度值;f(·)为目标函数。此时蚁狮的位置 M Antlion 和适应度值 MOAL可分别为

式中,ALnd为第n个蚁狮d维的值。
为了确保蚂蚁在搜索空间内随机游走,需要对蚂蚁的位置进行初始化,即
式中,ia和di分别为第i个变量随机游走蚂蚁的最小值和最大值![]() 分别为第t次迭代时第i个变量随机游走的最小值和最大值。
分别为第t次迭代时第i个变量随机游走的最小值和最大值。
3)蚂蚁滑落陷阱中心:当蚁狮发现有蚂蚁进入陷阱时,便将沙子向陷阱外抛去,使蚂蚁滑向陷阱中心。此时,蚂蚁的随机游走受到限制,以模拟蚁狮滑向蚂蚁的行为,可以定义为[23]

其中
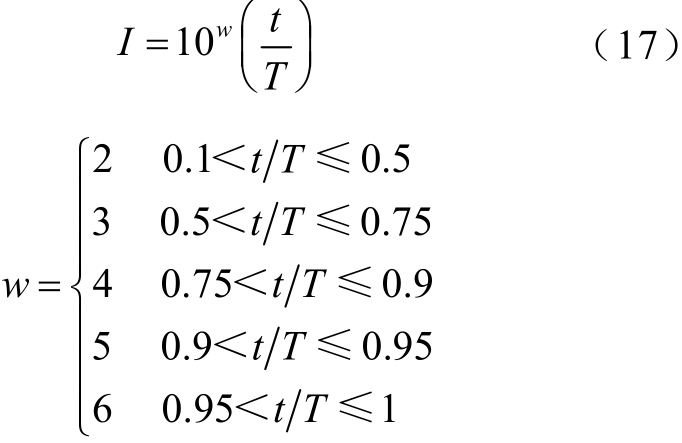
式中,t为当前迭代次数;T为迭代的最大次数;I为比率。
4)重建陷阱:蚁狮捕捉猎物后,评估蚂蚁新位置的适应度值。如果游走的蚂蚁种群中出现了适应度值高于蚁狮的个体,则该蚁狮将被替代。此时蚁狮的位置被更新为
式中,![]() 为蚁狮的位置;
为蚁狮的位置;![]() 为蚂蚁的位置。
为蚂蚁的位置。
5)精英化:蚂蚁的随机游走同时受到轮盘赌操作随机选择的蚁狮和精英蚁狮的影响。因此,蚂蚁的位置根据轮盘赌操作随机选择的蚁狮和精英蚁狮的平均值进行更新,其可表示为
式中,![]() 为通过轮盘赌所选中蚁狮的t次迭代的随机游走位置;
为通过轮盘赌所选中蚁狮的t次迭代的随机游走位置;![]() 为精英蚁狮的随机游走位置。
为精英蚁狮的随机游走位置。
通过对比PSO算法、布谷鸟搜索算法(Cuckoo Search, CS)及遗传算法(Genetic Algorithms, GA),ALO算法不仅具有较好的寻优效率,而且还具有较高的收敛精度[23]。因此,为SVR方法的两个参数选取提供了很好的决策。
1.3 改进蚁狮优化算法
ALO算法虽然能够较好地解决SVR模型参数问题,但ALO算法在迭代过程中易陷入局部最优解,本文通过引入Levy飞行算法来改善ALO算法的优化和搜索能力。
Levy飞行算法[24]是由Viswanathan提出的一种随机游走策略,可用来描述自然界中动物觅食行为。Levy飞行算法被广泛用于优化领域,其不仅能够扩大搜索范围,而且还能增加种群的多样性。因此,Levy飞行算法的引入能够很好地解决ALO算法易陷入局部最优解的问题。假设蚂蚁当前位置为![]() 则通过Levy飞行算法更新后的位置为
则通过Levy飞行算法更新后的位置为![]() 可将式(15)转换为
可将式(15)转换为
式中,α为步长控制因子;s为步长,其符合莱维分布,可表示为
式中,u和v均服从正态分布;通常β取值为1.5。
由于式(20)中α是固定常数,因此搜索能力很差,并且无法在搜索过程中提供准确性。因此,引入随机动态α为
式中,sign(⋅)为符号函数。
1.4 IALO-SVR方法
SVR方法的准确性取决于惩罚因子C和核参数γ,本文利用IALO算法来优化这两个参数,其详细流程框架如图1所示,其主要步骤如下:

图1 基于IALO-SVR的电池RUL预测流程
Fig.1 Flow chart of the RUL prediction of battery based on the IALO-SVR method
(1)数据处理:首先对数据集进行预处理,并将预处理后的数据分为训练集和测试集。
(2)设置模型参数:本文中,种群的数量Agents_no=30,变量参数dim=2,最大迭代次数Max_iter=100,下边界lb=0.01,上边界ub=1 000。
(3)设置适应度函数:利用实际容量值和预测容量值之间的方均误差(Mean Square Error, MSE)值建立适应度函数,即
式中,![]() 为预测容量;y为实际容量。
为预测容量;y为实际容量。
(4)IALO算法优化SVR模型参数:蚂蚁的位置由Levy飞行算法进行不断的更新,再根据适应度函数求出每个蚂蚁的适应度值。通过不断迭代,直到满足得到的极值小于设定的阈值或达到最大迭代次数,输出最佳参数,并利用最佳参数构建IALOSVR预测模型。
(5)锂离子电池的RUL预测:通过测试数据验证已训练完成的模型,从而完成锂离子电池RUL的预测。
2 锂离子电池健康因子分析及提取
2.1 锂离子电池数据集
本文采用的数据是来源于美国国家航空航天局卓越预测中心(National Aeronautics and Space Administration Prognostics Center of Excellence,NASA PCoE)提供的容量为2A·h的18650钴酸锂电池老化数据集[25]。每个充放电循环周期均包括充电和放电两个部分。具体操作过程如下:
1)充电模式:锂离子电池在1.5A的恒定电流(Constant Charge, CC)模式下充电直到电池电压达到4.2V,再以恒定电压(Constant Voltage, CV)4.2V充电,一直充到电流降至20mA为止。
2)放电模式:以恒定电流2A条件下进行放电,直到电压达到某一设定的截止电压。
对电池进行不断的充放电循环测试实验,当电池容量达到寿命失效阈值时,即当前容量为额定容量的70%,则实验终止,具体实验数据集信息见表1。
表1 实验数据集信息
Tab.1 Information of experimental dataset

?
由于B7号电池未降至失效阈值,考虑到此试验电池的寿命循环,将寿命终止条件设定为容量衰减到额定容量的72%,即2A⋅h降至为1.44A⋅h,四个锂离子电池容量退化曲线如图2所示。

图2 NASA电池容量退化曲线
Fig.2 Battery capacity change curves of NASA
2.2 健康因子分析及提取
电池实际运行过程中,像容量及内阻等直接性能参数难以获取,其不仅需要精密的仪器设备,而且还要排除外界环境干扰因素,实验操作条件十分苛刻。因此,从可监测的性能参数着手,即间接性能参数,考虑锂离子电池全寿命循环周期的过程,从中提取电压及电流等多方面外特性参量作为评估电池性能退化的健康因子。
随着锂离子电池不断地进行充放电循环实验,使得电池充放电总时间逐渐缩短,即电池的CC阶段与CV阶段充电总时间随着电池逐渐老化而不断缩短。以B5号电池为例,分别提取第2次、第50次、第100次和第150次循环周期的CC充电过程中的电压值变化曲线,其变化曲线如图3所示。

图3 CC充电过程中电压曲线变化
Fig.3 Change curves of voltage curve during constant current charging
等压升充电时间间隔:从图3中可知,第2次循环所需充电时间(即从开始电压值到截止电压时刻(4.2V)所需的充电时间)最长,而第150次循环所需充电时间最短。在到达截止电压4.2V这一相同条件下,随着充放电循环次数的不断增多,CC阶段充电时间逐渐缩短。由此可知,CC阶段充电电压隐含着电池性能退化的特征,可以间接表征电池健康状态信息。考虑使用者充电的行为习惯,根据电压值与电量之间的关系,选取3.8V的电压作为起始电压,4.2V的截止电压为终止电压。因此,从电压3.8V到4.2V时所需的充电时间作为表征电池健康状态的健康因子,并记作HI1。
等流降充电时间间隔:随着充放电循环次数不断增加,CV阶段充电时间也随之变化。同样地,以B5号电池为例,分别提取第2次、第50次、第100次和第150次循环周期中的CV充电过程中电流值变化曲线,如图4所示。随着充放电循环次数不断增加,由此可知,CV阶段充电电流变化较为明显,可以间接表征电池退化信息。考虑在实际应用中,存在不完全充电情况,而不能达到截止电流值,选取部分CV阶段,即选取1.5A电流值作为起始电流,0.5A电流作为终止电流。因此,CV阶段过程中电流值从1.5A降至0.5A时所需的充电时间作为表征电池健康状态的另一健康因子,记作HI2。
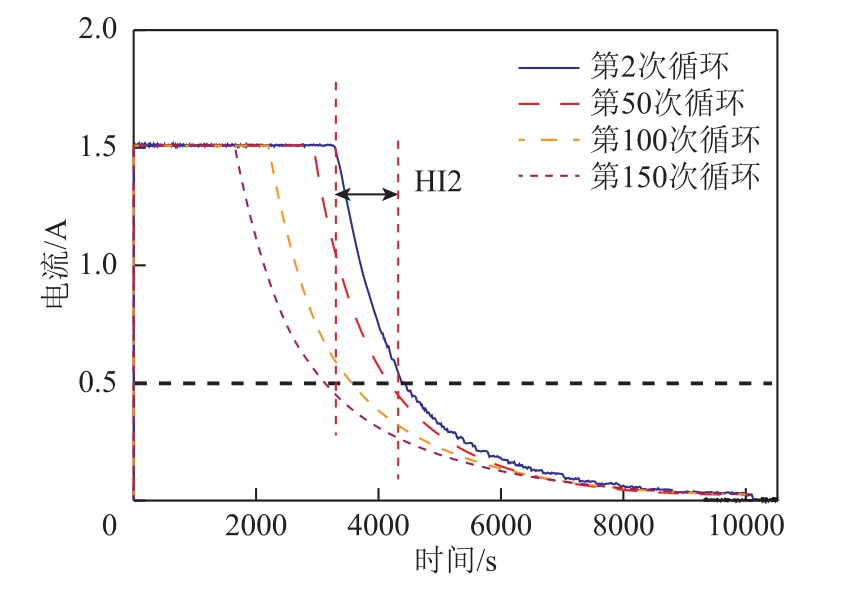
图4 CV充电过程中电流曲线变化
Fig.4 Change curves of current curve during constant voltage charging
循环次数:上述两个健康因子HI1及HI2均是随着充放电循环次数的增加而呈现明显的变化。随着循环次数的增加,电池内部活性材料不断地被消耗,可循环Li+元素也逐渐被消耗殆尽,导致内部可循环充放电能力逐渐下降,内部阻抗不断增加,使得电池容量不断衰减,最终可能导致电池内部结构破碎。随着循环次数的增加,无需知道影响电池的外部条件,也无需掌握电池内部发生的物理化学反应,其必然会使电池性能逐渐衰退。因此,本文将循环次数作为表征电池健康状态的第三个健康因子,记作HI3。
为验证所提取健康因子的可行性,利用Pearson及Spearman相关性分析法来分析与容量间的相关性。Pearson系数可以定量分析两组数据间的相似程度,假设给出两个变量 α = (α 1 ,α2 ,…,αn)和β=(β1,β2,…,βn ),则Pearson相关系数可表示为
式中,E为期望值。当两个向量具有极强的线性关系时,此时相关系数逼近-1或者1;如果两种变量相互独立时,则Pearson相关系数为0。
Spearman相关系数可表示为
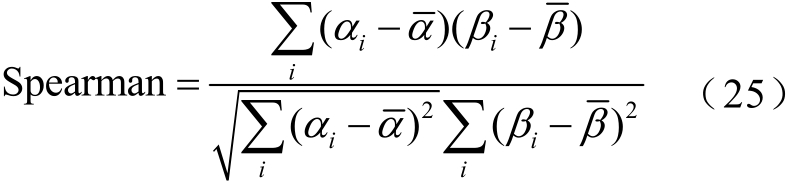
式中,![]() 分别为α和β的平均值;Spearman相关系数值的范围在-1~1之间。
分别为α和β的平均值;Spearman相关系数值的范围在-1~1之间。
在锂离子电池数据中,多种外特性参量以及容量值均随着循环次数的变化而变化,是一种时序数据。Pearson相关系数能够很好地描述这些外特性参量与容量之间是否存在线性关系,能够衡量这些外特性参量是否能够表征容量变化趋势;而在进行锂离子电池循环测试过程中,避免不了外界干扰因素的影响,且Pearson相关系数受异常值影响较大,而Spearman相关系数不受这些约束,能够很好地描述外特性参量与容量间的相关关系。
从NASA中选取的四块锂离子电池所提取的三个健康因子分别与容量之间的详细相关系数见表2。
表2 健康因子与容量间的相关系数结果
Tab.2 Results of correlation coefficient between health factor and capacity

?
由表2可知,所有实验锂离子电池与容量之间的相关系数均在±(0.7~1.0),说明所提取的健康因子与容量之间存在紧密的关系。因此,这三个健康因子可以间接表征电池容量退化特性,可以很好地描述电池健康状态信息。
3 基于IALO-SVR方法的锂离子电池RUL预测
本文利用NASA数据集对IALO-SVR预测方法进行实验验证,将其与BP神经网络和ALO-SVR方法进行对比分析,三种预测方法的参数设置[19]见表3。在BP方法中,学习速率Ir为0.05,最大训练次数epochs为1 000,显示训练迭代过程show为50;在SVR方法中,惩罚因子C=10和核参数 γ= 0.01;IALO-SVR方法的最大迭代次数Max_iter为100,且种群大小Ps均为30,参数β为1.5。分别利用四块试验电池的前65次(B5、B6及B7的为65,B18为45)和前80次(B5、B6及B7的为80,B18为60)循环周期数据作为训练样本。
表3 各种预测方法参数设置
Tab.3 Parameter setting of various prediction methods

?
当锂离子电池的前65次循环周期数据作为训练样本时,基于BP神经网络、SVR和IALO-SVR三种方法的锂离子电池的RUL预测结果如图5所示,测试集中的真实容量值与预测容量值间误差的绝对值如图6所示。

图5 三种方法的锂离子电池RUL预测结果(前65次周期数据作为训练样本)
Fig.5 RUL prediction of lithium-ion batteries based on three methods (The 65 cycles of data are used as training samples)

图6 三种方法的锂离子电池RUL预测误差(前65次周期数据作为训练样本)
Fig.6 RUL prediction error of lithium-ion batteries based on three methods (The 65 cycles of data are used as training samples)
统计BP、SVR和IALO-SVR三种方法的预测结果,见表4。
表4 三种方法的RUL预测结果(前65次周期数据作为训练样本)
Tab.4 RUL prediction of lithium-ion batteries based on three methods (the 65 cycles of data are used as training samples)
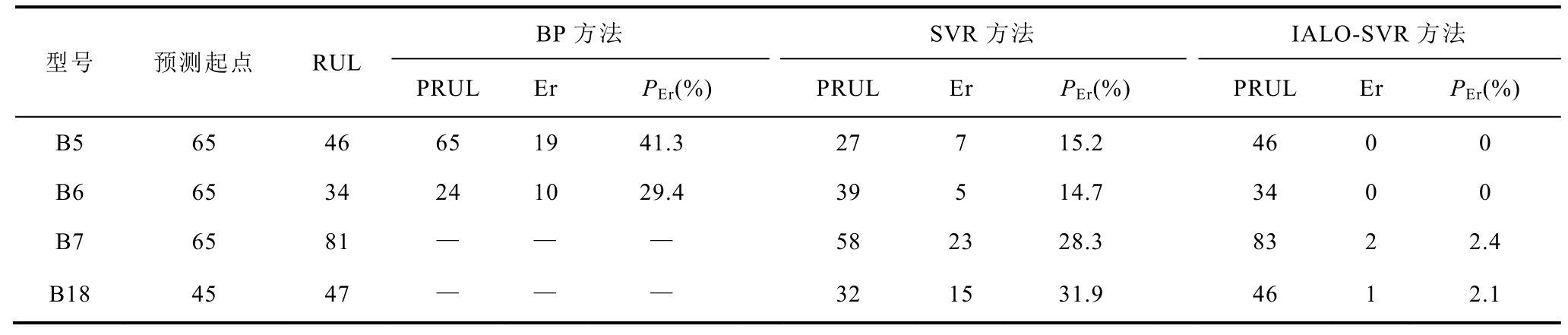
BP方法 SVR方法 IALO-SVR方法型号 预测起点 RUL PRUL Er PEr(%) PRUL Er PEr(%) PRUL Er PEr(%)B5 65 46 65 19 41.3 27 7 15.2 46 0 0 B6 65 34 24 10 29.4 39 5 14.7 34 0 0 B7 65 81 — — — 58 23 28.3 83 2 2.4 B18 45 47 — — — 32 15 31.9 46 1 2.1
表4 中,PRUL为RUL预测值,RUL为RUL真实值,Er表示PRUL与RUL之间误差的绝对值。当锂离子电池的容量衰退至失效阈值时,实际所经历的循环次数值与预测方法所预测的循环次数值之间的误差定义为
由表4可知,相较于BP和SVR方法,IALOSVR方法所得到的Er和PEr值更小(对于B7和B18号电池,BP方法预测得到的RUL值未达到失效阈值,因此用“—”表示)。例如,对于B5号电池,基于BP方法的Er和PEr值分别为19和41.3%,SVR方法的Er和PEr值分别为7和15.2%,而IALO-SVR方法所得到的Er和PEr值均为0。对于B7号电池,BP方法预测RUL均未达到失效阈值,SVR方法所得到的Er和PEr值分别为23和28.3%,而IALOSVR方法所得到的Er和PEr值均比SVR方法小10倍。由表4可知,BP方法的预测误差在19次循环周期内,SVR方法的预测误差在23次循环周期内,而IALO-SVR方法的预测误差在2次循环周期内。综上可知,IALO-SVR方法的锂离子电池RUL预测精度更高。
为了进一步分析三种方法的预测精度,将三种方法预测得到的平均绝对误差(Mean Absolute Error,MAE)和方均根误差(Root Mean Square Error, RMSE)值进行统计分析,见表5。
表5 三种方法的RUL预测误差(前65次周期数据作为训练样本)
Tab.5 RUL prediction error of lithium-ion batteries based on three methods (the 65 cycles of data are used as training samples)

?
表5 中,平均绝对误差(MAE)定义为
方均根误差(RMSE)为
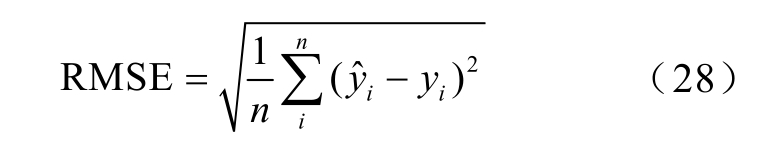
式中,![]() 为预测容量值;y为实际容量值。
为预测容量值;y为实际容量值。
从表5中的数据可知,IALO-SVR方法所得到的误差均比其他两种方法小。例如,对于B5号电池,BP方法的MAE和RMSE值分别为0.065 5和0.075 5,而SVR方法所得到的MAE和RMSE值为0.0741和0.095 7。此外,基于IALO-SVR方法所得到的MAE和RMSE值为BP方法的1/6和1/5左右。
当利用锂离子电池的前80次循环周期数据作为训练样本时,基于BP、SVR和IALO-SVR三种方法的锂离子电池的RUL预测结果如图7所示,预测误差如图8所示。

图7 三种方法的锂离子电池RUL预测结果(前80次周期数据作为训练样本)
Fig.7 RUL prediction of lithium-ion batteries based on three methods (the 80 cycles of data are used as training samples)

图8 三种方法的锂离子电池RUL预测误差(前80次周期数据作为训练样本)
Fig.8 RUL prediction error of lithium-ion batteries based on three methods (The 80 cycles of data are used as training samples)
为了更加直观地分析BP、SVR和IALO-SVR三种方法的预测效果,将预测结果进行统计,见表6。
表6 三种方法的RUL预测结果(前80次周期数据作为训练样本)
Tab.6 RUL prediction of lithium-ion batteries based on three methods (the 80 cycles of data are used as training samples)

?
由表6可知,对于B5号电池,IALO-SVR方法所得到的Er和PEr值都为0,均小于其他两种方法。此外,对于B6号电池,IALO-SVR方法所得到的Er和PEr值分别为2和10.5%,约为BP方法的1/5,约为SVR方法的1/6,由此可知,IALO-SVR方法所获得的误差更小。
为了进一步分析三种方法的预测精度,统计分析三种方法预测得到的MAE和RMSE值,见表7。
表7 三种方法的RUL预测误差(前80次周期数据作为训练样本)
Tab.7 RUL prediction error of lithium-ion batteries based on three methods (the 80 cycles of data are used as training samples)

?
从表7中的数据可知,对于B5号电池,IALOSVR方法所得到的MAE和RMSE值分别为0.009 7和0.014 9,均比其他两种方法小。相同的,对于B6、B7及B18号三个电池,IALO-SVR方法所得到的MAE和RMSE值也均小于其他两种方法,由此可得,IALO-SVR方法能够获得更小的预测误差。
此外,根据表4~表7中的数据,会发现B6号(或B18号)电池用前80次(或前60次)数据预测寿命比用前65次(前45次)数据预测的误差更大,这是由于数据存在容量再生的情况。例如B6号电池,前65次循环共发生了6次容量再生;在45~80次循环之间没有容量再生,退化趋势较为平缓;而80次循环之后又有容量再生的现象。然而MAE和RMSE的值是相对整体求取的,由于容量再生的情况,前65次预测误差基数整体较小于前80次预测误差基数。
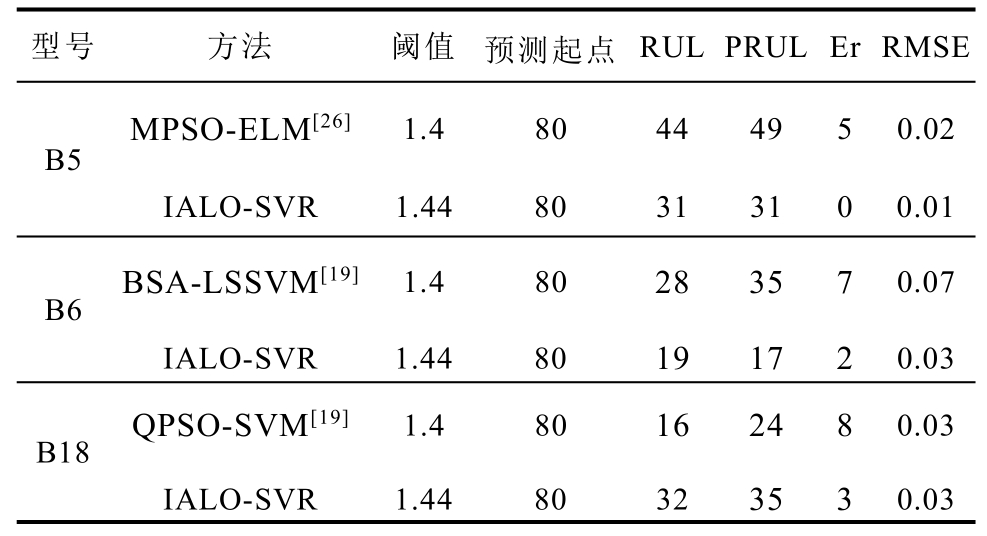
为进一步验证本文所提出的方法,与其他文献进行比较,结果见表8。
表8 IALO-SVR与其他预测方法的比较结果
Tab.8 Comparison results between IALO-SVR and other prediction methods
?
在相同预测起点下,对于电池B5号电池,MPSO-ELM方法的Er和RMSE值分别为5和0.02,而IALO-SVR方法所得到的Er值为0,RMSE值为MPSO-ELM方法的1/2。同样地,对于B6和B18号电池,本文提出的方法所得到的误差均比其他方法小,由此可知,本文提出的IALO-SVR方法能够提供更高的预测精度。
4 结论
锂离子电池凭借其优越的性能广泛用于电动汽车及储能领域,准确预测锂离子电池的RUL可以提高电池系统的安全性和可靠性。本文通过研究NASA 数据集,从充电中提取能够表征电池性能退化的间接健康因子,并利用Pearson及Spearman相关性分析法分析与容量之间的相关性,以验证所提取的间接健康因子的可行性;提出一种IALO优化算法,为SVR方法提供最优参数,从而实现基于间接健康因子的锂离子电池RUL在线准确预测;并利用NASA电池退化数据集来验证IALO-SVR方法的性能,相较于BP、SVR方法和其他文献方法的预测结果进行分析比较,验证了IALO-SVR方法的有效性。因此,本文提出的IALO-SVR预测方法能够为锂离子电池RUL提供更高的预测精度。在接下来的研究中,考虑电池充放电循环全周期过程和充放电过程中电压、电流及温度等参量的变化,提取具有极强相关性的外特性参量,实现更准确的锂离子电池RUL在线预测。
[1] 张振宇, 汪光森, 聂世雄, 等. 脉冲大倍率放电条件下磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2019, 34(8): 1769-1779.Zhang Zhenyu, Wang Guangsen, Nie Shixiong, et al.State of charge estimation of LiFePO4 battery under the condition of high rate pulsed discharge[J].Transactions of China Electrotechnical Society, 2019,34(8): 1769-1779.
[2] 李楠, 高峰. 基于储能型模块化多电平系统的多时间尺度控制策略[J]. 电工技术学报, 2017, 32(17):47-56.Li Nan, Gao Feng. Multi-time scale operational principle for battery integrated modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 47-56.
[3] 郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J].电工技术学报,2019, 34(19): 3968-3978.Guo Yongfang, Huang Kai, Li Zhigang. Fast state of health prediction of lithium-ion battery based on terminal voltage drop during rest for short time[J].Transactions of China Electrotechnical Society, 2019,34(19): 3968-3978.
[4] 焦自权, 范兴明, 张鑫, 等. 基于改进粒子滤波算法的锂离子电池状态跟踪与剩余使用寿命预测方法[J]. 电工技术学报, 2020, 35(18): 3979-3993.Jiao Ziquan, Fan Xingming, Zhang Xin, et al. State tracking and remaining useful life predictive method of Li-ion battery based on improved particle filter algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3979-3993.
[5] 孙丙香, 任鹏博, 陈育哲, 崔正韬, 姜久春. 锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测[J]. 电工技术学报, 2021,36(3): 666-674.Sun Bingxiang, Ren Pengbo, Chen Yuzhe, et al.Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 666-674.
[6] Kong S N, Moo C S, Chen Y P, et al. Enhanced coulomb counting method for estimating state-ofcharge and state-of-health of lithium-ion batteries[J].Applied Energy, 2009, 86(9): 1506-1511.
[7] Prasad G K, Rahn C D. Model based identification of aging parameters in lithium ion batteries[J]. Journal of Power Sources, 2013, 232: 79-85.
[8] Fan Guodong, Li Xiaoyu, Canova M. A reduced-order electrochemical model of Li-ion batteries for control and estimation applications[J]. IEEE Transactions on Vehicular Technology, 2018, 67(1): 76-91.
[9] He Wei, Williard N, Osterman M, et al. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method[J]. Journal of Power Sources, 2011, 196(23): 10314-10321.
[10] Zhang Xin, Miao Qiang, Liu Zhiwen. Remaining useful life prediction of lithium-ion battery using an improved UPF method based on MCMC[J].Microelectronics Reliability, 2017, 75: 288-295.
[11] Ma Yan, Chen Yang, Zhou Xiuwen, et al. Remaining useful life prediction of lithium-ion battery based on Gauss-Hermite particle filter[J]. IEEE Transactions on Control Systems Technology, 2019, 27(4): 1788-1795.
[12] Hariharan K S, Kumar V S. A nonlinear equivalent circuit model for lithium ion cells[J]. Journal of Power Sources, 2013, 222: 210-217.
[13] Zou Yuan, Li S E, Shao Bing, et al. State-space model with non-integer order derivatives for lithium-ion battery[J]. Applied Energy, 2016, 161: 330-336.
[14] Zhang Xin, Miao Qiang, Liu Zhiwen. Remaining useful life prediction of lithium-ion battery using an improved UPF method based on MCMC[J].Microelectronics Reliability, 2017, 75: 288-295.
[15] 刘月峰, 张公, 张晨荣, 等. 锂离子电池RUL预测方法综述[J]. 计算机工程, 2020, 46(4): 11-18.Liu Yuefeng, Zhang Gong, Zhang Chenrong, et al.Review of RUL prediction method for lithium-ion batteries[J]. Computer Engineering, 2020, 46(4):11-18.
[16] Patil M A, Tagade P, Hariharan K S, et al. A novel multistage support vector machine based approach for Li ion battery remaining useful life estimation[J].Applied Energy, 2015, 159: 285-297.
[17] Zhang Shuzhi, Zhai Baoyu, Guo Xu, et al.Synchronous estimation of state of health and remaining useful lifetime for lithium-ion battery using the incremental capacity and artificial neural networks[J]. Journal of Energy Storage, 2019, 26:100951.
[18] 刘健, 陈自强, 黄德扬, 等. 基于等压差充电时间的锂离子电池寿命预测[J]. 上海交通大学学报,2019, 53(9): 1058-1065.Liu Jian, Chen Ziqiang, Huang Deyang, et al.Remaining useful life prediction for lithium-ion batteries based on time interval of equal charging voltage difference[J]. Journal of Shanghai Jiaotong University, 2019, 53(9): 1058-1065.
[19] Li L L, Liu Z F, Tseng M L, et al. Enhancing the lithium-ion battery life predictability using a hybrid
method[J]. Applied Soft Computing, 2019, 74: 110-121.
[20] Gao Dong, Huang Miaohua. Prediction of remaining useful life of lithium-ion battery based on multi-kernel support vector machine with particle swarm optimization[J]. Journal of Power Electronics, 2017,17(5): 1288-1297.
[21] Liu Datong, Zhou Jianbao, Pan Dawei, et al. Lithiumion battery remaining useful life estimation with an optimized relevance vector machine algorithm with incremental learning[J]. Measurement, 2015, 63: 143-151.
[22] Cortes C, Vapnik V. Support-vector networks[J].Machine Learning, 1995, 20(3): 273-297.
[23] Mirjalili S. The ant lion optimizer[J]. Advances in Engineering Software, 2015, 83: 80-98.
[24] Viswanathan G M, Afanasyev V, Buldyrev S V, et al.Lévy flight search patterns of wandering albatrosses[J].Nature, 1996, 381: 413-415.
[25] Goebel K, Saha B, Saxena A, et al. Prognostics in battery health management[J]. IEEE Instrumentation and Measurement Magazine, 2008, 11(4): 33-40.
[26] Yang Jing, Peng Zhen, Wang Hongmin, et al. The remaining useful life estimation of lithium-ion battery based on improved extreme learning machine algorithm[J]. International Journal of Electrochemical Science, 2018, 13: 4991-5004.