0 引言
随着“全球能源互联网”战略的提出以及海洋能源工程的迅猛发展,海上风能发电和海洋油气资源开采等项目的开发规模不断扩大,近海经济快速发展,海上输电系统的建设已成为我国未来电力系统发展的重点[1-3]。电力电缆作为新能源跨海输电系统的重要组成部分,通过桥梁敷设电力电缆相比于海底电缆敷设具有更高的经济性和运行维护可靠性,已成为跨海输电系统的优先选择。然而,为了抑制接地电流对大桥钢管桩结构的腐蚀作用,电缆通常只能在大桥某些固定位置引下接地,如大桥钻孔灌注桩或大桥登陆处[4-5]。大桥引下接地的限制使得随桥电缆的接地方式成为决定输电系统安全可靠的关键,因此有必要对稳态运行条件下随桥电缆的接地方式开展研究。
稳态运行条件下,针对随桥电缆接地方式的研究主要有以下三个方面:一是电缆金属护套接地方式的设计,如单端接地、双端接地或交叉互联接地;二是电缆金属护套的感应电压,主要影响施工检修人员的人身安全;三是电缆金属护套的接地环流,主要决定了输电系统的损耗及能量传输效率。针对随桥电缆接地方式的设计,国内外学者开展了广泛的研究。文献[4]提出了Maracaibo地区的230kV随桥电缆工程的接地方案,即在大桥登陆处采取金属护套单端接地,大桥的中部采取两段交叉互联接地。文献[6]对东海大桥110kV电缆工程接地方式进行了设计,将长度为25km的随桥电缆分为四段,每段首尾端的金属护套采取单端接地,中间部分金属护套采取交叉互联接地,在最大负荷运行状态下,电缆护套的感应电压最高可以达到92V。
在电缆金属护套的感应电压和接地环流方面,文献[7-8]基于多导体分析方法,建立电缆的等效π型节点导纳矩阵,计算了地下电缆系统金属护套的感应电压分布。文献[9]建立了单回路电缆金属护套感应电压的三维简化模型,利用有限元软件计算分析了不同电导率下金属护套的感应电压。文献[10]运用矩阵级数展开的方法计算地下电缆系统的节点导纳矩阵,得到了电缆金属护套的感应电压和环流分布,并对电缆的降损措施进行了研究。文献[11]推导了双回路电缆金属护套的环流的计算公式,分析了不同因素对于双回路电缆护套环流的影响。文献[12]建立了单芯电缆交叉互联接地方式下接地电流的计算模型,分析了不同排列方式和负载电缆之间的关系。但是,上述研究主要针对地下电缆系统,而对于随桥电缆系统的相关研究还较少,因此有必要针对随桥电缆系统金属护套的感应电压和接地环流开展相关的研究工作。
本文考虑架空敷设环境对电缆电气特性的影响,推导随桥电缆的单位长度串联阻抗矩阵和并联导纳矩阵;然后采用节点导纳矩阵的非解耦形式简化节点电压方程的求解;基于随桥电缆系统的边界条件和节点约束条件,推导同阶和不同阶节点导纳矩阵的级联公式,构建随桥电缆系统稳态计算的矩阵解法。利用上述矩阵解法对舟岱大桥220kV随桥电缆工程开展接地方式研究,计算金属护套和回流电缆的感应电压及环流分布,求解随桥电缆系统的总损耗功率,并研究不同串联阻抗的降损效果。
1 随桥电缆节点导纳矩阵的构建
1.1 随桥电缆单位长度电气参数的计算
随桥电缆实质上属于架空电缆,其电气特性与地下电缆和海底电缆有较大差别[13]。目前的电缆电气参数计算公式主要针对地下电缆系统,而对于随桥电缆系统却不适用[14]。本节以图1所示的随桥电缆系统为例推导计算电缆线路的单位长度串联阻抗矩阵和单位长度并联导纳矩阵。
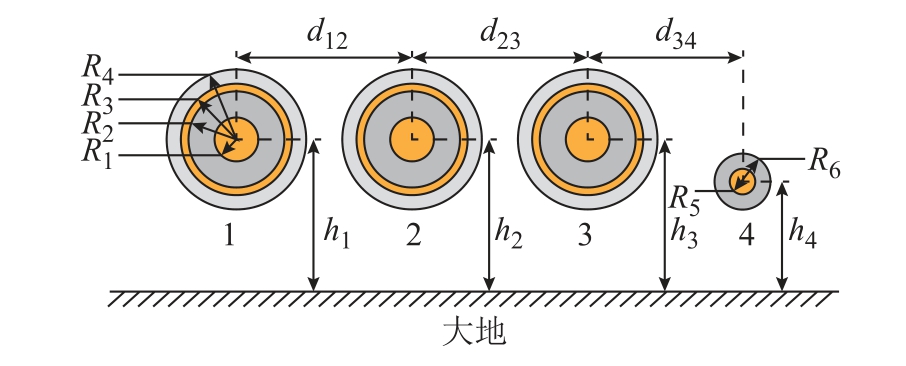
图1 随桥电缆系统结构示意图
Fig.1 Structure diagram of the bridge-cable system
图1 所示的随桥电缆系统中,1、2和3分别为A、B和C相电缆,4为回流电缆;R1为电缆缆芯半径,R2为电缆内绝缘层半径,R3为电缆金属护套半径,R4为电缆外绝缘层半径,R5为回流电缆缆芯半径,R6为回流电缆绝缘半径;hi为电缆i的离地高度;dik为电缆i和电缆k的水平距离。
1.1.1 随桥电缆单位长度串联阻抗矩阵的计算
考虑到架空敷设环境对随桥电缆的影响,将图1所示的随桥电缆系统分解为电缆及外部介质两部分,其单位长度串联阻抗矩阵为
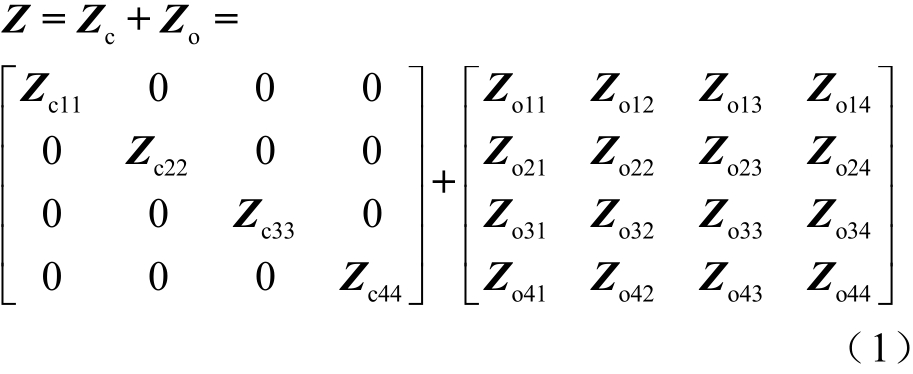
式中,Zc为随桥电缆系统中电缆部分的单位长度串联阻抗矩阵;Zo为随桥电缆系统中外部介质部分的单位长度串联阻抗矩阵。
电缆部分的单位长度串联矩阵可由式(2)求得。

式中,下标i为整数,代表相应的电缆序号;矩阵的各部分元素可由Schelkunhoff回路理论和Pollaczek理论给出[15-16]。
若土壤电导率为σ,真空磁导率为μ0,信号的角频率为ω,则外部介质中的单位长度串联阻抗矩阵的自阻抗部分

其中
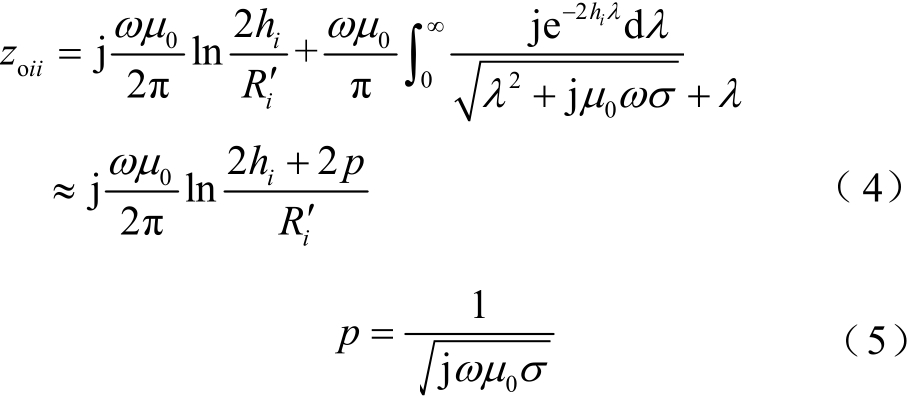
式中,zoii为外部介质部分中电缆i的对地串联自阻抗;zo44为外部介质部分中回流导体的对地串联自阻抗;iR′为电缆i的外绝缘层半径或回流电缆绝缘层的半径。
外部介质中的单位长度串联阻抗矩阵的互阻抗部分可由式(6)求得。

其中
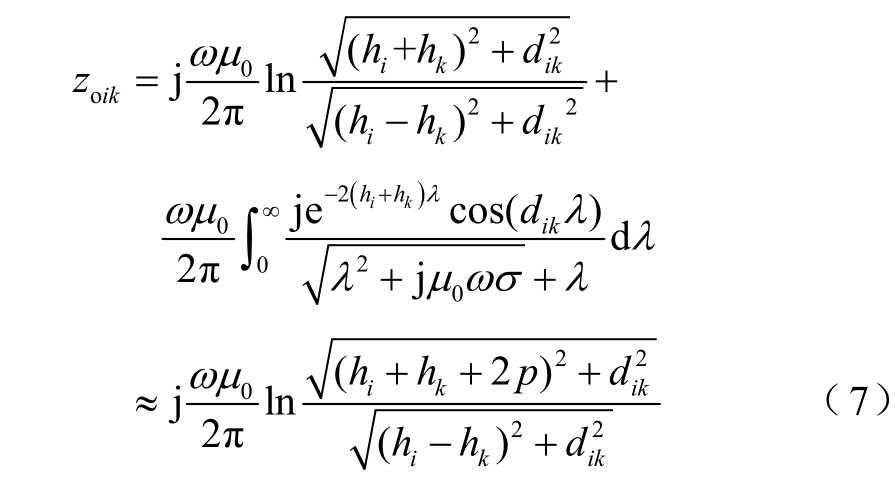
式中,下标i和k为整数,代表相应的电缆序号;zoik为外部介质部分中电缆i和k之间的对地互阻抗;zoi4为外部介质部分中电缆i与回流导体之间的对地互阻抗。
1.1.2 随桥电缆单位长度并联导纳矩阵的计算
考虑架空敷设环境对随桥电缆的影响,将图1所示的随桥电缆系统分解为电缆(不包括电缆外绝缘层)及外部介质(包括电缆外绝缘层)两部分,其单位长度并联导纳矩阵为
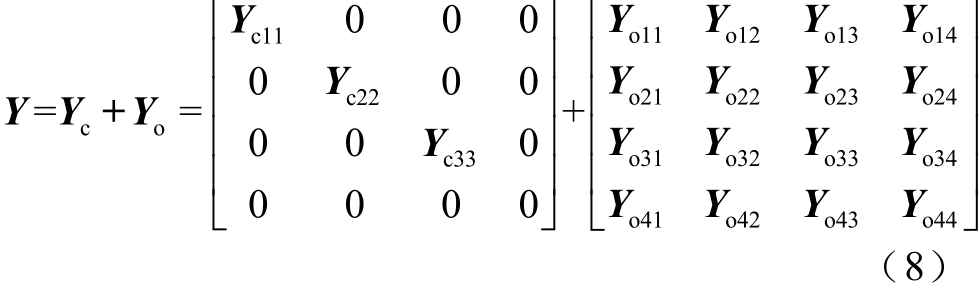
式中,Yc为随桥电缆系统中电缆部分(不包括电缆外绝缘层)的单位长度并联导纳矩阵;Yo为随桥电缆系统中外部介质部分(包括电缆外绝缘层)的单位长度并联导纳矩阵。
若信号角频率为ω,真空介电常数为ε0,则电缆部分(不包括电缆外绝缘层)的单位长度并联导纳矩阵为
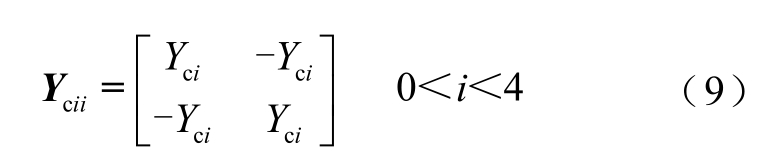
其中
式中,下标i为整数,代表相应的电缆序号;εin为电缆内绝缘层相对介电常数。
外部介质(包括电缆外绝缘层)中的单位长度并联导纳矩阵的互导纳部分可由式(11)求得。

其中
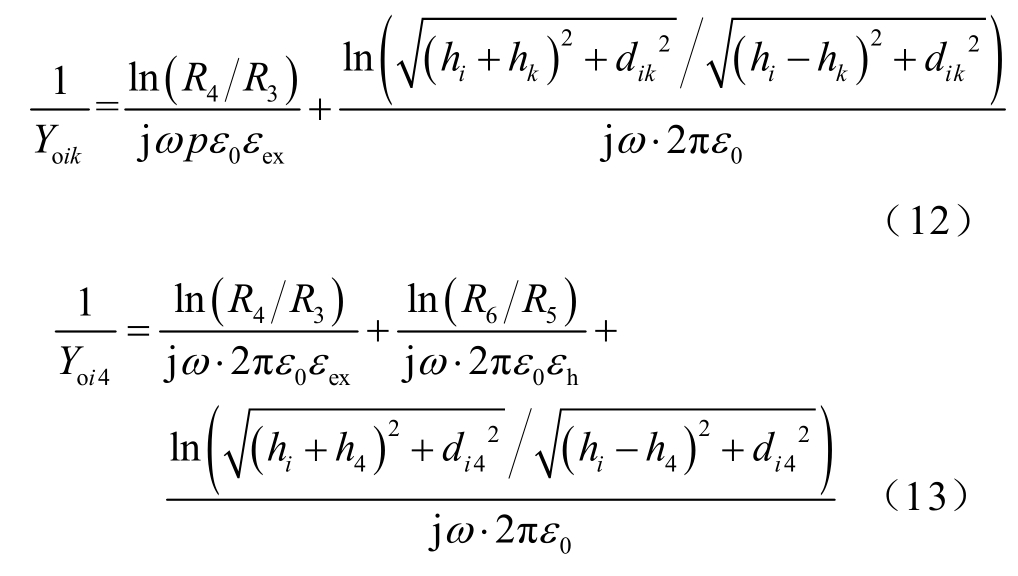
式中,εex为电缆外绝缘层相对介电常数;hε为回流电缆绝缘层的相对介电常数。
外部介质中的单位长度并联导纳矩阵的自导纳部分可表示为

其中
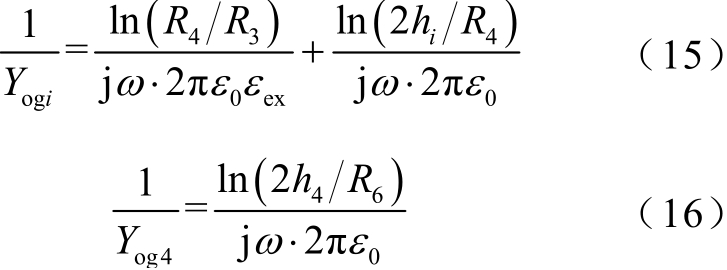
1.2 节点导纳矩阵的非解耦形式
根据多导体分析理论[17-18],图1所示的随桥电缆系统可以等效为7根互相耦合的平行输电导体,其等效电路模型如图2所示。其中,电缆线路长度为l,Z为单位长度串联阻抗矩阵,Y为单位长度并联导纳矩阵,U1为电缆首端的对地电压向量,U2为电缆末端的对地电压向量,I1为电缆首端的电流向量,电流方向朝右,I2为电缆末端的电流向量,电流方向朝左。

图2 等效电路模型
Fig.2 Equivalent circuit model
由频域的传输线电报方程和边界条件可以得到等效电路的节点电压方程为
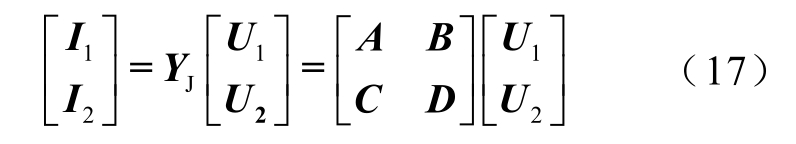
其中

式中,YJ为电缆线路的节点导纳矩阵;Γ为传输系数矩阵。
从式(18)中可以得到,节点导纳矩阵YJ的求解包括传输系数矩阵Γ,即必须进行矩阵对角化。但当矩阵的阶数较高时,对角化分解将会非常复杂,在某些情况下甚至无法进行矩阵的对角化。因此引入矩阵的非解耦形式,对节点导纳矩阵进行Laurent级数逼近,通过式(19)和式(20)进行求解[19-20]。

其中
式中,Bm为伯努利数,[m=0]表示m=0时取1,其余取0,B0=1;级数在0< Γl<π时收敛,即保证![]()
2 随桥电缆系统稳态计算的矩阵解法
在得到随桥电缆非解耦形式的节点导纳矩阵的情况下,可基于系统的边界条件和节点约束条件进行稳态计算,求取电缆金属护套和回流电缆上的感应电压及环流分布。本节以图3所示的随桥电缆系统为例介绍一种随桥电缆稳态计算的矩阵解法。其中,随桥电缆采取交叉互联接地,通过回流电缆与接地装置保持电气连接,变电站等效为带阻抗的三相电源,负载和电缆接地箱等效为阻抗。
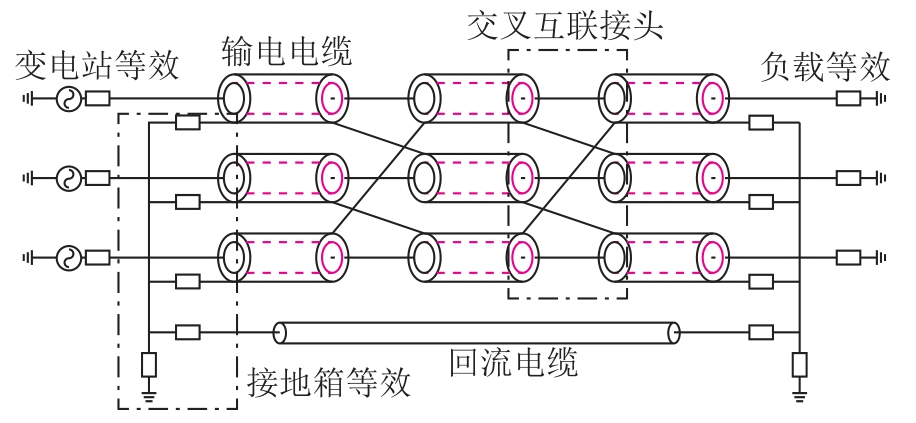
图3 随桥电缆系统结构
Fig.3 Structure of the bridge cable system
随桥电缆系统的等效节点电路如图4所示。根据电缆线路的结构特征,将其分为9段,Si和Si′为分段的端口名称,上标“′”表示该端口的节点数量为7,无上标代表该端口的节点数量为4。Yi_j和![]() 为相应端口之间的节点导纳矩阵,规定系统的电流正方向为右。
为相应端口之间的节点导纳矩阵,规定系统的电流正方向为右。
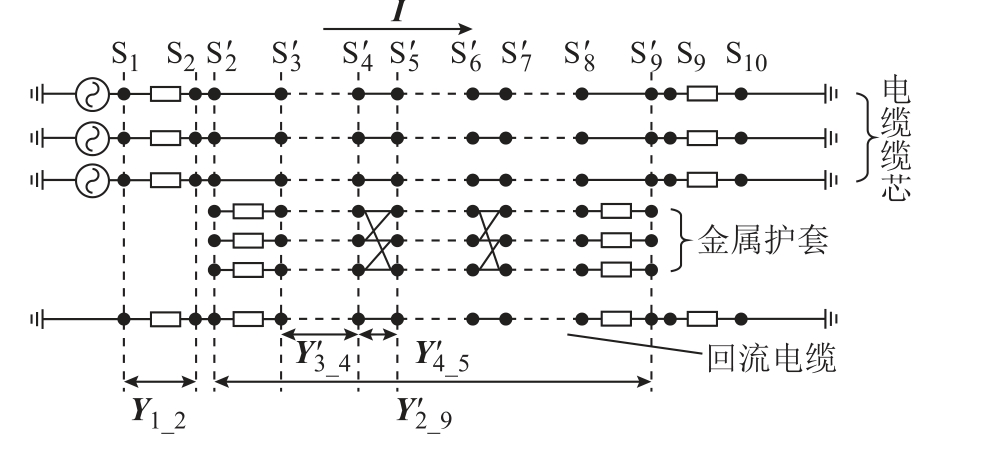
图4 等效节点电路
Fig.4 Equivalent node circuit
2.1 同阶节点导纳矩阵的级联
以等效节点电路图4中的节点导纳矩阵![]() 和
和![]() 为例,说明同阶节点导纳矩阵的级联。分别建立端口S3′和S4′之间的电缆段及端口S4′和S5′之间的换位接头段的节点电压方程,分别有
为例,说明同阶节点导纳矩阵的级联。分别建立端口S3′和S4′之间的电缆段及端口S4′和S5′之间的换位接头段的节点电压方程,分别有

式中,I′3、I′4和I′5分别为端口S′3、S′4和S′5的电流向量;下标a代表电流方向为正方向,下标b代表电流方向为负方向;U′3、U′4和U′5分别为端口S′3、S′4和S′5的对地电压向量。
由于流入及流出端口S′4的电流之和为0,即
结合式(22)和式(23),得到级联后的等效节点导纳矩阵Y′eq为

2.2 不同阶节点导纳矩阵的级联
以等效电路图4中的节点导纳矩阵Y1_2和Y′2_9为例,说明不同阶节点导纳矩阵的级联,节点导纳矩阵Y′2_9可由同阶矩阵的级联求得。分别建立端口S1和S2之间的线路分段及端口S′2和S′9之间的线路分段的节点电压方程,其结构分别如图5a和图5b所示。其中,I1a、I2b、U1和U2为4阶列向量,I′2a、I′9b、U′2和U′9为7阶列向量,Y1_2为8阶方阵,Y′2_9为14阶方阵。

图5 不同端口之间的节点电压方程
Fig.5 Node voltage equation between different ports
根据端口S2和端口S′2之间的节点约束条件,有关系式
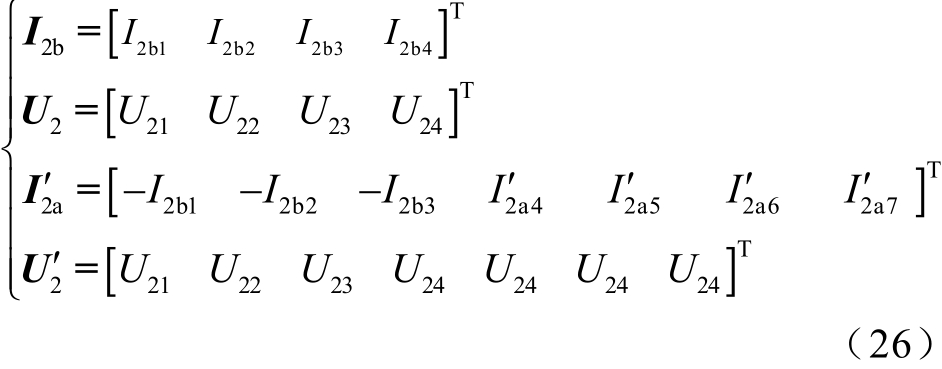
其中
根据以上关系式,引入电流变换矩阵T1、电压变换矩阵T2和节点导纳变换矩阵T3对图5b中虚线部分的行向量和列向量进行合并,T1、T2和T3的结构如图6所示。
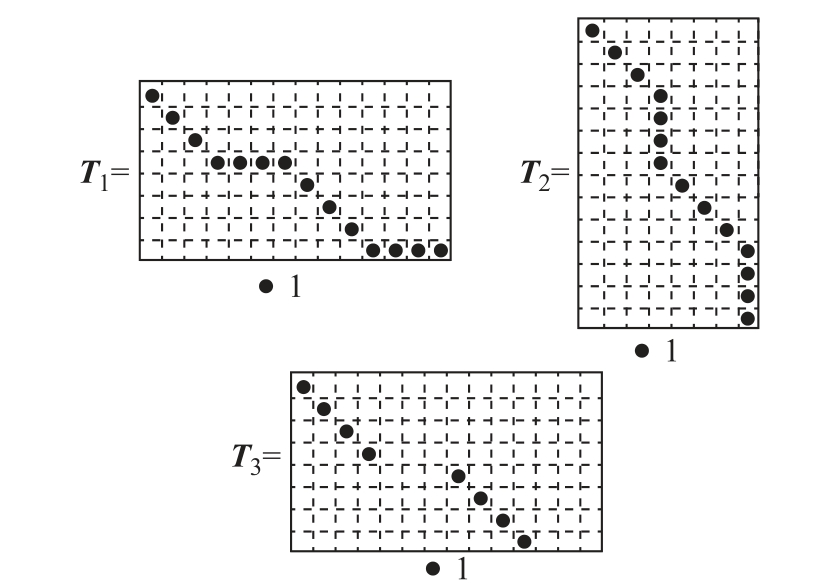
图6 T1、T2和T3的结构Fig.6 Structure of T1, T2 and T3
利用变换矩阵T1、T2和T3对图5b所示的节点电压方程进行变换,得到为
也即
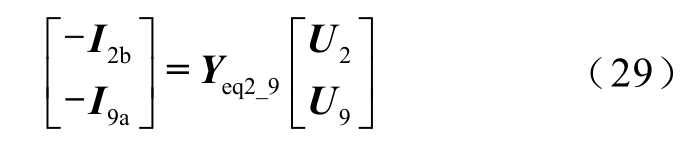
变换之后得到的等效节点导纳矩阵Yeq2_9为8阶矩阵,可以通过式(25)完成和节点导纳矩阵Y1_2的级联。
2.3 随桥电缆系统的稳态计算
在得到同阶矩阵和不同阶矩阵的级联公式情况下,可以分别求得电缆线路各段的节点导纳矩阵和电缆线路总的节点导纳矩阵。再由随桥电缆系统边界电压向量求得首尾端电流分布,根据以下公式逐段求取整个线路的金属护套和回流电缆中的感应电压及环流分布[21]。
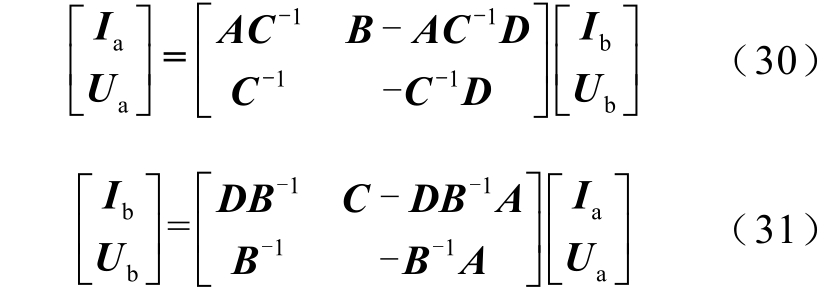
其中
式中,Ia为电缆首端电流向量;Ib为电缆末端电流向量;Ua为电缆首端电压向量;Ub为电缆末端电压向量;Y为电缆段的节点导纳矩阵。
3 随桥电缆接地方式研究
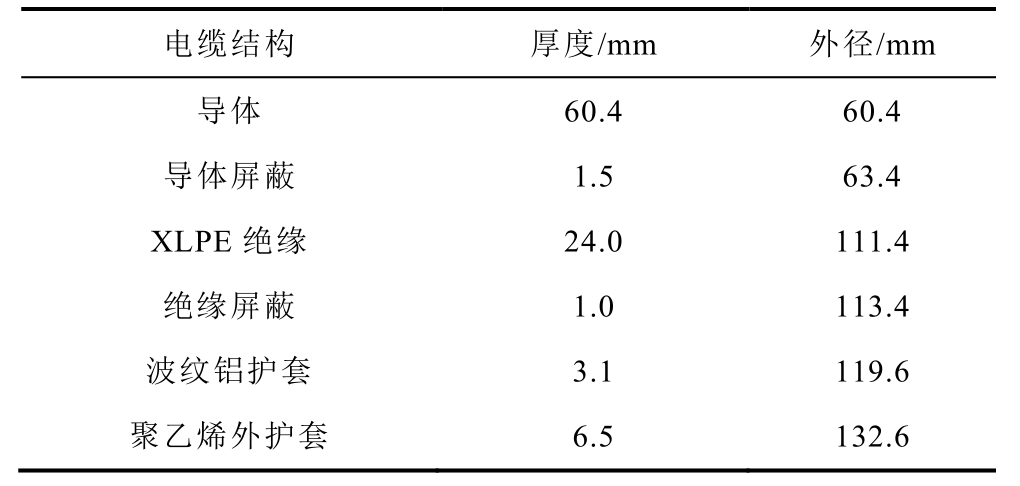
本节以浙江舟岱大桥中间段混凝土箱梁的220kV随桥电缆工程为对象开展接地方式研究。该电缆系统总长6 580m,采取首尾段电缆金属护套单端接地,中间电缆金属护套三段交叉互联接地,单端接地段长为590m,交叉互联单元长为600m,具体结构如图7所示。输电电缆的型号为127/220kVYJLW03,回流电缆的型号为VV-0.6/1-1×400,电缆采取水平布置,三相电缆之间间距为0.5m,回流电缆与C相电缆之间间距为1m,电缆的结构参数分别见表1和表2。
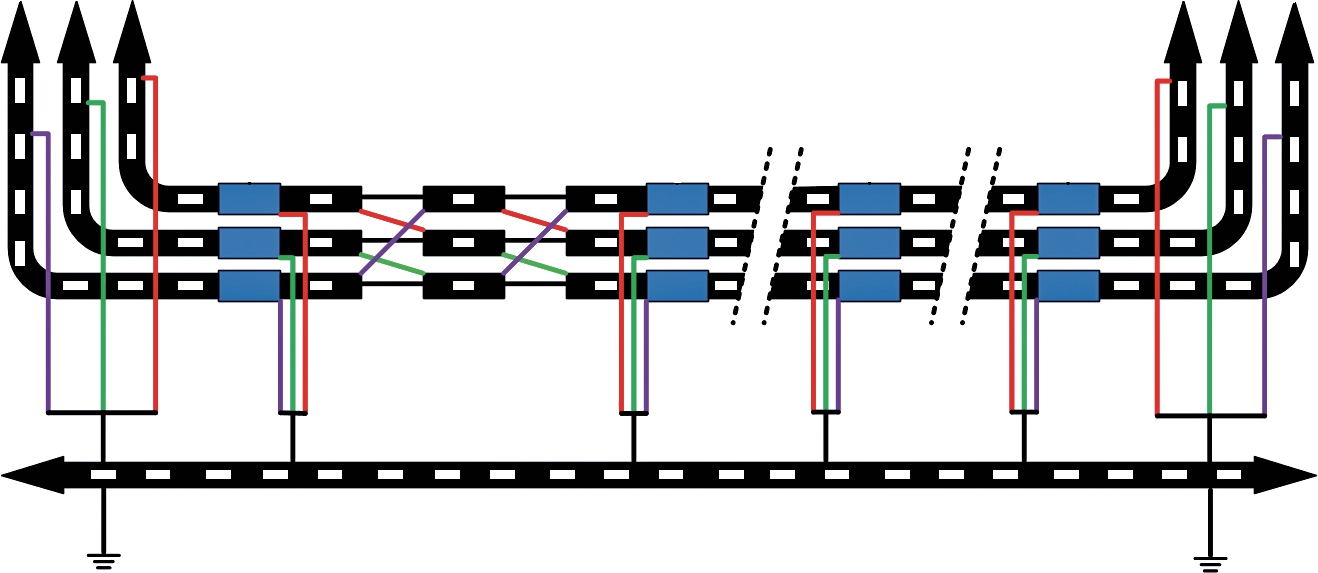
图7 舟岱大桥随桥电缆系统结构
Fig.7 Bridge-cable system structure of Zhoudai Bridge
表1 输电电缆的结构参数
Tab.1 Structural parameters of transmission cables
?
表2 回流电缆的结构参数
Tab.2 Structural parameters of return cable

?
3.1 随桥电缆的护套感应电压和环流分布
利用随桥电缆系统稳态计算的矩阵解法对图7所示系统进行求解,其中对称三相电源A相电压为220∠0°kV,输送的有功功率为528MW,电源等效阻抗为5Ω,回流电缆接地阻抗为1Ω,接地箱连接阻抗为1mΩ,得到A、B和C三相电缆的金属护套感应电压分布如图8所示。由图8可知,在电缆单端接地段,金属护套的感应电压幅值随距离变化呈现线性上升的趋势,在不接地端达到最高值;三相电缆中,A相电缆的金属护套上出现的感应电压大,其幅值最高可以达到83.76V。在电缆交叉互联接地段,金属护套上出现的感应电压在电缆交叉互联接头处最大,其幅值最高可以达到87.15V;三相电缆中,A相电缆的金属护套上出现的感应电压最大,B相和C相电缆金属护套上出现的感应电压较为接近,随距离呈现对称分布的趋势。结果表明,稳态运行条件下随桥电缆系统的金属护套感应电压最大值小于300V,符合国家标准规定的要求[22]。

图8 输电电缆的感应电压分布
Fig.8 Distribution of induced voltage of transmission cables
A、B和C三相电缆的金属护套环流分布如图9所示。由图9可知,在电缆单端接地段,金属护套的环流幅值随距离变化呈现线性下降的趋势,在不接地端处环流幅值降为0;三相电缆的护套环流分布基本一致,其幅值最高可以达到9.91A。在电缆交叉互联接地段,B相电缆的金属护套上出现的环流最大,其幅值最高可以达到40.76A,C相电缆的金属护套上出现的环流最小,其幅值最低为22.24A。结果表明,与交叉互联接地相比,单端接地能有效减小电缆金属护套环流。
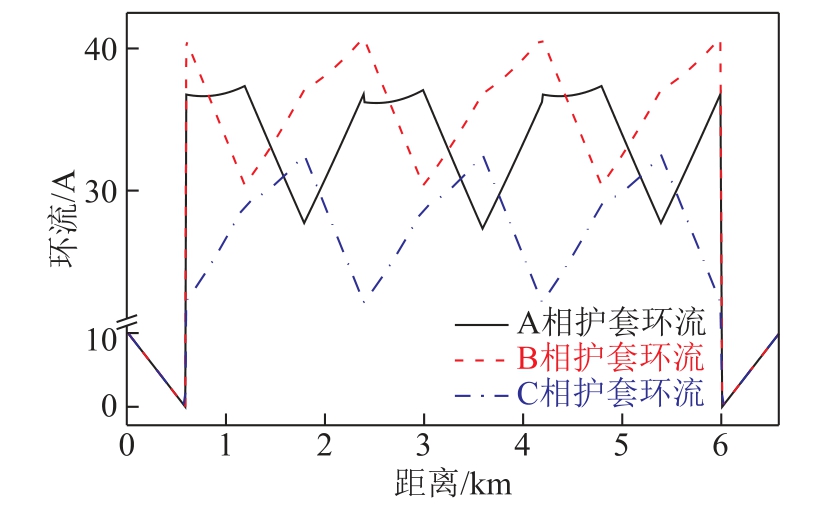
图9 输电电缆的环流分布
Fig.9 Circulating current distribution of transmission cables
回流电缆的感应电压和环流分布如图10所示。由图10可知,在输电电缆的单端接地段,回流电缆的感应电压随距离变化呈现线性下降的趋势,接地端处感应电压最大,其幅值最高可达到17.13V;回流电缆的环流随距离变化保持恒定,其幅值为17.51A。在输电电缆交叉互联接地段,回流电缆的感应电压随距离变化呈现先下降后上升的趋势,在输电电缆单端接地与交叉互联接地的交界处达到最高幅值14.32V;回流电缆的环流随距离变化保持恒定,其幅值为79.57A。结果表明,与输电电缆的金属护套相比,回流电缆的感应电压较小,接地环流较大。
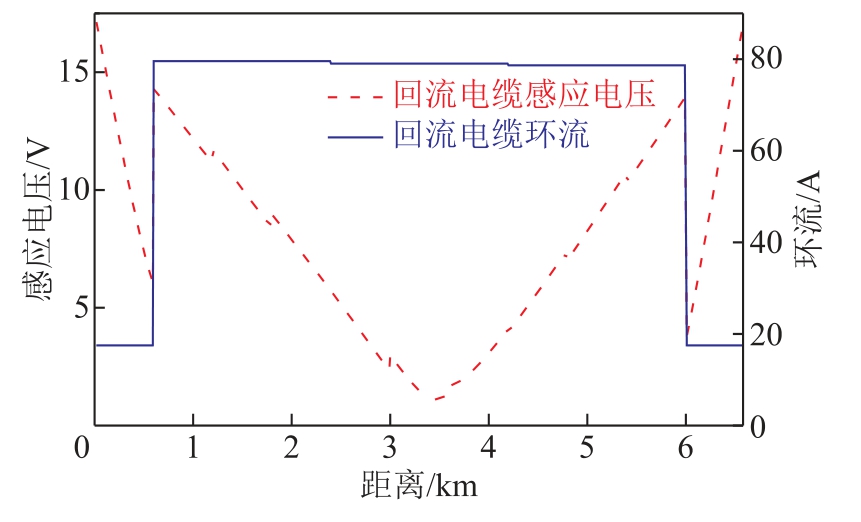
图10 回流电缆的感应电压和环流分布
Fig.10 Distribution of induced voltage and circulating current of return cable
3.2 随桥电缆护套损耗的计算
由随桥电缆系统的护套感应电压和环流分布结果可以得到:金属护套和回流电缆的接地环流是限制随桥电缆系统输电性能的主要因素。本节基于金属护套和回流电缆的接地环流分布,对随桥电缆金属护套和回流电缆的损耗进行计算。
将电缆划分为足够小的微元段,每个电缆微元段的环流视为恒定值,则随桥电缆的金属护套和回流电缆的损耗功率计算式为
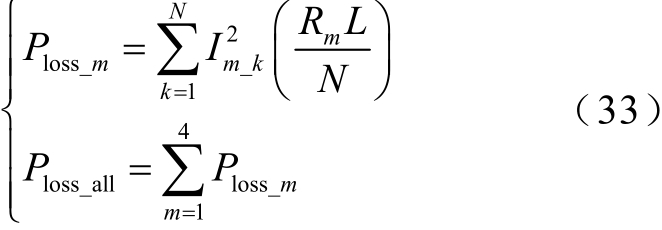
式中,Ploss_m为三相电缆金属护套和回流电缆的损耗功率,下标m=1~4,分别代表A、B、C相电缆金属护套及回流电缆的损耗功率(W);N为电缆划分的微元段个数;Im_k为对应电缆金属护套或回流电缆的第k微元段的环流,A;Rm为对应电缆金属护套或回流电缆的单位长度电阻(Ω);L为线路总长度(m);Ploss_all为随桥电缆系统总损耗功率(W)。
微元段长度取为1m,计算得到三相电缆金属护套、回流电缆及总损耗功率如图11所示。由图11可知,A相电缆的金属护套损耗功率为45.11kW,B相电缆的金属护套损耗功率为42.58kW,C相电缆的金属护套损耗功率为33.66kW,回流电缆的损耗功率为238.98kW,总损耗功率为360.34kW。结果表明,随桥电缆系统的损耗主要集中于回流电缆,回流电缆损耗功率占总体损耗功率的比例达到66.3%;随桥电缆系统的总体损耗较高,不可忽略。

图11 损耗功率分布
Fig.11 Power loss distribution diagram
3.3 随桥电缆的降损措施
目前,电缆系统常见的降损措施一般可采用电缆长度补偿,提高金属护套层的电阻率,在电缆终端接入补偿电感,以及在电缆交叉互联接头处串联阻抗等方法[23-25]。其中,在电缆交叉互联接头处串联阻抗不但能有效降低电缆损耗,而且投资成本较小,安装施工便利,具有较高的工程实践价值。本节针对随桥电缆的降损措施,研究不同串联阻抗特性下的降损性能。
3.3.1 不同串联电阻的降损性能
在电缆交叉互联接头处串联电阻,既能有效地降低护套环流损耗,在故障情况下也不会额外的引入电感复杂的电磁暂态效应,适用于过电压要求较为严格的线路,但需保证良好的散热环境。在电缆交叉互联接头处串联不同阻值的电阻,三相电缆护套损耗、回流电缆损耗及总损耗的计算结果分别如图12所示。由图12可知,当串联电阻小于0.5Ω时,随着电阻阻值的增大,损耗功率抑制效果显著,在电阻阻值为0.5Ω时,损耗降低达到初始总损耗的77.0%;当串联电阻大于0.5Ω时,随着电阻阻值的增大,损耗功率抑制效果较小,在电阻阻值为2.0Ω时,三相电缆护套损耗、回流电缆损耗及总损耗趋于恒定,损耗降低达到初始总损耗的96.2%。结果表明,在交叉互联接头处串联电阻能有效降低电缆损耗。
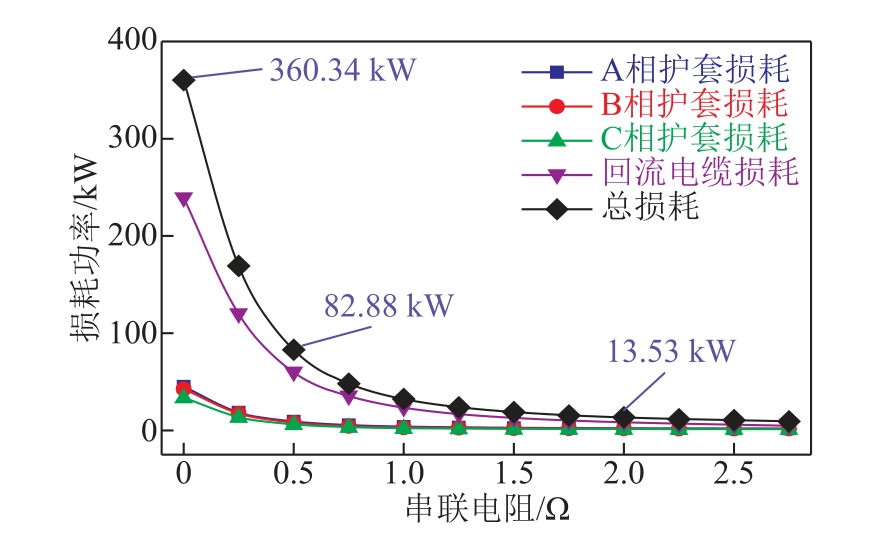
图12 不同串联电阻下的损耗功率
Fig.12 Power loss under different series resistance
在电缆交叉互联接头处串联不同阻值的电阻,计算得到三相电缆护套及回流电缆的最大感应电压如图13所示,图中UAmax为A相护套感应电压最大值,UBmax为B相护套感应电压最大值,UCmax为C相护套感应电压最大值,UHmax为回流电缆的感应电压最大值。由图13可知,随着串联电阻阻值的增大,三相电缆护套和回流电缆的感应电压最大值均有一定程度的上升。在串联电阻阻值为2.75Ω时,C相电缆金属护套的感应电压最大值达到峰值,为93.13V,远小于电缆护套感应电压的限制值300V。结果表明,在交叉互联接头处串联电阻对护套感应电压的影响程度不大。
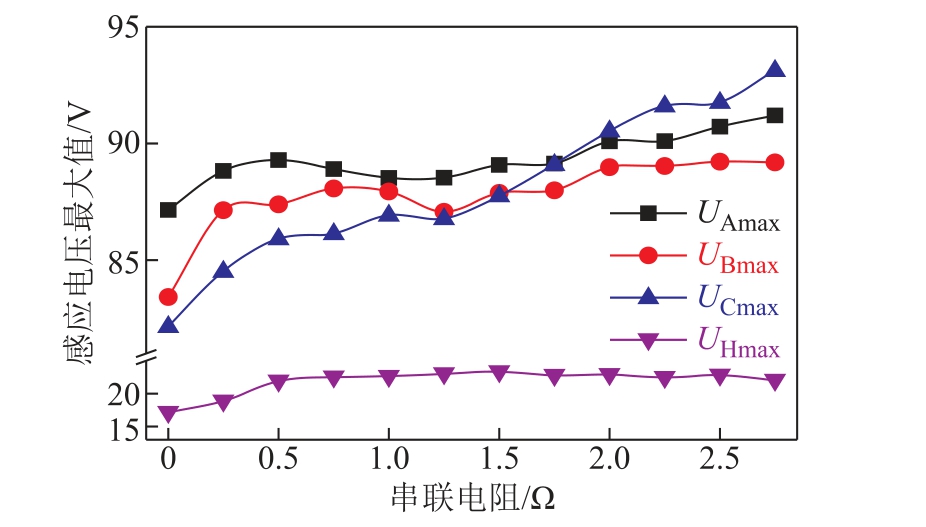
图13 不同串联电阻下的感应电压最大值
Fig.13 Maximum induced voltage under different series resistance
3.3.2 不同串联电感的降损性能
在电缆交叉互联接头处串联电感,既能有效降低护套环流损耗,装置本身也不会产生额外的热损耗,对散热环境的要求较低,但是需要校验故障情况下线路的过电压特性。在电缆交叉互联接头处串联不同阻值的电感,三相电缆护套损耗、回流电缆损耗及总损耗的计算结果分别如图14所示。由图14可知,当串联电感小于0.5Ω时,随着电感阻抗的增大,损耗功率抑制效果显著,在电感阻抗值为0.5Ω时,损耗降低达到初始总损耗的80.3%;当串联电感大于0.5Ω时,随着电感阻抗的增大,损耗功率抑制效果较小,在电感阻抗值为2.0Ω时,三相电缆护套损耗、回流电缆损耗及总损耗趋于恒定,损耗降低达到初始总损耗的96.3%。结果表明,在交叉互联接头处串联电感能有效的降低电缆损耗。
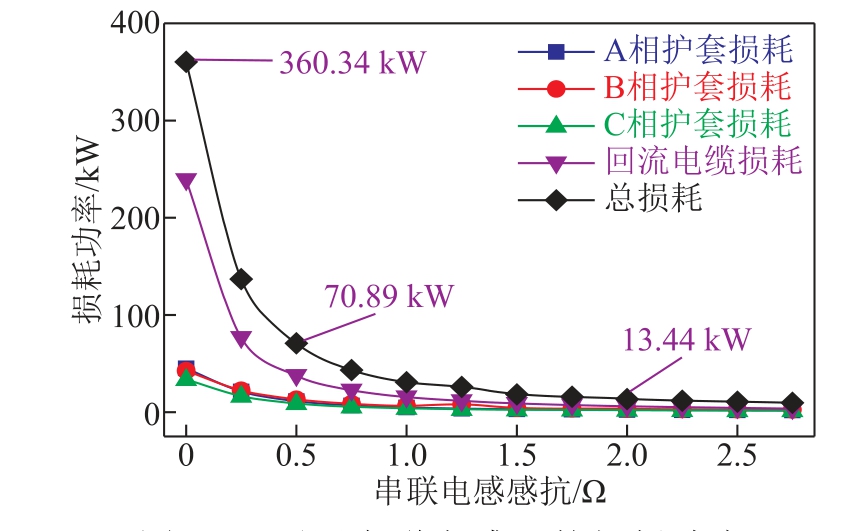
图14 不同串联电感下的损耗功率
Fig.14 Power loss under different series inductance
在电缆交叉互联接头处串联不同阻抗的电感,计算得到三相电缆护套及回流电缆的最大感应电压如图15所示。由图15可知,随着串联电感阻抗的增大,B相电缆护套和回流电缆的感应电压最大值有一定程度的上升,A相和C相电缆护套的感应电压最大值有一定程度的下降。在串联电感感抗值为0.5Ω时,A相电缆金属护套的感应电压最大值出现峰值,为89.93V,远小于电缆护套感应电压的限制值300V。结果表明,在交叉互联接头处串联电感对护套感应电压的影响程度不大。
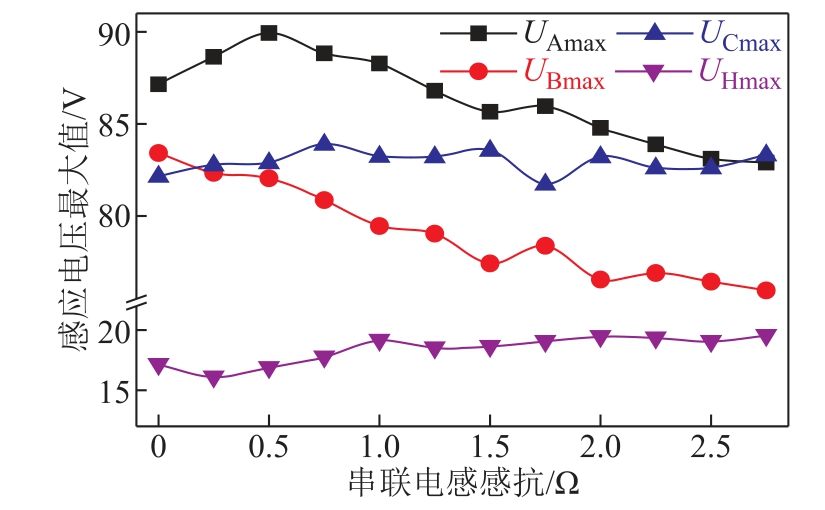
图15 不同串联电感下的感应电压最大值
Fig.15 Maximum induced voltage under different series inductance
3.3.3 不同相角串联阻抗的降损性能
在电缆交叉互联接头处串联阻抗,既能有效地降低护套环流损耗,装置产生的热损耗也较小,兼具了电阻和电感的优点。为了清晰地展示不同阻抗值下,串联阻抗的相角对降损性能的影响,对总损耗功率进行归一化处理,其表达式为
式中,PG为总损耗功率归一化值;Pzi表示串联阻抗为z,相角为i时的总损耗功率;Pz0表示串联阻抗为z,相角为0°时的总功率损耗。
计算得到不同阻抗值及阻抗相角下总损耗的归一化值如图16所示。由图16可知,同一阻抗值下,阻抗相角不为0°的总损耗功率归一化值总小于1,即电感和电阻配合使用的降损效果优于纯电阻;同一阻抗值下,阻抗角为60°时总损耗功率归一化值最小,即阻抗相角为60°时降损性能最优;阻抗相角不为0°时,随着阻抗值增大,相同阻抗角下的总损耗功率归一化值逐渐增大,即随着阻抗值增大,相同阻抗相角下的降损效果相对于纯电阻而言是逐渐减小的。结果表明,调节串联阻抗角能提高降损性能,且阻抗角为60°时降损性能最优。
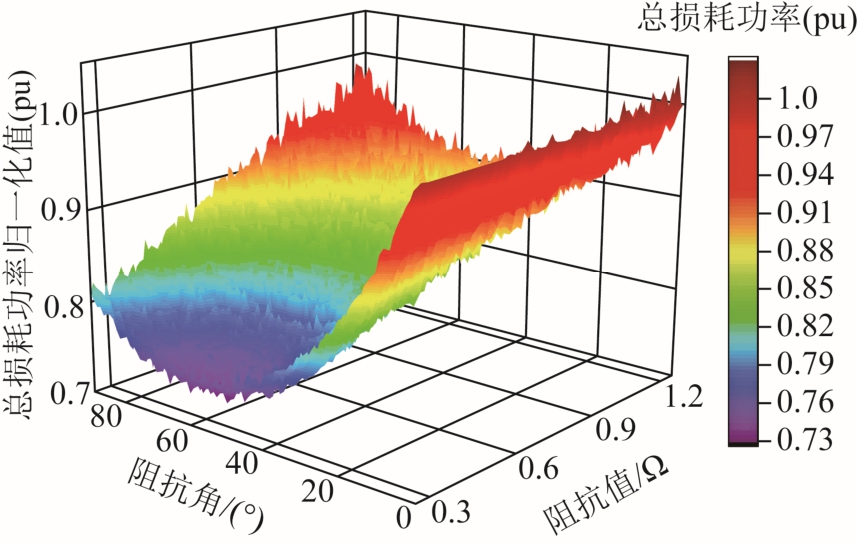
图16 总损耗归一化值分布
Fig.16 Distribution of normalized value of total loss
计算得到不同阻抗值及阻抗角下金属护套和回流电缆的感应电压最大值如图17所示。由图17可知,同一阻抗值下,随着阻抗角的增大,金属护套和回流电缆的感应电压最大值呈现先下降后上升的总体趋势,即纯电阻和纯电感下,感应电压的最大值出现峰值,阻抗角为50°时,感应电压的最大值出现谷值;同一阻抗相角下,随着阻抗值的增大,感应电压最大值呈现下降的总体趋势,且阻抗角越大,感应电压最大值下降的越明显;金属护套和回流电缆的感应电压最大值为97.6V,远小于电缆护套感应电压的限制值300V。结果表明,调节串联阻抗相角对感应电压的影响不大,感应电压最大值始终小于300V。
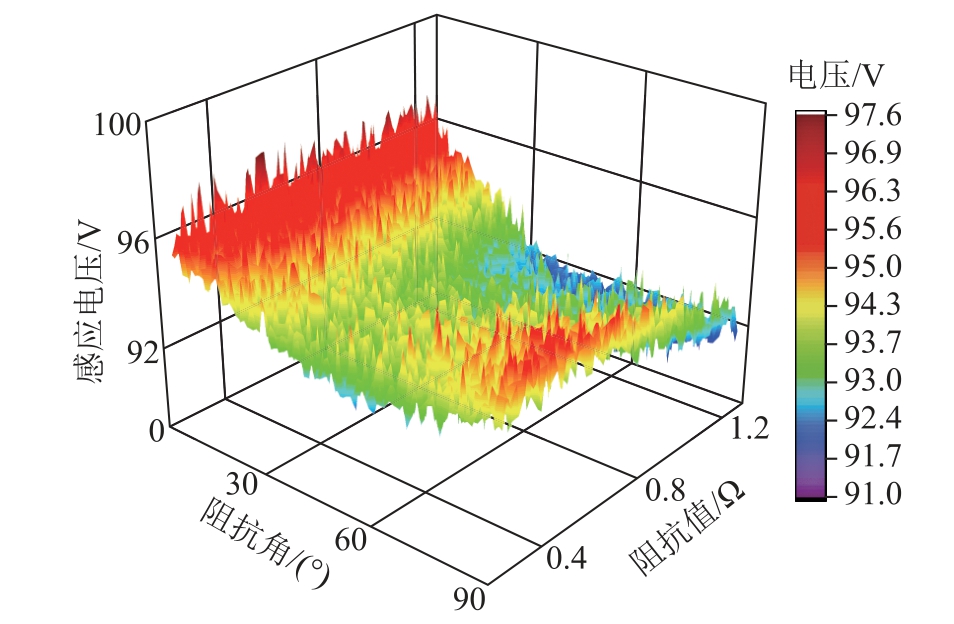
图17 感应电压最大值分布图
Fig.17 Distribution diagram of maximum induced voltage
4 结论
本文考虑架空敷设环境的影响,推导了随桥电缆系统的单位长度串联阻抗和并联导纳计算公式。针对高阶矩阵难以对角化的问题,引入节点导纳矩阵的非解耦形式,对节点导纳矩阵的计算进行了简化。同时基于随桥电缆系统的边界条件和节点约束条件,推导了同阶和不同阶节点导纳矩阵的级联公式,构建了随桥电缆系统稳态计算的矩阵解法。基于稳态计算的矩阵解法,以浙江舟岱大桥中间段混凝土箱梁的220kV随桥电缆工程为对象开展接地方式研究,得到以下结论:
1)稳态运行条件下,三相电缆金属护套和回流电缆上出现的感应电压较小,其幅值最高可以达到87.15V,符合相关国家标准要求;三相电缆金属护套和回流电缆上出现的环流较大,且主要集中于回流电缆,其幅值最高可以达到79.57A。
2)三相电缆金属护套和回流电缆的接地环流是限制随桥电缆系统输电性能的主要因素;随桥电缆系统的总损耗功率为360.34kW,其中回流电缆损耗占主要部分,占比达到66.3%;随桥电缆系统的总体损耗较高,不可忽略。
3)在交叉互联接头处串联电阻能有效的降低电缆损耗,在电阻阻值为2.0Ω时,损耗降低达到初始总损耗的96.2%,同时串联电阻对护套感应电压的影响程度不大,护套感应电压最大值为93.13V;在交叉互联接头处串联电感也能有效地降低电缆损耗,电感阻抗为2.0Ω时,损耗降低达到初始总损耗的96.3%,同时串联电阻对护套感应电压的影响程度不大,护套感应电压最大值为89.93V。
4)电感和电阻配合使用的降损效果优于纯电阻;相对于纯电阻而言,随着阻抗值增大,相同阻抗角下的降损效果逐渐减小;调节串联阻抗角为60°时,降损性能达到最优;调节串联阻抗角对感应电压的影响不大,感应电压最大值始终小于300V。
[1] 余晓丹, 徐宪东, 陈硕翼, 等. 综合能源系统与能源互联网简述[J]. 电工技术学报, 2016, 31(1): 1-13.Yu Xiaodan, Xu Xiangdong, Chen Shuoyi, et al. A brief review to integrated energy system and energy internet[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 1-13.
[2] 杨欢, 赵荣祥, 辛焕海, 等. 海岛电网发展现状与研究动态[J]. 电工技术学报, 2013, 28(11): 95-105.Yang Huan, Zhao Rongxiang, Xin Huanhai, et al.Development and research status of island power systems[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 95-105.
[3] 蔡游明,李征,蔡旭.计及控制时间窗内功率波动的风电场群无功电压分层优化控制[J]. 电工技术学报,2019, 34(6): 1240-1250.Cai Youming, Li Zheng, Cai Xu. Voltage hierarchical optimal control of a wind farm cluster in account of voltage fluctuation in control time window[J].Transactions of China Electrotechnical Society, 2019,34(6):1240-1250.
[4] Marquez R D, Ledezma O R, Noda N, et al. 230kV self-contained oil-filled cable line installed underneath a bridge located in Maracaibo,Venezuela[J]. IEEE Transactions on Power Apparatus and Systems, 1981, 100 (7): 3153-3165.
[5] 李星, 杨帆, 余晓, 等. 基于内源式电阻抗成像的接地网缺陷诊断逆问题研究[J]. 电工技术学报,2019, 34(5): 902-909.Li Xing, Yang Fan, Yu Xiao, et al. Research on the inverse problem of grounding grid fault diagnosis based on inner-source EIT[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 902-909.
[6] 孟毓, 龚尊. 东海大桥高压电缆工程设计[J]. 华东电力, 2007, 35(3): 62-65.Meng Yu, Gong Zun. Engineering designs for high voltage cable laying along Donghai Bridge[J]. East China Electric Power, 2007, 35(3): 62-65.
[7] Benato R, Carlini E M, Di Mario C, et al. Gas insulated transmission lines in railway galleries[J].IEEE Transactions on Power Delivery, 2005, 20(2):704-709.
[8] Benato R, Mario C D, Koch H. High-capability applications of long gas-insulated lines in structures[J]. IEEE Transactions on Power Delivery,2007, 22: 619-626.
[9] 高俊国, 于平澜, 李紫云, 等. 基于有限元法的电缆金属护套感应电压仿真分析[J]. 高电压技术,2014, 40(3): 714-720.Gao Junguo, Yu Pinglan, Li Ziyun, et al. Simulation analysis of induced voltage on metal sheath of power cable based on finite element method[J]. High Voltage Engineering, 2014, 40(3): 714-720.
[10] Lin Yong, Xu Zheng. Cable sheath loss reduction strategy research based on the coupled line model[J].IEEE Transactions on Power Delivery, 2015, 30(5):2303-2311.
[11] 刘英, 王磊, 曹晓珑. 双回路电缆护套环流计算及影响因素分析[J]. 高电压技术, 2007, 33(4): 143-146.Liu Ying, Wang Lei, Cao Xiaolong. Calculation of circulating current in sheaths of two-circuit arranged cables and analyses of influencing factors[J]. High Voltage Engineering, 2007, 33(4): 143-146.
[12] 杜伯学, 李忠磊, 张锴, 等. 220kV交联聚乙烯电力电缆接地电流的计算与应用[J]. 高电压技术, 2013,39(5): 1034-1039.Du Boxue, Li Zhonglei, Zhang Kai, et al. Calculation and application of 220kV crosslinked polyethylene power cable grounding current[J]. High Voltage Engineering, 2013, 39(5): 1034-1039.
[13] Itoh Y, Nagaoka N. Transient analysis of a crossbonded cable system underneath a bridge[J].IEEE Transactions on Power Delivery, 1990, 5(2):527-532.
[14] 钱洁. 电力电缆电气参数及电气特性研究[D]. 杭州: 浙江大学, 2013.
[15] Schelkunoff S A. The electromagnetic theory of coaxial transmission lines and cylindrical shields[J].Bell Labs Technical Journal, 2013, 13(4): 532-579.
[16] 徐政, 钱洁. 电缆电气参数不同计算方法及其比较[J].高电压技术, 2013, 39(3): 689-697.Xu Zheng, Qian Jie. Comparison of different methods for calculating electrical parameters of power cables[J].High Voltage Engineering, 2013, 39(3): 689-697.
[17] Paul C R. Analysis of multiconductor transmission lines[M]. New York: Wiley-IEEE Press, 1994.
[18] 赵亮, 王世山, 娄千层, 等. 基于三阈值概率分布的多导体传输线电磁参数特性[J]. 电工技术学报,2018, 33(8): 1663-1673.Zhao Liang, Wang Shishan, Lou Qianceng, et al.Characteristics of electromagnetic parameters of multiconductor transmission lines based on threethreshold probability distribution[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1663-1673.
[19] Weng Hua, Xu Zheng. Numerical harmonic modeling of long coupled transmission lines using matrix series theory and recursive approach[J]. International Journal of Numerical Modelling Electronic Networks Devices & Fields, 2013, 26(3): 225-237.
[20] 徐韬, 翁华, 徐政, 等. 高压直流输电非解耦线路模型改进算法[J]. 中国电机工程学报, 2011, 31(7):71-76.Xu Tao, Weng Hua, Xu Zheng, et al. An improved calculating method for the coupled line model of HVDC transmission[J]. Proceedings of the CSEE,2011, 31(7): 71-76.
[21] 林勇. 耦合线路电气特性分析与软件开发[D]. 杭州: 浙江大学, 2016.
[22] GB 50217—2018 电力工程电缆设计规范[S]. 北京:中国标准出版社, 2018.
[23] Gouda O E, Farag A A. Factors affecting the sheath losses in single-core underground power cables with two-points bonding method[J]. International Journal of Electrical & Computer Engineering, 2016, 2(1):2088-8708.
[24] 王雅芳. XLPE电力电缆接地系统与感应环流分析[D]. 杭州: 浙江大学, 2012.
[25] 王荣亮, 王浩鸣, 宗红宝, 等. 高压电缆金属护套接地环流平衡抑制方法分析[J]. 电力系统及其自动化学报, 2019, 31(11): 108-114.Wang Rongliang, Wang Haoming, Zong Hongbao, et al.Analysis of suppression method for grounding circular current in metal sheath of high-voltage cable[J].Proceedings of the CSU-EPSA, 2019, 31(11): 108-114.