0 引言
金属板材从完好到断裂一般经历三个过程:早期微裂纹的产生、裂纹的扩展以及板材最终的断裂[1]。对材料早期微裂纹的检测可以及时发现潜在的安全隐患,在损伤扩展前及时做出相应预防措施[2]。
非线性超声检测利用非线性系数来表征材料的损伤程度,从本质上反映了材料应力-应变的非线性[3]。但是由于实验仪器产生的非线性信号会对实验结果产生干扰,所以人们提出了混频非线性检测的方法[4-5]。非线性混频检测技术是利用两列不同频率的超声波与材料内部损伤发生的非线性调制作用进行检测[6]。当材料中不存在损伤时,接收信号中只有两个基频信号;当材料中存在损伤时,接收信号中会出现差频分量信号与和频分量信号。通过对该频率分量的相应分析可以实现对材料损伤程度的检测和评估。考虑到电磁超声换能器可以通过电磁耦合的方式激励各种类型的超声波[7],同时具有非接触性、高效性等优点[8-9],本文选用电磁超声换能器作为混合波的激励源。
国内外利用Lamb波混频非线性方法对材料中微裂纹进行定量的研究较少,大多数是进行定性的研究。D. J. Lee等[10]对Lamb波混频技术应用在板材的无损检测中的可行性进行了研究,结果表明Lamb波混频技术是一种很有潜力的检测技术。文献[11]指出,当同方向传播的A0模态Lamb波与S0模态Lamb波的频率满足一定条件时会产生一列反方向传播的A0模态Lamb波。通过控制两列波激发的延迟时间使混合波同时到达损伤区域时,接收到的波形混频调制效果最好,据此可以实现对损伤区域的定位。文献[12]研究了混合Lamb波在改变微裂纹长度、宽度等参数条件下的非线性行为,结果表明混合波对不同尺寸微裂纹的敏感性不同。文献[13]利用单向Lamb波混合的方法研究了混频非线性系数与微裂纹密度、微裂纹区域长度的关系,证明了单向Lamb波混合的方法可用于定量识别薄板中的微裂纹损伤。文献[14]通过设置两列Lamb波的延迟时间,使两列Lamb波同时到达微裂纹处,研究了混频非线性系数与微裂纹长度之间的关系。文献[15]研究了两列非共线剪切波与裂纹相互作用的关系。结果表明,产生最大振幅时两列波相互作用的角度与裂纹的取向有关。文献[16]推导了Lamb波单向混合时发生共振的条件,同时指出较短的脉冲可以提供更好的空间分辨率,适合定位并确定损坏区域的大小。文献[17]研究了两列沿相反方向传播的Lamb波在双层板中的混频响应。结果表明,使用空间扫描法可以用于评估和定位双层板中局部退化的界面。本文利用差频非线性系数与和频非线性系数定义综合系数因子,对微裂纹长度进行定量研究。
在对微裂纹的建模方面,目前的研究主要是建立在呼吸性模型的基础上[18]。但是微裂纹开合模型是将微裂纹的接触界面当作光滑界面处理,与实际情况中的微裂纹有较大差别[19]。文献[20]考虑了超声波与微裂纹之间有限程度的非线性相互作用。微裂纹是通过预加应力,并用库仑摩擦力以单边接触的形式来模拟。文献[21]基于弹簧模型,在复合材料的分层界面中使用弹簧-阻尼单元来模拟分层界面处发生的非线性行为。文献[22]利用COMSOL Multiphysics有限元软件在微裂纹引入界面力弹簧模型,建立了二维仿真模型。文献[23]提出了一个混频波与接触界面作用的分析模型,该模型的特点是界面处的法向应力、切向应力与界面上的相对法向位移、相对切向位移满足牵引定律。文献[24]基于Landau-Lifshitz公式并且考虑了材料的超弹性,利用弹簧模型的原理对材料中的疲劳裂纹进行建模。
本文综合考虑微裂纹界面呼吸作用的特点,将弹簧模型引入微裂纹中并考虑微裂纹界面的迟滞效应,使用COMSOL Multiphysics有限元软件建立了三维Lamb波混频非线性检测模型。在三维混频非线性检测模型的基础上,研究了微裂纹长度与深度对差频非线性系数、和频非线性系数的影响。最后搭建了混频激励下的非线性检测系统,提出用综合系数因子来定量分析微裂纹长度。根据实验结果拟合出了综合系数因子与微裂纹长度的关系,并利用关系曲线对微裂纹长度进行了预测,预测结果表明了该方法的可行性、有效性。
1 电磁超声Lamb波混频理论
电磁超声换能器主要由产生偏置磁场的磁铁、线圈及被测试件组成。当线圈中通入交变电流时,被测试件会受到交变电场与偏置磁场共同作用产生的洛仑兹力,在被测试件中激发出超声波。本文中选择曲折线圈,通过对曲折线圈中相邻导线间距的合理取值来满足超声波相长干涉的条件,激发出理想的电磁超声Lamb波。
在各向同性的弹性固体中的波动状态方程为
式中,u为固体内质点的位移;t为超声波传播的时间;x为声波传播的路程;c为超声波在该材料中的传播速度;β为非线性系数。
根据微扰动原理,可以得到近似波动方程为
式中,u(0)为质点线性波动的位移;u(1)为质点非线性波动的位移。将式(2)代入到式(1)中,经过整理可以得到超声波的非线性波动的方程为
当两列不同频率的超声波共同作用时,设频率ω1、频率ω2的超声波(ω 1> ω2)在固体介质中的衰减系数分别为1α和2α,忽略两列超声波的相位差,由线性波动引起的质点位移方程可表示[25]为
式中,![]() A1和A2分别为两列激励信号的幅值。结合式(2)、式(3)、式(4)并根据变动参数法,整理为
A1和A2分别为两列激励信号的幅值。结合式(2)、式(3)、式(4)并根据变动参数法,整理为
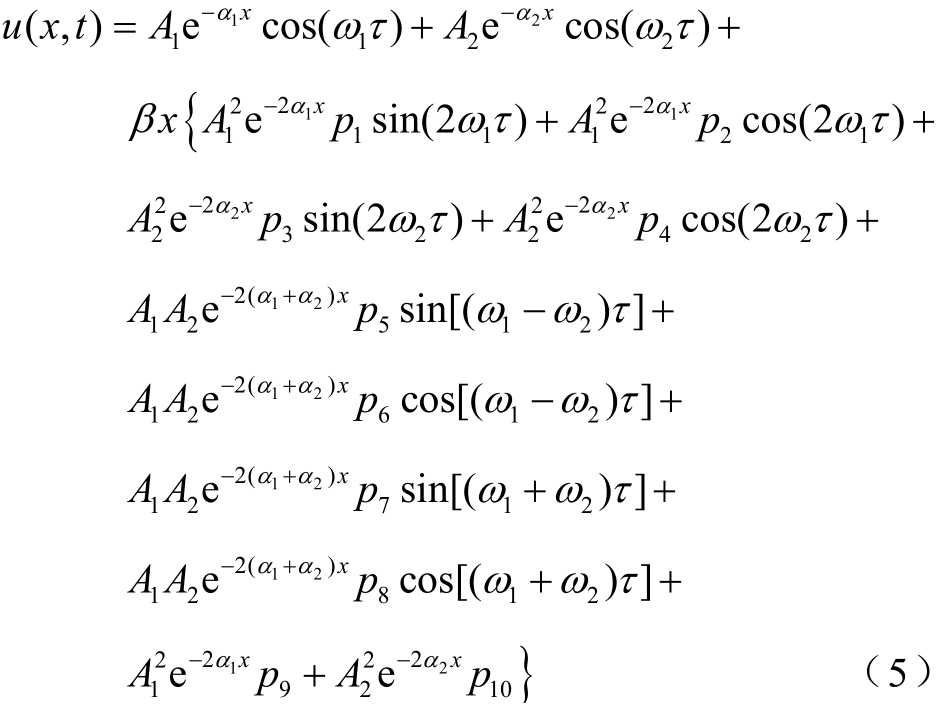
式中,pi(i=1,…,10)与波数以及衰减系数有关。
令A(ω1)、A(ω2)为两列超声波基波幅值,A (ω 1 −ω2)为差频分量幅值, A (ω 1 +ω2)为和频分量幅值,则
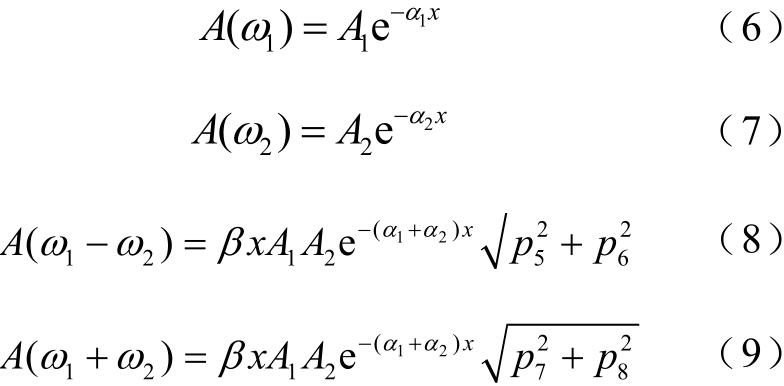
定义混频下的差频非线性系数β−与和频非线性系数β+为
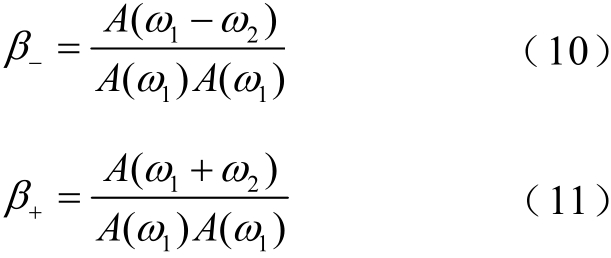
当材料中无损伤且处于理想条件下时,接收到的频域信号中差频分量与和频分量都为零。当材料中存在损伤时,混频Lamb波与损伤发生作用,使得接收到的频域信号中出现差频分量与和频分量,根据式(8)~式(11)可知,由于衰减系数的存在,不同频率的超声波衰减程度不同,差频非线性系数与和频非线性系数不相等,即差频非线性系数与和频非线性系数对材料损伤的敏感程度不同。
根据数据融合理论,定义综合系数因子为
式中,θ为综合系数因子。λ与δ之比为当微裂纹长度变化相同时,差频非线性系数的变化量与和频非线性系数的变化量的比值。比值根据多组数据的实验结果取平均值,令λ与δ之和为1。
通过综合系数因子消除差频非线性系数与和频非线性系数之间存在的冗余,加强互补性,改善提取材料损伤参数的可靠性。
2 电磁超声Lamb波混频非线性建模与分析
2.1 三维仿真模型的建立
微裂纹(如闭合裂纹、早期疲劳裂纹)存在一个相互接触的交界面。在外部应力的作用下,微裂纹存在张开与闭合两个状态。其中,微裂纹界面力与界面位移之间的关系可用弹簧模型来表示。外部应力会改变微裂纹接触面的位移,从而导致界面发生非线性效应。微裂纹界面力与弹簧力相似,其大小与界面位移成比例,但并非单纯的线性关系。微裂纹界面力F与界面相对位移 ςΔ 的关系如图1所示。在弹簧模型中引入迟滞效应与界面阻尼力,使建立的模型与实际情况更加贴近。
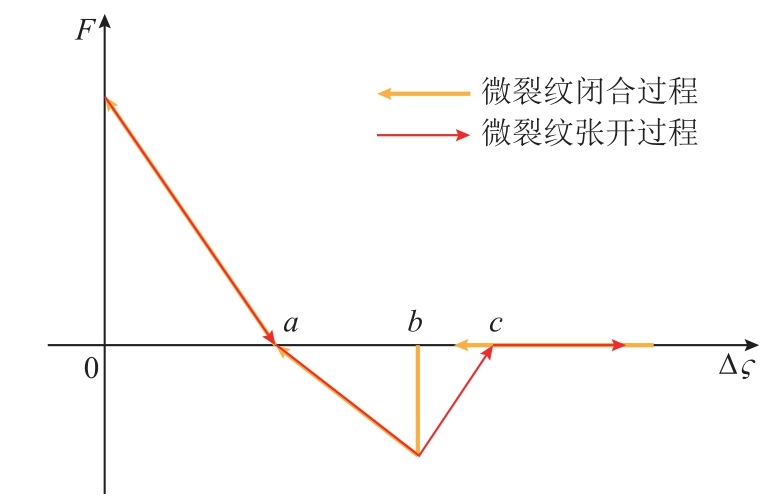
图1 界面力与界面的相对位移关系
Fig.1 The relation between interface force and relative displacement of interface
本文使用COMSOL软件进行仿真分析。以往基于弹簧模型与迟滞效应的微裂纹混频电磁超声模型,多数为二维模型。但是二维模型中,在研究微裂纹参数对混频非线性参数的影响时,由于受到二维仿真模型的限制,在模拟微裂纹发生波动开合时,微裂纹只是在深度方向上进行波动开合,不能分析微裂纹长度对混频非线性参数的影响,与实际情况存在一定的差别。为此,本文建立了含微裂纹的三维电磁超声混频模型,如图2所示。在三维模型中,利用两个矩形块间的接触面来模拟微裂纹的啮合界面,将两个矩形块的界面设置为线性拉伸。基于弹簧模型与迟滞效应,在定义模块中设置界面力函数,并在固体力学模块中调用设置好的界面力函数,引入矩形块的界面中。同时将矩形块与铝板接触的界面设置为连续接触对,使其在超声波透过时出现周期性的波动。
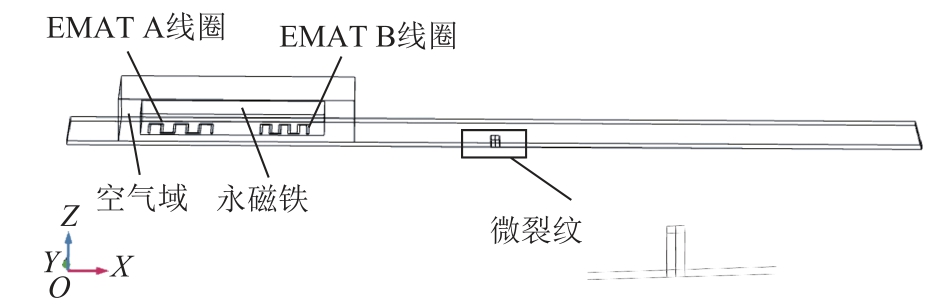
图2 含微裂纹的电磁混频仿真模型
Fig.2 Simulation model of electromagnetic mixing with micro crack
在三维模型中,铝板的尺寸设为200mm×26mm×1mm。除了铝板的上下两个端面,其余端面全部设置为低反射界面。电磁超声换能器线圈为曲折线圈,两个混频线圈相距25mm,混频线圈由两组线圈构成。导线中通入电流函数表达式为
式中,f与T分别为脉冲的中心频率与周期;N为激励电流的脉冲个数;I m为激励电流幅值,设置为25A。永磁铁磁感应强度设置为1.2T,磁场方向垂直于铝板。微裂纹距离铝板左端100mm。EMAT A线圈与微裂纹距离75mm,EMAT B与微裂纹距离50mm。接收点位于微裂纹右侧,距离微裂纹20mm。
2.2 激励频率的选择
研究厚度为1mm的含有微裂纹的铝板的非线性特征,选用Lamb波作为激励信号波,通过数值求解可以得到Lamb波的相速度和群速度随频厚积变化的关系,分别如图3和图4所示。从图3和图4中可以看出,频厚积越大,Lamb波同时存在的模态越多,且同一频厚积对应的Lamb波的模态数最少为两个。

图3 Lamb波相速度频散曲线
Fig.3 Dispersion curve of Lamb wave phase velocity
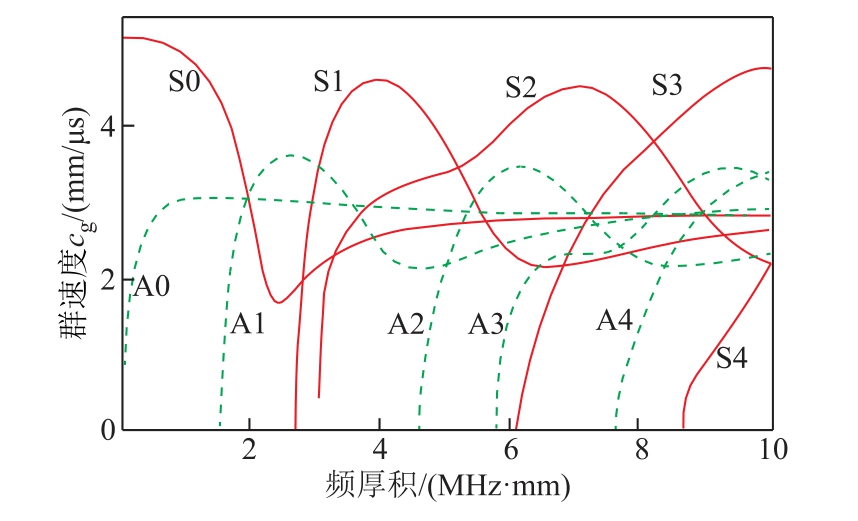
图4 Lamb波群速度频散曲线
Fig.4 Dispersion curves of Lamb wave group velocity
由于Lamb波S0与A0模态所包含的能量要高于其他模态,所以激励模态选择Lamb波的零阶模态。从图4中可以看出S0模态在低频时的群速度要高于A0模态的群速度,在接收到的时域图中容易区分,所以激发模态选择为S0模态。群速度的变化率越大,表示该模态对应的Lamb波频散性越大。从图4中可以看出当频率超过1MHz时,S0模态的Lamb波的频散性逐渐变大。结合相同模态时Lamb波的能量与频率大小相关(频率越高,Lamb波包含的能量越大),选择混频的两个激励频率为1MHz左右。最后考虑到两个激励频率的差频分量与和频分量,如果与激励频率相差过小,则在接收到的频域信号中基波分量会对差频分量与和频分量产生干扰。综合考虑,选择激励频率为0.9MHz和1.2MHz的S0模态Lamb波。EMAT B线圈中电流延迟4μs激发。
2.3 混合Lamb波的传播与微裂纹识别
为了更形象地描述微裂纹界面的波动情况,从三维仿真模型的x-y平面对铝板中微裂纹界面状态进行观察。图5为微裂纹波动状态示意图。当超声波能量未达到微裂纹处时,微裂纹界面处于闭合状态,如图5a所示。经过一定时间的传播,超声波到达微裂纹处,超声波的能量作用在微裂纹界面处,相当于给微裂纹啮合界面施加了一定的应力,导致微裂纹两接触面之间距离增大,微裂纹处于张开状态,如图5b所示。超声波完全经过微裂纹后,作用在微裂纹界面上的应力消失,微裂纹恢复闭合状态。微裂纹由闭合状态到张开状态,再到闭合状态这一过程与微裂纹在实际情况下的状态一致。
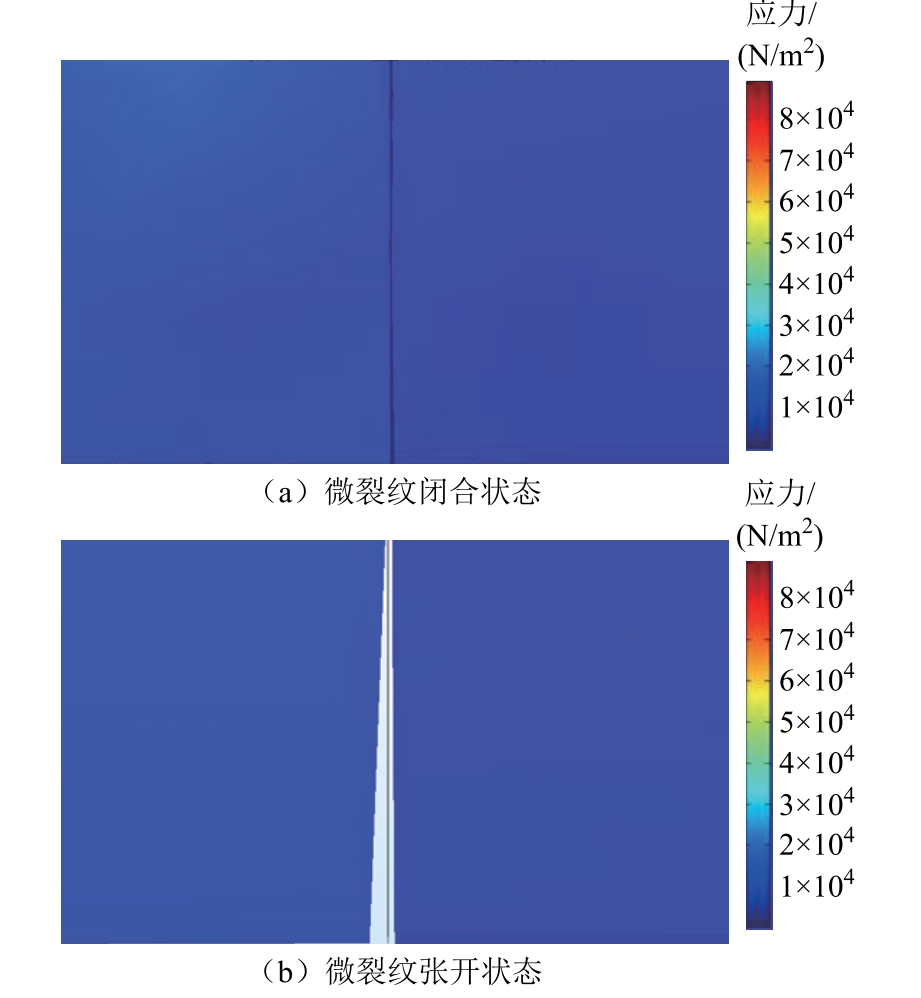
图5 微裂纹波动状态示意图
Fig.5 Schematic diagram of micro crack wave state
图6 为混合Lamb波在铝板中的位移传播情况。图6a是t=1μs 时铝板质点位移状态图。EMAT A线圈下方铝板表面质点振动明显,通过质点位移可以看出EMAT A线圈的大致轮廓。当t=5μs时,EMAT A线圈激发出的Lamb波已经到达EMAT B线圈的位置。此时EMAT B线圈中也已通入电流,开始产生Lamb波。两个线圈会激发出向左和向右两个方向传播的Lamb波。当t=13μs时,两个线圈组激发出的Lamb波同时到达微裂纹处。当t=40μs时,混合Lamb波完全通过微裂纹,部分混合Lamb波经过微裂纹发生反射,改变传播方向向左传播。由于两列Lamb波波速不同,所以穿过微裂纹后随着时间的增加逐渐分离,如图6d所示。
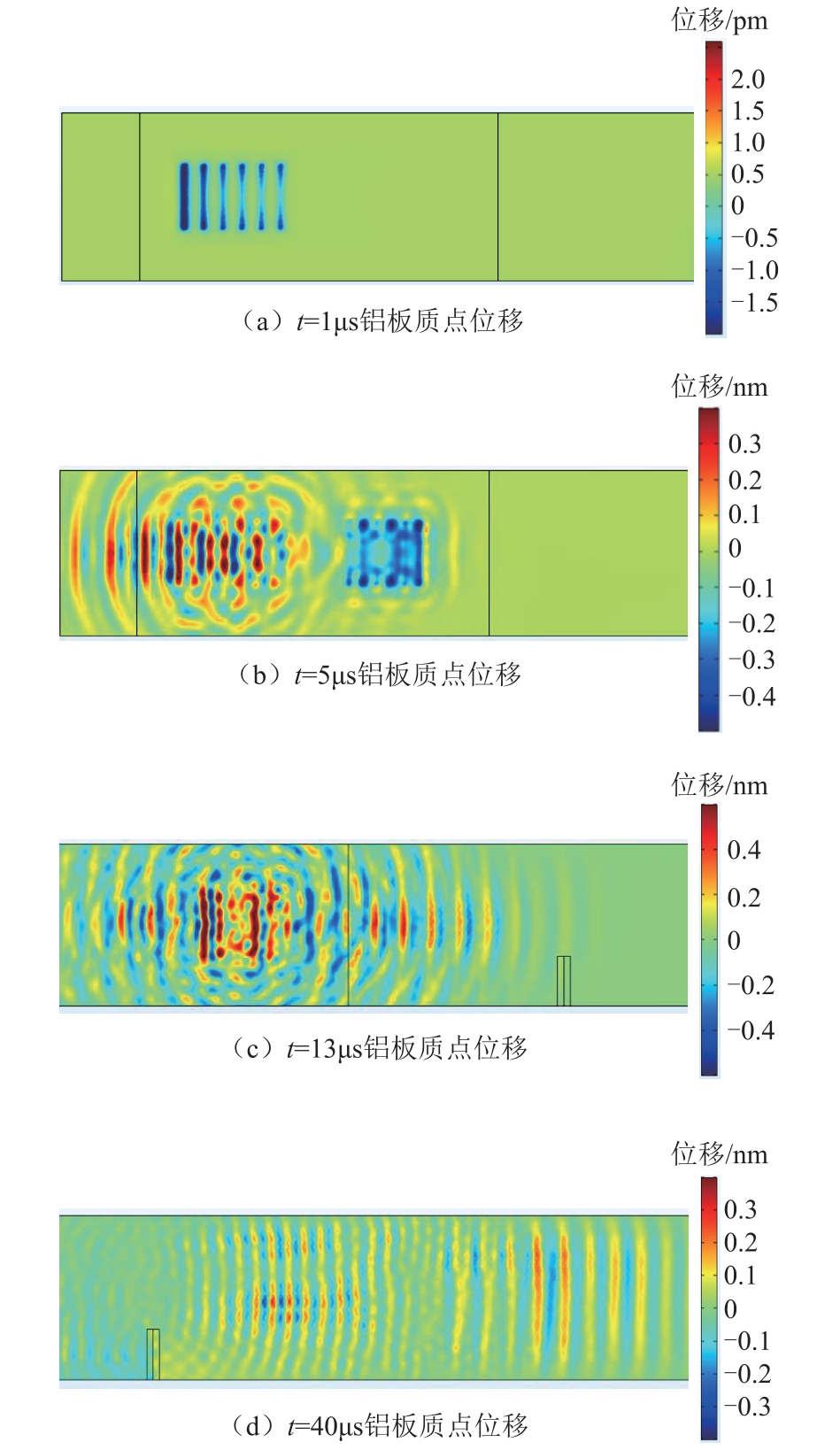
图6 铝板中混合Lamb波在不同时刻的位移传播情况
Fig.6 Displacement propagation of mixed Lamb waves in aluminum plates at different time
铝板中含有微裂纹时接收点的时域图和频域图如图7所示。由图7b可知,接收信号在频域上出现了明显的差频分量、和频分量与基波频率各自的2次谐波分量,其中差频分量的幅值明显高于和频分量的幅值。这是因为和频分量的频率高,透过微裂纹的啮合界面时衰减更大,导致幅值降低。
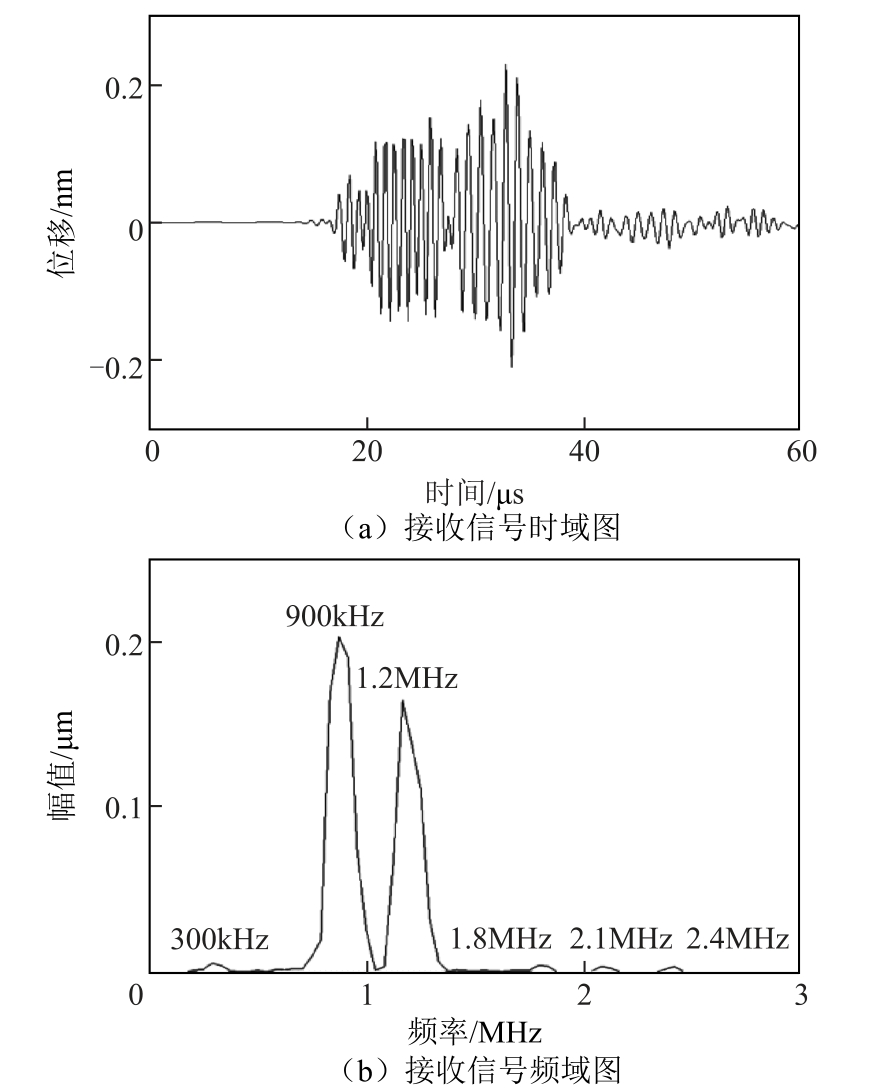
图7 含有微裂纹铝板接收点的时域图和频域图
Fig.7 Time domain and frequency domain diagrams of receiving points for aluminum plates with micro crack
图8 是完好铝板时接收信号的时域图和频域图。
由图8b可知,完好铝板接收信号的频域中没有差频分量、和频分量及高次谐波分量。
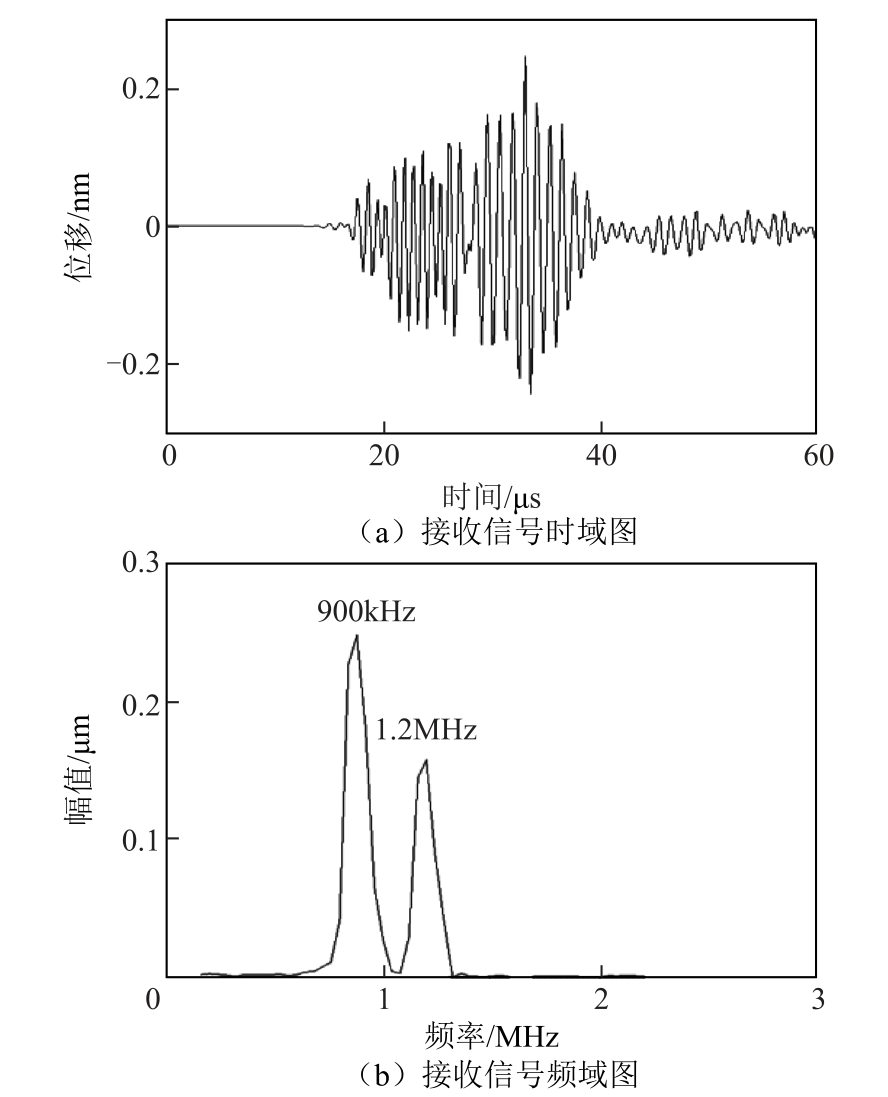
图8 完好铝板接收信号的时域图和频域图
Fig.8 Time domain diagram and frequency domain diagram of received signal of intact aluminum plate
对比图7b与图8b,图7b中由于微裂纹和两列超声波相互作用产生了非线性效应,出现了差频分量、和频分量以及高次谐波分量。这是因为当混合波穿过微裂纹时,微裂纹啮合界面受到应力作用会存在周期性的张开与闭合。微裂纹啮合界面张开时,造成介质分布不均匀,这也是产生混频非线性的根本原因。
2.4 微裂纹长度对混频调制效果的影响
在三维模型中改变微裂纹的长度,可以得到微裂纹长度与差频非线性系数、和频非线性之间的关系,如图9和图10所示。仿真模型中微裂纹长度在0~10mm之间变化。
微裂纹越长,与混合波作用的啮合界面面积越大。啮合面积的增加,一方面使得差频分量幅值与和频分量幅值增加;另一方面,使得基波幅值衰减,所以表现为非线性效应随微裂纹的增加越来越明显。图9、图10中,差频非线性系数与和频非线性系数都随着微裂纹长度的增加而增加。

图9 微裂纹长度与差频非线性系数的关系
Fig.9 Relationship between microcrack length and differential frequency nonlinear coefficient
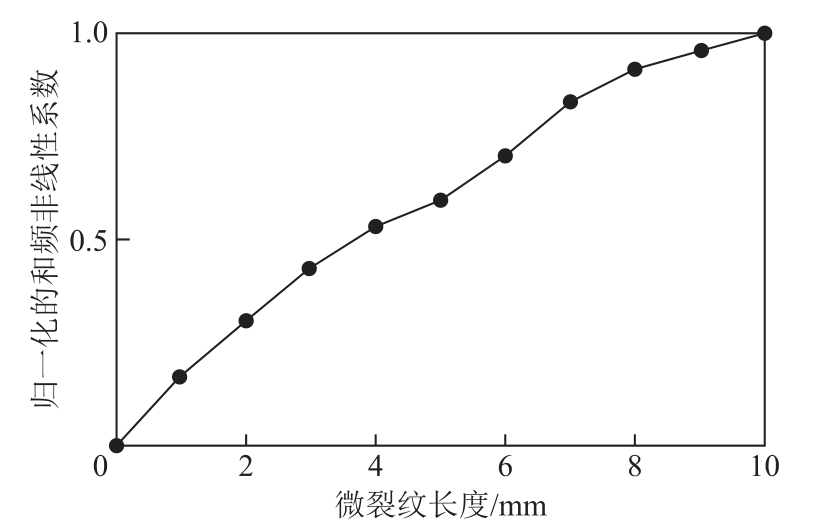
图10 微裂纹长度与和频非线性系数的关系
Fig.10 Relationship between microcrack length and sum frequency nonlinear coefficient
2.5 微裂纹深度对混频调制效果的影响
在三维模型中通过改变微裂纹的深度可以得到微裂纹深度与差频非线性系数、和频非线性之间的关系。仿真模型中微裂纹深度在0~0.8mm之间变化。
从图11与图12中可以看出,当微裂纹深度增加时,与混合波发生相互作用的微裂纹接触面面积增大,混合波的波形畸变程度增加,使得差频分量幅值与和频分量幅值增加,基波分量衰减,混频非线性系数增加。但当微裂纹深度进一步增加时,超声波能量衰减程度增大,使得差频分量幅值与和频分量幅值增加速度变缓。所以差频非线性系数与和频非线性系数呈现出单调增加且增加逐渐变缓的趋势。
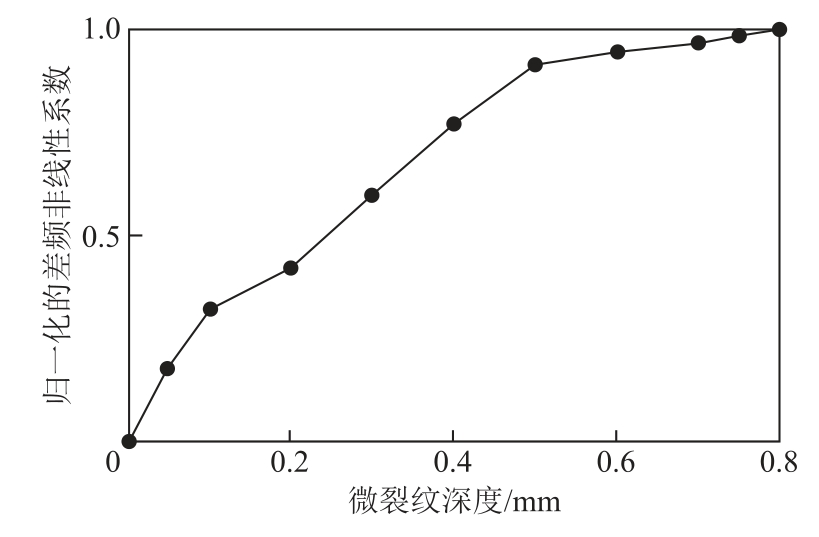
图11 微裂纹深度与差频非线性系数的关系Fig.11 Relationship between microcrack depth and differential frequency nonlinear coefficient
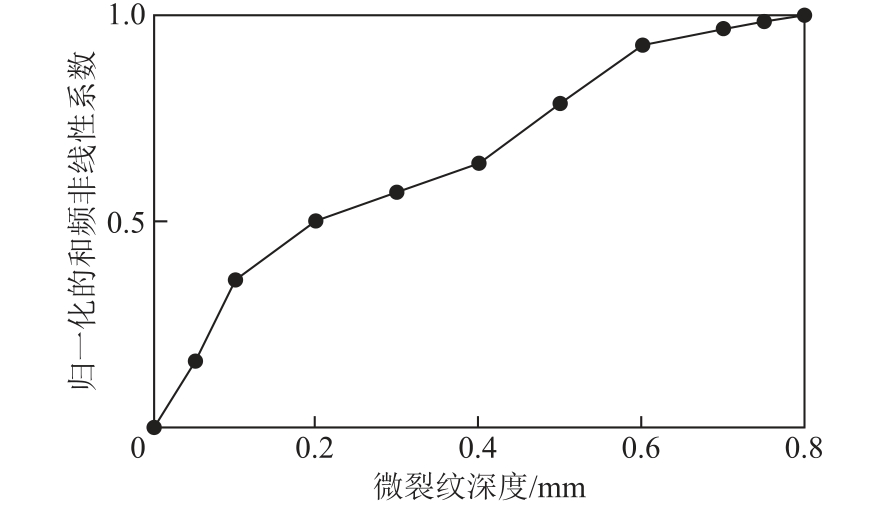
图12 微裂纹深度与和频非线性系数的关系
Fig.12 Relationship between microcrack depth and sum frequency nonlinear coefficient
3 实验结果及分析
实验试件选择铝板,使用MTS万能高频疲劳试验机对铝板进行疲劳循环加载。疲劳加载后铝板中微裂纹的局部放大图如图13所示。

图13 含有微裂纹铝板
Fig.13 Aluminum plate with micro crack
电磁超声非线性检测系统包括激励探头与接收探头、Ritec RAM-5000、前置放大器、高通滤波器与低通滤波器、阻抗匹配电路、声波信号采集系统与待测试件,如图14所示。利用Ritec RAM-5000产生两列频率不同的超声波并接收采集到的电压信号,通过接收到的电压信号对混频调制效果进行分析。
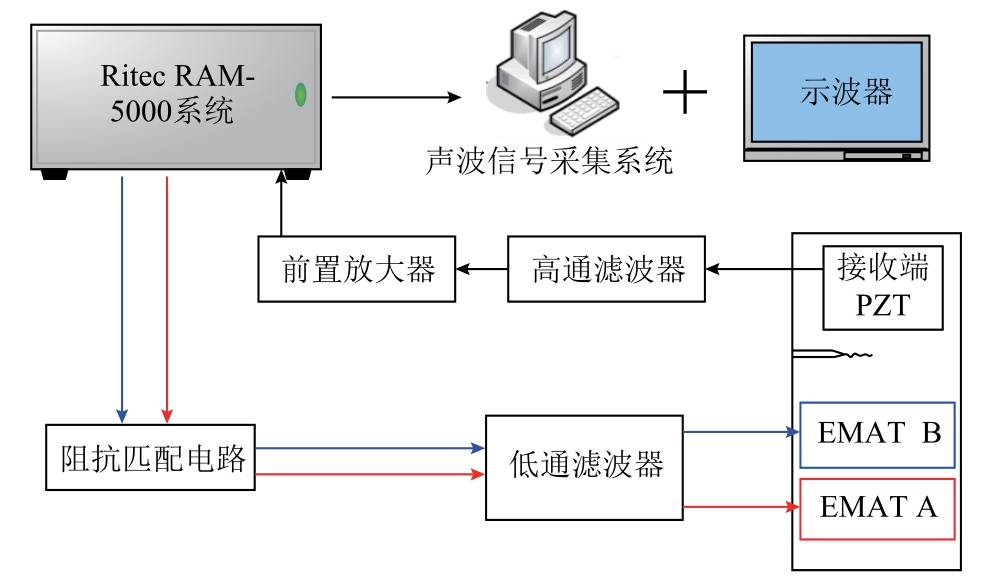
图14 混频非线性实验检测系统
Fig.14 Mixing nonlinear experimental detection system
实验中Lamb波选择S0模态,两个基波频率分别为0.9MHz与1.2MHz,偏置磁场剩磁为1.2T。将混频激励探头放置于铝板左侧。压电接收探头放置于微裂纹右侧,与微裂纹相距20mm。通过控制通入两个线圈中电流的延时使得两列Lamb波同时到达微裂纹。图15为完好铝板的频域信号图,图16为含有微裂纹的频域信号图。对比图15与图16可以看出,当铝板中含有微裂纹时,频域信号中出现了明显的差频分量、和频分量。
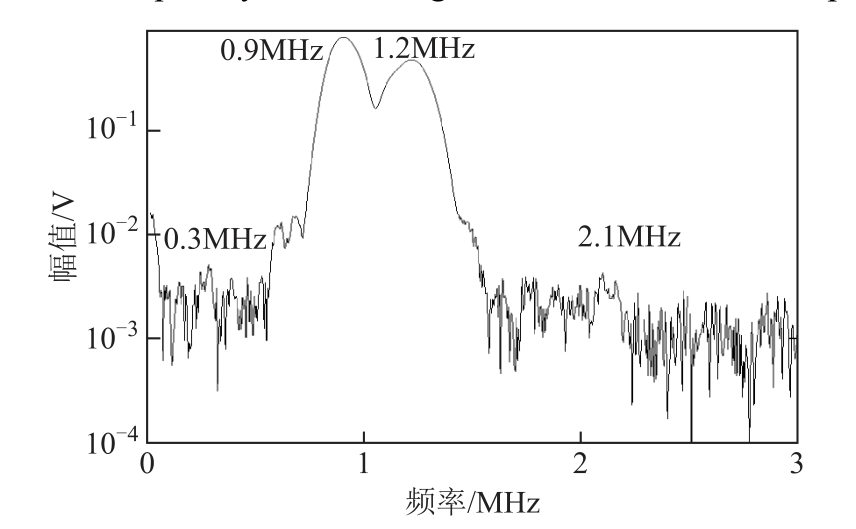
图15 完好铝板的频域信号
Fig.15 Frequency domain signal of intact aluminum plate
利用混频超声非线性检测方法对含有微裂纹的铝板进行检测,得到差频非线性系数、和频非线性系数与微裂纹长度的关系,如图17和图18所示。
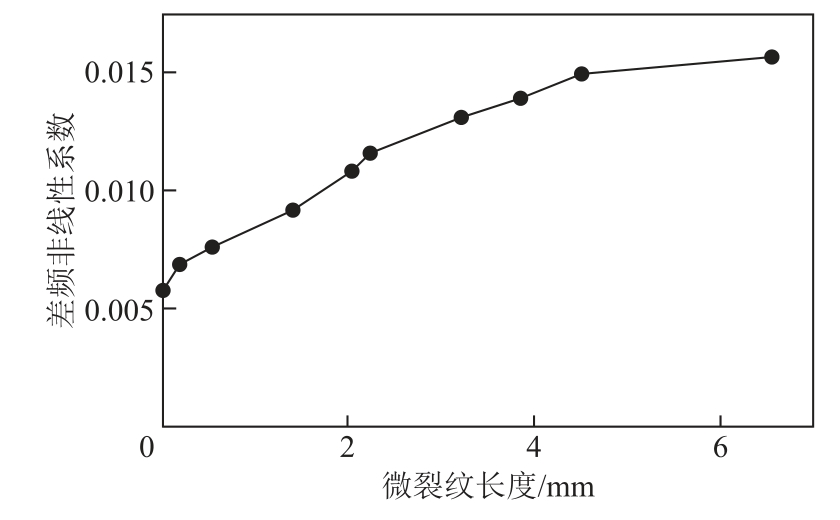
图17 微裂纹长度与差频非线性系数的关系Fig.17 Relationship between microcrack length and differential frequency nonlinear coefficient
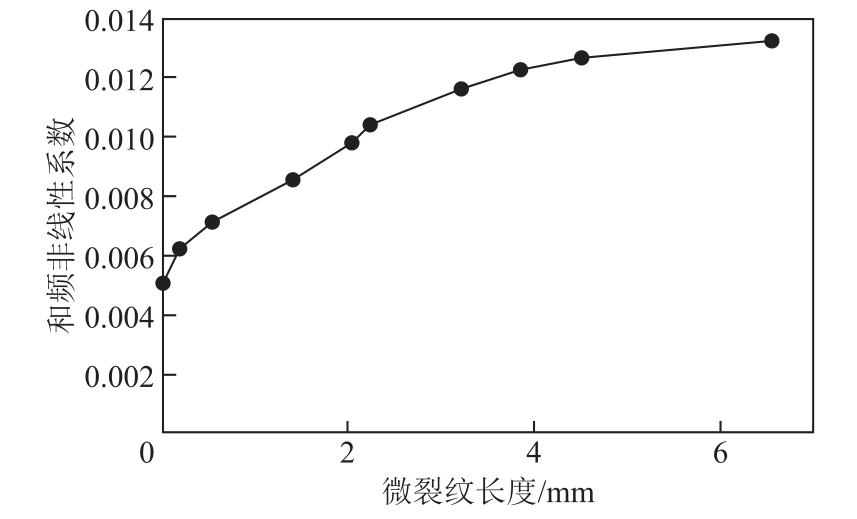
图18 微裂纹长度与和频非线性系数的关系
Fig.18 Relationship between microcrack length and sum frequency nonlinear coefficient
从图17和图18中可以看出,差频非线性系数与和频非线性系数都随着微裂纹长度的增加而增加,当微裂纹长度超过4mm时,差频非线性系数与和频非线性系数增加的速度明显放缓。仿真结果与实验结果中混频非线性系数变化的趋势一致,但不同的是实验结果中和频非线性系数与差频非线性系数的增加速度随微裂纹长度的增加而变缓。这主要是因为试件中的微裂纹是曲折的,而仿真中建立的微裂纹形状是规则的。在仿真中考虑的是微裂纹在理想状态下进行的呼吸作用,但是在试件中微裂纹的呼吸作用会受其他因素的影响。当试件中微裂纹长度超过4mm时,微裂纹接触面间的距离会逐渐变大,抑制了差频分量与和频分量的增加,使得混频非线性系数逐渐放缓。
根据综合系数因子的定义,可以得到微裂纹长度变化相同时差频非线性系数与和频非线性系数的变化量之比,取多组实验结果的平均值。最终,λ取为0.524,δ取为0.476,代入到式(12)中,可得综合系数因子表达式为
将通过实验得到的微裂纹长度与综合系数因子的关系绘于图19中,并拟合出它们之间的关系曲线为
式中,d为微裂纹长度(mm);θ为综合系数因子。由图19可得,在微裂纹较小时,随着微裂纹长度的增加,综合系数因子与微裂纹长度近似呈线性的关系。当微裂纹长度增加到一定程度后,差频非线性系数与和频非线性系数的增长速度逐渐变缓,对应到综合系数因子与微裂纹长度的关系中表现为拟合曲线斜率逐渐变大。

图19 微裂纹长度与综合因子的关系
Fig.19 Relationship between microcrack length and comprehensive factor
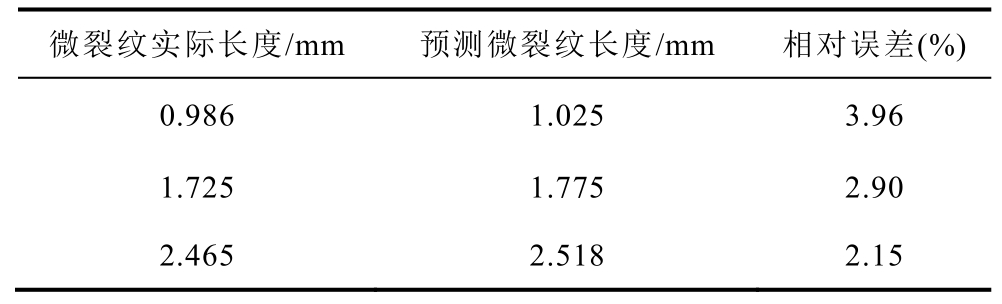
依据综合系数因子可以对微裂纹长度进行预测,预测结果见表1。
表1 综合系数因子对微裂纹长度的预测结果
Tab.1 Prediction results of comprehensive coefficient factor on microcrack length
?
由表1可以看出,根据综合系数因子预测出微裂纹长度的相对误差在5%以下,当微裂纹长度较大时,相对误差较小。当微裂纹长度较小时,测量得出的差频分量幅值与和频分量幅值易受杂波干扰,所以根据拟合曲线计算得到的微裂纹长度误差相对较大。实验结果表明通过定义综合系数因子来量化分析微裂纹长度是一种有效的方法。
4 结论
本文建立了三维Lamb波混频非线性检测模型,将微裂纹的迟滞效应引入到弹簧模型中,分析了混频超声波的传播状态,微裂纹啮合界面的波动状态与实际情况相符。通过三维模型的仿真分析,研究了微裂纹长度和深度的变化对混频调制效果的影响,并且根据差频非线性与和频非线性系数对微裂纹长度敏感性的不同定义了综合系数因子,量化分析微裂纹长度。得到的主要结论:
1)当铝板中含有微裂纹时,接收到的信号中会产生差频分量与和频分量,通过边频分量可以判断铝板的损伤程度。
2)当微裂纹长度增加时,差频非线性系数与和频非线性系数都会增加。当微裂纹深度增加时,差频非线性系数与和频非线性系数会随着微裂纹深度的增加而增加。
3)根据差频非线性系数与和频非线性系数对微裂纹长度的敏感性不同定义综合系数因子,拟合出裂纹长度与综合系数因子的关系曲线,利用关系曲线可以有效对微裂纹长度进行量化分析。实验结果表明利用综合系数因子对微裂纹长度进行预测是一种有效的方法。
[1] 刘素贞, 田钰霖, 张闯, 等. 铝合金拉伸塑性变形的非线性电磁超声检测[J]. 电工技术学报, 2020,35(15): 3153-3160.Liu Suzhen, Tian Yulin, Zhang Chuang, et al.Nonlinear electromagnetic acoustic detection of aluminum alloys with tensile plastic deformation[J].Transactions of China Electrotechnical Society , 2020,35(15): 3153-3160.
[2] 张闯, 曹晓琳, 刘素贞, 等. 基于累积效应的铝材塑性损伤电磁超声非线性检测[J]. 电工技术学报,2019, 34(19): 3961-3967.Zhang Chuang, Cao Xiaolin, Liu Suzhen, et al.Electromagnetic ultrasonic nonlinear detection of aluminum with plastic damage based on cumulative effect[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3961-3967.
[3] 门平, 董世运, 康学良, 等. 材料早期损伤的非线性超声诊断[J]. 仪器仪表学报, 2017, 38(5): 1101-1118.Men Ping, Dong Shiyun, Kang Xueliang, et al.Material early damage diagnosis with nonlinear ultrasound[J]. Chinese Journal of Scientific Instrument, 2017, 38(5): 1101-1118.
[4] 焦敬品, 樊仲祥, 吴斌, 等. 结构微裂纹混频非线性超声检测方法研究[J]. 声学学报, 2013, 38(6):648-656.Jiao Jingpin, Fan Zhongxiang, Wu Bin, et al. A frequency-mixing nonlinear ultrasonic technique for micro-crack detection[J]. Acta Acustica, 2013, 38(6):648-656.
[5] Cliff J Lissenden, Liu Yang, Vamshi K Chillara, et al.Nonlinear guided wave mixing for localized material state characterization[J]. Physics Proceda, 2015, 70:668-671.
[6] 苑博, 税国双, 汪越胜. 非线性超声混频检测技术在无损检测中的研究进展[J]. 机械工程学报, 2019,55(16): 33-46.Yuan Bo, Shui Guoshuang, Wang Yuesheng.Advances in research of nonlinear ultrasonic wave mixing detection technology in non-destructive evaluation[J]. Journal of Mechanical Engineering,2019, 55(16): 33-46.
[7] 刘素贞, 王淑娟, 张闯, 等. 钢板电磁超声表面波的仿真分析及缺陷定量检测[J]. 电工技术学报,2020, 35(1): 97-105.Liu Suzhen, Wang Shujuan, Zhang Chuang, et al.Simulation analysis of electromagnetic acoustic surface wave of steel plate and quantitative defect detection[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 97-105.
[8] 孙文秀, 刘国强, 夏慧, 等. 非铁磁材料的电磁超声接收过程数值模拟及实验研究[J]. 电工技术学报, 2018, 33(19): 4443-4449.Sun Wenxiu, Liu Guoqiang, Xia Hui, et al. Numerical simulation and experimental study of electromagnetic acoustic transducer receiving process in nonferromagnetic materials[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4443-4449.
[9] 金亮, 寇晓斐, 郭富坤, 等. 基于电磁超声换能器的铁磁材料电磁声发射检测方法[J]. 电工技术学报, 2017, 32(18): 98-105.Jin Liang, Kou Xiaofei, Guo Fukun, et al.Electromagnetic acoustic emission detection method of ferromagnetic materials based on EMAT[J].Transactions of China Electrotechnical Society, 2017,32(18): 98-105.
[10] Lee D J, Cho Y, Li Weibin.A feasibility study for lamb wave mixing nonlinear technique[C]//AIP Conference Proceedings, 2014, 1581(1): 662-666.
[11] Li Feilong, Zhao Youxuan, Cao Peng, et al. Mixing of ultrasonic Lamb waves in thin plates with quadratic nonlinearity [J]. Ultrasonics, 2018, 87: 33-43.
[12] Zhu Weiguang, Li Yifeng, Guan Liqiang, et al. Microcrack detection of nonlinear Lamb wave propagation in three-dimensional plates with mixed-frequency excitation[J]. Chinese Physics B, 2020, 29(1): 014302.
[13] Ding Xiangyan, Zhao Youxuan, Deng Mingxi, et al.One-way Lamb mixing method in thin plates with randomly distributed micro-cracks[J]. International Journal of Mechanical Sciences, 2020, 171: 105371.
[14] 刘素贞, 权泽, 张闯, 等. 疲劳裂纹的电磁超声混频非线性检测[J]. 中国电机工程学报, 2020, 40(5):1694-1703.Liu Suzhen, Quan Ze, Zhang Chuang, et al. Nonlinear detection of fatigue cracks by electromagnetic ultrasonic mixing[J]. Proceedings of the CSEE, 2020,40(5): 1694-1703.
[15] Lü Hongtao, Zhang Jie, Jiao Jingpin, et al. Fatigue crack inspection and characterization using noncollinear shear wave mixing[J]. Smart Materials and Structures, 2020, 29(5): 055024.
[16] Sun Maoxun, Qu Jianmin. Analytical and numerical investigations of one-way mixing of Lamb waves in a thin plate[J]. Ultrasonics, 2020, 108: 106180.
[17] Chen Han, Gao Guangjian, Hu Ning, et al. Modeling and simulation of frequency mixing response of two counterpropagating Lamb waves in a two-layered plate[J]. Ultrasonics, 2020, 104: 106109.
[18] 王芝, 吴维亮, 肖黎, 等. 闭合疲劳裂纹的亚谐波损伤识别方法[J]. 振动工程学报, 2015, 28(4): 567-573.Wang zhi, Wu Weiliang, Xiao Li, et al. Sub harmonic damage identification method for closed fatigue crack[J]. Journal of Vibration Engineering, 2015,28(4): 567-573.
[19] 郑慧峰, 凌田昊, 呼刘晨, 等. 振动声调制技术下微裂纹的非线性响应分析[J]. 声学学报, 2020,45(4): 571-577.Zheng Huifeng, Ling Tianhao, Hu Liuchen, et al.Nonlinear response analysis of microcracks under vibro acoustic modulation[J]. Acta Acustica, 2020,45(4): 571-577.
[20] Blanloeuil P, Meziane A, Bacon C. Numerical study of nonlinear interaction between a crack and elastic waves under an oblique incidence[J]. Wave Motion,2014, 51(3): 425-437.
[21] Steven Delrue, Koen Van Den Abeele. Threedimensional finite element simulation of closed delaminations in composite materials[J]. Ultrasonics,2012, 52(2): 315-324.
[22] 张闯, 周希运, 刘素贞, 等. 电磁加载下金属板闭合裂纹的超声调制实验研究[J]. 中国电机工程学报, 2019, 39(4): 1224-1230.Zhang Chuang, Zhou Xiyun, Liu Suzhen, et al.Experimental study on ultrasonic modulation of closed cracks in metal plates under electromagnetic loading[J]. Proceedings of the CSEE, 2019, 39(4): 1224-1230.
[23] Francis Rose L R, Blanloeuil P, Veidt M, et al.Analytical and numerical modelling of non-collinear wave mixing at a contact interface[J]. Journal of Sound and Vibration, 2020, 468: 115078.
[24] Rafal Radecki, Su Zhongqing, Cheng Li, et al.Modelling nonlinearity of guided ultrasonic waves in fatigued materials using a nonlinear local interaction simulation approach and a spring model[J].Ultrasonics, 2018, 84: 272-289.
[25] 胡海峰. 板状金属结构健康检测的非线性超声理论与关键技术研究[D]. 长沙: 国防科学技术大学, 2011.