0 引言
作为电力系统中的核心设备,变压器在整个电力系统运行中扮演着电压转换与电能传递的角色,其运行状况的好坏直接影响了整个电网的安全稳定[1-3]。随着我国电力行业的飞速发展,电力系统容量不断增加、电网规模不断扩大,对变压器提出了越来越高的要求[4]。但实际运行时变压器面临着复杂的运行环境,因变压器故障而引起的电网事故时有发生[5]。国家电网公司提出的“三杜绝、三防范”中就包含要“杜绝重特大设备事故”,作为电力系统中故障频发的设备之一,变压器一直是电力部门防范的重点区域。因此,及时掌握变压器的运行状况,防止其发生事故显得十分必要[6-7]。
变压器的故障类型主要有电热故障、绝缘故障、机械故障等,研究人员对此提出了多种故障判断方法。电热故障的出现通常伴随着气体,研究人员基于电热故障类型与变压器油中溶解气体成分的联系,提出了特征气体法、罗杰斯比值法、改良三比值法等。绝缘故障的产生多数与局部放电有关,基于对检测局部放电信号的分析,研究人员提出了超声波、超高频、脉冲电流法等方法[8-10]。机械故障大多数是铁心、绕组的松动、变形,研究人员基于机械故障时出现的变压器电容电感参数分布变化提出了低压脉冲法、短路阻抗法、频率响应分析法等方法[11]。目前针对电热故障的诊断已经有了较为全面可靠的在线与离线检测技术,而对于机械故障的检测目前仍只有离线检测较为可行[12]。基于振动信号的变压器故障诊断技术具有在线检测、与被测试变压器无电气连接、操作简单等优点,因此可以很好地弥补现有变压器故障检测技术的不足[13-14]。
对于变压器振动信号的相关研究开始于20世纪80年代。20世纪90年代中后期,国外的研究人员提出利用振动分析法分析变压器表面的振动信号[15-16]。B. Garcia、J. C. Burgos、C. Belén等初步研究了振动信号在变压器内传播时的变化,并发现了绕组、铁心100Hz的基频振幅与电流、电压二次方的关系[17-18]。国内在这方面的研究起步较晚,但目前成果较多。主要集中在变压器振动机理研究与故障诊断技术上[19-20]。如:吴晓文等提出了用于特高压交流变电站的振动噪声分离方法[21-22];汲胜昌等通过试验研究了变压器绕组和铁心共同作用时的振动传播特性[23];潘超等分析在直流影响下绕组异常电流和铁心振动加速度的变化特性[24];张鹏宁等在实验与仿真下对比研究了并联电抗器与变压器模型铁心的振动特性等[25]。
总的来说,目前基于变压器振动信号的机械故障诊断技术已有一定研究成果,但距离实际应用仍有较大距离。主要原因有:①对于变压器振动机理的研究常常局限于一台样机,所得结论规律没有普适性,无法推广;②在进行诊断时,特征量提取往往数目众多,导致进行故障诊断时步骤麻烦,程序繁琐;③测量得到的振动信号包含来自自身及外部环境的干扰,大多数诊断方法仅考虑了来自自身的低频干扰,忽视了高频干扰对故障诊断结果的影响。
针对第②点与③点,本文提出了一种基于点对称变换(Symmetrized Dot Pattern,SDP)和图像匹配的变压器机械故障诊断技术,该方法是在剔除了高频干扰的振动信号基础上进行诊断,具有步骤少、准确率高、不需要选取多个特征量等优点。先利用集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)对所得振动信号进行分解、重构,剔除来自自身及外界的高频干扰,在此基础上通过SDP将各类已知故障与未知故障振动信号变换为SDP图像,并在每类已知故障中选择部分图像,利用聚类方法提取共同特征获得典型故障模板,比较未知故障SDP图像与各典型故障模板SDP图像的相似度,通过最佳匹配完成变压器机械故障的诊断。
1 SDP与图像相似度提取
作为描述时间序列信号幅值与频率变化的方法之一,SDP变换是一种笛卡尔坐标系到极坐标系上的映射。20世纪90年代,SDP变换最初被提出是用于语音的视觉表征,之后被重新设计使用在风机故障检测上,其优势是通过简单算法实现了将信号从包含幅值、频率的一维时域复杂波形转换为简单易懂的二维极坐标对称图案[26]。
1.1 SDP的数学框架
时域信号上的每个点在SDP变换后会被分配一个角向量和两个径向量,用于生成极坐标下的图像。时域信号在经过SDP变换后一般会得到一条或一簇封闭曲线,不同时域信号变换后差异很大[27]。所得图像通常会被重复数次以覆盖整个极坐标区域,但重复次数不应过多以免形成重叠而丧失特征,时域信号的SDP变换为

式中,xi为时域信号上第i个点处的幅值;xmax、xmin分别为时域信号上最大、最小值;χ为滞后系数;θ为每部分图像的参考起始角度;ξ 为开合增益;ri为第i个点在极坐标上的半径;αi为开合角度的一半;βi、γi分别为第i个点变换后的上、下两个角度。某信号SDP变换前后如图1所示。

图1 某时域信号的SDP变换
Fig.1 SDP transform of a certain time domain signal
1.2 SDP的参数化
SDP变换过程中引入了滞后系数χ、角度开合增益ξ及起始角度θ三个参数,其决定了变换后图像的拓扑结构,影响着SDP图像的指纹特征。因此,研究其对SDP图像的影响有助于找寻较优参数值,以更好地实现变压器的机械故障诊断。
关于滞后系数、角度开合增益的选取,相关文献较少且大都集中在旋转机械领域,尚无程序化的选取方法,只能通过实际经验获得。起始角度一般取90°,具体要在选取滞后系数、角度开合增益之后再进行选取,其原则是尽量使SDP图像铺满极坐标且相邻旋臂不出现重叠。
对于fs采集频率下f频率的时域信号,其每周期内采集点数为T= fs/ f,因此滞后系数对SDP图像的影响呈现周期性变化,周期为T。当信号包含多个分量时,其变化周期为多个分量周期的最小公倍数。考虑到变压器振动信号特征,以采样频率25.6kHz、周期100Hz正弦信号为例,此时变化周期为256。起始角度为0°,开合增益为45时一个周期内SDP图像随滞后系数变化如图2和图3所示。
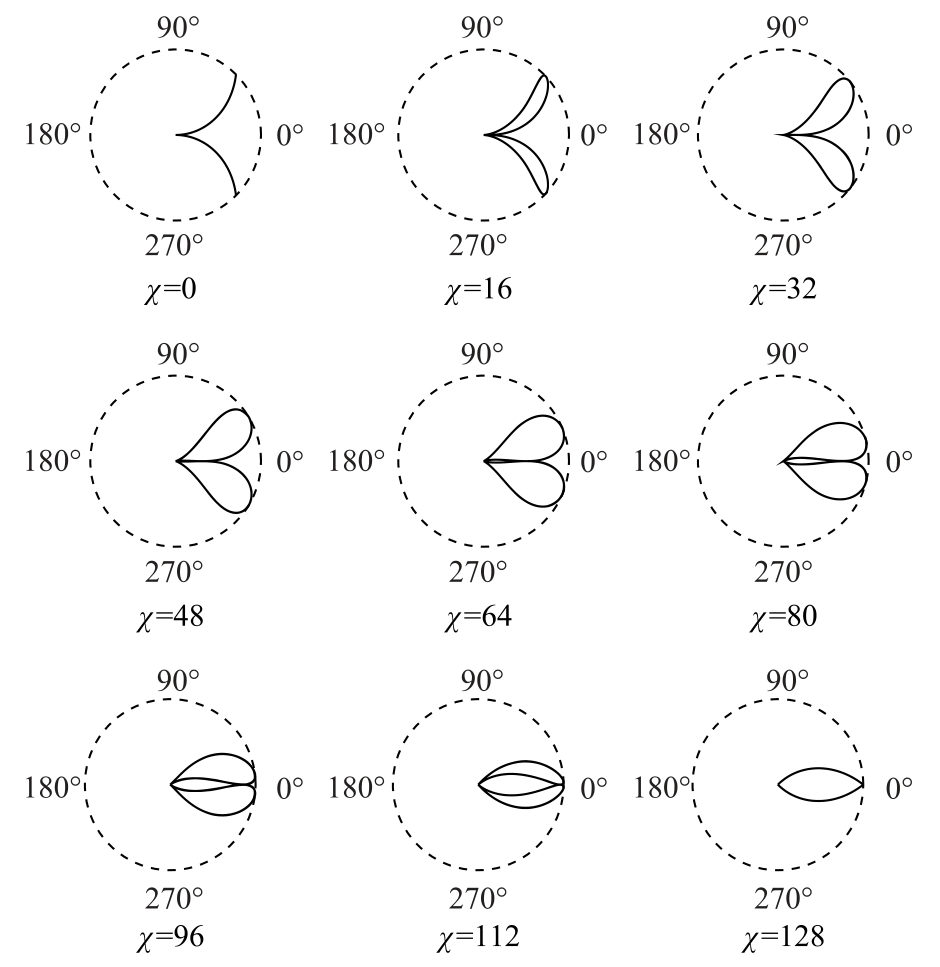
图2 上半周期内不同χ时的SDP图像
Fig.2 SDP image changes at different χ in the first half cycle

图3 下半周期内不同χ时的SDP图像
Fig.3 SDP image changes at different χ in the second half cycle
显然一个周期内滞后系数χ 对SDP图像的拓扑结构影响巨大,具体表现为:
1)上半周期:χ为0时,时域波形上的点经变换后都落在一条弧线上。随着滞后系数增大,两个旋臂由细长叶状逐渐变为水滴状,其与极坐标边界的两个连接点逐渐向起始角度方向开始聚拢;两个旋臂的边际逐渐舒展,宽度变宽,面积由0逐渐开始增大。随着旋臂与极坐标边界的两个连接点的不断移动,旋臂在达到最大宽度后开始变窄,旋臂面积增至最大后开始减小,旋臂形状由水滴状变为细长叶状。当旋臂与边界的两个连接点到达起始角度位置时,两条旋臂变为弧线并组成了瓣状图形,此时图像面积不为0。
2)下半周期:随着滞后系数增大,两个旋臂逐渐变为细长条状直至水滴状,旋臂与极坐标边界的两个连接点逐渐远离起始角度;旋臂边际逐渐舒展,宽度变宽,单个旋臂面积由0开始逐渐增大。随着旋臂与极坐标边界的两个连接点的移动,旋臂在达到最大宽度后开始变窄,旋臂面积增至最大后开始减小,旋臂形状开始由水滴状逐渐变为细长叶状。当旋臂与极坐标边界的两个连接点到达最远处时,两条旋臂重新变为弧线,此时图像面积变为0。
一个周期内SDP图像随滞后系数变化表明了随着滞后系数的增大旋臂面积先增加后减小再增大最后减小至0。为使诊断获得较好效果,在此选择SDP图像面积较大时的滞后系数为本次SDP变换的参数。对于变压器振动信号,其频谱分布一般在1 000Hz以内且各分量主要为100Hz及其倍频,因此振动信号滞后系数的选择范围缩小到半个周期即0~128之间。通过对不同SDP图像进行比较,最终选择了较优值χ=30。
仍以采样频率fs=25.6kHz、周期f=100Hz正弦信号为例,起始角度为0°,滞后系数为64时SDP图像随开合增益变化如图4所示。

图4 开合增益变化下的SDP图像
Fig.4 SDP image changes with opening and closing gain
开合角度增益对SDP图像的拓扑结构影响较大,这是由于其决定了SDP图像两条旋臂的面积。ξ 过小时各旋臂面积较小,不利于进行图像特征提取;ξ 过大时会使各旋臂间发生重叠而丧失信号特征。在此选择ξ=40,可以在变换后较好地体现信号特征并保证起始角度不同时各旋臂间不发生重叠。
1.3 SDP变换的性能分析
信号采集时的影响因素主要是采样频率、采样时间。采样频率会改变滞后系数的周期发生变化从而使得SDP图像发生变化,但在选择SDP参数时已考虑了其影响。以100Hz正弦信号为例,图5所示为不同采样时间下的SDP图像,显然采样时间的变化对SDP图案影响可忽略不计。

图5 不同采样时间下的SDP图像
Fig.5 SDP images at different sampling times
以100~10 000Hz正弦信号为例,测试了SDP变换的性能。结果表明随着正弦信号频率增大,变换后的SDP图案逐渐模糊,旋臂曲率逐渐增大,同时发现信号中低频分量占优时旋臂曲率较小。
1.4 SDP图像的相似度提取
SDP将时域信号变换为极坐标下的旋转对称图像,对所得图像进行灰度化、二值化处理后得到二值矩阵,通过比较矩阵相似度来实现故障诊断。
灰度化是将图像划分为若干个小区域,每个区域被视为一个像素。图案灰度化后会获得一个灰度化矩阵,具体转换为
式中,H为该图案灰度化后的矩阵;M、N为H矩阵的行数与列数;hnm为第n行第m列像素的灰度值,其数值范围在0~255之间。
转换后的灰度化矩阵通过设置阈值将其转换为仅包含0、1的二值矩阵,其中0表示背景像素,1表示图案像素,见式(3)。式(4)是转换后的二值矩阵,这里阈值的选择基于大津算法(OTSU)来实现。
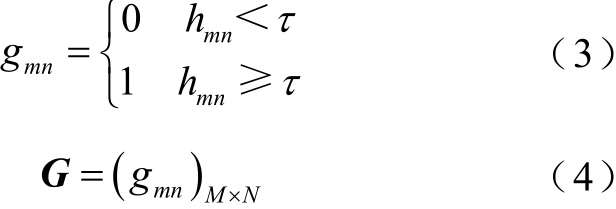
式中,τ 为二值化阈值,由大津算法计算得到;gmn为hnm二值化后的值(仅包含0、1);G为二值化后的二值矩阵。
大津算法的思想是根据灰度特性将整个图案分为图形与背景两个部分。当目标与背景间的类间差越大时将图案分割为背景与图形的正确率越高,因此通过计算每个灰度值内的类间方差,取最大的类间方差值为阈值。
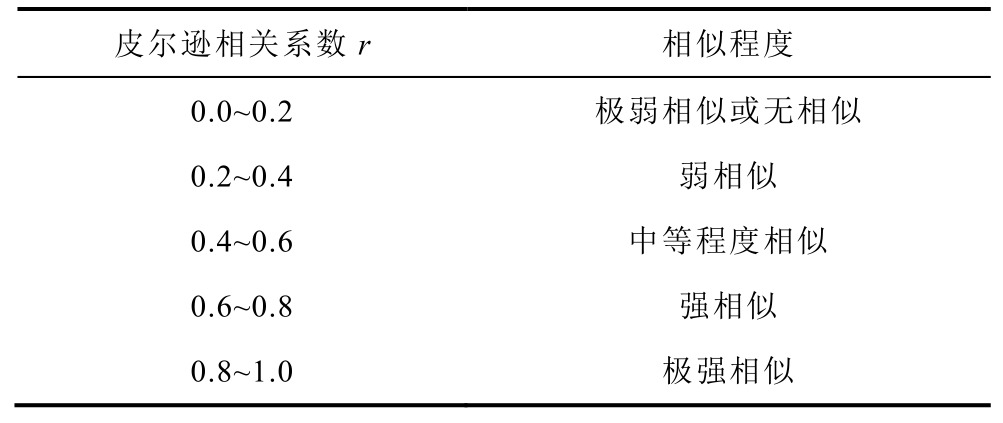
获得SDP的二值矩阵后,通过比较未知故障信号的二值矩阵与各已知故障的二值矩阵的相似程度来完成变压器机械故障的诊断。这里引入皮尔逊相关系数r来衡量两个矩阵间的相似程度,其取值的绝对值在0~1之间,数值越大表明两者相似程度越高,具体见式(5),皮尔逊相关系数r与相似程度的关系见表1。
表1 皮尔逊相关系数r与相似程度的关系Tab.1 The relationship between Pearson's correlation coefficient r and the degree of similarity
?
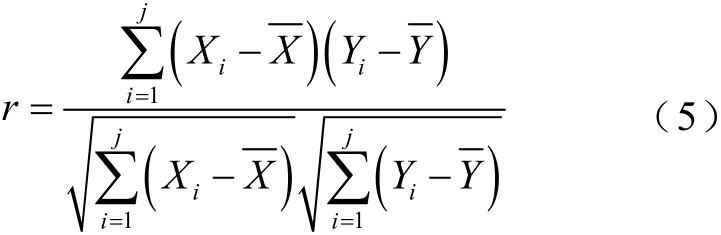
式中,![]() 分别为X、Y的样本均值;Xi为变量X在i点的观测值;Yi为变量Y在i点的观测值;j为样本总数。
分别为X、Y的样本均值;Xi为变量X在i点的观测值;Yi为变量Y在i点的观测值;j为样本总数。
2 变压器振动信号采集平台搭建与机械故障模拟设置
2.1 变压器振动信号采集平台搭建
本文参照DL/T 1540—2016中华人民共合国电力行业标准,搭建了变压器振动信号采集平台采集振动信号数据,平台接线如图6所示,主要设备有变压器、调压器、负载柜(相关参数见表2)、数据采集卡等。
表2 负载柜相关参数
Tab.2 Related parameters of load cabinet

?
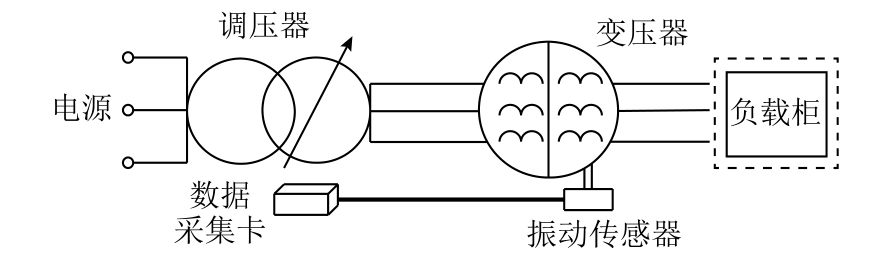
图6 变压器振动信号采集平台接线图
Fig.6 Wiring diagram of transformer vibration signal acquisition platform
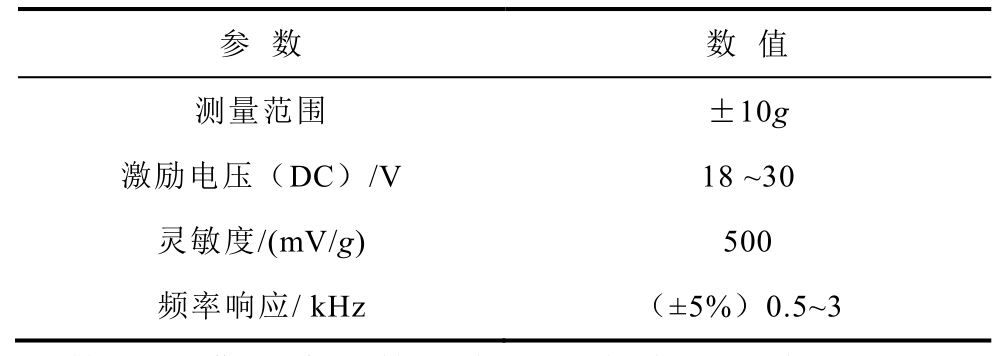
被测变压器为三相油浸式配电变压器,型号为S13-M-100/10/0.4。负载柜、调压器用于调节变压器负载、电压,通过PCB公司的365A振动传感器(相关参数见表3)进行箱壁表面振动信号的数据采集,经数据电缆传输到数据存储设备中进行存储,具体采集位置如图7所示。实验时采集记录变压器空载、短路、负载不同工况下正常运行与故障运行时各测点的振动信号数据,采集频率为25.6kHz。
表3 振动传感器相关参数
Tab.3 Vibration sensor related parameters
?
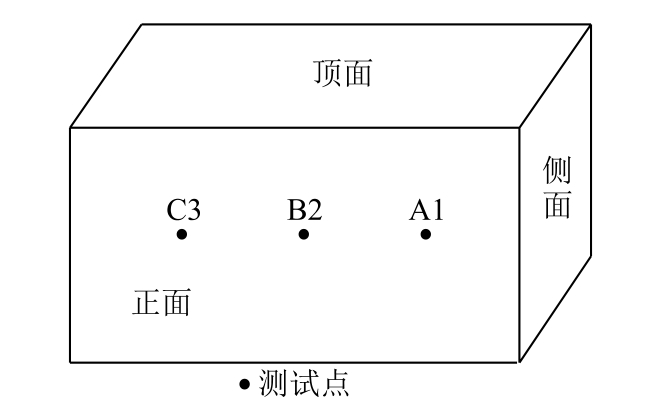
图7 变压器振动信号采集位置示意图
Fig.7 Schematic diagram of vibration signal sampling and location
2.2 变压器机械故障模拟设置
实验中模拟了变压器常见的机械故障类型,包括绕组松动、铁心松动、绕组变形等,如图8所示。本次故障设置未进行分级,每类故障仅考虑了一种情况,具体设置如下:

图8 机械故障设置
Fig.8 Mechanical fault settings
(1)绕组松动:松动A、B相绕组间的拉杆,降低压紧线圈的纵向预紧力,模拟A、B相绕组松动,松动位移为1cm。
(2)铁心松动:松动A相两颗紧固铁心横向角钢的螺栓和紧固铁心的横向拉杆螺栓,可以降低夹件对铁心的夹紧力,模拟A相铁心松动,松动位移为1cm。
(3)绕组变形:本次变压器绕组结构为层式结构,较为紧密,因此使用铁锤敲击橡胶垫块来模拟A相绕组变形,形变位移为0.5cm。
3 基于SDP的变压器振动信号特性分析
3.1 基于EEMD变压器振动信号的分解与重构
与实验室环境不同,实际运行中变压器的振动信号不仅受到自身的低频干扰,还常受到来自外界环境的高频干扰。
以A1测点铁心松动时为例,该测点处原始振动信号、剔除低频干扰保留外界高频干扰的振动信号、重构后振动信号的SDP图像分别如图9所示。对比重构前后的SDP图像,干扰的存在直接改变了图像的拓扑结构;对比保留高频干扰及重构后SDP振动信号的SDP图像,高频干扰的存在改变了图像边际弧线的曲率,影响着SDP图像的指纹特征,使得边际变得模糊、图形变得杂乱,不利于进行接下来的故障识别。
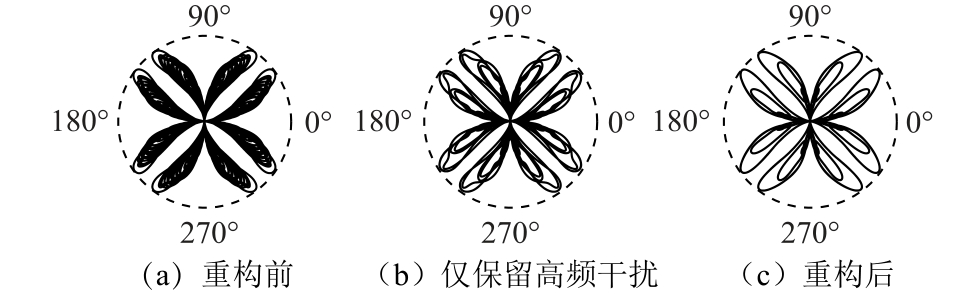
图9 A1测点处铁心松动时振动信号的SDP图像
Fig.9 The SDP image of the vibration signal when the iron core is loose at the measuring point A1
这里基于EEMD来实现对于低频干扰及高频干扰分量的同时剔除。限于篇幅,且因为三测点波形较为接近,在此仅选取B2测点来分析。
EEMD利用了所有频率上高斯白噪声能量相等的特点,通过在初始信号中添加白噪声并进行多次EMD处理,得到一系列线性、平稳的IMF分量,即将初始信号分解成若干单分量调幅、调频信号之和,该过程可视为线性滤波。其主要步骤如下:
(1)在被分解信号xi(t)中加入均值为0的高斯白噪声,并进行归一化。应用EMD算法分解归一化后的信号,获得各阶的IMF函数。
(2)重复步骤(1),并使每次添加的高斯白噪声强度相同而序列不同。
(3)将步骤(2)所得的IMF函数进行集成平均处理来获得初始信号的EEMD分解,即
式中,R(t)为残余分量;![]() 为分解所得的共S个IMF分量。
为分解所得的共S个IMF分量。
EEMD是通过在原始信号中添加白噪声实现对原始信号的分解,因此分解得到的众多IMF分量中可能存在虚假分量,可通过计算各个IMF分量与原始信号的皮尔逊相关系数,选择与原始信号强相似以上的IMF分量(r>0.6),认为此类分量是原始信号的一个真实分量,否则舍去。
对振动信号重构的基本步骤为:
(1)对采集的振动信号进行EEMD分解,得到一系列IMF分量。
(2)计算各IMF分量与原始信号的皮尔逊相关系数r,选择r>0.6的IMF分量叠加用以重构信号。
以负载工况下为例,振动信号经EEMD分解后各IMF分量如图10所示,重构前后振动信号的波形及频谱分布如图11所示,各IMF分量与原始信号的相似系数见表4。

图10 负载工况下B2测点处振动信号经EEMD分解后各IMF分量
Fig.10 Each IMF component of the vibration signal at the B2 measuring point under load conditions is decomposed by EEMD
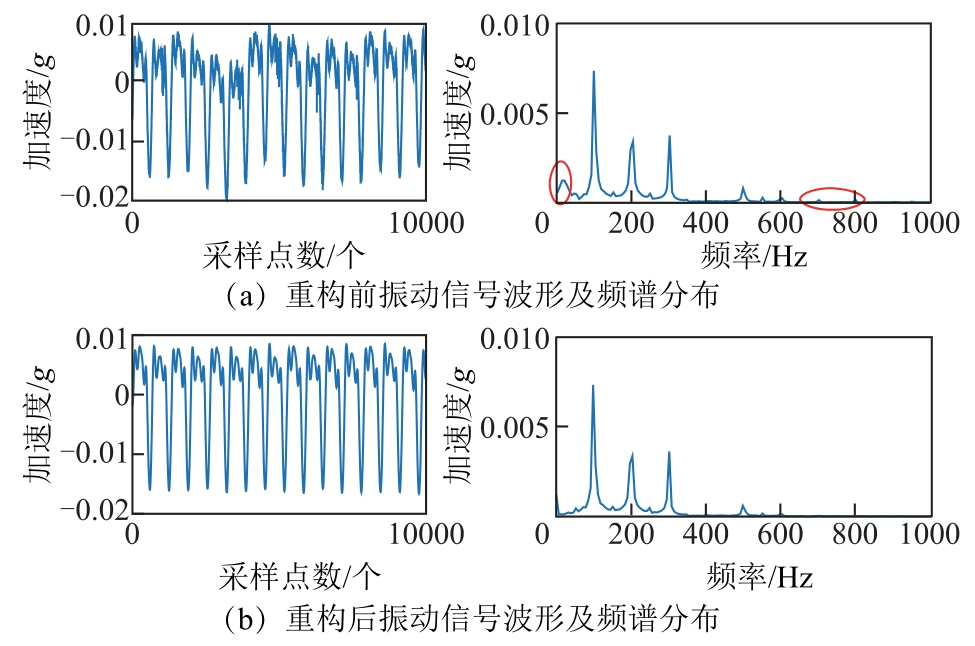
图11 负载工况下B2测点处振动信号重构前后的时域波形及频谱分布
Fig.11 The time-domain waveform and frequency spectrum distribution before and after reconstruction of the vibration signal at the B2 measuring point under load conditions

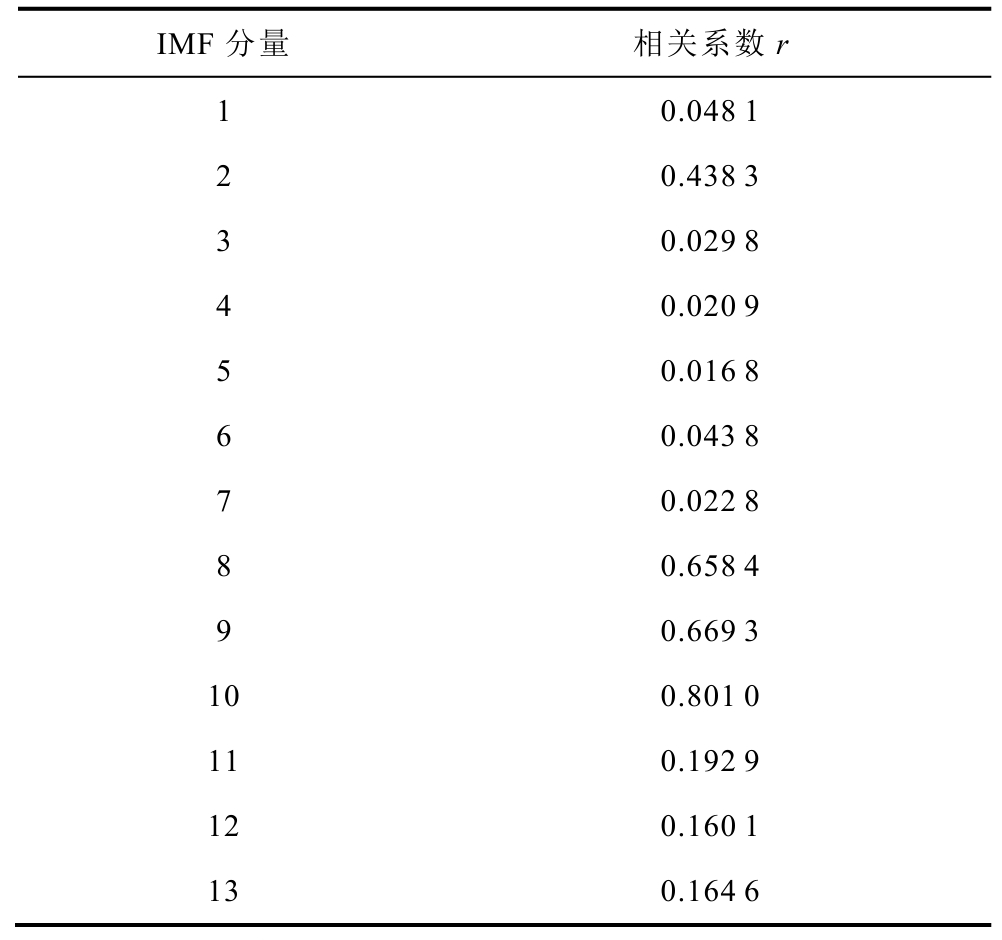
经EEMD分解后得到了13个IMF分量,结合表4,本次选择IMF8、IMF9、IMF10来重构信号,重构后的振动信号剔除了自身的低频干扰及外界的高频干扰,相对于重构前的振动信号波形更加规律,毛刺减少,更能够反映变压器的机械特性。限于篇幅,之后的分析仅显示重构后的振动信号波形及频谱分布。
表4 负载工况下B2测点处振动信号经EEMD分解后各IMF分量相似系数r
Tab.4 Correlation coefficient r of each IMF component after EEMD decomposition of vibration signal at B2 measuring point under load conditions
?
3.2 正常运行时振动信号特性及SDP图像分析
变压器空载时振动主要由铁心磁致伸缩产生,短路时主要是绕组电磁力导致振动,负载时由两者共同作用。短路工况、空载工况下重构前后振动信号的波形及频谱分布如图12和图13所示。
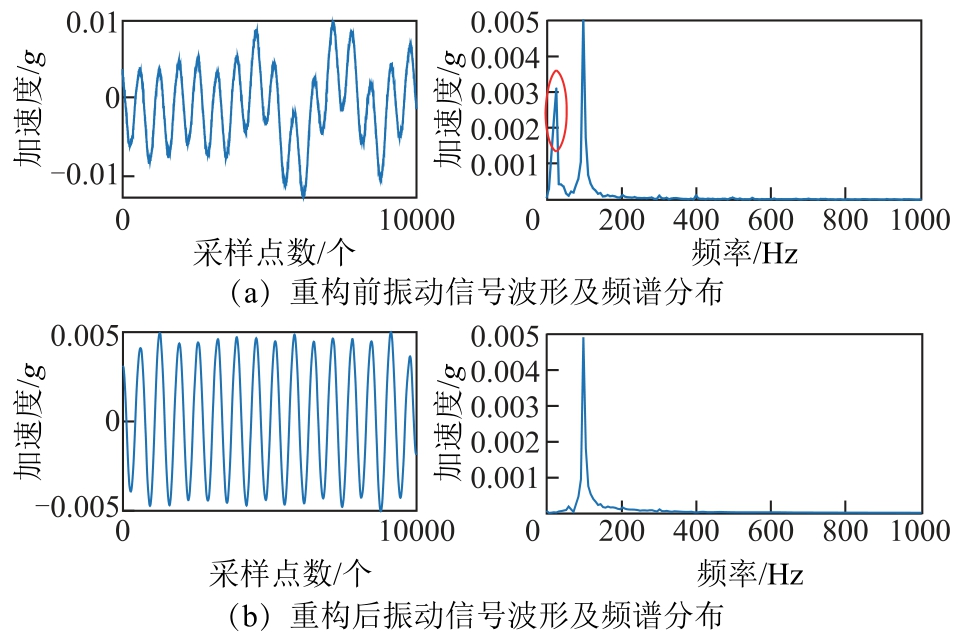
图12 短路工况下B2测点处重构前后振动信号波形及频谱分布
Fig.12 Vibration signal waveform and frequency spectrum distribution diagram before and after reconstruction at B2 measuring point under short-circuit conditions
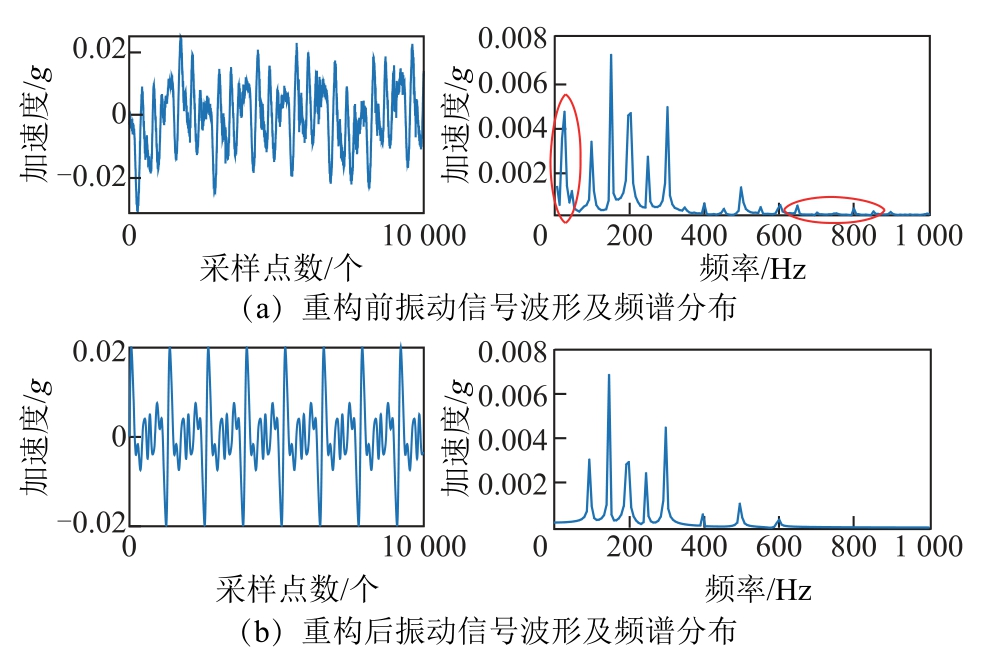
图13 空载工况下B2测点处重构前后振动信号波形及频谱分布图
Fig.13 Vibration signal waveforms and spectrum distribution diagram before and after reconstruction at B2 measuring point under no-load conditions
结果表明:短路时振动信号频谱较为单一,以100Hz基频为主。空载时振动信号成分较为复杂,频谱分布在100~600Hz内,范围较大,相应波形
相较于短路、负载下幅值增大一倍以上。除100Hz基频外还有如200Hz、300Hz等100Hz倍频,甚至出现了150Hz、250Hz等50Hz奇次倍频。导致出现100Hz倍频及50Hz奇次倍频的原因可能有以下几点:
(1)与电源电流有关,变压器外界电源中可能存在电流谐波。当电流中存在谐波时,可表示为
式中,k=1,3,5,…,K;Ik为各谐波电流幅值;fk为各谐波电流频率;φk为各谐波电流的初始相位。电流存在谐波时,绕组电磁力为
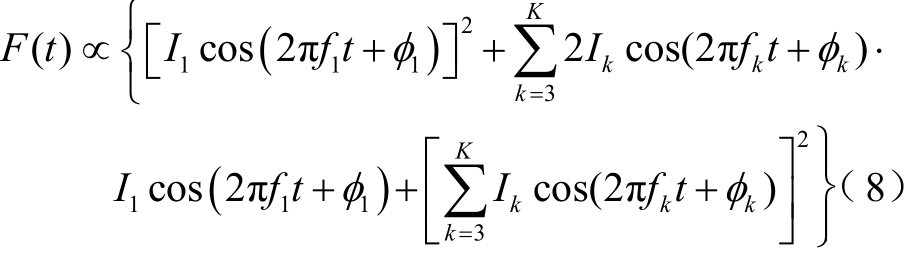
式(8)由三部分组成,第一部分表示基波电流分量的作用,频率为100Hz。第二部分基波电流与谐波电流的作用,该部分频率为|fk±50Hz|。第三部分是除基波外谐波电流间的相互作用,设相互作用间的谐波为fp、fq,则有:当fp=fq时,和基波分量作用效果类似,频率为2fp;当fp≠fq时,为不同阶次谐波间的相互作用,频率为|fp±fq|。
(2)与固有频率有关。变压器组成部件较多,不同部件具有其自身的固有频率,当振动信号中出现与固有频率接近的分量时,由于共振会极大增大该处的幅值。
(3)未考虑铁心与绕组间的相互作用。
(4)铁心磁致伸缩效应。
负载条件下振动信号仍有200Hz、300Hz、500Hz等分量,但150Hz、250Hz等奇次倍频成分不再出现,这种情况是绕组中交变电流改变了铁心主磁通,抑制了50Hz奇次频分量的产生[28]。
各工况下B2测点处重构后振动信号SDP图像如图14所示,结果表明:短路时SDP图像较为规则,各旋臂较为狭长,单个旋臂边际清晰,弧度较大。负载工况下各旋臂宽度明显增加,末端存在旋涡状空心椭圆,旋臂边际清晰,相较于短路、空载工况下弧度增大。空载状况下旋臂边际较细,相较于短路工况下图像较为复杂,旋臂变宽,但图形较为模糊;同负载工况相比,旋涡状空心椭圆由旋臂末端移至旋臂中部。

图14 各工况下B2测点处重构后振动信号SDP图像Fig.14 Reconstructed SDP image of vibration signal at B2 measuring point under various working conditions
3.3 机械故障时振动信号特性及SDP图像分析
B2测点模拟机械故障发生时振动信号重构后波形及频谱分布、变换后SDP图像如图15和图16所示,其中绕组故障包括绕组松动及绕组变形是在短路实验下进行的,而铁心故障是在空载实验下进行的。相较于正常状态下,故障发生时有以下变化:

图15 B2处机械故障下重构后信号波形及频谱分布图Fig.15 The waveforms and frequency spectrum distribution of the reconstructed vibration signal when the simulated mechanical fault occurs at the B2 point
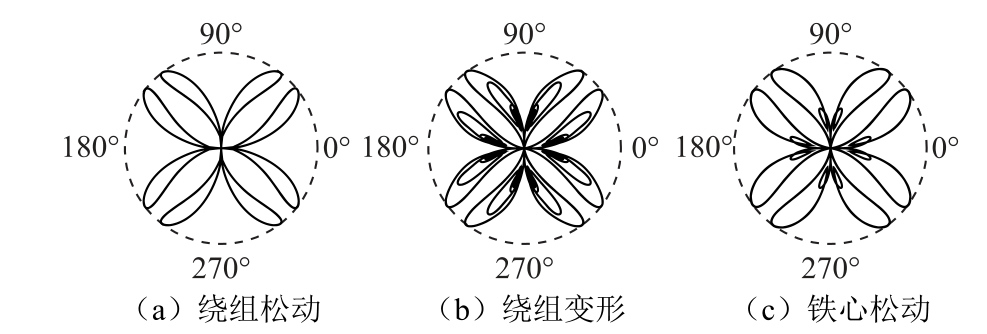
图16 机械故障下B2测点处重构后振动信号SDP图像
Fig.16 Reconstructed SDP image of vibration signal at B2 measuring point under mechanical failure
(1)绕组故障时振动信号时域波形较为规则,相应频谱成分较少,以100Hz、200Hz、300Hz为主。同短路工况下相比,时域波形幅值均增大30%以上,频谱成分增加了200Hz、300Hz分量;100Hz分量绕组松动时幅值增大30%以上,绕组变形时幅值减小了60%。
(2)铁心故障出现时信号幅值增大,频谱成分较多,主要以100Hz、200Hz、300Hz、500Hz为主,伴随着150Hz、250Hz分量。同空载工况相比,100Hz分量幅值增大了1倍以上。
(3)同短路工况下SDP图像相比,绕组松动时SDP图像旋臂宽度增加,末端弧度减小,图像面积增加,图形拓扑结构未出现明显变化;绕组变形时SDP图像旋臂宽度明显增加,末端弧度大幅减小,面积显著增加,旋臂内部靠近对称中心位置出现了旋涡状空心椭圆,图形拓扑结构变化较大。
(4)同空载工况下的SDP图像相比,旋臂宽度稍有增加,旋臂内部空心漩涡状椭圆位置由旋臂中部移动至靠近对称中心位置处,发生故障时旋涡状椭圆内出现了另外一个较小的细长椭圆,图形拓扑结构变化较大。
(5)不同故障间SDP图像特征差异较大。
总之,正常状态下与发生故障时的SDP图像的特征差异明显,不同类型故障间差异巨大,这为基于SDP图像匹配实现故障诊断提供了基础。
4 基于SDP与图像匹配的变压器机械故障诊断
不同故障下SDP图像的巨大差异性是实现故障诊断的基础,但测点位置、样本的个体特征等因素使得仅通过单一点的振动信号来完成诊断可能会出现误判,这里选择类聚模板解决这一问题。
4.1 基于SDP、EEMD分解与聚类模板匹配的变压器故障诊断流程
本文利用EEMD对振动信号进行分解、重构,并基于SDP和图像匹配,提出了一种变压器机械故障诊断模型,其流程如图17所示。

图17 变压器机械故障诊断流程
Fig.17 Transformer mechanical fault diagnosis process
(1)采集变压器正常和各类已知故障状态各工况下多测点处的振动信号,利用EEMD对信号进行分解与重构,通过变换获得重构后振动信号的SDP图像。
(2)选择每类已知故障中的部分SDP图像作为模板,并将剩余故障SDP图像作为测试,建立数据库。
(3)将未知故障振动信号的SDP图像变换为二值矩阵,计算未知故障SDP图像与各类故障模板图像的相关系数。
(4)当未知故障振动信号与某类故障模板图像的相关系数大于与其他类故障模板图像的相关系数,并大于所设置判定阈值δ(这里令δ=0.6),则认为变压器发生了这种故障;否则,认为此信号未发生故障。
4.2 基于SDP与聚类模板匹配的变压器故障诊断结果分析
当同一类故障SDP图像的模板数目较多时,会使得计算量增大,较为繁琐,应用聚类可以较好地解决这一点。
本次采用了聚类中心描述聚类准则:对变压器每类故障下各模板的图像矩阵进行求和,计算出聚类中心特征值的平均值,之后再对每类故障下由平均值构成的矩阵进行规范化处理,确定图像每一点或每一小块区域处上像素的阈值μ。μ决定了该像素是否可以作为判断故障的固有特征,本文将μ设为0.6,当同一位置上的像素在同类型故障的所有模板中出现了60%以上时,将该点视为该类型故障下具有的固有特征。具体为

式中,P(x,y)为SDP图像上(x,y)点处的灰度值;P(X,Y)为u个图像上(x,y)点处灰度值的平均值; Pmax和Pmin分别为该模板下灰度值的最大值与最小值;η为阈值μ对应的灰度值;u为每类模板包含样本数。本次将A1、B2、C3三处振动信号作为一组,聚类模板下每类故障模板的组数与诊断准确率关系如图18所示。
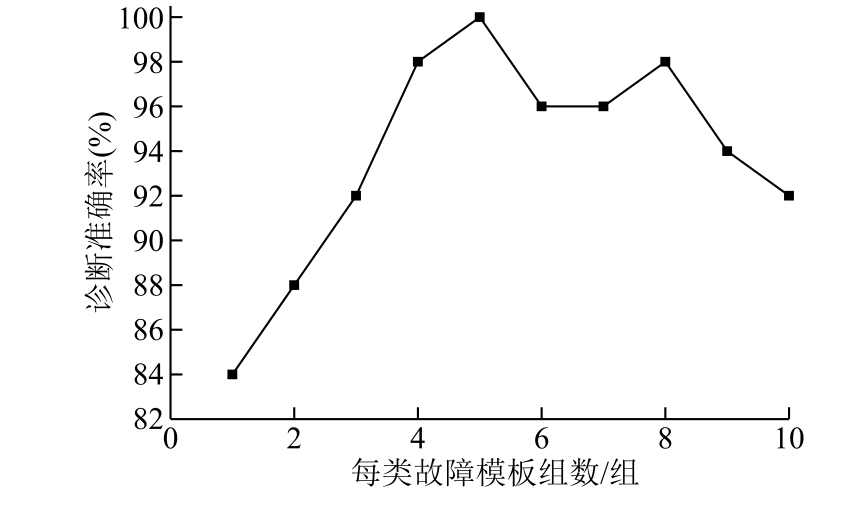
图18 每类故障模板不同组数下的诊断准确率
Fig.18 Diagnosis accuracy rate under different number of groups of each type of fault template
本次实验每个测点每类故障下采集数据为60个,将其中10个划为模板,剩下作为测试集。可以看出,随着组数的增加诊断准确率先增加后减小,在模板组数为5时准确率最高,达到了100%。
4.3 不同模式模板匹配下的结果分析
图19 显示了单一模板(每类故障下仅选择B2测点处一个模板)、多模板(每类故障下仅选择一组模板)及聚类模板(模板组数为5)时的诊断结果。其中状态1表示绕组变形,状态2表示绕组松动,状态3表示铁心松动,状态4表示无机械故障。

图19 不同模式模板匹配下的诊断结果
Fig.19 Diagnosis results under different pattern template matching
结果表明,相较于聚类模板匹配结果100%的诊断准确率,单一模板与多模板匹配下的诊断效果较差,分别为72%和78%。相较于单一模板、多模板匹配,聚类模板的诊断准确率分别提高了38.9%和28.2%。多模板相较于单一模板匹配结果,准确率提升了8.3%。
相较于单一模板与多模板匹配,聚类模板显著提升了诊断准确率,这是由于其加强了同类故障下各模板图像的共同特征,减弱了同类故障下各模板图像的个体特征,使所得每类模板图像更具代表性,有助于更好地完成变压器机械故障的诊断。与多模板匹配相比,使用聚类处理后将原有的多组故障模板减少到一组,实现了计算量的减小。
4.4 不同诊断模型的效果对比
以文献[29]作为对比,不同诊断模型的准确率见表5。二者的故障诊断思路相似,均是对信号进行处理后再识别,并都考虑到了未剔除外界干扰时的识别状况。图20为未剔除干扰下聚类模板(聚类组数为5)匹配的诊断结果。
表5 不同诊断模型的准确率
Tab.5 Vibration sensor related parameters

?
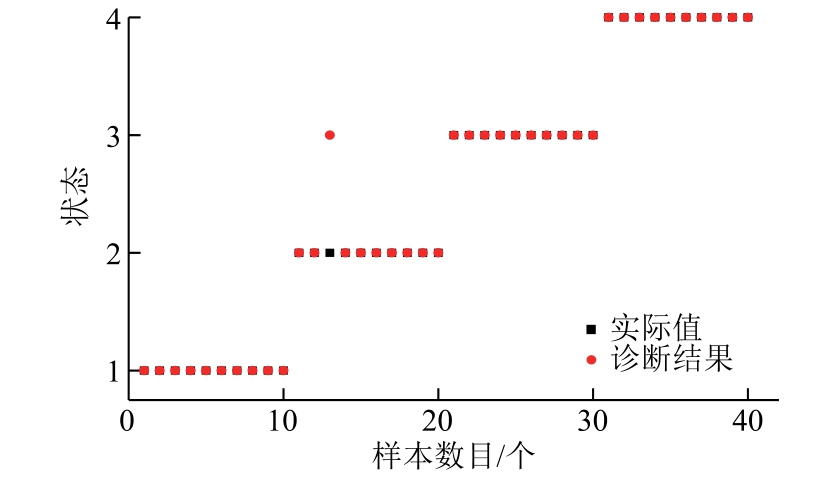
图20 未剔除干扰时应用聚类模板匹配诊断结果
Fig.20 Apply cluster template matching diagnosis result when interference is not eliminated
与未考虑干扰时的诊断结果相比,剔除干扰后在样本数增多的情况下仍实现了诊断准确率的提升。与文献[29]中变压器放电故障识别方法相比,本文中提出的模型诊断流程简单,准确率高,不需要针对特定故障选择特定参数,因此对于故障类型较多的情况更具推广性。
但目前本文提出方法仍存在一些问题:
(1)样本数目较少,需更多数据来进一步实现各类故障下SDP图像模板的特征细化。
(2)仅针对一台变压器进行测试,未设置故障分级,普适性有待商榷。
(3)本次诊断针对的机械故障种类较少,实际运行中还会存在其他机械故障或多故障,其SDP图像可能存在重叠而干扰诊断结果。
但相较于传统方法,本文中所提出的方法思路清晰、高效简洁,剔除了高频干扰对于振动信号的影响,工程实际中结合大数据等技术可以实现对于变压器的实时监测,为电力设备的机械故障诊断提供了新思路。
5 结论
本文基于变压器振动信号,在研究了SDP特性的基础上,利用图像匹配技术,提出了一种基于SDP与图像匹配的变压器故障诊断方法。该方法先利用EEMD对振动信号进行分解并重构,之后在重构信号的基础上进行变换,获得SDP图像,并在每类故障下选择部分图像应用聚类方法获得典型故障模板,通过计算相关系数进行图像最佳匹配,完成了变压器机械故障诊断。
在对SDP的特性研究分析时发现,滞后系数对SDP图像的影响存在周期性,周期内SDP图像拓扑结构随滞后系数变化很大;信号采样时间对SDP图案的拓扑结构影响很小。
通过EEMD重构后的振动信号剔除了外界环境及自身的干扰,能够更为真实地反映变压器的机械状态信息。
基于聚类模板的SDP图像匹配在单一模板、多模板的基础上加强了同类故障典型模板的共同特征,在未增加计算量的情况下大大提高了诊断准确率。
[1] 汲胜昌, 王世山, 李清泉, 等. 用振动信号分析法监测变压器绕组状况[J]. 高电压技术, 2002, 28(4):12-13, 15.Ji Shengchang, Wang Shishan, Li Qingquan, et al. The application of vibration method in monitoring the condition of transformer winding[J]. High Voltage Engineering, 2002, 28(4): 12-13, 15.
[2] 李存斌, 计丽妍, 赵德福, 等. 基于数据驱动的电力系统灾变演化及防控研究与展望[J]. 电力系统自动化, 2020, 44(9): 1-11.Li Cunbin, Ji Liyan, Zhao Defu, et al. Research and prospect of data-driven based disaster evolution and prevention of power system[J]. Automation of Electric Power System, 2020, 44(9): 1-11.
[3] 汲胜昌, 张凡, 师愉航, 等. 基于振动信号的电力变压器机械状态诊断方法研究综述[J]. 高电压技术, 2020, 46(1): 257-272.Ji Shengchang, Zhang Fan, Shi Yuhang, et al. Review on vibration-based mechanical condition monitoring in power transformers[J]. High Voltage Engineering,2020, 46(1): 257-272.
[4] 曹文斌, 尹项根, 王育学, 等. 高阻抗变压器涌流的特殊性比较分析 [J]. 电力系统自动化, 2019,43(16): 141-150.Cao Wenbin, Yin Xianggen, Wang Yuxue, et al.Analysis of the particularity of inrush current in high impedance transformer[J]. Automation of Electric Power System, 2019, 43(16): 141-150.
[5] 张凡, 汲胜昌, 师愉航, 等. 电力变压器绕组振动及传播特性研究[J]. 中国电机工程学报, 2018,38(9): 2790-2798, 2849.Zhang Fan, Ji Shengchang, Shi Yuhang, et al. Research on transformer winding vibration and propagation characteristics[J]. Proceedings of the CSEE, 2018, 38(9):2790-2798, 2849.
[6] 孙翔, 何文林, 詹江杨, 等. 电力变压器绕组变形检测与诊断技术的现状与发展[J]. 高电压技术,2016, 42(4): 1207-1220.Sun Xiang, He Wenlin, Zhan Jiangyang, et al. Current status and development of test and diagnostic technique of transformer winding deformation[J].High Voltage Engineering, 2016, 42(4): 1207-1220.
[7] 刘勇, 杨帆, 张凡, 等. 检测电力变压器绕组变形的扫频阻抗法研究[J]. 中国电机工程学报, 2015,35(17): 4505-4516.Liu Yong, Yang Fan, Zhang Fan, et al. Study on sweep frequency impedance to detect winding deformation within power transformer[J]. Proceedings of the CSEE,2015, 35(17): 4505-4516.
[8] 张大宁, 刘孝为, 詹江杨, 等. 变压器油纸绝缘频域介电谱的虚部分析[J]. 电工技术学报, 2019,34(4): 847-854.Zhang Daning, Li Xiaowei, Zhan Jiangyang, et al.Analysis of imaginary part of frequency domain spectroscopy for oil-paper insulation transformer[J].Transactions of China Electrotechnical Society, 2019,34(4): 847-854.
[9] 邹阳, 何倩玲, 蔡金锭. 基于组合赋权-双基点法的变压器油纸绝缘状态综合评估[J]. 电工技术学报,2019, 34(20): 4401-4408.Zou Yang, He Qianling, Cai Jinding. Comprehensive evaluation of transformer oil-paper state based on combined weight-double base point method[J].Transactions of China Electrotechnical Society, 2019,34(20): 4401-4408.
[10] 刘骥, 张明泽, 赵春明, 等. 基于频域介电响应分频段优化计算的变压器油纸绝缘老化参数定量计算方法[J]. 电工技术学报, 2020, 35(9): 2021-2031.Liu Ji, Zhang Mingze, Zhao Chunming, et al. Aging parameters based on frequency dielectric spectrum frequency range optimized calculation[J].Transactions of China Electrotechnical Society, 2020,35(9): 2021-2031.
[11] 马宏忠, 弓杰伟, 李凯, 等. 基于ANSYS Workbench的变压器绕组松动分析及判定方法[J].高电压技术, 2016, 42(1): 192-199.Ma Hongzhong, Gong Jiewei, Li Kai, et al. Analysis and determination method for transformer winding looseness based on ANSYS workbench[J]. High Voltage Engineering, 2016, 42(1): 192-199.
[12] 孙翔, 何文林, 詹江杨, 等. 电力变压器绕组变形检测与诊断技术的现状与发展[J]. 高电压技术,2016, 42(4): 1207-1220.Sun Xiang, He Wenlin, Zhan Jiangyang, et al. Current status and development of test and diagnostic technique of transformer winding deformation[J].High Voltage Engineering, 2016, 42(4): 1207-1220.
[13] Bagheri M, Naderi M S, Blackburn T. Advanced transformer winding deformation diagnosis: moving from off-line to on-line[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(6):1860-1870.
[14] 马宏忠, 耿志慧, 陈楷, 等. 基于振动的电力变压器绕组变形故障诊断新方法[J]. 电力系统自动化,2013, 37(8): 89-95.Ma Hongzhong, Geng Zhihui, Chen Kai, et al. A new fault diagnosis method for power transformer winding deformation based on vibration[J]. Automation of Electric Power Systems, 2013, 37(8): 89-95.
[15] Ertl M, Voss S. The role of load harmonics in audible noise of electrical transformers[J]. Journal of Sound and Vibration, 2014, 333(1): 2253-2270.
[16] Moses A J, Anderson P I, Phophongviwat T. Localized surface vibration and acoustic noise emitted from laboratory-scale transformer cores assembled from grainoriented electrical steel[J]. IEEE Transactions on Magnetics, 2016, 52(10): 1-15.
[17] Garcia B, Burgos J C, Alonso A M. Transformer tank vibration modeling as a method of detecting winding deformations-part II: experimental verification[J].IEEE Transactions on Power Delivery, 2005, 21(1):157-163.
[18] Belén G, Juan C B, Ángel M.A. Transformer tank vibration modelling as a method of detecting winding deformations-partⅡ: experimental verification[J].IEEE Trans-actions on Power Delivery, 2006, 21(1):164-169.
[19] 刘洪涛, 马宏忠, 高鹏, 等. 利用变压器箱体振动模型确定故障阈值[J]. 电力系统及其自动化学报,2012, 24(6): 36-40.Liu Hongtao, Ma Hongzhong, Gao Peng, et al. Method of determining the threshold of transformer fault using transformer tank vibration model[J]. Proceedings of the CSU-EPSA, 2012, 24(6): 36-40.
[20] 王丰华, 段若陈, 耿超, 等. 基于磁-机械耦合场理论的电力变压器绕组振动特性研究[J]. 中国电机工程学报, 2016, 36(9): 2555-2562.Wang Fenghua, Duan Ruochen, Geng Chao, et al.Research of vibration characteristics of power transformer winding based on magnetic-mechanical coupling field theory[J]. Proceedings of the CSEE,2016, 36(9): 2555-2562.
[21] 吴晓文, 周年光, 裴春明, 等. 特高压交流变电站可听噪声分离方法[J]. 高电压技术, 2016, 42(8):2625-2632.Wu Xiaowen, Zhou Nianguang, Pei Chunming, et al.Separation methodology of audible noises of UHV AC substations[J]. High Voltage Engineering, 2016, 42(8):2625-2632.
[22] 吴晓文, 周年光, 裴春明, 等. 特高压交流GIS变电站噪声特性测量与分析[J]. 高压电器, 2017,53(6): 13-18.Wu Xiaowen, Zhou Nianguang, Pei Chunming, et al.Measurement and analysis on characteristics of audible-noise in UHV AC GIS substations[J]. High Voltage Apparatus, 2017, 53(6): 13-18.
[23] 朱叶叶, 汲胜昌, 张凡, 等. 电力变压器振动产生机理及影响因素研究[J]. 西安交通大学学报, 2015,49(6): 115-125.Zhu Yeye, Ji Shengchang, Zhang Fan, et al. Vibration mechanism and influence factors in power transformers[J]. Journal of Xi’an Jiaotong University,2015, 49(6): 115-125.
[24] 潘超, 苏昊, 蔡国伟, 等. 变压器直流偏磁下异常电流表征振动特性研究[J]. 电工技术学报, 2020,35(9): 1869-1879.Pan Chao, Su Hao, Cai Guowei, et al. Research on characterization of core vibration by abnormal current of DC bias transformer[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1869-1879.
[25] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报,2018, 33(22): 5273-5281.Zhang Pengning, Li Lin, Cheng Zhiguang, et al.Vibration simulation and experiment comparison of shunt reactor and transformer model core[J].Transactions of China Electrotechnical Society, 2018,33(22): 5273-5281.
[26] José González, Jesús M Fernández Oro, Laura Delgado Z, et al. Symmetrized dot pattern analysis for the unsteady vibration state in a Sirocco fan unit[J].Applied Acoustics, 2019, 152: 1-12.
[27] Xu Xiaogang, Liu Haixiao, Zhu Hao, et al. Fan fault diagnosis based on symmetrized dot pattern analysis and image matching[J]. Journal of Sound and Vibration, 2016, 374: 297-311.
[28] 师愉航, 汲胜昌, 张凡, 等. 变压器绕组多倍频振动机理及特性[J]. 高电压技术, 2021, 4(5): 1-10.Shi Yuhang, Ji Shengchang, Zhang Fan, et al. Multifrequency vibration mechanism and characteristics of transformer windings[J]. High Voltage Engineering,2021, 4(5): 1-10.
[29] 舒畅, 金潇, 李自品, 等. 基于CEEMDAN的配电变压器放电故障噪声诊断方法[J]. 高电压技术,2018, 44(8): 2603-2611.Shu Chang, Jin Xiao, Li Zipin, et al. Noise diagnosis method of distribution transformer discharge fault based on CEEMDAN[J]. High Voltage Engineering,2018, 44(8): 2603-2611.