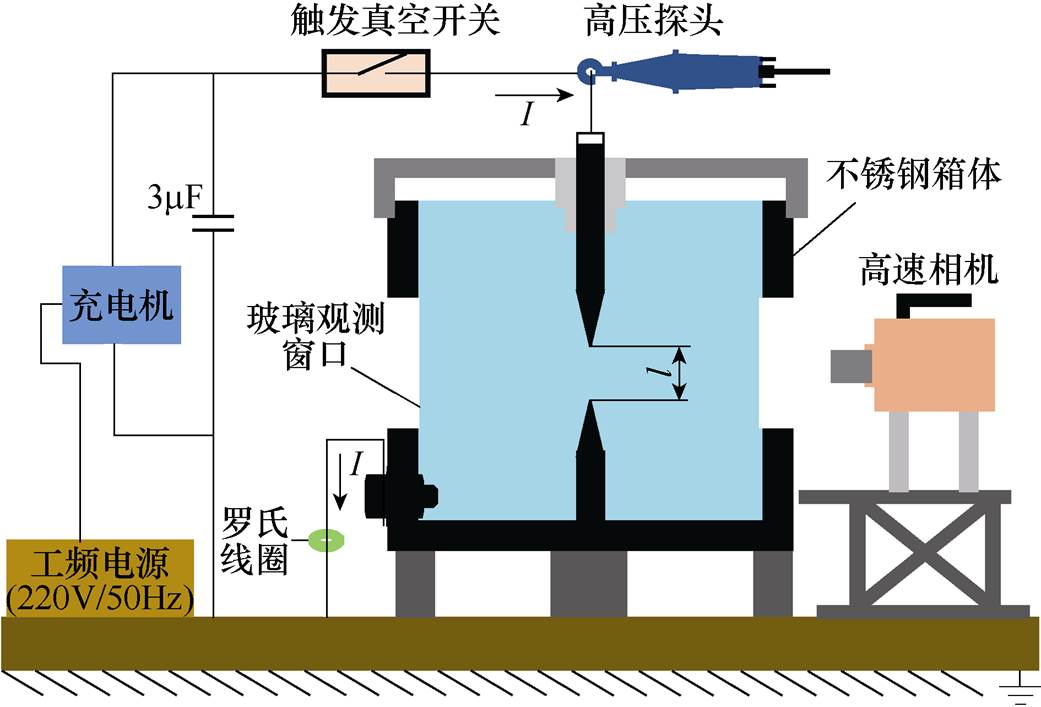
图1 水中放电综合观测平台结构
Fig.1 Structure diagram of the integrated observation platform for water discharge
摘要 针对基于Braginskii阻抗模型求解电弧通道注入能量时，与实验设置相关的放电系数求解过程复杂，且结果难以准确地反映电弧通道发展特性等问题，该文提出基于电弧通道电压、电流的水中大电流脉冲放电电弧通道发展过程分析方法。采用“活塞”模型阐述通道快速膨胀过程及激波产生机理，提出基于电弧通道电压、电流实测数据剥离电感分量计算注入通道能量的方法，借助能量平衡方程对通道发展过程进行建模分析。与基于传统Braginskii阻抗模型的求解结果对比表明，该文提出的方法可以更准确地描述电弧通道的加速膨胀特性，为深入探究电弧通道的发展机理提供依据。
关键词：水中放电 脉冲大电流 电弧通道 能量平衡方程 阻抗模型
在传统电力技术的基础上，近些年脉冲功率技术逐渐兴起，水中脉冲放电作为其中一个分支[1-4]，其产生的物理和化学效应在废弃物处理[5-6]、石油增产[7]和岩石破碎[8-9]等领域中应用十分广泛。电弧等离子体通道（简称“电弧通道”）是电能向机械能等转化的载体[10-12]。激波作为水中脉冲放电的主要产物，提高其能量的转换效率是实际应用需要考虑的问题。准确地分析电弧通道的发展过程，能够加深对液电脉冲激波产生机理的理解，为提高激波转化效率提供理论依据。
A. Claverie等认为水中脉冲放电过程按时间顺序分为电弧的膨胀与运动、激波的传播以及气泡的脉动与破裂等阶段[13]。初始电弧通道形成后向外急剧加速膨胀并辐射激波[14-17]。A. P. Smirnov等发现初始电弧通道存在一个短暂的加速膨胀过程，该过程中激波波阵面运动速度超过电弧通道膨胀速度，最终导致两者分离[18-19]。该过程历时较短，可以视为绝热过程，电弧边界尚来不及形成气鞘层。I. V. Lisitsyn等发现激波的初始速度远大于水中声速，并不断向外传播，逐渐衰减至水中声速[20-22]。Han Yibo等发现经过电弧通道的快速膨胀后，电弧通道与其周围液体之间出现了能见亮度较低的气体过渡鞘层，表明形成了外层气泡[23]。随着通道体积的扩大，维持通道加速膨胀的能量注入速率要求提高，外回路的能量注入难以满足要求，通道膨胀速度降低，直至停止。因此，电弧通道的加速膨胀过程影响着激波的产生过程，特别是决定了激波的峰值和上 升沿。
借鉴气体放电电弧通道建模理论，可建立水中电弧通道发展模型，并对通道电压、电流及注入功率等特性进行描述，预测通道的发展特性。但是模型不能完全反映通道阻抗的时变特性，同时与回路放电特性相关的模型参数受到试验条件（如电极形式、液体性质等）的影响。对于不同的试验设置，其数值需要重新确定[24-25]。而基于实测的电弧通道两端电压与通道电流波形实测数据，可以更好地分析电弧通道阻抗的时变特性，得到更加准确的通道注入功率，预测通道的发展特性，同时可以对电弧通道模型进行完善[9]。
为分析水中大电流脉冲放电电弧通道发展过程，更好地理解激波产生及传播机理，建立了水中大电流脉冲放电综合观测平台，通过高速摄影单元捕捉大电流作用下电弧通道的发展过程。本文提出一种改进的电弧通道发展过程计算模型，通过剥离电感分量得到电弧通道注入的实际有功功率，并与现有计算模型及实测数据进行对比分析，为分析电弧通道的发展特性提供理论基础。
水中放电综合观测平台结构如图1所示。主要由能量存储单元、脉冲放电单元和测量单元组成。
图1 水中放电综合观测平台结构
Fig.1 Structure diagram of the integrated observation platform for water discharge
能量存储单元主要由充电机、脉冲电容器（电容C=3mF，Uc为充电电压）组成。放电容器为边长为0.35m的正方体水箱，四周留有2 500mm×200mm的玻璃观测窗口。放电电极采用针-针形式，间隙距离为15mm。液体采用电导率为350mS/cm的自来水。通过触发真空开关控制放电回路的导通，上位机与触发器之间通过光电隔离传输触发信号，采用DG645精确控制触发信号与高速相机的同步信号。
由高压探头（Tektronix P6015A）、罗氏线圈（PEM CWT 600）、示波器（Agilent HD4034）分别测量放电间隙两端的电压与放电电流。采用高速相机（FASTCAM SA-X）拍摄电弧通道和气泡的形状变化和运动，采用减光（ND-1000、ND-400）处理，帧速为3ms/帧，曝光时间为1ms。
试验时，储能电容由充电机充至设定电压后，DG645通过光纤控制触发高速相机和触发真空开关；开关导通后，电容通过针-针电极向液体介质放电，高压探头和罗氏线圈记录放电过程中的电压、电流，高速相机通过玻璃观测窗口捕捉放电过程中电弧通道的形态变化。
水中脉冲放电（l=15mm，Uc=30kV）的电压、电流波形如图2所示。根据间隙两端的电压及电流波形可知，电极间隙的击穿时间t0=205ms，而高速相机在206ms捕捉到击穿后的第一张电弧通道照片，水中大电流脉冲放电的高速相机图像如图3所示。相机在拍摄时，防止间隙击穿瞬间电弧通道发光剧烈引起相机进光量饱和，加入减光片清晰记录了电弧通道的发展过程。相机拍摄重点是电弧通道本身难以记录清楚发光微弱的气鞘层及气泡的变化。
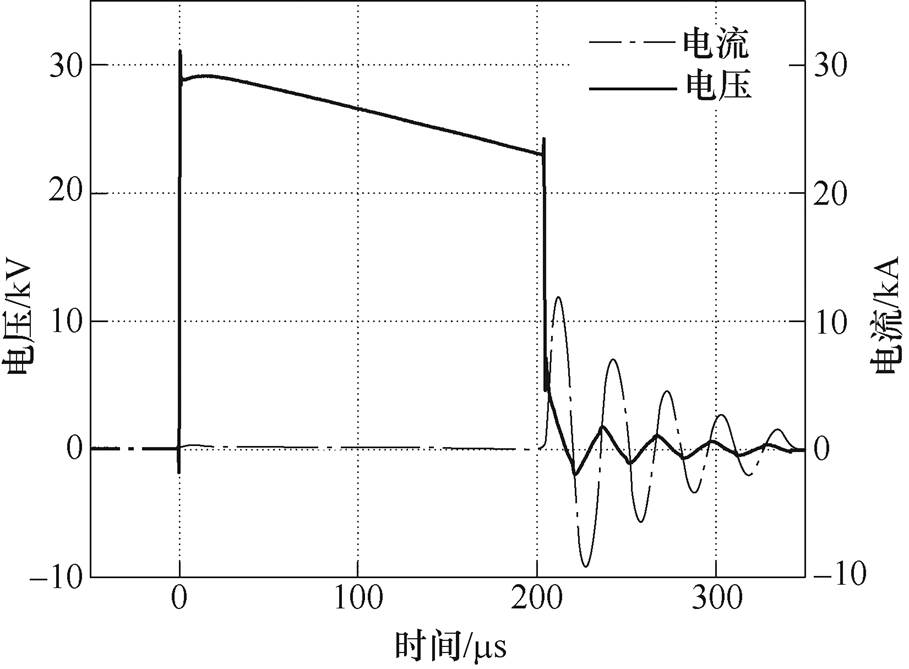
图2 水中脉冲放电的电压、电流波形
Fig.2 Voltage and current waveforms of pulse discharge in water
根据电压、电流曲线并结合高速相机捕捉的图像判断，t0=205ms时刻，电极间隙发生击穿，从发生击穿到tf=230ms，电弧的发展近似呈圆柱状。此后，电弧通道的形状开始变形，不再是圆柱形膨胀。后文电弧通道建模分析主要考虑通道的加速膨胀过程，将电弧通道考虑成圆柱形，因此不再作特殊说明，建模求解区间为t0～tf。
通过高速相机捕捉到图像测量电弧半径r(t)，得到第j张照片中电弧通道的平均膨胀速度v( j)为
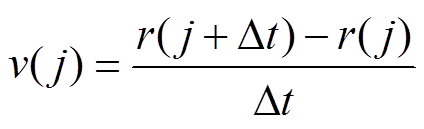（1） 式中，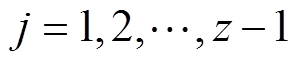
，z为图片的数量。得到平均速度后，电弧膨胀发展的加速度a( j)为
图3 水中大电流脉冲放电的高速相机图像
Fig.3 High speed camera images of underwater high current pulsed discharge
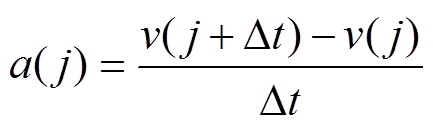（2）式中，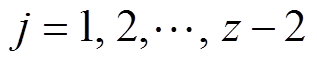
。
对应图3所观测的电弧通道发展过程，通道膨胀速度及加速度曲线如图4所示。电弧通道的加速膨胀持续时间约为6.5ms，达到最大平均速度267.16m/s。
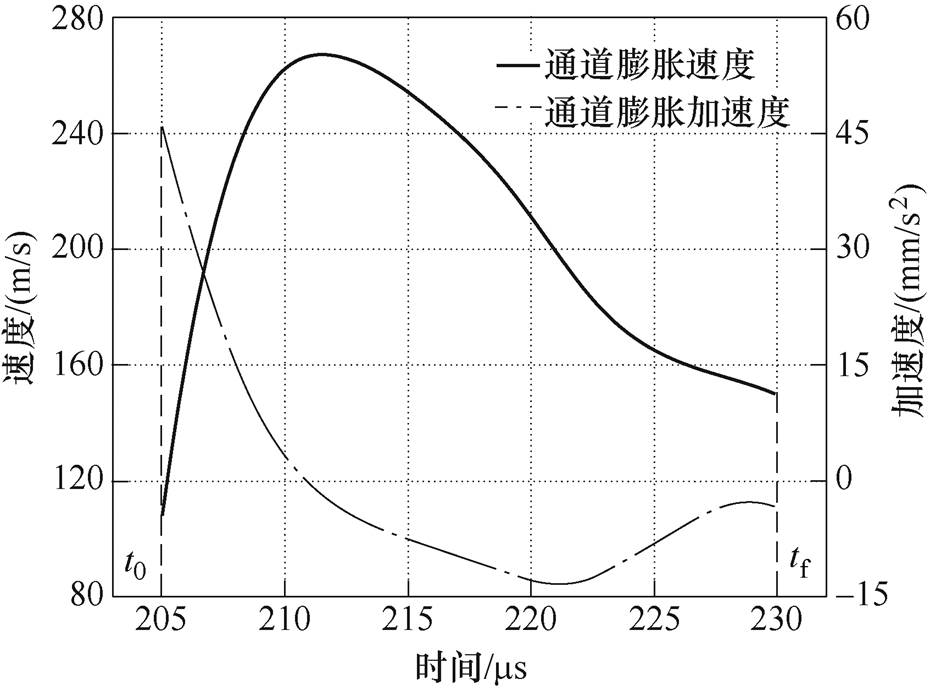
图4 通道膨胀速度与加速度曲线
Fig.4 Curves of channel expansion velocity and acceleration
电极间隙击穿后会形成贯穿电极两端的电弧通道，其发展过程宏观示意图如图5所示，图中，1为电弧通道，2为激波。图5a、图5b分别对应加速膨胀阶段中的间隙击穿时刻和通道膨胀速率最大时刻。随着电能的不断注入，电弧通道加速膨胀并辐射激波，此时通道边缘存在薄弱的气鞘层，但是通道发光剧烈，气鞘层难以观测。在加速膨胀阶段，电弧通道不断向外辐射激波，电弧通道产生激波过程如图6所示。图6中，0时刻为间隙击穿时刻，tn为从速度最快的激波追赶到第一个产生的激波时的耗时，t*为电弧通道膨胀速度最大时刻。电弧通道以速度v0向静止流体运动时，产生第一个激波，速度等于c0。随着电弧通道加速膨胀，由速度v0增大为v1，新产生激波的速度为v1+c1。t*时刻，电弧通道膨胀速度达到最大值vm，此时激波的速度为vm+cn。考虑到t*较小，在t*时刻前产生的激波传播距离很短，因此不考虑激波的衰减，则在t*之前产生的激波与t*时刻产生的激波将在时间tn和位置rn处相遇，并完成激波的“积累”，此后将合并为一个激波继续传播，速度为vn。因此，在远场中测量到的激波与电弧通道加速膨胀阶段产生的激波有关，即与加速膨胀阶段所吸收的能量有关。图5b所示为电弧通道膨胀达到最大速度时刻的图像。
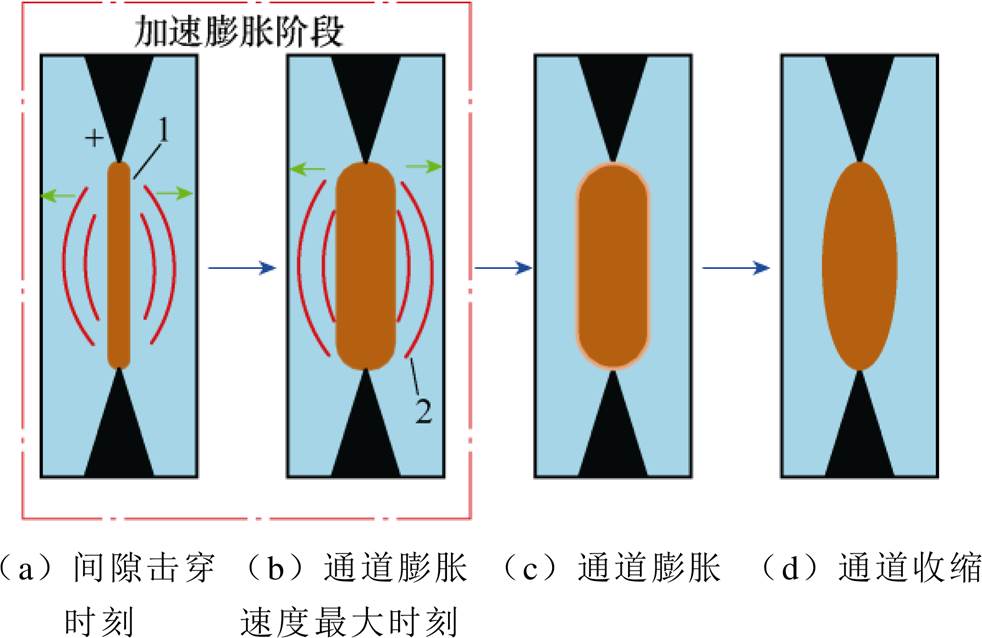
图5 电弧通道发展过程宏观示意图
Fig.5 Macro diagram of arc channel development process
电弧通道在注入能量的作用下径向膨胀，假设通道半径为r(t)，通道截面积为A(t)，二者具有时变特性。通过焦耳热注入通道的能量主要转化为通道内能、通道膨胀做功的机械能、光辐射等。E. A. Martin认为，光辐射占到电弧通道中能量的比例约为5%[14]。Sun Bing等发现紫外光辐射能量占放电过程中总能量的3.2%[26]。R. M. Roberts等认为等离子体-蒸汽混合物的内部能量和空腔完成的总机械功占电弧等离子体通道中耗散的总能量的99%以上[27]。Li Xingwen等认为热辐射等所占比例较大，空腔膨胀到最大半径时所占比例约为10%[17]。
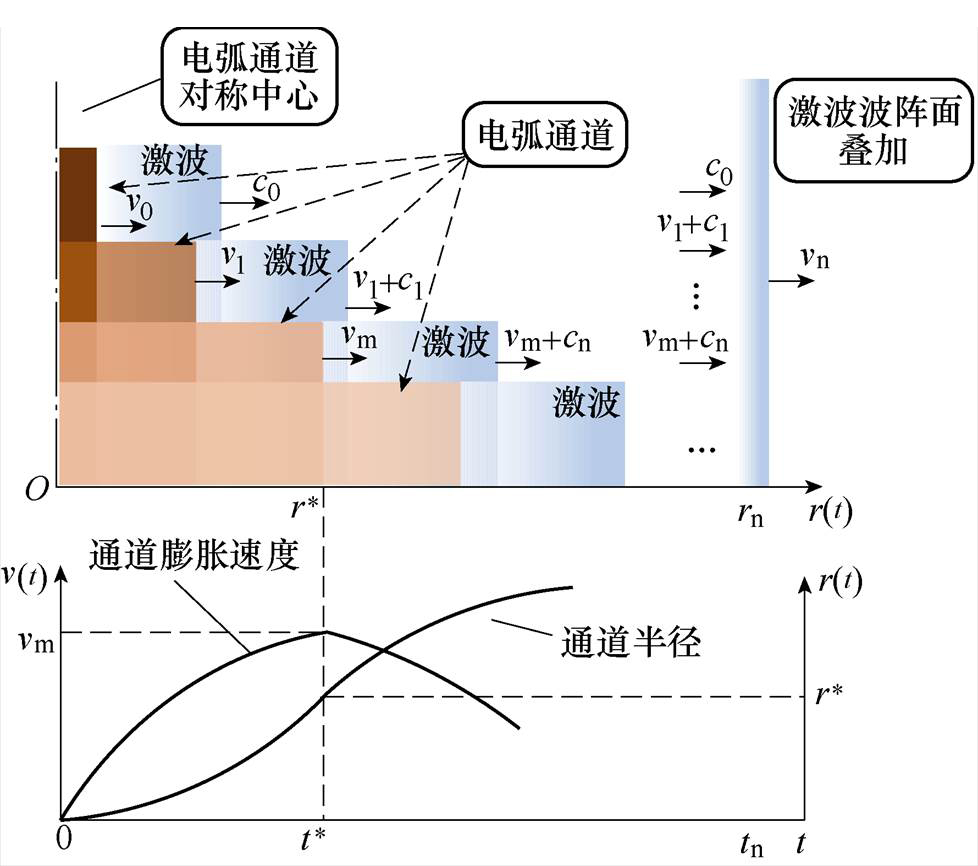
图6 电弧通道产生激波过程
Fig.6 Process diagram of shock waves generat ed by arc channel
因此，在通道膨胀阶段可以忽略热辐射和光辐射等，认为通过焦耳加热传递到电弧通道中的能量是电弧通道内能和电弧通道向外膨胀所做功之和，建立能量平衡方程为
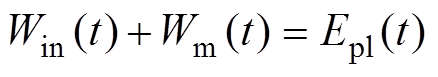（3）式中，Win(t)为电弧通道的内能；Wm(t)为电弧通道膨胀对周围液体所做功；Epl(t)为通过焦耳热注入电弧通道中的能量。通过对注入通道的有功功率积分可以得到Epl(t)为
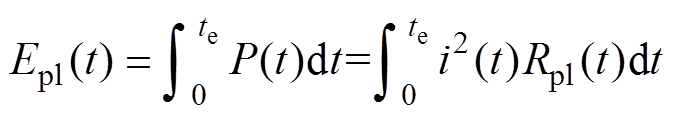（4）
式中，P(t)为注入电弧通道中的有功功率；i(t)为电弧通道的电流；Rpl(t)为电弧通道电阻；te为能量注入时间。
建立Win(t)表达式时，假设电弧通道内的气体由水电离形成，且绝热蒸汽混合物表现为具有恒定绝热系数g 的理想气体，在此条件下Win(t)表达式为
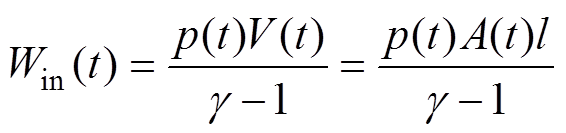（5）式中，p(t)为电弧通道内的压强；V(t)为电弧通道体积；A(t)为电弧通道的横截面积；l为电弧通道长度；g 为绝热系数。
Wm(t)表达式建立时存在一个前提条件：考虑到激波形成时前缘宽度较窄，激波前缘内的压力可视为均匀分布，因此在电弧通道与激波前沿的交界面上，电弧通道侧压力与激波前沿压力相同，则Wm(t)可表示为
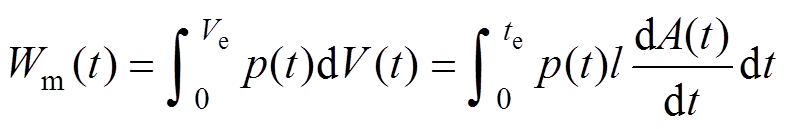（6）式中，Ve为能量注入结束后的空腔体积。
联立方程式（3）～式（6）得到
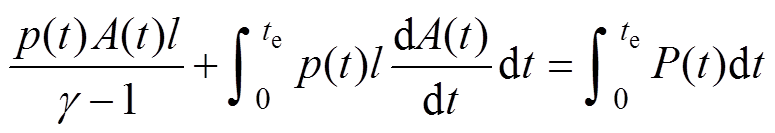（7）通过将式（7）微分并整理，得到电弧通道中的功率平衡方程为
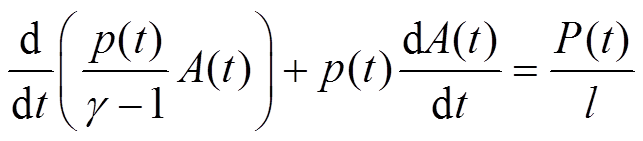（8）
再假设电弧通道侧压力与激波压力相同，在此条件下，水分子的质量守恒方程和动量守恒方程在激波前沿成立，分别为
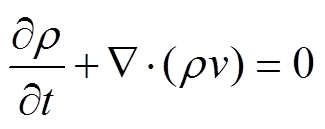（9）
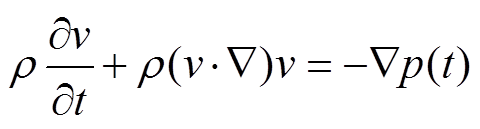（10）
假定未扰动水中的密度、速度和压强分别为r0、v0、p0，压缩区域中水的密度、速度和压强分别为r、v、p(t)，使用激波速度（v0=drc(t)/dt）代替激波前水分子的速度，则式（9）、式（10）变为
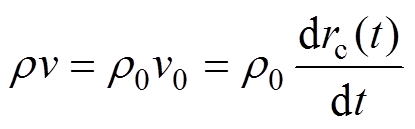（11）
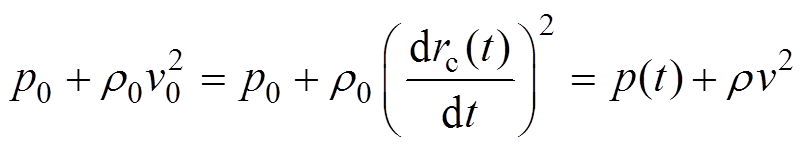（12）
式中，rc(t)为激波的运动位置。
为了求解激波压强，需要借助水的状态方程，有
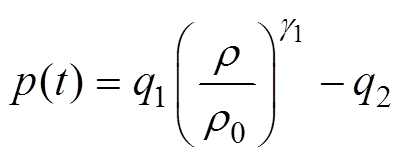（13）式中，p(t)为激波压强；q1、q2为常数；g1=7；q1= 3.001×108Pa；q2=3×108Pa。考虑到p(t)
p0，联立方程式（11）～式（13）得到激波的表达式为
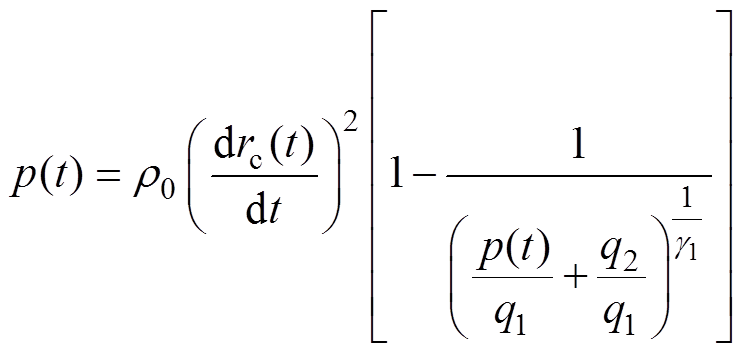（14）
等式最右侧一项变化范围很小，当压强在2～3MPa范围内变化时，其数值接近0.5。因此激波的表达式[25]可以简化为
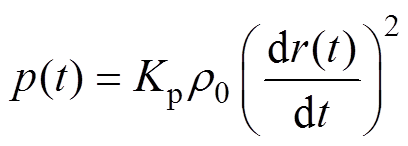（15）式中，r0为未扰动水的密度；Kp为比例系数；r(t)为电弧通道半径。将简化后的激波表达式（15）近似代替电弧通道的激波表达式（14）[28]，得到修正以后的功率平衡方程为
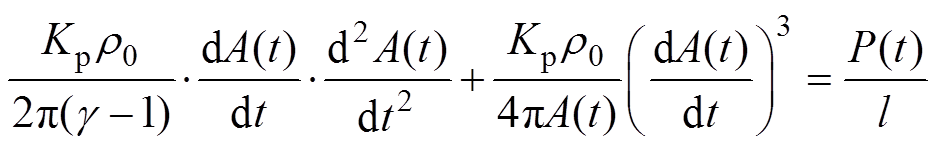（16）
其中
A(t)=pr2(t)
将式（16）做变量代换后得
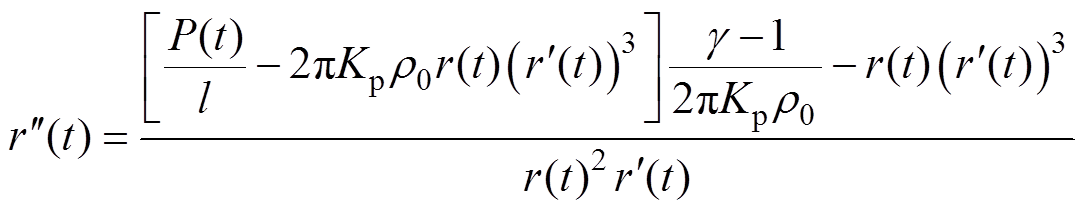（17）由式（17）可知，若要对通道的半径变化进行计算，需要求解电弧通道的电阻进而得到通过焦耳热计算注入电弧通道中的能量Epl(t)。通常可以借助水中电弧通道阻抗模型进行求解。
3.2.1 借助阻抗模型求解
S. I. Braginskii提出通道内等离子体-蒸汽混合物的内能由离子的动能、离解能和电离能组成，电弧通道阻抗与其内能建立的经验模型[25]为
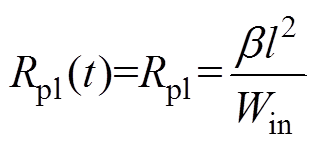（18）式中，b 为与试验装置相关的放电系数。考虑通道初期的能量主要转化内能，Liu Siwei等提出了一种改进的Braginskii经验公式，采用电弧通道的沉积能量Wpl代替电弧通道内能[29]，即
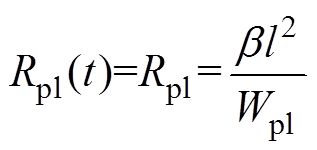（19）
式中，Wpl为电弧通道的沉积能量。Ren Yijia等给出了b 的确定方法，但是计算过程较为复杂，且b 参数受到试验平台特性（如电极形状、液体性质等）的影响，对于不同的试验设置，其数值需要重新计算且较为复杂[30]。
3.2.2 借助实测数据求解
通过实测的通道两端电压与通道电流可以更为准确地获取通道注入能量。但是通道电感的存在使得电压与电流存在相位差，直接计算注入能量会引起较大的误差。水中大电流脉冲放电时，测量得到的电压信号包含感性分量和阻性分量。所测量的间隙电压与间隙电流的关系[28]可表示为
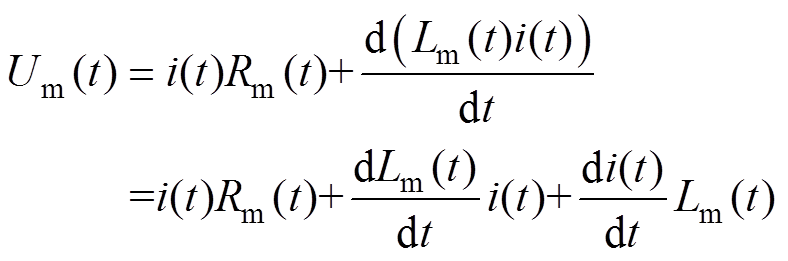（20）式中，Um(t)为试验中获得的间隙两端电压；Lm(t)为电弧通道的时变电感；Rm(t)为所测量的电阻，Rm(t)=Rpl(t)，Rpl(t)为电弧通道的时变电阻。另外，主放电时间内电弧通道的长度相对固定，电弧通道的电感随时间的变化量较小，i(t)dLm(t)/dt相对于Lm(t)di(t)/dt可忽略不计，式（20）可表示为
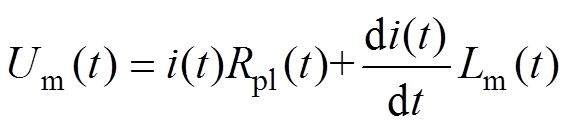（21）
对试验中获取的电压和电流波形数据分段拟合，借助电流波形的过零点并且计算电流的一阶导数值，可求取电弧通道时变电阻与电感。假设电流波形上某数据点为n，示波器的采样间隔为Dt，对任意时刻t有t=nDt（n=0, 1, 2,…, N），该点电感值为某一常数，即
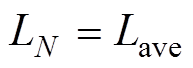（22）(n-1)Dt时刻对应的状态参量[UN-1, IN-1, RN-1, LN-1]和nDt时刻对应的状态参量[UN, IN, RN, LN]满足
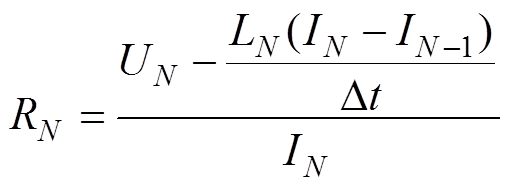（23）
考虑到采样间隔（本文为8ns）很短，电阻R的变化值可忽略不计，因此将n-1处的电阻定义为
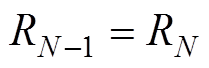（24）利用RN-1的值计算一个新的电感值，即
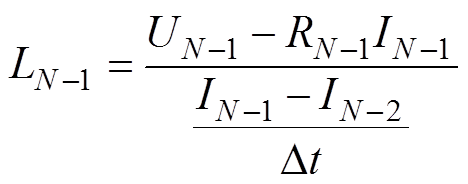（25）
然后再将n-2处的电感值设置为n-1处的电感值，将式（23）～式（25）进行迭代运算，即可求得不同时刻下的电弧电感Lm(t)与电弧电阻Rpl(t)。该方法原理简单，有效地剥离了电感和电阻分量，但是在求解过程中易出现结果不收敛，可对试验数据进行平滑预处理。通过剥离电感与电阻分量，就可以借助焦耳定律求取任意时刻注入到电弧通道中的有功功率及能量，即
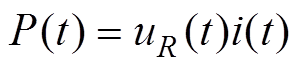（26）式中，uR(t)为电弧通道电压的电阻分量。
通过以上两种方法，计算注入电弧通道中的功率与电流曲线如图7所示。由图7可知，借助实测数据得到的有功功率峰值时间tpr1=210ms，峰值Pm1= 21.32MW，电流峰值时间tcr1=212ms，峰值Im1=12.17kA，有功功率及电流的第一个半周期T1=15ms；而借助阻抗模型得到的有功功率峰值时间tpr2=209ms，峰值Pm2=21.23MW，电流峰值时间tcr2=211ms，峰值Im2= 10.90kA，有功功率及电流的第一个半周期T2=17ms。采用电弧阻抗模型获得的功率曲线与实测结果仍存在较大的差异，这主要是模型的假设和参数选取引起的。
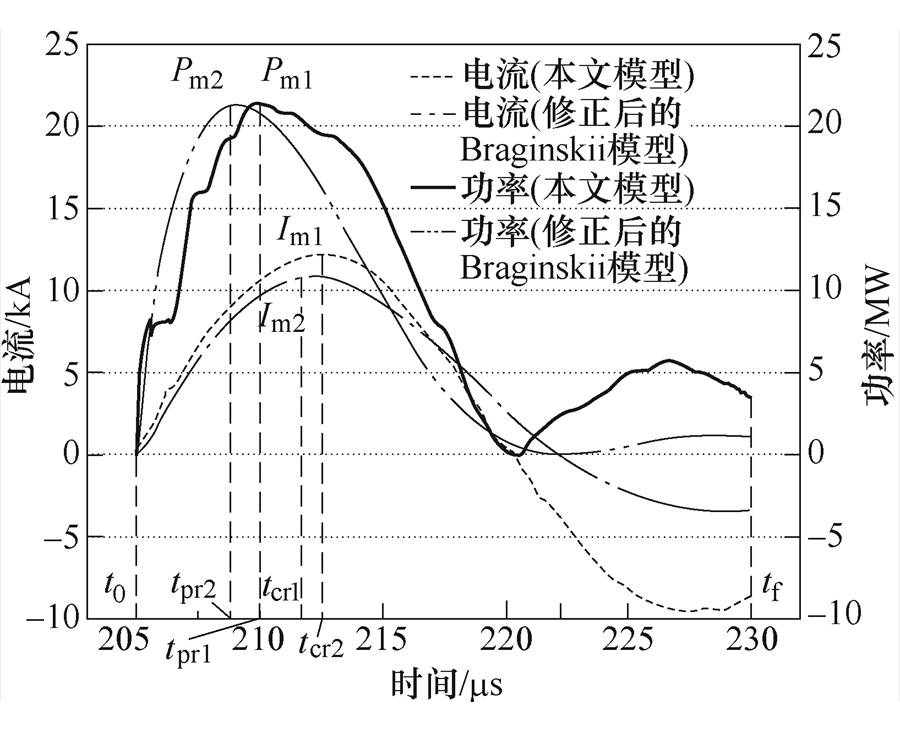
图7 注入电弧通道中的功率与电流曲线
Fig.7 Power curves and current curves injected into the arc channel
式（17）中，g 为绝热系数，因为水中大电流脉冲放电的非理想等离子体由许多不同的成分组成，因此确定热力学参数g 的计算非常复杂。I. Z. Okun研究计算了电弧通道内绝热系数的值，这些计算是基于氢氧等离子体的瞬态空穴含量，其中，离子总数等于电子数[31]。其假设电离气体内能包含动能、液体分子的离解能和电离能[31]三个主要部分。这种假设研究空腔内部粒子及其内能的方法与R. H. Mellen等的分析模型类似，最终得到的绝热系数 g ≈1.26[32]。G. L. Chahine等通过将水中电弧通道动力学试验数据与基于Rayleigh-Plesset方程的仿真结果进行对比分析，得出了g 值，发现g ≈1.4时匹配最佳[33]。g 在其他文献中取值有1.25[34]、1.33[35]和1.22～1.3[36]。综合考虑，本文模型中选择g =1.3。
L. K. Warne等给出了Kp=2[28]，l=0.015m；采用在室温下的密度r0=1×103kg/m3；将电压中的电感分量剥除以后，借助式（26）计算得到P(t)。
3.4.1 电弧通道发展不同求解过程对比
模型采用试验与仿真相结合的方式获得电弧通道发展过程，电弧通道发展过程分析流程如图8所示。水中放电综合观测平台搭建完成后，首先完成放电数据的获取，包括放电过程中电弧发展的高速相机图像、间隙电压及电流数据。得到数据后，一方面，对捕捉到图片进行处理，计算得到实测电弧通道半径及速度变化曲线；另一方面，剥离电压信号中的电感分量，借助焦耳定律得到注入到电弧通道中的功率P(t)并将其与通道能量平衡方程联立，求解得到电弧通道半径及速度变化曲线。同样借助阻抗模型求解注入通道的功率P(t)，可以得到电弧通道半径及速度半径变化曲线，将三种方式得到的结果进行对比。
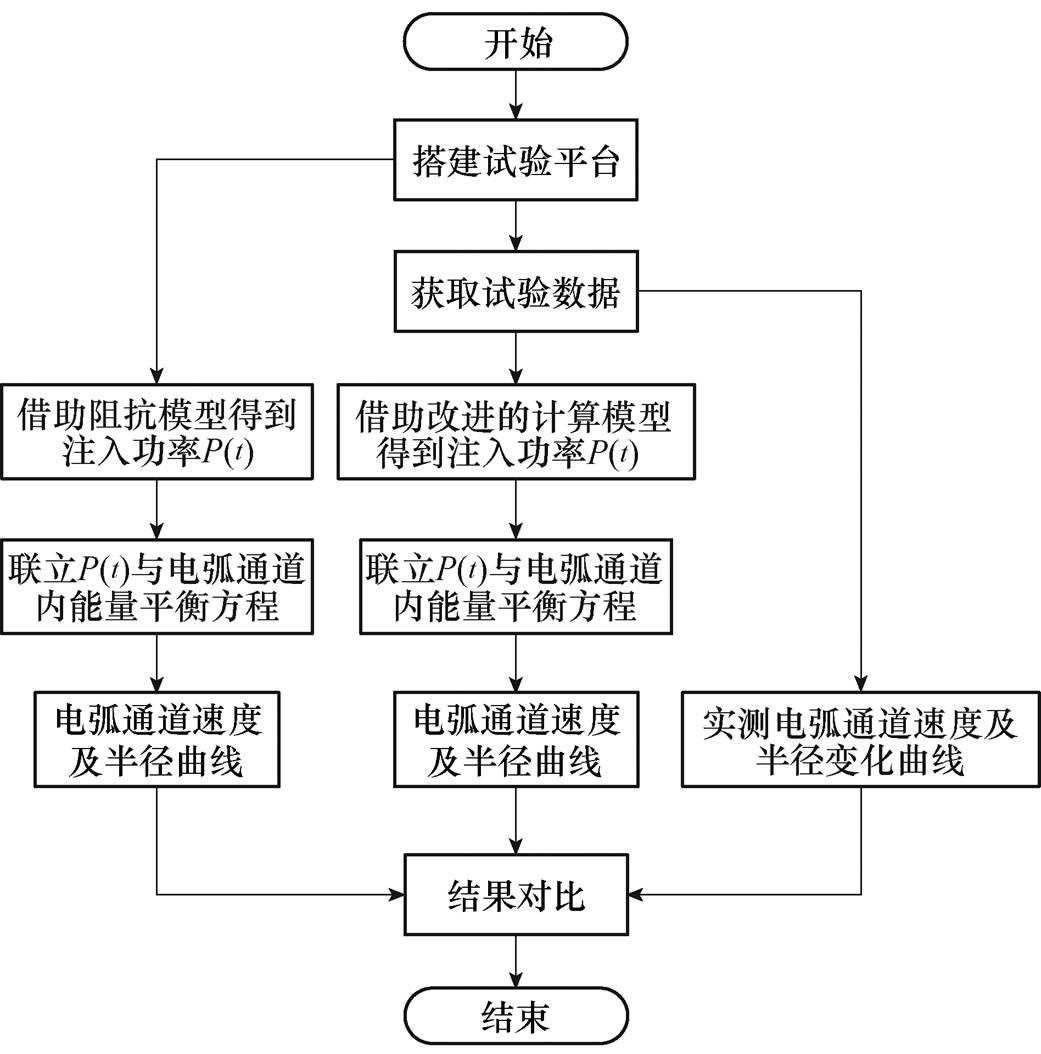
图8 电弧通道发展过程分析流程
Fig.8 Analysis flow chart of arc channel development process
3.4.2 仿真与试验结果对比分析
通过试验及仿真的方式可得到电弧通道半径及速度变化曲线。迭代发现，初始速度设置为100m/s，初始电弧半径为0.5mm，可以得到模型仿真结果，电弧通道半径仿真与试验结果对比如图9所示。
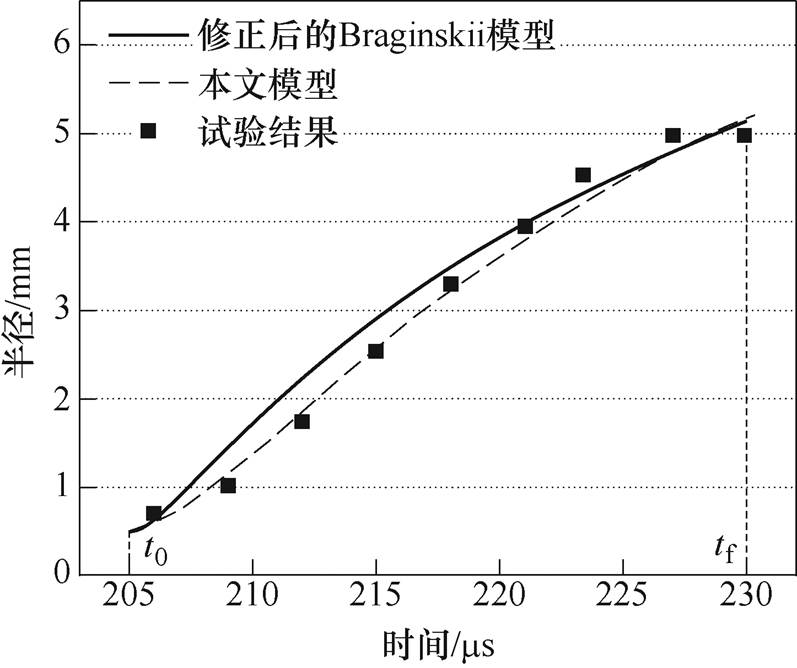
图9 电弧通道半径仿真与试验结果对比
Fig.9 Comparison of simulation and test results of arc expansion radius
根据图9可得，通过阻抗模型及剥离电感分量的方法均可以得到电弧通道半径变化曲线，但是在前期阶段（205ms＜t＜220ms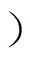
，本文模型吻合度 较好。
电弧通道膨胀速度变化仿真与试验对比如图10所示，图中，t0=205ms，tf =230ms。由图可知，峰值时间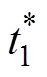
=210.64ms，
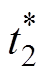=207.63ms，
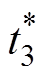=211.87ms，速度峰值Vm1=245.82m/s，Vm2=278.61m/s，Vm3= 267.21m/s。相比于实测值，本文模型峰值时间及峰值均较小，而对于借助阻抗模型得到的结果，其峰值时间小于实测值，而峰值大于实测值。
图10 电弧通道膨胀速度变化仿真与试验对比
Fig.10 Comparison of simulation and experiment of arc expansion speed change
据图9和图10可知，改进后的电弧通道发展过程计算模型在电弧通道膨胀加速阶段与实测数据吻合度较好，可以较好地反映电弧通道加速膨胀过程特性。
剥离电感分量后电压、电流曲线如图11所示，间隙击穿后，电压存在小幅抖动。由图7、图11可知，改进后模型得到的注入功率P(t)可以反映出击穿后的电压与电流抖动，得到实际的注入功率，这是借助阻抗模型所无法反映出的。
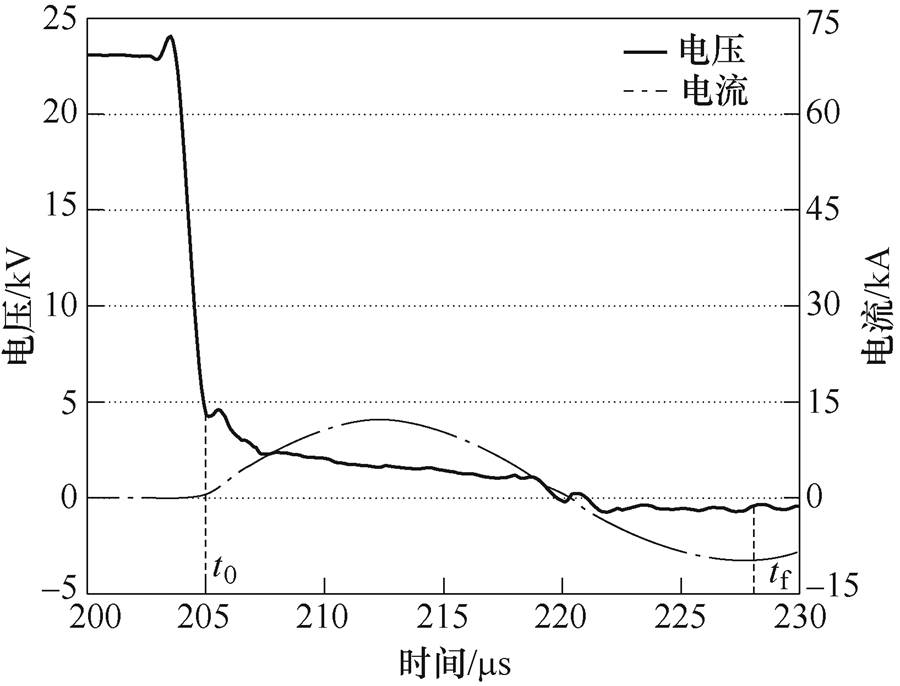
图11 剥离电感分量后电压、电流曲线
Fig.11 Voltage and current curves after stripping inductance component
改进后的模型在通道速度降低阶段吻合度较差，原因可能为：
（1）剥离电感分量时认为，电弧放电过程中电弧通道的长度相对固定，电弧通道的电感随时间的变化量较小，i(t)dLm(t)/dt相对于Lm(t)di(t)/dt可忽略不计，实际上在电流为脉冲信号时，直接忽略该项时会产生影响，造成的误差有待确定。
（2）考虑到相机的拍摄帧率较低（文中3ms），记录的电弧通道发展图像较少，得到的实测速度为平均速度，因此实测曲线的准确度也有待改进。
水中大电流脉冲放电产生激波的峰值主要取决于电弧通道的加速膨胀过程。利用能量平衡方程建立水中大电流脉冲放电通道发展分析计算模型，通过剥离电阻、电感分量，得到更加贴合实际的电弧通道注入功率，并通过求解能量平衡方程得到电弧通道半径及速度变化曲线。改进的电弧通道发展过程计算模型，在加速膨胀阶段可以更好地反映电弧通道的宏观发展过程。如果采用拍摄速率比较高的相机，可获得更加准确的实测曲线，从而对模型进行修正。
参考文献
[1] 徐箭, 廖思阳, 魏聪颖, 等. 基于广域量测信息的配电网协调控制技术展望[J]. 电力系统自动化, 2020, 44(18): 12-24.
Xu Jian, Liao Siyang, Wei Congying, et al. Prospect of distribution network coordinated control tech- nology based on wide area measurement infor- mation[J]. Automation of Electric Power Systems, 2020, 44(18): 12-24.
[2] 李军, 李世昌. 基于K-SVD-OMP的稀疏表示方法在电力负荷预测中的应用[J]. 电机与控制学报, 2020, 24(9): 156-164, 172.
Li Jun, Li Shichang. Application of sparse represent- ation method based on K-SVD-OMP in power load forecasting[J]. Electric Machines and Control, 2020, 24(9): 156-164, 172.
[3] 赵希梅, 刘超, 朱国昕. 永磁直线同步电机自适应非线性滑模控制[J]. 电机与控制学报, 2020, 24(7): 39-47.
Zhao Ximei, Liu Chao, Zhu Guoxin. Adaptive nonlinear sliding mode control of permanent magnet linear synchronous motor[J]. Electric Machines and Control, 2020, 24(7): 39-47.
[4] Zhang Dongdong, Liu Tianhao. Effects of voltage sag on the performance of induction motor based on a new transient sequence component method[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(3): 316-324.
[5] 刘克富, 赵海洋, 邱剑. 快脉冲放电等离子体用于难降解污水处理[J]. 高电压技术, 2009, 34(1): 12-16.
Liu Kefu, Zhao Haiyang, Qiu Jian. Fast pulsed discharge plasma for the treatment of refractory sewage[J]. High Voltage Engineering, 2009, 34(1): 12-16.
[6] 律方成, 詹振宇, 张立国, 等. 等离子体氟化改性微米AlN填料对环氧树脂绝缘性能的影响[J]. 电工技术学报, 2019, 34(16): 3522-3531.
Lü Fangcheng, Zhan Zhenyu, Zhang Liguo, et al. Effect of plasma fluorinated micron AlN fillers on the insulation properties of epoxy resin[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3522-3531.
[7] 张凯, 王瑞雪, 韩伟, 等. 等离子体重油加工技术研究进展[J]. 电工技术学报, 2016, 31(24): 1-15.
Zhang Kai, Wang Ruixue, Han Wei, et al. Research progress of plasma body weight oil processing technology[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 1-15.
[8] 王志强, 曹云霄, 邢政伟, 等. 高压脉冲放电破碎菱镁矿石的实验研究[J]. 电工技术学报, 2019, 34(4): 863-870.
Wang Zhiqiang, Cao Yunxiao, Xing Zhengwei, et al. Experimental study on crushing magnesite ore by high voltage pulse discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 863-870.
[9] 刘毅, 李志远, 李显东, 等. 水中脉冲激波对模拟岩层破碎试验[J]. 电工技术学报, 2016, 31(24): 71-78.
Liu Yi, Li Zhiyuan, Li Xiandong, et al. Test of simulated rock breaking by underwater pulsed shock waves[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 71-78.
[10] 孙昊, 张帅, 韩伟, 等. 纳秒脉冲火花放电高效转化甲烷的实验研究[J]. 电工技术学报, 2019, 34(4): 880-888.
Sun Hao, Zhang Shuai, Han Wei, et al. Experimental study on high-efficiency conversion of methane by nanosecond pulse spark discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 880-888.
[11] 吴世林, 杨庆, 邵涛. 低温等离子体表面改性电极材料对液体电介质电荷注入的影响[J]. 电工技术学报, 2019, 34(16): 3494-3503.
Wu Shilin, Yang Qing, Shao Tao. Effect of low temperature plasma surface modified electrode materials on charge injection in liquid dielectric[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3494-3503.
[12] 张开放, 张黎, 李宗蔚, 等. 高频正弦电应力下气-固绝缘沿面放电现象及特征分析[J]. 电工技术学报, 2019, 34(15): 3275-3284.
Zhang Kaifang, Zhang Li, Li Zongwei, et al. Analysis of the surface discharge phenomena and characteri- stics of gas-solid insulation under high frequency sinusoidal electrical stress[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3275-3284.
[13] Claverie A, Deroy J, Boustie M, et al. Experimental characterization of plasma formation and shockwave propagation induced by high power pulsed underwater electrical discharge[J]. Review of Scientific Instru- ments, 2014, 85(6): 625-636.
[14] Martin E A. Experimental investigation of a high- energy density, high-pressure arc plasma[J]. Journal of Applied Physics, 1960, 31(2): 255-267.
[15] Lu Xinpei, Pan Yuan, Liu Kefu, et al. Spark model of pulsed discharge in water[J]. Journal of Applied Physics, 2002, 91(1): 24-31.
[16] Chung K J, Lee S G, Hwang Y S, et al. Modeling of pulsed spark discharge in water and its application to well cleaning[J]. Current Applied Physics, 2015, 15(9): 977-986.
[17] Li Xingwen, Chao Youchuang, Wu Jian, et al. Study of the shock waves characteristics generated by underwater electrical wire explosion[J]. Journal of Applied Physics, 2015, 118(2): 023301.1-023301.8.
[18] Otsuka M, Itoh S. Destruction of concrete block using underwater shock wave generated by electric discharge[C]//ASME Pressure Vessels and Piping Conference, Vancouver, BC, Canada, 2006, 47551: 189-194.
[19] Smirnov A P, Zhekul V G, Poklonov S G. The influence of the hydrostatic pressure on the parameters of a pressure wave generated by an electric discharge in a fluid[J]. Surface Engineering and Applied Electrochemistry, 2014, 50(3): 233-237.
[20] Katsuki S, Tanaka K, Fudamoto T, et al. Shock waves due to pulsed streamer discharges in water[J]. Japanese Journal of Applied Physics, 2006, 45(1R): 239.
[21] Itoh S, Suzuki O, Nagano S, et al. Investigations of fundamental properties of underwater shock waves by high-speed photography[J]. Proceedings of SPIE-the International Society for Optical Engineering, 1995, 2513: 916-927.
[22] Lisitsyn I V, Muraki T, Akiyama H. Characterization of a shock wave generated by a wire explosion in water[J]. Journal of the Acoustical Society of Japan, 2011,18(2): 89-91.
[23] Han Yibo, Liu Yi, Lin Fuchang, et al. Experimental investigation of arc formation and bubble expansion initiated by pulse discharge in water[C]//2015 IEEE Pulsed Power Conference (PPC), Austin, TX, 2015: 1-5.
[24] Liu Siwei, Liu Yi, Ren Yijia, et al. Characteristic analysis of plasma channel and shock wave in electrohydraulic pulsed discharge[J]. Physics of Plasmas, 2019, 26(9): 093509.
[25] Braginskii S I. Theory of the development of a spark channel[J]. Soviet Physics JETP, 1958, 34(7): 1068- 1074.
[26] Sun Bing, Kunitomo S, Igarashi C. Characteristics of ultraviolet light and radicals formed by pulsed discharge in water[J]. Journal of Physics D: Applied Physics, 2006, 39(17): 3814.
[27] Roberts R M, Cook J A, Rogers R L, et al. The energy partition of underwater sparks[J]. The Journal of the Acoustical Society of America, 1996, 99(6): 3465- 3475.
[28] Warne L K, Jorgenson R E, Lehr J M. Resistance of a water spark[R]. Sandia National Laboratories, 2005.
[29] Liu Siwei, Liu Yi, Ren Yijia, et al. Influence of plasma channel impedance model on electrohydraulic shockwave simulation[J]. Physics of Plasmas, 2019, 26(2): 023522.
[30] Liu Yi, Ren Yijia, Lin Fuchang, et al. Determination of the discharge coefficient in improved empirical impedance model of plasma channel for underwater spark discharge[J]. IEEE Transactions on Plasma Science, 2019, 48(1): 196-203.
[31] Okun I Z. Plasma parameters in a pulsed discharge in a liquid[J]. Soviet Physics Technical Physics, 1971, 16: 227.
[32] Mellen R H. An experimental study of the collapse of a spherical cavity in water[J]. The Journal of the Acoustical Society of America, 1956, 28(3): 447-454.
[33] Chahine G L, Frederick G S, Lambrecht C J, et al. Spark-generated bubbles as laboratory-scale models of underwater explosions and their use for validation of simulation tools[C]//The 66th Shock and Vibration Symposium, Biloxi, MS, 1995, 2: 265-277.
[34] Vokurka K. A model of spark and laser generated bubbles[J]. Czechoslovak Journal of Physics B, 1988, 38(1): 27-34.
[35] Gidalevich E, Boxman R L, Goldsmith S. Hydro- dynamic effects in liquids subjected to pulsed low current arc discharges[J]. Journal of Physics D: Applied Physics, 2004, 37(10): 1509.
[36] Shneerson G A. Estimation of the pressure in a “slow” spark discharge in a cylindrical water-filled chamber[J]. Technical Physics, 2003, 48(3): 374-375.
Analysis on the Development Process of Arc Channel for Underwater High Current Pulsed Discharge
Abstract There are two problems in solving the arc channel injection energy with the help of the bragenskii impedance model. The first problem is that the process of solving the discharge coefficient related to the experimental setup is complicated, and the second problem is that the solution results are difficult to accurately reflect the channel development characteristics. Therefore, an analysis method of arc channel development process of underwater high current pulsed discharge based on arc channel voltage and current is proposed. The “piston” model was used to describe the rapid expansion process of the channel and the mechanism of shock wave generation. Based on the measured voltage and current of arc channel, removing the inductance component, a method to calculate the injected channel energy was proposed. The energy balance equation was used to model and analyze the channel development process. Compared with the solution results based on the Braginskii impedance model, the method proposed in this paper can more accurately describe the accelerated expansion characteristics of the arc channel, and can provide a basis for in-depth exploration of the development mechanism of the arc channel.
keywords：Discharge in water, high pulsed current, arc channel, energy balance equation, impedance model
DOI: 10.19595/j.cnki.1000-6753.tces.200541
中图分类号：TM85
刘 毅 男，1985年生，博士，副教授，研究方向为液电脉冲等离子体及其应用、电力设备故障诊断。E-mail: yiliu@hust.edu.cn（通信作者）
赵 勇 男，1997年生，硕士研究生，研究方向为液电脉冲等离子体及其应用。E-mail: 1046728699@qq.com
收稿日期 2020-05-25
改稿日期 2020-11-23
国家自然科学基金资助项目（51877095）。
（编辑 陈 诚）