针对直流偏移和谐波干扰的单相锁相环
曾 君1 岑德海1 陈 润1 刘俊峰2
(1. 华南理工大学电力学院 广州 510640 2. 华南理工大学自动化科学与工程学院 广州 510640)
摘要 针对电网普遍存在的直流偏移和谐波干扰等问题,提出一种基于二阶广义积分器锁相环(SOGI-PLL)的改进型锁相环算法。该方法在前级二阶广义积分器(SOGI)中增加积分支路并且改为固定频率结构,以抑制直流偏移和简化参数设计;在后级锁相环(PLL)环路中引入滑动平均值滤波器(MAF),去掉比例积分控制器的积分环节,以增强滤波性能和加快动态响应速度。利用伯德图分析和小信号模型推导等方法,指导改进结构设计,确定相应的参数。所提出的改进型单相锁相环技术可以有效地消除直流偏移和高频谐波,同时具备良好的动态性能和稳定性。最后,通过Matlab/Simulink仿真和相关实验验证了该方法的优越性。
关键词:二阶广义积分器 锁相环 直流偏移 谐波干扰
0 引言
全球性环境污染以及能源危机问题,极大地推动了分布式发电的发展。伴随着越来越多的以风能和太阳能等新能源为主的发电装置并入电网,对电力系统的并网控制技术提出了更严苛的要求[1-8]。锁相技术能够实时获取电网基波电压的相位、幅值,在实现安全稳定并网的过程中起着至关重要的作用。近年来,学者们提出了各种各样的相位同步技术,包括基于过零检测的方法[9]、卡尔曼滤波器[10]、加权最小二乘法估计[11]和递归离散傅里叶变换[12]等。其中,锁相环(Phase-Locked Loop, PLL)由鉴相器、环路滤波器和压控振荡器组成,结构简单、易于实现,在电力系统中得到了广泛应用[13]。
在理想三相并网系统中,使用最多的锁相技术是基于同步旋转坐标系的锁相环(Synchronous Reference Frame-Phase Locked Loop, SRF-PLL)[14],其特点是运用旋转坐标系变换的方法来完成鉴相器的功能,具有动态响应快、软件实现简单的特点。而在单相并网系统中,由于电压相量只有一个,不能直接进行坐标系变换,SRF-PLL实现起来比较困难[15]。为了解决这个问题,通常的做法是利用正交信号发生器(Quadrature Signal Generator, QSG)产生一个与输入电压等幅正交的电压相量,从而完成旋转坐标系变换。最早被提出的QSG是传输延时模块[16],该方法虽然能在电网电压频率处于额定值时得到满意的效果,但是当频率发生偏移时,QSG输出的信号不能保持正交,导致PLL的估算相位存在稳态误差。对输入信号进行求导运算,也能生成正交信号,然而会放大噪声[17]。文献[18]提出了基于Hilbert变换的QSG,该方法能在理想电网条件下无延时地生成正交信号,然而在频率偏移情况下性能会变差,并且计算量很大。基于卡尔曼滤波器的QSG即使在不理想电网条件下也能获得稳定的正交信号,但是复杂度高、不利于数字实现[19]。对比上述提到的QSG,二阶广义积分器(Second Order Generalized Integrator, SOGI)因为结构简单、计算量小、具有频率自适应性以及较好的滤波能力,近年来受到众多学者的关注,是构成单相PLL的理想选择[20-22]。
SOGI作为QSG,配合SRF-PLL构成的单相PLL,被广泛应用于单相并网系统,通常称为SOGI- PLL,其结构如图1所示。图中,v为输入电压信号,k为阻尼系数,va 和vb 为SOGI的输出正交信号,vd和vq为经过旋转坐标系变换获得的电压分量,kp和ki分别为比例系数、积分系数,wn为标称角频率,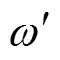 和
和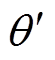 分别为估算角频率、估算相位。SOGI-PLL在理想正弦输入电压的条件下能够准确追踪基波电压相位,但仍存在以下不足:①虽然单相电压不存在基波负序分量,但是传统SOGI不能有效消除电压中的直流偏移,而且对高次谐波的抑制能力不足;②图1中,SOGI-PLL的频率自适应过程是通过SRF- PLL输出的估算频率反馈到SOGI来完成的,增加了控制的复杂性,并且使调谐敏感,从而降低稳定裕度;③SRF-PLL主要通过调节PI控制器参数来提高滤波能力,但是带宽必须相应地减小,动态响应变慢[14]。学者们为了解决上述问题,提出了一些改进型SOGI或SRF-PLL结构。文献[23]提出了通过加入低通滤波器(Low Pass Filter, LPF)来抑制直流分量和高次谐波的改进型SOGI结构,但是LPF的引入会产生延时,影响系统的动态性能。文献[24]提出了一种固定频率的SOGI结构,它不包含相互依赖的环路,从而增强了稳定性,但是依然存在不能有效抑制直流偏移的问题。
分别为估算角频率、估算相位。SOGI-PLL在理想正弦输入电压的条件下能够准确追踪基波电压相位,但仍存在以下不足:①虽然单相电压不存在基波负序分量,但是传统SOGI不能有效消除电压中的直流偏移,而且对高次谐波的抑制能力不足;②图1中,SOGI-PLL的频率自适应过程是通过SRF- PLL输出的估算频率反馈到SOGI来完成的,增加了控制的复杂性,并且使调谐敏感,从而降低稳定裕度;③SRF-PLL主要通过调节PI控制器参数来提高滤波能力,但是带宽必须相应地减小,动态响应变慢[14]。学者们为了解决上述问题,提出了一些改进型SOGI或SRF-PLL结构。文献[23]提出了通过加入低通滤波器(Low Pass Filter, LPF)来抑制直流分量和高次谐波的改进型SOGI结构,但是LPF的引入会产生延时,影响系统的动态性能。文献[24]提出了一种固定频率的SOGI结构,它不包含相互依赖的环路,从而增强了稳定性,但是依然存在不能有效抑制直流偏移的问题。
针对传统SOGI-PLL自身存在的缺点,本文提出了一种改进锁相环技术。首先,在SOGI结构中添加积分支路来抑制直流偏移,并把其改成固定频率结构以避免环路之间的相互干扰和优化参数设计。然后,在SRF-PLL环路中引入滑动平均值滤波器(Moving Average Filter, MAF)来消除高频谐波的影响,用P控制器代替PI控制器来提高系统的动态性能。该锁相环能够在复杂电网条件下准确获取基波正序电压的频率和相位,兼具动态响应快和鲁棒性强的特点。仿真和实验验证了该方法的有效性和优越性。
1 改进SOGI设计
1.1 传统SOGI
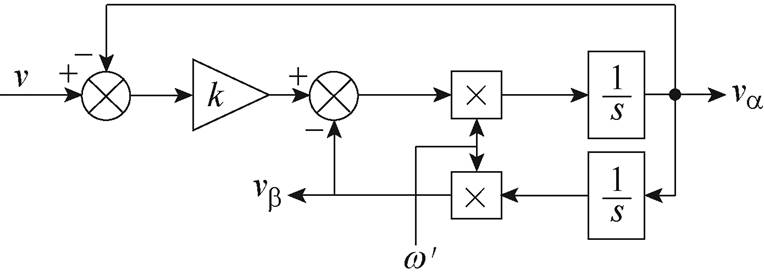
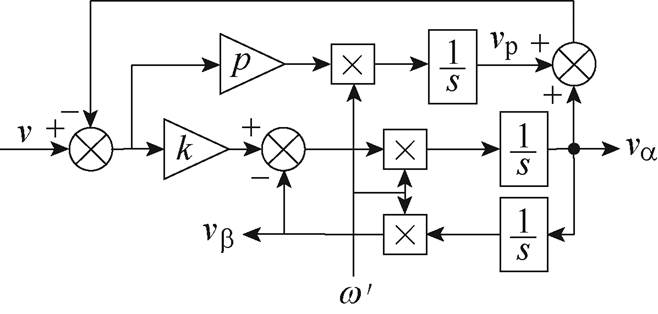
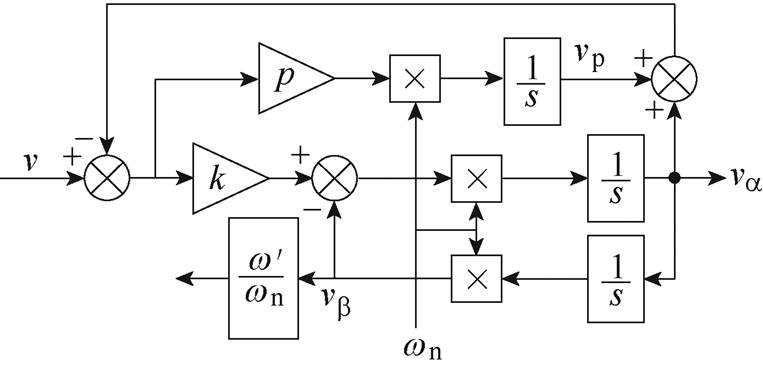
首先,介绍传统SOGI产生正交信号的原理,其结构框图如图2所示。
推导传递函数得到
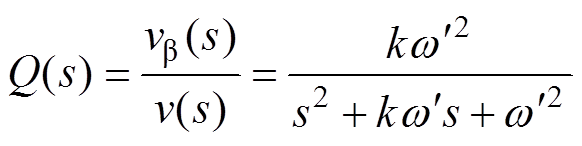 (2)
(2)
由式(1)、式(2)可知,D(s)是以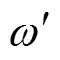 为中心角频率的二阶带通滤波器;Q(s)是以
为中心角频率的二阶带通滤波器;Q(s)是以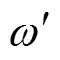 为交接角频率的二阶低通滤波器。当
为交接角频率的二阶低通滤波器。当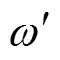 与输入电压角频率
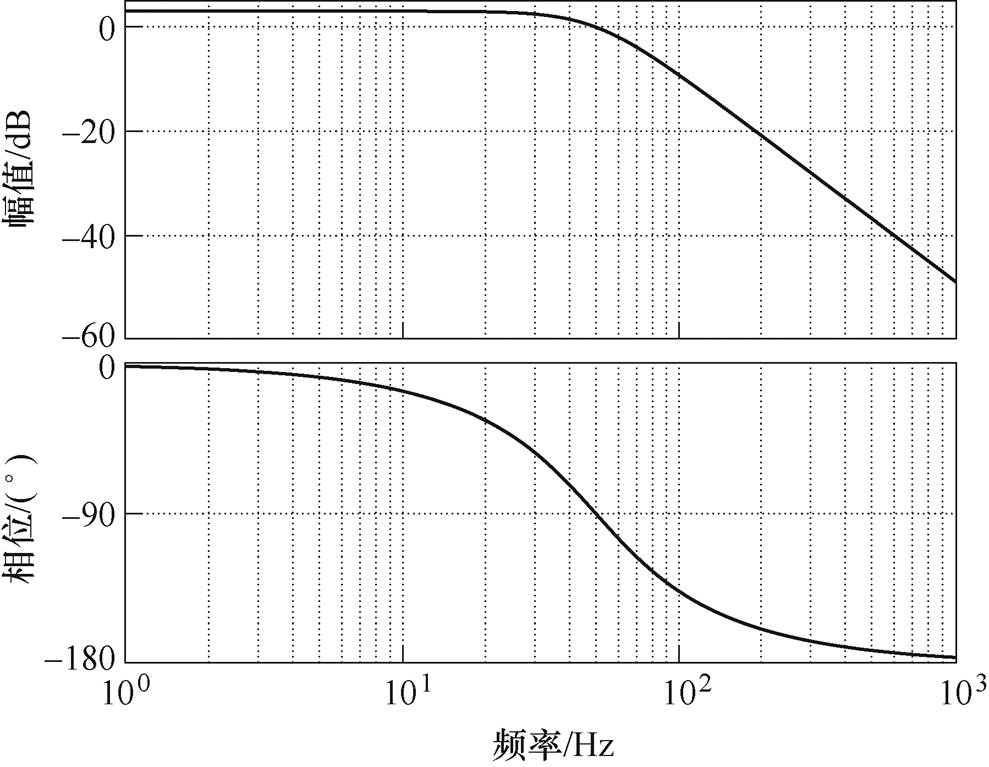
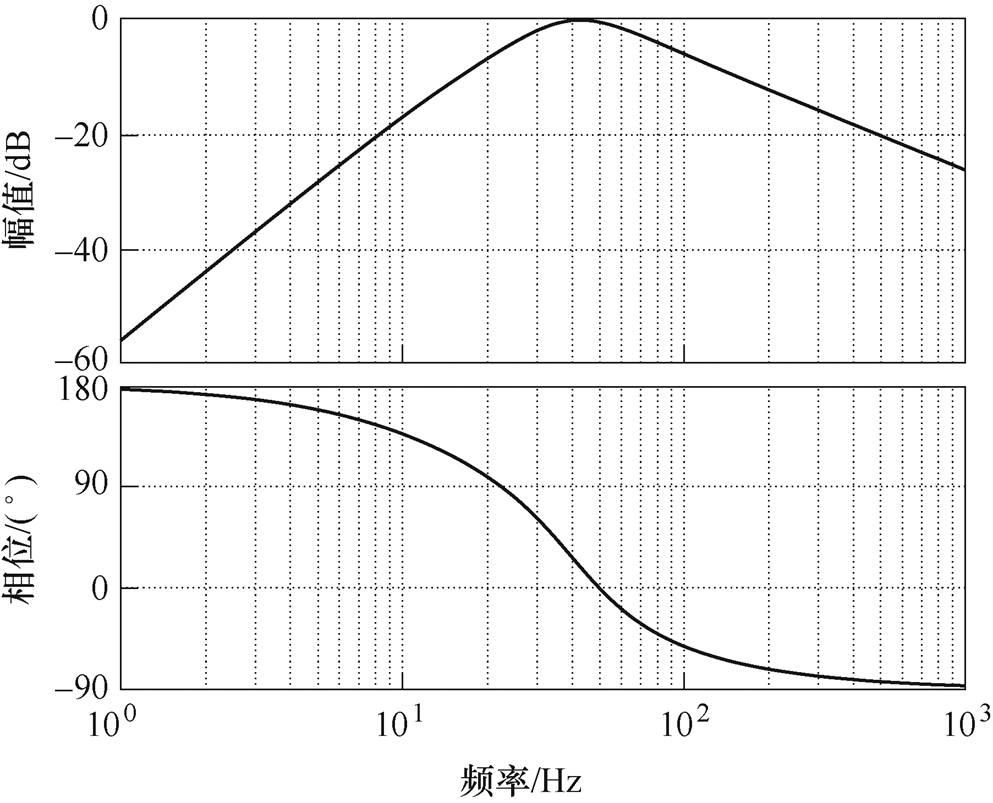
与输入电压角频率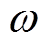 相等时,va 与v同相且幅值相等;vb 与v相位相差90°,幅值相等。因此,va 和vb 是一对正交等幅的电压信号,D(s)和Q(s)的伯德图分别如图3和图4所示。
相等时,va 与v同相且幅值相等;vb 与v相位相差90°,幅值相等。因此,va 和vb 是一对正交等幅的电压信号,D(s)和Q(s)的伯德图分别如图3和图4所示。
观察图3和图4可知,D(s)能有效消除输入电压中的直流偏移;但是Q(s)不能消除直流偏移,只能对高次谐波有一定的抑制作用。而且,D(s)和Q(s)都依赖于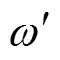 ,一旦
,一旦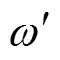 ≠
≠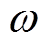 ,SOGI输出的正交信号会存在幅值衰减和相位偏差。因此,为了提高SOGI-PLL在复杂电网环境下的锁相性能,有必要对SOGI的结构进行改进和优化。
,SOGI输出的正交信号会存在幅值衰减和相位偏差。因此,为了提高SOGI-PLL在复杂电网环境下的锁相性能,有必要对SOGI的结构进行改进和优化。
1.2 改进的SOGI
本文在传统SOGI结构的基础上,通过添加第三个积分器的方式,增强正交信号发生器抑制直流偏移的能力,消除直流偏移的SOGI,如图5所示。图中,p为第三条积分支路的比例系数,vp为对应第三条积分支路的输出电压信号,其传递函数可表示为
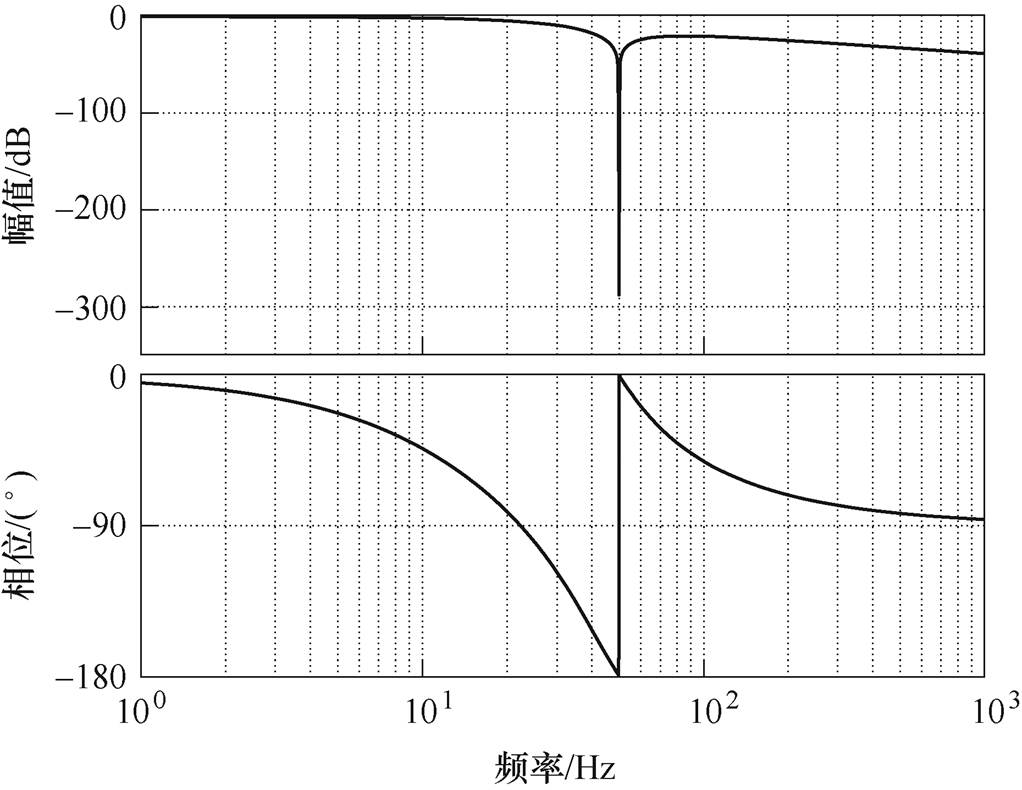
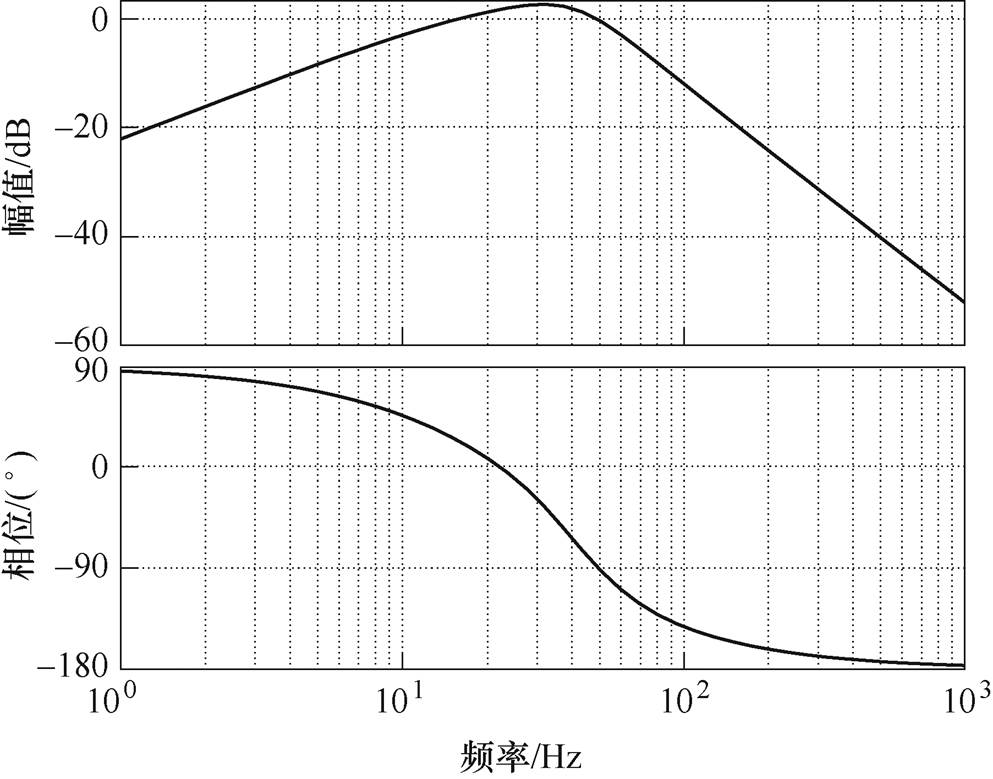
根据式(3)的表达式,可以画出其对应的伯德图,如图6所示。
显然,P1(s)是一个以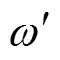 为带阻中心的陷波滤波器,很好地消除了角频率
为带阻中心的陷波滤波器,很好地消除了角频率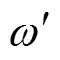 处的电压分量,而且对直流分量的增益为0dB,可以完整地保留直流偏移。当vp与va 共同构成负反馈支路返回输入端时,v就能在不影响基波电压信号的前提下消去直流偏移。为了进一步验证上述SOGI的性能,同理可推得其正交信号的传递函数及伯德图如图7所示。
处的电压分量,而且对直流分量的增益为0dB,可以完整地保留直流偏移。当vp与va 共同构成负反馈支路返回输入端时,v就能在不影响基波电压信号的前提下消去直流偏移。为了进一步验证上述SOGI的性能,同理可推得其正交信号的传递函数及伯德图如图7所示。
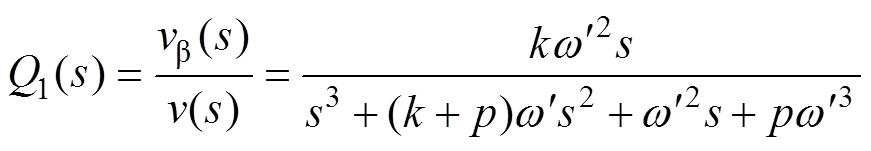 (5)
(5)
由式(4)和式(5)可知,当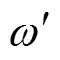 与输入电压角频率
与输入电压角频率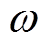 相等时,va 和vb 仍然是一对等幅正交的电压信号,因此第三条积分支路的引入并没有影响SOGI输出信号之间的相互关系。观察图3和图7,在低频段,D(s)的对数幅频特性是一条斜率为20dB/dec的直线,而D1(s)的对数幅频特性是一条斜率为40dB/dec的直线,抑制直流偏移的能力得到进一步的提升。对比图4和图8,Q(s)是低通滤波器,而Q1(s)是带通滤波器,抑制直流偏移的能力从无到有,发生了本质上的变化。
相等时,va 和vb 仍然是一对等幅正交的电压信号,因此第三条积分支路的引入并没有影响SOGI输出信号之间的相互关系。观察图3和图7,在低频段,D(s)的对数幅频特性是一条斜率为20dB/dec的直线,而D1(s)的对数幅频特性是一条斜率为40dB/dec的直线,抑制直流偏移的能力得到进一步的提升。对比图4和图8,Q(s)是低通滤波器,而Q1(s)是带通滤波器,抑制直流偏移的能力从无到有,发生了本质上的变化。
图5所示的SOGI结构虽然比传统SOGI具有更强的直流偏移抑制能力,但是仍存在一定的缺陷。D1(s)和Q1(s)都属于带通滤波器,依赖于中心角频率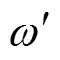 ,当输入电压发生频率偏移时,会造成输出信号的幅值衰减和相位偏差,在单相锁相环应用场合里,进一步导致估算相位存在稳态误差。通常情况下,如图1所示的频率自适应结构SOGI-PLL能够解决电网频率偏移带来的问题,然而SOGI和SRF-PLL之间存在反馈耦合回路,会增加控制难度和影响系统稳定性。此外,第三条积分支路引入参数p,加大了正交信号发生器参数设计的复杂程度。
,当输入电压发生频率偏移时,会造成输出信号的幅值衰减和相位偏差,在单相锁相环应用场合里,进一步导致估算相位存在稳态误差。通常情况下,如图1所示的频率自适应结构SOGI-PLL能够解决电网频率偏移带来的问题,然而SOGI和SRF-PLL之间存在反馈耦合回路,会增加控制难度和影响系统稳定性。此外,第三条积分支路引入参数p,加大了正交信号发生器参数设计的复杂程度。
针对上述问题,本文把可以消除直流偏移的SOGI改成固定频率结构,简称改进SOGI(Improved, ISOGI),其结构框图如图9所示。
观察图9可知,ISOGI在标称角频率wn处调谐。其中,wn=2p×50rad/s。被应用于单相锁相环时,无需频率反馈回路。因此,ISOGI与SRF-PLL之间没有相互依赖的环路,可以独立进行参数设计。同理,可由式(4)和式(5)推导得到ISOGI的传递函数分别为
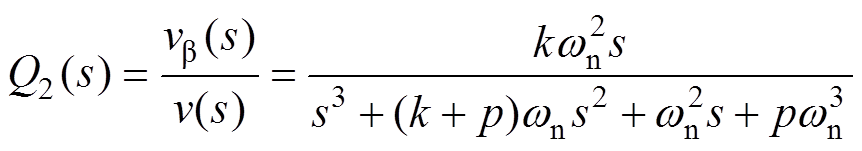 (7)
(7)
显然,va 和vb 的相位能够时刻保持正交关系。但是,当wn≠w 时,va 和vb 的幅值不相等,造成单相锁相环估算频率和估算相位中存在2次谐波[25]。仔细对比式(6)和式(7),vb(s)的幅值是va(s)的wn/w 倍,为了保持输出信号幅值大小一致,用va和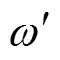 vb/wn代替va 和vb 作为正交信号发生器的输出信号。根据式(6)可知,当wn≠w 时,va 会滞后于v一个小相位j,其满足的关系式为
vb/wn代替va 和vb 作为正交信号发生器的输出信号。根据式(6)可知,当wn≠w 时,va 会滞后于v一个小相位j,其满足的关系式为
根据GB/T 15945《电能质量电力系统频率允许偏差》标准的规定,电力系统正常频率偏差允许值为±0.2Hz。一般情况下电网频率偏移很小,满足条件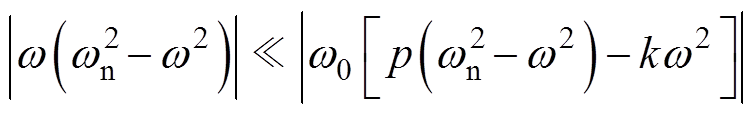 。令
。令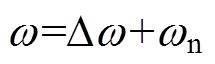 ,则滞后相位j 可近似计算为
,则滞后相位j 可近似计算为
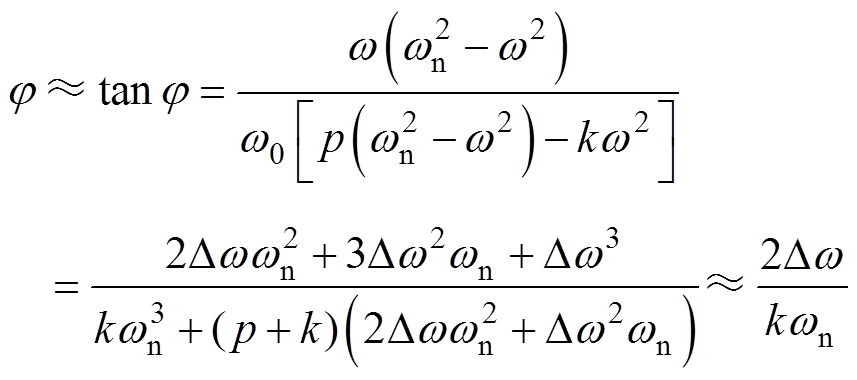 (9)
(9)
1.3 ISOGI的参数选择
从式(6)和式(7)能够看出,ISOGI传递函数的特征方程为D(s)=s3+(k+p)wns2+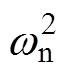 s+p
s+p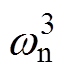 =0,可
=0,可
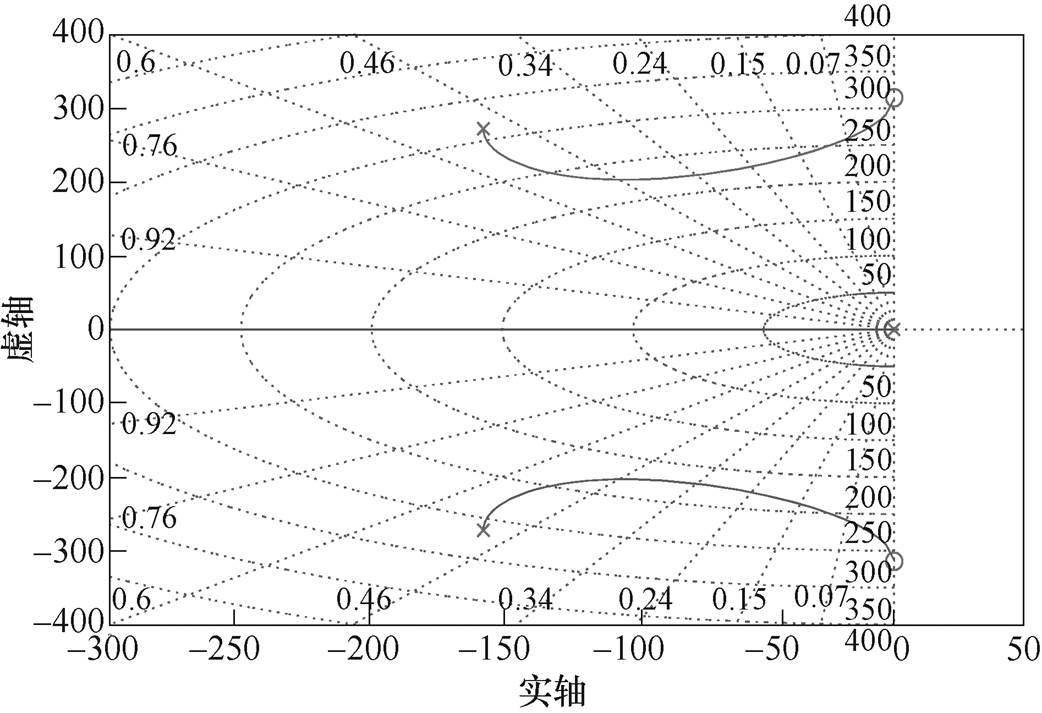
以根据特征方程的根来选择参数p。假设k=1,则D(s)关于参数p的根轨迹如图10所示。当p过小时,会造成直流偏移估算变慢;当p过大时,会引起输出正交信号的振荡。为了避免上述问题,需要对参数p进行折中选择。假设特征方程的三个根有相同的实部,即
根据式(10),求得p与k的函数关系式为
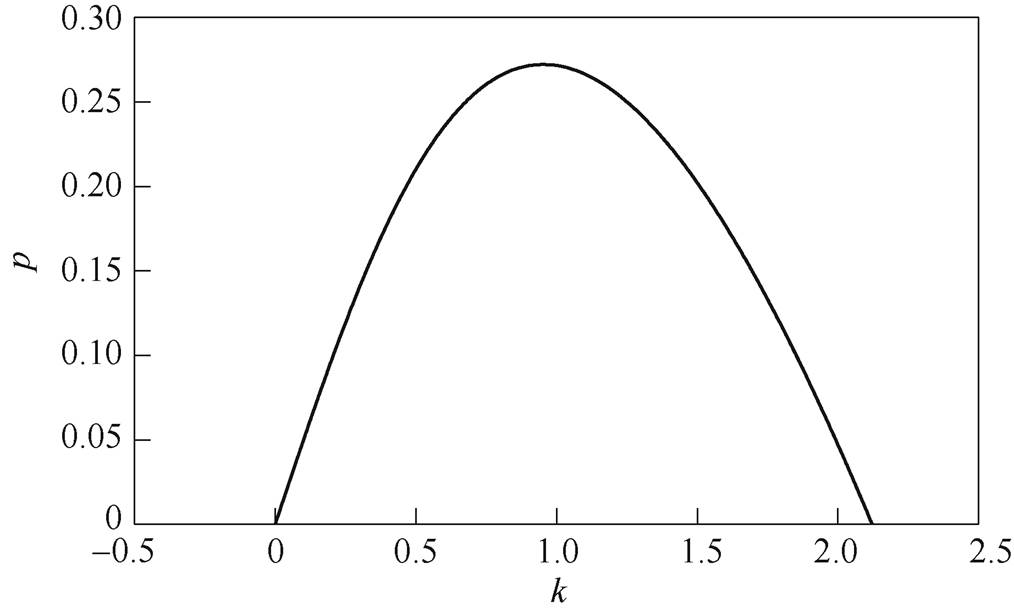
为了进一步验证上述参数设计方法的合理性,需要研究正交信号发生器的传递函数阶跃响应曲线。根据式(1)、式(6),可分别得到SOGI、ISOGI的传递函数阶跃响应为
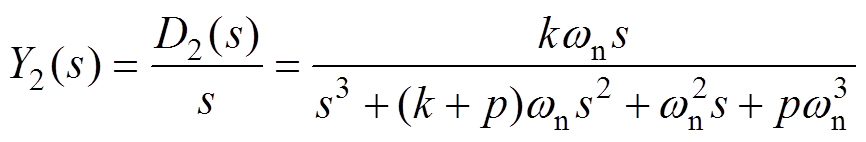 (13)
(13)
设定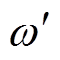 =wn,k=1,选取不同的p值,根据式(12)、式(13)绘制出D(s)和D2(s)的阶跃响应曲线如图12所示。观察图12,p取值的变化会影响ISOGI的动态响应速度。在一定范围内,p值越大,ISOGI的响应速度越快;当p>0.271 5时,ISOGI的响应速度逐渐变慢,开始出现振荡现象。图12中,SOGI的调节时间为29.6ms,而ISOGI的调节时间只有28.2ms。虽然,ISOGI通过添加第三个积分器来抑制直流偏移的方法会造成时间延迟,但是,采用本文提出的参数设计方法后,可以缩短ISOGI响应过程的调节时间,提升其动态性能。
=wn,k=1,选取不同的p值,根据式(12)、式(13)绘制出D(s)和D2(s)的阶跃响应曲线如图12所示。观察图12,p取值的变化会影响ISOGI的动态响应速度。在一定范围内,p值越大,ISOGI的响应速度越快;当p>0.271 5时,ISOGI的响应速度逐渐变慢,开始出现振荡现象。图12中,SOGI的调节时间为29.6ms,而ISOGI的调节时间只有28.2ms。虽然,ISOGI通过添加第三个积分器来抑制直流偏移的方法会造成时间延迟,但是,采用本文提出的参数设计方法后,可以缩短ISOGI响应过程的调节时间,提升其动态性能。
2 改进锁相结构设计
由1.2节分析可知,ISOGI能够有效地抑制输入电压中的直流偏移,然而电网谐波干扰的分布频段很广,ISOGI的滤波能力不足以完全消除。本文在SRF-PLL结构基础上,引入MAF来提升滤波性能,并把PI控制器改成P控制器以加快动态响应速度。本节主要介绍逐步改进锁相结构的过程。
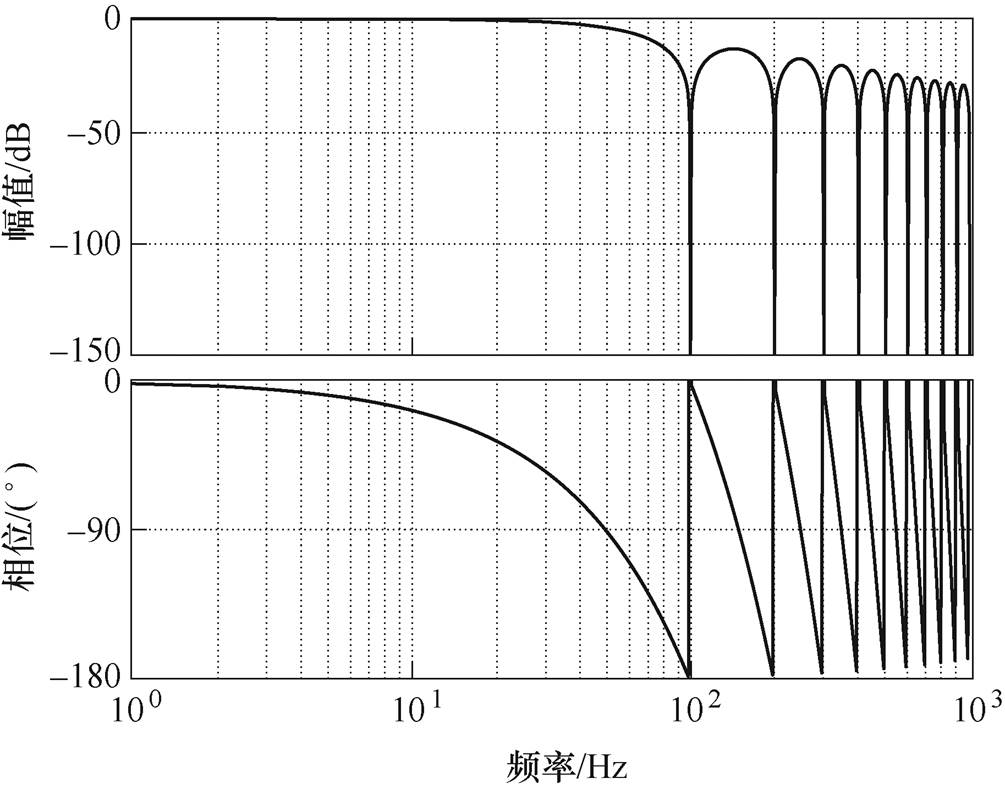
MAF是一种线性相位有限脉冲响应滤波器,其频域传递函数表示为
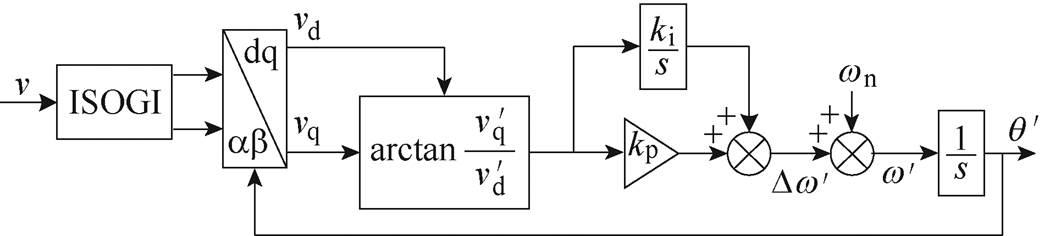
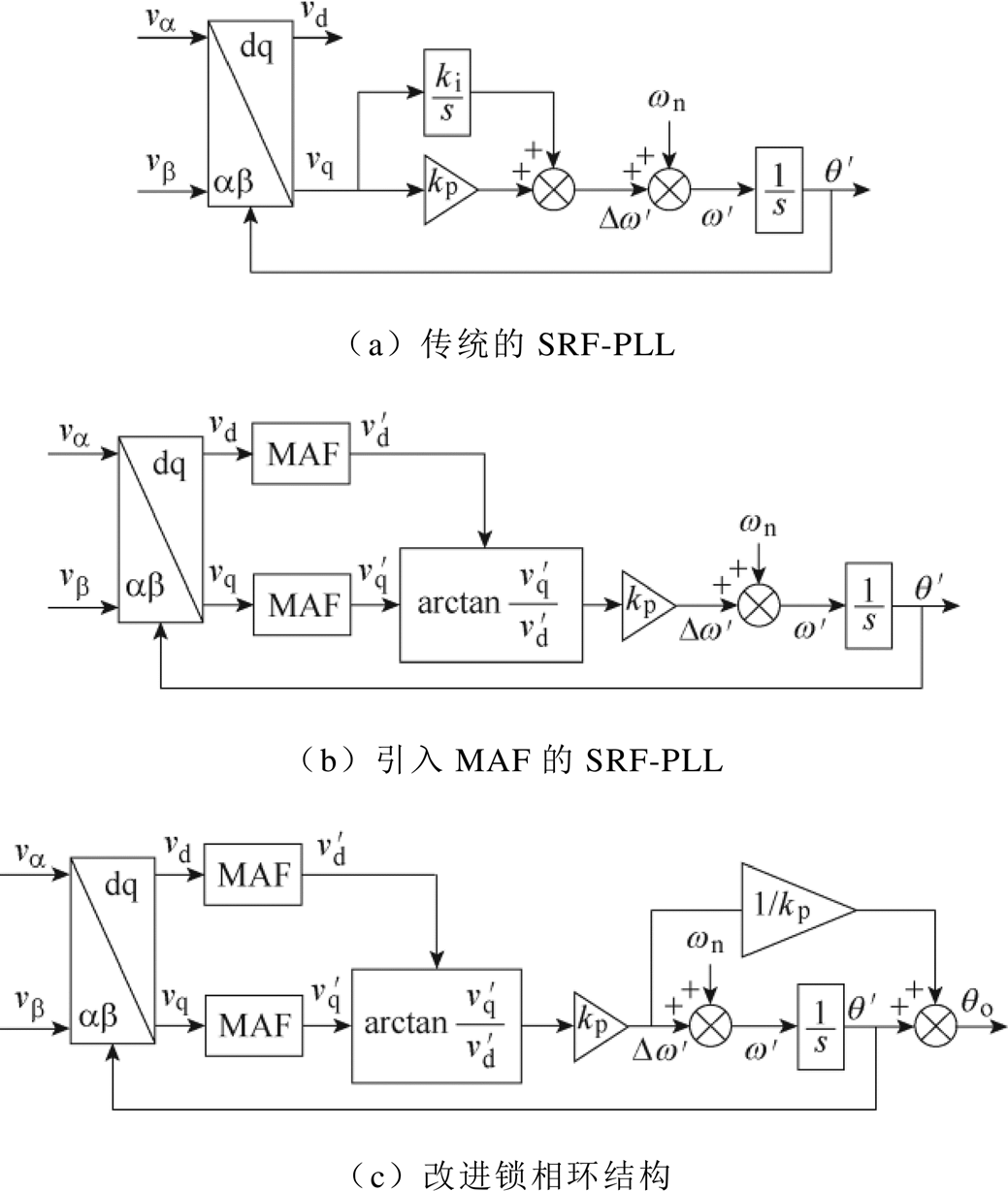
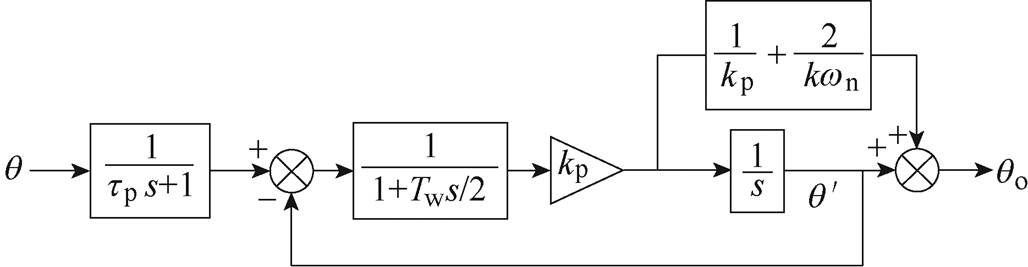
显然,MAF具有优越的陷波功能,能够完全滤除频率为1/Tw整数倍的谐波含量。图14a为传统SRF-PLL的结构,在环路中引入MAF后得到图14b所示的锁相环结构。由式(14)可知,MAF需要一个等于其窗口宽度的等待时间才能达到稳态,较大的窗口宽度将导致较慢的MAF瞬态响应。针对MAF造成的延时问题,本文把PI控制器换成P控制器以加快系统的响应速度。此外,对q轴电压分量除以d轴电压分量的商进行反正切函数运算,能够消除电压幅值变化对锁相环动态性能和稳定性的影响,并且使系统线性化。
但是,去掉PI控制器的积分作用之后,图14b所示锁相环无法追踪频率偏移,导致估算相位中存在稳态误差。因此,需要计算出相位偏差值,并进行偏差补偿。假设θ和θ′分别为输入电压相位和锁相环估算相位,其计算公式为
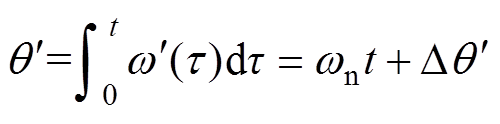 (16)
(16)
其中
为了使MAF线性化,通过一阶Pade近似逼近式(14)中的时延项,过程如下
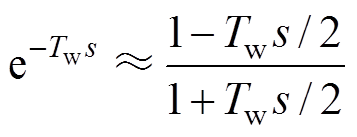 (17)
(17)
将式(17)代入式(14),得到
图15中,相位偏差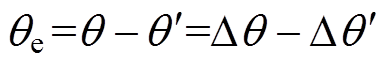 ,根据该模型,锁相系统的微分方程为
,根据该模型,锁相系统的微分方程为
式中,D为小扰动量;在相位锁定时,qe为常数。因此,可以求得式(19)分别在相位跳变和频率跳变情况下的锁相解,即
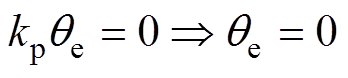 (20)
(20)
由式(20)和式(21)可以看出,图14b所示锁相环在相位跳变时可以稳定锁相;在频率跳变时却存在一个相位偏差Dw/kp。稳态时,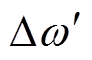 的平均值等于Dw,因此可以用
的平均值等于Dw,因此可以用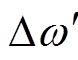 /kp来计算相位偏差,并在输出的估算相位中进行补偿。最终,图14c即为经过误差补偿之后的改进锁相环(Improve PLL, IPLL)结构。
/kp来计算相位偏差,并在输出的估算相位中进行补偿。最终,图14c即为经过误差补偿之后的改进锁相环(Improve PLL, IPLL)结构。
为了进一步验证IPLL的稳定性和稳态性能,需要研究其传递函数的特点。根据图15,同理可得到IPLL的线性模型如图16所示。根据图16,推导出IPLL的开环传递函数为
3 改进型单相锁相环
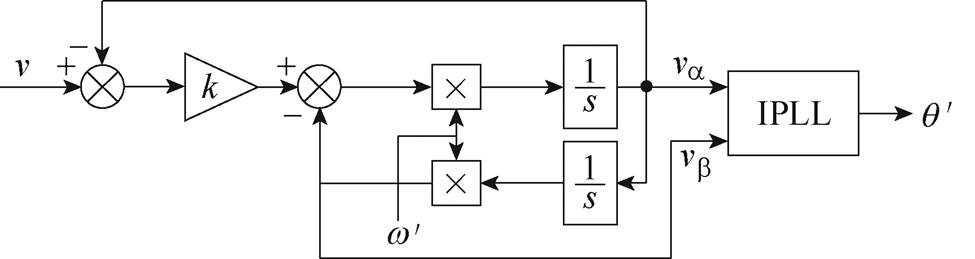
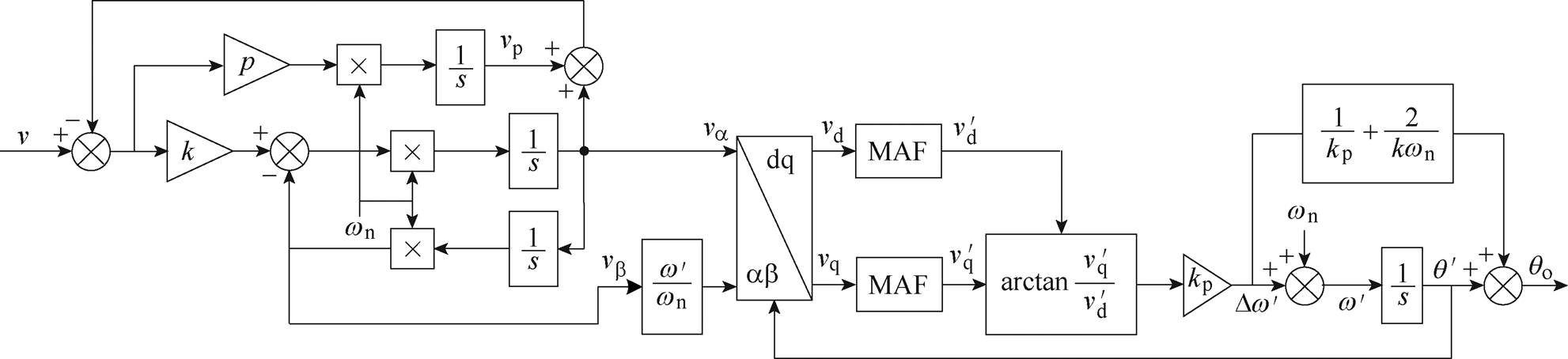
本文以ISOGI作为正交信号发生器,以IPLL作为锁相结构,提出了一种改进型单相锁相环,即ISOGI-IPLL,其结构框图如图17所示。其中,针对电网发生频率偏移时ISOGI所造成的滞后相位j,在锁相环的估算相位中进行了补偿。
文献[24]给出了基于固定频率结构SOGI-PLL的小信号模型。同理,根据图17可以推导得到ISOGI-IPLL的小信号模型,如图18所示。
图18中,tp=2/(kwn)。根据该模型,ISOGI-IPLL的闭环传递函数为
令2/Tw=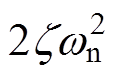 和2kp/Tw=
和2kp/Tw=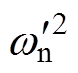 ,
, 和
和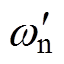 分别为阻尼系数和自然频率。前文已经采用k=1和Tw=0.01s,只要选择合适的
分别为阻尼系数和自然频率。前文已经采用k=1和Tw=0.01s,只要选择合适的 ,就能得到相应的
,就能得到相应的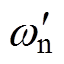 ,然后求出kp。本文选用二阶系统的最佳阻尼系数
,然后求出kp。本文选用二阶系统的最佳阻尼系数 =0.707,求得
=0.707,求得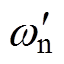 =141.42rad/s,kp=100。
=141.42rad/s,kp=100。
4 仿真和实验结果
为了验证所提ISOGI-IPLL的有效性,本文设置SOGI-PLL(见图1)、ISOGI-PLL的结构框图如图19所示和SOGI-IPLL的结构框图如图20所示作为比较对象,并且在仿真环境中搭建相应模型,在实验设备中进行算法编程。对于ISOGI-PLL,设置比例系数kp=100,同样,阻尼系数 =0.707,算出积分系数ki=5 000。对于SOGI-IPLL,为了兼顾SOGI的滤波效果和响应速度,取k=1.414[23]。对于SOGI-PLL,为了保持一致,其参数取值同上。锁相环控制参数见表1。
=0.707,算出积分系数ki=5 000。对于SOGI-IPLL,为了兼顾SOGI的滤波效果和响应速度,取k=1.414[23]。对于SOGI-PLL,为了保持一致,其参数取值同上。锁相环控制参数见表1。
表1 锁相环控制参数
Tab.1 The control parameters of PLLs

参数ISOGI-IPLLISOGI-PLLSOGI-IPLLSOGI-PLL k111.4141.414 p0.271 50.271 5—— Tw/s0.01—0.01— kp100100100100 ki—5 000—5 000
4.1 仿真分析
仿真模型搭建在Matlab/Simulink环境下,采样频率设置为10kHz,单相输入电压的额定值为220V/ 50Hz。为了检验ISOGI-IPLL的动态性能和稳定性,本文设置了谐波注入、直流偏移注入、相位跳变、频率跳变和电压暂降五组仿真条件,仿真结果如图21所示。
(1)谐波注入。在单相电压中注入0.05(pu)的-5次谐波和0.05(pu)的+7次谐波。图21a显示了单相锁相环稳态时的估算频率波形。显然,ISOGI- IPLL和SOGI-IPLL都能有效消除谐波分量,实现稳定锁频。但是,ISOGI-PLL受到谐波干扰,输出频率有明显的波动。这说明引入MAF之后,改进锁相结构IPLL的滤波能力得到了极大的提升。
(2)直流偏移注入。在单相交流电压中注入-20V的直流分量,其仿真结果如图21b所示。显然,直流偏移导致SOGI-IPLL在稳态时存在一倍工频的频率振荡,而ISOGI-IPLL却能够稳定无差锁频,说明ISOGI可以很好地抑制直流偏移。此外,ISOGI-PLL存在二倍工频的频率振荡,从侧面验证了IPLL的滤波能力。
(3)相位跳变。在0.04s时刻,输入电压发生40°的相位跳变,单相锁相环估算频率的动态响应过程如图21c所示。SOGI-IPLL动态过程的超调量大约为9.12%;而ISOGI-PLL和ISOGI-IPLL的超调量相对较小。ISOGI-PLL需要10个电网周期才能恢复对频率的准确估算,而SOGI-IPLL和ISOGI- IPLL的恢复时间只需5个电网周期。这说明,去掉积分环节之后,IPLL加快了系统的动态响应过程。
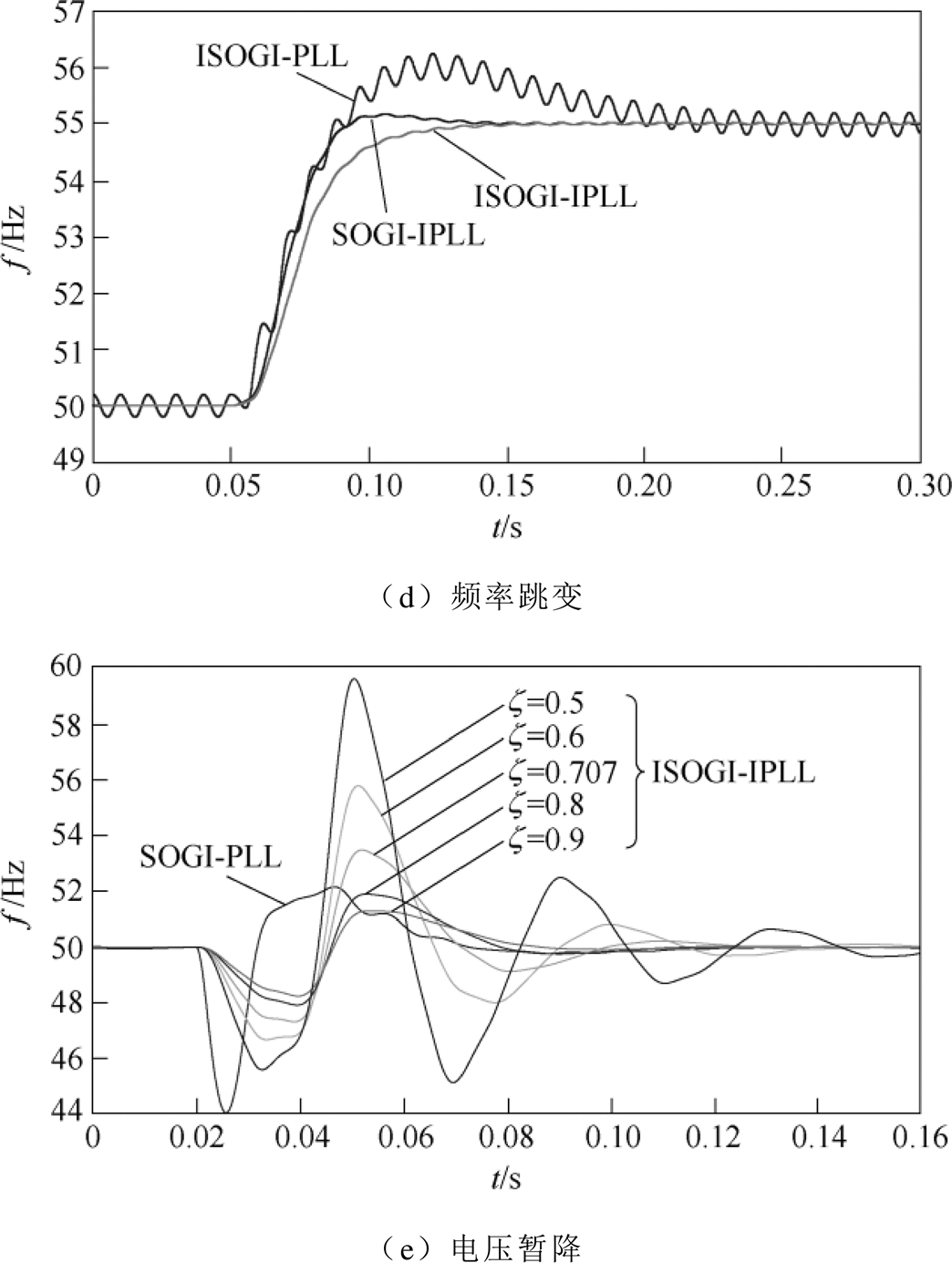
(4)频率跳变。在0.05s时刻,输入电压发生+5Hz的频率跳变,单相锁相环估算频率的动态响应过程如图21d所示。ISOGI-PLL动态过程存在较大的超调量,约为24%,而SOGI-IPLL和ISOGI-IPLL几乎不存在超调量,动态响应非常平稳,没有稳态误差,证明改进锁相结构IPLL能够很好地解决频率偏移带来的相位偏差问题。同样,ISOGI-PLL需要10个电网周期才能恢复对输入电压的频率追踪,大约是SOGI-IPLL和ISOGI-IPLL所需时间的两倍。因此,本文所提ISOGI-IPLL既能保持很快的动态响应速度,也能减少超调量,从而提高了动态性能。
(5)电压暂降。在0.02s时刻,输入电压发生-0.5(pu)的电压暂降,单相锁相环估算频率的动态响应过程如图21e所示。传统SOGI-PLL的动态响应过程只有4.34%的超调量和39.2ms的调节时间;而ISOGI-IPLL的动态响应过程受阻尼系数 取值的影响。当
取值的影响。当 <0.707时,ISOGI-IPLL的响应曲线存在明显的振荡现象,并且超调量过大,调节时间太长;当0.707≤
<0.707时,ISOGI-IPLL的响应曲线存在明显的振荡现象,并且超调量过大,调节时间太长;当0.707≤ ≤0.9时,随着
≤0.9时,随着 的取值逐渐增大,ISOGI-IPLL的超调量从7.62%减小为2.59%,减幅显著,ISOGI-IPLL的调节时间从46.1ms缩短到42.3ms,速度加快;当
的取值逐渐增大,ISOGI-IPLL的超调量从7.62%减小为2.59%,减幅显著,ISOGI-IPLL的调节时间从46.1ms缩短到42.3ms,速度加快;当 >0.9时,
>0.9时, 的数值过大,导致比例系数kp过小,ISOGI-IPLL响应曲线的上升时间太长,当电压频率/相位受到扰动时,锁相系统的追踪速度太慢,影响锁相精度。显然,改进结构在解决直流偏移和高次谐波问题的同时,也对锁相环的整体动态性能造成了一定的影响。由上述分析可知,合理选择
的数值过大,导致比例系数kp过小,ISOGI-IPLL响应曲线的上升时间太长,当电压频率/相位受到扰动时,锁相系统的追踪速度太慢,影响锁相精度。显然,改进结构在解决直流偏移和高次谐波问题的同时,也对锁相环的整体动态性能造成了一定的影响。由上述分析可知,合理选择 的数值,可以进一步优化ISOGI-IPLL的动态性能。根据实际需求,
的数值,可以进一步优化ISOGI-IPLL的动态性能。根据实际需求, 的取值可在区间[0.707, 0.9]内进行折中选择。
的取值可在区间[0.707, 0.9]内进行折中选择。
4.2 实验验证
为了验证所提单相锁相环的准确性,搭建了基于快速原型控制器YXSPACE的硬件平台进行实验验证,实验平台如图22所示。
南京研旭电气科技有限公司的快速原型控制器YXSPACE,采用TI公司的C2000系列DSP-F28xx作为核心控制器,控制算法模型在PC端的Matlab/ Simulink环境中搭建,模型中的接口与硬件驱动接口绑定后,再结合TI公司的CCS编译工具产生可执行文件,下载至YXSPACE控制器中运行。实验使用ITECH公司的可编程交流电源IT7600来产生单相电压信号,经过基于LV25-P电压传感器的信号调理电路获取采样电压,最后输入YXSPACE控制器中进行单相锁相环算法运行控制并导出实验波形数据,实验结果如图23所示。
整个实验的采样频率设定为10kHz,电压额定值为220V/50Hz。实验过程中的电网故障条件与仿真时的设定保持相同。对比图21的仿真结果以及图23的实验结果,二者在相同故障条件下的波形高度一致,验证了所提算法在理论上的正确性。图23a表明,相比于传统PLL,本文提出的IPLL结构具备更强的谐波抑制能力。图23b表明,输入电压存在直流偏移时,会导致输出端同时存在单频振荡和倍频振荡。所提ISOGI可以抑制直流偏移,有效消除单频振荡分量;所提IPLL能够滤除倍频振荡干扰。图23c和图23d表明,当输入电压发生相位/频率跳变时,SOGI-IPLL和ISOGI-IPLL的动态响应过程相似,调节时间较短,都有平滑的动态响应曲线;然而,ISOGI-PLL受到倍频振荡干扰,响应速度较慢。因此,所提IPLL在具有优越滤波功能的同时,兼备良好的动态性能。根据不同电网故障情况下的实验结果,本文提出的ISOGI-IPLL可以消除直流偏移,抑制谐波干扰,具备较快的响应速度和平滑的动态曲线,能够稳定无差锁频,从而准确地追踪电网的相位信息。
5 结论
针对传统SOGI-PLL的缺陷,本文提出了一种改进单相锁相环技术,适用于电网存在直流偏移和谐波干扰的条件。该方法利用添加积分支路和固定频率结构来改进SOGI,消除直流偏移和优化参数设计;通过引入MAF和去掉积分环节来改进SRF- PLL,抑制高频谐波和加快响应速度。仿真和实验结果一致,验证了理论分析的正确性。实验结果表明,改进的单相锁相环技术在直流偏移和谐波干扰的电网故障条件下都能稳定无差地锁定频率,进而准确地追踪电网同步相位,具有响应速度快和鲁棒性强的特点。由于所提改进锁相环方法添加了积分支路并引入MAF,无可避免地增加了结构复杂度,加大了运算量并造成一定的时间延迟。如何简化系统结构、选择更加简便和快速的方法来消除直流偏置和谐波干扰,还有待进一步研究。
参考文献
[1] 何宇, 漆汉宏, 罗琦, 等. 基于分数阶滤波器的三相锁相环技术[J]. 电工技术学报, 2019, 34(12): 2572-2583.
He Yu, Qi Hanhong, Luo Qi, et al. A novel three- phase phase-locked loop method based on fractional- order filter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2572-2583.
[2] 郭磊, 王丹, 刁亮, 等. 针对电网不平衡与谐波的锁相环改进设计[J]. 电工技术学报, 2018, 33(6): 1390-1399.
Guo Lei, Wang Dan, Diao Liang, et al. A modified design of phase-locked loop for unbalanced and distorted grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1390- 1399.
[3] 赵强松, 陈莎莎, 周晓宇, 等. 用于并网逆变器谐波抑制的重复-比例复合控制器分析与设计[J]. 电工技术学报, 2019, 34(24): 5189-5198.
Zhao Qiangsong, Chen Shasha, Zhou Xiaoyu, et al. Analysis and design of combination controller based on repetitive control and proportional control for harmonics suppression of grid-tied inverters[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5189-5198.
[4] 钟佩军, 孙建军, 司学振, 等. 基于电压扰动源的并网逆变器输出阻抗测量方法[J]. 电工技术学报, 2019, 34(22): 4739-4750.
Zhong Peijun, Sun Jianjun, Si Xuezhen, et al. Measurement method of inverter output impedance based on voltage disturbance source[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4739-4750.
[5] 张晓, 谭力, 鲜嘉恒, 等. LCL并网逆变器预测电流控制算法[J]. 电工技术学报, 2019, 34(增刊1): 189- 201.
Zhang Xiao, Tan Li, Xian Jiaheng, et al. Predictive current control algorithm for grid-connected inverter with LCL filter[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 189-201.
[6] 周鹏, 张新燕, 邸强, 等. 基于虚拟同步机控制的双馈风电机组预同步并网策略[J]. 电力系统自动化, 2020, 44(14): 71-84.
Zhou Peng, Zhang Xinyan, Di Qiang, et al. Pre- synchronous grid-connection strategy of DFIG-based wind turbine with virtual synchronous generator control[J]. Automation of Electric Power Systems, 2020, 44(14): 71-84.
[7] 赵清林, 宋文璐, 袁精, 等. 弱电网中基于调节器重构的多机并网稳定性研究[J]. 电机与控制学报, 2020, 24(1): 111-118.
Zhao Qinglin, Song Wenlu, Yuan Jing, et al. Stability analysis of multi-grid-connected inverters based on regulator reconstruction in weak grid[J]. Electric Machines and Control, 2020, 24(1): 111-118.
[8] 金楠, 窦智峰, 李琰琰, 等. 电压源并网变换器有限控制集预测电流控制[J]. 电机与控制学报, 2019, 23(9): 123-130.
Jin Nan, Dou Zhifeng, Li Yanyan, et al. Finite control sets predictive current control of voltage source grid-connected converter[J]. Electric Machines and Control, 2019, 23(9): 123-130.
[9] 侯立健, 朱长青, 陈雅, 等. 基于二阶广义积分器的单相并网系统锁相技术的研究[J]. 电测与仪表, 2016, 53(13): 84-89.
Hou Lijian, Zhu Changqing, Chen Ya, et al. Research on SOGI for phase lock technique of the single-phase grid-connected system[J]. Electrical Measurement & Instrumentation, 2016, 53(13): 84-89.
[10] Routray A, Pradhan A K, Rao K P. A novel Kalman filter for frequency estimation of distorted signals in power systems[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(3): 469-479.
[11] Song H S, Nam K. Instantaneous phase-angle estimation algorithm under unbalanced voltage-sag conditions[J]. IEE Proceedings-Generation, Trans- mission and Distribution, 2000, 147(6): 409-415.
[12] 吴振军, 秦方圆, 杨凯. 基于滑动离散傅里叶变换的锁相环设计[J]. 电器与能效管理技术, 2017(6): 78-82.
Wu Zhenjun, Qin Fangyuan, Yang Kai. Design of phase locked loop based on sliding discrete fourier transform[J]. Electrical & Energy Management Technology, 2017(6): 78-82.
[13] 陈四雄, 易龙强, 黄文俊, 等. 基于构造非正交向量的单相锁相技术研究[J]. 电工技术学报, 2019, 34(2): 398-408.
Chen Sixiong, Yi Longqiang, Huang Wenjun, et al. Single-phase phase-locked technique based on con- structing non-orthogonal vector[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 398-408.
[14] 回楠木, 王大志, 李云路. 基于复变陷波器的并网锁相环直流偏移消除方法[J]. 电工技术学报, 2018, 33(24): 5897-5906.
Hui Nanmu, Wang Dazhi, Li Yunlu. DC-offset elimination method for grid-connected phase-locked loop based on complex notch filter[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5897- 5906.
[15] 陈红兵, 闵晶妍. 基于正交信号发生器的单相锁相环的研究[J]. 电力电子技术, 2014, 48(11): 23-25.
Chen Hongbing, Min Jingyan. Research on single- phase phase-locked loop based on orthogonal signal generator[J]. Power Electronics, 2014, 48(11): 23-25.
[16] Akhtar M A, Saha S. An adaptive frequency-fixed second-order generalized integrator-quadrature signal generator using fractional-order conformal mapping based approach[J]. IEEE Transactions on Power Electronics, 2019, 35(6): 5548-5552.
[17] 严志星, 曾君, 赖臻, 等. 一种基于内置变压器的高增益双向DC-DC变换器[J]. 电源学报, 2020, 18(3): 4-12.
Yan Zhixing, Zeng Jun, Lai Zhen, et al. High voltage- gain bidirectional DC-DC converter based on built-in transformer[J]. Journal of Power Supply, 2020, 18(3): 4-12.
[18] 盘宏斌, 龙海鸿, 朱茂琨, 等. 基于Hilbert变换和预设旋转频率的无锁相环电网同步基准正弦信号检测方法[J]. 电工技术学报, 2018, 33(10): 2345- 2353.
Pan Hongbin, Long Haihong, Zhu Maokun, et al. Reference sinusoidal signal detection method of gird synchronization without phase-locked loop based on Hilbert transform and pre-set the rotation frequency[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2345-2353.
[19] Dong D, Thacker T, Burgos R, et al. On zero steady- state error voltage control of single-phase PWM inverters with different load types[J]. IEEE Transa- ctions on Power Electronics, 2011, 26(11): 3285- 3297.
[20] Rodriguez P, Luna A, Muñoz-Aguilar R S, et al. A stationary reference frame grid synchronization system for three-phase grid-connected power con- verters under adverse grid conditions[J]. IEEE Transactions on Power Electronics, 2012, 27(1): 99-112.
[21] Matas J, Martin H, Hoz J D L, et al. A family of gradient descent grid frequency estimators for the SOGI filter[J]. IEEE Transactions on Power Electro- nics, 2017, 33(7): 5796-5810.
[22] Singh B, Kumar S, Jain C. Damped-SOGI-based control algorithm for solar PV power generating system[J]. IEEE Transactions on Industry Appli- cations, 2017, 53(3): 1780-1788.
[23] 张纯江, 赵晓君, 郭忠南, 等. 二阶广义积分器的三种改进结构及其锁相环应用对比分析[J]. 电工技术学报, 2017, 32(22): 42-49.
Zhang Chunjiang, Zhao Xiaojun, Guo Zhongnan, et al. Three improved second order generalized integrators and the comparative analysis in phase locked loop application[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 42-49.
[24] Xiao Furong, Dong Lei, Li Li, et al. A frequency- fixed SOGI based PLL for single-phase grid- connected converters[J]. IEEE Transactions on Power Electronics, 2016, 32(3): 1713-1719.
[25] Golestan S, Guerrero J M, Vasquez J C. A nonadaptive window-based PLL for single-phase applications[J]. IEEE Transactions on Power Electronics, 2017, 33(1): 24-31.
Single-Phase Phase-Locked Loop for DC Offset and Harmonic Interference
Zeng Jun1 Cen Dehai1 Chen Run1 Liu Junfeng2
(1. School of Electric Power South China University of Technology Guangzhou 510640 China 2. School of Automation Science and Engineering South China University of Technology Guangzhou 510640 China)
Abstract Aiming at the common problems of DC offset and harmonic interference in power grids, an improved phase-locked loop algorithm based on second-order generalized integrator phase- locked loop (SOGI-PLL) is proposed. In order to suppress the DC offset and simplify the parameter design, an integral branch is added to the pre-stage second-order generalized integrator (SOGI), and the SOGI is changed to a fixed frequency structure. A moving average filter is introduced into the post-stage loop of phase-locked loop (PLL) to enhance filtering performance. For the purpose of speeding up dynamic response, the integral part of PI controller is removed. Bode diagram analysis and small signal model derivation are used to improve structure design and determine the corresponding parameters. The proposed improved single-phase phase-locked loop technology can effectively eliminate DC offset and high-frequency harmonics, while having good dynamic performance and stability. Finally, Matlab/Simulink simulation and related experiments verify the proposed method.
keywords:Second-order generalized integrator, phase-locked loop, DC offset, harmonic interference
DOI: 10.19595/j.cnki.1000-6753.tces.200595
中图分类号:TM761
作者简介
曾 君 女,1979年生,博士,教授,博士生导师,研究方向电力电子应用、分布式发电的能量管理和智能控制。E-mail: junzeng@scut.edu.cn
刘俊峰 男,1978年生,博士,副教授,研究方向为电力电子应用、高频配电系统、运动控制。E-mail: aujfliu@scut.edu.cn(通信作者)
收稿日期 2020-06-02
改稿日期 2020-08-12
(编辑 陈 诚)
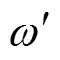 和
和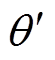 分别为估算角频率、估算相位。SOGI-PLL在理想正弦输入电压的条件下能够准确追踪基波电压相位,但仍存在以下不足:①虽然单相电压不存在基波负序分量,但是传统SOGI不能有效消除电压中的直流偏移,而且对高次谐波的抑制能力不足;②图1中,SOGI-PLL的频率自适应过程是通过SRF- PLL输出的估算频率反馈到SOGI来完成的,增加了控制的复杂性,并且使调谐敏感,从而降低稳定裕度;③SRF-PLL主要通过调节PI控制器参数来提高滤波能力,但是带宽必须相应地减小,动态响应变慢[14]。学者们为了解决上述问题,提出了一些改进型SOGI或SRF-PLL结构。文献[23]提出了通过加入低通滤波器(Low Pass Filter, LPF)来抑制直流分量和高次谐波的改进型SOGI结构,但是LPF的引入会产生延时,影响系统的动态性能。文献[24]提出了一种固定频率的SOGI结构,它不包含相互依赖的环路,从而增强了稳定性,但是依然存在不能有效抑制直流偏移的问题。
分别为估算角频率、估算相位。SOGI-PLL在理想正弦输入电压的条件下能够准确追踪基波电压相位,但仍存在以下不足:①虽然单相电压不存在基波负序分量,但是传统SOGI不能有效消除电压中的直流偏移,而且对高次谐波的抑制能力不足;②图1中,SOGI-PLL的频率自适应过程是通过SRF- PLL输出的估算频率反馈到SOGI来完成的,增加了控制的复杂性,并且使调谐敏感,从而降低稳定裕度;③SRF-PLL主要通过调节PI控制器参数来提高滤波能力,但是带宽必须相应地减小,动态响应变慢[14]。学者们为了解决上述问题,提出了一些改进型SOGI或SRF-PLL结构。文献[23]提出了通过加入低通滤波器(Low Pass Filter, LPF)来抑制直流分量和高次谐波的改进型SOGI结构,但是LPF的引入会产生延时,影响系统的动态性能。文献[24]提出了一种固定频率的SOGI结构,它不包含相互依赖的环路,从而增强了稳定性,但是依然存在不能有效抑制直流偏移的问题。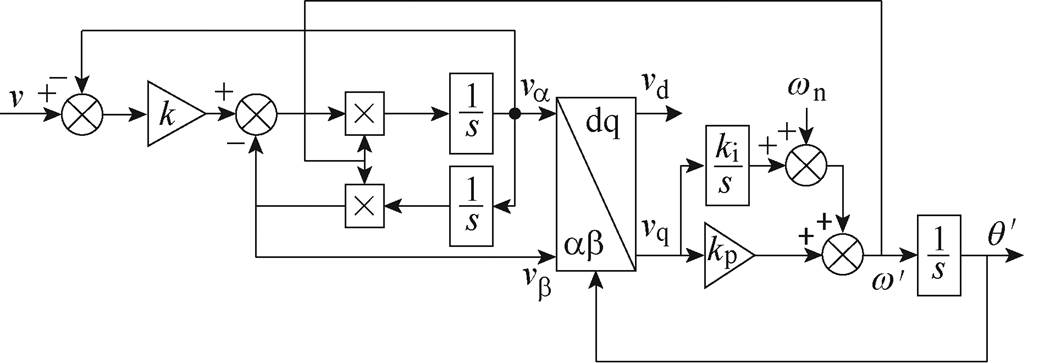
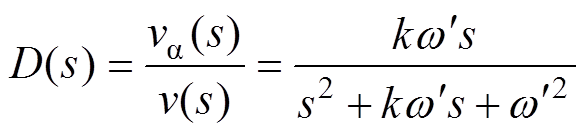 (1)
(1)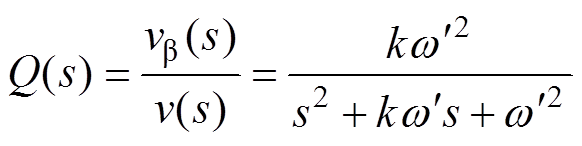 (2)
(2) 相等时,v
相等时,v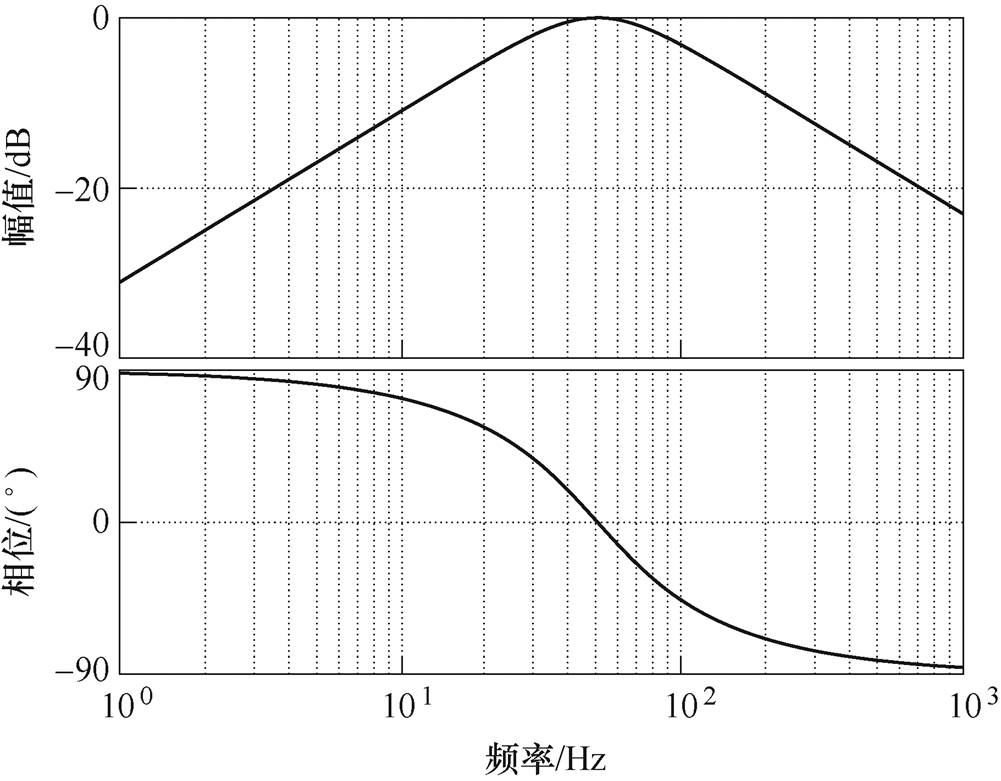
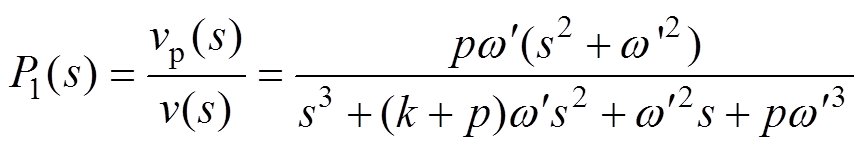 (3)
(3)
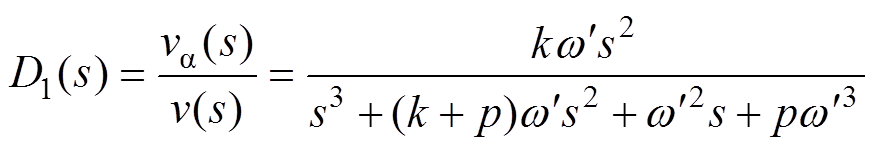 (4)
(4)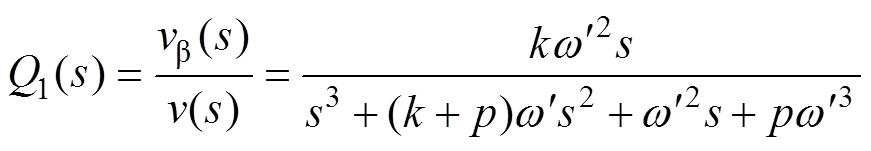 (5)
(5)
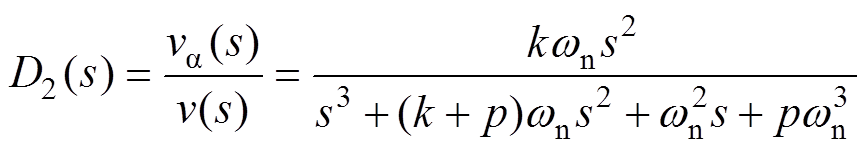 (6)
(6)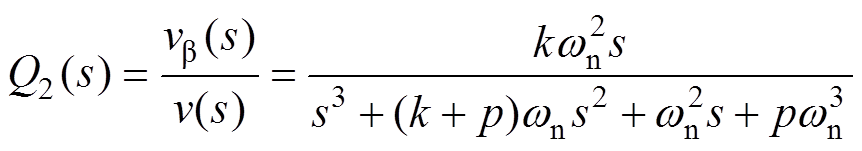 (7)
(7)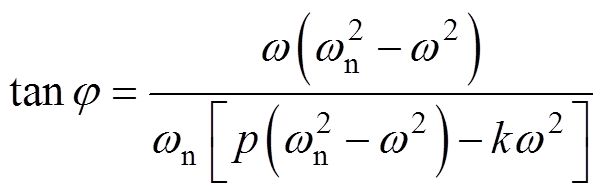 (8)
(8)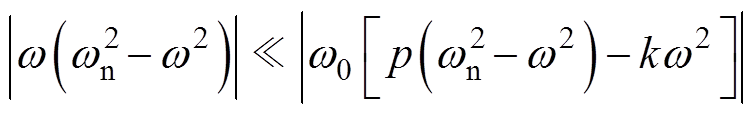 。令
。令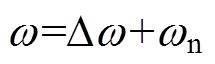 ,则滞后相位
,则滞后相位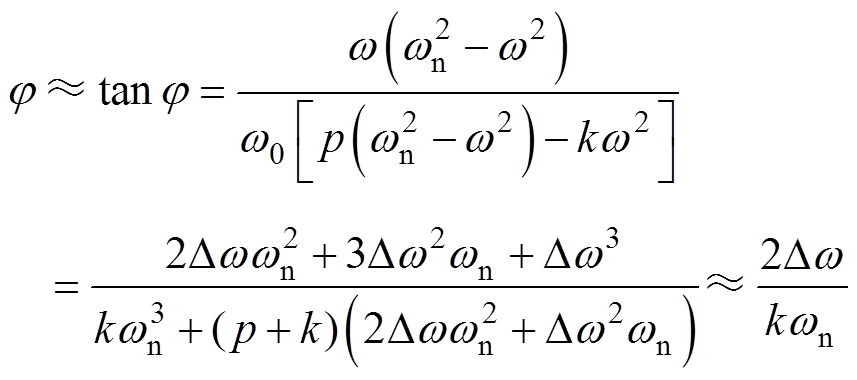 (9)
(9)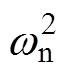 s+p
s+p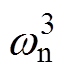 =0,可
=0,可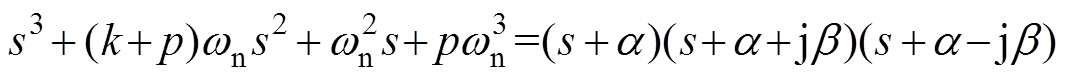 (10)
(10)
 (11)
(11) 
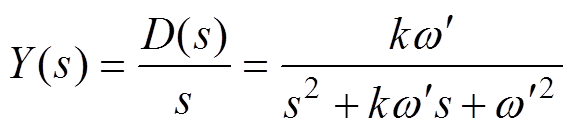 (12)
(12)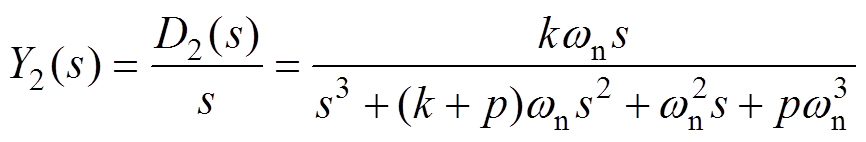 (13)
(13)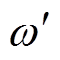 =
=
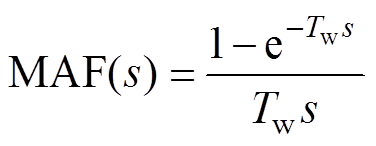 (14)
(14)
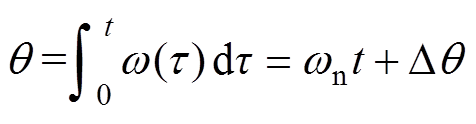 (15)
(15)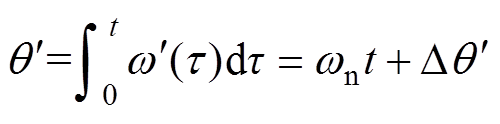 (16)
(16)
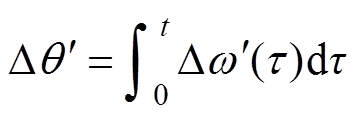
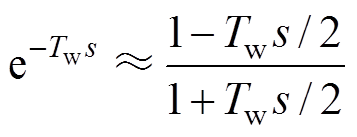 (17)
(17)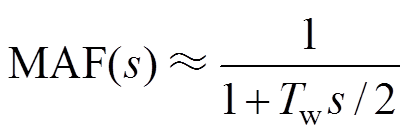 (18)
(18) 
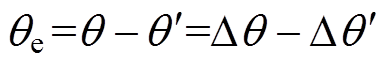 ,根据该模型,锁相系统的微分方程为
,根据该模型,锁相系统的微分方程为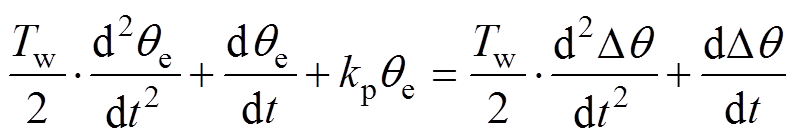 (19)
(19)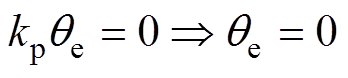 (20)
(20)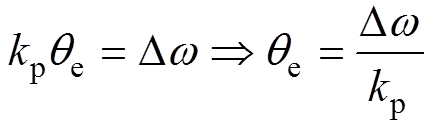 (21)
(21)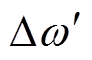 的平均值等于
的平均值等于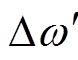 /k
/k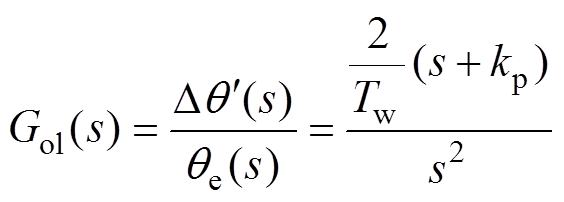 (22)
(22)
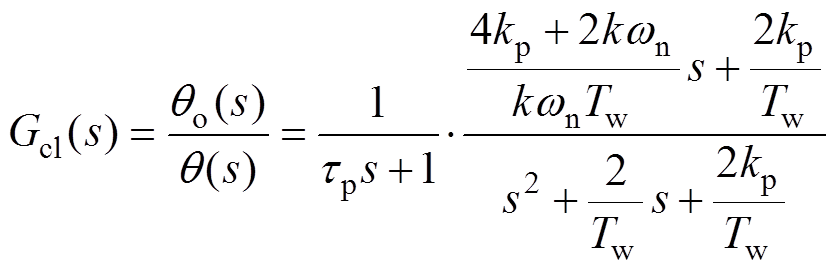 (23)
(23)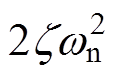 和2k
和2k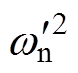 ,
, 和
和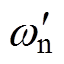 分别为阻尼系数和自然频率。前文已经采用k=1和T
分别为阻尼系数和自然频率。前文已经采用k=1和T